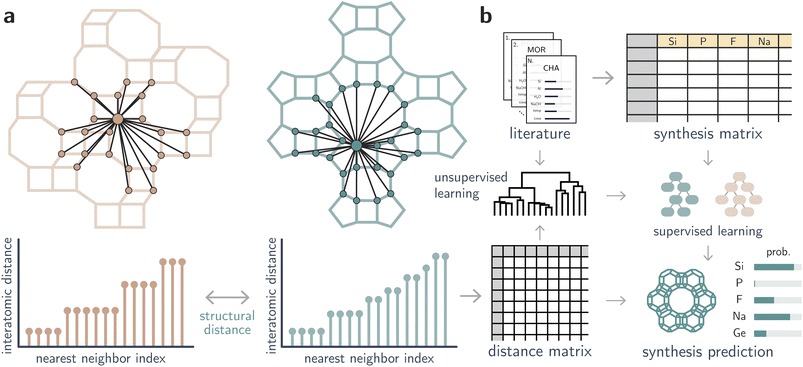
Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Inorganic synthesis-structure maps in zeolites with machine learning and crystallographic distances†
Daniel
Schwalbe-Koda
 *a,
Daniel E.
Widdowson
b,
Tuan Anh
Pham
*a,
Daniel E.
Widdowson
b,
Tuan Anh
Pham
 a and
Vitaliy A.
Kurlin
*b
a and
Vitaliy A.
Kurlin
*b
aLawrence Livermore National Laboratory, Livermore, CA, USA. E-mail: dskoda@llnl.gov; vitaliy.kurlin@gmail.com
bUniversity of Liverpool, Liverpool, UK
First published on 27th October 2023
Abstract
Zeolites are inorganic materials known for their diversity of applications, synthesis conditions, and resulting polymorphs. Although their synthesis is controlled both by inorganic and organic synthesis conditions, computational studies of zeolite synthesis have focused mostly on the design of organic structure-directing agents (OSDAs). In this work, we combine distances between crystal structures and machine learning (ML) to create inorganic synthesis maps in zeolites. Starting with 253 known zeolites, we show how the continuous distances between frameworks reproduce inorganic synthesis conditions from the literature without using labels such as building units. An unsupervised learning analysis shows that neighboring zeolites according to two different representations often share similar inorganic synthesis conditions, even in OSDA-based routes. In combination with ML classifiers, we find synthesis-structure relationships for 14 common inorganic conditions in zeolites, namely Al, B, Be, Ca, Co, F, Ga, Ge, K, Mg, Na, P, Si, and Zn. By explaining the model predictions, we demonstrate how (dis)similarities towards known structures can be used as features for the synthesis space, thus quantifying the intuition that similar structures often share inorganic synthesis routes. Finally, we show how these methods can be used to predict inorganic synthesis conditions for unrealized frameworks in hypothetical databases and interpret the outcomes by extracting local structural patterns from zeolites. In combination with OSDA design, this work can accelerate the exploration of the space of synthesis conditions for zeolites.
Introduction
Zeolites are inorganic porous materials widely recognized for their rich polymorphism and numerous applications.1–3 Their porous structure provides unique opportunities to tailor materials performance in catalysis, gas adsorption, selective membranes, and more.4–6 In principle, the performance of zeolites for each application can be controlled by adequate selection of polymorph and composition. However, this selection is often hindered by the high-dimensional synthesis routes required to produce the materials.7 Zeolites are often synthesized with hydrothermal treatments, with inorganic and organic precursors cooperating to crystallize the nanoporous structure.8 Certain organic molecules, often based on quaternary ammonium cations, are known to direct the formation of specific zeolite topologies, thus biasing the phase competition landscape to favor the structure that best matches the molecular shape instead of other worse-fitting hosts.8,9 Because of this effect, design of organic structure-directing agents (OSDAs) led to multiple successful examples of phase-selective zeolite synthesis and control of catalytic properties,10–12 especially when used in combination with computational methods.13–19On the other hand, computational design of inorganic synthesis conditions for zeolites has not yet achieved the same impact as OSDA design. Despite their promise in controlling active site distribution,20 phase selectivity,21 Si/Al ratio,22 morphology,23 or lowering the cost of syntheses,24 selection of inorganic conditions capable of synthesizing existing and novel zeolites is not easily modeled.25 Recent progress in quantifying the role of inorganic synthesis conditions in zeolites includes: coupling machine learning (ML) and literature extraction;26,27 obtaining structure-synthesis correlations from synthesis routes;21,28 predicting effects of inorganic cations in heteroatom distributions;17,20 or using ML to control composition and particle sizes from OSDA-free syntheses.22 Nevertheless, their reliance on reported data prevents them to propose inorganic conditions for the synthesis of novel or hypothetical frameworks. Whereas some inorganic synthesis-structure relationships can be derived from building units27,29,30 or alternative structural descriptors,28 automatically screening for new structures in hypothetical zeolite databases requires bypassing human-crafted labels such as building units. Furthermore, although graph-theoretical methods can detect composite building units (CBUs) in arbitrary structures, their computational cost may be prohibitive when exploring large datasets. Data-driven methods based in the topology of the structure also provide information on key factors that govern kinetics of zeolite crystallization,31,32 but do not immediately inform their synthesis conditions. Finally, aggregate framework information such as density-energy plots33,34 or local interatomic distances35 provide few correlations between different inorganic synthesis conditions and targeted frameworks, which motivate new data-driven approaches to synthesizability prediction.36 Thus, advancing towards a priori discovery of novel zeolite frameworks requires developing methods to: (1) uncover new synthesis-structure relationships in zeolites; (2) efficiently explore the inorganic synthesis space of zeolites; and (3) bypass the absence of labeled data in hypothetical zeolite databases.
In this work, we correlate inorganic synthesis conditions to zeolites using structural invariants that are independent of a unit cell and preserved under translations and rotations of a structure. In particular, two invariants are used to quantify distances between zeolites: the well-known Smooth Overlap of Atomic Positions (SOAP),37 and a newer method for comparing periodic crystals, the Average Minimum Distance (AMD)38 derived from the Pointwise Distance Distribution (PDD).39 The PDD is independent of a unit cell, continuous under small perturbations, is theoretically complete for generic crystals, and distinguished all periodic crystals in the Cambridge Structural Database. Importantly, it only requires a fast nearest neighbor search,40 and thus can be computed with low computational cost compared to graph-based approaches or more expensive representations. We show that, for both invariants, structural distances between zeolites can be used to predict inorganic synthesis conditions and recall a comprehensive dataset of synthesis conditions from the literature. Then, we demonstrate that unsupervised and supervised machine learning (ML) methods can be used to create structure-synthesis relationships for zeolites independently from OSDA design (see Fig. 1). Finally, we propose inorganic synthesis conditions to realize hypothetical frameworks based on distances toward structures whose synthesis is known, thus proposing interpretable synthesis-structure models to guide the synthesis of new zeolites.
Results and discussion
Inorganic synthesis maps from unsupervised learning
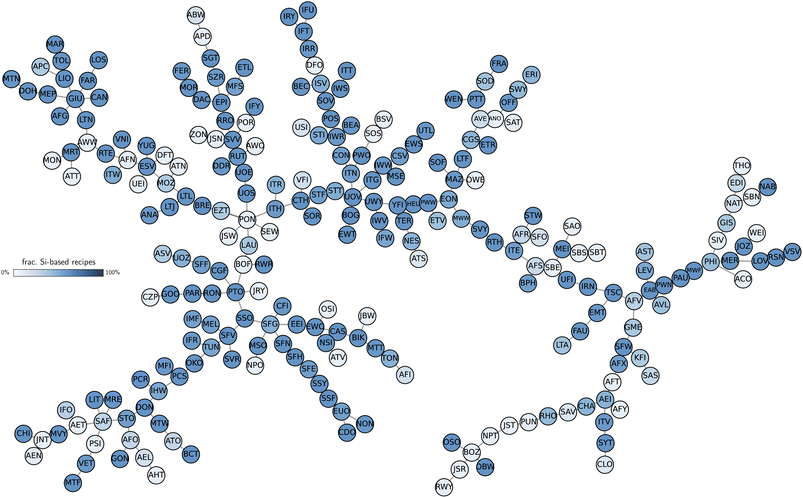
Designing synthesis-structure relationships in zeolites has long relied on intuitive patterns emerging from their natural structure. For example, some CBUs are typically known to be synthesized by different inorganic conditions, such as d6r in the presence of sodium ions or d4r in the presence of germanium or fluorine. Nevertheless, not all structures produced with certain inorganic agents exhibit the same CBUs, and CBUs are not necessarily realized only by one element. Data-driven methods showed promise in connecting zeolite synthesizability to their local structure35 or accelerating their screening,36 but interpreting large databases of structures can be challenging depending on the selected data invariants. To avoid crafting representations that both capture the diversity of structures and correlate them to synthesis conditions, we hypothesize that data-driven similarity between zeolite structures predicts similarity in their inorganic synthesis conditions. This allows us to compare zeolites and extract synthesis-structure relationships without relying on any structural labels except for the atomic positions (Fig. 1).To construct synthesis-structure maps in zeolites, we first calculated the distance between two idealized frameworks, as extracted from the IZA database, by comparing their AMD vectors (see Methods). Later, to demonstrate that the synthesis similarity hypothesis is not specific to the AMD, we show that structural similarity computed using SOAP also predicts inorganic synthesis conditions in these materials. To test the synthesis similarity hypothesis, we first computed the distance matrix between 253 known frameworks (denoted using their three-letter code, see Methods) in the International Zeolite Association (IZA) database and then performed a qualitative analysis of the results. We found that the AMD values correlated weakly with differences of density and with the SOAP distance between structures, but showed almost no correlation with graph-based distances from previous work41 (Fig. S1†). This can be understood by distorting a given framework without breaking covalent bonds, which leads to different structural fingerprints but equal connectivity. As such, graph and structural distances may be complementary in nature and can be used to model different phenomena.41 Moreover, we noted that some zeolites sharing the lowest distances according to the AMD have been synthesized together, as competing phases, intergrowths, or belonging to the same zeolite families (see Table S1 in the ESI†). Recovering pairs of structurally similar frameworks such as ITH-ITR,42ITG-IWW,43SBS-SBT,24MEL-*SFV,44 or MWF-PAU45 at low distance already suggests that the similarity values reproduce qualitatively some intuitive patterns observed in zeolite synthesis. To generalize this finding, we charted a map of zeolite structures based on their distances. Fig. 2 shows the minimum spanning tree created by converting the AMD distance matrix into a graph with weighted edges. Although the tree shows discrete connections between first-nearest neighbors and may not offer a complete picture with respect to outliers (see Methods), it facilitates the visualization of the results and may provide insights about synthesis-structure maps. Even without considering synthesis labels of the data in Fig. 2, known relationships between zeolites emerge naturally from the structural tree map. Several zeolites known for their similar building patterns are clustered together in the minimum spanning tree, demonstrating that their AMD values capture the space of zeolites without learnable features. Examples of such clusters include the ABC-6 zeolites, structures containing lov building units, six-membered rings frameworks (e.g., GIU cluster), Ge- or boron-containing zeolites (e.g., BEC or IRR and SFN-SSF branch, respectively), to name a few (see also Fig. S3 for a visual guide†). Similarly, structural outliers within the IZA dataset such as the low-density RWY or JSR, or interrupted frameworks such as -CLO, -SYT, and -ITV tend to cluster together, as their distances to all other zeolites is high (Fig. S2†). At the same time, other interrupted frameworks produced in different synthesis conditions, such as -IRY, -IFU, or -IFT synthesized with germanium, appear along with other germanosilicates in the synthesis map, not only with other interrupted frameworks. This ability to traverse the structural space in a continuous way allows drawing non-obvious connections that may be overlooked by building units alone. For example, the SOD and LTA zeolites may be intuitively regarded as similar because of their co-appearance in some synthesis routes and shared building unit sod, but they are not closely located in the graph from Fig. 2. Further analysis of the neighborhood of SOD indicates that this zeolite is instead closer to the FRA, PTT, DOH, and LOS frameworks. The first two explicitly contain the sod building unit, and the latter two are 0-dimensional frameworks analogous to SOD. All have higher framework density (∼17 T/1000 Å3) compared to LTA (∼14 T/1000 Å3), and can be accessed in synthesis routes similar to those typical from SOD. This observation illustrates how the data-driven analysis can be effective in drawing correlations between structural pairs that would not be otherwise obvious, given the diversity of zeolite structures. Beyond the SOD-LTA pair, several other similar zeolites, which are non-neighbors in the tree from Fig. 2, can be rationalized with the use of our distance, including the OFF-LTL, GME-AFI, and UTL-PCR-OKO (see ESI for an extended discussion†). Outliers can also propose new correlations not previously observed in the synthesis of zeolites. For example, the MEI framework lies within the SBS, SBT, SAO, SBE, and AFS cluster despite not having common CBUs with any of these zeolites. MEI also exhibits unusual 3- and 7-membered rings not seen in any of the zeolites in this group. However, the MEI structure was resolved by realizing the connection between its structure and its AFS counterpart, particularly in the presence of secondary building units with 3-fold point group symmetry connected either directly to each other (AFS building scheme) or through a 3-membered ring (MEI building scheme).46 A similar observation was also the key to characterize the STA-1 (SAO) zeolite47 and rationalize the selection of inorganic synthesis conditions for PST-32 (SBT) and PST-2 (SBS/SBT) as aluminosilicate zeolites.24 With this correlation, future computational investigations can help determine whether inorganic synthesis conditions play a role in directing these specific building patterns48 and inform the synthesis of structures such as SAO and SBE as aluminosilicates.
Despite the usefulness of the tree map in connecting zeolites with similar synthesis conditions, the visual analysis cannot determine whether the map consistently provides new insights on the synthesis of zeolites. To improve this qualitative analysis, we performed a hierarchical clustering of the data to quantify whether the structural distances cluster the data according to the literature synthesis conditions (see Methods). The dendrogram of AMD values (Fig. S5 and S6†) shows how zeolites are related to each other based on distances, thus providing a more quantitative view of the minimum spanning tree in Fig. 2. Then, to create labels for synthesis conditions, we started with a dataset of extensive synthesis conditions extracted from the zeolite literature from Jensen et al.49 After augmenting the data with frameworks not typically reported in publications, such as those found as minerals, we analyzed the frequency of occurrence of each synthesis condition for each framework. Although the initial dataset had information on both organic and inorganic conditions, we disregarded the OSDAs when labeling the data, thus assuming that inorganic and organic conditions can, to an extent, be predicted independently of each other. Furthermore, given the scarcity of data for some synthesis conditions, we focused only on the 14 inorganic conditions that have been used to synthesize at least 10 zeolites, namely Al, B, Be, Ca, Co, F, Ga, Ge, K, Mg, Na, P, Si, and Zn. Finally, we verify whether flat clusters formed by points with a maximum distance of each other share the same positive labels. This intuition is quantified by computing the homogeneity between data points given clusters formed by a given distance threshold50 (see Methods). If all clusters had only positive labels, their homogeneity would be 1, whereas zero homogeneity indicates perfect mixing of positive and negative labels. Fig. 3a shows that clusters with at least one positive data point tend to become more homogeneous as the distance threshold decreases. This supports the qualitative view that structures considered similar according to the AMD values also share similar synthesis conditions more often than not. On the other hand, as clusters become larger and the increasingly dissimilar structures are grouped together, the homogeneity decreases. Whereas the distribution of labels for some inorganic agents such as Al, Si, Be, F, or Na exhibit higher homogeneity at low distances (see Fig. S7†), others such as Co, Mg, or Zn show little predictive power. While this could be partly due to a lower number of data points for these synthesis conditions (see Table S5 for the total number of data points per element†), this could also be a consequence of weaker structure-synthesis correlations. Zeolites synthesized with beryllium, for example, are as scarce as Mg and have less data points than Co or Zn, but can be recalled correctly by the structural similarity tests. This suggests that structural distances computed with the AMD have stronger correlations with certain synthesis conditions than with others.
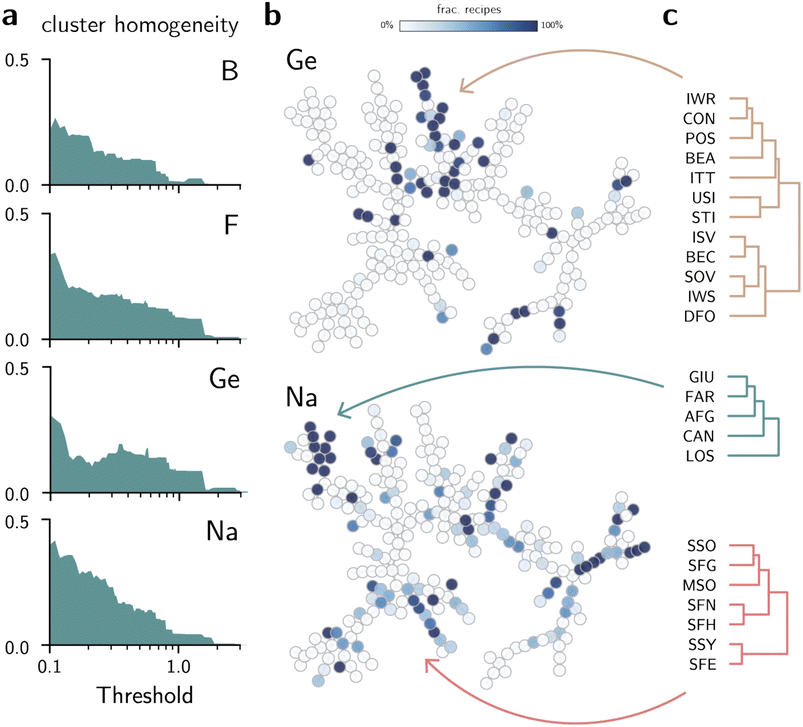 | ||
| Fig. 3 Unsupervised learning for inorganic synthesis of known zeolites. (a) Cluster homogeneity of zeolites for selected elements (see also Fig. S7†). (b) Minimum spanning tree of zeolites (Fig. 2) labeled according to frequency of Ge or Na in the synthesis of each zeolite (see also Fig. S4†). Darker (lighter) colors indicate that the inorganic synthesis condition is more (less) frequent in the synthesis of each zeolite. (c) Subset of the zeolite dendrogram for selected regions of the minimum spanning tree. | ||
To demonstrate that these findings are not limited to the AMD invariant and may be intrinsic to zeolite synthesis, we repeated the experiment by computing the distance between frameworks using SOAP (see Methods). Then, based on this new distance matrix, we repeated the analysis of the cluster homogeneity using the same data. Although the distance values in SOAP vectors are different from AMD (Fig. S1†), there is good agreement between the cluster homogeneities obtained with SOAP compared with those from AMD (see Fig. S8†). Interestingly, the SOAP vectors provides slightly better recall, as quantified by the higher homogeneity, for Co, Zn, and Mg, but slightly worse homogeneity scores for Al, Si, Na, and other conditions. Although the exact value of the homogeneity depends on the choice of threshold, these results demonstrate quantitatively that some synthesis-structure relationships can be established in zeolites using structural distances beyond a single choice of invariant.
Additional investigations of the data explain the patterns in homogeneity obtained above. Fig. 3b shows how the minimum spanning tree can be visualized according to the frequency of certain inorganic conditions in zeolite synthesis (see Fig. S4 for complete results using the AMD distance†). For example, some frameworks realizable with Ge or Na form their own groups in the tree, as also illustrated by the subclusters in dendrograms (Fig. 3c). Indeed, zeolites such as BEC, ISV, ITT or IWR are typical examples of large- and extra-large pore structures synthesized using germanium. Similarly, denser phases such as GIU, FAR, LOSetc. are often obtained in sodium-mediated syntheses. For common synthesis conditions such as silicon, trends can be derived from the visualization of silicon-free routes. The labeled trees from Fig. 2 and S4† show that non-silica zeolites are often located in similar regions of the structure space. Groups formed by zeolites such as NAT, EDI, and THO, or AFO, AEL, AHT show that non-silica zeolites also share structural patterns that may be harder to obtain in silica-based structures.
This unsupervised analysis demonstrates that structurally similar zeolites, according to invariants such as AMD and SOAP, share similar inorganic synthesis conditions. Although zeolite structures contain several outliers and lack true negative data, the structural patterns still provide a strong prior for exploring the synthesis conditions. In particular, as inorganic synthesis conditions can be inferred by the similarity between crystal structures, they can also help downselect structures for zeolites yet to be realized. Finally, although mainly we employed the AMD due to its computational efficiency and well-studied mathematical properties, other strategies could also recover this result from zeolite synthesis, as showcased by the example with SOAP.
Interpretable classifiers for predicting inorganic synthesis conditions
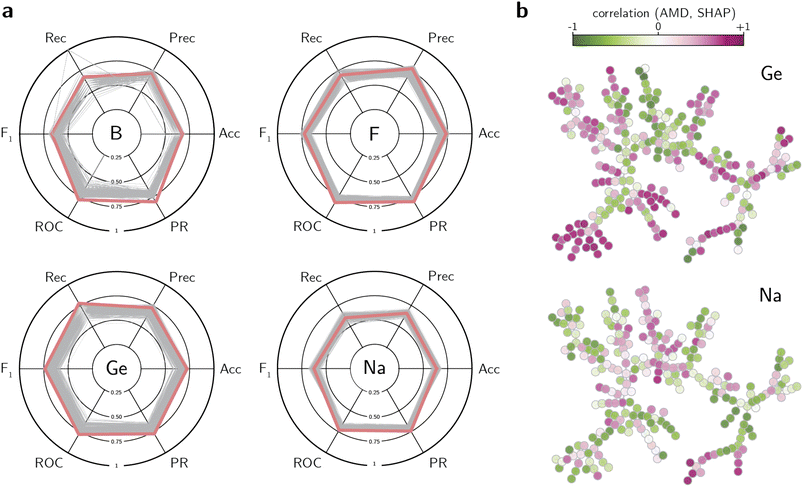
One disadvantage of the pure unsupervised learning approach is the suboptimal utilization of the available labels. Although similarity between crystal structures is a good indicator of common synthesis conditions, the dissimilarity between structures can also provide insights on which structures are less likely to be synthesized with a given composition. To perform this analysis, we use the labeled data to train supervised learning methods that predict the synthesis conditions of a zeolite given its distances to known frameworks. Specifically, we trained logistic regression, random forest, and XGBoost classifiers on literature data to predict each class label from their distance towards known zeolites. However, training models on the literature labels has two caveats: (1) the data is often unbalanced, i.e., the number of positive data points is much smaller than the number of negative data points; and (2) the negative data is not truly negative, as its lack of literature reporting does not imply that a zeolite cannot be synthesized under the synthesis conditions in analysis. To account for these problems, we trained balanced classifiers by subsampling the dataset for each synthesis conditions, thus ensuring that training sets had the same proportion of positive and negative data points, but validation/test sets were allowed to have more negative samples than positive ones. In that case, because models were tested on different negative splits, they were prevented from memorizing “negative” data points as truly negative, as exemplified by the cases discussed above. Finally, for each synthesis condition, we performed an extensive hyperparameter optimization for each of the three classifiers, evaluating the models according to their accuracy, precision, recall, F1 score, and areas under the receiving operating characteristic (ROC) and precision-recall (PR) curves.The results of the hyperparameter search are summarized in Fig. S9† for classifiers trained with AMD distances, and in S10† for those trained with SOAP distances. Whereas no classifier outperforms the other in all tasks, XGBoost models often show the best values of ROC and PR areas under the curve (AUC) for a variety of synthesis conditions. When the results for the XGBoost classifier are visualized according to all figures of merit at once (Fig. 4a), they demonstrate how the best hyperparameters lead to adequate figures of merit based on results from the validation set (see also Fig. S11, S12, and S16, and Tables S5 and S6†). When evaluated against a held-out test set, the model with best set of hyperparameters still exhibits high ROC and PR AUCs for a variety of synthesis conditions (Fig. S13 for the model with the AMD distance†). Nevertheless, this set of hyperparameters is far from being the only one that performs well in these conditions (Fig. S14 and S15†). As discussed in the analysis using unsupervised learning, the ability to correctly label zeolites whose synthesis contains Co or Zn is smaller than other labels, as indicated by the worse performance of all classifiers in labeling these conditions. However, some synthesis conditions that were not well-predicted by the unsupervised learning method, such as Mg, can now be predicted using XGBoost models, despite its low recall (Fig. S13†). Nevertheless, similar trends were found between classifiers trained with the AMD and SOAP invariants (Tables S5–S7†). Whereas classifiers trained on AMD values show a slightly better performance in predicting synthesizability with Al and Si, most of the other performance differences lie within the error bars. These results show that ML classifiers can predict inorganic synthesis conditions using distances between known zeolites as features, and that these structural similarities can be captured by different feature spaces. This has useful implications, as it bypasses the need to create representations specific for zeolites, and instead uses a set of points in the known zeolite space as references for new synthesis conditions.
To interpret the outcomes of the classifiers, explainability techniques can be used to probe what features most affect a positive (or negative) classification of a zeolite within certain synthesis conditions. Given that the input features are distances between known frameworks, a trained classifier decides how to assign a label to an input structure based on its similarity values. Using the Shapley value method (SHAP) and the classifiers trained on AMD values, we analyze what distances most affect the classification of a zeolite into a given class. As each SHAP value indicates how much each feature affects the probability of classifying a framework into a given class, we compute the Pearson correlation coefficient between the actual feature value and the SHAP value for each one of the inorganic synthesis conditions. This quantifies whether being close to a particular framework (feature) increases or decreases the likelihood of being assigned a positive label. The results for the interpretability of XGBoost classifiers are shown in Fig. 4b (see also Fig. S17 and S18†). As the correlation coefficient between AMD and SHAP values are computed on a per-feature (thus per-zeolite) basis, the nodes from the tree map in Fig. 2 are colored according to these coefficients. In this plot, a negative correlation (in green color) indicates that low distances increase the SHAP value and thus the likelihood of being classified as a positive label. Conversely, a positive correlation (in pink color) with a feature indicates that a given zeolite is more likely to be synthesized with a given synthesis condition if it is distant from the featurizing structure. The results not only support the observations highlighted by the unsupervised learning methods, but also complement them with new insights. For instance, zeolites synthesized with Ca and K have a wide overlap of positive and negative correlations (Fig. S18†), possibly due to the clustering of minerals in the tree map. There is also an overlap between boron-containing zeolites and germanium-containing zeolites, especially in the ISV branch. This result could be interesting if validated in practice, especially if the use of boron could help with the removal of Ge from the synthesis of certain zeolites. The central branch characterized by Ge-containing zeolites (such as BEC, ISV, IRR, ITT, see Fig. 2) also have features that correlate with F or Mg, but not Al or Ca. On the other hand, Be-containing zeolites are often complementary to Si-containing zeolites, as the former are found only in specific clusters or outliers in the tree map. This further supports the fact that the classifiers are able to obtain correlations beyond existing heuristics, thus providing data-driven ways to guide inorganic synthesis in zeolites.
Proposing inorganic synthesis conditions for hypothetical zeolites
Given that structural similarity is correlated to inorganic synthesis in zeolites and that supervised learning methods are able to predict synthesis using only inter-zeolite distances as inputs, we can use the models developed in this work to propose inorganic synthesis conditions for hypothetical zeolites. This approach complements previous work on the design of OSDAs for frameworks,51 thus enabling inorganic synthesis conditions to be predicted in silico whenever a new framework is proposed. To do that, we used the dataset of 331![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 171 hypothetical zeolites proposed by Pophale et al.,33 known as the “Deem dataset.” As structural features and densities from the hypothetical zeolites optimized with force fields may deviate from the experimental ones, we used the IZA and hypothetical zeolites from Erlebach et al.,52 which employed a neural network force field trained at the SCAN level of density functional theory calculations to reoptimize the hypothetical zeolites. Then, by comparing the hypothetical structures against all known zeolites using the AMD, we created a distance matrix that is used as input for the unsupervised and supervised learning methods shown in the previous section. Whereas this could also have been performed with SOAP, our results showing the similar performances of AMD and SOAP in recalling synthesis conditions from structural distances led us to choose the AMD invariant due to its computational inexpensiveness.38 Furthermore, as in the case of known zeolites, AMDs are correlated with differences of density, but are not solely determined by them (Fig. S19†). Using AMDs, a low-dimensional map can be created for all hypothetical structures, thus providing an intuitive way to visualize the space of structures. Fig. S20† shows a 2D projection of the distribution of hypothetical zeolites based on their distance matrix using UMAP. This plot shows that distance features are able to sort the space of zeolites according to energy and density despite not using this information as explicit inputs. The visualization also illustrates that most hypothetical frameworks do not have neighboring known structures. While 105 of all known zeolites have at least one other known zeolite up to 0.1 Å away (45% of structures, see Fig. S6†), only about 36
171 hypothetical zeolites proposed by Pophale et al.,33 known as the “Deem dataset.” As structural features and densities from the hypothetical zeolites optimized with force fields may deviate from the experimental ones, we used the IZA and hypothetical zeolites from Erlebach et al.,52 which employed a neural network force field trained at the SCAN level of density functional theory calculations to reoptimize the hypothetical zeolites. Then, by comparing the hypothetical structures against all known zeolites using the AMD, we created a distance matrix that is used as input for the unsupervised and supervised learning methods shown in the previous section. Whereas this could also have been performed with SOAP, our results showing the similar performances of AMD and SOAP in recalling synthesis conditions from structural distances led us to choose the AMD invariant due to its computational inexpensiveness.38 Furthermore, as in the case of known zeolites, AMDs are correlated with differences of density, but are not solely determined by them (Fig. S19†). Using AMDs, a low-dimensional map can be created for all hypothetical structures, thus providing an intuitive way to visualize the space of structures. Fig. S20† shows a 2D projection of the distribution of hypothetical zeolites based on their distance matrix using UMAP. This plot shows that distance features are able to sort the space of zeolites according to energy and density despite not using this information as explicit inputs. The visualization also illustrates that most hypothetical frameworks do not have neighboring known structures. While 105 of all known zeolites have at least one other known zeolite up to 0.1 Å away (45% of structures, see Fig. S6†), only about 36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 112 of the 331
112 of the 331![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 171 hypothetical structures have at least one known zeolite as neighbor when the same distance threshold is used (11% of zeolites in the dataset). This illustrates how the space of enumerated zeolites is often populated with structures far from known structural patterns of zeolites, as also demonstrated by previous studies (see also Fig. S21†).
171 hypothetical structures have at least one known zeolite as neighbor when the same distance threshold is used (11% of zeolites in the dataset). This illustrates how the space of enumerated zeolites is often populated with structures far from known structural patterns of zeolites, as also demonstrated by previous studies (see also Fig. S21†).
As demonstrated in this work, zeolites in the neighborhood of known frameworks are likely to share similar synthesis conditions as those known structures. Thus, downselecting frameworks for given synthesis conditions can benefit from the unsupervised and supervised methods developed here. This approach can be used in combination with previous “synthesizability descriptors” of zeolites, such as local interatomic distances35 or other data-driven predictions.53 However, we chose to evaluate them independently, as these synthesizability predictions do not take into account that certain known frameworks may be considered “unfeasible” depending on the synthesis conditions.34,54,55 For instance, structures containing three-connected rings, such as those with building units lov or vsv, could be ranked as “unsynthesizable,” despite being achieved with beryllium or borogermanate conditions. Thus, to propose synthesis conditions for zeolites, we evaluated all hypothetical frameworks for all synthesis conditions using an ensemble of 100 binary classifiers per inorganic condition (see Methods). As each classifier is trained on different negative data splits, the resulting classification varies for each model, allowing us to assess the degree of agreement between the models. By taking the average of the predictions, we obtain the agreement of the classifiers regarding the feasibility of the given pair of zeolite and synthesis condition.
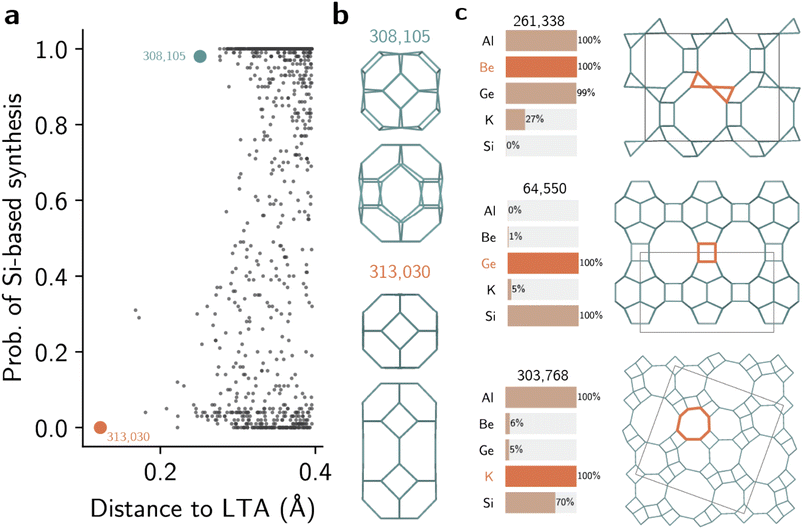
Fig. 5a depicts the distribution of hypothetical zeolites with Si-based recipes in the neighborhood of LTA zeolite. As all distances between known and hypothetical zeolites had been already computed, we can use both the distances and the class probabilities as criteria for navigating the space of hypothetical structures. This navigation using reference materials instead of features facilitates the selection process and can also inform their synthesis. For example, Fig. 5a and b illustrate two different hypothetical zeolites in the neighborhood of LTA. Although both have low distance towards LTA (compare with dendrogram in Fig. S6†), structure #308,105 is predicted to be more likely to be synthesized as a silicate than #313,030. Both contain the lta and sod cages characteristic of the LTA zeolite, but differ by the presence of a second cage similar to sod, shown in Fig. 5b. Whereas this new building unit resembles an expanded sod cage with distorted six-membered rings in #308,105, hypothetical framework #313,030 shows a new cage, formed by the merging of two sod cages, not seen in known zeolites. This increased distance towards known structural patterns drives the prediction of feasible synthesis using Si as unlikely, even when the distance towards the LTA zeolite is lower. This example shows how the combination of structural distances and classifier predictions facilitates the exploration of hypothetical zeolites using reference structures.
Beyond the exploration of the zeolite space, the models also uncover existing and new synthesis-structure relationships. Fig. 5c shows three examples of hypothetical frameworks predicted to be synthesized using three different elements: Be, Ge, and K. To obtain these frameworks, we filtered only frameworks within densities of 14 and 17 T/1000 Å3 that are predicted to have 100% probability of synthesis with the given element. Then, we ranked the frameworks by their relative energy. Despite not using explicit labels on the CBUs, the supervised learning models recovered the known heuristics of building units and inorganic synthesis conditions. For instance, framework #261,338, predicted to be synthesized in presence of Be, is formed mostly by lov building units, as found in other Be-zeolites such as RSN, LOV, or NAB. This same framework is predicted to be unlikely as a silicate, possibly following the trends seen in JSR or NPT structures. Hypothetical zeolite #64,550, predicted to be synthesized with germanium, also shows features similar to known ones. In addition to its three-dimensional pore structure, with 12 × 12 × 10 intersecting pores, the structure shows the d4r CBU typical of other structurally similar germanosilicates, such as POS or UOV, but with 7 symmetrically inequivalent T sites. Finally, one unrealized framework predicted to be synthesized with potassium is structure #303,768. Although this hypothetical structure does not exhibit typical CBUs, the local structures similar to d8r CBUs are predicted to be favored by K, in analogy with similar relationships in known zeolites. This demonstrates how data-driven models can not only recover known relationships between CBUs and inorganic conditions, but also propose new synthesis-structure relationships in zeolites based on distance patterns between known structures. When used to analyze the entire space of hypothetical frameworks, the models show that the distribution of predicted inorganic synthesis conditions is uneven across the space of zeolites (Fig. S24†). For instance, whereas about 27% of all known zeolites can be synthesized with germanium, according to the literature dataset we used in this work, only 8% of the hypothetical zeolites are predicted to being synthesizable under Ge conditions with an agreement of at least 80%. Similarly, the space of hypothetical structures is surprisingly lacking in structures predicted to be synthesizable with sodium. While about 45% of all known structures have at least one sodium-based synthesis, 17% of hypothetical structures are predicted to be realizable with Na given the 80% threshold probability. As most enumerated datasets are often created without considering synthesis conditions,56 comprehensive enumerations may introduce biases in structures that do not reflect the space of zeolite synthesis typically considered in practice. Thus, in combination with OSDA design17 and property screening,57,58 our methods to predict inorganic synthesis conditions in zeolites may help in synthesizing unrealized frameworks with targeted properties or formulating additional databases of hypothetical structures.
Conclusions
Mapping the space of inorganic conditions in materials synthesis is an outstanding challenge due to the complexity of chemical interactions during synthesis. In the case of zeolites, synthesis conditions are known to affect structural patterns in the materials, but finding correlations between structural patterns and inorganic syntheses often relies on heuristics. In this work, we used unsupervised and supervised learning methods to propose inorganic synthesis conditions for zeolite synthesis. In particular, we showed how structural distances between crystals can predict inorganic synthesis conditions in zeolites by using two different structural invariants as examples. This enables structural comparisons beyond human-crafted labels of building units or pore sizes/topologies. Clustering techniques demonstrate that our distance values consistently recall the inorganic synthesis conditions from literature datasets, thus providing predictive power even in the absence of labels. Then, we show that ML classifiers can predict synthesis conditions of a given framework based on its distribution of distances towards known structures. The classifiers were used to predict 14 different synthesis conditions for known and unrealized zeolites. When explaining the predictions, we showed how ML classifiers analyze synthesis conditions also from the dissimilarity between crystals, as well as from the similarity. The results from the explainability analysis reveals overlaps in inorganic synthesis conditions, such as boron and germanium, as well as complementary relationships, such as silicon and beryllium. Finally, we showcased how our methods can be used to predict inorganic synthesis conditions for hypothetical zeolites, facilitating the downselection of new structures for experimental attempts. This combination of data-driven methods can create a pathway for full in silico prediction of zeolite synthesis beyond the design of OSDAs.Methods
Pointwise distance distributions, average minimum distances and metrics
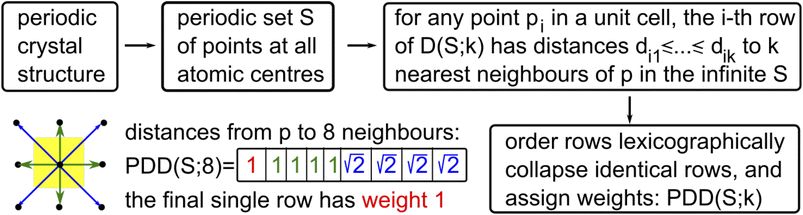
Any periodic crystal structure is modeled as a periodic set S of atomic centers considered as zero-sized points, with atomic types as optional labels. Any linear basis of vectors v1, v2, v3 in 3-dimensional space generates a lattice Λ = {c1v1 + c2v2 + c3v3∣ci are integers} and unit cell U = {t1v1 + t2v2 + t3v3∣0 ≤ ti < 1}. Any finite motif of points M ⊂ U defines the periodic point set S = {p + v∣p ∈ M, v ∈ Λ}. This conventional representation of a periodic crystal S by a unit cell and a motif is ambiguous because infinitely many different pairs (cell, motif) generate periodic sets that are equivalent up to rigid motion (a composition of translations and rotations). Fixing any reduced cells leads to unavoidable discontinuities59 even for 2-dimensional lattices.The ambiguity of crystal representations was theoretically resolved for all periodic point sets in any dimension by the complete isoset60 invariant. We define below the computationally faster Pointwise Distance Distribution (PDD) invariant, which distinguished all (more than 670![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000) periodic crystals in the Cambridge Structural Database (CSD) through more than 200 billion pairwise comparisons within two days on a typical desktop computer.
000) periodic crystals in the Cambridge Structural Database (CSD) through more than 200 billion pairwise comparisons within two days on a typical desktop computer.
Fix a number k ≥ 1 of atomic neighbors. Our experiments on zeolites and the CSD used k = 100. Let S be a periodic set with a motif M of points p1, …, pm. For each point pi, write down the sequence of increasing distances di1 ≤ ⋯ ≤ dik to its k nearest neighbors in the full infinite set S without considering any extended cell or cut-off radius. Collect these sequences of distances into an m × k matrix and lexicographically order the rows. If any l of the rows coincide (usually due to extra symmetries), collapse them into a single row with the weight l/m and put these weights into an additional first column (unique rows have weight 1/m). The resulting m × (k + 1) matrix PDD(S; k) is called the Pointwise Distance Distribution, a statistical distribution of rows with weights describing each point's environment. As an example, Fig. 6 shows the computation for a point in the square lattice S whose first k = 8 neighbours have distances 1,1,1,1 (in green) and 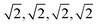 (in blue).
(in blue).
The Average Minimum Distance AMD(S; k) is the vector obtained by taking the weighted average of the last k columns in PDD(S; k), so AMD is a single vector of k average distances. To compare two AMD vectors of the same length, our experiments used the L∞ (Chebyshev) metric equal to the maximum absolute difference of corresponding coordinates. For a metric on PDDs, we use the Earth Mover's Distance (EMD)61 with the L∞ metric on rows. If any point of S is perturbed in its ε-neighborhood, then PDD(S; k) changes by at most 2ε in the EMD metric. If a periodic set S is generic, which is achievable by almost any perturbation of atoms, then S can be reconstructed from the number m of motif points, a (basis of a) lattice Λ and PDD(S; k) with a known upper bound on k. For the details on these results, see Definition C5 and proofs of Theorems 4.3 and 4.4 in the extended version of ref. 62.
Within this work, a metric is defined as a distance function d:χ × χ → [0,+∞) that satisfies the following axioms: (1) d(x, x) = 0 and d(x, y) > 0, ∀x ≠ y; (2) d(x, y) = d(y, x); and (3) d(x,z) ≤ d(x,y) + d(y,z), ∀x,y,z ∈ χ3. Generally, weaker concepts of distance relax the first constraint to d(x, y) ≥ 0. “Distances” between crystal structures, therefore, refer to distances between structural invariants (e.g., vectors) that are independent of a unit cell and is preserved under rotations and translations of the crystal structure.
SOAP representation
As an alternative invariant to the AMD, zeolite structures were also represented using the Smooth Overlap of Atomic Positions (SOAP).37 For each atom in the structure, the power spectrum was computed using 8 radial basis functions, 6 angular basis functions, and a cutoff of 5.0 Å using the package describe (v. 2.1.0).63 To represent the entire structure, the SOAP vectors were averaged over all environments prior to summing the magnetic quantum numbers (mode “inner” in describe.descriptors.SOAP). Then, the cosine SOAP kernel was used to measure the distance between two structures.It has been reported that local structural fingerprints such as SOAP may be unable to distinguish between certain atomic environments.64 While this may not be a problem when comparing zeolites, especially as cutoffs become larger,53 degeneracies in the descriptor space can limit the accuracy with which local environments — and, therefore, structures — can be distinguished. Specifically, as Pozdnyakov et al.64 demonstrate examples of degenerate manifolds in systems with typical tetrahedral coordination such as methane or silicon, it could be possible to find similar degeneracies in four-connected zeolite networks. Nevertheless, this method has also been widely successful in charting the space of materials, including other four-connected networks,65 and is not expected to interfere substantially with the ML results in this manuscript.
Zeolite structures data
The dataset of 253 known zeolite structures used in the unsupervised learning method was obtained from the International Zeolite Association (IZA) database66 (http://www.iza-structure.org/databases/). The dataset of hypothetical frameworks used in this work was developed by Pophale et al.,33 and re-optimized using a neural network force field trained on DFT-SCAN data by Erlebach et al.52 Because not all of the 253 known zeolites used previously were optimized by Erlebach et al., we used their subset of 236 known frameworks when computing distance matrices from the hypothetical frameworks and the known frameworks.Following the notation from the IZA, known zeolites are named in this manuscript according to their three-letter code in bold typeface. Known CBUs are represented with their three-letter code in lowercase and italic typeface.
Literature data
Literature data was obtained from public datasets of zeolite synthesis conditions from Jensen et al.,49 which has been extensively validated by Schwalbe-Koda et al. for the computational design of OSDAs.17 Whereas in those works only zeolite-OSDA pairs were considered, in this work only relationships between zeolites and non-organic synthesis conditions are analyzed. As the dataset was produced by collecting literature data from over 60 years of studies in synthetic zeolites, several natural frameworks were omitted from the table, as well as newer structures not captured at the time of that study. To address this issue, we manually inserted new rows on the table with the composition of the missing structures. The compositions were obtained with manual verification of the synthesis conditions in articles describing the mineral/synthetic zeolite, as also shown in the online IZA database. The resulting, cleaned data used in this study is available for download (see Code and data availability).In the literature analysis, a zeolite is classified as having a certain synthesis condition when at least 25% of its synthesis recipes exhibit that condition (excluding OSDAs). This label is used as a categorical variable when performing the classification task.
Unsupervised learning
A minimum spanning tree between zeolites was constructed by first creating a fully connected, undirected graph with weighted edges, where weights correspond to the distances between two structures. The tree was then obtained using NetworkX's (v. 2.5)67 minimum spanning tree algorithm, which minimizes the total length of the tree. Because the minimum spanning tree only connects the nearest neighbors, small differences in distance rankings can lead to substantial modifications in the graph of Fig. 2. As such, zeolites that can be regarded as outliers in the graph may be close to several structures, but only the closest one is depicted. Nevertheless, the visualization is able to capture several known relationships between inorganic syntheses, as also quantified by the analysis in Fig. 3, and offers a useful tool to traverse the space of frameworks. The ESI† provides an in-depth discussion on the outliers.The dendrogram of known zeolites was produced by creating a linkage matrix from the distance matrix using the Ward algorithm as implemented in SciPy (v. 1.10.0).68 The resulting clusters in Fig. S6† were obtained by forming flat clusters with the maximum AMD distance of a given threshold.
The homogeneity of the clustering was computed by calculating the Shannon entropy of flat clusters created with a given threshold,50 as implemented in scikit-learn (v. 1.2.0).69 As the literature dataset is not balanced and lacks true negative points, the homogeneity was only computed for clusters containing at least one positive data point. This ensures that a large homogeneity corresponds to recall of positive data points, which prevents biasing this metric in imbalanced datasets.
Dimensionality reduction was performed using UMAP,70 as implemented in the umap-learn package in Python (v. 0.5.3). The 2D UMAP plot was produced by comparing hypothetical frameworks using the cosine distance of their normalized distances to IZA structures, and using 10 neighbors as parameter.
Supervised learning
Classification of inorganic synthesis conditions was performed by training separate classifiers for each synthesis condition. The features used during training were the distances towards the 253 known frameworks, as computed with the AMD method described above. To obtain a statistically meaningful result, only elements used to synthesize at least 10 zeolites were considered. In particular, 14 inorganic conditions are considered: Al, B, Be, Ca, Co, F, Ga, Ge, K, Mg, Na, P, Si, and Zn.Train-validation-test sets were created starting with a 60-20-20 ratio, respectively, then subsampling the training set to have an equal number of points with positive and negative labels. Although techniques such as reweighting or resampling could have been employed to obtained balanced training sets, removing data points is a simple approach that prevents classifiers from treating negative data as “true negative”, resembling positive-unlabeled learning strategies.
Hyperparameter optimization of synthesis classifiers was performed using a grid-search method over relevant spaces of hyperparameters for logistic regression, random forest, and XGBoost71 methods. The full range of hyperparameters investigated in this hyperparameter search is shown in Tables S2–S4,† following the notation in the scikit-learn (v. 1.2.0) and xgboost (v. 1.7.5) Python packages. Model performances were compared using the same dataset splits, and the best model is selected according to its validation performance. The results on the paper showcase the performance on held-out test data. While training errors are always smaller than held-out data, the good performance of the models in the validation and test sets suggest their generalization power is not being degraded by overfitting.
One of the best models to classify synthesis conditions of zeolites was the XGBoost model with the following hyperparameters: colsample_bytree = 0.5, learning_rate = 0.1, max_depth = 6, min_child_weight = 1, n_estimators = 200, subsample = 0.5. This model and set of hyperparameters showed good performance across a range of inorganic synthesis conditions, as evaluated by the accuracy, precision, recall, F1 score, area under the receiving operator characteristic curve (ROC AUC), and area under the precision-recall curve (PR AUC). In particular, the best model was selected to maximize the ROC AUC and PR AUC for the balanced classifiers. As a comparison, the performance metrics and their baselines of unbalanced classifiers — thus trained on dataset splits with an uneven number of positive/negative labels — are shown in Fig. S13.†
Explainability of the classifiers was computed using the Shapley value method (SHAP)72 under the TreeExplainer framework,73 as implemented in the shap Python package (v. 0.41.0). The interventional feature perturbation method was used without limit for the tree explainer. Then, correlations between the SHAP values and the distance features were computed for each synthesis condition. To ensure that the correlations are not artifacts of particular train splits, we report the average correlation obtained from an ensemble of 100 XGBoost classifiers trained on splits with different negative data points.
Data and code availability
The code to compute PDDs and AMDs for arbitrary crystal structures is available on GitHub at https://github.com/dwiddo/average-minimum-distance (last access date on October, 9, 2023). The synthesis data was cleaned from the original source at GitHub, https://github.com/olivettigroup/OSDA_Generator (last access date on July, 20, 2023). The code and data required to reproduce all results and figures in this manuscript are available at https://github.com/dskoda/Zeolites-AMD (last access date on October, 9, 2023). Persistent links for the data/code are available at Zenodo under the following DOIs: 10.5281/zenodo.8422372 and 10.5281/zenodo.8422564.Author contributions
D. S.-K.: Conceptualization, methodology, software, validation, investigation, data curation, writing - original draft, writing - review & editing, visualization, supervision. D. E. W.: Methodology, software, validation, investigation, data curation, writing - original draft, writing - review & editing, visualization. T. A. P.: Methodology, writing - review & editing, supervision. V. A. K.: Conceptualization, methodology, writing - original draft, writing - review & editing, supervision.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This work was performed under the auspices of the U.S. Department of Energy by Lawrence Livermore National Laboratory (LLNL) under Contract DE-AC52-07NA27344. D. S.-K. acknowledges funding from the Laboratory Directed Research and Development (LDRD) Program at LLNL under project tracking code 22-ERD-055, and under the Postdoctoral Development Program. T. A. P. acknowledges funding from the Center for Enhanced Nanofluidic Transport (CENT), an Energy Frontier Research Center funded by the U.S. Department of Energy, Office of Science, Basic Energy Sciences under Award DE-SC0019112. D.E.W. and V. A. K. acknowledge funding from the EPSRC (EP/R018472/1, EP/X018474/1) and Royal Academy of Engineering (IF2122/186) in the UK. Manuscript released as LLNL-JRNL-851183.References
- M. E. Davis, Ordered porous materials for emerging applications, Nature, 2002, 417, 813–821 CrossRef CAS PubMed.
- Introduction to Zeolite Science and Practice, ed. J. Čejka, H. van Bekkum, A. Corma and F. Schueth, Elsevier, Amsterdam, Boston, 3rd edn, 2007, Studies in Surface Science and Catalysis 168, OCLC: ocn163318390 Search PubMed.
- W. Vermeiren and J.-P. Gilson, Impact of Zeolites on the Petroleum and Petrochemical Industry, Top. Catal., 2009, 52, 1131–1161 CrossRef CAS.
- Y. Li, L. Li and J. Yu, Applications of Zeolites in Sustainable Chemistry, Chem, 2017, 3, 928–949 CAS.
- Y. Li and J. Yu, Emerging Applications of Zeolites in Catalysis, Separation and Host–Guest Assembly, Nat. Rev. Mater., 2021, 6, 1156–1174 CrossRef CAS.
- M. Dusselier and M. E. Davis, Small-Pore Zeolites: Synthesis and Catalysis, Chem. Rev., 2018, 118, 5265–5329 CrossRef CAS PubMed.
- A. Corma, In Studies in Surface Science and Catalysis, ed. E. van Steen, I. Claeys and L. Callanan, Elsevier B.V., 2004, vol. 154A, pp. 25–40 Search PubMed.
- C. S. Cundy and P. A. Cox, The Hydrothermal Synthesis of Zeolites: History and Development from the Earliest Days to the Present Time, Chem. Rev., 2003, 103, 663–701 CrossRef CAS PubMed.
- R. F. Lobo, S. I. Zones and M. E. Davis, Structure-Direction in Zeolite Synthesis, J. Inclusion Phenom. Mol. Recognit. Chem., 1995, 21, 47–78 CrossRef CAS.
- R. M. Barrer, Zeolites and Their Synthesis, Zeolites, 1981, 1, 130–140 CrossRef CAS.
- S. K. Brand, J. E. Schmidt, M. W. Deem, F. Daeyaert, Y. Ma, O. Terasaki, M. Orazov and M. E. Davis, Enantiomerically Enriched, Polycrystalline Molecular Sieves, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 5101–5106 CrossRef CAS PubMed.
- E. M. Gallego, M. T. Portilla, C. Paris, A. León-Escamilla, M. Boronat, M. Moliner and A. Corma, Ab Initio” Synthesis of Zeolites for Preestablished Catalytic Reactions, Science, 2017, 355, 1051–1054 CrossRef CAS PubMed.
- D. W. Lewis, D. J. Willock, C. R. A. Catlow, J. M. Thomas and G. J. Hutchings, De novo design of structure-directing agents for the synthesis of microporous solids, Nature, 1996, 382, 604–606 CrossRef CAS.
- G. Sastre, A. Cantin, M. J. Diaz-Cabañas and A. Corma, Searching Organic Structure Directing Agents for the Synthesis of Specific Zeolitic Structures: An Experimentally Tested Computational Study, Chem. Mater., 2005, 17, 545–552 CrossRef CAS.
- J. E. Schmidt, M. W. Deem, C. Lew and T. M. Davis, Computationally-Guided Synthesis of the 8-Ring Zeolite AEI, Top. Catal., 2015, 58, 410–415 CrossRef CAS.
- T. M. Davis, A. T. Liu, C. M. Lew, D. Xie, A. I. Benin, S. Elomari, S. I. Zones and M. W. Deem, Computationally Guided Synthesis of SSZ-52: A Zeolite for Engine Exhaust Clean-Up, Chem. Mater., 2016, 28, 708–711 CrossRef CAS.
- D. Schwalbe-Koda, S. Kwon, C. Paris, E. Bello-Jurado, Z. Jensen, E. Olivetti, T. Willhammar, A. Corma, Y. Román-Leshkov, M. Moliner and R. Gómez-Bombarelli, A Priori Control of Zeolite Phase Competition and Intergrowth with High-Throughput Simulations, Science, 2021, 374, 308–315 CrossRef CAS PubMed.
- D. Schwalbe-Koda, A. Corma, Y. Román-Leshkov, M. Moliner and R. Gómez-Bombarelli, Data-driven design of biselective templates for intergrowth zeolites, J. Phys. Chem. Lett., 2021, 12, 10689–10694 CrossRef CAS PubMed.
- E. Bello-Jurado, D. Schwalbe-Koda, M. Nero, C. Paris, T. Uusimäki, Y. Román-Leshkov, A. Corma, T. Willhammar, R. Gómez-Bombarelli and M. Moliner, Tunable CHA/AEI zeolite intergrowths with A priori biselective organic structure-directing agents: controlling enrichment and implications for selective catalytic reduction of NOx, Angew. Chem., Int. Ed., 2022, 61, e202201837 CrossRef CAS PubMed.
- J. R. Di Iorio, S. Li, C. B. Jones, C. T. Nimlos, Y. Wang, E. Kunkes, V. Vattipalli, S. Prasad, A. Moini, W. F. Schneider and R. Gounder, Cooperative and Competitive Occlusion of Organic and Inorganic Structure-Directing Agents within Chabazite Zeolites Influences Their Aluminum Arrangement, J. Am. Chem. Soc., 2020, 142, 4807–4819 CrossRef CAS PubMed.
- J. Shin, D. Jo and S. B. Hong, Rediscovery of the Importance of Inorganic Synthesis Parameters in the Search for New Zeolites, Acc. Chem. Res., 2019, 52, 1419–1427 CrossRef CAS PubMed.
- X. Li, H. Han, N. Evangelou, N. J. Wichrowski, P. Lu, W. Xu, S.-J. Hwang, W. Zhao, C. Song and X. Guo, et al., Machine learning-assisted crystal engineering of a zeolite, Nat. Commun., 2023, 14, 3152 CrossRef CAS PubMed.
- S. Li, J. Li, M. Dong, S. Fan, T. Zhao, J. Wang and W. Fan, Strategies to control zeolite particle morphology, Chem. Soc. Rev., 2019, 48, 885–907 RSC.
- H. Lee, J. Shin, K. Lee, H. J. Choi, A. Mayoral, N. Y. Kang and S. B. Hong, Synthesis of Thermally Stable SBT and SBS/SBT Intergrowth Zeolites, Science, 2021, 373, 104–107 CrossRef CAS PubMed.
- M. D. Oleksiak and J. D. Rimer, Synthesis of Zeolites in the Absence of Organic Structure-Directing Agents: Factors Governing Crystal Selection and Polymorphism, Rev. Chem. Eng., 2014, 30, 1–49 CAS.
- Z. Jensen, E. Kim, S. Kwon, T. Z. H. Gani, Y. Román-Leshkov, M. Moliner, A. Corma and E. Olivetti, A Machine Learning Approach to Zeolite Synthesis Enabled by Automatic Literature Data Extraction, ACS Cent. Sci., 2019, 5, 892–899 CrossRef CAS PubMed.
- K. Muraoka, Y. Sada, D. Miyazaki, W. Chaikittisilp and T. Okubo, Linking Synthesis and Structure Descriptors from a Large Collection of Synthetic Records of Zeolite Materials, Nat. Commun., 2019, 10, 4459 CrossRef PubMed.
- K. Asselman, D. Vandenabeele, N. Pellens, N. Doppelhammer, C. E. Kirschhock and E. Breynaert, Structural Aspects Affecting Phase Selection in Inorganic Zeolite Synthesis, Chem. Mater., 2022, 34, 11081–11092 CrossRef CAS PubMed.
- K. Itabashi, Y. Kamimura, K. Iyoki, A. Shimojima and T. Okubo, A Working Hypothesis for Broadening Framework Types of Zeolites in Seed-Assisted Synthesis without Organic Structure-Directing Agent, J. Am. Chem. Soc., 2012, 134, 11542–11549 CrossRef CAS PubMed.
- J. Li, A. Corma and J. Yu, Synthesis of New Zeolite Structures, Chem. Soc. Rev., 2015, 44, 7112–7127 RSC.
- V. A. Blatov, G. D. Ilyushin and D. M. Proserpio, The Zeolite Conundrum: Why Are There so Many Hypothetical Zeolites and so Few Observed? A Possible Answer from the Zeolite-Type Frameworks Perceived as Packings of Tiles, Chem. Mater., 2013, 25, 412–424 CrossRef CAS.
- E. D. Kuznetsova, O. A. Blatova and V. A. Blatov, Predicting New Zeolites: A Combination of Thermodynamic and Kinetic Factors, Chem. Mater., 2018, 30, 2829–2837 CrossRef CAS.
- R. Pophale, P. A. Cheeseman and M. W. Deem, A Database of New Zeolite-like Materials, Phys. Chem. Chem. Phys., 2011, 13, 12407–12412 RSC.
- L. Li, B. Slater, Y. Yan, C. Wang, Y. Li and J. Yu, Necessity of Heteroatoms for Realizing Hypothetical Aluminophosphate Zeolites: A High-Throughput Computational Approach, J. Phys. Chem. Lett., 2019, 10, 1411–1415 CrossRef CAS PubMed.
- Y. Li, J. Yu and R. Xu, Criteria for Zeolite Frameworks Realizable for Target Synthesis, Angew. Chem., Int. Ed., 2013, 52, 1673–1677 CrossRef CAS PubMed.
- B. A. Helfrecht, R. Semino, G. Pireddu, S. M. Auerbach and M. Ceriotti, A New Kind of Atlas of Zeolite Building Blocks, J. Chem. Phys., 2019, 151, 154112 CrossRef PubMed.
- A. P. Bartók, R. Kondor and G. Csányi, On Representing Chemical Environments, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 184115 CrossRef.
- D. Widdowson, M. Mosca, A. Pulido, A. Cooper and V. Kurlin, Average Minimum Distances of periodic point sets - fundamental invariants for mapping all periodic crystals, MATCH, 2022, 87, 529–559 CrossRef.
- D. Widdowson and V. KurlinResolving the data ambiguity for periodic crystals, Advances in Neural Information Processing Systems (NeurIPS 2022) 2022, vol. 35, pp. 24625–24638 Search PubMed.
- Y. Elkin and V. KurlinA new near-linear time algorithm for k-nearest neighbor search using a compressed cover tree, International Conference on Machine Learning (ICML). 2023 Search PubMed.
- D. Schwalbe-Koda, Z. Jensen, E. Olivetti and R. Gómez-Bombarelli, Graph Similarity Drives Zeolite Diffusionless Transformations and Intergrowth, Nat. Mater., 2019, 18, 1177–1181 CrossRef CAS PubMed.
- T. Willhammar and X. Zou, Stacking disorders in zeolites and open-frameworks – structure elucidation and analysis by electron crystallography and X-ray diffraction, Z. Kristallogr. - Cryst. Mater., 2013, 228, 11–27 CrossRef CAS.
- M. Moliner, T. Willhammar, W. Wan, J. González, F. Rey, J. L. Jorda, X. Zou and A. Corma, Synthesis Design and Structure of a Multipore Zeolite with Interconnected 12- and 10-MR Channels, J. Am. Chem. Soc., 2012, 134, 6473–6478 CrossRef CAS PubMed.
- C. Baerlocher, T. Weber, L. B. McCusker, L. Palatinus and S. I. Zones, Unraveling the perplexing structure of the zeolite SSZ-57, Science, 2011, 333, 1134–1137 CrossRef CAS PubMed.
- P. Guo, J. Shin, A. G. Greenaway, J. G. Min, J. Su, H. J. Choi, L. Liu, P. A. Cox, S. B. Hong, P. A. Wright and X. Zou, A zeolite family with expanding structural complexity and embedded isoreticular structures, Nature, 2015, 524, 74–78 CrossRef CAS PubMed.
- S. L. Lawton and W. J. Rohrbaugh, The framework topology of ZSM-18, a novel zeolite containing rings of three (Si, Al)-O species, Science, 1990, 247, 1319–1322 CrossRef CAS PubMed.
- G. W. Noble, P. A. Wright, P. Lightfoot, R. E. Morris, K. J. Hudson, Å. Kvick and H. Graafsma, Microporous Magnesium Aluminophosphate STA-1: Synthesis with a Rationally Designed Template and Structure Elucidation by Microcrystal Diffraction, Angew. Chem., Int. Ed. Engl., 1997, 36, 81–83 CrossRef CAS.
- S. Hong, A. J. Mallette, J. J. Neeway, R. K. Motkuri, J. D. Rimer and G. Mpourmpakis, Understanding formation thermodynamics of structurally diverse zeolite oligomers with first principles calculations, Dalton Trans., 2023, 52, 1301–1315 RSC.
- Z. Jensen, S. Kwon, D. Schwalbe-Koda, C. Paris, R. Gómez-Bombarelli, Y. Román-Leshkov, A. Corma, M. Moliner and E. A. Olivetti, Discovering Relationships between OSDAs and Zeolites through Data Mining and Generative Neural Networks, ACS Central Science, 2021, 7, 858–867 CrossRef CAS PubMed.
- A. Rosenberg and J. V. Hirschberg, Measure: A Conditional Entropy-Based External Cluster Evaluation Measure, Proceedings of the 2007 Joint Conference on Empirical Methods in Natural Language Processing and Computational Natural Language Learning (EMNLP-CoNLL), Prague, Czech Republic, 2007, pp. 410–420 Search PubMed.
- D. Schwalbe-Koda, A. Corma, Y. Román-Leshkov, M. Moliner and R. Gómez-Bombarelli, Data-Driven Design of Biselective Templates for Intergrowth Zeolites, J. Phys. Chem. Lett., 2021, 12, 10689–10694 CrossRef CAS PubMed.
- A. Erlebach, P. Nachtigall and L. Grajciar, Accurate large-scale simulations of siliceous zeolites by neural network potentials, npj Comput. Mater., 2022, 8, 174 CrossRef CAS.
- B. A. Helfrecht, G. Pireddu, R. Semino, S. M. Auerbach and M. Ceriotti, Ranking the Synthesizability of Hypothetical Zeolites with the Sorting Hat, Digital Discovery, 2022, 1, 779–789 RSC.
- M. Mazur, P. S. Wheatley, M. Navarro, W. J. Roth, M. Položij, A. Mayoral, P. Eliášová, P. Nachtigall, J. Čejka and R. E. Morris, Synthesis of ’unfeasible’ Zeolites, Nat. Chem., 2016, 8, 58–62 CrossRef CAS PubMed.
- E. Verheyen, et al., Design of Zeolite by Inverse Sigma Transformation, Nat. Mater., 2012, 11, 1059–1064 CrossRef CAS PubMed.
- E. Argente, S. Valero, A. Misturini, M. M. Treacy, L. Baumes and G. Sastre, Computer Generation of Hypothetical Zeolites, AI-Guided Des. Prop. Predict. Zeolites Nanoporous Mater., 2023, 145–172 CAS.
- L.-C. Lin, A. H. Berger, R. L. Martin, J. Kim, J. A. Swisher, K. Jariwala, C. H. Rycroft, A. S. Bhown, M. W. Deem, M. Haranczyk and B. Smit, In Silico Screening of Carbon-Capture Materials, Nat. Mater., 2012, 11, 633–641 CrossRef CAS PubMed.
- D. Hewitt, T. Pope, M. Sarwar, A. Turrina and B. Slater, Machine learning accelerated high-throughput screening of zeolites for the selective adsorption of xylene isomers, Chem. Sci., 2022, 13, 13178–13186 RSC.
- V. A. Kurlin, Mathematics of 2-dimensional lattices, Found. Comput. Math., 2022, 1–59 Search PubMed.
- O. Anosova and V. Kurlin, An isometry classification of periodic point sets, Lect. Notes Comput. Sci., 2021, 229–241 Search PubMed.
- C. J. Hargreaves, M. S. Dyer, M. W. Gaultois, V. A. Kurlin and M. J. Rosseinsky, The Earth Mover's Distance as a Metric for the Space of Inorganic Compositions, Chem. Mater., 2020, 32, 10610–10620 CrossRef CAS.
- D. Widdowson and V. Kurlin, Pointwise Distance Distributions of periodic sets, arXiv, 2021, preprint, arXiv:2108.04798, DOI:10.48550/arXiv.2108.04798.
- J. Laakso, L. Himanen, H. Homm, E. V. Morooka, M. O. Jäger, M. Todorović and P. Rinke, Updates to the DScribe library: New descriptors and derivatives, J. Chem. Phys., 2023, 158 Search PubMed.
- S. N. Pozdnyakov, M. J. Willatt, A. P. Bartók, C. Ortner, G. Csányi and M. Ceriotti, Incompleteness of atomic structure representations, Phys. Rev. Lett., 2020, 125, 166001 CrossRef CAS PubMed.
- E. A. Engel, A. Anelli, M. Ceriotti, C. J. Pickard and R. J. Needs, Mapping uncharted territory in ice from zeolite networks to ice structures, Nat. Commun., 2018, 9, 2173 CrossRef PubMed.
- C. Baerlocher, McCusker, Database of Zeolite Structures, https://www.iza-structure.org/databases/, 2023 Search PubMed.
- A. A. Hagberg; D. A. Schult and P. J. Swart, Exploring Network Structure, Dynamics, and Function using NetworkX, Proceedings of the 7th Python in Science Conference, Pasadena, CA USA, 2008, pp. 11–15 Search PubMed.
- P. Virtanen, et al., SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python, Nat. Methods, 2020, 17, 261–272 CrossRef CAS PubMed.
- F. Pedregosa, et al., Scikit-learn: Machine Learning in Python, Journal of Machine Learning Research, 2011, 12, 2825–2830 Search PubMed.
- L. McInnes, J. Healy and J. Melville, UMAP: Uniform manifold approximation and projection for dimension reduction, arXiv, 2018, preprint, arXiv:1802.03426, DOI:10.48550/arXiv.1802.03426.
- T. Chen and C. GuestrinXGBoost: A Scalable Tree Boosting System. Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York, USA, 2016; pp. 785–794 Search PubMed.
- S. M. Lundberg and S.-I. Lee in Advances in Neural Information Processing Systems 30, ed. I. Guyon, U. V. Luxburg, S. Bengio, H. Wallach, R. Fergus, S. Vishwanathan and R. Garnett, Curran Associates, Inc., 2017; pp. 4765–4774 Search PubMed.
- S. M. Lundberg, G. Erion, H. Chen, A. DeGrave, J. M. Prutkin, B. Nair, R. Katz, J. Himmelfarb, N. Bansal and S.-I. Lee, From local explanations to global understanding with explainable AI for trees, Nature Machine Intelligence, 2020, 2, 2522–5839 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3dd00134b |
| This journal is © The Royal Society of Chemistry 2023 |