Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Understanding the patterns that neural networks learn from chemical spectra†
Laura Hannemose
Rieger
 a,
Max
Wilson
b,
Tejs
Vegge
a,
Max
Wilson
b,
Tejs
Vegge
 a and
Eibar
Flores
a and
Eibar
Flores
 *c
*c
aDepartment of Energy Conversion and Storage, Technical University of Denmark, DK-2800 Kgs. Lyngby, Denmark
bDepartment of Applied Mathematics and Computer Science, Technical University of Denmark, Kgs. Lyngby, Denmark
cSustainable Energy Technology, SINTEF Industry, Sem Sælands Vei 12, Trondheim, 7034, Norway. E-mail: eibar.flores.cedeno@sintef.no
First published on 10th November 2023
Abstract
Analysing spectra from experimental characterization of materials is time consuming, susceptible to distortions in data, requires specific domain knowledge, and may be susceptible to biases in general heuristics under human analysis. Recent work has shown the potential of using neural networks to solve this task, and assist spectral interpretation with automated and unbiased analysis on-the-fly. However, the black-box nature of most neural networks poses challenges when interpreting which patterns from the data are being used to make predictions. Understanding how neural networks learn is critical to assess their accuracy on unseen data, justify critical decision-making based on predictions, and potentially unravel meaningful scientific insights. We present a 1D neural network to classify infrared spectra from small organic molecules according to their functional groups. Our model is within range of state-of-the-art performance while being significantly less complex than previously used networks reported in the literature. A smaller network reduces the risk of overfitting and enables exploring what the model has learned about the patterns in the spectra that relate to molecular structure and composition. With a novel two-step approach for explaining the neural network's classification process, our findings not only demonstrate that the model learns the characteristic group frequencies of functional groups, but also suggest it uses non-intuitive patterns such as tails and overtones when classifying spectra.
1 Introduction
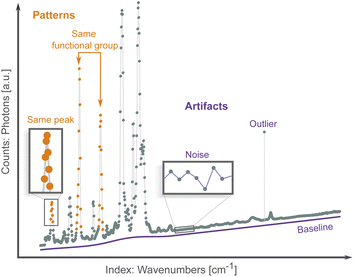
Spectroscopic techniques are one of the main tools in the scientific arsenal to characterize materials. They are routinely used to control the quality of drugs and find new ones, monitor the operation of industrial processes, investigate the properties and function of promising materials, etc.1 As radiation interacts with a material it excites the nuclei (e.g., nuclear magnetic resonance), core electrons (e.g., X-ray absorption spectroscopy), valence electrons (e.g., UV-Vis spectroscopy), or interatomic bonds (e.g., Raman spectroscopy). Spectroscopists then analyze the result of this interaction, which can occur via energy absorption, scattering, re-emission and/or resonance. The results are patterns of intensity vs. excitation energy, which are characteristic and descriptive fingerprints of the state of matter. Researchers use these patterns to infer properties such as phase, chemical composition and environment, purity, defects, stress/strain, etc. from the object of interest.2–4Virtually all spectra share the same data structure: an array of intensity counts (e.g., photons, electrons), and its corresponding array of indexes, i.e., the scanning variable such as absorption energy, scattering angle, or wavelength. Spectroscopic data differ from other more traditional data sources by being high-dimensional (each spectrum typically has hundred/thousand data points) and exhibiting both local (peaks and troughs) and non-local patterns (multiple peak belonging to the same compound or chemical environment), as shown in Fig. 1. Both types of patterns are needed to map a spectrum to a sample's properties.
Traditionally, spectral analysis involves comparing peaks and patterns to experimental databases,5 to simulations,6 or by visual inspection following heuristic rules.7 These methods can be time consuming, require specific domain knowledge, and are susceptible to spectral artifacts (Fig. 1) from, e.g., noise, outliers and baseline drift. Multiple correction algorithms have been proposed for spectral analysis.8,9 However, these traditional preprocessing techniques involve manual tuning of parameters and so are also susceptible to human biases. More importantly, even if the spectra can be successfully preprocessed, it is still highly challenging to establish spectrum–property relationships in the absence of accurate simulations and reference compounds. In the hope of addressing some of these issues, machine learning (ML) methods have been applied to the problem of spectra analysis. These algorithms can learn to directly map spectral patterns to material properties from a preexisting dataset.10–12 ML methods establish a statistical model between a large number of spectra and a property of interest, and potentially bypass the need for physics-based simulations and curated databases. Classification algorithms learn to assign spectra to one of several classes (e.g., species of bacteria13), while regression algorithms map spectra to a numerical property (e.g., the concentration of a specific chemical or compound within a mixture14). They can be susceptible, in the same way, to distortions or biases in the dataset. Addressing these artifacts manually becomes intractable given the large number of spectra needed to train an ML algorithm; instead, artifacts are mitigated in a high-throughput fashion with a variety of preprocessing routines, such as noise reduction15 and baseline correction.16–18
Convolutional neural networks (CNN) are a well-established type of neural network for recognizing patterns in images.19,20 CNNs can overcome the need of hand-engineering the data before training, since they learn low-dimensional patterns directly from the high-dimensional input. The low dimensional patterns are hierarchically combined into increasingly complex patterns. For instance, segments are combined into lines, and subsequently combined into shapes. In images, the shapes could be tails, ears and eyes to classify images of cats from dogs, or circles, arcs and triangles to classify images of hand-written digits.21–23 The hierarchical pattern recognition approach that CNNs leverage to classify images shows clear similarities to how experts infer properties from spectra. Spectroscopists typically search for lines that form baselines and peaks, in turn peaks that become shoulders, doublets, sextets, etc.; all while noting the position of these patterns within an energy axis. Naturally, such expert-based analysis is very time consuming, and constitutes a bottleneck in the data analysis from new high-throughput spectroscopic analysis techniques. It is no surprise that CNNs have been increasingly applied to the problem of spectra analysis24–30 and shown to perform comparatively better than other ML methods.31–36
CNNs share with other neural network methods a critical disadvantage: they are difficult to interpret. Given the dense connectedness of the network architecture, it becomes increasingly challenging to investigate the relations between inputs and outputs that lead to successful predictions. Understanding how the network learns is equally important as its accuracy, for three main reasons. One is assessing how well the network performs on unseen data. As with any ML model, the predictive power of a CNN might suffer when the input data is significantly different from the data used for training. CNN models might confuse spurious spectral artifacts for meaningful patterns. Therefore, ensuring that the model is learning patterns that carry physical information provides further guarantee on its ability to generalize. Secondly, interpretability enables delivering meaningful scientific outcomes. Using NNs for scientific discovery requires understanding how the learned patterns build upon existing scientific principles.37 The third reason pertains to justifying critical decision-making. When a network predicts an outcome that calls for a crucial decision, e.g., analysis and medical diagnosis of cancer specimens using spectroscopic imaging,38,39 data scientists must provide a satisfactory interpretation to justify a course of action. These interpretations have previously unraveled unexpected and undesirable behavior of deep learning models. For instance, models can choose shortcuts to make predictions, e.g. hospital metadata markers in lung X-ray images instead of using lung features to detect COVID-19.40,41
In this study, we use a convolutional neural network (CNN) to classify spectra, with a focus on interpreting the type patterns the network learns for making predictions. We use an openly available dataset of infrared spectra from small molecules and build a small CNN to classify the presence or absence of functional groups from spectra. Our CNN accuracy is within the range of the state-of-the-art while being comparatively less complex as measured by the number of parameters. Being smaller, our model is easier to interpret and more robust against overfitting. It is widely accepted in machine learning research that while simple models are not immune to overfitting, complex models are more prone to overfit the training data.42
This work builds upon previous research by Judge et al.,43 who used sensitivity factors computed from a trained multi-layered perceptron (MLP) to model the relation between a spectrum and the presence of a functional group. These sensitivity factors, interpreted as saliency profiles, highlighted regions of the spectra that were most relevant for predicting the presence of a functional group.43 Fine et al.44 implemented an autoencoder network followed by several fully connected layers, and used guided backpropagation to identify the regions of the spectra used to make classification of each functional group.45 Enders et al.46 used a 2D CNN to classify images of infrared and mass spectra, without assessing which patterns result in more confident predictions. Instead, in our work we focus not only on predictive performance but also the robustness of the prediction along with the interpretability. Similar to the concept bottleneck models introduced in Koh et al.,47 our model features a ‘bottleneck’ where human understandable features are converted into the final output classification. In contrast to their work, our model does not require the relevant features to be known beforehand or for all training inputs to be annotated with all features, since concept or prototype features are learnt automatically in our model. In this way the model might autonomously discover important features as these do not need to be known beforehand. Our approach of designing an inherently interpretable model by a bottleneck through which information must flow circumvents the known problems with the reliability of post-hoc attribution methods.48,49 To our knowledge this presents a novel method to explain the classifications of convolutional neural networks.
We implemented a simple 1-D CNN50 with convolutional layers followed by a single fully connected layer. Our contribution here is two-fold. Our stripped-down CNN architecture predicts functional groups with state-of-the-art performance. Due to the small architecture, we can further examine what features were relevant for the prediction. We show that patterns learnt by our model are aligned with the patterns experts use to assign spectra by visual inspection. In addition, we demonstrate that our approach uncovers new and non-intuitive patterns learnt by the neural network.
2 Methods
2.1 Data
We used the infrared spectra of small organic compounds from the Standard Reference Database Number 69, curated by the National Institute of Standards and Technology (NIST).51 The spectra were scraped from the web via the NIST API as in ref. 46. A total of 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 346 infrared spectra were available in the database; see ESI Fig. S1 and S2† for statistics on molecular size and composition. This initial pool was reduced to 8125 after preserving only gas-phase spectra and filtering out samples without a corresponding InChI (International Chemical Identifier) string. The spectra were preprocessed using simple transformations using an automated workflow procedure. First, we transformed all counts into absorbance units and all indexes into cm−1 units. Second, since the spectra differed in the range of wave numbers and sampling intervals, we applied a one-dimensional linear interpolation to transform every spectrum into a common x-axis of wave numbers, set between 400 and 4000 cm−1 and uniformly spaced at intervals of 4.2 cm−1. Third, we padded spectra narrower than the 400–4000 cm−1 range with zeros.
346 infrared spectra were available in the database; see ESI Fig. S1 and S2† for statistics on molecular size and composition. This initial pool was reduced to 8125 after preserving only gas-phase spectra and filtering out samples without a corresponding InChI (International Chemical Identifier) string. The spectra were preprocessed using simple transformations using an automated workflow procedure. First, we transformed all counts into absorbance units and all indexes into cm−1 units. Second, since the spectra differed in the range of wave numbers and sampling intervals, we applied a one-dimensional linear interpolation to transform every spectrum into a common x-axis of wave numbers, set between 400 and 4000 cm−1 and uniformly spaced at intervals of 4.2 cm−1. Third, we padded spectra narrower than the 400–4000 cm−1 range with zeros.
To obtain the target functional groups, we decoded the presence of functional groups from the InChI strings using a structural matching algorithm, feed with the substructural patterns expressed in SMILES arbitrary target specification syntax (SMARTS).52 Each functional group is encoded as a SMARTS pattern (see ESI Table S1†), which is used to search whether an InChI string encodes or not a particular functional group. Hence, for each InChI string we searched for 17 different SMARTS patterns, and encoded the results as a 17-element vector of “1”/“0”, representing the presence/absence of functional group in the InChI string. The algorithm matches a single molecule with multiple functional groups if they are present in the molecule; see the example of ethanol in Fig. S3.† This curated data pool was subsequently split randomly into 5687 (70%), 1218 (15%) and 1220 (15%) samples used for training, validation and testing, respectively. Data are then shuffled and randomly distributed to training, validation and test set. Spectra are normalised relative to their own maxima to be between 0 and 1.
2.2 Algorithm
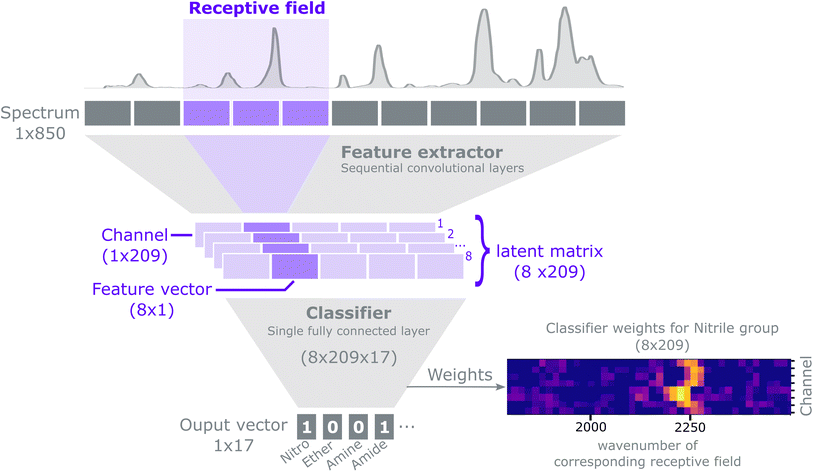
The purpose of this method is to predict the presence of functional groups (a discrete classification problem) given a spectrum. Each spectrum can potentially contain multiple functional groups, and we represent the predictions as a binary vector: y ∈ {0,1}.17For an extensive explanation of CNNs and common practices we refer to Goodfellow et al.53 Our model can conceptually be described as a feature extractor followed by a classifier, as shown in Fig. 2. The feature extractor consists of several 1-D convolutional layers that capture local and global patterns in a spectrum. Early convolutional layers learn simple patterns that are combined to recognise complex patterns in the subsequent layers. We use an architecture composed of convolutional layers with ReLU non-linearities and batch normalization54 interspersed with MaxPooling operations.21 The feature extractor outputs a latent matrix, i.e. a condensed representation of a spectrum, as learned during the training process. Each row in the matrix, a channel, models a specific spectral pattern (e.g. a peak). Each column in the matrix, a feature vector, attends to a specific spectral region; such region is called a receptive field. Stacking convolutional filters and MaxPool layers sequentially, effectively expands the size of the receptive field that each feature vector receives input from. The latent matrix is then flattened into a 1D vector by a Flatten layer and then fed to a classifier. The classifier consists of a single fully connected layer with sigmoid activation, which maps the flattened latent matrix into a format suitable to classify the presence of functional groups. The architecture of the CNN can be summarized in the following notation‡:
Conv(1, 4, 3, 1), ReLU, BatchNorm, Conv(4, 4, 3, 1), ReLU, BatchNorm, MaxPool(2),Conv(4, 8, 3, 1), ReLU, BatchNorm, Conv(8, 8, 3, 1), ReLU, MaxPool(2), BatchNorm, Flatten, Dense(1672, 17).
For the convolutional layers Conv(i, o, k, s), i, o, k, s, represent the number of input channels, output channels, kernel size and stride, respectively. For the MaxPool layers the numbers indicate the kernel size and stride. For the dense layer the first and second number indicate the number of inputs and outputs respectively. Zero padding is used for all layer types if it is applicable. The number of outputs of the dense layer is defined by the number of functional groups to be classified. The number of inputs to the dense layer is given by the number of channels, 8, times the length of the convolutional output, 209. Each receptive field is 16-elements wide with a stride of 4 elements, such that two adjacent inputs have an overlap of 12 elements. For a detailed explanation on how to compute the size of the receptive field for convolutional neural networks we refer to Araujo et al.55
Training the CNN involves updating its weights to improve its accuracy at detecting the presence of functional groups in the spectrum. In such a training scheme, gradients are computed for a batch at each update step by back-propagating the sum of the derivatives of the binary cross-entropy loss function as in eqn (1), applied to the value of the functional group prediction node yi for functional group index i, in a way equivalent to logistic regression. The loss is computed using the binary cross-entropy function:
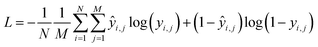 | (1) |
Some functional groups are only rarely present in the dataset, e.g., only 1.1% of the spectra originate from amide-containing molecules. As a result, the loss from the classes should be balanced during training such that their weights receive equal update signals from spectra with and without the functional group, i.e. spectra from the rarer group should be weighted more heavily. The proportion pj of class j is 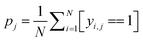 where N is the size of the training set, and yi,j is the class label for class j of sample i. We rebalance the loss resulting between labels indicating present/not present for the functional groups by introducing a loss reweighting factor that will reduce the loss impact of overrepresented functional groups. Overall, the loss reweighting factor becomes
where N is the size of the training set, and yi,j is the class label for class j of sample i. We rebalance the loss resulting between labels indicating present/not present for the functional groups by introducing a loss reweighting factor that will reduce the loss impact of overrepresented functional groups. Overall, the loss reweighting factor becomes
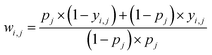 | (2) |
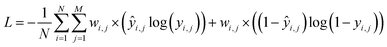 | (3) |
The model training was stopped after the validation loss had not improved for five concurrent epochs. Gradient updates were computed with the Adam optimization algorithm.56
2.3 Performance metrics
The loss is the quantity minimised during training of the neural network. However, understanding how this value relates to the success of the classification task can be challenging. It is therefore useful to compute and assess additional and more intuitive performance metrics. The accuracy is the proportion of correct predictions made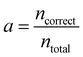 | (4) |
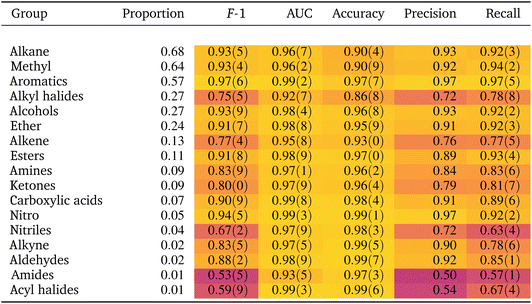
If the dataset is imbalanced, the overall accuracy may not give a complete description of the model performance. The model might perform well for some functional groups and poorly for others, as seen in Table 1. Computing additional metrics provides additional context on the way the model is performing. Precision quantifies the proportion of positive predictions made that were correct:
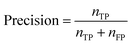 | (5) |
Recall quantifies the proportion of positive labels that were correctly predicted,
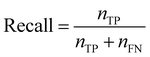 | (6) |
The F-1 score is the harmonic mean of the precision and recall,
 | (7) |
The AUC (area under the curve) is calculated as the area under the ROC (receiver operating characteristic) curve. The ROC curve is plotted as the rate of true positives over the rate of false positives when varying the classification threshold from 0 to 1. A model predicting the wrong result every time will get an AUC score of 0, a model predicting the right result every time will get an AUC score of 1. The AUC score is often used to indicate performance for imbalanced datasets as it is not dependent on the balance between the two classes.
2.4 A novel approach to explainability
In this section we outline how relevant insights about the classification are extracted from the neural network. Our approach to explainability is two-fold. We first identify the spectral patterns learnt by the network, i.e. peaks, shoulders, etc. Second, we inspect how relevant these patterns are to the classification of the individual functional groups. To the best of our knowledge, the proposed two-step approach represents a novel method to explain the inner workings of a CNN.To identify which patterns are typical and indicative for functional groups, we examine representative examples of those patterns from the dataset. For each channel, typical examples are subsets of a spectrum that maximize the corresponding feature variable in that channel. To identify those, we first extract the output of the final convolutional layer for the entire test set, resulting in a matrix with the shape [nSamples, nChannels, nFeatures] with nFeatures being the number of positional outputs of the last convolutional layer, i.e. the size of a channel vector.
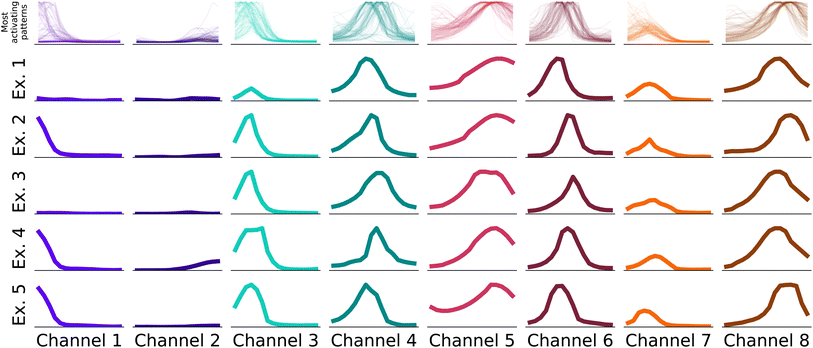
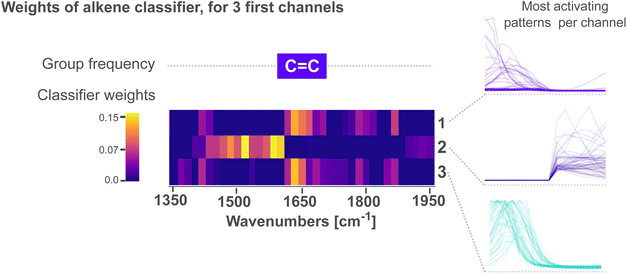
In the first step, we identify for each channel the 100 input samples with the highest output feature variables for this channel in the test set.§ The receptive fields causing the highest activation are linked to the feature variable activations by the structure of the neural network. We identify the most important patterns in the receptive fields, i.e. the parts of the spectrum that caused the high activations, and display them in Fig. 3.
The receptive fields span 16 elements in the input vector, which translate to windows of ca. 67 cm−1 width. Hence, as the receptive fields are small enough to consist e.g. of a single peak, the viewer can identify common patterns across a small number of examples as in Fig. 3. In Fig. 3 we show examples for all eight channels of the neural network. In the first row, the receptive fields that caused the highest output values of the feature extractor for the respective channel are displayed. In the rows below, we display examples randomly chosen from these 100 receptive fields. While not identical, it's evident that receptive fields within a single channel exhibit consistent patterns.
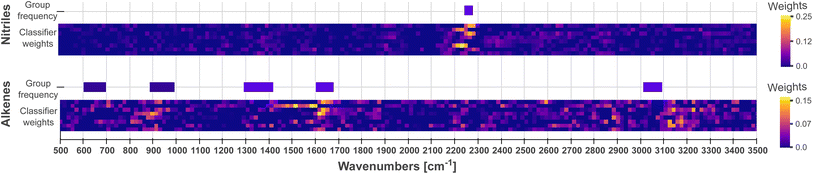
As the second step, we conduct an examination of the classifier (the final fully connected layer), which uses these patterns and their location in the spectra to carry out classifications. Each neuron in the classifier can be mapped to a channel and a feature vector in the latent matrix, which in turn can be mapped to a pattern (as in Fig. 3) and a wave number range in the input spectra, respectively. Therefore, a neuron exhibiting a high weight indicates that the pattern and spectral region associated to it have high importance when classifying a functional group. The output for each functional group is connected to the channel output of the CNN via [nChannels × nPositions] neurons. In Fig. 5, we visualize the weights for nitrile and alkene as a comparison. In particular, we see that the middle channels is important for both. From Fig. 3, we can identify those as a broad peak and a flat region.
By combining the learnt features and their connection to the prediction for each functional group, we can make concise statements about the patterns the CNN learnt such as “a peak at 2200 cm−1 is strongly correlated with nitrile”. These observational statements allow us to study whether the patterns the network uses compare well to empirical practices in spectrum identification, and further investigate instances where the CNN uses unexpected patterns.
3 Results and discussion
3.1 Model performance
As shown in Table 1 the model achieves good performance on most functional groups across most metrics. Compared to the F-1 score from the model of Fine et al.,44 considered state-of-the-art, our scores are slightly worse, which are nonetheless mostly within the range of the previous results (as compared to Table S5† in Fine et al.44). Other studies in the literature tackling the problem in similar ways, but providing only (worse) accuracy results, are not included in Table 2.46| Molecular perfection | Molecular F-1 | |
|---|---|---|
| Rieger, Wilson and Flores (ours) | 0.59(2) | 0.895(5) |
| Fine et al.44 | 0.63 | 0.905 |
Spectra classification is a multi-label problem, where each spectrum can correspond to more than one label (the functional group) and the classes are not mutually exclusive. Hence, to obtain a broader picture of model performance, we also compute two additional metrics, the molecular perfection and molecular F-1 defined in Fine et al.,44 which are designed to capture the ability of a model to correctly predict all functional groups of a molecule. Briefly, Molecular Perfection is the proportion of spectra in the test set for which the prediction of all functional groups is correct. For a definition of the molecular F-1 we refer to Fine et al.44. These metrics are computed for the functional groups listed in Table S1 (see ESI†).
Before analysing this comparison, we note a key difference between the approach used by Fine et al.44 and ours. The authors did not use a test set in their work and instead reported results on the validation set. Here, we randomly split the training/validation/test sets 70/15/15 and report results on the test set, following standard practice in machine learning research. In Table 2, we compare the molecular metrics between our approach and Fine et al.44 directly. We observe that the performance metrics are comparable, although our approach performs slightly worse. In return, our approach allows for human-understandable explanations both for individual decisions as well as patterns the CNN has learnt to classify functional groups. In Section 2.4.1, we explain how we utilize the bottleneck in the feature space to extract insights about the classification from the trained neural network, resulting in slightly worse predictive performance in return for increased interpretability, similar to findings in Koh et al.47.
Finally, our results were computed as the average across 10 seeded models. Table 1 also shows the standard deviation across the seeded models as values within parenthesis, with the precision of the last significant digit of the mean. The standard deviation values are low across most metrics and functional groups, indicating our model architecture yields consistent predictions across random initializations.
3.2 Consistency between neural networks
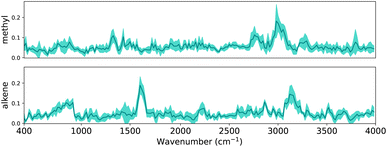
In Section 2.4.1, we outlined how explanations can be extracted from a trained CNN. In this section, we evaluate whether the same patterns are found across multiple CNNs. In Section 3 it is shown that the performance variance between CNN trained with different random seeds is small. To examine the difference between the trained CNNs, we can inspect either the patterns that have been learnt or inspect how aligned important locations are between CNNs. Since the first task requires assumptions about the commutability of channels, we focus on the alignment of locations. As a reminder, the final dense layer outputs the classification for each functional group, and has a weight matrix with dimensions 8 × 209 × 17. Since we are interested in the alignment of important locations, for each functional group we obtain the maximum of the weight matrix across all channels.Intuitively, if the differently seeded neural networks learnt similar important regions, the vectors with the dimensions 1 × 209 for each functional group will look similar across neural networks. To verify this, we visualize the linear layer weights for two exemplary functional groups in Fig. 6 (the extended version with all functional groups is shown in Fig. S4†). To facilitate better understanding we have mapped the dense layer weights back to the corresponding wave number scale in the input spectra, similar to Fig. 5. Since the inputs of the dense layer are normalized by the final batch normalization to have zero mean and standard deviation one, the dense layer weights indicate how much each region contributes to the final classification.
For each linear layer we plot the mean and standard deviation of the maximum value across the channels. We see that – on average – the CNNs highlight distinctive peaks for methyl and alkene groups, indicating these regions to be important when classifying the functional groups. The low standard deviation (as indicated by the shaded area around the mean) also indicates that all neural networks have learnt that e.g. the region around 3000 cm−1 – characteristic of C–H stretch – is important to classify methyl groups; likewise, the region around 1600 cm−1 – distinctive of C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretch – is important to classify alkenes.
C stretch – is important to classify alkenes.
We further note that the important regions emphasized by our CNNs compare well to those in Fine et al.,44e.g. the “alkene bending motion around 900 cm−1.”. We therefore conclude that CNNs learn consistent patterns across diversely seeded networks to classify functional groups, and these patterns seem related to characteristic group frequencies. In the following sections we will examine these patterns in depth using explainability methods.
3.3 Scientific insights by explainability
We compare the patterns learned by the CNN to those used by experts when carrying out spectrum assignment. Experts systematically examine the absorptions at group frequencies, i.e., the frequencies characteristic of a functional group. An initial discrimination focuses on peaks in sparse regions, e.g., above 3000 cm−1, or in regions with strong and distinctive absorptions, e.g., carbonyl groups found ca. 1700 cm−1. Whether absorptions are present or not in these regions rules out some functional groups. Further analysis might focus on examining the fingerprint region (400–1500 cm−1) used to uniquely recognize a compound; however, the fingerprint region is seldom used because it is typically crowded with a large number of peaks. Finally, experts use the evidence, previous knowledge on the sample and heuristic rules to assign a spectrum.![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N stretching vibrations from nitriles. The same applies to alkenes: even if the weight heatmap is not as clean as for nitriles, the classifier weights shown in Fig. 5 emphasize the spectral regions at ca. 1600 cm−1 and 3100 cm−1, which correspond to the group frequencies that characterize the stretching vibrations of C
N stretching vibrations from nitriles. The same applies to alkenes: even if the weight heatmap is not as clean as for nitriles, the classifier weights shown in Fig. 5 emphasize the spectral regions at ca. 1600 cm−1 and 3100 cm−1, which correspond to the group frequencies that characterize the stretching vibrations of C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bonds and C–H bonds, respectively. Fig. S6–S22† indeed show that most classifiers emphasize spectral regions in the receptive field where group frequencies are found. Crucially, CNNs initialized with different random seeds use the same patterns as shown and described in the example in Fig. 6. These observations provide qualitative assurances that the model will generalize well on unseen data, since it makes predictions based on meaningful patterns, i.e. the characteristic frequencies of functional groups.
C bonds and C–H bonds, respectively. Fig. S6–S22† indeed show that most classifiers emphasize spectral regions in the receptive field where group frequencies are found. Crucially, CNNs initialized with different random seeds use the same patterns as shown and described in the example in Fig. 6. These observations provide qualitative assurances that the model will generalize well on unseen data, since it makes predictions based on meaningful patterns, i.e. the characteristic frequencies of functional groups.
However, when we revisit the results for nitriles we note that, while the CNN has clearly learned the location of C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N vibrations, the precision, recall and F1 scores of the nitrile classifier are relatively poor (Table 1). Only 4% of the spectra come from nitrile compounds so it is possible that the dataset has too few instances of nitriles to learn other relevant features besides the main C
N vibrations, the precision, recall and F1 scores of the nitrile classifier are relatively poor (Table 1). Only 4% of the spectra come from nitrile compounds so it is possible that the dataset has too few instances of nitriles to learn other relevant features besides the main C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N band. Class imbalance is known to skew the classifier's bias towards the majority class.57 Hence the model misclassifies a substantial number of instances in the minority class, leading to poor precision and recall. This argument is further supported by the high AUC (0.97) which is a metric robust against class imbalance. Upon closer examination, however, even less represented classes such as alkynes and aldehydes (proportion 0.02, Table 1) are classified with better precision and recall scores than nitriles, suggesting that class imbalance is not the only reason for the poor classification metrics of nitriles; separability issues might also be at play. We expect functional groups with more and stronger characteristic IR bands to be easier to identify. Nitriles exhibit only a single and relatively weak distinctive vibration: the C
N band. Class imbalance is known to skew the classifier's bias towards the majority class.57 Hence the model misclassifies a substantial number of instances in the minority class, leading to poor precision and recall. This argument is further supported by the high AUC (0.97) which is a metric robust against class imbalance. Upon closer examination, however, even less represented classes such as alkynes and aldehydes (proportion 0.02, Table 1) are classified with better precision and recall scores than nitriles, suggesting that class imbalance is not the only reason for the poor classification metrics of nitriles; separability issues might also be at play. We expect functional groups with more and stronger characteristic IR bands to be easier to identify. Nitriles exhibit only a single and relatively weak distinctive vibration: the C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N stretching band. In contrast, both aldehydes and alkynes exhibit several characteristic bands, with comparatively stronger intensities, that might make them easier to classify. In short, the relatively poor classification performance of nitriles might be related not only to class imbalance, but also to an inherent difficulty to classify them as they exhibit only one weak characteristic band. These observations imply that, even if a classifier has learned the group frequencies, it might not produce accurate results given the class imbalance in the dataset and separability challenges between spectra.
N stretching band. In contrast, both aldehydes and alkynes exhibit several characteristic bands, with comparatively stronger intensities, that might make them easier to classify. In short, the relatively poor classification performance of nitriles might be related not only to class imbalance, but also to an inherent difficulty to classify them as they exhibit only one weak characteristic band. These observations imply that, even if a classifier has learned the group frequencies, it might not produce accurate results given the class imbalance in the dataset and separability challenges between spectra.
Fig. 4 zooms into the first three feature variables of the alkene classifier within 1350–1950 cm−1. The characteristic group frequency of alkene is added for comparison, alongside the patterns that lead to the strongest activation for each channel. We see in the figure that peaks followed by a tail (channels 1 and 3) activate the most above 1620 cm−1. In contrast, patterns of tails followed by a peak (channel 2) activate the most below 1620 cm−1. In all cases, the peak in the patterns is oriented towards the wave number where C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C vibrations are expected, while the tails orient away from this region. We interpret these patterns as the CNN learning to emphasize that ca. 1620 cm−1, a single peak – without any neighbors – is a characteristic to classify alkenes. For context, the C
C vibrations are expected, while the tails orient away from this region. We interpret these patterns as the CNN learning to emphasize that ca. 1620 cm−1, a single peak – without any neighbors – is a characteristic to classify alkenes. For context, the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C absorption bands ca. 1650 cm−1 are not the only ones within this region; a variety of vibrations from carbonyl C
C absorption bands ca. 1650 cm−1 are not the only ones within this region; a variety of vibrations from carbonyl C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bonds are also expected. Acyl halides, esters, aldehydes, carboxilic acids, ketones and amides, all share C
O bonds are also expected. Acyl halides, esters, aldehydes, carboxilic acids, ketones and amides, all share C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O absorptions ca. 1650 cm−1. Moreover, these absorptions are highly sensitive to the electronic environment in the vicinity of the bond, often resulting in many overlapping bands with complex shapes. As the region at ca. 1650 cm−1 is crowded with peaks from multiple functional groups, we believe the CNN places extra emphasis on distinguishing peaks from C
O absorptions ca. 1650 cm−1. Moreover, these absorptions are highly sensitive to the electronic environment in the vicinity of the bond, often resulting in many overlapping bands with complex shapes. As the region at ca. 1650 cm−1 is crowded with peaks from multiple functional groups, we believe the CNN places extra emphasis on distinguishing peaks from C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C vibrations – characteristic of alkenes – from those of C
C vibrations – characteristic of alkenes – from those of C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O vibrations. The network thus assigns high weights to tail-peak and peak-tail patterns that outline a single peak with no neighbors.
O vibrations. The network thus assigns high weights to tail-peak and peak-tail patterns that outline a single peak with no neighbors.
Not all activated regions on the classifier weights coincide with group frequencies. For instance, carboxylic acids have group frequencies within 1500–1700 cm−1, yet their network weights (Fig. S18†) show strong activations >3500 cm−1. This is expected given that carboxylic acids share with alcohols O–H bonds that vibrate at ca. 3570 cm−1, and both groups co-occur frequently in the dataset (Fig. S23†). Their activation weights are consequently similar.
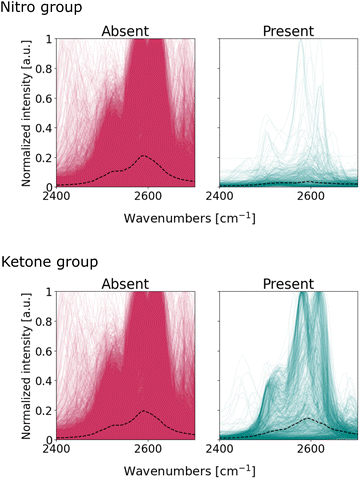
However, the same argument cannot be made for the nitro and ketone compounds. Their classifier weights share relatively strong activations between 2400 and 2700 cm−1, a region usually devoid of characteristic bands. At this point it is unclear what the CNN has learnt from this region since the region is activated across all channels, meaning it uses most patterns – peaks, peak shoulders, tails – to make classifications. We further investigate whether the network uses spurious patterns such as post-processing artifacts or non-apparent spectroscopic signals.
We visualize the spectra within the 2400–2700 cm−1, and segregate these into two subgroups: one where a particular functional group is present, the other where said functional group is absent. Fig. 7 illustrates the overlap of these subgroups for nitro and ketone groups; Fig. S24† completes the series for all functional groups. The spectra exhibit symmetric peaks of Lorentzian and pseudo-Voight lineshape, as expected from infrared absorption bands. Notably, there are no spurious patterns typical from spectral noise (e.g. outliers) nor from pre-processing (e.g. discontinuities or asymmetrical curves). We conclude that the patterns within the 2400–2700 cm−1 region originate from infrared absorption bands, even if these are not typically considered to be characteristic of functional groups. Bands within the 2400–2700 cm−1 are usually assigned to anharmonic vibrations: overtones that result from higher-energy harmonics of fundamental vibrations, or combination bands that derive from the simultaneous excitation of multiple vibrational modes in the molecule.58,59 These vibrations result in weak absorption bands in the spectrum and so experts seldom used them for molecule identification.7Fig. 7 suggests, however, that these bands are detectable and suitable enough for the CNN to make classification more certain.
The presence of bands within the 2400–2700 cm−1 region does not imply that they effectively discriminate between functional groups. For the case of ketones, the median intensity in Fig. 7 is similar for both spectra with and without the functional group. The role of these bands in the classifier's decision for ketones is unclear: the classifier exhibits high activations in this region, even if the spectra are not very different from each other upon visual inspection. On the other hand, the median lines for nitro subgroups are clearly different: the spectra of nitro-containing molecules exhibit – on average – fewer bands within 2400–2700 cm−1 compared to molecules without the nitro group. Therefore, these bands are suitable to distinguish spectra with and without nitro compounds, and thus explains the high attention the nitro classifier assigns to this region. In summary, our observations suggest that the CNN uses not only fundamental vibrations characteristic of the functional groups, but also overtone and combination bands, to maximize the accuracy of its classifications.
4 Conclusion
In this work we report on the development of a 1D convolutional neural network to classify the spectra of small organic molecules according to their functional groups. Despite being comparatively smaller than previously reported models, our 1D CNN classifies the presence of functional groups with performance metrics comparable to the state-of-the-art. We also demonstrate that our simplified model architecture provides consistent predictions across randomly initialized instances of the model, and consistently attends to the same spectral regions when classifying functional groups. We extend this investigation and analyse the patterns the neural network discovers in the spectral data. We employ a novel two-step explainability technique, where we visualize (i) the spectral patterns (lines, curves, peaks) strongly activating the latent representation of the spectra, and (ii) the receptive fields resulting in the most salient weights in the linear classifier. In combination, these analyses enable unraveling the location and shape of the spectral patterns that improve classification certainty. We find that many of the patterns learnt by the model are consistent with symmetric peaks at the location of the well-documented functional group frequencies, which provide qualitative assurances that the model will perform well on unseen data. Unexpectedly, the network also seems to use the absence of peaks and anharmonic molecular vibrations (overtones and combination bands) to make classifications. Our explainability approach also reveals potential limitations of the model. In nitriles, for instance, class imbalance and the presence of only one characteristic band result in poor classification accuracy, even if the CNN learns to attend to the C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N vibration band. In addition, the halide classifier attends to C–H wag vibrations due to their prevalence in the dataset, even if these vibrations are not intrinsic to the functional group. As a result, the nitrile and halide classifier might perform poorly in unseen data.
N vibration band. In addition, the halide classifier attends to C–H wag vibrations due to their prevalence in the dataset, even if these vibrations are not intrinsic to the functional group. As a result, the nitrile and halide classifier might perform poorly in unseen data.
More broadly, the patterns learnt by the CNN can be rationalized in terms of the principles of infrared absorption: chemical moieties absorb infrared light at characteristic group frequencies, such absorptions are peak-shaped, and might give rise to anharmonic siblings such as overtones and combination bands. This clear connection between physico-chemical principles and CNN patterns enables us to qualitatively assess the generalization abilities of the network, and further clears the path to leverage more chemical/physics-based knowledge in future model design. Physics-based intuition can be incorporated into the model, for example using IR tables to (smart-)initialize parameters, initializing filters that optimally recognize peaks, and/or transferring understanding from pretrained models60 to new datasets (potentially even from different spectral regions). Our results also highlight that bigger models are not always better; through a judicious balance between performance and explainability considerations, we deliver a predictive model that maintains transparency without compromising on predictive performance.
Data availability
The code used for this project is available at the public GitHub repository: https://github.com/laura-rieger/SpectraML-Classification.Conflicts of interest
There are no conflicts to declare.Notes and references
- J. C. Lindon, G. E. Tranter and D. Koppenaal, Encyclopedia of Spectroscopy and Spectrometry, Academic Press, 2016 Search PubMed.
- G. Gauglitz and D. S. Moore, Handbook of Spectroscopy, Wiley-VCH, Weinheim, 2014, vol. 1 Search PubMed.
- M. H. Penner, Food Analysis, Springer, 2017, pp. 79–88 Search PubMed.
- J. I. Steinfeld, Molecules and Radiation: An Introduction to Modern Molecular Spectroscopy, Courier Corporation, 2012 Search PubMed.
- W. Zhou, Y. Ying and L. Xie, Appl. Spectrosc. Rev., 2012, 47, 654–670 CrossRef.
- V. Barone, S. Alessandrini, M. Biczysko, J. R. Cheeseman, D. C. Clary, A. B. McCoy, R. J. DiRisio, F. Neese, M. Melosso and C. Puzzarini, Nat. Rev. Methods Primers, 2021, 1, 1–27 CrossRef.
- J. Coates, in Interpretation of Infrared Spectra, A Practical Approach, John Wiley & Sons Ltd, Chichester, 2000, pp. 10815–10837 Search PubMed.
- Å. Rinnan, Anal. Methods, 2014, 6, 7124–7129 RSC.
- G. Schulze, A. Jirasek, M. Marcia, A. Lim, R. F. Turner and M. W. Blades, Appl. Spectrosc., 2005, 59, 545–574 CrossRef CAS PubMed.
- T. Specht, H. Hasse and F. Jirasek, J. Chem. Inf. Model., 2021, 61, 143–155 CrossRef CAS PubMed.
- Y. Wei, R. S. Varanasi, T. Schwarz, L. Gomell, H. Zhao, D. J. Larson, B. Sun, G. Liu, H. Chen and D. Raabe, et al. , Patterns, 2021, 2, 100192 CrossRef CAS PubMed.
- R. Nalla, R. Pinge, M. Narwaria and B. Chaudhury, Proceedings of the ACM India Joint International Conference on Data Science and Management of Data, 2018, pp. 201–209 Search PubMed.
- U. Sharaha, E. Rodriguez-Diaz, O. Sagi, K. Riesenberg, I. Lapidot, Y. Segal, I. J. Bigio, M. Huleihel and A. Salman, Anal. Chem., 2019, 91, 2525–2530 CrossRef CAS PubMed.
- A. Angulo, L. Yang, E. S. Aydil and M. A. Modestino, Digital Discovery, 2022, 1, 35–44 RSC.
- L. DeNoyer and J. G. Dodd, Handbook of Vibrational Spectroscopy, 2006 Search PubMed.
- A. Travert and C. Fernandez, SpectroChemPy, a framework for processing, analyzing and modeling spectroscopic data for chemistry with Python, 2022, https://github.com/spectrochempy/spectrochempy.
- C. Le Losq, Rampy: a Python library for processing spectroscopic (IR, Raman, XAS...) data, Zenodo, 2018 Search PubMed.
- E. Flores, N. Mozhzhukhina, X. Li, P. Norby, A. Matic and T. Vegge, Chem.: Methods, 2022, e202100094 CAS.
- L. Chen, S. Li, Q. Bai, J. Yang, S. Jiang and Y. Miao, Remote Sens., 2021, 13, 4712 CrossRef.
- A. Krizhevsky, I. Sutskever and G. E. Hinton, Adv. Neural Inf. Process. Syst., 2012, 1–9 Search PubMed.
- K. Simonyan, A. Vedaldi and A. Zisserman, arXiv preprint arXiv:1312.6034, 2013.
- M. T. Ribeiro, S. Singh and C. Guestrin, Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, 2016, pp. 1135–1144 Search PubMed.
- L. Rieger, P. Chormai, G. Montavon, L. K. Hansen and K.-R. Müller, Explainable and Interpretable Models in Computer Vision and Machine Learning, 2018, pp. 115–131 Search PubMed.
- J. Yang, J. Xu, X. Zhang, C. Wu, T. Lin and Y. Ying, Anal. Chim. Acta, 2019, 1081, 6–17 CrossRef CAS PubMed.
- C. Zhang, Y. Idelbayev, N. Roberts, Y. Tao, Y. Nannapaneni, B. M. Duggan, J. Min, E. C. Lin, E. C. Gerwick and G. W. Cottrell, et al. , Sci. Rep., 2017, 7, 1–17 CrossRef PubMed.
- F. Lussier, V. Thibault, B. Charron, G. Q. Wallace and J.-F. Masson, TrAC, Trends Anal. Chem., 2020, 124, 115796 CrossRef CAS.
- L.-N. Li, X.-F. Liu, F. Yang, W.-M. Xu, J.-Y. Wang and R. Shu, Spectrochim. Acta, Part B, 2021, 180, 106183 CrossRef CAS.
- D. D. Matyushin, A. Y. Sholokhova and A. K. Buryak, Anal. Chem., 2020, 92, 11818–11825 CrossRef CAS PubMed.
- L. Pan, P. Zhang, C. Daengngam, S. Peng and M. Chongcheawchamnan, J. Raman Spectrosc., 2021, 6–19 Search PubMed.
- B. Debus, H. Parastar, P. Harrington and D. Kirsanov, TrAC, Trends Anal. Chem., 2021, 116459 CrossRef CAS.
- J. Liu, M. Osadchy, L. Ashton, M. Foster, C. J. Solomon and S. J. Gibson, Analyst, 2017, 142, 4067–4074 RSC.
- J. Zhu, A. S. Sharma, J. Xu, Y. Xu, T. Jiao, Q. Ouyang, H. Li and Q. Chen, Spectrochim. Acta, Part A, 2021, 246, 118994 CrossRef CAS PubMed.
- J. Acquarelli, T. van Laarhoven, J. Gerretzen, T. N. Tran, L. M. Buydens and E. Marchiori, Anal. Chim. Acta, 2017, 954, 22–31 CrossRef CAS PubMed.
- S. Malek, F. Melgani and Y. Bazi, J. Chemom., 2018, 32, e2977 CrossRef.
- X. Zhang, T. Lin, J. Xu, X. Luo and Y. Ying, Anal. Chim. Acta, 2019, 1058, 48–57 CrossRef CAS PubMed.
- M. R. Carbone, S. Yoo, M. Topsakal and D. Lu, Phys. Rev. Mater., 2019, 3, 033604 CrossRef CAS.
- R. Roscher, B. Bohn, M. F. Duarte and J. Garcke, IEEE Access, 2020, 8, 42200–42216 Search PubMed.
- N. M. Ralbovsky and I. K. Lednev, Chem. Soc. Rev., 2020, 49, 7428–7453 RSC.
- S. Mittal, T. P. Wrobel, M. Walsh, A. Kajdacsy-Balla and R. Bhargava, Clinical Spectroscopy, 2021, 3, 100006 CrossRef.
- L. Rieger, C. Singh, W. Murdoch and B. Yu, International Conference on Machine Learning, 2020, pp. 8116–8126 Search PubMed.
- A. J. DeGrave, J. D. Janizek and S.-I. Lee, Nat. Mach. Intell., 2021, 3, 610–619 CrossRef.
- M. M. Bejani and M. Ghatee, Artif. Intell. Rev., 2021, 1–48 Search PubMed.
- K. Judge, C. W. Brown and L. Hamel, Anal. Chem., 2008, 80, 4186–4192 CrossRef CAS PubMed.
- J. A. Fine, A. A. Rajasekar, K. P. Jethava and G. Chopra, Chem. Sci., 2020, 11, 4618–4630 RSC.
- J. Springenberg, A. Dosovitskiy, T. Brox and M. Riedmiller, ICLR (Workshop Track), 2015 Search PubMed.
- A. A. Enders, N. M. North, C. M. Fensore, J. Velez-Alvarez and H. C. Allen, Anal. Chem., 2021, 93, 9711–9718 CrossRef CAS PubMed.
- P. W. Koh, T. Nguyen, Y. S. Tang, S. Mussmann, E. Pierson, B. Kim and P. Liang, International Conference on Machine Learning, 2020, pp. 5338–5348 Search PubMed.
- L. Sixt, M. Granz and T. Landgraf, International Conference on Machine Learning, 2020, pp. 9046–9057 Search PubMed.
- J. Adebayo, J. Gilmer, M. Muelly, I. Goodfellow, M. Hardt and B. Kim, Adv. Neural Inf. Process. Syst., 2018, 31, 1–11 Search PubMed.
- K. O'Shea and R. Nash, arXiv preprint arXiv:1511.08458, 2015.
- N. I. of Standards and Technology, NIST Standard Reference Database Number 69, 2022, https://webbook.nist.gov/chemistry/, data retrieved from https://webbook.nist.gov/chemistry/.
- G. Landrum, P. Tosco, B. Kelley, Ric, sriniker, gedeck, R. Vianello, NadineSchneider, E. Kawashima, A. Dalke, D. N. D. Cosgrove, B. Cole, M. Swain, S. Turk, AlexanderSavelyev, G. Jones, A. Vaucher, M. Wójcikowski, I. Take, D. Probst, K. Ujihara, V. F. Scalfani, guillaume godin, A. Pahl and F. Berenger, JLVarjo, strets123, JP and DoliathGavid, rdkit/rdkit: 2021_09_5 (Q3 2021) Release, 2022, DOI:10.5281/zenodo.6330241.
- I. Goodfellow, Y. Bengio and A. Courville, Deep Learning, MIT Press, 2016 Search PubMed.
- S. Ioffe and C. Szegedy, International Conference on Machine Learning, 2015, pp. 448–456 Search PubMed.
- A. Araujo, W. Norris and J. Sim, Distill, 2019, e21 Search PubMed.
- D. P. Kingma and J. Ba, arXiv preprint arXiv:1412.6980, 2014.
- V. García, J. Sánchez and R. Mollineda, Knowl. Base Syst., 2012, 25, 13–21 CrossRef.
- D. Lin-Vien, N. B. Colthup, W. G. Fateley and J. G. Grasselli, The Handbook of Infrared and Raman Characteristic Frequencies of Organic Molecules, Elsevier, 1991 Search PubMed.
- V. Barone, S. Alessandrini, M. Biczysko, J. R. Cheeseman, D. C. Clary, A. B. McCoy, R. J. DiRisio, F. Neese, M. Melosso and C. Puzzarini, Nat. Rev. Methods Primers, 2021, 1, 38 CrossRef CAS.
- O. Vinyals, C. Blundell, T. Lillicrap and D. Wierstra, et al. , Adv. Neural Inf. Process. Syst., 2016, 29, 1–9 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3dd00203a |
| ‡ The code to further inspect the architecture and reproduce the results is available at https://github.com/laura-rieger/SpectraML-Classification. |
| § The number was chosen ad-hoc. Considering the ≈1.200 spectra in the test set, each with 209 receptive windows (∼240.000 samples), we consider the top 0.04% examples. |
| This journal is © The Royal Society of Chemistry 2023 |