Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Multi-fidelity Bayesian optimization of covalent organic frameworks for xenon/krypton separations†
Nickolas
Gantzler
a,
Aryan
Deshwal
b,
Janardhan Rao
Doppa
*b and
Cory M.
Simon
 *c
*c
aDepartment of Physics, Oregon State University, Corvallis, OR, USA
bSchool of Electrical Engineering and Computer Science, Washington State University, Pullman, WA, USA. E-mail: jana.doppa@wsu.edu
cSchool of Chemical, Biological, and Environmental Engineering, Oregon State University, Corvallis, OR, USA. E-mail: cory.simon@oregonstate.edu
First published on 16th October 2023
Abstract
Our objective is to search a large candidate set of covalent organic frameworks (COFs) for the one with the largest equilibrium adsorptive selectivity for xenon (Xe) over krypton (Kr) at room temperature. To predict the Xe/Kr selectivity of a COF structure, we have access to two molecular simulation techniques: (1) a high-fidelity, binary grand canonical Monte Carlo simulation and (2) a low-fidelity Henry coefficient calculation that (a) approximates the adsorbed phase as dilute and, consequently, (b) incurs a smaller computational runtime than the higher-fidelity simulation. To efficiently search for the COF with the largest high-fidelity Xe/Kr selectivity, we employ a multi-fidelity Bayesian optimization (MFBO) approach. MFBO constitutes a sequential, automated feedback loop of (1) conduct a low- or high-fidelity molecular simulation of Xe/Kr adsorption in a COF, (2) use the simulation data gathered thus far to train a surrogate model that cheaply predicts, with quantified uncertainty, the low- and high-fidelity simulated Xe/Kr selectivity of COFs from their structural/chemical features, then (3) plan the next simulation (i.e., choose the next COF and fidelity) in consideration of balancing exploration, exploitation, and cost. We find that MFBO acquires the optimal COF among the candidate set of 609 structures using only 30 low-fidelity and seven high-fidelity simulations, incurring only 2%, 4% on average, and 20% on average of the computational runtime of a single-[high-]fidelity exhaustive, random, and BO search, respectively.
Introduction
Bayesian optimization for materials discovery
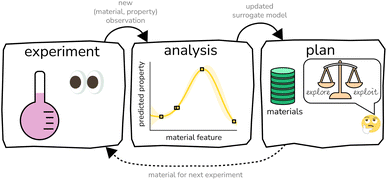
The discovery and development of new materials is vital for both sustaining and technologically-advancing our society. Computational methods, including electronic structure calculations, molecular simulations, and materials informatics/machine learning, can predict the properties of materials and thus be employed to optimize, screen, and design new materials rapidly and cost-effectively—accelerating the rate of materials optimization and discovery.1–6Bayesian optimization (BO)7–10 combines supervised machine learning, uncertainty quantification, and decision-making algorithms to automatically and efficiently design a sequence of experiments—in the lab or a computer simulation—to find materials with an optimal property for some application.11–13 Given (i) a pool or constructed space14 of candidate materials and (ii) an experimental protocol—in the lab or a simulation—to measure/evaluate/predict the relevant property of a material, BO iteratively designs experiments (i.e., chooses materials to synthesize then subject to a measurement) to find the optimal material with the fewest costly experiments. The two ingredients of BO for iterative, automated experiment planning are:
• A surrogate model, a supervised machine learning model that computationally predicts—inexpensively, and with quantified uncertainty—the property of any material from its compositional, chemical, and/or structural features. This model serves as a surrogate for the experiment by approximating the structure–property relationship of the materials.
• An acquisition function, which uses the surrogate model to score the utility of each material for the next experiment. The acquisition function is designed to balance (i) exploitation (“acquire a material with the optimal predicted property”) to greedily pursue the material we believe may be optimal under the limited information we currently possess and (ii) exploration (“acquire a material whose predicted property is highly uncertain”) to gather more information about the structure–property relationship.
The experiment–analysis–plan feedback loop15 that constitutes BO (see Fig. 1) iterates through (i) conduct an experiment to obtain a (material, property) observation, (ii) update the surrogate model in light of this new experimental data, then (iii) select the next material for an experiment by maximizing the acquisition function. BO accounts for all data observed thus far, summarizes the information in the data with a surrogate model, then leverages the surrogate model to make principled decisions of which material to pursue for the next experiment. By design, BO tends to acquire the optimal material much earlier in the sequential search than random search; hence, it provides value by allowing us to find the optimal material with many fewer costly and time-consuming experiments than a random or exhaustive search.
Because the acquisition function paired with an optimization algorithm negates the need for humans to design the experiments inside the experiment–analysis–plan feedback loop, BO can orchestrate autonomous, “self-driving” labs15–22 that employ automated instrumentation and/or robots to conduct a sequence of experiments with the goal of resource-efficient materials discovery and optimization.
BO has been deployed for the optimization and discovery of many different materials12,23–26 in the lab or a computer simulation, including nanoporous materials,27–31 nanoparticles,32 light emitting diodes,33 carbon nanotubes,34 photovoltaics,35–37 additively manufactured structures,38 polymers,39–43 thermoelectrics,44 anti-microbial active surfaces,45 quantum dots,46 luminescent materials,47 catalysts,48–52 thin films,53 solid chemical propellants,54 alloys,55 and phase-change memory materials.56 More, BO has been used to optimize processes to synthesize materials and chemicals57–63 or to employ materials for an industrial-scale task.64
Multi-fidelity Bayesian optimization for materials discovery
Often, we have multiple options of different experiments to measure/evaluate/predict the relevant property of the material—experiments that trade (1) fidelity, i.e. the extent to which the experiment faithfully measures/evaluates/predicts the property of the material, for (2) affordability. For example, a computer simulation is usually a low-fidelity and -cost estimation of the material property compared to a high-fidelity and -cost measurement of the material property in the laboratory.Multi-fidelity Bayesian optimization (MFBO)10,65–71 takes advantage of multiple types of experiments that trade fidelity and affordability to search for a material with an optimal property while incurring the minimal cost.72 MFBO modifies the experiment–analysis–plan loop of standard BO in Fig. 1 by extending: (i) the surrogate model, to (a) predict the property of materials according to experiments of all fidelities and (b) capture the correlations between the material properties according to the experiments of varying fidelity, enabling observed outcomes of low-fidelity experiments to inform predicted outcomes of high-fidelity experiments, and (ii) the acquisition function, to pick the next material and the next experimental fidelity, while balancing exploration, exploitation, and the cost of the different experiments. In turn, MFBO leverages low-fidelity experiments to cheaply scope out which regions of materials space contain (i) poor-performing materials, to avoid wasting resources on high-fidelity experiments there, and (ii) high-performing materials, to focus high-fidelity experiments there. MFBO (or its parent, multi-information-source BO73) has been scarcely applied to materials discovery.72,74–77
Our contribution
In this work, we employ MFBO to search a pool of ∼600 covalent organic framework (COF) crystal structures78 for the one with the highest simulated xenon/krypton selectivity at room temperature, while incurring the minimal computational expense. We are armed with two molecular simulation methods to predict the Xe/Kr selectivity of a COF: (higher-fidelity & -cost) Markov-chain Monte Carlo simulation of the binary grand-canonical ensemble, where the COF hosts multiple adsorbates (both Xe and Kr) during the simulation; and, (lower-fidelity & -cost) Monte Carlo integration to calculate the Xe and Kr Henry coefficients in the COF, which makes the dilute approximation, so the COF hosts only a single adsorbate during the simulation. Our task constitutes solving an optimization problem (objective function = high-fidelity Xe/Kr selectivity) over a finite set of materials14 with access to bi-fidelity molecular simulations to evaluate the material property. Our MFBO routine employs (i) a multi-fidelity Gaussian process (GP)69 surrogate model to predict the simulated Xe/Kr selectivity of a COF from its structural and chemical features and (ii) a cost-aware, multi-fidelity expected improvement79 acquisition function to design the next simulation. MFBO acquires the COF with the largest high-fidelity simulated Xe/Kr selectivity using only 30 low- and seven high-fidelity simulations, incurring only 2%, 4% on average, and 20% on average of the computational run time of a single-fidelity exhaustive, random, and BO search, respectively, using only high-fidelity simulations. More, MFBO robustly out-performs single-fidelity BO, over randomly chosen COFs used to initialize the surrogate model. Our results demonstrate the promise of MFBO to cost-effectively discover materials for a variety of applications when in possession of multiple options of laboratory experiments and/or computer simulations, that trade fidelity for affordability, to measure/evaluate/predict the property of materials.COFs for Xe/Kr separations
Results
Problem setup
We possess a candidate set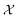 of 609 experimentally-reported covalent organic frameworks (COFs)78 for the task of Xe/Kr separations (at this point, abstractly think of
of 609 experimentally-reported covalent organic frameworks (COFs)78 for the task of Xe/Kr separations (at this point, abstractly think of 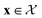 as the crystal structure of a COF. Later, we construct a continuous vector space in which COFs abstractly lie;14 then, x is instead a vector representation of the COF, listing features of its crystal structure that are relevant to Xe/Kr adsorption). Our objective is to find the COF
as the crystal structure of a COF. Later, we construct a continuous vector space in which COFs abstractly lie;14 then, x is instead a vector representation of the COF, listing features of its crystal structure that are relevant to Xe/Kr adsorption). Our objective is to find the COF 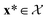 that exhibits the highest equilibrium adsorptive Xe/Kr selectivity (:=y) when immersed in a 20 mol%/80 mol% Xe/Kr mixture at 1 bar and 298 K.
that exhibits the highest equilibrium adsorptive Xe/Kr selectivity (:=y) when immersed in a 20 mol%/80 mol% Xe/Kr mixture at 1 bar and 298 K.
To computationally predict the Xe/Kr selectivity of a COF, we are armed with two different molecular simulation techniques. Each molecular simulation employs Lennard-Jones interatomic potentials (parameters from Universal Force Field103) to describe the potential energy of a configuration of a rigid COF hosting Xe and/or Kr adsorbate(s). Given a COF, our choice of which simulation to perform to predict its Xe/Kr selectivity involves a trade-off between fidelity and computational runtime.
 High-fidelity
High-fidelity  simulation. Run-time: ca. 230 min.
The high-fidelity simulation constitutes a Markov chain Monte Carlo (MC) simulation of the COF in the binary grand-canonical (BGC) ensemble. During the molecular simulation of adsorption in the COF, generally the COF hosts both and multiple Xe and Kr adsorbates; these adsorbates [implicitly] enter/leave the COF from/to the gas phase and move around in the pores of the COF. The key measurable during the BGCMC simulation is the average number of adsorbates in the COF system, 〈n〉, with n := [nXe, nKr]. Our high-fidelity prediction of the adsorptive Xe/Kr selectivity of the COF is then
simulation. Run-time: ca. 230 min.
The high-fidelity simulation constitutes a Markov chain Monte Carlo (MC) simulation of the COF in the binary grand-canonical (BGC) ensemble. During the molecular simulation of adsorption in the COF, generally the COF hosts both and multiple Xe and Kr adsorbates; these adsorbates [implicitly] enter/leave the COF from/to the gas phase and move around in the pores of the COF. The key measurable during the BGCMC simulation is the average number of adsorbates in the COF system, 〈n〉, with n := [nXe, nKr]. Our high-fidelity prediction of the adsorptive Xe/Kr selectivity of the COF is then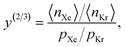 | (1) |
 Low-fidelity
Low-fidelity 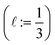 simulation. Run-time: ca. 15 min.
The low-fidelity prediction of the Xe/Kr selectivity of a COF relies on the dilute approximation in the BGC ensemble and models adsorption in the COF with Henry's law
simulation. Run-time: ca. 15 min.
The low-fidelity prediction of the Xe/Kr selectivity of a COF relies on the dilute approximation in the BGC ensemble and models adsorption in the COF with Henry's law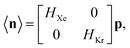 | (2) |
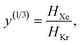 | (3) |
See Methods for details about both molecular simulation techniques.
Given access to (only) these two molecular simulation techniques that trade fidelity and computational runtime, we reframe the objective as:
 Find the COF
Find the COF 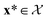 with the highest adsorptive Xe/Kr selectivity according to the high-fidelity BGCMC simulation, y(2/3), while incurring the minimal computational cost, measured by the sum of run times of the (both low- and high-fidelity) simulations we conduct to find x*.
with the highest adsorptive Xe/Kr selectivity according to the high-fidelity BGCMC simulation, y(2/3), while incurring the minimal computational cost, measured by the sum of run times of the (both low- and high-fidelity) simulations we conduct to find x*.
Multi-fidelity Bayesian optimization (MFBO) of COFs for Xe/Kr separations
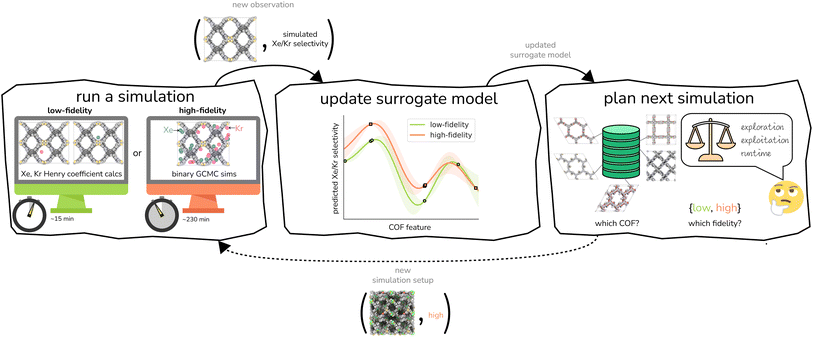
We provide an overview of multi-fidelity Bayesian optimization (MFBO) to efficiently find the COF with the largest high-fidelity Xe/Kr selectivity. that lies in a continuous space, listing its following structural (computed from Zeo++105) and compositional features derived from its crystal structure: density, gravimetric surface area, void fraction, largest included sphere diameter, and mole-fractions of metals, halogens, phosphorus, sulfur, nitrogen, silicon, hydrogen, carbon, oxygen, and boron. See Fig. 3. We min–max normalized the features.
that lies in a continuous space, listing its following structural (computed from Zeo++105) and compositional features derived from its crystal structure: density, gravimetric surface area, void fraction, largest included sphere diameter, and mole-fractions of metals, halogens, phosphorus, sulfur, nitrogen, silicon, hydrogen, carbon, oxygen, and boron. See Fig. 3. We min–max normalized the features.
 Simulation.
We conduct either a low- or high-fidelity simulation of Xe/Kr adsorption in a COF structure to obtain its predicted Xe/Kr selectivity. This generates a new data point—a COF structure “labeled” with its simulated Xe/Kr selectivity under that fidelity.
Simulation.
We conduct either a low- or high-fidelity simulation of Xe/Kr adsorption in a COF structure to obtain its predicted Xe/Kr selectivity. This generates a new data point—a COF structure “labeled” with its simulated Xe/Kr selectivity under that fidelity.
 Analysis.
We use this new data point to update our surrogate model of the simulations. This surrogate model is a supervised machine learning model that can, with negligible computational runtime, predict both the low- and high-fidelity simulated Xe/Kr selectivity of a COF not simulated before—and quantify uncertainty in this prediction. The inputs to the surrogate model for its prediction about a COF are (cheaply computed) structural and chemical features of its crystal structure. The surrogate model is trained on all labeled data—i.e., all (COF features, simulated Xe/Kr selectivity) pairs—gathered from simulations we have conducted thus far in the search. Thus, the surrogate model summarizes our knowledge, thus far in the search, about (i) the relationship between (a) the structural and chemical features of the COFs and (b) their simulated Xe/Kr selectivity and (ii) correlations between the low- and high-fidelity simulated Xe/Kr selectivities.
Analysis.
We use this new data point to update our surrogate model of the simulations. This surrogate model is a supervised machine learning model that can, with negligible computational runtime, predict both the low- and high-fidelity simulated Xe/Kr selectivity of a COF not simulated before—and quantify uncertainty in this prediction. The inputs to the surrogate model for its prediction about a COF are (cheaply computed) structural and chemical features of its crystal structure. The surrogate model is trained on all labeled data—i.e., all (COF features, simulated Xe/Kr selectivity) pairs—gathered from simulations we have conducted thus far in the search. Thus, the surrogate model summarizes our knowledge, thus far in the search, about (i) the relationship between (a) the structural and chemical features of the COFs and (b) their simulated Xe/Kr selectivity and (ii) correlations between the low- and high-fidelity simulated Xe/Kr selectivities.
 Plan.
Completing the loop, we judiciously select the (a) COF and (b) fidelity for the next simulation. An acquisition function relies on the surrogate model to score each (COF, fidelity) pair according to its appeal for the next simulation; the plan for the new simulation follows from the (COF, fidelity) pair with the maximal score. The acquisition function is designed to balance three often competing desires: (i) exploitation, to select a COF that the surrogate model predicts to have a large high-fidelity simulated Xe/Kr selectivity; (ii) exploration, to select a COF with a high-fidelity simulated Xe/Kr selectivity about which the surrogate model is highly uncertain; and (iii) cost reduction, which incentivizes choosing a low-fidelity simulation that provides useful but incomplete information about the high-fidelity selectivity.
Plan.
Completing the loop, we judiciously select the (a) COF and (b) fidelity for the next simulation. An acquisition function relies on the surrogate model to score each (COF, fidelity) pair according to its appeal for the next simulation; the plan for the new simulation follows from the (COF, fidelity) pair with the maximal score. The acquisition function is designed to balance three often competing desires: (i) exploitation, to select a COF that the surrogate model predicts to have a large high-fidelity simulated Xe/Kr selectivity; (ii) exploration, to select a COF with a high-fidelity simulated Xe/Kr selectivity about which the surrogate model is highly uncertain; and (iii) cost reduction, which incentivizes choosing a low-fidelity simulation that provides useful but incomplete information about the high-fidelity selectivity.
 In practice, we cannot know for certain when we have recovered the optimal COF. Possible strategies to terminate the iterative MFBO search include when: (i) computational resources are exhausted, (ii) a COF with a sufficiently large high-fidelity Xe/Kr selectivity has been recovered, or (iii) a large runtime has elapsed since we last discovered a COF with an improved high-fidelity Xe/Kr selectivity over those COFs we have acquired thus far.
In practice, we cannot know for certain when we have recovered the optimal COF. Possible strategies to terminate the iterative MFBO search include when: (i) computational resources are exhausted, (ii) a COF with a sufficiently large high-fidelity Xe/Kr selectivity has been recovered, or (iii) a large runtime has elapsed since we last discovered a COF with an improved high-fidelity Xe/Kr selectivity over those COFs we have acquired thus far.
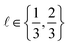 simulated Xe/Kr selectivity of a COF represented by x,
simulated Xe/Kr selectivity of a COF represented by x, 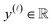 , as a realization of a random variable Y(
, as a realization of a random variable Y(![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) )(x). The surrogate model specifies a probability density for Y(
)(x). The surrogate model specifies a probability density for Y(![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) )(x). Suppose we have conducted n iterations of MFBO and possess simulation data
)(x). Suppose we have conducted n iterations of MFBO and possess simulation data 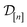 composed of ((COF feature vector, simulation fidelity), simulated Xe/Kr selectivity) pairs:
composed of ((COF feature vector, simulation fidelity), simulated Xe/Kr selectivity) pairs: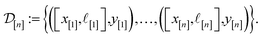 | (4) |
Under a Bayesian perspective, the posterior probability density of 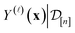 reflects our beliefs, grounded by the simulation data
reflects our beliefs, grounded by the simulation data 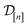 collected thus far, about the fidelity-
collected thus far, about the fidelity-![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) simulated Xe/Kr selectivity of the COF represented by x. This density concentrates in the region of the line where we believe the selectivity of the COF lies, and the spread of this density reflects our uncertainty about the selectivity of the COF. The mean of the posterior density of the conditional random variable
simulated Xe/Kr selectivity of the COF represented by x. This density concentrates in the region of the line where we believe the selectivity of the COF lies, and the spread of this density reflects our uncertainty about the selectivity of the COF. The mean of the posterior density of the conditional random variable 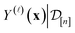 is a point-prediction of the fidelity-
is a point-prediction of the fidelity-![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) Xe/Kr selectivity of COF x, and the variance of it is a measure of our uncertainty about the predicted selectivity. The density of
Xe/Kr selectivity of COF x, and the variance of it is a measure of our uncertainty about the predicted selectivity. The density of 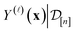 is particularly valuable for a COF-fidelity pair (x,
is particularly valuable for a COF-fidelity pair (x, ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) ) absent from the simulation data
) absent from the simulation data 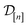 , since then we can use the predictions to decide if this simulation is worth doing next.
, since then we can use the predictions to decide if this simulation is worth doing next.
We adopt a multi-fidelity Gaussian process (GP)69,106,107 surrogate model:
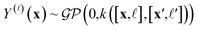 | (5) |
![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) ) and (x′,
) and (x′, ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) ′) as a scaled (by factor α, a hyperparameter) product of a symmetric material and fidelity kernel function:
′) as a scaled (by factor α, a hyperparameter) product of a symmetric material and fidelity kernel function: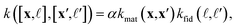 | (6) |
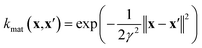 | (7) |
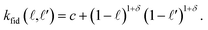 | (8) |
• The material kernel function 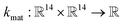 is a squared exponential kernel with a length-scale hyperparameter γ. Roughly, kmat quantifies the similarity between any pair of COFs. If two COFs are nearby in COF space, they are declared to be similar by the kernel; γ modulates how close two COFs must be to be declared “nearby”.
is a squared exponential kernel with a length-scale hyperparameter γ. Roughly, kmat quantifies the similarity between any pair of COFs. If two COFs are nearby in COF space, they are declared to be similar by the kernel; γ modulates how close two COFs must be to be declared “nearby”.
• The fidelity kernel function 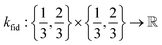 is a down-sampling kernel69,108 with offset and power hyperparameters c and δ. Roughly, kfid quantifies the similarity between any pair of simulation fidelities. It can take on only three distinct values—expressing the low–low, high–high, and low–high fidelity simulation similarities.
is a down-sampling kernel69,108 with offset and power hyperparameters c and δ. Roughly, kfid quantifies the similarity between any pair of simulation fidelities. It can take on only three distinct values—expressing the low–low, high–high, and low–high fidelity simulation similarities.
Empirically, GPs tend to be effective surrogate models for Bayesian optimization of molecules in the small-data regime.109
In Methods, we precisely explain the meaning behind the notation of the multi-fidelity GP in eqn (5), following the Bayesian paradigm110 of (i) specifying a prior distribution, (ii) collecting the simulation data, then (iii) updating the prior to a posterior distribution. The resulting posterior distribution is Gaussian
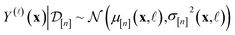 | (9) |
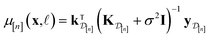 | (10) |
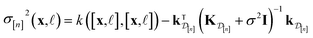 | (11) |
•  : the vector of simulated Xe/Kr selectivities of COFs we observed thus far in
: the vector of simulated Xe/Kr selectivities of COFs we observed thus far in  (see eqn (31)).
(see eqn (31)).
• 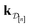 : the vector giving the kernel between (i) the (COF, fidelity) pair (x,
: the vector giving the kernel between (i) the (COF, fidelity) pair (x, ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) ) in question and (ii) the (COF, fidelity) pairs
) in question and (ii) the (COF, fidelity) pairs 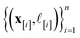 in the simulation data
in the simulation data 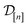 (see eqn (30)).
(see eqn (30)).
• 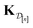 : the matrix giving the kernel between the (COF, fidelity) pairs
: the matrix giving the kernel between the (COF, fidelity) pairs 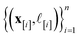 in the simulation data
in the simulation data 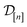 (see eqn (29)).
(see eqn (29)).
• σ2: the variance of the noise contaminating the simulated Xe/Kr selectivity (see eqn (26)).
Intuitively:
• The mean μ[n](x, ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) ) in eqn (10), a point prediction for the Xe/Kr selectivity of COF x according to a fidelity-
) in eqn (10), a point prediction for the Xe/Kr selectivity of COF x according to a fidelity-![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) simulation, is a weighted combination of the observed simulated Xe/Kr selectivities
simulation, is a weighted combination of the observed simulated Xe/Kr selectivities 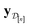 , with the similarity between the simulation in question (x,
, with the similarity between the simulation in question (x, ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) ) and the previously conducted simulations in
) and the previously conducted simulations in 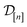 involved in forming the weights.
involved in forming the weights.
• The variance 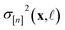 in eqn (11), quantifying uncertainty about the Xe/Kr selectivity of COF x according to a fidelity-
in eqn (11), quantifying uncertainty about the Xe/Kr selectivity of COF x according to a fidelity-![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) simulation, is that of the prior reduced according to the similarity between the simulation in question (x,
simulation, is that of the prior reduced according to the similarity between the simulation in question (x, ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) ) and the previously conducted simulations in
) and the previously conducted simulations in 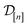 .
.
The subscript [n] in our notation emphasizes that the surrogate model changes over iterations; we expect the surrogate model to improve its predictions as the search progresses and the simulation data 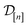 grows in size.
grows in size.
 The GP in eqn (5) is designed to (i) through the material kernel function, incorporate our domain knowledge that COFs with similar pore size, surface area, composition, etc. will tend to exhibit similar Xe/Kr selectivities and (ii) learn, from the simulation data
The GP in eqn (5) is designed to (i) through the material kernel function, incorporate our domain knowledge that COFs with similar pore size, surface area, composition, etc. will tend to exhibit similar Xe/Kr selectivities and (ii) learn, from the simulation data 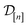 , (a) the relationship between the simulated Xe/Kr selectivity y(
, (a) the relationship between the simulated Xe/Kr selectivity y(![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) ) and the structural and compositional features of COFs listed in x and (b) through the fidelity kernel, correlations between the low- and high-fidelity simulations, allowing outcomes of low-fidelity simulations to inform us about the high-fidelity Xe/Kr selectivity we ultimately wish to maximize. Fig. 4, middle panel, visualizes a toy multi-fidelity GP for a one-dimensional COF space: the dark lines show the mean function μ(x,
) and the structural and compositional features of COFs listed in x and (b) through the fidelity kernel, correlations between the low- and high-fidelity simulations, allowing outcomes of low-fidelity simulations to inform us about the high-fidelity Xe/Kr selectivity we ultimately wish to maximize. Fig. 4, middle panel, visualizes a toy multi-fidelity GP for a one-dimensional COF space: the dark lines show the mean function μ(x,![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) ); the shaded bands highlight μ(x,
); the shaded bands highlight μ(x,![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) ) ± σ(x,
) ± σ(x,![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) ), quantifying uncertainty by showing a credible interval for the predicted selectivity of any given COF x; the points show the multi-fidelity data
), quantifying uncertainty by showing a credible interval for the predicted selectivity of any given COF x; the points show the multi-fidelity data 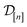 on which the toy GP is trained.
on which the toy GP is trained.
![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) [n+1] of the molecular simulation. The plan is judicious because it employs (i) the surrogate model—particularly, the posterior in eqn. (9)—and (ii) running averages of the computational runtime of the low- and high-fidelity simulations,
[n+1] of the molecular simulation. The plan is judicious because it employs (i) the surrogate model—particularly, the posterior in eqn. (9)—and (ii) running averages of the computational runtime of the low- and high-fidelity simulations, 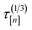 and
and 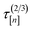 , to design the next simulation setup, (x[n+1],
, to design the next simulation setup, (x[n+1], ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) [n+1]), so as to balance exploration, exploitation, and cost.
[n+1]), so as to balance exploration, exploitation, and cost.
Particularly, we rely on an augmented, cost-aware expected improvement acquisition function79 to score the appeal of each setup (x, ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) ) for the next simulation. The simulation plan follows from maximizing the acquisition function in eqn (12):
) for the next simulation. The simulation plan follows from maximizing the acquisition function in eqn (12):
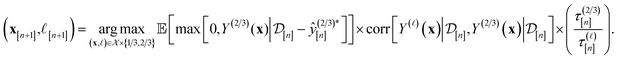 | (12) |
The acquisition function being maximized is a product of three terms:
• Expected improvement (EI): the amount that the high-fidelity simulated Xe/Kr selectivity of COF x is expected to improve upon the largest high-fidelity Xe/Kr selectivity we observed thus far, 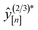 . Owing to the max[0, ·] operator, the integral constituting this expectation
. Owing to the max[0, ·] operator, the integral constituting this expectation 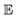 has a contribution only from density of the predicted high-fidelity Xe/Kr selectivity
has a contribution only from density of the predicted high-fidelity Xe/Kr selectivity 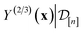 greater than
greater than 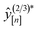 . Because both (a) a large posterior variance
. Because both (a) a large posterior variance 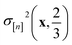 (reflecting uncertainty) and (b) a large mean
(reflecting uncertainty) and (b) a large mean 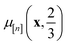 will contribute density to this region, maximizing this EI term balances exploitation and exploration, by favoring COFs whose predicted high-fidelity selectivity is large and/or uncertain.
will contribute density to this region, maximizing this EI term balances exploitation and exploration, by favoring COFs whose predicted high-fidelity selectivity is large and/or uncertain.
• Correlation with the high-fidelity selectivity: the correlation between the simulated Xe/Kr selectivity of the COF x under (i) the fidelity-![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) simulation and (ii) a high-fidelity simulation. If
simulation and (ii) a high-fidelity simulation. If ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) = 1/3 and this term is small (large), this simulation setup is downgraded (upgraded) because the outcome of this low-fidelity simulation cannot (can) inform us about the high-fidelity selectivity we ultimately wish to optimize.
= 1/3 and this term is small (large), this simulation setup is downgraded (upgraded) because the outcome of this low-fidelity simulation cannot (can) inform us about the high-fidelity selectivity we ultimately wish to optimize.
• Cost ratio: The ratio of the runtime of a high-fidelity simulation to the fidelity-![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) simulation, to promote low-fidelity simulations owing to their smaller runtime.
simulation, to promote low-fidelity simulations owing to their smaller runtime.
Owing to these three components, maximizing the acquisition function at each iteration gives a simulation plan (x[n+1], ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) [n+1]) for the next iteration with a high utility per cost for our objective of finding the COF with the largest high-fidelity Xe/Kr selectivity soon.
[n+1]) for the next iteration with a high utility per cost for our objective of finding the COF with the largest high-fidelity Xe/Kr selectivity soon.
Since the acquisition function relies on the surrogate model, it also changes from iteration-to-iteration.
Maximizing the acquisition function. Because (i) the acquisition function is computationally cheap to evaluate and (ii) we are searching over a relatively small, finite set of COFs
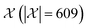 , we elected to find (x[n+1],
, we elected to find (x[n+1], ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) [n+1]) at each iteration via exhaustive search.
[n+1]) at each iteration via exhaustive search.
The acquired set of COFs. We refer to the set of COFs in
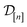 at iteration n, automatically chosen by sequentially maximizing the acquisition function, as the set of acquired COFs.
at iteration n, automatically chosen by sequentially maximizing the acquisition function, as the set of acquired COFs.
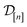 :
: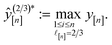 | (13) |
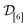 consisting of three diverse COFs “labeled” with their simulated—both low- and high-fidelity—Xe/Kr selectivities. We select the initial COF as the most “average”, defined as the one closest to the mean (normalized) COF vector. For the two subsequent COFs, we select (2) the COF most distal in COF space from the initial COF then (3) the COF with the maximal minimum distance to the first two COFs.
consisting of three diverse COFs “labeled” with their simulated—both low- and high-fidelity—Xe/Kr selectivities. We select the initial COF as the most “average”, defined as the one closest to the mean (normalized) COF vector. For the two subsequent COFs, we select (2) the COF most distal in COF space from the initial COF then (3) the COF with the maximal minimum distance to the first two COFs.
MFBO performance
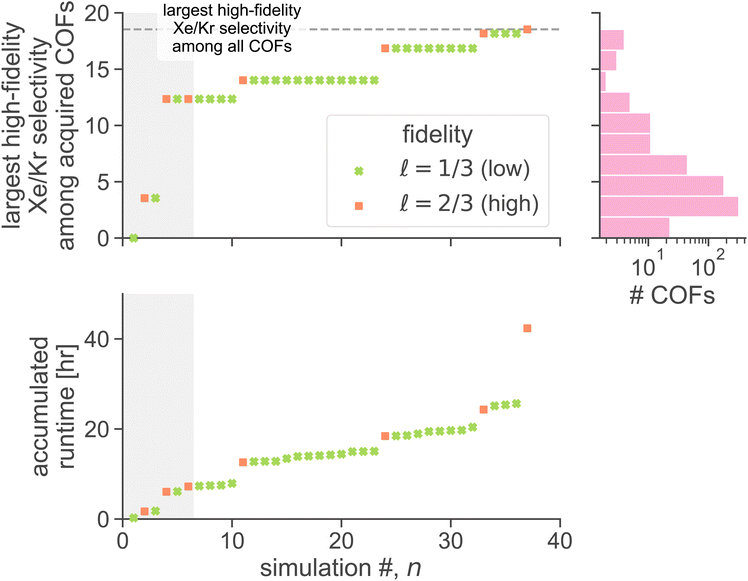
We now execute the MFBO loop in Fig. 4 to iteratively search for the COF with the largest high-fidelity simulated Xe/Kr selectivity.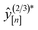 in eqn (13), and (ii, bottom panel) the accumulated computational runtime (see Methods for our compute hardware specifications). The gray region highlights the n = 6 simulations used to initialize the surrogate model.
in eqn (13), and (ii, bottom panel) the accumulated computational runtime (see Methods for our compute hardware specifications). The gray region highlights the n = 6 simulations used to initialize the surrogate model.
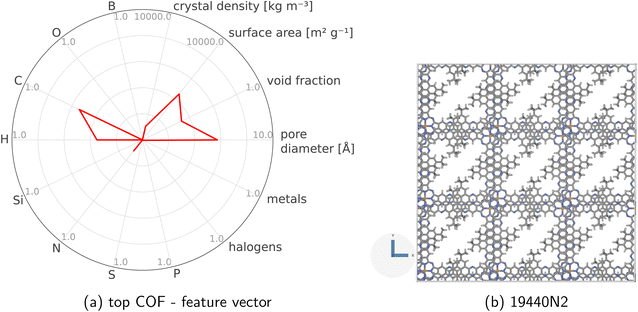
 The MFBO algorithm acquires the COF x* (19440N2 = CuPc-pz COF;111 surprise, Fig. 3b shows its crystal structure!) with the largest high-fidelity Xe/Kr selectivity y(2/3)* (18.53) after conducting only 37 molecular simulations—seven high-fidelity, 30 low-fidelity—incurring a computational runtime of 42.4 h. Recall, there are 609 COF candidates. Thus, MFBO recovers the top COF early in the search. Terminating the MFBO search early, before all materials are exhausted, then, would circumvent many wasteful molecular simulations in non-optimal COFs.
The MFBO algorithm acquires the COF x* (19440N2 = CuPc-pz COF;111 surprise, Fig. 3b shows its crystal structure!) with the largest high-fidelity Xe/Kr selectivity y(2/3)* (18.53) after conducting only 37 molecular simulations—seven high-fidelity, 30 low-fidelity—incurring a computational runtime of 42.4 h. Recall, there are 609 COF candidates. Thus, MFBO recovers the top COF early in the search. Terminating the MFBO search early, before all materials are exhausted, then, would circumvent many wasteful molecular simulations in non-optimal COFs.
For context, the distribution of high-fidelity Xe/Kr selectivities for all COFs, shown in Fig. 5 (top right), is skewed right. MBFO acquired the optimal COF x*, early in the search, from the thin tail (note the log-scale) of the distribution.
The most dramatic increases in accumulated runtime owe to high-fidelity simulations. Despite that the majority of simulations performed were low-fidelity, the high-fidelity simulations account for ∼84% of the accumulated runtime to find the optimal COF x*. Molecular simulations of the same fidelity vary in runtime among different COFs owing to different unit cell sizes, numbers of framework atoms, and, for high-fidelity simulations, average numbers of adsorbates hosted by the COF during the simulation. This explains why some jumps in accumulated runtime, within a given fidelity, are larger than others.
As evidence that MFBO is allocating computational resources intelligently, (1) several low-fidelity simulations precede each high-fidelity simulation (thus, MFBO is utilizing the cheaper, low-fidelity simulations to inform predictions about high-fidelity simulations we ultimately care about) and (2) all four of the MFBO-acquired COFs for high-fidelity simulations resulted in an improvement of the largest high-fidelity Xe/Kr selectivity observed.
(At the iteration preceding the acquirement of the optimal COF, Fig. S1† shows the predictivity of the surrogate model, and Fig. S2† shows the observed correlation between low- and high-fidelity selectivities. The prediction accuracy of the surrogate model is not impressive, but importantly it does recall the most selective COFs and provide useful direction/guidance112 for MFBO).
 Of course, in practice, we cannot know with certainty when we have recovered the optimal COF x* until we have exhaustively conducted high-fidelity simulations in all of the COF candidates. For the purposes of benchmarking MFBO, for this study, we actually did conduct an exhaustive search, to know the optimal COF x* with certainty and judge the performance of MFBO. See our previous discussion of stopping criteria that must be implemented in practice.
Of course, in practice, we cannot know with certainty when we have recovered the optimal COF x* until we have exhaustively conducted high-fidelity simulations in all of the COF candidates. For the purposes of benchmarking MFBO, for this study, we actually did conduct an exhaustive search, to know the optimal COF x* with certainty and judge the performance of MFBO. See our previous discussion of stopping criteria that must be implemented in practice.
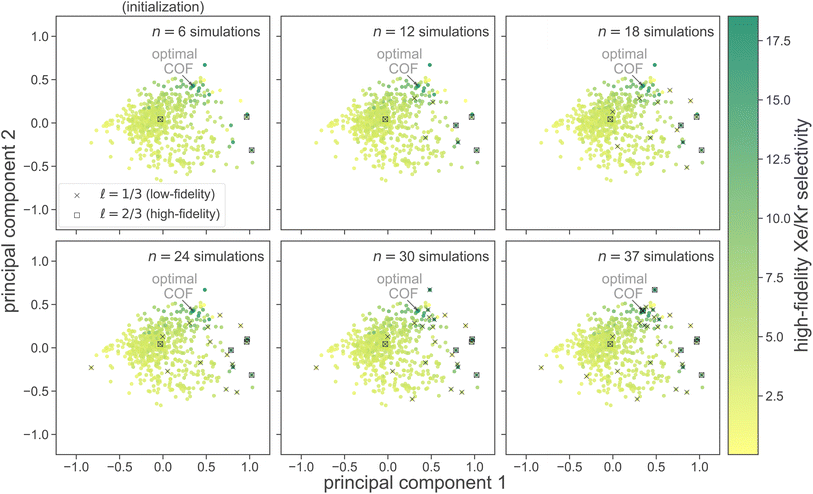
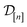 at six different stages of the search. Low- and high-fidelity simulations are distinguished by marker shape.
at six different stages of the search. Low- and high-fidelity simulations are distinguished by marker shape.
We used principal component analysis (PCA) to reduce the dimensionality of the COF feature vectors {x1, …, x609} from 14 to two, for visualization. Each panel in Fig. 6 shows the first two principal components of COF feature space; each point represents a COF, colored according to its high-fidelity Xe/Kr selectivity. Note, the COFs with the largest high-fidelity Xe/Kr selectivities tend to concentrate in the upper-right region of COF PC space.
Judging by the location of the acquired set of COFs in PC COF space, MFBO explores diverse regions of COF space, yet concentrates its COF acquires in the regions containing the highest performers. Interestingly, each high-fidelity simulation in a COF was preceded by a low-fidelity simulation in the same COF. This suggests that the MFBO algorithm is cautious to conduct expensive high-fidelity simulations and conservatively utilizes the low-fidelity simulations to explore COF space.
Exhaustive search. An exhaustive search runs a high-fidelity simulation of Xe/Kr adsorption in each of the 609 COFs in
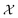 . While guaranteed to find the optimal COF x*, an exhaustive search incurs a high cost because it fails to exploit (i) the cheap, low-fidelity simulations available and (ii) the information contained in the simulation data
. While guaranteed to find the optimal COF x*, an exhaustive search incurs a high cost because it fails to exploit (i) the cheap, low-fidelity simulations available and (ii) the information contained in the simulation data 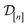 , about the relationship between the Xe/Kr selectivity of the COFs and their structural and compositional features in x, as the search proceeds, to reject simulations in COFs likely to be poorly-selective.
, about the relationship between the Xe/Kr selectivity of the COFs and their structural and compositional features in x, as the search proceeds, to reject simulations in COFs likely to be poorly-selective.
 The runtime of the exhaustive search was ∼2331 h. By comparison, MFBO incurred 2% of the runtime of the exhaustive search.
The runtime of the exhaustive search was ∼2331 h. By comparison, MFBO incurred 2% of the runtime of the exhaustive search.
Two-stage screening. A two-stage screening (1) runs a low-fidelity simulation of Xe/Kr adsorption in each of the 609 COFs in
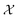 , then (2) (a) sorts the COFs according to their low-fidelity simulated Xe/Kr selectivity, in descending order, then (b) runs high-fidelity simulations of Xe/Kr adsorption in the COFs starting with the COF at the top of the list and working down. This search strategy leverages the cheap, low-fidelity simulations available in stage (1) to recover the optimal COF early in the sequence of stage (2). However, it still fails to leverage the information contained in the simulation data
, then (2) (a) sorts the COFs according to their low-fidelity simulated Xe/Kr selectivity, in descending order, then (b) runs high-fidelity simulations of Xe/Kr adsorption in the COFs starting with the COF at the top of the list and working down. This search strategy leverages the cheap, low-fidelity simulations available in stage (1) to recover the optimal COF early in the sequence of stage (2). However, it still fails to leverage the information contained in the simulation data 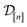 as the search proceeds to (i) avoid running low-fidelity simulations in every COF during stage (1) and (ii) adjust the sequence of high-fidelity simulations as high-fidelity simulation data is collected in stage (2).
as the search proceeds to (i) avoid running low-fidelity simulations in every COF during stage (1) and (ii) adjust the sequence of high-fidelity simulations as high-fidelity simulation data is collected in stage (2).
 This two-stage search incurs a runtime of ∼189 h to find the optimal COF x*, still more than MFBO (42 h).
This two-stage search incurs a runtime of ∼189 h to find the optimal COF x*, still more than MFBO (42 h).
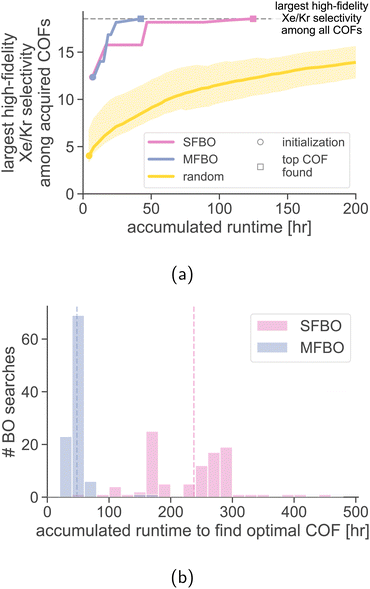
Random search with the high-fidelity simulations. A random search sequentially chooses a COF at random (without replacement) for a high-fidelity simulation of Xe/Kr adsorption. We conduct 1000 random searches and show the mean and two standard deviations of the search efficiency curves in Fig. 7a. MFBO recovers the optimal COF x* with much less accumulated runtime compared to a typical random search.
 The average run time incurred during by a random search to acquire the optimal COF is 1176 h. By comparison, MFBO incurred 4% of the average runtime of the random search.
The average run time incurred during by a random search to acquire the optimal COF is 1176 h. By comparison, MFBO incurred 4% of the average runtime of the random search.
Single-fidelity Bayesian optimization (SFBO). Finally, we assess the performance of single-fidelity (SF) BO of COFs for Xe/Kr separations—standard Bayesian optimization with the high-fidelity simulation of Xe/Kr adsorption using, for a controlled comparison to MFBO, (i) the same three COFs for initialization,‡ (ii) the expected improvement acquisition function, and (iii) a GP surrogate model with an identical material kernel.
 Fig. 7a shows the search efficiency curve of SFBO compared to MFBO. SFBO incurred a runtime of ∼125 h, about three times that of MFBO (42 h).
Fig. 7a shows the search efficiency curve of SFBO compared to MFBO. SFBO incurred a runtime of ∼125 h, about three times that of MFBO (42 h).
Feature permutation baseline. The surrogate model in MFBO relies upon both (1) the chemical and structural features of the COFs and (2) the low- and high-fidelity simulation data available, to make predictions of the high-fidelity Xe/Kr selectivity of COFs. We next aim to measure the cumulative value of the features for the search efficiency of MFBO. To do so, we (1) for each feature, randomly permute its values among the COFs—thus, preserving the distribution of each feature, but decorrelating each feature from the high-fidelity Xe/Kr selectivity—then (2) run MFBO with all of the features jumbled. We repeat this process 15 times. The deterioration in the search efficiency of MFBO with permuted features is indicative of the cumulative value of the features for MFBO. Note, a per-feature permutation could quantify the importance of each feature individually for MFBO (which we did not do).
 Fig. S4† shows that the search efficiency of MFBO is severely diminished when the features of the COFs are randomly permuted, incurring an average runtime of 254 h. Thus, the features of the COFs are valuable for MFBO.
Fig. S4† shows that the search efficiency of MFBO is severely diminished when the features of the COFs are randomly permuted, incurring an average runtime of 254 h. Thus, the features of the COFs are valuable for MFBO.
Robustness of MFBO performance to initialization. How robust is the MFBO performance to different initialization schemes? We conduct 100 MFBO and SFBO searches whose surrogate model is initialized with training data from simulations in three COFs: the first randomly selected (as opposed to the “average” COF), the next two chosen according to max-min distance for diversity. Fig. 7b shows the distribution of accumulated runtimes to find the optimal COF x* over random initializing COFs (each individual search efficiency trace is shown in Fig. S3†). While the runtime exhibits significant variance (standard deviations: 81 h for SFBO, 19 h for MFBO), the distribution of the runtime of MFBO is shifted far to the left of that of SFBO (means: 238 h for SFBO, 48 h for MFBO).
Post-MFBO analysis of our simulated adsorption data
During the iterative, MFBO-guided COF search, especially in the early stages, the surrogate model lacks complete knowledge of how the high-fidelity simulated Xe/Kr selectivities are related to (i) the structural and chemical features of the COFs and (ii) the low-fidelity selectivities. Nonetheless, post-MFBO, we now examine these relationships using the exhaustive simulation data for all COFs to gain insights. Fig. S5† shows the [strong, but diminishing at high Xe/Kr selectivities] correlation between the Xe/Kr selectivity of the COFs according to high vs. low-fidelity simulations, and Fig. S6† shows the correlation between the high-fidelity Xe/Kr selectivity and the features of the COFs. To further assess our ability to discriminate between the COFs with the highest and lowest simulated Xe/Kr selectivity based on their features, the radar plot in Fig. S7† visualizes the feature vectors of the top- and bottom-15 COFs. Consistent with previous computational studies of Xe/Kr adsorption,87,93,97e.g., the COFs with the largest high-fidelity simulated Xe/Kr selectivity exhibit pore diameters that fall within a narrow interval situated a little to the right of the diameter of a Xe adsorbate. Finally, unsurprisingly, the parity plot in Fig. S8† shows a single-[high-]fidelity GP trained on 80% of all of the data performs dramatically better than the multi-fidelity GP immediately preceding the acquirement of the top COF (Fig. S1†), trained with only 36 examples.Conclusions
Our goal was to efficiently search a database of ∼600 COFs for the one exhibiting the largest adsorptive Xe/Kr selectivity. We had access to two molecular simulations of Xe/Kr adsorption to predict the selectivity of a COF: a high-fidelity binary grand-canonical Monte Carlo simulation and a low-fidelity Henry coefficient calculation with a smaller runtime. We employed multi-fidelity Bayesian optimization (MFBO) to orchestrate the sequential search for the COF with the largest high-fidelity Xe/Kr selectivity. MFBO constituted an iterative feedback loop of (1) conduct a low- or high-fidelity simulation of Xe/Kr adsorption in a COF, (2) use the simulation data gathered so far to train a surrogate model that predicts the selectivity of COFs, according to both low- and high-fidelity simulations, based on their structural and chemical features, with quantified uncertainty, then (3) choose the COF and fidelity for the next simulation via maximizing an acquisition function that balances exploration, exploitation, and cost. MFBO acquired the optimal COF—the one with the largest high-fidelity Xe/Kr selectivity—among the ∼600 candidates using only 30 low-fidelity and seven high-fidelity simulations, incurring only 4% and 20% of the average runtime to find the top COF via random sequential search and single-fidelity BO, respectively, with high-fidelity simulations only. Visualizing the location of the acquired COFs in the design space as the search proceeds revealed that MFBO judiciously planned the sequence of simulations to balance exploration, exploitation, and the cost of the two types of simulations.Despite within a computer simulation and pertaining to the specific task of discovering COFs for Xe/Kr separations, our proof-of-concept study broadly hints at the potential for MFBO to reduce the time and cost to discover new materials in both the virtual and physical laboratory.
Discussion
MFBO performance depends on: surrogate model, acquisition function, and precision of the experiment/simulation
Generally, the performance of MFBO for materials discovery depends on the surrogate model, the acquisition function, and the precision/reproducibility of the synthesis of the targeted materials and subsequent measurements of their properties. The surrogate model must (i) be fed features of the materials that are informative about the property (engineering such features relies on domain knowledge), (ii) be data-efficient (i.e., require a small number of examples to learn to make accurate predictions), and (iii) express well-calibrated uncertainty.109,113,114 The acquisition function for experimental planning must balance exploration, exploitation, and cost. The surrogate model and acquisition function must be cheap to train and evaluate, respectively, relative to the simulations/experiments to evaluate the material property. Finally, if the synthesis of targeted materials is not well-controlled (resulting in e.g., variations in crystallinity, defects, and impurities) and/or the measurement of the material property is noisy owing to an imprecise instrument or poorly-controlled conditions, the surrogate model will require many examples to learn to predict the [average] material property.Note, the sample-efficiency of MFBO can be improved by incorporating prior beliefs/hypotheses (grounded in chemical intuition or information) of expert chemists about the region of materials space in which the optimal material belongs.115,116
Translating MFBO to the bona fide lab
Most intriguingly, MFBO may direct a human- or robot-operated lab aimed at the discovery of new molecules or materials. In this setting, (i) a high-fidelity experiment constitutes the synthesis, activation, and characterization of a material and a measurement of its performance for some engineering application, and (ii) the low-fidelity experiment(s) constitute (a) a physics-based simulation of the material to predict its performance or (b) a quick, cheap, accessible measurement of a property of the material in the lab—some property that serves as a proxy for the property we ultimately wish to maximize for the engineering application.The materials discovery costs incurred in the lab—reagents, consumable vials, instrumentation time and depreciation, salaries of operators, etc.—are much more significant in scale than the costs due to computational runtime herein. Consequently, MFBO is poised to make a bigger impact when applied to the bona fide lab.
In the lab, imprecision in the materials synthesis and property-measurements (e.g., adsorption measurements in porous materials sometimes vary dramatically across labs;117,118 automated labs are likely to improve reproducibility, though119) will reduce the sample-efficiency of MFBO. Herein, such imprecision was not a major issue because our molecular simulations were well-converged.
Prototyping MFBO variants on a frugal twin120 of a physical system—or toy systems121—may accelerate translation and adaption of MFBO to the bona fide lab.
Relationship between MFBO and MF active-learning
MFBO is closely related to multi-fidelity active learning,122 where we iteratively design a sequence of experiments of multiple fidelities (like MFBO) to efficiently gather training data for a predictor of the [high-fidelity] property of materials.123 For active learning, we wish to pick experiments that will reduce the uncertainty of the predictor. We may adapt the MFBO framework herein for active learning by installing an acquisition function that seeks full exploration (i.e., no exploitation component). Active learning can e.g. reduce the number of experiments to characterize the adsorption isotherm of a gas in a porous material.124Remark on acquisition functions
MFBO constitutes an outer loop, visualized in Fig. 4, for the outer optimization problem of finding the material with the optimal property, of (1) conducting an experiment/simulation, (2) updating the surrogate model, then (3) picking the next material and fidelity for an experiment/simulation. Task (3) constitutes the inner optimization problem—finding the material and fidelity that optimize the acquisition function. The cost-performance of MFBO deteriorates when the cost of solving the inner optimization grows.125Herein, we solved the inner-optimization problem via a brute-force inner loop over all COFs. The runtime for this was negligible compared to our molecular simulations because (i) we are optimizing over a finite and relatively small set of COFs and (ii) we possess an analytical expression for the acquisition function in eqn (12). Other acquisition functions, grounded in different principles (e.g., information about the minimum,126–128 knowledge gradient,129 non-myopic look-ahead,130,131 or portfolios132) than the improvement-based, myopic one in eqn (12), may be more expensive to compute (involving intractable integrals that must be approximated through sampling133 and/or rollout). The choice/design of an acquisition function for MFBO may involve balancing (i) the cost to evaluate it and (ii) how well it scores the utility-per-cost of material–fidelity pairs.
Scaling MFBO to larger sets of materials
Herein, we executed MFBO for optimization over a finite, small (∼600) set of materials. For MFBO to scale to larger search spaces (i.e., larger sets of materials) and experimental sample sizes, we can (1) employ surrogate models that are more scalable than GPs, such as Bayesian linear regression128 (perhaps, using features learned from a neural network134), sparse GPs,135–137 Bayesian neural networks,138 or random forests139 (though, random forests poorly extrapolate uncertainty7) and (2) to speed up finding the solution to the inner optimization problem, maximize the acquisition function over the continuous materials space with a generic continuous optimization algorithm (e.g., gradient descent), then decode to a viable material by e.g., selecting the material in the candidate set that is closest to the maximizer. For materials with structured (non-vector) representations such as strings or graphs, one can learn a continuous representation of the materials via an autoencoder and execute MFBO in this continuous latent space;140–142 then in strategy (2) we use the decoder to map the continuous latent representation to a material structure.Future work on MFBO algorithm development
Future work for MFBO algorithm development includes (1) inventing new (a) predictive, uncertainty-calibrated, data-efficient, and scalable multi-fidelity surrogate models and (b) exploration-, exploitation-, cost-balancing, and cheap-to-evaluate multi-fidelity acquisition functions; (2) benchmarking the performance of other multi-fidelity acquisition functions7 and their robustness across a variety of materials discovery tasks; (3) extending MFBO to (a) the batch setting, where experiments can be conducted in parallel (i.e., multiple materials are selected at each iteration)7,143,144 and (b) the multi-objective setting,145,146 where we seek the Pareto-optimal set of materials.Another search strategy using material properties measured with low fidelity
Similar in spirit to multi-fidelity machine learning and two-stage search, the cheap-, low-fidelity calculations of dilute adsorption properties could serve as features (inputs) to a supervised machine learning model to predict the high-fidelity adsorption property.147 In Fig. S8,† we show that augmenting the standard chemical and structural features of the COFs with the low-fidelity Xe/Kr selectivity treated as an additional input can dramatically improve the predictivity of a GP on the high-fidelity Xe/Kr selectivity.Methods
The COF crystal structures
We obtained the crystal structures of the 609 COF candidates from the Clean, Uniform, Refined with Automatic Tracking from Experimental Database (CURATED).78The two molecular simulation techniques to predict the Xe/Kr selectivity of a COF
The chemical potential μ is set by the Xe/Kr gas mixture; the ideal gas law gives μ in terms of the temperature T and partial pressures of Xe and Kr, p = [pXe, pKr]:
μg = kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log[βpgΛg3] for g ∈ {Xe, Kr}, log[βpgΛg3] for g ∈ {Xe, Kr}, | (14) |
A microstate of the system is defined by (i) the number of adsorbates n and (ii) their positions
| R(n) := [rXe,1⋯rXe,nXerKr,1⋯rKr,nKr] | (15) |
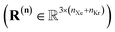 . Approximating the COF as rigid, the positions of the atoms of the COF are fixed.
. Approximating the COF as rigid, the positions of the atoms of the COF are fixed.
Let E = E(n, R(n)) be the potential energy of a microstate (n, R(n)). Of course, E = E(n, R(n)) is COF-dependent. We will model E(n, R(n)) using Lennard-Jones interatomic pair potentials.
In the BGC ensemble, the partition function is a sum/integral over microstates148–150
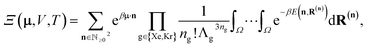 | (16) |
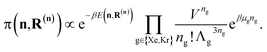 | (17) |
In each molecular simulation technique below, the ultimate goal is to predict the expected number of adsorbates in the system under the BGC ensemble:
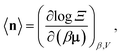 | (18) |
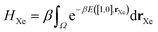 | (19) |
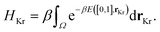 | (20) |
For the low-fidelity prediction of Xe/Kr selectivity, we compute HXe and HKr of a COF from two ordinary Monte Carlo integrations (500 insertions per Å3), i.e. Widom particle insertions.149
Of course, this cost comparison depends on the number of MC cycles/insertions dedicated to each simulation; we allocated 500 cycles/insertions per Å3 volume of the system in an attempt to grant each simulation with reasonably comparable errors in the average 〈n〉.
N.b., with further approximation, the computational expense of the Henry coefficient calculations can be reduced by biasing the samples of adsorbate configurations to lie nearby the internal surface (pore walls) of the COF.151
| Nodes 1–4 | Model | Dell PowerEdge R740 |
| Processor | 2× 10-core 2.20 GHz Intel Xeon Silver 4114 w/16896 KB cache | |
| Memory | 128 GB RAM @2666 MT s−1 | |
| Nodes 5–8 | Model | Dell PowerEdge R740 |
| Processor | 2× 22-core 2.10 GHz Intel Xeon Gold 6152 w/30976 KB cache | |
| Memory | 128 GB RAM @2666 MT s−1 |
The multi-fidelity Gaussian process surrogate model
We explain our multi-fidelity GP in the context of the Bayesian paradigm of (i) impose a prior distribution, (ii) collect data, then (iii) in light of the data, update the prior distribution to a posterior distribution.For more understanding about GPs, see ref. 106 and 107.
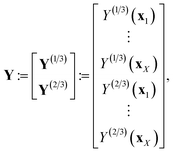 | (21) |
The joint prior distribution expressed by the GP in eqn (5) is a Gaussian distribution with (i) a mean of the zero-vector and (ii) a covariance matrix exhibiting a block structure:
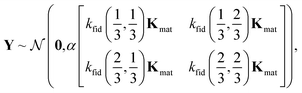 | (22) |
We elucidate the assumption behind eqn (22) and the intuition behind the kernel functions by inspecting the marginal prior distribution of
• The fidelity-![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) simulated Xe/Kr selectivity of a COF x,
simulated Xe/Kr selectivity of a COF x,
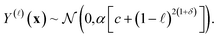 | (23) |
Apparently, the hyperparameters c and δ forming the variance express our fidelity-dependent, COF-independent prior uncertainty about the simulated Xe/Kr selectivity of any given COF.
• A pair of simulated Xe/Kr selectivities, Y(![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) )(x) and Y(
)(x) and Y(![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) ′)(x′), whose covariance is given by the kernel function k in eqn (6):
′)(x′), whose covariance is given by the kernel function k in eqn (6):
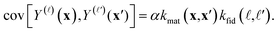 | (24) |
With the kernel functions quantifying our notion of “similarity”, our prior belief is that the simulated selectivity of two COFs will be similar (dissimilar) for (i) two similar (dissimilar) COFs under (ii) two similar (dissimilar) simulation fidelities. Importantly, the material kernel function in eqn (7) paired with our design of COF space captures our domain knowledge that COFs with closeby composition, pore size, surface area, etc. tend to exhibit similar adsorption properties.89,90,93,97 Note, for ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) ≠
≠ ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) ′ but x = x′, it is apparent that the hyperparameters c and δ of the fidelity kernel function also capture the correlation between the high- and low-fidelity Xe/Kr selectivities for a given COF. This allows observed low-fidelity simulated Xe/Kr selectivities to appropriately inform the predictions about the high-fidelity selectivities we ultimately wish to maximize.
′ but x = x′, it is apparent that the hyperparameters c and δ of the fidelity kernel function also capture the correlation between the high- and low-fidelity Xe/Kr selectivities for a given COF. This allows observed low-fidelity simulated Xe/Kr selectivities to appropriately inform the predictions about the high-fidelity selectivities we ultimately wish to maximize.
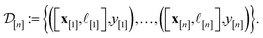 | (25) |
I.e., x[i] is the vector representation of the COF, ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) [i] is the fidelity, and y[i] is the observed Xe/Kr selectivity of the simulation conducted at iteration i. In light of this simulation data
[i] is the fidelity, and y[i] is the observed Xe/Kr selectivity of the simulation conducted at iteration i. In light of this simulation data 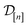 , we wish to update our prior distribution in eqn (22).
, we wish to update our prior distribution in eqn (22).
We view each observed fidelity-![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) simulated Xe/Kr selectivity y(
simulated Xe/Kr selectivity y(![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) ) of a COF represented by x as a noisy evaluation of a black-box function f(x,
) of a COF represented by x as a noisy evaluation of a black-box function f(x,![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) ) that represents the relationship between the fidelity-
) that represents the relationship between the fidelity-![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) Xe/Kr selectivity of a COF and its features x. Particularly, we assume
Xe/Kr selectivity of a COF and its features x. Particularly, we assume
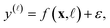 | (26) |
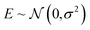 . The source of this noise is the inherent stochasticity involved in the Monte Carlo simulation; however, the noise may also have a contribution from the lack of information contained about the selectivity within the COF features x.
. The source of this noise is the inherent stochasticity involved in the Monte Carlo simulation; however, the noise may also have a contribution from the lack of information contained about the selectivity within the COF features x.
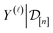 .
The posterior distribution of Y(
.
The posterior distribution of Y(![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) )(x) expresses our beliefs about the fidelity-
)(x) expresses our beliefs about the fidelity-![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) simulated Xe/Kr selectivity of a COF with features xin light of the simulation data
simulated Xe/Kr selectivity of a COF with features xin light of the simulation data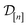 . The posterior is an update to our prior distribution, obtained by conditioning the prior distribution in eqn (22) on the observations
. The posterior is an update to our prior distribution, obtained by conditioning the prior distribution in eqn (22) on the observations 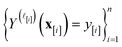 in the data
in the data 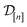 .
.
We find the marginal posterior distribution of 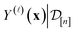 by first writing the marginal prior distribution, following from eqn (22), of (i) the fidelity-
by first writing the marginal prior distribution, following from eqn (22), of (i) the fidelity-![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) simulated Xe/Kr selectivity of COF represented by x and (ii) the observed (i.e., noise-contaminated) selectivities in the simulations we have already done in
simulated Xe/Kr selectivity of COF represented by x and (ii) the observed (i.e., noise-contaminated) selectivities in the simulations we have already done in 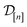 :
:
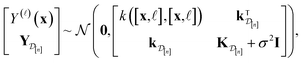 | (27) |
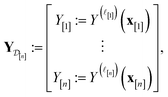 | (28) |
(2) The kernel matrix between the simulation setups in the data 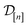 ,
, 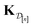 , whose element (i, j) is
, whose element (i, j) is
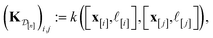 | (29) |
![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) ] and those in the data
] and those in the data 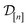
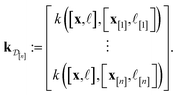 | (30) |
We obtain the posterior distribution of Y(![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) )(x) by conditioning the prior in eqn (27) on the observed simulated Xe/Kr selectivities of the COFs in the data
)(x) by conditioning the prior in eqn (27) on the observed simulated Xe/Kr selectivities of the COFs in the data 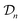 :
:
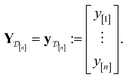 | (31) |
Upon conditioning, the posterior distribution of Y(![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) )(x) is also a Gaussian distribution, given in eqn (9).
)(x) is also a Gaussian distribution, given in eqn (9).
Sources of uncertainty. Uncertainty in the Xe/Kr selectivity of a COF may owe to (i) a lack of simulations on COFs in the neighborhood of COF space around x, (ii) a lack of mutual information between outcomes of simulations of different fidelities, (iii) a lack of information about the selectivity contained in the features, and/or (iv) inherent variability/noise in the outcome of the Monte Carlo simulation.
Centering the outputs. For the zero-mean prior in eqn (22) to be reasonable, we center the simulated Xe/Kr selectivities (the y[i]'s) in the data
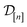 at each iteration.
at each iteration.
Hyperparameters. The kernel function in eqn (6) contains four hyperparameters: α, γ, c, and δ. And, we have the noise hyperparameter σ from eqn (26). At each iteration, these hyperparameters are tuned to maximize the marginal likelihood of the data
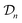 .
.
Function space view of a GP. For our problem of searching a fixed pool of COFs, we are only interested in the joint distribution of the random variables listed in Y in eqn (22). However, an alternative view of the GP in eqn (5) is that it specifies a (prior and posterior) distribution over functions F(x,
![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) ) that aim to approximate the black-box input (COF x, fidelity
) that aim to approximate the black-box input (COF x, fidelity ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) ) – output (simulated Xe/Kr selectivity, y(
) – output (simulated Xe/Kr selectivity, y(![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) )) relationship underlurking the simulations—the black-box function f(x,
)) relationship underlurking the simulations—the black-box function f(x,![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) ) in eqn (26). This perspective is illustrated in the middle panel of Fig. 4, where the dark line shows the posterior mean function μ[n](x,
) in eqn (26). This perspective is illustrated in the middle panel of Fig. 4, where the dark line shows the posterior mean function μ[n](x,![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) ) and the bands show a posterior credible region for these functions, μ[n](x,
) and the bands show a posterior credible region for these functions, μ[n](x,![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) ) ± σ[n](x,
) ± σ[n](x,![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) ).
).
GP implementation. We use the implementation of the multi-fidelity GP in the BoTorch162 library in Python, which builds upon GPyTorch.163 Note, Atlas164 is a Python package for BO tailored to self-driving chemical labs.
Data availability
All computer codes and simulation data to reproduce our results are available at https://github.com/SimonEnsemble/multi-fidelity-BO-of-COFs-for-Xe-Kr-seps.Conflicts of interest
None to declare.Acknowledgements
For funding and support, N. G. and C. M. S. acknowledge the U.S. Department of Defense (DoD) Defense Threat Reduction Agency (HDTRA-19-31270) and A. D. and J. D. acknowledge the National Science Foundation Grants IIS-1845922 and OAC-1910213. C. M. S. and N. G. thank the Oregon State University College of Engineering High-Performance Computing Cluster manager Robert Yelle.References
- F. Formalik, K. Shi, F. Joodaki, S. Wang and R. Q. Snurr, Exploring the Structural, Dynamic, and Functional Properties of Metal-Organic Frameworks through Molecular Modeling, Adv. Funct. Mater., 2023, 2308130 CrossRef
, https://onlinelibrary.wiley.com/doi/10.1002/adfm.202308130.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, Commentary: The Materials Project: A materials genome approach to accelerating materials innovation, APL Mater., 2013, 1, 011002 CrossRef
.
- E. O. Pyzer-Knapp, C. Suh, R. Gómez-Bombarelli, J. Aguilera-Iparraguirre and A. Aspuru-Guzik, What is high-throughput virtual screening? A perspective from organic materials discovery, Annu. Rev. Mater. Res., 2015, 45, 195–216 CrossRef CAS
.
- K. T. Butler, D. W. Davies, H. Cartwright, O. Isayev and A. Walsh, Machine learning for molecular and materials science, Nature, 2018, 559, 547–555 CrossRef CAS PubMed
.
- K. M. Jablonka, D. Ongari, S. M. Moosavi and B. Smit, Big-data science in porous materials: materials genomics and machine learning, Chem. Rev., 2020, 120, 8066–8129 CrossRef CAS PubMed
.
- J. A. Keith, V. Vassilev-Galindo, B. Cheng, S. Chmiela, M. Gastegger, K.-R. Müller and A. Tkatchenko, Combining machine learning and computational chemistry for predictive insights into chemical systems, Chem. Rev., 2021, 121, 9816–9872 CrossRef CAS PubMed
.
- B. Shahriari, K. Swersky, Z. Wang, R. P. Adams and N. De Freitas, Taking the human out of the loop: A review of Bayesian optimization, Proc. IEEE, 2015, 104, 148–175 Search PubMed
.
- A. Agnihotri and N. Batra, Exploring Bayesian Optimization, Distill, 2020 Search PubMed
, https://distill.pub/2020/bayesian-optimization.
- P. I. Frazier, A tutorial on Bayesian optimization, arXiv, 2018, preprint, arXiv:1807.02811, DOI:10.48550/arXiv.1807.02811.
-
R. Garnett, Bayesian Optimization, Cambridge University Press, 2023 Search PubMed
.
- Q. Liang, A. E. Gongora, Z. Ren, A. Tiihonen, Z. Liu, S. Sun, J. R. Deneault, D. Bash, F. Mekki-Berrada, S. A. Khan, K. Hippalgaonkar, B. Maruyama, K. A. Brown, J. F. Fisher III and T. Buonassisi, Benchmarking the performance of Bayesian optimization across multiple experimental materials science domains, npj Comput. Mater., 2021, 7, 188 CrossRef
.
-
D. Packwood, Bayesian Optimization for Materials Science, Springer, 2017 Search PubMed
.
-
P. I. Frazier and J. Wang, Information science for materials discovery and design, Springer, 2015, pp. 45–75 Search PubMed
.
- C. W. Coley, Defining and exploring chemical spaces, Trends Chem., 2021, 3, 133–145 CrossRef CAS
.
- E. Stach,
et al., Autonomous experimentation systems for materials development: A community perspective, Matter, 2021, 4, 2702–2726 CrossRef
.
- F. Häse, L. M. Roch and A. Aspuru-Guzik, Next-Generation Experimentation with Self-Driving Laboratories, Trends Chem., 2019, 1, 282–291 CrossRef
.
- B. Burger, P. M. Maffettone, V. V. Gusev, C. M. Aitchison, Y. Bai, X. Wang, X. Li, B. M. Alston, B. Li, R. Clowes, N. Rankin, B. Harris, R. S. Sprick and A. I. Cooper, A mobile robotic chemist, Nature, 2020, 583, 237–241 CrossRef CAS PubMed
.
- A. M. K. Nambiar, C. P. Breen, T. Hart, T. Kulesza, T. F. Jamison and K. F. Jensen, Bayesian Optimization of Computer-Proposed Multistep Synthetic Routes on an Automated Robotic Flow Platform, ACS Cent. Sci., 2022, 8, 825–836 CrossRef CAS PubMed
.
- Y. Jiang, D. Salley, A. Sharma, G. Keenan, M. Mullin and L. Cronin, An artificial intelligence enabled chemical synthesis robot for exploration and optimization of nanomaterials, Sci. Adv., 2022, 8, eabo2626 CrossRef CAS PubMed
.
- A. Pomberger, N. Jose, D. Walz, J. Meissner, C. Holze, M. Kopczynski, P. Müller-Bischof and A. Lapkin, Automated pH Adjustment Driven by Robotic Workflows and Active Machine Learning, Chem. Eng. J., 2023, 451, 139099 CrossRef CAS
.
- R. Shimizu, S. Kobayashi, Y. Watanabe, Y. Ando and T. Hitosugi, Autonomous materials synthesis by machine learning and robotics, APL Mater., 2020, 8, 111110 CrossRef CAS
.
- K. L. Snapp and K. A. Brown, Driving School for Self-Driving Labs, Digital Discovery, 2023, 2, 1620–1629 RSC
.
- R. Arróyave, D. Khatamsaz, B. Vela, R. Couperthwaite, A. Molkeri, P. Singh, D. D. Johnson, X. Qian, A. Srivastava and D. Allaire, A perspective on Bayesian methods applied to materials discovery and design, MRS Commun., 2022, 1–13 Search PubMed
.
- K. Wang and A. W. Dowling, Bayesian optimization for chemical products and functional materials, Curr. Opin. Chem. Eng., 2022, 36, 100728 CrossRef
.
- Y. Comlek, T. D. Pham, R. Snurr and W. Chen, Rapid Design of Top-Performing Metal-Organic Frameworks with Qualitative Representations of Building Blocks, npj Comput. Mater., 2023, 9, 170 CrossRef CAS
.
- E. O. Pyzer-Knapp, J. W. Pitera, P. W. Staar, S. Takeda, T. Laino, D. P. Sanders, J. Sexton, J. R. Smith and A. Curioni, Accelerating materials discovery using artificial intelligence, high performance computing and robotics, npj Comput. Mater., 2022, 8, 84 CrossRef
.
- A. Deshwal, C. M. Simon and J. R. Doppa, Bayesian optimization of nanoporous materials, Mol. Syst. Des. Eng., 2021, 6, 1066–1086 RSC
.
- E. Taw and J. B. Neaton, Accelerated Discovery of CH4 Uptake Capacity Metal–Organic Frameworks Using Bayesian Optimization, Adv. Theory Simul., 2022, 5, 2100515 CrossRef CAS
.
- H. Tang and J. Jiang, Active learning boosted computational discovery of covalent–organic frameworks for ultrahigh CH4 storage, AIChE J., 2022, 68, e17856 CrossRef CAS
.
- E. O. Pyzer-Knapp, L. Chen, G. M. Day and A. I. Cooper, Accelerating computational discovery of porous solids through improved navigation of energy-structure-function maps, Sci. Adv., 2021, 7, eabi4763 CrossRef CAS PubMed
.
- S. Ghude and C. Chowdhury, Exploring Hydrogen Storage Capacity in Metal-Organic Frameworks: A Bayesian Optimization Approach, Chem.–Eur. J., 2023, e202301840 CrossRef PubMed
.
- K. Vaddi, H. T. Chiang and L. D. Pozzo, Autonomous retrosynthesis of gold nanoparticles via spectral shape matching, Digital Discovery, 2022, 1, 502–510 RSC
.
- B. Rouet-Leduc, K. Barros, T. Lookman and C. J. Humphreys, Optimisation of GaN LEDs and the reduction of efficiency droop using active machine learning, Sci. Rep., 2016, 6, 1–6 CrossRef PubMed
.
- J. Chang, P. Nikolaev, J. Carpena-Núñez, R. Rao, K. Decker, A. E. Islam, J. Kim, M. A. Pitt, J. I. Myung and B. Maruyama, Efficient closed-loop maximization of carbon nanotube growth rate using Bayesian optimization, Sci. Rep., 2020, 10, 9040 CrossRef CAS
.
- H. C. Herbol, W. Hu, P. Frazier, P. Clancy and M. Poloczek, Efficient search of compositional space for hybrid organic–inorganic perovskites via Bayesian optimization, npj Comput. Mater., 2018, 4, 51 CrossRef
.
- S. Sun,
et al., A data fusion approach to optimize compositional stability of halide perovskites, Matter, 2021, 4, 1305–1322 CrossRef CAS
.
- Y. Zhang, D. W. Apley and W. Chen, Bayesian optimization for materials design with mixed quantitative and qualitative variables, Sci. Rep., 2020, 10, 1–13 CrossRef CAS
.
- A. E. Gongora, K. L. Snapp, E. Whiting, P. Riley, K. G. Reyes, E. F. Morgan and K. A. Brown, Using simulation to accelerate autonomous experimentation: A case study using mechanics, iScience, 2021, 24, 102262 CrossRef PubMed
.
- S. Langner, F. Häse, J. D. Perea, T. Stubhan, J. Hauch, L. M. Roch, T. Heumueller, A. Aspuru-Guzik and C. J. Brabec, Beyond Ternary OPV: High-Throughput Experimentation and Self-Driving Laboratories Optimize Multicomponent Systems, Adv. Mater., 2020, 32, 1907801 CrossRef CAS PubMed
.
- P. S. Ramesh and T. K. Patra, Polymer sequence design via molecular simulation-based active learning, Soft Matter, 2023, 19, 282–294 RSC
.
- M. Reis, F. Gusev, N. G. Taylor, S. H. Chung, M. D. Verber, Y. Z. Lee, O. Isayev and F. A. Leibfarth, Machine-learning-guided discovery of 19F MRI agents enabled by automated copolymer synthesis, J. Am. Chem. Soc., 2021, 143, 17677–17689 CrossRef CAS PubMed
.
- C. Li, D. Rubín de Celis Leal, S. Rana, S. Gupta, A. Sutti, S. Greenhill, T. Slezak, M. Height and S. Venkatesh, Rapid Bayesian optimisation for synthesis of short polymer fiber materials, Sci. Rep., 2017, 7, 1–10 CrossRef PubMed
.
- M. J. Tamasi, R. A. Patel, C. H. Borca, S. Kosuri, H. Mugnier, R. Upadhya, N. S. Murthy, M. A. Webb and A. J. Gormley, Machine Learning on a Robotic Platform for the Design of Polymer–Protein Hybrids, Adv. Mater., 2022, 34, 2201809 CrossRef CAS PubMed
.
- A. Seko, A. Togo, H. Hayashi, K. Tsuda, L. Chaput and I. Tanaka, Prediction of low-thermal-conductivity compounds with first-principles anharmonic lattice-dynamics calculations and Bayesian optimization, Phys. Rev. Lett., 2015, 115, 205901 CrossRef PubMed
.
- H. Zhai and J. Yeo, Computational Design of Antimicrobial Active Surfaces via Automated Bayesian Optimization, ACS Biomater. Sci. Eng., 2022, 9(1), 269–279 CrossRef PubMed
.
- R. W. Epps, M. S. Bowen, A. A. Volk, K. Abdel-Latif, S. Han, K. G. Reyes, A. Amassian and M. Abolhasani, Artificial Chemist: An Autonomous Quantum Dot Synthesis Bot, Adv. Mater., 2020, 32, 2001626 CrossRef CAS PubMed
.
- Y. Kitamura, H. Toshima, A. Inokuchi and D. Tanaka, Bayesian optimization of the composition of the lanthanide metal-organic framework MIL-103 for white-light emission, Mol. Syst. Des. Eng., 2023, 8, 431–435 RSC
.
- Y. Zhang, T. C. Peck, G. K. Reddy, D. Banerjee, H. Jia, C. A. Roberts and C. Ling, Descriptor-Free Design of Multicomponent Catalysts, ACS Catal., 2022, 12, 10562–10571 CrossRef CAS
.
- J. K. Pedersen, C. M. Clausen, O. A. Krysiak, B. Xiao, T. A. A. Batchelor, T. Löffler, V. A. Mints, L. Banko, M. Arenz, A. Savan, W. Schuhmann, A. Ludwig and J. Rossmeisl, Bayesian Optimization of High-Entropy Alloy Compositions for Electrocatalytic Oxygen Reduction, Angew. Chem., 2021, 133, 24346–24354 CrossRef
.
- B. Rohr, H. S. Stein, D. Guevarra, Y. Wang, J. A. Haber, M. Aykol, S. K. Suram and J. M. Gregoire, Benchmarking the acceleration of materials discovery by sequential learning, Chem. Sci., 2020, 11, 2696–2706 RSC
.
- M. C. Ramos, S. S. Michtavy, M. D. Porosoff and A. D. White, Bayesian Optimization of Catalysts With In-context Learning, arXiv, 2023, preprint, arXiv:2304.05341, DOI:10.48550/arXiv.2304.05341.
- L. Kavalsky, V. I. Hegde, E. Muckley, M. S. Johnson, B. Meredig and V. Viswanathan, By how much can closed-loop frameworks accelerate computational materials discovery?, Digital Discovery, 2023, 2, 1112–1125 RSC
.
- B. P. MacLeod,
et al., Self-driving laboratory for accelerated discovery of thin-film materials, Sci. Adv., 2020, 6(20), eaaz8867 CrossRef CAS PubMed
.
- S. G. Baird, J. R. Hall and T. D. Sparks, Compactness matters: Improving Bayesian optimization efficiency of materials formulations through invariant search spaces, Comput. Mater. Sci., 2023, 224, 112134 CrossRef CAS
.
- T. Mohanty, K. S. R. Chandran and T. D. Sparks, Machine learning guided optimal composition selection of niobium alloys for high temperature applications, APL Mach. Learn., 2023, 1, 036102 CrossRef
.
- A. G. Kusne,
et al., On-the-fly closed-loop materials discovery via Bayesian active learning, Nat. Commun., 2020, 11, 5966 CrossRef CAS PubMed
.
- W. Xu, Z. Liu, R. T. Piper and J. W. P. Hsu, Bayesian Optimization of photonic curing process for flexible perovskite photovoltaic devices, Sol. Energy Mater. Sol. Cells, 2023, 249, 112055 CrossRef CAS
.
- J. A. G. Torres, S. H. Lau, P. Anchuri, J. M. Stevens, J. E. Tabora, J. Li, A. Borovika, R. P. Adams and A. G. Doyle, A Multi-Objective Active Learning Platform and Web App for Reaction Optimization, J. Am. Chem. Soc., 2022, 144, 19999–20007 CrossRef CAS PubMed
.
- B. J. Shields, J. Stevens, J. Li, M. Parasram, F. Damani, J. I. M. Alvarado, J. M. Janey, R. P. Adams and A. G. Doyle, Bayesian reaction optimization as a tool for chemical synthesis, Nature, 2021, 590, 89–96 CrossRef CAS PubMed
.
- A. M. Schweidtmann, A. D. Clayton, N. Holmes, E. Bradford, R. A. Bourne and A. A. Lapkin, Machine learning meets continuous flow chemistry: Automated optimization towards the Pareto front of multiple objectives, Chem. Eng. J., 2018, 352, 277–282 CrossRef CAS
.
- Y. K. Wakabayashi, T. Otsuka, Y. Krockenberger, H. Sawada, Y. Taniyasu and H. Yamamoto, Stoichiometric growth of SrTiO3 films via Bayesian optimization with adaptive prior mean, APL Mach. Learn., 2023, 1, 026104 CrossRef
.
- J. Guo, B. Ranković and P. Schwaller, Bayesian Optimization for Chemical Reactions, Chimia, 2023, 77, 31 CrossRef CAS
.
- K. J. Kanarik, W. T. Osowiecki, Y. Lu, D. Talukder, N. Roschewsky, S. N. Park, M. Kamon, D. M. Fried and R. A. Gottscho, Human–machine collaboration for improving semiconductor process development, Nature, 2023, 616, 707–711 CrossRef CAS PubMed
.
- A. Ward and R. Pini, Efficient Bayesian Optimization of Industrial-Scale Pressure-Vacuum Swing Adsorption Processes for CO2 Capture, Ind. Eng. Chem. Res., 2022, 61, 13650–13668 CrossRef CAS
.
-
R. Lam, D. L. Allaire and K. E. Willcox, Multifidelity Optimization using Statistical Surrogate Modeling for Non-Hierarchical Information Sources, 56th AIAA/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, 2015, p. 0143 Search PubMed
.
- K. Kandasamy, G. Dasarathy, J. B. Oliva, J. Schneider and B. Póczos, Gaussian process bandit optimisation with multi-fidelity evaluations, Adv. Neural Inf. Process. Syst., 2016, 29 Search PubMed
.
- A. Tran, T. Wildey and S. McCann, sMF-BO-2CoGP: A sequential multi-fidelity constrained Bayesian optimization framework for design applications, J. Comput. Inf. Sci. Eng., 2020, 20, 031007 CrossRef
.
- S. Takeno, H. Fukuoka, Y. Tsukada, T. Koyama, M. Shiga, I. Takeuchi and M. Karasuyama, Multi-fidelity Bayesian optimization with max-value entropy search and its parallelization, Int. Conf. Mach. Learn., 2020, 9334–9345 Search PubMed
.
-
J. Wu, S. Toscano-Palmerin, P. I. Frazier and A. G. Wilson, Practical Multi-fidelity Bayesian Optimization for Hyperparameter Tuning, Uncertainty in Artificial Intelligence, 2020, pp. 788–798 Search PubMed
.
-
K. Kandasamy, G. Dasarathy, J. Schneider and B. Póczos, Multi-fidelity Bayesian optimisation with continuous approximations, International Conference on Machine Learning, 2017, pp. 1799–1808 Search PubMed
.
- M. Poloczek, J. Wang and P. Frazier, Multi-information source optimization, Adv. Neural Inf. Process. Syst., 2017, 30 Search PubMed
.
- C. Fare, P. Fenner, M. Benatan, A. Varsi and E. O. Pyzer-Knapp, A multi-fidelity machine learning approach to high throughput materials screening, npj Comput. Mater., 2022, 8, 257 CrossRef
.
- H. C. Herbol, M. Poloczek and P. Clancy, Cost-effective materials discovery: Bayesian optimization across multiple information sources, Mater. Horiz., 2020, 7, 2113–2123 RSC
.
- A. Tran, J. Tranchida, T. Wildey and A. P. Thompson, Multi-fidelity machine-learning with uncertainty quantification and Bayesian optimization for materials design: Application to ternary random alloys, J. Chem. Phys., 2020, 153, 074705 CrossRef CAS PubMed
.
- Z. Z. Foumani, M. Shishehbor, A. Yousefpour and R. Bostanabad, Multi-fidelity cost-aware Bayesian optimization, Comput. Methods Appl. Mech. Eng., 2023, 407, 115937 CrossRef
.
- A. Palizhati, M. Aykol, S. Suram, J. S. Hummelshøj and J. H. Montoya, Multi-fidelity Sequential Learning for Accelerated Materials Discovery, ChemRxiv, 2021, preprint, DOI:10.26434/chemrxiv.14312612.v1.
- A. Palizhati, S. B. Torrisi, M. Aykol, S. K. Suram, J. S. Hummelshøj and J. H. Montoya, Agents for sequential learning using multiple-fidelity data, Sci. Rep., 2022, 12, 4694 CrossRef CAS PubMed
.
-
D. Ongari, A. V. Yakutovich, L. Talirz and B. Smit, Building a consistent and reproducible database for adsorption evaluation in Covalent-Organic Frameworks, Materials Cloud Archive, 2021 Search PubMed
.
- D. Huang, T. T. Allen, W. I. Notz and R. A. Miller, Sequential kriging optimization using multiple-fidelity evaluations, Struct. Multidiscip. Optim., 2006, 32, 369–382 CrossRef
.
-
P. Häussinger, R. Glatthaar, W. Rhode, H. Kick, C. Benkmann, J. Weber, H.-J. Wunschel, V. Stenke, E. Leicht and H. Stenger, Noble Gases, Ullmann's Encyclopedia of Industrial Chemistry, 2001 Search PubMed
.
- D. Banerjee, C. M. Simon, S. K. Elsaidi, M. Haranczyk and P. K. Thallapally, Xenon Gas Separation and Storage Using Metal-Organic Frameworks, Chem, 2018, 4, 466–494 CAS
.
- D. Banerjee, A. J. Cairns, J. Liu, R. K. Motkuri, S. K. Nune, C. A. Fernandez, R. Krishna, D. M. Strachan and P. K. Thallapally, Potential of Metal–Organic Frameworks for Separation of Xenon and Krypton, Acc. Chem. Res., 2015, 48, 211–219 CrossRef CAS PubMed
.
- C. S. Diercks and O. M. Yaghi, The atom, the molecule, and the covalent organic framework, Science, 2017, 355(6328), eaal1585 CrossRef PubMed
.
- A. P. Côté, A. I. Benin, N. W. Ockwig, M. O'Keeffe, A. J. Matzger and O. M. Yaghi, Porous, Crystalline, Covalent Organic Frameworks, Science, 2005, 310, 1166–1170 CrossRef PubMed
.
- H. Wang and J. Li, General strategies for effective capture and separation of noble gases by metal–organic frameworks, Dalton Trans., 2018, 47, 4027–4031 RSC
.
- M. Yuan, X. Wang, L. Chen, M. Zhang, L. He, F. Ma, W. Liu and S. Wang, Tailoring Pore Structure and Morphologies in Covalent Organic Frameworks for Xe/Kr Capture and Separation, Chem. Res. Chin. Univ., 2021, 37, 679–685 CrossRef CAS
.
- D. Banerjee, C. M. Simon, A. M. Plonka, R. K. Motkuri, J. Liu, X. Chen, B. Smit, J. B. Parise, M. Haranczyk and P. K. Thallapally, Metal–organic framework with optimally selective xenon adsorption and separation, Nat. Commun., 2016, 7, 1–7 Search PubMed
.
- Z. Jia, Z. Yan, J. Zhang, Y. Zou, Y. Qi, X. Li, Y. Li, X. Guo, C. Yang and L. Ma, Pore Size Control via Multiple-Site Alkylation to Homogenize Sub-Nanoporous Covalent Organic Frameworks for Efficient Sieving of Xenon/Krypton, ACS Appl. Mater. Interfaces, 2020, 13, 1127–1134 CrossRef PubMed
.
- M. Tong, Y. Lan, Q. Yang and C. Zhong, Exploring the structure-property relationships of covalent organic frameworks for noble gas separations, Chem. Eng. Sci., 2017, 168, 456–464 CrossRef CAS
.
- E. Ren and F.-X. Coudert, Thermodynamic exploration of xenon/krypton separation based on a high-throughput screening, Faraday Discuss., 2021, 231, 201–223 RSC
.
- J. Wang, M. Zhou, D. Lu, W. Fei and J. Wu, Virtual screening of nanoporous materials for noble gas separation, ACS Appl. Nano Mater., 2022, 5, 3701–3711 CrossRef CAS
.
- W.-q. Lin, X.-l. Xiong, H. Liang and G.-h. Chen, Multiscale Computational Screening of Metal–Organic Frameworks for Kr/Xe Adsorption Separation: A Structure–Property Relationship-Based Screening Strategy, ACS Appl. Mater. Interfaces, 2021, 13, 17998–18009 CrossRef CAS PubMed
.
- C. M. Simon, R. Mercado, S. K. Schnell, B. Smit and M. Haranczyk, What Are the Best Materials to Separate a Xenon/Krypton Mixture?, Chem. Mater., 2015, 27, 4459–4475 CrossRef CAS
.
- I. Cooley, L. Efford and E. Besley, Computational Predictions for Effective Separation of Xenon/Krypton Gas Mixtures in the MFM Family of Metal–Organic Frameworks, J. Phys. Chem. C, 2022, 126, 11475–11486 CrossRef CAS
.
- N. Gantzler, M.-B. Kim, A. Robinson, M. W. Terban, S. Ghose, R. E. Dinnebier, A. H. York, D. Tiana, C. M. Simon and P. K. Thallapally, Computation-informed optimization of Ni(PyC)2 functionalization for noble gas separations, Cell Rep. Phys. Sci., 2022, 3, 101025 CrossRef CAS
.
- P. Ryan, O. K. Farha, L. J. Broadbelt and R. Q. Snurr, Computational Screening of Metal-Organic Frameworks for Xenon/Krypton Separation, AIChE J., 2010, 57, 1759–1766 CrossRef
.
- B. J. Sikora, C. E. Wilmer, M. L. Greenfield and R. Q. Snurr, Thermodynamic analysis of Xe/Kr selectivity in over 137 000 hypothetical metal–organic frameworks, Chem. Sci., 2012, 3, 2217 RSC
.
- M. V. Parkes, C. L. Staiger, J. J. P. IV, M. D. Allendorf and J. A. Greathouse, Screening metal–organic frameworks for selective noble gas adsorption in air: effect of pore size and framework topology, Phys. Chem. Chem. Phys., 2013, 15, 9093 RSC
.
- Y. G. Chung, E. Haldoupis, B. J. Bucior, M. Haranczyk, S. Lee, H. Zhang, K. D. Vogiatzis, M. Milisavljevic, S. Ling, J. S. Camp, B. Slater, J. I. Siepmann, D. S. Sholl and R. Q. Snurr, Advances, Updates, and Analytics for the Computation-Ready, Experimental Metal–Organic Framework Database: CoRE MOF 2019, J. Chem. Eng. Data, 2019, 64, 5985–5998 CrossRef CAS
.
- C. Gu, Z. Yu, J. Liu and D. S. Sholl, Construction of an anion-pillared MOF database and the screening of MOFs suitable for Xe/Kr separation, ACS Appl. Mater. Interfaces, 2021, 13, 11039–11049 CrossRef CAS PubMed
.
- R. Anderson and D. A. Gómez-Gualdrón, Deep learning combined with IAST to screen thermodynamically feasible MOFs for adsorption-based separation of multiple binary mixtures, J. Chem. Phys., 2021, 154, 234102 CrossRef CAS PubMed
.
- X.-m. Du, S.-t. Xiao, X. Wang, X. Sun, Y.-f. Lin, Q. Wang and G.-h. Chen, Combination of High-Throughput Screening and Assembly to Discover Efficient Metal–Organic Frameworks on Kr/Xe Adsorption Separation, J. Phys. Chem. B, 2023, 127(38), 8116–8130 CrossRef CAS PubMed
.
- A. K. Rappe, C. J. Casewit, K. S. Colwell, W. A. Goddard and W. M. Skiff, UFF, a full periodic table force field for molecular mechanics and molecular dynamics simulations, J. Am. Chem. Soc., 1992, 114, 10024–10035 CrossRef CAS
.
- K. Mukherjee and Y. J. Colón, Machine learning and descriptor selection for the computational discovery of metal-organic frameworks, Mol. Simul., 2021, 47, 857–877 CrossRef CAS
.
- T. F. Willems, C. H. Rycroft, M. Kazi, J. C. Meza and M. Haranczyk, Algorithms and tools for high-throughput geometry-based analysis of crystalline porous materials, Microporous Mesoporous Mater., 2012, 149, 134–141 CrossRef CAS
.
- J. Görtler, R. Kehlbeck and O. Deussen, A Visual Exploration of Gaussian Processes, Distill, 2019 Search PubMed
, https://distill.pub/2019/visual-exploration-gaussian-processes.
-
C. E. Rasmussen and C. K. I. Williams, Gaussian processes for machine learning; Adaptive computation and machine learning, MIT Press, 2006 Search PubMed
.
-
P. Mikkola, J. Martinelli, L. Filstroff and S. Kaski, Multi-Fidelity Bayesian Optimization with Unreliable Information Sources, Proceedings of the 26th International Conference on Artificial Intelligence and Statistics, 2023 Search PubMed
.
- G. Tom, R. J. Hickman, A. Zinzuwadia, A. Mohajeri, B. Sanchez-Lengeling and A. Aspuru-Guzik, Calibration and generalizability of probabilistic models on low-data chemical datasets with DIONYSUS, Digital Discovery, 2023, 2, 759–774 RSC
.
- R. van de Schoot, S. Depaoli, R. King, B. Kramer, K. Märtens, M. G. Tadesse, M. Vannucci, A. Gelman, D. Veen, J. Willemsen and C. Yau, Bayesian statistics and modelling, Nat. Rev. Methods Primers, 2021, 1, 1–26 CrossRef CAS
.
- M. Wang,
et al., Unveiling Electronic Properties in Metal–Phthalocyanine-Based Pyrazine-Linked Conjugated Two-Dimensional Covalent Organic Frameworks, J. Am. Chem. Soc., 2019, 141, 16810–16816 CrossRef CAS PubMed
.
- J. Schrier, A. J. Norquist, T. Buonassisi and J. Brgoch,
In Pursuit of the Exceptional: Research Directions for Machine Learning in Chemical and Materials Science, J. Am. Chem. Soc., 2023, 145(40), 21699–21716 CrossRef CAS PubMed
.
- K. Tran, W. Neiswanger, J. Yoon, Q. Zhang, E. Xing and Z. W. Ulissi, Methods for comparing uncertainty quantifications for material property predictions, Mach. Learn.: Sci. Technol., 2020, 1, 025006 Search PubMed
.
- G. Scalia, C. A. Grambow, B. Pernici, Y.-P. Li and W. H. Green, Evaluating scalable uncertainty estimation methods for deep learning-based molecular property prediction, J. Chem. Inf. Model., 2020, 60, 2697–2717 CrossRef CAS PubMed
.
-
C. Hvarfner, D. Stoll, A. Souza, M. Lindauer, F. Hutter and L. Nardi, πBO: Augmenting acquisition functions with user beliefs for Bayesian optimization, International Conference on Learning Representations (ICLR), 2022 Search PubMed
.
- A. Cisse, X. Evangelopoulos, S. Carruthers, V. V. Gusev and A. I. Cooper, HypBO: Expert-Guided Chemist-in-the-Loop Bayesian Search for New Materials, arXiv, 2023, preprint, arXiv:2308.11787, DOI:10.48550/arXiv.2308.11787.
- R. Han, K. S. Walton and D. S. Sholl, Does chemical engineering research have a reproducibility problem?, Annu. Rev. Chem. Biomol. Eng., 2019, 10, 43–57 CrossRef PubMed
.
- J. Park, J. D. Howe and D. S. Sholl, How reproducible are isotherm measurements in metal–organic frameworks?, Chem. Mater., 2017, 29, 10487–10495 CrossRef CAS
.
- M. Seifrid, R. Pollice, A. Aguilar-Granda, Z. Morgan Chan, K. Hotta, C. T. Ser, J. Vestfrid, T. C. Wu and A. Aspuru-Guzik, Autonomous chemical experiments: Challenges and perspectives on establishing a self-driving lab, Acc. Chem. Res., 2022, 55, 2454–2466 CrossRef CAS PubMed
.
- S. Lo, S. Baird, J. Schrier, B. Blaiszik, S. Kalinin, H. Tran, T. Sparks and A. Aspuru-Guzik, Review of Low-cost Self-driving Laboratories: The “Frugal Twin Concept, ChemRxiv, 2023, preprint, DOI:10.26434/chemrxiv-2023-6z9mq.
- S. G. Baird and T. D. Sparks, What is a minimal working example for a self-driving laboratory?, Matter, 2022, 5, 4170–4178 CrossRef
.
- D. A. Cohn, Z. Ghahramani and M. I. Jordan, Active learning with statistical models, J. Artif. Intell. Res., 1996, 4, 129–145 CrossRef
.
- T. Lookman, P. V. Balachandran, D. Xue and R. Yuan, Active learning in materials science with emphasis on adaptive sampling using uncertainties for targeted design, npj Comput. Mater., 2019, 5, 21 CrossRef
.
- E. Osaro, K. Mukherjee and Y. J. Colón, Active Learning for Adsorption Simulations: Evaluation, Criteria Analysis, and Recommendations for Metal–Organic Frameworks, Ind. Eng. Chem. Res., 2023, 62, 13009–13024 CrossRef CAS
.
-
M. A. Gelbart, J. Snoek and R. P. Adams, Bayesian optimization with unknown constraints, UAI'14: Proceedings of the Thirtieth Conference on Uncertainty in Artificial Intelligence, 2014, pp. 250–259 Search PubMed
.
- O. Chapelle and L. Li, An empirical evaluation of Thompson sampling, Adv. Neural Inf. Process. Syst., 2011, 24 Search PubMed
.
- P. Hennig and C. J. Schuler, Entropy Search for Information-Efficient Global Optimization, J. Mach. Learn. Res., 2012, 13, 1809–1837 Search PubMed
.
- T. Ueno, T. D. Rhone, Z. Hou, T. Mizoguchi and K. Tsuda, COMBO: An efficient Bayesian optimization library for materials science, Mater. Discovery, 2016, 4, 18–21 CrossRef
.
- P. Frazier, W. Powell and S. Dayanik, The knowledge-gradient policy for correlated normal beliefs, Inf. J. Comput., 2009, 21, 599–613 CrossRef
.
- R. Lam, K. Willcox and D. H. Wolpert, Bayesian optimization with a finite budget: An approximate dynamic programming approach, Adv. Neural Inf. Process. Syst., 2016, 29 Search PubMed
.
-
X. Yue and R. A. Kontar, Why non-myopic Bayesian optimization is promising and how far should we look-ahead? a study via rollout, International Conference on Artificial Intelligence and Statistics, 2020, pp. 2808–2818 Search PubMed
.
-
E. Brochu, M. W. Hoffman and N. de Freitas, Portfolio allocation for Bayesian optimization, Proceedings of the Twenty-Seventh Conference on Uncertainty in Artificial Intelligence, 2011, pp. 327–336 Search PubMed
.
- J. Wilson, F. Hutter and M. Deisenroth, Maximizing acquisition functions for Bayesian optimization, Adv. Neural Inf. Process. Syst., 2018, 32 Search PubMed
.
- J. Snoek, O. Rippel, K. Swersky, R. Kiros, N. Satish, N. Sundaram, M. Patwary, M. Prabhat and R. Adams, Scalable Bayesian optimization using deep neural networks, Int. Conf. Mach. Learn., 2015, 2171–2180 Search PubMed
.
-
M. W. Seeger, C. K. Williams and N. D. Lawrence, Fast forward selection to speed up sparse Gaussian process regression, International Workshop on Artificial Intelligence and Statistics, 2003, pp. 254–261 Search PubMed
.
- E. Snelson and Z. Ghahramani, Sparse Gaussian processes using pseudo-inputs, Adv. Neural Inf. Process. Syst., 2005, 18 Search PubMed
.
-
J. Hensman, A. Matthews and Z. Ghahramani, Scalable variational Gaussian process classification, Artificial Intelligence and Statistics, 2015, pp. 351–360 Search PubMed
.
- J. T. Springenberg, A. Klein, S. Falkner and F. Hutter, Bayesian optimization with robust Bayesian neural networks, Adv. Neural Inf. Process. Syst., 2016, 29 Search PubMed
.
-
F. Hutter, H. H. Hoos and K. Leyton-Brown, Sequential model-based optimization for general algorithm configuration, Learning and Intelligent Optimization: 5th International Conference, 2011, pp. 507–523 Search PubMed
.
- R. Gómez-Bombarelli, J. N. Wei, D. Duvenaud, J. M. Hernández-Lobato, B. Sánchez-Lengeling, D. Sheberla, J. Aguilera-Iparraguirre, T. D. Hirzel, R. P. Adams and A. Aspuru-Guzik, Automatic chemical design using a data-driven continuous representation of molecules, ACS Cent. Sci., 2018, 4, 268–276 CrossRef PubMed
.
- A. Deshwal and J. Doppa, Combining latent space and structured kernels for Bayesian optimization over combinatorial spaces, Adv. Neural Inf. Process. Syst., 2021, 34, 8185–8200 Search PubMed
.
- N. Maus, H. Jones, J. Moore, M. J. Kusner, J. Bradshaw and J. Gardner, Local latent space Bayesian optimization over structured inputs, Adv. Neural Inf. Process. Syst., 2022, 35, 34505–34518 Search PubMed
.
-
D. Ginsbourger, R. Le Riche and L. Carraro, Computational Intelligence in Expensive Optimization Problems, Springer, 2010, vol. 2, pp. 131–162 Search PubMed
.
- L. D. González and V. M. Zavala, New paradigms for exploiting parallel experiments in Bayesian optimization, Comput. Chem. Eng., 2023, 170, 108110 CrossRef
.
-
S. Belakaria, A. Deshwal and J. R. Doppa, Max-value Entropy Search for Multi-Objective Bayesian Optimization, Conference on Neural Information Processing Systems, 2019, pp. 7823–7833 Search PubMed
.
- K. M. Jablonka, G. M. Jothiappan, S. Wang, B. Smit and B. Yoo, Bias free multiobjective active learning for materials design and discovery, Nat. Commun., 2021, 12, 2312 CrossRef CAS PubMed
.
- E. Ren and F.-X. Coudert, Enhancing Gas Separation Selectivity Prediction through Geometrical and Chemical Descriptors, Chem. Mater., 2023, 35(17), 6771–6781 CrossRef CAS
.
-
V. I. Kalikmanov, Statistical physics of fluids: basic concepts and applications, Springer Science & Business Media, 2013 Search PubMed
.
-
D. Frenkel and B. Smit, Understanding Molecular Simulation: From Algorithms to Applications, Elsevier Science, 2001 Search PubMed
.
- D. Dubbeldam, A. Torres-Knoop and K. S. Walton, On the inner workings of Monte Carlo codes, Mol. Simul., 2013, 39, 1253–1292 CrossRef CAS
.
- E. Ren and F.-X. Coudert, Rapid Adsorption Enthalpy Surface Sampling (RAESS) to Characterize Nanoporous Materials, Chem. Sci., 2023, 14, 1797–1807 RSC
.
- J. A. Mason, T. M. McDonald, T.-H. Bae, J. E. Bachman, K. Sumida, J. J. Dutton, S. S. Kaye and J. R. Long, Application of a High-throughput Analyzer in Evaluating Solid Adsorbents for Post-Combustion Carbon Capture via Multicomponent Adsorption of CO2, N2, and H2O, J. Am. Chem. Soc., 2015, 137, 4787–4803 CrossRef CAS PubMed
.
- S. Vandenhaute, M. Cools-Ceuppens, S. DeKeyser, T. Verstraelen and V. Van Speybroeck, Machine learning potentials for metal-organic frameworks using an incremental learning approach, npj Comput. Mater., 2023, 9, 19 CrossRef
.
- C.-T. Yang, I. Pandey, D. Trinh, C.-C. Chen, J. D. Howe and L.-C. Lin, Deep learning neural network potential for simulating gaseous adsorption in metal–organic frameworks, Mater. Adv., 2022, 3, 5299–5303 RSC
.
- J. Heinen and D. Dubbeldam, On flexible force fields
for metal–organic frameworks: Recent developments and future prospects, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1363 Search PubMed
.
- M. I. Hossain, J. D. Cunningham, T. M. Becker, B. E. Grabicka, K. S. Walton, B. D. Rabideau and T. G. Glover, Impact of MOF defects on the binary adsorption of CO2 and water in UiO-66, Chem. Eng. Sci., 2019, 203, 346–357 CrossRef CAS
.
- A. Nandy, C. Duan and H. J. Kulik, Using Machine Learning and Data Mining to Leverage Community Knowledge for the Engineering of Stable Metal–Organic Frameworks, J. Am. Chem. Soc., 2021, 143, 17535–17547 CrossRef CAS PubMed
.
- P. Z. Moghadam, S. M. Rogge, A. Li, C.-M. Chow, J. Wieme, N. Moharrami, M. Aragones-Anglada, G. Conduit, D. A. Gomez-Gualdron and V. Van Speybroeck,
et al., Structure-mechanical stability relations of metal-organic frameworks via machine learning, Matter, 2019, 1, 219–234 CrossRef
.
- M. Islamov, H. Babaei, R. Anderson, K. B. Sezginel, J. R. Long, A. J. H. McGaughey, D. A. Gomez-Gualdron and C. E. Wilmer, High-throughput screening of hypothetical metal-organic frameworks for thermal conductivity, npj Comput. Mater., 2023, 9, 11 CrossRef CAS
.
- T. Van Heest, S. L. Teich-McGoldrick, J. A. Greathouse, M. D. Allendorf and D. S. Sholl, Identification of metal–organic framework materials for adsorption separation of rare gases: applicability of ideal adsorbed solution theory (IAST) and effects of inaccessible framework regions, J. Phys. Chem. C, 2012, 116, 13183–13195 CrossRef CAS
.
- A. Rajendran, S. G. Subraveti, K. N. Pai, V. Prasad and Z. Li, How Can (or Why Should) Process Engineering Aid the Screening and Discovery of Solid Sorbents for CO2 Capture?, Acc. Chem. Res., 2023, 56, 2354–2365 CrossRef CAS PubMed
.
- M. Balandat, B. Karrer, D. R. Jiang, S. Daulton, B. Letham, A. G. Wilson and E. Bakshy, BoTorch: A Framework for Efficient Monte-Carlo Bayesian Optimization, Adv. Neural Inf. Process. Syst., 2020, 33 Search PubMed
.
- J. R. Gardner, G. Pleiss, D. Bindel, K. Q. Weinberger and A. G. Wilson, GPyTorch: Blackbox Matrix-Matrix Gaussian Process Inference with GPU Acceleration, Adv. Neural Inf. Process. Syst., 2018 Search PubMed
.
- R. Hickman, M. Sim, S. Pablo-García, I. Woolhouse, H. Hao, Z. Bao, P. Bannigan, C. Allen, M. Aldeghi and A. Aspuru-Guzik, A Brain for Self-driving Laboratories, ChemRxiv, 2023, preprint, DOI:10.26434/chemrxiv-2023-8nrxx.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3dd00117b |
| ‡ Note that the initialization cost of MFBO is higher than that of its SFBO counterpart due to the inclusion of the additional low-fidelity simulations. We include the runtime incurred for initialization. |
| This journal is © The Royal Society of Chemistry 2023 |