Pre-zeolite framework super-MIEC anodes for high-rate lithium-ion batteries

Abstract

Zeolites, Prussian blue analogues (PBAs), and metal–organic frameworks (MOFs) rely on surface-like internal pore diffusions, which have generically low activation barriers to enable the rapid uptake of chemical species. Here we show that Wadsley–Roth oxides (WROs) with pore diameters of 2.5 Å < d < 2.8 Å, while excluding molecules, enable very rapid diffusion of Li⁺ in single-crystal particles >10 μm size. This supports full charge cycles at high rates of ∼30C, which would rival the filling up of gasoline vehicles, while reducing the contact and side reactions with the electrolyte and enhancing the cycle life up to 10 000 cycles. Pore diffusion in WRO mixed ionic and electronic conductors (MIECs) differs from that in lithium intercalation compounds in the off-centered Li storage and low-coordination saddle points for migration. The reduced topological constraints per atom and large free volume in the host also lead to abnormally low or even negative thermal expansion and soft phonons, similar to other open frameworks such as zeolites, PBAs, and MOFs. Based on these guidelines, we have synthesized new composition (Nb₉W₄Ti₄O_42.5) and crystal size-coarsened H-Nb₂O₅ (>20 μm single crystals) with unprecedented performance.

---

Broader context

The key components in lithium-ion batteries are battery electrodes, which must be superfast mixed ionic and electronic conductors (super-MIECs) with an effective activation energy of less than 250 meV. Across different material classes, diffusion energy barriers less than 250 meV are rare for lattice diffusion, yet frequently encountered in surface diffusion that usually requires a host framework with a pore diameter d > 2 Å. Well-known frameworks such as zeolites with internal pore diameters ranging from ∼3 Å to 10 Å and other nanoporous materials can take up large quantities of H₂O (molecular diameter 2.8 Å), H₂, and CO₂ molecules. However, these large-pore open frameworks will not store too many alkali metal atoms due to their excessively large pore sizes, and are thus not suitable for energy-dense fast-charging lithium-ion batteries. Here we define “pre-zeolite” frameworks to mean crystals with percolating open pores with a diameter smaller than the size of H₂O, and therefore excluding water adsorption and molecular adsorption in general, while allowing surface-diffusion like superfast transport of Li⁺. This work offers unique physical insights and a robust approach to developing super-MIEC anodes for high-rate batteries. It also bridges two general material families—nanoporous framework materials and conductive oxides.

Introduction

Mixed ionic and electronic conductors (MIECs) are widely used in solid oxide fuel/electrolysis cells, batteries, electrochromic devices, neuromorphic computing, etc.^1–5 Lithium-ion battery (LIB)'s cathode and anode must be MIECs, and need to store large quantities of Li⁰ on-demand in the lattice interior, accompanied by the redox of certain host elements, often transition metals (TMs). Rapid Li⁺ and e⁻ transport (thus effective Li⁰ “atomic” diffusivity D_Li) should be maintained at all depths of discharge (DODs), which is the most crucial factor for fast charging and high discharge power batteries used in heavy transportation (e.g., boats, trains, and trucks), industrial equipment (e.g., cranes), household products, and electrical-grid regulation.^5–15 Drawing an analogy to superionic solid electrolytes, we define super-MIECs in the LIB context to mean having an effective activation energy Q of D_Li inside the MIEC of less than 250 meV or about 10 k_BT at T = 300 K, which would give D_Li ∼ ν_Lih_Li²e⁻¹⁰ ∼ 5 × 10⁻¹³ m² s⁻¹, for a typical hopping trial frequency ν_Li = 1 THz and a hopping distance h_Li = 1 Å. This means in t = 100 seconds (the typical duration it takes to fill up a gasoline car), or in a full charge/discharge cycle at 36C, the diffusion distance L = (2D_Lit)^1/2 = 10 μm, which is the desirable battery electrode particle size for slurry coating. Note that a super-MIEC with a large DOD range would allow fully dense, single-crystal particles of 10 μm size to be used without requiring electrolyte infiltration into polycrystalline secondary particles, greatly increasing the volumetric energy density and reducing the side reactions. This is superior to nano Li₄Ti₅O₁₂ (the most widely studied and commercialized anode for fast charging¹⁶) with low D_Li. Some reported oxide anodes can be viewed as super-MIECs^12,17–19 (especially for Nb-based materials with >1 μm size, Table S1, ESI†), which can support a full charge/discharge cycle within several minutes.

The dual demands of large “Li adsorption” per volume and maintaining D_Li ≥ 5 × 10⁻¹³ m² s⁻¹ put stringent requirements on transition-metal oxide MIECs. Across material classes, diffusion barriers generically less than 250 meV are frequently encountered only in surface diffusion. Diffusion in tight-fitting atomic channels for the Li⁺ cation (Shannon ionic diameters of 1.18 Å for 4-fold coordinated, 1.52 Å for 6-fold coordinated and 1.84 Å for 8-fold coordinated Li⁺), such as inside LiFePO₄, typically gives Q values ranging from 270 meV to 500 meV.²⁰ By tight-fitting, we mean that the diffusing species at some point strongly interact with the host on two or more sides (e.g., in the LiCoO₂ lattice; stoichiometric LiCoO₂ in a fully lithiated state has sluggish Li⁺ diffusivity), unlike surface diffusion where the mobile species mainly interact with the host on one side. If the host framework has a large enough pore diameter > 2 Å, then this allows for the Li⁺ to adsorb on the side wall of the pore, rather than be constrained at the center of a channel. Adsorption/uptake of external species is well-known in the realm of framework materials and molecular sieves. For example, zeolites have internal pore diameters ranging from ∼3 Å to 10 Å, which can take up large quantities of H₂O (molecular diameter 2.8 Å), H₂, and CO₂ molecules.²¹ The word “zeolite” originated from its hygroscopicity, which literally meant “stones that give off water steam when heated”.²² The open aluminosilicate framework of zeolite A often gives entropic elasticity and a negative coefficient of thermal expansion (CTE) when dehydrated, which however turns positive in its fully hydrated state, when the pore is filled up.²³ Well-known framework crystals also include Prussian blue analogues (PBAs) and metal–organic frameworks (MOFs). These open frameworks often have a negative CTE, tolerance for a wide variety of molecules inside the pores, and surface-diffusion-like rapid mass transport for molecules that can fit inside the pores, making them ideal gas storage media.^24–26 Some PBAs and MOFs are even electronically conductive, making them super-MIECs.^27–29 But these large-pore open frameworks, even though generally showing diffusivity >5 × 10⁻¹³ m² s⁻¹, will not store too many alkali metal atoms per volume due to the excessively large pore sizes, and thus are not optimal for high-volumetric-energy density fast-charging electrodes.

As H₂O is the second smallest simple molecule (slightly larger than NH₃), a basic question is if it is possible to exclude molecular adsorption, while still allowing alkali ions to have surface-like adsorption and diffusion on the sidewalls of the “internal pore surfaces” of the framework structures. In this work, we define a pre-zeolite framework to mean crystals with percolating open pores with a diameter smaller than 2.8 Å, and therefore exclude water adsorption and generally all molecular adsorptions, while allowing surface-diffusion-like transport of Li⁺. We are mainly interested in multi-valent TM-containing pre-zeolite frameworks, and will show that these frameworks, if electronically conductive, are generally all super-MIECs. We will demonstrate the structural and chemical design criteria for such pre-zeolite frameworks, in particular Wadsley–Roth structures containing multi-valent Nb, W, and Ti and having an anion-to-cation ratio (ACR) around 2.5 (mostly between 2.33 and 2.8). While some of the compositions have been shown before, the universality and robustness of these open-pore design rules provide a cornucopia of surface-diffusion-like high-capacity super-MIECs, that would allow 10 μm sized single crystals with >30C charging/discharging rates, rivaling fossil-fuel vehicles in the charging rate.

Results and discussion

Wadsley–Roth pore with 2.5 Å < d < 2.8 Å is a sufficient condition for ultrafast Li⁺ diffusion

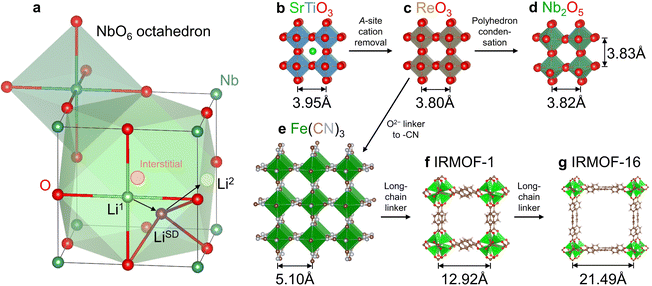
We selected a representative Wadsley–Roth oxide (WRO) H-Nb₂O₅, and conducted first-principles calculations to clarify the physical picture of surface-like diffusion. As shown in Fig. S1a, ESI,† there are 14 open pores within the a–c plane of an H-Nb₂O₅ unit cell containing 28 Nb and 70 O. To study the storage and migration mechanism of Li⁺ in the dilute lithiated state, we added one Li atom into a 1 × 3 × 1 supercell (containing 84 Nb and 210 O). Pore P6 (the same as P3 by symmetry) was picked randomly and Li⁺ was placed on the interstitial site in the center of a pore surrounded by 12 O (consisting of six square planes, including two within the a–c plane perpendicular to the b axis and four parallel to the b axis on the sidewalls of the cage; see the schematic for a cubic cage in Fig. 1 where lattice distortions were neglected for simplicity). In conventional transition-metal oxides, such high-symmetry interstitial sites are typically preferred sites for Li⁺ storage, for example, octahedral sites in layered LiCoO₂ and lithiated Li₄Ti₅O₁₂ (Li₇Ti₅O₁₂) and tetrahedral sites in spinel LiMn₂O₄. However, this does not apply to H-Nb₂O₅, whose interstitial site (pore) is so large that a pore-centered Li⁺ would automatically relax to a sidewall and adopt a square planar geometry (such as sites Li¹ and Li² in Fig. 1(a)). We refer to such one-sided behavior as “surface adsorption” like. Such a storage mechanism has been reported in ReO₃ experimentally using the diffraction technique³⁰ and in Nb₂TiO₇³¹ and Nb₁₂WO₃₃³² by atomistic simulations.

Fig. 1 Structural features of Wadsley–Roth pores. (a) Schematic Li⁺ storage (sites Li¹ and Li²) and migration pathway (from Li¹ to Li²via Li^SD) within a “cubic” Wadsley–Roth pore. Lattice distortions are neglected for simplicity. Structural relationship among (b) cubic SrTiO₃, (c) ReO₃, (d) H-Nb₂O₅ around the T6 tunnel, (e) Prussian blue analogue Fe(CN)₃, and (f) metal–organic frameworks IRMOF-1 and (g) IRMOF-16 with varying pore sizes. Marked in (b)–(g) are the cation–cation distances, which divided by 2^1/2 gives the characteristic pore size. WROs are termed “pre-zeolite frameworks” due to their considerably smaller pore size than zeolites with 3–10 Å, while PBAs and MOFs may be considered as “zeolite-like” and “post-zeolite” frameworks.

We next used the climbing image nudged elastic band (NEB) method to calculate the migration path and energy barrier for Li⁺ hopping between two neighbouring square-planar sites from one on the sidewall to the one in the a–c plane. We found the former has an energy of 130 meV lower than the latter, with a forward migration barrier of 190 meV and a backward barrier of 60 meV (Fig. S1b, ESI†). Such low barriers are surface-diffusion like, which supports the super-MIEC behavior. Yet a more striking feature is the saddle-point configuration, where the coordination number of Li⁺ decreases from 4 in the square-planar ground-state (see the schematic Li⁺ migration pathway from sites Li¹ to Li² in Fig. 1(a)) to a remarkably low coordination of 3 (marked as Li^SD), which is rare for lattice diffusion in crystals (The critical role of the ultra-low coordination number at the saddle point of Li⁺ hopping was not realized in previous studies.^31,32). We recall that surface diffusion can take place via low-coordination-number adatoms which reside on adsorption sites on the surface plane, and it does not cost much elastic energy because these adatoms can veer into the vacuum half-space (with zero moduli) instead of the solid. The analogy is thus: the saddle-point Li⁺ veers into the pore with a large free volume like an adatom, and this minimizes elastic energy penalty, which typically applies to the crowded saddle-point configuration and slows down diffusion due to steric hindrance (for example, octahedral-to-tetrahedral-to-octahedral Li⁺ diffusion in LiCoO₂). Therefore, one can justifiably call Li⁺ diffusion in Wadsley–Roth H-Nb₂O₅ surface-like diffusion, and these “internal surfaces” are distinguishable from physical surfaces as the pores are not large enough to allow even the smallest molecules like H₂O to enter. The latter was proved by thermogravimetric analysis for wet WRO powders (Fig. S2, ESI†), where no weight loss occurred above 100 °C (surface water was mostly removed below 100 °C). Indeed, WROs have been reported as bulk intercalation pseudocapacitors, and the bulk Li⁺ diffusion kinetics share a similar dependence on the charge/discharge rate as the one observed for electric double-layer supercapacitors.³³

From a crystallographic perspective, WROs are related to the ReO₃ structure³⁴ (Fig. 1(c), which differs from the parent perovskite structure ABO₃, e.g., SrTiO₃ in Fig. 1(b), by removing the A-site cation) by condensing some of the corner-sharing octahedra in ReO₃ to edge-sharing ones on the boundaries of “blocks”.³⁵ This results in better structural rigidity and d–d orbital coupling. (Compared to corner-sharing ones, edge-sharing octahedra give shorter metal–metal distance and suitable orbital orientations—d_xy, d_yz, and d_xz point to edge centers—for d–d coupling). Meanwhile, there are still sufficient numbers of corner-sharing octahedra inside the “blocks”³⁵ that form pores for Li⁺ surface-like diffusion. For cubic SrTiO₃ and ReO₃, one may estimate the pore size by the cation–cation distance (marked in Fig. 1(b)–(g)) divided by 2^1/2, thus being 2.79 Å for SrTiO₃ and 2.69 Å for ReO₃. A similar pore size is also noted in H-Nb₂O₅, for example, 2.70–2.71 Å for P6 (Fig. 1(d)), despite the lattice distortion and lower symmetry. Such pores allow for adatom-like Li⁺ storage and internal surface-like diffusion, and are even large enough for interstitial Na⁺ and K⁺ storage (but not Na⁺/K⁺ surface-like diffusion), as cubic NaNbO₃ and KNbO₃ have cage sizes of 2.84 Å and 2.87 Å (e.g., see atomic structures at materialsproject.org³⁶), respectively. Therefore, the off-center Li⁺ storage and Li⁺ migration without steric hindrance are both verifiable, distinguishable features. Meanwhile, the framework oxygen can be replaced by other groups if large pore sizes are desired. The examples beyond LIB applications include replacing the O²⁻ for corner-sharing octahedra by (CN)⁻ in Fe(CN)₃ (Fig. 1(e)) and other PBAs for Na⁺ battery cathodes³⁷ and proton battery cathodes (H₃O⁺ storage in the cage²⁹), and by larger chain-molecules in mesoporous metal–organic frameworks such as IRMOF-1 (Fig. 1(f)) and IRMOF-16 (Fig. 1(g)), with varying pore sizes for gas storage and catalysis.³⁴ A WRO is thus identified as a pre-zeolitic framework that does not have strong hygroscopy, but can take up a large amount of Li atoms electrochemically.

The calculations above rationalize the superfast Li⁺ transport in a model WRO. The insights into surface-like diffusion, as opposed to diffusion in tight-fitting channels of lithium intercalation oxides, should apply to all open pore structures with pre-zeolitic pore diameters 2.5 Å < d < 2.8 Å. We thus hypothesize that the Wadsley–Roth structure by itself, with a pore channel locally similar to ReO₃, has already ensured facile bulk diffusion. Thus in real batteries, bulk diffusion in these compounds is likely not the bottleneck. The real challenge is in the boundary conditions, where side reactions and solid electrolyte interphases (SEIs) at the oxide surface build up impedance and degrade the battery during both early and prolonged cycles. As long as the 2.5 Å < d < 2.8 Å pores are maintained, we can tune the compositional space to optimize anode–electrolyte interactions to improve the cyclability. Finally, the large free volume gives rise to other structural and physical properties, such as anomalously low coefficient of thermal expansion (CTE) and formation of planar defects, which suggest soft phonon modes that could buffer strain and facilitate transport during electrochemical cycling. These shall be investigated in the following sections.

Rate parities: super-MIEC anodes with a large free volume and low CTE

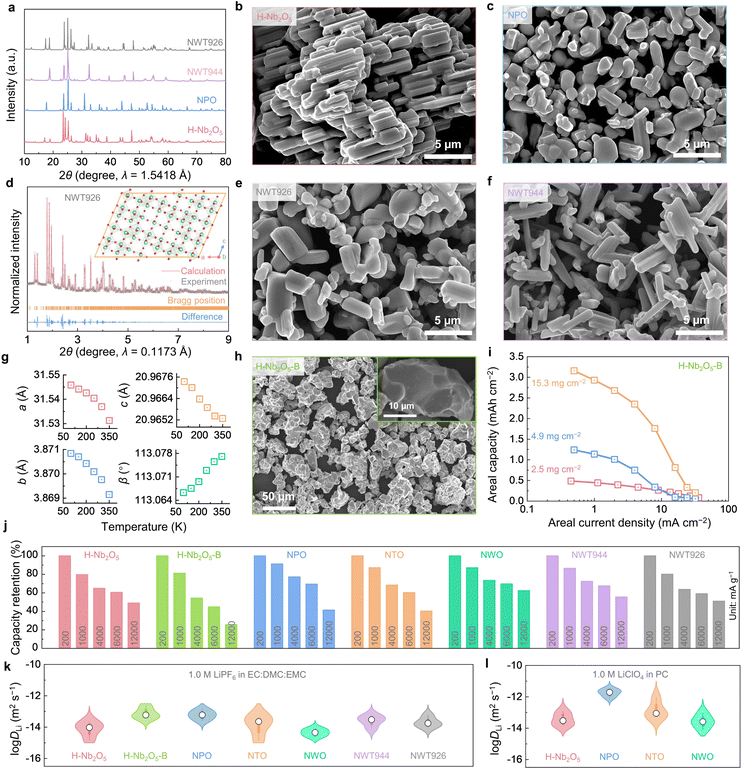
We have synthesized H-Nb₂O₅, Nb₉PO₂₅ (PNb₉O₂₅, NPO), a well-studied WRO Nb₂TiO₇ (TiNb₂O₇, NTO), a closely-related tungsten bronze structure oxide Nb₁₈W₁₆O₉₃ (NWO, also with a large pore size), and two new ternary oxides Nb₉W₂Ti₆O_40.5 (NWT926) and Nb₉W₄Ti₄O_42.5 (NWT944) via solid-state synthesis.^9,17,38,39 For all the samples, we heat-treated the powders at high temperatures (1100–1125 °C) to grow them into micron-sized single crystals. The powders obtained are phase-pure (shown by X-ray diffraction (XRD) in Fig. 2(a)) with crystal sizes shown by scanning electron microscopy (SEM) in Fig. 2(b), (c), (e) and (f). Using synchrotron powder XRD data (Fig. 2(d)), we analyzed the crystal structure of NWT926 and confirmed that it is a new phase with large pores and monoclinic symmetry (crystal structure in the inset of Fig. 2(d); data listed in Table S2, ESI†). To shed light on the free volume in the crystal lattice (critical for surface-like diffusion), we calculated the average atomic volume (defined as the supercell volume divided by the number of atoms in the supercell) of H-Nb₂O₅, NPO, NTO, NWO, and NWT926, which are in the range of 13.2–14.4 ų. The average atomic volume has been shown to correlate well with the CTE, a phonon-controlled property, and could be abnormally low or even negative in framework materials like zeolites.⁴⁰ The obtained values in our materials are close to the critical value that leads to a crossover from positive to a negative CTE (Fig. S3, ESI†). (Local average atomic volume at the pores of WROs can also be estimated from the geometry by neglecting lattice distortion and assuming a cubic ReO₃-type local structure. For example, for P6 of H-Nb₂O₅ in Fig. 1(e), it is around 3.82³/4 = 13.9 ų.) We measured the CTEs of our powder samples using in situ XRD measurements (Fig. S4–S8, ESI†) conducted at 100–650 K, and the linear CTE α was obtained from the refined primary-cell volume V₀(T). Compared to the CTE database for 260 compounds centered around ∼7 × 10⁻⁶ K⁻¹ (Fig. S9 and Table S3, ESI†), H-Nb₂O₅, NPO, NTO, NWO, and NWT926 indeed all have negative or close-to-zero CTEs (Fig. S4–S8, ESI†). Of particular interest is NWT926 which has negative CTEs along all three lattice axes (Fig. 2(g)), which are rare and termed triaxial negative CTEs. The reason may be that the transverse vibrations of oxygen atoms in the M–O–M (M = Nb, Ti, W) with increasing temperature lead to the rotation of corner-sharing MO₆ polyhedra, giving rise to the contraction.^24,41,42 Such anomalously low CTEs, similar to other open frameworks such as zeolites, PBAs, and MOFs, indirectly support the notion of surface-like adsorption and diffusion in all WRO super-MIECs.

Fig. 2 Structural characterization and electrochemical performances of super-MIEC anodes. (a) XRD patterns of H-Nb₂O₅, NPO, NWT944 and NWT926. SEM images of (b) H-Nb₂O₅, (c) NPO, (e) NWT926, (f) NWT944, and (h) H-Nb₂O₅-B. (d) The high-energy synchrotron diffraction pattern and the refinement analysis of NWT926, and the inset shows the structural illustration of the new phase. (g) Primary-cell parameters as a function of temperature T of NWT926. (i) The effect of current densities and mass loadings on the areal capacities of H-Nb₂O₅-B. (j) Capacity retention at different rates and (k), (l) electrochemically measured D_Li of H-Nb₂O₅, H-Nb₂O₅-B, NPO, NTO, NWO, NWT944 and NWT926.

We next measured the electrochemical performances of H-Nb₂O₅, NPO, NWT926, and NWT944 as LIB anodes in half cells and compared them with NTO and NWO references. By definition, super-MIEC materials should have high intrinsic electronic conductivity to assist electronic percolation. Therefore, we minimized the usage of conductive carbon in the composite electrode and tested all the anodes with >85 wt% active materials. At a low rate of 200 mA g⁻¹ and a lower cutoff voltage of 1.0 V (vs. Li⁺/Li), H-Nb₂O₅, NPO, NTO, NWO, NWT926, and NWT944 have specific capacities of 192 mA h g⁻¹, 210 mA h g⁻¹, 236 mA h g⁻¹, 180 mA h g⁻¹, 187 mA h g⁻¹, and 204 mA h g⁻¹, respectively. They all have suitable average voltage (1.5–1.7 V vs. Li⁺/Li), high Coulombic efficiency (CE), and a stable charge–discharge profile upon cycling (Fig. S10–S12, ESI†). When tested at higher rates (for both charge and discharge) up to 16 000 mA g⁻¹ (roughly 200∼300C), we found all six materials have good capacity retention (for the capacity at 200 mA g⁻¹, Fig. 2(j)). At 6000 mA g⁻¹, the capacity retentions are >50%, offering 116 mA h g⁻¹ capacity for H-Nb₂O₅, 146 mA h g⁻¹ for NPO, 142 mA h g⁻¹ for NTO, 125 mA h g⁻¹ for NWO, 110 mA h g⁻¹ for NWT926, and 138 mA h g⁻¹ for NWT944. These correspond to ∼60C, which would satisfy many high-rate applications, shifting the rate-limiting consideration to the cathode or electrolyte in the full cells.

D _Li is the composite of the Li⁺ ion and e⁻ polaron diffusivities in ambipolar diffusion theory. First, the electronic conductivities of Nb₂O₅ and Li_0.1Nb₂O₅ were calculated to be 1.0 × 10⁻⁶ S m⁻¹, and 6.6 S m⁻¹, respectively, by measuring the 2-probe electronic resistance, area, and thickness of the pellet samples. Therefore, slightly lithiated Nb₂O₅ can be regarded as a good electronic conductor. To enable facile kinetics at 60C for ∼1 μm single crystals, D_Li needs to be ∼10⁻¹⁴ m² s⁻¹. To verify, galvanostatic intermittent titration technique (GITT) measurements (Fig. S13, ESI†) were conducted at different states of charge and at temperatures of 10–50 °C relevant for LIB operations. As shown by the violin plots in Fig. 2(k), D_Li values from GITT measurements are within the range of 10⁻¹⁵–10⁻¹² m² s⁻¹ for all the anodes. These values are comparable to the D_Li values of 10⁻¹⁶–10⁻¹² m² s⁻¹ in famous cathodes of LiCoO₂ and LiNi_0.33Co_0.33Mn_0.33O₂ (Fig. S14, ESI,† similarly calculated from GITT measurements). The measurements above were from half cells using ethylene carbonate (EC)-based electrolytes. Interestingly, when we switched to propylene carbonate (PC)-based electrolytes, H-Nb₂O₅, NPO, NTO, and NWO showed 1–2 orders of magnitude higher D_Li (Fig. 2(l) and Fig. S15, ESI†) than their respective values measured by the GITT in EC-based ones. It suggests that the measured diffusivities may not be the intrinsic ones in the crystal lattice but are likely to be constrained by SEIs formed during electrochemical tests. This inspires us to further modify the morphology and grow larger single crystals with less electrochemically active surfaces. We have made successful attempts to grow H-Nb₂O₅ in ∼20 μm-sized particles (abbreviated as H-Nb₂O₅-B; XRD in Fig. S16c, ESI;† SEM in Fig. 2(h) and a particle size analyzer in Fig. S16d, ESI† were used to obtain an agglomeration size of D₅₀ = 49.0 μm) and again tested its electrochemical performance (216 mA h g⁻¹ capacity at 200 mA g⁻¹, Fig. S16b, ESI†). Remarkably, H-Nb₂O₅-B shows superior rate capability at different mass loadings (Fig. 2(i)), which is similar to H-Nb₂O₅ (Fig. 2(j)), despite ∼10 times larger grain size, and it can deliver an impressive capacity of 110 mA h g⁻¹ at 6000 mA g⁻¹ (∼60C). The D_Li value of H-Nb₂O₅-B from GITT measurements is also >10 times larger than H-Nb₂O₅. Therefore, we conclude that WROs have high D_Li in electrochemical cells and superior rate performance, which is relatively insensitive to oxide compositions but more sensitive to SEIs. The formation and growth of SEIs depend on the electro-chemo-mechanical interactions between active electrode materials and the electrolytes, which affect the rate capability and cycling stability of the anode and the full cell.

Cyclability disparities: towards the long cycle life of high-rate LIBs

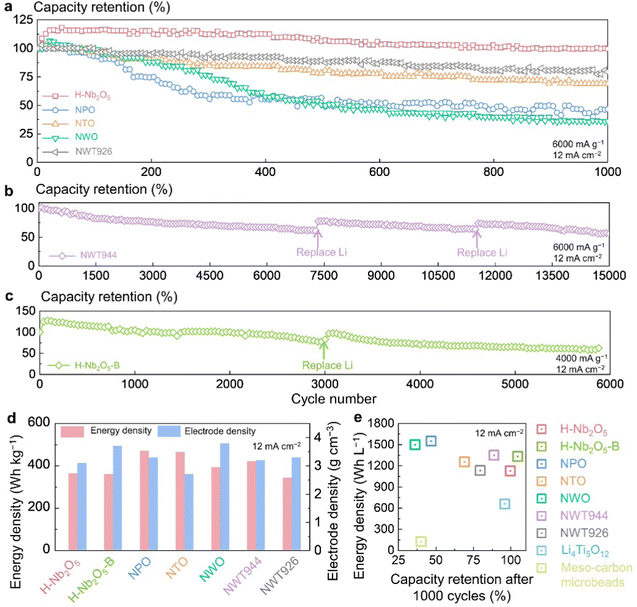
High-rate LIBs require an extended cycle life, and >10 000 cycle life has been demonstrated by the LiFePO₄ cathode and Li₄Ti₅O₁₂ anode. We therefore evaluated the cycling stability of the synthesized super-MIEC anodes in half cells (i.e., with excess electrolyte and Li reservoir). As shown in Fig. 3(a), when cycled at 6000 mA g⁻¹ (12 mA cm⁻², ∼60C), NTO, NPO, and NWO rapidly decay and have capacity retentions of 69%, 47%, and 36% after 1000 cycles, respectively. H-Nb₂O₅ and NWT926 have better cycling stability, with 100% and 80% capacity retentions after 1000 cycles. In comparison, NWT944 shows remarkably improved stability (Fig. 3(b)), with 62% capacity retention after 7000 cycles (5.4% decay per 1000 cycles). To exclude capacity decay drivers from the other battery components, we replaced the Li metal counter electrode and the electrolytes after 7300 and 11 500 cycles (severe degradation of the Li metal electrode is shown in Fig. S17, ESI†). 56% capacity retention over 15 000 cycles has thus been achieved in NWT944. On the other hand, by tailoring the morphology and increasing the particle size, we show in Fig. 3(c) that H-Nb₂O₅-B has 5% higher capacity after 1000 cycles than its initial capacity (attributed to the activation process occurring in electrochemical cycling⁴³), and it also has capacity retentions of 77% after 3000 cycles, and 60% after 5800 cycles when cycled at 4000 mA g⁻¹ (similar areal current density of 12 mA cm⁻²), representing improvements over H-Nb₂O₅. Therefore, our new composition (NWT944) and crystal size-coarsened H-Nb₂O₅-B both demonstrate a superior cycle life compared with previous WROs^{9,12,17–19,44–48} (Table S1, ESI†). With suitable coatings and electrolyte modifications, we believe extended cycle life can be realized in full cells in all WROs, as the lattice volume change is small. (Preliminary investigations have been conducted in coin-type full cells using the H-Nb₂O₅ anode paired with the LiNi_0.5Mn_1.5O₄ or LiFePO₄ cathode, and in pouch-type full cells using the H-Nb₂O₅ anode paired with the LiNi_0.6Co_0.2Mn_0.2O₂ cathode and the H-Nb₂O₅-B anode paired with the LiCoO₂ cathode, as shown in Fig. S18, ESI†).

Fig. 3 Cyclability comparison among the Super-MIEC anodes. Capacity retention of (a) H-Nb₂O₅, NPO, NTO, NWO, NWT926, and (b) NWT944 at 6000 mA g⁻¹, and (c) capacity retention of H-Nb₂O₅-B at 4000 mA g⁻¹. (d) Gravimetric energy density and electrode density of super-MIEC anodes including H-Nb₂O₅, H-Nb₂O₅-B, NPO, NTO, NWO, NWT944, and NWT926. (e) Volumetric energy density and capacity retention of super-MIEC anodes including H-Nb₂O₅, H-Nb₂O₅-B, NPO, NTO, NWO, NWT944, NWT926, Li₄Ti₅O₁₂ and meso-carbon microbeads.

Super-MIEC anodes compete with Li₄Ti₅O₁₂ in high-rate applications. We compared the gravimetric energy density and electrode density of super-MIEC anodes in Fig. 3(d), which gives volumetric energy density in the range of 1128∼1550 W h L⁻¹ (at 6000 mA g⁻¹, Fig. 3(e)) with the rank of NPO > NWO > NWT944 > H-Nb₂O₅-B > NTO > NWT926 > H-Nb₂O₅. (More detailed comparisons on characterized particle size, electrode density, initial Coulombic efficiency, capacity, rate retention, average voltage, energy density, and cyclability are listed in Tables S4 and S5, ESI†.) These values are much higher than 658 W h L⁻¹ for Li₄Ti₅O₁₂ and 127 W h L⁻¹ for meso-carbon microbeads, which are the commercially prevailing high-rate anodes. Through trial and error, it appears that Nb is the baseline element to form the Wadsley–Roth oxide structure, W is beneficial for increasing the crystal density and energy density, and Ti is beneficial for enhancing the structural stability. We note that in many applications, the cycle life is an important metric, which sets NWT944 and H-Nb₂O₅-B to be the best candidates among the super-MIEC anodes investigated.

Other lattice-structural and microstructural features

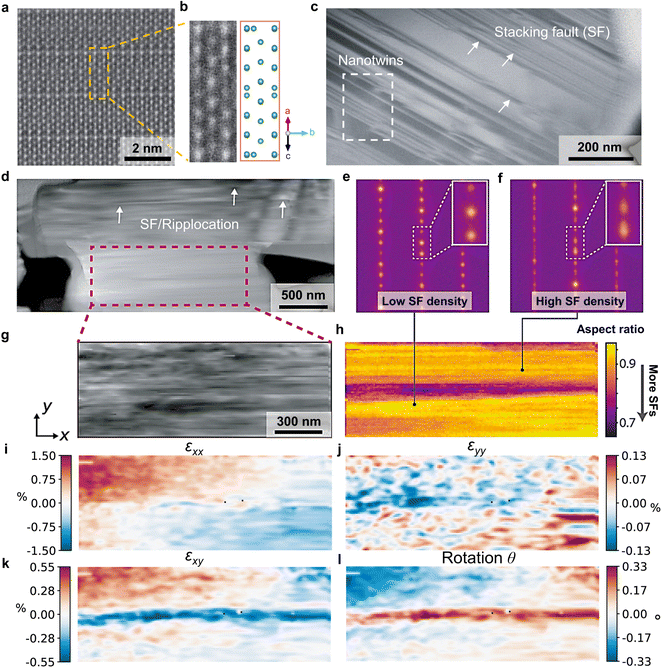
As an anode must host and disgorge a great amount of excess lithium reversibly, a robust atomic structure is required. As shown by the top surfaces and cross-sections of H-Nb₂O₅, NPO, and NWT944 electrodes (Fig. S19, ESI†), the single-crystal WRO particles did not fracture after cycling. This means the particles could survive the mechanical stresses and stress-corrosion cracking during cyclic electrochemical loading, which would benefit the long-term cycling stability. Indeed, the scanning transmission electron microscopy – high-angle annular dark-field (STEM-HAADF) image in Fig. 4(a) shows well-ordered crystal lattices without point defects (corresponding atomic structure for the Nb sublattice in Fig. 4(b)).

Fig. 4 Lattice-structural features of Super-MIEC anodes. (a) High-resolution scanning transmission electron microscopy-high-angle annular dark-field (STEM-HAADF) image of H-Nb₂O₅ as well as (b) the corresponding crystal structure. (c), (d), and (g) Low-magnification STEM-HAADF images showing the focused ion beam (FIB) lift-out transmission electron microscopy (TEM) foil of H-Nb₂O₅. (e) and (f) Nanobeam electron diffraction patterns showing the spatial fluctuations in the SF density of the selected area of (h). 4D-STEM lattice strain mapping of components (i) ε_xx, (j) ε_yy, and (k) ε_xy, and (l) lattice rotation angle θ within the x–y plane.

However, over a larger length scale of a few hundred nanometers, extended defects including stacking faults, nano-twins, and ripplocations⁴⁹ were found in the WRO single crystals (Fig. 4(c), (d) and Fig. S20, ESI†). Different levels of diffuse scattering exist in the nanobeam electron diffraction patterns (Fig. 4(e) and (f)) at different locations of Fig. 4(d), and mapping of stacking fault density in Fig. 4(g) and (h) further indicates spatial variations. As these planar defects are formed in pristine H-Nb₂O₅ synthesized from high-temperature heat treatment, the observations indicate their relatively low formation energies. It is in contrast with the high formation energy of point defects, but consistent with the fact that the large free volume and low CTE in WROs are a result of low polyhedral packing density and their collective twisting/relaxation. In addition, strain mapping by four-dimensional scanning transmission electron microscopy (4D-STEM) at 10 nm spatial resolution (Fig. 4(g)) visualizes the lattice at the mesoscale, with a standard deviation of 1.53% for ε_xx, 1.44% for ε_yy, 0.20% for ε_xy, and 0.12% for the rotation angle θ (Fig. 4(i)–(l)).

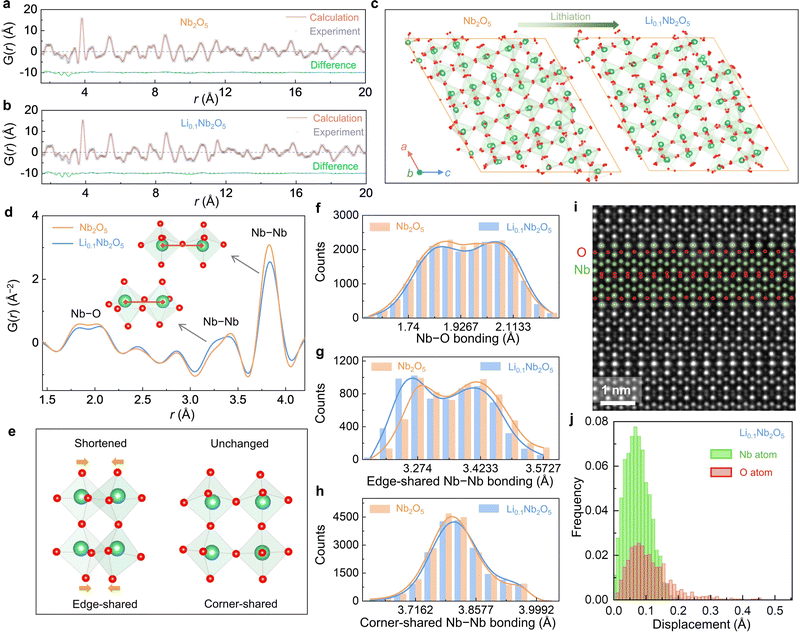
Pair distribution function (PDF) analysis was conducted on unlithiated (Nb₂O₅ in Fig. 5(a)) and slightly lithiated (Li_0.1Nb₂O₅ in Fig. 5(b)) H-Nb₂O₅ powders using synchrotron X-ray total scattering. Experimentally, the raw total scattering data were collected and then transformed into the real-space PDF G(r).^50,51 For Nb₂O₅, we noted the measured G(r) significantly deviates from the calculated one from the “perfect” H-Nb₂O₅ structure (Fig. 1(a)), especially at large r up to 20 Å. We thus conducted reverse Monte Carlo (RMC) simulations to fit the experimental data (calculated G(r) shown in Fig. 5(a), (b)) and to analyze the structure. As shown by simulated atomic structures (Fig. 5(c)) after converged RMC simulations, there are distortions at both Nb and O sublattices, even though O displacements (average value 0.06 Å for Nb₂O₅ and 0.05 Å for Li_0.1Nb₂O₅) are larger than Nb displacements (average value 0.01 Å for Nb₂O₅ and 0.01 Å for Li_0.1Nb₂O₅, Fig. S21, ESI†). To compare the structure before and after lithiation, we focused on G(r) data at 1.5∼4.0 Å (Fig. 5(d)), especially the ∼1.9 Å double peaks for nearest Nb–O bonds, the ∼3.3 Å double peaks for nearest Nb–Nb bonds for edge-sharing NbO₆ octahedra, and the ∼3.8 Å peak for Nb–Nb bonds for corner-sharing NbO₆ octahedra. When lithiating from Nb₂O₅ to Li_0.1Nb₂O₅, we found minimum changes in ∼1.9 Å Nb–O bonds (Fig. 5(f)) and ∼3.8 Å Nb–Nb bonds (Fig. 5(h)) but shortened Nb–Nb bonds at ∼3.3 Å (Fig. 5(g)). It indicates the pore structure is relatively robust and does not involve much structural change upon lithiation. To confirm, we conducted STEM-HAADF on Li_0.1Nb₂O₅, which provides contrasts for light-element O. As shown in Fig. 5(i), the lattice is again well ordered, yet slight distortions on the O sublattice are notable. Quantitative analysis of the atomic positions (Fig. 5(j)) shows 0.004 Å (with a standard deviation of 0.008 Å) displacements in the Nb sublattice and 0.02 Å (with a standard deviation of 0.02 Å) displacements in the O sublattice, and some O atoms are displaced further up to ∼0.45 Å. These results agree with the diffraction and RMC data.

Fig. 5 Microstructural features of Super-MIEC anodes. Pair distribution function (PDF) measurements as well as Reverse Monte Carlo (RMC) simulation for (a) Nb₂O₅ and (b) Li_0.1Nb₂O₅. (c) Structural comparison between Nb₂O₅ and Li_0.1Nb₂O₅ by using the results of RMC simulation. (d) Comparison of original PDF experimental data and (e) schematic diagram of the structural changes before and after lithiation. Comparison of bonding lengths of (f) Nb–O, (g) edge-sharing Nb–Nb, and (h) corner-sharing Nb–Nb of Nb₂O₅ and Li_0.1Nb₂O₅. (i) Variable-angle HAADF image in scanning transmission electron microscopy as well as the (j) distribution of displacement for Li_0.1Nb₂O₅.

Lastly, we used in situ XRD to measure the CTEs of lithiated H-Nb₂O₅ at 100–200 K (Fig. S22 and S23, ESI†). Interestingly, negative CTEs of −8.80 × 10⁻⁶ K⁻¹ and −4.21 × 10⁻⁶ K⁻¹ were obtained for Li_0.2Nb₂O₅ and Li_1.6Nb₂O₅, respectively, which are lower than that of −0.53 × 10⁻⁶ K⁻¹ for non-lithiated H-Nb₂O₅. This again suggests that the large free volume holds even upon electrochemical lithiation.

Conclusions and outlook

We have explained why the WROs have fast Li⁺ diffusion ability and abnormally low CTEs. The low topological constraints per atom and large free volume in the crystal lattice should be the fundamental cause of soft phonons, low CTE, low-coordination-number Li⁺ storage, and surface-like diffusion, similar to other open frameworks such as zeolites, PBAs, and MOFs. But unlike those frameworks that take up molecules, the WRO frameworks with 2.5 Å < d < 2.8 Å can only take up atoms like Li. The phonon anomalies are expected to influence the pre-exponential factor of the Arrhenius-type diffusivity. There is literature on D_Li measured by pulsed-field-gradient nuclear magnetic resonance (PFG NMR) spectroscopy, which is a bulk measurement and not sensitive to SEIs. In Fig. S2a, ESI† of ref. 9, in Li_xNb_yW_zO_(5y+6z)/2, we note that larger activation energy gives higher D_Li values, because a large pre-exponential term not only compensates but also dominates (Table S6, ESI†), signifying perhaps collective Li motion in pores.

Another question is why Nb (group-5, period-5) is essential in forming WRO super-MIEC anodes. Turning back to the parent structure ReO₃, partial condensation of the corner-sharing octahedra to edge-sharing ones is necessary to enhance the structural rigidity (to suppress extensive phase transitions during electrochemical cycling; unalloyed ReO₃ has multiple phase transitions upon lithiation, which leads to slow kinetics, voltage hysteresis, and poor cycling⁵²) and d–d coupling for better electron transport. Therefore, an ACR around 2.5 is expected, which requires a +5 average cation valence, and thus group-5 elements (Zr/Hf likes to be +4, Mo/W likes to be +6). Meanwhile, as the octahedron majority should be maintained, the fact—that V⁵⁺ is so small that it prefers to be coordinated by four neighboring O²⁻ as is the case for various V₂O₅ polymorphs; while Ta⁵⁺ is so large that it prefers mixed TaO₆/TaO₇ occupancy as is the case for L- and H-Ta₂O₅—sets group-5 and period-5 Nb⁵⁺ to be the best candidate for the major cation. Other elements (Ti, W) can be alloyed into the lattice, to tune the bulk redox and surface stability.

Finally, we provide some guidance on the search for other candidates in the multi-element compositional space. As Roth and Wadsley categorized, the “block” structured oxides M_xO_y can be represented by a series of chemical formulas with one single integer variable n, including M_3nO_8n−3 for Group A, M_3n+1O_8n−2 (n odd) for Group B, M_3n+1O_8n−2 (n even) for Group C, M_3n+1O_8n+1 for Group D, M_4n+1O_11n for Group E, and M_5n+1O_14n−1 for Group F.^35,53 Taking the limiting cases as n → ∞ and known small n compositions (e.g., n = 3 for Nb₂TiO₇ in Group A, n = 7 for Nb₂₂O₅₄ in Group B, n = 8 for Nb₂₄TiO₆₂ in Group C, n = 3 for Nb₉TPO₂₅ in Group D, n = 3 for Nb₁₂WO₃₃ in Group E, and n = 4 for Nb₁₆W₅O₅₅ in Group F), we obtained the O/M ratio in the range of 2.33–2.8. Applying such boundaries to the NbO_2.5–WO₃–TiO₂ ternary phase diagram offers the potential compositional ranges to synthesize new WROs (Fig. S24, ESI†) to optimize bulk redox and SEIs. Indeed, all the known materials within this category fall into the colored compositional space, including our newly synthesized NWT944 and NWT926. The O/M = 2.5 tie-line is of particular interest, which is achieved by alloying WO₃ and TiO₂ with a 1 : 1 molar ratio into the NbO_2.5 matrix. This, together with the coarsened crystal size and suitable coatings, enables the prolonged cycle lives of super-MIEC anodes in high-rate LIBs.

Author contributions

S. W., L. Z., Y. D., J. Z., Z. T., and J. L. conceived the project. L. Z. synthesized the materials and conducted electrochemical testing. H. Z. and H. X. contributed to the PDF analysis and RMC simulation. H. W. and Y. D. conducted the bond-valence sum simulations and first-principles calculations. Y. Yang, B. W., Y. S., and A. M. contributed to the FIB sample preparation, spherical aberration TEM and atomic resolution STEM-HAADF imaging, and 4D-STEM characterization and stacking fault mapping analysis. Y. Yuan and Q. H. contributed to the displacement analysis of the HAADF image. S. W. and Y. H. analyzed the GITT data. H. Z., Q. L., Y. R., C. S., and Q. L. contributed to the synchrotron measurement for structural analysis and CTE analysis. R. F. contributed to Li nuclear magnetic resonance measurements confirming ultrafast Li⁺ diffusion. X. H., Y. C., X. X., and W. L. contributed to the X-ray scanning nano-diffraction measurements. W. Q., Y. L., Z. X., and Z. Z. contributed to the pouch cells assembling and measurement. S. W., Y. D., and J. L. wrote the paper. All authors discussed and contributed to the writing.

Conflicts of interest

The authors declare that they have no competing interests.

Acknowledgements

J. Z. acknowledges the support from the State Key Laboratory of New Ceramic and Fine Processing, Tsinghua University (No. KF201801). Z. T. acknowledges support from the National Natural Science Foundation of China (No. 51772163, 52172210). J. L. acknowledges the support from Honda Research Institute USA, Inc. Y. Y. was supported by the Director, Office of Science, Office of Basic Energy Sciences, Materials Sciences and Engineering Division, the U.S. Department of Energy under contract no. DE-AC02-05-CH11231 within the Mechanical Behavior of Materials (KC 13) program at the Lawrence Berkeley National Laboratory. A. M. was supported by the Toyota Research Institute. The authors acknowledge support from the Molecular Foundry at Lawrence Berkeley National Laboratory, which is supported by the U.S. Department of Energy under contract no. DE-AC02-05-CH11231. This research used resources of the Advanced Photon Source, a U.S. Department of Energy (DOE) Office of Science user facility operated for the DOE Office of Science by Argonne National Laboratory under contract no. DE-AC02-06CH11357. Q. L. acknowledges the Shenzhen Science and Technology Innovation Commission under grant SGDX2019081623240948. X. H acknowledges the support from the U.S. Department of Energy under contract no. DE-SC0012704. R. F. acknowledges the support from the NSF Cooperative Agreement DMP-1644779 and the State of Florida.

References

1. Y. Chen, Z. Wang, X. Li, X. Yao, C. Wang, Y. Li, W. Xue, D. Yu, S. Y. Kim, F. Yang, A. Kushima, G. Zhang, H. Huang, N. Wu, Y. W. Mai, J. B. Goodenough and J. Li, Nature, 2020, 578, 251–255.
2. A. Sood, A. D. Poletayev, D. A. Cogswell, P. M. Csernica, J. T. Mefford, D. Fraggedakis, M. F. Toney, A. M. Lindenberg, M. Z. Bazant and W. C. Chueh, Nat. Rev. Mater., 2021, 6, 847–867.
3. P. C. Harikesh, A. Surendran, B. Ghosh, R. A. John, A. Moorthy, N. Yantara, T. Salim, K. Thirumal, W. L. Leong, S. Mhaisalkar and N. Mathews, Adv. Mater., 2020, 32, 1906976.
4. I. Riess, Solid State Ionics, 2003, 157, 1–17.
5. H. Sun, L. Mei, J. Liang, Z. Zhao, C. Lee, H. Fei, M. Ding, J. Lau, M. Li, C. Wang, X. Xu, G. Hao, B. Papandrea, I. Shakir, B. Dunn, Y. Huang and X. Duan, Science, 2017, 356, 599–604.
6. Y. Liu, Y. Zhu and Y. Cui, Nat. Energy, 2019, 4, 540–550.
7. H. Liu, Z. Zhu, Q. Yan, S. Yu, X. He, Y. Chen, R. Zhang, L. Ma, T. Liu, M. Li, R. Lin, Y. Chen, Y. Li, X. Xing, Y. Choi, L. Gao, H. S.-Y. Cho, K. An, J. Feng, R. Kostecki, K. Amine, T. Wu, J. Lu, H. L. Xin, S. P. Ong and P. Liu, Nature, 2020, 585, 63–67.
8. W. Zhang, D. H. Seo, T. Chen, L. Wu, M. Topsakal, Y. Zhu, D. Lu, G. Ceder and F. Wang, Science, 2020, 367, 1030–1034.
9. K. J. Griffith, K. M. Wiaderek, G. Cibin, L. E. Marbella and C. P. Grey, Nature, 2018, 559, 556–563.
10. Y. Li, S. Wang, Y. Dong, Y. Yang, Z. Zhang and Z. Tang, Adv. Energy Mater., 2019, 10, 1903411.
11. S. T. Wang, Y. H. Dong, F. J. Cao, Y. T. Li, Z. T. Zhang and Z. L. Tang, Adv. Funct. Mater., 2020, 30, 2001026.
12. B. Babu, P. Simon and A. Balducci, Adv. Energy Mater., 2020, 10, 2001128.
13. Q. Ai, Q. Fang, J. Liang, X. Xu, T. Zhai, G. Gao, H. Guo, G. Han, L. Ci and J. Lou, Nano Energy, 2020, 72, 104657.
14. S. Wang, W. Quan, Z. Zhu, Y. Yang, Q. Liu, Y. Ren, X. Zhang, R. Xu, Y. Hong, Z. Zhang, K. Amine, Z. Tang, J. Lu and J. Li, Nat. Commun., 2017, 8, 627.
15. C. Choi, D. S. Ashby, D. M. Butts, R. H. DeBlock, Q. Wei, J. Lau and B. Dunn, Nat. Rev. Mater., 2019, 5, 5–19.
16. T. Yuan, Z. Tan, C. Ma, J. Yang, Z.-F. Ma and S. Zheng, Adv. Energy Mater., 2017, 7, 1601625.
17. Y. Yang and J. Zhao, Adv. Sci., 2021, 8, 2004855.
18. Q. Deng, Y. Fu, C. Zhu and Y. Yu, Small, 2019, 15, 1804884.
19. K. J. Griffith, Y. Harada, S. Egusa, R. M. Ribas, R. S. Monteiro, R. B. Von Dreele, A. K. Cheetham, R. J. Cava, C. P. Grey and J. B. Goodenough, Chem. Mater., 2020, 33, 4–18.
20. Z. Liu and X. Huang, Solid State Ionics, 2010, 181, 907–913.
21. N. Rangnekar, N. Mittal, B. Elyassi, J. Caro and M. Tsapatsis, Chem. Soc. Rev., 2015, 44, 7128–7154.
22. C. J. Jacobsen, C. Madsen, J. Houzvicka, I. Schmidt and A. Carlsson, J. Am. Chem. Soc., 2000, 122, 7116–7117.
23. T. Carey, C. C. Tang, J. A. Hriljac and P. A. Anderson, Chem. Mater., 2014, 26, 1561–1566.
24. Q. Gao, J. Chen, Q. Sun, D. Chang, Q. Huang, H. Wu, A. Sanson, R. Milazzo, H. Zhu, Q. Li, Z. Liu, J. Deng and X. Xing, Angew. Chem., Int. Ed., 2017, 56, 9023–9028.
25. Z. Chang, D. H. Yang, J. Xu, T. L. Hu and X. H. Bu, Adv. Mater., 2015, 27, 5432–5441.
26. J. Li, P. M. Bhatt, J. Li, M. Eddaoudi and Y. Liu, Adv. Mater., 2020, 32, 2002563.
27. L. S. Xie, G. Skorupskii and M. Dinca, Chem. Rev., 2020, 120, 8536–8580.
28. K. Hurlbutt, S. Wheeler, I. Capone and M. Pasta, Joule, 2018, 2, 1950–1960.
29. X. Y. Wu, J. J. Hong, W. Shin, L. Ma, T. C. Liu, X. X. Bi, Y. F. Yuan, Y. T. Qi, T. W. Surta, W. X. Huang, J. Neuefeind, T. P. Wu, P. A. Greaney, J. Lu and X. L. Ji, Nat. Energy, 2019, 4, 123–130.
30. R. J. Cava, A. Santoro, D. W. Murphy, S. M. Zahurak and R. S. Roth, J. Solid State Chem., 1983, 50, 121–128.
31. K. J. Griffith, I. D. Seymour, M. A. Hope, M. M. Butala, L. K. Lamontagne, M. B. Preefer, C. P. Kocer, G. Henkelman, A. J. Morris, M. J. Cliffe, S. E. Dutton and C. P. Grey, J. Am. Chem. Soc., 2019, 141, 16706–16725.
32. C. P. Kocer, K. J. Griffith, C. P. Grey and A. J. Morris, Chem. Mater., 2020, 32, 3980–3989.
33. Y. Liu, S. P. Jiang and Z. Shao, Mater. Today Adv., 2020, 7, 100072.
34. H. A. Evans, Y. Wu, R. Seshadri and A. K. Cheetham, Nat. Rev. Mater., 2020, 5, 196–213.
35. R. Roth and A. Wadsley, Acta Crystallogr., 1965, 19, 42–47.
36. S. P. Ong, A. Jain, G. Hautier, B. Kang and G. Ceder, Electrochem. Commun., 2010, 12, 427–430.
37. Q. N. Liu, Z. Hu, M. Z. Chen, C. Zou, H. L. Jin, S. Wang, S. L. Chou, Y. Liu and S. X. Dou, Adv. Funct. Mater., 2020, 30, 1909530.
38. L. Zhao, S. Wang, Y. Dong, W. Quan, F. Han, Y. Huang, Y. Li, X. Liu, M. Li, Z. Zhang, J. Zhang, Z. Tang and J. Li, Energy Storage Mater., 2021, 34, 574–581.
39. T. Li, G. Nam, K. Liu, J.-H. Wang, B. Zhao, Y. Ding, L. Soule, M. Avdeev, Z. Luo, W. Zhang, T. Yuan, P. Jing, M. G. Kim, Y. Song and M. Liu, Energy Environ. Sci., 2022, 15, 254–264.
40. Q. Gao, J. Wang, A. Sanson, Q. Sun, E. Liang, X. Xing and J. Chen, J. Am. Chem. Soc., 2020, 142, 6935–6939.
41. Z. Liu, Q. Li, H. Zhu, K. Lin, J. Deng, J. Chen and X. Xing, Chem. Commun., 2018, 54, 5712–5715.
42. Q. Gao, N. Shi, Q. Sun, A. Sanson, R. Milazzo, A. Carnera, H. Zhu, S. H. Lapidus, Y. Ren, Q. Huang, J. Chen and X. Xing, Inorg. Chem., 2018, 57, 10918–10924.
43. Z. Song, H. Li, W. Liu, H. Zhang, J. Yan, Y. Tang, J. Huang, H. Zhang and X. Li, Adv. Mater., 2020, 32, 2001001.
44. F. Shen, Z. Sun, Q. He, J. Sun, R. B. Kaner and Y. Shao, Mater. Horiz., 2021, 8, 1130–1152.
45. X. Han, Q. Meng, X. Wan, B. Y. Sun, Y. Zhang, B. C. Shen, J. L. Gao, Y. L. Ma, P. J. Zuo, S. F. Lou and G. P. Yin, Nano Energy, 2021, 81, 105635.
46. T. F. Yi, H. M. K. Sari, X. Z. Li, F. F. Wang, Y. R. Zhu, J. H. Hu, J. J. Zhang and X. F. Li, Nano Energy, 2021, 85, 105955.
47. J.-T. Han and J. B. Goodenough, Chem. Mater., 2011, 23, 3404–3407.
48. Y. Yang, H. Zhu, J. Xiao, H. Geng, Y. Zhang, J. Zhao, G. Li, X. L. Wang, C. C. Li and Q. Liu, Adv. Mater., 2020, 32, 1905295.
49. A. Kushima, X. Qian, P. Zhao, S. Zhang and J. Li, Nano Lett., 2015, 15, 1302–1308.
50. H. Zhu, Y. Huang, J. Ren, B. Zhang, Y. Ke, A. K. Jen, Q. Zhang, X. L. Wang and Q. Liu, Adv. Sci., 2021, 8, 2003534.
51. Q. Li, H. Zhu, L. Zheng, L. Fan, N. Wang, Y. Rong, Y. Ren, J. Chen, J. Deng and X. Xing, Nano Lett., 2017, 17, 7892–7896.
52. N. H. Bashian, S. Zhou, M. Zuba, A. M. Ganose, J. W. Stiles, A. Ee, D. S. Ashby, D. O. Scanlon, L. F. J. Piper, B. Dunn and B. C. Melot, ACS Energy Lett., 2018, 3, 2513–2519.
53. A. Wadsley, S. Andersson, J. Dunitz and J. Ibers, Perspectives in Structural Chemistry, Wiley, New York, 1970, vol. 3, pp. 1–58.

---

Footnotes

† Electronic supplementary information (ESI) available: Experimental and computational details, supplementary figures, supplementary tables, and supplementary references. See DOI: https://doi.org/10.1039/d2ee02918a

‡ These authors contributed equally to this work.

---