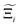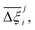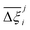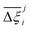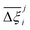Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A process-level perspective of the impact of molecular force fields on the computational screening of MOFs for carbon capture†
Conor
Cleeton
 *a,
Felipe Lopes
de Oliveira
bc,
Rodrigo F.
Neumann
b,
Amir H.
Farmahini
*a,
Felipe Lopes
de Oliveira
bc,
Rodrigo F.
Neumann
b,
Amir H.
Farmahini
 a,
Binquan
Luan
a,
Binquan
Luan
 d,
Mathias
Steiner
b and
Lev
Sarkisov
d,
Mathias
Steiner
b and
Lev
Sarkisov
 a
a
aThe University of Manchester, Manchester, UK. E-mail: conor.cleeton@postgrad.manchester.ac.uk
bIBM Research, Av. República do Chile, 330, CEP 20031-170, Rio de Janeiro, RJ, Brazil
cInstituto de Quımica, Universidade Federal do Rio de Janeiro, Rio de Janeiro, RJ, Brazil
dIBM Research, 1101 Kitchawan Road, Yorktown Heights, 10519, NY, USA
First published on 31st July 2023
Abstract
The question we pose in this study is to what extent the ranking of metal organic frameworks (MOFs) for adsorption-based carbon capture, and the selection of top performers identified in Pressure Swing Adsorption (PSA) process modelling, depends on the choice of the commonly available forcefields. To answer this question, we first generated distributions of CO2 and N2 adsorption isotherms via molecular simulation in 690 MOFs using six typical forcefields: the UFF or Dreiding sets of Lennard-Jones parameters, in combination with partial charges derived from ab initio calculations or by charge equilibration schemes. We then conducted a systematic uncertainty quantification study using PSA process-level modelling. We observe that: (i) the ranking of MOFs significantly depends on the choice of forcefield; (ii) partial charge assignment is the prevailing source of uncertainty, and that charge equilibration schemes produce results which are inconsistent with ab initio-derived charges; (iii) the choice of Lennard-Jones parameters is a considerable source of uncertainty. Our work highlights that is not really possible to obtain material rankings with high resolution using a single molecular modelling approach and that, as a minimum, some uncertainty should be estimated for the performance of MOFs shortlisted using high throughput computational screening workflows. Future prospects for computational screening studies are also discussed.
Broader contextTo avoid the most severe impacts of climate change, we need to deploy carbon capture and sequestration (CCS) technologies on a scale that matches human industrial activity's emissions. However, the differences in scale, composition, and technical requirements between various emission sectors require technologies that can be optimised for various applications. Adsorption-based processes using metal organic frameworks (MOFs) for carbon capture offer a significant advantage because they can be tailored for specific CO2 capture sources by optimising the adsorption cycle and MOF properties. While high throughput computational screening (HTCS) studies are routinely conducted to identify the best MOFs for various CCS applications, very few of these materials are tested at the lab-scale. In this article, we argue that a lack of accurate, reproducible, and consistent implementation of HTCS workflows is one of the primary technological barriers between theoretical and experimental studies. We demonstrate that the molecular parameter sets used to simulate CO2 and N2 adsorption significantly impact the final recommendations made using process modelling. Given the uncertainties we observe, the community must take steps to improve the current simulation strategy. We offer several recommendations in the article on how to enhance the reliability of predictions derived from HTCS studies. |
Introduction
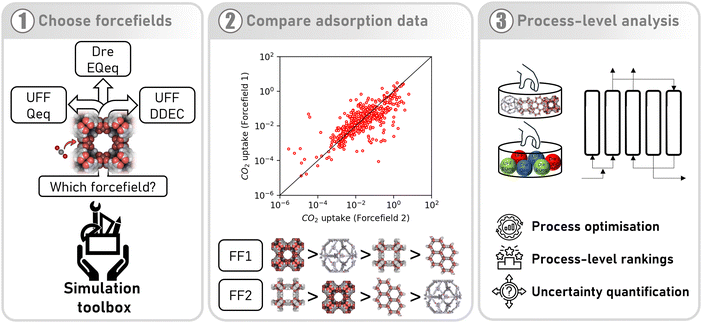
High throughput computational screening (HTCS) has emerged as an important strategy in the efforts to identify the most promising metal organic frameworks (MOFs) for carbon capture applications.1,2 Consider two academic groups as an example: both are seeking to determine the best MOF for carbon capture from flue gas using computational screening. Their simulation protocols are identical, including the database of MOF candidates. To rank the performance of materials, both groups use pressure swing adsorption (PSA) process modelling, with an identical process configuration and parameters. They both operate under the assumption that the results obtained using their workflows can be used to inform experimentalists on which MOFs to synthesise and test. The only difference between the groups is the choice of force fields used to describe intermolecular interactions, which are required by molecular simulations to generate equilibrium adsorption data. In this article, we question whether the rankings produced by the two groups, and therefore the final recommendations of their screening studies, will be similar and to what extent.Let us first look in more detail at the steps and the assumptions typically involved in HTCS workflows. Generally speaking, HTCS can be conducted at the material level or the process level. Material-level screening studies filter MOFs for a desired property. For example, the CO2/N2 adsorption selectivity, percent regenerability, and CO2 working capacity are key performance indicators (KPIs) that have been used to organise MOF databases on several occasions.2–4 However, for complex, dynamic processes such as PSA, it has been convincingly demonstrated that these properties alone do not provide enough information to determine the separation potential of an adsorbent.5 For that reason, process-level screening workflows must be utilised. This approach relies on atomistic Grand Canonical Monte Carlo (GCMC) simulations to obtain microscale properties of the adsorbent (in particular, equilibrium adsorption data). This data is then passed onto detailed PSA process models whereby MOFs are evaluated under realistic separation conditions.6 At this level, we are interested in KPIs which reflect the economic drivers of the separation, such as high CO2 product purity and recovery, or low energy penalty (energy required to capture a unit amount of CO2) and high productivity (how much CO2 is captured per kg of adsorbent per second). These properties depend on the properties of the adsorbent as well as the variables of the PSA cycle (pressures of each step, duration of each step, etc.). However, there is no unique combination of the PSA cycle variables which satisfies all of the process-level KPIs simultaneously, and so the trade-off between competing objectives can be represented as a series of Pareto-optimal solutions known as a Pareto front. Comparing Pareto fronts for two different materials has therefore become an established protocol for ranking MOFs based on their performance.7–11 Among the several design choices one is posed with when constructing a process-level simulation pipeline, the first (and perhaps most important) choice is how to generate the adsorption data using molecular simulations. To understand the importance of this step, it is instructive to briefly review the primary components of a typical GCMC simulation of adsorption.
The interactions between all atoms, and therefore the potential energy, must be accurately described in order to predict CO2 and N2 adsorption in MOFs. In classical GCMC, this is typically achieved by defining an appropriate set of equations and molecular parameters known as a forcefield (FF), whereby short-range repulsion/dispersion interactions are described by a Lennard-Jones (LJ) potential, and long-range electrostatic interactions by a coulombic potential.12,13 Specialised FFs have been developed to accurately describe the LJ contributions in specific subclasses of MOFs,12,14,15 however these lack the large-scale predictive capabilities needed for screening purposes. On the other hand, generic FFs such as Dreiding16 and the Universal Force Field (UFF)17 are transferable (albeit less accurate) as they describe the same types of framework atoms in many different materials with the same parameters. Therefore, Dreiding or UFF are the common and practical choices for HTCS of MOFs.18–22 They are typically combined with the Transferable Potentials for Phase Equilibria (TraPPE)23 FF (which describes the CO2 and N2 adsorbates) using mixing rules such as Lorentz–Berthelot. For the electrostatic interactions, partial charges must be assigned to each atom in the system. Several assignment schemes have been developed so far and have been reviewed elsewhere,24 each differing in their level of accuracy, philosophy, and computational cost. The most accurate (but computationally expensive) approach would be to determine the electrostatic potential within a material using ab initio calculations and then assign point charges that best represents this electronic environment.24 While many ab initio approaches exist,25–33 density derived electrostatic and chemical (DDEC)28–32 charges and Repeating Electrostatic Potential Extracted ATomic (REPEAT) charges33 are considered to be the best options for periodic structures. Less accurate, but computationally inexpensive, charges can also be obtained using charge equilibration (Qeq)34 schemes such as the Extended Qeq (EQeq)35 and Periodic Qeq (PQeq)36 methods, among others.37,38 These approaches are based on the principle of electronegativity equalisation between bonded atoms, and have been used extensively in MOF screening studies despite their semiempirical nature.18,39–42
Despite the consensus that ab initio charges are the preferred choice for HTCS, several practical considerations (such as the availability of computational resources) can motivate the choice of charge equilibration schemes. Additionally, it is currently nontrivial to obtain a set of LJ parameters capable of screening thousands of MOFs with high accuracy. Therefore, it is quite common to see an almost arbitrary combination of the LJ parameters and charge assignment schemes used in HTCS of MOFs. This raises some concerns on the quality of the FFs used for predicting equilibrium adsorption data in molecular simulations.43–45 Several studies have endeavoured to understand how the choice of charge scheme27,39,46,47 or LJ FF44,48 changes the rankings of MOFs for CO2 capture. However, these studies do not extend beyond a simple material-level analysis (i.e., up to step 2 in Fig. 1). In order to align with the advancements achieved in HTCS, the uncertainty embedded within the process-level KPIs must be understood (i.e., up to step 3 in Fig. 1), given that the adsorption data plays a pivotal role in PSA-based CO2 capture processes.5,49–51 Without this level of analysis, a shadow of doubt on the outcomes of theoretical studies will remain, which only serves to hinder the transition of the recommended materials to the experimental campaign and ultimately to practical, industrial systems.
To explore these issues, we carry out a multiscale HTCS where we assess the suitability of six FFs commonly chosen to simulate CO2 and N2 adsorption in MOFs. Our goal is to understand how the material rankings are impacted by this choice, not necessarily on how well the FFs reproduce experimental data, and so we deliberately avoid making any comparisons to experimental measurements of adsorption. As a process-level case study, we consider the separation of CO2 (15 vol%) and N2 (85 vol%) binary mixtures using a modified Skarstrom PSA cycle at conditions representative of dry flue gas streams from coal-fired power plants. We generate distributions of CO2 and N2 adsorption isotherms in 690 MOFs at multiple temperatures using LJ parameters from either Dreiding or UFF, in combination with partial charges assigned by the DDEC, EQeq, or Qeq schemes. We then determine the distributions in process-level performances for every MOF using a combination of high-fidelity PSA process modelling and machine learning. Using these data, we generate material ranking lists for each FF and reflect on the consistency of the results. Our analysis will show moderate-to-poor correlations between the process-level rankings obtained using different FFs, and that this disagreement stems primarily from the significant deviations which manifest at the material level of description. We then quantify the average uncertainties between FFs from their process-level responses and reveal that the prevailing source of uncertainty is the choice of charge scheme. We finally explore a potential pathway towards uncertainty mitigation in multiscale simulations of PSA-based CO2 capture processes and discuss future prospects for HTCS of materials.
Methodology
Grand canonical Monte Carlo simulations
The computation-ready, experimental (CoRE) MOF 2014 DDEC database52,53 is chosen as the starting point for adsorbent selection. To ensure a fair comparison in GCMC modelling approaches, only MOF structures that contain all the atom types present in both the UFF and Dreiding force fields are included. This filtering process results in a reduced dataset of 726 structures from the original 2932. A further 36 MOFs are removed due to the presence of unbound water molecules, counter-ions and/or hydrogen atoms with incorrect bond lengths/angles, leaving 690 computation-ready structures available for this study.Simulations of CO2 and N2 adsorption are performed using the atomistic GCMC method implemented in RASPA.54 For framework atoms, LJ parameters were taken from UFF17 or Dreiding.16 For CO2 and N2 adsorbates, the TraPPE FF is used.23 For the coulombic interactions, three partial charge assignment schemes are considered here: DDEC,28 EQeq,35 and Qeq.34 DDEC charges are taken from the original CoRE MOF 2014 DDEC database, while the EQeq and Qeq partial charges are calculated using the EQeq v1.1.055 and RASPA v2.0.47 simulation codes, respectively.
For each adsorbent, single-component isotherms are generated at 273 K, 298 K, and 323 K on a logarithmic pressure scale between 10−3–10 bar for CO2 and 10−3–1 bar for N2. As there are 6 possible FF combinations, this results in 18 isotherms for both CO2 and N2 using 378 unique adsorption points. In total, 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 840 isotherms are generated across 690 MOFs which span different pressures, temperatures, charge assignment methods, and generic forcefield parameters. We refer to the data generated using this subset of MOFs as the charge-dependent, reproducible, accessible, forcefield-dependent, and temperature-dependent exploratory database of isotherms, or CRAFTED isotherms for brevity. To provide an initial seed for future benchmarking efforts, we make the CRAFTED database (v1.1.1)56 and scripts available to the broader scientific community in a dedicated Zenodo repository at https://zenodo.org/record/7689919. This data was obtained using a HTCS workflow that has been developed56 and validated elsewhere.57,58 For more technical details on the GCMC simulations, see the ESI,† supplementary note 1.
840 isotherms are generated across 690 MOFs which span different pressures, temperatures, charge assignment methods, and generic forcefield parameters. We refer to the data generated using this subset of MOFs as the charge-dependent, reproducible, accessible, forcefield-dependent, and temperature-dependent exploratory database of isotherms, or CRAFTED isotherms for brevity. To provide an initial seed for future benchmarking efforts, we make the CRAFTED database (v1.1.1)56 and scripts available to the broader scientific community in a dedicated Zenodo repository at https://zenodo.org/record/7689919. This data was obtained using a HTCS workflow that has been developed56 and validated elsewhere.57,58 For more technical details on the GCMC simulations, see the ESI,† supplementary note 1.
Equilibrium adsorption model
Process-level simulations require an analytical model to determine the equilibrium molar loadings of CO2/N2 mixtures over various pressure and temperature domains. The dual-site Langmuir (DSL) model (eqn (1)) is well suited for this purpose. Within the DSL approach, competitive adsorption may be calculated by a simple extension of the single-component DSL models;59 many practical systems of interest are known to be described by this behaviour.7,60,61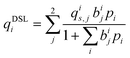 | (1) |
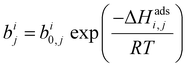 | (2) |
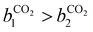 condition. This constraint reflects the energetic heterogeneity of CO2 adsorption. For N2, in cases where the adsorption isotherm is linear over the pressure range, we adopt the Equal Energy Site (EES) formulation of the extended DSL model.64,65 This formulation recognises the energetic homogeneity of N2 adsorption by setting the interaction energy parameters (i.e.,
condition. This constraint reflects the energetic heterogeneity of CO2 adsorption. For N2, in cases where the adsorption isotherm is linear over the pressure range, we adopt the Equal Energy Site (EES) formulation of the extended DSL model.64,65 This formulation recognises the energetic homogeneity of N2 adsorption by setting the interaction energy parameters (i.e., 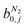 and
and 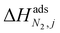 ) to the same value at both sites.51,66 In cases where N2 adsorption deviates substantially from linearity, this constraint is relaxed, and the fitting protocol used to model CO2 adsorption is utilised. This approach has been validated using binary mixture GCMC simulations (see supplementary note 1.3, ESI†).
) to the same value at both sites.51,66 In cases where N2 adsorption deviates substantially from linearity, this constraint is relaxed, and the fitting protocol used to model CO2 adsorption is utilised. This approach has been validated using binary mixture GCMC simulations (see supplementary note 1.3, ESI†).
PSA simulation and optimisation strategy
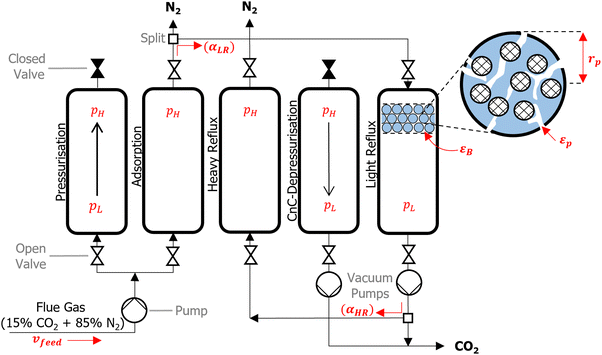
We consider a modified Skarstrom PSA cycle which consists of five steps: (1) pressurisation; (2) adsorption; (3) heavy reflux; (4) counter-current depressurisation; and (5) light reflux, as shown in Fig. 2. The cycle variables consist of high (adsorption) and low (evacuation) pressures (pH and pL [bar]), durations of the pressurisation, adsorption, and counter-current depressurisation steps (tpres, tads, and tcnCDepres [s]), velocity of the feed (vfeed [m s−1]), and light and heavy reflux ratios (αLR and αHR [−]). Other important properties highlighted in Fig. 2 are the porosity of the bed and pellet (εB and εp [−]), and the pellet radius (rp [m]). The role and purpose of individual steps are described in detail elsewhere.7 The main feature of this cycle is that it utilises a dual reflux configuration, which avoids the need to pull deep vacuum below the practical limits of industrial vacuum pumps.67 This presents an important advantage over the more commonly used 4-step VSA cycle with light product pressurisation, which often requires unphysically low evacuation pressures to achieve high CO2 purities and recoveries.51To accurately simulate the separation of CO2/N2, partial differential equations which describe the mass, energy, and momentum transfer phenomena taking place in the adsorption column are required. A complete description of the governing equations, model parameters, boundary conditions and mathematical criterion used to determine cyclic steady state are provided in supplementary note 2 (ESI†), while other technical details of the PSA simulation are provided elsewhere.7,68 We summarise here the key assumptions adopted in our process model as the following: (1) the Ideal Gas law describes the gas phase; (2) the gas phase and solid phase are in thermal equilibrium; (3) mass transfer is controlled by molecular diffusion in the macropores, which is valid for most microporous adsorbents with pore openings greater than 4 Å.69 Furthermore, the mass transfer rate is described by the linear driving force (LDF) approximation; (4) an axially dispersed plug flow model is employed, meaning there are no radial distributions in concentration, pressure, and temperature for both the solid and gas phase; (5) the column is operated adiabatically; (6) the Ergun equation describes the axial pressure drop. These assumptions are largely consistent with the assumptions of several previous studies.7–11
Four key performance indicators (KPIs) are extracted from the PSA simulations, namely: CO2 purity [−], CO2 recovery [−], energy penalty [kWh tonCO2−1], and productivity [molCO2 kgads−1 s−1]. Regulatory bodies such as the US Department of Energy have specified 95% purity and 90% recovery targets for CO2 capture processes. Viable adsorbents must therefore be able to achieve this product specification in any given PSA cycle. For the purposes of our investigation, we relax the purity requirement to 90%,7,66 and simply refer to the 90% purity and recovery targets as carbon capture and sequestration (CCS) constraints. The energy penalty corresponds to the amount of energy required to capture a unit of CO2, whereas productivity specifies how much CO2 a unit of the adsorption bed (e.g., a kg or m3) can capture per unit of time. These KPIs are related to the operating and capital costs of the separation, and have been widely adopted in previous screening studies as the indicative metrics of material performance.7–11,70 Mathematical definitions for each KPI are provided in supplementary note 2 (ESI†).
The performance of the PSA cycle is optimised by coupling the PSA process model with the Non-dominated Sorting Genetic Algorithm (NSGA-II).71–73 11 decision variables (DVs) are initially considered for the process optimisation. These included all of the PSA cycle variables as well as εB, εp and rp. Parameters εB, εp and rp are included as DVs in light of the recent work by Farmahini et al.74 who demonstrated that significant performance gains can be obtained by optimising properties of the pellet as well as the cycle variables. We then reduced the dimensionality of the optimisation landscape to 7 DVs by fixing the values of pL, tpres, tcnCDepres, and αHR after some preliminary sensitivity analysis. This decision is motivated by the fact that these 4 parameters contributed very little to the overall performance of the cycle; they either converged to the boundaries defined by physical limitations, or they varied within a narrow window of the optimisable range (see supplementary note 3, ESI†). A summary of the final DVs considered in this work and their operating ranges are provided in Table 1.
| p H [bar] | t ads [s] | α LR [−] | v feed [m s−1] | ε B [−] | ε p [−] | r p [m] | |
|---|---|---|---|---|---|---|---|
| a Competitive adsorption of CO2/N2 mixtures are well described by the extended DSL model up to 5 bar, see Fig. S1 (ESI). | |||||||
| Lower bound | 1 | 5 | 0.01 | 0.1 | 0.35 | 0.3 | 0.5 × 10−3 |
| Upper bound | 5 | 500 | 0.2 | 2.0 | 0.45 | 0.7 | 2.5 × 10−3 |
We conduct two separate optimisation stages in this study. The first is an unconstrained maximisation of the CO2 purity and recovery. For this stage, the genetic algorithm is terminated after 70 generations. The second stage is a multi-objective optimisation, whereby we maximise the productivity while simultaneously minimising the energy penalty subject to the two CCS constraints: CO2 purity ≥0.9 and CO2 recovery ≥0.9. For this stage, the genetic algorithm is terminated after 250 generations. We confirm that 70 and 250 generations for the CO2 purity-recovery and energy-productivity optimisations, respectively, are sufficient to guarantee convergence of the Pareto fronts.
Machine learning surrogate model for the prediction of PSA performance indicators.
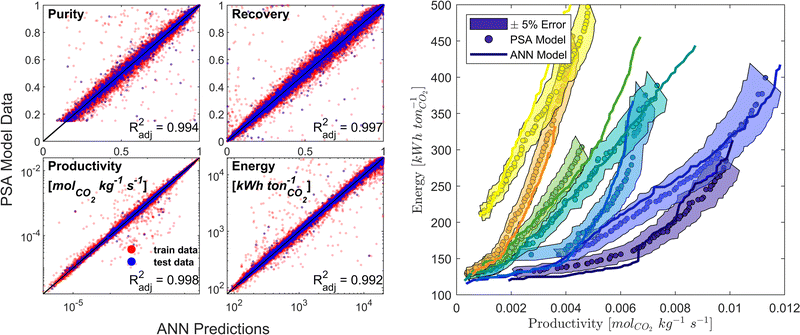
We developed a machine learning (ML) surrogate model of the modified Skarstrom cycle which can predict the process KPIs for any arbitrary combination of DVs and material properties. We use this surrogate model to expedite the calculation of CO2 purity-recovery and energy penalty-productivity Pareto fronts. Similar to, and guided by, our previous efforts in this domain,66 we use an artificial neural network (ANN) as our choice of ML model. There are overall 7 DVs and 14 material-specific parameters (crystal density ρs [kg m−3], crystal specific heat capacity cp,s [J kg−1 K−1], and the 12 DSL parameters which describe CO2 and N2 adsorption), resulting in 21 inputs, while the outputs of interest are the 4 KPIs (i.e., CO2 purity, CO2 recovery, energy penalty, and productivity). Appropriate training limits are defined for each of the material-specific parameters to sufficiently cover the distributions of CRAFTED MOF material properties, and training limits for the 7 DVs are defined as the optimisable ranges given in Table 1.Training data is generated by a combination of Latin Hypercube sampling (LHS) of the input phase space as well as a guided search of high quality, Pareto-optimal points through a bootstrap optimisation technique. The data obtained using these sampling techniques is then cleaned and pre-processed by applying log-like transformations to each of the KPIs.75 Next, the data is partitioned into train/test/validation datasets using a ratio of 90/5/5. MATLAB's machine-learning toolbox is subsequently used to train a dense feedforward ANN model architecture of 3 hidden layers with 45 neurons per hidden layer by Levenberg–Marquardt back-propagation. The ANN model predictive performance is evaluated by calculating the adjusted coefficient of determination (Radj2) for all KPIs using the test dataset. Model training and refinement is terminated once predictions of both the individual cycle configurations and fully resolved Pareto fronts no longer improved (Fig. 3). Additional details on the surrogate model training protocol and on how the CRAFTED MOF material properties are calculated are provided in the supplementary note 4 (ESI†).
Uncertainty metrics for high performing adsorbents
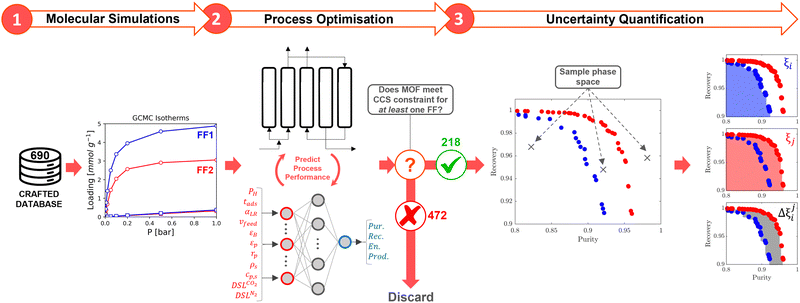
High performing adsorbents are characterised by their ability to minimise the cost of CO2 capture while meeting the CCS requirements. It is not a priori evident what combination of material properties leads to these requirements being satisfied, so we conduct preliminary purity-recovery optimisations in two stages. Low performing adsorbents are first identified by their ANN-generated Pareto fronts and discarded from our subsequent analysis. We define a low performing material as one which does not satisfy the CCS constraints for any FF. For the 218 materials that remain after this pre-screening, high quality Pareto data is generated by refining the ANN results with the PSA process model for an additional 10 NSGA-II generations. This mitigates any potential bias in the ML process and ensures that the conclusions drawn are established using accurate process simulation data. Moving forwards, we only consider the 218 MOFs in our uncertainty calculations. We designate this subset of MOFs as CRAFTED-u.We seek to quantify the level of agreement between FFs at the molecular and process simulation levels. To do so, we make use of a number of statistical metrics which are both local, i.e., relating to a single material, and global, i.e., relating to the entire CRAFTED-u MOF database. Let us first focus on molecular simulations, used to generate equilibrium adsorption data. In addition to the comparison of individual adsorption isotherms generated from different FFs, we also employ the Spearman correlation coefficient, ρ, to measure the global extent of the correlation between adsorbate uptakes predicted by different FFs. Perfect positive correlations result in ρ = 1, perfect negative correlations in ρ = −1, and no correlation in ρ = 0.
At the process level, for each CRAFTED-u MOF, the uncertainty between Pareto fronts that emerges from the use of different molecular FFs to generate the adsorption data as input, is quantified using the hypervolume. The hypervolume, ξ, measures the area enclosed by all solutions on the Pareto front and a user-defined reference point r.76,77 We measure ξ by querying N = 104 uniformly distributed random points within the Pareto phase space bounded by r, where r is determined such that the entire Pareto front for every FF is covered in the sampling. The difference in hypervolumes between FFs i and j, which we call the hypervolume error Δξji, is taken as the uncertainty measure for a single material. The process of calculating Δξji is visually represented in Fig. 4.
Now, in order to quantify the global uncertainties between two different FFs i and j across all CRAFTED-u MOFs, we must determine a single numerical value from the full distribution of Δξji values. We take the mean of the hypervolume error distribution, 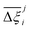 , as the indicative metric of global uncertainty. Qualitatively we would also like to understand if FF i has a propensity to generate adsorption behaviours that produce better process performances overall compared to FF j. Establishing this connection between the adsorption behaviours and process-level responses helps to reveal the biases in performances that may arise in particular FFs. We therefore introduce a normalised metric,
, as the indicative metric of global uncertainty. Qualitatively we would also like to understand if FF i has a propensity to generate adsorption behaviours that produce better process performances overall compared to FF j. Establishing this connection between the adsorption behaviours and process-level responses helps to reveal the biases in performances that may arise in particular FFs. We therefore introduce a normalised metric, 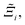 to understand the general process-level behaviours of different FFs across many materials which may dominate different areas of KPI phase space. The protocol for calculating
to understand the general process-level behaviours of different FFs across many materials which may dominate different areas of KPI phase space. The protocol for calculating 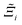 for FF i is as follows. For a single MOF, six Pareto fronts are generated for each of the six possible FFs. One of these FFs generates a Pareto front which performs the best, and therefore has the greatest hypervolume. We treat this hypervolume as the upper limit of performance (i.e., ξmax = 100%) and normalise the hypervolume of FF i relative to ξmax such that Ξi = ξi/ξmax × 100. This operation is applied to every CRAFTED-u MOF, resulting in a distribution of Ξi values. Similar to the hypervolume error, we measure the central tendency of the Ξi distribution by a single numerical value. In this case, we take the median, Ξi. If
for FF i is as follows. For a single MOF, six Pareto fronts are generated for each of the six possible FFs. One of these FFs generates a Pareto front which performs the best, and therefore has the greatest hypervolume. We treat this hypervolume as the upper limit of performance (i.e., ξmax = 100%) and normalise the hypervolume of FF i relative to ξmax such that Ξi = ξi/ξmax × 100. This operation is applied to every CRAFTED-u MOF, resulting in a distribution of Ξi values. Similar to the hypervolume error, we measure the central tendency of the Ξi distribution by a single numerical value. In this case, we take the median, Ξi. If 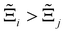 , then FF i tends to dominate over FF j overall. Note that the mean of Δξji and the median of Ξi were determined to be the most appropriate statistical measures of central tendency given the spread and skewness of the underlying data distributions. They are therefore the best metrics to indicate the overall trends of the CRAFTED-u MOF dataset.
, then FF i tends to dominate over FF j overall. Note that the mean of Δξji and the median of Ξi were determined to be the most appropriate statistical measures of central tendency given the spread and skewness of the underlying data distributions. They are therefore the best metrics to indicate the overall trends of the CRAFTED-u MOF dataset.
Finally, we measure the correlation between process-level rankings using the Spearman coefficient. Note that, as a matter of convention, we indicate that any of the metrics discussed above are being calculated with respect to a particular FF by the subscript notation and are being compared to another FF using the superscript notation. As an example, ξi refers to the hypervolume calculated for FF i, and ρji refers to the correlation in rankings obtained using FFs i and j.
Results & discussion
We begin our discussion by delving into the most crucial and practical consideration of this work, i.e., to what extent the selection of a particular FF impacts the process-level rankings of materials. We then consider specific adsorption patterns and the level of agreement between different FFs in predicting the uptake of CO2 and N2. The objective here will be to reason some of the important differences in molecular modelling approaches, seeking to understand the nature of the (dis)agreement by exploring correlations in simulated CO2 and N2 uptakes. Next, we quantify the uncertainty between different FFs at the process-level. For this, we will utilise a number of figures and statistical measures to map process-level responses onto the underlying adsorption patterns. Finally, we explore potential pathways towards uncertainty mitigation in multiscale simulations of PSA-based CO2 capture processes and discuss future prospects for HTCS of materials.Level of agreement between process-level rankings obtained using different molecular forcefields
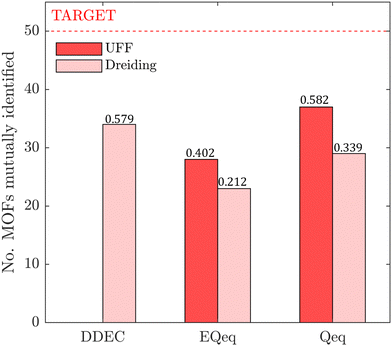
In this section, we inquire whether the ranking of porous materials and the identification of top performers through process modelling depends on the use of a specific FF. For this, we must first generate a material ranking list for each molecular FF using some process-level performance metric. The energy-productivity Pareto front, subject to the CCS constraints, is often used to rank materials in multiscale HTCS studies.7,66,70,74 However, the CCS constraints are not satisfied by every CRAFTED-u MOF across all FFs, and so it is not possible to evaluate every material behaviour using energy-productivity KPIs. We therefore ranked materials according to the maximum CO2 purity they can achieve in the modified Skarstrom cycle (Fig. 2), subject to the constraint of CO2 recovery ≥0.9, using the HTCS workflow shown in Fig. 4.Then, we extracted the top 50 MOFs from each ranking, consistent with the philosophy of previous screening studies which typically seek to narrow the candidate list to only the top performers.2,19,21,22,70 We find that the material rankings are poorly-to-moderately positively correlated, and that the identity of the top performing MOFs can change significantly, depending on the FF. To demonstrate this point, let us make comparisons amongst the different FFs by choosing UFF with DDEC charges as the reference. Note that by doing so, we do not suggest that UFF + DDEC is more accurate in reproducing experimentally observed adsorption behaviours, it is simply a matter of convention. With this in mind, we identify the number of MOFs from each FF-specific ranking which overlap with the top 50 materials from the UFF + DDEC baseline and visualise the results in Fig. 5.
Let us first focus on the comparison between UFF and Dreiding in Fig. 5, with each of these LJ parameter sets combined with the DDEC charges. We see that 35 MOFs are shared in the list of top performers between these two variants of the forcefields. Turning now to the combinations of UFF with other charge schemes, the greatest level of agreement is between DDEC and Qeq, with 36 MOFs appearing in both lists of the top 50 materials. It is also quite apparent that the EQeq charges provide a much poorer level of agreement, with only 27 MOFs appearing in the ranking obtained using the DDEC charges. We find that even if we take a different molecular FF as the baseline (Fig. S9, ESI†) or focus on a shorter list of candidate materials, i.e., the top 20 (Fig. S10, ESI†), that generally: (1) there is consistently better agreement in the rankings between Qeq and DDEC charges than in EQeq and DDEC charges; (2) depending on one's choice of the charge scheme, the overlap in the materials identified by any two different schemes ranges between 50% and 70% (Fig. S9, ESI†), not to mention the order of materials which changes significantly depending on the set of parameters; (3) the screening results remain sensitive to the choice of LJ parameters and the two lists of top materials produced by two different FFs may share approximately 70% of the materials. These tendencies are supported by the Spearman ranking correlation coefficients, which are provided above each bar plot in Fig. 5.
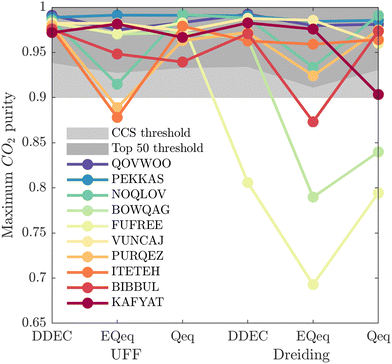
While Fig. 5 is a useful tool to visualise how the identity of the top performers can change with molecular FF, we do not yet understand how close the materials are in terms of their numerical performance. The two possible explanations for poor-to-moderate agreement between material rankings is either: (1) many materials perform similarly, and small differences in the performance estimates give rise to large differences in the relative rankings across different FFs, or (2) the process performances, and therefore the rankings, are highly variable parameters. In Fig. 6 we provide a snapshot of how the numerical performance values used to rank the top 10 materials for UFF + DDEC change with molecular FF. From this plot we identify some materials, such as QOVWOO and PEKKAS, which show fairly minor deviations using different FFs, and so are consistently ranked in the top 10 candidates. Other materials, such as VUNCAJ, always remain within the top 50 threshold. Finally, we have some materials with such a strong volatility in their process KPIs that they may fall far below the top 50 threshold, depending on the choice of FF. These constitute the largest proportion of materials, and in many instances the difference in performance is sufficient to classify the same material as suitable (in other words, meeting the CCS constraints) by one FF and not suitable by another FF. Note that these trends persist when the other FFs are taken as the baseline for comparison (Fig. S11, ESI†).
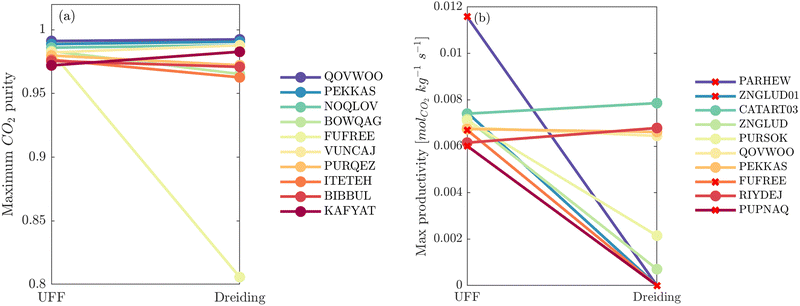
So far it appears that the process performances and material rankings depend on both the definition of the LJ and the electrostatic potentials, however it seems that the choice of charge scheme has a stronger impact (Fig. 5). In practice, (E)Qeq may be chosen over DDEC in HTCS78–80 due to restricted computational resources, or they may be used to pre-screen large databases and shortlist top performers for further refinement using higher accuracy charge assignment schemes.81,82 In an ideal scenario, DDEC charges are available or can be calculated for all candidate materials. In this case, the uncertainty embedded in one's choice of partial charge assignment would be eliminated as ab initio charges are the preferred level of molecular theory for HTCS of materials for carbon capture.2 If we confine the scope of our analysis to this ideal scenario, the only additional degree of freedom remaining is how to model the LJ interactions. In Fig. 7(a), a direct comparison of the maximum CO2 purity predicted by either UFF or Dreiding in combination with DDEC charges reflects this ideal case study. Apart from FUFREE, the MOFs in this top performing subset show similar process-level responses. While it is tempting to attribute this behaviour to minor scattering in the adsorption data, we show later in our discussion of the process-level uncertainties that this may not strictly be the case as different adsorption patterns can lead to the same CO2 purity-recovery performances. On the contrary, differences between LJ FFs become much more pronounced at the energy-productivity Pareto level. For example, in Fig. 7(b) we rank materials according to the maximum productivity they can achieve on their energy-productivity Pareto front (subject to the CCS constraints), and make a similar comparison between the top performers identified by UFF + DDEC and Dreiding + DDEC. It is evident from Fig. 7 that the predictions between LJ FFs are substantially more uncertain when the energy-productivity process KPIs are used. This observation is notable because the energy-productivity Pareto front more accurately reflects the separation potential of an adsorbent and, unlike the choice of charge scheme, the uncertainty that arises between different LJ parameter sets is unavoidable as the choice of UFF vs Dreiding is still somewhat arbitrary.
What then are the practical implications of these observations for HTCS of materials for CO2 capture? At this point it is important to recognise that the correlations between rankings are in some cases much greater than zero, i.e., between UFF + DDEC and Dreiding + DDEC. This suggests that HTCS retains its utility as a guided search platform even in the presence of considerable uncertainties. Indeed, Chung et al.83 and Boyd et al.82 have demonstrated this to good effect as studies which have experimentally verified the structures predicted by HTCS workflows. However, in light of our results, the preliminary conclusion of this section is that it is very likely that two separate studies utilising different levels of molecular theory will still come to different conclusions on what the top performing material candidates are. The picture that is emerging from the process-level results cannot be complete without a complementary understanding of the adsorption behaviours. Our objective in the next section is to therefore understand the nature of the disagreement between FFs at the material level. This will provide us with the molecular insights needed to reason why such differences in process performances arise.
Analysis of the underlying adsorption patterns and the extent of consistency in CO2 and N2 uptakes predicted using different molecular forcefields
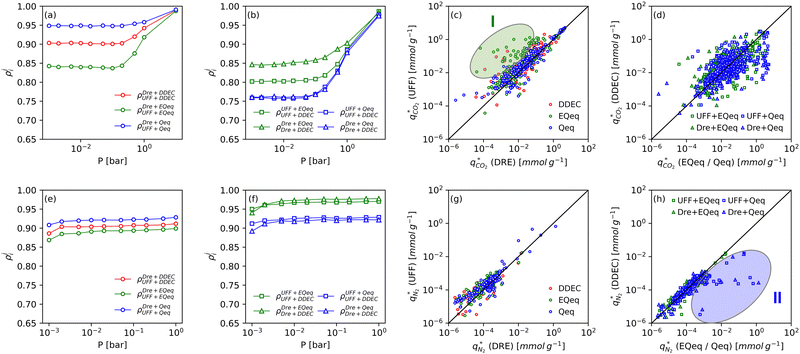
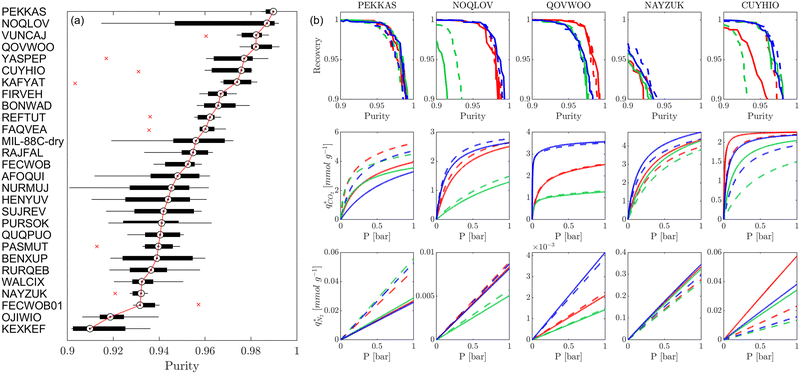
Fig. 8 provides a birds-eye-view of the extent of agreement in simulated uptakes of CO2 and N2 between different FFs. Fig. 8(a, b, e and f) show the Spearman correlations in simulated uptakes for all pressure points. Subplots (a) and (e) show correlations between LJ FFs using fixed charges for CO2 and N2, respectively, while subplots (b) and (f) consider fixed LJ FF parameters and different charge schemes. Parity plots of simulated uptakes for both CO2 and N2 relevant to each of these scenarios are provided in Fig. 8(c, d, g and h) at 0.001 bar, i.e., in the Henry's regime. We begin the discussion by comparing the behaviours of both adsorbates, after which we will explore the differences between molecular FFs. Note that the results presented here are qualitatively similar at higher pressures (see supplementary note 6, ESI†).From Fig. 8(a, b, e and f), both CO2 and N2 there is a greater degree of scattering, and therefore a lower correlation, between different FFs at lower pressures. We note that CO2 simulated uptakes exhibit a higher degree of scattering than N2 and seem more sensitive to the electrostatics than to the parameters of the LJ FF, as seen by the stronger correlations in Fig. 8(a) compared to Fig. 8(b); for N2, the opposite trend is observed. The observations above are easy to rationalise. It is known that the most favourable adsorption sites on a MOF will be occupied preferentially at lower pressures.44 The strength of the interactions between the adsorbing species and the framework is mediated by the partial charges assigned to framework atoms and the cross-interactions between the adsorbate and adsorbent (and hence the parameters of the LJ FF). Therefore, a higher degree of scattering in the uptakes is expected in the low pressure regime. CO2 also exhibits more pronounced uncertainties than N2 because: (1) it has more LJ sites available to interact with the MOF, and (2) it has a larger quadrupole moment which strongly interacts with the partial charges assigned to framework atoms.84 Finally, as the electrostatic contributions in CO2 adsorption are more significant than in N2 adsorption, the variation in the charge schemes produces a more pronounced scattering in the results compared to variations in the LJ parameters.
Now, we explore in more detail individual adsorption behaviours that contribute to the overall picture in Fig. 8. Intuitively, we can expect three primary scenarios for when predictions between FFs deviate significantly from each other: (1) when adsorption occurs in MOFs with small pores; (2) when the LJ parameters for framework atoms are significantly different between UFF and Dreiding; and (3) when charge equilibration methods fail to reproduce DDEC charges. In addition, it is possible that there are combinations of these scenarios for particular MOFs leading to strongly coupled effects. The aim of the following discussion is to explain how these FF deviations arise, and in doing so to provide more insights into the molecular origins of the correlation results in Fig. 8(a, b, e and f). To achieve this, we explore each of these three scenarios, touching on both the general trends and some material specific deviations.
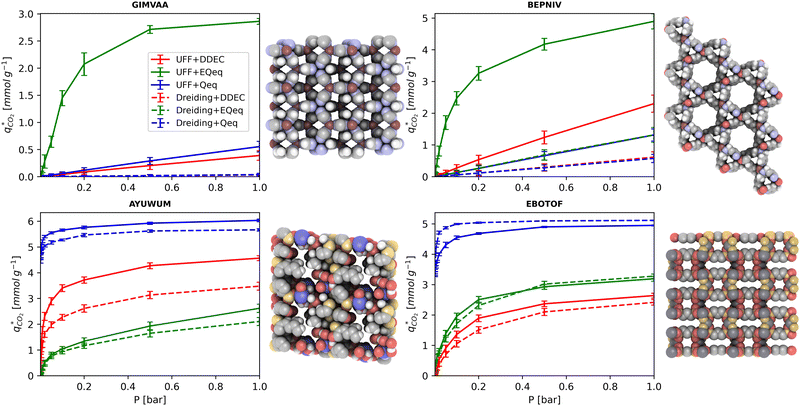
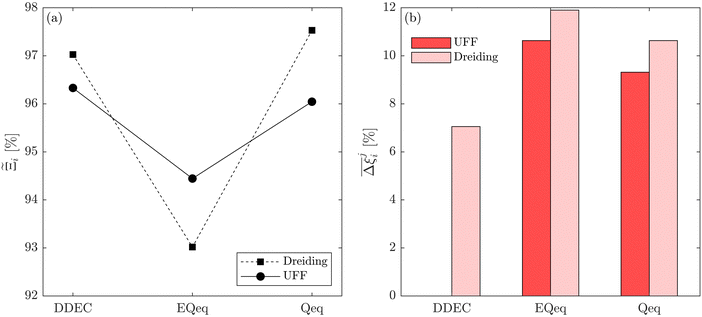
MOFs with smaller pores, and therefore a higher density of framework atoms, are more sensitive to the LJ parameters. These materials are typically associated with lower adsorbate uptakes, and so we generally see higher scattering in the data at lower loadings, as shown in e.g., Fig. 8(c). This is further demonstrated in Fig. S12 (ESI†), where the relative uptake of CO2 at 0.1 bar is plotted against the accessible void fraction of MOFs. In specific cases, confinement effects may also lead to very strong deviations in the adsorptive behaviours depending on the choice of the LJ parameters. For instance, OSOMIT, HELCUY, and GIMVAA – materials which contain Zn and have very narrow pore spaces – represent such exceptional cases. As an example, let us consider the adsorption isotherms of GIMVAA, as shown in the top left panel of Fig. 9. The first feature to note about the behaviour of this material is the very strong uptake observed for the UFF + EQeq combination of parameters (green line). This is associated with the EQeq charges assigned to metal atoms in this structure, which are substantially higher than the charges assigned by the DDEC and Qeq schemes. Focusing on the other data in this panel (blue and red lines), we note that only UFF predicts an appreciable uptake of CO2, and much lower uptake for any other combination of parameters. This behaviour stems primarily from the difference in LJ diameters assigned to Zn by UFF and Dreiding (σUFFZn = 2.462 Å and σDreZn = 4.045 Å). Due to the larger size of the framework atoms, the cross-potential interactions between the adsorbate and adsorbent are unfavourable in the small pores of GIMVAA for Dreiding, and favourable for UFF. This leads to negligible CO2 uptake when using Dreiding-based parameters and non-negligible uptake when the UFF models are employed. Returning to the outlier behaviour of the models based on EQeq charges, GIMVAA is representative of several materials in this class, forming a cluster of green points (cluster I) far above the parity line in Fig. 8(c).
Let us now consider the second scenario, when the LJ parameters for framework atoms are significantly different between UFF and Dreiding. If a MOF contains atom types for which the depth of the well in the interaction potential, ε, between UFF and Dreiding is very different, we can anticipate some sensitivity of the adsorption behaviour to the choice of LJ FF.48 From Fig. 8(c and g), we see that UFF generally predicts higher adsorbate uptakes. This can be tentatively attributed to the fact that many (approximately 65%) of the CRAFTED-u MOFs contain Zn as the metal which, in the UFF framework, is modelled with εUFFZn = 62.35 K compared to the Dreiding value of εDreZn = 27.68 K. Then, depending on the type of framework atoms and their abundance within the unit cell, it should be possible to determine which MOFs will be sensitive to the choice of LJ FF before performing any molecular simulations. Indeed, Dokur and Keskin developed a simple factor, calculated using the difference in εi between LJ FFs and the number, ni, of atoms i, to distinguish MOFs which are relatively insensitive, and MOFs which significantly depend on the choice of the LJ parameters (see supplementary note 6.2, ESI†).45 Turning our attention now to some specific materials, we find that, similar to the previous scenario, often a particular feature of a MOF tends to magnify the expected deviations between LJ FFs. For example, in addition to OSOMIT, HELCUY, and GIMVAA, cluster I in Fig. 8(c) contains other Zn-metal MOFs such as BEPNIV (Fig. 9, top panel on the right) for which confinement effects cannot explain the observed sensitivities as these structures are quite open and feature relatively larger pores. These materials do however contain open metal sites (OMS).85 As Zn is defined by a smaller LJ collision diameter in UFF, the closest distance of approach between adsorbing CO2 and the OMS is shorter, which leads to an exponential increase in the electrostatic contributions to the interactions in these systems. This generally results in more sporadic adsorption behaviours using UFF parameters. From this observation we expect that large uncertainties are likely to be encountered when: (1) MOFs contain OMS that are accessible to the adsorbates; (2) the OMS belongs to a metal in which the difference in atomic diameters between LJ FFs is significant (e.g., Zn, Fe, Ti, Tc, and Ru); and (3) the partial charge assigned to the metal is sufficiently large. Caution is therefore warranted when interpreting the adsorption behaviours in MOFs with OMS using generic LJ FFs, particularly as they often fail to reproduce the adsorption data of their experimental counterparts.85–89 Combined, the materials described here and in the previous scenario explain why poorer correlations between LJ FFs are observed using EQeq (Fig. 8(a and e)), and why 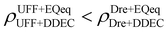 for CO2 in Fig. 8(b).
for CO2 in Fig. 8(b).
Finally, the third scenario is concerned with the accuracy of charge assignment using simplified schemes such as Qeq and EQeq. In many instances, charge equilibration methods do not capture the subtle differences in chemical bonding environments that are reflected by DDEC charges. Therefore, only modest agreement between DDEC and (E)Qeq charge schemes is observed over the entire CRAFTED-u database. A good example is given in Fig. S14 (ESI†), whereby (E)Qeq returns similar charges for all Zn atoms in all CRAFTED-u MOFs, while DDEC charges range between 0 and +1.5e (where e is the elementary charge). For specific materials, charge equilibration methods can fail spectacularly. In particular, we found that the Qeq scheme can return inappropriately high – and in some instances unphysical – charges. Such is the case for the MOFs populating the cluster of blue points (cluster II) below the parity line in Fig. 8(h). The spurious charges assigned in these materials arise for different reasons. For example, in EBOTOF (Fig. 9, lower panel on the right), Al metals are coordinated to highly electronegative atoms such as F, which represents a particular bonding environment for which Qeq fails. Similarly, abnormal Qeq charges are assigned in MOFs where Na, Ga, or In metals are present, such as in AYUWUM (Fig. 9, lower left panel). Ongari et al. noticed similar abnormalities in their study.47 As to why Qeq fails in this regard, and EQeq does not, stems from the fact that Qeq uses a neutral charge-centre to express the Taylor series expansion in electric energy, while EQeq considers the Taylor series expansion around charge-positive metal cations. The neutral charge-centring is not able to accurately reproduce DDEC charges in alkali metals such as Na, but more generally it appears to fail for MOFs containing metals with a single electron in their outer orbital,47 thus leading to similar deviations in In- and Ga-metal MOFs in the CRAFTED-u dataset. These outlier adsorption behaviours, which exist primarily for the Qeq scheme, are what contributes to the difference between Qeq and EQeq correlation lines in Fig. 8(b and f).
At this point, it is clear that the choice of the FF has a very strong impact on the adsorption behaviour, often leading to profound differences in the isotherms for the same material. These differences are likely to manifest in the material-level KPIs that depend on adsorption data from molecular simulations (see for example Fig. S16, ESI†), as well as in the performance estimates obtained using process simulations, discussed in the next section. Our results further emphasise that using simplified charge equilibration schemes in application to a heterogeneous database of materials is likely to result in unreliable predictions, which can further lead to significant scattering in the results and a lack of confidence in the rankings. From this analysis, we are now better equipped to establish a general connection between the different molecular FFs and the process performance distributions that arise from such modelling choices.
Quantifying process-level uncertainties emerging from the use of different molecular forcefields
In this section, we quantify the uncertainty between different FFs at the process-level. The objective here is two-fold: (1) we attempt to connect the material uncertainties described in the previous section to the process-level uncertainties in a systematic way; and (2) benchmarking protocols that quantify the impact of different FFs in conditions relevant to the desired application, e.g., carbon capture, will be required as improvements in molecular simulations continue to develop. Through our analysis, we aim to demonstrate the generality of our framework for evaluating future generations of molecular FFs.For the above purposes, we make use of the metrics described in the Methodology section to map between distributions in adsorption isotherms and CO2 purity-recovery Pareto fronts. A Pareto-dominance plot, constructed from 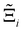 for each molecular FF i, is displayed in Fig. 10(a). This plot demonstrates the tendency of a particular FF to dominate, or not dominate, relative to other FFs. In Fig. 10(b), the process-level uncertainties are visualised using the average hypervolume error,
for each molecular FF i, is displayed in Fig. 10(a). This plot demonstrates the tendency of a particular FF to dominate, or not dominate, relative to other FFs. In Fig. 10(b), the process-level uncertainties are visualised using the average hypervolume error, 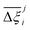 . Consistent with the discussion so far, we make comparisons amongst the different FFs by taking UFF + DDEC as the reference. For a complete comparison of the uncertainties between all pairwise FFs i and j, see supplementary note 7.1 (ESI†).
. Consistent with the discussion so far, we make comparisons amongst the different FFs by taking UFF + DDEC as the reference. For a complete comparison of the uncertainties between all pairwise FFs i and j, see supplementary note 7.1 (ESI†).
Focusing on Fig. 10(a) first, it is clear that 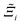 values constructed from the models based on EQeq charges are consistently lower than those using DDEC or Qeq charges. This means that the adsorption behaviours of materials generated using the EQeq charge scheme typically yield poorer process-level performances compared to DDEC and Qeq. Another interesting feature to note is the interaction between LJ FFs and the different charge schemes. Dreiding yields better average process performances than UFF when coupled with either DDEC or Qeq but poorer average process performances when coupled with EQeq. The molecular origin behind this inverse Pareto-dominance relationship is explained in supplementary note 7.2 (ESI†). Now, turning our attention to Fig. 10(b), we note a number of important trends. Relative to the UFF + DDEC baseline: (1) larger
values constructed from the models based on EQeq charges are consistently lower than those using DDEC or Qeq charges. This means that the adsorption behaviours of materials generated using the EQeq charge scheme typically yield poorer process-level performances compared to DDEC and Qeq. Another interesting feature to note is the interaction between LJ FFs and the different charge schemes. Dreiding yields better average process performances than UFF when coupled with either DDEC or Qeq but poorer average process performances when coupled with EQeq. The molecular origin behind this inverse Pareto-dominance relationship is explained in supplementary note 7.2 (ESI†). Now, turning our attention to Fig. 10(b), we note a number of important trends. Relative to the UFF + DDEC baseline: (1) larger 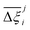 are typically observed when the charge scheme is changed rather than when the LJ FF is changed, i.e.,
are typically observed when the charge scheme is changed rather than when the LJ FF is changed, i.e., 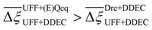 ; (2) models based on EQeq charges are associated with larger
; (2) models based on EQeq charges are associated with larger 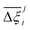 compared to the models based on Qeq charges; and (3) the uncertainties associated with the choice of LJ FF is non-negligible. To expand on this final point, QOVWOO and XOVVIO are the 1st and 47th ranked materials according to the UFF + DDEC forcefield. Their performance curves deviate by a hypervolume of approximately 7%, which is equivalent to the average error between UFF and Dreiding in Fig. 10(b). The results presented here reasonably support the conclusions outlined in our discussion of the agreement between process-level rankings. In particular, they corroborate that the predictions are overall more sensitive to the choice of the charge scheme than to the choice of the LJ parameters, that the models based on EQeq charges agree less favourably with the DDEC baseline, and that the LJ FF can have a considerable impact on the process-level results.
compared to the models based on Qeq charges; and (3) the uncertainties associated with the choice of LJ FF is non-negligible. To expand on this final point, QOVWOO and XOVVIO are the 1st and 47th ranked materials according to the UFF + DDEC forcefield. Their performance curves deviate by a hypervolume of approximately 7%, which is equivalent to the average error between UFF and Dreiding in Fig. 10(b). The results presented here reasonably support the conclusions outlined in our discussion of the agreement between process-level rankings. In particular, they corroborate that the predictions are overall more sensitive to the choice of the charge scheme than to the choice of the LJ parameters, that the models based on EQeq charges agree less favourably with the DDEC baseline, and that the LJ FF can have a considerable impact on the process-level results.
On the contrary, we find that the connection between the process-level uncertainties and material-level correlations in Fig. 8(a, b, e and f) is not as straightforward. For example, given that a stronger correlation in the Henry's regime is observed between DDEC and EQeq in Fig. 8(b and f), one might expect that lower process-level uncertainties in Fig. 10(b) would be observed between DDEC and EQeq rather than DDEC and Qeq. However, different FFs often give rise to variations in several important features of both the CO2 and N2 adsorption isotherms simultaneously, such as the Henry's coefficient, local slope, nonlinearity, and total saturation capacity. The performance of an adsorbent is determined by an interplay of all of these features and by the competitive adsorption between CO2 and N2,5,49–51,66 and so it is difficult to capture the process-level effects from a single metric such as the correlation between uptakes at low pressure. This makes establishing a general connection between molecular FFs and their process-level uncertainties a challenging task. It is possible to link individual materials to their process-level responses by a more in-depth analysis (for example, see supplementary note 7.2, ESI†), however the material-to-process mappings are in general nonlinear.
Exploring potential pathways towards uncertainty mitigation in multiscale HTCS workflows
In the previous sections we demonstrated that the typical choices and combinations of the FF parameters lead to inconsistent selection of the top performing materials and the relative rankings of the materials. We showed that both selection of the LJ parameters (UFF vs. Dreiding) and selection of the charge scheme has an impact on the predictions, however the inconsistency introduced by the charge scheme seems to be more significant compared to the choice of the LJ parameters. Furthermore, our results indicate that charge equilibration schemes may lead to unphysical results (Qeq) and strong deviations in the adsorption behaviours predicted by DDEC charges (both EQeq and Qeq).These findings have significant implications for any further effort to implement fully in silico multiscale screening of porous materials. On the one hand, a strong statement would be that none of the combinations of the parameters are fully validated in experiments and, given the sensitivity of the process predictions to the selection of the FFs, it is unlikely that fully computational workflows will be able to produce reliable results. On the other hand, we argue that meaningful results can be obtained using this approach provided the parameter inputs and data outputs are handled with care. It is clear that shortcut methods such as (E)Qeq should not be used in HTCS studies, and so future screening studies should adopt ab initio levels of theory for partial charge assignment. The process performance of shortlisted materials identified using ab initio charges should therefore (ideally) be robust against perturbations in the LJ parameters. As a minimum, some estimate of the uncertainty introduced by different LJ parameter sets should be considered to build confidence in the predictions of these workflows. In either case, an accurate and comprehensive FF is the key bottleneck in computational screening, and we will return to this point in more detail in the next section. For now, we would like to explore two ideas to improve the consistency of predictions within the current state-ot-the-art.
The first idea is based on the hypothesis that amongst the CRAFTED MOFs, a group of materials exists whose adsorption behaviours are rather insensitive to the choice of the FF. It is further possible that among these materials, there are those that meet the required purity and recovery constraints and, in general, show good performance at the process level. We speculate that, given the insensitivity of the materials to the FF, it is likely that they will retain their performance in experiments as well. In this case, one can argue that the screening protocols could focus on searching for the materials in this class.
The second idea is as follows. We assert that ab initio charges are required for HTCS of MOFs for carbon capture. Unfortunately, it is still computationally challenging to employ these approaches for large databases of materials. Therefore, we would like to explore whether ML-based models90–92 such as the message passing neural network (MPNN) model90 and partial atomic charges in metal–organic frameworks (PACMOF) model92 can be used as a scalable but accurate alternative to the DDEC method.
Let us focus on these ideas in turn. To explore our initial hypothesis that there exists a subset of high performing MOFs that are relatively insensitive to the FF, we first define a taxonomy for describing CRAFTED MOFs by their ability to meet the CCS constraints for different FFs using four distinct consistency classes (Table 2). A small subset of 28 MOFs meets the CO2 purity and recovery constraints on a consistent basis, regardless of the particular variation of the FF chosen. We denote these materials as being at the highest level of consistency: consistency level 1 (CL1).
| Classa | Label | Number of molecular forcefields (out of 6) for which a material meets the CCS constraints | Number of materials in class |
|---|---|---|---|
| a The lists of CSD codes for each of these classes are provided in supplementary note 8. b CL1 and CL2 class materials are differentiated from CL3 and CL4 on the basis of statistical significance. That is, the spread and skewness of the performance distributions for materials in these classes can be visualised using box-and-whisker plots which require a minimum of 5 measurements to construct. | |||
| CL1b | Consistent CCS adsorbents | 6 | 28 |
| CL2a | Semi-consistent CCS adsorbents | 5 | 22 |
| CL3 | Inconsistent CCS adsorbents | [1–4] | 168 |
| CL4 | Non-CCS adsorbents | 0 | 472 |
The next question we pose is whether the high level of consistency in the CL1 group is because the adsorption behaviours in these materials are insensitive to the parameters of the FF or due to some other factors. To address this question, in Fig. 11(a) we visualise the relative ranking of CL1 class MOFs, using a box-and-whisker plot to represent the underlying distributions in process performances. It is evident from this subplot that the CL1 class contains materials which are characterised by both narrow distributions in performance, i.e., PEKKAS, and broad distributions in performance, i.e., NOQLOV. This suggests that a search for materials which consistently meet the CCS constraints is not sufficient to guarantee that their performance is insensitive to the choice of FF. Still, within the CL1 subset there are materials such as PEKKAS, QOVWOO, FIRVEH, and NAYZUK, whose narrow boxplots have the potential to confirm our hypothesis. By inspection of the individual adsorption behaviours and performance curves for select materials in Fig. 11(b), we observe a diversity of responses to the choice of FF. In every case however, some scattering in the adsorption data is observed. This means that the MOFs which are (rather fortuitously) characterised by narrow performance distributions achieve this level of consistency through different pathways. That is to say, the CO2 purity-recovery Pareto fronts in these materials converge to similar high performing solutions (despite the scattering seen in the adsorption data) by using very different combinations of the PSA cycle parameters. Therefore, the results in Fig. 11 do not provide us with the type of evidence one would like to confirm our initial hypothesis. We arrive then to the conclusion that, in order to achieve consistent process performances in multiscale HTCS workflows for the right reasons, the inconsistencies which propagate from the material level must first be addressed.
This brings us onto our second idea. Here, we test whether the uncertainties which are introduced by charge equilibration schemes can be effectively mitigated by using the ML-based MPNN and PACMOF models. As a case study, we continue with the CL1 class of MOFs. These materials satisfy the CCS constraints across all FFs, and so we evaluate the accuracy of MPNN and PACMOF charges by optimising the energy penalty and productivity performances subject to the CCS constraints. This protocol is more robust than an unconstrained CO2 purity-recovery optimisation as the energy-productivity process responses are more sensitive to changes in the adsorption behaviours.66 The optimisations were first conducted using the ANN model and then refined using the PSA process model in order to calculate the hypervolume errors between Pareto fronts generated using different molecular FFs. The results are provided in Fig. 12, taking UFF + DDEC as the baseline for comparison.
Disregarding the MPNN and PACMOF charges in Fig. 12 for a moment, we observe a similar response in the energy-productivity results to changes in the FF as the CO2 purity-recovery results. However, it is clear that scattering in the adsorption data has a stronger influence on these KPIs. For instance, the average hypervolume error of 24% between LJ FFs (combined with DDEC charges) in Fig. 12 represents a 3-fold increase in the errors calculated at the CO2 purity-recovery Pareto level (Fig. 10). While these results are determined for a reduced subset of MOFs, we generally expect an uncertainty of approximately 30% between LJ FFs using energy-productivity KPIs (see supplementary note 8.3, ESI†). Upon introducing the MPNN and PACMOF charges back into the discussion, the lowest uncertainties in Fig. 12 no longer occur between UFF and Dreiding using fixed DDEC charges. Instead, they occur between DDEC and MPNN/PACMOF charges using fixed UFF parameters, meaning that the prevailing sources of uncertainty identified previously (the choice of charge) has been effectively mitigated by modelling the electrostatics with ML-based charges. Interestingly, the uncertainty that is introduced by the MPNN and PACMOF models is comparable to the scattering seen between surrogate model predictions and PSA process simulations (Fig. 3). Efficient pre-screening of MOF databases could therefore be achieved by combining ML models for both the partial charge calculations and the PSA cycle optimisations without a significant loss of accuracy. Overall, our results suggest that MPNN and PACMOF can be used to assign charges in lieu of the DDEC method (see Fig. S18, S19 and S21, ESI†). This is further demonstrated in Fig. 13 whereby we see that, of the materials shown here, the adsorption behaviours and process-level predictions obtained using ML-based charges are in closer agreement with the DDEC baseline for all materials apart from NOQLOV.
Future prospects for HTCS of materials for carbon capture
While we strongly advocate for ab initio charges whenever possible, the results presented in Fig. 12 and 13 support our argument that ML-based charges are the next best option available to practitioners. Nonetheless, we recognise some of the shortcomings in our analysis (see supplementary note 9, ESI†) and understand that 28 MOFs cannot represent the diverse chemical landscape of all known MOFs. It is likely that expanding the scope of our study to more materials would expose some regions of poor agreement between ML-based and DDEC charges. Indeed, Liu and Luan39 recently benchmarked several charge assignment methods and determined that charge predictions from PACMOF significantly deteriorated in MOFs which contained transition metals. However, as larger MOF databases with pre-computed ab initio charges begin to emerge,93 we expect that improvements in the current ML models can be achieved by simply extending the training set to cover more materials with greater chemical diversity. Future efforts should therefore be directed towards developing more advanced MOF representations and ML architectures.A problem still remains when we are posed with the question of which LJ FF to use. Both UFF and Dreiding are designed to be as generic as possible and thus are rather crude approximations of the complex interatomic interactions taking place during adsorption. These interactions are relatively weak compared to the energy variations in chemical bonds, and so the development of more reliable LJ FFs for adsorption in MOFs remains an open and important challenge. As with most areas of material science, ML has a possible role to play here. The interatomic potentials which describe short range interactions can be constructed using ML methods by approximating the high-dimensional potential energy surface (PES) using training data obtained from ab initio calculations.94 The general and flexible nature of neural network models makes them a viable ML architecture for this purpose. Indeed, the so-called high-dimensional neural network potential (HDNNP) was introduced as early as 2007 by Behler and Parrinello,95 and in principle considers the PES to be a sum of environment-dependent atomic energy contributions. HDNNPs can be computed many orders of magnitude faster than e.g., DFT calculations, they retain the accuracy of reference ab initio data, and can be scaled to large systems or time scales.94
These concepts are only beginning to emerge in the field of MOFs. The first application of HDNNPs for MOFs was introduced by Eckhoff and Behler, where they predicted the negative thermal expansion of MOF-5 as well as its phonon density of states using HDNNPs.96 Zheng et al. also recently developed a HDNNP to study to the chemisorption and diffusion of CO2 in Mg-MOF-74.97 While promising, this approach comes with its own set of open challenges. These include, but are not limited to, the construction of more informative feature vectors which can capture both the local chemical environments and MOF pore attributes, in developing an approach which can model material classes with a large number of chemical elements (the feature vector often scales with the number of chemical elements98), and in generating the reference training data for MOFs with a large number of atoms in their unit cells.99 Furthermore, extending this approach to predict adsorption in chemically diverse material databases would require transferable models: the training set must represent the problem at hand. A good example is the general-purpose ANI-2 potential,100 which was trained on reference data for a large number of organic molecules and is thus capable of simulating systems containing (H, C, N, O, F, Cl, and S). One can envision a similar approach being adopted for mixed organic–inorganic complexes. An alternative, less data-intensive avenue would be to use active learning as a means to reliably explore the chemical space of MOFs.99,101 In either case, a viable pathway towards developing a general-purpose, highly accurate ML potential for MOF screening applications exists provided that the appropriate training data, ML architecture, and feature vector can be combined. If such a method were to emerge, it has the potential to shift paradigms not only in the screening of MOFs for carbon capture, but in materials modelling in general.
Conclusions
In this multiscale computational screening study, we aimed to address the question: to what extent will the ranking of porous materials, and the selection of top performers identified in process modelling, depend on the choice of molecular forcefield? To do so, we generated distributions of CO2 and N2 adsorption isotherms in 690 MOFs using different forcefields (FFs) which represent the modelling choices commonly encountered in high-throughput computational screenings (HTCS) of materials for CO2 capture. We then conducted a systematic uncertainty quantification study using PSA process-level modelling to determine one's ability to identify top-performing candidate materials consistently across different FF definitions.Our results allow us to draw a number of general conclusions:
(i) Indeed, the computational ranking of materials appears to depend on the choice of the molecular FF to a significant extent.
(ii) From the pool of molecular modelling choices considered in this investigation, the choice of charge assignment scheme represents the largest source of uncertainty at the process-level.
(iii) Partial charges assigned by charge equilibration methods such as Qeq and EQeq are unable to reproduce the adsorption behaviours of charges derived from ab initio calculations such as DDEC with sufficient accuracy to guarantee consistent process-level rankings. As such, we recommend avoiding using charge equilibration methods when the electrostatic interactions are important for adsorption, such as CO2 adsorption in MOFs. When ab initio charges are not available and are computationally unfeasible to obtain, ML-based charges are an attractive alternative that can effectively minimise the uncertainties originating from partial charge assignment. A simple extension in the pool of training materials can provide a quick remedy to the potential pitfalls of existing ML models, while future efforts should strive towards advanced MOF representations and machine learning architectures.
(iv) The process-level correlations between LJ FFs indicate that approximately 70% of the top performing MOFs may be mutually identified. This suggests that, in spite of considerable uncertainty, the search for MOFs using state-of-the-art multiscale HTCS is still more efficient than a random search. Nevertheless, we still lack a consistent, experimentally validated set of molecular parameters to describe the LJ interactions. Until this issue is addressed, one has to accept the considerable uncertainties embedded within process-level predictions which make use of adsorption data generated using generic LJ FFs.
We believe our work is an important step towards understanding the level of accuracy one can expect from multiscale screenings of materials for PSA-based carbon capture processes. The picture that emerges from our study is that, while HTCS remains a useful tool in the computational chemist's arsenal, it is not really possible to obtain material rankings with high resolution using this approach. In light of these observations, we see two ways to proceed with HTCS studies.
The first is to strive towards more consistent implementations of these workflows. As we mention above, the most direct route is to only use ab initio charges and, failing that, ML-based charges, to model the electrostatic interactions. Moving towards more consistent models of the short-range range dispersion/repulsion interactions would require two stages of implementation, we expect. In the short-term and until a truly universal methodology can be developed, opting for internally consistent LJ parameters within the community is an admirable pursuit. The rational choice would be to use the UFF forcefield, given its ability to simulate MOF databases with greater chemical diversities. However, we still recommend that the performance of shortlisted MOFs should be checked for robustness against perturbations in the LJ parameter sets. In the longer-term, we foresee great possibilities in the use of machine learned interatomic potentials as a means to simulate the short-range interactions in MOFs and, provided such a method can be developed, expect this approach to radicalise the way in which HTCS studies are conducted.
The second option is to alter the perceived utility of HTCS. Many technical barriers exist between identifying MOFs through HTCS and translating them into real, industrially viable separation materials. To name a few, a MOF must demonstrate good mechanical, thermal and moisture stability, low cost, and scalable synthesisability. A prime example is CALF-20102 which, despite its relatively modest process-level performance (see supplementary note 10, ESI†), is the only known MOF to satisfy enough of these technical requirements to succeed as a viable industrial-scale adsorbent. Therefore, rather than identifying the best performers via material rankings which we understand suffers from some reliability issues, one can instead try to identify good performers using HTCS and then shortlist materials based on all other factors which dictate the feasibility of an adsorbent. Given the importance of these material attributes, this approach could provide more meaning to the results obtained using HTCS and help expedite the transition between identifying promising MOFs and eventually tasking them to bench scale.
Author contributions
Conor Cleeton contributed to the data curation, conceptualisation, formal analysis, investigation, methodology, software, validation, visualisation, and writing – original draft. Felipe Lopes Oliveira contributed to the data curation, conceptualisation, methodology, and writing – review & editing. Rodrigo F. Neumann contributed to conceptualisation, methodology, and writing – review & editing. Amir H. Farmahini contributed to the conceptualisation, methodology, and writing – review and editing. Binquan Luan contributed to conceptualisation and writing – review & editing. Mathias Steiner contributed to conceptualisation and writing – review & editing. Lev Sarkisov contributed to the conceptualisation, formal analysis, methodology, validation, writing – original draft.Code availability
All code created in this work is available on GitHub (https://github.com/ConorNCleeton/uncertainty_screening_mofs).Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors would like to acknowledge the assistance given by Research IT and the use of the Computational Shared Facility at the University of Manchester.References
- A. Li, R. Bueno-Perez, D. Madden and D. Fairen-Jimenez, Chem. Sci., 2022, 13, 7990–8002 RSC.
- A. H. Farmahini, S. Krishnamurthy, D. Friedrich, S. Brandani and L. Sarkisov, Chem. Rev., 2021, 121(17), 10666–10741 CrossRef CAS.
- S. Li, Y. G. Chung, C. M. Simon and R. Q. Snurr, J. Phys. Chem. Lett., 2017, 8, 6135–6141 CrossRef CAS PubMed.
- D. Wu, Q. Yang, C. Zhong, D. Liu, H. Huang, W. Zhang and G. Maurin, Langmuir, 2012, 28, 12094–12099 CrossRef CAS PubMed.
- A. K. Rajagopalan, A. M. Avila and A. Rajendran, Int. J. Greenhouse Gas Control, 2016, 46, 76–85 CrossRef CAS.
- T. D. Burns, K. N. Pai, S. G. Subraveti, S. P. Collins, M. Krykunov, A. Rajendran and T. K. Woo, Environ. Sci. Technol., 2020, 54, 4536–4544 CrossRef CAS PubMed.
- D. Yancy-Caballero, K. T. Leperi, B. J. Bucior, R. Richardson, T. Islamoglu, O. K. Farha, F. You and R. Q. Snurr, Mol. Syst. Des. Eng., 2020, 5, 1–26 RSC.
- K. T. Leperi, D. Yancy-Caballero, R. Q. Snurr and F. You, Ind. Eng. Chem. Res., 2019, 58, 18241–18252 CrossRef CAS.
- A. H. Farmahini, D. Friedrich, S. Brandani and L. Sarkisov, Energy Environ. Sci., 2020, 13, 1018–1037 RSC.
- S. Krishnamurthy, J. Boon, C. Grande, A. Lind, R. Blom, R. de Boer, H. Willemsen and G. de Scheemaker, Chem. Ing. Tech., 2021, 1–13 Search PubMed.
- S. G. Subraveti, K. N. Pai, A. K. Rajagopalan, N. S. Wilkins, A. Rajendran, A. Jayaraman and G. Alptekin, Appl. Energy, 2019, 254, 1–13 CrossRef.
- D. Dubbeldam, K. S. Walton, T. J. H. Vlugt and S. Calero, Adv. Theory Simul., 2019, 2(11), 1900135 CrossRef CAS.
- F.-X. Coudert and A. H. Fuchs, Coord. Chem. Rev., 2016, 307, 211–236 CrossRef CAS.
- E. Haldoupis, J. Borycz, H. Shi, K. D. Vogiatzis, P. Bai, W. L. Queen, L. Gagliardi and J. I. Siepmann, J. Phys. Chem. C, 2015, 119, 16058–16071 CrossRef CAS.
- T. M. Becker, J. Heinen, D. Dubbeldam, L. C. Lin and T. J. H. Vlugt, J. Phys. Chem. C, 2017, 121, 4659–4673 CrossRef CAS.
- S. L. Mayo, B. D. Olafson and W. A. Goddard, J. Phys. Chem., 1990, 94, 8897–8909 CrossRef CAS.
- A. K. Rappe, C. J. Casewit, K. S. Colwell, W. A. Goddard and W. M. Skiff, J. Am. Chem. Soc., 1992, 10024–10035 CrossRef CAS.
- E. Braun, A. F. Zurhelle, W. Thijssen, S. K. Schnell, L. C. Lin, J. Kim, J. A. Thompson and B. Smit, Mol. Syst. Des. Eng., 2016, 1, 175–188 RSC.
- L. C. Lin, A. H. Berger, R. L. Martin, J. Kim, J. A. Swisher, K. Jariwala, C. H. Rycroft, A. S. Bhown, M. W. Deem, M. Haranczyk and B. Smit, Nat. Mater., 2012, 11, 633–641 CrossRef CAS PubMed.
- N. S. Bobbitt and R. Q. Snurr, Mol. Simul., 2019, 45, 1069–1081 CrossRef CAS.
- M. J. Chiau Junior, Y. Wang, X. Wu and W. Cai, Int. J. Hydrogen Energy, 2020, 45, 27320–27330 CrossRef CAS.
- Y. J. Colón and R. Q. Snurr, Chem. Soc. Rev., 2014, 43, 5735–5749 RSC.
- J. Stoll, J. Vrabec and H. Hasse, AIChE J., 2003, 49, 2187–2198 CrossRef CAS.
- S. Hamad, S. R. G. Balestra, R. Bueno-perez, A. R. Ruiz-salvador and M. Carlo, J. Solid State Chem., 2015, 223, 144–151 CrossRef CAS.
- C. I. Bayly, P. Cieplak, W. D. Cornell and P. A. Kollman, J. Phys. Chem., 1993, 97, 10269–10280 CrossRef CAS.
- C. Breneman and K. Wilberg, J. Comput. Chem., 1989, 11, 361–373 CrossRef.
- K. Sladekova, C. Campbell, C. Grant, A. J. Fletcher, J. R. B. Gomes and M. Jorge, Adsorption, 2020, 26, 663–685 CrossRef CAS.
- T. A. Manz and D. S. Sholl, J. Chem. Theor. Comput., 2010, 6, 2455–2468 CrossRef CAS PubMed.
- T. A. Manz and N. G. Limas, RSC Adv., 2016, 6, 47771–47801 RSC.
- N. G. Limas and T. A. Manz, RSC Adv., 2016, 6, 45727–45747 RSC.
- T. A. Manz, RSC Adv., 2017, 7, 45552–45581 RSC.
- N. G. Limas and T. A. Manz, RSC Adv., 2018, 8, 2678–2707 RSC.
- C. Campañá, B. Mussard and T. K. Woo, J. Chem. Theory Comput., 2009, 5, 2866–2878 CrossRef PubMed.
- A. K. Rappe and W. A. Goddard, J. Phys. Chem., 1991, 95, 3358–3363 CrossRef CAS.
- C. E. Wilmer, K. C. Kim and R. Q. Snurr, J. Phys. Chem. Lett., 2012, 3, 2506–2511 CrossRef CAS PubMed.
- S. Ramachandran, T. G. Lenz, W. M. Skiff and A. K. Rappé, J. Phys. Chem., 1996, 100, 5898–5907 CrossRef CAS.
- B. A. Wells, C. De Bruin-Dickason and A. L. Chaffee, J. Phys. Chem. C, 2015, 119, 456–466 CrossRef CAS.
- M. Zhang and R. Fournier, J. Phys. Chem. A, 2009, 113, 3162–3170 CrossRef CAS PubMed.
- S. Liu and B. Luan, Nanoscale, 2022, 14, 9466–9473 RSC.
- C. E. Wilmer, O. K. Farha, Y. S. Bae, J. T. Hupp and R. Q. Snurr, Energy Environ. Sci., 2012, 5, 9849–9856 RSC.
- Z. Sumer and S. Keskin, Ind. Eng. Chem., 2016, 55, 10404–10419 CrossRef CAS.
- C. Altintas, G. Avci, H. Daglar, A. Nemati Vesali Azar, S. Velioglu, I. Erucar and S. Keskin, ACS Appl. Mater. Interfaces, 2018, 10, 17257–17268 CrossRef CAS PubMed.
- M. J. Lennox, M. Bound, A. Henley and E. Besley, Mol. Simul., 2017, 43, 828–837 CrossRef CAS.
- J. G. Mcdaniel, S. Li, E. Tylianakis, R. Q. Snurr and J. R. Schmidt, J. Phys. Chem. C, 2015, 119, 3143–3152 CrossRef CAS.
- H. Fang, H. Demir and D. S. Sholl, J. Mater. Chem. A, 2014, 2, 274–291 RSC.
- C. Altintas and S. Keskin, Mol. Syst. Des. Eng., 2020, 5, 532–543 RSC.
- D. Ongari, P. G. Boyd, O. Kadioglu, A. K. Mace, S. Keskin and B. Smit, J. Chem. Theory Comput., 2019, 15, 382–401 CrossRef CAS PubMed.
- D. Dokur and S. Keskin, Ind. Eng. Chem. Res., 2018, 57, 2298–2309 CrossRef CAS PubMed.
- A. K. Rajagopalan and A. Rajendran, Int. J. Greenhouse Gas Control, 2018, 78, 437–447 CrossRef CAS.
- K. T. Leperi, Y. G. Chung, F. You and R. Q. Snurr, ACS Sustainable Chem. Eng., 2019, 7, 11529–11539 CrossRef CAS.
- A. H. Farmahini, S. Krishnamurthy, D. Friedrich, S. Brandani and L. Sarkisov, Ind. Eng. Chem. Res., 2018, 57, 15491–15511 CrossRef CAS.
- Y. G. Chung, J. Camp, M. Haranczyk, B. J. Sikora, W. Bury, V. Krungleviciute, T. Yildirim, O. K. Farha, D. S. Sholl and R. Q. Snurr, Chem. Mater., 2014, 26, 6185–6192 CrossRef CAS.
- D. Nazarian, S. Camp and D. S. Sholl, Chem. Mater., 2016, 28, 785–793 CrossRef CAS.
- D. Dubbeldam, S. Calero, D. E. Ellis, R. Q. Snurr, D. Dubbeldam, S. Calero, D. E. Ellis and R. Q. Snurr, Mol. Simul., 2016, 42, 81–101 CrossRef CAS.
- danieleongari/EQeq: Charge equilibration method for crystal structures, https://github.com/danieleongari/EQeq, (accessed 21 July 2022).
- F. L. Oliveira, C. Cleeton, R. Neumann Barros Ferreira, B. Luan, A. H. Farmahini, L. Sarkisov and M. Steiner, Sci. Data, 2023, 10, 1–12 CrossRef PubMed.
- W. Lou, J. Li, W. Sun, Y. Hu, L. Wang, R. F. Neumann, M. Steiner, Z. Gu, B. Luan and Y. Zhang, Chem. Eng. J., 2023, 452, 139296 CrossRef CAS.
- Y. Hu, Y. Jiang, J. Li, L. Wang, M. Steiner, R. F. Neumann, B. Luan, Y. Zhang, Y. Hu, Y. Jiang, J. Li, L. Wang, Y. Zhang, M. Steiner, R. F. Neumann and B. Luan, Adv. Funct. Mater., 2023, 33, 2213915 CrossRef CAS.
- J. A. Ritter, K. C. Bumiller, K. J. Tynan and A. D. Ebner, Adsorption, 2019, 25, 1511–1523 CrossRef CAS.
- P. Nugent, Y. Belmabkhout, S. Burd, A. Cairns, R. Luebke, K. Forrest, T. Pham, S. Ma, B. Space, L. Wojtas, M. Eddaoudi and M. Zaworotko, Nature, 2013, 495, 80–84 CrossRef CAS PubMed.
- V. Benoit, R. S. Pillai, A. Orsi, P. Normand, H. Jobic, F. Nouar, P. Billemont, E. Bloch, S. Bourrelly, T. Devic, P. A. Wright, G. De Weireld, C. Serre and P. L. Llewellyn, J. Mater. Chem. A, 2016, 1383–1389 RSC.
- Non-Linear Least-Squares Minimization and Curve-Fitting for Python—Non-Linear Least-Squares Minimization and Curve-Fitting for Python, https://lmfit.github.io/lmfit-py/, (accessed 5 December 2022).
- A. L. Myers, AIChE J., 1983, 29, 691–693 CrossRef CAS.
- N. S. Wilkins and A. Rajendran, Adsorption, 2019, 25, 115–133 CrossRef CAS.
- S. J. Bhadra, A. D. Ebner and J. A. Ritter, Langmuir, 2012, 28, 6935–6941 CrossRef CAS PubMed.
- C. Cleeton, A. H. Farmahini and L. Sarkisov, Chem. Eng. J., 2022, 437, 135395 CrossRef CAS.
- M. Khurana and S. Farooq, Chem. Eng. Sci., 2016, 152, 507–515 CrossRef CAS.
- K. T. Leperi, R. Q. Snurr and F. You, Ind. Eng. Chem. Res., 2016, 55, 3338–3350 CrossRef CAS.
- J. C. Abanades, B. Arias, A. Lyngfelt, T. Mattisson, D. E. Wiley, H. Li, M. T. Ho, E. Mangano and S. Brandani, Int. J. Greenhouse Gas Control, 2015, 40, 126–166 CrossRef CAS.
- T. D. Burns, K. N. Pai, S. G. Subraveti, S. P. Collins, M. Krykunov, A. Rajendran and T. K. Woo, Environ. Sci. Technol., 2020, 54, 4536–4544 CrossRef CAS PubMed.
- K. Deb and H. Jain, IEEE Trans. Evol. Comput., 2014, 18, 577–601 Search PubMed.
- K. Deb, A. Pratap, S. Agarwal and T. Meyarivan, IEEE Trans. Evol. Comput., 2002, 6, 182–197 CrossRef.
- L. Estupiñan Perez, P. Sarkar and A. Rajendran, Sep. Purif. Technol., 2019, 224, 553–563 CrossRef.
- A. H. Farmahini, D. Friedrich, S. Brandani and L. Sarkisov, Energy Environ. Sci., 2020, 13, 1018–1037 RSC.
- J. Beck, D. Friedrich, S. Brandani and E. S. Fraga, Comput. Chem. Eng., 2015, 82, 318–329 CrossRef CAS.
- M. T. M. Emmerich and A. H. Deutz, Nat. Comput., 2018, 17, 585–609 CrossRef CAS PubMed.
- Y. Cao, B. J. Smucker and T. J. Robinson, J. Stat. Plan. Inference, 2015, 160, 60–74 CrossRef.
- X. Deng, W. Yang, S. Li, H. Liang, Z. Shi and Z. Qiao, Appl. Sci., 2020, 10, 569 CrossRef CAS.
- G. Avci, I. Erucar and S. Keskin, ACS Appl. Mater. Interfaces, 2020, 12, 41567–41579 CrossRef CAS PubMed.
- Y. Yan, Z. Shi, H. Li, L. Li, X. Yang, S. Li, H. Liang and Z. Qiao, Chem. Eng. J., 2022, 427, 131604 CrossRef CAS.
- S. Li, Y. G. Chung and R. Q. Snurr, Langmuir, 2016, 32, 10368–10376 CrossRef CAS PubMed.
- P. G. Boyd, A. Chidambaram, E. García-Díez, C. P. Ireland, T. D. Daff, R. Bounds, A. Gładysiak, P. Schouwink, S. M. Moosavi, M. M. Maroto-Valer, J. A. Reimer, J. A. R. Navarro, T. K. Woo, S. Garcia, K. C. Stylianou and B. Smit, Nature, 2019, 576, 253–256 CrossRef CAS PubMed.
- Y. G. Chung, D. A. Gómez-Gualdrón, P. Li, K. T. Leperi, P. Deria, H. Zhang, N. A. Vermeulen, J. F. Stoddart, F. You, J. T. Hupp, O. K. Farha and R. Q. Snurr, Sci. Adv., 2016 DOI:10.1126/sciadv.1600909.
- J. A. Dunne, M. Rao, S. Sircar, R. J. Gorte and A. L. Myers, Langmuir, 1996, 12, 5896–5904 CrossRef CAS.
- M. Fischer, J. R. B. Gomes and M. Jorge, Mol. Simul., 2014, 40, 537–556 CrossRef CAS.
- G. Garberoglio, A. I. Skoulidas and J. K. Johnson, J. Phys. Chem. B, 2005, 109, 13094–13103 CrossRef CAS PubMed.
- S. Vandenbrande, T. Verstraelen, J. J. Gutiérrez-Sevillano, M. Waroquier and V. Van Speybroeck, J. Phys. Chem. C, 2017, 121, 25309–25322 CrossRef CAS PubMed.
- J. Zang, S. Nair and D. S. Sholl, J. Phys. Chem. C, 2013, 117, 7519–7525 CrossRef CAS.
- R. Mercado, B. Vlaisavljevich, L. C. Lin, K. Lee, Y. Lee, J. A. Mason, D. J. Xiao, M. I. Gonzalez, M. T. Kapelewski, J. B. Neaton and B. Smit, J. Phys. Chem. C, 2016, 120, 12590–12604 CrossRef CAS.
- A. Raza, A. Sturluson, C. M. Simon and X. Fern, J. Phys. Chem. C, 2020, 124, 19070–19082 CrossRef CAS.
- V. V. Korolev, A. Mitrofanov, E. I. Marchenko, N. N. Eremin, V. Tkachenko and S. N. Kalmykov, Chem. Mater., 2020, 32, 7822–7831 CrossRef CAS.
- S. Kancharlapalli, A. Gopalan, M. Haranczyk and R. Q. Snurr, J. Chem. Theory Comput., 2021, 17, 3052–3064 CrossRef CAS PubMed.
- J. Burner, J. Luo, A. White, A. Mirmiran, O. Kwon, P. G. Boyd, S. Maley, M. Gibaldi, S. Simrod, V. Ogden and T. K. Woo, Chem. Mater., 2023, 16, 54 Search PubMed.
- J. Behler, Chem. Rev., 2021, 121, 10037–10072 CrossRef CAS PubMed.
- J. Behler and M. Parrinello, Phys. Rev. Lett., 2007, 146401 CrossRef PubMed.
- M. Eckhoff and J. Behler, J. Chem. Theory Comput., 2019, 15, 3793–3809 CrossRef CAS PubMed.
- B. Zheng, F. L. Oliveira, R. Neumann, B. Ferreira, M. Steiner, H. Hamann, G. X. Gu and B. Luan, ACS Nano, 2023, 17, 5579–5587 CrossRef CAS PubMed.
- J. Behler, J. Chem. Phys., 2016, 145, 170901 CrossRef PubMed.
- P. Friederich, F. Häse, J. Proppe and A. Aspuru-Guzik, Nat. Mater., 2021, 20, 750–761 CrossRef CAS PubMed.
- C. Devereux, J. S. Smith, K. K. Huddleston, K. Barros, R. Zubatyuk, O. Isayev and A. E. Roitberg, J. Chem. Theory Comput., 2020, 16, 37 Search PubMed.
- N. Bernstein, G. Csányi and V. L. Deringer, npj Comput. Mater., 2019, 5, 1–9 CrossRef.
- J.-B. Lin, T. T. T. Nguyen, R. Vaidhyanathan, J. Burner, J. M. Taylor, H. Durekova, F. Akhtar, R. K. Mah, O. Ghaffari-Nik, S. Marx, N. Fylstra, S. S. Iremonger, K. W. Dawson, S. Partha, P. Hovington, A. Rajendran, T. K. Woo and G. K. H. Shimizua, Science, 2021, 374, 1464–1469 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ee00858d |
| This journal is © The Royal Society of Chemistry 2023 |