The impact of electrode conductivity on electrolyte interfacial structuring and its implications on the Na0/+ electrochemical performance†
Dmitrii A.
Rakov
 *ab,
Ju
Sun
*ab,
Ju
Sun
 a,
Pavel V.
Cherepanov
c,
Khryslyn
Arano
a,
Patrick C.
Howlett
ab,
Alexandr N.
Simonov
a,
Pavel V.
Cherepanov
c,
Khryslyn
Arano
a,
Patrick C.
Howlett
ab,
Alexandr N.
Simonov
 c,
Fangfang
Chen
c,
Fangfang
Chen
 *ab and
Maria
Forsyth
*ab
*ab and
Maria
Forsyth
*ab
aInstitute for Frontier Materials, Deakin University, Geelong, Victoria 3217, Australia. E-mail: dmitrii.rakov@research.deakin.edu.au; maria.forsyth@deakin.edu.au; fangfang.chen@deakin.edu.au
bARC Centre of Excellence for Electromaterials Science (ACES), Deakin University, Burwood, Victoria 3125, Australia
cSchool of Chemistry, Monash University and the ARC Centre of Excellence for Electromaterials Science, Clayton, 3800, Australia
First published on 19th July 2023
Abstract
Molecular and ionic assemblies at electrode/liquid electrolyte interfaces, i.e., the electric double layer (EDL), define battery performance by directing the formation of stable interphases. An unstable interphase can hamper metal-cation diffusion, lead to continuous electrolyte consumption, and also promote non-uniform electrochemical processes like dendrite formation. The co-selection of electrolyte chemistry and initial cycling conditions together are generally considered for the design of desirable interphases. At the same time, the dielectric nature of the electrode material is largely ignored, notwithstanding the high unreliability of the assumption that the nature of the EDL and the mechanism of the interphase formation at metallic and semiconductive electrodes are identical. Here we show that the dielectric nature of the charged electrode greatly affects the interfacial metal–anion–solvent composition; therefore, different interphase chemistry will be formed, suggesting different initial cycling conditions need to be established on a case-by-case basis to form the desired interphase. This phenomenon correlates with the metal ion solvation chemistry and the adsorption of species at the electrified electrode due to the competition of van der Waals and coulombic interactions.
Broader contextThe well-established lithium-ion and the emerging sodium-ion battery technologies are at the forefront of energy storage solutions, but both face durability limitations associated with the irreversible processes at electrode/electrolyte interfaces. To overcome this, an ionically conductive and robust solid electrolyte interphase (SEI) needs to be formed, which is commonly achieved through optimisations of electrolyte chemistry and SEI formation protocols (i.e., initial cycling conditions, with specific current/voltage conditions). At the same time, the role of the electrode material in this process has received significantly less attention, notwithstanding it inherently affects the initial steps of the SEI formation. To address this knowledge gap, our present work explores the effects of the physicochemical properties of the electrode on the mechanism of the SEI formation for the ionic liquid and carbonate-based sodium electrolytes. Using a combination of experimental and theoretical tools, we demonstrate that the structure of the electrolyte–electrode interface and the properties of the SEI are substantially affected by the polarizability of the electrode, and explain these phenomena in the context of the ability of charged electrodes to adsorb electrolyte species. Our work shows that the SEI formation protocols should take all key factors into consideration including the electrolyte composition, cycling conditions, and electrode nature to produce high-performance, robust battery devices. |
Lithium-ion batteries (LIBs) are the leading battery technology in the energy storage landscape; however, the demand to further reduce their cost and improve safety, and the growing concern related to lithium resources motivate the accelerated development of sodium-ion batteries (SIBs). An electric double layer (EDL) is an essential part of these batteries as with all electrochemical devices. This structure originates at the solid–liquid interface and can extend up to a few nanometres from the electrode surface to the bulk electrolyte phase.1,2 Such interfacial behavior originates from different forces, e.g., local coulombic order and van der Waals forces. The EDL structure affects capacitive charge storage due to molecular/ionic packing near the electrode,3 as well as the mechanism of heterogeneous charge transfer, the chemistry of the solid electrolyte interphase (SEI) and its morphology in the batteries.4–7 Both LIBs and SIBs suffer from deficient reversibility of redox processes which is associated with the formation of mechanically unstable and reactive interphases as well as hampered solid-state ion diffusion through these poor interphases. This leads to continuous electrolyte consumption and/or non-uniform metal deposition (i.e., dendrite formation in the case of metal anodes) causing battery failure and safety concerns. Understanding these processes is at the forefront of the development of stable and efficient LIBs/SIBs,8–12 and requires a comprehensive analysis of the EDL structure and its potential-driven changes in different electrolytes.
Battery electrolyte engineering, e.g., the chemical structure of the solvent and salt, their ratio, presence of additives, etc.,13–16 and the application of the SEI formation protocols with specific current/voltage conditions are widely used to optimize the interphase chemistry and morphology to enable reversible charge transfer.13,17–22 The structural changes and transport properties within the EDL were also explored with respect to these parameters. For example, the role of applied current/voltage in defining the interface composition and dynamics of ions within the EDL were examined in the case of different ionic liquids and carbonate-based electrolytes.13,17,22,23
In contrast, the role of the electrode material in the structure and ion transport within the electrified interfaces is often neglected and thus the distinctions in the EDL at different electrodes, e.g., metal or semiconductor, in battery electrolytes are not well understood.
Here, we demonstrate that potential-driven structural changes at the interface with sodium electrolytes based on ionic liquids (ILs) and carbonates as solvents are greatly affected by the dielectric nature of the electrode material. This structural difference is mainly due to the different van der Waals forces between the electrode and the electrolyte, which is significant enough in the case of metallic electrodes promoting anion-solvated sodium clusters near the negatively charged metallic surface depending on the applied potential. This is contrasted by the preference of organic species, i.e., solvent molecules, on the semiconductive electrode. These dissimilarities, therefore, result in different interphase chemistries (anion-derived or solvent-derived), and the requirement for the use of different formation protocols, as discussed below.
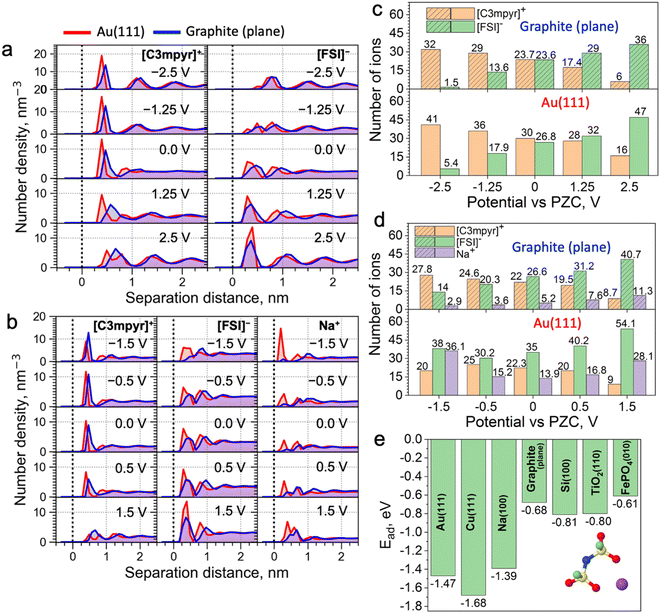
Classical molecular dynamics (MD) simulations were conducted to study the difference in EDL structures of IL electrolytes in both metallic Au(111)||Au(111) and semi-metallic graphite (plane)||graphite (plane) electrode models (Fig. 1a–d). Here, a neat IL, i.e., N-methyl-N-propylpyrrolidinium ([C3mpyr]+) bis(fluorosulfonyl)imide ([FSI]−), and an equimolar mixture of the IL with sodium salt, i.e., 50 mol% Na[FSI] salt with a 50 mol% [C3mpyr][FSI] IL were investigated. In what follows, the latter composition is also referred as the superconcentrated IL (for details, see the Methods section). As shown in Fig. 1a and Fig. S1 (ESI†), the charging of the neat IL leads to very similar interfacial changes for both electrodes. Specifically, the calculated number density in Fig. 1a and the number of ions within the innermost layer (0.6 nm from the surface in this case) in Fig. 1c show that both Au and graphite electrode models demonstrate an increase in the interfacial population of the IL cation [C3mpyr]+ (24 to 32 for graphite and 30 to 41 for gold), and a decrease in the number of anions [FSI]− (24 to 1.5 for graphite and 27 to 5.4 for gold) when the potential is changed from 0.0 to −2.5 V vs. potential of zero charge (PZC). An exact opposite trend was seen on the positive electrode side. The angular distribution function (Fig. S2, ESI†) analyses the orientation of ions near the electrodes. The orientation of the [C3mpyr]+ ring that is parallel to the negatively charged electrode surface (indicated by two peaks near 0 and 180 degrees) shows a higher probability near the Au(111) surface compared to the semi-metallic graphite (plane). Such observations are expected in the case of non-symmetrical [C3mpyr]+ which appears closer to the Au(111) surface compared to the graphite plane (Fig. 1a), i.e., at a distance of ∼3.9 Å vs. 4.7 Å for the nitrogen-atom of [C3mpyr]+, while the orientation of more symmetrical [FSI]− is less affected by the nature of the electrode (Fig. S2, ESI†).
In contrast to the neat IL, the interface of superconcentrated IL is much more susceptible to the dielectric nature of the electrode (Fig. 1b and d and Fig. S3, ESI†). Charging of the metallic Au(111) electrode increases the concentration of the molten-salt-like NaxFSIy clusters within the innermost layer (the x![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) y ratio of these clusters varies with the applied potential) (Fig. 1d), and promotes the migration of [C3mpyr]+ into the bulk electrolyte phase. Importantly, charging of the semi-metallic graphite (plane) surface does not lead to similar interfacial changes with the superconcentrated IL as was seen for the Au(111) case. The composition of this graphite (plane)/superconcentrated IL electrolyte interface reorganizes like in the NaFSI salt-free IL, namely, the increase in the negative surface charge only attracts organic cations [C3mpyr]+, while the NaxFSIy clusters move away from the electrode surface (Fig. 1b and d). Besides, the positive potential on the graphite (plane) electrode accumulates at least twice less Na+ in the form of NaxFSIy at the interface compared to that on Au(111) (Fig. 1b and d).
y ratio of these clusters varies with the applied potential) (Fig. 1d), and promotes the migration of [C3mpyr]+ into the bulk electrolyte phase. Importantly, charging of the semi-metallic graphite (plane) surface does not lead to similar interfacial changes with the superconcentrated IL as was seen for the Au(111) case. The composition of this graphite (plane)/superconcentrated IL electrolyte interface reorganizes like in the NaFSI salt-free IL, namely, the increase in the negative surface charge only attracts organic cations [C3mpyr]+, while the NaxFSIy clusters move away from the electrode surface (Fig. 1b and d). Besides, the positive potential on the graphite (plane) electrode accumulates at least twice less Na+ in the form of NaxFSIy at the interface compared to that on Au(111) (Fig. 1b and d).
Angular distribution analysis of the [C3mpyr]+ and [FSI]− orientations within the innermost layer of the superconcentrated IL shows similar changes to the applied charge as those seen for the neat IL (Fig. S4, ESI†). Also, after charging the electrode, the Na-FSI coordination in the innermost layer of the superconcentrated IL undergoes structural changes, viz. alternations in the ionic bond distance and the number of shared oxygens (Fig. S5, ESI†), which was also discussed in our earlier publications.13,21,22
The classical MD can employ either surface charge (μC cm−2) or electrostatic potential (V vs. PZC) to model the electrified interfaces, which is done by a uniform charge distribution to each of the electrode atoms, i.e. the constant charge method (CCM). Herein, these two methods of charging produced similar outcomes (Fig. S6, ESI†). Also, certain modelling codes, in particular the constant potential method (CPM), enable surface charge fluctuation of the electrode, which might affect the energy barrier for certain ions to reach the surface.24 To estimate such an effect on the accuracy of our MD results with respect to Au(111) and graphite (plane) systems, we conducted CPM MD simulations (Note S1, ESI†). It was found that the implementation of the CPM method does not alter the conclusions derived from the CCM MD method (Fig. 1).
Trends discussed above and demonstrated in Fig. 1 can be related to the difference in the adsorption energies of the electrolyte species on different electrodes. For example, as shown in Fig. 1e and Fig. S12, ESI,† the adsorption energy of the Na-FSI complex on different electrodes with explicit metallic nature calculated using the density functional theory (DFT) method is much stronger and almost twice that with semi-metallic and semiconductive surfaces. This is caused by the higher electrical conductivity/electronic polarizability of metals forming strong multipole interactions, viz. dispersion forces or van der Waals interactions, with adsorbates (in this case the IL cations and/or salt complexes).25,26 This is also evident from the reported Lennard-Jones (LJ) potential parameters for modelling surfaces of different dielectric nature (Table S1, ESI†). Indeed, the metal elements, such as Au and Cu, have much higher values of ε (good depth of the LJ potential) than elements like C and Si. This concept was further tested and confirmed in Fig. S13 (ESI†), where weak LJ parameters of the graphite were used for the calculations with the Au(111) electrode and vice versa. This allows for the formation of the NaxFSIy aggregate-rich interface for the graphite electrode and an IL cation-rich interface for Au when the same negative surface charge is applied. This also indicates the importance of using accurate LJ parameters to describe surface adsorption phenomena in classical MD.
Those results explain why the negative Au electrode can accommodate the NaxFSIy complexes easier than the semi-metallic graphite electrode, and the latter has a higher affinity toward the positively charged IL cation, e.g., [C3mpyr]+ or [P1222]+, compared to neutral or negatively charged NaxFSIy clusters. This also explains why an additional energy barrier has been experienced for metal deposition from the IL electrolytes with semiconductive electrodes compared to that with metals.27,28 Such strong dispersion forces of metals allow negatively-charged NaxFSIy complexes to remain near the anode surface, and subsequently reduce the number of [C3mpyr]+ with the increase of Na+ in the clusters.
These differences in potential-driven EDL changes between metallic and semiconductive electrodes were also seen for the phosphonium-based superconcentrated IL electrolyte (Fig. S10 and S11, ESI†) and other IL electrolytes with different metal salt concentrations and chemistries.22,29–32 Thus, such behaviour is likely to be general for the IL electrolytes, as metal cations move in the anion-coordinated clusters having a negative charge up to high salt concentrations.33 However, we acknowledge that it would be useful to validate the generic nature of the phenomenon for a broader range of IL electrolytes. It is also noted though that the polarity of the IL cation can affect this interfacial phenomenon to some extent.34
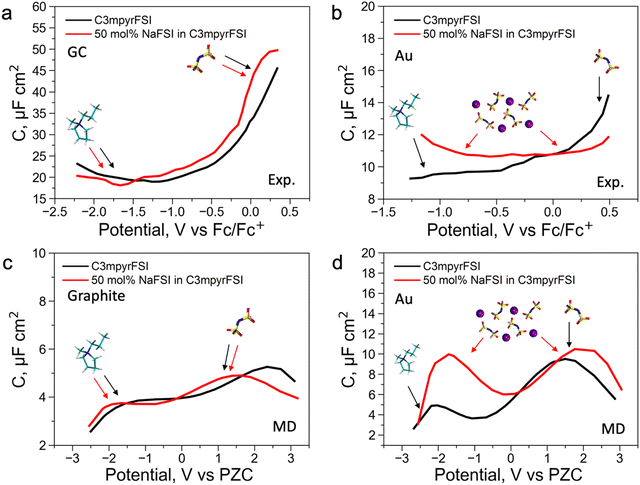
To further understand the EDL structure of neat and superconcentrated IL with different electrode materials, we performed differential capacitance measurements by recording electrochemical impedance spectra (EIS) at varying applied potentials within the non-faradaic region. Cyclic voltammetry data for the examined electrolytes, with and without the addition of 50 mol% NaFSI, are shown in Fig. S14 (ESI†). The non-faradaic region is affected by both the dielectric nature of the working electrode and the presence of the NaFSI salt, and this was considered for differential capacitance (C) measurements in Fig. 2. As shown in Fig. 2a and b, the C–E curve for neat C3mpyrFSI exhibits a descending shape from the positive to the negative potential region, which was also reported for other ILs.35,36 This phenomenon is likely caused by the difference in the ion size and shape. Specifically, the relatively symmetrical [FSI]− pack is tighter per volume at the interface compared to [C3mpyr]+ which results in an increase of charge accumulating at the interface and hence higher capacitance.3 When comparing neat [C3mpyr][FSI] and 50 mol% NaFSI in [C3mpyr][FSI] with different surfaces, the shape of the C–E curve with a metallic gold electrode is significantly affected by the presence of the NaFSI salt (Fig. 2b). In contrast, with a semiconductive glassy carbon (GC) electrode, both neat and superconcentrated IL demonstrate differential capacitance curves of similar shapes (Fig. 2a). The C–E relationships for the GC electrode were recorded over a wider potential region compared to the gold system, which is due to the higher buildup of [C3mpyr]+ at the interface and lesser faradaic contribution from the NaxFSIy decomposition around −1.3 V vs. ferrocene0/+ (Fc0/+).28 Both neat [C3mpyr][FSI] and 50 mol% NaFSI in [C3mpyr][FSI] electrolytes on GC show higher capacitances than those on the metallic gold electrode, consistent with previous reports.35–37
To obtain a molecular-level understanding of the experimental differential capacitance trends (Fig. 2c and d), the interface for the same pyrrolidinium-based IL electrolytes with idealistic graphite (plane) and Au(111) electrodes was analyzed by means of classical MD (for details, see Methods). As shown in Fig. 2b and c, the MD model represents only an EDL part (CEDL) of experimental differential capacitance which is higher for a gold electrode than that for graphite (plane) regardless of the electrolyte nature. This is due to the tighter ionic packing resulting from greater interactions with metallic surfaces.38 The higher experimental capacitance of the non-metallic GC electrode compared to the gold system can be explained by splitting the total experimental capacitance (Cexp) into two main parts, i.e., the EDL part (CEDL) including Helmholtz/diffuse layer capacitance and a quantum capacitance (CQ) component related to the space charge region within the electrode material (eqn (1)).
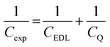 | (1) |
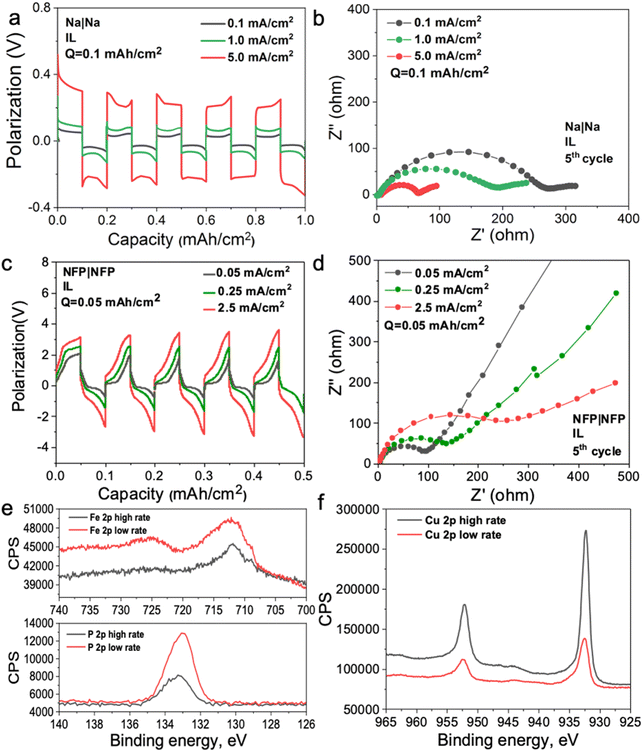
To investigate the mechanism of the interphase formation with the superconcentrated IL electrolytes in the light of these new findings, we conducted several symmetrical cell cycling experiments with 50 mol% NaFSI in [C3mpyr][FSI] and electrodes of different dielectric nature. Each cell was cycled under various current densities (leading to different surface charges) with a fixed depth of charge. This study included symmetrical cells with sodium iron phosphate (NFP) electrodes (non-metallic with low electric conductivity) commonly used as cathodes in sodium-ion batteries, as well as Na and Cu as two distinct metallic systems. Fig. 3a shows Na metal symmetrical cell cycling with a sodium salt superconcentrated IL at different current densities. In this case, we used higher current density to control the initial cell voltage to mimic the higher negative potential values used in the MD simulations. Fig. 3b shows that the cell cycled at the highest rate used herein exhibits the lowest interphase resistance which correlates with the presence of a favorable SEI, and hence, better overall cycling performance. In contrast, the symmetrical cell cycling with the semiconductive NFP, under a similar protocol, leads to the most resistive interphase when the cell is preconditioned at the highest current density examined (Fig. 3c and d). We note here that the cathodes in these symmetric NFP cells were not fully sodiated and hence the electrochemical processes are expected to include Na insertion/de-insertion during cycling. A symmetric Cu/Cu electrochemical cell was also investigated using the same [Na][FSI] superconcentrated IL electrolyte (Fig. S15, ESI†). The electrochemistry, in this case, is likely to be quite complex but still influenced by the EDL layer and its forming interphase which we will also denote as the SEI. The Cu anode, which is often used to study electrochemical processes in sodium electrolytes,45,46 was used herein to investigate the chemistry of the formed interphase. The use of the copper electrode facilitates discrimination between the electrode substrate and the formed SEI.
In our earlier studies,13,21,22,47 we showed that an improved electrochemical behavior of the Na and Li anodes with superconcentrated ILs preconditioned at a high current density originates from the interface dominated by NaxFSIy or LixFSIy clusters and the expulsion of the IL cation. This interface enables a uniform and dense deposition morphology and a desirable anion-derived inorganic-rich SEI. The self-heating of the electrode surface at a high rate might also contribute to a dendrite-free morphology.17 In this work, we conducted an X-ray photoelectron spectroscopy (XPS) analysis of other electrode materials, viz. NFP and Cu, which were not previously considered in the context of the interface/interphase relationships.
The XPS data obtained for NFP suggests that low and high current cycling conditions have a different impact on the SEI composition/morphology as compared to those observed for Na and Li. According to the EDL discussion presented above, the SEI layer at more negative potentials on NFP is expected to be dominated by the IL cation and hence a rapid formation cycle could be detrimental to the creation of a low-resistive inorganic-rich SEI layer. To investigate this phenomenon, we conducted XPS analysis on the cycled electrodes after different periods of Ar+ etching to analyze the chemistry of the deposition products at different depths into the SEI. The Cu surfaces were also analyzed and compared to determine the proportion of organic/inorganic components in the deposition products after cycling at different rates.
Fig. S16 (ESI†) shows XPS data for neat [C3mpyr][FSI], NaFSI, and 50 mol% NaFSI in [C3mpyr][FSI]. All recorded spectra confirm the elemental content and their oxidation states in examined compounds,48 and that partial decomposition of [FSI]− anions to NaF takes place upon drying of the NaFSI salt.49 Keeping the NFP and Cu electrodes in contact with 50 mol% NaFSI in [C3mpyr][FSI] with no potential applied for 24 h results in the formation of polysulfides and some other oxidized species, which are collectively denoted as the initial/native SEI (Fig. S17, ESI†).22 Electrochemical cycling with 50 mol% NaFSI in [C3mpyr][FSI] at a high rate produces a thicker SEI on the NFP surface as compared to the experiments at a low rate, as concluded from the comparisons of the intensities of the Fe 2p and P 2p spectra recorded for the cycled electrodes (Fig. 3e). The metallic Cu system demonstrates an opposite trend by forming a thinner SEI at the high rather than at the low rate (Fig. 3f). The thick SEI on the NFP surface at the high rate is likely associated with the formation of a porous organic-based film,50,51 which increases the Na+ diffusion pathway, and increases the interfacial resistance with sluggish Na+ diffusion kinetics.
To obtain further insights into the composition of the SEI, we performed the XPS analysis of the cycled electrodes that were etched by Ar+. The F 1s spectra exhibit peaks characteristic of NaF (684.0 eV) and S–F at (687.4 eV),52 both being the decomposition products from the FSI− anion but present at different ratios at the surface and within the SEI of NFP electrodes (Fig. S18, ESI†). Analysis of the Na 1s and O 1s spectra also suggests the presence of Na2O throughout the SEI (Fig. S18, ESI†).52 The XPS depth profiles for NFP cycled at the low rate indicate that relative concentrations of C and F decline, while the contributions of O and Na increase upon increasing the Ar+ etching time (Fig. S19 and S20a, ESI†). These observations suggest that the inorganic SEI components Na2O and NaF dominate the inner layer, while the surface layers majorly contain organic species formed through the electrochemically induced decomposition of the organic [C3mpyr]+ cations. Interestingly, a different trend was found for the NFP electrodes cycled at a high rate, with progressively increasing contribution of C and decreasing relative concentrations of Na, F and O with the duration of etching (Fig. S19 and S20b, ESI†). Hence, we conclude that inorganic species are major components of the outer layer of the SEI, while organic compounds are concentrated deeper into the SEI. Regarding the chemistry of the SEI on Cu anodes (Fig. S19–S21, ESI†), the low-rate cycling generates higher C % compared to that when the high current density is used. Both these systems show a decreasing trend for the C element, indicative of an organic–inorganic SEI layer on the Cu surface. Additionally, higher amounts of O, F, and S elements at high cycling rate suggest that there are more inorganic species (NaF, Na2O, Na2S, etc.) in the inner layer of the SEI, while there are barely inorganic species decomposed from the NaxFSIy clusters for the Cu electrode cycled at a low rate (Fig. S19b and S20e, f, ESI†).
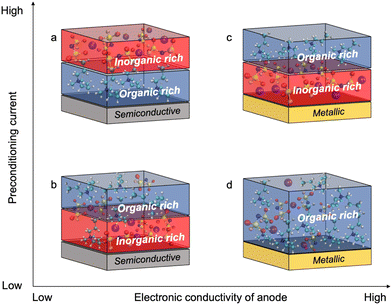
Fig. 4 shows the proposed chemistry of the SEI formed at different current densities with superconcentrated IL electrolytes and electrodes of different dielectric nature. The non-metallic NFP electrode forms an organic-rich SEI near its surface at high cycling rate (Fig. 4a), which is due to the predominance of the IL cation at the interface (Fig. 1b and d). As a result, the [C3mpyr]+ actively participates in the reduction processes and/or blocks Na+ intercalation. Both phenomena result in a more resistive interphase and therefore deteriorated performance (Fig. 3c and d). The observed inorganic-rich layer on the top of the organic-rich [C3mpyr]+ decomposition layer under high current density cycling might come from the subsequent decomposition of the NaxFSIy clusters. This is observed in the MD simulations in the case of the semiconductive electrode where anion-solvated Na+ are present in the outer layer adjacent to [C3mpyr]+. Meanwhile, the inorganic-rich film near the surface of the NFP forms during low current density cycling (Fig. 4b), which in turn leads to decreased interphase resistance (Fig. 3c and d).
The Cu anode with the superconcentrated IL electrolyte forms an inorganic-rich SEI near the surface when high current density cycling is applied (Fig. 4c), whereas the low-rate cycling leads to the organic-rich SEI (Fig. 4d). This behaviour is similar to that observed earlier for the Na and Li electrodes.13,47 These observations correlate with the difference in the structure of the electrode/electrolyte interface for metallic and semiconductive surfaces with superconcentrated ILs discussed above.
To confirm that the interfacial resistance for the examined cells is affected by the EDL structuring near the electrode rather than its state of charge, we further expanded our understanding to the mono-cationic carbonate electrolyte, i.e., 1.0 M NaPF6 electrolyte in ethylene carbonate (EC) and dimethyl carbonate (DMC) (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
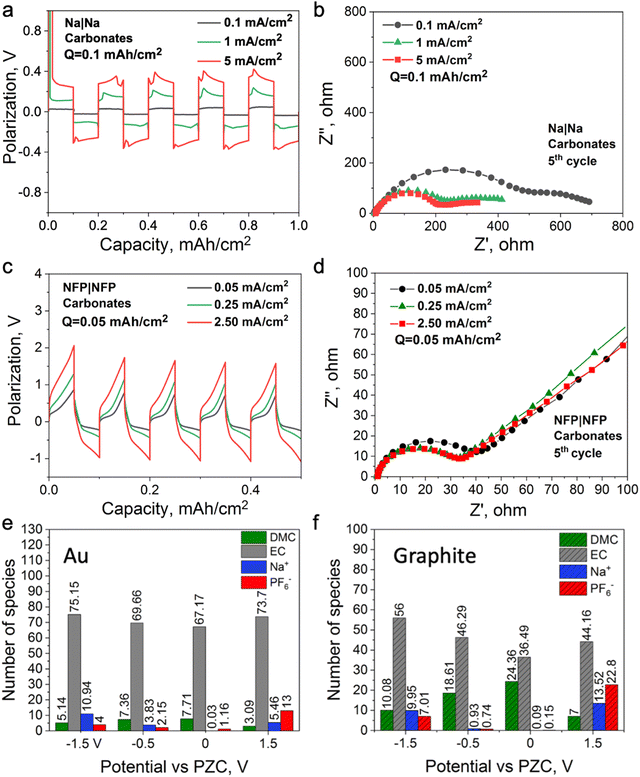
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 vol.). In this case, Na+ is surrounded by a neutral solvent53 which does not require a strong dispersion force for its retention at the electrified interface; hence, the formation protocols might be different from the ionic liquid electrolytes. Fig. 5a and b show Na symmetrical cell cycling with this electrolyte, where the cell cycled at a higher current density demonstrates lower interfacial resistance. A similar observation was reported for a Li symmetrical cell cycled with 1.2 M LiPF6 in the same solvent system, where a high cell voltage was used instead of a high current density to control the reduction and oxidation rates during cycling.19Fig. 5c and d show that the interfacial resistance of the NFP symmetrical cells with the carbonate-based electrolyte decreases after cycling at a high current density, which is opposite to the case observed with the IL electrolyte (Fig. 3d and c). This also suggests that changes in the interfacial resistance of the NFP electrodes correlate with the EDL structure, and do not solely depend on the state of charge of the NFP, i.e., how much Na0 is in it. It was also shown that the use of high-rate formation cycling for the semiconductive full cell (graphite||NMC) and metallic symmetrical cell (Li||Li) with the same electrolyte leads to lower interfacial resistance and stable cycling behavior.18–20
1 vol.). In this case, Na+ is surrounded by a neutral solvent53 which does not require a strong dispersion force for its retention at the electrified interface; hence, the formation protocols might be different from the ionic liquid electrolytes. Fig. 5a and b show Na symmetrical cell cycling with this electrolyte, where the cell cycled at a higher current density demonstrates lower interfacial resistance. A similar observation was reported for a Li symmetrical cell cycled with 1.2 M LiPF6 in the same solvent system, where a high cell voltage was used instead of a high current density to control the reduction and oxidation rates during cycling.19Fig. 5c and d show that the interfacial resistance of the NFP symmetrical cells with the carbonate-based electrolyte decreases after cycling at a high current density, which is opposite to the case observed with the IL electrolyte (Fig. 3d and c). This also suggests that changes in the interfacial resistance of the NFP electrodes correlate with the EDL structure, and do not solely depend on the state of charge of the NFP, i.e., how much Na0 is in it. It was also shown that the use of high-rate formation cycling for the semiconductive full cell (graphite||NMC) and metallic symmetrical cell (Li||Li) with the same electrolyte leads to lower interfacial resistance and stable cycling behavior.18–20
To interpret this phenomenon at a molecular level, the structure of electrified interfaces of Au(111) and graphite (plane) electrodes with 1 M NaPF6 in EC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMC (1
DMC (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 vol.) was investigated using MD simulations (extended discussions are provided in Note S2, ESI†). Two different electrode configurations were modelled, namely, Au(111)||Au(111) and graphite(basal plane)||graphite(basal plane) (Fig. S23–S25, ESI†). In contrast to ILs, at the high negative/positive electrode charging, we can observe the increased Na+ and PF6− in the innermost layer near both Au(111) and graphite(basal plane) electrodes (Fig. 5e and f), and the most polar and strongly Na+ coordinated solvent molecule (EC in this case) saturate the majority of the electrified interface. The Au(111) plane has a stronger affinity towards this highly polar EC solvent than the graphite (plane) electrode. Such a distinction compared with the IL system arises from the absence of a competing cationic species near the negative electrode, viz., the IL cation. This explains why both metallic and semiconductive electrodes form favourable SEI chemistry/morphology with the carbonate electrolyte after high current/voltage formation cycling.18–20 However, apart from the optimum SEI chemistry/composition such aspects as optimum cell capacity and its retention should be also considered to design optimal formation protocols for batteries with different electrode and electrolyte materials.54 Moreover, the current densities and areal capacities used in this work should not be treated as the ideal cycling conditions for a given device. The electrode formation protocols are complex and will surely depend on the cell configuration, electrolyte composition, temperature, etc. Nevertheless, our data demonstrates that the formation conditions are at the very least dependent on the nature of the electrode and additional case studies are still required to optimize the performance of a given device.
1 vol.) was investigated using MD simulations (extended discussions are provided in Note S2, ESI†). Two different electrode configurations were modelled, namely, Au(111)||Au(111) and graphite(basal plane)||graphite(basal plane) (Fig. S23–S25, ESI†). In contrast to ILs, at the high negative/positive electrode charging, we can observe the increased Na+ and PF6− in the innermost layer near both Au(111) and graphite(basal plane) electrodes (Fig. 5e and f), and the most polar and strongly Na+ coordinated solvent molecule (EC in this case) saturate the majority of the electrified interface. The Au(111) plane has a stronger affinity towards this highly polar EC solvent than the graphite (plane) electrode. Such a distinction compared with the IL system arises from the absence of a competing cationic species near the negative electrode, viz., the IL cation. This explains why both metallic and semiconductive electrodes form favourable SEI chemistry/morphology with the carbonate electrolyte after high current/voltage formation cycling.18–20 However, apart from the optimum SEI chemistry/composition such aspects as optimum cell capacity and its retention should be also considered to design optimal formation protocols for batteries with different electrode and electrolyte materials.54 Moreover, the current densities and areal capacities used in this work should not be treated as the ideal cycling conditions for a given device. The electrode formation protocols are complex and will surely depend on the cell configuration, electrolyte composition, temperature, etc. Nevertheless, our data demonstrates that the formation conditions are at the very least dependent on the nature of the electrode and additional case studies are still required to optimize the performance of a given device.
In summary, the results presented herein suggest that the mechanism of interphase formation on battery electrodes, especially with IL electrolytes, is significantly affected by the dielectric nature of the electrode material, which can cause different electrode/electrolyte interface structuring in response to different applied electrode charges. For achieving stable and low-resistance charge transfer, the interphase that is derived predominantly from the anion decomposition products appears favourable as these are likely to be insoluble, electronically insulating and ionically conductive.
The composition of the electrode/electrolyte interface depends on interfacial van der Waals and coulombic interactions, e.g., the charged semiconductive electrode is less likely to retain highly polar molecules or ions of the same charge near its surface owing to their low electronic polarizability and weak dispersion forces. This is especially important in the case of IL electrolytes because organic IL cations and anion-coordinated Li+/Na+ complexes compete near a negatively charged surface. The formation of an anion-derived interphase with IL electrolytes on a semiconductive electrode can occur at a low current density. In contrast, a higher current density leads to the formation of a thick organic-rich interphase with high resistance. This is due to the increase the number of IL cations near the surface of the semiconductive electrode with an increase in the applied negative charging.
High negatively charged metallic electrodes can retain anions near their surface. This is due to the high electronic polarizability and strong dispersion forces in the case of metallic surfaces which require a high current density to enable the anion-derived interphase to form a molten-salt-like rich interface.
In the case of carbonates electrolytes which only have alkali metal cations, the application of high current, i.e., the rapid formation cycling, for both metallic and semiconductive electrodes leads to a similar trend for the system investigated herein. Namely, this method enhances the formation of an anion-derived interphase from increased Nax(PF6)y clusters attracted to the negative electrode. At the same time, the electrode nature affects the interfacial concentration of a specific solvent depending on its polarity, and this could be used for controlled SEI formation from the selected species to, especially, if only certain organic molecules are fluorinated. In this regard, the rational design of batteries requires not only the consideration of new electrolyte chemistries, the optimization of their transport properties and interphase formation protocols, but also the role of the dielectric nature of the electrode material. These factors should all be considered when designing electrode formation protocols for reversible charge transfer with stable/efficient interphases. These findings open new prospects for future implications in the field of electrochemical systems for controlled electrocatalysis, rare-metal recovery, and the design of EDL capacitors, batteries, etc.
Methods
Molecular dynamics simulations
All-atom classic molecular dynamic simulations were conducted with the GROMACS software package (version 2022.2).55 The Canongia Lopes-Padua (CL&P) force field parameters were used in this work for [C3mpyr][FSI] and [P1222][FSI] ionic liquids, which were previously studied for bulk-phase investigation.56,57 The Lennard-Jones potential parameters ((ε = 22.1333 kJ mol−1 and σ = 0.2629 nm) and (ε = 0.2305 kJ mol−1 and σ = 0.3412 nm)) for Au and graphite electrodes were adopted to describe van der Waals interaction at the interface.58,59 The bulk phase densities of [P1222][FSI] and 50 mol% NaFSI in [P1222][FSI] were calculated first and the computational details are described in the literature.13 The simulation density errors for neat [P1222][FSI] and 50 mol% NaFSI in [P1222][FSI] with 0.7 scaling factor were −4.43% and −1.13% at 333 K compared to experimentally obtained values of 1.2873 kg m−3 and 1.5232 kg m−3, respectively. The density errors for neat [C3mpyr][FSI] and 50 mol% NaFSI in [C3mpyr][FSI] with the same 0.7 charge scale factor are mentioned in the literature.13 The interface models were constructed with the IL electrolytes confined between two Au(111) face-centered cubic or two graphite (plane) electrodes (Fig. S27, ESI†). The simulation box consisting of two electrodes and an electrolyte has the same the x and y dimension as that the of gold or graphite electrode, and the z-length was calculated based on the bulk phase density of electrolytes. An extra vacuum space twice the length of electrode separation was also introduced outside one side of the electrode to eliminate the artefact images resulting from the simulation in the slab geometry when applying periodical boundary conditions along the z-direction.60 An annealing process was simulated at first upon changing the temperature from 393 K to 700 K and then to 393 K again before a long equilibration calculation at 393 K for a total of 15 ns using an NVT ensemble and the Nose–Hoover thermostat. The annealing procedure allows the system to gain sufficient dynamics to obtain a reasonable initial structure for equilibration calculation. Both energies and pressures were checked to determine whether the system reaches equilibrium. An additional 40 ns production run was performed at 393 K for structural and dynamics analyses. The trajectory file was written every 2 ps. The constant charge method (CCM) with a uniform distribution of point charges across the top layer of the electrode surface was used thoroughly unless it is specified somewhere else. The electrode potential was determined according to the Poisson equation,61 by calculating the electric double layer (EDL) potential drop between two electrodes UEDL = ψelectrode − ψbulk. The UEDL value of the uncharged electrode was defined as the potential of zero charge (PZC). The electrode potential vs. PZC is defined as UEDL = ψelectrode − ψbulk − PZC. The surface charges used to achieve the electrode potential are given in Fig. S28 (ESI†). The MD differential capacitance (Cdiff) was calculated by taking the derivative of the first order from the plot in Fig. S28 (ESI†), namely,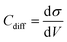 . The σ is the surface charge of the electrode in μC cm−2 and V is the potential vs. PZC. The DC curve was obtained through the global fitting of the Cdiff-V data points to a polynomic function of the fifth order, as described in the literature.62 The customized Python code was used for trajectory analysis unless the required tool was available in the GROMACS package.55,63
. The σ is the surface charge of the electrode in μC cm−2 and V is the potential vs. PZC. The DC curve was obtained through the global fitting of the Cdiff-V data points to a polynomic function of the fifth order, as described in the literature.62 The customized Python code was used for trajectory analysis unless the required tool was available in the GROMACS package.55,63
Density functional theory calculations
DFT calculations have been conducted to calculate the adsorption energy using the Gaussian Plane Wave scheme based on CP2K version 6.1.064 with the Perdew–Burke–Ernzerhof (PBE) functional,65 TZVP MOLOPT basis set for all atoms,66 and Goedecker–Teter–Hutter pseudopotentials.67 The orbital transform method was used with the full kinetic predictioner and conjugated gradient as a minimizer. The DFT-D3 Grimme dispersion correction with the PBE exchange correlation function was used for all calculations.68 The SCF convergence factor was set up at 10−6 for geometry optimization and at 10−8 for the following scf energy calculations. The NaFSI adsorption energy on the slab of different electrode materials was calculated in a 2D periodic setup with z dimension 2.5 times longer than that of the largest x or y. Poisson solver Analytic and surface dipole correction along the z axis were applied to avoid improper treatment of periodicity.69 The coordinate positions and cell dimensions of all four layers of slabs were initially optimized, and then, further fixed for geometry optimization with an absorbed NaFSI complex. All calculations have been done at the Γ point due to the large size of supercells resulting in a small Brillouin zone.Materials
Na metal was purchased from Sigma-Aldrich. Sodium iron phosphate (NaFePO4 or NFP) was synthesized and characterized in CIC energiGUNE as previously reported.70 The electrode was prepared by mixing NFP, carbon black and the polyvinylidene fluoride (PVDF) binder at a weight ratio of 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 into the N-methyl-2-pyrrolidone (NMP) solvent and cast onto an Al foil. Cu was purchased from Gelon LIB Co., Ltd. All the electrodes were punched into 8 mm diameter disks. The NFP mass loading was 2.0 mg cm−2. Sodium bis(fluorosulfonyl)imide (NaFSI, 99.7%) and N-propyl-N-methylpyrrolidinium bis(fluorosulfonyl)imide ([C3mpyr][FSI], 99.9%) were obtained from Solvionic Corporation. They were dried under vacuum using a Schlenk line at 50 °C before any electrolyte preparations. The superconcentrated ILs were prepared by adding 50 mol% NaFSI into [C3mpyr][FSI]. The water content of IL electrolytes used for battery cycling was tested by means of an 831 Karl Fisher coulometer with Hydranal Coulomat AG as the titrant and does not exceed 50 ppm. The procedure was conducted under an argon-filled glovebox with water and oxygen level <0.1 ppm. The organic ester electrolyte (1.0 M NaPF6 in EC/DEC 1
1 into the N-methyl-2-pyrrolidone (NMP) solvent and cast onto an Al foil. Cu was purchased from Gelon LIB Co., Ltd. All the electrodes were punched into 8 mm diameter disks. The NFP mass loading was 2.0 mg cm−2. Sodium bis(fluorosulfonyl)imide (NaFSI, 99.7%) and N-propyl-N-methylpyrrolidinium bis(fluorosulfonyl)imide ([C3mpyr][FSI], 99.9%) were obtained from Solvionic Corporation. They were dried under vacuum using a Schlenk line at 50 °C before any electrolyte preparations. The superconcentrated ILs were prepared by adding 50 mol% NaFSI into [C3mpyr][FSI]. The water content of IL electrolytes used for battery cycling was tested by means of an 831 Karl Fisher coulometer with Hydranal Coulomat AG as the titrant and does not exceed 50 ppm. The procedure was conducted under an argon-filled glovebox with water and oxygen level <0.1 ppm. The organic ester electrolyte (1.0 M NaPF6 in EC/DEC 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 by volume) was purchased from Kishida Chemical Co., Ltd.
1 by volume) was purchased from Kishida Chemical Co., Ltd.
Three-electrode setup measurements
Experimental differential capacitance curves were obtained by means of electrochemical impedance spectroscopy (EIS) in a three-electrode setup, namely, the working electrode was either a gold or glassy carbon electrode (BAS inc., Japan) with a surface area of 0.02 cm−2, platinum wire as a counter electrode, and the Ag0/Ag+ reference electrode containing 10 mM silver triflate in [C3mpyr][FSI] (eDAQ Pty Ltd, Australia). The reference electrodes were calibrated with the ferrocene redox couple (Sigma-Aldrich), and the potential reference scale at 0.0 V vs. Ag0/Ag+ was −0.361 V vs. Fc0/Fc+ for [C3mpyr][FSI]. Prior to measurements, the working electrode was cleaned according to the method described previously.29 The counter Pt wire was sonicated for 15 minutes with ethanol/deionized water, and dried under the same conditions as a working electrode with Ar flow initially and later in a 70 °C oven, and then Pt wire was annealed with a butane torch. The setup was equilibrated for 30 minutes at 50 °C before performing any electrochemical measurements. Cycling voltammetry tests were performed with a scan rate of 25 mV s−1 to define a non-faradaic region for all the following DC measurements.Capacitance is extracted within a potential region of +0.70–−1.85 V vs. Ag0/Ag+ for the GC electrode and of +0.85–−1.85 V vs. Ag0/Ag+ for the gold electrode with a step of 50 mV, and a chronoamperometry of 30 s was applied to reorganize the double layer at the fixed potential. EIS spectra were collected from a Biologic VSP potentiostat using the PEIS test from 400 kHz to 1 Hz with an amplitude of 10 mV. A relaxation step of 8 min was applied prior to switching to another potential. The capacitance was extracted by fitting the PEIS data to a circuit model with a constant phase element (CPE) in Fig. S29 (, ESI†). High frequencies (f), i.e., >10 kHz, were ignored in the fitting as they are likely associated with the inductance/capacitance of the electrode connections.
The experimental capacitance value was extracted using 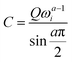 , where C is a differential capacitance (F); Q is a component of CPE (F·s(a−1)); ω is the angular frequency (Hz), and ω = 2πf; and a is a phase constant. All electrochemical measurements should be repeated several times to ensure that the observed trend is reproducible. The frequency (f) of 40 Hz related to capacitive behaviour (close to the 90-degree phase angle) is used for all calculations (Fig. S30, ESI†). The phase constants (a) calculated from the fitting of EIS data were ≥0.938 for the gold electrode or ≥0.824 for the glassy carbon electrode. The potential of zero charge (PZC) for superconcentrated [C3mpy][FSI]-based electrolytes was previously measured by the electrode immersion method with the gold electrode as approximately −0.35 V vs. Fc/Fc+.22 It should be recognised though that the direct conversion of V vs. PZC to V vs. Fc/Fc+ within the theory of classical MD is not accurate as the calculated potential drop does not include the complete polarizability of the system. All measurements were conducted at 50 °C in an argon-filled glove box with H2O and O2 levels <0.1 ppm.
, where C is a differential capacitance (F); Q is a component of CPE (F·s(a−1)); ω is the angular frequency (Hz), and ω = 2πf; and a is a phase constant. All electrochemical measurements should be repeated several times to ensure that the observed trend is reproducible. The frequency (f) of 40 Hz related to capacitive behaviour (close to the 90-degree phase angle) is used for all calculations (Fig. S30, ESI†). The phase constants (a) calculated from the fitting of EIS data were ≥0.938 for the gold electrode or ≥0.824 for the glassy carbon electrode. The potential of zero charge (PZC) for superconcentrated [C3mpy][FSI]-based electrolytes was previously measured by the electrode immersion method with the gold electrode as approximately −0.35 V vs. Fc/Fc+.22 It should be recognised though that the direct conversion of V vs. PZC to V vs. Fc/Fc+ within the theory of classical MD is not accurate as the calculated potential drop does not include the complete polarizability of the system. All measurements were conducted at 50 °C in an argon-filled glove box with H2O and O2 levels <0.1 ppm.
Symmetrical cell cycling
R2032 symmetrical cells were assembled by putting two identical electrodes (Na||Na, NFP||NFP, and Cu||Cu) with 60 mL of superconcentrated ionic liquid electrolyte (50 mol% NaFSI in [C3mpyr][FSI]) or an organic electrolyte (1.0 M NaPF6 in EC/DEC). The Solupor® polyethylene (19 mm in diameter) was used as a separator in all cells. The cells were then rested for 24 h before the charge/discharge test under 50 °C for IL and under 30 °C for carbonates. The areal capacity used for NFP||NFP is 0.05 mA h cm−2 with 0.05, 0.25 and 2.5 mA cm−2 and for Cu||Cu it is 0.05 μAh cm−2 with 0.05, 0.25 and 2.5 μA cm−2 current densities. This low current for the Cu||Cu setup was chosen to adjust an equal amount of consumed Na and enable the same capacity per cycle for each condition. The areal capacity used in Na||Na cell is 0.1 mA h cm−2 with 0.1, 1.0 and 5.0 mA cm−2 current densities. EIS data for interfacial resistance was collected from the Biologic VSP potentiostat from 1 MHz to 100 MHz with 10 mV potential perturbation. EIS spectra were recorded after five cycles, and the electrodes were then taken from the disassembled cells and sent for XPS tests.X-Ray photoelectron spectroscopic characterization
X-Ray photoelectron spectroscopy (XPS) analysis was performed using a Nexsa Surface Analysis System from ThermoFisher Scientific with a monochromatic Al Kα source (1486.6 eV). The X-ray spot size was set to 400 μm. The analysis chamber was maintained at a pressure of 1.0 × 10−8 bar or less. Survey scans were recorded at a pass energy of 200 eV and a step size of 1 eV, while high resolution data were obtained at a pass energy of 50 eV and a step size of 0.1 eV. Samples were loaded onto the holder inside the Ar-filled glovebox and left under vacuum in the glovebox antechamber for 10 min before being transported to the instrument without coming into contact with the ambient environment at any stage. The samples were kept in an ultra-high vacuum overnight before XPS measurements were carried out. No electrical contact between the sample and the instrument ground was present, and the samples were charge neutralised before the analysis. Collected spectral data were energy corrected by adjusting the maximum of the aliphatic C–C peak in C 1s spectra to 284.8 eV. When required, Ar+ etching was performed in a monoatomic regime at a pass energy of 420 eV at an estimated etching rate of 0.08 nm s−1.Author contributions
M. F. proposed the research. D. A. R. designed experiments, conducted MD and DFT modelling studies and three-electrode setup measurements including data analysis, interpretation, manuscript drafting and editing. J. S. conducted symmetrical cell cycling. P. V. C. conducted XPS measurements. All authors contributed to the discussion of the results, writing, and editing of the final manuscript.Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
D. A. R., F. C., M. F., and P. C. H. acknowledge the Australian Research Council (ARC) for funding via the Australian Centre for Electromaterials Science, grant CE140100012. M. F., F. C. and P. C. H. acknowledge ARC grant DP210101172. ANS acknowledges ARC funding through the Future Fellowship (FT200100317). The simulation work was undertaken with the assistance of resources provided at the NCI National Facility systems at the Australian National University through the National Computational Merit Allocation Scheme supported by the Australian Government. The authors gratefully acknowledge CIC energiGUNE for providing the NaFePO4 cathode material.References
- J. Hernández-Muñoz, et al., Subnanometer interfacial forces in three-dimensional atomic force microscopy: water and octane near a mica surface, J. Phys. Chem. C, 2020, 124, 26296–26303 CrossRef.
- M. A. Gebbie, et al., Long range electrostatic forces in ionic liquids, Chem. Commun., 2017, 53, 1214–1224 RSC.
- M. V. Fedorov and A. A. Kornyshev, Ionic liquids at electrified interfaces, Chem. Rev., 2014, 114, 2978–3036 CrossRef CAS PubMed.
- Z. Liu, et al., Dendrite-Free Nanocrystalline Zinc Electrodeposition from an Ionic Liquid Containing Nickel Triflate for Rechargeable Zn-Based Batteries, Angew. Chem., Int. Ed., 2016, 55, 2889–2893 CrossRef CAS PubMed.
- M. Gauthier, et al., Electrode–electrolyte interface in Li-ion batteries: current understanding and new insights, J. Phys. Chem. Lett., 2015, 6, 4653–4672 CrossRef CAS PubMed.
- X. Wang, et al., Electrode material–ionic liquid coupling for electrochemical energy storage, Nat. Rev. Mater., 2020, 5, 787–808 CrossRef CAS.
- M. Li, C. Wang, Z. Chen, K. Xu and J. Lu, New concepts in electrolytes, Chem. Rev., 2020, 120, 6783–6819 CrossRef CAS PubMed.
- L. Wang, et al., Identifying the components of the solid–electrolyte interphase in Li-ion batteries, Nat. Chem., 2019, 11, 789–796 CrossRef CAS PubMed.
- X. He, et al., The passivity of lithium electrodes in liquid electrolytes for secondary batteries, Nat. Rev. Mater., 2021, 6, 1036–1052 CrossRef CAS.
- Y. Huang, et al., Electrolytes and Electrolyte/Electrode Interfaces in Sodium-Ion Batteries: From Scientific Research to Practical Application, Adv. Mater., 2019, 31, 1808393 CrossRef PubMed.
- C.-X. Yu, et al., Surface engineering based on in situ electro-polymerization to boost the initial coulombic efficiency of hard carbon anode for sodium-ion battery, Rare Met., 2022, 41, 1616–1625 CrossRef CAS.
- Y.-D. Guo, et al., Enhanced performance of core–shell structured sodium manganese hexacyanoferrate achieved by self-limiting Na+ –Cs+ ion exchange for sodium-ion batteries, Rare Met., 2022, 41, 3740–3751 CrossRef CAS.
- D. A. Rakov, et al., Engineering high-energy-density sodium battery anodes for improved cycling with superconcentrated ionic-liquid electrolytes, Nat. Mater., 2020, 19, 1096–1101 CrossRef CAS PubMed.
- Y. Yin, et al., Fire-extinguishing, recyclable liquefied gas electrolytes for temperature-resilient lithium-metal batteries, Nat. Energy, 2022, 7, 548–559 CrossRef CAS.
- S. Tan,
et al., Additive engineering for robust interphases to stabilize high-Ni layered structures at ultra-high voltage of 4.8
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) V, Nat. Energy, 2022, 7, 484–494 CrossRef CAS.
V, Nat. Energy, 2022, 7, 484–494 CrossRef CAS. - Y. Jin, et al., Low-solvation electrolytes for high-voltage sodium-ion batteries, Nat. Energy, 2022, 7, 718–725 CrossRef CAS.
- L. Li, et al., Self-heating–induced healing of lithium dendrites, Science, 2018, 359, 1513–1516 CrossRef CAS PubMed.
- S. J. An, J. Li, Z. Du, C. Daniel and D. L. Wood III, Fast formation cycling for lithium ion batteries, J. Power Sources, 2017, 342, 846–852 CrossRef CAS.
- A. Aleshin, S. Bravo, K. Redquest and K. N. Wood, Rapid Oxidation and Reduction of Lithium for Improved Cycling Performance and Increased Homogeneity, ACS Appl. Mater. Interfaces, 2021, 13, 2654–2661 CrossRef CAS PubMed.
- B. Kishore, L. Chen, C. E. J. Dancer and E. Kendrick, Electrochemical formation protocols for maximising the life-time of a sodium ion battery, Chem. Commun., 2020, 56, 12925–12928 RSC.
- T. Pathirana, et al., Improving Cycle Life through Fast Formation Using a Superconcentrated Phosphonium Based Ionic Liquid Electrolyte for Anode-Free and Lithium Metal Batteries, ACS Appl. Energy Mater., 2021, 4, 6399–6407 CrossRef CAS.
- D. Rakov, et al., Stable and Efficient Lithium Metal Anode Cycling through Understanding the Effects of Electrolyte Composition and Electrode Preconditioning, Chem. Mater., 2021, 34(1), 165–177, DOI:10.1021/acs.chemmater.1c02981.
- X. Wang, et al., Inhibiting Dendrite Growth via Regulating the Electrified Interface for Fast-Charging Lithium Metal Anode, ACS Cent. Sci., 2021, 7, 2029–2038 CrossRef CAS PubMed.
- Z. Wang, Y. Yang, D. L. Olmsted, M. Asta and B. B. Laird, Evaluation of the constant potential method in simulating electric double-layer capacitors, J. Chem. Phys., 2014, 141, 184102 CrossRef PubMed.
- R. A. Bowling, An analysis of particle adhesion on semiconductor surfaces, J. Electrochem. Soc., 1985, 132, 2208 CrossRef CAS.
- T. Tian, et al., Electronic polarizability as the fundamental variable in the dielectric properties of two-dimensional materials, Nano Lett., 2019, 20, 841–851 CrossRef PubMed.
- K. Periyapperuma, J. M. Pringle, L. Sanchez-Cupido, M. Forsyth and C. Pozo-Gonzalo, Fluorine-free ionic liquid electrolytes for sustainable neodymium recovery using an electrochemical approach, Green Chem., 2021, 23, 3410–3419 RSC.
- M. Tułodziecki, J.-M. Tarascon, P.-L. Taberna and C. Guéry, Catalytic reduction of TFSI-containing ionic liquid in the presence of lithium cations, Electrochem. Commun., 2017, 77, 128–132 CrossRef.
- K. Arano, et al., Tuning the Formation and Structure of the Silicon Electrode/Ionic Liquid Electrolyte Interphase in Superconcentrated Ionic Liquids, ACS Appl. Mater. Interfaces, 2021, 13, 28281–28294 CrossRef CAS PubMed.
- J. B. Haskins, J. J. Wu and J. W. Lawson, Computational and experimental study of li-doped ionic liquids at electrified interfaces, J. Phys. Chem. C, 2016, 120, 11993–12011 CrossRef CAS PubMed.
- S. S. D. Begić, F. Chen, E. Jónsson and M. Forsyth, Overscreening and crowding in electrochemical ionic liquid systems, Phys. Rev. Mater., 2019, 3, 1–8 Search PubMed.
- T. Méndez-Morales, et al., Molecular dynamics simulations of the structure of the graphene–ionic liquid/alkali salt mixtures interface, Phys. Chem. Chem. Phys., 2014, 16, 13271–13278 RSC.
- N. Molinari, J. P. Mailoa and B. Kozinsky, General trend of a negative Li effective charge in ionic liquid electrolytes, J. Phys. Chem. Lett., 2019, 10, 2313–2319 CrossRef CAS PubMed.
- D. A. Rakov, et al., Polar Organic Cations at Electrified Metal with Superconcentrated Ionic Liquid Electrolyte and Implications for Sodium Metal Batteries, ACS Mater. Lett., 2022, 4, 1984–1990 CrossRef CAS.
- M. Jitvisate and J. R. T. Seddon, Direct measurement of the differential capacitance of solvent-free and dilute ionic liquids, J. Phys. Chem. Lett., 2018, 9, 126–131 CrossRef CAS PubMed.
- J. M. Klein, E. Panichi and B. Gurkan, Potential dependent capacitance of [EMIM][TFSI],[N 1114][TFSI] and [PYR 13][TFSI] ionic liquids on glassy carbon, Phys. Chem. Chem. Phys., 2019, 21, 3712–3720 RSC.
- R. Costa, C. M. Pereira and A. F. Silva, Charge storage on ionic liquid electric double layer: the role of the electrode material, Electrochim. Acta, 2015, 167, 421–428 CrossRef CAS.
- M. Trulsson, J. Algotsson, J. Forsman and C. E. Woodward, Differential capacitance of room temperature ionic liquids: the role of dispersion forces, J. Phys. Chem. Lett., 2010, 1, 1191–1195 CrossRef CAS.
- C. Zhan, Y. Zhang, P. T. Cummings and D. Jiang, Computational insight into the capacitive performance of graphene edge planes, Carbon N. Y., 2017, 116, 278–285 CrossRef CAS.
- O. Oll, T. Romann, C. Siimenson and E. Lust, Influence of chemical composition of electrode material on the differential capacitance characteristics of the ionic liquid| electrode interface, Electrochem. Commun., 2017, 82, 39–42 CrossRef CAS.
- C. Cannes, et al., Double layer at [BuMeIm][Tf2N] ionic Liquid–Pt or− C material interfaces, J. Phys. Chem. C, 2013, 117, 22915–22925 CrossRef CAS.
- T.-C. Kuo and R. L. McCreery, Surface Chemistry and Electron-Transfer Kinetics of Hydrogen-Modified Glassy Carbon Electrodes, Anal. Chem., 1999, 71, 1553–1560 CrossRef CAS.
- A. J. P. Neto and E. E. Fileti, Differential Capacitance and Energetics of the Electrical Double Layer of Graphene Oxide Supercapacitors: Impact of the Oxidation Degree, J. Phys. Chem. C, 2018, 122, 21824–21832 CrossRef CAS.
- K. Ma, C. E. Woodward and J. Forsman, Classical density functional study on interfacial structure and differential capacitance of ionic liquids near charged surfaces, J. Phys. Chem. C, 2014, 118, 15825–15834 CrossRef CAS.
- S. A. M. Noor, P. C. Howlett, D. R. MacFarlane and M. Forsyth, Properties of sodium-based ionic liquid electrolytes for sodium secondary battery applications, Electrochim. Acta, 2013, 114, 766–771 CrossRef.
- K. Matsumoto, et al., The Na [FSA]–[C2C1im][FSA](C2C1im +: 1-ethyl-3-methylimidazolium and FSA−: bis (fluorosulfonyl) amide) ionic liquid electrolytes for sodium secondary batteries, J. Power Sources, 2014, 265, 36–39 CrossRef CAS.
- K. Periyapperuma, et al., High Current Cycling in a Superconcentrated Ionic Liquid Electrolyte to Promote Uniform Li Morphology and a Uniform LiF-Rich Solid Electrolyte Interphase, ACS Appl. Mater. Interfaces, 2020, 12, 42236–42247 CrossRef CAS PubMed.
- H. J. Lee, et al., Ordered LiNi0. 5Mn1. 5O4 Cathode in Bis (fluorosulfonyl) imide-Based Ionic Liquid Electrolyte: Importance of the Cathode–Electrolyte Interphase, Chem. Mater., 2021, 33, 1238–1248 CrossRef CAS.
- M. Kerner, N. Plylahan, J. Scheers and P. Johansson, Thermal stability and decomposition of lithium bis (fluorosulfonyl) imide (LiFSI) salts, RSC Adv., 2016, 6, 23327–23334 RSC.
- B. Heidrich, L. Pritzlaff, M. Börner, M. Winter and P. Niehoff, Comparative X-ray Photoelectron Spectroscopy Study of the SEI and CEI in Three Different Lithium Ion Cell Formats, J. Electrochem. Soc., 2022, 169, 30533 CrossRef CAS.
- Y. Zhou, et al., Real-time mass spectrometric characterization of the solid–electrolyte interphase of a lithium-ion battery, Nat. Nanotechnol., 2020, 15, 224–230 CrossRef CAS PubMed.
- S. A. Ferdousi, et al., High-Performance Cycling of Na Metal Anodes in Phosphonium and Pyrrolidinium Fluoro(sulfonyl)imide Based Ionic Liquid Electrolytes, ACS Appl. Mater. Interfaces, 2022, 14, 15784–15798 CrossRef CAS PubMed.
- D. Monti, et al., Towards standard electrolytes for sodium-ion batteries: physical properties, ion solvation and ion-pairing in alkyl carbonate solvents, Phys. Chem. Chem. Phys., 2020, 22, 22768–22777 RSC.
- D. L. Wood III, J. Li and S. J. An, Formation challenges of lithium-ion battery manufacturing, Joule, 2019, 3, 2884–2888 CrossRef.
- E. Lindahl, B. Hess and D. van der Spoel, GROMACS 3.0: a package for molecular simulation and trajectory analysis, Mol. Model. Annu., 2001, 7, 306–317 CrossRef CAS.
- F. Chen, P. Howlett and M. Forsyth, Na-Ion solvation and high transference number in superconcentrated ionic liquid electrolytes: a theoretical approach, J. Phys. Chem. C, 2018, 122, 105–114 CrossRef CAS.
- F. Chen, R. Kerr and M. Forsyth, Cation effect on small phosphonium based ionic liquid electrolytes with high concentrations of lithium salt, J. Chem. Phys., 2018, 148, 193813 CrossRef PubMed.
- R. Wang, S. Bi, V. Presser and G. Feng, Systematic comparison of force fields for molecular dynamic simulation of Au(111)/Ionic liquid interfaces, Fluid Phase Equilib., 2018, 463, 106–113 CrossRef CAS.
- P. Hirunsit and P. B. Balbuena, Effects of confinement on water structure and dynamics: a molecular simulation study, J. Phys. Chem. C, 2007, 111, 1709–1715 CrossRef CAS.
- I.-C. Yeh and M. L. Berkowitz, Ewald summation for systems with slab geometry, J. Chem. Phys., 1999, 111, 3155–3162 CrossRef CAS.
- J. Vatamanu, L. Xing, W. Li and D. Bedrov, Influence of temperature on the capacitance of ionic liquid electrolytes on charged surfaces, Phys. Chem. Chem. Phys., 2014, 16, 5174–5182 RSC.
- J. Vatamanu, O. Borodin and G. D. Smith, Molecular insights into the potential and temperature dependences of the differential capacitance of a room-temperature ionic liquid at graphite electrodes, J. Am. Chem. Soc., 2010, 132, 14825–14833 CrossRef CAS PubMed.
- N. Michaud-Agrawal, E. J. Denning, T. B. Woolf and O. Beckstein, MDAnalysis: a toolkit for the analysis of molecular dynamics simulations, J. Comput. Chem., 2011, 32, 2319–2327 CrossRef CAS PubMed.
- J. VandeVondele, et al., Quickstep: Fast and accurate density functional calculations using a mixed Gaussian and plane waves approach, Comput. Phys. Commun., 2005, 167, 103–128 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- J. VandeVondele and J. Hutter, Gaussian basis sets for accurate calculations on molecular systems in gas and condensed phases, J. Chem. Phys., 2007, 127, 114105 CrossRef PubMed.
- S. Goedecker, M. Teter and J. Hutter, Separable dual-space Gaussian pseudopotentials, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 1703 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- K. M. Bal and E. C. Neyts, Modelling molecular adsorption on charged or polarized surfaces: a critical flaw in common approaches, Phys. Chem. Chem. Phys., 2018, 20, 8456–8459 RSC.
- C. Berlanga, et al., Cost-Effective Synthesis of Triphylite-NaFePO4 Cathode: A Zero-Waste Process, ACS Sustainable Chem. Eng., 2020, 8, 725–730 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ee00864a |
| This journal is © The Royal Society of Chemistry 2023 |