Diamond-XII: a new type of exotic cubic carbon allotrope

Abstract

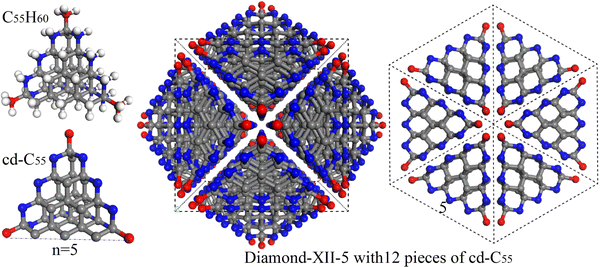
Based on the tetragonal diamond segments (CH₄, C₅H₁₂, C₁₄H₂₄, C₃₀H₄₀, C₅₅H₆₀ and C₉₁H₈₄), a new type of cubic carbon crystalline structure (Diamond-XII) with 12-fold distorted diamond segments was proposed and investigated by first-principles calculations. The phonon band structures and elastic properties show that all these Diamond-XII structures are both mechanically and dynamically stable. They are more stable than the previously proposed T-carbon, BC-8 and C3-205 phases and are confirmed to be transparent superhard insulators. Especially, the lattice constants for Diamond-XII-4 and Diamond-XII-5 of 12.83 Å and 15.68 Å are very close to that (14.7 Å) of the superhard transparent cubic carbon phase discovered in the Popigai crater [A. El Goresy et al., C. R. Geoscience, 2003, 335, 889–898]. Their simulated XRD results can explain many of the XRD peaks from the experiment. The matches in lattice, hardness, XRD and electronic properties provide us with an inaugural and fundamental understanding of the super-size cubic carbon for the first time.

---

I. Introduction

The energy landscape of the element carbon is exceedingly complex, hosting diverse and important metastable phases, including diamond, fullerenes, nanotubes and graphene. In the past decades, many efforts from both experimental^1–4 and theoretical^5–8 points of view have been paid on searching for new meta-stable carbon crystals. Many structurally unknown carbon samples have been experimentally reported. For example, the large-size hexagonal chaoite (a = b = 8.948 Å and c = 14.078 Å) discovered in the Ries Crater in Germany⁹, which was synthesized again through graphite sublimation in high temperature and low-pressure conditions;^10,11 the middle-size hexagonal carbon IV (a = b = 5.33 Å and c = 12.24 Å), which was synthesized again through graphite sublimation in high temperature and low-pressure conditions;¹¹ and the super-size cubic phase (a = 14.7 Å) with transparent and superhard properties discovered in the Popigai crater.¹² To search for structural candidates for these large-size carbon structures is challenging for present crystal prediction methods.^13–19 There are large numbers of carbon crystals that have been theoretically predicted in previous literature.^19–29 However, only a few of them have been suggested as the candidates for some of the previously discovered small size experimental carbons. For example, the M-carbon,^17,30 W-carbon,³¹ Z-carbon,^32,33 H-carbon and S-carbon³⁴ proposed for explaining the superhard carbon phase synthesized through cold-compressing graphite;² the cubic C20-sc,³⁵ C21-sc and C22-sc³⁶ predicted as the candidates of the simple cubic carbon sample shock-synthesized by compression of the mixture of carbon black and tetracyanoethylene;¹ the 3D-C24³⁷ and C3-205³⁸ proposed for the cubic carbon phase synthesized by cold compressing graphite;³⁹ and the cubane,⁴⁰ BC8⁴¹ and Bcc-C6^35,42 suggested for superdense carbon.⁴⁰

According to our knowledge, no crystal structures have been proposed for the super-size cubic carbon phase.¹² The crystal structures for chaoite,^9–11 carbon IV¹¹ and the super-size cubic carbon¹² are still mysteries and are challenging for present popular crystal prediction methods.^13–19 In this letter, we report our discovery of a new type of cubic diamond allotrope (Diamond-XII) containing 12 pieces of tetragonal diamond segments (TDS) as shown in Fig. 1. With the increase of the size (defined as the length of the tetragon as shown in Fig. S1, ESI†) of the used TDS as indicated in Fig. S1 (ESI†), a series of Diamond-XII-n shown in Fig. S2 and S3 (ESI†) can be constructed (see the method as sketched in Fig. 1). We notice that the total atom number N_i per cubic cell in Diamond-XII-i can be described as a general term N_i = N_i−1 + 12i² when i when ubic c₁ = 12 and i indicates the size of the TDS. We investigate the structures, stabilities and electronic properties of the fist-six Diamond-XII-n with computing-acceptable sizes, in which n = 1, 2, 3, 4, 5 and 6 contain 1, 2, 4, 7 12 and 16 inequivalent carbon atoms in the cells, respectively. We find that the optimized lattice constants of Diamond-XII-4 (12.83 Å) and Diamond-XII-5 (15.68 Å) are very close to that (14.7 Å) of super-size cubic carbon.¹² Furthermore, the simulated X-ray diffraction patterns (XRD) of these Diamond-XII phases can help us to understand the experimental results, which indicate that Diamond-XII-4 and Diamond-XII-5 can be considered as structural candidates for super-size cubic carbon.

Fig. 1 The crystalline views of tetragonal diamond segments with (C₅₅H₆₆) and without (cd-C₅₅). The sketch map of constructing Diamond-XII through diamond segments in the perspective cubic view and 111 direction primitive views. Each cubic cell contains 12 pieces of tetragonal diamond segments.

II. Method

The density functional theory (DFT) based first-principles method as implemented in the Vienna ab initio simulation package (VASP)^43,44 is employed in our calculations. The interactions between the nucleus and the 2s²2p² valence electrons of carbon are described by the projector augmented wave (PAW) method.^45,46 The interactions between the valence electrons are also accounted for by generalized gradient approximations (GGA) developed by Perdew, Burke and Ernzerhof (PBE).⁴⁷ The cut-off energies are set to be 500 eV and the Brillouin Zone sample meshes were set to be dense enough (less than 0.21 Å⁻¹) for each system. All the structures are fully optimized up to the residual force on every atom less than 0.01 eV Å⁻¹. The vibrational spectra are simulated by the open-free code-package PHONOPY^48,49 with forces calculated from VASP. We have used the HSE06 functional⁵⁰ to calculate the band gap of cubic diamond to evaluate the movement, and then to evaluate the HSE06-based band gaps of these new carbon phase by pulsing the movement on the PBE-based gaps.

To further confirm the mechanical stabilities of these new materials, we have systematically investigated their symmetry-dependent elastic constants (C_ij) through a well-developed method⁵¹ as implemented in the newest VASP code by setting IBRION = 6 in the input file (INCAR). With the calculated independent elastic constants (C_ij), we can evaluate their elastic stabilities according to their symmetries⁵² and further evaluate their corresponding bulk modules (B) and shear modules (G). In our calculations, both Reiss's and Voigt's formulas are employed to obtain the averaged results. Finally, with the recently developed model,⁵³ we can calculate their Vicker's hardness (Hv) as Hv = 2*(G³/B²)^0.585 – 3, which can help us to classify these crystals as soft (<10 GPa), hard (10 GPa – 40 GPa) or superhard materials (>40 GPa).

III. Results and discussion

In fact, Diamond-XII-1 and Diamond-XII-2 containing 12/1 and 60/2 total/inequivalent carbon atoms in their cubic cells are the previously proposed bcc-C6³⁵ and cl60,²² respectively. Such small-size configurations can be quickly discovered by our recently developed RG²-code¹⁹, which is a powerful code for generating crystal structures with well-defined geometrical features.^54–59 The new Diamond-XII-3 with a larger size can also be uncovered by RG². It contains 168/84 carbon atoms in its cubic/primitive cell, in which only 4 of them are inequivalent. After studying the topology characteristics of Diamond-XII-1, Diamond-XII-2 and Diamond-XII-3, we find that they can be constructed through combining 12 pieces of the TDS (CH₄, C₅H₁₂ and C₁₄H₂₄ as shown in Fig. S1, ESI†). In Fig. 1, we show such a simple idea of combining the TDS to construct new cubic carbons. With the increase of the size n of the used TDS (C₃₀H₄₀, C₅₅H₆₀ and C₉₁H₈₄), three large-size cubic carbon phases (Diamond-XII-4, Diamond-XII-5 and Diamond-XII-6) are obtained. They contain 360/7, 660/12 and 1092/16 total/inequivalent carbon atoms in their cubic cells, respectively, which are too large for the present crystal predicting software.

The optimized crystal structures of these Diamond-XII allotropes in the perspective cubic view and 111 direction views are shown in Fig. S2 and S3 (ESI†), respectively. One can easily know their common topological characteristics from their crystal structures as provided in the ESI.† After optimizing, the lattice constants of Diamond-XII-1 and Diamond-XII-2 are 4.37 Å and 7.16 Å, respectively, which are in good agreement with those reported in previous literature.^22,35 The optimized lattice constants of Diamond-XII-n are 9.99 Å, 12.83 Å, 15.65 Å and 18.51 Å for n equal to 3, 4, 5 and 6, respectively. We can see that Diamond-XII-4 and Diamond-XII-5 possess lattice constants very close to that of the super-size cubic carbon discovered in the Popigai crater.¹²

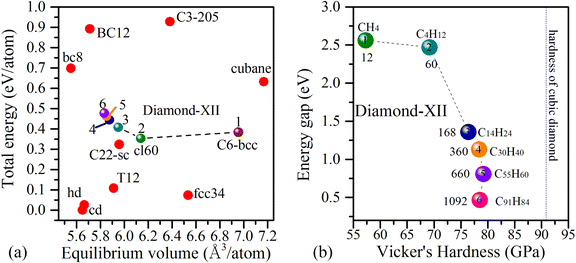
To show the relative stabilities of these Diamond-XII allotropes, we compared their average energies to those of some well-known cubic carbon phases, such as BC8,⁴¹ BC12,⁶ C3-205,³⁸ Cubane,⁴⁰ C22-sc³⁶ and cubic diamond (cd). As shown in Fig. 2(a), the calculated average energies of Diamond-XII-1 and Diamond-XII-2 are 383 meV per atom and 352 meV per atom higher than that of cd (set to be zero). These results are good agreement those reported in previous literature^22,35. With the size increase, the average energies of Diamond-XII allotropes (n = 3, 4, 5 and 6) slightly increase to be 407 meV per atom, 441 meV per atom, 463 meV per atom and 477 meV per atom, respectively. They are energetically more stable than cubane (631 meV per atom), BC8 (698 meV per atom), BC12 (892 meV per atom) and C3-205 (927 meV per atom). Especially, they are more favorable than the experimentally synthesized T-carbon (1171 meV per atom),^3,60 which indicate that they can be expected to be synthesized in future experiments.

Fig. 2 The calculated average energies (eV per atom relative to cubic diamond) and equilibrium volumes of Diamond-XII allotropes and some well-known carbon crystals (a); the calculated band gaps and Vicker's hardness of Diamond-XII allotropes (b).

The dynamical stabilities of Diamond-XII-1 and Diamond-XII-2 have been previously confirmed to be positive.^22,35 We then calculated the vibrational phonon spectra of Diamond-XII-3, Diamond-XII-4, Diamond-XII-5 and Diamond-XII-6 to check their dynamical stabilities. The calculated results of the phonon band structures of Diamond-XII-3, Diamond-XII-4, Diamond-XII-5 and Diamond-XII-6, are shown in Fig. 3(a)–(d), respectively. We can see that no imaginary frequencies appear in the phonon band structures, which indicates that these four new Diamond-XII allotropes are dynamically viable carbon phases. As shown in Table S1 (ESI†), we also calculated the elastic properties of these Diamond-XII allotropes. The calculated elastic constants for all Diamond-XII allotropes satisfy the mechanical stability criteria of a cubic lattice, namely C₁₁ > 0, C₄₄ > 0, C₁₁ − C₁₂ > 0 and C₁₁ + 2C₁₂ > 0, which indicate that all of them are mechanically stable. As shown in Fig. 2(b) and Table S1 (ESI†), the calculated Vicker's hardness of Diamond-XII-n (n = 1, 2, 3, 4, 5 and 6) are 57.27 GPa, 69.17 GPa, 76.49 GPa, 80.33 GPa, 83.66 GPa and 86.44 GPa, respectively. These values indicate that all these Diamond-XII allotropes are superhard materials. For intuitive presentation of the anisotropy in mechanical properties of these Diamond-XII allotropes, we plotted the Young's modulus and Poisson's ratio in three-dimensional form in Fig. S4 and S5 (ESI†). It is clear that the anisotropy is enhanced as the size-index n increases.

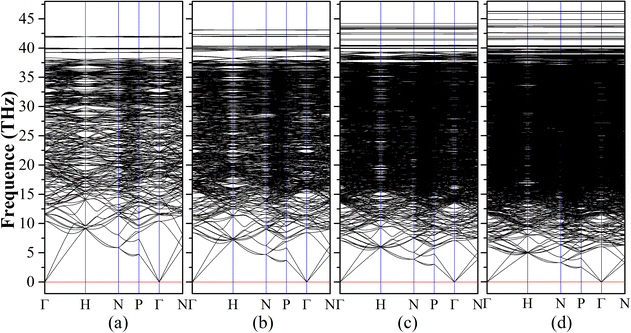Fig. 3 The calculated phonon band structures of our new Diamond-XII-3 (a), Diamond-XII-4 (b), Diamond-XII-5 (c) and Diamond-XII-6 (d).

We then investigated the electronic properties of these Diamond-XII allotropes. Fig. 4(a)–(d) are the density functional theory (DFT) based bands structures of Diamond-XII-3, Diamond-XII-4, Diamond-XII-5 and Diamond-XII-6, respectively. The DFT-based band gaps of all the Diamond-XII allotropes are shown in Fig. 2(b) and Table S1 (ESI†). We can see that the calculated band gaps for these four new Diamond-XII allotropes (n = 3, 4, 5 and 6) are 1.357, 1.129, 0.806 and 0.465 eV, respectively. Although DFT always under-evaluates the band gap of semiconductors, we did not employ the HSE06 method to recalculate the bands structures of these Diamond-XII allotropes because of the computational costs. We evaluated a proper movement of about 1.2 eV for the HSE06-based band gaps of these carbon allotropes based on the difference between the HSE06-based gap (5.32 eV) and the PBE-based gap (4.12 eV) of cd. Thus, the HSE06-based band gaps of these four new Diamond-XII allotropes (n = 3, 4, 5 and 6) are evaluated to be 2.557, 2.329, 2.006 and 1.665 eV, respectively. That is to say, Diamond-XII-4 and Diamond-XII-5 cannot absorb most of all visible light, which indicates that they may be transparent for most visible light. Such results are also in good agreement with the experiment conclusion that the super-size cubic carbon is a transparent phase.¹²

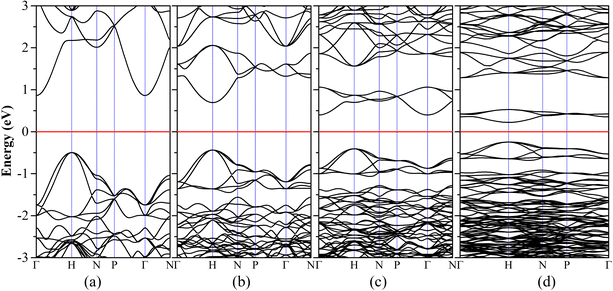Fig. 4 The calculated electronic band structures of our new Diamond-XII-3 (a), Diamond-XII-4 (b), Diamond-XII-5 (c) and Diamond-XII-6 (d).

With well-matched lattice constants, mechanical and electronic properties, Diamond-XII-4 (12.83 Å) and Diamond-XII-5 (15.65 Å) are expected to explain the super-size cubic carbon (14.7 Å) reported in previous literature.¹² We simulated their XRD patterns to compare them with that reported in a previous experiment, and Fig. 5(a) shows the XRD patterns of Diamond-XII-1, Diamond-XII-2 and Diamond-XII-3. Fig. 5(d) plots the XRD pattern of Diamond-XII-6. In views of the mismatch in lattice constant, the XRD patterns in Fig. 5(a) and (d) cannot explain the XRD of the super-size cubic carbon. However, we can see that the XRD patterns in Fig. 5(b) and (c) for Diamond-XII-4 and Diamond-XII-5 can explain many of the XRD peaks in the experiment.¹² For example, the experimental XRD peaks in the ranges of [8–12°], [13–14°] and [16–22°] can be well understood based on the XRD patterns of Diamond-XII-4 and Diamond-XII-5. These results indicate that Diamond-XII-4 and Diamond-XII-5 are possible structural candidates for the super-size cubic carbon sample.

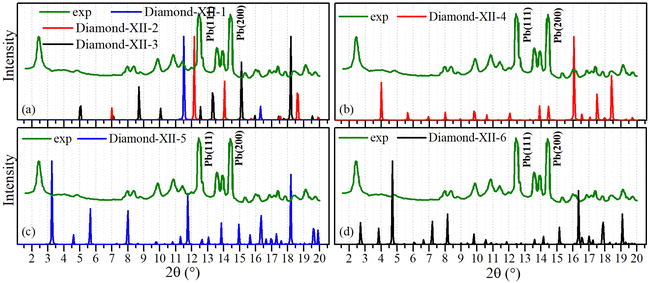Fig. 5 Simulated X-ray diffraction patterns of Diamond-XII-1, Diamond-XII-2, Diamond-XII-3 (a), Diamond-XII-4 (b), Diamond-XII-5 (c) and Diamond-XII-6 (d) compared with experimental results.

IV. Conclusion

In summary, a new type of cubic carbon crystalline structure (Diamond-XII) with 12-fold distorted diamond segments was proposed and investigated. They are confirmed to be both mechanically and dynamically metastable carbon phases that are more favorable than the previously proposed BC8, BC12 and C3-205 as well as the experimentally synthesized T-carbon. The calculated results show that these Diamond-XII allotropes are superhard materials. Five of them are evaluated to be transparent phases for visible light. In view of the well-matched lattice constant, electronic and mechanical properties, Diamond-XII-4 and Diamond-XII-5 are suggested to be structural candidates for the super-size, superhard and transparent cubic carbon sample discovered in the Popigai crater. Their simulated XRD results can explain many of the XRD peaks from the experiment.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work is supported by the National Natural Science Foundation of China (No. 11974300, 11974299, and 11874316), the Science Fund for Distinguished Young Scholars of Hunan Province of China (No. 2021JJ10036), the Natural Science Foundation of Hunan Province, China (No. 2019JJ50577, 2021JJ40524, and 2022JJ30554), the Scientific Research Fund of Hunan Provincial Education Department (No. 19C1746, 20K127, 20A503, and 20B582), and the Program for Changjiang Scholars, Innovative Research Team in University (No. IRT13093) and the Hunan Provincial Innovation Foundation for Postgraduates (Grant No. CX20210616).

References

1. K. Yamada, Carbon, 2003, 41, 1309–1313.
2. W. L. Mao, H.-k Mao, P. J. Eng, T. P. Trainor, M. Newville, C.-c Kao, D. L. Heinz, J. Shu, Y. Meng and R. J. Hemley, Science, 2003, 302, 425–427.
3. J. Zhang, R. Wang, X. Zhu, A. Pan, C. Han, X. Li, D. Zhao, C. Ma, W. Wang and H. Su, Nat. Commun., 2017, 8, 1–7.
4. X. Yang, M. Yao, X. Wu, S. Liu, S. Chen, K. Yang, R. Liu, T. Cui, B. Sundqvist and B. Liu, Phys. Rev. Lett., 2017, 118, 245701.
5. A. Mujica, C. J. Pickard and R. J. Needs, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 214104.
6. Z.-Z. Li, C.-S. Lian, J. Xu, L.-F. Xu, J.-T. Wang and C. Chen, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 214106.
7. C. J. Pickard and R. Needs, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 014106.
8. Q. Zhu, A. R. Oganov, M. A. Salvadó, P. Pertierra and A. O. Lyakhov, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 193410.
9. A. El Goresy and G. Donnay, Science, 1968, 161, 363–364.
10. A. G. Whittaker and P. Kintner, Science, 1969, 165, 589–591.
11. A. G. Whittaker and G. M. Wolten, Science, 1972, 178, 54–56.
12. A. El Goresy, L. S. Dubrovinsky, P. Gillet, S. Mostefaoui, G. Graup, M. Drakopoulos, A. S. Simionovici, V. Swamy and V. L. Masaitis, C. R. Geosci., 2003, 335, 889–898.
13. C. J. Pickard and R. Needs, Phys. Rev. Lett., 2006, 97, 045504.
14. C. J. Pickard and R. Needs, J. Phys.: Condens. Matter, 2011, 23, 053201.
15. Y. Wang, J. Lv, L. Zhu and Y. Ma, Comput. Phys. Commun., 2012, 183, 2063–2070.
16. Y. Wang, J. Lv, L. Zhu and Y. Ma, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 094116.
17. A. R. Oganov and C. W. Glass, J. Chem. Phys., 2006, 124, 244704.
18. C. W. Glass, A. R. Oganov and N. Hansen, Comput. Phys. Commun., 2006, 175, 713–720.
19. X. Shi, C. He, C. J. Pickard, C. Tang and J. Zhong, Phys. Rev. B, 2018, 97, 014104.
20. R. Hoffmann, A. A. Kabanov, A. A. Golov and D. M. Proserpio, Angew. Chem., Int. Ed., 2016, 55, 10962–10976.
21. M. Takagi, T. Taketsugu, H. Kino, Y. Tateyama, K. Terakura and S. Maeda, Phys. Rev. B, 2017, 95, 184110.
22. Z. Li, M. Hu, M. Ma, Y. Gao, B. Xu, J. He, D. Yu, Y. Tian and Z. Zhao, Carbon, 2016, 105, 151–155.
23. C. He, L. Sun, C. Zhang, X. Peng, K. Zhang and J. Zhong, Phys. Chem. Chem. Phys., 2012, 14, 8410–8414.
24. C. He, L. Sun and J. Zhong, J. Superhard Mater., 2012, 34, 386–399.
25. C. He and J. Zhong, Solid State Commun., 2014, 181, 24–27.
26. D. Selli, I. A. Baburin, R. Martoňák and S. Leoni, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 161411.
27. Z.-Z. Li, J.-T. Wang, L.-F. Xu and C. Chen, Phys. Rev. B, 2016, 94, 174102.
28. Y. J. Oh, S. Kim, I.-H. Lee, J. Lee and K. J. Chang, Phys. Rev. B, 2016, 93, 085201.
29. M. O’Keeffe, G. B. Adams and O. F. Sankey, Phys. Rev. Lett., 1992, 68, 2325.
30. Q. Li, Y. Ma, A. R. Oganov, H. Wang, H. Wang, Y. Xu, T. Cui, H.-K. Mao and G. Zou, Phys. Rev. Lett., 2009, 102, 175506.
31. J.-T. Wang, C. Chen and Y. Kawazoe, Phys. Rev. Lett., 2011, 106, 075501.
32. Z. Zhao, B. Xu, X.-F. Zhou, L.-M. Wang, B. Wen, J. He, Z. Liu, H.-T. Wang and Y. Tian, Phys. Rev. Lett., 2011, 107, 215502.
33. M. Amsler, J. A. Flores-Livas, L. Lehtovaara, F. Balima, S. A. Ghasemi, D. Machon, S. Pailhes, A. Willand, D. Caliste and S. Botti, Phys. Rev. Lett., 2012, 108, 065501.
34. C. He, L. Sun, C. Zhang, X. Peng, K. Zhang and J. Zhong, Solid State Commun., 2012, 152, 1560–1563.
35. F. J. Ribeiro, P. Tangney, S. G. Louie and M. L. Cohen, Phys. Rev. B, 2006, 74, 172101.
36. C. He, C. Zhang, H. Xiao, L. Meng and J. Zhong, Carbon, 2017, 112, 91–96.
37. V. Pokropivny and A. Pokropivny, Phys. Solid State, 2004, 46, 392–394.
38. J.-T. Wang, C. Chen and Y. Kawazoe, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 214104.
39. R. Aust and H. Drickamer, Science, 1963, 140, 817–819.
40. A. Bakai and V. Strel’nitskii, Sov. Phys. Tech. Phys, 1981, 26, 1425–1426.
41. R. L. Johnston and R. Hoffmann, J. Am. Chem. Soc., 1989, 111, 810–819.
42. M. Hu, F. Tian, Z. Zhao, Q. Huang, B. Xu, L.-M. Wang, H.-T. Wang, Y. Tian and J. He, J. Phys. Chem. C, 2012, 116, 24233–24238.
43. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169.
44. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
45. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953.
46. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758.
47. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
48. A. Togo and I. Tanaka, Scr. Mater., 2015, 108, 1–5.
49. A. Togo, F. Oba and I. Tanaka, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 134106.
50. J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215.
51. Y. Le Page and P. Saxe, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 104104.
52. R. Hill, Proc. Phys. Soc., London, Sect. A, 1952, 65, 349.
53. H. Niu, P. Wei, Y. Sun, X.-Q. Chen, C. Franchini, D. Li and Y. Li, Appl. Phys. Lett., 2011, 99, 031901.
54. H. Yin, X. Shi, C. He, M. Martinez-Canales, J. Li, C. J. Pickard, C. Tang, T. Ouyang, C. Zhang and J. Zhong, Phys. Rev. B, 2019, 99, 041405.
55. N. Zhou, P. Zhou, J. Li, C. He and J. Zhong, Phys. Rev. B, 2019, 100, 115425.
56. Z. Gong, X. Shi, J. Li, S. Li, C. He, T. Ouyang, C. Zhang, C. Tang and J. Zhong, Phys. Rev. B, 2020, 101, 155427.
57. Y. Liao, X. Shi, T. Ouyang, J. Li, C. Zhang, C. Tang, C. He and J. Zhong, J. Phys. Chem. Lett., 2021, 12, 8889–8896.
58. Y. Wei, J. Li, X. Shi, J. Li and C. He, Scr. Mater., 2022, 219, 114843.
59. L. Su, S. Li, J. Li, C. He, X.-T. Zeng, X.-L. Sheng, T. Ouyang, Z. Chunxiao, C. Tang and J. Zhong, ACS Mater. Lett., 2022, 4, 1726–1733.
60. X.-L. Sheng, Q.-B. Yan, F. Ye, Q.-R. Zheng and G. Su, Phys. Rev. Lett., 2011, 106, 155703.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2ma00920j

---