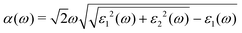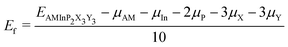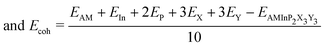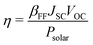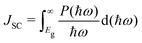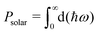Theoretical design of two-dimensional AMInP₂X₃Y₃ (AM = Li, Na, K; X/Y = S, Se, Te) monolayers for highly efficient excitonic solar cells

Abstract

Two-dimensional materials are regarded as promising candidates for use in photovoltaic solar cells. On the basis of first-principles calculations, we show that the 2D alkali metal indium phosphorus trichalcogenides AMInP₂X₃Y₃ (AM = Li, Na, or K; X/Y = S, Se, or Te) monolayers possess excellent stability and great potential for solar energy conversion applications. The cohesive energies, phonon spectra, and elastic constants of these materials demonstrate their high thermodynamic, kinetic, and mechanical stabilities. The 2D NaInP₂Te₆ (NT), KInP₂Te₆ (KT), and AMInP₂Te₃Se₃ (LTS,NTS, and KTS) monolayers are promising donor materials for excitonic solar cells with high photovoltaic performance. More importantly, the appropriate donor bandgaps and small conduction band offsets of these type II heterostructures result in power conversion efficiencies (PCE) of up to 22.12% (NT/InSe), 18.23% (KT/MoGe₂N₄), 21.93% (NTS/MoGe₂N₄) and 18.00% (KTS/T-HfSe₂), making them promising candidates for solar energy conversion applications. Our findings reveal the great potential of 2D alkali metal indium phosphorus trichalcogenides for the design of high-performance excitonic solar cells.

---

1 Introduction

Solar cells that directly convert solar energy into electricity are among the most promising clean energy technologies. Since the first solar cells were developed in the 1950s,¹ the search has continued for solar cell materials with higher power conversion efficiencies (PCEs).^2–10 Solar cells can be divided into two categories according to their photoelectric conversion mechanism, namely, conventional solar cells^3,4 and excitonic solar cells (XSCs).^5,11–15 Conventional solar cells are pn-junction cells fabricated from bulk inorganic semiconductors such as Si, GaAs, and CdTe,² which suffer from non-radiative recombination of photogenerated electron–hole pairs, severely limiting their solar energy conversion efficiency. Excitonic solar cells consist of heterostructures formed from donor–acceptor composite networks, including dye-sensitized solar cells (DSSCs),¹¹ organic solar cells (OSCs),^12,13 and two-dimensional (2D) heterojunction solar cells.^5–8 Light-induced excitons can be dissociated with high yields at material interfaces with different electron affinities and ionization potentials in XSCs,¹⁶ leading to remarkable energy conversion efficiency. Compared with other XSCs, 2D heterojunction solar cells show great promise for high-efficiency solar cell applications, owing to their excellent interfacial properties.

Efficient 2D heterojunction solar cells share two common characteristics. First, the acceptor and donor materials have a type II band arrangement in the heterostructure. Such a band alignment facilitates the accumulation of photogenerated electrons and holes in different layers, thereby reducing their recombination. Also, with this alignment, the conduction band offset between the donor and the acceptor is small, leading to less energy loss and hence higher open-circuit voltage. Second, the donor materials of these heterostructures have bandgaps in the range of 0.90–1.70 eV,^5,7,8 ensuring efficient light absorption. High absorbed light and carrier mobility and efficient exciton separation also have a significant impact on PCE.⁶ Therefore, 2D materials are considered to be promising candidates for heterojunction solar cells because of their tunable bandgaps and good light absorption efficiency with high carrier mobility.^17,18 Experimentally, however, most of the heterojunction solar cells still exhibit efficiencies of less than 12%.^19–21 It has been theoretically found that the maximum PCEs of 2D heterojunction solar cells consisting of heterobilayers lie in the range of 10–20%,^{5,6,8–10,22–26} with only a few of 2D heterojunction solar cells (e.g., α-AsP/GaN, In₂STe/Al₂ SSe, GaAs/InAs, HfSe₂/GeO₂, TiNF/TiNCl, h-BAs/h-BP, boron pnictide/MoSSe, β-PdTe₂/MoSe₂, and β-PdTe₂/MoTe₂) being capable of achieving large PCEs over 20%.^5–10,27,28 However, most of the compositing 2D materials have not been experimentally realized. Thus, these 2D heterojunction solar cells cannot be constructed and their performance cannot be measured. Therefore, it is of great importance to design suitable and experimentally synthesizable donor and acceptor materials to construct 2D heterojunction solar cells with high PCE.

Among the wide variety of 2D materials, layered metal phosphorus trichalcogenides (MPX₃) composed of M and P atoms located between two layers of X atoms through strong ionic bonds have attracted much attention.^18,29–31 Metal cations (M^II or M^IM^III) stabilize the [P₂S₆]⁴⁻ or [P₂Se₆]⁴⁻ frameworks, and their interlayers are bound by van der Waals (vdW) interactions. Here, the metal cations can be from the first row of transition metals (M = V, Mn, Fe, Co, Ni, Zn), from the alkaline earth metals of group II, or some other metal ions. With the experimental synthesis of LiInP₂Se₆,³² the range of possible metal cations has been extended to the alkali metals of group I. The cations in the MPX₃ family members have a wide variety of species and valences, offering vast possibilities for achieving the desired physical and chemical properties.^30,33,34 The optical and electronic properties of these materials can be tuned by changing the elemental composition and material thickness. Both theoretical and experimental results have revealed that the MPX₃ compounds are very interesting functional materials,³⁴ with their bandgaps of 1.3–3.5 eV³⁴ indicating that MPX₃ monolayers have higher light absorption efficiencies and wider absorption ranges than TMDs.²⁹ Therefore, we have reason to believe that they are promising candidates for solar energy conversion applications.

In the work reported in this paper, using first-principles density functional theory (DFT) simulations, we constructed 57 new metal phosphorus trichalcogenides and calculated their energy and phonon spectra, screening 17 stable semiconductor materials. It is worth noting that the NaInP₂Te₆ (NT), KInP₂Te₆ (KT), LiInP₂Te₃Se₃ (LTS), NaInP₂Te₃Se₃ (NTS), and KInP₂Te₃Se₃ (KTS) monolayers are direct bandgap semiconductors with bandgaps of 1.49 eV, 1.41 eV, 0.89 eV, 1.16 eV, and 0.82 eV, respectively, suggesting that they can be suitable donor materials for 2D heterojunction solar cells. The PCEs of the NT/InSe, KT/MoGe₂N₄, NTS/MoGe₂N₄, and KTS/T-HfSe₂ heterostructures are calculated as 22.12%, 18.23%, 21.93%, and 18.00%, respectively, which are higher than those of most other 2D heterostructures. In addition, the 2D LiInP₂S₆, LiInP₂Se₆, LiInP₂Se₃S₃, NaInP₂S₆, NaInP₂Se₆, NaInP₂Te₆, and KInP₂Te₆ monolayers exhibit semiconducting characteristics with suitable bandgaps, appropriate band alignments, and high solar-to-hydrogen (STH) efficiencies, confirming their good photoelectronic performances. Furthermore, these metal phosphorus trichalcogenides exhibit substantial optical absorption in the visible and ultraviolet (UV) region. Our results reveal the great potential of metal phosphorus trichalcogenides for photonics, optoelectronics, and solar energy harvesting applications, and call for more comprehensive computational and experimental studies of metal phosphorus trichalcogenide materials.

2 Computational method

All DFT calculations were carried out by using the DFT method,³⁵ within the generalized gradient approximation of Perdew–Burke–Ernzerhof (GGA-PBE) implemented in the Vienna Ab initio Simulation Package (VASP).^36,37 The phonon spectra were calculated by the finite displacement method as implemented in the Phonopy code.³⁸ The geometry and electronic structures of MX nanosheets were calculated using a 15 × 15 × 1 Monkhorst–Pack k-mesh over the Brillouin zone.³⁹ A plane-wave cutoff energy of 520 eV was employed. The atomic positions were fully relaxed until the maximum force on each atom was less than 10⁻² eV Å⁻¹. A vacuum distance of about 20 Å was used to avoid interaction between adjacent layers. The van der Waals interaction was taken into account using the semiempirical DFT-D3 approach.⁴⁰ The sophisticated Heyd–Scuseria–Ernzerhof (HSE06) hybrid functional⁴¹ was also used for calculating the electronic structures. The spin–orbit coupling (SOC) effect⁴² was also taken into account in the band structure computations, because of the presence of heavy elements in the 2D alkali metal indium phosphorus trichalcogenides. The Device Studio program provides a number of functions for performing visualization, modeling, and simulation.⁴³

The calculations of the quasiparticle and optical absorption properties were carried out using rigorous many-body perturbation theory (MBPT) implemented by the BerkeleyGW package.⁴⁴ For the calculations implemented in the Quantum Espresso code,^45,46 the SG15 optimized norm-conserving Vanderbilt (ONCV) pseudopotentials⁴⁷ were used, and the KS states were obtained by solving the Kohn–Sham equations using the PBE exchange-correlation functional. The Coulomb interaction was truncated in the out-of-plane direction. After careful convergence tests (Fig. S6 (ESI†)),⁴⁸ the kinetic cutoff energy of the plane waves was set as 55 Ry and the Coulomb cutoff in the GW calculations was set as 20 Ry. The number of empty bands was set as 1300 to ensure bandgap convergence within 0.05 eV. A coarse k-mesh of 10 × 10 × 1 was used to perform the mean-field calculations, and a fine k-mesh of 20 × 20 × 1 was used for the Bethe–Salpeter equation (BSE) calculation. The degeneracy-allowed 16 highest valence bands and 16 lowest conduction bands were incorporated during the BSE calculations. The GW approximation in conjunction with the BSE was adopted to calculate the absorption coefficients through the following equation:

3 Results and discussion

3.1 Geometric structure and stability

The atomic structure of 2D metal phosphorus trichalcogenide monolayers is shown in Fig. 1. The general formula for these monolayers can be expressed as AM^IM^IIIP₂X₃Y₃, with the alkali metal AM^I = Li, Na, K, Rb, or Cs, M^III = In or Bi, and the chalcogen X/Y = O, S, Se, or Te. The laminar form of these materials comes about because they contain (PX₃) anions that assemble with their P–P bonds aligned like a bed of nails that is then covered by two parallel sheets of X/Y atoms. Between the sheets, the alkali metal and In/Bi atoms embed into nominally octahedral holes formed between the X/Y atoms of different anions. A total of 55 new materials were constructed, their crystal structures were thoroughly optimized, and the phonon spectra and phonon density of states were calculated along the high-symmetry direction of the hexagonal Brillouin zone using the finite displacement method, as shown in Fig. S1 (ESI†). The negative phonon density of states of the 2D AMBiP₂X₃Y₃ and AMInP₂X₃O₃ monolayers indicate that they are kinetically unstable. Also, the apparent virtual phonon mode at the Γ point of the LiInP₂Te₆ monolayer shows that this is dynamically unstable. Except for a small patch of negative frequencies near the Γ point in the phonon spectra of the remaining AMInP₂X₃Y₃ monolayers, no imaginary frequency traces were observed in their Brillouin zones, indicating the dynamic stability of these monolayers.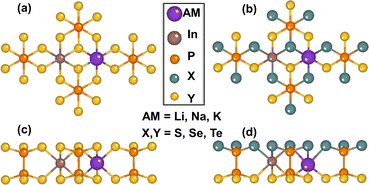

Fig. 1 Top and side views of pristine monolayers ((a) and (c)) and Janus monolayers ((b) and (d)) of alkali metal phosphorous trichalcogenides AMInP₂X₃Y₃.

To further evaluate the stability of the 2D AMInP₂X₃Y₃ monolayers and the possibility of experimental synthesis, we calculated their cohesive energies E_coh and formation energies E_f as follows:

where E_AMInP2X3Y3, E_AM, E_In, E_P, E_X, and E_Y are the total energy and the energies of isolated AM, In, P, X, and Y atoms, respectively, μ_AM, μ_In, μ_P, μ_X, and μ_Y are the chemical potentials of the atoms in their bulk crystals, and the number 10 in the denominator represents the total number of atoms. The negative formation energies and the high value of the cohesive energy suggest that the resulting compounds are energetically stable. As shown in Table S2 (ESI†), the cohesive energies of AMInP₂X₃Y₃ lie in the range 2.64–3.55 eV and are thus comparable to those of the synthesized 2D materials LiInP₂Se₆ (3.16 eV),³² silicene (3.94 eV),⁴⁹ and phosphorene (3.48 eV).⁵⁰ In addition, all monolayers have negative energies, which confirms their high stability and the possibility of experimental synthesis.

The elastic constants of 2D AMInP₂X₃Y₃ monolayers were also computed to enable examination of their mechanical stability. Table S2 (ESI†) displays the calculated results for these elastic constants, which satisfy the Born elastic stability criteria⁵¹: C₁₁C₂₂−C²₁₂ > 0 and C₆₆ > 0 for 2D trigonal materials, suggesting the mechanical stability of these monolayers. Compared with most previously studied 2D materials, 2D AMInP₂X₃Y₃ monolayers show excellent flexibility, with in-plane stiffness in the range 4.26–49.50 N m⁻¹ (Table S2 (ESI†)), which is lower than those of metal phosphorus trichalcogenides (MPX₃, 60–120 N m⁻¹),⁵² h-BN (271 N m⁻¹),⁵³ borophene (398 N m⁻¹),⁵⁴ graphene (350 N m⁻¹),⁵⁵ and Ti₃C₂T_x (326 N m⁻¹).⁵⁶ The lower the value of Young's modulus of a material, the more flexible is that material. The stability of material under shear deformation is determined by Poisson's ratio v. When v is between −1.0 and 0.50, the material is relatively stable.⁵⁷ The larger the value of v, the greater the plasticity of the material. As shown in Table S2 (ESI†), Poisson's ratio v of AMInP₂X₃Y₃ monolayers ranges from 0.26 to 0.45, except for KInP₂Te₆ (0.53) and KInP₂Te₃S₃ (0.93), which are in the range of −1.0 to 0.5. Therefore, these AMInP₂X₃Y₃ monolayers are stable and elastic materials. We also explored their orientation-dependent Young's modulus Y(θ) and Poisson's ratio υ(θ), which are plotted as functions of angle in Fig. S2 (ESI†). The 2D AMInP₂X₃Y₃ monolayers are isotropic with identical Young's modulus Y(θ) and Poisson's ratio υ(θ).

3.2 Electronic properties

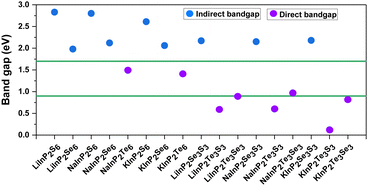
After investigating the stability and feasibility of experimental synthesis of 2D AMInP₂X₃Y₃ monolayers, we went on to explore the electronic properties of these materials. The band structures were evaluated at the HSE06 level with or without the SOC effect as shown in Fig. S3 (ESI†). We noticed that the SOC effect not only changes the band gap but also alters the band edge position of the studied materials due to the presence of heavy elements, which will inevitably affect the application of these materials in solar energy conversion. The AMInP₂X₃Y₃ monolayers are indirect bandgap semiconductors, except for the 2D NaInP₂Te₆, KInP₂Te₆, AMInP₂Te₃S₃, and AMInP₂Te₃Se₃ monolayers (all of whose conduction band minima (CBM) and valence band maxima (VBM) are located in Γ). Among the direct bandgap materials, NaInP₂Te₆, KInP₂Te₆, LiInP₂Te₃Se₃, NaInP₂Te₃Se₃, and KInP₂Te₃Se₃ monolayers have a bandgap of 0.88–1.49 eV (Fig. 2), which is consistent with the ideal bandgap of 1.0–1.7 eV for the best light absorption properties of conventional single-crystal-based p–n junction solar cells,⁵⁸ indicating that these five materials are potential donor materials for heterojunction solar cells.

Fig. 2 Bandgaps of 2D alkali metal phosphorous trichalcogenide AMInP₂X₃Y₃ monolayers at the HSE06 level, taking account of spin–orbit coupling. The blue circles represent the indirect bandgap and the purple circles the direct bandgap. The green lines represents the ideal bandgap of 0.9–1.7 eV for the best light absorption properties.

The bandgaps of 2D LiInP₂X₆, NaInP₂X₆, KInP₂Te₆, AMInP₂Se₃S₃ monolayers lie in the range 1.41–2.83 eV, which means that these materials may be suitable as photocatalysts for water splitting. To assess this possibility, we further aligned the band edge positions of these materials with vacuum level corrections and compared them with the potentials for the hydrogen reduction (−4.44 eV) and water oxidation (−5.67 eV) reactions. As shown in Fig. S4 (ESI†), the electrostatic potential difference in Janus AMInP₂Se₃S₃ monolayers is particularly small, and so we ignore the effect of the electrostatic potential difference on the position of the band edges in these materials. Except for the 2D NaInP₂Se₃S₃, KInP₂S₆, KInP₂Se₆, and KInP₂Se₃S₃ monolayers, the VBM and CBM of the remaining potential photocatalysts span the oxidation (O₂/H₂O) and reduction (H⁺/H₂) potentials of water at pH = 0, fulfilling the thermodynamic requirements for overall water splitting (see Fig. S5 (ESI†)).

3.3 Optical properties

To investigate the light-harvesting ability of the 2D AMInP₂X₃Y₃ monolayers, we calculated the optical absorption spectra along the in-plane (XY) direction using the G₀W₀ + BSE method, which includes the electron–hole interaction. As shown in Fig. 3, an increase in the atomic number of the chalcogen element induced a redshift of the absorption edge for the AMInP2X6 monolayers. The absorption peaks of the 2D AMInP₂S₆ monolayers lie in the ultraviolet (UV) region because of their large bandgap. The 2D AMInP₂Se₆ (blue lines) and AMInP₂Te₆ (yellow lines) monolayers exhibit remarkably high absorbance coefficients (exceeding 10⁵ cm⁻¹) in the visible and UV regions of the spectrum, which are higher than that of the well-known 2D photocatalyst g-C₃N₄.⁵⁹ The absorption edge of the LiInP₂Se₃S₃ monolayer (red line) is redshifted with respect to that of the LiInP₂S₆ and LiInP₂Se₆ monolayers, indicating a wider range of light absorption in the visible region. The AMInP₂Te₃Se₃ monolayers (green lines) exhibit remarkably high absorbance coefficients (10⁵ cm⁻¹) within broadband (ranging from infrared to ultraviolet). Therefore, their broad absorption ranges and large absorbance coefficients make the 2D AMInP₂X₃Y₃ monolayers potential materials for photovoltaic solar cells and photocatalysts.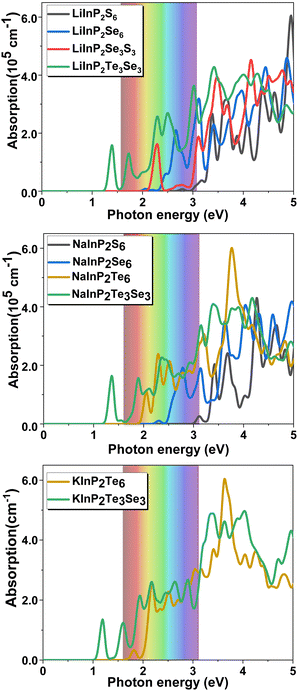

Fig. 3 Absorbance of AMInP₂X₃Y₃ monolayers computed using the G₀W₀ + BSE method for the light incidence in-plane (XY) direction. The iridescent colors mark the visible spectrum.

3.4 2D heterojunction solar cells

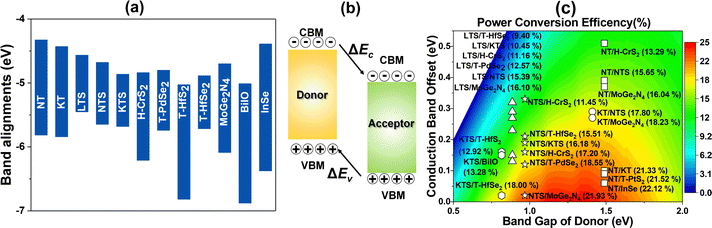
The appropriate bandgap and good solar light-harvesting capability make the 2D NaInP₂Te₆ (NT), KInP₂Te₆ (KT), and AMInP₂Te₃Se₃ (LTS, NTS, and KTS) monolayers promising solar cell donor materials. Nevertheless, these potential donor materials need to pair with suitable acceptor materials to build the high-performing heterojunction solar cells, where we adopted a three-step screening procedure. We first selected 37 2D semiconductors with appropriate band gap and band edge positions that can potentially form type II heterojunctions with these potential donor materials at the HSE06 level through literature survey^{5,6,15,60–62} and 2D materials database⁶³ searching. Then the band structures of these screened semiconductors were recalculated at the HSE06 + SOC level and aligned according to the vacuum level. To achieve high PCE, the conduction band offset (CBO) between the donor and the acceptor should be as small as possible to suppress the energy loss. Finally, based on the low CBO (< 0.4 eV) criteria, 2D H-CrS₂,⁵ T-PdSe₂,⁵ T-HfS₂,⁵ T-HfSe₂,⁵ MoGe₂N₄,⁶⁰ BiIO,⁶ and InSe⁶¹ monolayers were chosen as proper acceptor materials to construct the heterojunction solar cells with these potential donor materials. The CBM and VBM positions of individual monolayers calculated at the HSE06 + SOC level are shown in Fig. 4(a). 23 type II heterojunctions with less than 0.9% lattice mismatch (Table S3 (ESI†)) were constructed, which allow their lattices can form a coherent interface with continuous crystalline arrangements without significant strain, irreversible deformation, and defects.⁶⁴ As summarized in Table S3 (ESI†), the negative binding energy indicates the exothermicity and high feasibility of constructing heterojunctions from these two groups of materials. To obtain deep insight into their band alignment, a model of charge transfer in the proposed solar-cell device is illustrated schematically in Fig. 4(b). Encouragingly, the conduction band offset of NT/InSe, LTS/NTS, NTS/MoGe₂N₄, and KTS/T-HfSe₂ heterostructures are calculated as 62 meV, 0.11 eV, 21 meV and 24 meV, implying their high PCE.

Fig. 4 (a) Band alignments of 2D NaInP₂Te₆ (NT), KInP₂Te₆ (KT), and AMInP₂Te₃Se₃ (LTS, NTS, and KTS) compared with those of other 2D materials (H-CrS₂, T-PdSe₂, T-HfSe₂ and so on) at the HSE06 level with account taken of spin–orbit coupling. The upper and lower edges of the bars show the CBM and the VBM positions relative to the vacuum. (b) Schematic of type II donor–acceptor band alignments, where ΔE_c and ΔE_v are the conduction and valence band offsets, respectively. (c) Computed exciton solar energy efficiency contours as a function of the conduction band offset (CBO) and donor bandgap E_g of the designed vdW heterostructures. Squares, circles, triangles, stars, and hexagons represent heterojunctions composed of NT, KT, LTS, NTS, and KTS monolayers as the donor material, respectively. The heterostructures are labeled in the form “donor/acceptor”.

According to Bernardi and Scharber,¹⁶ the PCE of an excitonic solar cell is given by

Here, β_FF is the electrical fill factor, with a value of 0.65 deduced from the Shockley–Queisser limit,⁶⁵J_SC is the short–circuit current, which is given by an integral in the limit of external quantum efficiency of 100%, V_OC is an estimate of the maximum open-circuit voltage, and P_solar is the incident solar radiation, which can be obtained by integrating the AM1.5 solar energy flux:

V_OC = E_g − ΔE_c − 0.3

where P(ħω) is the AM 1.5 solar energy flux at a photon energy of ħω, E_g is the bandgap of the donor segment, and ΔE_c the conduction band offset between the donor and acceptor materials.

As donor materials, the bandgaps of the 2D NT, KT, LTS, NTS, and KTS monolayers are in the range of 0.82–1.49 eV and are thus suitable for absorbing the solar spectrum. The PCE also depends critically on the band alignment between donor and acceptor materials. The lower the CBO, the higher the energy conversion efficiency. The PCEs of the 23 type II heterostructures were estimated, and the results are summarized in Fig. 4(c) and Table S3 (ESI†). As shown in Fig. 4(c), the PCEs of the 23 heterostructures are in the range of 9.40–22.12% and are thus larger than the best value (about 9%) of existing XSCs.²¹ We can identify 15 heterostructures with PCEs larger than or equal to 15%. Furthermore, four of these have PCEs higher than 20%. The PCEs of the NT/InSe, KT/MoGe₂N₄, NTS/MoGe₂N₄, and KTS/T-HfSe₂ XSCs are calculated as 22.12%, 18.23%, 21.93%, and 18.00%, respectively, all of which are higher than the best-certified efficiencies of organic solar cells (13%),^12,13 ternary polymer solar cells (PM6:PDHP-Th: Y6 ternary PSCs, 16.8%),⁶⁶ and dye-sensitized solar cells (12%),²¹ and competitive with the theoretical values of most other 2D heterostructures (e.g., g-SiC₂ based systems (12–20%),⁶⁷ ZrS₃/HfS₃ (16–18%),²⁵ MoS₂/phosphorene (17.5%),^24,68 GeSe/SnS (18%),⁶⁹ In₂STe/Al₂ SSe (21.41%),⁹ boron pnictide/MoSSe (22.97%),²⁸ Janus TMDs based XSCs (15–23%)^14,70 and of perovskite solar cells (22.1%)⁷¹). Moreover, we also calculated the PCE for these heterojunction solar cells by excluding the SOC effect for comparison as presented in Table S3 (ESI†). As we can see, the PCE is quite different with or without the SOC effect, indicating the SOC effect indeed has a huge influence on the photovoltaic performance of the studied heterojunction solar cells as we mentioned above. Our results suggest that it is crucial to consider the SOC effect for the investigation of solar cells based on materials with heavy elements.

3.5 Photocatalytic water splitting

To explore the photocatalytic water splitting reactions over AMInP₂X₆ and LiInP₂Se₃Se₃ monolayers, we calculated the free energy of oxygen evolution reactions (OERs) (Fig. S7 (ESI†)) and hydrogen evolution reactions (HERs) (Fig. S8 (ESI†)). In the absence of any light irradiation (U = 0) at pH = 0–3 (black line), the free energy change of the OER is always uphill (endothermic), implying that the water oxidation half-reaction cannot proceed spontaneously. The ΔG_i values of all these proposed materials decrease greatly under illumination, but still require the assistance of an external potential (green line). Interestingly, the ΔG_i (blue lines) of the LiInP₂S₆ and NaInP₂S₆ monolayers are all negative under light irradiation (Fig. S7 (ESI†)). We next explored the performance of the AMInP₂X₆ and LiInP₂Se₃Se₃ monolayers in the HERs. The external potential provided by photogenerated electrons from the AMInP₂X₆ and LiInP₂Se₃Se₃ monolayers is between 0.02 V and 0.23 V at pH = 0. As shown in Fig. S8 (ESI†), the ΔG_H values of the AMInP₂X₆ and LiInP₂Se₃Se₃ monolayers at pH = 0 in the absence of light irradiation are in the range 0.53–1.71 eV, far exceeding the potentials that these monolayers could provide. This means that the AMInP₂X₆ and LiInP₂Se₃Se₃ monolayers are inert to HERs, similar to some other 2D materials, including MoS₂,⁷² MoSe₂,⁷³ AgBiP₂Se₆,⁷⁴ and MnPS₃²⁹ monolayers. To estimate solar energy utilization for photocatalytic water splitting, we examined the STH efficiency to evaluate the energy conversion efficiencies of the AMInP₂X₆ and LiInP₂Se₃Se₃ monolayers, based on the results of the band alignments above (Table 1). It is worth noting that the η_STH of the remaining potential photocatalysts all meet the critical value (>10%) for economical production of hydrogen from photocatalytic water splitting and are larger than that for the reported similar AgBiP₂Se₆ (10.3%).⁷⁴ In particular, the STH efficiencies of the NaInP₂Te₆ (∼19%) and KInP₂Te₆ (∼19%) monolayers exceed the traditional theoretical limit (∼18%),⁷⁵ owing to their smaller bandgaps (1.49 eV and 1.41 eV), respectively.

Table 1 Calculated χ(H₂) and χ(O₂), energy conversion efficiency of light absorption (η_abs), carrier utilization (η_cu), and STH (η_STH) of AMInP₂X₆ and LiInP₂Se₃Se₃ monolayers

Material	χ(H2) (eV)	χ(O2) (eV)	η abs (%)	η cu (%)	η STH (%)
LiInP2S6	0.23	1.37	14	38	5
LiInP2Se6	0.09	0.67	42	41	17
NaInP2S6	0.13	1.44	14	34	5
NaInP2Se6	0.07	0.82	35	36	13
NaInP2Te6	0.11	0.15	66	28	19
KInP2Te6	0.01	0.17	60	31	19
LiInP2Se3S3	0.18	0.78	34	45	15

---

4 Conclusions

On the basis of first-principles calculations, we have proposed the 2D alkali metal indium phosphorus trichalcogenides AMInP₂X₃Y₃ monolayers for efficient solar energy conversion applications. We have systematically explored the stability, optoelectronic, photocatalytic, and photovoltaic properties of these monolayers, all of which have been found to have good thermodynamic, kinetic, and mechanical stabilities. The pronounced light absorption ability of these monolayers makes them suitable for energy conversion devices. The 2D LiInP₂S₆, LiInP₂Se₆, LiInP₂Se₃S₃, NaInP₂S₆, NaInP₂Se₆, NaInP₂Te₆, and KInP₂Te₆ monolayers can be considered as potential candidates for photocatalytic water splitting, since they have appropriate bandgaps, efficient optical absorption under visible-light irradiation, and appropriate band edge positions to meet the requirements of the reduction and oxidation levels. In addition, the NT, KT, LTS, NTS, and KTS monolayers are characterized by moderate bandgaps in the range 0.82–1.49 eV and are therefore suitable donor materials for constructing heterostructures as excitonic solar cells. We have identified 15 heterostructures with PCE > 15% as promising for use in ultrathin high-PCE excitonic solar cells. The PCEs of the NT/InSe, KT/MoGe₂N₄, LTS/NTS, NTS/MoGe₂N₄, and KTS/T-HfSe₂ heterostructures are calculated as 22.12%, 18.23%, 16.80%, 21.93%, and 18.00%, respectively. The calculations presented here provide a basis for further developments in nanoscale solar energy conversion using 2D AMInP₂X₃Y₃ monolayers.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (Grant No. 12022408). We gratefully acknowledge HZWTECH for providing computation facilities. This paper is dedicated to the 70th anniversary of the physics of Jilin University.

References

1. D. M. Chapin, C. S. Fuller and G. L. Pearson, J. Appl. Phys., 1954, 25, 676–677.
2. D. Ginley, M. A. Green and R. Collins, MRS Bull., 2011, 33, 355–364.
3. C. Battaglia, A. Cuevas and S. De Wolf, Energy Environ. Sci., 2016, 9, 1552–1576.
4. L. C. Andreani, A. Bozzola, P. Kowalczewski, M. Liscidini and L. Redorici, Adv. Phys.: X, 2018, 4, 126–148.
5. J. Linghu, T. Yang, Y. Luo, M. Yang, J. Zhou, L. Shen and Y. P. Feng, ACS Appl. Mater. Interfaces, 2018, 10, 32142–32150.
6. Y. Liang, Y. Dai, Y. Ma, L. Ju, W. Wei and B. Huang, J. Mater. Chem. A, 2018, 6, 2073–2080.
7. M. Jakhar and A. Kumar, J. Mater. Chem. A, 2022, 10, 6785–6795.
8. C. Wang, Y. Jing, X. C. Zhou and Y. F. Li, ACS Omega, 2021, 6, 20590–20597.
9. B. Sa, R. Hu, Z. Zheng, R. Xiong, Y. Zhang, C. Wen, J. Zhou and Z. Sun, Chem. Mater., 2022, 34, 6687–6701.
10. Y. Chen, B. Jia, X. Guan, L. Han, L. Wu, P. Guan and P. Lu, Appl. Surf. Sci., 2022, 586, 152799.
11. J. W. Gong, K. Sumathy, Q. Q. Qiao and Z. P. Zhou, Renewable Sustainable Energy Rev., 2017, 68, 234–246.
12. J. Zhao, Y. Li, G. Yang, K. Jiang, H. Lin, H. Ade, W. Ma and H. Yan, Nat. Energy, 2016, 1, 1–7.
13. W. Zhao, S. Li, H. Yao, S. Zhang, Y. Zhang, B. Yang and J. Hou, J. Am. Chem. Soc., 2017, 139, 7148–7151.
14. A. Rawat, M. K. Mohanta, N. Jena, Dimple, R. Ahammed and A. D. Sarkar, J. Phys. Chem. C, 2020, 124, 10385–10397.
15. R. Ahammed, A. Rawat, N. Jena, Dimple, M. K. Mohanta and A. D. Sarkar, Appl. Surf. Sci., 2020, 499, 143894.
16. M. C. Scharber, D. Mühlbacher, M. Koppe, P. Denk, C. Waldauf, A. J. Heeger and C. J. Brabec, Adv. Mater., 2006, 18, 789–794.
17. K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666–668.
18. J. Dai and X. C. Zeng, Angew. Chem., Int. Ed., 2015, 54, 7572–7576.
19. L. Britnell, R. M. Ribeiro, A. Eckmann, R. Jalil, B. D. Belle, A. Mishchenko, Y. J. Kim, R. V. Gorbachev, T. Georgiou, S. V. Morozov, A. N. Grigorenko, A. K. Geim, C. Casiraghi, A. H. Castro Neto and K. S. Novoselov, Science, 2013, 340, 1311–1314.
20. M.-L. Tsai, S.-H. Su, J.-K. Chang, D.-S. Tsai, C.-H. Chen, C.-I. Wu, L.-J. Li, L.-J. Chen and J.-H. He, ACS Nano, 2014, 8, 8317–8322.
21. M. A. Green, K. Emery, Y. Hishikawa, W. Warta and E. D. Dunlop, Prog. Photovoltaics: Res. Appl., 2015, 23, 1–9.
22. M. Bernardi, M. Palummo and J. C. Grossman, Nano Lett., 2013, 13, 3664–3670.
23. V. Dheivanayagam, J. J. Linghu, C. Zhang, Y. P. Feng and L. Shen, Appl. Phys. Lett., 2016, 108, 122105.
24. J. Dai and X. C. Zeng, J. Phys. Chem. Lett., 2014, 5, 1289–1293.
25. Q. Zhao, Y. Guo, Y. Zhou, Z. Yao, Z. Ren, J. Bai and X. Xu, Nanoscale, 2018, 10, 3547–3555.
26. A. Rawat, R. A. Dimple, N. Jena, M. K. Mohanta and A. De Sarkar, J. Phys. Chem. C, 2019, 123, 12666–12675.
27. M. Xie, S. Zhang, B. Cai, Y. Huang, Y. Zou, B. Guo, Y. Gu and H. Zeng, Nano Energy, 2016, 28, 433–439.
28. M. K. Mohanta and A. De Sarkar, Nanoscale, 2020, 12, 22645–22657.
29. X. Zhang, X. Zhao, D. Wu, Y. Jing and Z. Zhou, Adv. Sci., 2016, 3, 1600062.
30. L. H. Zhang, X. Y. Guo and S. P. Huang, Int. J. Hydrogen Energy, 2021, 46, 26950–26960.
31. D. Zhang and B. Zhou, RSC Adv., 2022, 12, 13765–13773.
32. D. G. Chica, Y. He, K. M. McCall, D. Y. Chung, R. O. Pak, G. Trimarchi, Z. Liu, P. M. De Lurgio, B. W. Wessels and M. G. Kanatzidis, Nature, 2020, 577, 346–349.
33. J. Liu, X. B. Li, D. Wang, W. M. Lau, P. Peng and L. M. Liu, J. Chem. Phys., 2014, 140, 054707.
34. F. M. Wang, T. A. Shifa, P. Yu, P. He, Y. Liu, F. Wang, Z. X. Wang, X. Y. Zhan, X. D. Lou, F. Xia and J. He, Adv. Funct. Mater., 2018, 28, 1802151.
35. B. Y. Tong and L. J. Sham, Phys. Rev., 1966, 144, 1–4.
36. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
37. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561.
38. A. Togo and I. Tanaka, Scr. Mater., 2015, 108, 1–5.
39. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192.
40. S. Grimme, J. Comput. Chem., 2004, 25, 1463–1473.
41. J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215.
42. N. J. Turro, G. Kavarnos, V. Fung, A. L. Lyons and T. Cole, J. Am. Chem. Soc., 1972, 94, 1392–1394.
43. Hongzhiwei Technology, Device Studio; Version 2021A, China, 2021. Available online: https://iresearch.net.cn/cloudSoftware.
44. J. Deslippe, G. Samsonidze, D. A. Strubbe, M. Jain, M. L. Cohen and S. G. Louie, Comput. Phys. Commun., 2012, 183, 1269–1289.
45. P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502.
46. P. Giannozzi, O. Andreussi, T. Brumme, O. Bunau, M. Buongiorno Nardelli, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, M. Cococcioni, N. Colonna, I. Carnimeo, A. Dal Corso, S. de Gironcoli, P. Delugas, R. A. DiStasio Jr, A. Ferretti, A. Floris, G. Fratesi, G. Fugallo, R. Gebauer, U. Gerstmann, F. Giustino, T. Gorni, J. Jia, M. Kawamura, H. Y. Ko, A. Kokalj, E. Kucukbenli, M. Lazzeri, M. Marsili, N. Marzari, F. Mauri, N. L. Nguyen, H. V. Nguyen, A. Otero-de-la Roza, L. Paulatto, S. Ponce, D. Rocca, R. Sabatini, B. Santra, M. Schlipf, A. P. Seitsonen, A. Smogunov, I. Timrov, T. Thonhauser, P. Umari, N. Vast, X. Wu and S. Baroni, J. Phys.: Condens. Matter, 2017, 29, 465901.
47. D. R. Hamann, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 085117.
48. D. Y. Qiu, F. H. da Jornada and S. G. Louie, Phys. Rev. B, 2016, 93, 235435.
49. S. Cahangirov, V. O. Özçelik, L. Xian, J. Avila, S. Cho, M. C. Asensio, S. Ciraci and A. Rubio, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 035448.
50. V. Vierimaa, A. V. Krasheninnikov and H. P. Komsa, Nanoscale, 2016, 8, 7949–7957.
51. F. Mouhat and F.-X. Coudert, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 224104.
52. Z. Cheng, T. A. Shifa, F. Wang, Y. Gao, P. He, K. Zhang, C. Jiang, Q. Liu and J. He, Adv. Mater., 2018, 30, 1707433.
53. R. C. Andrew, R. E. Mapasha, A. M. Ukpong and N. Chetty, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 125428.
54. A. J. Mannix, X. F. Zhou, B. Kiraly, J. D. Wood, D. Alducin, B. D. Myers, X. L. Liu, B. L. Fisher, U. Santiago, J. R. Guest, M. J. Yacaman, A. Ponce, A. R. Oganov, M. C. Hersam and N. P. Guisinger, Science, 2015, 350, 1513–1516.
55. C. Lee, X. Wei, J. W. Kysar and J. Hone, Science, 2008, 321, 385–388.
56. A. Lipatov, H. D. Lu, M. Alhabeb, B. Anasori, A. Gruverman, Y. Gogotsi and A. Sinitskii, Sci. Adv., 2018, 4, eaat0491.
57. G. N. Greaves, A. L. Greer, R. S. Lakes and T. Rouxel, Nat. Mater., 2011, 10, 823–837.
58. J. J. Loferski, J. Appl. Phys., 1956, 27, 777–784.
59. X. Ma, Y. Lv, J. Xu, Y. Liu, R. Zhang and Y. Zhu, J. Phys. Chem. C, 2012, 116, 23485–23493.
60. C. C. Tho, C. Yu, Q. Tang, Q. Wang, T. Su, Z. Feng, Q. Wu, C. V. Nguyen, W.-L. Ong, S.-J. Liang, S.-D. Guo, L. Cao, S. Zhang, S. A. Yang, L. K. Ang, G. Wang and Y. S. Ang, arXiv:2206.11765, 2022.
61. Y. Yan, S. Li, J. Du, H. Yang, X. Wang, X. Song, L. Li, X. Li, C. Xia, Y. Liu, J. Li and Z. Wei, Adv. Sci., 2021, 8, 1903252.
62. M. Jakhar, A. Kumar, P. K. Ahluwalia, K. Tankeshwar and R. Pandey, Materials, 2022, 15, 2221.
63. M. N. Gjerding, A. Taghizadeh, A. Rasmussen, S. Ali, F. Bertoldo, T. Deilmann, N. R. Knøsgaard, M. Kruse, A. H. Larsen, S. Manti, T. G. Pedersen, U. Petralanda, T. Skovhus, M. K. Svendsen, J. J. Mortensen, T. Olsen and K. S. Thygesen, 2D Mater., 2021, 8, 044002.
64. P. A. Gabrys, S. E. Seo, M. X. Wang, E. Oh, R. J. Macfarlane and C. A. Mirkin, Nano Lett., 2018, 18, 579–585.
65. Y. L. Xu, T. Gong and J. N. Munday, Sci. Rep., 2015, 5, 13536.
66. J. H. Han, X. C. Wang, D. Huang, C. M. Yang, R. Q. Yang and X. C. Bao, Macromolecules, 2020, 53, 6619–6629.
67. L. J. Zhou, Y. F. Zhang and L. M. Wu, Nano Lett., 2013, 13, 5431–5436.
68. H. Guo, N. Lu, J. Dai, X. Wu and X. C. Zeng, J. Phys. Chem. C, 2014, 118, 14051–14059.
69. Y. Mao, C. Xu, J. Yuan and H. Zhao, J. Mater. Chem. A, 2019, 7, 11265–11271.
70. M. Bikerouin and M. Balli, Appl. Surf. Sci., 2022, 598, 153835.
71. M. A. Green and A. Ho-Baillie, ACS Energy Lett., 2017, 2, 822–830.
72. C. Tsai, H. Li, S. Park, J. Park, H. S. Han, J. K. Norskov, X. Zheng and F. Abild-Pedersen, Nat. Commun., 2017, 8, 15113.
73. H. Shu, D. Zhou, F. Li, D. Cao and X. Chen, ACS Appl. Mater. Interfaces, 2017, 9, 42688–42698.
74. L. Ju, J. Shang, X. Tang and L. Z. Kou, J. Am. Chem. Soc., 2020, 142, 1492–1500.
75. C. F. Fu, J. Sun, Q. Luo, X. Li, W. Hu and J. Yang, Nano Lett., 2018, 18, 6312–6317.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2ma00937d

---