Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Fabrication of doped ferrites and exploration of their structure and magnetic behavior
Reda E.
El-Shater
a,
Hassan
El Shimy
bc,
Samia A.
Saafan
a,
Moustafa A.
Darwish
a,
Di
Zhou
d,
Kadiyala Chandra Babu
Naidu
e,
Mayeen U.
Khandaker
fg,
Z.
Mahmoud
h,
Alex V.
Trukhanov
 ij,
Sergei V.
Trukhanov
ij,
Sergei V.
Trukhanov
 *ij and
Fatma
Fakhry
a
*ij and
Fatma
Fakhry
a
aPhysics Department, Faculty of Science, Tanta University, Tanta 31527, Egypt
bPhysics Department, Faculty of Science, Ain Shams University, Cairo 11566, Egypt
cPhysics Department, Faculty of Advanced Basic Science, Galala University, New Galala City 43511, Egypt
dElectronic Materials Research Laboratory, Key Laboratory of the Ministry of Education & International Center for Dielectric Research, School of Electronic Science and Engineering, Xi’an Jiaotong University, Xi'an 710049, Shannxi, China
eGitam School of Science, Gitam Deemed to be University Bangalore Campus, Karnataka 562163, India
fCentre for Applied Physics and Radiation Technologies, School of Engineering and Technology, Sunway University, Bandar Sunway, 47500, Selangor, Malaysia
gDepartment of General Educational Development, Faculty of Science and Information Technology, Daffodil International University, DIU Rd, Dhaka 1341, Bangladesh
hDepartment of Physics, College of Sciences, King Khalid University, P.O. Box 9004, Abha, Saudi Arabia
iSmart Sensors Laboratory, Department of Electronic Materials Technology, National University of Science and Technology MISiS, Leninski ave., 4, 119049, Moscow, Russia. E-mail: s.v.trukhanov@gmail.com
jLaboratory of Magnetic Films Physics, SSPA “Scientific and Practical Materials Research Centre of NAS of Belarus”, 19, P. Brovki str., 220072, Minsk, Belarus
First published on 12th June 2023
Abstract
Manganese-doped MnxFe3−xO4 (x = 0.0, 0.2, 0.6, 0.8) spinel ferrites were produced via co-precipitation using the ethanolamine. XRD results confirmed the formation of the spinel phase. The well-crystallized particles of the ferrite spinel phase had linear sizes in the range of 5–9 nm. It was found that the lattice parameter increases gradually as the Mn concentration is increased. XPS data supported the presence of Mn3+ and Mn4+ in the nanosized crystallites. A large specific surface area of 124–143 m2 g−1 was calculated using HRTEM and BET. The spontaneous magnetization increases monotonically from ∼51 emu g−1 for x = 0.0 up to ∼106 emu g−1 for x = 0.8. By contrast, the remanent magnetization changed non-monotonically from ∼3 emu g−1 for x = 0.0 up to ∼11 emu g−1 for x = 0.8, with a local maximum of ∼7 emu g−1 for x = 0.2 and a local minimum of ∼3 emu g−1 for x = 0.6. The coercivity also changed non-monotonically from ∼4 Oe for x = 0.0 up to ∼9 Oe for x = 0.8, with a minimum of ∼1 Oe for x = 0.2. The ordered magnetic moments for each sub-lattice were computed. The large values of the specific surface area indicate that the samples are good candidates for chemical and biological applications. The FT-IR and Raman spectra obtained supported the Rietveld refinement of XRD without forming any impurity phases. With an increase in the Mn concentration, magnetic investigations indicated an enhancement in the magnetic parameters of the obtained nanostructured samples.
1. Introduction
Ferrite nanoparticles with a spinel structure1 have attracted the interest of many researchers due to their intriguing properties compared with bulk samples. The miniature sizes of nanosized particles have contributed to the development of theoretical concepts and the introduction of practical applications.2 Also, the small particle sizes have aided an understanding of many physical phenomena and processes that occur in complex iron oxides.3 Along with traditional applications, such as in microwave devices,4 transformer cores,5 solid-state gas sensors,6 high-frequency magnets,7 high-temperature catalysts,8 and targeted drug delivery,9,10 superparamagnetic nanoparticles of ferrite spinels are also promising for use as liquid fillers in heat transfer fluids,11 in magnetoviscous12 and magnetorheological fluids,13 for storing high-density information,14,15 and in devices with advanced intelligent technologies.16It should be noted that the low saturation magnetization values of nanometer particles limit their practical use. At the same time, the intriguing properties of nanosized ferrite spinel particles with superparamagnetic properties have attracted extensive interest in the design, synthesis, and use of such materials in many necessary applications.17–20 The antibacterial activity of ferrites obtained using plant extracts21–23 makes them excellent candidates for new applications, including water purification,24 as chip-sized nanolaboratories,25 in tissue engineering,26 hyperthermia treatment27 and medical supplies.28
Complex iron oxide with a spinel structure and its manganese-substituted derivatives represent an important direction in a variety of ferrites from the perspective of biomedical applications.29 Nanosized magnetite powder with manganese substitution has mainly been considered as a contrast agent in magnetic resonance imaging (MRI).30–32
Various methods33–38 have previously been used to obtain nanosized particles of Mn-doped spinel ferrite. The superparamagnetic behavior of ferromanganese spinels with nanosized (15–17 nm) particles was established via their S-shaped magnetization and the absence of magnetic hysteresis.39–41 A reduced value of saturation magnetization was also found in comparison with their bulk counterparts. It is interesting to note that the calculated magnetic particle size (Dm) is smaller than the crystallite size, as estimated from XRD results. This fact was explained by the presence of a dead magnetic layer on the nanoparticle surface.
Nanosized MnFe2O4 powders were obtained via the sol–gel autocombustion method.42 The phase of the normal ferrite spinel was identified. It was found that with an increase in the annealing temperature, the Fe3+ cations filling the octahedral sites are gradually reduced to Fe2+ cations. This was explained by the oxidation of Mn2+ cations to the Mn3+ state. In addition, nanosized MnFe2O4 powders were also obtained by Zhang et al.43 using the co-precipitation method. The effect of a surfactant (CTAB) on the particle size of these compositions was studied. The maximal saturation magnetization of 54.5 emu g−1 was observed.
In the current work, our activity was directed towards obtaining samples of ferrite spinel doped with manganese cations via organic co-precipitation. The method of synthesis using an organic base44 for the co-precipitation is one of the most optimal methods for obtaining superparamagnetic nanosized samples. This is due to its simplicity, better control over the morphology and size of the crystallites, mass use, economy, and time economy.45 Ethanolamine was used as the precipitating agent in the current work. The structure, morphology and magnetic properties of the obtained nanosized Mn-doped spinel ferrites were studied.
2. Experimental
2.1. Reagents and synthesis
Nanosized Mn-doped ferrite spinel samples (NMFSs; MnxFe3−xO4 (x = 0.0, 0.2, 0.6, 0.8)) were prepared using the co-precipitation organic base method with ethanolamine solution. First, 5 mM solutions of manganese chloride (MnCl2·4H2O; LOBA Chemie, LOT # L129411409) and ferrous chloride (FeCl2·4H2O; ALPHA CHEMIKA, Mumbai – 400 002 (INDIA)) with 0.5 mL (37 wt%) HCl and 2 mL water were added together and stirred thoroughly. Second, the 10 mM ferrous chloride FeCl3·6H2O (Sisco Research Laboratories Pvt. Ltd. 26, Navketan Mumbai 93, India) was dissolved in 20 mL water. These two solutions were combined and stirred at 50 °C. Thereafter, the resulting product was quickly diluted with 100 mL of 2.0 M ethanolamine (C2H7NO; ALPHA CHIMIKA S. No. AL9686) with mechanical mixing for ∼60 min. This obtained mixture was stirred for about 2 h at 90 °C and then cooled to room temperature (RT). The precipitate that formed was removed using a magnet and purified with distilled water before being dried in a drying chamber at 80 °C for 12 h.2.2. Measurements
Phase analysis and determination of the lattice parameters of the NMFSs at RT were performed via XRD using a PHILIPS® X’Pert diffractometer. The current–voltage characteristics of the copper tube were 40 kV and 30 mA. The Bragg angle was changed from 20° to 80° with a step size of 0.025° and a holding time of 4 s. The crystal structure parameters were determined using the Rietveld MAUD program.46,47 Reliability parameters such as Rb, Rwp and GOF were achieved in the intervals of 6.8–7.6%, 9.21–10.44% and 0.84–1.31, respectively. The LaB6 standard was used to evaluate the instrumental parameters. The experimental conditions established using the standard were maintained. Energy dispersive X-ray spectra (EDX; Hitachi S-4800) were used to determine the proportion of metal ions in the NMFSs.XPS spectra were obtained using an Ulvac-Phi QuanteraSXM instrument with Al-Kα radiation. The C–C hump at ∼284.8 eV was applied for charge correction. Fourier transform infrared spectra (Bruker FT-IR) were obtained at RT in the range of 200–2000 cm−1. The Raman spectra were fixed using a JASCO NRS-1000 microspectrometer with excitation radiation of ∼514.5 nm using a green argon laser. The specific surface area of the NMFSs was determined using a Brunauer–Emmett–Teller (BET) Micrometrics Instrument Corporation TriStar II 3020 V1.03 instrument. The grain size was determined using a high-resolution transmission electron microscope (HRTEM; JEOL-TEM-2100F) operated at a voltage of 200 kV.
Ferromagnetic resonance (FMR) investigations were realized using an X-band EMX spectrometer (Bruker, Germany), at the National Center of Radiation Research and Technology of Egypt (NCRRT). The spin moment values were computed using eqn (1):
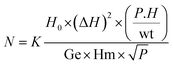 | (1) |
A lab-made vibrating sample magnetometer (VSM)48 of up to 8 kOe was used at RT to investigate the hysteresis loops49 for all the NMFSs.
3. Results and discussion
3.1. XRD investigation
Fig. 1(a–d) display the XRD patterns of the NMFSs with various x at RT. The form and positions of all the Bragg reflections are in good agreement with an earlier report50 for the cubic spinel structure with the Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group (ICDD number: 01-088-1965). The peak widening of the NMFSs suggests the nanometer sizes of the obtained powders. It should be recalled that the experimentally established ae unit cell parameter was computed using Rietveld analysis.51
m space group (ICDD number: 01-088-1965). The peak widening of the NMFSs suggests the nanometer sizes of the obtained powders. It should be recalled that the experimentally established ae unit cell parameter was computed using Rietveld analysis.51
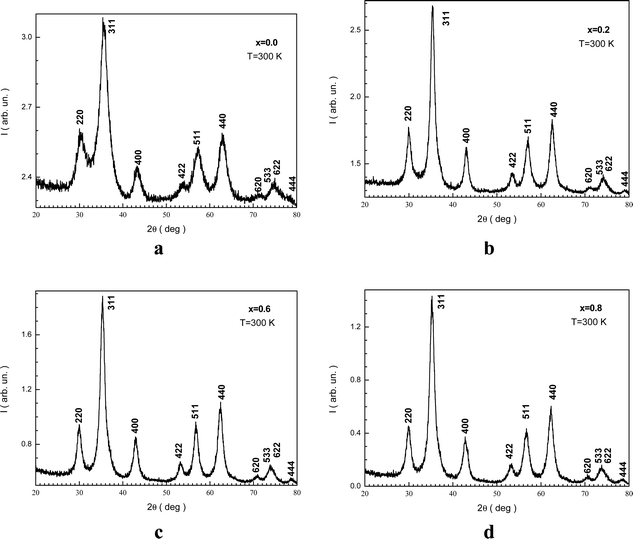 | ||
| Fig. 1 XRD patterns for the NMFSs with different Mn ion contents at RT: x = 0.0 (a), x = 0.2 (b), x = 0.6 (c), and x = 0.8 (d). | ||
Rietveld refinement of the XRD pattern for x = 0.0 is presented in Fig. 2. The reliability factors were Rb ≈ 7%, Rwp ≈ 10.44%, and GOF ≈ 0.84. These data will help to discuss latter the distribution of cations between different atomic positions. The ae unit cell parameters are summarized in Table 1. The ae magnification can be associated with the replacement of Fe3+ ions by Mn3+ ions.
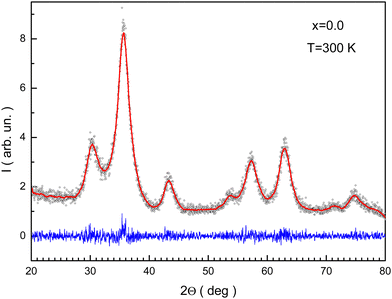 | ||
| Fig. 2 Rietveld processed XRD pattern for the NMFSs with x = 0.0. Symbols are experimental data, the red line shows the fitting curve, and the blue line shows the differences curve. | ||
| x | a e (Å) | R x (nm) | D x (g cm−3) | D e (g cm−3) | P e (%) | S x (m2 g−1) | S e (m2 g−1) | R e (nm) | ε × 10−4 | R b (%) | R wp (%) | GOF |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.0 | 8.373 | 5 | 5.237 | 2.987 | 42.9 | 238 | 143 | 14 | 6 | 6.8 | 9.21 | 0.89 |
| 0.2 | 8.380 | 10 | 5.223 | 2.872 | 45.0 | 117 | 127 | 17 | 13 | 7.6 | 10.02 | 1.21 |
| 0.6 | 8.414 | 9 | 5.152 | 2.634 | 48.8 | 133 | 124 | 18 | 16 | 7.3 | 10.12 | 1.31 |
| 0.8 | 8.427 | 9 | 5.122 | 2.517 | 50.8 | 137 | 130 | 18 | 23 | 7.1 | 10.44 | 0.84 |
The theoretical calculation of the unit cell parameter can be performed taking into account the radii of the Fe2+/3+/4+ and Mn2+/3+/4+ ions that occupy tetrahedral and octahedral positions in the spinel structure. Such charge configurations were obtained via XPS measurements (Section 3.5), which gave Fe2+, Fe3+, Fe4+, Mn3+ and Mn4+. A theoretical calculation of the at unit cell parameter using the high-spin state of these ions revealed that these values decrease with increasing Mn concentration. However, this behavior contradicts the experimental results. To solve this problem, a low-spin Fe2+ ion with a radius of 0.610 Å at the octahedral position and a high-spin Mn3+ ion with a radius of 0.645 Å in an octahedral position were used.52 The set of theoretically calculated at unit cell parameters with replacement by Mn is given in Table 2. The experimentally obtained value of the ae parameter is somewhat lower than the theoretically obtained value of at. This behavior agrees satisfactorily with the reasonable notion that at should be greater than ae, since at is calculated assuming that all the 96 ionic positions are occupied. This condition is not always met in practice. In contrast to this, ae is determined when all the crystallographic positions are actually occupied by various cations.53 In addition, Mn3+ ions tend to be located exclusively in A-positions. An increase in the x concentration of Mn3+ ions at the A-positions creates a certain disorder in the crystal lattice. This arrangement of Mn3+ ions pushes the smaller Fe3+ ions into the B-positions, increasing the radius of the A-position. This leads to an increase in ε deformation inside the crystal structure. A detailed full calculation of the specific value of the deformation of the crystal lattice of the spinel ferrite upon doping with manganese cations is a significant task, and such results will be presented in future work. The ε lattice strain is given in Table 1.
| x | γ | r t (nm) | r o (nm) | a t (nm) | u (Å) | θ 1 (°) | θ 2 (°) | θ 3 (°) | θ 4 (°) | θ 5 (°) |
|---|---|---|---|---|---|---|---|---|---|---|
| 0.0 | 0.00 | 0.0595 | 0.0595 | 0.8452 | 0.3822 | 123.02 | 143.35 | 93.49 | 126.11 | 73.49 |
| 0.2 | 0.20 | 0.0592 | 0.0592 | 0.8462 | 0.3817 | 123.18 | 144.04 | 93.24 | 126.05 | 73.91 |
| 0.6 | 0.36 | 0.0602 | 0.0593 | 0.8481 | 0.3796 | 123.84 | 147.05 | 92.21 | 125.82 | 75.74 |
| 0.8 | 0.48 | 0.0608 | 0.05926 | 0.8489 | 0.3791 | 124.00 | 147.81 | 91.97 | 125.77 | 76.19 |
The Rx XRD crystallite sizes were calculated using the Rietveld method. The Sx specific surface area of the NMFS crystallites was determined using the following equations:
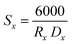 | (2) |
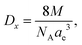 | (3) |
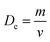 , where m is the mass and v is and the volume of the sample, which satisfactorily agreed with the fact that it is always lower than the Dx theoretical XRD density. This is observed because real crystals always contain defects in the form of vacancies.54 With an increase in the concentration of manganese, the difference between the theoretical Dx and experimental De densities increases, and with it, the porosity
, where m is the mass and v is and the volume of the sample, which satisfactorily agreed with the fact that it is always lower than the Dx theoretical XRD density. This is observed because real crystals always contain defects in the form of vacancies.54 With an increase in the concentration of manganese, the difference between the theoretical Dx and experimental De densities increases, and with it, the porosity 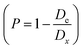 also increases. This is well demonstrated in Table 1. In addition, the increase in the Rx XRD crystallite size with increasing manganese concentration satisfactorily corresponds to the change in the experimentally determined ae unit cell parameter. The Rx XRD crystallite size varies within 5–10 nm. This behavior is generally recognized.55–58 A change in the size of the crystallites with an increase in the x concentration of manganese ions can be associated with the presence of defects in the crystal structure, including substitutional ones, and the resulting ε deformations are the cause of the dispersion of the Rx XRD crystallite size59 with an increase in the concentration of manganese.
also increases. This is well demonstrated in Table 1. In addition, the increase in the Rx XRD crystallite size with increasing manganese concentration satisfactorily corresponds to the change in the experimentally determined ae unit cell parameter. The Rx XRD crystallite size varies within 5–10 nm. This behavior is generally recognized.55–58 A change in the size of the crystallites with an increase in the x concentration of manganese ions can be associated with the presence of defects in the crystal structure, including substitutional ones, and the resulting ε deformations are the cause of the dispersion of the Rx XRD crystallite size59 with an increase in the concentration of manganese.
The part of Mn ions at the A-position used for calculations for the NMFSs is given in Table 2. Taking into account the distribution of ions over the sublattices, the rt tetrahedral position radius, the ro octahedral position radius, the rt0 tetrahedral position radius without substitution, the ro0 octahedral position radius without substitution, and the theoretical at unit cell parameter were computed using the following:
| rA = (x − p)rMn3+ + (1 − x + p)rFe3+ | (4) |
| rB = (p)rMn3+ + (1 − x)rFe2+ + (1 + x − p)rFe3+ | (5) |
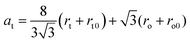 | (6) |
As is well known, the intensity of Fei+–O2−–Fei+ indirect superexchange interactions depends critically on structural parameters such as bond angles. In ferrite spinels, they are represented by the values θ1, θ2, θ3, θ4 and θ5. The intensity of the exchange is directly proportional to the bond angles, but inversely proportional to the bond lengths.62 To a first approximation, the exchange integral between the A–B positions depends on the bond angles θ1 and θ2, while between the A–A positions it depends on the bond angle θ5. The bond angles θ3 and θ4 determine the exchange integral between the B–B positions.63 An increase in the bond angles θ1, θ2 and θ5 leads to an increase in the A–B and A–A exchange interaction, while a decrease in the bond angles θ3 and θ4 leads to a weakening of the B–B exchange interaction. The low concentration of Mn ions did not cause any significant migration of 3d-ions between the octahedral and tetrahedral positions. However, at higher concentrations such as x = 0.6 and 0.8, migration of a certain portion of the 3d-ions from the A-position to the B-position was observed, which, as expected, changed the bond angles.
3.2. EDX investigation
The SEM and EDX spectra are shown in Fig. 3(a–d). These data demonstrate the formation of the planned NMFSs. Some results are given in Table 3. The experimentally determined concentrations of the Mn ions satisfactorily correspond to the planned values within the measurement error. The δ oxygen ion deficit can be calculated by subtracting the number of oxygen ions experimentally determined using EDX from its ideal number of 4. The crystal lattice of samples x = 0.0–0.6 can be considered almost ideal, since the oxygen deficit is almost zero. This indicates that the co-precipitation method using an organic base as a precipitating agent is an excellent method for producing NMFSs. | ||
| Fig. 3 SEM images (left panels) and EDX spectra (right panels) for the NMFSs at RT: x = 0.0 (a and b) and x = 0.8 (c and d). | ||
| x | Fe | Mn | O | Δ |
|---|---|---|---|---|
| 0.0 | 47.72 | — | 51.59 | 0.3887 |
| 0.2 | 39.35 | 3.11 | 57.54 | −0.0278 |
| 0.6 | 31.69 | 8.93 | 59.37 | −0.1559 |
| 0.8 | 37.21 | 10.5 | 52.29 | 0.3397 |
3.3. HRTEM investigation
HRTEM was applied to study the morphology and microstructure of the nanosized particles. Fig. 4 shows the HRTEM images of some of the NMFSs. The nanometer sizes of the obtained particles are visible in all the images. It is clearly seen that the crystallites of the sample are closely adjacent to each other and thus form certain agglomerations. The Re size of an such agglomeration was computed knowing the value Se for the specific surface area using the equation: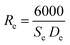 | (7) |
The features of the crystal structure of the NMFSs were studied using the selected area electron diffraction (SAED) method. Such a reciprocal diffraction image is shown in Fig. 5a, where periodically nested diffraction rings can be clearly seen. Such a diffraction pattern corresponds to the nanometer size of the crystallites. It confirms that nanometer crystallites are cubic particles with a spinel structure and contain practically no defects.67 The identified lines of the reciprocal lattice, as shown in Fig. 5a, correspond to the (440), (333), (400), (311) and (220) planes of the cubic symmetry of the spinel structure with an interplanar spacing of ∼0.15 nm, ∼0.16 nm, ∼0.20 nm, ∼0.25 nm and ∼0.29 nm, respectively. Fig. 5b clearly shows two such characteristic distances between the corresponding lattice planes. These are distances of ∼0.25 nm and ∼0.29 nm, which correspond to the (311) and (220) planes, respectively, of the cubic lattice.68
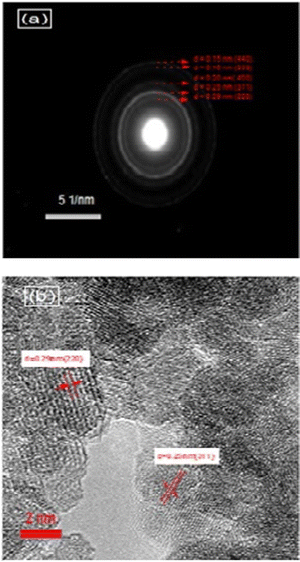 | ||
| Fig. 5 SAED images of the NMFSs with x = 0.4 at RT: reciprocal diffraction at a scale of 5 nm−1 (a) and SAED at a scale of 2 nm (b). | ||
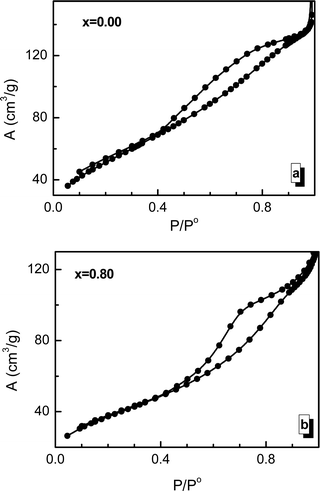
3.4. Specific surface area (Se) investigation
Using the adsorption/desorption hysteresis data of the BET measurements presented in Fig. 6, it is possible to calculate the specific surface area of the investigated sample and its change during the process of substitution by manganese ions. The experimentally determined specific surface area values (Se) of the nanosized crystallites are large compared with those previously reported for similar spinel ferrites prepared using other methods.69–71 The measured Se and calculated Sx values have a similar behavior depending on the concentration of manganese ions. The Se and Sx values are in good agreement with the grain size results. It should be noted that the Se values are lower than the Sx values because the grain size is larger than the crystallite size. It should be noted that the specific surface of a crystallite is also determined by some other factors, such as the amorphization of part of the crystallite surface, chemical disorder, and deformation and strain inside the lattice.723.5. XPS investigation
Fig. 7 shows the XPS spectra of the NMFSs for Fe2+/3+ ions. It is clearly seen that with an increase in the concentration of manganese ions, the humps of the non-monotonic dependences are shifted towards a low binding energy. This behavior confirms that the binding energy of the manganese ions is lower in magnitude.73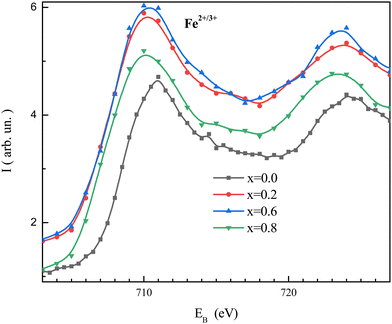 | ||
| Fig. 7 XPS spectra for the NMFSs at RT, with x = 0.0 (black line and symbols), x = 0.2 (red line and symbols), x = 0.6 (blue line and symbols), and x = 0.8 (green line and symbols). | ||
Fitted XPS spectra of the NMFSs for iron ions are shown in Fig. 8(a–d). The Fe2p spectra consist of an Fe2p3/2 jump in the vicinity of ∼710 eV and an Fe2p1/2 jump in the vicinity of ∼723 eV. The Fe2p3/2 jump can be represented as being split into three humps for the Fe2+, Fe3+, and Fe4+ ions at about ∼709, ∼711, and ∼714 eV, respectively. The Fe2p1/2 jump can be represented as being split into two humps for the Fe2+ and Fe3+ ions at about ∼721 and ∼723 eV, respectively.73
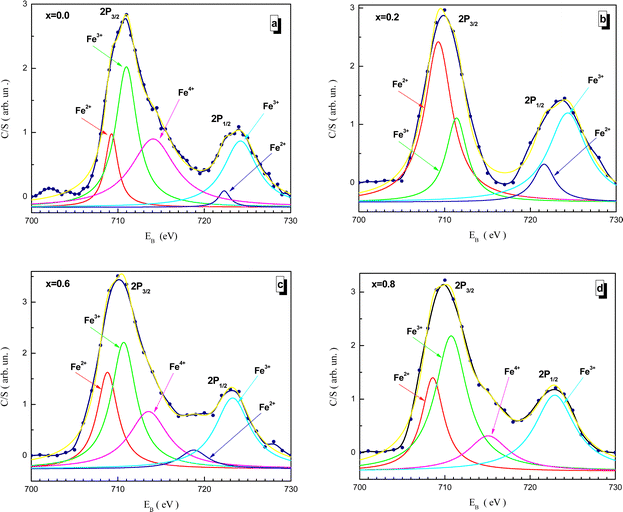 | ||
| Fig. 8 Fitted XPS spectra of the NMFSs at RT for iron ions: x = 0.0 (a), x = 0.2 (b), x = 0.6 (c), and x = 0.8 (d). | ||
Fitted XPS spectra of the NMFSs for manganese ions are shown in Fig. 9(a–c). The Mn2p spectra consist of a Mn2p3/2 jump in the vicinity of ∼642 eV and a Mn2p1/2 jump in the vicinity of ∼653 eV. The Mn2p3/2 jump splits into two humps for the Mn3+ and Mn4+ ions at about ∼642 and ∼645 eV, respectively. The Mn2p1/2 jump can be represented by a single hump corresponding to Mn3+ at about ∼653 eV.68,74,75
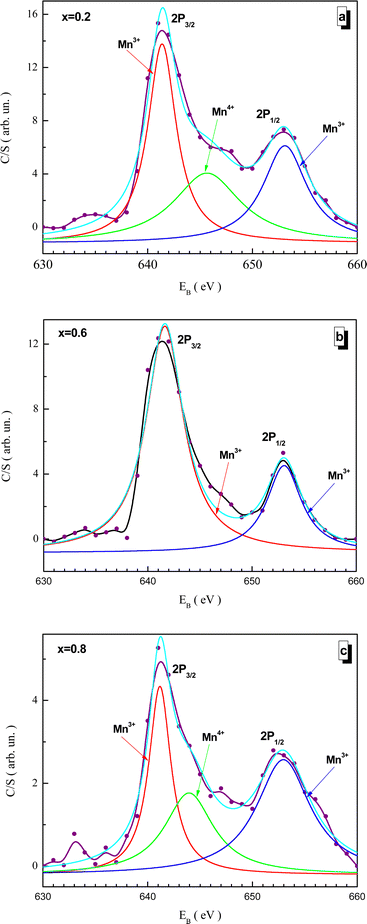 | ||
| Fig. 9 Fitted XPS spectra of the NMFSs at RT for manganese ions: x = 0.2 (a), x = 0.6 (b), and x = 0.8 (c). | ||
3.6. FT-IR investigation
The resulting spectra from the FT-IR study of the NMFSs, which are showed in Fig. 10, confirmed the proposed model on the distribution of ions and provided additional information on the valence of the ions and the position of the electronic bands of the metals.14 It should be recalled that spinel ferrites are characterized by four active IR bands, i.e., ν1, ν2, ν3, and ν4. Tetrahedral and octahedral complexes are responsible for the existence of the first three bands, while the fourth band is generated by lattice vibrations.76 The obtained FT-IR spectra of the NMFSs are shown in Fig. 10.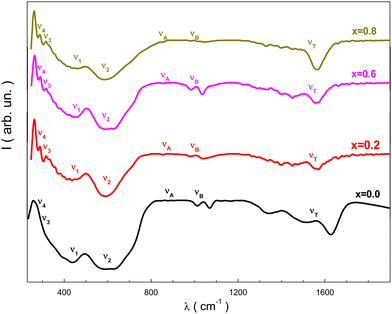 | ||
| Fig. 10 FT-IR spectra for the NMFSs at RT: x = 0.0 (black line), x = 0.2 (red line), x = 0.6 (magenta line), and x = 0.8 (dark yellow line). | ||
It is possible to emphasize some peculiarities of the dependencies in Fig. 10:
• Two extrema, designated as ν1 and ν2, are located in the vicinity of ∼440 cm−1 and ∼600 cm−1. With an increase in the concentration of manganese ions, the geometrical center of the ν1 extremum shifts towards a decrease in frequency, while the geometrical center of the ν2 extremum shifts towards an increase in frequency.
• The ν4 extremum located near ∼250 cm−1 is clearly detected for all the NMFSs with an almost constant position, while the ν3 extremum appearing at substitution near ∼280 cm−1 in the parent compound was not recorded.
• With an increase in the substitution concentration, the νA and νB extrema, which were initially recorded not far from ∼870 cm−1 and ∼1008 cm−1, respectively, shift towards higher frequencies.
Fig. 10 shows wide tetrahedral extrema in the region of 1545–1636 cm−1. They are due to the valence band of Fe3+ ions in the tetrahedral position of the spinel.77–79 As the substitution concentration increases, the size of the tetrahedral position increases, while the size of the octahedral position decreases. This behavior is determined by an increase in the number of covalent bonds of the emerging Fe3+ ions, as well as by the redistribution of some of the Mn3+ ions from the octahedral positions to the tetrahedral ones in the spinel structure. An increase in the size of the tetrahedral position (see Table 2) reduces the base frequency of the corresponding extremum, which is clearly fixed with substitution. A decrease in the size of the octahedral position (see Table 2) shifts the frequency of the extremum towards a low frequency.
The presence of the ν3 extremum in the vicinity of ∼280 cm−1 upon substitution for the NMFSs with x > 0.0 (see Fig. 7), is due to the strong interaction between trivalent Fe3+ and Mn3+ ions located in octahedral positions with divalent Fe2+ ions located in tetrahedral positions or due to the divalent bond Fe2+–O2− from octahedral positions.76 It should be noted that the appearance of the ν3 extremum with substitution can be considered as a splitting of the ν2 extremum as a result of the appearance of trivalent Fe3+ and Mn3+ ions in octahedral sites and an increase in their number. It is also known that the presence of the ν4 extremum is determined by the mass of the divalent cation located in the tetrahedral position and depends on a certain type of vibration associated with the displacement of the tetrahedral cation.80
The νA extremum is determined by divalent Fe2+ ions located in the octahedral position. The νB extremum is determined by the tetravalent Fe4+ and Mn4+ ions located in the tetrahedral position. Moreover, it should be noted that various tetravalent ions can appear in the dynamic mode as a result of electron hopping exchange. This interpretation satisfactorily agrees with the XPS data.73
The expansion of the tetrahedral ν1 extremum also has a contribution from the Jahn–Teller distortion of Fe2+ ions in the low spin state.76 This situation leads to a non-cubic contribution to the potential of the crystal field, which causes local deformations. The sharpening of the shape of this ν1 extremum with increasing substitution may indicate a change in the degree of inversion of the spinel structure.81 This result confirms the distribution of ions over the sub-lattices mentioned above.
The main reason for the sharpening of the tetrahedral ν1 extremum is the presence of divalent Fe2+ ions in the tetrahedral position. Fe2+ ions can be displaced from tetrahedral positions to octahedral positions when the Mn3+ ions enter, converting a corresponding number of Fe3+, Fe4+, Mn3+, and Mn4+ ions to octahedral positions. The transition of some Fe3+ ions to the octahedral position instead of Fe2+ ions causes a certain deformation in the form of this tetrahedral ν1 extremum, as well as splitting of the octahedral ν2 extremum, which indicates that divalent Fe2+ ions in such samples are spatially ordered.
The Kt and Ko, strength coefficients for tetrahedral and octahedral positions, respectively, were calculated using the corresponding equations:82
| Kt = 7.62 × Mt × νA2 × 10−7, | (8) |
| Ko = 5.31 × Mo × νB2 × 10−7 | (9) |
| x | v 1 (cm−1) | v 2 (cm−1) | v 3 (cm−1) | v 4 (cm−1) | v A (cm−1) | v B (cm−1) | d A (nm) | d B (nm) | K t (N m−1) | K o (N m−1) |
|---|---|---|---|---|---|---|---|---|---|---|
| 0.0 | 601 | 437 | — | — | 864 | 1012 | 0.1955 | 0.20147 | 380.026 | 185.74 |
| 0.2 | 600 | 440 | 282 | 254 | 871 | 1012 | 0.1972 | 0.20091 | 201.972 | 188.31 |
| 0.6 | 586 | 445 | 279 | 254 | 873 | 1008 | 0.2008 | 0.20016 | 191.197 | 192.62 |
| 0.8 | 584 | 448 | 279 | 254 | 878 | 1014 | 0.2025 | 0.19966 | 190.283 | 195.21 |
3.7. Raman investigation
Fig. 11 shows the fitted Raman spectra of the NMFSs at RT. Since the samples have a cubic spinel structure with the Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group, five active Raman modes, i.e., A1g, Eg, 1T2g, 2T2g, and 3T2g, can be distinguished in the spectra presented. The main results of this experiment are given in Table 5. The main features of the Raman spectra are as follows:
m space group, five active Raman modes, i.e., A1g, Eg, 1T2g, 2T2g, and 3T2g, can be distinguished in the spectra presented. The main results of this experiment are given in Table 5. The main features of the Raman spectra are as follows:
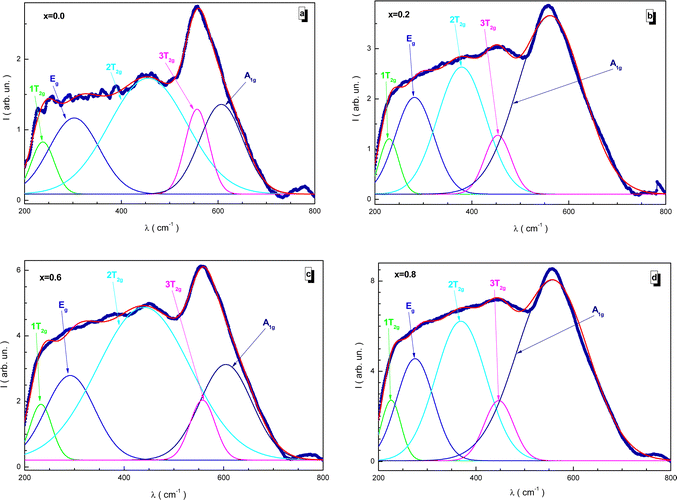 | ||
| Fig. 11 Fitted Raman spectra for the NMFSs at RT: x = 0.0 (a), x = 0.2 (b), x = 0.6 (c), and x = 0.8 (d). | ||
| x | 1T2g | Eg | 2T2g | 3T2g | A1g |
|---|---|---|---|---|---|
| 0.0 | 237.8 | 302.7 | 455.8 | 556.6 | 606.8 |
| 0.2 | 229.5 | 281.6 | 379.3 | 453.4 | 561.3 |
| 0.6 | 232.7 | 291.5 | 439.8 | 557.6 | 604.5 |
| 0.8 | 225.8 | 275.2 | 369.1 | 447.4 | 557.3 |
• The A1g mode is located in the frequency range of 557–607 cm−1 and is responsible for the symmetrical stretching of the distances between the iron and oxygen ions according to the Fe–O bonds.
• The Eg mode is located in the frequency range of 275–303 cm−1, while the 3T2g mode is located in the frequency range of 447–558 cm−1. These modes are responsible for the symmetric and asymmetric stretching of the bond lengths of oxygen and iron ions.
• The 2T2g mode is located in the frequency range of 369–456 cm−1. It determines the asymmetry of the bond length between oxygen and iron ions.
• The 1T2g mode is located in the frequency range of 225–238 cm−1. It determines the vibrations of the FeO4 tetrahedron.
The tetrahedral position is determined mainly by the A1g mode, while the octahedral position is described mainly by the 3T2g mode. The presence of these pronounced vibrational modes also indicates the existence of the spinel structure.83,84 With an increase in the substitution concentration, a certain uniform monotonic shift towards lower frequencies is clearly recorded for all the modes without exception. This behavior is explained by changes associated with the distribution of ions between the tetrahedral and octahedral positions. During the process of substitution, the sizes of the tetrahedral and octahedral positions are redistributed as a result of the displacement of manganese and iron ions between these positions. The larger radius of the Mn3+ ion replaces the smaller radius of the Fe3+ ion in the tetrahedral position and the larger radius of the Fe2+ ion in the octahedral position. This behavior is confirmed by the XPS data, as well as the behavior of the bond lengths. The position of the Raman modes is also determined via the lattice disorder, substitutional defects, and by the surface pressure or the phonon confinement effect, which usually manifests itself in nanosized particles.85
3.8. FMR investigation
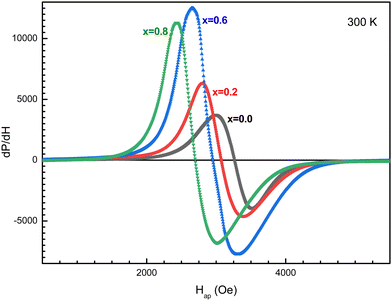
The field dependence of the differential electromagnetic absorption spectra for all the NMFSs is shown in Fig. 12. The concentration dependence of the main absorbing parameters, such as the resonance field (Hr), the line width (ΔH), the number of spins (ns) and the asymmetry ratio (ra), were extracted from the shape of the spectra interpolated by the Gaussian distribution33 and plotted in Fig. 13.86 With an increase in the manganese ion content, the internal local magnetic field increases rapidly. At the same time, it was determined that the resonance is observed at low values of the magnetic field, which decreases with an increase in the concentration of manganese ions.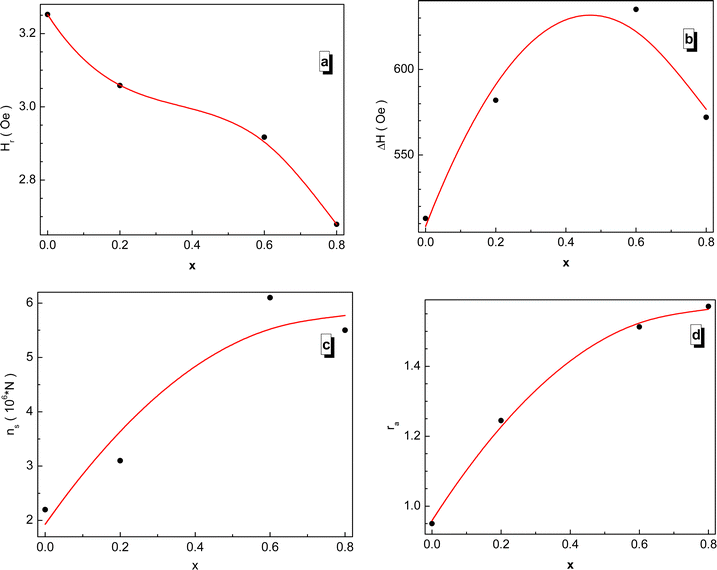 | ||
| Fig. 13 Concentration dependence of the fitting parameters for all the NMFSs at RT: Hr resonance field (a), ΔH line width (b), ns spin number (c), and ra asymmetry ratio (d). | ||
The results on the absorption of electromagnetic radiation show that the ΔH line width is determined by the composition of the sample. As is known, White87 emphasized that the introduction of a transition element into the lattice of a sample with an electron singlet increases the line width. Thus, the line width decreases with decreasing spontaneous magnetization. The shape and quality of the material, which includes but is not limited to spinel ferrite, affects the resonant parameters. So the random orientation of the crystallites and the presence of pores change the resonance parameters from point to point inside the material. This is expressed in the broadening and displacement of the resonant hump. The nanometer shape of the sample is expressed in the asymmetry of the resonant hump (see Fig. 12). These curves exhibit a steep rise with increasing field followed by a slow fall. The same behavior is typical for materials with long-range ferrimagnetic order. Thus, the absorption curve for all the NMFSs is asymmetric and steep towards a weak field, and the steepness increases with an increase in the concentration of manganese ions. This behavior is confirmed by the ra asymmetry ratio plot presented in Fig. 13d.
The dependence of the ΔH line width can be understood on the basis of the theory of indirect superexchange and magnetic dipole interactions between manganese and iron ions in tetrahedral and octahedral positions.88 The substitution of iron ions by manganese ions increases the magnetic dipole interaction. The decrease in the ΔH line width and the ns number of spins for x = 0.8 is explained by the redistribution of manganese ions into octahedral positions from tetrahedral positions,32 as established by the results of X-ray diffraction analysis. This redistribution of ions also weakens their indirect superexchange interaction through oxygen ions. Thus, with an increase in the concentration of manganese ions, an increase in the ΔH line width and ns number of spins should be observed.89 However, a decrease in the line width at high concentrations of manganese ions can be explained by the nanometer size of the crystallite. Moreover, it is known that nanoscale samples exhibit a smaller line width than that previously reported for other spinel ferrites.90 This behavior may contribute to the use of the NMFSs for low-loss electrical applications in the microwave range and in biomedicine.91
3.9. Magnetic investigation
Fig. 14 presents the field dependence of the NMFSs at RT. From these dependences, we can conclude that the samples are characterized by an insignificant saturation magnetization, while the coercivity is almost negligible Hc < 9 Oe. The shape of the presented magnetization curves indicates a superparamagnetic or spin glass state of the NMFSs. Such a form of hysteresis loops is observed for materials consisting of nanosized crystallites.92 It can be concluded that the energies of magnetic anisotropy and thermal fluctuations are comparable for the studied samples.93 With an increase in the concentration of manganese ions, the coercivity and remanence decrease, and become almost equal to zero for x = 0.6. This magnetic behavior is explained by an increase in the content of manganese ions in tetrahedral positions. However, some increase in these magnetic parameters for x = 0.8 may indicate the location of a small amount of manganese ions in octahedral positions.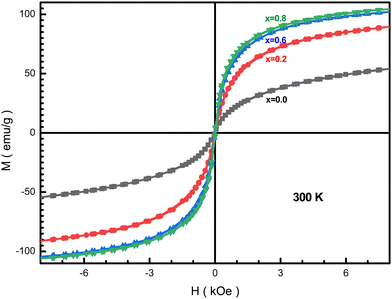 | ||
| Fig. 14 Hysteresis loops for the NMFSs at RT: x = 0.0 (black line and symbols), x = 0.2 (red line and symbols), x = 0.6 (blue line and symbols), and x = 0.8 (green line and symbols). | ||
As the manganese concentration increases, the Ms saturation magnetization increases, as can be seen from Table 6. The measured μm magnetic moment also increases with an increase in the concentration of manganese ions x due to an increase in the magnitude of local spins and the intensity of the Fei+(Mnj+)–O2−–Fei+(Mnj+) (i, j = 2, 3, 4) indirect superexchange interactions. It should be recalled here that iron ions have a strong tendency to occupy the octahedral positions, while manganese ions prefer to occupy the tetrahedral positions.42 Such a distribution of ions was confirmed by a combination of results from XRD experiments using the Rietveld method and the frequency shift of the FT-IR absorption humps.94
| x | M s (emu g−1) | M r (emu g−1) | H C (Oe) |
|---|---|---|---|
| 0.0 | 51 | 3 | 4 |
| 0.2 | 90 | 7 | 1 |
| 0.6 | 100 | 3 | 3 |
| 0.8 | 106 | 11 | 9 |
The MT total magnetization of the sample with the ferrimagnetic lattice, in accordance with the Néel model, can be computed as the difference between the magnetizations of the sub-lattices MB – MA, where MB and MA are the total magnetic moments of the B sub-lattice and A sub-lattice, respectively.95 The μt theoretical values of the magnetic moment according to the Néel model in Bohr magnetons per formula unit μB/f.u. can be determined taking into account the probable distribution of ions over the sub-lattices and knowing the ionic magnetic moments for μt(Mn3+) = 4μB, μt(Fe2+) = 4μB, and μt(Fe3+) = 5μB.96 Here it should be recalled (see Table 2) that the rt size of the tetrahedral position monotonically increases with an increase in the concentration of manganese ions, and the ro size of the octahedral position first decreases at small x down to x = 0.2, and then increases at large x up to x = 0.8, which is explained by the redistribution of ions over the positions.
It can be seen from Table 6 that the Ms saturation magnetization values for all x are higher than those of the unsubstituted nanoferrite, which is ∼53 emu g−1. Such a significant difference in the saturation magnetization values proves the existence of a non-collinear magnetic structure of the substituted compounds. In addition, the high saturation magnetization is determined by the high degree of crystallinity, which was obtained via the HRTEM method (see Fig. 4(a and b)) and the high degree of coherence obtained from the clear X-ray diffraction spectra (see Fig. 1(a–d)).
The crystallite sizes of the studied samples lie in the range of 14–18 nm (see Table 1), which is comparable to some previously published values for similar manganese magnetites (11–14 nm and 9–12 nm), but with a lower saturation magnetization.41–43 For nanometer crystallites, the Dm magnetic diameter is small, and the thermal energy of chaotic motion becomes higher than the energy of magnetic crystallographic anisotropy. Therefore, for nanometer crystallites, the saturation magnetization does not have a preferred spatial orientation. Since the vibrations of ions are random, the nanosamples are characterized by paramagnetic, or rather, superparamagnetic properties.41
The slope of the field magnetization near zero can give the value of the Dm magnetic diameter. Since the largest crystallites make the main contribution to superparamagnetic magnetization, the upper limit of the Dm magnetic diameter can be found from the relation:
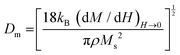 | (10) |
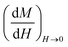 is the initial magnetization slope near zero field, which was determined via extrapolation of the linear part of the data.
is the initial magnetization slope near zero field, which was determined via extrapolation of the linear part of the data.
The Re experimentally determined sizes of the crystallites (see Table 1) were compared with the calculated Dm magnetic sizes (see Table 7). The number of exchange-coupled spins is directly proportional to the particle size. The Rx crystallite sizes estimated via XRD are smaller than the Re grain sizes determined from the BET results. This may indicate the possible presence of a disordered layer on the particle surface.97
| x | μ m (μB/ion) | μ A (μB/ion) | μ m (μB/ion) | μ t (μB/ion) | θ Y–K | D m (nm) |
|---|---|---|---|---|---|---|
| 0.0 | 2.114 | 5.02 | 9.04 | 4.02 | 37.77 | 7.76 |
| 0.2 | 3.728 | 5.04 | 9.03 | 4.03 | 14.12 | 7.35 |
| 0.6 | 4.135 | 4.76 | 9.24 | 4.48 | 15.68 | 8.21 |
| 0.8 | 4.380 | 4.64 | 9.36 | 4.72 | 15.47 | 8.19 |
More profoundly, after considering the particle size of the prepared samples and the magnetic diameter, it is also essential to discuss the vital role of the Yafet–Kittel angle (Y–K angle), which may affect the resultant magnetic moment. Measured magnetic moment μm values (corresponding to Ms) lower than the theoretical values may be explained by referring to the three-sublattice model suggested by Yafet and Kittel (Y–K model), which assumes the existence of the nonlinear spin arrangement in the system.98 The presence of a canted spin and the behavior of the magnetic moment with an increasing Mn concentration may be proved by determining the Y–K angle according to the Y–K model (eqn (11)):
μm = μB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θY–K − μA θY–K − μA | (11) |
It can be seen that the calculated value of the Y–K angle decreases dramatically with a small doping ratio of Mn concentration (x = 0.2) then decreases slightly afterwards with more doping of Mn ions, which is in good agreement with the saturation magnetization behavior, i.e., a significant increase at x = 0.2 then a slight increase afterwards. Non-zero Y–K angles suggest that the magnetization behavior is better explained by a non-collinear spin structure than a two-sublattice ideal model.98 However, with x > 0.0, the decrease in spin canting angle (θY–K) with increasing Mn content, which confirms the increased favor of collinear spin arrangements on the B sites, leads to an increase in the A–B exchange interaction inconsistency with the slight increase in the calculated bond angles (θ1, θ2, and θ5) and the slight decrease of the calculated bond angles (θ3 and θ4) (see Table 2) supporting the strengthening of A–B exchange interaction and weakening of the B–B interaction, respectively.
In addition, it is found that the net number of magnetic spins calculated using FMR measurement increases upon increasing the value of x. In these samples, the improvement of collinear Néel type of magnetic ordering with Mn substitution may be attributed intrinsically to the increase in dominant A–B superexchange interaction and extrinsically to the increase in particle size. Also, the calculation of bond angles based on the proposed cation distribution indicates an increase in the superexchange interaction, in agreement with the magnetic calculations (see Table 2 and Table 7, respectively).
Besides, each nanoparticle is assumed to consist of ordered spins at the grain having the Dm magnetic diameter and canted spins on the surface, dead layer of the grain boundary. The increase in Mn doping is leading to a slight increase in the Dm magnetic diameter, resulting in a consequent decrease of the magnetically dead layer (the canted spins), and in turn, this leads to an increase in the magnetic moments, as observed in Table 7 and Fig. 13c.
The obtained and studied nanoparticles of doped spinel ferrite have great prospects for the delivery of drugs for cancer therapy,99 including boron neutron capture therapy, upon modification of their surface with therapeutic substances. The samples also have broad biomedical prospects as anti-cancer agents for hyperthermia.
4. Conclusions
Four cubic spinel nanoparticle ferrite samples MnxFe3–xO4, with x = 0.0, 0.2, 0.6, and 0.8, were successfully obtained via the co-precipitation method using the organic base ethanolamine as the chelating agent. The XPS spectra, the FT-IR absorption peaks, and Raman spectral behavior confirmed the existence of different metallic ions of Mn and Fe. Both XRD and HRTEM proved the excellent crystallization of the as-prepared nanoparticles. Large specific surface areas have been estimated via BET measurements. The BET measurements enabled the successful calculation of the grain size to overcome the agglomeration of particles in the TEM images. FMR and VSM measurements have revealed superparamagnetic properties with a relatively high saturation magnetization of the prepared samples.Author contributions
Conceptualization – R. E. E., M. A. D., A. V. T., S. V. T., and F. F.; methodology – R. E. E., H. E. S., S. A. S., M. U. K., and Z. M.; formal analysis – H. E. S., M. A. D., M. U. K., Z. M., H. M., K. C. B. N., A. V. T., S. V. T., and F. F.; investigation – R. E. E., H. E. S., S. A. S., M. A. D., A. V. T., and S. V. T.; resources – H. E. S., S. A. S., K. C. B. N., M. U. K., Z. M., F. F., A. V. T., and S. V. T.; data curation – M. A. D., M. U. K., M. A. I., A. V. T., S. V. T., and F. F.; writing (original draft preparation) – R. E. E., M. A. D., A. V. T., and S. V. T.; review and editing – M. A. D., A. V. T., and S. V. T.; visualization – H. E. S., S. A. S., K. C. B. N., and Z. M.; supervision – A. V. T., S. V. T, and F. F.; project administration – M. A. D., M. U. K., Z. M., A. V. T., S. V. T., and F. F.; funding acquisition – M. U. K., A. V. T. and S. V. T.Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
The authors acknowledge Prof. A. Matsuda (Matsuda Lab., Toyohashi University) for performing some measurements like HRTEM, BET, SEM, and EDX in his Lab. The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University, Saudi Arabia for funding this work through Large Research Groups Program under grant number R.G.P2/274/44. Alex V. Trukhanov thanks NUST MISIS for support within the framework of the «Priority 2030» (K6-2022-043).References
- M. A. Almessiere, Y. Slimani, H. Güngüneş, A. D. Korkmaz, T. Zubar, S. Trukhanov, A. Trukhanov, A. Manikandan, F. Alahmari and A. Baykal, Influence of Dy3+ ions on microstructure, magnetic, electrical and microwave properties of [Ni0.4Cu0.2Zn0.4](Fe2-xDyx)O4 (0.00 < x < 0.04) spinel ferrites, ACS Omega, 2021, 6, 10266–10280, DOI:10.1021/acsomega.1c00611.
- M. A. Almessiere, Y. Slimani, A. V. Trukhanov, A. Baykal, H. Gungunes, E. L. Trukhanova, S. V. Trukhanov and V. G. Kostishin, Strong correlation between Dy3+ concentration, structure, magnetic and microwave properties of the [Ni0.5Co0.5](DyxFe2-x)O4 nanosized ferrites, J. Ind. Eng. Chem., 2020, 90, 251–259, DOI:10.1016/j.jiec.2020.07.020.
- M. Mostafa, O. Saleh, A. M. Henaish, S. A. A. El-Kaream, R. Ghazy, O. M. Hemeda, A. M. Dorgham, H. Al-Ghamdi, A. H. Almuqrin, M. I. Sayyed, S. V. Trukhanov, E. L. Trukhanova, A. V. Trukhanov, D. Zhou and M. A. Darwish, Structure, morphology and electrical/magnetic properties of Ni-Mg nano-ferrites from a new perspective, Nanomaterials, 2022, 12, 1045, DOI:10.3390/nano12071045.
- V. A. Turchenko, S. V. Trukhanov, V. G. Kostishin, F. Damay, F. Porcher, D. S. Klygach, M. G. Vakhitov, D. Lyakhov, D. Michels, B. Bozzo, I. Fina, M. A. Almessiere, Y. Slimani, A. Baykal, D. Zhou and A. V. Trukhanov, Features of structure, magnetic state and electrodynamic performance of SrFe12-xInxO19, Sci. Rep., 2021, 11, 18342, DOI:10.1038/s41598-021-97684-8.
- M. Sugimoto, The past, present, and future of ferrites, J. Am. Ceram. Soc., 1999, 82, 269–280, DOI:10.1111/j.1551-2916.1999.tb20058.x.
- M. A. Njoroge, N. M. Kirimi and K. P. Kuria, Spinel ferrites gas sensors: a review of sensing parameters, mechanism and the effects of ion substitution, Crit. Rev. Solid State Mater. Sci., 2021, 30, 1040–8436, DOI:10.1080/10408436.2021.1935213.
- M. A. Almessiere, S. Güner, Y. Slimani, M. Hassan, A. Baykal, M. A. Gondal, U. Baig, S. V. Trukhanov and A. V. Trukhanov, Structural and magnetic properties of Co0.5Ni0.5Ga0.01Gd0.01Fe1.98O4/ZnFe2O4 spinel ferrite nanocomposites: Comparative study between sol-gel and pulsed laser ablation in liquid approaches, Nanomaterials, 2021, 11, 2461, DOI:10.3390/nano11092461.
- D.-W. Jeong, A. Jha, W.-J. Jang, W.-B. Han and H.-S. Roh, Performance of spinel ferrite catalysts integrated with mesoporous Al2O3 in the high temperature water–gas shift reaction, Chem. Eng. J., 2015, 265, 100–109, DOI:10.1016/j.cej.2014.12.045.
- A. M. Davarpanah, A. Rahdar, M. A. Dastnae, O. Zeybek and H. Beyzaei, 1-x)BaFe12O19/xCoFe2O4 hard/soft magnetic nanocomposites: Synthesis, physical characterization, and antibacterial activities study, J. Molec. Struct., 2019, 1175, 445–449, DOI:10.1016/j.molstruc.2018.07.092.
- M. A. Almessiere, A. V. Trukhanov, F. A. Khan, Y. Slimani, N. Tashkandi, V. A. Turchenko, T. I. Zubar, D. I. Tishkevich, S. V. Trukhanov, L. V. Panina and A. Baykal, Correlation between microstructure parameters and anti-cancer activity of the [Mn0.5Zn0.5](EuxNdxFe2-2x)O4 nanoferrites produced by modified sol-gel and ultrasonic methods, Ceram. Int., 2020, 46, 7346–7354, DOI:10.1016/j.ceramint.2019.11.230.
- M. Amani, P. Amani, A. Kasaeian, O. Mahian, F. Kasaeian and S. Wongwises, Experimental study on viscosity of spinel-type manganese ferrite nanofluid in attendance of magnetic field, J. Magn. Magn. Mater., 2017, 428, 457–463, DOI:10.1016/j.jmmm.2016.12.129.
- J. P. McTague, Magnetic resonance lineshape and chemical shift of molecules in clathrates, J. Chem. Phys., 1969, 51, 47–51, DOI:10.1063/1.1670822.
- M. Arana, P. G. Bercoff and S. E. Jacobo, Thermomagnetic characterization of organic-based ferrofluids prepared with Ni ferrite nanoparticles, Mater. Sci. Eng. B, 2017, 215, 1–8, DOI:10.1016/j.mseb.2016.10.006.
- R. Sharma, P. Thakur, P. Sharma and V. Sharma, Ferrimagnetic Ni doped Mg-Zn spinel ferrite nanoparticles for high density information storage, J. Alloys Compd., 2017, 704, 7–17, DOI:10.1016/j.jallcom.2017.02.021.
- Z. A. Gilani, M. S. Shifa, H. M. Noor ul Huda Khan Asghar, M. A. Khan, M. N. Anjum, M. N. Usmani, R. Ali and M. F. Warsi, New LiCo0.5PrxFe2−xO4 nanoferrites: Prepared via low cost technique for high density storage application, Ceram. Int., 2018, 44, 1881–1885, DOI:10.1016/j.ceramint.2017.10.126.
- M. F. Warsi, Z. A. Gilani, N. F. Al-Khalli, M. Sarfraz, M. A. Khan, M. N. Anjum and I. Shakir, New LiNi0.5PrxFe2−xO4 nanocrystallites: Synthesis via low cost route for fabrication of smart advanced technological devices, Ceram. Int., 2017, 43, 14807–14812, DOI:10.1016/j.ceramint.2017.07.228.
- H. Bayrakdar, O. Yalçın, S. Vural and K. Esmer, Effect of different doping on the structural, morphological and magnetic properties for Cu doped nanoscale spinel type ferrites, J. Magn. Magn. Mater., 2013, 343, 86–91, DOI:10.1016/j.jmmm.2013.04.079.
- R. A. Bohara, H. M. Yadav, N. D. Thorat, S. S. Mali, C. K. Hong, S. G. Nanaware and S. H. Pawar, Synthesis of functionalized Co0.5Zn0.5Fe2O4 nanoparticles for biomedical applications, J. Magn. Magn. Mater., 2015, 378, 397–401, DOI:10.1016/j.jmmm.2014.11.063.
- M. A. Almessiere, Y. Slimani, H. Güngüneş, V. G. Kostishyn, S. V. Trukhanov, A. V. Trukhanov and A. Baykal, Impact of Eu3+ ion substitution on structural, magnetic and microwave traits of Ni–Cu–Zn spinel ferrites, Ceram. Int., 2020, 46, 11124–11131, DOI:10.1016/j.ceramint.2020.01.132.
- D. A. Vinnik, V. E. Zhivulin, D. P. Sherstyuk, A. Y. Starikov, P. A. Zezyulina, S. A. Gudkova, D. A. Zherebtsov, K. N. Rozanov, S. V. Trukhanov, K. A. Astapovich, A. S. B. Sombra, D. Zhou, R. B. Jotania, C. Singh and A. V. Trukhanov, Ni substitution effect on the structure, magnetization, resistivity and permeability of zinc ferrites, J. Mater. Chem. C, 2021, 9, 5425–5436, 10.1039/D0TC05692H.
- A. Thakur, N. Sharma, M. Bhatti, M. Sharma, A. V. Trukhanov, S. V. Trukhanov, L. V. Panina, K. A. Astapovich and P. Thakur, Synthesis of barium ferrite nanoparticles using rhizome extract of Acorus Calamus: Characterization and its efficacy against different plant phytopathogenic fungi, Nano-Struct. Nano-Objects., 2020, 24, 100599, DOI:10.1016/j.nanoso.2020.100599.
- C. C. Chauhan, T. Gupta, S. S. Meena, M. F. Desimone, A. Das, C. S. Sandhu, K. R. Jotania and R. B. Jotania, Tailoring magnetic and dielectric properties of SrFe12O19/NiFe2O4 ferrite nanocomposites synthesized in presence of Calotropis gigantea (crown) flower extract, J. Alloys Compd., 2022, 900, 163415, DOI:10.1016/j.jallcom.2021.163415.
- C. C. Chauhan, A. A. Gor, T. Gupta, M. F. Desimone, N. Patni and R. B. Jotania, Investigation of structural, optical, magnetic, and dielectric properties of calcium hexaferrite synthesized in presence of Azadirachta indica and Murraya koenigii leaves extract, Ceram. Int., 2022, 48, 20134–20145, DOI:10.1016/j.ceramint.2022.03.292.
- K. K. Kefeni, B. B. Mamba and T. A. M. Msagati, Application of spinel ferrite nanoparticles in water and wastewater treatment: A review, Sep. Pur. Techn., 2017, 188, 399–422, DOI:10.1016/j.seppur.2017.07.015.
- W. Hu, N. Qin, G. Wu, Y. Lin, S. Li and D. Bao, Opportunity of spinel ferrite materials in nonvolatile memory device applications based on their resistive switching performances, J. Am. Chem. Soc., 2012, 134, 14658–14661, DOI:10.1021/ja305681n.
- K. K. Kefeni, T. A. M. Msagati, T. T. I. Nkambule and B. B. Mamba, Spinel ferrite nanoparticles and nanocomposites for biomedical applications and their toxicity, Mat. Sci. Eng. C, 2020, 107, 110314, DOI:10.1016/j.msec.2019.110314.
- G. Nandhini and M. K. Shobana, Role of ferrite nanoparticles in hyperthermia applications, J. Magn. Magn. Mater., 2022, 552, 169236, DOI:10.1016/j.jmmm.2022.169236.
- T. M. Hakami, A. M. Davarpanah, A. Rahdar and S. D. Barrett, Structural and magnetic study and cytotoxicity evaluation of tetrametallic nanoparticles of Co0.5Ni0.5CrxFe2-xO4 prepared by co-precipitation, J. Molec. Struct., 2018, 1165, 344–348, DOI:10.1016/j.molstruc.2018.04.016.
- H. Alijani, S. Iravani, S. Pourseyedi, M. Torkzadeh-Mahani, M. Barani and M. Khatami, Biosynthesis of spinel nickel ferrite nanowhiskers and their biomedical applications, Sci. Rep., 2021, 11, 17431, DOI:10.1038/s41598-021-96918-z.
- L. Khanna, N. K. Verma and S. K. Tripathi, Burgeoning tool of biomedical applications superparamagnetic nanoparticles, J. Alloys Compd., 2018, 752, 332–353, DOI:10.1016/j.jallcom.2018.04.093.
- S. V. Trukhanov, Peculiarities of the magnetic state in the system La0.70Sr0.30MnO3-γ (0 ≤ γ ≤ 0.25), J. Exp. Theor. Phys., 2005, 100, 95–105, DOI:10.1134/1.1866202.
- S. V. Trukhanov, L. S. Lobanovski, M. V. Bushinsky, V. A. Khomchenko, N. V. Pushkarev, I. O. Tyoyanchuk, A. Maignan, D. Flahaut, H. Szymczak and R. Szymczak, Influence of oxygen vacancies on the magnetic and electrical properties of La1-xSrxMnO3-x/2 manganites, Eur. Phys. J. B, 2004, 42, 51–61, DOI:10.1140/epjb/e2004-00357-8.
- J. M. Soares, V. B. Galdino, O. L. A. Conceic, M. A. Morales, J. H. de Araujo and F. L. A. Machado, Critical dimension for magnetic exchange-spring coupled core/shell CoFe2O4/CoFe2 nanoparticles, J. Magn. Magn. Mater., 2013, 326, 81–84, DOI:10.1016/j.jmmm.2012.08.040.
- B. Hadjarab, M. Trari and M. Kebir, Physical characterization of the semiconducting deficient perovskite BaSnO3−δ, Mater. Sci. Sem. Proc., 2015, 29, 283–287, DOI:10.1016/j.mssp.2014.04.041.
- J. Das, V. S. Moholkar and S. Chakma, Structural, magnetic and optical properties of sonochemically synthesized Zr-ferrite nanoparticles, Powd. Techn., 2018, 328, 1–6, DOI:10.1016/j.powtec.2017.11.057.
- P. Jadoun, J. Sharma, S. Kumar, S. N. Dolia, D. Bhatnagar and V. K. Saxen, Structural and magnetic behavior of nanocrystalline Cr doped Co-Mg ferrite, Ceram. Int., 2018, 44, 6747–6753, DOI:10.1016/j.ceramint.2018.01.091.
- G. Mustafa, M. U. Islam, M. Ahmad, W. Zhang, Y. Jamil, A. W. Anwar and M. Hussain, Investigation of structural and magnetic properties of Ce3+-substituted nanosized Co–Cr ferrites for a variety of applications, J. Alloys Compd., 2015, 618, 428–436, DOI:10.1016/j.jallcom.2014.07.132.
- M. A. Gabal, W. A. Bayoumy, A. Saeed and Y. M. Al Angari, Structural and electromagnetic characterization of Cr-substituted Ni–Zn ferrites synthesized via Egg-white route, J. Mol. Str., 2015, 1097, 45–51, DOI:10.1016/j.molstruc.2015.04.032.
- M. L. Esteves, A. Cortes, M. T. Lugo and C. Rinaldi, Synthesis and characterization of carboxymethyl dextran-coated Mn/Zn ferrite for biomedical applications, J. Magn. Magn. Mater., 2009, 321, 3061–3066, DOI:10.1016/j.jmmm.2009.05.023.
- H. Yang, C. Zhang, X. Shi, H. Hu, X. Du, Y. Fang, Y. Ma, H. Wu and S. Yang, Water-soluble superparamagnetic manganese ferrite nanoparticles for magnetic resonance imaging, Biomater., 2010, 31, 3667–3673, DOI:10.1016/j.biomaterials.2010.01.055.
- P. Iranmanesh, S. Saeednia, M. Mehran and S. R. Dafeh, Modified structural and magnetic properties of nanocrystalline MnFe2O4 by pH in capping agent free co-precipitation method, J. Magn. Magn. Mater., 2017, 425, 31–36, DOI:10.1016/j.jmmm.2016.10.105.
- S. V. Bhandare, R. Kumar, A. V. Anupama, H. K. Choudhary, V. M. Jali and B. Sahoo, Annealing temperature dependent structural and magnetic properties of MnFe2O4 nanoparticles grown by sol-gel auto-combustion method, J. Magn. Magn. Mater., 2017, 433, 29–34, DOI:10.1016/j.jmmm.2017.02.040.
- Y. Zhang and Z. Nan, Modified magnetic properties of MnFe2O4 by CTAB with co-precipitation method, Mater. Lett., 2015, 149, 22–24, DOI:10.1016/j.matlet.2015.02.096.
- A. Soufi, H. Hajjaoui, R. Elmoubarki, M. Abdennouri, S. Qourzal and N. Barka, Spinel ferrites nanoparticles: Synthesis methods and application in heterogeneous Fenton oxidation of organic pollutants – A review, Appl. Surf. Sci. Adv., 2021, 6, 100145, DOI:10.1016/j.apsadv.2021.100145.
- S. Kalia, A. Kumar, N. Munjal and N. Prasad, Synthesis of ferrites using various parts of plants: a mini review, J. Phys.: Conf. Ser., 2021, 1964, 032003, DOI:10.1088/1742-6596/1964/3/032003.
- L. Lutterotti, P. Scardi and P. Maistrelli, LS1- a computer program for simultaneous refinement of material structure and microstructure, J. Appl. Crystallogr., 1992, 25, 459–462, DOI:10.1107/s0021889892001122.
- L. Lutterotti, MAUD version 1.85, 2002, http://www.ing.unitn.it/~luttero/maud.
- T. M. El-Alaily, M. K. El-Nimr, M. M. Kamel, T. M. Meaz and S. T. Assar, Construction and calibration of a low cost and fully automated vibrating sample magnetometer, J. Magn. Magn Mater., 2015, 386, 25–30, DOI:10.1016/j.jmmm.2015.03.051.
- S. V. Trukhanov, A. V. Trukhanov, A. N. Vasiliev, A. M. Balagurov and H. Szymczak, Magnetic state of the structural separated anion-deficient La0.70Sr0.30MnO2.85 manganite, J. Exp. Theor. Phys., 2011, 113, 819–825, DOI:10.1134/S1063776111130127.
- D. A. Vinnik, V. E. Zhivulin, D. P. Sherstyuk, A. Y. Starikov, P. A. Zezyulina, S. A. Gudkova, D. A. Zherebtsov, K. N. Rozanov, S. V. Trukhanov, K. A. Astapovich, V. A. Turchenko, A. S. B. Sombra, D. Zhou, R. B. Jotania, C. Singh and A. V. Trukhanov, Electromagnetic properties of zinc-nickel ferrites in frequency range of 0.05-10 GHz, Mater. Today Chem., 2021, 20, 100460, DOI:10.1016/j.mtchem.2021.100460.
- M. A. Almessiere, Y. Slimani, N. A. Algarou, M. G. Vakhitov, D. S. Klygach, A. Baykal, T. I. Zubar, S. V. Trukhanov, A. V. Trukhanov, H. Attia, M. Sertkol and I. A. Auwal, Tuning the structure, magnetic and high frequency properties of Sc-doped Sr0.5Ba0.5ScxFe12-xO19/NiFe2O4 hard/soft nanocomposites, Adv. Electr. Mater., 2022, 8, 2101124, DOI:10.1002/aelm.202101124.
- R. D. Shannon, Revised Effective Ionic Radii and Systematic Studies of Interatomie Distances in Halides and Chaleogenides, Acta Cryst. A, 1976, 32, 751–767, DOI:10.1107/s0567739476001551.
- D. V. Kurmude, R. S. Barkule, A. V. Raut, D. R. Shengule and K. M. Jadhav, X-Ray diffraction and cation distribution studies in zinc-substituted nickel ferrite nanoparticles, J. Supercond. Nov. Magn., 2014, 27, 547–553, DOI:10.1007/s10948-013-2305-2.
- S. Anjum, G. H. Jaffari, A. K. Rumaiz, M. S. Rafique and S. I. Shah, Role of vacancies in transport and magnetic properties of nickel ferrite thin films, J. Phys. D: Appl. Phys., 2010, 43, 265001, DOI:10.1088/0022-3727/43/26/265001.
- N. Kumari, V. Kumarn, S. Khasa and S. K. Singh, Chemical synthesis and magnetic investigations on Cr3+ substituted Zn-ferrite superparamagnetic nano-particles, Ceram. Int., 2015, 41, 1907–1911, DOI:10.1016/j.ceramint.2014.09.118.
- S. Jauhar and S. Singhaln, Substituted cobalt nano-ferrites, CoMxFe2−xO4 (M = Cr3+, Ni2+, Cu2+, Zn2+; 0.2 ≤ x ≤ 1.0) as heterogeneous catalysts for modified Fenton's reaction, Ceram. Int., 2014, 40, 11845–11855, DOI:10.1016/j.ceramint.2014.04.019.
- M. Raghasudha, Characterization of nano-structured magnesium-chromium ferrites synthesized by citrate-gel auto combustion method, Adv. Mat. Lett., 2013, 4, 910–916, DOI:10.5185/amlett.2013.5479.
- L. Z. Li, X. Q. Tu, R. Wang and L. Peng, Structural and magnetic properties of Cr-substituted NiZnCo ferrite nanopowders, J. Magn. Magn. Mater., 2015, 38, 328–331, DOI:10.1016/j.jmmm.2015.01.020.
- D. C. Ghosh and R. Biswas, Theoretical calculation of absolute radii of atoms and ions. Part 2. The ionic radii, Int. J. Mol. Sci., 2003, 4, 379–407, DOI:10.3390/i4060379.
- D. Makovec, A. Kodre, I. Arčon and M. Drofenik, Structure of manganese zinc ferrite spinel nanoparticles prepared with co-precipitation in reversed microemulsions, J. Nanopart. Res., 2009, 11, 1145–1158, DOI:10.1007/s11051-008-9510-0.
- H. Mahajan, S. K. Godara and A. K. Srivastava, Synthesis and investigation of structural, morphological, and magnetic properties of the manganese doped cobalt-zinc spinel ferrite, J. Alloys Compd., 2022, 896, 162966, DOI:10.1016/j.jallcom.2021.162966.
- P. G. Radaelli, G. Iannone, M. Marezio, H. Y. Hwang, S.-W. Cheong, J. D. Jorgensen and D. N. Argyriou, Structural effects on the magnetic and transport properties of perovskite A1−xA′xMnO3 (x = 0.25, 0.30), Phys. Rev. B, 1997, 56, 8265, DOI:10.1103/PhysRevB.56.8265.
- V. K. Lakhani, T. K. Pathak, N. H. Vasoya and K. B. Modi, Structural parameters and X-ray Debye temperature determination study on copper-ferrite-aluminates, Sol. State Sci., 2011, 13, 539–547, DOI:10.1016/j.solidstatesciences.2010.12.023.
- Y. H. Chen, Thermal properties of nanocrystalline goethite, magnetite, and maghemite, J. Alloys Compd., 2013, 553, 194–198, DOI:10.1016/j.jallcom.2012.11.102.
- I. V. Chernyshova, M. F. Hochella Jr and A. S. Madden, Size-dependent structural transformations of hematite nanoparticles. 1. Phase transition, Phys. Chem. Chem. Phys., 2007, 9, 1736–1750, 10.1039/b618790k.
- P. R. Chetana, X. Siddaramaiah and P. G. Ramappa, TGA studies of metoclopramide complexes of cobalt(II) in the solid state, Thermochim. Acta, 2005, 425, 13–21, DOI:10.1016/j.tca.2003.10.012.
- Z. Xu, J. Fan, T. Liu, Y. Han and H. Zhang, Calcination induced phase transformation in MnZn ferrite powders, J. Alloys Compd., 2020, 814, 152307, DOI:10.1016/j.jallcom.2019.152307.
- S. Liu, L. J. Wang and K. Chou, Synthesis of metal-doped Mn-Zn ferrite from the leaching solutions of vanadium slag using hydrothermal method, J. Magn. Magn. Mater., 2018, 449, 49–54, DOI:10.1016/j.jmmm.2017.10.001.
- C. M. Srivastava and T. T. Srinivasan, Effect of Jahn-Teller distortion on the lattice vibration frequencies of nickel ferrite, J. Appl. Phys., 1982, 53, 8148–8150, DOI:10.1063/1.330276.
- B. Pourgolmohammad, S. M. Masoudpanah and M. R. Aboutalebi, Synthesis of CoFe2O4 powders with high surface area by solution combustion method: Effect of fuel content and cobalt precursor, Ceram. Int., 2017, 43, 3797–3803, DOI:10.1016/j.ceramint.2016.12.027.
- B. Kalska-Szostko, U. Wykowska, D. Satula and P. Nordblad, Thermal treatment of magnetite nanoparticles, Beilstein J. Nanotechnol., 2015, 6, 1385–1396, DOI:10.3762/bjnano.6.143.
- S. Kumar, P. B. Barman and R. R. Singh, Estimation and association of structural, elastic and magnetic properties of magnesium-nickel-ferrite nanoparticles annealed at different temperatures, Mater. Sci. Eng. B, 2021, 272, 115362, DOI:10.1016/j.mseb.2021.115362.
- M. A. Amer, A. Matsuda, G. Kawamura, R. El-Shater, T. Meaz and F. Fakhry, Characterization and structural and magnetic studies of as- synthesized Fe2+CrxFe(2-x)O4 nanoparticles, J. Magn. Magn. Mater., 2017, 439, 373–383, DOI:10.1016/j.jmmm.2017.05.048.
- D. R. Abd El-Hafiz, A. A.-E. Sakr and M. A. Ebiad, Methane Bi-reforming for direct ethanol production over smart Cu/Mn- ferrite catalysts, Renewable Energy, 2021, 167, 236–247, DOI:10.1016/j.renene.2020.11.078.
- X. Gao, J. Chen, H. Liu, S. Yin, Y. Tian, X. Cao, G. Zou, H. Hou, W. Wei, L. Chen and X. Ji, Copper-substituted NaxMO2 (M = Fe, Mn) cathodes for sodium ion batteries: Enhanced cycling stability through suppression of Mn(III) formation, Chem. Eng. J., 2021, 406, 126830, DOI:10.1016/j.cej.2020.126830.
- V. Rathod, A. V. Anupama, R. V. Kumar, V. M. Jali and B. Sahoo, Correlated vibrations of the tetrahedral and octahedral complexes and splitting of the absorption bands in FTIR spectra of Li-Zn ferrites, Vibrat. Spectr., 2017, 92, 267–272, DOI:10.1016/j.vibspec.2017.08.008.
- V. A. Potakova, N. D. Zverev and V. P. Romanov, On the cation distribution in Ni1-x-yFex2+ZnyFe23+O4 spinel ferrites, Phys. Stat. Sol. (a), 1972, 13, 623–627, DOI:10.1002/pssa.2210120235.
- G. Padmapriya, A. Manikandan, V. Krishnasamy, S. K. Jaganathan and S. A. Antony, Enhanced catalytic activity and magnetic properties of spinel MnxZn1-xFe2O4 (0.0 ≤ x ≤ 1.0) nano-photocatalysts by microwave irradiation route, J. Supercond. Nov. Magn., 2016, 29, 2141–2149, DOI:10.1007/s10948-016-3527-x.
- U. Kurtan, D. Dursun, H. Aydın, M. S. Toprak and A. Baykal, Influence of calcination rate on morphologies and magnetic properties of MnFe2O4 nanofibers, Ceram. Int., 2016, 42, 18189–18195, DOI:10.1016/j.ceramint.2016.08.135.
- J. Preudhomme, Etude par spectroscopie infra-rouge des solutions solides germanate de cobalt-ferrite de cobalt, Spectrochim. Acta, 1964, 20, 275–283, DOI:10.1016/0371-1951(64)80023-0.
- S. A. Patil, V. C. Mahajan, A. K. Ghatage and S. D. Lotke, Structure and magnetic properties of Cd and Ti/Si substituted cobalt ferrites, Mater. Chem. Phys., 1998, 57, 86–91, DOI:10.1016/s0254-0584(98)00202-8.
- S. M. Patange, S. E. Shirsath, S. P. Jadhav, V. S. Hogade, S. R. Kamble and K. M. Jadhav, Elastic properties of nanocrystalline aluminum substituted nickel ferrites prepared by co-precipitation method, J. Mol. Str., 2013, 1038, 40–44, DOI:10.1016/j.molstruc.2012.12.053.
- D. Varshney, K. Verma and A. Kumar, Structural and vibrational properties of ZnxMn1-xFe2O4 (x = 0.0, 0.25, 0.50, 0.75, 1.0) mixed ferrites, Mater. Chem. Phys., 2011, 131, 413–419, DOI:10.1016/j.matchemphys.2011.09.066.
- R. Kumar, R. K. Singh, M. K. Zope and M. Kar, Tuning of magnetic property by lattice strain in lead substituted cobalt ferrite, Mater. Sci. Eng. B, 2017, 220, 73–81, DOI:10.1016/j.mseb.2017.03.012.
- K. Sabri, A. Rais, K. Taibi, M. Moreau, B. Ouddane and A. Addou, Structural Rietveld refinement and vibrational study of MgCrxFe2-xO4 spinel ferrites, Phys. B, 2016, 501, 38–44, DOI:10.1016/j.physb.2016.08.011.
- S. V. Trukhanov, A. V. Trukhanov, V. G. Kostishin, L. V. Panina, I. S. Kazakevich, V. A. Turchenko, V. V. Oleinik, E. S. Yakovenko and L. Y. Matsui, Magnetic and absorbing properties of M-type substituted hexaferrites BaFe12-xGaxO19 (0.1 < x < 1.2), J. Exp. Theor. Phys., 2016, 123, 461–469, DOI:10.1134/S1063776116090089.
- R. L. White, Ferrimagnetic resonance line widths and g-factors in ferrites, Phys. Rev. Lett., 1959, 2, 465, DOI:10.1103/PhysRevLett.2.465.
- R. Arias and D. L. Mills, Theory of collective spin-wave modes of interacting ferromagnetic spheres, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 104425, DOI:10.1103/physrevb.70.104425.
- Y. S. Chen, J. G. Lin, I. S. Titov and A. B. Granovsky, Electron spin resonance probed competing states in NiMnInSi Heusler alloy, J. Magn. Magn. Mater., 2016, 407, 365–368, DOI:10.1016/j.jmmm.2016.01.079.
- L. Gama, E. P. Hernandez, D. R. Cornejo, A. A. Costa, S. M. Rezende, R. H. G. A. Kiminami and A. C. F. M. Costa, Magnetic and structural properties of nanosize Ni–Zn–Cr ferrite particles synthesized by combustion reaction, J. Magn. Magn. Mater., 2007, 317, 29–33, DOI:10.1016/j.jmmm.2007.04.007.
- S. Thota, S. C. Kashyap, S. K. Sharma and V. R. Reddy, Micro Raman, Mossbauer and magnetic studies of manganese substituted zinc ferrite nanoparticles: Role of Mn, J. Phys. Chem. Solids, 2016, 91, 136–144, DOI:10.1016/j.jpcs.2015.12.013.
- V. E. Zhivulin, D. P. Sherstyuk, O. V. Zaitseva, N. A. Cherkasova, D. A. Vinnik, S. V. Taskaev, E. A. Trofimov, S. V. Trukhanov, S. I. Latushka, D. I. Tishkevich, T. I. Zubar and A. V. Trukhanov, Creation and magnetic study of ferrites with magnetoplumbite structure multisubstituted by Al3+, Cr3+, Ga3+, and In3+ cations, Nanomaterials, 2022, 12, 1306, DOI:10.3390/nano12081306.
- A. N. Birgani, M. Niyaifar and A. Hasanpour, Study of cation distribution of spinel zinc nano-ferrite by X-ray, J. Magn. Magn. Mater., 2015, 374, 179–181, DOI:10.1016/j.jmmm.2014.07.066.
- J. Li, H. Yuan, G. Li, Y. Liu and J. Leng, Cation distribution dependence of magnetic properties of sol–gel prepared MnFe2O4 spinel ferrite nanoparticles, J. Magn. Magn. Mater., 2010, 322, 3396–3400, DOI:10.1016/j.jmmm.2010.06.035.
- L. Néel, Étude théorique du couplage ferro-antiferromagnétique dans les couches minces, Ann. Phys., 1967, 14, 61–80, DOI:10.1051/anphys/19671402061.
- R. Sharma, P. Thakur, M. Kumar, P. B. Barman, P. Sharma and V. Sharma, Enhancement in A-B superexchange interaction with Mn2+ substitution in Mg-Zn ferrites as a heating source in hyperthermia applications, Ceram. Int., 2017, 43, 13661–13669, DOI:10.1016/j.ceramint.2017.07.076.
- M. Satalkara and S. N. Kane, On structural studies and cation distribution of La added Zn-Ni-Mg-Cu spinel nano ferrite, J. Phys.: Conf. Ser., 2016, 755, 012047, DOI:10.1088/1742-6596/755/1/012047.
- D. S. Nikam, S. V. Jadhav, V. M. Khot, R. A. Bohara, C. K. Hong, S. S. Mali and S. H. Pawar, Cation distribution, structural, morphological and magnetic properties of Co1-xZnxFe2O4 (x = 0–1) nanoparticles, RSC Adv., 2015, 5, 2338–2345, 10.1039/c4ra08342c.
- K. Dukenbayev, I. V. Korolkov, D. I. Tishkevich, A. L. Kozlovskiy, S. V. Trukhanov, Y. G. Gorin, E. E. Shumskaya, E. Y. Kaniukov, D. A. Vinnik, M. V. Zdorovets, M. Anisovich, A. V. Trukhanov, D. Tosi and C. Molardi, Fe3O4 nanoparticles for complex targeted delivery and boron neutron capture therapy, Nanomaterials, 2019, 9, 494, DOI:10.3390/nano9040494.
| This journal is © The Royal Society of Chemistry 2023 |