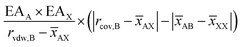Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Machine learning the vibrational free energy of perovskites†
Krishnaraj
Kundavu
 ,
Suman
Mondal
and
Amrita
Bhattacharya
,
Suman
Mondal
and
Amrita
Bhattacharya
 *
*
Ab initio Computational Materials Science Laboratory, Department of Metallurgical Engineering and Materials Science, Indian Institute of Technology, Bombay, Maharashtra 400076, India. E-mail: b_amrita@iitb.ac.in
First published on 9th August 2023
Abstract
Scanning the potential energy surface of a given compositional space via Ehull analysis is not sufficient to comment on thermodynamic stability, since the contribution stemming from the vibrational free energy is typically ignored in high-throughput searches of compositional spaces for stable compounds. The calculation of the vibrational free energy through first principles can be computationally very expensive owing to the complexity of the structures, which is directly proportional to the number of symmetrically non-unique terms to be evaluated for the creation of the dynamical matrix. In this work, we use machine learning (ML) to predict the free energy of a given compositional space (ternary perovskite compounds belonging to different symmetric structures) using the elemental and structural descriptors as fingerprints. The temperature dependence of the free energy is modeled using a 3rd-order polynomial fit, where the coefficients are learned and predicted using ML. Thereby, a highly accurate model is built for the zero-point energy (with a root mean square error (RMSE) of 18.9 meV per atom), which is further improved by employing a symbolic regression technique, SISSO, giving a very low RMSE of 8 meV per atom. This model, while providing a computationally inexpensive means for predicting the harmonic vibrational free energy of compounds, also provides an aid to obtain the free energy and hence assess the thermodynamic stability of a given composition at any temperature. This work also provides important insights on how the elemental and compound properties are related to the vibrational free energy and hence, may aid in its prediction.
1 Introduction
Perovskites are one of the most earth-abundant material classes, with several million compositional variants. They exhibit a wide range of electronic, optical, magnetic, and thermal properties, leading to their enormous technological advantages1–4 as ferroelectrics,5,6 ferromagnets,7–9 superconductors,10–12 photovoltaics,13,14 piezoelectrics,15–17etc. Even though research in this field had been going on for the past few decades, each day a new perovskite compound with an interesting application is discovered. Pertaining to their huge compositional space, it is practically impossible to explore the stability and the application potential of each one of them individually. Naturally, ab initio first-principles-based density functional theory (DFT) calculations can lead to the cost-effective prescreening of the compositional space before the experimental realization of the compounds.18–21 High-throughput loops have been designed to scan for new stable perovskite compounds,22,23 which is the foremost vital step that should be taken, even before the compounds are scanned for their physical properties.Several groups have attempted to explore this problem.24–29 However, it is not a trivial one, owing to the huge compositional space of perovskites. Ideally, a perovskite compound (chemical formula ABX3) will have a cubic unit cell with A and B cations occupying the center and corners of the cube, respectively, and X anions occupying the edge centers to form octahedra around the B cations. However, not all ABX3 compounds can be realized in an ideal perovskite structure. Distortions are created in the octahedra depending on the ionic radii of the cations and anions.30 The realization of ABX3 compounds in the perovskite structure has been related to the ionic radii of the constituent elements. In this regard, Goldschmidt31 gave an empirical parameter, t, for realization of the ideal perovskite structure:
 | (1) |
Data-driven methods can be used as an alternative aid to solve similar problems and gain further insight. These methods can be applied on a data set containing ab initio results of a given physical property under consideration (called the target property) and some relatively less complex and physically meaningful properties (called descriptors). The descriptors can be used as fingerprints to explain and analyze the target property. These methods, while aiding in the discovery of new materials with improved properties, allow prediction of new trends, hidden traits, anomalies, etc. Naturally, enormous computational effort has been spent to build online repositories containing different physical properties of compounds, which may be used to build meaningful machine-learning (ML) models.32–42 Many works have been carried out in this regard. ML models are being built to predict the inter-atomic potentials to circumvent the problems associated with the use of DFT in predicting various properties of materials, which may be computationally expensive.43,44 While these methods are yet to be tested for a wide variety of compound classes, researchers are using ML to predict the stability of compounds. For instance, tolerance factors, ionic radii, bond distances, etc., have been used to build an ML model to categorize perovskites from nonperovskites.45,46 ML models have also been built to predict the crystal structure based on the tolerance factor.24 Structure maps have been developed based on the bond lengths of A and B cations with X anions, and formability has been predicted using the tolerance factor.28 Bartel et al.47 defined a new tolerance factor, by considering multiple A- and B-site cations in double perovskites. They used SISSO,48 which is one of the compressed-sensing techniques, for formulating this new factor. Xu et al.49 built a machine-learning model using the data available in the Materials Project database32 to identify formable single and double B-cation perovskites. Similar to formability, machine-learning models have also been built to study the thermodynamic stability of perovskites.50 Li et al.51 predicted the thermodynamic phase stability of ABO3 compounds based on convex hull analysis. Balachandran et al.52 used the ionic radii of elements to build an ML model for predicting new cubic perovskite materials using an experimental database of 390 perovskite compounds. Talapatra et al.53 studied the overlap between the formable and thermodynamically stable perovskites predicted using machine-learning models, and predicted around 300 new compounds that are stable in their perovskite structures.
All these works provide some critical insights for the prediction and realization of new perovskite compounds. However, the vibrational (or thermal) free-energy content of a composition, at any given temperature, plays a very crucial role in determining its thermodynamic phase stability. The Ehull analysis reported in most literature focusing on high-throughput studies, however, does not take this into account. Hence, the energetically most stable phase, as concluded, may still not be the most stable phase thermodynamically. To completely define the thermodynamical stability, one needs to incorporate the vibrational free energy of the compound at constant volume (Helmholtz free energy, FH) and at constant pressure (Gibbs free energy, FG). The vibrational free energy can be estimated from the phonon frequency of the vibrational modes of a given composition. Using ab initio DFT-based methods, one can either employ finite displacement or perturbative approaches to calculate these phonon frequencies. However, the procedure is non-trivial, since it involves several force calculations for the displaced or the perturbed structures. The exact number of calculations that need to be performed depends on the symmetry of the considered unit cell. The lower the symmetry of the crystal, typically the larger the number of force calculations that are required for constructing the dynamical matrix.54,55 Hence, most of the materials databases do not contain the vibrational properties of the compounds. Few research groups have tried to predict free energy using ML models with their own databases. Legrain et al.56 built ML models for the vibrational free energy and entropy of 292 compounds from Inorganic Crystal Structure Database (ICSD) entries in aflow.org repositories. They used the elemental descriptors to predict various thermal properties. They achieved an RMSE of 18.76 meV per atom for the vibrational free energy. Bartel et al.57 used the SISSO (sure independence screening and sparsifying operator) approach to predict the experimental Gibbs free energy of inorganic compounds. Yoon et al.58 used adaptive learning techniques to build a generalized ML model for the Gibbs free energy of 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ICSD compounds. However, these works focus on the generalization of models to predict the Gibbs free energy, ignoring the temperature-dependent phase transition, which cannot be represented by just the chemical composition. Building ML models by incorporating inherent features of a compound class is required to solve this problem.
000 ICSD compounds. However, these works focus on the generalization of models to predict the Gibbs free energy, ignoring the temperature-dependent phase transition, which cannot be represented by just the chemical composition. Building ML models by incorporating inherent features of a compound class is required to solve this problem.
We, therefore, perform harmonic vibrational calculations on a set of perovskite compounds from the ICSD database with Ehull ≤ 80 meV. We first classify them as vibrationally stable (with all real modes) or unstable (with large phonon instabilities) by analyzing their harmonic phonon spectrum. A considerable number (∼32%) of compounds lying at the surface of the hull are found to be vibrationally unstable. We thus prepare a data set of 80 vibrationally stable compounds, along with their elemental and structural features. We employ one unique strategy to predict the variation of vibrational free energy, FH, as a function of temperature. We find that a third-order polynomial fit is adequate to represent the temperature variation of FH. Thus, we use ML to predict the coefficients of the polynomial fit. A flowchart illustrating the steps in our study is given in Fig. 1. Using our approach, a very accurate ML model is built to predict the variation of free energy with temperature. Thus, using only elemental and a few simple compound descriptors, the vibrational free energy of the compounds can be predicted, in a way that is fast, reasonably accurate and computationally inexpensive. Finally, we analyze the role of different descriptors in constituting the vibrational free energy.
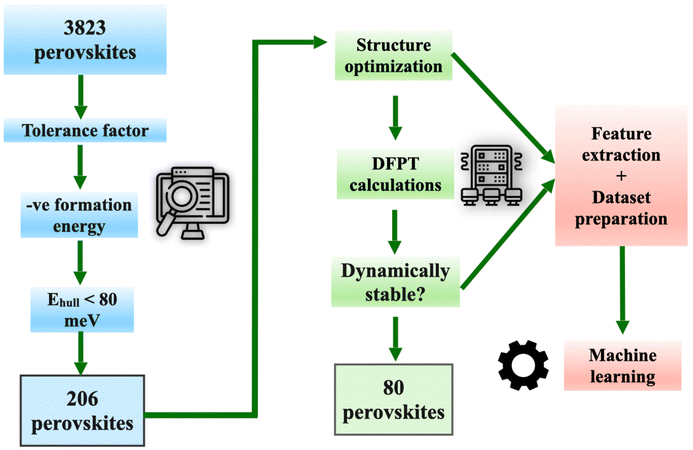 | ||
| Fig. 1 Schematic diagram showing the criteria for screening of vibrationally stable perovskite compounds and construction of the data set containing the descriptors for machine learning. | ||
2 Methodology
Classification of compounds
As the first step, a database is built by searching the literature49,53 and existing materials databases, i.e. Aflowlib, Materials Project, Inorganic Crystal Structure Database (ICSD), and Open Quantum Materials Database (OQMD), for compounds (Fig. S1 of the ESI†) with elements in the given stoichiometry, i.e. 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3, as in perovskite. A preliminary run through more than 50
3, as in perovskite. A preliminary run through more than 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 compounds gives a list of 3823 perovskite compounds. Out of these, 206 perovskite compounds are filtered in steps using three criteria, viz. (a) a tolerance factor of 0.7 < t < 1.1, (b) a negative formation energy and (c) an Ehull less than 80 meV. These compound are shortlisted for DFT calculations. DFT calculations (cf. Computational details) are performed for complete structural relaxation and subsequently, density functional perturbation theory calculations (cf. Computational details) are performed for plotting their phonon dispersions. Since the thermodynamic properties depend on the frequency of vibration of the phonons, very accurate force calculations are carried out and the convergence of the phonon spectrum is checked by using the supercell method. Compounds having no vibrational instability, i.e. no negative phonon modes, in the phonon spectrum (Fig. 2(a)) are considered as vibrationally stable. Compounds with very small phonon instabilities (i.e., up to 0.3 THz in frequency) are also included in this list. This is because such small phonon instabilities may be a result of some computational artifacts. All other compounds with large phonon instabilities are concluded to be vibrationally unstable and discarded.
000 compounds gives a list of 3823 perovskite compounds. Out of these, 206 perovskite compounds are filtered in steps using three criteria, viz. (a) a tolerance factor of 0.7 < t < 1.1, (b) a negative formation energy and (c) an Ehull less than 80 meV. These compound are shortlisted for DFT calculations. DFT calculations (cf. Computational details) are performed for complete structural relaxation and subsequently, density functional perturbation theory calculations (cf. Computational details) are performed for plotting their phonon dispersions. Since the thermodynamic properties depend on the frequency of vibration of the phonons, very accurate force calculations are carried out and the convergence of the phonon spectrum is checked by using the supercell method. Compounds having no vibrational instability, i.e. no negative phonon modes, in the phonon spectrum (Fig. 2(a)) are considered as vibrationally stable. Compounds with very small phonon instabilities (i.e., up to 0.3 THz in frequency) are also included in this list. This is because such small phonon instabilities may be a result of some computational artifacts. All other compounds with large phonon instabilities are concluded to be vibrationally unstable and discarded.
Construction of the descriptor sets
The descriptors used in this work are broadly classified as elemental and compound descriptors. The elemental descriptors, i.e. the physical properties of the elemental constituents (cf.Table 2), are collected mainly from the python Mendeleev library59 and also from Matminer.60 19 elemental descriptors are collected for each of the three elements, totaling to 57 descriptors.Since the compound descriptors may vary with different numerical settings used in the theoretical calculations, we extract them from the output of our DFT calculations (cf. Computational details). Thereby, 12 compound descriptors are collected (cf.Table 2), which are explained individually below.
1. The density, ρ, of the relaxed structures (in kg m−3).
2. Cohesive energy, Ecoh per f.u. (in eV), of the compound as calculated from its total energy (E[ABX3]) and that of the isolated atoms (taken as the reference chemical potential, viz. μA, μB and μX)
| Ecoh[ABX3] = E[ABX3] − μA − μB − 3μX | (2) |
3. The tolerance factor (1) and octahedron factor (3), which are calculated using the Shannon ionic radii61 of the A, B, and X ions;
 | (3) |
4. The nearest-neighbor distances between various atoms in the unit cell of the relaxed structure are generalized and considered as a set of descriptors. To keep all descriptors identical for the cubic as well as non-cubic structures, the means (![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) AB,
AB, ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) AX, and
AX, and ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) BX) and standard deviations (σAB, σAX, and σBX) of the three non-unique bond distances (viz. A–B, B–X, and A–X) are extracted from the relaxed geometry.
BX) and standard deviations (σAB, σAX, and σBX) of the three non-unique bond distances (viz. A–B, B–X, and A–X) are extracted from the relaxed geometry.
Target property
The target property in our problem is the Helmholtz free energy (FH), as calculated using:| FH = F(0)vib − TS | (4) |
| FH = A × T3 + B × T2 + C × T + D | (5) |
Machine-learning model
To build the ML model, the performance of several different ML algorithms is compared, viz. linear regression (LR), least absolute shrinkage and selection operator regression (LASSO), random forest (RF) regression, gradient boosting (GB) regression and Gaussian process regression (GPR), using the radial-basis function (RBF) along with the white kernel and rational quadratic kernel (henceforth referred to as GPR-1 and GPR-2, respectively), which are available as part of the scikit-learn package.62 Since our filtered data set comprises only 80 compounds, the K-fold cross-validation method is first used to make sure of the suitability of the model and avoid bias/overfitting. In K-fold cross-validation, the data set is divided into K subsets. The machine-learning model is then built using K-1 subsets and tested on the rest. This process is repeated multiple times with randomly selected subsets until convergence in accuracy is reached. The performance of these models is then judged based on two factors: the accuracy (R2 score) and the root mean square error (RMSE). The accuracy gives an estimation of the ability of the model to predict the accurate target values. The closer the R2 score to unity, the better the performance of the model. The R2 score is calculated as: | (6) |
The RMSE indicates the variance of the residuals, which is given by:
 | (7) |
Machine-learning strategy
The ML models are built in several steps. In the first step, only the elemental descriptors are used. A correlation heat map is plotted for each of the individual elemental constituents. All the highly correlated features with a correlation score of ±0.9 are dropped. Recursive feature elimination (RFE) is carried out to identify the feature's importance. The R2 score of the model is plotted as a function of the number of features. The same procedure is repeated after inclusion of the compound features in the feature list. This entire procedure is repeated with different ML algorithms and their performance is compared. Finally, one of the compressed-sensing methods, SISSO48 is used to build a model for the ZPE with combined but reduced dimensions using the elemental and simple compound descriptors (see Computational details section for details of the numerical settings used in SISSO).Testing on unseen data
The coefficients obtained using the best-performing ML models are used to predict the Helmholtz free energy of a set of perovskite compounds that is unknown to the sample space used to generate the models. Results of a few experimentally observed compounds are then compared with the literature to ascertain the utility of the ML models.3 Results and discussion
Construction of the data set
As already mentioned before, our dataset contains 206 perovskite compounds, which have negative formation energy and an Ehull value of ≤80 meV in the Materials Project database.32 To remove any bias imposed from the symmetry of the compounds, an equal distribution of cubic as well as non-cubic structures has been maintained in the dataset. As the first step, ionic as well as geometric relaxation of these structures is carried out. Subsequently, the cohesive energies of the compounds are calculated from the static total energy calculations of the relaxed structures, which are found to be negative in all cases. For all these structures, harmonic phonon calculations are performed, whereby we have filtered the vibrationally stable compounds (with no or negligible negative phonon modes) and subsequently extracted the thermal properties of the compounds. The final data set contains an even distribution of compounds with different symmetries. Thereby, the final data set comprises 21 cubic structures (i.e., in the Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space-group), 26 trigonal structures (i.e., in space-groups R3c, R3m, R
m space-group), 26 trigonal structures (i.e., in space-groups R3c, R3m, R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c, R
c, R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m, etc.) and 33 other structures (i.e. in space-groups Cmcm, Pnma, etc.) as provided in Table 1 of the ESI.†
m, etc.) and 33 other structures (i.e. in space-groups Cmcm, Pnma, etc.) as provided in Table 1 of the ESI.†
| Category | Descriptors |
|---|---|
| Elemental | Atomic number (Z), atomic mass (M), period (P), and group (G) number of the constituent elements in the periodic table, first ionization energy (IEI), second ionization energy (IEII), electron affinity (EA), Pauling electronegativity (χP), Allen electronegativity (χA), van der Waals radius (rvdw), covalent radius (rcov), atomic radius (ratomic), melting point (MP), boiling point (BP), density (ρ), heat of fusion (ΔHfus), heat of vaporization (ΔHvap), thermal conductivity (κ) and specific heat (cv) |
| Compound | Density (ρ), cohesive energy per f.u. (Ecoh), tolerance factor (t), octahedron factor (μ), and mean and standard deviation of neighbour distances (![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) AB, AB, ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) AX, AX, ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) BX, σAB, σAX, σBX) BX, σAB, σAX, σBX) |
The thermal properties of the vibrationally stable compounds are further calculated. The phonon spectrum (Fig. 2(a)) and thermal properties of BaLiF3 have been discussed as a representative case study. The Helmholtz free energy FH (kJ mol−1), entropy S (J K−1 mol−1) and specific heat at constant volume Cv (J K−1 mol−1) are plotted as a function of temperature T in Fig. 2(b). As already discussed in the methods section, the main motivation of our study is to learn the T dependence of FH. Fig. 2(c) shows the comparison of the 2nd- and 3rd-order polynomial fit for the Helmholtz free energy FH as a function of T. The 3rd-order fit (eqn (5)) ideally captures the variation. Hence, the four coefficients (A, B, C and D) of this fit are learned and predicted using ML.
Thus, the final data set of 80 perovskite compounds with 57 descriptors in total is obtained. As the first step, we analyze the feature correlation to eliminate the strongly correlated features. A high correlation between the descriptors may lead to overfitting of the model and hence, may decrease the accuracy of the model. The Pearson correlation coefficient heat maps for both elemental and compound descriptors are shown in Fig. 3. Pearson correlation coefficient between features is calculated as given below.
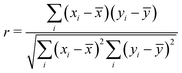 | (8) |
![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) and ȳ are the averages of all values of these two descriptors in the data set.
and ȳ are the averages of all values of these two descriptors in the data set.
 | ||
| Fig. 3 Correlation heat map plotted for (a) descriptors of one of the elements, viz. the element B presented as a representative case study (the heat maps for elements A and X are provided as a part of the ESI†), and (b) compound descriptors of perovskites in our database. Descriptors with a correlation score of ±0.9 are concluded to be strongly correlated (symbols have their usual meaning as given in Table 1). | ||
Using the above correlation score, strongly correlated features (with correlation of >±0.9) are dropped. Thus, out of the correlated features, viz. atomic number, atomic mass, and period, only atomic mass is chosen based on it's highest feature importance. The higher importance of atomic mass may be related to the crucial role of mass in lattice vibration. Similarly, all three different radii are found to be correlated and thus, only the van der Waals radius of A and X elements is retained. Also, the Pauling electronegativity, boiling point, and heat of vaporization are removed, while retaining their significantly correlated counterparts i.e., Allen electronegativity, melting point, and heat of fusion, respectively. The correlation between compound descriptors is further calculated, which has been shown in Fig. 3(b). The compound features are found to be uncorrelated. After dropping all the correlated descriptors, a total of 52 descriptors are left with which the ML models are built.
ML is performed on the processed data set to build a regression model for the zero-point energy (ZPE), i.e. the coefficient D of eqn (5), of the compounds. A 10-fold cross-validation (CV) method is used for evaluating our models to make sure that there is no bias due to the small size of our data set. In the first step, the performance of models is compared to decide the scaling method that is to be used. Since the descriptors used in our models belong to different dimensions, their magnitude varies in different ranges and thus, they need to be scaled to improve the performance of our models. This is illustrated in Fig. 4(a), where the performance of the models for unscaled, standard scaled and min-max scaled datasets is compared. As can be observed in the figure, scaling improves the performance of the models considerably for GPR-1 and GPR-2. In particular, the performance of GPR-2 is found to be very poor for the unscaled data and hence it's R2 score is not shown in the figure. The standard scaler is chosen, which gives the best results (with GPR-2) among all the models. To understand the critical role of descriptors in the target property, the descriptors are classified into three groups, viz. (a) elemental, (b) compound, and (c) mixed. Subsequently, the R2 scores of the models built using the elemental, compound, and mixed descriptor sets are compared. The final set of 80 compounds and their compound descriptors used in our data set are listed in Tables S2 and S3 of the ESI.†Fig. 4(b) compares the performance of the chosen algorithms for the different descriptor sets. As can be seen from the bar chart, the combined set of descriptors yields the best performance, while the elemental descriptor set is a close second.
Once the descriptor set and scaling methods are decided, the number of descriptors required is optimized to build the best-performing model for the ZPE. The performance of various ML algorithms is compared for the set of top 50, 40, 30, 20, and 10 descriptors in our data set. The top descriptors are decided using the SelectKBest method provided by scikit-learn. The comparison of the R2 scores for different models is shown in Fig. 4(c). As can be observed, the GPR-2 algorithm gives the best results with a CV score of 0.95 with the top 30 features. Except for the LASSO algorithm, the performance of other models is found to be comparable.
The top 15 descriptors for describing the ZPE are shown with their importance score as per the SelectKBest method, which is shown in Fig. 4(d). The atomic number and electron affinity of the X atoms are found to be very important descriptors. This is mainly due to the wide difference in the range of ZPE that is observed depending upon the variation of X elements in the perovskite. Other important features are found to be the bond-distance averages and standard deviations, the radius of A and X elements, heat of fusion of the B element, the first ionization energy of the A atom, etc. These properties directly or indirectly contribute to the bond strength of the atoms in the crystal and hence to the vibrational frequencies of phonons.
A CV score of 0.95 is obtained, from which it can be concluded that our data set does not have a huge bias in the samples and hence the model is built by splitting the data set into test and train subsets. The train subset is used to build the ML model and the test set is used as the unseen data to validate the model’s performance. To decide the optimum size of the training subset, we compare the R2 score and RMSE as a function of the number of data samples in the train set. Both R2 score and RMSE saturate at a train-subset size of 64 samples. Hence, 64 out of 80 compounds are randomly selected for the train set using scikit-learn methods and the remaining 16 compounds are used for testing. With this data set, we obtain a best test R2 score of 0.97 and RMSE of 1.84 kJ mol−1 (18.9 meV per atom) for the zero-point energy, i.e. the coefficient D, which is comparable to the results of Legrain et al.56 The scatter plot of the testing set is shown in Fig. 5(d).
The above-mentioned approach is also used to build the ML models for coefficients A, B, and C of eqn (5) (as shown in Fig. 5(a)–(c)). Comparisons of cross-validation R2 scores of different algorithms for coefficients A, B, and C are shown in Fig. S3 of the ESI.† Fig. S4 in the ESI† depicts the important features in the models built for these coefficients. The GPR-2-based model worked best for coefficient A with an R2 score of 0.88 with 40 descriptors. For coefficient B, the maximum R2 score using GPR-2 is obtained as 0.93 with standard scaling and 40 top descriptors. For coefficient C, GPR-2 gave a best CV score of 0.93 with 30 top descriptors using standard scaling. The R2 scores obtained for these models using test–train splitting are found to be very high (i.e. 0.94).
To increase the accuracy of predictions and to gain further insight into the role of descriptors, SISSO48 is used. With this method, the descriptors can be reduced to highly important compressed dimensions obtained by combining the original descriptors. Details of the seven dimensions obtained from SISSO are listed in Table 2, and yield a very highly accurate model for the ZPE. By analyzing the top features, we observe that most descriptors found in these complex dimensions are also found to have good correlation with our target property. For the ZPE, SISSO gives a dimension with a correlation score as high as 0.96. This feature involves a square root relation to the atomic radius of B and average AX bond length. The bond distance and radii of the constituent elements dominate 6 out of the 7 important features given by the SISSO algorithm. Some exceptions are the electron affinities and the thermal features like the melting points of constituent elements. Using the non-linear dimensions from SISSO, a linear regression model is trained, which yields a maximum R2 score of 0.99 and RMSE of 0.74 kJ mol−1 (8 meV per atom). Fig. 6 shows the scatter plot of predicted vs. calculated ZPE of the perovskite compounds in our data set. The ML models built for the different coefficients are used to predict the FH of several unknown compounds that are not present in our original dataset. As a tentative case study, the Imma and Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phases of EuNbO3 are selected, which are known to show phase transition,63i.e., at room temperature, EuNbO3 exists in the orthorhombic (Imma) structure and undergoes phase transition to the cubic (Pm
m phases of EuNbO3 are selected, which are known to show phase transition,63i.e., at room temperature, EuNbO3 exists in the orthorhombic (Imma) structure and undergoes phase transition to the cubic (Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) structure at 460 K. To verify the capability of our model to predict the FH and the thermodynamic phase transition, the total energy, i.e., the sum of the DFT static energy (electronic and ionic) and free energy (predicted from the model), is plotted as a function of temperature for both the phases in Fig. 7. The phase transition can be seen at ∼450 K, which is highlighted by the crossover between the blue (Imma phase) and the green (Pm
m) structure at 460 K. To verify the capability of our model to predict the FH and the thermodynamic phase transition, the total energy, i.e., the sum of the DFT static energy (electronic and ionic) and free energy (predicted from the model), is plotted as a function of temperature for both the phases in Fig. 7. The phase transition can be seen at ∼450 K, which is highlighted by the crossover between the blue (Imma phase) and the green (Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) curves. Similar verification is also performed for phase transitions within different phases of BaBiO3, KCaCl3, CsSrCl3 and LaAlO3, which are also found to be in agreement with the literature.64–67 Even in compounds (viz. ErMnO3 and EuZrO3) where phase transitions are not observed, the predicted stabilities of different phases are found to be in agreement with literature. The results for these compounds are given in the ESI,† and the inputs and codes used for these predictions are supplied in the github repository link included in the ESI.†
m) curves. Similar verification is also performed for phase transitions within different phases of BaBiO3, KCaCl3, CsSrCl3 and LaAlO3, which are also found to be in agreement with the literature.64–67 Even in compounds (viz. ErMnO3 and EuZrO3) where phase transitions are not observed, the predicted stabilities of different phases are found to be in agreement with literature. The results for these compounds are given in the ESI,† and the inputs and codes used for these predictions are supplied in the github repository link included in the ESI.†
 | ||
| Fig. 6 Calculated vs. predicted zero-point energy (ZPE) plotted using the 7 dimensions obtained from the SISSO algorithm. | ||
One of the main goals of our study is to understand the underlying science in the variation of the free energy and compound properties. By analyzing the correlation between the different descriptors and their importance in the ML models with good accuracy, further insights can be obtained. The analysis of the correlation between the descriptors and the target variables brings out some trends in the nature of the vibrational free energy. It is observed that for higher free-energy values, the 3rd-order variation of temperature, i.e., the contribution arising from coefficient A, is negligible. Also, an increase in the ZPE leads to a decrease in the curvature of the variation of the ZPE with temperature. This can also be observed in the bar charts in Fig. 8(a and b). The correlation of −0.99 between coefficients A and B can also be exploited to increase the prediction accuracy of models for coefficient A. Coefficient B (predicted from our model) can be incorporated as a descriptor to predict coefficient A.
A comparison of elemental descriptors shows that descriptors corresponding to the X-site element are more correlated to our target properties as compared to those corresponding to A- and B-site elements. Fig. 8(a) shows a clear trend in the variation of the ZPE (coefficient D) as the X-site element is varied. ZPE values decrease as we move down the periodic table within the same group (example: O → S → Se). Similarly, the ZPE decreases as we move to the right in the periodic table (example: N → O → F). This correlates with the variation in the atomic radius of these elements, which in turn plays a role in the bond formation in the perovskite structure. Elements at the A and B sites do not show such high correlation with our target properties (Fig. S6 and S7 in the ESI†). The atomic number, electron affinity and atomic radius of the X element have >0.7 correlation with all four coefficients in our study. Descriptors of element A also follow a similar trend, although with a lower correlation. Descriptors of element B show low correlation (<0.5) with the coefficients. Similarly, when comparing the correlation of elemental descriptors to the different coefficients, the element at site B becomes more prominent in determining coefficient D or the ZPE. These correlations are translated exactly to the feature importance for different ML models built in our study.
Comparing the correlation of compound descriptors to our target variables, it is more evident that compound descriptors have higher correlation to the coefficients of fit. In particular, mean bond lengths between the A and B elements and A and X elements are found to be very important. However the standard deviation between these bond lengths becomes less important to coefficients A, B and C as compared to D. Fig. 8(c) shows the scatter plot of ZPE as a function of mean A–X bond length, indicating that moderate correlation exists between these two. However, this correlation is enhanced by SISSO using non-linear operators to combine multiple descriptors, as shown in Fig. 8(d). The dependence of FH on the bond lengths is driven by its direct correlation with the force constant required to form the dynamical matrix, which depends on the strength of the bonds and hence, the bond lengths. Thus, this is directly reflected in the top descriptors obtained in our models.
4 Conclusion
In the context of perovskite research, predicting new stable ones prior to their synthesis in the laboratory is a problem that has acquired immense attention in the past. To date, many researchers have attempted to solve this problem by performing high-throughput calculations using ab initio density functional theory. The vibrational free-energy contribution to the total energy is absolutely vital for the prediction of a given perovskite composition as thermodynamically stable/unstable in different temperature ranges. However, the calculation of the free energy of vibration of a solid is computationally very expensive, owing to the basic symmetry of the structure. The lower the symmetry, the more force calculations are required for constructing the dynamical matrix. In order to reduce the computational cost of calculating the vibrational free energy, machine-learning (ML) methods can be used. We perform structural relaxation and harmonic vibrational calculations on a set of 206 compounds with Ehull < 80 meV. Thereby, we filter 80 dynamically stable compounds with no/negligible negative phonon modes by ensuring all the convergence criteria are met. The phonon frequencies are used to calculate the Helmholtz free energy of these compounds as a function of temperature. We use polynomial fitting of the third order to depict the temperature dependence of the vibrational free energy. Using ML, we build regression models to predict the coefficients of the polynomial fit using elemental and simple compound descriptors. We obtain a highly accurate model for the zero-point energy, as well as for all the other coefficients, with a maximum R2 score of 0.97 and RMSE of 1.84 kJ mol−1 (18.9 meV per atom). Further, we use SISSO to reduce the dimensions and with 7 combined dimensions, an unprecedented accuracy is achieved. Our models succeed in correctly predicting the phase stability of many unseen compounds (viz. EuNbO3, BaBiO3, CsSrCl3, etc.), which provides validation of the utility of our models. This study thus offers a simple route to predict the vibrational free energy of perovskite compounds. Although the performance of the model may improve with the inclusion of more sample points, the existence of the model definitely hints towards a cost-effective pathway to predict the thermodynamic stability of a given compositional space.5 Computational details
Structure relaxation
We employ first-principles density functional theory (DFT)68,69 to calculate the structural and thermal descriptors of the perovskite compounds. The calculations are performed using a popular DFT code, VASP (Vienna Ab initio Simulation Program),70 which is a plane-wave-based electronic structure code. The generalized gradient approximation of Perdew, Burke, and Ernzerhof (PBE)71 is used for the treatment of electronic exchange and correlation. All numerical settings are chosen so as to ensure convergence in energy differences to better than 10−5 eV and a plane-wave cutoff energy of 520 eV. The atomic positions and lattice vectors are fully relaxed for all structures using the conjugate gradient minimization algorithm. The forces are converged to less than 10−3 eV Å−1. For all calculations, a converged Monkhorst–Pack k-mesh grid is applied for the unit cell. For each structure, ionic as well as geometric relaxations are performed.Phonon calculations
With the relaxed geometry, the phonon band structure is calculated using the density functional perturbation theory (DFPT) method as implemented in the phonopy code.72 A converged supercell of 2 × 2 × 2 is used to calculate the phonon band structure and thermal properties. The amplitude of the displacements is fixed to 0.01 Å, and the forces are converged to an accuracy of 10−3 eV Å−1. From the phonon frequency details obtained using phonopy, we can get the energy E of the phonon system as | (9) |
 | (10) |
SISSO
In order to build a regression model with reduced dimensional space for the ZPE, SISSO48 is used on our data set with elemental and compound descriptors. We start with a total of 50 non-correlated elemental and compound features with ZPE as the target property. All features are scaled between 0 and 1 to avoid imaginary features in the SISSO algorithm. The mathematical operations used to generate the complex non-linear dimensions include the operations . The combined features were built in 3 steps with descriptor sets Φ1, Φ2, and Φ3 corresponding to increasing feature complexity. The numbers of descriptors in Φ1, Φ2 and Φ3 are 1905, 1
. The combined features were built in 3 steps with descriptor sets Φ1, Φ2, and Φ3 corresponding to increasing feature complexity. The numbers of descriptors in Φ1, Φ2 and Φ3 are 1905, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 740
740![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 446 and 1
446 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 853
853![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 192
192![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 759
759![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 494, respectively. The magnitude of correlation of each feature is calculated during sure independence screening (SIS) at each iteration, and subsequently, only the top 20 ranked features are retained. At each iteration, O operates on all available combinations, and ∼1012 features are constructed using a complexity cutoff of 3 and dimensionality of 7.
494, respectively. The magnitude of correlation of each feature is calculated during sure independence screening (SIS) at each iteration, and subsequently, only the top 20 ranked features are retained. At each iteration, O operates on all available combinations, and ∼1012 features are constructed using a complexity cutoff of 3 and dimensionality of 7.
Author contributions
Krishnaraj Kundavu: methodology, investigation, data curation, visualisation, writing – original draft preparation, writing – reviewing and editing. Suman Mondal: writing – reviewing and editing. Amrita Bhattacharya: conceptualization, supervision, writing – reviewing and editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
AB acknowledges the IIT B seed grant (RD/0517-IRCCSH0-043), SERB ECRA grant (ECR/2018/002356), SERB POWER grant (SPG/2021/003874), and BRNS regular grant (BRNS/37098) for the financial assistance. The high-performance computational facilities, viz. Aron (AbCMS lab, IITB), Dendrite (MEMS dept., IITB), Spacetime-IITB, and CDAC Pune (Param Yuva-II), are acknowledged for providing the computational hours.Notes and references
- M. L. Medarde, J. Phys.: Condens. Matter, 1997, 9, 1679 CrossRef CAS.
- J. Blasco, J. Garcia, J. De Teresa, M. Ibarra, P. Algarabel and C. Marquina, J. Phys.: Condens. Matter, 1996, 8, 7427 CrossRef CAS.
- S. Brittman, G. W. P. Adhyaksa and E. C. Garnett, MRS Commun., 2015, 5, 7–26 CrossRef CAS PubMed.
- L. Chouhan, S. Ghimire, C. Subrahmanyam, T. Miyasaka and V. Biju, Chem. Soc. Rev., 2020, 49, 2869–2885 RSC.
- R. Ding, Y. Lyu, Z. Wu, F. Guo, W. F. Io, S.-Y. Pang, Y. Zhao, J. Mao, M.-C. Wong and J. Hao, Adv. Mater., 2021, 33, 2101263 CrossRef CAS PubMed.
- J. J. Wang, D. Fortino, B. Wang, X. Zhao and L.-Q. Chen, Adv. Mater., 2020, 32, 1906224 CrossRef CAS PubMed.
- G. Jonker and J. Van Santen, Physica, 1950, 16, 337–349 CrossRef CAS.
- G. Blasse, J. Phys. Chem. Solids, 1965, 26, 1969–1971 CrossRef CAS.
- D. Serrate, J. De Teresa and M. Ibarra, J. Phys.: Condens. Matter, 2007, 19, 023201 CrossRef.
- F. S. Galasso, Perovskites and high-Tc superconductors, Gordon and Breach Science Publishers Inc., United States, 1990 Search PubMed.
- B. Raveau, C. Michel, M. Hervieu, D. Groult and J. Provost, Adv. Mater., 1990, 2, 299–304 CrossRef CAS.
- D. W. Murphy, S. Sunshine, R. B. Van Dover, R. J. Cava, B. Batlogg, S. Zahurak and L. Schneemeyer, Phys. Rev. Lett., 1987, 58, 1888 CrossRef CAS PubMed.
- H. J. Snaith, Nat. Mater., 2018, 17, 372–376 CrossRef CAS PubMed.
- H. Min, D. Y. Lee, J. Kim, G. Kim, K. S. Lee, J. Kim, M. J. Paik, Y. K. Kim, K. S. Kim, M. G. Kim, T. J. Shin and S. Il Seok, Nature, 2021, 598, 444–450 CrossRef CAS PubMed.
- L. Bellaiche and D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 61, 7877 CrossRef CAS.
- T. Zheng, J. Wu, D. Xiao and J. Zhu, Prog. Mater. Sci., 2018, 98, 552–624 CrossRef CAS.
- K. Uchino, Sci. Technol. Adv. Mater., 2015, 16, 046001 CrossRef PubMed.
- F. Calle-Vallejo, J. I. Martnez, J. M. Garca-Lastra, M. Mogensen and J. Rossmeisl, Angew. Chem., Int. Ed., 2010, 49, 7699–7701 CrossRef CAS PubMed.
- S. Körbel, M. A. Marques and S. Botti, J. Mater. Chem. C, 2016, 4, 3157–3167 RSC.
- A. A. Emery, J. E. Saal, S. Kirklin, V. I. Hegde and C. Wolverton, Chem. Mater., 2016, 28, 5621–5634 CrossRef CAS.
- P. R. Raghuvanshi, S. Mondal and A. Bhattacharya, J. Mater. Chem. A, 2020, 8, 25187–25197 RSC.
- J. E. Saal, S. Kirklin, M. Aykol, B. Meredig and C. Wolverton, JOM, 2013, 65, 1501–1509 CrossRef CAS.
- A. Jain, O. Voznyy and E. H. Sargent, J. Phys. Chem. C, 2017, 121, 7183–7187 CrossRef CAS.
- M. W. Lufaso and P. M. Woodward, Acta Crystallogr., Sect. B: Struct. Sci., 2001, 57, 725–738 CrossRef CAS PubMed.
- Z. Li, Q. Xu, Q. Sun, Z. Hou and W.-J. Yin, Adv. Funct. Mater., 2019, 29, 1807280 CrossRef.
- P. M. Woodward, Acta Crystallogr., Sect. B: Struct. Sci., 1997, 53, 32–43 CrossRef.
- P. M. Woodward, Acta Crystallogr., Sect. B: Struct. Sci., 1997, 53, 44–66 CrossRef.
- H. Zhang, N. Li, K. Li and D. Xue, Acta Crystallogr., Sect. B: Struct. Sci., 2007, 63, 812–818 CrossRef CAS PubMed.
- A. A. Emery and C. Wolverton, Sci. Data, 2017, 4, 170153 CrossRef CAS PubMed.
- R. J. D. Tilley, The ABX3 Perovskite Structure, in Perovskites: Structure-Property Relationships, John Wiley & Sons, Ltd, 2016, ch. 1, pp. 1–41 Search PubMed.
- V. M. Goldschmidt, Naturwissenschaften, 1926, 14, 477–485 CrossRef CAS.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, APL Mater., 2013, 1, 011002 CrossRef.
- S. Kirklin, J. E. Saal, B. Meredig, A. Thompson, J. W. Doak, M. Aykol, S. Rühl and C. Wolverton, npj Comput. Mater., 2015, 1, 15010 CrossRef CAS.
- C. Oses, C. Toher and S. Curtarolo, MRS Bull., 2018, 43, 670–675 CrossRef.
- D. Hicks, M. J. Mehl, E. Gossett, C. Toher, O. Levy, R. M. Hanson, G. Hart and S. Curtarolo, Comput. Mater. Sci., 2019, 161, S1–S1011 CrossRef CAS.
- M. J. Mehl, D. Hicks, C. Toher, O. Levy, R. M. Hanson, G. Hart and S. Curtarolo, Comput. Mater. Sci., 2017, 136, S1–S828 CrossRef CAS.
- R. Yuan, Z. Liu, P. V. Balachandran, D. Xue, Y. Zhou, X. Ding, J. Sun, D. Xue and T. Lookman, Adv. Mater., 2018, 30, 1702884 CrossRef PubMed.
- J. Kim, E. Kim and K. Min, Adv. Theory Simul., 2019, 2100263 Search PubMed.
- J. Li, B. Pradhan, S. Gaur and J. Thomas, Adv. Energy Mater., 2019, 9, 1901891 CrossRef CAS.
- D. Bhattacharjee, K. Kundavu, D. Saraswat, P. R. Raghuvanshi and A. Bhattacharya, ACS Appl. Energy Mater., 2022, 5, 8913–8922 CrossRef CAS.
- C. W. Myung, A. Hajibabaei, J.-H. Cha, M. Ha, J. Kim and K. S. Kim, Adv. Energy Mater., 2022, 2202279 CrossRef CAS.
- V. Gladkikh, D. Y. Kim, A. Hajibabaei, A. Jana, C. W. Myung and K. S. Kim, J. Phys. Chem. C, 2020, 124, 8905–8918 CrossRef CAS.
- A. Hajibabaei, C. W. Myung and K. S. Kim, Phys. Rev. B, 2021, 103, 214102 CrossRef CAS.
- A. Hajibabaei, M. Ha, S. Pourasad, J. Kim and K. S. Kim, J. Phys. Chem. A, 2021, 125, 9414–9420 CrossRef CAS PubMed.
- Y. Zhang, R. Ubic, D. Xue and S. Yang, Mater. Focus, 2012, 1, 57–64 CrossRef CAS.
- G. Pilania, P. Balachandran, J. E. Gubernatis and T. Lookman, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2015, 71, 507–513 CrossRef CAS PubMed.
- C. J. Bartel, C. Sutton, B. R. Goldsmith, R. Ouyang, C. B. Musgrave, L. M. Ghiringhelli and M. Scheffler, Sci. Adv., 2019, 5, eaav0693 CrossRef CAS PubMed.
- R. Ouyang, S. Curtarolo, E. Ahmetcik, M. Scheffler and L. M. Ghiringhelli, Phys. Rev. Mater., 2018, 2, 083802 CrossRef CAS.
- Q. Xu, Z. Li, M. Liu and W.-J. Yin, J. Phys. Chem. Lett., 2018, 9, 6948–6954 CrossRef CAS PubMed.
- H. Liu, J. Cheng, H. Dong, J. Feng, B. Pang, Z. Tian, S. Ma, F. Xia, C. Zhang and L. Dong, Comput. Mater. Sci., 2020, 177, 109614 CrossRef CAS.
- W. Li, R. Jacobs and D. Morgan, Comput. Mater. Sci., 2018, 150, 454–463 CrossRef CAS.
- P. V. Balachandran, A. A. Emery, J. E. Gubernatis, T. Lookman, C. Wolverton and A. Zunger, Phys. Rev. Mater., 2018, 2, 043802 CrossRef CAS.
- A. Talapatra, B. P. Uberuaga, C. R. Stanek and G. Pilania, Chem. Mater., 2021, 33, 845–858 CrossRef CAS.
- J. Zhang, Y. Cheng, W. Lu, E. Briggs, A. J. Ramirez-Cuesta and J. Bernholc, J. Chem. Theory Comput., 2019, 15, 6859–6864 CrossRef CAS PubMed.
- P. Pavone, R. Bauer, K. Karch, O. Schütt, S. Vent, W. Windl, D. Strauch, S. Baroni and S. De Gironcoli, Phys. B, 1996, 219–220, 439–441 CrossRef.
- F. Legrain, J. Carrete, A. van Roekeghem, S. Curtarolo and N. Mingo, Chem. Mater., 2017, 29, 6220–6227 CrossRef CAS.
- C. J. Bartel, S. L. Millican, A. M. Deml, J. R. Rumptz, W. Tumas, A. W. Weimer, S. Lany, V. Stevanović, C. B. Musgrave and A. M. Holder, Nat. Commun., 2018, 9, 4168 CrossRef PubMed.
- J. Yoon, E. Choi and K. Min, J. Phys. Chem. A, 2021, 125, 10103–10110 CrossRef CAS PubMed.
- L. Mentel, mendeleev - A Python resource for properties of chemical elements, ions and isotopes, ver. 0.7.0, https://github.com/lmmentel/mendeleev, 2014 Search PubMed.
- L. Ward, A. Dunn, A. Faghaninia, N. E. Zimmermann, S. Bajaj, Q. Wang, J. Montoya, J. Chen, K. Bystrom and M. Dylla, et al. , Comput. Mater. Sci., 2018, 152, 60–69 CrossRef.
- R. t Shannon and C. Prewitt, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1970, 26, 1046–1048 CrossRef CAS.
- F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss, V. Dubourg, J. Vanderplas, A. Passos, D. Cournapeau, M. Brucher, M. Perrot and E. Duchesnay, J. Mach. Learn. Res., 2011, 12, 2825–2830 Search PubMed.
- Y. Kususe, S. Yoshida, K. Fujita, H. Akamatsu, M. Fukuzumi, S. Murai and K. Tanaka, J. Solid State Chem., 2016, 239, 192–199 CrossRef CAS.
- Q. Zhou and B. J. Kennedy, Solid State Commun., 2004, 132, 389–392 CrossRef CAS.
- M. Midorikawa, Y. Ishibashi and Y. Takagi, J. Phys. Soc. Jpn., 1979, 46, 1240–1244 CrossRef CAS.
- Z. Wen-Chen, Phys. B, 2000, 291, 266–269 CrossRef.
- H. Lehnert, H. Boysen, J. Schneider, F. Frey, D. Hohlwein, P. Radaelli and H. Ehrenberg, Z. Kristallogr. - Cryst. Mater., 2000, 215, 536–541 CrossRef CAS.
- P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864 CrossRef.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133 CrossRef.
- V. Blum, R. Gehrke, F. Hanke, P. Havu, V. Havu, X. Ren, K. Reuter and M. Scheffler, Comput. Phys. Commun., 2009, 180, 2175–2196 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- A. Togo and I. Tanaka, Scr. Mater., 2015, 108, 1–5 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: The data set and the codes and models used in this work are available in github repository and link is provided in the supplementary pdf file. See DOI: https://doi.org/10.1039/d3ma00216k |
| This journal is © The Royal Society of Chemistry 2023 |