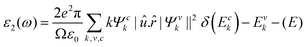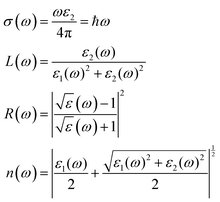Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Pressure-dependent comparative study of the mechanical, electronic, and optical properties of CsPbX3 (X = Cl, Br, I): a DFT study for optoelectronic applications†
M.
Aktary
 *a,
M.
Kamruzzaman
*a,
M.
Kamruzzaman
 *b and
R.
Afrose
b
*b and
R.
Afrose
b
aDepartment of Materials Science and Engineering, King Fahd University of Petroleum and Minerals, Saudi Arabia. E-mail: aktarymahbuba@gmail.com; Tel: +966 532754870
bDepartment of Physics, Begum Rokeya University, Rangpur, Rangpur-5400, Bangladesh. E-mail: kzaman.phy11@gmail.com
First published on 11th September 2023
Abstract
Inorganic metal-halide perovskite (MHP) materials are potential candidates for optoelectronic and energy-storage device applications. In this work, a systematic hydrostatic pressure-dependent investigation of the elastic, electronic, optical, and photocatalytic properties of CsPbX3 (X = Cl, Br and I) was performed based on ab initio simulations. This study revealed that the mechanical stability of Cl- and Br-containing perovskites could be sustained up to 20 and 25 GPa, respectively, while CsPbI3 could survive up to 75 GPa applied pressure. It was also found that the mechanical properties of CsPbX3 perovskites were ductile under ambient conditions and their ductility significantly improved (decreased) with pressure. The electronic property calculations suggested that CsPbX3 perovskites have a direct energy band gap, which decreases with increasing pressure due to structural change and/or a shifting of the conduction band minimum toward the Fermi level. The band gap became zero under pressures of 20.0, 15.0, and 10.0 GPa for Cl-, Br-, and I-based halides, indicating the transition of the crystal structure. The absorption peak of CsPbX3 perovskites radically shifted toward the low photon energy region with applied pressure. The photoconductivity, reflectivity, and dielectric constant showed an increasing tendency under pressure. These findings would be beneficial for experimental study and suggest that pressure has significant effect on the physical properties of CsPbX3 perovskites, which might be a promising avenue for exploitation in optoelectronic and photonic applications.
1. Introduction
With a growing global population and a worsening energy problem, demands for more efficient PV cells, optoelectronics, and electronic devices have become a major concern.1 Researchers are highly concerned about the health of ecosystems because of the pressure from rising demands on resources. The demand for innovative forms of efficient, environmentally friendly, and renewable energy-harvesting technology has attracted a lot of interest from the scientific community.2–11 To this end, photovoltaic technology has attracted the most research interest for solving the aforementioned problems. Photovoltaic device can directly convert renewable solar energy into electrical energy. It is well known that Si-based solar cells currently dominate the photovoltaic market12,13 but due to their low efficiency and high maintenance costs of the purification process, this may not last for very long.1 These involve the use of an indirect band gap semiconductor but reduced optical absorption and carrier mobility have made it uncompetitive for use in more functional devices. Though, amorphous Si technology is both affordable and easy to manufacture, its poor stability and low photoconversion efficiency (PCE) are major causes of concern.14,15 However, the alternatives to Si, including some inorganic photovoltaic materials, such as iron disulfide (FeS2), gallium arsenide (GaAs), and cadmium telluride (CdTe), are promising but their efficiency is not yet satisfactory. Multi-junction AlGaInP-, AlGaAs-, GaAs-, and GaInAs-based solar cells are another alternative, and being around 47.1% more efficient have attracted a great deal of attention from the scientific community.16 Although, current research is encouraging, all these mixtures are expensive due to the inclusion of scarce elements, such as In or Ga, and also hazardous due to the prescence of As and P. As a result, scientists are keen to identify new solar cell materials that are inexpensive, abundant on earth, and easily processed. To this goal, organic–inorganic halide perovskites are of tremendous interest as they fulfill these requirements. Extended research into the development of perovskites began in the 1990s with an aim to replace Si and to produce multipurpose solar cell technology. Miyasaka and co-workers introduced a perovskites solar cell in 2006 for the first time, with a PCE of 2.2%,17 which had reached 3.8% by 2009.18 Researchers reported a much increased PCE of 27.6% in 2018, while the US National Renewable Energy Laboratory verified a perovskite solar cell with a maximum PCE of 25.5% in 2020.19 Thus, by carefully choosing the right atoms and placing them in the right places, metal-halide perovskites solar cells have a great chance of replacing the dominant Si-based solar cells.20–25 Organic–inorganic halide perovskites with the formula ABX3 (where, A = monovalent organic–inorganic cation, reported as Cs+ or CH3NH3+, etc.; B = a divalent inorganic cation: Pb2+ or Sn2+etc.; X = a halide: Cl-, Br-, I-)1 are highly efficient26–29 due to their excellent absorption coefficient,30–32 carrier mobility, long carrier life, and suitable band gaps.33–36Inorganic perovskites have received a lot of attention from researchers despite the fact that organic–inorganic perovskites are physically and chemically not very stable.1 For the next generation of advanced electrical, optoelectronic, and other devices, Cs-based inorganic perovskites CsPbX3 (X = Cl, Br, I) are considered the most promising materials.37
To improve the performance of optoelectronic devices, like LEDs, photodetectors, and lasers, the characteristics of CsPbX3 need to be modified by adding metal halides or combining with halides.38–59 Due to its higher binding energy of 64 meV, CsPbCl3 (X = Cl, Br, I) has a larger band gap and superior thermal stability, making it the preferred choice for many optomagnetic and optoelectronic,60 single,61 and multiphoton pumping-based laser devices.62 CsPbBr3 has demonstrated a band gap of 3.153 eV,62 and cubic bulk CsPbI3 a band gap of 1.73 eV.4 It has been shown that direct band gap semiconductors with the formula of CsPbX3 (X = Cl, Br, I) absorb visible and ultraviolet light. As perovskites are a smart class of materials with significant potential for photovoltaic and optoelectronic applications, all-inorganic perovskites have a very flexible crystal structure and are attracting great interest.
As pressure is a key factor in adjusting the physical characteristics of any material,63–65 by adjusting the pressure, the optical, electronic, and optoelectronic properties can be tuned as well as the material phase transitions.66–70 For example, Zou et al. (2017) reported that at considerably greater pressures, the Jahn–Teller effect might eventually result in a direct to indirect band-gap electrical transition.71 This research established high pressure as a reliable tool for controlling the structure along with the band gap of CsPbBr3 NCs, revealing the nano-scale physiochemical process of these squeezed MHP nanosystems. So, the pressure-dependent properties are crucial for optoelectronic quantum dot applications. In this way, research conducted under high pressure frequently provides insights into the optoelectronic characteristics of perovskite materials for photoluminescence kinetics.
However, extensive theoretical research on the pressure-dependent comparisons of the elastic, mechanical, electronic, and optical characteristics of CsPbX3 has not yet been published. The compound is more beneficial for applications in optoelectronic devices thanks to the tuning of the band gap, which can improve electron movement from the valence band to the conduction band, boosting the optical absorption and conductivity.
2. Method
The lattice constants of bulk perovskites of CsPbX3 (X = Cl, Br, I) are 5.734, 6.017, and 6.38 Å, respectively, and they have a cubic structure with the space group Pmm (221) (Table 5). DFT calculations were carried out using the CASTEP code in the Materials Studio simulation software to compare and analyze the results of the structural, mechanical, electronic, and optical properties.72–77 Electrostatic interactions between component atoms’ valence shell and ion core were examined using the Perdew–Burke–Ernzerhof (PBE) in the framework of the generalized gradient approximation (GGA) and ultrasoft pseudopotentials. Electronic band edge diagram calculations were also used to calculate the photocatalytic property. To begin with, we decided to perform numerical operations on a cubic structure.A five-atom CsPbCl3 primitive cell was thus developed, as shown in Fig. 1. In this cell, one Cs atom is located at the Wyckoff site (0, 0, 0), one Pb atom is located at the site of (0.5, 0.5, 0.5), and three Cl atoms are located at (0, 0.5, 0.5) fractional coordinates. The valence sets interact as follows: Cs: 5s2 5p6 6s1, Pb: 5s2 5p6 5d10 6s2 6p2, Cl: 3s2 3p5, Br: 4s2 4p5, and I: 5s2 5p5. Identical software functional treatments were used to optimize all the crystals. CsPbCl3 was first simulated with the lattice parameter set to a = 5.734 Å.78 The optimized structure with the lowest formation enthalpy was then verified with the plane-wave basic set and k-points of 6 × 6 × 6 and a 520 eV cutoff energy, SCF tolerance of 2 × 10−6 eV per atom, convergence tolerance energy of 2 × 10−5 eV per atom, and maximum force and stress of 0.05 eV Å−1 and 0 GPa, respectively. The largest atomic displacement was limited to 0.002.
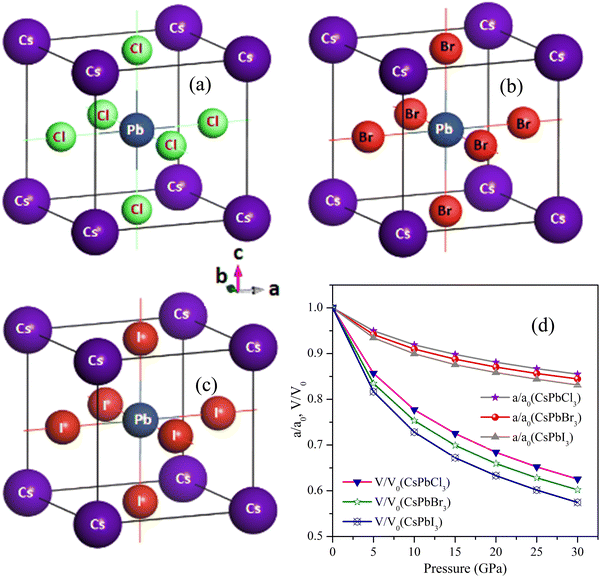 | ||
| Fig. 1 Pressure response for the structures of (a) CsPbCl3 (b) CsPbBr3, and (c) CsPbI3 depicted with their atomic orientations. | ||
After substituting Br and I atoms (100%) for the Cl atoms in CsPbBr3 and CsPbI3 under the same conditions, we determined the elastic, electrical, and optical properties of each compound.
3. Results and discussion
3.1 Structural and mechanical properties
To do the numerical calculations, we mostly chose the cubic structure of CsPbCl3 among cubic, tetragonal, and orthorhombic structures due to its high-temperature tolerance. In order to achieve structural analysis, like to obtain the lattice constant, a (Å), bulk moduli, B (GPa), and its pressure responses, the volume of the unit cell of each CsPbX3 (X = Cl, Br, I) was tuned by optimization of the parameters. After discovering the CsPbCl3 cell's optimized structure, the Cl atom was substituted for the Br and I atoms, which made the cell optimized for the CsPbBr3 and CsPbI3 perovskite structures. The optimized crystal structures, normalized parameters, and volumetric pressure responses of CsPbCl3, CsPbBr3, and CsPbI3 are shown in Fig. 1(a)–(d) and Table 5 shows the optimal cell parameters for the matching perovskites. From Table 5, it can be seen that CsPbCl3's optimum lattice parameter a was 5.734 Å, which was elongated by 4.8% and 11.6%, respectively, after the replacement of the Cl atom by Br and I atoms. It was seen that the optimized lattice parameter a decreased to 5.02%, 8.07%, 10.1%, and 11.8% for CsPbCl3 as the pressure was increased to 5, 10, 15, and 20 GPa, respectively. For CsPbBr3 and CsPbI3, the decrement was 5.8% and 6.5% at 5 GPa, 8.9% and 10.0% at 10 GPa, and 13.3% and 12.4% at 15 GPa, respectively, as result of the replacement of the halide Cl atom by Br and I atoms. The resulting values were in good accordance with other theoretical as well as experimental results reported.79 From these results for CsPbX3 (X = Cl, Br, I), a relation was established and can be expressed as: VCsPbCl3 < VCsPbBr3 < VCsPbI3 (Table 5) with a volume increment of 15.4% and 39.3% for CsPbBr3 and CsPbI3, respectively, as a result of lattice expansion due to the comparatively larger ionic radii of Br and I atoms.Three separate elastic tensors, C11, C12, and C44, were used to independently calculate the explicit and implicit mechanical properties of the cubic perovskites of CsPbX3. The computed values for the isostructural forms of CsPbCl3, CsPbBr3, and CsPbI3 are displayed visually in Fig. 2(a) and recorded in Table 1. From Fig. 2(a) and Table 1, it is obvious that they were mechanically stable because all these crystals met the conditions of C11 + 2C12 > 0, C44 > 0 and C11 − C44 > 0 as well as the additional stability criterion of C12 < B < C11.80 The mechanical stability was justified under Born's criteria for these crystals.81 The association of 2C44 = C11 − C1282 and a non-zero Zener's anisotropy factor A both demonstrated that each of these bulks was elastically anisotropic.83 The materials exhibited greater resistance to longitudinal deformation than to shape deformation under the circumstances of C11 > C12 > C44, with CsPbBr3 having the highest value of C11. The capacity of materials scientists to create novel materials with specific mechanical reactions is constrained by the absence of experimental data. With anisotropic materials, it is much more important to examine and depict the directional elastic characteristics as opposed to their averages, such as Young's modulus, linear compressibility, shear modulus, and Poisson's ratio. At the threshold value of Poisson's ratio 0.26 (known as brittle/ductile borderline), the material can be distinguished as a brittle or ductile crystalline material. Table 1 makes it very obvious that the CsPbX3 materials had values larger than 0.26, proving their high degree of ductility. Among them, CsPbI3 was more ductile because it could withstand higher pressure.
| Materials | C 11 | C 12 | C 44 | B | G | E | σ |
|---|---|---|---|---|---|---|---|
| CsPbCl3 | 48.35 | 7.88 | 4.92 | 21.37 | 9.05 | 23.79 | 0.31 |
| CsPbBr3 | 51.94 | 16.47 | 4.18 | 28.30 | 7.81 | 21.47 | 0.37 |
| CsPbI3 | 39.32 | 6.75 | 5.35 | 17.61 | 8.52 | 22.01 | 0.29 |
ELATE Code is a reliable computational method to observe elastic moduli in 2D as well as 3D views. To observe the elastic properties in different crystallographic planes, the Young's modulus, linear compressibility, and shear modulus were plotted with ELATE code only for the zero pressure condition in 2D plane projections. For CsPbX3, all the above-mentioned parameters showed similar responses along the xy, xz, and yz planes. So only the xy-plane responses are shown in Fig. 2. The Young's modulus exhibited the highest values along the horizontal and vertical axes, and at least at 45° between the abscissa and ordinate.
The linear compressibility showed direction-independent responses for CsPbX3 (Fig. 2(b), (e) and (h)). According to Fig. 2(c), (f) and (i), the shear modulus showed a direction-based inverse response with Young's modulus. The maximum and minimum anisotropy in the shear modulus were obtained at 45° and in the axial directions respectively.
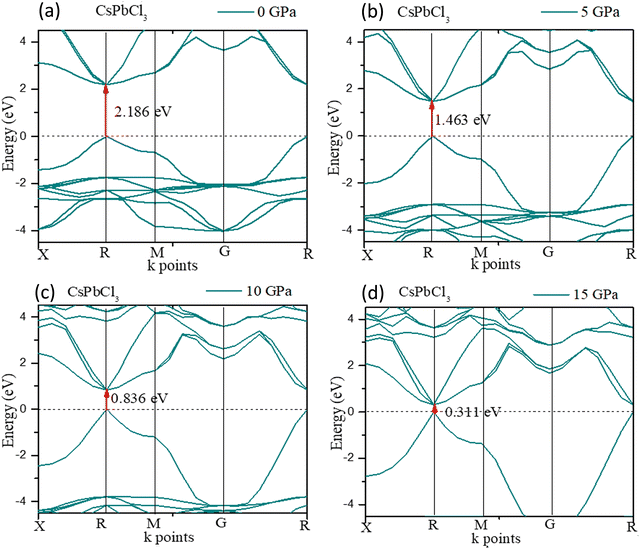
The negative value of C12 presented in Table 2, calculated by the norm-conserving pseudopotential, gave a negative value of Poisson's ratio σ (which is unacceptable) and did not satisfy Born's condition of mechanical stability. That is why this research utilized ultrasoft pseudopotentials. According to this study, iodine-containing perovskites could withstand pressures of up to 75 GPa, whereas the Cl- and Br-containing perovskites could withstand pressures of up to 20 and 25 GPa, respectively, as confirmed by the negative value of C44 presented in Table 3.
| Elastic constants | C 11 | C 12 | C 44 | |||
|---|---|---|---|---|---|---|
| Pseudopotential | Norm-conserving | Ultrasoft | Norm-conserving | Ultrasoft | Norm-conserving | Ultrasoft |
| CsPbCl3 | 20.3 | 39.32 | −9.178 | 6.75 | 7.589 | 5.35 |
| CsPbBr3 | 22.699 | 51.94 | −6.928 | 16.47 | 5.487 | 4.18 |
| CsPbI3 | 14.923 | 48.35 | −5.519 | 7.88 | 4.511 | 4.92 |
| Materials | CsPbI3 | CsPbBr3 | CsPbCl3 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| P (GPa) | a (Å) | C 11 | C 12 | C 44 | a (Å) | C 11 | C 12 | C 44 | a (Å) | C 11 | C 12 | C 44 |
| 0 | 6.4 | 39.32 | 6.75 | 5.35 | 6.01 | 51.94 | 16.47 | 4.18 | 5.73 | 48.35 | 7.88 | 4.92 |
| 5 | 5.98 | 81.66 | 12.25 | 4.67 | 5.66 | 90.46 | 13.99 | 3.61 | 5.44 | 97.06 | 16.58 | 4.06 |
| 10 | 5.76 | 119.43 | 15.97 | 1.34 | 5.47 | 125.74 | 14.11 | 2.88 | 5.27 | 145.49 | 29.86 | 2.91 |
| 15 | 5.6 | 170.4 | 27.37 | 6.43 | 5.33 | 173.83 | 28.69 | 2.14 | 5.15 | 175.01 | 27.9 | 1.68 |
| 20 | 5.49 | 207.43 | 35.46 | 5.79 | 5.23 | 211.2 | 35.27 | 1.28 | 5.05 | 214.4 | 36.14 | 0.48 |
| 25 | 5.4 | 238.25 | 38.76 | 3.17 | 5.15 | 248.17 | 43.08 | 0.33 | 4.97 | 249.95 | 43.19 | −0.71 |
| 30 | 5.32 | 288.88 | 50.85 | 7.06 | 5.07 | 283.31 | 49.76 | −0.66 | — | — | — | — |
| 35 | 5.25 | 323.53 | 58.81 | 6.71 | — | — | — | — | — | — | — | — |
| 40 | 5.2 | 357.61 | 66.84 | 6.36 | — | — | — | — | — | — | — | — |
| 45 | 5.15 | 388.58 | 72.78 | 5.46 | — | — | — | — | — | — | — | — |
| 50 | 5.1 | 419.99 | 79.41 | 3.5 | — | — | — | — | — | — | — | — |
| 55 | 5.06 | 449.5 | 84.78 | 1.32 | — | — | — | — | — | — | — | — |
| 60 | 5.02 | 483.76 | 93.12 | 0.97 | — | — | — | — | — | — | — | — |
| 65 | 4.98 | 523.28 | 103.91 | 3.34 | — | — | — | — | — | — | — | — |
| 70 | 4.95 | 560.19 | 114.31 | 4.65 | — | — | — | — | — | — | — | — |
| 75 | 4.92 | 588.96 | 119.87 | 2.62 | — | — | — | — | — | — | — | — |
| 80 | 4.89 | 615 | 124.42 | −0.96 | — | — | — | — | — | — | — | — |
3.2 Electronic properties
Table 4 shows the values of Eg, and Table 5 shows the pressure-dependent lattice parameter, volume, and band gap values of CsPbX3.| Materials | Method | P (GPa) | Lattice parameters | Band gap Eg (eV) | Bulk type | |
|---|---|---|---|---|---|---|
| a (Å) | V (Å3) | |||||
| CsPbCl3 | Calc. | 0 | 5.734 | 188 | 2.186 | Cubic |
| 5 | 5.446 | 161 | 1.463 | |||
| 10 | 5.271 | 146 | 0.836 | |||
| 15 | 5.151 | 136 | 0.311 | |||
| 20 | 5.052 | 128 | 0 | |||
| CsPbBr3 | Calc. | 0 | 6.014 | 217 | 1.80 | Cubic |
| 5 | 5.663 | 181 | 1.008 | |||
| 10 | 5.473 | 163 | 0.384 | |||
| 15 | 5.339 | 152 | 0 | |||
| CsPbI3 | Calc. | 0 | 6.403 | 262 | 1.479 | Cubic |
| 5 | 5.985 | 214 | 0.715 | |||
| 10 | 5.761 | 191 | 0.125 | |||
| 15 | 5.608 | 176 | 0 | |||
Though the norm-conserving data for the band gap were closer to the reported experimental values (Table 4), the ultrasoft pseudopotential method provided greater accuracy in the case of the mechanical stability measurement. Material of interest must follow Born's criteria mentioned in Section 3.1 (Structural and mechanical properties), and ultrasoft pseudopotential enabled keeping to that standard (Table 2).
The crystal structure could be densified under high pressure with structural renovation. The evolution of the band gap of CsPbCl3 under pressure is shown in Fig. 4. It could be found that the band gap (Eg) decreased with an increase in pressure and finally decreased to zero at 20 GPa pressure.
For CsPbCl3, the direct band gap was 2.186 eV as calculated with the ultrasoft pseudopotential, which was in good agreement with the experimental value.82 This decreased to 1.463 eV at 5 GPa which is still suitable for photovoltaic applications in tandem solar cells, and is really ideal for high power conversion efficiency single solar cells. In this study, the band gap was reduced to 0 eV at hydrostatic pressures ≤ 20 GPa.
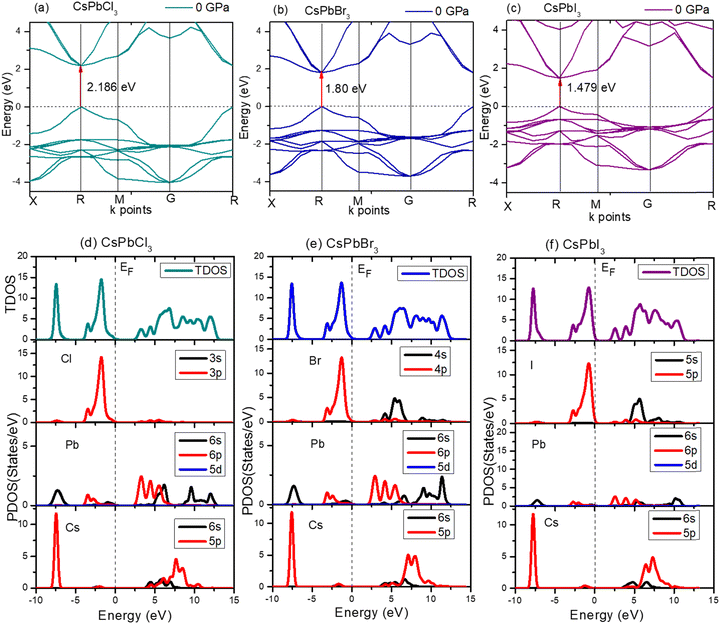
To further understand the electronic properties of CsPbCl3 under pressure, the partial density of states (PDOS) of CsPbCl3 were also calculated. The states at the valence band and conduction band near the Fermi level were mainly formed by the hybridization of the Cl-3p and Pb-6p states, respectively. The band gap decreased with the increase in pressure, due to delocalization of the bands and the energy range broadened as the pressure increased.
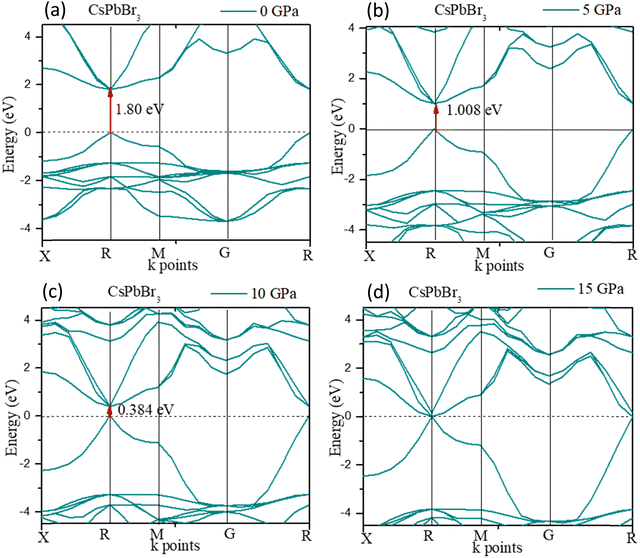
The electronic structure of CsPbBr3 under pressure was investigated. Fig. 5 displays the variation of the band gap of CsPbBr3 as a function of pressure. The ground state band gap of CsPbBr3 at 0 GPa possessed a value of 1.80 eV, but the band gap decreased with the increase in pressure, which was similar to the experimental results. From Fig. 5, it could be clearly seen that the band gap of the cubic CsPbBr3 decreased with the increasing pressure, and ultimately reached 0 eV at 15 GPa. The lattice parameter a also reached a smaller value compared to at 0 GPa, and showed a similar variation to the band gap when the pressure increased (Table 5).
The expansion and/or shrinkage of the lattice parameter a may shift the bands and change the band gaps. The minimum of the lattice parameter ‘a’ caused the band gap to reach the minimum value. The band gap could change to zero and CsPbBr3 could become metallic if the pressure was further increased.
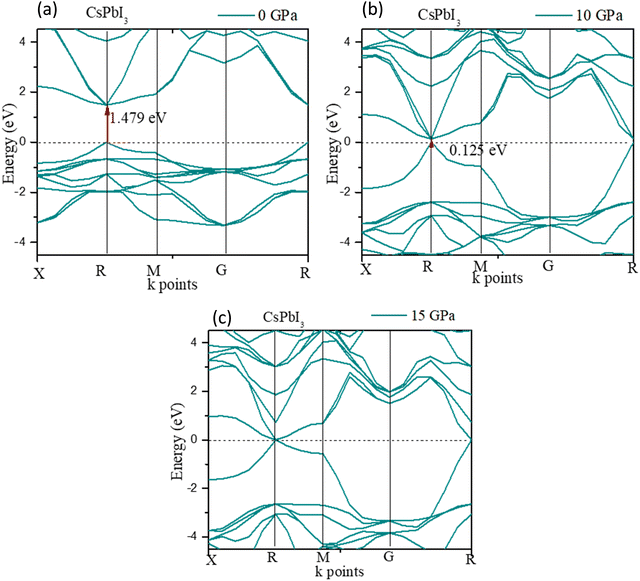
Fig. 6 shows the band gap of cubic CsPbI3. The band gap was 1.479 eV at 0 GPa, which decreases to 0 eV at ≤15 GPa. The deviation of the band gap was associated with the lattice parameter ‘a’, which slightly decreased from 0 to 15 GPa, as shown in Fig. 6(c).
The high-pressure structure had a greater electronic charge density overlap between the Pb and X (= Cl, Br, I) atoms than the ambient structure. The CBM mostly exhibited a nonbonding Pb 6p character, while the VBM could be classified as an antibonding hybridized state, consisting of p orbitals of X (= Cl, Br, I) and a tiny number of Pb 6s orbitals. It was amazing that the electronic levels from the Cs+ cations were positioned far from the VBM and CBM (Fig. 3); as a result, they could only compensate for the charge valence and did not directly contribute to the band edge states, suggesting that PbX6 octahedra primarily control the optoelectronic properties of CsPbX3. Compression of the Pb–X bond strengthened the coupling between the X p and Pb 6s orbitals, which raised the VBM and increased band dispersion. The CBM was not responsive to pressure when it was mostly in a nonbonding localized condition. By pushing the VBM higher, the enhanced orbital coupling reduced the band gap.
3.3 Optical properties
The potential use of a material in optoelectronic devices depends on its pressure-dependent optical characteristics. There have been several papers on the optical characteristics of perovskites, but none have compared the optical properties of CsPbX3, which are highly relevant since they are used in thin-film transistors and solar cells. For this reason, here we studied the pressure-dependent optical properties (absorption, photoconductivity, reflectivity, refractive index, and the real and imaginary parts of the dielectric function) of CsPbX3 for many application fields. Such applications of material depend on its optical responses. The photonic interaction of a material can provide light on the perspective, characteristics, and application forecasts as a function of energy when there are external electromagnetic waves present. Owing to their optical spectra, these features were examined for electrical shifts between filled and vacant states, band constructions, bond types, and the internal structure of the materials. The Kramers–Kronig transformation was followed by the frequency-dependent complex dielectric function, which is connected to the demonstration of relative permittivity and has the formula ε(ω) = ε1(ω) + iε2(ω). The imaginary portion of this complex dielectric function is,where ω = 2πν is the angular frequency of an incoming photon; and e,
![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) and û are the electronic charge, radius vector, and polarization vector of the incident field, respectively; whereas, Ψck and Ψvk represent the wave functions of the conduction band and valence band at k, respectively. Optical properties, such as absorption, conductivity, loss function.reflectivity, and refractive index can be calculated explicitly in terms of ε1 and ε285 as,
and û are the electronic charge, radius vector, and polarization vector of the incident field, respectively; whereas, Ψck and Ψvk represent the wave functions of the conduction band and valence band at k, respectively. Optical properties, such as absorption, conductivity, loss function.reflectivity, and refractive index can be calculated explicitly in terms of ε1 and ε285 as,The charge-carrier recombination rate of specific materials used in solar cells is affected by a basic characteristic known as the dielectric function.86,87 It provides a precise understanding of how optoelectronic devices function.88 Lower recombination rates are revealed by perovskite solar cells with higher dielectric constant values.
Fig. 7(a) and (b) show the pressure-dependent real and imaginary parts of the dielectric function of CsPbX3 perovskites. The real part of the dielectric function (Fig. 7(a)) showed a higher value at low photon energy and then decreased rapidly with the increase in photon energy. Whereas the pressure-induced perovskite exhibited a higher dielectric constant in the visible range. It is well known that normally a perovskite material with such a higher value of the real part of the dielectric function would exhibit a lower band gap,89 which is related to the Penn model. It could also be seen in the electronic band structure (shown in Fig. 3 and 7(b)) that the band gap decreased with increase in applied pressure, which was consistent with the behavior of the imaginary part of the dielectric function. It was evident that the imaginary part dielectric function could be correlated with the optical absorption/transition and the material's band gap. It could be found that the values of the imaginary part of the dielectric function were enhanced with applied pressure and the peaks were shifted toward the lower incident photon energy, which was similar to the optical absorption in Fig. 8(a). On the other hand, the values of the imaginary part of the dielectric function decreased to zero in the higher photon energy region.
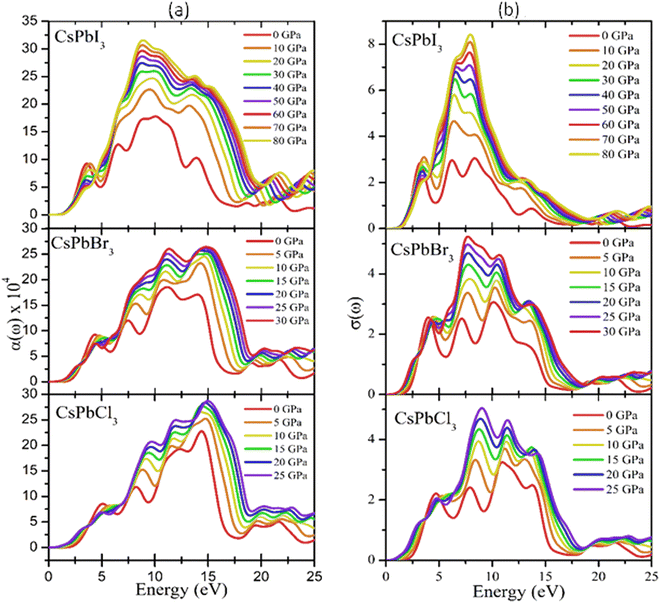 | ||
| Fig. 8 Optical responses in terms of the (a) absorption coefficients and (b) conductivity of CsPbX3. | ||
It is well known that the performance of solar cells is determined by various optical properties, among which the absorption coefficient (α) is the crucial property. The variation of the optical absorption of CsPbX3 perovskites with pressure can be seen in Fig. 8(a). It could be clearly seen that the optical absorption edge of cubic CsPbX3 perovskites was shifted to the low energy region, indicating a shifting of the band gap with applied pressure within the visible range. Furthermore, the value of α of the I-based perovskite demonstrated the maximum intensity in the ultraviolet region, rather than the Br- and Cl-based perovskites. The width of the absorption peak of CsPbI3 was higher than that of CsPbCl3 and CsPbBr3 in the UV region. Fig. 8(b) shows the pressure-dependent real part of the photoconductivity. From the figure, it is evident that when the absorption of photons is enhanced, the rate of photoconductivity tended to increase. Thereby the greater absorption and photoconductivity that could be observed in the I-based perovskite compound could be due to lower band gap relative to the Br- and Cl-based perovskite compounds with applied pressure.
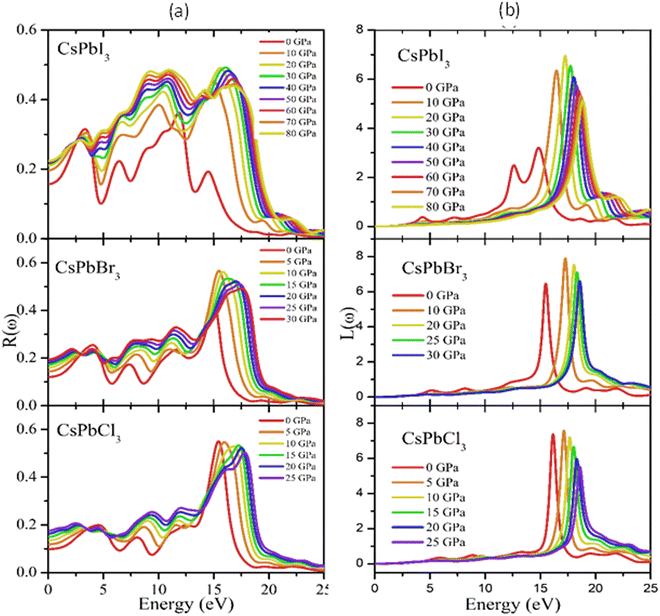
Reflectivity is an important optical property that determines the surface nature of materials for optoelectronic and solar cell applications.90Fig. 9(a) shows the pressure-dependent reflectivity spectra of the CsPbX3 perovskites. From these graphs, it can be seen that at zero pressure the reflectivity was very low for all the studied cubic perovskite compounds. Then, when pressure was applied, the value of the reflectivity and loss function increased significantly with the increase in applied pressure, which could be due to changes of the band gap and/or structure (Fig. 9(a) and (b)).
Fig. 7(a) and (b) show the pressure-dependent real and imaginary parts of the dielectric function of CsPbX3 perovskites. The real part of the dielectric function (Fig. 7a) showed a higher value with low photon energy and then decreased rapidly with the increase in photon energy. Whereas the pressure-induced perovskite exhibited a higher dielectric constant in the visible range. It is well known that normally a perovskite material with such a higher value of the real part of the dielectric function would exhibit a lower band gap.91 This could also be seen in the electronic band structure in Fig. 3. Fig. 7(b) shows the behavior of the imaginary part of the dielectric function with the applied pressure. The imaginary part of the dielectric function was correlated with the optical absorption and the material's band gap. It could be found that the values of the imaginary part of the dielectric function was enhanced with applied pressure and the peaks were shifted toward lower incident photon energy, which was similar to the optical absorption in Fig. 8(a). On the other hand, the values of the imaginary part of the dielectric function decreased to zero in the higher photon energy region. It should be noted that a few peaks appeared at 3.9, 7.8, 11.0, and 14.1 eV for CsPbCl3; 3.5, 7.3, 10.3, and 13.9 eV for CsPbBr3; and 3.0, 6.3, 8.5, and 13.9 eV for CsPbI3. The first peak was due to the generation of electron–hole pairs for conduction. The 2nd and 3rd peaks were due to interband optical transitions from the valence bands to the conduction bands. The fourth peak around 14.0 eV was due to collecting excitons of the free carriers, which is the so-called plasma frequency and the peak is called the plasmon peak. These irregular photoresponses of the materials caused the differences in the band gaps among them.
It is well known that the performance of solar cells is determined by various optical properties, among them absorption coefficient (α) is the crucial property. The variation of optical absorption of CsPbX3 perovskites with pressure can be seen in Fig. 8(a). It is clearly seen that the optical absorption edge of cubic CsPbX3 perovskites is shifted to the low energy region with applied pressure within the visible ranges. In Fig. 8(a) the absorption edges are remarkably enhanced under pressure within the visible ranges. Furthermore, the value of α of the I-based perovskite demonstrates maximum intensity in the ultraviolet region rather than Br and Cl based perovskites. The width of the absorption peak of CsPbI3 is higher than that of CsPbCl3 and CsPbBr3 in the UV region. The first peak of α indicates the optical transition of electrons from Cl-3p of the valence band to Pb-6p of the conduction band at higher energy compared to that of the interband transitions of electrons in the case of CsPbBr3 and CsPbI3. The optical band gaps can be seen from the absorption peaks of the corresponding materials as Eg (CsPbCl3) > Eg (CsPbBr3) > Eg (CsPbI3), which was consistent with the calculated values of Eg of CsPbX3 perovskites (Table 4). The highest absorption peaks for all the materials occurred at the same energy of 14.6 eV (Fig. 8(a)).
Fig. 8(b) shows the pressure-dependent real part of the photoconductivity. From the figure, it was evident that when the absorption of photons was enhanced, the rate of photoconductivity tended to increase. Thereby, greater absorption and photoconductivity could be observed in the I-based perovskite compound relative to the Br- and Cl-based perovskite compounds with applied pressures. The photoconductivity comparison of these materials showed some peaks over a wide range of the energy spectrum. The conductivity initiatives and the first peaks could be ordered in terms of the energy as σ (CsPbI3) > σ (CsPbBr3) > σ (CsPbCl3). The photoconductivity increased at the energy edges 4.2, 7.8, 11.3, and 14.1 eV for CsPbCl3; 3.8, 7.3, 10.2, and 14.1 eV for CsPbBr3; and 3.0, 6.4, 8.3, and 14.1 eV for CsPbI3 as a result of the photonic energy absorption, which is shown in Fig. 8(b).
Reflectivity is an important optical property that determines the surface nature of materials for optoelectronic and solar cell applications.92Fig. 9(a) shows the pressure-dependent reflectivity spectra of the CsPbX3 perovskites. From these graphs, it could be seen that at zero pressure the reflectivity was very low for all the studied cubic perovskite compounds. However, the reflectivity was the maximum for CsPbI3 and the minimum for CsPbCl3 perovskites, respectively. There were also some peaks that appeared in each spectrum that were the responses that still held true for the infra-red and visible regions. In the visible region, the first peaks were observed at 4.2, 3.8, and 3.3 eV for CsPbCl3, CsPbBr3, and CsPbI3, respectively. Some other peaks appeared at 7.8, 11.5, 15.6, and 20.4 eV for CsPbCl3; at 7.3, 10.9, 15.4, for CsPbBr3; and at 6.3, 9.0, 11.3, 15.8 eV for CsPbI3. From a comparison of the reflectivity, it could be clearly seen that CsPbI3 showed the most homogeneous responses over a wide energy range in the ultraviolet region. When pressure was applied, the values of the reflectivity and loss function increased significantly with the increased applied pressure in the UV region.
4. Conclusions
Hydrostatic pressure's effects on the cubic perovskites CsPbX3 were studied by DFT. All the direct band gap materials mentioned here showed a red-shifted nature of the electronic and optical band gap. The application of pressure resulted in strong attractive interaction between the valence band and the conduction band. The increment of pressure caused more overlapping of the CB and VB; whereby the semiconductor perovskites appeared as conductor after a certain amount pressure was applied. The electronic as well as optical responses were enhanced without any deformation of the crystal structure. Our investigation can expand the practical utilization of metal-halide perovskites in optoelectronics, photovoltaics, and quantum dot applications.Author contributions
M. Aktary performed conceptualization, design the study, interpreted the data, and wrote the manuscript. M. Kamruzzaman helped to study, data analysis and wrote the manuscript. R. Afrose helped to understand software, DFT calculations, data curation, writing-review, write and editing the manuscript.Conflicts of interest
The authors declare no competing financial interests.Acknowledgements
The authors would like to thank Department of Physics, Begum Rokeya University, Rangpur, Bangladesh for supporting the computer facility. The research was funded by The Ministry of Science and Technology, Bangladesh. Authors are expressing gratitude to American Physical Society (APS) for appreciating this research. The author is dedicating this article to her beloved friends Popy, Pritha, and Dana.References
- A. Hagfeldt, G. Boschloo, L. Sun, L. Kloo and H. Pettersson, Dye-Sensitized Solar Cells, Chem. Rev., 2010, 110, 6595–6663 CrossRef CAS PubMed.
- J. H. Bang and P. V. Kamat, Quantum Dot Sensitized Solar Cells. A Tale of Two Semiconductor Nanocrystals: CdSe and CdTe, ACS Nano, 2009, 3, 1467–1476 CrossRef CAS PubMed.
- T. R. Cook, et al., Solar Energy Supply and Storage for the Legacy and Nonlegacy Worlds, Chem. Rev., 2010, 110, 6474–6502 CrossRef CAS.
- C.-H. Chiang, M. K. Nazeeruddin, M. Grätzel and C.-G. Wu, The synergistic effect of H 2 O and DMF towards stable and 20% efficiency inverted perovskite solar cells, Energy Environ. Sci., 2017, 10, 808–817 RSC.
- M. M. Lee, J. Teuscher, T. Miyasaka, T. N. Murakami and H. J. Snaith, Efficient Hybrid Solar Cells Based on Meso-Superstructured Organometal Halide Perovskites, Science, 2012, 338, 643–647 CrossRef CAS PubMed.
- N. J. Jeon, et al., Compositional engineering of perovskite materials for high-performance solar cells, Nature, 2015, 517, 476–480 CrossRef CAS PubMed.
- A. Yella, et al., Porphyrin-Sensitized Solar Cells with Cobalt (II/III)–Based Redox Electrolyte Exceed 12 Percent Efficiency, Science, 2011, 334, 629–634 CrossRef CAS PubMed.
- H.-J. Park, et al., Inverted Organic Solar Cells with ZnO Thin Films Prepared by Sol–Gel Method, J. Nanoelectron. Optoelectron., 2010, 5, 135–138 CrossRef CAS.
- W. B. Xiao, M. M. Liu and C. Yan, Extracting and Studying Solar Cell Five Parameters Based on Lambert W Function, J. Nanoelectron. Optoelectron., 2017, 12, 189–195 CrossRef CAS.
- M. Liu, M. B. Johnston and H. J. Snaith, Efficient planar heterojunction perovskite solar cells by vapour deposition, Nature, 2013, 501, 395–398 CrossRef CAS PubMed.
- J. Burschka, et al., Sequential deposition as a route to high-performance perovskite-sensitized solar cells, Nature, 2013, 499, 316–319 CrossRef CAS PubMed.
- M. Jørgensen, K. Norrman and F. C. Krebs, Stability/degradation of polymer solar cells, Sol. Energy Mater. Sol. Cells, 2008, 92, 686–714 CrossRef.
- Z. Pan, et al., Near Infrared Absorption of CdSex Te1–x Alloyed Quantum Dot Sensitized Solar Cells with More than 6% Efficiency and High Stability, ACS Nano, 2013, 7, 5215–5222 CrossRef CAS PubMed.
- M. D. Kelzenberg, et al., Enhanced absorption and carrier collection in Si wire arrays for photovoltaic applications, Nat. Mater., 2010, 9, 239–244 CrossRef CAS PubMed.
- K. Yoshikawa, et al., Silicon heterojunction solar cell with interdigitated back contacts for a photoconversion efficiency over 26%, Nat. Energy, 2017, 2, 17032 CrossRef CAS.
- J. F. Geisz,
et al., Six-junction III–V solar cells with 47.1% conversion efficiency under 143
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Suns concentration, Nat. Energy, 2020, 5, 326–335 CrossRef CAS.
Suns concentration, Nat. Energy, 2020, 5, 326–335 CrossRef CAS. - A. M. M. Tanveer Karim, et al., Structural, opto-electronic characteristics and second harmonic generation of solution processed CH3NH3PbI3-xClx thin film prepared by spray pyrolysis, Mater. Sci. Eng., B, 2020, 259, 114599 CrossRef CAS.
- A. Kojima, K. Teshima, Y. Shirai and T. Miyasaka, Organometal Halide Perovskites as Visible-Light Sensitizers for Photovoltaic Cells, J. Am. Chem. Soc., 2009, 131, 6050–6051 CrossRef CAS PubMed.
- M. Jošt, et al., Textured interfaces in monolithic perovskite/silicon tandem solar cells: advanced light management for improved efficiency and energy yield, Energy Environ. Sci., 2018, 11, 3511–3523 RSC.
- P. Ramasamy, et al., All-inorganic cesium lead halide perovskite nanocrystals for photodetector applications, Chem. Commun., 2016, 52, 2067–2070 RSC.
- Q. A. Akkerman, et al., Strongly emissive perovskite nanocrystal inks for high-voltage solar cells, Nat. Energy, 2016, 2, 16194 CrossRef.
- W.-J. Yin, T. Shi and Y. Yan, Unique Properties of Halide Perovskites as Possible Origins of the Superior Solar Cell Performance, Adv. Mater., 2014, 26, 4653–4658 CrossRef CAS PubMed.
- K. P. Marshall, M. Walker, R. I. Walton and R. A. Hatton, Enhanced stability and efficiency in hole-transport-layer-free CsSnI3 perovskite photovoltaics, Nat. Energy, 2016, 1, 16178 CrossRef CAS.
- A. Swarnkar, et al., Quantum dot–induced phase stabilization of α-CsPbI3 perovskite for high-efficiency photovoltaics, Science, 2016, 354, 92–95 CrossRef CAS PubMed.
- W. Zhang, G. E. Eperon and H. J. Snaith, Metal halide perovskites for energy applications, Nat. Energy, 2016, 1, 16048 CrossRef CAS.
- Sandeep, et al., Study of electronic and magnetic properties in 4 f electron based cubic EuAlO 3: a first-principles calculation, Phys. Scr., 2015, 90, 065803 CrossRef.
- S. Chettri, et al., GGA + U and mBJ + U study of the optoelectronic, magnetic and thermoelectric properties of the SmAlO 3 compound with spin–orbit coupling, Int. J. Mod. Phys. B, 2016, 30, 1650078 CrossRef CAS.
- Sandeep, et al., A first principles study of Nd doped cubic LaAlO3 perovskite: mBJ + U study, J. Magn. Magn. Mater., 2016, 417, 313–320 CrossRef CAS.
- D. P. Rai, et al., Electronic and optical properties of cubic SrHfO3 at different pressures: A first principles study, Mater. Chem. Phys., 2017, 186, 620–626 CrossRef CAS.
- G. Murtaza and I. Ahmad, First principle study of the structural and optoelectronic properties of cubic perovskites CsPbM3 (M = Cl, Br, I), Phys. B, 2011, 406, 3222–3229 CrossRef CAS.
- L. Lang, J.-H. Yang, H.-R. Liu, H. J. Xiang and X. G. Gong, First-principles study on the electronic and optical properties of cubic ABX3 halide perovskites, Phys. Lett. A, 2014, 378, 290–293 CrossRef CAS.
- J. Qiu, et al., All-solid-state hybrid solar cells based on a new organometal halide perovskite sensitizer and one-dimensional TiO2 nanowire arrays, Nanoscale, 2013, 5, 3245 RSC.
- H. J. Snaith, Perovskites: The Emergence of a New Era for Low-Cost, High-Efficiency Solar Cells, J. Phys. Chem. Lett., 2013, 4, 3623–3630 CrossRef CAS.
- H.-S. Kim, et al., Lead Iodide Perovskite Sensitized All-Solid-State Submicron Thin Film Mesoscopic Solar Cell with Efficiency Exceeding 9%, Sci. Rep., 2012, 2, 591 CrossRef PubMed.
- Z. Ku, Y. Rong, M. Xu, T. Liu and H. Han, Full Printable Processed Mesoscopic CH3NH3PbI3/TiO2 Heterojunction Solar Cells with Carbon Counter Electrode, Sci. Rep., 2013, 3, 3132 CrossRef PubMed.
- C. Katan, N. Mercier and J. Even, Quantum and Dielectric Confinement Effects in Lower-Dimensional Hybrid Perovskite Semiconductors, Chem. Rev., 2019, 119, 3140–3192 CrossRef CAS PubMed.
- M. A. Fadla, B. Bentria, T. Dahame and A. Benghia, First-principles investigation on the stability and material properties of all-inorganic cesium lead iodide perovskites CsPbI3 polymorphs, Phys. B, 2020, 585, 412118 CrossRef CAS.
- Z.-K. Tan, et al., Bright light-emitting diodes based on organometal halide perovskite, Nat. Nanotechnol., 2014, 9, 687–692 CrossRef CAS PubMed.
- H. Zhu, et al., Lead halide perovskite nanowire lasers with low lasing thresholds and high quality factors, Nat. Mater., 2015, 14, 636–642 CrossRef CAS PubMed.
- C. C. Stoumpos, et al., Crystal Growth of the Perovskite Semiconductor CsPbBr3: A New Material for High-Energy Radiation Detection, Cryst. Growth Des., 2013, 13, 2722–2727 CrossRef CAS.
- J. Deng, J. Li, Z. Yang and M. Wang, All-inorganic lead halide perovskites: a promising choice for photovoltaics and detectors, J. Mater. Chem. C Mater., 2019, 7, 12415–12440 RSC.
- X. Li, et al., All-Inorganic CsPbBr3 Perovskite Solar Cells with 10.45% Efficiency by Evaporation-Assisted Deposition and Setting Intermediate Energy Levels, ACS Appl. Mater. Interfaces, 2019, 11, 29746–29752 CrossRef CAS PubMed.
- H. Zhang, et al., Centimeter-Sized Inorganic Lead Halide Perovskite CsPbBr3 Crystals Grown by an Improved Solution Method, Cryst. Growth Des., 2017, 17, 6426–6431 CrossRef CAS.
- D. N. Dirin, I. Cherniukh, S. Yakunin, Y. Shynkarenko and M. V. Kovalenko, Solution-Grown CsPbBr 3 Perovskite Single Crystals for Photon Detection, Chem. Mater., 2016, 28, 8470–8474 CrossRef CAS PubMed.
- P. Ramasamy, et al., All-inorganic cesium lead halide perovskite nanocrystals for photodetector applications, Chem. Commun., 2016, 52, 2067–2070 RSC.
- Y. Lee, et al., High-Performance Perovskite-Graphene Hybrid Photodetector, Adv. Mater., 2015, 27, 41–46 CrossRef CAS PubMed.
- Y. Wang, et al., Hybrid Graphene-Perovskite Phototransistors with Ultrahigh Responsivity and Gain, Adv. Opt. Mater., 2015, 3, 1389–1396 CrossRef CAS.
- W. Nie, et al., High-efficiency solution-processed perovskite solar cells with millimeter-scale grains, Science, 2015, 347, 522–525 CrossRef CAS PubMed.
- M. A. Green, A. Ho-Baillie and H. J. Snaith, The emergence of perovskite solar cells, Nat. Photonics, 2014, 8, 506–514 CrossRef CAS.
- G. Xing, et al., Long-Range Balanced Electron- and Hole-Transport Lengths in Organic-Inorganic CH3 NH3 PbI3, Science, 2013, 342, 344–347 CrossRef CAS PubMed.
- X. Li, et al., All Inorganic Halide Perovskites Nanosystem: Synthesis, Structural Features, Optical Properties and Optoelectronic Applications, Small, 2017, 13, 1603996 CrossRef PubMed.
- X. Li, et al., Intercrossed Carbon Nanorings with Pure Surface States as Low-Cost and Environment-Friendly Phosphors for White-Light-Emitting Diodes, Angew. Chem., Int. Ed., 2015, 54, 1759–1764 CrossRef CAS PubMed.
- J. Song, et al., Quantum Dot Light-Emitting Diodes Based on Inorganic Perovskite Cesium Lead Halides (CsPbX3), Adv. Mater., 2015, 27, 7162–7167 CrossRef CAS PubMed.
- K. Lin, et al., Perovskite light-emitting diodes with external quantum efficiency exceeding 20 per cent, Nature, 2018, 562, 245–248 CrossRef CAS PubMed.
- Y. Wang, et al., All-Inorganic Colloidal Perovskite Quantum Dots: A New Class of Lasing Materials with Favorable Characteristics, Adv. Mater., 2015, 27, 7101–7108 CrossRef CAS PubMed.
- Q. Zhang, et al., Advances in Small Perovskite-Based Lasers, Small Methods, 2017, 1, 1700163 CrossRef.
- R. J. Sutton, et al., Bandgap-Tunable Cesium Lead Halide Perovskites with High Thermal Stability for Efficient Solar Cells, Adv. Energy Mater., 2016, 6, 1502458 CrossRef.
- E. M. Sanehira, et al., Enhanced mobility CsPbI3 quantum dot arrays for record-efficiency, high-voltage photovoltaic cells, Sci. Adv., 2017, 3 DOI:10.1126/sciadv.aao4204.
- J. Li, et al., 50-Fold EQE Improvement up to 6.27% of Solution-Processed All-Inorganic Perovskite CsPbBr3 QLEDs via Surface Ligand Density Control, Adv. Mater., 2017, 29, 1603885 CrossRef PubMed.
- N. Pandey, A. Kumar and S. Chakrabarti, Investigation of the structural, electronic, and optical properties of Mn-doped CsPbCl3: theory and experiment, RSC Adv., 2019, 9, 29556–29565 RSC.
- L. Protesescu, et al., Nanocrystals of Cesium Lead Halide Perovskites (CsPbX3, X = Cl, Br, and I): Novel Optoelectronic Materials Showing Bright Emission with Wide Color Gamut, Nano Lett., 2015, 15, 3692–3696 CrossRef CAS PubMed.
- O. Yu Posudievsky, et al., Structural and Spectral Characteristics of Mechanochemically Prepared CsPbBr3, Theor. Exp. Chem., 2017, 53, 235–243 CrossRef CAS.
- M. Coduri, et al., Origin of pressure-induced band gap tuning in tin halide perovskites, Mater. Adv., 2020, 1, 2840–2845 RSC.
- M. I. Kholil and M. T. H. Bhuiyan, Effects of pressure on narrowing the band gap, visible light absorption, and semi-metallic transition of lead-free perovskite CsSnBr3 for optoelectronic applications, J. Phys. Chem. Solids, 2021, 154, 110083 CrossRef CAS.
- G. Liu, L. Kong, W. Yang and H. Mao, Pressure engineering of photovoltaic perovskites, Mater. Today, 2019, 27, 91–106 CrossRef CAS.
- Y. Li, et al., Electrical transport properties of Weyl semimetal WTe2 under high pressure, J. Mater. Sci., 2020, 55, 14873–14882 CrossRef CAS.
- J.-H. Lee, A. Jaffe, Y. Lin, H. I. Karunadasa and J. B. Neaton, Origins of the Pressure-Induced Phase Transition and Metallization in the Halide Perovskite (CH3NH3)PbI3, ACS Energy Lett., 2020, 5, 2174–2181 CrossRef CAS.
- O. V. Oyelade, et al., Pressure-Assisted Fabrication of Perovskite Solar Cells, Sci. Rep., 2020, 10, 7183 CrossRef CAS PubMed.
- S. Yalameha, P. Saeidi, Z. Nourbakhsh, A. Vaez and A. Ramazani, Insight into the topological phase and elastic properties of halide perovskites CsSnX3 (X
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
= ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) l, Br, Cl) under hydrostatic pressures, J. Appl. Phys., 2020, 127, 085102 CrossRef CAS.
l, Br, Cl) under hydrostatic pressures, J. Appl. Phys., 2020, 127, 085102 CrossRef CAS. - R. Y. Alyoubi, B. M. Raffah, F. Hamioud and A. A. Mubarak, Effect of pressure on the mechanical, electronic and optical characters of CsSnBr3 and CsSnI3: ab-initio study, Mod. Phys. Lett. B, 2021, 35, 2150056 CrossRef CAS.
- G. Xiao, et al., Pressure Effects on Structure and Optical Properties in Cesium Lead Bromide Perovskite Nanocrystals, J. Am. Chem. Soc., 2017, 139, 10087–10094 CrossRef CAS PubMed.
- S. J. Clark, et al., First principles methods using CASTEP, Z Kristallogr Cryst. Mater., 2005, 220, 567–570 CrossRef CAS.
- W. Kohn and L. J. Sham, Self-Consistent Equations Including Exchange and Correlation Effects, Phys. Rev., 1965, 140, A1133–A1138 CrossRef.
- P. Hohenberg and W. Kohn, Inhomogeneous Electron Gas, Phys. Rev., 1964, 136, B864–B871 CrossRef.
- S. Idrissi, H. Labrim, S. Ziti and L. Bahmad, Investigation of the physical properties of the equiatomic quaternary Heusler alloy CoYCrZ (Z = Si and Ge): a DFT study, Appl. Phys. A, 2020, 126, 190 CrossRef CAS.
- S. Idrissi, H. Labrim, S. Ziti and L. Bahmad, Structural, electronic, magnetic properties and critical behavior of the equiatomic quaternary Heusler alloy CoFeTiSn, Phys. Lett. A, 2020, 384, 126453 CrossRef CAS.
- S. Idrissi, H. Labrim, S. Ziti and L. Bahmad, Characterization of the Equiatomic Quaternary Heusler Alloy ZnCdRhMn: Structural, Electronic, and Magnetic Properties, J Supercond Nov Magn, 2020, 33, 3087–3095 CrossRef.
- J. Hutton, R. J. Nelmes, G. M. Meyer and V. R. Eiriksson, High-resolution studies of cubic perovskites by elastic neutron diffraction: CsPbCl3, J. Phys. C-Solid State Phys., 1979, 12, 5393–5410 CrossRef CAS.
- M. Aktary, M. Kamruzzaman and R. Afrose, A comparative study of the mechanical stability, electronic, optical and photocatalytic properties of CsPbX3 (X = Cl, Br, I) by DFT calculations for optoelectronic applications, RSC Adv., 2022, 12, 23704–23717 RSC.
- M. M. Lee, J. Teuscher, T. Miyasaka, T. N. Murakami and H. J. Snaith, Efficient Hybrid Solar Cells Based on Meso-Superstructured Organometal Halide Perovskites, Science, 2012, 338, 643–647 CrossRef CAS PubMed.
- M. Jørgensen, K. Norrman and F. C. Krebs, Stability/degradation of polymer solar cells, Sol. Energy Mater. Sol. Cells, 2008, 92, 686–714 CrossRef.
- K. Yoshikawa, et al., Silicon heterojunction solar cell with interdigitated back contacts for a photoconversion efficiency over 26%, Nat. Energy, 2017, 2, 17032 CrossRef CAS.
- M. D. Kelzenberg, et al., Enhanced absorption and carrier collection in Si wire arrays for photovoltaic applications, Nat. Mater., 2010, 9, 239–244 CrossRef CAS PubMed.
- T. Paul, et al., Tunable cathodoluminescence over the entire visible window from all-inorganic perovskite CsPbX3 1D architecture, J. Mater. Chem. C Mater., 2018, 6, 3322–3333 RSC.
- M. Aktary, et al., Mechanical and optoelectronic properties of ternary telluride NbFeTe2: A DFT approach, Comput. Condensed Matter., 2023, 34, e00788 CrossRef.
- G. E. Eperon, et al., Formamidinium lead trihalide: a broadly tunable perovskite for efficient planar heterojunction solar cells, Energy Environ. Sci., 2014, 7, 982 RSC.
- L. Lang, et al., Three-step approach for computing band offsets and its application to inorganicABX3 halide perovskites, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 075102 CrossRef.
- K. Heidrich, et al., Electronic structure, photoemission spectra, and vacuum-ultraviolet optical spectra of CsPbCl3 and CsPbBr3, Phys. Rev. B: Condens. Matter Mater. Phys., 1981, 24, 5642–5649 CrossRef CAS.
- R. J. Sutton, et al., Bandgap-Tunable Cesium Lead Halide Perovskites with High Thermal Stability for Efficient Solar Cells, Adv. Energy Mater., 2016, 6, 1502458 CrossRef.
- J. B. Hoffman, A. L. Schleper and P. V. Kamat, Transformation of Sintered CsPbBr3 Nanocrystals to Cubic CsPbI 3 and Gradient CsPbBrx I3–x through Halide Exchange, J. Am. Chem. Soc., 2016, 138, 8603–8611 CrossRef CAS PubMed.
- L. Lang, et al., Three-step approach for computing band offsets and its application to inorganic ABX3 halide perovskites, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 075102 CrossRef.
- Md. S. Hossain, A. S. Roy and Md. S. Islam, In silico analysis predicting effects of deleterious SNPs of human RASSF5 gene on its structure and functions, Sci. Rep., 2020, 10, 14542 CrossRef CAS PubMed.
Footnote |
| † The author is dedicating this article to her beloved friends Popy, Pritha, Shahina and Dana. |
| This journal is © The Royal Society of Chemistry 2023 |