Open Access Article
Open Access ArticleDesign and screening of B–N functionalized non-fullerene acceptors for organic solar cells via multiscale computation†
Rudranarayan
Khatua
and
Anirban
Mondal
 *
*
Department of Chemistry, Indian Institute of Technology, Gandhinagar, Gujarat, 382355, India. E-mail: amondal@iitgn.ac.in
First published on 24th August 2023
Abstract
The molecular engineering of small molecule non-fullerene acceptors (NFAs) is central to enhancing organic solar cell (OSC) performance. One of the effective strategies is the chemical tailoring of the ladder-type central π-core unit of NFAs. Especially boron–nitrogen (B–N) functionalized heterocycles in ladder-type π-cores is considered a promising approach to boost the device performance by regulating energy levels, band gap, and photovoltaic properties of organic materials. Here, we employ a multiscale computational workflow to design acceptor–donor–acceptor (A–D–A) type B–N functionalized NFAs starting from well-defined building blocks representing the donor and acceptor units. Initial assessment of the dataset generated via quantum mechanical calculations revealed that B–N functionalization in the designed NFAs leads to a bathochromic shift in the absorption maximum in the near-infrared region with ΔLUMO below 0.3 eV required for improved solar cell efficiency. Further, crucial threshold parameters are imposed on an initial database of 120 NFAs to screen and identify five potential candidate structures on which molecular dynamics simulations are performed to generate amorphous morphologies. Charge transport simulations on these morphologies exhibit ambipolar character with superior mobilities for holes and electrons compared to the parent molecule. Our design principle guides us in identifying novel NFAs with promising photovoltaic characteristics and highlights that precisely manipulating boron–nitrogen functionalization is a possible way toward high-efficiency OSCs.
1 Introduction
Over the past decade, the performance of bulk-heterojunction (BHJ) organic solar cells has increased markedly owing to the paradigm shift from fullerene acceptors to small molecule non-fullerene acceptors (NFAs) emerging from the rapid growth of the A–D–A-type and the A-DA′D–A-type materials.1–4 The power conversion efficiencies (PCEs) of organic solar cells (OSCs) comprising blends of NFAs and suitable donor polymers have reached beyond 19%,5–9 by collective research efforts in the development of efficient photon absorbers, device fabrication techniques, and morphological or photophysical characterizations. Although the recent breakthroughs in OSC are very encouraging, tackling the well-known trade-off between open-circuit voltage (VOC) and short-circuit current density (JSC) to maximize the power conversion efficiencies (PCEs) is still one of the paramount issues to be addressed in the field.Engineering ladder-type π-core is an effective strategy to induce desired modifications in photon absorption and material characteristics of the NFA-based dyes. Several chemical tailoring routes have been adapted, including conjugation length adjustment,10 tuning of electron-withdrawing groups,11 desymmetrization,12etc., which have shown great potential in regulating the photophysical properties of the NFA molecules. In particular, boron (B)-substituted heterocycles in ladder-type π-cores are beneficial in many aspects to boost the device performance.13,14 Inclusion of isoelectronic and isosteric boron–nitrogen (B–N) sub-unit bonded with a carbon atom in the π-conjugated systems has been shown a promising approach to tune the energy levels, band gap, and optoelectronic properties of organic materials.15–18 However, only a handful of efforts employing B–N-embedded NFAs have been reported so far.19–23 For instance, Morgan et al. synthesized B–N-decorated dihydroindeno[1,2-b]fluorenes core and achieved tunable light absorption properties of the materials when functionalized with suitable end groups.24 More recently, employing a theoretical approach, Yang et al. investigated boron–nitrogen-based A–D–A-type non-fullerene small molecules and demonstrated that the designed acceptors exhibit a wide absorption spectrum with enhanced electron mobility than the bare molecule.25 Dong et al. synthesized the B–N embedded donor–acceptor (D–A) type conjugated polymer. They observed a downshift of the energy levels compared to the bare system.26 In another study, donor polymer decorated with a B–N unit for enhanced photovoltaic performance was reported by Zhang and coworkers. They observed that polymer PCPDT functionalized with B–N system showed an improved VOC and PCE, lower HOMO/LUMO levels with a narrower optical bandgap as compared to bare PCPDT polymer.27 Despite these merits of B-containing π-cores, the development of novel NFAs exhibiting wider absorption in the near-infrared region,28 and n-type charge transport25 is a key challenge for further improvement of PCEs in organic solar cells.
The potential of organic synthesis in creating novel NFA molecules for versatile OSC applications can be explored efficiently with reliable models that allow the realistic prediction of properties. Therefore, it is unsurprising that computational modeling has accompanied the development and characterization of numerous NFAs.29 The emerging trend in computational modeling is a rational, application-driven generation of a database of potential candidate structures filtered using high-throughput screening methods, guiding the discovery of new materials.30,31 The strategy involves pre-screening molecules with a predefined set of properties followed by extensive multiscale simulations to establish clear structure–property relationships.32
In this work, we employ a multiscale computational workflow to design and screen B–N incorporated A–D–A type NFA molecules, starting with a combination of ten unique ladder-type π-core units and twelve potential terminal groups. The molecular design originates from a well-known experimentally reported small molecule acceptor, INIC3 (6,6,12,12-tetrakis(4-hexylphenyl)-indacenobis(dithieno[3,2-b;2′,3′-d]thiophene) as the electron-rich unit and 1,1-dicyanomethylene-3-indanones with two fluorine substituents as the electron-deficient units), which showed a power conversion efficiency of 11.5%, as reported in ref. 33. Three essential pillars drive the generation of the π-core units – shortening of non-polar side chains, extending the conjugation length, and B–N embedding into the system. Initial pre-screening driven by key threshold parameters led us to identify a small number of potentially high-performing NFA materials exhibiting low exciton binding energy, adequate VOC, and complementary absorption in the near-infrared region. Molecular dynamics simulations followed by charge-transport calculation on these selected compounds revealed promising electron and hole mobilities.
This article is organized as follows: Section 2 discusses the multiscale workflow. The analyses of the initial database, results obtained, and the performance of selected NFA materials are discussed in Section 3. The last section provides a summary of the work.
2 Computational details
2.1 Structure generation
Efficient designing of NFAs is critical in optimizing the photovoltaic characteristics to obtain improved performance of the OSC. Typically NFA system consists of an acceptor–donor–acceptor-based architecture, where the donor is fused with the acceptor in a single covalent bond. In this regard, selecting the appropriate donor and acceptor building blocks to construct a new NFA molecule is vital. We chose the experimentally reported, well-known acceptor INIC3 as our base framework for the π-core unit.33 Based on the INIC3 core unit, we designed ten new donor building blocks primarily by incorporating B–N embedding in place of C–C single bond and elongation of the π-conjugation length, as shown in Fig. 1. The designed donor building blocks (D2–D4) consist of six thiophene rings (three thiophenes are symmetrically distributed on both sides of the central benzene ring) attached with an alkyl linker. D2 is formed from bare D1 (INIC3) by adding B–N functionalization in place of the C–C single bond of the core–thiophene ring linked with the phenyl–hexyl (Ph–HE) chain. The D3 unit originates from D1 by reducing the alkyl chain from phenyl–hexyl to phenyl–methyl. The introduction of a shorter alkyl chain to replace the hexyl group was primarily to reduce the system size and, thus, the associated computational cost. In a real scenario, an acceptor molecule with such shortened side chain may also not show good solubility. However, trimming alkyl chains help enormously in converging the quantum chemical calculations. Like D2, B–N functionalization of D3 yielded a D4 donor block (Fig. 1). The remaining donors are then designed by changing the π-conjugation length from six to eight thiophenes in the ladder-type π-core unit. Specifically, D5 originated by adding one more thiophene ring at both ends of the D3 system. On the other hand, shifting the thiophene-linked phenyl–methyl to the two ends of the D5 yielded D7 and D9 donor blocks. Lastly, units D6, D8, and D10 are built from the donors D5, D7, and D9 by adding B–N functionalization on the thiophene ring linked with the alkyl chain. Modifying the six thiophene rings to eight thiophenes in the donor moiety helps expand the π-conjugation and is expected to offer better photophysical properties. Incorporating B–N into the donor moieties may substantially impact the material's properties, including energy levels, absorption, bandgaps, and device functionality.15–18 On the other hand, trimming hexyl to methyl lowers computational efficiency, which may impact molecular packing. In addition to these donor building blocks, twelve well-known acceptors with high efficiency are selected from the available organic solar cell database.34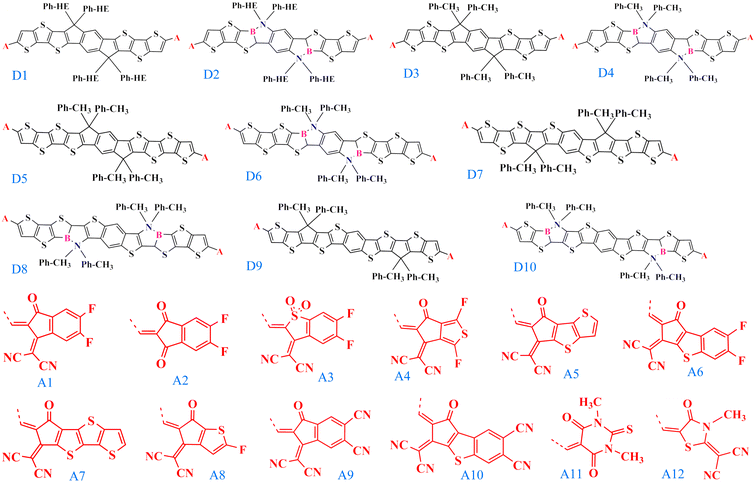 | ||
| Fig. 1 The chemical structures of the donor (D1–D10) and acceptor (A1–A12) building blocks used to construct NFA molecules studied in this work. A is the linker between the donor and the acceptor. | ||
We constructed the database of A–D–A type NFA molecules using the selected building blocks. The simplified molecular-input line-entry system (SMILES) strings of compounds were created by combining the SMILES strings of the composing donor and acceptor building blocks. Based on these SMILES strings, we created the initial 3D structures of each molecular formula by employing the empirical MMFF94 force field parameters35–39via the gen3d option as implemented in Open Babel.40 This step yielded 120 equilibrium structures.
2.2 Multiscale workflow
Fig. 2 summarizes the computational workflow applied in this study to design and screen NFA molecules. Next, we describe the individual steps in detail.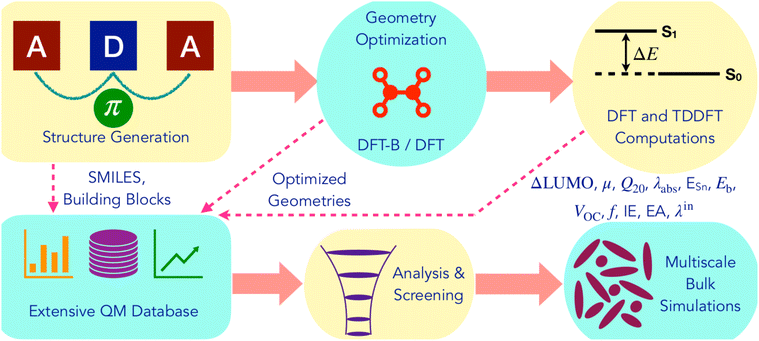 | ||
| Fig. 2 Illustration of the computational workflow for the design and screening of non-fullerene acceptors. | ||
DFT-based simulations were carried out employing the Gaussian 09 program.50 The suitable computational method was chosen based on validating the computed absorption maximum against the experimental measurement for three compounds. Toward this end, we tested a few DFT functionals such as B3LYP, B3LYP-D3, CAM-B3LYP, ωB97XD, and M062X in combination with 6-31G(d,p) basis sets considering chloroform (CHCl3, ε = 4.7113) as the solvent using the polarizable conductor calculation model (CPCM).51 Details of validation tests are summarized in Table S1 of the ESI.† Among the tested combinations, the B3LYP/6-31G(d,p) method showed the best agreement with a maximum wavelength of 736 nm compared to the experimental measurements of 710 nm for the INIC3 molecule.33 Similar agreement between experiment and simulation was seen for the other two complexes. Therefore, we continued with the same level of theory for all the DFT and time-dependent DFT (TD-DFT) calculations. To describe excited states, we employ linear-response time-dependent density functional theory with Tamm–Dancoff approximation (TDA/TD-DFT) to compute the excitation energies and oscillator strengths.
The reorganization energy of a few selected NFA molecules was calculated as follows: λ = (EnCi − EnNi) + (EcNj − EcCj), for molecule i and j, where the lowercase represents the neutral (n) or charged (c) molecule, and the uppercase represents the neutral (N) or charged (C) geometry. In the current framework, external contribution to the reorganization energy is ignored since in the amorphous organic semiconductors (e.g., NFAs), the Pekar factor is on the order of 0.01, leading to a relatively small contribution to the total reorganization energy.52 The ionization potential and electron affinity was estimated as; IP = (EcC − EnN) and EA = (EnN − EaA). The exciton binding was evaluated using the following relation; Eb = EHOMO–LUMO − Ex. Here, EHOMO–LUMO is the energy difference between HOMO and LUMO energy levels, and Ex represents the first excitation energy (S0 → S1). Theoretical VOC values are calculated using the relation VOC = (|EDHOMO| − |EALUMO|) − 0.3, where EDHOMO and EALUMO are the HOMO and LUMO energy levels of the donor and NFA molecules, respectively.53,54 In this study, we have considered one unit of FTAZ polymer as the donor molecule, as the experimental measurements were done for the bulk mixture between INIC3 and this polymer.33 The geometry and energy of the polymer unit were computed at the same level of theory as described for the NFA molecules (Fig. S1 of the ESI†). We found that for the INIC3 molecule, the predicted VOC overestimated the experimental measurement by 0.387 V. Thus, we applied this difference as the correction factor to obtain the corrected VOC for all the designed NFA compounds.
Classical molecular dynamics (MD) simulations were performed using the GROMACS engine, v.2022.60,61 A two-step procedure, including an annealing step followed by rapid quenching to lock the molecules in a local energy minimum, was applied to generate the amorphous state. Such a strategy has been used earlier to prepare amorphous structures of organic hole transport materials.62,63 Initial configurations were generated by randomly placing 1000 molecules in a cubic simulation box by the Packmol program.64 These initial structures were energy-minimized and annealed from 300–800 K within five ns, followed by rapid quenching to 300 K in three ns. Further equilibration for five ns was performed at 300 K. All simulations were performed in the NPT ensemble using a canonical velocity rescaling thermostat,65 a Berendsen barostat for pressure coupling,66 and the smooth particle mesh Ewald technique for long-range electrostatic interactions. A time step of 0.005 ps was used to integrate the equations of motion. Non-bonded interactions were computed with a realspace cutoff of 1.3 nm.
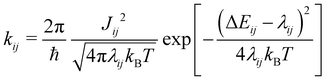 | (1) |
The electron coupling (Jij) elements were estimated using eqn (2).
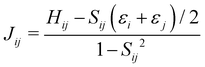 | (2) |
The charge carrier mobility of the NFAs was estimated from the diffusion process, in which the charge carriers hop from one site to another of the molecular fragments in a dimer. In the low external electric field limit, the Einstein relation was employed to compute the hole and electron mobilities in the NFA systems.70,71
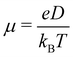 | (3) |
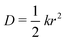 | (4) |
3 Results and discussion
3.1 Initial assessment
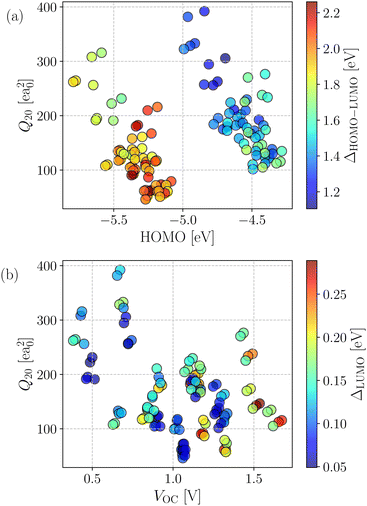
The generated database was initially assessed by exploring correlations among key computed quantities. In this regard, the quadrupole moment (Q20) is one of the critical parameters which governs the charge separation/recombination at the donor–acceptor interfaces and thus regulates the short-circuit current (JSC) and hence, the power conversion efficiency (PCE) of the solar cell.72 In general, a higher Q20 value leads to a larger magnitude of JSC.73 However, a substantial quadrupole moment negatively impacts the open-circuit voltage (VOC).74 Therefore, it is imperative to optimize the trade-off between the JSC and VOC.Fig. 3a depicts the comparison between the computed Q20 values against each compound's highest and lowest occupied molecular orbital (HOMO and LUMO) energy levels. An inverse correlation between Q20 and HOMO energy levels is apparent; a more significant HOMO–LUMO gap yields smaller Q20. It can be justified as in an A–D–A type NFA molecule, the presence of electron-withdrawing acceptor units results in a reduced HOMO–LUMO gap. However, for the same reason, there will be a net increase in the charge flow and an improved molecular quadrupole moment. Fig. 3a shows two distinct patterns in the computed HOMO energy levels. All points with a HOMO energy above −5 eV represent B–N functionalized 6T and 8T-based NFAs, while others with HOMO energy below −5 eV indicate bare 6T and 8T-based NFAs. We observed that B–N functionalization helps increase the HOMO/LUMO energy and decrease the band gap compared to bare NFAs. In addition, Q20 values are enhanced significantly (in the range of 100–210 ea02, except a few are above 210 ea02) in the B–N functionalized NFAs.
The correlation between computed molecular quadrupole moment and VOC in the investigated compounds is shown in Fig. 3b. As expected, overall, we observed an inverse correlation between VOC and Q20 following earlier reports.54,72–74 Interestingly, all of the NFAs with VOC values between 0.5 and 1.2 V have higher Q20 and lower (LUMO+1)–LUMO (referred to as ΔLUMO) gap. As reported by Troisi and coworkers,75 a small ΔLUMO value with a sufficiently low-lying LUMO+1 of the acceptor promotes electron acceptance probability from the LUMO of the donor. Hence, it results in a significant improvement in the PCE. Moreover, a small ΔLUMO gap enables a high energy charge transfer (CT) state, which in turn leads to an efficient formation of charge separation (CS) state.76 Therefore, ΔLUMO is an essential parameter and plays a vital role in discriminating between good and bad electron acceptors. As can be seen from Fig. 3b, most of the designed NFAs exhibit ΔLUMO below 0.3 eV.
3.2 Screening criteria
To identify the novel NFAs, we apply a layer-by-layer screening criterion. The screening conditions are applied sequentially to reduce the size of the system to a fewer number and achieve the potential candidates. However, the result is independent of the order.(i) Criteria I: The LUMO energy of an NFA is lower than the LUMO of the FTAZ donor polymer. A low-lying LUMO level contributes to a faster charge separation at the interface.
(ii) Criteria II: The energy gap between LUMO+1 and LUMO is lower than 0.3 eV. As stated in ref. 31, 75, a small ΔLUMO (<0.3 eV) is beneficial for high PCE solar cells. All candidate molecules fulfilled the first two conditions.
(iii) Criteria III: Exciton binding energy (Eb) below 0.3 eV. A low Eb facilitates the exciton dissociation process, yielding separated charge carriers and an improved current density.77 This condition reduces the overall number of candidates to 38.
(iv) Criteria IV: Open circuit voltage (VOC) of the NFAs lies in the range of 0.5–1.2 V, with respect to the FTAZ donor, further reducing the set to 32 NFAs.
(v) Criteria V: One of our goals was to find complementary absorbing NFA dyes with maximum absorption in the near IR region. Hence applying a condition of absorption wavelength (λ) in the range of ∼800–1200 nm further reduced to 18 NFAs.
(vi) Criteria VI: We identified the five best NFAs based on the most suitable combinations of VOC (close to 1.2 V), λ (∼1200 nm), Eb (<0.3 eV), and the oscillator strength (>1.0).
Fig. 4 shows a correlation between the computed VOC and Eb, where each point is color coded as per the respective absorption maximum. It is apparent that only a small set of designed compounds fulfills the benchmarks mentioned above. Also, these few NFAs possess high oscillator strength (f) and large Q20 as depicted in Fig. 3b. These NFAs are A1–D4–A1, A4–D4–A4, A1–D6–A1, A4–D6–A4, and A4–D8–A4. It is important to note that the charge transport simulations are computationally demanding since they involve morphology predictions via molecular dynamics simulations followed by quantum chemical calculations on near-neighbor charge hopping pairs. Hence, restricting us from treating only a few selected compounds from the database.
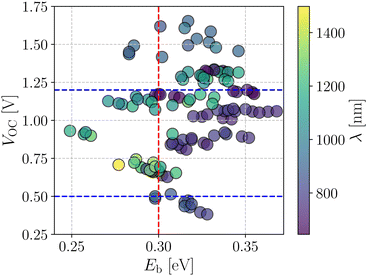 | ||
| Fig. 4 Screening criteria of the investigated NFA systems based on their correlation between VOC and Eb. The color of each point represents the corresponding absorption wavelength value. | ||
3.3 Energy levels and photophysics of the selected NFAs
Ionization potential (IP), electron affinity (EA), and reorganization energy are crucial parameters for determining the charge transport efficiencies of organic semiconductors. The computed IP, EA, and reorganization energy of the selected NFAs (A1–D4–A1, A4–D4–A4, A1–D6–A1, A4–D6–A4, and A4–D8–A4) are summarized in Table 1. As can be seen, the structural modifications of bare A1–D3–A1 molecule offer significant differences in the calculated energy levels. Compared to the bare A1–D3–A1, six thiophene-linked A1–D4–A1 and A4–D4–A4 acceptors exhibit a reduced IP and EA. The elongation from six to eight thiophene ring further reduces the IP and EA. However, a slight increment in the energy levels is observed when B–N fuzed-thiophene incorporated phenyl–methyl (A4–D6–A4) is shifted towards the end-group acceptor (A4–D8–A4). The investigated systems' hole and electron reorganization energies (λh and λe) are summarized in Table 1. Compared to bare A1–D3–A1, the B–N embedded thiophene ring linked with phenyl–methyl materials (A1–D4–A1 and A4–D4–A4) possess smaller λe, which indicates better electron transport characteristics in these systems. However, the larger λh suggests a poorer hole transport efficiency.| Compounds | IP (eV) | EA (eV) | λ h (eV) | λ e (eV) | μ h (cm2 V−1 s−1) | μ e (cm2 V−1 s−1) |
|---|---|---|---|---|---|---|
| A1–D3–A1 | 6.129 | 2.786 | 0.179 | 0.124 | 2.60 × 10−2 | 3.45 × 10−2 |
| A1–D4–A1 | 5.238 | 2.503 | 0.199 | 0.111 | 3.38 × 10−1 | 2.52 × 10−1 |
| A4–D4–A4 | 5.245 | 2.532 | 0.194 | 0.106 | 2.59 × 10−1 | 2.41 × 10−1 |
| A1–D6–A1 | 5.145 | 2.545 | 0.192 | 0.091 | 1.24 × 10−1 | 1.15 × 10−1 |
| A4–D6–A4 | 5.151 | 2.572 | 0.188 | 0.087 | 7.25 × 10−2 | 1.12 |
| A4–D8–A4 | 5.257 | 2.598 | 0.199 | 0.099 | 1.20 × 10−1 | 1.68 × 10−1 |
The optical absorption spectra of the designed NFA molecules are examined at TD-DFT/B3LYP/6-31G(d,p) level considering the polarizable conductor calculation model (CPCM, solvent = chloroform). The absorption wavelength (λmax), excitation energy (Ex), oscillator strength (f), and exciton binding energy (Eb) are summarized in Table S2 of the ESI.† Table S2 shows that the computed maximum wavelength of the INIC3 compound agreed well with the available experimental value. The λmax of the designed compounds are found in the visible to near-infrared (NIR) region with a significant value of oscillator strength. Notably, λmax of the selected five acceptor molecules fall in the NIR region, 1074.7 to 1171.8 nm, resulting from a bathochromic shift compared to the bare INIC3 compound. The above shift can be justified by incorporating B–N in the π-core unit, elongating the thiophene rings, and strong acceptor motifs in the molecular architecture. Thus, these potential NFAs can complement donor photon absorption in the middle of the visible region, eventually guiding to an efficient photon harvesting blend.
The open-circuit voltage is one of the key parameters that determine a material's efficiency and influence the overall performance of the OSC.78VOC is calculated considering FTAZ donor (Fig. S1 of ESI†), as reported in ref. 31 and values are listed in Table S2 of SI. We observe that VOC of the five potential NFAs are greater than the INIC3 (A1–D1–A1) compound. The net increase of the VOC falls in the 0.219 to 0.284 V range. The enhancement of VOC can be explained by B–N functionalization and elongation of thiophene rings on the donor moiety. However, the increase in the VOC on the six and eight thiophene-based acceptors are quite similar and follows the trend A1–D4–A1 (1.136 V) > A1–D6–A1 (1.121 V) > A4–D4–A4 (1.106 V) > A4–D6–A4 (1.093 V) > A4–D8–A4 (1.071 V).
3.4 Morphology and charge transport simulations
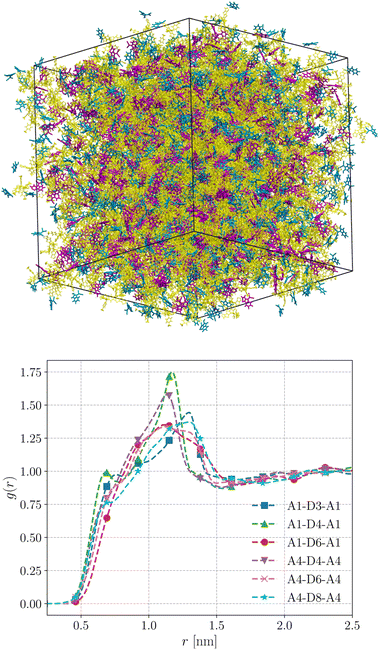
We performed MD simulations on the five selected NFA molecules (potentially high-performing) to generate their amorphous morphology. These simulations involved 1000 acceptor molecules initially packed into a cubic box, followed by simulated annealing and rapid quenching to obtain glassy amorphous morphology. Fig. 5 shows a representative snapshot of such morphology where the π-core and the two terminal electron-withdrawing moieties are depicted in yellow, blue, and magenta colors, respectively. Further, we have evaluated the nematic order parameter to (S) to quantify the structural ordering in the MD simulated morphologies. S is defined as the largest eigenvalue of the order tensor,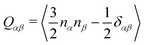 . Here n is the unit vector along the long molecular axis. A morphology of perfectly aligned molecules is represented by S = 1 whereas S = 0 corresponds to an isotropic orientational distribution. In the five systems, we observed the values of S to be in the range of 0.02 to 0.08, indicating that we indeed have an amorphous morphology.
. Here n is the unit vector along the long molecular axis. A morphology of perfectly aligned molecules is represented by S = 1 whereas S = 0 corresponds to an isotropic orientational distribution. In the five systems, we observed the values of S to be in the range of 0.02 to 0.08, indicating that we indeed have an amorphous morphology.
The radial distribution functions (RDFs) obtained from the simulated amorphous mesophases are displayed in Fig. 5. As can be seen, the RDFs exhibit a prominent peak around 1.2–1.3 nm with a minor shoulder at sub-nanometer length scales. The prominent peaks in all systems are broad, substantiating that these morphologies lack orientational order and are purely amorphous.
Based on these MD-simulated amorphous morphologies, we extracted 110 molecular dimers within the centroid-to-centroid distance of 10 Å for all the systems. On each of these dimers, quantum chemical calculations yielded the electronic coupling elements and the site energy differences as defined in eqn (2).68 Following that, the rate of charge carrier transfer and their mobilities were estimated viaeqn (1) and (3). The distributions of the site energy differences (ΔEij) for hole and electron transfer, estimated from the site energies of the fragments in a dimer, are shown in Fig. 6. It is evident that ΔEij follows a Gaussian distribution for both hole and electron with a standard deviation of 0.19 eV and 0.18 eV, respectively. Such distribution in site energies is in accordance with earlier reports on IDIC-based non-fullerene acceptors.79 ΔEij quantifies the energetic disorder, and the predicted disorder for hole and electron transfer in the investigated systems are of the same order as reported in ref. 79 for amorphous NFAs.
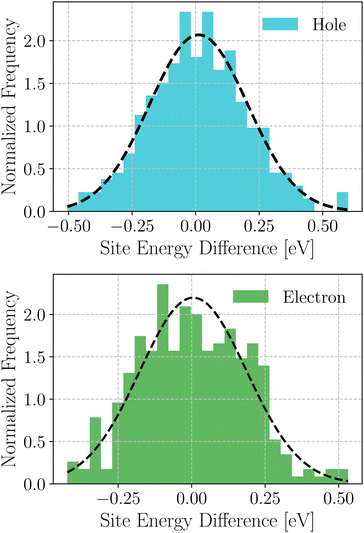 | ||
| Fig. 6 Distribution of site energy differences for hole and electron transfer process in the selected NFA systems. | ||
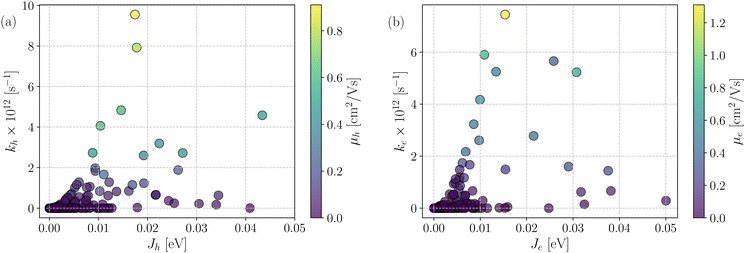
Fig. 7 shows a correlation between the computed charge transfer rates (kh/ke) and electronic coupling (Jh/Je) for hole and electron in the six-thiophene systems, where each point is color coded as per the respective charge carrier mobilities. A similar correlation for the eight-thiophene systems is shown in Fig. S2 of the ESI.† As evident from Fig. 7, the electronic couplings for hole and electron transfer in these systems are within 0.01 eV for most of the molecular dimers. The coupling elements were found to be as large as 0.05 eV for a few exceptional charge-hopping pairs. Consequently, these pairs exhibit a large magnitude of charge transfer rate and, thus, mobility. Such a high magnitude of charge carrier mobility is justified, as these dimers are separated by short distances yielding a significant constructive overlap between HOMO or LUMO orbitals attributed to hole or electron transport. The computed average mobility for holes and electrons in the six systems are summarized in Table 1. As can be seen, the simulated average electron mobility in the A1–D3–A1 compound is 3.45 × 10−02 cm2 V−1 s−1 which is two orders of magnitude higher than the experimental measurement performed on INIC3 acceptor. It is important to note that simple methyl groups in the A1–D3–A1 system replace the hexyl linkers present in the INIC3 compound. Shortening such alkyl linkers strongly affects the molecular packing and hence, the charge transport properties. Another justification could be that the mobility was computed based on a molecular dimer extracted from the MD simulation trajectory neglecting the effect of their surrounding. Although the final mobility was averaged over hundreds of dimers, individually, they lack the presence of the surrounding environment. To incorporate such effects, a multiscale simulation technique, as reported in ref. 62 and 63, can be employed, where the charge-hopping sites are dressed by their neighbors' electrostatic and induction effects. Kinetic Monte Carlo simulations followed it to obtain the charge carrier dynamics and mobilities. Although accurate enough, the latter approach is very expensive regarding computational time, and it would be impossible to apply such an expensive method to perform extensive scale screening. Instead, the present method70,71 has been widely used in the literature to give qualitative insights into the charge transport properties and mobility values within a few orders of magnitudes compared to the experiment. Our work shows that the deviation is consistent across the experimentally studied systems within two orders of magnitude (see Table S1 of the ESI†). Therefore, the relative trend in computed mobilities among the designed NFAs would be interesting even though the absolute number is overestimated. Interestingly, from Table 1, we observe an enhanced charge carrier mobility in all the designed NFAs when compared to the A1–D3–A1 system. Among the systems examined, A4–D6–A4 exhibited the largest average electron mobility value of 1.12 cm2 V−1 s−1, which is approximately 15 times larger than the hole mobility 7.25 × 10−02 cm2 V−1 s−1. Important to note that ambipolar and n-type organic semiconducting materials are highly required due to the rapid growth in demand in the organic electronics field. Ambipolar charge transport generally refers to balanced charge transfer characteristics considering equivalent hole and electron mobility of the organic materials. Ambipolar charge transport plays a vital role in achieving multiple charge transfer routes without accumulating charge carriers, consequently enhancing the OSCs' short-circuit current density.80 In the present context, except for the A4–D6–A4, all the screened potential candidate NFAs demonstrate ambipolar charge transport, a characteristic generally desired for enhanced device performance. These observations based on charge transport characteristics demonstrate our design principle's efficacy for the next-generation NFAs. B–N Functionalization of the ladder-type π-core unit not only improves the photophysics but also yields charge carrier mobility enhanced by at least two orders of magnitude compared to the parent system. Therefore, such a chemical design rule would be a possible way to design novel NFAs for improved solar cell performance.
4 Conclusions
In summary, we presented a computational approach to design and screen novel small molecule non-fullerene acceptor for organic solar cells. Our chemical design rules primarily rely on functionalizing the ladder-type π-core unit by incorporating boron and nitrogen atoms and extending the conjugation length by increasing the length of thiophene rings from three to four units on either side of the phenyl ring in the core. In addition, we considered shifting the B–N-linked thiophene ring toward the end-group acceptor; and, to reduce the computational expenses, trimming the phenyl–hexyl to phenyl–methyl attached to the core unit of the small acceptor molecules. In this multilayer computational strategy, we first generate the 3D-molecular architecture based on individual SMILE strings of core and acceptor units by applying an automated method. Initial geometries of each NFAs are optimized via tight-binding followed by density functional theory. Based on the energy-minimized structures, electronic structure calculations are performed to acquire critical parameters to evaluate the merits of each designed NFAs.Initial assessment of the dataset generated via quantum mechanical calculations revealed that B–N functionalization in the designed NFAs leads to a bathochromic shift in the absorption maximum in the NIR region. All NFA molecules created satisfy the ΔLUMO condition below 0.3 eV for improved solar cell efficiency, as reported in ref. 31 and 75. For further screening and identification of potential candidate structures, three crucial threshold parameters are imposed – exciton binding energy below 0.3 eV, open-circuit voltage between 0.5 to 1.2 V, and absorption wavelength in the range of ∼800–1200 nm. These filtering conditions resulted in eighteen NFAs, of which five were selected to further investigate their charge transport properties.
On the five selected compounds, molecular dynamics simulations are carried out to obtain amorphous morphologies. Based on these morphologies, near-neighbor pairs are extracted within a distance cutoff of 10 Å. These molecular dimers are then used to compute the electronic coupling elements for hole and electron transfer. Finally, charge transfer rates and mobilities are estimated within the hopping formalism as described by eqn (1) and (3). Our results reveal that all the screened potential NFA compounds exhibit superior charge transport characteristics with hole and electron mobilities two orders of magnitude higher than the parent A1–D3–A1 system. In addition, most of the designed compounds possess an ambipolar character which is highly desired for enhancing short-circuit current density (JSC) and improved solar cell efficiency. Overall our design principle of embedding boron and nitrogen center within the central π-core unit leads us to identify novel NFA molecules with promising photophysical and charge transport properties. This outcome certainly provides an avenue for tailoring and developing next-generation non-fullerene acceptors for organic solar cells.
Author contributions
AM conceived the problem. RK conducted all the simulations. AM and RK analyzed the results and prepared the draft.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors gratefully acknowledge the Indian Institute of Technology Gandhinagar, India, for providing research facilities and financial support. AM acknowledges the SERB (SRG/2022/001532) project for funding. RK and AM thank PARAM Ananta for computational resources.References
- S. Li, W. Liu, C.-Z. Li, M. Shi and H. Chen, Small, 2017, 13, 1701120 CrossRef PubMed.
- C. Yan, S. Barlow, Z. Wang, H. Yan, A. K.-Y. Jen, S. R. Marder and X. Zhan, Nat. Rev. Mater., 2018, 3, 18003 CrossRef CAS.
- P. Meredith, W. Li and A. Armin, Adv. Energy Mater., 2020, 10, 2001788 CrossRef CAS.
- A. Armin, W. Li, O. J. Sandberg, Z. Xiao, L. Ding, J. Nelson, D. Neher, K. Vandewal, S. Shoaee, T. Wang, H. Ade, T. Heumüller, C. Brabec and P. Meredith, Adv. Energy Mater., 2021, 11, 2003570 CrossRef CAS.
- L. Zhu, M. Zhang, J. Xu, C. Li, J. Yan, G. Zhou, W. Zhong, T. Hao, J. Song and X. Xue, et al. , Nat. Mater., 2022, 21, 656–663 CrossRef CAS PubMed.
- R. Sun, Y. Wu, X. Yang, Y. Gao, Z. Chen, K. Li, J. Qiao, T. Wang, J. Guo and C. Liu, et al. , Adv. Mater., 2022, 34, 2110147 CrossRef CAS PubMed.
- Z. Zheng, J. Wang, P. Bi, J. Ren, Y. Wang, Y. Yang, X. Liu, S. Zhang and J. Hou, Joule, 2022, 6, 171–184 CrossRef CAS.
- C. Han, J. Wang, S. Zhang, L. Chen, F. Bi, J. Wang, C. Yang, P. Wang, Y. Li and X. Bao, Adv. Mater., 2023, 35, 2208986 CrossRef CAS PubMed.
- C. He, Y. Pan, Y. Ouyang, Q. Shen, Y. Gao, K. Yan, J. Fang, Y. Chen, C.-Q. Ma and J. Min, et al. , Energy Environ. Sci., 2022, 15, 2537–2544 RSC.
- J. Song, F. Cai, C. Zhu, H. Chen, Q. Wei, D. Li, C. Zhang, R. Zhang, J. Yuan, H. Peng, S. K. So and Y. Zou, Sol. RRL, 2021, 5, 2100281 CrossRef CAS.
- X. Li, S. Luo, H. Sun, H. H.-Y. Sung, H. Yu, T. Liu, Y. Xiao, F. Bai, M. Pan, X. Lu, I. D. Williams, X. Guo, Y. Li and H. Yan, Energy Environ. Sci., 2021, 14, 4555–4563 RSC.
- C. Zhang, J. Yuan, J. K. W. Ho, J. Song, H. Zhong, Y. Xiao, W. Liu, X. Lu, Y. Zou and S. K. So, Adv. Funct. Mater., 2021, 31, 2101627 CrossRef CAS.
- S. K. Mellerup and S. Wang, Trends Chem., 2019, 1, 77–89 CrossRef CAS.
- A. Escande and M. J. Ingleson, Chem. Commun., 2015, 51, 6257–6274 RSC.
- F. Jakle, Chem. Rev., 2010, 110, 3985–4022 CrossRef CAS PubMed.
- P. G. Campbell, A. J. Marwitz and S.-Y. Liu, Angew. Chem., Int. Ed., 2012, 51, 6074–6092 CrossRef CAS PubMed.
- C. R. McConnell, F. Haeffner, A. W. Baggett and S.-Y. Liu, J. Am. Chem. Soc., 2019, 141, 9072–9078 CrossRef CAS PubMed.
- T. A. Welsh, A. Laventure, A. F. Alahmadi, G. Zhang, T. Baumgartner, Y. Zou, F. Jakle and G. C. Welch, ACS Appl. Energy Mater., 2019, 2, 1229–1240 CrossRef CAS.
- X. Long, Z. Ding, C. Dou, J. Zhang, J. Liu and L. Wang, Adv. Mater., 2016, 28, 6504–6508 CrossRef CAS PubMed.
- K. Liu, R. A. Lalancette and F. Jakle, J. Am. Chem. Soc., 2019, 141, 7453–7462 CrossRef CAS PubMed.
- K. Liu, R. A. Lalancette and F. Jakle, J. Am. Chem. Soc., 2017, 139, 18170–18173 CrossRef CAS PubMed.
- F. Liu, Z. Ding, J. Liu and L. Wang, Chem. Commun., 2017, 53, 12213–12216 RSC.
- K. Liu, Z. Jiang, R. A. Lalancette, X. Tang and F. Jakle, J. Am. Chem. Soc., 2022, 144, 18908–18917 CrossRef CAS PubMed.
- M. M. Morgan, M. Nazari, T. Pickl, J. M. Rautiainen, H. M. Tuononen, W. E. Piers, G. C. Welch and B. S. Gelfand, Chem. Commun., 2019, 55, 11095–11098 RSC.
- J. Yang, X. Wu, Q.-S. Li and Z.-S. Li, Mater. Adv., 2022, 3, 3229–3237 RSC.
- C. Dong, B. Meng, J. Liu and L. Wang, ACS Appl. Mater. Interfaces, 2020, 12, 10428–10433 CrossRef CAS PubMed.
- Z. Zhang, Z. Ding, C. Dou, J. Liu and L. Wang, Polym. Chem., 2015, 6, 8029–8035 RSC.
- Z. Jia, Q. Ma, Z. Chen, L. Meng, N. Jain, I. Angunawela, S. Qin, X. Kong, X. Li and Y. Yang, et al. , Nat. Commun., 2023, 14, 1236 CrossRef CAS PubMed.
- Ö. H. Omar, M. del Cueto, T. Nematiaram and A. Troisi, J. Mater. Chem. C, 2021, 9, 13557–13583 RSC.
- C. Schober, K. Reuter and H. Oberhofer, J. Phys. Chem. Lett., 2016, 7, 3973–3977 CrossRef CAS PubMed.
- Z.-W. Zhao, O. H. Omar, D. Padula, Y. Geng and A. Troisi, J. Phys. Chem. Lett., 2021, 12, 5009–5015 CrossRef CAS PubMed.
- N. C. Forero-Martinez, K. Lin, K. Kremer and D. Andrienko, Adv. Sci., 2022, 9, 2200825 CrossRef CAS PubMed.
- S. Dai, F. Zhao, Q. Zhang, T.-K. Lau, T. Li, K. Liu, Q. Ling, C. Wang, X. Lu and W. You, et al. , J. Am. Chem. Soc., 2017, 139, 1336–1343 CrossRef CAS PubMed.
- B. Schweda, M. Reinfelds, P. Hofstadler, G. Trimmel and T. Rath, ACS Appl. Energy Mater., 2021, 4, 11899–11981 CrossRef CAS PubMed.
- T. A. Halgren, J. Comput. Chem., 1996, 17, 490–519 CrossRef CAS.
- T. A. Halgren, J. Comput. Chem., 1996, 17, 520–552 CrossRef CAS.
- T. A. Halgren, J. Comput. Chem., 1996, 17, 553–586 CrossRef CAS.
- T. A. Halgren and R. B. Nachbar, J. Comput. Chem., 1996, 17, 587–615 CAS.
- T. A. Halgren, J. Comput. Chem., 1996, 17, 616–641 CrossRef CAS.
- N. M. O'Boyle, M. Banck, C. A. James, C. Morley, T. Vandermeersch and G. R. Hutchison, J. Cheminform., 2011, 3, 33 CrossRef PubMed.
- G. Seifert, D. Porezag and T. Frauenheim, Int. J. Quantum Chem., 1996, 58, 185–192 CrossRef CAS.
- M. Elstner, D. Porezag, G. Jungnickel, J. Elsner, M. Haugk, T. Frauenheim, S. Suhai and G. Seifert, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 7260–7268 CrossRef CAS.
- M. Gaus, Q. Cui and M. Elstner, J. Chem. Theory Comput., 2011, 7, 931–948 CrossRef CAS PubMed.
- A. Tkatchenko, R. A. DiStasio, R. Car and M. Scheffler, Phys. Rev. Lett., 2012, 108, 236402 CrossRef PubMed.
- A. Ambrosetti, A. M. Reilly, R. A. DiStasio and A. Tkatchenko, J. Chem. Phys., 2014, 140, 18A508 CrossRef PubMed.
- M. Stöhr, G. S. Michelitsch, J. C. Tully, K. Reuter and R. J. Maurer, J. Chem. Phys., 2016, 144, 151101 CrossRef PubMed.
- M. Mortazavi, J. G. Brandenburg, R. J. Maurer and A. Tkatchenko, J. Phys. Chem. Lett., 2018, 9, 399–405 CrossRef CAS PubMed.
- B. Aradi, B. Hourahine and T. Frauenheim, J. Phys. Chem. A, 2007, 111, 5678–5684 CrossRef CAS PubMed.
- A. H. Larsen, J. J. Mortensen, J. Blomqvist, I. E. Castelli, R. Christensen, M. Dułak, J. Friis, M. N. Groves, B. Hammer, C. Hargus, E. D. Hermes, P. C. Jennings, P. B. Jensen, J. Kermode, J. R. Kitchin, E. L. Kolsbjerg, J. Kubal, K. Kaasbjerg, S. Lysgaard, J. B. Maronsson, T. Maxson, T. Olsen, L. Pastewka, A. Peterson, C. Rostgaard, J. Schiøtz, O. Schütt, M. Strange, K. S. Thygesen, T. Vegge, L. Vilhelmsen, M. Walter, Z. Zeng and K. W. Jacobsen, J. Phys.: Condens. Matter, 2017, 29, 273002 CrossRef PubMed.
- M. J. Frisch et al. , Gaussian 09 Revision E.01, Gaussian Inc., Wallingford CT, 2009 Search PubMed.
- V. Barone, M. Cossi and J. Tomasi, J. Comput. Chem., 1998, 19, 404–417 CrossRef CAS.
- V. Rühle, A. Lukyanov, F. May, M. Schrader, T. Vehoff, J. Kirkpatrick, B. Baumeier and D. Andrienko, J. Chem. Theory Comput., 2011, 7, 3335–3345 CrossRef PubMed.
- M. C. Scharber, D. Mühlbacher, M. Koppe, P. Denk, C. Waldauf, A. J. Heeger and C. J. Brabec, Adv. Mater., 2006, 18, 789–794 CrossRef CAS.
- R. Khatua, B. Das and A. Mondal, Phys. Chem. Chem. Phys., 2023, 25, 7994–8004 RSC.
- W. L. Jorgensen, D. S. Maxwell and J. Tirado-Rives, J. Am. Chem. Soc., 1996, 118, 11225–11236 CrossRef CAS.
- W. L. Jorgensen and J. Tirado-Rives, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 6665–6670 CrossRef CAS PubMed.
- D. J. Cole, J. Z. Vilseck, J. Tirado-Rives, M. C. Payne and W. L. Jorgensen, J. Chem. Theory Comput., 2016, 12, 2312–2323 CrossRef CAS PubMed.
- T. A. Manz and N. G. Limas, RSC Adv., 2016, 6, 47771–47801 RSC.
- A. Tkatchenko and M. Scheffler, Phys. Rev. Lett., 2009, 102, 073005 CrossRef PubMed.
- B. Hess, C. Kutzner, D. Van Der Spoel and E. Lindahl, J. Chem. Theory Comput., 2008, 4, 435–447 CrossRef CAS PubMed.
- S. Pronk, S. Páll, R. Schulz, P. Larsson, P. Bjelkmar, R. Apostolov, M. R. Shirts, J. C. Smith, P. M. Kasson, D. van der Spoel, B. Hess and E. Lindahl, Bioinformatics, 2013, 29, 845–854 CrossRef CAS PubMed.
- N. B. Kotadiya, A. Mondal, S. Xiong, P. W. M. Blom, D. Andrienko and G.-J. A. H. Wetzelaer, Adv. Electron. Mater., 2018, 4, 1800366 CrossRef.
- A. Mondal, L. Paterson, J. Cho, K.-H. Lin, B. van der Zee, G.-J. A. H. Wetzelaer, A. Stankevych, A. Vakhnin, J.-J. Kim, A. Kadashchuk, P. W. M. Blom, F. May and D. Andrienko, Chem. Phys. Rev., 2021, 2, 031304 CrossRef.
- L. Martínez, R. Andrade, E. G. Birgin and J. M. Martínez, J. Comput. Chem., 2009, 30, 2157–2164 CrossRef PubMed.
- G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 014101 CrossRef PubMed.
- H. J. C. Berendsen, J. P. M. Postma, W. F. van Gunsteren, A. DiNola and J. R. Haak, J. Chem. Phys., 1984, 81, 3684–3690 CrossRef CAS.
- R. A. Marcus, J. Chem. Phys., 1956, 24, 966–978 CrossRef CAS.
- E. F. Valeev, V. Coropceanu, D. A. da Silva Filho, S. Salman and J.-L. Brédas, J. Am. Chem. Soc., 2006, 128, 9882–9886 CrossRef CAS PubMed.
- Brown's Open Access Toolset BOAT, https://joshuasbrown.github.io/docs/CATNIP/catnip_home.html, Accessed: 2023-01-09.
- V. Coropceanu, J. Cornil, D. A. da Silva Filho, Y. Olivier, R. Silbey and J.-L. Brédas, Chem. Rev., 2007, 107, 926–952 CrossRef CAS PubMed.
- L. Wang, G. Nan, X. Yang, Q. Peng, Q. Li and Z. Shuai, Chem. Soc. Rev., 2010, 39, 423–434 RSC.
- S. Karuthedath, J. Gorenflot, Y. Firdaus, N. Chaturvedi, C. S. De Castro, G. T. Harrison, J. I. Khan, A. Markina, A. H. Balawi and T. A. D. Peña, et al. , Nat. Mater., 2021, 20, 378–384 CrossRef CAS PubMed.
- J. I. Khan, M. A. Alamoudi, N. Chaturvedi, R. S. Ashraf, M. N. Nabi, A. Markina, W. Liu, T. A. Dela Peña, W. Zhang and O. Alévêque, et al. , Adv. Energy Mater., 2021, 11, 2100839 CrossRef CAS.
- A. Markina, K.-H. Lin, W. Liu, C. Poelking, Y. Firdaus, D. R. Villalva, J. I. Khan, S. H. K. Paleti, G. T. Harrison, J. Gorenflot, W. Zhang, S. De Wolf, I. McCulloch, T. D. Anthopoulos, D. Baran, F. Laquai and D. Andrienko, Adv. Energy Mater., 2021, 11, 2102363 CrossRef CAS.
- A. Kuzmich, D. Padula, H. Ma and A. Troisi, Energy Environ. Sci., 2017, 10, 395–401 RSC.
- T. Liu and A. Troisi, J. Phys. Chem. C, 2011, 115, 2406–2415 CrossRef CAS.
- L. Zhu, Y. Yi and Z. Wei, J. Phys. Chem. C, 2018, 122, 22309–22316 CrossRef CAS.
- X. Duan, W. Song, J. Qiao, X. Li, Y. Cai, H. Wu, J. Zhang, X. Hao, Z. Tang and Z. Ge, et al. , Energy Environ. Sci., 2022, 15, 1563–1572 RSC.
- M. Andrea, K. Kordos, E. Lidorikis and D. Papageorgiou, Comput. Mater. Sci., 2022, 202, 110978 CrossRef CAS.
- D. Luo, Z. Jiang, W. Yang, X. Guo, X. Li, E. Zhou, G. Li, L. Li, C. Duan and C. Shan, et al. , Nano Energy, 2022, 98, 107186 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Chemical structure of donor polymer, energy levels, absorption spectra, exciton binding energy, quadrupole moment, open-circuit voltage and charge carrier mobility. See DOI: https://doi.org/10.1039/d3ma00460k |
| This journal is © The Royal Society of Chemistry 2023 |