Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
DFT investigation of the oxygen reduction reaction over nitrogen (N) doped graphdiyne as an electrocatalyst: the importance of pre-adsorbed OH* and the solvation effect†
Yuelin
Wang
 a,
Thanh Ngoc
Pham
a,
Thanh Ngoc
Pham
 a,
Harry H.
Halim
a,
Likai
Yan
a,
Harry H.
Halim
a,
Likai
Yan
 c and
Yoshitada
Morikawa
c and
Yoshitada
Morikawa
 *ab
*ab
aDepartment of Precision Engineering, Graduate School of Engineering, Osaka University, 2-1, Yamada-oka, Osaka 565-0871, Suita, Japan. E-mail: morikawa@prec.eng.osaka-u.ac.jp
bResearch Center for Precision Engineering, Graduate School of Engineering, Osaka University, 2-1 Yamada-oka, Suita 565-0871, Osaka, Japan
cInstitute of Functional Material Chemistry, Key Laboratory of Polyoxometalate Science of Ministry of Education, Faculty of Chemistry, Northeast Normal University, Changchun, 130024, P. R. China
First published on 22nd September 2023
Abstract
Searching for novel electrocatalysts that can replace precious platinum for oxygen reduction reaction (ORR) is important for developing fuel cells. Recently, nitrogen (N) doped graphdiyne (GDY) has been synthesized and proved that the ORR electrocatalytic activity catalyzed by N-doped GDY is significantly improved, however, the roles of sp-N (including sp-N1 and sp-N2) and pyridinic (Pyri)-N dopants in mediating the ORR are still unclear. To clarify which sp-N or Pyri-N creates the active site for ORR, we systematically studied the ORR mechanism on sp-N1GDY and pyri-NGDY supported on graphene (G) with the solvation effect, which was performed using density functional theory (DFT) and ab initio molecular dynamics (AIMD) simulations. Firstly, we found that the dissociative mechanism is preferred on sp-N1GDY/G and the surface is easily terminated by the OH* intermediates, while the OH* pre-adsorbed surface (sp-N1GDY(OH)/G) prefers the associative mechanism. Pyri-NGDY/G also prefers the associative mechanism without any termination. Then, the solvation effect stabilizes all ORR intermediates in both cases. From the calculated free energy diagram, a model with water solvent gives a more appropriate estimation of the overpotential than the one without the water solvent, and sp-N1GDY/G with OH* pre-adsorbed has a lower overpotential (0.46 V), which is close to the experimental value (0.36 V), compared with Pyri-NGDY/G (0.75 V). Our study provides useful information for understanding the reaction mechanisms of ORR at the solid/liquid interface on the N-doped GDY surface.
1. Introduction
Fuel cells provide an innovative and efficient energy conversion technology and operate via electrochemical reactions. The use of clean and renewable fuels, such as hydrogen, methanol, and biomass, reduces dependence on fossil fuels and their associated environmental impacts.1–3 The oxygen reduction reaction (ORR) is a key electrochemical reaction that takes place at the cathode of the fuel cells.4 Traditionally, platinum (Pt) and Pt-based materials have been widely used as electrocatalysts for ORR due to their excellent electrocatalytic activity, durability, and stability;5 however, the high cost and scarcity of Pt have led to significant research efforts to find alternative electrocatalysts that can perform as effectively as Pt-based materials while being more cost-effective and environmentally sustainable.4,6 In 2009, Dai et al. reported that nitrogen-doped carbon nanotube arrays possessed high electrocatalytic activity for the ORR in alkaline media, even superior to Pt.7 This finding led to the development of an interesting field of carbon-based metal-free ORR electrocatalysts because of their advantages, including relatively abundant raw materials, economic feasibility, adjustable surface chemistry, easy processing, large specific surface area, high chemical stability, fast transfer kinetics, and a wide operating temperature range.6 Based on many findings,8–11 N-doping is a particularly advantageous method to modify carbon materials for energy conversion, such as hydrogen evolution reaction (HER), oxygen evolution reaction (OER), ORR, nitrogen reduction reaction (N2RR), and carbon dioxide reduction reaction (CO2RR).Recently, a new type of carbon material named graphdiyne (GDY), a rising star of 2D carbon allotropes with one-atom-thick planar layers, has achieved the co-existence of sp and sp2 hybridized carbon atoms in a 2D planar structure.12–14 GDYs with unique chemical and physical properties have attracted more attention in energy conversion.15–17 However, pure GDY has low ORR electrocatalytic activity, and structural modification, including doping with metal or nonmetal atoms is a good way to improve the activity. Gao et al.18 reported that Fe-doped GDY (Fe@GDY) showed high catalytic activity towards ORR at even higher activity than the benchmark commercial Pt/C (20 wt%). Dai et al.19 predicted that Ni@GDY and Pt@GDY catalysts possessed comparable electrocatalytic activity for ORR and OER in alkaline media based on DFT studies. Li et al.20 reported that N-doped GDY, especially sp-N doping showed much better ORR electrocatalytic performance than the commercial Pt-based catalyst in alkaline media and comparable activity in acidic media. On the other hand, Huang et al.21 reported that pyridinic (Pyri)-NGDY is mainly produced by N doping and Pyri-NDGY exhibits excellent ORR and OER catalytic activity. Despite experimental evidence demonstrating the excellent ORR electrocatalytic activity of N-doped GDY, the nature of the active sites and the dopants involved are still controversial. Recently, a few theoretical ORR studies on N-doped GDY with sp-N configurations have been reported.22–24 Li et al.22 found that ORR proceeds on sp-N(II)GDY with the associative mechanism. The highest ORR electrocatalytic activity has a theoretical onset potential of 0.76 V with metastable adsorption of all the ORR intermediates. Lee et al.23 found that double N-doped GDY has better ORR activity. In the above studies, it turns out that the metastable adsorption sites of ORR intermediates govern the ORR performance. However, the role of the most stable adsorption sites in the ORR mechanism on N-doped GDY remains unclear.
Density functional theory (DFT) calculation is a powerful tool to explore the ORR mechanism using the computational hydrogen electrode (CHE) model,25 however, to accurately elucidate the ORR activity, it is important to incorporate the solvation effect. There are two approaches: (1) the explicit model, and (2) the implicit model. The former approach involves adding water molecules around the reactant or above the surface to represent the solvation effect,26–29 and the latter approach replaces the liquid environment with a polarizable continuous medium (PCM).30,31 Previous theoretical studies on metal-free catalysts mostly used the implicit model, which tends to underestimate the solvation effect during the ORR process. Boresch et al.32 reported that PCM cannot describe any direct solvent effects and might be inaccurate for specific hydrogen bonds. Wang et al.33 reported that the explicit model can give a correct estimation of the ORR overpotential on MnN4–graphene catalyst than the gas-phase model. Hansen et al.34 investigated the solvation energy of ORR intermediates on N-doped graphene using the explicit and implicit models, and found that including explicit H2O molecules is essential for a correct description of the adsorption energy of ORR intermediates on carbon materials, while continuum solvation models are unable to accurately describe the solvation energy.
In this study, we systemically investigated the ORR activity on sp-N1 and Pyri-N-doped GDY with graphene (G) support. DFT calculations and ab initio molecular dynamics (AIMD) simulations were carried out to investigate the ORR mechanism as well as the solvation effect for ORR in both cases. Free energy diagrams showed that the active sites of sp-N1-doped GDY surfaces are easily terminated by OH*, and the neighboring C sites of the –COH–N moiety become real active sites for ORR to proceed with low overpotentials compared with those in Pyri-N. Moreover, the explicit solvation model can give a more consistent overpotential (0.46 V) with the experimental value (0.36 V) compared with that under vacuum conditions (0.72 V).
2. Computational methods
Most of our DFT calculations were performed using the Simulation Tool from the Atom Technology (STATE) program package.35–38 Ionic cores were described using the ultrasoft pseudopotentials,39 and valence electron states were expanded using a plane wave basis set with the kinetic energy cutoffs of 36 and 400 Ry for wave functions and augmented charge density, respectively. A 2 × 4 × 1 Monkhorst–Pack k-point sampling was used for the N-doped GDY 2 × 1 × 1 supercell. The revised PBE (RPBE) functional40 with the Grimme's van der Waals (vdW) correction (D2)41 was employed to describe the weak dispersion interactions between various intermediates and surfaces as well as to describe water–water interactions more accurately.29Spin-polarized calculations were performed whenever triplet O2 was simulated. We considered the intersystem crossing (ISC) upon O2 adsorption on the substrate. The isolated O2 in the triplet state (3Σg−) as its ground electronic state is relatively unreactive due to its low energy. However, when O2 approaches surfaces such as carbon nanotubes and diamond (100),42,43 it can undergo the intersystem crossing (ISC) to a more reactive singlet state (1Δg). In our calculations, the adsorbed O2 in 3Σg− was modeled by fixing the difference between the number of spin-up and spin-down electrons to two, while the adsorbed O2 in 1Δg was modeled by a spin-restricted calculation to obtain a closed-shell configuration, which was necessary to prevent spin contamination. Activation reaction barriers (Ea) were calculated using the climbing image nudge elastic band method (CI-NEB).44,45
According to the experimental conditions,20 the overall reaction of O2 reduction to H2O on N-doped GDY under alkaline conditions is O2(g) + 2H2O(l) + 4e− → 4OH−. The adsorption Gibbs free energy changes (ΔGads) of all the elementary steps in ORR on this N-doped GDY/G using the CHE method24 were computed as:
| ΔGads(X*) = ΔEX* + (ΔHX* − TΔSX*)−neURHE + ΔSol(X*) |
3. Results and discussions
3.1 Atomic and electronic structures of the N-doped GDY catalysts
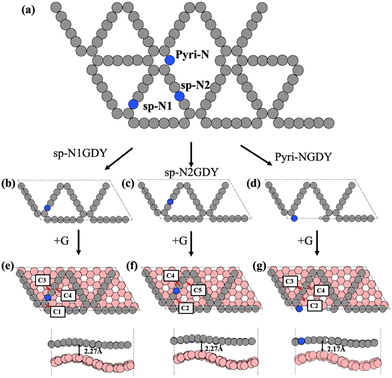
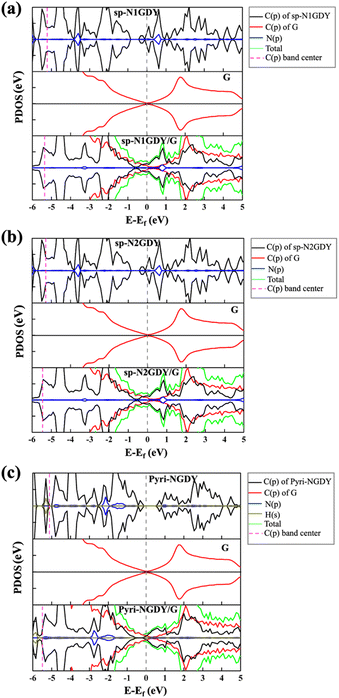
Based on the experimental results,20,21 we constructed two types of N-doped GDY (NGDY), namely sp-NGDY and Pyri-NGDY. As shown in Fig. 1, the carbon atom in the diacetylene linkage (sp hybridized C) is replaced by N to generate two types of sp-N (Fig. 1(b) and (c)), i.e., sp-N1GDY and sp-N2GDY. Pyri-NGDY is the sp2 hybridized N atom bonded with two sp2 hybridized carbon (C) neighbors in the carbon ring and with H-terminated C atoms (Fig. 1(d)). In the experiment,20 N-doped GDY was supported onto glassy carbon, herein, to simplify the model, graphene (G) was applied as a support underneath the N-doped GDY. The obtained optimized lattice constants of the N-doped GDY (9.46 Å), and graphene (2.46 Å) unit cells were consistent with those from previous results.48,49 Considering the lattice matching between the two components, the p(8 × 4) supercell of G and the p(2 × 1) supercell of N-doped GDY were employed to create the interface model (Fig. 1(e)–(g)) by applying a mixed tensile/compressive strain (4%) to the graphene phase, resulting in corrugated graphene. The calculated minimum distances between sp-NGDY or Pyri-NGDY, and the top of graphene were 2.27 and 2.17 Å, respectively, which are close to those of other heterostructures.50 The band gap (Eg) of the isolated G, NGDY in three N configurations (sp-N1, sp-N2, and Pyri-N) and their interface models (sp-N1GDY/G, sp-N2GDY/G, and pyri-NGDY/G) were calculated using the PBE51 and HSE06 functionals52,53 using the VASP code,54,55 as shown in Table S1 (ESI†). We find that Pyri-NGDY is a semiconductor with a band gap of 0.60 eV by PBE and 0.97 eV by HSE06, while sp-N1GDY and sp-N2GDY are metallic, as predicted by both functionals. After introducing the G substrate as the support, all sp-N1GDY, sp-N2GDY, and Pyri-NGDY showed metallicity.To explore the charge transfer of the three N-doped GDY/G interfaces, we calculated the projected density of states (PDOS) (Fig. 2), charge density difference (CDD), and Bader charge of the three cases (Fig. S1, ESI†). The PDOS results showed that after the introduction of G, the Dirac point of G in sp-N1GDY/G, sp-N2GDY/G, and Pyri-NGDY/G is upshifted above the Fermi level, on the other hand, the C(p)s of sp-N1GDY, sp-N2GDY, and Pyri-NGDY in sp-N1GDY/G, sp-N2GDY/G, and Pyri-NGDY/G are downshifted below the Fermi level. The C (p) band centers in the three N-doped GDYs are shifted to a lower energy region upon the introduction of G (Fig. 2). The above results indicate that the use of G can increase the conductivity of N-doped GDY and induce the charge transfer from G to N-doped GDY. The CDD (Fig. S1, ESI†) results also revealed that the charge densities are redistributed by forming electron- and hole-rich regions within the three N-doped GDY/G interfaces. Charge depletion occurs on the G surfaces, resulting in the hole-rich sites. However, strong charge accumulation occurred on the three N-doped GDY surfaces, forming electron-rich sites. Therefore, the electrons are mainly transferred from G to the three N-doped GDY surfaces. To confirm this, the Bader charge analysis (Fig. S1, ESI†) and work function change (Table S2, ESI†) were also conducted. From the Bader charge analysis, 0.11 e− are transferred from the G substrate to sp-N1GDY or sp-N2GDY, and 0.13 e− are transferred from the G substrate to Pyri-NGDY. As shown in Table S2 (ESI†), the work functions of planar G (4.20 eV) and corrugated G (4.10 eV) are smaller than those of pure GDY (5.10 eV), sp-NGDY (4.53 eV), and Pyri-NGDY (4.93 eV), which is the fundamental cause for charge transfer from G to GDY and NGDY.
3.2 ORR mechanism and free energy analysis of sp-N1GDY/G, sp-N2GDY/G, and Pyri-NGDY/G under vacuum conditions
| Structure | ΔEads(O2)/eV | ΔEads(OOH)/eV | E a/eV | |||
|---|---|---|---|---|---|---|
| O2 dissociation | O2 protonation | |||||
| O2 → O2* → 2O* | O2 → 2O* | O2 → 2O* with one H2O | O2 + H2O → OOH* + OH* | |||
| sp-N1GDY/G | −0.6 | — | 0.25 | 0.22 | 0.09 | 0.88 |
| sp-N1GDY(OH)/G | −0.15 | −1.23 | — | 1.86 | 1.64 | 1.40 |
| Pyri-NGDY/G | −0.10 | −0.93 | — | 1.52 | 1.35 | 1.17 |
Next, we examined the reaction barriers for O2 dissociation to 2O* and O2 protonation to OOH* using the CI-NEB method with the consideration of the ISC. We considered two probable pathways for O2 dissociation cases, namely (1) gas-phase O2 adsorption on the surface followed by O2* dissociation to 2O* (O2 → O2* → 2O*); (2) direct dissociative adsorption of gas-phase O2 to 2O* (O2 → 2O*). The triplet and singlet potential energy surfaces (PES) are shown in Fig. S3 (ESI†). For all reaction processes, O2 starts in a triplet state, reaches the ISC state, and changes to a singlet state. The activation reaction energies (Ea) of O2 dissociation and protonation on the three N-doped GDY/G are shown in Table 1 and Fig. S3 (ESI†). We found that on two sp-NGDY/G systems (sp-N1GDY/G and sp-N2GDY/G), the direct O2 → 2O* path is kinetically the most preferable with relatively low Ea (∼0.22 eV on sp-N1GDY/G, and ∼0.08 eV on sp-N2GDY/G). Moreover, water induces O2 dissociation by lowering the activation barrier by ∼0.2 eV on all substrates due to the H bond effect between water and O2.56,57 In contrast, O2 protonation to OOH* exhibits higher activation energy (∼0.88 eV on sp-N1GDY/G and ∼1.41 eV on sp-N2GDY/G) compared with that of O2 dissociation. Consequently, we assume that the ORR mechanism on sp-N-doped catalysts will follow the dissociative mechanism (O2 → 2O* → O* + OH* → O* → OH* → OH−). On the Pyri-NGDY/G surface, the O–O bond of O2 does not activate upon the adsorption due to its physisorption state.
From Table 1, protonation to OOH* has a lower activation energy than its dissociation with one water (1.17 eV vs. 1.35 eV), however, this protonation barrier (1.17 eV) is still rather high; thus protonation process is kinetically unfavorable due to physisorption O2.
It is noted that even though O2 is weakly adsorbed and the activation barrier for the direct protonation of the adsorbed O2 is high, ORR can still proceed with high activities on carbon materials via a different reaction pathway, namely, a process of long-range electron transfer (ET) to nonadsorbed O2 in the outer Helmholtz plane (ET-OHP).58,59 Choi et al.59 recently revealed that the first proton-coupled electron transfer (PCET) step (O2(aq) + (H+ + e−) → ˙OOH (aq)) can occur via ET-OHP, where O2 directly forms ˙OOH (aq). Then, ˙OOH (aq) subsequently adsorbs on the catalytic site as OOH* (i.e., ET-OHP mechanism). This explains the problem of not finding suitable sites for O2 binding on N-doped graphene and shows that the O2 chemisorption is not essential for the occurrence of ORR on carbon-based catalysts. We found that O2 could not chemisorb and that the O2 protonation barrier (1.17 eV) was high on Pyri-NGDY/G. However, OOH* can chemisorb on the surface with ΔEads of −0.93 eV (Table 1). Therefore, we assume that the ORR on Pyri-NGDY/G follows ET-OHP associative mechanism (O2 → OOH* → O* → OH* → OH−).
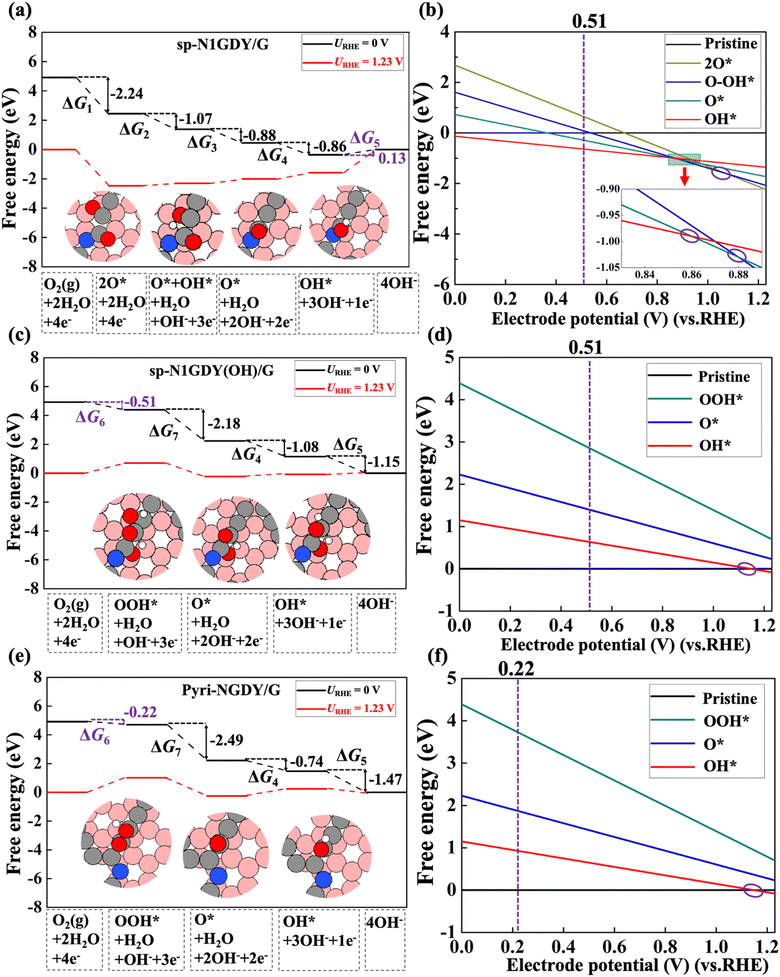
Then, the reaction and adsorption Gibbs free energies of each ORR intermediate on three N-doped models, i.e., sp-N1GDY/G, sp-N2GDY/G, and Pyri-NGDY/G, were calculated and are shown in Fig. 3, Fig. S4, and Tables S4–S6 (ESI†), respectively, for all the considered systems. We find that ORR proceeds with a rather high overpotential (η) on the three substrates. For Pyri-NGDY/G (Fig. 3e), η is 1.01 V, and the potential-determining step (PDS) is the O2 → OOH* (ΔG6). High η of ORR on sp-N1GDY/G (Fig. 3(a)), and sp-N2GDY/G (Fig. S4(a), ESI†) arises from the strong interactions of ORR intermediates with the substrate. The PDS for ORR on the N-doped catalyst in sp-N configurations is found to be the last step OH* → OH− (ΔG5). The third ORR step (O* + OH* → O*) is exergonic and becomes endergonic upon applying a potential of 1.23 V. The last steps (OH* → OH−) are endergonic reactions even at URHE = 0 V (0.13 eV on sp-N1GDY/G and 0.38 eV on sp-N2GDY/G), showing that OH* has a strong binding energy with the surface and is difficult to further hydrogenate. As a result, the first ORR could not be completed, and some ORR intermediates, such as O* or OH*, remain adsorbed on sp-NGDY/G.
To confirm this, the adsorption Gibbs free energy of each ORR intermediate as a function of the electrode potential (URHE) was evaluated. As shown in Fig. 3(b), sp-N1GDY/G was terminated by OH* at 0 V < URHE < 0.86 V, by O* at 0.86 V < URHE < 0.88 V, by O* + OH* at 0.88 V < URHE < 1.07 V, and by 2O* at 1.07 V < URHE < 1.23 V. Similarly, for sp-N2GDY/G (Fig. S4(b), ESI†), sp-N2GDY/G was terminated by OH* at 0 V< URHE < 0.49 V, by O* at 0.49 V < URHE < 0.73 V, and by 2O*at 0.73 V < URHE < 1.23 V. In contrast, on the Pyri-NGDY/G surface, the most stable structure is the Pyri-NGDY/G pristine surface under 0 V < URHE <1.11 V (Fig. 3(f)). It should be noted that in this work, we only considered single ORR intermediates as a function of potential, the coverage60 of ORR intermediates may or may not affect the results, this subject will be investigated in the next project.
Consequently, upon applying a limiting potential of 0.22 V, the complete ORR process occurring on Pyri-NGDY/G, and ORR species will never be terminated on the surface. In contrast, OH* will be terminated on sp-N1GDY/G and sp-N2GDY/G surfaces without any applied potential (sp-N1GDY(OH)/G and sp-N2GDY/G hereafter). Therefore, we explored the ORR mechanism of sp-N1GDY(OH)/GDY and sp-N2GDY(OH)/GDY in the next subsection.
The free energy diagram, reaction, and adsorption Gibbs free energy of ORR intermediates on sp-N1GDY(OH)/GDY and sp-N2GDY(OH)/GDY are shown in Fig. 3(c), Fig. S4(c), and Tables S4–S6 (ESI†). For sp-N1GDY(OH)/GDY, the stabilities of the three ORR intermediates, i.e., OOH*, O*, and OH* were estimated. We find that all ORR intermediates preferably adsorb on top sites of the neighboring C atom of the –COH–N moiety. Interactions between sp-N1GDY(OH) and intermediates become weak after involving the pre-adsorbed OH*. The ΔGOH* of sp-N1GDY(OH)/G is 1.15 eV larger than that of sp-N1GDY/G (−0.13 eV), indicating that the pre-adsorbed OH* is improving rather than poisoning. Moreover, the PDS is O2 → OOH* with a limiting potential of 0.51 eV and η of 0.72 V (Table 2). As shown in Fig. 3(b) and (d), we can also prove that under URHE = 0.51 V, sp-N1GDY(OH) is the most stable structure. For sp-N2GDY(OH)/G, we found 2O* → O* + OH* is a strongly endergonic reaction with ΔG2 of 1.06 eV (Fig. S4(c) and Table S5, ESI†), which may cause possible poisoning of active sites by 2O*. Therefore, sp-N2GDY/G cannot be used as an ORR electrocatalyst.
| RPBE + D2 | PBE + D2 | |||
|---|---|---|---|---|
| η | PDS | η | PDS | |
| sp-N1GDY(OH) | 0.75 | O2 → OOH* | — | — |
| sp-N1GDY(OH)/G | 0.72 | O2 → OOH* | 0.54 | O2 → OOH* |
| sp-N1GDY(OH)/G with water | 0.46 | O2 → OOH* | 0.54 | OH* → OH− |
| Pyri-NDGY | 1.17 | O2 → OOH* | — | — |
| Pyri-NDGY/G | 1.01 | O2 → OOH* | 0.89 | O2 → OOH* |
| Pyri-NDGY/G with water | 0.75 | O2 → OOH* | 0.65 | O* → OH* |
| Experiment20 | η = 0.36 | |||
Under vacuum conditions, we found that sp-N1GDY(OH)/G can create a conceivable active site for ORR with low overpotential. The clean sp-N1GDY/G surfaces are easily terminated by OH* intermediate and the neighboring C site of -the COH-N moiety of sp-N1GDY(OH)/G is the real active site for ORR to proceed with low η compared with Pyri-NGDY/G.
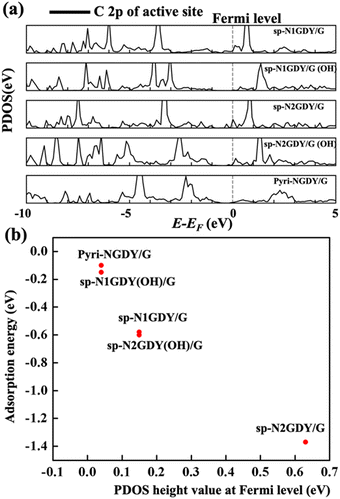
We plotted the PDOS of C2p of the active site in sp-N1GDY/G, sp-N2GDY/G, sp-N1GDY(OH)/G, sp-N2GDY(OH)/G, and Pyri-NGDY/G. In Fig. 4(a), at the Fermi level, there is almost no partially occupied state of C 2p in sp-N1GDY(OH)/G and Pyri-NGDY/G, while for sp-N1GDY/G, sp-N2GDY/G, and sp-N2GDY(OH)/G, there exists partially occupied state of C 2p. From Fig. 4(b), we also found that there is a linear relationship between the PDOS height value at the Fermi level and the adsorption energy of O2. The results can also prove that the presence of a partially occupied state of the C 2p of the active site can induce O2 adsorption. Upon adsorption of O2, there is almost no hybridization in sp-N1GDY(OH)/G and Pyri-NGDY/G, thus the adsorption energies are weak (−0.15 eV and −0.10 eV) and O2 dissociation barrier is high (1.9 eV and 1.57 eV). On the other hand, O2 has strong hybridizations with C on sp-N1GDY/G, sp-N2GDY/G, and sp-N2GDY(OH)/G due to the presence of partially occupied states. The adsorption energy (−0.6 eV, −1.37 eV, and −0.58 eV) and NEB barrier (0.22 eV, 0.08 eV, and 0.81 eV) results show that O2 is chemisorbed and easily dissociates on sp-N1GDY/G, sp-N2GDY/G, and sp-N2GDY(OH)/G, respectively.
3.3 ORR mechanism and free energy analysis on sp-N1GDY/G and Pyri-NGDY/G under water conditions
Experimentally, electrochemical reactions occur at solid–liquid interfaces, thus it is necessary to incorporate the solvation effects in an explicit water environment when investigating the ORR using the CHE model. The solvation energy of the ORR intermediate can be estimated from the AIMD simulation of the adsorbed systems with water solvents explicitly. However, this approach incurs a huge computational cost. To this end, we first simulated the interfaces of NGDY's, namely sp-N1GDY/G and Pyri-NGDY/G with water to elucidate the H bond networks. Next, we only kept the water configurations in the contact region with the surface of the five most stable AIMD snapshots of the clean systems and replaced one nearest water molecule above the active site by each ORR intermediate to construct the H bond networks of ORR intermediate and water. The ΔSol of each ORR intermediate is then elucidated from an average of five AIMD snapshots. Moreover, we also constructed H bond networks using the ice-like bilayer model. The details of the AIMD analysis are summarized in the ESI,† Fig. S7–S9, and Table S7.H bond networks of water on sp-N1GDY/G and Pri-NGDY/G surfaces are shown in Fig. S10 (ESI†). On both substrates, the water layer of the H bond networks at the contact region with N-doped GDY is mainly composed of six-membered ring components after optimization, i.e., one H2O has three H bonds with three neighboring H2O. This is similar to the ice-like bilayer that is often observed for water/flat metal interfaces.28,61 The ΔSol of 2O*, O* + OH*, O*, and OH* on sp-N1GDY/G and the ΔSol of OOH*, O*, and OH* on sp-N1GDY(OH)/G or Pyri-NGDY/G are shown in Tables S8 and S9 (ESI†). We found that water stabilizes all the ORR intermediates, which arise from H bonds with water. Moreover, we also calculated the ΔSol of each ORR intermediate using an ice-like bilayer (Tables S8 and S9, ESI†). The results showed that the difference in the ΔSol‘s between the H bond networks model from AIMD and the ice-like bilayer model varies by only ∼0.06 eV. We found that the ΔSol of these surfaces is independent of the water model, which arises from a similar H bond between adsorbates and water in the ice-like bilayer and AIMD H bond networks.
The free energy diagrams of ORR with water on sp-N1GDY/G, sp-N1GDY(OH)/G, and Pyri-NGDY/G are shown in Fig. 5. Because of the stabilization driven by the solvation effect, the reaction Gibbs free energies of all ORR intermediates are more stable than those under vacuum conditions. Thus, OH* is more easily terminated on the sp-N1GDY/G surface (Fig. 5(a) and (b)), and further ORR steps are considered on sp-N1GDY(OH)/G (Fig. 5(c) and (d)). The PDS of ORR on sp-N1GDY(OH)/G in water remains the same as that under vacuum conditions (O2 → OOH*), while the limiting potential is changed from 0.51 V under vacuum condition to 0.77 V under water conditions. At URHE = 0.77 V (Fig. 5(b) and 5(d)), sp-N1GDY(OH) is the most stable structure under water conditions. Therefore, introducing ΔSol, the η of sp-N1GDY(OH)/G is 0.46 V (Table 2), which is close to the experimentally reported value (0.36 V). Similarly, on Pyri-NGDY/G, even though the solvation effect is included, the PDS of ORR on Pyri-NGDY/G in water conditions does not change compared with that under vacuum conditions (O2 → OOH*). We obtained a limiting-potential increase to 0.48 eV (Fig. 5(e) and (f)) and an η decrease to 0.75 V (Table 2), which is higher than that of sp-N1GDY(OH)/G. Finally, we conclude that ORR easily proceeds on sp-N1 doping with pre-adsorbed OH*.
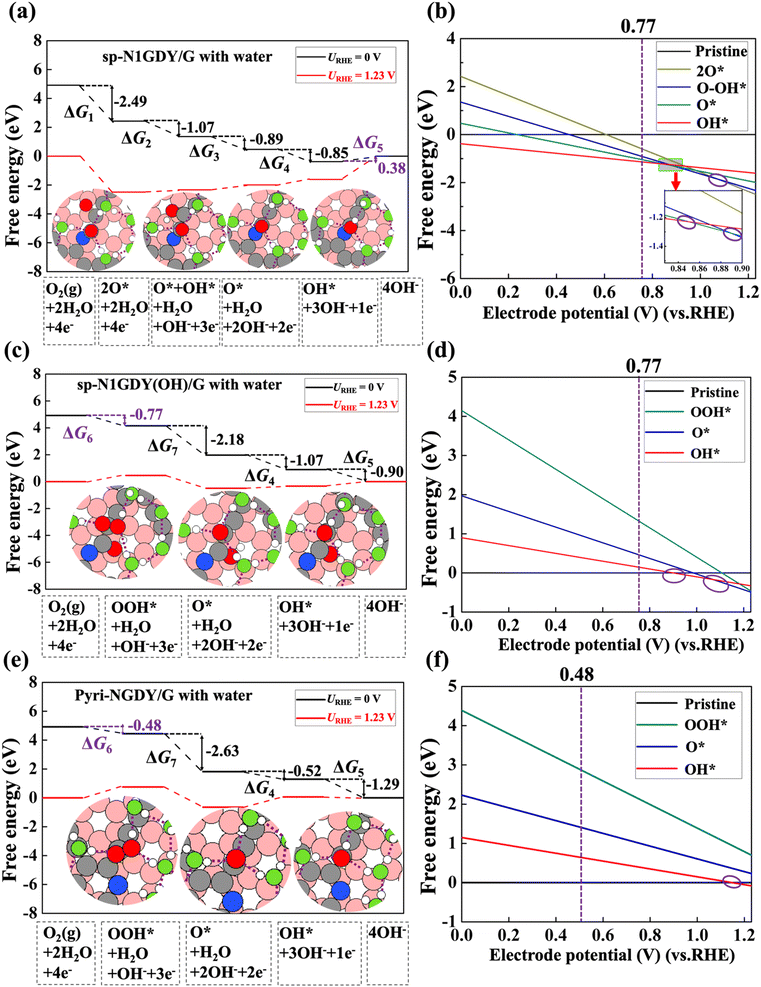 | ||
| Fig. 5 (a) Free energy diagram and structures of each ORR intermediate with water on sp-N1GDY/G. (b) Free energy of each ORR intermediate with water versus electrode potential (vs. RHE) on sp-N1GDY/G. (c) Free energy diagram and structures of each ORR intermediate with water on sp-N1GDY(OH)/G. (d) Free energy of each ORR intermediate with water versus electrode potential (vs. RHE) on sp-N1GDY(OH)/G. (e) Free energy diagram and structures of each ORR intermediate with water on Pyri-NGDY/G. (f) Free energy of each ORR intermediate versus electrode potential (vs. RHE) on Pyri-NGDY/G. Pristine in (b), (d), and (f) represents sp-N1GDY/G, sp-N1GDY(OH), and Pyri-NGDY/G, respectively. URHE is the potential of the electrode relative to the RHE. Red, green, white, gray, pink, and blue balls are O atoms in ORR intermediates, O atoms in water, H atoms, C atoms in N-doped GDY, and C atoms in G, and N atoms, respectively. The purple dashed lines in structures of (a), (c), and (e) represent the H bonds. Purple circles in (b), (d), and (f) represent the lowest lines crossed at different potentials. We regard an H bond as being formed when the O–O distance of adjacent water molecules is smaller than 3.5 Å and the angle between the O–H vector of one molecule and the O–O vector is smaller than 30° in ref. 62. | ||
3.4 Effects of exchange–correlation energy functionals and graphene support on ORR
Here, we discuss the effect of exchange–correlation energy functionals on the adsorption Gibbs free energy of ORR. We employed the PBE + D2 energy functional to perform the adsorption Gibbs free energy of ORR on sp-N1GDY/G, sp-N1GDY(OH)/G, and Pyri-NGDY/G with and without water. As shown in Table S10 (ESI†), we found that PBE tends to overestimate the binding energy of chemisorption species. This is due to the overestimation of attractive interactions in molecular systems. Under vacuum conditions, the adsorption Gibbs free energies of ORR intermediates on sp-N1GDY/G, sp-N1GDY(OH)/G, and Pyri-NGDY/G are more stable using PBE + D2 compared with RPBE + D2. Thus, the η of ORR on sp-N1GDY(OH)/G and Pyri-NGDY/G is slightly decreased using PBE + D2 compared with RPBE + D2. However, the trend of ORR activity remains the same, which is sp-N1GDY(OH)/G > Pyri-NGDY/G. Under water conditions, we only used the ice-like bilayer water to simulate the ΔSol because we already proved that the ΔSol using the H bond networks from AIMD is not much different from that using the ice-like bilayer water based on RPBE + D2 energy functional. Table S11 (ESI†) shows that the ΔSol of each ORR intermediate is more negative using the PBE + D2 energy functional compared with that using the RPBE + D2 energy functional. For Pyri-NGDY/G with water, η is decreased to 0.65 V (Table 2) and PDS is changed from O2 → OOH* (vacuum conditions) to O* → OH* (water conditions). For sp-N1GDY(OH)/G, PDS is changed from O2 → OOH* (vacuum conditions) to OH* → OH− (water conditions) but η is coincidentally not changed (0.54 V) (Table 2). Although the trend of ORR activity in water is unchanged, the η of sp-N1GDY(OH)/G using RPBE + D2 (0.46 V) is closer to the experimental result (0.36 V) compared with that using PBE + D2 (0.54 V). Therefore, the RPBE + D2 energy functional gives more reasonable binding energies and solvation energies of adsorbates.In Section 3.1, we discussed that the G support on NGDY enhances the metallic property and causes charge transfer from G to NGDY. To investigate the effect of G support on ORR electrocatalytic activity, calculated adsorption Gibbs free energies of ORR with G support and without G support are shown in Tables S5 and S6 (ESI†), respectively. The results revealed that the G support stabilizes all ORR intermediates in these cases, especially on Pyri-NGDY, which stabilizes ∼0.2 eV on OOH*, O*, and OH* (Table S6, ESI†). Higher charge transfer from G to the substrate as indicated by work function change upon graphene support (0.31 eV for Pyri-NGDY/G vs. 0.13 eV for sp-N1GDY/G) results in a strong interaction of ORR intermediate with N-doped GDY. Briefly, the introduction of the G support enhances the ORR electrocatalytic activity of N-doped GDY.
4. Conclusions
In this study, we performed DFT calculations and AIMD simulations to investigate the ORR mechanism on the sp-N1GDY/G and Pyri-NGDY/G with and without the solvation effect. We obtained the following important results:(1) Under both vacuum and water conditions, ORR firstly proceeds on sp-N1GDY/G via a dissociative mechanism because O2 can be chemisorbed on a clean surface and easily dissociated rather than protonated to OOH*. However, OH* is strongly adsorbed on the sp-N1GDY/G surface, resulting in the weakening of the second O2 adsorption, and ORR occurs via the ET-OHP associative mechanism. Pyri-NGDY/G also prefers the ET-OHP associative mechanism.
(2) From the AIMD simulation, the H bond networks at the contact region of water and NGDY are mainly composed of six-membered ring components. H bond with water stabilizes each ORR intermediate and the free energy diagram with solvation effect agrees well with the experimental data. Moreover, we found that using the ice-like bilayer model to construct the H bond networks can also give a reasonable estimation of ΔSol. Therefore, the ΔSol of these surfaces is independent of the water model, which arises from a similar H bond between adsorbates and water in the ice-like bilayer and AIMD H bond networks.
(3) sp-N1GDY/G with OH* pre-adsorbed surface has the highest ORR electrocatalytic activity and the neighboring C site of –COH–N moiety is the active site for ORR. Incorporation of the solvation effect is of importance because η with the solvation effect (0.46 V) is much closer to the experimental one (0.36 V). Our work highlights the importance of considering solvation effects in designing and optimizing catalysts for ORR and other chemical reactions.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by a Grant-in-Aid for Transformative Research Areas (A) “Hyper-Ordered Structure Science” (grant no. JP20H05883) and a Grant-in-Aid for Scientific Research (B) (grant no. JP20H02569) and JSPS Fellows (22J10937) from the Japan Society for the Promotion of Science (JSPS) and Elements Strategy Initiative for Catalysts and Batteries (ESICB) (grant no. JPMXP0112101003) from the Ministry of Education, Culture, Sports, Science, and Technology, Japan (MEXT). The computations were performed using computer resources at the Research Center for Computational Science, Okazaki; the Cyberscience Center, Tohoku University; the Center for Computational Materials Science, Institute for Materials Research, Tohoku University; the Institute for Solid State Physics, University of Tokyo. This work was also supported by MEXT as “Program for Promoting Researches on the Supercomputer Fugaku” (Fugaku battery & Fuel Cell Project) and used the computational resources of the supercomputer Fugaku provided by the RIKEN Center for Computational Science.Notes and references
- B. C. H. Steele and H. Angelika, Nature, 2001, 414, 345–352 CrossRef CAS PubMed.
- J. Kui, J. Xuan, Q. Du, Z. Bao, B. Xie, B. Wang, Y. Zhao, L. Fan, H. Wang, Z. Hou, S. Hu, N. P. Brandon, Y. Yin and M. D. Guiver, Nature, 2021, 595, 361–369 CrossRef PubMed.
- D. Larcher and J. M. Tarascon, Nat. Chem., 2015, 7, 19–29 CrossRef CAS PubMed.
- R. Ma, G. Lin, Y. Zhou, Q. Liu, T. Zhang, G. Shan, M. Yang and J. Wang, npj Comput. Mater., 2019, 5, 78 CrossRef.
- S. Sui, X. Wang, X. Zhou, Y. Su, S. Riffat and C. J. Liu, J. Mater. Chem. A, 2017, 5, 1808–1825 RSC.
- L. Dai, Y. Xue, L. Qu, H. J. Choi and J. B. Baek, Chem. Rev., 2015, 115, 4823–4892 CrossRef CAS PubMed.
- K. Gong, F. Du, Z. Xia, M. Durstock and L. Dai, Science, 2009, 323, 760–764 CrossRef CAS PubMed.
- D. Guo, R. Shibuya, C. Akiba, S. Saji, T. Kondo and J. Nakamura, Science, 2016, 351, 361–365 CrossRef CAS PubMed.
- S. Tang, X. Zhou, T. Liu, S. Zhang, T. Yang, Y. Luo, E. Sharman and J. Jiang, J. Mater. Chem. A, 2019, 7, 26261–26265 RSC.
- S. Tang, Q. Dang, T. Liu, S. Zhang, Z. Zhou, X. Li, X. Wang, E. Sharman, Y. Luo and J. Jiang, J. Am. Chem. Soc., 2020, 142, 19308–19315 CrossRef CAS PubMed.
- C. Z. Yuan, H. B. Li, Y. F. Jiang, K. Liang, S. J. Zhao, X. X. Fang, L. B. Ma, T. Zhao, C. Lin and A. W. Xu, J. Mater. Chem. A, 2019, 7, 6894–6900 RSC.
- L. Jian, X. Gao, B. Liu, Q. Feng, X. B. Li, M. Y. Huang, Z. Liu, J. Zhang, C. H. Tung and L. Z. Wu, J. Am. Chem. Soc., 2016, 138, 3954–3957 CrossRef PubMed.
- G. Xin, H. Liu, D. Wang and J. Zhang, Chem. Soc. Rev., 2019, 48, 908–936 RSC.
- Y. Fang, Y. Liu, L. Qi, Y. Xue and Y. Li, Chem. Soc. Rev., 2022, 51, 2681–2709 RSC.
- Y. Li, L. Xu, H. Liu and Y. Li, Chem. Soc. Rev., 2014, 43, 2572–2586 RSC.
- C. Huang, Y. Li, N. Wang, Y. Xue, Z. Zuo, H. Liu and Y. Li, Chem. Rev., 2018, 118, 7744–7803 CrossRef CAS PubMed.
- Z. Zuo and Y. Li, Joule, 2019, 3, 899–903 CrossRef.
- Y. Gao, Z. Cai, X. Wu, Z. Lv, P. Wu and C. Cai, ACS Catal., 2018, 8, 10364–10374 CrossRef CAS.
- Z. Feng, R. Li, Y. Ma, Y. Li, D. Wei, Y. Tang and X. Dai, Phys. Chem. Chem. Phys., 2019, 21, 19651–19659 RSC.
- Y. Zhao, J. Wan, H. Yao, L. Zhang, K. Lin, L. Wang, N. Yang, D. Liu, L. Song, J. Zhu, L. Gu, L. Liu, H. Zhao, Y. Li and D. Wang, Nat. Chem., 2018, 10, 924–931 CrossRef CAS PubMed.
- T. Lu, X. Hu, J. He, R. Li, J. Gao, Q. Lv, Z. Yang, S. Cui and C. Huang, Nano Energy, 2021, 85, 106024 CrossRef CAS.
- X. Chen, W. J. Ong, Z. Kong, X. Zhao and N. Li, Sci. Bull., 2020, 65, 45–54 CrossRef CAS PubMed.
- B. Kang, S. Wu, J. Ma, H. Ai and J. Y. Lee, Nanoscale, 2019, 11, 16599–16605 RSC.
- J. Gu, S. Magagula, J. Zhao and Z. Chen, Small Methods, 2019, 1800550 CrossRef.
- J. K. Nørskov, J. Rossmeisl, A. Logadottir, L. Lindqvist, J. R. Kitchin, T. Bligaar and H. Jónsson, J. Phys. Chem. B, 2004, 108, 17886–17892 CrossRef.
- L. Yu, X. Pan, X. Cao, P. Hu and X. Bao, J. Catal., 2011, 282, 183–190 CrossRef CAS.
- P. S. Rice, Y. Mao, C. Guo and P. Hu, Phys. Chem. Chem. Phys., 2019, 21, 5932–5940 RSC.
- S. Schnur and A. Groß, New J. Phys., 2009, 11, 125003 CrossRef.
- A. Groß and S. Sung, Chem. Rev., 2022, 122, 10746–10776 CrossRef PubMed.
- S. N. Steinmann, P. Sautet and C. Michel, Phys. Chem. Chem. Phys., 2016, 18, 31850–31861 RSC.
- J. Ho and M. Z. Ertem, J. Phys. Chem. B, 2016, 120, 1319–1329 CrossRef CAS PubMed.
- G. König and B. Stefan, J. Phys. Chem. B, 2009, 113, 8967–8974 CrossRef PubMed.
- H. Cao, G. J. Xia, J. W. Chen, H. M. Yan, Z. Huang and Y. G. Wang, J. Phys. Chem. C, 2020, 124, 7287–7294 CrossRef CAS.
- M. Reda, H. A. Hansen and T. Vegge, Catal. Today, 2018, 312, 118–125 CrossRef CAS.
- Y. Morikawa, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51, 14802–14805 CrossRef CAS PubMed.
- Y. Hamamoto, I. Hamada, K. Inagaki and Y. Morikawa, Phys. Rev. B: Condens. Matter Mater. Phys., 2016, 93, 245440 CrossRef.
- Y. Morikawa, K. Iwata and K. Terakura, Appl. Surf. Sci., 2000, 11, 169–170 Search PubMed.
- S. A. Wella, Y. Hamamoto, F. Iskandar, Suprijadi, Y. Morikawa and I. Hamada, J. Chem. Phys., 2020, 152, 104707 CrossRef CAS PubMed.
- D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 7892–7895 CrossRef PubMed.
- B. Hammer, L. B. Hansen and J. K. Nørskov, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 7413 CrossRef.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- G. Henkelman and H. Jonsson, J. Chem. Phys., 2000, 113, 9978–9985 CrossRef CAS.
- G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904 CrossRef CAS.
- S. P. Chan, G. Chen, X. G. Gong and Z. F. Liu, Phys. Rev. Lett., 2003, 90, 086403 CrossRef PubMed.
- J. I. Enriquez, F. Muttaqien, M. Michiuchi, K. Inagaki, M. Geshi, I. Hamada and Y. Morikawa, Carbon, 2021, 174, 36–51 CrossRef CAS.
- J. K. Nørskov, F. Studt, F. Abild-Pedersen and T. Bligaard, Fundamental Concepts in Heterogeneous Catalysis, Wiley, New York, NY, 2014 Search PubMed.
- R. Iftimie, P. Minary and M. E. Tuckerman, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 6654–6659 CrossRef CAS PubMed.
- X. Chen, Y. Zhang, Y. Ren, D. Wang and J. Yun, Mater. Res. Express, 2019, 6, 095610 CrossRef CAS.
- V. M. Karpan, G. Giovannetti, P. A. Khomyakov, M. Talanana, A. A. Starikov, M. Zwierzycki, J. V. D. Brink, G. Brocks and P. J. Kelly, Phys. Rev. Lett., 2007, 99, 176602 CrossRef CAS PubMed.
- A. S. Haile, H. A. Hansen, W. Yohannes and Y. S. Mekonnen, J. Phys. Chem. Lett., 2021, 12, 3552–3559 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- J. Heyd and G. E. Scuseria, J. Chem. Phys., 2004, 121, 1187–1192 CrossRef CAS PubMed.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215 CrossRef CAS.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS PubMed.
- M. Yan, Z. Q. Huang, Y. Zhang and C. R. Chang, Phys. Chem. Chem. Phys., 2017, 19, 2364–2371 RSC.
- T. N. Pham, M. Sugiyama, F. Muttaqien, S. E. M. Putra, K. Inagaki, D. N. Son, Y. Hamamoto, I. Hamada and Y. Morikawa, J. Phys. Chem. C, 2018, 122, 11814–11824 CrossRef CAS.
- N. Ramaswamy and S. Mukerjee, J. Phys. Chem. C, 2011, 115, 18015–18026 CrossRef CAS.
- C. H. Choi, H. K. Lim, M. W. Chung, J. C. Park, H. Shin, H. Kim and S. I. Woo, J. Am. Chem. Soc., 2014, 136, 9070–9077 CrossRef CAS PubMed.
- Y. Wang, Y. J. Tang and K. Zhou, J. Am. Chem. Soc., 2019, 141, 14115–14119 CrossRef CAS PubMed.
- A. Groß, F. Gossenberger, X. Lin, M. Naderian, S. Sakong and T. Roman, J. Electrochem. Soc., 2014, 161, E3015 CrossRef.
- A. Luzar and D. Chandler, Nature, 1996, 379, 55–57 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ma00502j |
| This journal is © The Royal Society of Chemistry 2023 |