Machine learning-based q-RASPR predictions of detonation heat for nitrogen-containing compounds

Abstract

The quantitative Read-Across Structure–Property Relationship (q-RASPR) is a novel method for the property predictions derived from the integrated concept of both similarity-based predictions (i.e., Read-Across or RA) and statistical modelling-based predictions (i.e., Quantitative Structure–Property Relationship or QSPR). The main performance index of ammunition used in air-to-air and underwater weapons is the detonation heat energy. In the present work, we have applied the q-RASPR modeling approach and various Machine Learning (ML) algorithms to predict the detonation heat (an intrinsic property) of different N-containing compounds. The data set was collected from the literature, curated, and further divided into training and test sets using the Euclidean distance-based algorithm. The feature selection was done on the basis of internal validation metrics of Genetic Algorithm (GA) models. A Multiple Linear Regression (MLR) QSPR model with 6 descriptors was selected, and the model features were used to calculate the similarity and error-based RASPR descriptors. The RASPR descriptor matrix was then merged with the features of the QSPR model. A grid search was performed for the selection of a combination of descriptors which were then subjected to Partial Least Squares (PLS) regression to obviate the inter-correlation among the descriptors. We have also employed various ML algorithms by optimizing the hyperparameters based on a cross-validation approach and compared the final test set prediction results. The PLS q-RASPR model was selected to be the best model based on the external validation metrics and it also shows enhanced prediction quality using 2D-descriptors compared to the previous model reported with 3D-descriptors. The developed model can be used for the detection of the detonation heat of compounds containing nitrogen with an effective performance.

---

1. Introduction

Compounds or combinations of compounds with explosive groups or oxidants and incendiary materials are known as high energy density materials (HEDMs), as these are tiny, compact, sensitive, and energetic.¹ Depending upon the properties, constitutions, and intentional applications, HEDMs can be explosives, propellants, or pyrotechnics. Modern HEDMs should possess a higher detonation performance (i.e., high detonation velocity, high detonation pressure, and high heat of explosion) along with higher stability (least chemical degradation, refuse phase transition, non-responsive to unintentional mechanical shock, friction, or non-mechanical stimuli like disclosure to light, radiation in the infrared spectrum, electrostatic discharge, etc.).² Nowadays, civil and military are the prominent fields where HEDMs are widely used. In terms of time and money, the development, manufacturing, and testing of a new energetic material is very costly. Therefore, the detection and elimination of any poor-performing candidate through predictive capabilities is highly efficient in the early stages of development.

Detonation is a chemical reaction that involves an explosive material resulting in the production of a shock wave.³ The heat of detonation (Q) refers to the quantity of heat energy liberated by an energetic compound per unit mass when detonated. It is one of the major thermodynamic features associated with the performance of HEDMs.⁴ The heat of detonation is an intrinsic property of HEDMs composed of chemical and physical parameters. Other performance parameters such as detonation pressure and detonation velocities can also be calculated using the heat of detonation.⁵ Chemically it depends on the type and proportion of the detonation product, the heat of formation of products, and the heat of formation of the energetic compound, and physical factors governing the heat of detonation are the loading density and the expansion ratio (of the gaseous products).⁶ For estimating the detonation heat of the explosive materials one can use the condensed phase heat of formation of the explosives and the standard heat of formation of the detonation product. A positive heat of formation (per unit weight) is advantageous for an energetic compound in order to gain a higher release of energy upon explosion and an improvement in performance.^7–9 Structurally, explosives comprise various energetic functionalized groups known as explosophores linked with carbon-rich backbones that act as fuel. External oxidizers like ammonium perchlorate (NH₄ClO₄) and ammonium nitrate (NH₄NO₃) are used to facilitate oxidation and detonation of the main fuel. Combining fuel with oxidizer fragments in explosives leads to the development of ‘green explosives’.¹⁰ The introduction of nitrogen in the parent structure (i.e. an increase in the nitrogen/carbon ratio) leads to the production of new high-performing, stable, and safer HEDMs as their energy content is predominantly derived from the heat of formation due to a large number of dynamic N–N and C–N bonds instead of coming thoroughly from the heat of combustion. Also, after detonation, the major product formed is the dinitrogen (N₂) gas which is nontoxic in nature so is less hazardous for the user and is eco-friendly.^11,12 N-containing 4-membered heterocyclic or heterocyclic compounds having explosophores like nitro (–NO₂), nitroso (–RNO), nitramino (–NHNO₂), amino (–NH₂), azides (–N₃), azo bridge (–N=N–), nitrito (–ONO₂), etc. are good candidates for designing newer HEDMs. Energetic materials incorporated with ring/cage compounds have the advantage of excess strain energy released upon ring opening during the decomposition process and thus possess high detonation energy.¹³ Some powerful HEDMs contain units of 5-membered heterocyclic rings like furazan, furoxan, isofurazan, and tetrazole leading to a higher compact framework and positive higher enthalpies of formation resulting in excellent detonation performances.¹⁴ The heat of detonation of aromatic energetic compounds is different from the detonation heat of non-aromatic compounds. So, separate strategies have been developed to estimate the detonation heat of aromatic and non-aromatic energetic compounds respectively.^7,15,16 Among the measured and predicted molecular properties, the heat of detonation is found to be straightforwardly related to the impact sensitivities of the explosives, particularly within chemical families.¹⁷

The rapid growth and advancement in the computational approaches for the prediction of the characteristic behavior of compounds not only give promising results but also reduce the hazard risk, and high cost for experimentation, and can screen large data in a short period of time. Chemoinformatics models can be used to calculate many physical and chemical properties that are difficult to derive using theoretical methods such as density functional theory (DFT) or molecular dynamics (MD).¹⁸ Because of the robustness and computational tractability, the quantitative structure–property relationship (QSPR) has gained a lot of attention for the prediction of the properties of compounds. The primary algorithm in QSPR modeling is that it includes one or more properties (dependent variables) along with one or more descriptors/features (independent variables) contributing to the property.¹⁹ Chemical read-across (RA) was originally an unsupervised similarity-based approach for predicting the activity/property/toxicity of compounds. RA based on similarity levels recognizes the close source compound for each query compound. RA-based predictions either use the analogue approach or the category approach to identify similar compounds.²⁰ The analogue approach uses a small number of structurally-similar compounds with irregular patterns on the properties. The simplest case of the analogue approach uses only a single chemical as a source chemical for a single target. If it uses more than one source or target, the evaluation has to be repeated for each source and/or target compound. The category approach uses a group of chemicals as source chemicals having structural similarities. The groups are prepared on the basis of defined structural similarities and differences among the compounds.²¹ A combination of QSPR (supervised learning) with RA (unsupervised learning) forms the basis of a supervised learning algorithm called the Read-Across Structure–Property Relationship (RASPR) which shows a better predictive ability of the model than the conventional QSPR technique.²² The fundamental premise of the quantitative RASPR (q-RASPR) is the combination of important structural and physicochemical descriptors with Read-Across-derived similarity and error-based measures. The calculation of these similarities and error-based measures uses the structural and physiochemical descriptors and similarity-based approach (Euclidean distance-based, Gaussian kernel similarity-based, and Laplacian kernel similarity-based).²³ q-RASPR models can be developed using a variety of statistical techniques like multiple linear regression (MLR), partial least squares (PLS),²⁴ apart from sophisticated machine learning (ML) techniques. Machine learning (ML) has emerged as one of the most admissible and effective techniques for creating precise models, particularly when dealing with complex nonlinear data. Supervised learning (SL), unsupervised learning (UL), and reinforcement learning (RL) are the three basic domains of the ML technique. SL deals with labelled data having inputs and known outputs, and thus is used to solve regression and classification problems.^25,26 Random forest (RF), artificial neural networks (ANN), and support vector machines (SVM) are commonly used machine learning algorithms for numerous experimental studies.²⁷

In the present work, we have established a q-RASPR model by employing various ML algorithms for the determination of chemical features contributing to the heat of detonation of N-containing HEDMs and for the prediction of new query compounds without having experimental heat of detonation. As mentioned above, the incorporation of a nitrogen into the parent structure or the addition of a nitrogen-containing substituent enhances the heat of detonation of the energetic materials because of N–N and C–N energetic bonds. The replacement of C-atom with nitrogen also leads to more release of N₂ gas simultaneously, lowering the amount of CO₂ or CO produced after decomposition and reducing the ill effect on the environment. Our dataset contains both aromatic and non-aromatic energetic compounds, and the prediction of the detonation heat does not involve any calculation of heat of formation of either the energetic compound or of the detonation product. This study uses a data set of 162 compounds collected from the literature cited under the methods and material section.

2. Material and methods

2.1. Data set

The values of detonation heat (expressed in KJ kg⁻¹) of 162 N-containing compounds were collected from previously published literature¹ and are available in the form of an Excel sheet in the ESI† SI-1. The structures were prepared in MarvinSketch²⁸ (version- 5.5.0.1), the explicit hydrogen was added, the structure was cleaned, and the aromatic rings were aromatized as applicable. A chemical diversity plot (Fig. 1) was prepared using the molecular weight and logP_cons which shows the diversity in the chemical nature of the compounds.

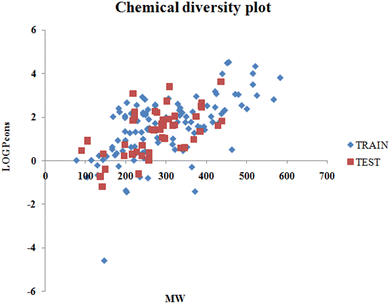Fig. 1 Chemical diversity plot.

2.2. Descriptor calculation and data pre-treatment

Molecular descriptors are the quantitative values derived from the structural information of the molecules. Different classes of 2D descriptors like molecular properties, 2D atom pairs, atom type E-state indices, atom-centered fragments, functional group counts, connectivity indices, ring descriptors, constitutional indices, and extended topochemical atom (ETA) indices were calculated using alvaDesc v2.0.6.²⁹ These different classes of descriptors are so chosen as they are highly interpretable and are also efficient in the development of models as evident from our previous experiences. A total of 689 molecular descriptors were calculated initially.

The obtained descriptors were then subjected to a pretreatment process using a java-based tool DataPreTreatmentGUI 1.2 available from https://teqip.jdvu.ac.in/QSAR_Tools/ to remove the intercorrelated descriptors with a variance cut-off of 0.0001 and a correlation coefficient cut-off value of 0.95. In this process, descriptors that are highly inter-correlated to each other and descriptors with null or constant values for each data point are obviated. After the pre-treatment process, a total of 473 descriptors were left which were used for further study.

2.3. Data division

The division of the dataset is a necessary step prior to the model development. To establish a powerful QSPR model with good predictive ability the data set is divided into a training set and a test set. In this work, the dataset was divided in a ratio of 75 : 25, constituting 122 compounds in the training set and 40 compounds in the test set using the Euclidean Distance-based division algorithm³⁰ with the help of a java-based tool datasetDivisionGUI1.2 available from https://teqip.jdvu.ac.in/QSAR_Tools/. After division, the training and test sets were subjected to pretreatment with the help of dataPreTreatmentTrainTest1.0 tool from https://teqip.jdvu.ac.in/QSAR_Tools/ to remove intercorrelated descriptors. The development of the model is done using the training set whereas the test set is used to check the predictive ability and external validation of the developed model.

2.4. Feature selection and QSPR model development

The selection of important features contributing to the property of compounds is a crucial step during the development of a QSPR model.³¹ We have prepared several Genetic Algorithm (GA)³² models using a java-based tool GeneticAlgorithm_v4.1 from https://teqip.jdvu.ac.in/QSAR_Tools/ and selected the descriptors that appeared frequently in a maximum number of models. The generation of GA models and feature selection is done using the training set only without the involvement of the test set. The training set and test set matrices with the selected features were prepared. Furthermore, we have used the Best Subset Selection v2.1 tool available from https://teqip.jdvu.ac.in/QSAR_Tools/ to generate different MLR models with all possible combinations of a given number of descriptors. A good robust model was selected based on the cross-validation result which is used for further q-RASPR analysis.

2.5. Optimization of the Read-Across hyperparameters

Identification of the optimized setting of hyperparameters (σ, γ, number of close source/training compounds, and best similarity-based algorithm) is an essential step for Read-Across based prediction. As per the QSPR prediction principles, hyperparameter optimization should be done on the basis of training/source set only without any involvement of the test/query set. The training set containing the descriptors involved in the QSPR model was further divided into the corresponding sub-train and sub-test sets. With the help of a java-based tool Auto_RA_Optimizer-v1.0 available from https://sites.google.com/jadavpuruniversity.in/dtc-lab-software/home, we have selected the values for σ and γ to be 0.5, the number of close training compounds to be 8, and the Gaussian kernel-based similarity as our best similarity-based algorithm. Here, the selection of hyperparameters was based on the maximum occurrence frequency of individual hyperparameters obtained during optimization using different sub-training and sub-test sets prepared through the division of the training set via different algorithms.

2.6. Calculation of the RASPR descriptors

Before proceeding with the q-RASPR study, the prominent step is to calculate the similarity and error-based RASPR descriptors³³ (Table 1, ESI†) for the individual training set and the test set. Unlike the calculation of structural and physiological descriptors, the RASPR descriptors are calculated after the division process. This is because the RASPR descriptors are calculated on the basis of the similarity of query set compounds to the training set compounds. The Gaussian kernel-based similarity descriptors with σ value 0.5 were calculated using a java-based tool RASAR-Desc-Calc-v2.0 available from https://sites.google.com/jadavpuruniversity.in/dtc-lab-software/home. For the calculation of RASPR descriptors for the test set, we have used the training set and the test set containing the selected physiochemical descriptors as the input whereas for the computation of training set RASPR descriptors only the training set is used as the input.

Table 1 Detailed list of RASPR descriptors and their definition

S. No.	RASPR descriptors	Definition
1.	RA function	A composite function derived from Read-Across
2.	MaxPos	Similarity score of the closest positive source compound (with an observed response value greater than the mean activity of the training set)
3.	MaxNeg	Similarity score of the closest negative source compound (with an observed response value less than the mean activity of the training set)
4.	Abs MaxPos-MaxNeg	Absolute difference between the MaxPos and MaxNeg levels
5.	SE	Weighted standard error of the close source compounds’ response values
6.	CVact	Coefficient of variation of the close source compounds’ observed response values
7.	SD_Activity	Weighted standard deviation of the close source compounds’ observed response values
8.	CVsim	Coefficient of variation of the similarity values of the close source compounds
9.	SD_similarity	The standard deviation of the close source compounds’ similarity levels
10.	Pos.Avg.Sim	The positive close source compounds’ average similarity levels
11.	Neg.Avg.Sim	The negative close source compounds’ average similarity levels
12.	Avg.Sim	Average similarity level of the close source compounds
13.	g m	A novel concordance measure also known as Banerjee-Roy Coefficient
14.	g m*SD_Similarity	Product of the gm and SD similarity levels
15.	g m*Avg.Sim	Product of the gm and Avg. Sim levels

---

2.7. Feature selection and development of the q-RASPR model

Since the q-RASPR study is the combination of both QSPR and RA-based predictions, it is necessary to combine the structural and physiological descriptors with the similarity and error-based RASPR descriptors. The 15 similarity and error-based descriptors are fused with the previously selected structural and physiological descriptors for respective training and test sets. A grid search was performed to generate an MLR q-RASPR model with all the possible combinations of a given number of descriptors using the Best Subset Selection v2.1 tool available from https://teqip.jdvu.ac.in/QSAR_Tools/. The optimization of the number of descriptors was based on the Q²_LOO (cross-validation) metric. The final PLS q-RASPR model was developed with the selected features.

2.8. Application of other machine learning (ML) algorithms

The predictive performance of the developed q-RASPR model was further evaluated by applying various supervised Machine Learning (ML) algorithms. We have used 7 different ML algorithms to develop various regression models such as Random Forest (RF),³⁴ Adaptive Boosting (AdaBoost/AB),³⁵ Gradient boosting (GB),³⁶ Extreme Gradient Boosting (XGB),³⁷ Support Vector Machine (SVM),³⁸ Linear Support Vector Machine (LSVM), and Ridge Regression (RR).³⁹ Scaling of the training and test sets data values was achieved using a Java-based tool Scale1.0 from https://sites.google.com/jadavpuruniversity.in/dtc-lab-software/home. With the help of a Python-based tool Hyperparameter Optimizer v1.2 and the scaled data of the training set, we have calculated the optimized hyperparameters for each ML algorithm. The selection of the hyper-parameters was based on the MAE results. Using the optimized settings of the hyperparameters and the scaled training and test sets, we have developed several ML models using a Python-based tool Machine Learning Regressor v 2.0 available from https://sites.google.com/jadavpuruniversity.in/dtc-lab-software/home. The final selection of the best predictive model was done based on MAE_Test results.

2.9. Statistical validation metrics

The developed models were evaluated for their predictability and reliability in terms of various internal and external validation parameters. Internally the model was evaluated on the basis of determination coefficient (R²), adjusted R² (R²_adj), Leave-One-Out cross-validated Q² (Q²_LOO), and root mean squared error of calibration (RMSE_C) while the external statistical parameters involve the calculation of R²_pred or Q²_F1, Q²_F2, Q²_F3, CCC, and root mean squared error of prediction (RMSE_P).⁴⁰ Both internal and external validation tests were done using the mean absolute error (MAE) based criteria⁴¹ as Q²_ext does not always provide exact prediction quality because of its dependence on the response range and response value distribution in the training and test set compounds.

2.10. Applicability domain (AD)

The validity of the q-RASPR model is denoted by a defined domain of applicability (OECD principle 3).⁴² AD⁴³ represents the response and chemical structure space which is defined by the chemicals used in the development of the model (in the training set). The distance to model X (DModX) approach⁴⁴ was used with a 99% confidence level with the help of SIMCA software (https://landing.umetrics.com/downloads-simca) to check whether the compounds in the sets are within the AD. In the DModX technique, the residuals of X and Y act as diagnostic values for the quality of the model. The standard deviation (SD) of X-residuals corresponds to the respective row of residual matrix E. As SD is directly proportional to the distance between the data points and the model plane in X-space, it is commonly called DModX (distance to the model in X-space). Those compounds which are present in the chemical space can be predicted precisely and those lying outside the AD are termed as outliers.

The detailed workflow is represented in Fig. 2.

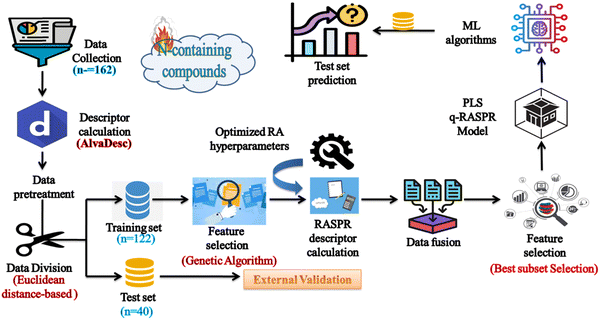Fig. 2 Workflow of the q-RASPR model development to estimate the detonation heat of N-containing compounds.

3. Results and discussion

3.1. QSPR model development

The data set comprising 162 compounds with the detonation heat energy and computed descriptors is provided in the ESI† section. The training set consists of 122 compounds, while the predictions and external validation were carried out using a test set with 40 compounds. After the feature selection process, a total of 6 descriptors were used to develop the final PLS QSAR model with 5 latent variables as shown in eqn (1)

Q = 2504.432 + 264.478 × F01[N–O] − 151.749 × X% + 156.626 × SddsN + 297.997 × nCt + 2393.524 × Eta_epsiD − 284.446 × F01[C–F] (1)

n_(Training) = 122, n_(Test) = 40

R²_(Train) = 0.851, Q²_(LOO) = 0.832, R²_(adj) = 0.843, MAE_(Train) = 482.451

Q²_F1 = 0.921, Q²_F2 = 0.920, Q²_F3 = 0.916, CCC = 0.960, MAE_(Test) = 430.542

The developed model was statistically reliable as the internal as well as external validation metrics were far above the required threshold values.

3.2. Chemical Read-Across (RA) prediction

To perform the similarity-based Read-Across predictions, the structural and physiochemical parameters of the developed QSPR model were used. Hyper-parameters (similarity approach, the number of close source compounds, σ, and γ) optimization was done using the training set containing the selected variables. The training and test sets with the selected features were used as the inputs for the RA predictions based on the different similarity approaches like Euclidean distance-based similarity, Gaussian kernel-based similarity, and Laplacean kernel-based similarity. The results obtained show that the Gaussian kernel-based similarity has the best predictive quality for the test set (or query set) using the default hyper-parameters (close source compounds = 8, σ = 0.5, and γ = 0.5) with Q²_F1 = 0.906, Q²_F2 = 0.905, MAE_Test = 418.004, and RMSE_P = 580.938. The same information of the hyper-parameters and Gaussian kernel-based similarity were used to calculate the similarity and error-based RASPR descriptors for individual training and test sets respectively.

3.3. q-RASPR model development

Clubbing of the structural and physiochemical features with the similarity and error-based measures was carried out before further model development. The new descriptor matrix contains information on both chemical structure attributes and RA-based similarities. The training set formed after clubbing the features was used for the selection of the important contributing descriptors for the development of the models. A 5-descriptor combination MLR model was prepared based on internal validation metrics. Finally, a PLS model was developed using the selected 5 descriptors with 4 latent variables and was evaluated for its robustness, reliability, and predictive ability using various internal and external validation parameters. Eqn (2) (vide infra) shows the corresponding q-RASPR model and the descriptors involved. Detailed information of the descriptors is listed in Table 2. The Scatter plot (Fig. 3) represents the observed and predicted detonation heat energy values of individual training and test set compounds. The graph infers that there is a low difference between observed and corresponding predicted values of compounds present in both the training set and the test set.

Q = 1930.622 + 217.106 × F01[N–O] − 78.832 × X% + 130.881 × SddsN + 237.814 × nCt + 0.536 × RA function (GK) (2)

n_(Training) = 122, n_(Test) = 40

R²_(Train) = 0.846, Q²_(LOO) = 0.828, R²_(adj) = 0.839

Q²_F1 = 0.927, Q²_F2 = 0.927, Q²_F3 = 0.923, CCC = 0.963

MAE_(Train) = 489.865, MAE_(Test) = 395.705, RMSE_c = 723.177, RMSE_P = 510.755

Table 2 List of descriptors and their contribution in the final PLS q-RASPR model

S. No.	Descriptor	Type	Description	Contribution
1.	X%	Constitutional indices	Percentage of halogen atoms	Negative (−ve)
2.	F01[N–O]	2D Atom Pairs	Frequency of N–O at topological distance 1	Positive (+ve)
3.	nCt	Functional group counts	Total number of tertiary carbon	Positive (+ve)
4.	SddsN	Atom-type E-state indices	Sum of ddsN E-states (–N=)	Positive (+ve)
5.	RA function (GK)	RASPR descriptor	All structural information	Positive (+ve)

---

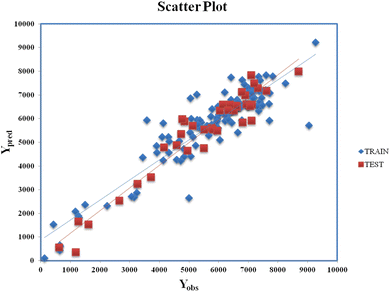Fig. 3 Scatter Plot (Y_obsvs. Y_pred) for eqn (2).

Additionally, we also checked for the structural outliers in the training and test sets using the Williams Plot (Fig. 4). The plot infers that two of the compounds from the training set and one compound from the test set are structural outliers.

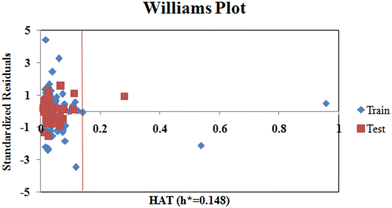Fig. 4 Williams plot (standardized cross-validated residuals vs. leverage values).

3.4. Descriptor interpretation of the PLS q-RASPR model

The descriptor RA function (GK) is a composite RASPR descriptor that contains all the selected atomic as well as structural information of the compounds. The RA function (GK) descriptor contributes positively to the prediction of detonation heat energy of N-containing compounds which is easily visualized in 3,6-Bis(1H-1,2,3,4-tetrazolyl-5-amino)-1,2,4,5-tetrazine (12) where the value of the RA function (GK) is more resulting in high detonation heat energy while in 3,3′-Azobis(6-amino-1,2,4,5-tetrazine) (13), the RA function (GK) is low resulting in a low detonation heat energy.

The descriptor nCt defines the number of tertiary carbons in the compound and it contributes positively to the prediction of detonation heat energy. Octanitrocubane (97) due to its cage-like structure represents a total of 8 such tertiary carbons in its structure present at the vertices. Compounds with ring/cage structures can liberate more energy at the time of detonation because of the excess strain energy associated with the ring.⁴⁵ In isopentanetriol trinitrate (156), the value of detonation heat energy is less as it contains only a single tertiary-carbon.

The descriptor F01[N–O] defines the frequency of N-O bonds at the topological distance 1. This descriptor contributes positively to the value of detonation heat energy which can be seen in 4,4′-heavy (N-trinitroethyl-N-nitro)-3,3′-difurazan (47) and heavy (N-trinitroethyl-N-nitro)furazan (48) having 20 and 18 N–O bonds respectively and high detonation heat values, while 3-nitro-1,2,4-triazole (8) and 1-methyl-2,4-dinitrobenzene (19) have 2 and 4 N–O in their structures respectively; hence, they have low values of detonation heat. In the compounds, F01[N–O] corresponds to the presence of explosophores in the form of nitro (NO₂), nitrito (ONO₂), furazan ring, furaxan ring, etc. leading to the production of more detonation heat energy.¹⁴

The descriptor X% depicts the percentage of halogen present in the compound. This descriptor contributes negatively to the value of detonation heat energy. This can be seen in 2,2-difluoro-2-nitroethyl trifluoromethane-sulfonate (65) with a high halogen percentage and showing the least value of detonation heat among all the 162 compounds whereas methyl 4-fluoro-4,4-dinitrobutyrate (76) has the lowest halogen percentage and have a greater value of detonation heat energy. In trifluoromethane-sulfonate (65), the electronegative fluorine atom is situated close to the positively charged nitrogen (more energy, less stable), therefore stabilizing its energy due to ion–dipole interaction resulting in a decrease in detonation energy.

The descriptor SddsN describes the atom-type E-state index for –N= groups (nitro) and contributes positively to the detonation energy. The nitrogen present in the form of the nitro group is in a high energy state (higher oxidation state in nitro) which after explosion forms inert N₂ gas (lowest oxidation state) and hence releases more energy.¹⁰ Pentaerythritol tetranitrate (135) and 1-nitropiperazine-2,3-co(1′,3′-dinitroimidazolidinone-2′)-5,6-nafurazan (45) have higher SddsN values compared to hexanitrodiphenyl sulfide (38) and tetranitroglycoluril (108), respectively, with a lower E-state index for the –N= group showing lower detonation energy.

The descriptors with their respective VIP levels and compounds with higher and lower detonation heat energy values associated with individual descriptors are represented in Fig. 5.

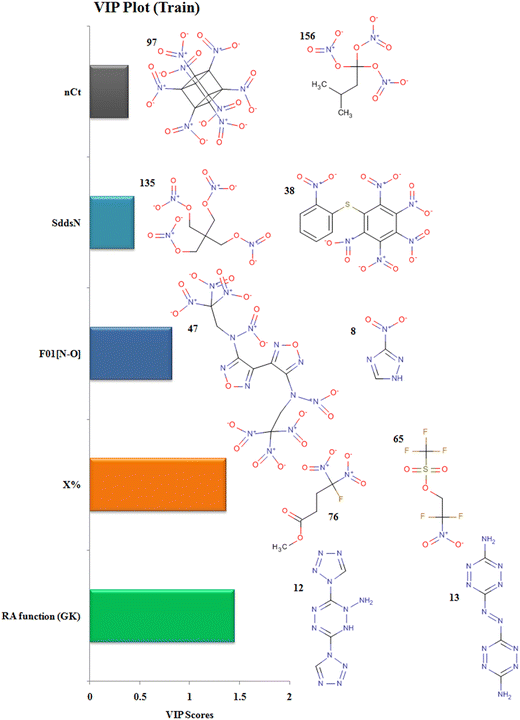Fig. 5 Variable importance plot with structural representations of molecules with higher and lower Q values.

3.5. Predictions through various ML models

We have also employed different machine-learning algorithms for the prediction of the detonation heat energy of N-containing compounds. Here, in this work, we have applied 7 different ML algorithms to develop our models and check their predictive performance. Before applying different ML methods, we have scaled both the descriptor matrix and the response values of individual training and test sets using a java-based tool Scale1.0 available from https://sites.google.com/jadavpuruniversity.in/dtc-lab-software/home. For the optimization process, we have used a python-based tool Hyperparameter Optimizer v1.2 available from https://sites.google.com/jadavpuruniversity.in/dtc-lab-software/home and performed a grid search for optimizing the hyper-parameters of each method using the scaled training set as the input. The results of RF and Adaboost/AB show that these models are not robust as the difference between the values of R² and Q²_LOO is high and hence are not reliable. The predictive performance of Gradient boost, XGBoost, and ridge regression are almost similar to our developed PLS model. Based on the MAE_Test results, the Gradient boost model shows the best predictive performance with the lowest error. To check the quality of the models we have checked MAE from cross-validation (CV), i.e. leave-one-out CV, 20 times 5 fold CV, and shuffle-split CV with n_splits = 1000. The MAE CV results of RF, AB, GB, and SVM models have increased significantly which shows the models are of inferior quality in comparison to other models. In comparison, it was found that the PLS and RR models have efficient predictive performance in terms of Q²_F1, Q²_F2, MAE_P, and RMSE and RMSE_p. So, on the basis of RMSE_P criteria, we have selected the PLS q-RASPR model as the best model for the prediction of both the training and test sets. The validation metrics of all the models are represented in Table 3.

Table 3 Comparison between the performances of different q-RASPR models

q-RASPR models	Training set statistics							Test set statistics				Optimized hyperparameters
	R ^2	Q ^2 LOO	MAEC	MAELOO	MAE ± SEM (20 times 5 fold CV)	MAE ± SEM (Shufflesplits CV n_splits = 1000)	RMSEC	Q ^2 F1	Q ^2 F2	MAEP	RMSEP
PLS	0.846	0.828	0.265	0.28	0.29 ± 0.006	0.29 ± 0.0016	0.391	0.927	0.927	0.214	0.276	(LV = 4)
RF	0.957	0.722	0.142	0.36	0.36 ± 0.007	0.36 ± 0.0016	0.206	0.885	0.884	0.242	0.347	(n = 120, leaf = 1, split = 3, depth = none)
AB	0.864	0.677	0.301	0.41	0.42 ± 0.008	0.41 ± 0.0016	0.367	0.859	0.858	0.284	0.385	(n = 60, loss = linear)
GB	0.878	0.750	0.226	0.33	0.34 ± 0.007	0.34 ± 0.0016	0.349	0.925	0.925	0.199	0.280	(n = 150, leaf = 1, split = 2, depth = 1)
XGB	0.840	0.825	0.267	0.28	0.29 ± 0.006	0.29 ± 0.0025	0.399	0.926	0.925	0.213	0.279	(n = 60, depth = 5, booster = gblinear, learning rate = 0.1)
SVM	0.885	0.747	0.212	0.31	0.32 ± 0.008	0.32 ± 0.0016	0.337	0.854	0.853	0.224	0.391	(C = 5.0, Degree = 2, Gamma = auto)
LSVM	0.831	0.824	0.270	0.28	0.29 ± 0.006	0.29 ± 0.0016	0.409	0.916	0.915	0.223	0.297	(C = 25.0)
RR	0.847	0.829	0.264	0.28	0.29 ± 0.006	0.29 ± 0.0013	0.390	0.927	0.926	0.214	0.277	(α = 1.0)

---

3.6. Interpretation of the PLS plots

To identify the outliers in the respective training set and test set, the DModX (distance to model X) AD plots (see Fig. S1 in the ESI† SI-2) were prepared for the training set and the test set, and it shows that there are 2 outlier compounds in the training set while no compounds from the test set were outside the applicability domain (AD). To determine the relationship between the X-variables (descriptors) and the Y-variable (property) and also obtain an idea about the variable importance, we have prepared the loading plot (see Fig. S2 in the ESI† SI-2) developed using the first and second PLS components. The interpretation of the plot depicts that the descriptors situated at a greater distance from the origin have more impact on the Y-variable (here the property). In the plot, RA function (GK) and X% descriptors were the farthest from the origin showing their larger impact on the prediction of detonation heat which can also be verified from the VIP plot (Fig. 5) showing their VIP score >1. The coefficient plot (see Fig. S3 in the ESI† SI-2) shows the standardized regression coefficient values of each descriptor of the model. The bubble plot (Fig. 6) shows the standardized regression coefficient of the descriptors on the Y-axis and the size of the bubble corresponds to their importance (VIP levels). The score plot (Fig. 7) was prepared using the first two PLS components for the training set. The score plot for the training set contains a total of 4 outliers. We have also performed Shapley Additive exPlanations (SHAP) analysis⁴⁶ (Fig. 8) to determine the contribution of each feature to the outcome of the model (i.e. detonation heat). The SHAP analysis for the training set shows that the F01[N-O] is the most important descriptor for the prediction of detonation heat while in the case of the test set, the RA function (GK) has the highest impact on the detonation heat prediction. The nCt descriptor is of the least importance for both the training and test sets.

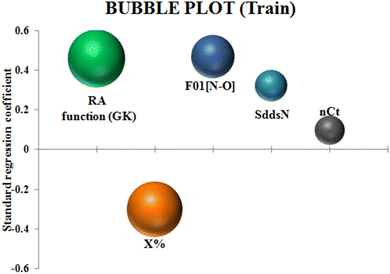Fig. 6 Bubble plot of the q-RASPR model depicting the contribution of the descriptors.

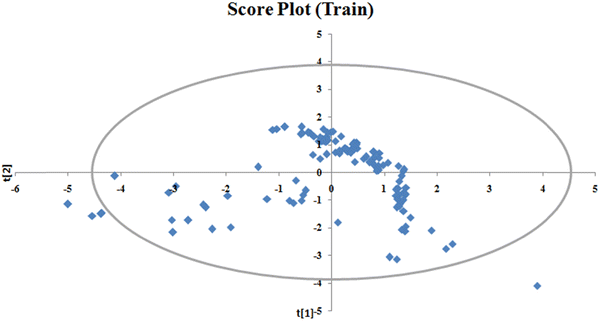Fig. 7 Score plot of the q-RASPR model for the training set.

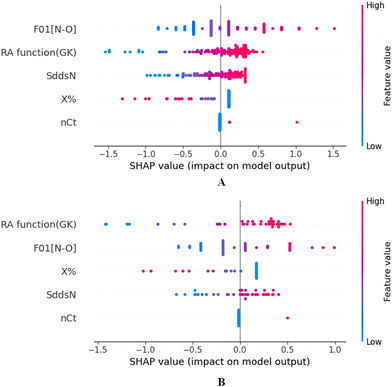Fig. 8 SHAP analysis for the training set (A) and test set (B) for the developed PLS model.

4. Comparison of the q-RASPR model with other models

4.1. Comparison with the present QSPR model

We have compared the results of the developed q-RASPR model with our own QSPR model (Section 3.1). The chemical information associated with both the models is the same as the features appearing in the QSPR model and was used for the RASPR descriptor calculation and further model development. Although the internal validation metrics were comparable for both QSPR (R²_(Train) = 0.851, Q²_(LOO) = 0.832, MAE_(Train) = 482.451) and q-RASPR (R²_(Train) = 0.846, Q²_(LOO) = 0.828, MAE_(Train) = 489.865) models, the results of the test set prediction of the q-RASPR model (Q²_F1 = 0.927, Q²_F2 = 0.927, MAE_(Test) = 395.705) were better than the QSPR model (Q²_F1 = 0.921, Q²_F2 = 0.920, MAE_(Test) = 430.542) in terms of MAE_(Test). The external validation results show that there is an enhancement in the prediction quality of the q-RASPR model. It should also be noted that the q-RASPR model is developed using 5 descriptors while the QSPR model has 6 descriptors. This depicts that the q-RASPR model with a lower number of descriptors is more efficient in the prediction of detonation heat with the same type of chemical information.

4.2. Comparison with the previous model

The previous QSPR study was performed using the random forest (RF) algorithm using a set of 3D-descriptors. Our q-RASPR model shows better predictive results in terms of Q²_F1 and RMSE_P with a lower number of descriptors. It should also be noted here that we have only used the 2D-descriptors which do not need prior structure optimization, unlike computing 3D-descriptors. A comparison of different validation metrics of our model with the previously developed model is given in Table 4.

Table 4 Comparative results of the previous model with our q-RASPR model

Models	No. of descriptors	R ^2	RMSEC	Q ^2F1	RMSEP
He et al.^1	7	0.965	377.8	0.880	641.8
Our q-RASPR model	5	0.846	723.177	0.927	510.755

---

5. Conclusion

The present work reports a q-RASPR model developed using a step-wise process of data point collection, computation of molecular structures, descriptor calculation, pre-treatment, data division, feature selection, QSPR model development, Read-Across predictions, calculation of RASPR descriptors, data fusion and finally feature selection to develop the final q-RASPR model. Initially, an MLR q-RASPR model was selected based on the cross-validation result, and thereafter the corresponding PLS model was developed with a lower number of latent variables. The authors have also employed various ML algorithms for predicting the detonation heat through the generation of different ML-based models. Furthermore, different cross-validation strategies such as leave-one-out (LOO), 20 times 5-fold CV, and shuffle-split CV (n-splits = 1000) were performed for each model to detect any over-fitting in the models. A comparison between the predictive performances of all the developed models was made as shown in Table 3. The selection of the final model (here PLS) was done on the ground of an error-based measure, i.e. Root Mean Squared Error of Predictions (RMSEP) of the test set compounds, i.e. RMSE_P. The purpose of this study was to develop an efficient model to predict the detonation property of N-containing compounds in terms of detonation heat. The study represents the development of a novel q-RASPR model in accordance with the OECD guidelines and is highly robust, easily interpretable, and reproducible. The developed model can be used to prepare new and efficient nitrogenous compounds with better detonation performance in measures of the detonation heat and to predict the detonation heat of a new compound.

Author contributions

SKP – data curation, formal analysis, validation, writing – original draft. AB – methodology, software. KR – conceptualization, resources, supervision, writing – review & editing.

Conflicts of interest

None declared.

Acknowledgements

SKP conveys his sincere gratitude to the All India Council for Technical Education (AICTE), New Delhi for the PG-scholarship and AB thanks the Life Sciences Research Board, DRDO, New Delhi (LSRB/01/15001/M/LSRB-394/SH&DD/2022) for funding the research.

References

1. T. He, W. Lai, M. Li, Y. Feng, Y. Liu, T. Yu, H. Tang, T. Zhang and H. Li, The detonation heat prediction of nitrogen-containing compounds based on quantitative structure-activity relationship (QSAR) combined with random forest (RF), Chemom. Intell. Lab. Syst., 2021, 213, 104249.
2. X. Huang, C. Li, K. Tan, Y. Wen, F. Guo, M. Li, Y. Huang, C. Q. Sun, M. Gozin and L. Zhang, Applying machine learning to balance performance and stability of high energy density materials, Iscience, 2021, 24.
3. N. Vedang and K. C. Patil, High energy materials: A brief history and chemistry of fireworks and rocketry, Resonance, 2015, 20, 431–444.
4. R. Infante-Castillo and S. P. Hernández-Rivera, Predicting Heats of Explosion of Nitroaromatic Compounds through NBO Charges and 15N NMR Chemical Shifts of Nitro Groups, Adv. in Phy. Chem, 2012.
5. M. H. Keshavarz and H. R. Pouretedal, An empirical method for predicting detonation pressure of CHNOFCl explosives, Thermochim. Acta, 2004, 414, 203–208.
6. P. Politzer and J. S. Murray, Impact sensitivity and the maximum heat of detonation, J. mol. model., 2015, 21, 1–11.
7. M. H. Keshavarz, Determining heats of detonation of non-aromatic energetic compounds without considering their heats of formation, J. Hazard. Mater., 2007, 142, 54–57.
8. M. H. Keshavarz, Theoretical prediction of condensed phase heat of formation of nitramines, nitrate esters, nitroaliphatics and related energetic compounds, J. Hazard. Mater., 2006, 136, 145–150.
9. M. H. Keshavarz, A simple procedure for calculating condensed phase heat of formation of nitroaromatic energetic materials, J. Hazard. Mater., 2006, 136, 425–431.
10. D. Kumar and A. J. Elias, The Explosive Chemistry of Nitrogen: A Fascinating Journey From 9th Century to the Present, Resonance, 2019, 24, 1253–1271.
11. M. Jaidann, S. Roy, H. Abou-Rachid and L. S. Lussier, A DFT theoretical study of heats of formation and detonation properties of nitrogen-rich explosives, J. Hazard. Mater., 2010, 176, 165–173.
12. P. Yin, Q. Zhang and J. N. M. Shreeve, Dancing with energetic nitrogen atoms: versatile N-functionalization strategies for N-heterocyclic frameworks in high energy density materials, Acc. Chem. Res., 2016, 49, 4–16.
13. R. Ameen, P. M. Fasila and A. R. Biju, Theoretical studies of azete based high energy density materials with trinitromethane functional group, Comput. Theo. Chem., 2021, 1203, 113346.
14. L. Wang, L. Zhai, W. She, M. Wang, J. Zhang and B. Wang, Synthetic strategies toward nitrogen-rich energetic compounds via the reaction characteristics of cyanofurazan/furoxan, Front. Chem., 2022, 10, 871684.
15. M. H. Keshavarz, Simple procedure for determining heats of detonation, Thermochim. Acta, 2005, 428, 95–99.
16. M. H. Keshavarz, Quick estimation of heats of detonation of aromatic energetic compounds from structural parameters, J. Hazard. Mater., 2007, 143, 549–554.
17. B. M. Rice and J. J. Hare, A quantum mechanical investigation of the relation between impact sensitivity and the charge distribution in energetic molecules, J. Phys. Chem. A, 2002, 106(9), 1770–1783.
18. J. Mao, J. Akhtar, X. Zhang, L. Sun, S. Guan, X. Li, G. Chen, J. Liu, H. N. Jeon, M. S. Kim and K. T. No, Comprehensive strategies of machine-learning-based quantitative structure-activity relationship models, Iscience, 2021, 24.
19. A. R. Katritzky, V. S. Lobanov and M. Karelson, QSPR: the correlation and quantitative prediction of chemical and physical properties from structure, Chem. Soc. Rev., 1995, 24, 279–287.
20. S. Manganelli and E. Benfenati, in Use of read-across tools, Silico Methods for Predicting Drug Toxicity, ed. E. Benfenati, Humana Press, 2016, pp. 305–322.
21. Assessment, Read-Across. Framework (RAAF). 2017, https://echa.europa.eu/documents/10162/13628/raaf_en.pdf/614e5d61-891d-4154-8a47-87efebd1851a (accessed on 07 May 2023).
22. A. Banerjee, A. Gajewicz-Skretna and K. Roy, A machine learning q-RASPR approach for efficient predictions of the specific surface area of perovskites, Mol. Inform., 2022, 42, 2200261.
23. A. Banerjee and K. Roy, First report of q-RASAR modeling toward an approach of easy interpretability and efficient transferability, Mol. Divers., 2022, 26, 2847–2862.
24. S. Wold, M. Sjöström and L. Eriksson, PLS-regression: a basic tool of chemometrics, Chemometr. Intell. Lab. Syst., 2001, 58, 109–130.
25. K. Yeturu, Machine learning algorithms, applications, and practices in data science, Handbook of Statistics, Elsevier, 2020, vol. 43, pp. 81–206.
26. V. N. Gudivada and C. R. Rao, Computational Analysis and Understanding of Natural Languages: Principles, Methods and Applications, Handbook of Statistics, Elsevier, 2018, vol. 38, pp. 197–228.
27. A. Varnek and I. Baskin, Machine learning methods for property prediction in chemoinformatics: Quo Vadis?, J. Chem. Inf. Model., 2012, 52, 1413–1437.
28. MarvinSketch software, https://www.chemaxon.com (accessed on 13 February 2023).
29. A. Mauri, in alvaDesc: a tool to calculate and analyze molecular descriptors and fingerprints, Ecotoxicological QSARs. Methods in Pharmacology and Toxicology, ed. K. Roy, Humana, 2020, pp. 801–820.
30. P. E. Danielsson, Euclidean distance mapping, Comp. Graph. Img. Process, 1980, 14, 227–248.
31. Z. Bursac, C. H. Gauss, D. K. Williams and D. W. Hosmer, Purposeful selection of variables in logistic regression, Sour. Code Bio. Med, 2008, 3, 1–8.
32. S. Katoch, S. S. Chauhan and V. Kumar, A review on genetic algorithm: past, present, and future, Multimed. Tool Appl., 2021, 80, 8091–8216.
33. A. Banerjee and K. Roy, On some novel similarity-based functions used in the ML-based q-RASAR approach for efficient quantitative predictions of selected toxicity end points, Chem. Res. Toxi., 2023, 36, 446–464.
34. L. Breiman, Random forests, Mach. Learn., 2001, 45, 5–32.
35. Q. Wu, C. J. C. Burges, K. M. Svore and J. Gao, Adapting boosting for information retrieval measures, Inf. Retr., 2010, 13, 254–270.
36. J. H. Friedman, Stochastic gradient boosting, Comput. Stat. Data Anal., 2002, 38, 367–378.
37. T. Chen and C. Guestrin XGBoost: A Scalable Tree Boosting Sysytem. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, 2016, 785–794.
38. W. S. Noble, What is a support vector machine?, Nat. Biotechnol., 2006, 24.12, 1565–1567.
39. A. E. Hoerl and R. W. Kennard, Ridge Regression: Applications to nonorthogonal problems, Technometrics., 1970, 12, 69–82.
40. K. Roy, On some aspects of validation of predictive quantitative structure–activity relationship models, Expet Opin. Drug Discovery, 2007, 2, 1567–1577.
41. K. Roy, R. N. Das, P. Ambure and R. B. Aher, Be aware of errormeasures. Further studies on validation of predictive QSAR models, Chemometr. Intell. Lab. Syst., 2016, 152, 18–33.
42. K. Roy, S. Kar and R. N. Das, A Primer on QSAR/QSPR Modeling: Fundamental Concepts, Springer, 2015, pp. 45–46.
43. K. Roy, S. Kar and P. Ambure, On a simple approach for determining applicability domain of QSAR models, Chemometr. Intell. Lab. Syst., 2015, 145, 22–29.
44. K. Roy, S. Kar and R. N. Das, Understanding the basics of QSAR for applications in pharmaceutical sciences and risk assessment, Academic press, 2015, pp. 247–248.
45. J. Li, An evaluation of nitro derivatives of cubane using ab initio and density functional theories, Theo. Chem. Acc., 2009, 122, 101–106.
46. R. Rodriguez-Perez and J. Bajorath, Interpretation of machine learning models using shapley values: application to compound potency and multi-target activity predictions, J. Comput.-Aided Mol. Des., 2020, 34, 1013–1026.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ma00535f

---