Elucidating correlated defects in metal organic frameworks using theory-guided inelastic neutron scattering spectroscopy†
Lucas S. R.
Cavalcante
 *a,
Makena A.
Dettmann
*a,
Makena A.
Dettmann
 a,
Tyler
Sours
a,
Dong
Yang
a,
Tyler
Sours
a,
Dong
Yang
 a,
Luke L.
Daemen
b,
Bruce C.
Gates
a,
Luke L.
Daemen
b,
Bruce C.
Gates
 a,
Ambarish R.
Kulkarni
*a and
Adam J.
Moulé
a,
Ambarish R.
Kulkarni
*a and
Adam J.
Moulé
 *a
*a
aDepartment of Chemical Engineering, University of California, Davis, CA 95616, USA. E-mail: arkulkarni@ucdavis.edu; amoule@ucdavis.edu
bNeutron Scattering Division, Oak Ridge National Laboratory, Oak Ridge, Tennessee 37831, USA
First published on 31st October 2022
Abstract
Metal organic frameworks (MOFs) that incorporate metal oxide cluster nodes, exemplified by UiO-66, have been widely studied, especially in terms of their deviations from the ideal, defect-free crystalline structures. Although defects such as missing linkers, missing nodes, and the presence of adventitious synthesis-derived node ligands (such as acetates and formates) have been proposed, their exact structures remain unknown. Previously, it was demonstrated that defects are correlated and span multiple unit cells. The highly specialized techniques used in these studies are not easily applicable to other MOFs. Thus, there is a need to develop new experimental and computational approaches to understand the structure and properties of defects in a wider variety of MOFs. Here, we show how low-frequency phonon modes measured by inelastic neutron scattering (INS) spectroscopy can be combined with density functional theory (DFT) simulations to provide unprecedented insights into the defect structure of UiO-66. We are able to identify and assign peaks in the fingerprint region (<100 cm−1) which correspond to phonon modes only present in certain defective topologies. Specifically, this analysis suggests that our sample of UiO-66 consists of predominantly defect-free fcu regions with smaller domains corresponding to a defective bcu topology with 4 and 2 acetate ligands bound to the Zr6O8 nodes. Importantly, the INS/DFT approach provides detailed structural insights (e.g., relative positions and numbers of acetate ligands) that are not accessible with microscopy-based techniques. The quantitative agreement between DFT simulations and the experimental INS spectrum combined with the relative simplicity of sample preparation, suggests that this methodology may become part of the standard and preferred protocol for the characterization of MOFs, and, in particular, for elucidating the structure defects in these materials.
New conceptsProgress in relating metal organic framework (MOF) structure and chemistry to materials properties like catalytic activity and structural/chemical stability is limited by the lack of techniques that provide atomic-level structural details. We combine density functional theory (DFT) simulations with inelastic neutron scattering (INS) data to develop a general approach for spectroscopically characterizing defects in MOFs. Through this new approach, the number and relative position of missing linkers in a UiO-66 MOF is investigated. The measured UiO-66 was characterized as an almost defect free (12 linkers per cluster) sample with the coexistence of lower linker density topologies (8 linkers per cluster). We simulate an ensemble of possible topologies with acetic acid and formic acid defects and demonstrate that low-frequency vibrational modes (<100 cm−1) can be used to identify the arrangement of adventitious node defects around the metal oxide core. The measured INS spectrum and DFT simulations proved to be sensitive to the defect chemistry, arrangement of defects around the node, and arrangement of defects on neighboring nodes. Our approach, using combined INS spectroscopy with DFT simulations, provides unprecedented molecular details about the organization and coordination of defect sites in MOFs and enhances our understanding of active site molecular geometry and consequently catalytic activity. |
1 Introduction
As investigations of metal–organic frameworks (MOFs) have developed beyond synthesis, discovery, and bulk structure determination, researchers have increasingly focused on novel applications such as removal of water1 and of CO22 from air. These potentially disruptive technologies require the MOF to be sufficiently stable under ambient conditions. MOF stability depends on the prevalence of structural defects and imperfections in the underlying structure.3 Defects include missing linkers and nodes and the presence of adventitious node ligands that arise during the synthesis. Defects have thus become central topics in MOF science; the associated challenges and opportunities have been recently reviewed. Fang et al.,4 Sholl and Lively,5 Dissegna et al.,6 Feng et al.,7 Ma et al.8Although several studies have leveraged defect engineering in improving the catalytic and separation properties of MOFs, the role of defects on other properties (e.g., for energy storage,9,10 water purification,11 supercapacitors,12 electrocatalysis,13,14 mechanical properties,15–17 conductivity,18–21 optical properties8,22,23) is not well understood. Additionally, although we focus on porous MOF materials, we anticipate that defects play an important role in related materials such as dense MOFs24–26 and porous organic cages.27
More specifically to the subject of this work, defects in UiO-66 MOFs are of great interest because they can act as catalytically active sites28,29 or as support sites for metal complexes.30,31 Investigations of the synthesis chemistry of MOFs such as UiO-66 provide insight into the control of defects.32 The elucidation of the defect chemistry of MOFs is progressing using combined characterization techniques. Combined use of diffuse X-ray scattering, electron microscopy, and anomalous X-ray diffraction (XRD) demonstrated correlations between defects in a UiO-66 (Hf) MOF and phase separation between defective and defect-free regions on the nanoscale in hafnium-containing metal oxide cluster nodes.33 High-resolution transmission electron microscopy (TEM) images have shown the evolution of defect distributions as function of MOF crystallization time.34 Indirect characterization methods including thermogravimetric analysis,35 acid–base titration,36 nitrogen adsorption,3 and analysis of the products of MOFs digested in NaOH in D2 O by 1H NMR spectroscopy37 also enable quantification of defect chemistry and density, but cannot co-locate the chemical species with the physical structure. Table 1 summarizes the advantages and disadvantages of the mentioned techniques for characterizing defects in MOFs.
| Methods | Advantages | Disadvantages |
|---|---|---|
| RAMAN/FTIR | Able to derive some local defect details | Not enough to characterize defect occupancy and define defect type |
| XRD | Able to derive crystal structure detecting missing clusters | No organic linker information (linker defects) |
| HRTEM | Detailed atomic observation of defects | Impractical to define/quantify all defects in the sample |
| Thermogravimetric analysis | Able to quantify defects | No atomic detail of the structures of defects |
| Acid–base titration | Able to quantify defects and reactive site information | No definition of the defects types (cluster or linker) and positions |
| Nitrogen adsorption | Indicate existence of defects | No information on the definition/quantification of defects |
| 1H NMR | Robust quantification of modulator species and linkers | No atomic detail of the structure of defects |
| INS | Provide atomic-level structural/chemical details of the defects | Semiquantitative assessment of defects |
Notwithstanding these excellent characterization options, progress in relating MOF structure and chemistry to materials properties like catalytic activity and structural/chemical stability is limited by the lack of characterization techniques that provide atomic-level structural details. Here, we combine density functional theory (DFT) simulations with inelastic neutron scattering (INS) data to develop a general approach for spectroscopically characterizing defects in MOFs. We quantify the dynamics of missing linker defects and adventitious ligands in MOF UiO-66 using the low-frequency vibrational modes (<100 cm−1), measured by INS. Then we create an ensemble of possible defect configurations (e.g., the density and positions of missing linkers) in various topologies (e.g., fcu, bcu, reo, scu) with DFT. Quantitative comparison between the measured and simulated spectra is used to fingerprint the exact positions, density, and chemistry of missing linker defects and adventitious node ligands.
INS is effective for investigating structure and dynamic disorder in a wide range of materials.38–40 Although INS has been used to investigate gas adsorption and phase changes in MOFs,41,42 this technique has not been used to elucidate the structure of defects in these materials. INS is ideally suited to address the challenge of defect structure because, in contrast to XRD (which probes the structures of crystalline domains), INS is a quantitative spectroscopic technique that probes the dynamics of the whole sample. Unlike optical vibrational spectroscopies (e.g., Raman and infrared) that measure the energy exchanged by scattered photons which obey selection rules, INS is not limited by photon selection rules since it measures the exchanged energy of neutrons scattered by the atomic nuclei. Also, INS samples the complete Brillouin zone, not just the gamma point as for the optical spectroscopies, enabling resolution of phonons that cannot be detected using optical spectroscopies. In the ESI,† we present a comparison between optical spectroscopy methods (Raman and infrared) and INS, so the differences are made clear to the reader.43 Finally, owing to the high neutron scattering cross-section of the 1H nucleus, INS is particularly sensitive to the molecular environment of organic linkers and node ligands. Because the 1H atoms are present in a wide range of locations in the structural organic backbone, they are remarkably sensitive to subtle changes in the intermolecular environment.
We now illustrate the value of INS for structural characterization of UiO-66 samples that have been synthesized using modulators to incorporate node formate, acetate, and trifluoroacetate ligands. The extensive literature of UiO-66 provides a foundation for placing the new results in a broad context.3,7,32,34,35,37,44–52 Since INS probes all the coupled vibrational modes involving hydrogen atoms, the interpretation of INS spectra is computationally challenging. Detailed modeling of the phonon modes (typically done with DFT) is necessary to link experimentally observed peak positions and intensities with specific vibrational modes. The high costs of the DFT calculations have, for the most part, limited this approach to simple crystalline materials with high structural symmetry (including a few nearly defect-free MOFs).53,54 For example, Deacon et al.42 combined DFT calculations with INS spectra to show the pressure-induced phase transition of ZIF-L to ZIF-8. Because defects in MOFs reduce the overall symmetry of the structure, INS simulations of defective MOFs require larger simulation volumes and are orders of magnitude more computationally expensive than those of their pristine analogs.
To work toward overcoming these limitations, we developed a Python-based workflow (denoted as DCS-Flow55) that facilitates seamless integration between the separate components of an INS simulation. DCS-Flow is an accurate, reproducible, efficient workflow for calculating phonon modes and the INS spectrum using DFT. The flowchart in Fig. S1 in the ESI† summarizes our approach, which allows comparisons of experimental spectra with predictions from a library of candidate defect structures. We now illustrate the method by comparing predicted spectra with INS data characterizing UiO-66 with various node ligands. The results provide unprecedented insights into the structure of the missing linker defects and the ligands that reside on the Zr-nodes. We posit that this integrated experiment-theory approach can be broadly extended to a wide family of MOFs.
2 Results and discussion
The structure of defect-free UiO-66 includes Zr6O8 nodes that are interconnected to form a fcu topology, where each node is bound to 12 linkers. The average connectivity of the nodes is controlled during synthesis by the use of modulators (e.g., acetic acid), which form anions that compete with the linker precursor anions during synthesis. For example, use of acetic acid (AA) as the modulator (with a modulator to ZrCl4 mol ratio of 30) resulted a UiO-66 sample with 10.9(4) linkers/node (i.e., 1.0(6) missing linkers/node) where the number in parentheses is the numerical value of the standard uncertainty. We denote this material as UiO-66-AA. When trifluoroacetic acid (TFA) was used as a modulator instead of acetic acid, with the same modulator to ZrCl4 ratio, the pKa of the synthesis solution was lower, the crystallization time was reduced, and the resulting MOF had 3.52 missing linkers per node. The experimental characterization (IR Spectroscopy, Powder X-ray Diffraction, Scanning Electron Microscopy, Transmission Electron Microscopy, Brunauer–Emmett–Teller (BET) Surface Area, Thermal Gravimetric Analysis, and 1H NMR Spectroscopy) of the sample measured here was published previously by Wei et al.37The linkers/node ratio, derived from 1H NMR Spectroscopy, does not determine the relative positions of the missing linkers in the MOFs. The interpretation of linker and defect structure from the molar ratio is further complicated by the presence of other less-coordinated topologies in the UiO-66 samples.33
All the experiments were done at 5 K because the dynamics of the system can strongly suppress all neutron intensities at high temperatures, such as room temperature. A room-temperature spectrum is almost the same for any organic compound.40 This point can be confirmed by the Debye–Waller factor, an exponential temperature-dependent term present in the scattering law that is used to model all modern neutron spectroscopy data.
2.1 Simulating defect free topologies
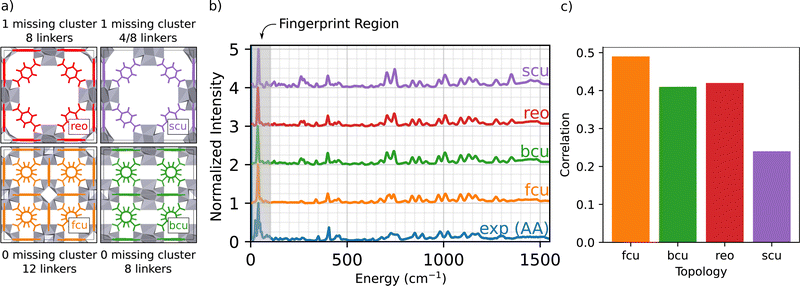
The main goal of this work is to develop an atomic-scale picture of the defective MOF structure. An appropriate starting point to understanding defects in UiO-66 topologies is to simulate defect free and under-coordinated structures, shown in Fig. 1(a).34 These under-coordinated topologies include varying numbers of missing linkers per node. The sites on the nodes where linkers are missing in UiO-66 are often occupied by adventitious ligands, including acetate derived from the acetic acid modulator and formate derived from DMF.34 For example, the bcu topology presents the same density of Zr6O8 nodes as fcu (1 node per unit cell), but has 8 linkers per node instead of 12 linkers per node; thus there are four sites on each node that might either be capped by a proton or occupied by adventitious ligands. The reo and scu topologies have lower node densities per unit cell, meaning a more open MOF framework. The reo topology incorporates 8 linkers per node. The scu topology is more complex, with either 8 or 4 linkers per node. Fig. 1(b) presents the simulated INS spectra of defect-free fcu, and defected bcu, reo, and scu topologies where the linker-occupied sites in the less-coordinated topologies (bcu, scu, and reo) are occupied by formate ligands derived from the DMF solvent. The simulation results are compared with the INS data for a UiO-66 sample synthesized with acetic acid modulator (i.e., UiO-66-AA).The INS data characterizing the four topologies show some similar features, and excellent agreement between experiment and the INS simulations for the fcu topology over the entire energy range. The simulated INS spectra for the other topologies are less consistent with the data, especially in the regions of 250 and 1450 cm−1; the peaks in these regions arise from the increased abundance of formate ligands in the under-coordinated topologies (details in ESI†). Two central conclusions emerge from this comparison:
(1) Our computational methods and the DCS-flow approach are quantitatively accurate in predicting the vibrational modes and the resulting INS spectrum of UiO-66 over an energy range of 5–5000 cm−1 (Fig. S2, ESI†).
(2) The defect-free fcu topology provides the best overall representation of the UiO-66-AA sample among those investigated (details on how the correlation was calculated are given in the ESI†).
Conclusion 2 is especially encouraging because the experimental UiO-66-AA sample contains only 1.0(6) missing linkers per node.37Fig. 1(c) shows a quantitative comparison between the experimental and simulated spectra from Fig. 1(b). The fcu structure shows the highest correlation, followed by equally good correlations between the bcu and reo topologies and a much poorer correlation with the scu structure. Assuming that the sample contains only pure fcu and bcu topologies that phase separate, then a sample with 1.0 missing linkers per node would be 75% fcu with no missing linkers and 25% bcu with 4.0 missing linkers per node.
We emphasize that the above analysis required a thorough testing of the parameters that are relevant for the INS simulation. Specifically, we evaluated the effect of DFT functionals, energy cutoffs, and mesh sampling of the phonon Brillouin zone to achieve optimal agreement with experiment, as reported previously.38 We posit that such high-cost, high-quality simulations are necessary for direct comparison and correct interpretation of MOF INS experiments.
A fundamental advantage of INS over other vibrational spectroscopies is the high signal-to-noise ratio obtained at low wavenumbers (e.g., <100 cm−1). These low-frequency phonon modes are often associated with coupled motions (e.g., wagging, twisting, bending, rocking, breathing) that span several unit cells and involve multiple atoms in the structure. In the following sections, we demonstrate that this low-frequency INS data set serves as a fingerprint region for identifying the type (e.g., AA, formate, TFA), density, and relative positions of linkers and adventitious ligands bound to the Zr6O8 nodes in UiO-66.
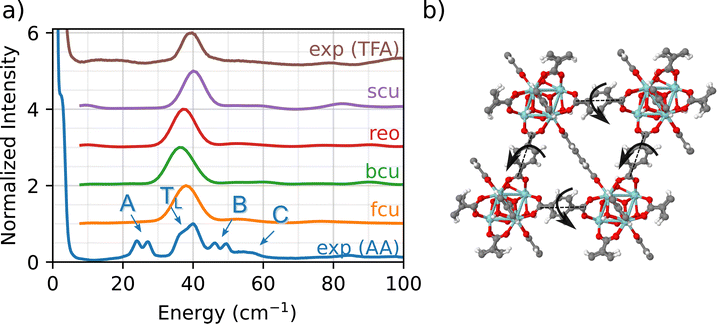
Fig. 2 compares the experimental INS measurement for UIO-66-AA (blue) with the DFT simulations of the INS spectrum in the low-frequency fingerprint region. The experimental INS data for UiO-66-AA data are characterized by four key features:
(1) A major peak (denoted TL) at about 40 cm−1 with a small, red-shifted shoulder (∼35 cm−1).
(2) A red-shifted double peak (∼25 cm−1, designated as A peak).
(3) A blue-shifted double peak (∼50 cm−1, designated as B peak).
(4) A broad shoulder at 55 cm−1 (designated as C peak).
Although the A, B, and C peaks are not observed in the simulations, all four topologies show a phonon mode close to TL (i.e., 35–40 cm−1 region). To identify the specific molecular vibration corresponding to this peak, we calculate the eigenvalues and eigenvectors of the DFT-simulated dynamical matrix (determined using finite displacement, as implemented in Phonopy).56 With this normal mode analysis approach, the eigenvalue for each phonon mode corresponds to the characteristic energy (i.e., the wavenumber), while the molecular motion itself is determined by the eigenvector (one vector for each atom in the system). Importantly, the eigenvectors are further analyzed to determine which atoms contribute to the phonon mode (e.g., node, linker, acetate ligand, etc.)
The above analysis shows that the TL peak originates from a back and forth rocking/twisting motion about the longitudinal axis of the linker (Fig. 2(b), see fcu_40 cm-1.gif animation in the ESI†). Since the phonon mode is dominated by linker motions (i.e., Zr6O8 nodes are not involved), it is observed at similar energies (and wavenumbers) across the different topologies. The slight differences in the position of the peak arise due to the small variations in the lattice constants for the four topologies. To the best of our knowledge, this is the first unambiguous assignment of a linker-specific phonon mode in the fingerprint region for any MOF. (The study by Deacon et al. was unable to identify modes below 200 cm−1.42)
We now explain the origin of A, B, and C peaks in the experimental INS. Since these features are not observed in the simulated INS spectra for any of the four topologies, we conclude that chemical defects due to the presence of adventitious synthesis-derived node ligands in UiO-66-AA are responsible for the peaks A, B, and C. Further evidence for this conclusion comes from comparison between the UiO-66-AA (blue) and UiO-66-TFA (brown) spectra (Fig. 2(a)). The spectrum of UiO-66-TFA lacks the A, B, and C peaks and the TFA synthesized sample does not contain any acetate groups. Thus, we associate these peaks with the presence of acetate ligands in the structure. This assignment is consistent with earlier work that shows that methyl groups in ZIF-8 are associated with a 25 cm−1 peak in the INS spectrum.57 The computational models that consider only connectivity defects are incomplete and fail to capture the structural and chemical complexity of the experimental sample.
2.2 Simulating acetate ligands
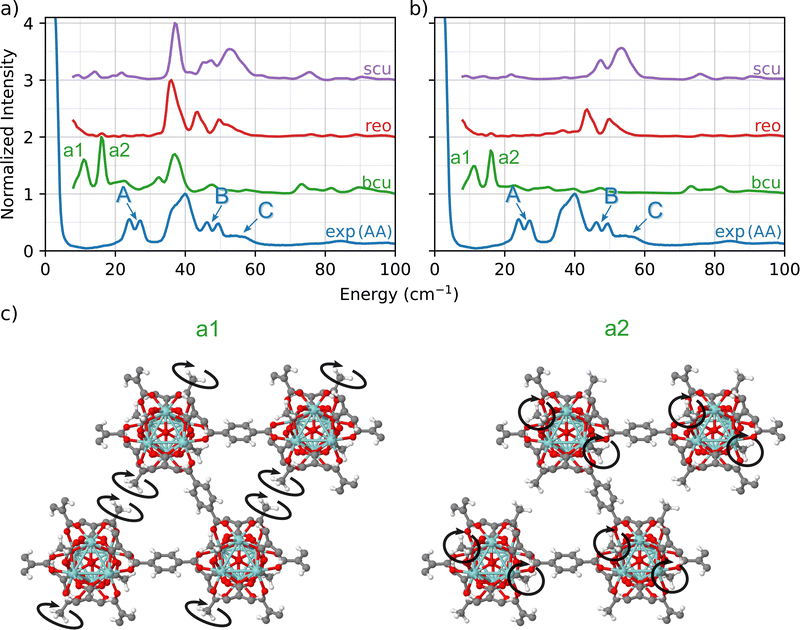
To further investigate how the modulator acetic acid led to changes in the INS spectra, we created a library of UiO-66 models in which the formate ligands in the bcu, reo, and scu topologies were replaced with acetate ligands. This replacement resulted in a well-defined set of topologies with varying numbers of linkers and acetate ligands bonded to the nodes. In each of the three cases, the total coordination number of the node is 12.A comparison of the predicted INS spectra of the three under-coordinated topologies with experiment is shown in Fig. 3(a). In contrast to the pristine fcu topology and the formate-containing bcu, reo, and scu topologies (Fig. 2), we now observe many more peaks in the fingerprint region, indicative of the acetate ligands.
A central advantage of our DFT-based DCS-flow approach is the ability it provides to computationally set the scattering cross-sections of individual atoms to zero. Thus, to isolate the vibrational modes that are related to these peaks, we set the cross-section of each atom except those of the acetate groups to zero. The resulting spectra in Fig. 3(b) provides strong evidence that the low-energy doublets indeed originate from acetate groups bonded to the Zr6O8 clusters at defect sites.
The results show that the acetate group contributes differently to the INS spectrum depending on the topology, which means that the molecular environment around the acetate group strongly affects the correlated wag and twist motions of the methyl groups. Using bcu as an example (green in Fig. 3(b)), we observe two main features at 12 cm−1 (a1) and at 16 cm−1 (a2). This doublet corresponds to coupled twisting motions of two methyl groups (from the acetate) on opposing sides of the Zr6O8 node in a diagonal fashion (see Fig. 3(c)). There are two different peaks because there are two different symmetric arrangements of methyl groups on each node. These modes are localized only on the methyl groups of the acetate ligand. Neither the linker (which dominates the TL peak) nor the Zr6O8 node is coupled to the doublet modes (see animations bcu-4A_a1.gif and bcu-4A_a2.gif in the ESI†).
In both the reo and scu cases, two different groups of acetate structures are involved in rocking motions that couple with the surrounding linkers. The coupling of the acetate motion with the linkers' motion increases the total energy of the mode. The scu simulated spectrum presents a stronger signal of peak C (Fig. 3) because it contains a smaller number of linkers and a correspondingly larger number of acetate ligands.
This analysis shows that the A, B, and C peaks originate from the acetate defects and are associated with different phonon modes depending on the motions that are specific to the bonding environment in each topology. The slight disagreement in the peak positions (∼10 cm−1, 1.24 meV) of the bcu case is due to the fact that the INS simulations are performed using a 1 × 1 × 1 unit cell of the MOF, which corresponds to an infinite network of defective nodes. Nevertheless, our simulations provide strong evidence that the experimental A peaks arise from the coupled twisting of the methyl groups bound to the Zr6O8 node of UiO-66-AA. The phonon modes corresponding to a1 (bcu-4A_a1.gif) and a2 (bcu-4A_a2.gif) are presented in the ESI† as movie files.
We showed, in Fig. 1, that the simulated INS spectrum from a non-defective lattice provides the best fit to the UiO-66-AA spectrum. This assignment was expected considering that the NMR measurements show an average ratio of one missing linker per node. This would correspond to a 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 volume ratio of fcu
1 volume ratio of fcu![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) bcu or fcu
bcu or fcu![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) reo topologies. The analysis in Fig. 3 makes a strong case that the A peaks come from coupled acetate linkers in the bcu topology, because there were no peaks with energy below 40 cm−1 in the simulated INS spectra of the acetate defect reo and scu topologies. The B and C peaks however cannot be unambiguously assigned. Our analysis shows that the modes above 40 cm−1 in the fingerprint region are strongly coupled with the linker and the Zr6O8 node, but it is not unambiguous which acetate/linker geometry causes the doublet at B and the shoulder at C.
reo topologies. The analysis in Fig. 3 makes a strong case that the A peaks come from coupled acetate linkers in the bcu topology, because there were no peaks with energy below 40 cm−1 in the simulated INS spectra of the acetate defect reo and scu topologies. The B and C peaks however cannot be unambiguously assigned. Our analysis shows that the modes above 40 cm−1 in the fingerprint region are strongly coupled with the linker and the Zr6O8 node, but it is not unambiguous which acetate/linker geometry causes the doublet at B and the shoulder at C.
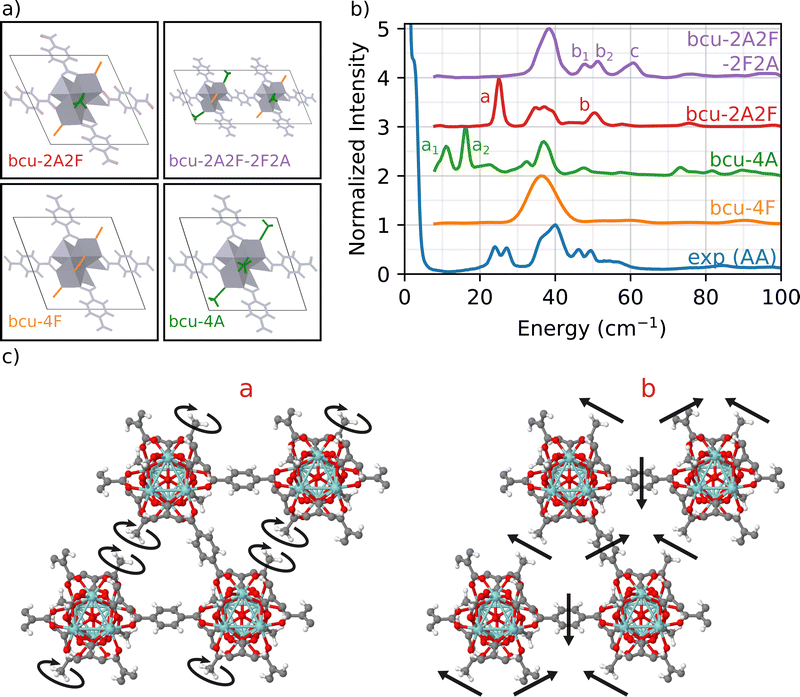
2.3 Effect of defect symmetry
To address this issue, we focus on the bcu topology because it has the smallest unit cell, it has the same number of nodes as the fcu structure, and it provides a better fit to the full INS simulation in Fig. 1 than either the reo or scu topologies. Indeed, the bcu topology can be considered as a defective fcu topology with four missing linkers per node. We consider four different variations of the bcu topology to demonstrate the structure sensitivity of the DFT-INS approach (Fig. 4(a)). The four open missing linker sites on the bcu topology (i.e., missing linkers compared to fcu) can be occupied by either formate or acetate ligands. The simulated INS spectrum with all formate ligands (bcu-4F) was presented in Fig. 1 and reproduced here (orange). The simulated INS spectrum with all acetate ligands (bcu-4A) was depicted in Fig. 3 and reproduced here (green). Since the 1H NMR data characterizing digested UiO-66-AA indicates the presence of both formate and acetate ligands on the node defect sites,37 we next consider the possibility that the four missing linker sites in the bcu topology were occupied by two acetate and two formate ligands. When the acetate groups are oriented diagonally with each other (bcu-2A2F, red spectrum in Fig. 4(b)), we observe a single peak at 25 cm−1 at the correct energy for an A peak and a single peak at 52 cm−1, which is the correct energy for a B peak. In Fig. 4(c), we present the mode corresponding to the peak at 25 cm−1 which consists of localized rotations of the acetate groups. The peak at 52 cm−1 includes significant contributions from the MOF linkers and involves coupled rocking motions of the acetate groups with the whole framework. The modes are also presented as animations (bcu-2A2F_a.gif and bcu-2A2F_b.gif in the ESI†). The absence of the doublet (similar to peaks A and B in the experimental spectrum) arises because of the presence of a single diagonally opposite pair of acetate groups bound to the Zr6O8 node. The comparison suggests that the diagonal location of the acetate group results in vibrational motions at the correct frequencies, but the simple unit cell does not represent the heterogeneity of the environment surrounding the acetate in the measured sample.To probe a greater degree of structural complexity, we simulated a 2 × 1 × 1 unit cell of the bcu topology with diagonal defects on one node and off-diagonal defects on the other (bcu-2A2F-2F2A, purple spectrum in Fig. 4). The simulated INS spectrum shows a doublet at 48 cm−1 and 52 cm−1 along with a broader peak centered at 60 cm−1. The measured spectrum has a nearly identical doublet for the measured b1 and b2 peaks at 46 cm−1 and 50 cm−1 and the shoulder C peak is at 55 cm−1. The slight offsets in the peak positions likely arise from the differences in the lattice constants of the computational model and the experimental sample. The motions corresponding to the doublet b involve coupled vibrations to the framework of neighboring acetate groups whereby one acetate rotates and the other rocks (b1), and vice versa (b2). Moreover, peak c is related to vibrations of all acetate groups from both the diagonals coupled to the framework (see the animations bcu-2A2F-2F2A_b1.gif, bcu-2A2F-2F2A_b2.gif, and bcu-2A2F-2F2A_c.gif in the ESI†). These results provide strong evidence that the experimental UiO-66-AA contains domains of the bcu-2A2F-2F2A defect structure that span multiple unit cells. Although the reo and scu topologies capped with acetates are able to reproduce peaks in the region of double peak b and shoulder c (see Fig. 3), the INS simulation of the bcu-2A2F-2F2A defect structure is a much closer match to the experimental results.
In summary, the investigated sample, UiO-66-AA, has Zr-oxide nodes that have 12 possible linker attachment sites. The sample was prepared with adventitious node ligand acetate that occupies on average 1 of the 12 attachment sites. Formate was a second adventitious node ligand that was adventitiously introduced during synthesis. We first simulated all four of the known UiO-66 topologies (fcu, bcu, reo, scu) and compared them to the measured INS spectrum. The fcu produced the best fit across the full energy range, which tells us that the majority of the volume (75%) is a defect free fcu topology. We also showed that a series of INS peaks at frequencies below 100 cm−1 (labeled A, B and C) serve as fingerprint spectra for the acetate defect site. Next we simulated the bcu, reo, and scu topologies with all missing linker sites filled with acetate. Only the fully substituted bcu topology reproduced the A-peaks matching the doublet at 25 cm−1 which comes from a twisting motion of the acetate defect. The higher energy B and C peaks couple rocking motions of the acetate methyl group to twisting of the linkers, but none of the fully substituted acetate spectra matched the measured data, indicating again that the reo and scu topologies were not present in the measured sample. Finally, we simulated the bcu topology with combined acetate and formate defects. Only geometries with acetate on opposite sides of the node and alternating orientation between neighboring nodes accurately reproduced the B-peak doublet and C-shoulder from the measured INS spectrum. We can therefore assign that 75% of the volume was the fcu topology with no defects. We assume, based on excellent previous work,33 that the different topologies phase separate into domains. The remaining 25% of the volume seems to be roughly equally divided between the bcu topology with 100% of the adventitious node site occupied by acetate and the bcu topology with a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of acetate and formate on the adventitious node sites. In the very roughly 12.5% of the volume with mixed acetate and formate, the sites ligands assume ordered arrangements, including occupying the opposite sides of the node and with alternating orientation between neighboring nodes. While our conclusions are consistent with a previous study by Liu2019, the INS/DFT approach provides detailed structural insights (e.g., relative positions and number of acetate ligands) that are not possible with microscopy-based techniques.
1 mixture of acetate and formate on the adventitious node sites. In the very roughly 12.5% of the volume with mixed acetate and formate, the sites ligands assume ordered arrangements, including occupying the opposite sides of the node and with alternating orientation between neighboring nodes. While our conclusions are consistent with a previous study by Liu2019, the INS/DFT approach provides detailed structural insights (e.g., relative positions and number of acetate ligands) that are not possible with microscopy-based techniques.
3 Conclusions
We present a combined INS spectroscopic and simulation investigation of UiO-66 to characterize the geometry of adventitious defect sites occupied by ligands such as acetate and formate. INS spectroscopy is highly sensitive to the vibrational motions of linkers and defect species on MOF node defect sites because of the high resolution at low energies. Vibrations in the <100 cm−1 range include subtle wag and twist motions that capture details of the molecular-scale environment around the defect site, in this case coupling between wag motions by the methyl group on the acetate with twist motions on the terephthalate linker. We show a near quantitative match between the experimental INS spectrum and DFT simulated INS spectra, which demonstrates that this combination of experiment and theory is well-suited to characterization of heterogeneous reactive sites in MOFs. We suggest that this methodology should become part of the standard protocol for characterization of MOF structures.58Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was supported by the Department of Energy, Basic Energy Sciences, Award DE-SC0010419, including salary for L. S. R. C., M. A. D. and A. J. M. T. S. and A. K. acknowledge partial support from NSF # 2048260. D. Y. and B. C. G. acknowledge support as part of the Inorganometallic Catalyst Design Center, an Energy Frontier Research Center funded by the U.S. Department of Energy (DOE), Office of Science, Basic Energy Sciences (DE-SC0012702). This research used resources of the National Energy Research Scientific Computing Center (NERSC), a DOE Office of Science User Facility supported by the Office of Science of the U.S. Department of Energy under Contract no. DE-AC02-05CH11231. The INS spectrum was measured at the Spallation Neutron Source, a DOE Office of Science User Facility operated by the Oak Ridge National Laboratory, partly supported by LLNL under Contract DE-AC52-07NA27344.Notes and references
- H. Furukawa, F. Gándara, Y. B. Zhang, J. Jiang, W. L. Queen, M. R. Hudson and O. M. Yaghi, J. Am. Chem. Soc., 2014, 136, 4369–4381 CrossRef CAS PubMed
.
- G. Rim, F. Kong, M. Song, C. Rosu, P. Priyadarshini, R. P. Lively and C. W. Jones, JACS Au., 2022, 2, 380–393 CrossRef CAS PubMed
.
- B. Bueken, N. Van Velthoven, A. Krajnc, S. Smolders, F. Taulelle, C. Mellot-Draznieks, G. Mali, T. D. Bennett and D. De Vos, Chem. Mater., 2017, 29, 10478–10486 CrossRef CAS
.
- Z. Fang, B. Bueken, D. E. De Vos and R. A. Fischer, Angew. Chem., Int. Ed., 2015, 54, 7234–7254 CrossRef CAS
.
- D. S. Sholl and R. P. Lively, J. Phys. Chem. Lett., 2015, 6, 3437–3444 CrossRef CAS
.
- S. Dissegna, K. Epp, W. R. Heinz, G. Kieslich and R. A. Fischer, Adv. Mater., 2018, 30, 1704501 CrossRef
.
- Y. Feng, Q. Chen, M. Jiang and J. Yao, Ind. Eng. Chem. Res., 2019, 58, 17646–17659 CrossRef CAS
.
- X. Ma, L. Wang, Q. Zhang and H.-L. Jiang, Angew. Chem., Int. Ed., 2019, 58, 12175–12179 CrossRef CAS PubMed
.
- A. E. Baumann, D. A. Burns, B. Liu and V. S. Thoi, Commun. Chem., 2019, 2, 1–14 CrossRef
.
- A. E. Baumann, D. A. Burns, J. C. Díaz and V. S. Thoi, ACS Appl. Mater. Interfaces, 2019, 11, 2159–2167 CrossRef CAS
.
- Y. Cao, X. Mi, X. Li and B. Wang, Front. Chem., 2021, 9, 673738 CrossRef CAS
.
- N. Ferhi, B. Desalegn Assresahegn, C. Ardila-Suarez, N. Dissem, D. Guay and A. Duong, ACS Appl. Energy Mater., 2022, 5, 1235–1243 CrossRef CAS
.
- J. Morales-Vidal, R. García-Muelas and M. A. Ortuño, Catal. Sci. Technol., 2021, 11, 1443–1450 RSC
.
- Z.-D. Wang, Y. Zang, Z.-J. Liu, P. Peng, R. Wang and S.-Q. Zang, Appl. Catal., B, 2021, 288, 119941 CrossRef CAS
.
- T. D. Bennett, A. K. Cheetham, A. H. Fuchs and F.-X. Coudert, Nat. Chem., 2016, 9, 11–16 CrossRef
.
- A. K. Cheetham, T. D. Bennett, F.-X. Coudert and A. L. Goodwin, Dalton Trans., 2016, 45, 4113–4126 RSC
.
- B. Zheng, F. Fu, L. L. Wang, J. Wang, L. Du and H. Du, J. Phys. Chem. C, 2018, 122, 4300–4306 CrossRef CAS
.
- J. Y. Choi and J. Park, ACS Appl. Electron. Mater., 2021, 3, 4197–4202 CrossRef CAS
.
- A. A. Talin, A. Centrone, A. C. Ford, M. E. Foster, V. Stavila, P. Haney, R. A. Kinney, V. Szalai, F. E. Gabaly, H. P. Yoon, F. Léonard and M. D. Allendorf, Science, 2014, 343, 66–69 CrossRef CAS PubMed
.
- O. Basu, S. Mukhopadhyay, S. Laha and S. K. Das, Chem. Mater., 2022, 34, 6734–6743 CrossRef CAS
.
- M. Islamov, H. Babaei and C. E. Wilmer, ACS Appl. Mater. Interfaces, 2020, 12, 56172–56177 CrossRef CAS
.
- H. S. Jena, A. M. Kaczmarek, C. Krishnaraj, X. Feng, K. Vijayvergia, H. Yildirim, S.-N. Zhao, R. Van Deun and P. V. Der Voort, Cryst. Growth Des., 2019, 19, 6339–6350 CrossRef CAS
.
- M. Taddei, G. M. Schukraft, M. E. A. Warwick, D. Tiana, M. J. McPherson, D. R. Jones and C. Petit, J. Mater. Chem. A, 2019, 7, 23781–23786 RSC
.
- L. Xin, Z. Fan, G. Li, M. Zhang, Y. Han, J. Wang, K. P. Ong, L. Qin, Y. Zheng and X. Lou, New J. Chem., 2017, 41, 151–159 RSC
.
- G. Lorusso, E. Natividad, M. Evangelisti and O. Roubeau, Mater. Horiz., 2019, 6, 144–154 RSC
.
- Y. Wu, T. Binford, J. A. Hill, S. Shaker, J. Wang and A. K. Cheetham, Chem. Commun., 2018, 54, 3751–3754 RSC
.
- G. Zhu, Y. Liu, L. Flores, Z. R. Lee, C. W. Jones, D. A. Dixon, D. S. Sholl and R. P. Lively, Chem. Mater., 2018, 30, 262–272 CrossRef CAS
.
- M. Rimoldi, A. J. Howarth, M. R. DeStefano, L. Lin, S. Goswami, P. Li, J. T. Hupp and O. K. Farha, ACS Catal., 2017, 7, 997–1014 CrossRef CAS
.
- D. Yang, M. A. Ortuño, V. Bernales, C. J. Cramer, L. Gagliardi and B. C. Gates, J. Am. Chem. Soc., 2018, 140, 3751–3759 CrossRef CAS
.
- V. Bernales, D. Yang, J. Yu, G. GümüÅŸlü, C. J. Cramer, B. C. Gates and L. Gagliardi, ACS Appl. Mater. Interfaces, 2017, 9, 33511–33520 CrossRef CAS
.
- D. Yang, S. O. Odoh, J. Borycz, T. C. Wang, O. K. Farha, J. T. Hupp, C. J. Cramer, L. Gagliardi and B. C. Gates, ACS Catal., 2016, 6, 235–247 CrossRef CAS
.
- F. E. Chen, T. A. Pitt, D. J. Okong'o, L. G. Wetherbee, J. J. Fuentes-Rivera and P. J. Milner, Chem. Mater., 2022, 34, 3383–3394 CrossRef CAS
.
- M. J. Cliffe, W. Wan, X. Zou, P. A. Chater, A. K. Kleppe, M. G. Tucker, H. Wilhelm, N. P. Funnell, F. X. Coudert and A. L. Goodwin, Nat. Commun., 2014, 5, 1–8 Search PubMed
.
- L. Liu, Z. Chen, J. Wang, D. Zhang, Y. Zhu, S. Ling, K. W. Huang, Y. Belmabkhout, K. Adil, Y. Zhang, B. Slater, M. Eddaoudi and Y. Han, Nat. Chem., 2019, 11, 622–628 CrossRef CAS PubMed
.
- H. Wu, T. Yildirim and W. Zhou, J. Phys. Chem. Lett., 2013, 4, 925–930 CrossRef CAS
.
- R. C. Klet, Y. Liu, T. C. Wang, J. T. Hupp and O. K. Farha, J. Mater. Chem. A, 2016, 4, 1479–1485 RSC
.
- R. Wei, C. A. Gaggioli, G. Li, T. Islamoglu, Z. Zhang, P. Yu, O. K. Farha, C. J. Cramer, L. Gagliardi, D. Yang and B. C. Gates, Chem. Mater., 2019, 31, 1655–1663 CrossRef CAS
.
- T. F. Harrelson, V. Dantanarayana, X. Xie, C. Koshnick, D. Nai, R. Fair, S. A. Nuñez, A. K. Thomas, T. L. Murrey, M. A. Hickner, J. K. Grey, J. E. Anthony, E. D. Gomez, A. Troisi, R. Faller and A. J. Moulé, Mater. Horiz., 2019, 6, 182–191 RSC
.
- T. F. Harrelson, Y. Q. Cheng, J. Li, I. E. Jacobs, A. J. Ramirez-Cuesta, R. Faller and A. J. Moulé, Macromolecules, 2017, 50, 2424–2435 CrossRef CAS
.
-
C. H. Philip, S. F. Parker, A. J. Ramirez-Cuesta and J. Tomkinson, Vibrational spectroscopy with neutrons: With applications in chemistry, biology, materials science and catalysis, World Scientific Publishing Co., 2005, pp. 1–642 Search PubMed
.
- M. E. Casco, J. Fernández-Catalá, Y. Cheng, L. Daemen, A. J. Ramirez-Cuesta, C. Cuadrado-Collados, J. Silvestre-Albero and E. V. Ramos-Fernandez, ChemistrySelect, 2017, 2, 2750–2753 CrossRef
.
- A. Deacon, L. Briquet, M. Malankowska, F. Massingberd-Mundy, S. Rudić, T. L. Hyde, H. Cavaye, J. Coronas, S. Poulston and T. Johnson, Commun. Chem., 2022, 5, 1–10 CrossRef
.
- D. Vong, T. Nematiaram, M. A. Dettmann, T. L. Murrey, L. S. R. Cavalcante, S. M. Gurses, D. Radhakrishnan, L. L. Daemen, J. E. Anthony, K. J. Koski, C. X. Kronawitter, A. Troisi and A. J. Moulé, J. Phys. Chem. Lett., 2022, 13, 5530–5537 CrossRef CAS
.
- L. Valenzano, B. Civalleri, S. Chavan, S. Bordiga, M. H. Nilsen, S. Jakobsen, K. P. Lillerud and C. Lamberti, Chem. Mater., 2011, 23, 1700–1718 CrossRef CAS
.
- H. Wu, Y. S. Chua, V. Krungleviciute, M. Tyagi, P. Chen, T. Yildirim and W. Zhou, J. Am. Chem. Soc., 2013, 135, 10525–10532 CrossRef CAS
.
- S. Øien, D. Wragg, H. Reinsch, S. Svelle, S. Bordiga, C. Lamberti and K. P. Lillerud, Cryst. Growth Des., 2014, 14, 5370–5372 CrossRef
.
- M. Vandichel, J. Hajek, F. Vermoortele, M. Waroquier, D. E. D. Vos and V. V. Speybroeck, CrystEngComm, 2014, 17, 395–406 RSC
.
- T. D. Bennett, T. K. Todorova, E. F. Baxter, D. G. Reid, C. Gervais, B. Bueken, B. Van De Voorde, D. De Vos, D. A. Keen and C. Mellot-Draznieks, Phys. Chem. Chem. Phys., 2016, 18, 2192–2201 RSC
.
- F. Zhou, N. Lu, B. Fan, H. Wang and R. Li, J. Energy Chem., 2016, 5, 874–879 CrossRef
.
- C. Atzori, G. C. Shearer, L. Maschio, B. Civalleri, F. Bonino, C. Lamberti, S. Svelle, K. P. Lillerud and S. Bordiga, J. Phys. Chem. C, 2017, 121, 9312–9324 CrossRef CAS
.
- D. N. Johnstone, F. C. N. Firth, C. P. Grey, P. A. Midgley, M. J. Cliffe and S. M. Collins, J. Am. Chem. Soc., 2020, 142, 13081–13089 CrossRef CAS PubMed
.
- K. Tan, H. Pandey, H. Wang, E. Velasco, K. Y. Wang, H. C. Zhou, J. Li and T. Thonhauser, J. Am. Chem. Soc., 2021, 143, 6328–6332 CrossRef CAS PubMed
.
- Y. Q. Cheng, L. L. Daemen, A. I. Kolesnikov and A. J. Ramirez-Cuesta, J. Chem. Theory Comput., 2019, 15, 1974–1982 CrossRef CAS PubMed
.
- M. A. Dettmann, L. S. Cavalcante, C. Magdaleno, K. Masalkovaitė, D. Vong, J. T. Dull, B. P. Rand, L. L. Daemen, N. Goldman, R. Faller and A. J. Moulé, J. Chem. Theory Comput., 2021, 17, 7313–7320 CrossRef CAS
.
- L. S. Cavalcante, L. L. Daemen, N. Goldman and A. J. Moulé, J. Chem. Inf. Model., 2021, 61, 4486–4496 CrossRef CAS PubMed
.
- A. Togo and I. Tanaka, Scr. Mater., 2015, 108, 1–5 CrossRef CAS
.
- M. E. Casco, Y. Q. Cheng, L. L. Daemen, D. Fairen-Jimenez, E. V. Ramos-Ferná Ndez, A. J. Ramirez-Cuesta and J. Silvestre-Albero, Chem. Commun., 2016, 52, 3639 RSC
.
- C. Gropp, S. Canossa, S. Wuttke, F. Gándara, Q. Li, L. Gagliardi and O. M. Yaghi, ACS Cent. Sci., 2020, 6, 1255–1273 CrossRef CAS PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2mh00914e |
| This journal is © The Royal Society of Chemistry 2023 |