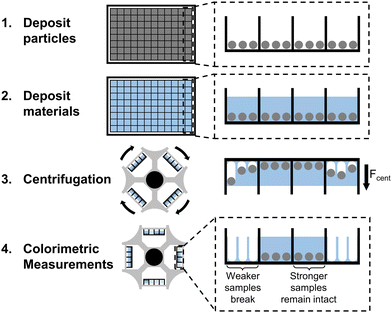
Quantitative high-throughput measurement of bulk mechanical properties using commonly available equipment†
Justin E.
Griffith‡
 a,
Yusu
Chen‡
a,
Qingsong
Liu
a,
Yusu
Chen‡
a,
Qingsong
Liu
 a,
Qifeng
Wang
b,
Jeffrey J.
Richards
a,
Qifeng
Wang
b,
Jeffrey J.
Richards
 a,
Danielle
Tullman-Ercek
a,
Danielle
Tullman-Ercek
 a,
Kenneth R.
Shull
a,
Kenneth R.
Shull
 b and
Muzhou
Wang
b and
Muzhou
Wang
 *a
*a
aDepartment of Chemical and Biological Engineering, Northwestern University, Evanston, Illinois 60208, USA. E-mail: mwang@northwestern.edu
bDepartment of Materials Science & Engineering, Northwestern University, Evanston, Illinois 60208, USA
First published on 18th October 2022
Abstract
Machine learning approaches have introduced an urgent need for large datasets of materials properties. However, for mechanical properties, current high-throughput measurement methods typically require complex robotic instrumentation, with enormous capital costs that are inaccessible to most experimentalists. A quantitative high-throughput method using only common lab equipment and consumables with simple fabrication steps is long desired. Here, we present such a technique that can measure bulk mechanical properties in soft materials with a common laboratory centrifuge, multiwell plates, and microparticles. By applying a homogeneous force on the particles embedded inside samples in the multiwell plate using centrifugation, we show that our technique measures the fracture stress of gels with similar accuracy to a rheometer. However, our method has a throughput on the order of 103 samples per run and is generalizable to virtually all soft material systems. We hope that our method can expedite materials discovery and potentially inspire the future development of additional high-throughput characterization methods.
New conceptsAs machine learning becomes more and more transformational in our materials community, it is increasingly important to support these efforts with simple approaches to accurately measure large libraries of materials properties. While most common experimental approaches rely on robotic measurement, not all materials scientists have access to large capital equipment budgets or in-house automation support teams. To enable the masses to contribute to the new revolution in AI-based materials design, there is a crucial need for clever and elegant methods that can quantitatively measure properties at high-throughput, using only common lab equipment and inexpensive consumables. Here, our work demonstrates one such approach, that can measure the mechanical properties of soft materials. Our key concept is the use of centrifugation, which can apply a uniform force to many samples, and is readily available to most research labs. This is thus a natural vehicle for multiplexing, and we hope that readers are inspired by our work to think about creative uses of a centrifuge for their own needs. Additionally, we apply careful analysis of the underlying mechanics to show that our technique is much more than a screening tool, as it can quantitatively measure modulus and fracture strength with similar accuracy to more standard methods. |
1 Introduction
In the era of Big Data and AI, there is a pressing demand for large datasets of materials properties to train machine learning models that can aid in materials discovery.1–10 While advances in combinatorial chemistry have greatly accelerated the synthesis of novel materials,11–13 characterization methods have not kept up with this increased throughput, creating a bottleneck in materials development. To address these issues, high-throughput characterization methods have previously measured properties such as melting temperature,14 oxidation behavior,15 and electrical conductivity.16 However, measuring mechanical properties at high throughput is significantly more challenging, as existing methods are often limited by slow, complex fabrication steps or expensive custom instrumentation.17–19 A simple and widely-accessible high-throughput mechanical test could significantly speed up the discovery and development of novel materials.Existing high-throughput mechanical characterization methods are often hindered by their accessibility or complicated fabrication steps. Many such techniques already exist, including scanning nanoindentation,19 micromachined cantilever beams,20 microelectromechanical systems,21 microtensile testing,18,22 and microrheology.23 These methods can measure properties such as elastic modulus, hardness, thin film thermomechanical behavior, and ultimate tensile strength.17,18 For example, scanning nanoindentation can measure hardness and elastic modulus in a high-throughput manner, but requires expensive and uncommon instrumentation.19 Microrheology has also been utilized to measure elastic modulus and viscosity at high throughput,23–26 but it requires complex custom instrumentation and is optimized for materials with a very low modulus or viscosity.24,25 Finally, parallel microtensile testing can characterize mechanical properties in a high-throughput manner,18,22 but samples must be fabricated into a specific form and aligned precisely, limiting the overall throughput of the method.18
Soft materials present an important target for high-throughput mechanical characterization. The mechanical properties of such materials are highly tunable, especially by adding extra components to form composites with enhanced properties.27–29 However, the presence of these additives significantly increases the number of possible formulations, so far more testing is required to fully explore the materials library. Sequence-specific polymers are another interesting class of soft materials that allow precise control of material properties by directly tailoring monomeric sequences.10 Fully unlocking the potential of these materials, however, requires a deep understanding of the sequence–structure–function paradigm, which again necessitates large-scale experimentation because the sequence space is exponentially large.10 Fortunately, the preparation of many soft materials is simple enough that samples across a wide range of compositions can be synthesized in a high-throughput manner. For example, automated pipetting systems have been shown to be effective at creating various hydrogels at high throughput.27,30 This synthesis technique takes advantage of the fact that post-treatment is often not necessary for soft materials, so gels of different compositions can quickly be fabricated by simply combining reactants in varying amounts. This is far simpler than the formation of composition gradients for hard materials such as alloys, which often requires very slow diffusion processing.19 Unfortunately, high throughput studies of soft materials are frequently bottlenecked by the mechanical characterization step, which is often still performed with standard one-at-a-time testing.27 More accessible high-throughput characterization methods are necessary to keep up with the increased throughput of soft materials synthesis.
Centrifugation is uniquely suited for widely adoptable high-throughput mechanical testing due to its ability to apply a homogenous force across many samples while only requiring commonly available laboratory equipment. This has previously been utilized for high-throughput measurement techniques such as single-particle force spectroscopy.31,32 Recently, we developed a method that uses centrifugation to pull particles off thin adhesive films, enabling high-throughput characterization of the adhesive strength of soft materials.33 We show here that a similar strategy can characterize bulk mechanical properties of soft materials. Rather than placing the particles on top of films as was done previously, we now embed the particles within material samples on a multiwell plate before centrifuging the plate at higher and higher rotational velocities. We can thus quantify the mechanical properties of bulk materials instead of adhesive strength, by measuring the centrifugal force required to pull the particles out of the sample. The particles provide a colorimetric signal, so results are immediately visible to the naked eye (Fig. 1).
In contrast to existing high-throughput methods for mechanical properties,17–23 our method only requires a common laboratory centrifuge and commercially available particles and well plates, so it is much more widely accessible. Sample fabrication is simple and does not limit the throughput of our method, especially when using multi-channel pipettes or automated pipetting systems. With four 384-well plates able to fit in the centrifuge at once, we show that our method can reach a throughput of up to 1536 samples per run, a massive improvement over traditional one-at-a-time mechanical characterization techniques. This throughput could potentially be even further increased using 1536-well plates or by using a centrifuge rotor that can hold additional plates.
We begin by showing results from our method for poly(methyl methacrylate)–poly(n-butyl acrylate)–poly(methyl methacrylate) (PMMA–PnBA–PMMA) triblock copolymer gels, using particles of varying density and size. To better understand the fracture mechanism in this test, we investigate a similar scenario where we physically pull a particle attached to a wire out of a gel. Using this experiment as a starting point, we present an analytical solution that indicates that our method can measure the shear fracture stress of soft materials. We then test this theory by comparing the results from our method to those from a standard rheometer test, demonstrating excellent agreement for two different materials systems. Finally, we perform our method on a full 384-well plate to illustrate its significantly increased throughput over standard tests.
2 Results and discussion
Our method utilizes centrifugation to apply a homogeneous force across hundreds of samples on a multiwell plate. The centrifugal force pulls on the particles embedded in each sample, eventually causing them to break through the gel. We can then use the magnitude of centrifugal force at fracture as a metric for the bulk mechanical strength of the corresponding material. We begin by proving the basic concept on poly(methyl methacrylate)–poly(n-butyl acrylate)–poly(methyl methacrylate) (PMMA–PnBA–PMMA) triblock copolymers dissolved in 2-ethylhexanol. At room temperature, this is a good solvent for PnBA but a poor solvent for the PMMA endblocks, which thus serve as physical crosslinks that form a gel. Above 90 °C, PMMA becomes soluble and the gel becomes a liquid, allowing us to pipette hot solution into the well plate before it solidifies at room temperature.34 We chose this material because its mechanical properties can be tuned by simply adjusting the concentration of the copolymer in the solvent. Additionally, this material is highly adhesive, enabling it to stick to the well plate and not detach during centrifugation.The preparation steps in our method are relatively simple and do not limit the throughput of characterization. First, we deposit a single layer of particles at the bottom of each well on the plate. We then heat and pipette triblock gel solutions of varying concentrations into each well and then allow them to cool and solidify around the particles. After the samples solidify completely, we centrifuge the plate facing outwards multiple times at successively increasing speeds. After each speed, we remove the well plate from the centrifuge, take photos of the plate, and then return it to the centrifuge for the next speed. Our results show that centrifugation can distinguish between materials of varying strengths, validating the feasibility of this method for measuring bulk mechanical properties (Fig. 2).
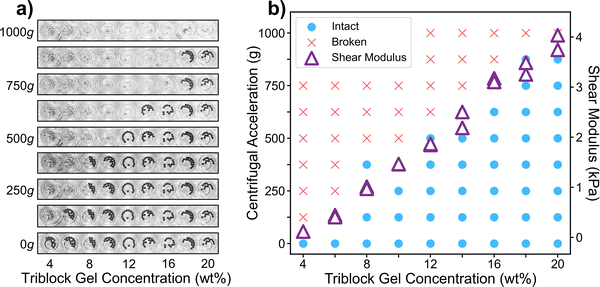 | ||
| Fig. 2 (a) Photos of centrifugation experiment with 1 mm diameter tungsten carbide particles embedded in PMMA–PnBA–PMMA gels at various concentrations. 100 μL of triblock gel solution was added to each well in a 96-well plate. The same row in the well plate is shown from the bottom after cycles at increasing speeds. When a sample fractures, the particles break through to the top of the well plate and are thus not visible in subsequent photos. (b) Graphical representation of data in part a along with shear modulus of the same gels (Table S1, ESI†). Centrifugal results are interpreted in a binary fashion, with “intact” meaning that the majority of the particles were still inside the gel at the specified speed and “broken” meaning that the majority had broken out of the gel. | ||
We observed that when one particle breaks through a sample, the rest of the particles in that well would usually break through all at once. We thus define the critical centrifugal speed as the midpoint between the highest speed at which a sample was intact and the speed at which most of the particles broke through the sample. Critical centrifugal speed was observed to be independent of the duration of centrifugation above ∼30 seconds. To investigate whether the number or location of particles in a well has any effect on the critical centrifugal speed, we compared our results from several particles in a flat-bottomed well to results obtained from a single particle in the center of a U-shaped well. The critical centrifugation speed was consistent across both scenarios (Fig. S1 and S2, ESI†), which suggests that the number and location of particles in each well is not significant.
To correlate our results to those from more classical mechanical tests, we compared them to related mechanical properties. We observed a serendipitous correlation between the shear modulus of the triblock gel measured by oscillatory rheology and the centrifugal acceleration at which that gel fractures (Fig. 2b). To determine the origin of this correlation, we first hypothesized that the correct metric for the material strength is the centrifugal force at break normalized by the particle's cross-sectional area, i.e., a “centrifugal stress,”
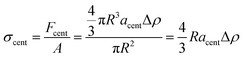 | (1) |
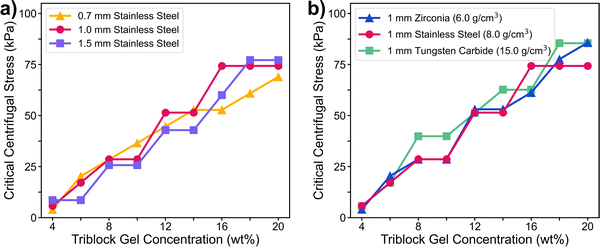 | ||
| Fig. 3 Critical centrifugal stress (eqn (1)) for different gel concentrations, with particles of different diameters (a) and densities (b). Results were consistent across different particle types (Fig. S3, ESI†). Centrifugation was performed in a 96-well plate, and 100 μL of triblock gel solution was added to each well. | ||
To investigate the mechanism of gel fracture in our centrifugation method, we set up a similar experiment in which we physically pulled a particle out of a gel using a thin wire (Fig. 4). As the wire was connected to an inchworm motor, load transducer, and optical sensor, we could directly measure the force and displacement during the pulling process. A side camera also enabled visual monitoring. To estimate the forces on the particle alone, we ran a control experiment consisting of a wire with no particle. After subtracting the load of this control experiment from the total load (Fig. S4, ESI†), we found that the force on the particle increases nonlinearly from zero, when the particle is at the bottom, to a plateau value (Fig. 4b). This plateau is reached at a displacement of ∼0.5 mm for a 3 mm diameter particle, and the force eventually falls off when the gel completely fractures.
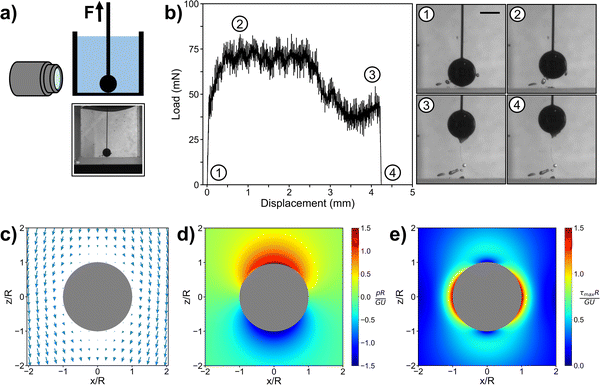 | ||
| Fig. 4 (a) Diagram of particle pulling experiment with full camera image shown before pulling began. (b) Load-displacement curve for particle pulling experiment after wire load was subtracted from total load (Fig. S4, ESI†). A 15 mm tall 10 wt% triblock gel in a small glass container was used for this experiment, with a 3 mm diameter stainless steel particle starting at the bottom surface. Zoomed-in images are shown for the starting point, when the force plateaus, just before fracture, and just after fracture. The scale bar is 2 mm, and all images are at the same magnification. (c–e) Analytical solution for the displacement field, pressure, and maximum shear stress around particle that has moved a distance in the +z direction in an infinite medium, in the frame of reference of the particle. | ||
Direct quantitative comparison of pulling the particle using a wire vs. centrifugation is difficult because of a few issues. Generally, we observed that adhesion of the gel to the wire contributes between 60% and 85% of the total measured load at fracture (Fig. S4, ESI†). Even after subtracting the wire's adhesive force, the pulling force drastically underestimated the centrifugal force that one would expect for a particle of similar size and density (Fig. S5, ESI†). To explain this, we hypothesize that the wire generates a pathway of broken gel that the particle easily tunnels through as it moves up, while the gel above the particles is pristine in the centrifugal experiment. The presence of the wire thus limits the quantitative results we can draw from this experiment.
Nevertheless, the wire pulling experiment contributes an important insight into our analysis of the mechanics of centrifugation. While the plateau in pulling force does not quantitatively match the centrifugal results, it does correspond to when the particle experiences its maximum force, which only occurs when the particle is a considerable distance away from the bottom surface. This suggests that if a particle begins at the bottom surface, the critical centrifugal force at break should be the same as if the particle had begun far away from the bottom. While we could not perform this specific comparison in the centrifugal test, we instead varied the thickness of the gel above the particles on the bottom surface of the well plates (Fig. S6, ESI†). We found that as this thickness increased above a few particle diameters, our results were generally insensitive to the thickness (until it was so large that the centrifugal force exceeded the tensile strength of the gel, and the gel itself broke out of the well plate). This is all consistent with the same picture: a particle that begins at the bottom of the well plate must eventually move up, through the entire gel, before it breaks out. The critical centrifugal stress for a particle starting at the bottom surface should thus be identical to that of a particle in an infinitely large gel.
The stress and strain fields associated with a force exerted on a solid sphere in an infinite elastic medium have a well-known analytical solution. From the frame of reference of a particle of radius R that has moved a distance U in the +z direction (up), the deformation field (Fig. 4c) in the surrounding medium is given by,
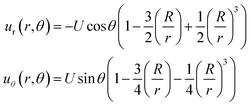 | (2) |
| F = 6πGRU, | (3) |
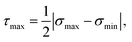 | (4) |
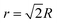 , where the gel experiences uniaxial compression and tension, respectively. Notably, the highest stress regions occur closest to the sphere's surface at the equator (θ = 90°), where the deformation mode is simple shear. Although we reach this conclusion by examining the Tresca stress measure, we note that the stress at these regions is much higher than anywhere else in the material, so selecting other failure criteria will ultimately result in the same conclusion. Therefore, during centrifugation the gel first breaks near the equatorial surfaces.
, where the gel experiences uniaxial compression and tension, respectively. Notably, the highest stress regions occur closest to the sphere's surface at the equator (θ = 90°), where the deformation mode is simple shear. Although we reach this conclusion by examining the Tresca stress measure, we note that the stress at these regions is much higher than anywhere else in the material, so selecting other failure criteria will ultimately result in the same conclusion. Therefore, during centrifugation the gel first breaks near the equatorial surfaces.
Because the point of failure occurs at a region experiencing simple shear, we can potentially determine the correct mechanical property corresponding to the critical centrifugal stress by comparing the stress fields to a shear rheology experiment. The shear stress at the equatorial surfaces is given by,
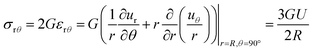 | (5) |
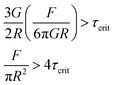 | (6) |
| σcent > 4τcrit | (7) |
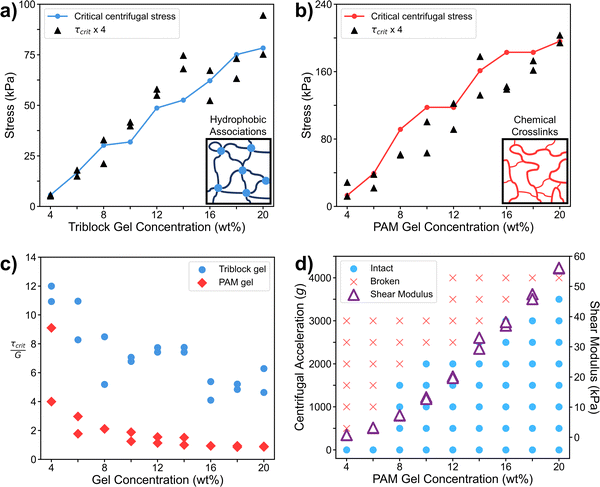
We can test this key prediction by performing shear rheology on triblock gels over the same range of concentrations as in the centrifugal experiment. We interpret our centrifugal method as a quasi-static test, as stress is ramped up during startup until fracture occurs at maximum stress. Because of this, we chose to compare our centrifugal results to those from a static shear stress growth rheology experiment. We found that the critical σcent values from Fig. 3 are readily superimposable with the results from the rheometer, linearly shifted by the factor of 4 from eqn (7) (Fig. 5a). This agreement is remarkable and worth additional emphasis, as the prediction from our analysis was confirmed with no fitting parameters, and the centrifugal test indeed quantitatively measures the shear fracture stress of the gels. To further confirm this, we performed both centrifugal and shear rheology tests over a range of hydrogels composed of chemically crosslinked polyacrylamide (PAM). This new system was selected as a completely different category of soft material compared to the triblock gels, using water vs. organic solvents, crosslinked through covalent bonds vs. physical associations, and containing different microstructures and fracture mechanisms. However, the agreement between the two techniques was similarly striking in the PAM hydrogels (Fig. 5b), confirming that our centrifugal method and its analysis are extremely robust, even for quantitative measurement.
The success of our centrifugal method requires that there is no debonding between the gel samples and the bottom of the well plate. If debonding were to occur, failure would be observed at an artificially low centrifugal speed because the particles would never penetrate through the gel. Several scenarios could potentially cause debonding or similar behavior. Larger amounts of sample in each well results in larger centrifugal forces at the sample-plate interface, causing adhesive failure at the interface or cohesive failure in the material if this force exceeds the tensile strength of the gel. We took pains to avoid this in our experiments (Fig. S6, ESI†). An excessive number of particles could also cause debonding, by adding to the sample mass during centrifugation, and potentially introducing unnecessary defects at the sample-plate interface. We investigated this effect by confirming that the critical centrifugal stress is similar for a single particle in a well vs. several particles (Fig. S1 and S2, ESI†), though we never explored a full layer of particles covering the bottom of the well plate. Finally, debonding is obviously problematic when there is poor adhesion between the materials comprising the sample and the well plate. In our triblock gel system, this material naturally adheres to common polypropylene plates, and no debonding was observed. In PAM hydrogels, the water-based materials do not easily adhere to plastic, so debonding is potentially a severe issue.
To avoid debonding during centrifugation of our PAM hydrogels, we used separable glass-bottomed plates, which were surface-functionalized with methacrylamide groups that covalently bond with the network (Fig. S7, ESI†). Our solution here is widely applicable to other classes of soft materials, as other functionalization schemes could be easily adapted by choosing a silane coupling agent that can bond to the chosen material. For some systems, storing the functionalized plates in a cool, dry environment is required to ensure long-term stability of surface treatment. Using high-density particles such as stainless steel or tungsten carbide is optimal, because the acceleration required to cause fracture is lower, so there is less occurrence of debonding. Moreover, because material fracture occurs rapidly when the critical centrifugal stress is exceeded, it is recommended to utilize short centrifugation periods (30 seconds or less) to avoid placing unnecessary excess stress on the point of adhesion to the plate. While we took pains to avoid debonding of the PAM hydrogel at the bottom of the well plate through surface functionalization, no such effort is necessary for the surface of the particles. This is because the shear stress in the material is maximized at the interface with the spheres, at the equatorial region as our analysis showed (Fig. 4e). Therefore, adhesive failure at the particle-gel interface is indistinguishable from cohesive failure, which would also occur at the same location. Centrifugation thus removes the particles from the material through decohesion.
The serendipitous correlation with shear modulus in the triblock gels (Fig. 2b) can be explained by noting that the ratio of fracture stress to shear modulus at break (i.e. critical strain) in shear rheology happens to be relatively constant with concentration above a certain point (Fig. 5c). Specifically, τcrit ∼ 6G for triblock gels above ∼8 wt%. A similar constant trend is observed in polyacrylamide for higher percentage gels, and thus the shear modulus correlates well to the centrifugal fracture stress in this system as well (Fig. 5d). Therefore, in cases where critical strain is constant, our centrifugal method can also be used as a measure of mechanical modulus, even though it quantitatively measures the fracture stress.
The quantitative agreement between eqn (7) and Fig. 5a and b implicitly assumes that shear stress at the point of failure (shown in Fig. 4e) directly leads to the actual force required to pull the particle out of the gel during centrifugation. This assumption deserves further analysis, particularly as the force to continue pulling the particle through the gel after initial failure, i.e. a propagation force, may also be significant. The propagation of this fracture process is equivalent to the puncture experiments of Fakhouri, et al.,39 where an indenter with a spherical tip is pushed through identical triblock gels as in our experiment. In that study, the indentation fracture stress was determined to be σindent ∼ 10G, where σindent is defined as Findent/πR2, similarly to eqn (1) here. However, our study determined the critical centrifugal stress was σcent ∼ 24G, as this is ∼4 times the τcrit shown in Fig. 5c for the triblock gels. As σcent is significantly larger than σindent which is equivalent to a propagation stress, we confirm that the stress to initiate failure dominates the fracture process, as expected. Our centrifugal method thus measures σcent = 4τcrit as we have defined.
Our method can measure fracture stress over multiple orders of magnitude. Here we show strong agreement between 3 and 50 kPa for PAM hydrogels. However, it is possible to extend the dynamic range of this method even further by using higher density particles, larger particles, or higher centrifugal speeds. For example, a centrifugal test at 4700g with 1.5 mm diameter tungsten carbide particles could reach a centrifugal stress of over 640 kPa, which could break much stronger gels.
To demonstrate the high throughput of our method, we performed a test using every single well of a 384-well plate. We deposited 3 different PAM concentrations with different strengths into a predetermined pattern, and then photographed the plate from the top after multiple spins in the centrifuge (Fig. 6). With four 384-well plates able to fit in the centrifuge, our method can characterize up to 1536 samples at once. Preparing samples and running a full centrifugation sweep across multiple speeds can take up to a few hours, dramatically improving the throughput of mechanical characterization. If more thorough data collection is required, our method can be followed up by classic mechanical testing on a smaller subset of the best performing candidates from our method. In this way, our method is well-suited to complement classic mechanical testing by offering the ability to quickly characterize large libraries of materials at once while requiring only common equipment and inexpensive consumables.
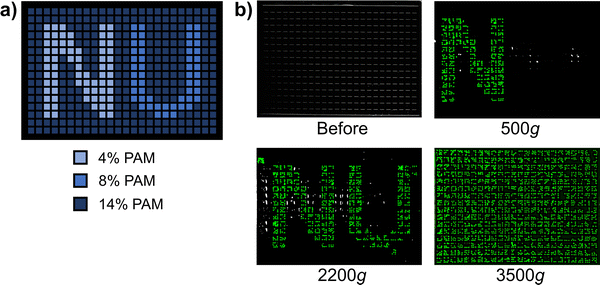 | ||
| Fig. 6 Full 384-well plate centrifugation experiment using 1 mm diameter stainless steel particles. (a) Pre-determined pattern of material samples. 40 μL of polyacrylamide solution at the specified weight percent was added to each well. (b) Photographs of experimental results of full plate experiment. The plate is shown from the top after centrifugation cycles at different speeds, so particles are only visible once they break out of the gel. Particles start at the bottom of the wells, so none are visible prior to centrifugation, and more particles in the pattern become visible at higher speeds. A post-processing algorithm was used to artificially color the particles green for better visibility (Fig. S8, ESI†). | ||
3 Methodology
Materials synthesis
PMMA–PnBA–PMMA copolymer was obtained from Kuraray Co. and used as received. The molecular weight of the PMMA endblocks was 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g mol−1, the molecular weight of the PnBA midblock was 116
000 g mol−1, the molecular weight of the PnBA midblock was 116![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g mol−1, and the polydispersity of the copolymer was ∼1.16. Triblock copolymer was dissolved in 2-ethylhexanol solvent at 140 °C at the desired concentration and subsequently cooled to room temperature to solidify the resulting gels. Polyacrylamide gels of varying concentration were prepared by diluting a 30 wt% stock solution with a 37.5
000 g mol−1, and the polydispersity of the copolymer was ∼1.16. Triblock copolymer was dissolved in 2-ethylhexanol solvent at 140 °C at the desired concentration and subsequently cooled to room temperature to solidify the resulting gels. Polyacrylamide gels of varying concentration were prepared by diluting a 30 wt% stock solution with a 37.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio of acrylamide to bisacrylamide (Bio-Rad). Each polyacrylamide gel additionally contained 0.1 wt% ammonium persulfate initiator (Bio-Rad) in water, and 0.077 wt% tetramethylethylenediamine (TEMED, Bio-Rad). Polyacrylamide gels were left to react for 30 minutes before experimentation to ensure that gelation had finished.
1 ratio of acrylamide to bisacrylamide (Bio-Rad). Each polyacrylamide gel additionally contained 0.1 wt% ammonium persulfate initiator (Bio-Rad) in water, and 0.077 wt% tetramethylethylenediamine (TEMED, Bio-Rad). Polyacrylamide gels were left to react for 30 minutes before experimentation to ensure that gelation had finished.
Centrifugation
Stainless steel particles were purchased in diameters of 0.7 mm (Cospheric Inc.), 1 mm (MSE Supplies LLC), and 1.5 mm (Life Science Products). Tungsten carbide particles (1 mm diameter, MSE Supplies LLC) and yttria-stabilized zirconia particles (0.9–1.1 mm diameter, MSE Supplies LLC) were also purchased. For accurate and consistent results, it is necessary to add only a single layer of particles to each well in the plate. To accomplish this, particles were first poured into each well such that the bottom of the well was completely covered. We then attached a polypropylene adhesive plate seal (Thermo Fisher Scientific) to the top of the plate and inverted it, causing a single layer of particles to stick to the adhesive. Next, we removed this cover and poured out the excess particles from the plate. We then put the adhesive sheet back on the well plate and centrifuged it at 4700g for 30 seconds to get the particles to detach and fall back into the wells, resulting in a single layer of particles in each well.Next, the material samples were added to the wells. PMMA–PnBA–PMMA samples were heated to 140 °C to allow pipetting, and polyacrylamide samples were pipetted immediately after the TEMED was added and before gelation occurred. For 96-well plates (Greiner CELLSTAR® 96 well plates), 100 μL of each sample was added to the well; for 384-well plates (PolyAn), 40 μL of each sample was added to the well. This results in a gel of height ∼2.1 mm above the 1 mm diameter particles in the 96-well plate, and a gel of height ∼2.6 mm above the 1 mm diameter particles in the 384-well plate. After depositing the samples, the plate was covered with a fresh adhesive sheet and left to sit for 30 minutes to allow the samples to solidify before centrifugation was performed.
Centrifugation was carried out in a benchtop centrifuge (Sorvall Legend XFR centrifuge with a TX-750 swinging bucket rotor, Thermo Scientific). After the samples solidified in the covered well plate, a photo was taken of the plate. Then, the plate was placed top-down in the centrifuge, such that the top of the well plate would face outwards while spinning. For the triblock gel with stainless steel particles, we centrifuged the plate at increments of 250g up to 1750g. For the polyacrylamide gel with stainless steel particles, we centrifuged the plate at increments of 500g up to 4000g. In both cases, the centrifuge was run for 30 seconds at each desired speed. After each spin, the plate was removed, and photos were taken of the plate to document the state of each sample. The speed was increased incrementally until all samples were broken.
Particle pulling
Particle pulling was performed using a custom apparatus as described in Wang et al.40 A hole was drilled into a 3 mm diameter stainless steel particle, and a 0.01 inch diameter metal wire was then glued into the hole and connected to the piezoelectric stepping motor of the custom apparatus. The particle and wire were then lowered into a small cubic glass container until the particle was barely touching the bottom. PMMA–PnBA–PMMA triblock gel (7 mL) was heated to 140 °C until it liquified and then poured into the glass container with the particle, resulting in a 15 mm tall gel. After waiting 15 minutes for the gel to cool and fully solidify around the particle and wire, the particle was pulled upwards at 20 μm s−1. The custom apparatus measured the displacement and force at each point using an optical sensor (Philtec) and a load transducer (Honeywell), respectively. The particle was pulled until the gel fractured, at which point a sharp decrease in force was observed.Rheological measurements
Rheological measurements were carried out using a stress-controlled rheometer (DHR-2, TA Instruments, New Castle, DE) at 25 °C with a 25 mm parallel plate geometry with a 500 μm gap. The storage (G′) and loss moduli (G′′) were recorded over a frequency range of 0.1–100 rad s−1 at 5% strain (Fig. S9, ESI†). Stress growth tests were conducted at 0.05 s−1 to obtain the fracture stress and the critical strain of each sample (Fig. S10, ESI†). The fracture stress and the critical strain were recorded at the highest stress reached during the test. Prior to loading the triblock samples, the samples were heated on a hot plate at 155 °C for at least 20 minutes, and the Peltier plate of the rheometer was set to be 95 °C. Samples were then loaded on the rheometer and the geometry gap was set to be 500 μm initially. The Peltier plate was then set to be 25 °C and the axial force control was activated while cooling to compensate for thermal shrinkage. Testing on triblock gels began 10 seconds after the sample reached 25 °C. PAM gel samples were made in situ on the Peltier plate and cured for 30 minutes before testing. Initiator and catalyst were first added to vials containing monomer solutions and mixed before loading on the rheometer. The geometry gap was set to be 500 μm initially, and the gel formed at 25 °C with axial force control activated.Surface functionalization
We purchased separable well plates from PolyAn and Grace Bio Labs. This allowed us to functionalize the glass bottom separately before attaching the plastic wells on top. (3-methacrylamido)triethoxysilane (Gelest) was used as a silane coupling agent for the polyacrylamide gel. First, the glass bottom of the 384-well plates was heated in Piranha solution at 80 °C overnight. Following this, the glass was removed from the solution, rinsed with diH2O, and dried thoroughly. The glass was then submerged in silane coupling agent (5 vol%) in toluene (95 vol%) and heated again at 80 °C overnight. After this, the glass was removed from the solution, rinsed with acetone, and fully dried once more. The plastic wells were then attached to the glass plate bottom with pressure-sensitive adhesive, forming a tight seal.4 Conclusion
We have developed a high-throughput colorimetric centrifugal method to measure the bulk fracture stress of soft materials using only common laboratory equipment and inexpensive consumables. Sample preparation is simple, and the colorimetric results are immediately interpretable by the naked eye. Furthermore, we have been able to better understand the mechanisms of fracture through close observation of a related particle pulling experiment. Most importantly, we can quantitatively correlate our centrifugal measurements to those from a more standard rheometer test without requiring any fitting parameters or calibration. Our method can dramatically cut down on the time required to measure bulk mechanical properties of large sets of materials, helping to alleviate the bottleneck of materials characterization in combinatorial or high-throughput experiments. We hope that our method improves the accessibility of high-throughput mechanical testing, expedites materials discovery and optimization, and inspires the development of additional high-throughput methods to measure other mechanical properties.Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
This work was sponsored by the MRSEC at Northwestern University under NSF Award Number DMR-1720139. J. E. G. acknowledges the generous support of a McCormick summer research grant.References
- S. P. Ong, Comput. Mater. Sci., 2019, 161, 143 CrossRef CAS
.
- K. Kim, L. Ward, J. He, A. Krishna, A. Agrawal and C. Wolverton, Phys. Rev. Mater., 2018, 2, 123801 CrossRef CAS
.
- Y. Liu, T. Zhao, W. Ju and S. Shi, J. Materiomics, 2017, 3, 159 CrossRef
.
- C. Suh, C. Fare, J. A. Warren and E. O. Pyzer-Knapp, Annu. Rev. Mater. Res., 2020, 50, 1 CrossRef CAS
.
- M. Moliner, Y. Román-Leshkov and A. Corma, Acc. Chem. Res., 2019, 52, 2971 CrossRef CAS PubMed
.
- J. Schmidt, M. R. G. Marques, S. Botti and M. A. L. Marques, npj Comput. Mater., 2019, 5, 83 CrossRef
.
- N. Wagner and J. M. Rondinelli, Front. Mater., 2016, 3, 28 Search PubMed
.
- C. B. Wahl, M. Aykol, J. H. Swisher, J. H. Montoya, S. K. Suram and C. A. Mirkin, Sci. Adv., 2021, 7, eabj5505 CrossRef CAS PubMed
.
- R. Potyrailo, K. Rajan, K. Stoewe, I. Takeuchi, B. Chisholm and H. Lam, ACS Comb. Sci., 2011, 13, 579 CrossRef CAS
.
- A. J. DeStefano, R. A. Segalman and E. C. Davidson, JACS Au, 2021, 1, 1556 CrossRef CAS PubMed
.
- H. Koinuma and I. Takeuchi, Nat. Mater., 2004, 3, 429 CrossRef CAS PubMed
.
- A. Ludwig, npj Comput. Mater., 2019, 5, 70 CrossRef
.
- A. Kafizas and I. P. Parkin, Chem. Soc. Rev., 2012, 41, 738 RSC
.
- S. Ding, J. Gregoire, J. J. Vlassak and J. Schroers, J. Appl. Phys., 2012, 111, 114901 CrossRef
.
- C. A. Stewart, A. Suzuki, T. M. Pollock and C. G. Levi, Oxid. Met., 2018, 90, 485 CrossRef CAS
.
- J. García-Cañadas and G. Min, Rev. Sci. Instrum., 2014, 85, 043906 CrossRef PubMed
.
- X. Zhang and Y. Xiang, J. Materiomics, 2017, 3, 209 CrossRef
.
- T. Oellers, V. G. Arigela, C. Kirchlechner, G. Dehm and A. Ludwig, ACS Comb. Sci., 2020, 22, 142 CrossRef CAS PubMed
.
- J.-C. Zhao, M. R. Jackson, L. A. Peluso and L. N. Brewer, MRS Bull., 2002, 27, 324 CrossRef CAS
.
- H.-J. Kim, J.-H. Han, R. Kaiser, K. H. Oh and J. J. Vlassak, Rev. Sci. Instrum., 2008, 79, 045112 CrossRef
.
- A. Ludwig, J. Cao, J. Brugger and I. Takeuchi, Meas. Sci. Technol., 2005, 16, 111 CrossRef CAS
.
- B. C. Salzbrenner, J. M. Rodelas, J. D. Madison, B. H. Jared, L. P. Swiler, Y.-L. Shen and B. L. Boyce, J. Mater. Process. Technol., 2017, 241, 1 CrossRef CAS
.
- V. Breedveld and D. J. Pine, J. Mater. Sci., 2003, 38, 4461 CrossRef CAS
.
- R. C. Spero, L. Vicci, J. Cribb, D. Bober, V. Swaminathan, E. T. O’Brien, S. L. Rogers and R. Superfine, Rev. Sci. Instrum., 2008, 79, 083707 CrossRef PubMed
.
- J. Cribb, L. D. Osborne, J. P.-L. Hsiao, L. Vicci, A. Meshram, E. T. O’Brien, R. C. Spero, R. Taylor and R. Superfine, Rev. Sci. Instrum., 2015, 86, 023711 CrossRef PubMed
.
- K. Joyner, S. Yang and G. A. Duncan, APL Bioeng., 2020, 4, 041508 CrossRef CAS PubMed
.
- Y. Ding, H. Tang, C. Zhang, W. Li, G. Li, Y. Zhang, C. Xu, F. Zhao, Q. Guo, C. F. Guo and X.-D. Xiang, Adv. Funct. Mater., 2021, 31, 2100489 CrossRef CAS
.
- E. Wang, M. S. Desai and S.-W. Lee, Nano Lett., 2013, 13, 2826 CrossRef CAS PubMed
.
- A. J. Silvaroli, T. R. Heyl, Z. Qiang, J. M. Beebe, D. Ahn, S. Mangold, K. R. Shull and M. Wang, ACS Appl. Mater. Interfaces, 2020, 12, 44125 CrossRef CAS
.
- F. Xu, B. Corbett, S. Bell, C. Zhang, M. Budi Hartono, Z. J. Farsangi, J. MacGregor and T. Hoare, Biomacromolecules, 2020, 21, 214 CrossRef CAS PubMed
.
- K. Halvorsen and W. P. Wong, Biophys. J., 2010, 98, L53 CrossRef CAS PubMed
.
- D. Yang, A. Ward, K. Halvorsen and W. P. Wong, Nat. Commun., 2016, 7, 11026 CrossRef CAS PubMed
.
- Y. Chen, Q. Wang, C. E. Mills, J. G. Kann, K. R. Shull, D. Tullman-Ercek and M. Wang, ACS Cent. Sci., 2021, 7, 1135 CrossRef CAS PubMed
.
- M. E. Seitz, W. R. Burghardt, K. T. Faber and K. R. Shull, Macromolecules, 2007, 40, 1218 CrossRef CAS
.
-
A. C. Pipkin, Lectures on Viscoelastic Theory, Springer-Verlag, New York, 1986 Search PubMed
.
-
E. M. Furst and T. M. Squires, Microrheology, Oxford University Press, 2017 Search PubMed
.
-
W. M. Deen, Analysis of Transport Phenomena, Oxford University Press, 2011 Search PubMed
.
-
R. M. Jones, Deformation Theory of Plasticity, Bull Ridge Publishing, 2009 Search PubMed
.
- S. Fakhouri, S. B. Hutchens and A. J. Crosby, Soft Matter, 2015, 11, 4723 RSC
.
- Q. Wang, W. B. Griffith, M. Einsla, S. Zhang, M. L. Pacholski and K. R. Shull, Macromolecules, 2020, 53, 6975 CrossRef CAS
.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2mh01064j |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2023 |