Open Access Article
Open Access ArticleUltrafast hot-carrier cooling in quasi freestanding bilayer graphene with hydrogen intercalated atoms†
Sachin
Sharma
a,
Rachael L.
Myers-Ward
b,
Kurt D.
Gaskill
c and
Ioannis
Chatzakis
 *a
*a
aTexas Tech University Department of Physics & Astronomy, Lubbock, Texas TX 79409, USA. E-mail: Ioannis.chatzakis@ttu.edu
bU.S. Naval Research Laboratory, Washington, DC20375, USA
cInstitute for Research in Electronics and Applied Physics, University of Maryland, College Park, MD, USA
First published on 3rd January 2023
Abstract
Femtosecond-THz optical pump probe spectroscopy is employed to investigate the cooling dynamics of hot carriers in quasi-free standing bilayer epitaxial graphene with hydrogen interacalation. We observe longer decay time constants, in the range of 2.6 to 6.4 ps, compared to previous studies on monolayer graphene, which increase nonlinearly with excitation intensity. The increased relaxation times are due to the decoupling of the graphene layer from the SiC substrate after hydrogen intercalation which increases the distance between graphene and substrate. Furthermore, our measurements show that the supercollision mechanism is not related to the cooling process of the hot carriers, which is ultimately achieved by electron optical phonon scattering.
Introduction
For over a decade, graphene has been among the most widely explored optoelectronic materials.1,2 A large number of investigations have established the significance of graphene in photodetection, data communication, biosensors, ultrafast systems and THz technology and more, due to high mobility of the carriers and the strong interaction of light over an extraordinary broad spectral range.1–15 These applications rely on the optoelectronic properties of graphene that are determined by the dynamics of the energy relaxation of the hot carriers. Thus, understanding the mechanisms that contribute to the relaxation processes is pivotal. Because pump-probe spectroscopy is an excellent tool to probe relaxation processes, many experiments exploiting this technique using different combinations of pump and probe wavelengths ranging from visible to terahertz (THz) region have been reported. Such experiments commonly use THz pump-probe spectroscopy where carrier excitation is triggered with an optical or near infrared radiation (NIR) pulse and subsequently the carrier dynamics are observed by recording the THz transmission through the material for different time delays.16–22 Since the THz photon energy is a few meV, this is significantly smaller than the Fermi energy for most graphene samples. Consequently, THz (probe-field) contribution to the carrier excitation can be ignored and the inter-band processes can be exclusively associated with the excitation (pump) pulse. The ultrafast optical-pump THz-probe spectroscopy is a very successful method to study the nonequilibrium dynamics of hot carriers and phonons and has been extensively applied to a wide variety of materials including other carbonic materials such as carbon nanotubes for investigating intraexcitonic transitions23 and phonon dynamics.24 At room temperature, carrier relaxation in graphene is extremely fast and typically occurs on a time scale of a few picoseconds.8,16–20,25–38 When the pump pulse arrives on a graphene sample it creates a highly nonequilibrium “hot” electron distribution, which first relaxes on an ultrafast time scale on order of tens of femtoseconds to a thermalized Fermi-Dirac distribution with a characteristic temperature Te. The relaxation of the hot carriers is primarily controlled by electron–electron (e–e) interactions that are sensitive to the doping. Subsequently electrons slowly cool down, either via coupling to optical phonons (at Γ and K-point of the Brillouin zone) that are coupled to acoustic phonon,39 or by direct coupling of hot electrons to acoustic phonon40 giving large decay times (few hundred ps that are not relevant to our observations). Additional studies at low electron temperatures emphasized the role of the disorder as a source of momentum needed for direct coupling of hot carriers to acoustic phonons via supercollision (SC) scattering.27,41–44 Another scenario for cooling includes the interaction of hot carriers with phonons of a polar substrate.45 In the optical pump THz-probe experiment the relative long THz-pulse width (∼1 ps) compared to the carrier–carrier scattering time of a few hundred fs cannot be resolved. Instead, the long decay of the quasi-equilibrium Fermi–Dirac distribution can be effectively probed. Various experimental studies have been also conducted using this method to investigate the sign of the transient conductivity from hot carriers and the role the Fermi energy plays in the relevant process. These experiments utilize THz photoconductivity deduced from THz transmission among pumped and unpumped high-mobility graphene samples16,20 and have shown that THz photoconductivity can both be negative and positive. Shi et al.,16 demonstrated that hot carriers in graphene lead to an unusual conductivity behaviour that can be switched from semiconductor-like to metal-like response depending on the doping level of the sample. It has been also showed by Tierlooij et al.,46 that induced THz transient transparency can be obtained by heating the carriers in graphene using optical excitation, and Jnawali et al.,18 showed that within the Drude model, this increase in the THz transmission is due to the increased scattering rate of hot electrons. It was claimed that these observations were due to optical phonon scattering and carrier heating effects, however, a full justification is lacking. These claims were addressed in a comprehensive study by Tomadin et. al.,17 where carrier dynamics and photoconductivity of graphene were reported for varying Fermi energies. Tomadin concluded that the sign of photoconductivity is determined by the type of electronic transitions. In case of low EF, interband transitions dominate over intraband transitions and vice versa is true for high EF. Winnerl et al.,30,47 performed diverse experiments using multilayer epitaxial graphene (70 layers) with different combinations of pump and probe pulses ranging from 10 to 250 meV. They observed a slower relaxation dynamic for excitation energies <160 meV (K-point phonons) above the Fermi energy, but with the optical phonon still playing important role. Mihnev et al.,25 demonstrated that interlayer Coulomb coupling in multilayer epitaxial graphene (more than 60 layers samples were used) provides a cooling mechanism for the hot carriers.25 Also, electrical transport measurements have been used and optical phonon-mediated carrier cooling mechanisms have been identified. However, this mechanism is relevant only for carriers at high temperature. For electron temperatures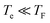 supercollisions plays significant role in the relaxation process.
supercollisions plays significant role in the relaxation process.
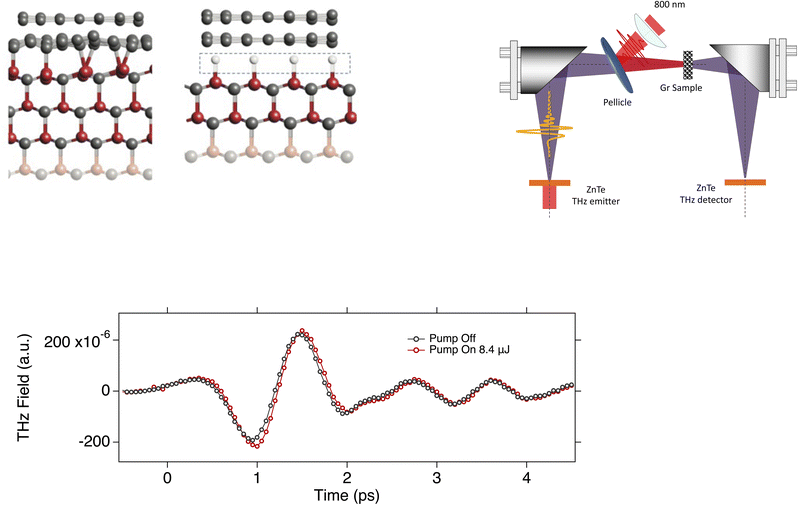
Nonetheless, while the energy relaxation in graphene prepared either by CVD or exfoliation method has been extensively studied, much less literature exist for epitaxial graphene (EG) on SiC substrate. Particularly of interest is hydrogen intercalated EG. For standard epitaxial graphene on the SiC surface, the first graphene layer, called buffer layer or zero-layer graphene (ZLG), is between the SiC substrate and the epitaxial graphene. The ZLG is bound to the SiC substrate (Fig. 1 Top Left) and strongly interacts with the substrate via the pz orbitals thus, the π bands with the characteristic linear dispersion of graphene cannot be developed. A true monolayer of graphene, which possess typical graphene band structure, can be formed on top of the buffer by further annealing of the sample. It has been demonstrated48–50 by different groups that the buffer layer and the monolayer can be decoupled from the substrate by hydrogen atoms intercalation as it is shown in Fig. 1. With the intercalation method, large areas of high-quality quasi free-standing graphene can be produced for practical applications, thus it is critical to understand its carrier cooling mechanisms.
In this work we explore the cooling dynamics of hot carriers in H-intercalated quasi free standing bilayer graphene utilizing ultrafast pump-probe THz spectroscopy. We demonstrate (i) a significant deviation from the supercollision cooling mechanism and, (ii) that the relaxation of the hot carriers mostly occurs due to electron–optical phonon interactions. In accordance with previous measurements, we also observe an increase of the pump induced conductivity, Δσ, and of the relaxation time with the excitation fluence.
In quasi free standing epitaxial graphene, the graphene layer is sitting on top of a graphene-like carbon layer which forms a large unit-cell superstructure with a 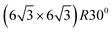 periodicity, called buffer layer or zero-layer graphene (ZLG). The ZLG has same geometrical atomic arrangement as graphene. However, about 30% of the carbon atoms in ZLG, are covalently bound to the top of Si atoms of the SiC surface which prevents the formation of the linear dispersion of π bands typical for graphene, so that the latter cannot be observed by ARPES50 (see Fig. 1(a)). Thus, the ZLG lacks bands with linear dispersion and is electronically inactive. With the penetration of the hydrogen atoms under the ZLG, the bonds between the C and the Si break and the Si dangling bonds are saturated with hydrogen atoms as shown in Fig. 1(a). The Si–H bonds are electronically inactive and the inetrface between SiC–graphene is expected to be defects free. The ZLG turns to quasi free-standing epitaxial graphene (QFSEG) and the monolayer graphene turns to into a decoupled bilayer.51 Presumably the reduced mobility in epitaxial graphene is due to presence of the dangling bonds between the C and Si atoms. By breaking these covalent bonds, a QFSEG that possess the typical graphene structure, can be obtained. Riedl et. al.,50 demonstrated that the elimination of the covalent bonds to decouple the epitaxial graphene layers from the substrate can be achieved by intercalation of hydrogen atoms between the ZGL and the SiC. Because the epitaxial graphene doesn't grow as a simple AB staked graphite films but with high density of rotational faults, the adjacent layers are rotated relative to each other. Hass et. al.,52 demonstrated by first principles calculations that the adjacent rotated layers become electronically decoupled, preserving the linear band structure at the K-point and thus the bilayer graphene behaves as an isolated graphene sheet. Epitaxial graphene on SiC reveals a pronounce n-type doping that can be explained by electron transfer from, interface (SiC/graphene) density of states associated with carbon or silicon dangling bonds to the graphene layer.
periodicity, called buffer layer or zero-layer graphene (ZLG). The ZLG has same geometrical atomic arrangement as graphene. However, about 30% of the carbon atoms in ZLG, are covalently bound to the top of Si atoms of the SiC surface which prevents the formation of the linear dispersion of π bands typical for graphene, so that the latter cannot be observed by ARPES50 (see Fig. 1(a)). Thus, the ZLG lacks bands with linear dispersion and is electronically inactive. With the penetration of the hydrogen atoms under the ZLG, the bonds between the C and the Si break and the Si dangling bonds are saturated with hydrogen atoms as shown in Fig. 1(a). The Si–H bonds are electronically inactive and the inetrface between SiC–graphene is expected to be defects free. The ZLG turns to quasi free-standing epitaxial graphene (QFSEG) and the monolayer graphene turns to into a decoupled bilayer.51 Presumably the reduced mobility in epitaxial graphene is due to presence of the dangling bonds between the C and Si atoms. By breaking these covalent bonds, a QFSEG that possess the typical graphene structure, can be obtained. Riedl et. al.,50 demonstrated that the elimination of the covalent bonds to decouple the epitaxial graphene layers from the substrate can be achieved by intercalation of hydrogen atoms between the ZGL and the SiC. Because the epitaxial graphene doesn't grow as a simple AB staked graphite films but with high density of rotational faults, the adjacent layers are rotated relative to each other. Hass et. al.,52 demonstrated by first principles calculations that the adjacent rotated layers become electronically decoupled, preserving the linear band structure at the K-point and thus the bilayer graphene behaves as an isolated graphene sheet. Epitaxial graphene on SiC reveals a pronounce n-type doping that can be explained by electron transfer from, interface (SiC/graphene) density of states associated with carbon or silicon dangling bonds to the graphene layer.
After the intercalation of hydrogen graphene exhibits a strong p-type doping, with a Fermi energy usually few hundreds meV. The change of the doping type from n to p is due to spontaneous polarization53 that it is an intrinsic characteristic of the most SiC polytypes. It should be noted that the type of doping n or p depends on the polytypes of the SiC, e.g. the p-type character vanishes for the quasi free standing graphene when going from the hexagonal SiC to the cubic 3C polytype which is due to spontaneous polarization of the SiC substrate.53
Experimental details
The laser source was a 1 kHz Ti:Sapphire regenerative amplifier system that produced 7 mJ, 100 fs pulses centered at 800 nm. A part of the output of the laser amplifier was used to generate and detect the THz radiation. Quasi-single cycle THz pulses with bandwidth ∼2.3 THz centered at 1.2 THz generated via optical rectification in a 1 mm thick ZeTe (110) nonlinear crystal. The emitted THz radiation was focused on the graphene samples by an off-axis parabolic mirror at normal incidence. The spot size of the THz beam on the sample was about 0.7 mm, measured by the knife-edge method. The transmitted radiation through the sample was collected and refocused by parabolic mirrors onto a second 1 mm thick ZnTe (110) crystal and detected by electro-optic sampling (EOS) method.46 Another part of the laser beam was used as a sampling beam that was scanned via an adjustable optical delay line and was used to sample the temporal electric field profile of the THz transients. Schematic illustartion of the optical-pump THz-probe measurement technique is shown in Fig. 1. All the measurements were performed at room temperature. A phased-locked chopper in combination with a lockin-amplifier was used in the pump path to modulate the beam at 500 Hz to reduce the noise of the signal. The photon energies of the pump pulses we used to excite the graphene samples was 1.55 eV (800 nm) and the excitation fluence in the range of 27 to 270 μJ cm−2. The spot size of the pump beam was 2 mm to ensure uniform excitation of the probed area. The pump-induced changes in the THz transmission were measured by scanning a second optical delay line that introduces a time-delay between the near infrared (NIR) pump pulse and the maximum amplitude of the THz probe pulses.The samples we used in this study was pH-doped quasi freestanding epitaxially grown bilayer graphene on hexagonal SiC semi-insulating substrate with hydrogen intercalated atoms. To determine the sheet carrier density and mobility, we performed Hall measurements (see ESI†) and found (9.14 ± 0.11) × 1012 cm−2 and determined μ = (4291 ± 66) cm2 V−1 s−1 respectively that are typical values for quasi free standing bilayer graphene on 6H–SiC substrate.54,55 The carrier density we found corresponds to Fermi energies EF = 0.38 eV.
Results and discussion
To characterize the THz conductivity of the unexcited sample we recorded the time dependent THz electric fields transmitted through the quasi-freestanding graphene on the SiC substrate denoted as Egr(t), and through of a blank SiC substrate similar to the one used for the graphene, denoted Eref.(t) in order to normalize the data. Typical time-domain THz electric-fields transients Egr(t) and Eref.(t) are shown in Fig. 1. The THz field complex transmission coefficient T*(ω) is obtained from the ratio between the two Fourier transformed spectra Egr(t) and Eref.(t). We derive the complex transmission coefficient as T*(ω) = |T (ω)|eiφ (ω), where |T (ω)| and φ(ω) are the amplitude and the phase, respectively. Applying the thin-film approximation,1–3 we have,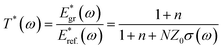 | (1) |
In eqn (1), n = 3.124 is the refractive index of the SiC substrate. The number of the graphene layers is denoted by N, and Z = 377 Ω is the vacuum impedance. To get insight into the graphene response under photoexcitation conditions a pump pulse was focused on the graphene at a spot size of 2 mm determined by a metallic aperture placed in front of the sample. The pump photon energies Eph was 1.55 eV to excite electrons/holes in conduction/valence band states with energies |Eph| above/below the Dirac point. We probe the pump-induced change in the transmission of the THz pulse after a time delay of ∼400 fs that is much longer than the thermalization time of the electronic distribution, so the electronic system is in a quasi-equilibrium state. To obtain the photoinduced conductivity of the graphene samples, we directly recorded the pump-induced changes of the THz-waveform peak amplitude transmission (ΔT(t)/T0) = (TPump ON − TPump OFF)/TPump OFF, by placing the chopper in the pump path and normalized to the THz transmission without photo-excitation. For thin samples the differential transmission (ΔT/T0) is related to the photoinduced conductivity by the relation.18
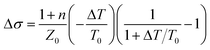 | (2) |
The negative change of the transmission (−ΔT/T0) we measured here indicates Δσ > 0, i.e. the conductivity increases as a result of the photoexcitation, similar to what has been observed in previous studies on monolayer graphene.16 However, in contrast to previous studies on monolayer graphene, our measurements do not show that the supercollision mechanism is relevant to the cooling process of the hot carriers, as it will be discussed later in details. To investigate the relaxation dynamics in graphene we record the ΔT(t) as a function of probe delay time τ. Fig. 2 illustrates the corresponding data. For all excitation fluences we used in this study the THz transmission increases rapidly in about 1 ps after photoexcitation and then recovers the initial value within few picoseconds. The max amplitude of the corresponding photoinduced conductivity extracted form Fig. 2 (Right panel) is also shown in Fig. 3(d). The decrease of the transparency of the graphene after the photoexcitation corresponds to an increase of the conductivity due to the increase of the conducting carrier concentration. This effect occurs in conventional semiconductors with photoexcitation. However, the opposite effect has also been observed where the increase of the ΔT results in decreased conductivity, which is due to increased carrier scattering rate.18 In the context of the electronic temperature, in conventional semiconductors the increase of the Te implies increase of the conductivity through the increase of the Drude weight D. In graphene the Drude weight D is given by
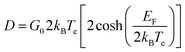 | (3) |
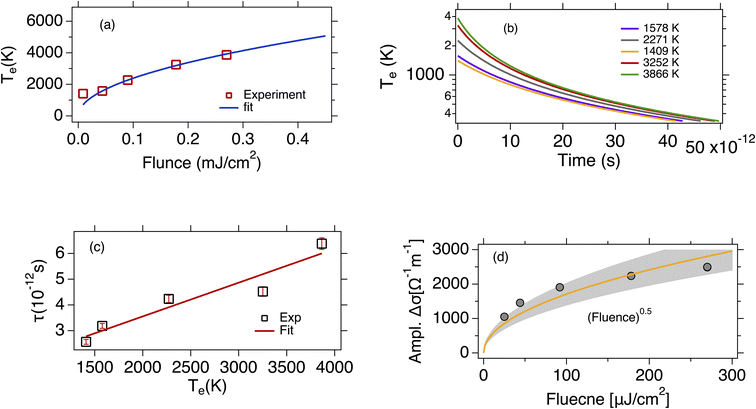 | ||
| Fig. 3 (a) The initial electron temperature is plotted as a function of the excitation fluence. The blue line is the fit with the square root function. (b) The dynamics of the electron temperature calculated from eqn (5) (see text) as a function of the time delay in a semi log plot. Different color represents different initial temperature of the electrons. The significant deviation of the disorder-assited cooling of carriers model (supercollisions mechanism) from the monoexponental function, confirms that the supercollisions is not the dominant mechanism in the cooling process. (c) The carriers cooling time plotted as a function of the electron initial temperature. The red solid line is a linear fit to the experimental data, (d) the max amplidute of the pump induced conductivity is plotted as afunction of the excitation fluence. The data are fitted with the square root function shown by the yellow solid line and the gray shaded area is the confidence interval. | ||
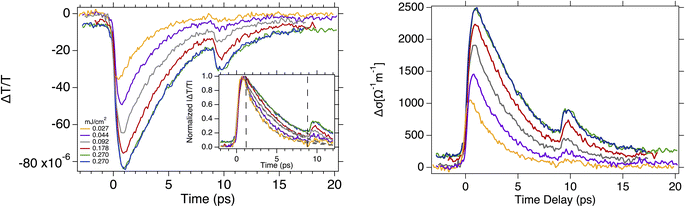
The contributions from the Drude weight and the scattering rate depends on the initial Fermi energy and a positive or negative conductivity. In Fig. 2 (Left) are depicted typical results of the time-domain transient transmission of THz pulses through graphene at different excitation fluences ranging from 27 to 270 μJ. The dynamical traces we recorded show sub picosecond rise time followed by few picoseconds decay time. The experimental data were fitted using a mono-exponential function −ΔT/T0 = C exp (−t/τd) where, τd is the cooling time constant that we found it as of 2.6 to 6.4 ps for the lowest and highest excitation fluences we used, respectively. The longer decay constant observed here is due to hydrogen intercalation that causes the decoupling of graphene and, its vertical displacement by ∼0.21 nm48 from the SiC substrate. Mihnev's et. al.,25 demonstrated that the heat transfer from one layer graphene to another is due to the coulomb interaction between electrons in different layers, and that a decoupling of the layers will lead to the reduced heat transfer rate. Thus, the reduced coupling due to broken covalent bonds between the graphene and the substrate we observed in our samples, naturally causes a decrease in the cooling rate. The secondary peak at about 10 ps is due to round trip of the excitation pulse inside the SiC substrate that re-excites the graphene. As seen at ∼10 ps where the secondary peak rises, the cooling of the carriers has not be completed. Thus, to deduce the decay time constants we limit the exponential fit to the time window between ∼1 ps to ∼9 ps excluding the secondary peak, in order to avoid any influence on the dynamics from the back-reflected excitation pulse. As shown in Fig. 2 (Left) in the first ∼1 ps the negative terahertz transmission ΔT/T decreases after photoexcitation, but the corresponding conductivity increases (increase of D) and has a positive sign. This is mainly due to two reasons. First, the increases the conductivity is due to the higher density of free carriers in the conduction band created by photoexcitation. Second, due to the temperature dependence of the conductivity, the absorption of the pump energy causes an increase in the temperature of the electrons leading to a higher conductivity (see eqn.(3)).
Beyond few picoseconds a decrease in the photogenerated carrier density occurs as the carriers cool down, that results in an increase of the transmission but the opposite occurs in the conductivity as it is shown in Fig. 2 (Right). For excitation energies above the Fermi energy once the quasi-Fermi Dirac distribution is realized after the photoexcitation, it is typical to justify the cooling process predominantly via optical phonons (will be discussed later) rather than acoustic phonons. This is a faster process and at 295 K, is widely reported to take few picoseconds.18 In addition, the relatively weaker acoustic phonon coupling also contributes and leads to significantly longer decay times (hundreds of ps),40 that are not relevant to time scales we deduced in this study. We infer from the experimental data in Fig. 2 longer decay times by more than of a factor of two, comparable to the decay times observed in monolayer graphene in previous studies.34 In our quasi-free-standing graphene samples, due to presence of the intercalated hydrogen atoms, there are not additional bonds between ZLG and SiC substrate, a decoupling between graphene and substrate occurs converting the ZLG into a new graphene layer as shown in Fig. 1. The same reason applies for the weak or even non-existent contribution of the substrate phonons to the cooling process of the energy of the hot carriers.
To get further insight into hot carriers cooling we examine the fluence dependence of the photoinduced THz conductivity Δσ. Based on our experimental conditions, Δσ is proportional to the electron temperature. Using the electronic heat capacity Ce and assuming a small fraction η of the incident power density is absorbed by the sample, we can calculate the initial hot electron temperature Te. For highly doped graphene we have 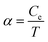 with
with 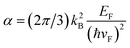 , which is the heat capacity coefficient. Then for the hot electron temperature
, which is the heat capacity coefficient. Then for the hot electron temperature
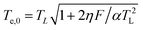 | (4) |
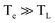 we then infer ΔTe∝F1/2. As it is illustrated in Fig. 3(a) our experimental data show a nonlinear dependence of the electron temperature on the excitation fluence that is scaling as F1/2.
we then infer ΔTe∝F1/2. As it is illustrated in Fig. 3(a) our experimental data show a nonlinear dependence of the electron temperature on the excitation fluence that is scaling as F1/2.
We now consider an intrinsic mechanism of cooling of the hot carriers in graphene. In graphene the strong electron–optical phonon coupling results in a very efficient channel that the hot carriers lose their energy by emission of optical phonons at the K and Γ points of the Brillouin zone with energies ∼160 meV and 196 meV respectively, the so-called strong coupled optical phonons (SCOPs). The hot carriers with energy ≥160 meV can efficiently lose their energy through the electron–optical phonon interactions that results in a rapid decrease of their temperature Te within few hundreds of femtoseconds. This produces a significant non equilibrium phonon population that subsequently decays towards lower energy acoustic phonon via anharmonic coupling.39 In the case that the density of the emitted optical phonons is so high, then they cannot completely decay to low energy acoustic phonons, and a phonon bottleneck occurs. Part of their energy is reabsorbed by the electronic system that leads to an increase of the cooling time of graphene hot carriers. An important component in the intrinsic cooling process in graphene is the continuous rethermalization of the electronic gas. That means that the electrons with excess energy larger than the 0.16 eV above the Fermi energy have relaxed by coupling to SCOPs, the remaining electrons will thermalize through carrier–carrier scattering. That enables a continuous emission of optical phonons which operates as a continuous heat sink even at electron temperature of 300 K. The analytical model developed by Pogna et. al.,56 captures the time evolution of this cooling channel. For carriers with excess energies <160 meV with respect the Fermi energy the hot carriers lose their energy by acoustic phonon emission with energy determined by kBTBG per scattering event as it is determined by conservation of momentum. The TBG is the Bloch–Gruneisen temperature57 which is our case is calculated to be 98 K. Furthermore, Song et. al.,27 identified an unconventional, disorder-assisted electron-phonon mechanism that is highly efficient in cooling of carriers, and dominate in a wide range of temperatures. Since then, several groups have observed role of the supercollisions in the cooling process of the hot carriers in graphene.41,42,44 The cooling times increases with decreasing the temperature from ∼10 ps at 300 K to 200 ps below 50 K. In the high temperature limit 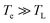 , that characterizes our experiment the time dependent electron temperature Te is given by
, that characterizes our experiment the time dependent electron temperature Te is given by
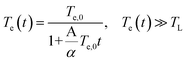 | (5) |
where Te,0 is the initial electron temperature, TL = 295 K is the lattice temperature, and the ratio A/α = 5.49 × 107 K−1 s−1 (the calculation of the ratio A/α is included in the ESI†).27 Using the eqn (4) and (5) we calculated the time dependence of the electron temperature illustrated in Fig. 3(b). However, the dynamics of the photoinduced conductivity, shown in Fig. 2 and described by a single exponential form, is inconsistent with the temperature dynamics shown in Fig. 3(b). This leads us to the conclusion that the disorder assisted cooling is not the dominant cooling mechanism but can provide a parallel cooling channel of the carriers in time resolved THz spectroscopy experiments. Similarly, Mihnev et. al.,25 also concluded that the disorder assisted cooling of carriers is not the primary cooling process for multilayer graphene. In Fig. 3(c) is depicted the cooling time as a function of the electron temperature. As the electron temperature increases, the cooling time increases as well. A similar trend of the decay time as a function of the excitation fluence has been also observed in chemical vapor deposition grown graphene.21 A reasonable explanation is that the higher the temperature of the electrons, the longer it takes for them to cool down especially in the case that the Fermi energy is not near the charge neutrality point. The shift of the Fermi energy away from the charge neutrality point reflects large density of states that means higher electron heat capacity. Fig. 3(d) illustrates the maximum of the pump induced conductivity extracted from the data in Fig. 2(b). The increase of the conductivity maximum with the fluence is compatible with the corresponding increases of the electron temperatures as shown in Fig. 3(a). The relatively high pump fluence increases the Drude weight which is also expressed in terms of the density of the photogenerated carriers and gives rise to the conductivity. It is shown that the amplitude is ∼ (fluence)1/2 (solid yellow line) as it is expected. Furthermore, the lateral diffusion mechanism that also contribute to the relaxation process of the hot electron temperature is not relevant in the time scale of our measurements. The spot size of the excitation beam is ∼2 mm so the lateral spreading of the excitation heat, despite the large in-plane diffusion rate occurs on a time scale much larger than the time scale we observed here. From the discussion above, we see that the dominant cooling process is the intrinsic cooling mechanism in which highly energetic hot carriers with energies >0.16 eV emit optical phonons.
In conclusion, we employed optical-pump THz-probe spectroscopy to investigate the cooling dynamics of hot carriers in quasi freestanding bilayer epitaxial grown graphene on SiC with H-intercalation. Considering negligible contribution of the substrate's optical phonons to the cooling process along with the inefficient cooling channel by supercollisions, we conclude that the cooling of carriers is primarily due to intrinsic mechanisms that involves the SCOPs and their subsequent relaxation by lower energy acoustic phonons. Interestingly, our results show a longer cooling time by more than twice the relaxation time observed in monolayer graphene in previous studies. This can be attributed to decoupling of the graphene layers form the SiC substrate due to the broken covalent bonds by the H intercalation. These results are important especially for optoelectronic devices based on quasi free-standing hydrogenated epitaxial graphene as the hot carriers can retain their energy longer time before cooling down, which is pivotal for processes such as energy transfer, high-field electron transport, and thermoelectric effect.
Methods
Sample preparation
The growth of the bilayer graphene samples was conducted on a semi insulating 6H–SiC(0001), <0.2 deg off-axis substrate. Prior to growth, the sample was etched in H2 during the ramp to growth temperature (1580 °C, 200 mbar) process to remove any polishing damage and prepare the surface for epitaxial graphene growth. Once the temperature was reached, epitaxial graphene was synthesized in 10 slm Ar at 100 mbar for 20 min. After growth, the sample was cooled to 1050 °C and H2 replaced Ar to perform H intercalation using 80 slm H2 at 950 mbar for 60 min. During the H intercalation process, the buffer layer which is present in epitaxial graphene converts to a second graphene layer, making a quasi-freestanding bilayer epitaxial graphene. A similar method used for the sample preparation in the work.58 The Hall effect measurements of the graphene on semi-insulating SiC were performed on 8 × 8 mm2 samples at room temperature in a van der Pauw configuration. Hall measurements are repeatable and known to be uniform (±10%) over samples synthesized on 100 mm substrates. These measurements are accepted by the graphene synthesis community.58Author contributions
I. C. conceived and supervised the experiments, R. M. W. and D. K. G. synthesized the samples, and performed the hall measurements, I. C. and S. S. carried out the experiment, I. C. wrote the paper, and all authors contributed to improving the manuscript.Conflicts of interest
“There are no conflicts to declare”.Acknowledgements
Ioannis Chatzakis gratefully acknowledges the College of Art & Science, VPR office, and Provost office for their contribution to start-up funding and Rachael L. Myers-Word the financial support from the Office of Naval Research (ONR) for the research performed at the Naval Research Laboratory. We would also like to thank Paola Barbara at Georgetown University for her comments for improving this manuscript.Notes and references
- K. S. Novoselov, et al., Two-dimensional gas of massless Dirac fermions in graphene, Nature, 2005, 438, 197–200 CrossRef.
- Y. Zhang, Y.-W. Tan, H. L. Stormer and P. Kim, Experimental observation of the quantum Hall effect and Berry's phase in graphene, Nature, 2005, 438, 201–204 CrossRef.
- K. I. Bolotin, et al., Ultrahigh electron mobility in suspended graphene, Solid State Commun., 2008, 146, 351–355 CrossRef.
- F. Bonaccorso, Z. Sun, T. Hasan and A. C. Ferrari, Graphene photonics and optoelectronics, Nat. Photon, 2010, 4, 611–622 CrossRef.
- P. Avouris, Graphene: Electronic and Photonic Properties and Devices, Nano Lett., 2010, 10, 4285–4294 CrossRef.
- K. F. Mak, et al., Measurement of the Optical Conductivity of Graphene, Phys. Rev. Lett., 2008, 101, 196405 CrossRef PubMed.
- R. R. Nair, et al., Fine Structure Constant Defines Visual Transparency of Graphene, Science, 2008, 320, 1308 CrossRef CAS PubMed.
- J. M. Dawlaty, et al., Measurement of the optical absorption spectra of epitaxial graphene from terahertz to visible, Appl. Phys. Lett., 2008, 93, 131905 CrossRef.
- H. Yan, et al., Infrared Spectroscopy of Wafer-Scale Graphene, ACS Nano, 2011, 5, 9854–9860 CrossRef CAS.
- M. C. Lemme, T. J. Echtermeyer, M. Baus and H. Kurz, A Graphene Field-Effect Device, IEEE Electron Device Lett., 2007, 28, 282–284 CAS.
- M. Jablan, H. Buljan and M. Soljačić, Plasmonics in graphene at infrared frequencies, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 245435 CrossRef.
- Y.-M. Lin, et al., 100-GHz Transistors from Wafer-Scale Epitaxial Graphene, Science, 2010, 327, 662 CrossRef CAS.
- L. Ju, et al., Graphene plasmonics for tunable terahertz metamaterials, Nat. Nanotechnol., 2011, 6, 630–634 CrossRef CAS PubMed.
- L. Liao, et al., High-speed graphene transistors with a self-aligned nanowire gate, Nature, 2010, 467, 305–308 CrossRef CAS PubMed.
- Q. Bao and K. P. Loh, Graphene Photonics, Plasmonics, and Broadband Optoelectronic Devices, ACS Nano, 2012, 6, 3677–3694 CrossRef CAS.
- S.-F. Shi, et al., Controlling Graphene Ultrafast Hot Carrier Response from Metal-like to Semiconductor-like by Electrostatic Gating, Nano Lett., 2014, 14, 1578–1582 CrossRef.
- A. Tomadin, et al., The ultrafast dynamics and conductivity of photoexcited graphene at different Fermi energies, Sci. Adv., 2018, 4, eaar5313 CrossRef PubMed.
- G. Jnawali, Y. Rao, H. Yan and T. F. Heinz, Observation of a Transient Decrease in Terahertz Conductivity of Single-Layer Graphene Induced by Ultrafast Optical Excitation, Nano Lett., 2013, 13, 524–530 CrossRef PubMed.
- P. A. George, et al., Ultrafast Optical-Pump Terahertz-Probe Spectroscopy of the Carrier Relaxation and Recombination Dynamics in Epitaxial Graphene, Nano Lett., 2008, 8, 4248–4251 CrossRef PubMed.
- S. Kar, D. R. Mohapatra, E. Freysz and A. K. Sood, Tuning photoinduced terahertz conductivity in monolayer graphene: Optical-pump terahertz-probe spectroscopy, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 165420 CrossRef.
- T. Jia, et al., Role of the Optical–Acoustic Phonon Interaction in the Ultrafast Cooling Process of CVD Graphene, J. Phys. Chem. C, 2021, 125, 27283–27289 CrossRef.
- S. Kar, S. Jayanthi, E. Freysz and A. K. Sood, Time resolved terahertz spectroscopy of low frequency electronic resonances and optical pump-induced terahertz photoconductivity in reduced graphene oxide membrane, Carbon, 2014, 80, 762–770 CrossRef.
- L. Luo, I. Chatzakis, A. Patz and J. Wang, Ultrafast Terahertz Probes of Interacting Dark Excitons in Chirality-Specific Semiconducting Single-Walled Carbon Nanotubes, Phys. Rev. Lett., 2015, 114, 107402 CrossRef PubMed.
- T. Kampfrath, L. Perfetti, F. Schapper, C. Frischkorn and M. Wolf, Strongly Coupled Optical Phonons in the Ultrafast Dynamics of the Electronic Energy and Current Relaxation in Graphite, Phys. Rev. Lett., 2005, 95, 187403 CrossRef.
- M. T. Mihnev, et al., Electronic cooling via interlayer Coulomb coupling in multilayer epitaxial graphene, Nat. Commun., 2015, 6, 8105 CrossRef PubMed.
- R. Bistritzer and A. H. MacDonald, Electronic Cooling in Graphene, Phys. Rev. Lett., 2009, 102, 206410 CrossRef.
- J. C. W. Song, M. Y. Reizer and L. S. Levitov, Disorder-Assisted Electron-Phonon Scattering and Cooling Pathways in Graphene, Phys. Rev. Lett., 2012, 109, 106602 CrossRef PubMed.
- J. C. Johannsen, et al., Direct View of Hot Carrier Dynamics in Graphene, Phys. Rev. Lett., 2013, 111, 027403 CrossRef.
- T. Low, V. Perebeinos, R. Kim, M. Freitag and P. Avouris, Cooling of photoexcited carriers in graphene by internal and substrate phonons, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 045413 CrossRef.
- S. Winnerl, et al., Carrier Relaxation in Epitaxial Graphene Photoexcited Near the Dirac Point, Phys. Rev. Lett., 2011, 107, 237401 CrossRef.
- J. N. Heyman, et al., Carrier heating and negative photoconductivity in graphene, J. Appl. Phys., 2015, 117, 015101 CrossRef.
- D. Sun, et al., Spectroscopic Measurement of Interlayer Screening in Multilayer Epitaxial Graphene, Phys. Rev. Lett., 2010, 104, 136802 CrossRef.
- I. Gierz, et al., Snapshots of non-equilibrium Dirac carrier distributions in graphene, Nat. Mater., 2013, 12, 1119–1124 CrossRef PubMed.
- J. M. Dawlaty, S. Shivaraman, M. Chandrashekhar, F. Rana and M. G. Spencer, Measurement of ultrafast carrier dynamics in epitaxial graphene, Appl. Phys. Lett., 2008, 3, 042116 CrossRef.
- M. R. Amer, A. Bushmaker and S. B. Cronin, The Influence of Substrate in Determining the Band Gap of Metallic Carbon Nanotubes, Nano Lett., 2012, 12, 4843–4847 CrossRef CAS PubMed.
- M. Massicotte, G. Soavi, A. Principi and K.-J. Tielrooij, Hot carriers in graphene – fundamentals and applications, Nanoscale, 2021, 13, 8376–8411 RSC.
- T. Li, et al., Femtosecond Population Inversion and Stimulated Emission of Dense Dirac Fermions in Graphene, Phys. Rev. Lett., 2012, 108, 167401 CrossRef PubMed.
- J. H. Strait, et al., Very Slow Cooling Dynamics of Photoexcited Carriers in Graphene Observed by Optical-Pump Terahertz-Probe Spectroscopy, Nano Lett., 2011, 11, 4902–4906 CrossRef PubMed.
- I. Chatzakis, H. Yan, D. Song, S. Berciaud and T. F. Heinz, Temperature dependence of the anharmonic decay of optical phonons in carbon nanotubes and graphite, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 205411 CrossRef.
- A. C. Betz, et al., Hot Electron Cooling by Acoustic Phonons in Graphene, Phys. Rev. Lett., 2012, 109, 056805 CrossRef PubMed.
- A. C. Betz, et al., Supercollision cooling in undoped graphene, Nat. Phys., 2013, 9, 109–112 Search PubMed.
- M. W. Graham, S.-F. Shi, D. C. Ralph, J. Park and P. L. McEuen, Photocurrent measurements of supercollision cooling in graphene, Nat. Phys., 2013, 9, 103–108 Search PubMed.
- T. V. Alencar, M. G. Silva, L. M. Malard and A. M. de Paula, Defect-Induced Supercollision Cooling of Photoexcited Carriers in Graphene, Nano Lett., 2014, 14, 5621–5624 CrossRef PubMed.
- A. El Fatimy, et al., Effect of defect-induced cooling on graphene hot-electron bolometers, Carbon, 2019, 154, 497–502 CrossRef CAS.
- V. Perebeinos and P. Avouris, Inelastic scattering and current saturation in graphene, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 195442 CrossRef.
- K. J. Tielrooij, et al., Photoexcitation cascade and multiple hot-carrier generation in graphene, Nat. Phys., 2013, 9, 248–252 Search PubMed.
- S. Winnerl, et al., Time-resolved spectroscopy on epitaxial graphene in the infrared spectral range: relaxation dynamics and saturation behavior, J. Phys.: Condens. Matter, 2013, 25, 054202 CrossRef.
- J. D. Emery, et al., Structural consequences of hydrogen intercalation of epitaxial graphene on SiC(0001), Appl. Phys. Lett., 2014, 105, 161602 CrossRef.
- S. Forti and U. Starke, Epitaxial graphene on SiC: from carrier density engineering to quasi-free standing graphene by atomic intercalation, J. Phys. D: Appl. Phys., 2014, 47, 094013 CrossRef.
- C. Riedl, C. Coletti, T. Iwasaki, A. A. Zakharov and U. Starke, Quasi-Free-Standing Epitaxial Graphene on SiC Obtained by Hydrogen Intercalation, Phys. Rev. Lett., 2009, 103, 246804 CrossRef PubMed.
- S. Forti, et al., Large-area homogeneous quasifree standing epitaxial graphene on SiC(0001): Electronic and structural characterization, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 125449 CrossRef.
- J. Hass, et al., Why Multilayer Graphene on 4 H − SiC (0001) Behaves Like a Single Sheet of Graphene, Phys. Rev. Lett., 2008, 100, 125504 CrossRef CAS PubMed.
- J. Ristein, S. Mammadov and Th. Seyller, Origin of Doping in Quasi-Free-Standing Graphene on Silicon Carbide, Phys. Rev. Lett., 2012, 108, 246104 CrossRef CAS.
- J. L. Tedesco, et al., Hall effect mobility of epitaxial graphene grown on silicon carbide, Appl. Phys. Lett., 2009, 95, 122102 CrossRef.
- F. Speck, et al., The quasi-free-standing nature of graphene on H-saturated SiC(0001), Appl. Phys. Lett., 2011, 99, 122106 CrossRef.
- E. A. A. Pogna, et al., Hot-Carrier Cooling in High-Quality Graphene Is Intrinsically Limited by Optical Phonons, ACS Nano, 2021, 15, 11285–11295 CrossRef CAS PubMed.
- J. K. Viljas and T. T. Heikkilä, Electron-phonon heat transfer in monolayer and bilayer graphene, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 245404 CrossRef.
- K. M. Daniels, et al., Narrow plasmon resonances enabled by quasi-freestanding bilayer epitaxial graphene, 2D Mater., 2017, 4, 025034 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Details on the supercollision model. See DOI: https://doi.org/10.1039/d2na00678b |
| This journal is © The Royal Society of Chemistry 2023 |