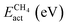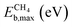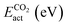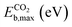Open Access Article
Open Access ArticleStability and reactivity of metal nanoclusters supported on transition metal carbides†
Hector
Prats
 * and
Michail
Stamatakis
* and
Michail
Stamatakis

Department of Chemical Engineering, University College London, Roberts Building, Torrington Place, London WC1E 7JE, UK. E-mail: h.garcia@ucl.ac.uk
First published on 25th May 2023
Abstract
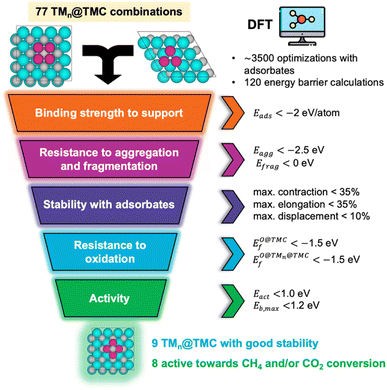
Small particles of transition metals (TM) supported on transition metal carbides (TMC) – TMn@TMC – provide a plethora of design opportunities for catalytic applications due to their highly exposed active centres, efficient atom utilisation and the physicochemical properties of the TMC support. To date, however, only a very small subset of TMn@TMC catalysts have been tested experimentally and it is unclear which combinations may best catalyse which chemical reactions. Herein, we develop a high-throughput screening approach to catalyst design for supported nanoclusters based on density functional theory, and apply it to elucidate the stability and catalytic performance of all possible combinations between 7 monometallic nanoclusters (Rh, Pd, Pt, Au, Co, Ni and Cu) and 11 stable support surfaces of TMCs with 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 stoichiometry (TiC, ZrC, HfC, VC, NbC, TaC, MoC and WC) towards CH4 and CO2 conversion technologies. We analyse the generated database to unravel trends or simple descriptors in their resistance towards metal aggregate formation and sintering, oxidation, stability in the presence of adsorbate species, and study their adsorptive and catalytic properties, to facilitate the discovery of novel materials in the future. We identify 8 TMn@TMC combinations as promising catalysts, all of them being new for experimental validation, thus expanding the chemical space for efficient conversion of CH4 and CO2.
1 stoichiometry (TiC, ZrC, HfC, VC, NbC, TaC, MoC and WC) towards CH4 and CO2 conversion technologies. We analyse the generated database to unravel trends or simple descriptors in their resistance towards metal aggregate formation and sintering, oxidation, stability in the presence of adsorbate species, and study their adsorptive and catalytic properties, to facilitate the discovery of novel materials in the future. We identify 8 TMn@TMC combinations as promising catalysts, all of them being new for experimental validation, thus expanding the chemical space for efficient conversion of CH4 and CO2.
1. Introduction
The abundance of CH4 and CO2, two well-known greenhouse gases, makes them attractive raw materials for the synthesis of fuels and chemicals.1 Large amounts of CH4 are available in nature in the form of natural gas, while substantial amounts of CO2 are generated by human activity, for instance from the combustion of fossil fuels. The conversion of these two gases to produce more valuable chemicals and/or clean fuels is critical to overcoming ever-increasing energy demands and achieving a more sustainable future.2 Methane has a high C–H bond strength of 4.5 eV, and due to the absence of low-energy empty orbitals and high-energy filled orbitals it is a very unreactive molecule, making its activation at low temperature a real challenge.3 There are various processes to convert CH4 into more valuable chemicals and fuels, such as reforming to produce syngas (i.e., a mixture of CO and H2 which can be later transformed to hydrocarbons via the Fischer–Tropsch reaction), the oxidative coupling to produce hydrocarbons, or its conversion to oxygenates. Carbon dioxide, on the other hand, has a C–O bond strength of 5.5 eV and a large negative Gibbs free energy of formation (−394.6 kJ mol−1) which also makes it a very stable and inert molecule. The most promising approach for the conversion of CO2 to more valuable chemicals is the CO2 hydrogenation to alkanes, alkenes or oxygenates.4 In this context, precious metal catalysts have been extensively studied due to their high activities and resistance to carbon deposition,5 but their implementation for industrial application is hindered by their high cost. A way to increase metal atom utilisation and therefore reduce cost is by using supported metal clusters, which possess distinct geometric and electronic structures and thus can exhibit enhanced activity and desired selectivity.6 Transition metal carbides (TMCs) are excellent substrates to disperse metallic particles due to their strong covalent interactions between metal particles and the surface C atoms,7 which immobilise the supported clusters.8,9 For instance, small Ni clusters supported on TiC have been shown to activate CH4 at room temperature,10 and small Au, Cu and Ni particles are more active towards CO2 hydrogenation when supported on TiC than when supported on traditional oxide supports.11 The enhanced activity is attributed to the polarisation that the TMC surface inflicts on the electronic density of the supported particle,8,12 which drastically reduces the dissociation energy barriers for CO2 and H2.13 Unlike traditional support materials which are inert, TMCs exhibit catalytic properties similar to those of Pt-group metals for a wide range of reactions,14 so the deposition of metal particles on TMCs leads to bifunctional catalysts with multiple active sites allowing for cooperative effects.15,16 To our knowledge, however, only the aforementioned four combinations of metal clusters on TMCs have been experimentally tested.In this work, we set out to design novel catalysts for the efficient catalytic conversion of CH4 and CO2 based on transition metal (TM) nanoclusters supported on TMCs, namely TMn@TMC. To achieve this goal, we developed a high-throughput screening approach specifically designed for catalysts consisting of supported nanoclusters and based on density functional theory (DFT). We apply it to assess the stability and reactivity of 77 TMn@TMC systems consisting of small clusters (n = 3, 4) of precious metals (Rh, Pd, Pt and Au) and more affordable metals (Co, Ni and Cu) supported on TMCs with 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 stoichiometry (TiC, ZrC, HfC, VC, NbC, TaC, MoC and WC). Note that Cr carbides were omitted from the screening as they do not form a TMC with 1
1 stoichiometry (TiC, ZrC, HfC, VC, NbC, TaC, MoC and WC). Note that Cr carbides were omitted from the screening as they do not form a TMC with 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 stoichiometry,17 and the reason for not considering other transition metals is simply to keep time and computational resources within reasonable limits, while taking care to explore materials that are representative and relevant to practical applications. For the chosen materials, we evaluate the resistance of the supported clusters against aggregation, fragmentation, and oxidation, and propose two simple descriptors to predict the stability of these clusters in the presence of adsorbates. The potential catalytic activity is then estimated based on the energy barrier of the first rate determining step which, for the case of CH4 and CO2 conversion technologies corresponds to the dissociation of the reactant molecules.
1 stoichiometry,17 and the reason for not considering other transition metals is simply to keep time and computational resources within reasonable limits, while taking care to explore materials that are representative and relevant to practical applications. For the chosen materials, we evaluate the resistance of the supported clusters against aggregation, fragmentation, and oxidation, and propose two simple descriptors to predict the stability of these clusters in the presence of adsorbates. The potential catalytic activity is then estimated based on the energy barrier of the first rate determining step which, for the case of CH4 and CO2 conversion technologies corresponds to the dissociation of the reactant molecules.
The rest of this manuscript is organised as follows. The ‘Computational models and methods’ section describes the bulk and slab models adopted and provides the details of the DFT calculations and the relevant formulae used to estimate all stability, adsorptive and catalytic properties. The ‘Results and discussion’ section begins with an analysis on the energetic stability of the clean catalysts, followed by the evaluation of their stability in the presence of adsorbates, and finishes with the results on the predicted catalytic activity towards CH4 and CO2 conversion along with a selection of the most promising candidates. Finally, in the ‘Conclusions’ section, a brief summary of the main trends and results is provided.
2. Computational models and methods
2.1. Dataset
The present screening focuses on the stability, adsorptive properties, and reactivity of 77 TMn@TMC combinations described in the previous section. For all TMCs under consideration except MoC and WC we have only considered the most stable phase, which corresponds to a fcc crystal packing, with the (001) facet being the lowest energy one.18 For MoC19 and WC,20,21fcc and hcp phases can be synthesised with high stability, so both phases are considered. The (001) facet is the lowest energy one for fcc MoC22 and WC,18 while the most stable facet for their hcp phase is the (0001).20,22 Note that the latter can be terminated with metal atoms or C atoms. For hcp MoC, both Mo- and C-terminated (0001) facets have been theoretically predicted to have similar stability22 and are included in this study, while for hcp WC, the W-terminated (0001) face is significantly more stable than the C-terminated (0001) one,20 so only the C-termination is considered. To ease the notation, the cubic fcc and hexagonal hcp phases for MoC and WC are referred to as cTMC and hTMC, respectively. The size of the metal cluster is 4 atoms on cTMCs and 3 atoms on hTMCs. These sizes feature compact, high symmetry structures that maximise the atomic coordination with the support and are thus likely to be energetically stable. Moreover, previous experimental11,23,24 and theoretical8,10,13 studies have shown that the activity is higher when the size of these nanoclusters is very small (<0.6 nm). Finally, for each TMn@TMC system, the supported cluster can adopt many different configurations (Fig. S2†). In our previous work7 we determined the most stable configuration for each one of the TMn@TMCs. Here, we consider the most stable configuration for each cluster except if it corresponds to a 3D configuration (i.e., tetrahedral), which is the case of 8 systems. In these cases, the high variety of adsorption sites results in complexity during the screening and the subsequent kinetic modelling. Therefore, these systems will not be selected as promising potential candidates. However, we have also included them in the screening for completeness, taking into account their most stable 2D configuration, which in most cases has a similar stability to the tetrahedral one (Table S1†).2.2. Computational details and models
Periodic spin polarised DFT calculations were performed using the Vienna Ab-initio Simulation Package (VASP), version 5.4.4.25 The PBE exchange correlation functional26 was used, which has been demonstrated to provide most accurate results among GGA functionals in describing the atomic and electronic structure of TMCs.27 Dispersion (van der Waals) interactions were included through the D3 method as proposed by Grimme and coworkers.28 Plane-wave kinetic energy cutoffs of 520 and 415 eV were used for bulk and surface calculations, respectively, and the core electrons were accounted for using the projector-augmented wave (PAW) method.29,30 The bulk structures for all TMCs were obtained from the Materials Project open dataset31 (see Table S2†).For bulk geometry relaxation, electronic and force convergence tolerances of 10−6 eV and 10−3 eV Å−1, respectively, were imposed, and a dense Γ-centred k-point grid of 80/a × 80/b × 80/c was used, with non-integer values rounded up to the nearest integer. The slab models for the surfaces were constructed from the optimised bulk structures. For the relaxation of the clean slabs, adsorbed configurations, and transition state calculations, electronic and force convergence tolerances of 10−5 eV and 10−2 eV Å−1, respectively, were imposed, and a Γ-centred k-point grid of 60/a × 60/b × 1 was used, with non-integer values rounded up to the nearest integer. In all systems, the bottom half of the slab in the vertical z-direction was constrained at the bulk positions, while the top half of the slab, the metal clusters and the adsorbed species were fully relaxed. A supercell of 27 Å in the z-direction was used for all slab calculations, ensuring that periodic slab images were separated by at least 18 Å of vacuum, and a dipole correction was applied. Transition states (TS) were located using CatLearn's Bayesian transition state search module (ML-NEB)32 and the vibrational frequencies of the TS were analysed to check that they had only one imaginary mode. The few cases where more than one imaginary mode was found were refined using the improved Dimer method33 and, if needed, further refined with the quasi-Newton algorithm as implemented in VASP, using a more stringent convergence criterion. All crystal structure manipulations and data analysis were carried out using the Python Materials Genomics package (pymatgen)34 and the Atomic Simulation Environment (ASE).35
3. Calculated properties
3.1. Stability of supported clusters
The thermodynamic stability of supported clusters is evaluated by computing the adsorption energy (Eads), aggregation energy (Eagg) and fragmentation energy (Efrag) as follows: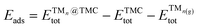 | (1) |
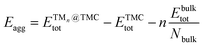 | (2) |
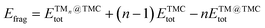 | (3) |
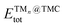 is the total (DFT) energy of the TMC-supported cluster, ETMCtot is the total energy of the clean TMC slab,
is the total (DFT) energy of the TMC-supported cluster, ETMCtot is the total energy of the clean TMC slab, 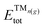 is the total energy of the relaxed cluster in the gas-phase (i.e., vacuum), Ebulktot and Nbulk are the total energy and number of atoms in the bulk metal unit cell, respectively, and ETM@TMCtot is the total energy of a single metal atom on a TMC slab. The adsorption energy is a measure of the binding strength of the cluster to the TMC support, with negative values corresponding to favourable adsorption. On the other hand, the aggregation energy and the fragmentation energy are measures of stability of the supported cluster compared to the bulk metal and the supported single atoms, respectively. Therefore, they can be used as descriptors for resistance to metal aggregate formation (Eagg) and fragmentation (Efrag), with negative values indicating that the cluster configuration is thermodynamically preferred over the bulk and the single atoms, respectively.
is the total energy of the relaxed cluster in the gas-phase (i.e., vacuum), Ebulktot and Nbulk are the total energy and number of atoms in the bulk metal unit cell, respectively, and ETM@TMCtot is the total energy of a single metal atom on a TMC slab. The adsorption energy is a measure of the binding strength of the cluster to the TMC support, with negative values corresponding to favourable adsorption. On the other hand, the aggregation energy and the fragmentation energy are measures of stability of the supported cluster compared to the bulk metal and the supported single atoms, respectively. Therefore, they can be used as descriptors for resistance to metal aggregate formation (Eagg) and fragmentation (Efrag), with negative values indicating that the cluster configuration is thermodynamically preferred over the bulk and the single atoms, respectively.
3.2. Stability of adsorbed species
The formation energy of each adsorbed species is defined relative to the clean slab and a common set of gas-phase molecules (H2(g), CH4(g) and CO2(g)), thereby allowing the stability of different fragments to be compared to one another within the same reference. In the case of a generic adsorbate i, Ei@slabf, is defined as: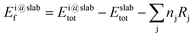 | (4) |
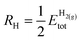 | (5) |
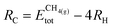 | (6) |
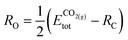 | (7) |
3.3. Reactivity of supported clusters
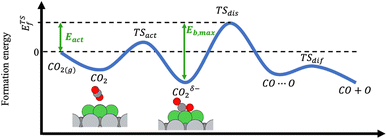
The adsorption and dissociation of CH4 and CO2 on the supported cluster may involve several elementary steps, as illustrated in Fig. 1. For instance, the reactant molecule can approach the cluster and adopt a first physisorbed configuration following a non-activated adsorption step. Then, the substrate can activate it through charge transfer, in the case of CO2 leading to a bent anionic CO2δ− species. Finally, the activated adsorbate dissociates to coadsorbed products but, in some cases, a first metastable configuration (i.e., CH3⋯H or CO⋯O) is adopted, in which both species are very close together, and then they diffuse towards a neighbouring adsorption site adopting a more stable configuration. Typically, the highest-energy TS corresponds to the dissociation step. With all the possible minima and transition state configurations, the definition of the energy barriers is not straightforward. In this work, we define the activation energy of the reaction (Eact) as the relative energy of the highest-energy TS with respect to gas-phase. Because both CH4 and CO2 belong to the reference set of gas-phase molecules used to compute the formation energies, their formation energy in the gas-phase is zero, and Eact can be calculated as:| Eact = max(ETSf, 0) | (8) |
| Eb,max = max(ETSf − Eadsf, 0) | (9) |
3.4. Data sharing
A dataset containing all VASP output files has been made available in the NOMAD repository36 (https://doi.org/10.17172/NOMAD/2023.01.31-1). Moreover, a comma-separated values (CSV) file with the calculated values of all properties has been included in the ESI.†4. Results and discussion
4.1. Stability of the clean catalysts
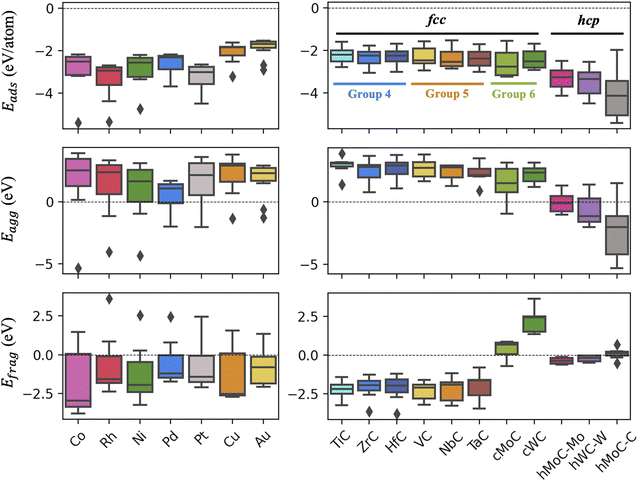
The computed values on the three metrics of stability for the clean catalysts are reported in Fig. 2. All clusters are strongly bonded to the TMC support, with adsorption energies lower than −2 eV per atom in most cases. TM clusters bind more strongly to hexagonal TMCs than to cubic ones, as the latter present more surface states near the Fermi level.37 For the hexagonal surfaces, the most negative Eads values correspond to the C-termination, since TM atoms form stronger bonds with the TMC C atoms than the TMC metal atoms.8 Among the different TMs considered, Cu and Au clusters show the weakest binding to the TMC, presumably due to the fact that both are coinage metals and have filled d states that are lower in energy. Despite the overall strong binding, the aggregation energies are positive for most clusters on cubic TMCs, meaning that the formation of bigger particles is thermodynamically favoured. Even so, the aggregation of clusters might be suppressed by the diffusion barriers which, due to the formation of strong covalent bonds between the cluster atoms and the surface C atoms, are expected to be high. On hexagonal TMCs, clusters are more resistant against aggregation, especially for the case of the C-termination, as the strong TM–C bonds are stronger than the intrametallic bonds within the cluster in big nanoparticles. On the other hand, most clusters present negative fragmentation energies, especially those supported on group 4 and 5 cubic TMCs, while clusters supported on cWC are significantly weak against fragmentation. However, positive Efrag values do not imply a spontaneous cleavage of the clusters, as there is an energy barrier for breaking of the cluster bonds that must be overcame. Note that the left panels in Fig. 2 combine TMn clusters with different nuclearities (n = 3, 4), but the same trends are observed when only considering clusters with the same number of atoms, as shown in Fig. S3.†4.2. Stability in the presence of adsorbates
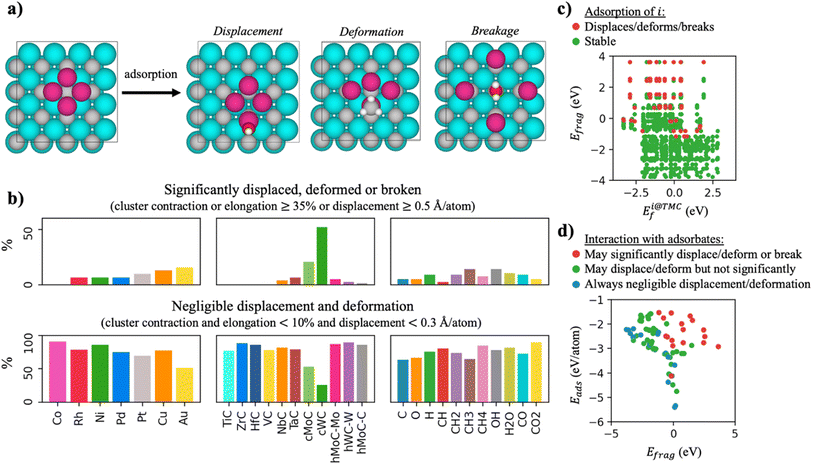
Small, supported clusters do not have the rigidity of larger structures such as big nanoparticles, but are generally labile systems, in which the bonds between the cluster atoms can be extended or contracted to accommodate the different reactants. This lability was predicted to be critical in the strong CH4 adsorption on Nin/TiC,10 but the disadvantage is that sometimes the clusters can deform significantly or even break during the interaction with adsorbed species, as shown in Fig. 3a. In other cases where the cluster is loosely bound to the carbide, interaction with other adsorbates can cause the cluster to be displaced from its original position. It is therefore of critical importance to assess the stability of the cluster in the presence of adsorbates and to identify simple descriptors that can predict it. To assess this issue, we have studied the interaction of the 77 TMn@TMCs with CH4, CO2, H2O, CO, and an array of catalytically relevant molecular fragments (C, CH, CH2, CH3, O, OH and H) and quantified their structural stability by computing the maximum bond contraction and elongation, and the displacement of the cluster from its original position.Fig. 3b shows that the stability depends mainly on the support, and to a lesser extent on the nature of the cluster or adsorbed species. In essence, the most unstable clusters are those supported on fcc WC and MoC, with 52 and 21% of clusters that are broken, deformed, or displaced when interacting with the species considered in this study, and therefore these supports are not suitable for catalysis. Notably, out of all the carbides considered here, these are the only ones that are not found in their most stable crystalline structure, which is hcp (Section 2.1), and thus, they favour the formation of surface C vacancies much more compared to the other carbides (Table S3†). The surface C atom closest to the cluster can rise in the direction perpendicular to the surface to form a strong bond with the adsorbed species, which in many cases deforms or breaks the cluster.
Regarding the nature of the metal cluster, Fig. 3b shows that the tendency to break or significantly deform/displace follows the trend: group 9 (Co, Rh) < group 10 (Ni, Pd, Pt) < group 11 (Cu, Au), and the tendency increases when going down in a group. Thus, Co clusters are always stable (regardless of the carbide support or the adsorbate species), while the clusters with more tendency to displace, deform or break are those of Cu (13%) and Au (16%). Interestingly, Cu and Au are the two metals considered in this study with the lowest bond energies in their bulk phase,38 which could explain why the Cu–Cu and Au–Au bonds within the cluster are easier to compress, elongate or break. Note that the above-mentioned trend is not related to the charge states of the supported clusters, since their oxidation state when supported on the TMC depends on their period (i.e., period VI clusters more electron-rich than period IV) and not the group.7 Finally, the adsorbates that seem to be more detrimental to the stability of the cluster are CH3 and OH, both species having one dangling bond (Fig. 3b, top right panel). Ideally, only those clusters that have negligible deformation or displacement in the presence of reaction intermediates should be selected. In fact, this is the case for the majority of TMnTMC combinations, as shown by the bottom panels in Fig. 3b, with the exception of systems containing Au or hcp TMCs. As expected, the adsorbed species that least affect the integrity of the cluster are CH4, H2O and CO2, since these are stable molecules without dangling bonds that in principle should interact weaklier than the other reaction intermediates.
At this point, the question arises as to whether it is possible to predict the stability of clusters from simple descriptors. Intuition tells us that those clusters in which the atoms are more strongly bonded to each other (as quantified by Efrag) and which in turn are strongly bonded to the support (as quantified by Eads) will be more stable. In addition, those species that interact more strongly with the TMC support will have a greater tendency to break the cluster in order to bond directly to the TMC. The interaction between the adsorbates and the support can be quantified from Ei@TMCf. Fig. 3c demonstrates that indeed, the vast majority of the systems that deform, break, or displace, correspond to those clusters with Efrag > 0 (i.e., single atoms are thermodynamically preferred) and in which the adsorbates interact strongly with the support (Ei@TMCf < 0). Some industrially relevant chemical reactions, however, involve dozens of elementary steps, with a considerable number of intermediate species, and hence it is not practical to compute Ei@TMCf for each species. It is therefore desirable, from a more general perspective, to develop a simple approach to predict which clusters are stable in the presence of any adsorbate species. In Fig. 3d we show that calculations of Eads and Efrag, are already insightful enough in assessing cluster stability in the presence of adsorbates. In the first place, the stability depends on Efrag, and for those clusters with intermediate values of Efrag, it is Eads that determines whether the system will be stable or not. These two quantities can be easily calculated as they do not involve considering the adsorbate species.
4.3. Resistance against oxidation
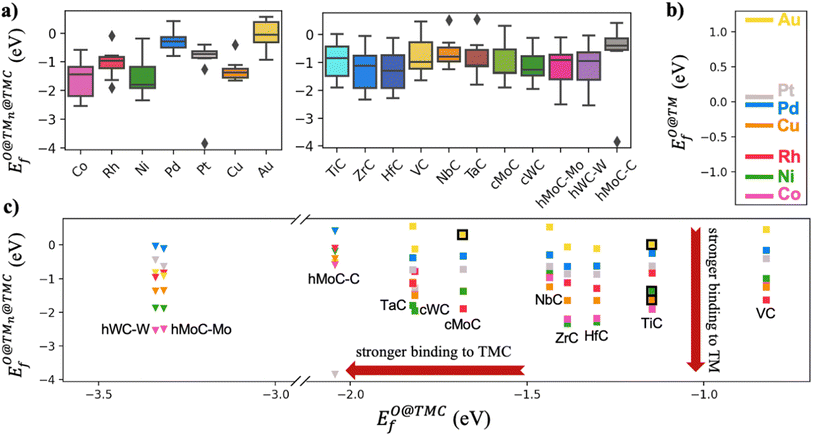
TMCs can be oxidized by air at high temperatures in a process that removes C atoms from the surface and ultimately leads to the formation of oxycarbides,39 drastically modifying their chemical properties.40,41 For instance, oxycarbide formation is known to undermine the Mo2C catalytic performance for the water-gas shift reaction, where O moieties are created from H2O decomposition.42 Porosoff et al.43 showed in an experimental and computational study that the catalytic activity of TMCs for CO2 hydrogenation is correlated to the oxygen binding energy; in particular, carbides that do not bond to O too strongly facilitate oxygen exchange by removal of adsorbed O, therefore increasing the catalytic activity. We have quantified the binding strength of O by computing the formation energies of O on the clean TMCs (EO@TMCf) and on the supported clusters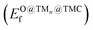 . Although the tendency to form oxycarbides also depends on other factors, the formation energy of O is a simple descriptor that can be considered when screening the vast materials space of TMn@TMCs catalysts for chemical reactions in oxidative environments.
. Although the tendency to form oxycarbides also depends on other factors, the formation energy of O is a simple descriptor that can be considered when screening the vast materials space of TMn@TMCs catalysts for chemical reactions in oxidative environments.
Fig. 4a shows that the binding energy of O on the supported clusters does not depend much on the carbide support but on the nature of the cluster, where the noble metal clusters Au, Pt and Pd exhibit the weakest binding. This result follows the trend of O binding on extended TM surfaces (Fig. 4b), where the weakest binding corresponds to Au(111), followed by Pt(111) and Pd(111). Fig. 4c shows a scatter plot of EO@TMCfversus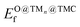 . Ideally, a promising TMn@TMC catalyst should exhibit weak O binding on both the cluster and the support regions (top right corner). The squares highlighted with a black outline correspond to the only TMn@TMCs that, to our knowledge, have been tested experimentally and proven to be stable. Specifically, they were tested for CO2 hydrogenation11 (Aun@TiC, Cun@TiC and Nin@TiC) and the water-gas shift reaction15 (Aun@cMoC), exhibiting catalytic activities that are orders of magnitude higher than those of their corresponding extended TM surfaces. It should be noted that, in some cases, a high O coverage may not be detrimental but even beneficial for its catalytic activity. For instance, Kurlov et al. showed that an O* coverage of ca. 0.7 monolayer provides a high activity of Mo2C MXene (i.e., 2D carbide) in DRM and operating away from this optimal O* coverage decreases the reaction rate.44
. Ideally, a promising TMn@TMC catalyst should exhibit weak O binding on both the cluster and the support regions (top right corner). The squares highlighted with a black outline correspond to the only TMn@TMCs that, to our knowledge, have been tested experimentally and proven to be stable. Specifically, they were tested for CO2 hydrogenation11 (Aun@TiC, Cun@TiC and Nin@TiC) and the water-gas shift reaction15 (Aun@cMoC), exhibiting catalytic activities that are orders of magnitude higher than those of their corresponding extended TM surfaces. It should be noted that, in some cases, a high O coverage may not be detrimental but even beneficial for its catalytic activity. For instance, Kurlov et al. showed that an O* coverage of ca. 0.7 monolayer provides a high activity of Mo2C MXene (i.e., 2D carbide) in DRM and operating away from this optimal O* coverage decreases the reaction rate.44
4.4. Catalytic activity
The potential catalytic activity of TMn@TMCs towards CH4 and CO2 conversion is estimated in terms of their ability to adsorb and dissociate those molecules, as quantified by Eact (eqn (8)) and Eb,max (eqn (9)). A general observation from Fig. 5 is that TMn@TMC structures dissociate CO2 easier than CH4 (i.e., many systems exhibit ETSf < 0 for CO–O, meaning Eact = 0, while only few of them exhibit ETSf < 0 for CH3–H). This can be explained by the ability of CO2 to accept electrons into its lowest unoccupied molecular orbital to form negatively charged bent species (CO2δ−, Fig. 1), resulting in a significant weakening of the C–O bonds due to the π-antibonding occupation of the molecule, while the absence of low-energy empty orbitals in CH4 makes its dissociation more challenging. However, there are more TMn@TMCs with ETSf > 1 eV for CO–O than for CH3–H. These correspond to clusters that cannot bend CO2 by charge transfer, and the higher Ef,TSmax for CO–O is a result of the higher strength of the C–O double bond from linear CO2 compared to the first C–H bond in CH4 (i.e., 5.51 and 4.50 eV, respectively). Therefore, the ability of some clusters and the inability of others to bend CO2 explains why the range of ETSf values shown in Fig. 5a for CO2 is wider than for CH4.Pt clusters are the most active for CH4 and CO2 dissociation, with negative ETSf values or close to 0 (i.e., Eact ∼ 0), making them potential candidates for DRM, where both molecules must be activated. While the vast majority of TMn@TMCs are fairly reactive (ETSf < 0.7 eV), clusters of Cu, Pd and Au are in general less active than the others. In fact, extended Cu(111), Pd(111) and Au(111) surfaces are also among the least active TM fcc(111) facets for CO2 dissociation, while Pt(111) exhibits a moderate activity.45 Regarding the effect of the TMC support, the lowest values of ETSf are exhibited by group 4 TMCs and TaC, as shown in the right panels in Fig. 5a. Interestingly, ETSf seems to decrease when going down a group, so that the most active clusters for each TMC-metal group are in general those supported on period VI TMCs (i.e., HfC, TaC and cWC). This trend can be rationalised based on the electronic charge of the supported clusters as follows. The charge transfer from the TMC to the cluster increases when going down a group (e.g., VC < NbC < TaC) due to the lower electronegativity of the TMC metal atom.7 This excess charge can help activate and dissociate more effectively reactant molecules, especially CO2 by promoting the formation of the bent anionic CO2δ− species. Another interesting observation is that, despite hcp TMC surfaces being more reactive than fcc ones, the metal clusters supported on hcp TMCs are in general less reactive than those supported on fcc, especially for CO2 activation, where clusters supported on hMoC and hWC exhibit the highest ETSf values.
The scatter plot in Fig. 5b shows that there are 5 TMn@TMC combinations were the activation of CH4 and CO2 proceeds with no energy barrier (Eact = 0). These correspond to Ni clusters on ZrC and HfC, and Pt clusters on TiC, HfC and TaC. Apart from these, there are 12 additional TMn@TMCs that can activate CO2 with no barrier, while there is only one other extra system with 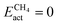 . The activation energy barriers for all systems, along with all other calculated properties, can be found in the CSV file provided in the ESI,† while data for selected systems is summarised in Table 1. As discussed in Section 3, a very low Eact suggests but does not guarantee a high catalytic activity towards CH4 or CO2 dissociation, because Eact is calculated with respect to the gas phase. The dissociation energy barriers from the adsorbed configuration might be high if the adsorbate binds too strongly to the cluster. This is especially important for CO2 dissociation, where the bent CO2δ− configuration might be also very stable. Therefore, we have identified the highest energy barrier (eqn (9)) for each TMn@TMC, and the results are shown in Fig. 5c. Contrary to what is observed for Eact, the number of systems with very low Eb,max (i.e., <0.5 eV) are similar for CH4 and CO2 dissociation, and a total of 4 combinations exhibit Eb,max < 0.5 eV for both processes. Equivalent boxplots to Fig. 5a for Eb,max are shown in Fig. S4.† Finally, it is worth mentioning that, due to the structural complexity of the supported clusters and their great variety of adsorption sites, they do not follow the simple Brønsted–Evans–Polanyi relationships that are found for extended metal surfaces46 (Fig. S5†).
. The activation energy barriers for all systems, along with all other calculated properties, can be found in the CSV file provided in the ESI,† while data for selected systems is summarised in Table 1. As discussed in Section 3, a very low Eact suggests but does not guarantee a high catalytic activity towards CH4 or CO2 dissociation, because Eact is calculated with respect to the gas phase. The dissociation energy barriers from the adsorbed configuration might be high if the adsorbate binds too strongly to the cluster. This is especially important for CO2 dissociation, where the bent CO2δ− configuration might be also very stable. Therefore, we have identified the highest energy barrier (eqn (9)) for each TMn@TMC, and the results are shown in Fig. 5c. Contrary to what is observed for Eact, the number of systems with very low Eb,max (i.e., <0.5 eV) are similar for CH4 and CO2 dissociation, and a total of 4 combinations exhibit Eb,max < 0.5 eV for both processes. Equivalent boxplots to Fig. 5a for Eb,max are shown in Fig. S4.† Finally, it is worth mentioning that, due to the structural complexity of the supported clusters and their great variety of adsorption sites, they do not follow the simple Brønsted–Evans–Polanyi relationships that are found for extended metal surfaces46 (Fig. S5†).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 for Pd and 27
500 for Pd and 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 for Pt
800 for Pt
| TMn@TMC | Stability | Reactivity | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Binding strength | Aggregation | Fragmentation | Oxidation | CH4 | CO2 | ||||
| E ads (eV per atom) | E agg (eV) | E frag (eV) | E O@TMCf (eV) | ||||||
| Pd4@TiC | −2.25 | 1.38 | −1.41 | −0.24 | −1.15 | 0.98 | 1.46 | 0.62 | 1.44 |
| Pd4@ZrC | −2.40 | 0.78 | −1.26 | −0.64 | −1.39 | 0.35 | 0.79 | 0.27 | 1.10 |
| Pt4@ZrC | −3.04 | 1.99 | −1.47 | −0.86 | −1.39 | 0.05 | 0.47 | 0.00 | 0.37 |
| Pd4@HfC | −2.33 | 1.08 | −1.19 | −0.62 | −1.30 | 0.33 | 0.78 | 0.03 | 0.87 |
| Pt4@HfC | −3.01 | 2.11 | −1.42 | −0.87 | −1.30 | 0.00 | 0.43 | 0.00 | 0.29 |
| Ni4@VC | −2.57 | 1.63 | −3.22 | −0.99 | −0.82 | 1.05 | 1.26 | 0.81 | 1.06 |
| Pd4@VC | −2.18 | 1.68 | −1.59 | −0.16 | −0.82 | 0.46 | 0.88 | 0.69 | 1.27 |
| Ni4@NbC | −2.66 | 1.26 | −3.24 | −0.79 | −1.44 | 1.13 | 1.31 | 0.61 | 0.84 |
| Pd4@NbC | −2.25 | 1.37 | −1.72 | −0.28 | −1.44 | 0.56 | 0.90 | 0.49 | 0.78 |
4.5. Novel catalysts for CH4 and CO2 conversion
The selection steps to identify the most promising candidates are illustrated in Fig. 6 and described below. In addition to low Eact and Eb,max values, the potential CH4 and/or CO2 conversion catalysts should be stable against aggregation, fragmentation, oxidation, and displacement/deformation due to interaction with adsorbate species. To integrate all these considerations, we impose the following requirements for promising supported clusters: (i) strong binding to the support, i.e., Eads < −2 eV per atom, (ii) high resistance to metal aggregate formation and fragmentation, i.e., Eagg < 2.5 eV and Efrag < 0 eV, (iii) never displace/deform significantly or break when interacting with adsorbate species, i.e., maximum bond contraction/elongation lower than 35% and maximum displacement lower than 0.5 Å/atom after the adsorption of any of the studied adsorbates, (iv) moderate or low binding to O of the cluster and the support, i.e.,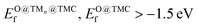 , and (v) modest energy barriers for dissociation of reactant(s), i.e., Eact < 1.0 eV and Eb,max < 1.2 eV. An additional requirement, which is a technical one, is that the most stable configuration must be 2D, as for 3D tetragonal clusters the high variety of adsorption sites triggers the complexity of the reaction profile and subsequent kinetic modelling. Fortunately, the vast majority of supported clusters prefer to adopt a 2D configuration (see Table S1†). Table 1 summarises stability and reactivity data of all TMn@TMCs that meet the requirements (i)–(iv) and hence are predicted to be stable. Among the nine TMn@TMCs with superior stability listed in Table 1, many of them feature promising catalytic activity for CH4 conversion, CO2 conversion or both, and, to the best of our knowledge, none of them have been studied either experimentally or theoretically.
, and (v) modest energy barriers for dissociation of reactant(s), i.e., Eact < 1.0 eV and Eb,max < 1.2 eV. An additional requirement, which is a technical one, is that the most stable configuration must be 2D, as for 3D tetragonal clusters the high variety of adsorption sites triggers the complexity of the reaction profile and subsequent kinetic modelling. Fortunately, the vast majority of supported clusters prefer to adopt a 2D configuration (see Table S1†). Table 1 summarises stability and reactivity data of all TMn@TMCs that meet the requirements (i)–(iv) and hence are predicted to be stable. Among the nine TMn@TMCs with superior stability listed in Table 1, many of them feature promising catalytic activity for CH4 conversion, CO2 conversion or both, and, to the best of our knowledge, none of them have been studied either experimentally or theoretically.
A general observation from Table 1 is that hcp TMCs and Co, Cu, Rh and Au clusters are not included, despite many of them showing very low energy barriers. The main problem is their stability; for instance, hcp TMCs bind O too strongly (Fig. 4c), which can cause O poisoning or full oxidation. The same applies to fcc TaC, MoC and WC. Regarding Au clusters, some of them prefer to adopt a 3D tetrahedral configuration and therefore are excluded, and most of those that adopt a 2D configuration are significantly displaced/deformed or break when interacting with adsorbates (Fig. 3b). For Cu clusters, the main problem is their weak Eads (Fig. 2), which can pose a stability problem. Co and Rh clusters suffer from relatively high Eagg, making them particularly sensitive to deactivation caused by metal aggregate formation, and the ones with the required Eagg < 2.5 eV adsorb O too strongly. Therefore, only some combinations of Ni, Pd and Pt clusters supported on TiC, ZrC, HfC, VC or NbC pass all stability tests. From the 9 stable candidates, all of them except Pdn@TiC show promising catalytic activity towards CH4 conversion, CO2 conversion or both.
Within the CH4-active candidates, Ptn@ZrC and Ptn@HfC have negligible activation energy barriers (0.05 and 0.00 eV, respectively), and the energy difference between the most stable reactant configuration and the highest TS is less than 0.5 eV. All calculated stability metrics for these two materials are almost identical, making them the best candidates for CH4 conversion. The next promising candidates with 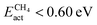 are Pd clusters on ZrC, HfC, VC and NbC. All of them have similar
are Pd clusters on ZrC, HfC, VC and NbC. All of them have similar 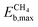 values (i.e., 0.78–0.90 eV), but Pdn@VC has significantly weaker O binding on both the metal cluster and the support. Finally, Ni clusters on VC and NbC are not as active as the previous ones, but they feature excellent resistance to fragmentation (Efrag ≈ −3.2 eV).
values (i.e., 0.78–0.90 eV), but Pdn@VC has significantly weaker O binding on both the metal cluster and the support. Finally, Ni clusters on VC and NbC are not as active as the previous ones, but they feature excellent resistance to fragmentation (Efrag ≈ −3.2 eV).
Amongst the CO2 active candidates, Ptn@ZrC and Ptn@HfC again stand out as the most promising candidates, with 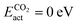 and
and 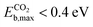 . Due to their excellent stability and activity metrics for both CH4 and CO2 conversion, they are bright candidates for their simultaneous conversion, such as in dry reforming or oxidative coupling of methane. Another potential candidate for CO2 conversion is Pdn@HfC, with has a negligible
. Due to their excellent stability and activity metrics for both CH4 and CO2 conversion, they are bright candidates for their simultaneous conversion, such as in dry reforming or oxidative coupling of methane. Another potential candidate for CO2 conversion is Pdn@HfC, with has a negligible 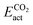 , a slightly higher
, a slightly higher 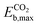 of 0.87 eV and weaker O binding to the cluster. Finally, Nin@NbC and Pdn@NbC can also dissociate CO2 with relatively low energy barriers, with Nin@NbC being extremely resistant to fragmentation (Efrag = −3.24 eV) but Pdn@NbC more resistant to cluster oxidation
of 0.87 eV and weaker O binding to the cluster. Finally, Nin@NbC and Pdn@NbC can also dissociate CO2 with relatively low energy barriers, with Nin@NbC being extremely resistant to fragmentation (Efrag = −3.24 eV) but Pdn@NbC more resistant to cluster oxidation 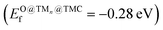 .
.
In addition to stability under reaction conditions and catalytic activity performance, the promising catalysts should be affordable and consist of earth-abundant materials,48i.e., accessible, and free of supply risk, in order to develop large-scale sustainable conversion technologies. These considerations can be included by using the analysis by Gaultois et al.,49 which is based on the crustal abundance of the elements and the Herfindahl–Hirschman index (HHI) as a measure of the concentration or monopoly character of the resources and the market. Among all listed materials in Table 1, Nin@VC and Nin@NbC consist of earth abundant elements only. Despite not being as active as Pt clusters, their moderate activity for the conversion of CH4 and CO2 is compensated by their excellent stability metrics.
5. Conclusions
In summary, we have developed a high-throughput framework to discover stable and active CH4 and CO2 conversion catalysts based on metal nanoclusters supported on TMCs. All clusters bind strongly to the TMC support but, while those supported on fcc TMCs are very resistant against fragmentation and weak against aggregation, the opposite behaviour is observed for clusters supported on hcp TMCs. Weaker binding to O (thereby preventing O poisoning and possible cluster oxidation and/or oxycarbide formation) can be achieved by combining Pd, Pt or Au clusters with group 4 or 5 TMCs. We also observe that those TMn@TMCs not including Au, fcc MoC and fcc WC are in general very stable in the presence of adsorbates, with negligible displacement and deformation. The stability with adsorbates can be predicted from two simple descriptors: the adsorption energy and the fragmentation energy of the clean cluster. Regarding their catalytic activity, many TMn@TMC combinations can dissociate CO2 and CH4 with negligible energy barriers, with Pt clusters being in general the most reactive ones, and those supported on TMCs made from group 4 elements (Ti, Zr and Hf) or Ta. By considering all stability and activity metrics, we identify Pdn@ZrC, Ptn@ZrC, Pdn@HfC, Ptn@HfC, Nin@VC, Pdn@VC, Nin@NbC and Pdn@NbC as promising candidates exhibiting high stability and catalytic performance. Among them, Nin@VC and Nin@NbC stand out as the only candidates that consist of earth abundant elements only. The systematic framework developed in this work is especially designed for supported clusters and can be used for the discovery of other types of functional materials, opening up opportunities towards the development of novel catalysts with superior performance for a wide range of industrially important reactions.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This project has received funding from the European Union's Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie Grant Agreement No. 891756. We gratefully acknowledge the use of the UCL High Performance Computing Facility Kathleen@UCL in the completion of the simulations of this work. We are grateful to the UK Materials and Molecular Modelling Hub for computational resources, which is partially funded by EPSRC (EP/P020194/1 and EP/T022213/1).References
- V. Havran, M. P. Dudukovic and C. S. Lo, Ind. Eng. Chem. Res., 2011, 50, 7089–7100 CrossRef CAS
.
- S. Chu, Y. Cui and N. Liu, Nat. Mater., 2017, 16, 16–22 CrossRef PubMed
.
- P. Tang, Q. Zhu, Z. Wu and D. Ma, Energy Environ. Sci., 2014, 7, 2580–2591 RSC
.
- R. W. Dorner, D. R. Hardy, F. W. Williams and H. D. Willauer, Energy Environ. Sci., 2010, 3, 884–890 RSC
.
- D. Pakhare and J. Spivey, Chem. Soc. Rev., 2014, 43, 7813–7837 RSC
.
- C. Dong, Y. Li, D. Cheng, M. Zhang, J. Liu, Y.-G. Wang, D. Xiao and D. Ma, ACS Catal., 2020, 10, 11011–11045 CrossRef CAS
.
- H. Prats and M. Stamatakis, J. Mater. Chem. A, 2022, 10, 1522–1534 RSC
.
- J. A. Rodriguez, F. Viñes, F. Illas, P. Liu, Y. Takahashi and K. Nakamura, J. Chem. Phys., 2007, 127, 211102 CrossRef CAS PubMed
.
- J. A. Rodriguez and F. Illas, Phys. Chem. Chem. Phys., 2012, 14, 427–438 RSC
.
- H. Prats, R. A. Gutiérrez, J. J. Piñero, F. Viñes, S. T. Bromley, P. J. Ramírez, J. A. Rodriguez and F. Illas, J. Am. Chem. Soc., 2019, 141, 5303–5313 CrossRef CAS PubMed
.
- J. A. Rodriguez, J. Evans, L. Feria, A. B. Vidal, P. Liu, K. Nakamura and F. Illas, J. Catal., 2013, 307, 162–169 CrossRef CAS
.
- P. Lozano-Reis, R. Sayós, J. A. Rodriguez and F. Illas, Phys. Chem. Chem. Phys., 2020, 22, 26145–26154 RSC
.
- P. Lozano-Reis, H. Prats, R. Sayós, J. A. Rodriguez and F. Illas, J. Phys. Chem. C, 2021, 125, 12019–12027 CrossRef CAS
.
- H. Prats, J. J. Piñero, F. Viñes, S. T. Bromley, R. Sayós and F. Illas, Chem. Commun., 2019, 55, 12797–12800 RSC
.
- S. Posada-Pérez, R. A. Gutiérrez, Z. Zuo, P. J. Ramírez, F. Viñes, P. Liu, F. Illas and J. A. Rodriguez, Catal. Sci. Technol., 2017, 7, 5332–5342 RSC
.
- H. Prats, S. Posada-Pérez, J. A. Rodriguez, R. Sayós and F. Illas, ACS Catal., 2019, 9, 9117–9126 CrossRef CAS
.
- Q. Zhang, L. Pastor-Pérez, S. Gu and T. R. Reina, Catalysts, 2020, 10, 955 CrossRef CAS
.
- M. G. Quesne, A. Roldan, N. H. de Leeuw and C. R. A. Catlow, Phys. Chem. Chem. Phys., 2018, 20, 6905–6916 RSC
.
- T. Xiao, A. P. E. York, K. S. Coleman, J. B. Claridge, J. Sloan, J. Charnock and M. L. H. Green, J. Mater. Chem., 2001, 11, 3094–3098 RSC
.
- D. J. Siegel, L. G. M. Hector Jr and J. B. Adams, Surf. Sci., 2002, 498, 321–336 CrossRef CAS
.
- A. M. Nartowski, I. P. Parkin, M. MacKenzie, A. J. Craven and I. MacLeod, J. Mater. Chem., 1999, 9, 1275–1281 RSC
.
- J. R. d. S. Politi, F. Viñes, J. A. Rodriguez and F. Illas, Phys. Chem. Chem. Phys., 2013, 15, 12617–12625 RSC
.
- J. A. Rodriguez, L. Feria, T. Jirsak, Y. Takahashi, K. Nakamura and F. Illas, J. Am. Chem. Soc., 2010, 132, 3177–3186 CrossRef CAS PubMed
.
- J. A. Rodriguez, P. Liu, F. Viñes, F. Illas, Y. Takahashi and K. Nakamura, Angew. Chem., Int. Ed., 2008, 120, 6787–6791 CrossRef
.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed
.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed
.
- P. Janthon, S. M. Kozlov, F. Viñes, J. Limtrakul and F. Illas, J. Chem. Theory Comput., 2013, 9, 1631–1640 CrossRef CAS PubMed
.
- S. Grimme, J. Antony and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed
.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed
.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS
.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, APL Mater., 2013, 1, 011002 CrossRef
.
- J. A. Garrido Torres, M. H. Hansen, P. C. Jennings, J. R. Boes and T. Bligaard, Phys. Rev. Lett., 2019, 122, 156001 CrossRef CAS PubMed
.
- P. G. Henkelman and H. Jónsson, J. Chem. Phys., 1999, 111, 7010–7022 CrossRef
.
- S. P. Ong, W. D. Richards, A. Jain, G. Hautier, M. Kocher, S. Cholia, D. Gunter, V. Chevrier, K. A. Persson and G. Ceder, Comput. Mater. Sci., 2013, 68, 314–319 CrossRef CAS
.
- A. Hjorth Larsen, J. Jørgen Mortensen, J. Blomqvist, I. E. Castelli, R. Christensen, M. Dułak, J. Friis, M. N. Groves, B. Hammer, C. Hargus, E. D. Hermes, P. C. Jennings, P. B. Jensen, J. Kermode, J. R. Kitchin, E. L. Kolsbjerg, J. Kubal, K. Kaasbjerg, S. Lysgaard, J. B. Maronsson, T. Maxson, T. Olsen, L. Pastewka, A. Peterson, C. Rostgaard, J. Schiøtz, O. Schütt, M. Strange, K. S. Thygesen, T. Vegge, L. Vilhelmsen, M. Walter, Z. Zeng and K. W. Jacobsenet, J. Phys.: Condens. Matter, 2017, 29, 273002 CrossRef PubMed
.
- C. Draxl and M. Scheffler, MRS Bull., 2018, 43, 676–682 CrossRef
.
- L. I. Johansson, Surf. Sci. Rep., 1995, 21, 177 CrossRef CAS
.
- J. G. Eberhard and S. Horner, J. Chem. Educ., 2010, 87, 608–612 CrossRef
.
- J. A. Rodriguez, P. Liu, J. Gomes, K. Nakamura, F. Viñes, C. Sousa and F. Illas, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 75427 CrossRef
.
- R. B. Levy and M. Boudart, Science, 1973, 181, 547–549 CrossRef CAS PubMed
.
- F. Viñes, C. Sousa, F. Illas, P. Liu and J. A. Rodriguez, J. Phys. Chem. C, 2007, 111, 1307–1314 CrossRef
.
- P. Liu and J. A. Rodriguez, J. Phys. Chem. B, 2006, 110, 19418–19425 CrossRef CAS PubMed
.
- M. D. Porosoff, S. Kattel, W. Li, P. Liu and J. G. Chen, Chem. Commun., 2015, 51, 6988–6991 RSC
.
- A. Kurlov, E. B. Deeva, P. M. Abdala, D. Lebedev, A. Tsoukalou, A. Comas-Vives, A. Fedorov and C. R. Müller, Nat. Commun., 2020, 11, 4920 CrossRef CAS PubMed
.
- Z. Liu and W. Q. Deng, J. Phys. Chem. C, 2018, 122, 8306–8314 CrossRef
.
- S. Wang, B. Temel, J. Shen, G. Jones, L. C. Grabow, F. Studt, T. Bliggard, F. Abild-Pedersen, C. H. Christensen and J. K. Nørskov, Catal. Lett., 2011, 141, 370–373 CrossRef CAS
.
- Preismonitor report, Federal Institute for Geosciences and Natural Resources, 22 January 2020, Available online at: https://www.bgr.bund.de/DE/Themen/Min_rohstoffe/Produkte/Preisliste/pm_19_12.pdf, accessed 15 May 2022.
- R. M. Bullock, J. G. Chen, L. Gagliardi, P. J. Chirik, O. K. Farha, C. H. Hendon, C. W. Jones, J. A. Keith, J. Klosin, S. D. Minteer, R. H. Morris, A. T. Radosevich, T. B. Rauchfuss, N. A. Strotman, A. Vojvodic, T. R. Ward, J. Y. Yang and Y. Surendranath, Science, 2020, 369, eabc3183 CrossRef CAS PubMed
.
- M. W. Gaultois, T. D. Sparks, C. K. H. Borg, R. Seshadri, W. D. Bonificio and D. R. Clarke, Chem. Mater., 2013, 25, 2911–2920 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3na00231d |
| This journal is © The Royal Society of Chemistry 2023 |