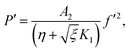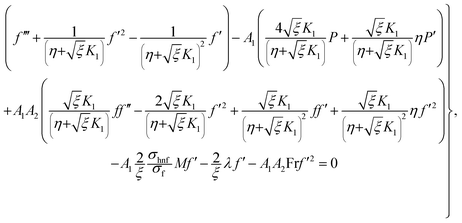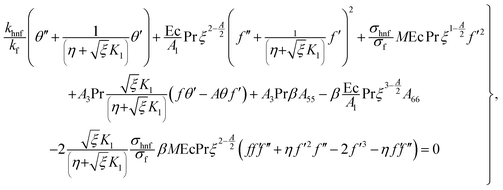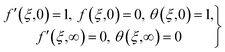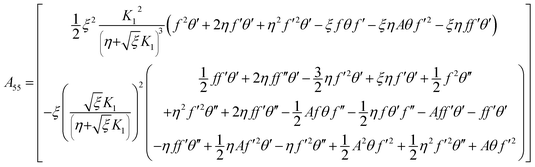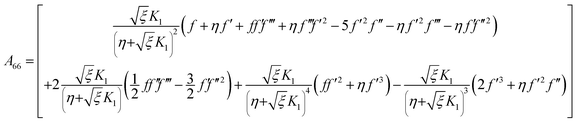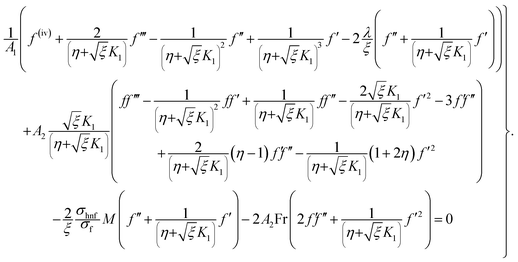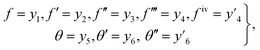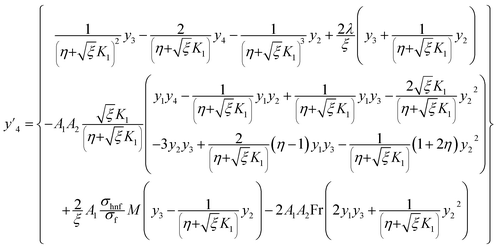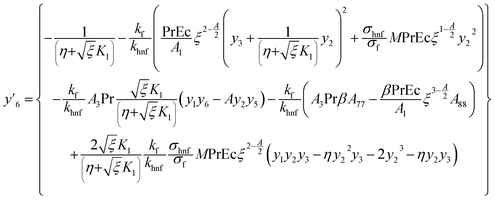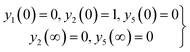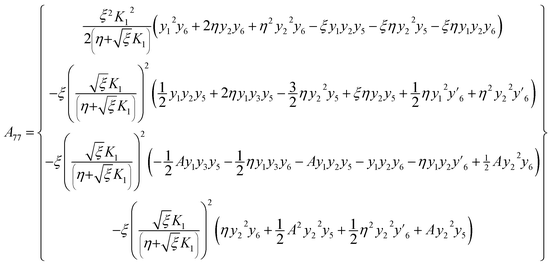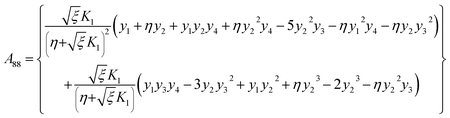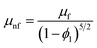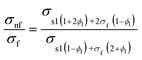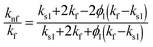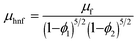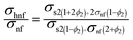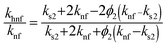DOI:
10.1039/D3NA00453H
(Paper)
Nanoscale Adv., 2023,
5, 4819-4832
Modeling and simulation for Cattaneo–Christov heat analysis of entropy optimized hybrid nanomaterial flow
Received
25th June 2023
, Accepted 7th August 2023
First published on 8th August 2023
Abstract
Here, the hydromagnetic entropy optimized flow of a hybrid (Pb + Fe2O3/C2H6O2) nanoliquid by a curved stretchable surface is addressed. The Darcy–Forchheimer model is utilized for porous space. Lead (Pb) and ferric oxide (Fe2O3) are considered the nanoparticles and ethylene glycol (C2H6O2) as the base liquid. Thermal expression consists of dissipation and ohmic heating. Entropy generation is under consideration. The Cattaneo–Christov heat flux impact is discussed. Non-dimensional partial expressions by adequate transformations have been reduced to ordinary differential systems. The ND-solve technique is implemented for numerical solutions of dimensionless systems. Graphical illustrations of velocity, thermal field and entropy against influential variables for both nanoliquid (Pb/C2H6O2) and hybrid nanoliquid (Pb + Fe2O3/C2H6O2) are presented. Graphical illustrations of velocity, thermal field and entropy against sundry variables for both nanoliquid (Pb/C2H6O2) and hybrid nanoliquid (Pb + Fe2O3/C2H6O2) are presented. Influences of sundry variables on the Nusselt number and drag force for both nanoliquid (Pb/C2H6O2) and hybrid nanoliquid (Pb + Fe2O3/C2H6O2) are examined. A higher thermal relaxation time tends to intensify the heat transport rate and temperature. An increment in the magnetic variable leads to an enhancement of the entropy and thermal field. An improvement in liquid flow is seen for volume fraction variables. Velocity against the porosity variable and Forchheimer number is reduced. The Brinkman number leads to maximization of entropy generation.
1. Introduction
During the past few decades, hybrid nano-fluids have become popular among researchers, scientists and engineers due to their superior heat transport properties. Hybrid nano-fluids are suspensions of two or more nano-particles in the base fluid. The heat conductive performance of convectional materials (like blood, water, engine oil, ethylene glycol, etc.) can be enhanced by inserting nano-particles (like silica, carbon nanotubes, silver alumina, gold, lead, ferric oxide, etc.). Hybrid nano-fluids possess higher thermal conductivity for heat transfer phenomena such as those relevant to engines, vehicle radiators, machining, biomedicine, warming procedure on buildings, hybrid powered engines, pharmaceutical industries, paper production and many others. The concept of heat transport enhancement of the base liquid through addition of nanoparticles was initially given by Choi and Eastman et al.1,2 Hassan et al.3 examined the partial slip effect for the flow of hybrid ferro-liquids. Radiation and porous space effects were addressed. Chabani et al.4 examined the electrically conducting hybrid (Ag–Al2O3/H2O) nanomaterial flow inside a modified trapezoidal permeable enclosure. Thermal transport analysis for hybrid nanoliquids with suction/injection in a rotating system was reported by Abdollahi et al.5 Cattaneo–Christov analysis in the magnetohydrodynamic flow of ternary nanomaterials with nonlinear radiation was studied by Alqawasmi et al.6 Few latest developments related to hybrid nano-fluid flow under different geometric configurations are given in ref. 7–15.
Heat transfer is induced in view of temperature differences and subsequent temperature changes and distribution in different bodies. Heat transfer plays a significant role in industries, and biomedical and engineering processes such as those relevant to heat exchangers, air conditioning, refrigeration, equipment power collectors, fuel cells, drug targeting, microelectronics, heat conduction in tissues, etc. The mechanism of heat transfer was initially given by Fourier.16 Fourier's law through parabolic expression predicts the infinite speed of heat waves. It is not acceptable physically. Therefore the thermal relaxation time was taken into account by Cattaneo.17 For material invariant formulation to the Cattaneo's frame work Christov18 introduced Oldroyd's upper convected derivative. Razaq et al.19 explored the convective flow of the Reiner–Rivlin fluid subject to Cattaneo–Christov fluxes and MHD. Radiation impact for the magnetized flow of Prandtl nanoliquid with Cattaneo–Christov fluxes theory was given by Salmi et al.20 Haneef et al.21 analyzed heat transport for Oldroyd-B material flow with Cattaneo–Christov fluxes. Random motion and thermophoresis effects in magnetohydrodynamic Oldroyd-B nanoliquid flow were studied by Hayat et al.22 Latest articles for Cattaneo–Christov heat and mass fluxes are mentioned in ref. 23–28.
Entropy minimization (EM) optimizes thermal system performance by exploring associated irreversibility through heat and mass transfer, Joule heating and liquid friction. Entropy is a measure of uncertainty and disorderness of a system and its surroundings. All natural processes are thermodynamically irreversible. Entropy is inversely proportional to the temperature of a system. Entropy has a direct proportion to the reversible change in heat. Entropy generation is the loss of energy in thermodynamical systems due to diffusion processes, temperature difference, electric resistance, fluid mixing, chemical reaction, radiation and resistive forces. Applications of entropy generation are found in electronic cooling systems, geothermal reservoirs, thermal and nuclear reactors and heat exchanger pumps. Entropy optimization in thermally convection flow was studied in Bejan.29–31 Iftikhar et al.32 analyzed entropy generation for non-Newtonian biviscosity fluid in a square cavity. Hayat et al.33 addressed the magnetized entropy optimized flow of the Reiner–Rivlin material. Maiti et al.34 reported entropy generation analysis for time-dependent hybrid nanoliquid flow by shrinking a disk. Latest investigations for entropy analysis are highlighted in studies.35–42
This communication discusses the magnetohydrodynamic Darcy–Forchheimer flow of a hybrid nanomaterial. The Cattaneo–Christov heat relation is under consideration. Ferric oxide (Fe2O3) and lead (Pb) are used as nanoparticles. Ethylene glycol (C2H6O2) is used as a conventional liquid. Joule heating and dissipation are considered in thermal relation. Entropy generation analysis is carried out. Governing nonlinear expressions are made dimensionless by implementation of suitable transformations. ND-solve is utilized for numerical solutions. Liquid flow, entropy and temperature for both nanoliquid (Pb/C2H6O2) and hybrid nanoliquid (Fe2O3 + Pb/C2H6O2) are explored. Surface drag force and heat transport rate against emerging variables for nanoliquid (Pb/C2H6O2) and hybrid nanoliquid (Fe2O3 + Pb/C2H6O2) are numerically discussed.
2. Modeling
Two-dimensional magnetized flow of the hybrid (Fe2O3 + Pb/C2H6O2) nanoliquid by the curved stretching surface is addressed. Darcy–Forchheimer model analysis is carried out. Lead (Pb) and ferric oxide (Fe2O3) are used as nanoparticles and ethylene glycol (C2H6O2) as the base liquid. Cattaneo–Christov heat flux with ohmic heating and dissipation is under consideration. Entropy analysis is carried out. The surface has stretching velocity (uw = u0es/L) with u0 reference velocity. The magnetic field of constant strength (B0) is applied. Fig. 1 comprises a physical model.43
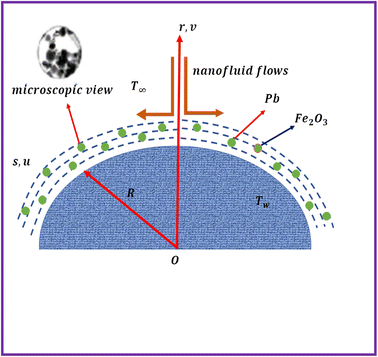 |
| | Fig. 1 Flow sketch. | |
The governing equations satisfy:44–49
| | 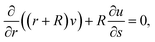 | (1) |
| | 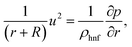 | (2) |
| | 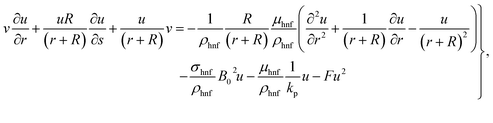 | (3) |
| | 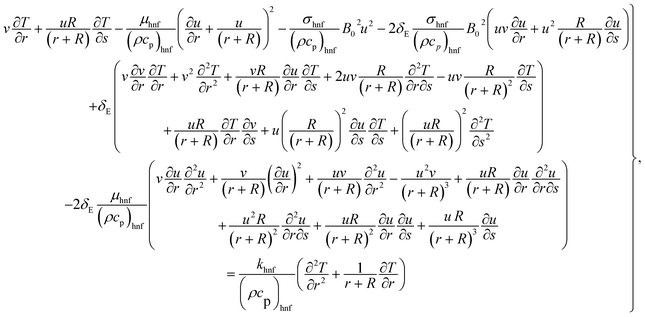 | (4) |
with
50–52| | 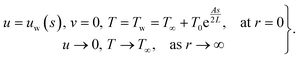 | (5) |
In the above expressions (
u,
v) depict velocity components,
μhnf the dynamic viscosity,
ρhnf the density, (
r,
s) signify the Cartesian coordinates,
σhnf the electrical conductivity,
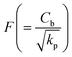
the inertia coefficient,
kp the porous medium permeability coefficient,
R the radius of curvature, (
ρcp)
hnf the heat capacitance,
Cb the drag force coefficient,
L the reference length,
T the temperature,
khnf the thermal conductivity,
cp the specific heat,
T∞ the ambient temperature,
δE the heat relaxation time,
B0 the magnetic field strength,
Tw the wall temperature and
p the pressure.
2.1. Thermophysical characteristics
Mathematical expressions for nanofluid and hybrid nanomaterials and numerical values of conventional fluid and nanoparticles have been given through Tables 1 and 2.53,54
Table 1 Mathematical expressions for thermophysical characteristics53,54
| Properties |
Nanoliquid |
| Viscosity |
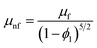
|
| Density |
ρ
nf = (1 − ϕ1)ρf + ϕ1ρs1 |
| Heat capacity |
(ρcp)nf = (1 − ϕ1)(ρcp)f + ϕ1(ρcp)s1 |
| Electrical conductivity |
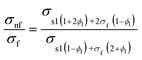
|
| Thermal conductivity |
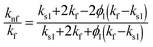
|
| Properties |
Hybrid nanoliquid |
| Viscosity |
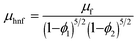
|
| Density |
ρ
hnf = (1 − ϕ2){(1 − ϕ1)ρf + ϕ1ρs1} + ϕ2ρs2 |
| Heat capacity |
(ρcp)hnf = (1 − ϕ2){(1 − ϕ1)(ρcp)f + ϕ1(ρcp)s1} + ϕ2(ρcp)s2 |
| Electrical conductivity |
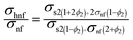
|
| Thermal conductivity |
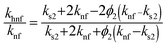
|
Table 2 Thermophysical characteristics of ethylene glycol (C2H6O2), lead (Pb) and ferric oxide (Fe2O3)53,54
| Properties |
ρ (kg m−3) |
k (W m−1 K−1) |
c
p (J k−1 g−1 K−1) |
σ (Ω−1 m−1) |
| Ethylene glycol |
1116.6 |
0.249 |
2382 |
1.07 × 10−7 |
| Lead (Pb) |
11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 343 343 |
35 |
130 |
4.55 × 106 |
| Ferric oxide (Fe2O3) |
5200 |
80.2 |
670 |
0.74 × 106 |
Letting
| | 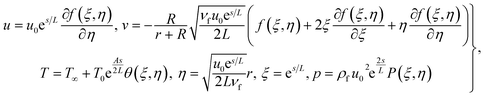 | (6) |
one obtains
| | 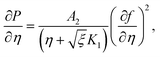 | (7) |
| | 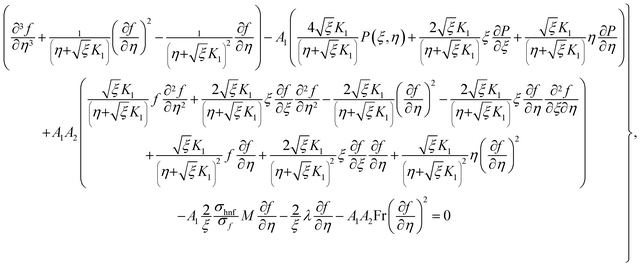 | (8) |
| | 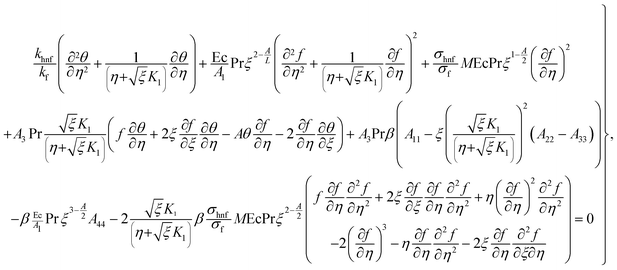 | (9) |
| | 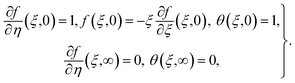 | (10) |
Here
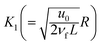
shows the material parameter,
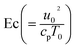
the Eckert number,
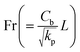
theForchheimer number,
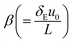
the thermal relaxation time,
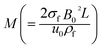
the magnetic variable,
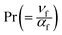
the Prandtl number and
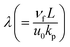
the porosity parameter. Here
A1,
A2,
A3,
A11,
A22,
A33 and
A44 are expressed as
| | 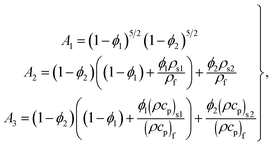 | (11) |
| | 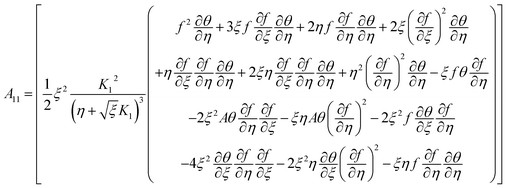 | (12) |
| | 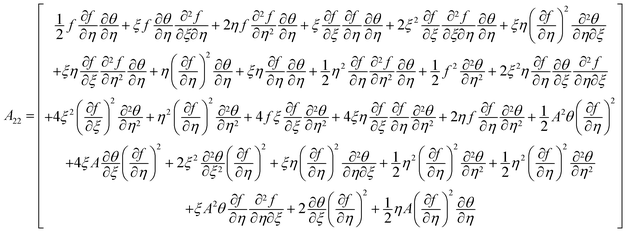 | (13) |
| | 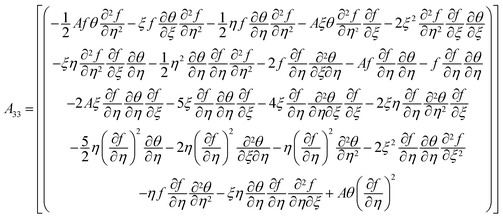 | (14) |
| | 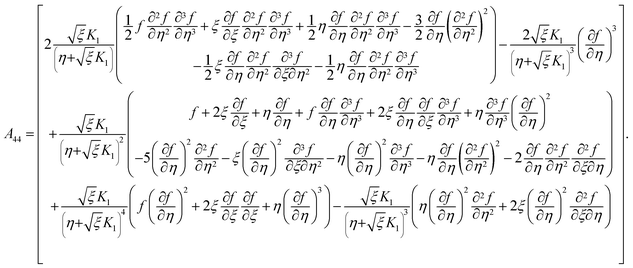 | (15) |
3. Interesting quantities
3.1. Surface drag force
One may write| | 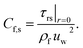 | (16) |
Here τrs wall shear stress is| | 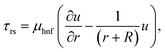 | (17) |
Dimensionless version is
| | 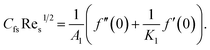 | (18) |
3.2. Nusselt number
Considering| | 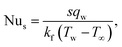 | (19) |
and heat flux qw| | 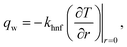 | (20) |
we can express that| | 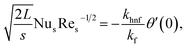 | (21) |
in which 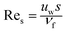 indicates the local Reynolds number.
indicates the local Reynolds number.
4. Entropy formulation
Mathematical expression is given by| | 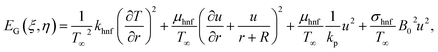 | (22) |
or| | 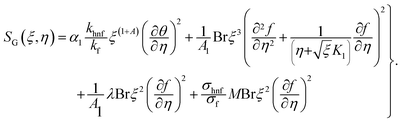 | (23) |
Here 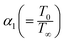 represents the heat ratio parameter,
represents the heat ratio parameter, 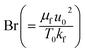 the Brinkman number and
the Brinkman number and 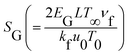 the entropy rate.
the entropy rate.
5. Solutions methodology
Considering the derivatives with respect to ξ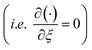 in eqn (7)–(10) we arrive at
in eqn (7)–(10) we arrive at| | 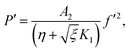 | (24) |
| | 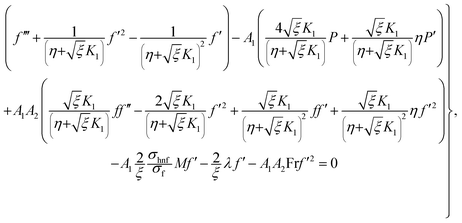 | (25) |
| | 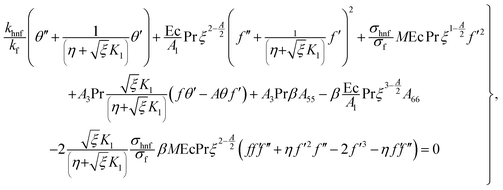 | (26) |
| | 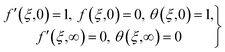 | (27) |
with A55 and A66 as| | 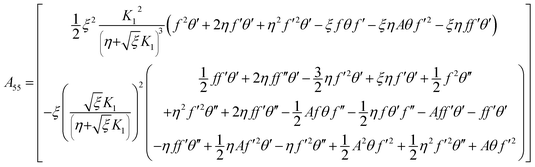 | (28) |
| | 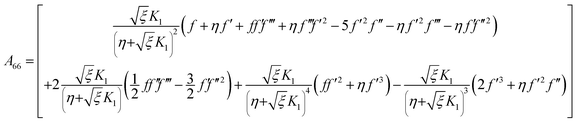 | (29) |
Elimination of pressure from eqn (22) and (23) yields
| | 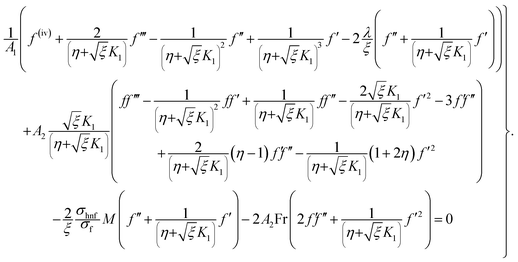 | (30) |
5.1. Numerical approach
Governing problems are solved by the ND-solve algorithm. The Mathematica software is utilized to develop the computational results. For this we converted the boundary value problem to the initial value situation as follows:| | 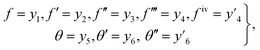 | (31) |
| | 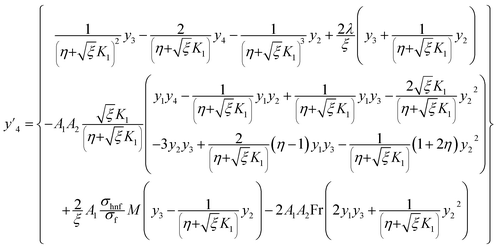 | (32) |
| | 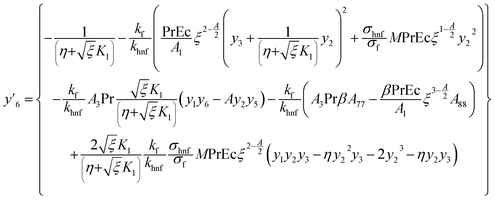 | (33) |
| | 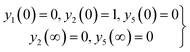 | (34) |
with A77 and A88 given below:| | 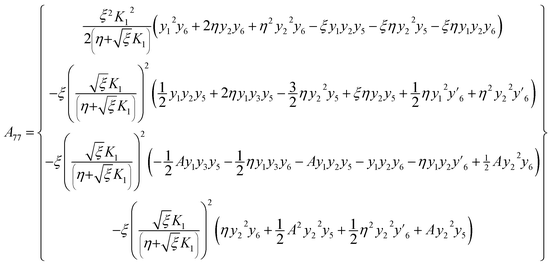 | (35) |
| | 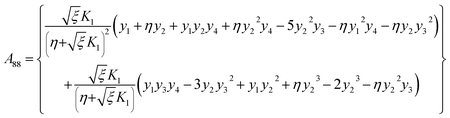 | (36) |
6. Discussion
The influence of emerging variables on liquid flow, entropy rate and temperature for both nanoliquid (Pb/C2H6O2) and hybrid nanoliquid (Fe2O3 + Pb/C2H6O2) is discussed. Here dotted lines show nanoliquid (Pb/C2H6O2) behaviors and solid lines characterize the hybrid (Pb + Fe2O3/C2H6O2) nanoliquid characteristics. Engineering quantities like the skin friction coefficient and heat transport rate are discussed through tabulated forms. Comparison of recent analysis with previous results in the literature is constructed in Table 3. Here we discussed the comparison of the coefficient of skin friction versus a higher approximation of the curvature variable with Okechi et al.55 for a limiting case (viscous fluid flow). Clearly a good consensus is noticed.
Table 3 Coefficient of skin friction comparison with Okechi et al.55
|
K
1
|
Okechi et al.55 |
Present results |
| 5 |
1.4196 |
1.41963 |
| 10 |
1.3467 |
1.34675 |
| 20 |
1.3135 |
1.31354 |
| 30 |
1.3028 |
1.30281 |
6.1. Velocity
Fig. 2 illustrates the flow behavior against the magnetic variable (M). An increment in the magnetic variable leads to intensification of the Lorentz force which declines the liquid flow. The influence of (λ) on (f′(η)) is portrayed in Fig. 3. Higher porosity corresponds to diminished velocity in both nanoliquid (Pb/C2H6O2) and hybrid (Pb + Fe2O3/C2H6O2) nanoliquid cases. Fig. 4 shows the velocity impact against the Forchheimer number (Fr). A reduction in liquid flow (f′(η)) is noticed versus the Forchheimer number for both nanoliquid (Pb/C2H6O2) and hybrid (Pb + Fe2O3/C2H6O2) nanomaterials. Fig. 5 and 6 elucidate the impact for flow versus nanoparticle volume fractions (ϕ1 and ϕ2). It is noticed that there is an enhancement in liquid flow versus higher nanoparticle volume fractions (ϕ1 and ϕ2).
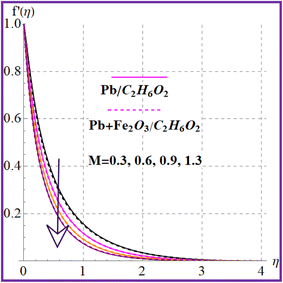 |
| | Fig. 2
f′(η) variation versus M. | |
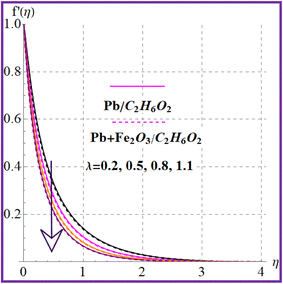 |
| | Fig. 3
f′(η) variation versus λ. | |
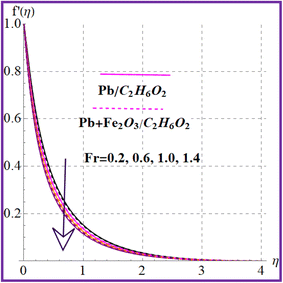 |
| | Fig. 4
f′(η) variation versus Fr. | |
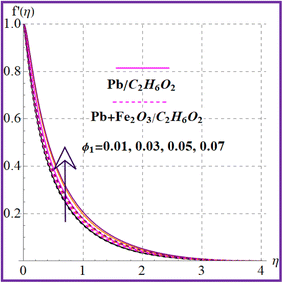 |
| | Fig. 5
f′(η) variation versus ϕ1. | |
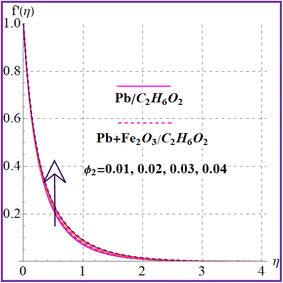 |
| | Fig. 6
f′(η) variation versus ϕ2. | |
6.2. Thermal field
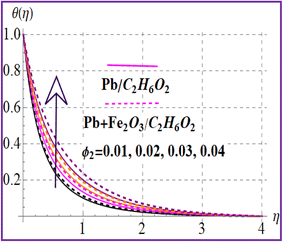
Fig. 7 presents the trend of temperature against the thermal relaxation time variable (β). A higher estimation of thermal relaxation time corresponds to an increase of the thermal field. Fig. 8 indicates the importance for (M) on θ(η). A larger approximation of the magnetic variable intensifies the Lorentz force which raises the resistance to flow. Therefore, the temperature is increased. The influence of the Eckert number on (θ(η)) is depicted in Fig. 9. The outcome for the Eckert number (Ec) leads to creation of an additional kinetic energy and consequently the thermal field is improved. Characteristics of nanoparticle volume fractions (ϕ1 and ϕ2) on the thermal field are disclosed in Fig. 10 and 11. Clearly, higher nanoparticle volume fractions (ϕ1 and ϕ2) enhance the thermal field for both nanoliquid (Pb/C2H6O2) and hybrid (Pb + Fe2O3/C2H6O2) nanomaterials.
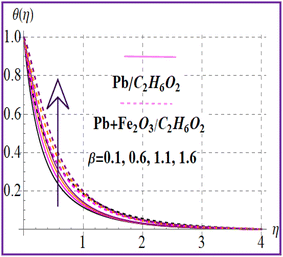 |
| | Fig. 7
θ(η) versus β. | |
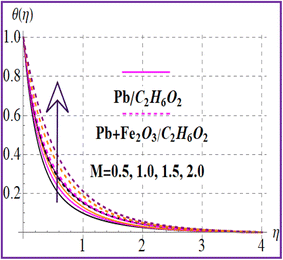 |
| | Fig. 8
θ(η) versus M. | |
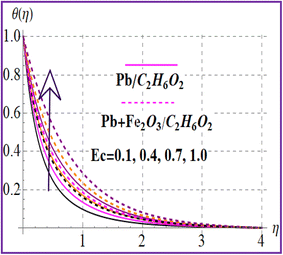 |
| | Fig. 9
θ(η) versus Ec. | |
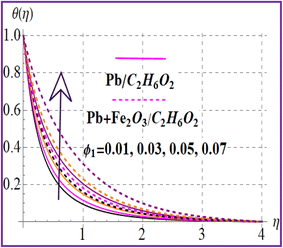 |
| | Fig. 10
θ(η) versus ϕ1. | |
 |
| | Fig. 11
θ(η) versus ϕ2. | |
6.3. Entropy rate
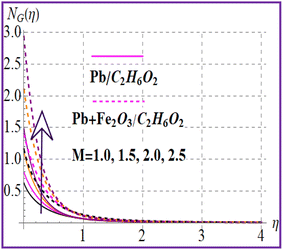
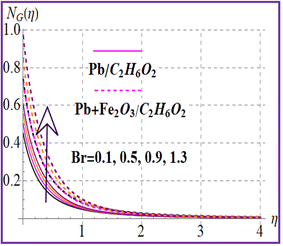
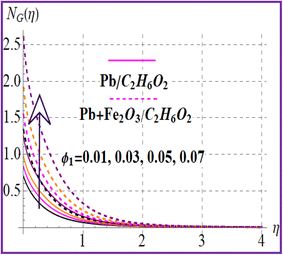
Fig. 12 reveals the impact of the magnetic variable on NG(η). Increasing values of the magnetic variable enhance the resistive force in the flow region which produces an additional energy in the system and therefore entropy is maximized. Fig. 13 depicts the importance of entropy for the Brinkman number. The entropy rate rises versus a higher Brinkman number due to the viscous force. Fig. 14 and 15 show entropy characteristics against nanoparticle volume fractions (ϕ1 and ϕ2). A higher estimation of volume fractions (ϕ1 and ϕ2) leads to augmentation of the entropy rate for both nanoliquid (Pb/C2H6O2) and hybrid (Pb + Fe2O3/C2H6O2) nanomaterials.
 |
| | Fig. 12
N
G(η) versus M. | |
 |
| | Fig. 13
N
G(η) versus Br. | |
 |
| | Fig. 14
N
G(η) versus ϕ1. | |
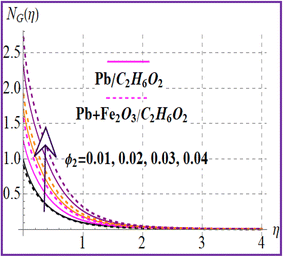 |
| | Fig. 15
N
G(η) versus ϕ2. | |
6.4. Physical quantities
Engineering quantities like the skin friction coefficient (Res1/2Cfs) and heat transport rate (Res−1/2Nus) for nanoliquid (Pb/C2H6O2) and hybrid (Pb + Fe2O3/C2H6O2) nanomaterials are discussed through tabulated forms.
6.4.1. Skin friction.
Table 4 highlights the characteristics of the skin friction (Res1/2Cfs) coefficient against sundry parameters for both nanoliquid (Pb/C2H6O2) and hybrid (Pb + Fe2O3/C2H6O2) nanomaterials. It is found that larger Forchheimer number (Fr), porosity (λ), material (K1) and magnetic (M) parameters result in skin friction reduction.
Table 4 Numerical results of the skin friction (Res1/2Cfs) coefficient
|
M
|
K
1
|
λ
|
Fr |
Res1/2Cfs |
| Pb/C2H6O2 |
Pb + Fe2O3/C2H6O2 |
| 0.4 |
0.1 |
0.1 |
0.2 |
8.4631 |
19.9922 |
| 0.8 |
|
|
|
7.35445 |
17.5033 |
| 0.12 |
|
|
|
6.57457 |
15.7212 |
| 0.3 |
0.45 |
0.1 |
0.2 |
0.475582 |
1.04693 |
|
|
0.45 |
|
|
0.34613 |
0.754253 |
|
|
0.51 |
|
|
0.231708 |
0.496568 |
| 0.3 |
0.45 |
0.2 |
0.2 |
0.344601 |
0.738767 |
|
|
|
0.3 |
|
0.223838 |
0.453805 |
|
|
|
0.4 |
|
0.11172 |
0.188597 |
|
|
|
|
0.1 |
0.564833 |
1.20704 |
|
|
|
|
0.4 |
0.313042 |
0.748393 |
|
|
|
|
0.7 |
0.0991132 |
0.343877 |
6.4.2. Heat transport rate.
Table 5 shows the heat transport rate (Res−1/2Nus) variation versus influential variables for both nanoliquid (Pb/C2H6O2) and hybrid (Pb + Fe2O3/C2H6O2) nanomaterials. Decay in the thermal transport rate is witnessed for larger Eckert number (Ec), thermal relaxation time (β) and magnetic (M) variables. An increment in the temperature gradient is detected for the Prandtl number.
Table 5 Computational values for Res−1/2Nus
|
β
|
M
|
Pr |
Ec |
Res−1/2Nus |
| Pb/C2H6O2 |
Pb + Fe2O3/C2H6O2 |
| 0.01 |
0.1 |
5.0 |
0.4 |
2.94351 |
3.10761 |
| 0.03 |
|
|
|
2.81501 |
2.44288 |
| 0.05 |
|
|
|
2.68726 |
2.09427 |
| 0.01 |
0.4 |
5.0 |
0.4 |
2.59787 |
2.34593 |
|
|
|
|
0.5 |
2.48648 |
1.82663 |
|
|
|
|
0.6 |
2.37692 |
1.59412 |
| 0.01 |
0.1 |
3.5 |
0.4 |
2.45597 |
2.38122 |
|
|
|
4.0 |
|
2.62835 |
2.52681 |
|
|
|
4.5 |
|
2.79038 |
2.6638 |
| 0.01 |
0.1 |
5.0 |
0.2 |
3.23399 |
3.85736 |
|
|
|
|
0.7 |
2.50778 |
1.71628 |
|
|
|
|
0.11 |
1.92682 |
0.280292 |
7. Closing remarks
Main findings are listed below.
• A higher magnetic parameter decays fluid flow whereas temperature enhances.
• Velocity for the Forchheimer number and porosity parameter is the same.
• A larger thermal relaxation time variable raises temperature.
• A larger estimation of nanoparticle volume fractions corresponds to an amplified fluid flow and thermal field.
• Entropy shows increasing behavior due to the Brinkman number.
• A Higher magnetic parameter leads to entropy rate enhancement.
• Surface drag force shows decreasing behavior for Forchheimer, porosity, material and magnetic parameters.
• The Prandtl number leads to Nusselt number enhancement.
• Nusselt number improvement against thermal relaxation time and magnetic parameters is ensured.
Conflicts of interest
There are no conflicts to declare.
References
-
S. U. S. Choi and J. A. Eastman, Enhancing thermal conductivity of fluids with nanoparticles, ASME International Mechanical Engineering Congress and Exposition, San Francisco, California, vol. 231, 1995, pp. 99–105 Search PubMed.
- J. A. Eastman, S. U. S. Choi, S. Li, W. Yu and L. J. Thompson, Anomalously increased effective thermal conductivities of ethylene glycol-based nanofluids containing copper nanoparticles, Appl. Phys. Lett., 2001, 78, 718–720 CrossRef CAS.
- A. Hassan, N. Alsubaie, F. M. Alharbi, A. Alhushaybari and A. M. Galal, Scrutinization of Stefan suction/blowing on thermal slip flow of ethylene glycol/water based hybrid ferro-fluid with nano-particles shape effect and partial slip, J. Magn. Magn. Mater., 2023, 565, 170276 CrossRef CAS.
- I. Chabani, F. M. Oudina, H. Vaidya and A. I. Ismail, Numerical analysis of magnetic hybrid nano-fluid natural convective flow in an adjusted porous trapezoidal enclosure, J. Magn. Magn. Mater., 2022, 564, 170142 CrossRef CAS.
- S. A. Abdollahi, A. Alizadeh, I. C. Esfahani, M. Zarinfar and P. Pasha, Investigating heat transfer and fluid flow betwixt parallel surfaces under the influence of hybrid nanofluid suction and injection with numerical analytical technique, Alexandria Eng. J., 2023, 70, 423–439 CrossRef.
- K. Alqawasmi, K. A. M. Alharbi, U. Farooq, S. Noreen, M. Imran, A. Akgül, M. Kanan and J. Asad, Numerical approach toward ternary hybrid nanofluid flow with nonlinear heat source-sink and Fourier heat flux model passing through a disk, Int. J. Thermofluids, 2023, 18, 100367 CrossRef.
- H. Maiti, A. Y. Khan, S. Mondal and S. K. Nandy, Scrutinization of unsteady MHD fluid flow and entropy generation: hybrid nanofluid model, Journal of Computational Mathematics and Data Science, 2023, 6, 100074 CrossRef.
- A. Rauf, F. Hussain, A. Mushtaq, N. A. Shah and M. R. Ali, MHD mixed convection flow for Maxwell hybrid nanofluid with Soret, Dufour and morphology effects, Arabian J. Chem., 2023, 16, 104965 CrossRef CAS.
- S. Qayyum, Dynamics of Marangoni convection in hybrid nanofluid flow submerged in ethylene glycol and water base fluids, Int. Commun. Heat Mass Transfer, 2020, 119, 104962 CrossRef CAS.
- A. Y. Sayed, S. I. Ahmed, K. S. Mekheimer and M. S. Abdel-wahed, Electromagnetohydrodynamic effects with single-walled carbon nanotubes particles in a corrugated microchannel, Chaos, Solitons Fractals, 2023, 168, 113126 CrossRef.
- S. S. Ghadikolaei and M. Gholinia, Terrific effect of H2 on 3D free convection MHD flow of C2H6O2 single bond H2O hybrid base fluid to dissolve Cu nanoparticles in a porous space considering the thermal radiation and nanoparticle shapes effects, Int. J. Hydrogen Energy, 2019, 44, 17072–17083 CrossRef CAS.
- T. Salahuddin, M. Khan, S. Sakinder and B. A. Alwan, A flow analysis of hybrid nanoparticles near a solid sphere, Int. J. Hydrogen Energy, 2022, 47, 16640–16648 CrossRef CAS.
- A. Ali, S. Sarkar, S. Das and R. N. Jana, Investigation of Cattaneo–Christov double diffusions theory in bioconvective slip flow of radiated magneto-cross-nanomaterial over stretching cylinder/plate with activation energy, Int. J. Appl. Comput. Math., 2021, 7, 208 CrossRef.
- M. V. Krishna, N. A. Ahammad and A. J. Chamkha, Radiative MHD flow of Casson hybrid nanofluid over an infinite exponentially accelerated vertical porous surface, Case Stud. Therm. Eng., 2021, 27, 101229 CrossRef.
- P. Sreedevi, P. S. Reddy and A. J. Chamkha, Heat and mass transfer analysis of unsteady hybrid nanofluid flow over a stretching sheet with thermal radiation, SN Appl. Sci., 2020, 2, 1222 CrossRef CAS.
-
J. B. J. Fourier, Théorie Analytique De La Chaleur, 1822 Search PubMed.
-
C. Cattaneo, Sulla conduzione del calore, Atti Semin, Mat Fis Univ Modena Reggio Emilia, 1948, vol. 3, pp. 83–101 Search PubMed.
- C. I. Christov, On frame indifferent formulation of the Maxwell-Cattaneo model of finite-speed heat conduction, Mech. Res. Commun., 2009, 36, 481–486 CrossRef.
- A. Razaq, S. A. Khan, T. Hayat and A. Alsaedi, Entropy optimization in radiative flow of Reiner-Rivlin material with heat source and modified Cattaneo-Christov
heat and mass fluxes, Case Stud. Therm. Eng., 2023, 45, 102985 CrossRef.
- A. Salmi, H. A. Madkhali, B. Ali, M. Nawaz, S. O. Alharbi and A. S. Alqahtani, Numerical study of heat and mass transfer enhancement in Prandtl fluid MHD flow using Cattaneo-Christov heat flux theory, Case Stud. Therm. Eng., 2022, 33, 101949 CrossRef.
- M. Haneef, M. Nawaz, S. O. Alharbi and Y. Elmasry, Cattaneo-Christov heat flux theory and thermal enhancement in hybrid nano Oldroyd-B rheological fluid in the presence of mass transfer, Int. Commun. Heat Mass Transfer, 2021, 126, 105344 CrossRef CAS.
- T. Hayat, S. A. Khan, M. I. Khan, S. Momani and A. Alsaedi, Cattaneo-Christov (CC) heat flux model for nanomaterial stagnation point flow of Oldroyd-B fluid, Comput. Methods Programs Biomed., 2020, 187, 105247 CrossRef CAS PubMed.
- S. A. Lone, S. Anwar, Z. Raizah, M. Y. Almusawa and A. Saeed, A magnetized Maxwell nanofluid flow over a stratified stretching surface with Cattaneo-Christov double diffusion theory, J. Magn. Magn. Mater., 2023, 575, 170722 CrossRef.
- A. Alsaedi, S. A. Khan and T. Hayat, Cattaneo-Christov double diffusive and model development for entropy optimized flow of Reiner-Rivlin material in thermal system and environmental effect, Alexandria Eng. J., 2023, 72, 67–82 CrossRef.
- S. Bilal, M. I. Shah, N. Z. Khan, A. Akgül and K. S. Nisar, Onset about non-isothermal flow of Williamson liquid over exponential surface by computing numerical simulation in perspective of Cattaneo Christov heat flux theory, Alexandria Eng. J., 2022, 61, 6139–6150 CrossRef.
- M. Yasir, M. Khan, A. S. Alqahtani and M. Y. Malik, Heat generation/absorption effects in thermally radiative mixed convective flow of Zn−TiO2/H2O hybrid nanofluid, Case Stud. Therm. Eng., 2023, 45, 103000 CrossRef.
- T. Salahuddin, M. Awais, M. Khan and M. Altanji, Analysis of transport phenomenon in cross fluid using Cattaneo-Christov theory for heat and mass fluxes with variable viscosity, Int. Commun. Heat Mass Transfer, 2021, 129, 105664 CrossRef CAS.
- S. A. Khan, T. Hayat and A. Alsaedi, Cattaneo Christov (CC) heat and mass fluxes in Stagnation point flow of Jeffrey nanoliquids by a stretched surface, Chin. J. Phys., 2022, 76, 205–216 CrossRef CAS.
- A. Bejan, A study of entropy generation in fundamental convective heat transfer, ASME J. Heat Mass Transfer, 1979, 101, 718–725 CrossRef.
- A. Bejan, Entropy generation through heat and fluid flow, J. Appl. Mech., 1983, 50, 475 CrossRef.
- A. Bejan, Entropy generation minimization, J. Appl. Phys., 1996, 79, 1191–1218 CrossRef CAS.
- B. Iftikhar, T. Javed and M. A. Siddiqu, Entropy generation analysis during MHD mixed convection flow of non-Newtonian fluid saturated inside the square cavity, J. Comput. Sci., 2023, 66, 101907 CrossRef.
- T. Hayat, A. Razaq, S. A. Khan and A. Alsaedi, Entropy generation in chemically reactive and radiative Reiner-Rivlin fluid flow by stretching cylinder, J. Magn. Magn. Mater., 2023, 573, 170657 CrossRef CAS.
- H. Maiti, A. Y. Khan, S. Mondal and S. K. Nandy, Scrutinization of unsteady MHD fluid flow and entropy generation: hybrid nanofluid model, Journal of Computational Mathematics and Data Science, 2023, 6, 100074 CrossRef.
- A. Alsaedi, S. A. Khan and T. Hayat, A model development for thermal and solutal transport analysis in radiating entropy optimized and magnetized flow of nanomaterial by convectively heated stretched surface, Chaos, Solitons Fractals, 2023, 171, 113424 CrossRef.
- M. O. Oni and B. K. Jha, Entropy generation analysis of electroosmotic mixed convection flow in vertical microannulus with asymmetric heat fluxes, Int. Commun. Heat Mass Transfer, 2023, 145, 106813 CrossRef CAS.
- L. S. Sundar and H. K. Mewada, Experimental entropy generation, exergy efficiency and thermal performance factor of CoFe2O4/water nanofluids in a tube predicted with ANFIS and MLP models, Int. J. Therm. Sci., 2023, 190, 108328 CrossRef CAS.
- H. Zhao, D. Zhao and S. Becker, Entropy production and enhanced thermal performance studies on counter-flow double-channel hydrogen/ammonia-fuelled micro-combustors with different shaped internal threads, Int. J. Hydrogen Energy, 2022, 47, 36306–36322 CrossRef CAS.
- M. O. Oni and B. K. Jha, Entropy generation analysis of electroosmotic mixed convection flow in vertical microannulus with asymmetric heat fluxes, Int. Commun. Heat Mass Transfer, 2023, 145, 106813 CrossRef CAS.
- T. Siva, S. Jangili and B. Kumbhakar, Entropy generation on EMHD transport of couple stress fluid with slip-dependent zeta potential under electrokinetic effects, Int. J. Therm. Sci., 2023, 191, 108339 CrossRef.
- A. Ali, S. Sarkar, S. Das and R. N. Jana, A report on entropy generation and Arrhenius kinetics in magneto-bioconvective flow of cross nanofluid over a cylinder with wall slip, Int. J. Ambient Energy, 2022 DOI:10.1080/01430750.2022.2031292.
- A. J. Chamkha and A. R. A. Khaled, Hydromagnetic combined heat and mass transfer by natural convection from a permeable surface embedded in a fluid-saturated porous medium, Int. J. Numer. Methods Heat Fluid Flow, 2000, 10, 455–477 CrossRef CAS.
- H. Waqas, F. F. Bukhari, U. Farooq, M. S. Alqarni and T. Muhammad, Numerical computation of melting heat transfer in nonlinear radiative flow of hybrid nanofluids due to permeable stretching curved surface, Case Stud. Therm. Eng., 2021, 27, 101348 CrossRef.
- E. N. Maraj, Z. Khatoon, S. Ijaz and R. Mehmood, Effect of Arrhenius activation energy and medium porosity on mixed convective diluted ethylene glycol nanofluid flow towards a curved stretching surface, Int. Commun. Heat Mass Transfer, 2021, 129, 105691 CrossRef CAS.
- A. J. Chamkha, Non-Darcy hydromagnetic free convection from a cone and a wedge in porous media, Int. Commun. Heat Mass Transfer, 1996, 23, 875–887 CrossRef CAS.
- S. Das, A. Ali and R. N. Jana, Numerically framing the impact of magnetic field on nanofluid flow over a curved stretching surface with convective heating, World J. Eng., 2021, 18, 938–947 CrossRef CAS.
- M. V. Krishna and A. J. Chamkha, Hall and ion slip effects on MHD rotating boundary layer flow of nanofluid past an infinite vertical plate embedded in a porous medium, Results Phys., 2019, 15, 102652 CrossRef.
- K. Hosseinzadeh, M. R. Mardani, M. Paikar, A. Hasibi, T. Tavangar, M. Nimafar, D. D. Ganji and M. B. Shafii, Investigation of second grade viscoelastic non-Newtonian nanofluid flow on the curve stretching surface in presence of MHD, Results Eng., 2023, 17, 100838 CrossRef CAS.
-
A. Ali, R. N. Jana and S. Das, Radiative CNT-based hybrid magneto-nanoliquid flow over an extending curved surface with slippage and convective heating, Heat Transfer, 2021, 50, 2997–3020 Search PubMed.
- H. Waqas, F. F. Bukhari, U. Farooq, M. S. Alqarni and T. Muhammad, Numerical computation of melting heat transfer in nonlinear radiative flow of hybrid nanofluids due to permeable stretching curved surface, Case Stud. Therm. Eng., 2021, 27, 101348 CrossRef.
- T. Hayat, R. S. Saif, R. Ellahi, T. Muhammad and B. Ahmad, Numerical study for Darcy-Forchheimer flow due to a curved stretching surface with Cattaneo-Christov heat flux and homogeneous-heterogeneous reactions, Results Phys., 2017, 7, 2886–2892 CrossRef.
- B. Ullah, B. M. Fadhl, B. M. Makhdoum, K. S. Nisar, H. A. Wahab and U. Khan, Heat transfer analysis in Darcy Forchheimer flow of hybrid nanofluid for multiple shape effects over a curved stretching surface, Case Stud. Therm. Eng., 2022, 40, 102538 CrossRef.
- L. Zhang, M. M. Bhatti, E. E. Michaelides, M. Marin and R. Ellahi, Hybrid nanofluid flow towards an elastic surface with tantalum and nickel nanoparticles, under the influence of an induced magnetic field, Eur. Phys. J.: Spec. Top., 2022, 231, 521–533 CAS.
- T. Hayat, A. Razaq, S. A. Khan and A. Alsaedi, An induced magnetic field utilization for hybrid nanoliquid flow subject to entropy generation, J. Magn. Magn. Mater., 2023, 576, 170742 CrossRef CAS.
- N. F. Okechi, M. Jalil and S. Asghar, Flow of viscous fluid along an exponentially stretching curved surface, Results Phys., 2017, 7, 2851–2854 CrossRef.
|
| This journal is © The Royal Society of Chemistry 2023 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a,
Tasawar
Hayat
a,
Sohail A.
Khan
*a,
Tasawar
Hayat
a,
Sohail A.
Khan
 *a and
Ahmed
Alsaedi
*a and
Ahmed
Alsaedi
 b
b
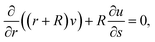
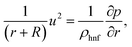
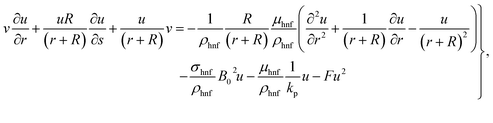
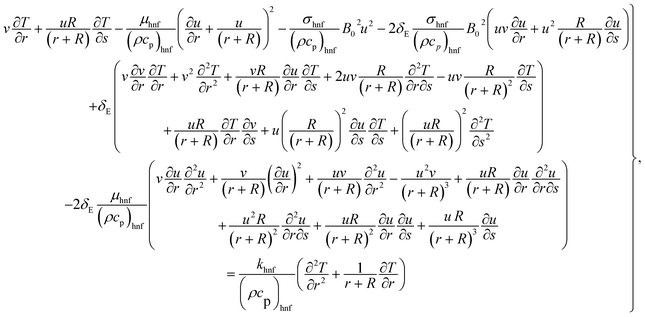
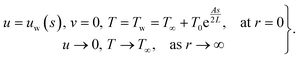
 the inertia coefficient, kp the porous medium permeability coefficient, R the radius of curvature, (ρcp)hnf the heat capacitance, Cb the drag force coefficient, L the reference length, T the temperature, khnf the thermal conductivity, cp the specific heat, T∞ the ambient temperature, δE the heat relaxation time, B0 the magnetic field strength, Tw the wall temperature and p the pressure.
the inertia coefficient, kp the porous medium permeability coefficient, R the radius of curvature, (ρcp)hnf the heat capacitance, Cb the drag force coefficient, L the reference length, T the temperature, khnf the thermal conductivity, cp the specific heat, T∞ the ambient temperature, δE the heat relaxation time, B0 the magnetic field strength, Tw the wall temperature and p the pressure.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 343
343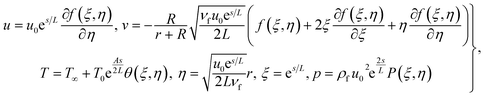
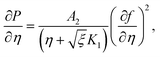
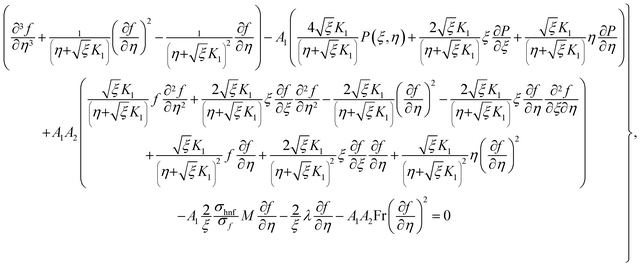
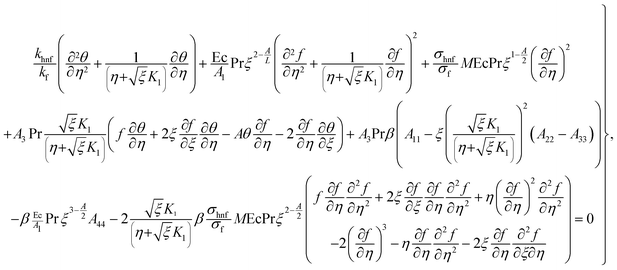
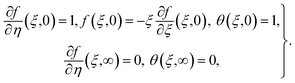
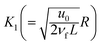 shows the material parameter,
shows the material parameter, 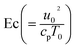 the Eckert number,
the Eckert number, 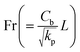 theForchheimer number,
theForchheimer number, 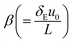 the thermal relaxation time,
the thermal relaxation time, 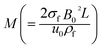 the magnetic variable,
the magnetic variable, 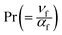 the Prandtl number and
the Prandtl number and 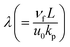 the porosity parameter. Here A1, A2, A3, A11, A22, A33 and A44 are expressed as
the porosity parameter. Here A1, A2, A3, A11, A22, A33 and A44 are expressed as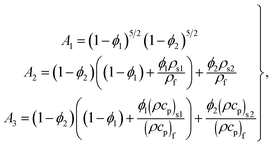
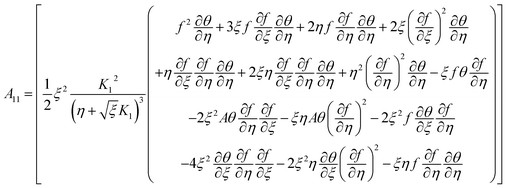
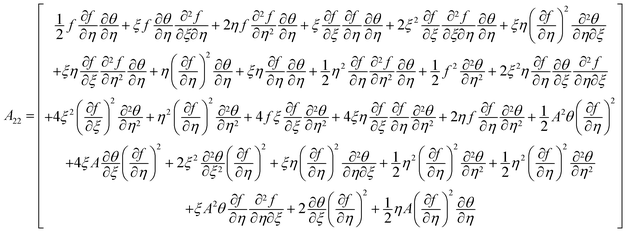
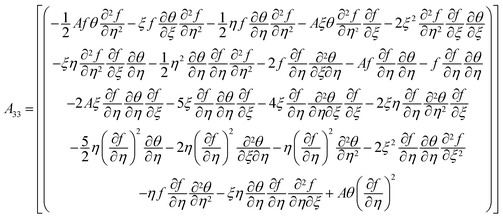
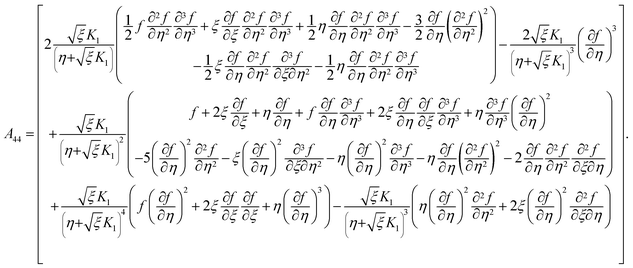
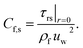
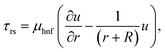
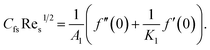
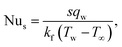
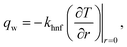
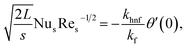
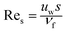 indicates the local Reynolds number.
indicates the local Reynolds number.
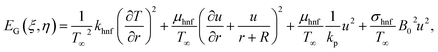
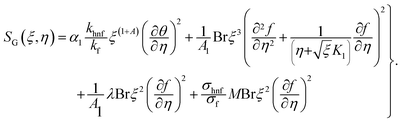
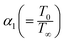 represents the heat ratio parameter,
represents the heat ratio parameter, 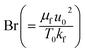 the Brinkman number and
the Brinkman number and 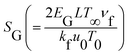 the entropy rate.
the entropy rate.
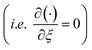 in eqn (7)–(10) we arrive at
in eqn (7)–(10) we arrive at