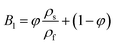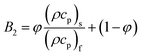DOI:
10.1039/D3NA00654A
(Paper)
Nanoscale Adv., 2023,
5, 5819-5828
Flow and heat transfer of Al2O3 and γ-Al2O3 through a channel with non-parallel walls: a numerical study
Received
17th August 2023
, Accepted 12th September 2023
First published on 4th October 2023
Abstract
Nanofluids are referred to as nanometer suspensions in standard nanometer-sized fluid transfer. In this study, our focus was to examine the flow and transmission of heat through a non-parallel walled channel of nanofluids. For this purpose, we used the thermal transport in H2O composed of Al2O3 and γ-Al2O3 nanomaterials within the convergent/divergent channel for stretching/shrinking parameters. The flow was considered two-dimensional and unsteady. As a result, the flow of an unstable fluid, including various nanoparticles, was modeled within the convergent/divergent channel. A suitable similarity transformation was used to convert the complicated coupled system of differential equations into a non-dimensional form. For numerical solutions, the complicated system of equations was first transformed into a set of first-order differential equations using the shooting method. The Runge–Kutta (RK-4) method was then used to solve the reduced first-order equations. To comprehend the flow pattern and temperature and velocity profile deviations caused by dimensionless parameters, a graphical investigation was performed. Graphs were also used to investigate the variation in the velocity and temperature profiles for various emerging factors.
Introduction
Scientists and engineers have experimented with various methods to control temperature rise in mechanical and industrial operations over the years. Poor thermal performance of everyday fluids results in poor conduction, which is the cause of inefficient heat transmission. Low thermal conductivity ratings in everyday fluids, such as water, kerosene oil, and ethylene glycol, cause inefficient heat transmission, which elevates the total temperature of the system. Nanofluids have been developed to address this issue. Nano-sized solid particles are added to low thermal conductivity fluids to significantly improve heat transfer performance. In recent years nanofluid has become an inseparable feature of energy transport-related phenomena. Its effects rely on the physical elements of modern manufacturing and thermal processes, including heating power and thermal conductivity. One of the significant subjects of computer fluid dynamics among researchers is the modelling of transport phenomena in nanofluids in the last decade. Applications for the system's enhanced heat transfer properties range from solar synthesis to gas sensing, biological sensing, nuclear chemical reactors, and the chemical sector. In order to increase the efficiency of heat transfer in regular fluids, the idea of using nanoparticles in similar locations was suggested.
Gamma nanofluids were added to the system to improve the heat transfer rates and overall thermal performance. These are nanofluids that have been extended. Two concepts are used in these fluids. The first method incorporates two types of nanoparticles into a single base fluid. This significantly improves the thermal properties of the final product. Second, the final modified conventional fluids gain thermal conductivity by combining two base fluids with a single nanoparticle. A solid understanding of thermal energy exchange between physical systems or products is required for physical transport challenges. The rate of heat transmission is influenced by the temperature and quality of the medium between the two systems.
The flows of different types of fluids between converging and diverging channels have been extensively studied owing to their manufacturing, engineering, and technological applications, cavities, and canals, for instance, flow. Another example of fluid flowing through converging or diverging channels is the circulatory system of the human body, where blood flows through arteries and capillaries. These applications include an improved heat transport rate in the process of the heat exchanger for milk streams, molten polymer extrusion by converging dies, and polymer industry cold drawing operations.
Flow analysis across converging/diverging channels is becoming very important due to its diverse industrial and technology applications. These applications include improvements in heat transport rates in the molten polymer extrusion heating exchanger process using converging dies. The first work by Jeffery1 and Ganie2 demonstrated the pioneering work on the flow along the converging/divergent direction, which is the flow between two planes at an angle. Many researchers have followed the ground-breaking, highly successful studies of the Jeffery–Hamel flow.
The influence of thermal radiation on the flow of non-parallel stretching and shrinking walls was investigated by Khan et al.3 The ability of water-based nanofluids to transmit heat across the convergent/divergent channels was studied by W. Khan et al.4 Ullah et al.5 recently proposed a numerical analysis to investigate the movement of thermal resources during the flow of convergent and divergent ribs. Ahmed6 created a new form of fluid called nanofluids, which is made up of solid metallic or metal-oxide nanoparticles suspended in a liquid. They discovered that adding 1–5% volume of solid oxide particles to a base fluid can increase thermal conductivity by 20%.
In recent years, the nanofluid industry, including shipping, has become an inseparable part of the phenomenon. Its consequences in modern manufacturing and thermal processes rely on physical properties, such as heat capability and thermal conductivity. Owing to poor thermal behavior, the conversion of heat to operating fluids such as water, ethylene glycol, and silicone oil has declined. The thermal efficiency of fluid is a key industrial issue, so scientists have tried to build new nanoparticles for better thermal and cooling systems. Alumina nanofluids have attracted the scientific community because of their application in many cooling systems. An experimental analysis on the cooling application of γ-Al2O3–H2O was performed by Qahtani et al.;7 water was used as the base fluid. Scientists have studied this field based on attractive cooling applications for gamma alumina nanofluids. Appropriate literature on this subject can be found in related studies.8,9 M. M Rashidi et al.10 have studied gamma alumina with various base fluids and used gamma alumina with base fluids such as water and ethylene. Ganie et al.11 investigated the movement of nanofluid across a stretching sheet. Khan et al.12 showed that the nanofluid flow through a stretched sheet is affected by thermal radiation and sliding. The effects of temperature on the thermal conductivity of nanofluid were investigated by Das et al.13
The first empirical correlation for computing the Nusselt number in both laminar and turbulent tube flow using nanofluids composed of water, and Cu and γ-Al2O3 particles has been provided by Umavathi14 and Parvin,15 which is particularly relevant to the topic of the thermal performance of nanofluids in confined flow situations. The next researcher to look at fluid flow in shrinking/stretching divergent/convergent Jeffery–Hamal channels was Turkyilmazoglu.16 By explicitly solving the governing nonlinear equations, he demonstrated that a larger value for the stretching parameter increased the heat transfer rate in the direction of the channel walls. Makinde et al.17 employed the DRA to investigate the influence of thermal radiation on magnetohydrodynamic nanofluid flow produced by stretchable/shrinkable channels. They discovered that as the stretching parameter is increased, the fluid velocity increases. Parvin18 proposed studying the analytical results of MHD copper–water nanofluid flow using the RVI approach in two non-comparable converging/diverging channels. They found that as the Eckert number grew, the Nusselt number grew along with it. The impact of Radiation on Jeffry fluid's flow towards stretchy diverging and converging channels was first postulated by Kumar et al.19 Their research showed that as the Reynolds number increased, the divergent channel's speed dropped while the convergent channel's speed increased. Many scientists have studied convergent and divergent channels in different environmental settings.20–22 Water-based copper and silver nanofluids were studied by Izadi et al.23 on a stretched surface.
The boundary layer flow of alumina and aluminum gamma nanofluids on a horizontal stretch sheet was recently studied by Alharbi et al.,24 but they neglected to account for the effective Prandtl number. To the best of our knowledge, the problem of taking gamma nanofluid into account through a convergent channel has not been examined in the literature. We hope that this research will help strengthen the established literature. Uses for gamma alumina single crystals in jewelry include setting rubies. Gamma alumina's superior mechanical qualities make it suitable for use in cutting tools. Other applications for gamma alumina include polishing compounds and antiwear devices. Aluminum oxide, or alpha alumina in the materials science community, is also known as alundum (in its fused state) or aloxite in the mining and ceramics industries. In 2015, the world produced over 115 million tons of aluminum oxide annually, with more than 90% going toward the production of aluminum metal. Refractories, ceramics, polishing, and abrasives are where specialist aluminum oxides really shine. Alumina is formed from aluminum hydroxide, which is used in large quantities in the production of zeolites, the coating of titanium pigments, and the suppression of fire and smoke. More than 90% of aluminum oxide, also known as smelter-grade alumina (SGA), is used in the Hall–Heroult process to create aluminum. The rest, known as specialty alumina, is used in numerous industries, because of its inertness, thermal stability, and electrical conductivity.
Description and the problem
The flow of Al2O3–H2O and γ-Al2O3–H2O nanofluids was taken between two non-parallel and inclined plane walls. It is assumed that the under-considered nanoparticles and the conventional fluid are in thermal equilibrium. The flow of the nanofluid in the channel is due to a source or sink present at the culmination of the walls. These walls are separated through an angle 2α and flow is purely radial and unidirectional. Thus, only the u component of the velocity survives, and it depends on r and θ. It is important to mention that the parameter alpha represents a convergent channel when it is negative and positive alpha represents a diverging channel. Using the stated assumption, the governing motion equations are presented below (Fig. 1).
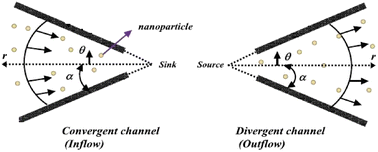 |
| | Fig. 1 Geometry of the problem. | |
Using the stated assumption, the governing motion equations are presented as follows26,27
Governing equations
Mass conservation equation| | 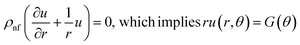 | (1) |
Momentum conservation equations
| | 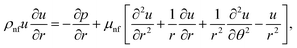 | (2) |
| | 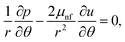 | (3) |
| | 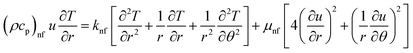 | (4) |
For boundary conditions, see ref. 28.
| | 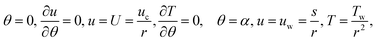 | (5) |
Here, the effective density is
ρnf, the effective dynamic viscosity is
μnf, specific heat capacity is (
ρcP)
nf, effective thermal conductivity is k
nf,
T is temperature, and
μ the velocity at the channel centerline,
μc defines the rate of movement at the channel centerline and
s indicates the stretching/shrinking parameter.
The effective dynamic density (ρnf) and the heat capacitance (ρccp)nf of the nanofluid are:
| | | ρnf = (1 − ϕ)ρf + ϕρs = A1 | (6) |
| | | (ρcp)nf = (1 − φ)(ρcp)f + φ(ρcp)s = A2 | (7) |
| | | ρnf = (1 − ϕ)ρf + ϕρs = B1 | (8) |
where,
ϕ is the solid volume fraction.
| | 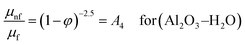 | (9) |
| | 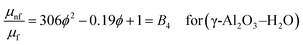 | (10) |
| | 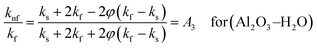 | (11) |
| | 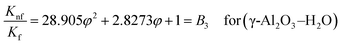 | (12) |
| | 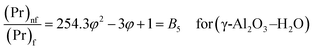 | (13) |
| | | Pr = 6.2 for (Al2O3–H2O) | (14) |
Using similarity transformations,
| | 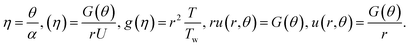 | (15) |
Equations with an effective Prandtl number
| | | B4(f′′′(η)) + 4B4α2(f′(η)) + 2B1Reα(f(η))(f′(η)) = 0 for (γ-Al2O3–H2O) | (16) |
| | 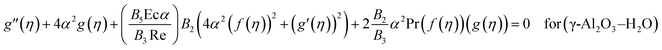 | (17) |
where
| B3 = 4.97φ2 + 2.72φ + 1, (the effective thermal conductivity of nanofluid) |
| B4 = 123φ2 + 7.3φ + 1, (the dynamic viscosity of nanofluid) |
Boundary Conditions
| f(0) = 1, f′(0) = 0, g′(0) = 0, f(1) = χ, g(1) = 1 |
Solution procedure
The numerical program solves the mathematical formulae (16)–(19) for the nanofluid flow. The associative equation was first converted into a solved initial value problem. We designed a recovery strategy to accomplish this. The problem was then solved using the Runge–Kutta-4 technique, which is a number system. All graphical analyses and simulations were performed using Mathematica mathematics software.
When the above equations are combined with the normal velocity equation and the temperature equation, the following results are obtained.
| A4(y4) + 4A4α2(y2) + 2A1Reα(y1)(y2) = 0 |
| | 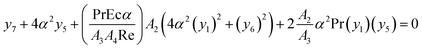 | (18) |
With an effective Prandtl number
| B4(y4) + 4B4α2(y2) + 2B1Reα(y1)(y2) = 0 |
| | 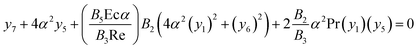 | (19) |
Interpretation of the results
Changes in the involvement features impact program performance, which will be discussed in this study. The thermophysical properties of water and alumina are shown in Table 1. Dimensionless parameter discrepancies in all profiles can be studied using a variety of provided images. The volume fractions of water (H2O) nanoparticles and aluminium nanoparticles vary greatly. Based on the stretching/shrinking option, below are the three examples. (a) χ < 0 i.e., the shrinking parameter (b) χ > 0 i.e., the stretching parameter (c) χ = 0 i.e., the walls are at rest on the velocity and the temperature profile.
Table 1 Physical properties of water and nanoparticles
| Nanoparticles |
ρ (kg m−3) |
C
p (J kg−1 K−1) |
k (W mK−1) |
Pr |
| H2O |
998.3 |
4182 |
0.60 |
6.2 |
| Al2O3 |
3970 |
765 |
40 |
— |
The results of the R-K-4 approach are contrasted with the results of the R-K-4 method in Table 2. This table also considers the shooting technique. Both choices are entirely congruent with one another in every respect. These details are computed ϕ = 0.02, Ec = 0.2, and the Prandtl number is equal to 6.2.
Table 2 Comparison of the current result with that found in ref. 25
|
α (Radian) |
Ref. 25 |
Current result |
| 0.0174533 |
0.5289 |
0.5289 |
| 0.0349066 |
0.6139 |
0.6139 |
| 0.0523599 |
0.3158 |
0.3158 |
| 0.0698132 |
0.2847 |
0.2847 |
Velocity profile for Al2O3/water and γ-Al2O3/water with an effective Prandtl number
The investigation of the turning factor distribution velocity is discussed in this section. These graphs can be used to determine how well a flow operates when various inputs are used. As a consequence, the values of alpha increase and decrease, resulting in an increase and decrease in the velocity distribution for χ = 0.5 and χ = −0.5 values shown in Fig. (2–17). When α > 0, it shows the divergent channel, and when α < 0 it shows the divergent channel.
Variations in the velocity profile are depicted in Fig. (2), which was created when the value was lowered. It should come as no surprise that in the convergent channel/stretching situation, velocity increases when α decreases. As can be seen in Fig. (3), the velocity profile shifts whenever we change to α. In the event of a converging channel or shrinking, it is self-evident that the velocity will increase as α decreases. As illustrated in Fig. (4), the velocity profile shifts whenever the value of α is altered. It should come as no surprise that the velocity will increase in the event that the channel is stretched or diverges. Fig. 5 shows how the velocity profile changes when the value of α is changed. It should come as no surprise that the velocity decreases as the height increases in the case of the divergent channel and the decreasing channel. For a given value of χ, the velocity increases in the convergent channel/stretching scenario. These differences in the velocity profile for different values of χ are depicted in Fig. (6). The variations in the velocity profile that occur for different values of χ are depicted in Fig. 7. Within the context of the convergent channel/shrinking scenario, the velocity decreases for a given value of χ.
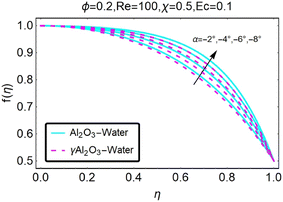 |
| | Fig. 2 Variation in the velocity profile with changes in α. | |
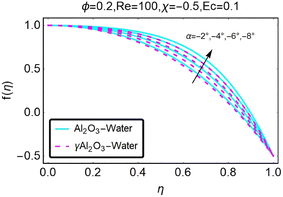 |
| | Fig. 3 Variation in the velocity profile with changes in α. | |
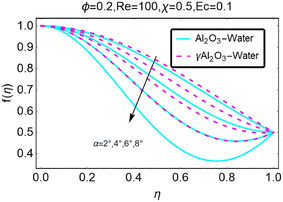 |
| | Fig. 4 Variation in the velocity profile with changes in α. | |
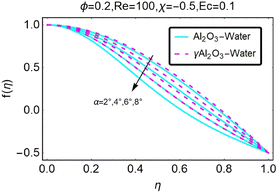 |
| | Fig. 5 Variation in the velocity profile with changes in α. | |
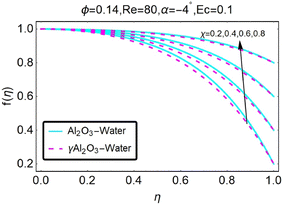 |
| | Fig. 6 Variation in the velocity profile with changes in χ. | |
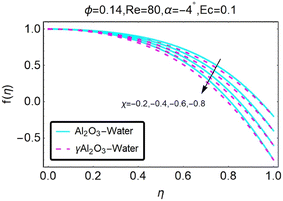 |
| | Fig. 7 Variation in the velocity profile with changes in χ. | |
Fig. 8 illustrates how variations in the velocity profile occur for different values of the variable χ. In the case of the diverging channel and stretching, the velocity increased when the value of χ was increased to higher levels. The variations in the velocity profile that occurred for different values of χ are depicted in Fig. (9). The situation of the diverging channel and diminishing space results in a decrease in velocity for any given value of χ. As shown in Fig. (10), the velocity profile can take on a variety of forms depending on the value of the parameter ϕ. When there is a convergence of flow, also known as stretching, the velocity decreases as the angle of convergence increases. The variations in the velocity profile are depicted for various ϕ values in Fig. (11). When a convergent channel or shrinking scenario is present, a higher value of ϕ results in a decrease in velocity. In the scenario of a diverging channel or stretching, as depicted in Fig. (12), the velocity profile shifts depending on the value of ϕ, with an increase in velocity occurring when ϕ values are higher. Variations in the velocity profile are depicted for a variety of ϕ values in Fig. (13). When the value of ϕ increases, the divergent channel's shrinking condition experiences a greater increase in the velocity. As seen in Fig. (14), the velocity distribution changes depending on the value of Re taken into consideration. When Re increases, the convergent channel/stretching condition experiences a greater increase in velocity. Fig. 15 illustrates how the velocity profile shifts depending on the value of Re, as discussed previously. When the value of Re is increased, the convergent channel or the shrinking instance experiences a greater increase in velocity. Variations in the velocity profile are shown for a range of different Re values in Fig. (16). In the event of a channel that is stretching or diverging, the velocity will decrease while Re will increase. The variations that occur in the velocity profile at varying levels of Re are depicted in Fig. (17). In the scenario of a narrowing and diverging channel, an increase in Re decreases in velocity.
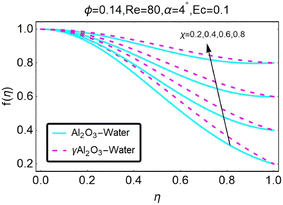 |
| | Fig. 8 Variation in the velocity profile with changes in χ. | |
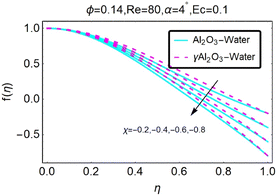 |
| | Fig. 9 Variation in the velocity profile with changes in χ. | |
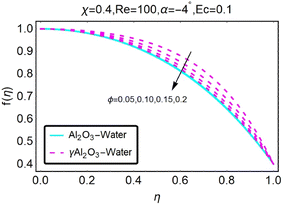 |
| | Fig. 10 Variation in the velocity profile as a function of changes in ϕ. | |
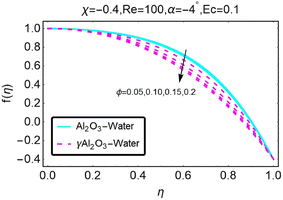 |
| | Fig. 11 Variation in the velocity profile as a function of changes in ϕ. | |
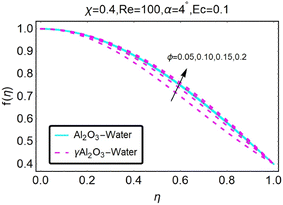 |
| | Fig. 12 Variation in the velocity profile as a function of changes in ϕ. | |
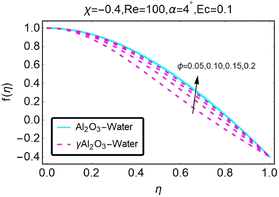 |
| | Fig. 13 Variation in the velocity profile with changes in ϕ. | |
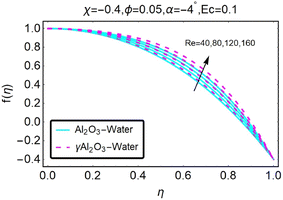 |
| | Fig. 14 Variation in the velocity profile as a function of changes in Re. | |
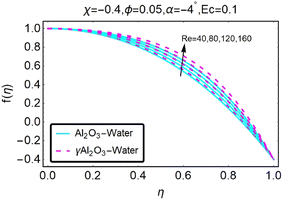 |
| | Fig. 15 Variation in the velocity profile with changes in Re. | |
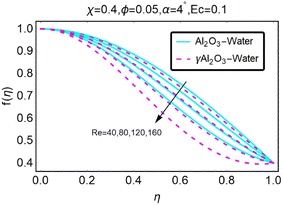 |
| | Fig. 16 Variation in the velocity profile with changes in Re. | |
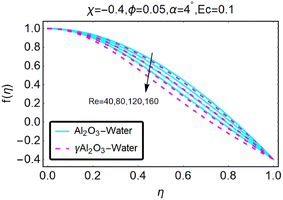 |
| | Fig. 17 Variation in the velocity profile as a function of changes in Re. | |
Temperature profile for Al2O3/water and γ-Al2O3/water with an effective Prandtl number
Next, we examined the behavior of the temperature profile as well as the standard deviations of the pertinent parameters. As a critical factor, the temperature distribution was considered during the development of this part. Based on numerous input variables, these graphs can be used to determine how well the flow functions. As a consequence, increasing or decreasing distinct factors have different impacts on temperature distribution for both values of χ = 0.5 and χ = −0.5 values. Fig. 18–29 illustrates this. When α > 0, it shows the divergent channel and when α < 0 it shows the divergent channel.
The temperature distribution was considered during the process that was occurring in this part because it was an important aspect. The fluctuation in the temperature profile is depicted in Fig. (18). In the case of a convergent channel or stretching, it is self-evident that the temperature will increase as a result of a change in the value of α. The temperature profile is depicted in Fig. (19) for a variety of different (a) values. When the value of α is altered for the convergent channel/shrinking example, it is clear that this results in an increase in temperature. The temperature curve for a variety of α values is shown in Fig. (20). An increase in the value of α for the diverging channel/stretching situation may be investigated, and it can be found that this leads to an increase in temperature.
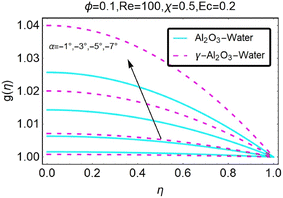 |
| | Fig. 18 Variation in the temperature profile with changes in α. | |
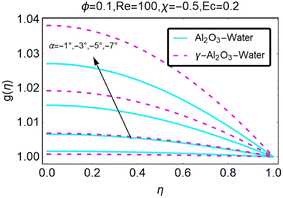 |
| | Fig. 19 Variation in the temperature profile with changes in α. | |
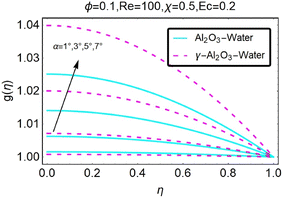 |
| | Fig. 20 Variation in the temperature profile as a function of changes in α. | |
The temperature curve for a variety of α values can be seen in Fig. (21). It is clear that a higher value for α in the diverging channel/shrinking situation results in a higher temperature being reached by the system. The temperature profile is depicted for a variety of values of χ in Fig. (22). It has been observed that an increase in the value of χ results in a rise in temperature when the scenario involves convergent channels and stretching. The temperature curve for a variety of χ values is shown in Fig. (23). Changing the value of χ in the case of convergent channels and shrinking can be seen to result in a decrease in temperature, as can be seen here. The temperature profile is depicted in Fig. (24) for a variety of various χ values. One can make the observation that, in the instance of the divergent channel/stretching, raising the value of χ results in a higher temperature being reached.
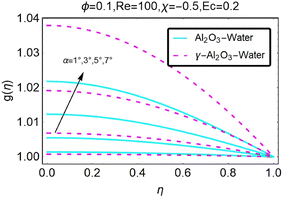 |
| | Fig. 21 Variation in the temperature profile with changes in α. | |
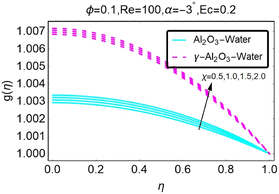 |
| | Fig. 22 Variation in the temperature profile as a function of changes in χ. | |
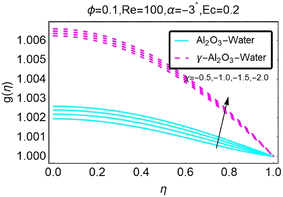 |
| | Fig. 23 Variation in the temperature profile as a function of changes in χ. | |
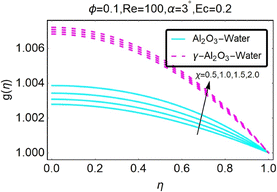 |
| | Fig. 24 Variation in the temperature profile as a function of changes in χ. | |
The temperature profile is depicted in Fig. (25) for a variety of various values of the variable χ. Altering the value of χ in the case of the diverging channel and shrinking can be seen to result in a decrease in temperature. This is something that can be noticed. Fig. (26) illustrates how the temperature profile shifts depending on the value of the temperature field. As can be observed, a decrease in temperature occurs in the convergent channel/stretching situation when the value of ϕ is increased. As shown in Fig. (27), the temperature profile changes for various values of ϕ, the temperature distribution in this region for the occurrence of the turning factor ϕ; raising the value of ϕ leads the temperature in the convergent channel/shrinking scenario to decline, as can be demonstrated in the figure. The temperature distribution in this region for the occurrence of the turning factor ϕ is given in the figure.
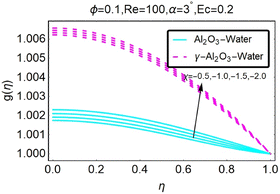 |
| | Fig. 25 Variation in the temperature profile as a function of changes in χ. | |
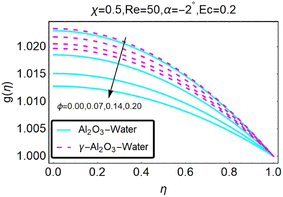 |
| | Fig. 26 Variation in the temperature profile as a function of changes in ϕ. | |
 |
| | Fig. 27 Variation in the temperature profile with changes in ϕ. | |
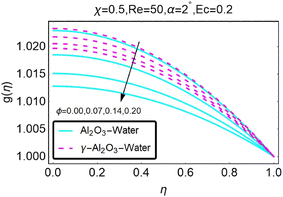
As shown in Fig. (28), the temperature profile changes for different values of ϕ, which represents the temperature distribution in this region for the occurrence of the turning factor. An increase in the value of ϕ produces a decrease in temperature in the divergent channel/stretching scenario, as can be seen in the figure. The temperature profile shifts in response to the occurrence of the turning factor ϕ in Fig. (29), which occurs when the temperature field in this region takes on a range of different values. When the value of ϕ is increased, the diverging channel/shrinking scenario experiences a drop in temperature as a result.
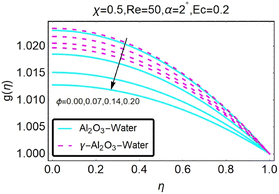 |
| | Fig. 28 Variation in the temperature profile with changes in ϕ. | |
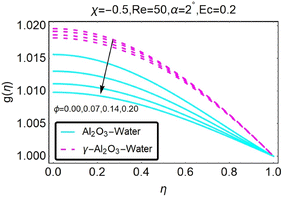 |
| | Fig. 29 Variation in the temperature profile with changes in ϕ. | |
Conclusions
We investigated the constant flow, two-dimensional, nonlinear flow of viscous incompressible gamma nanofluids in a convergent/divergent channel. By completing the parameter analysis, we were able to physically understand the problem. A novel kind of nanofluid, comprising Al2O3/water and γ-Al2O3/water was used. We obtained the following conclusions after numerically and graphically estimating the model. The parameter analysis will provide a better physical understanding of the problem. One of the new types of gamma nanofluids is a mixture of γ-Al2O3/water and Al2O3/water nanofluid:
• If the value of χ for a convergent channel in the stretched case is increased, then the velocity profile will also grow; however, if the value of χ for a convergent channel in the shrinking case is reduced, then the velocity profile will decrease.
• For a channel that is diverging (the stretched case), a greater value of χ will result in a higher velocity profile, whereas for a channel that is shrinking (the contracted case), a lower value of χ will result in a lower velocity profile.
• If the value of χ becomes greater, the temperature profile will change so that it will decrease in the convergent channel (in the case of stretching) while it will grow in the divergent channel (in the case of stretching).
• If the value of χ is decreased, the temperature profile of the convergent/divergent channel (stretching/shrinking) instance will decrease.
• In the case of the convergent channel, also known as the example of stretching and shrinking, the temperature profile rises as α decreases.
• If α becomes larger, the temperature profile for the divergent channel (in either the stretching or shrinking situation) will become larger.
Conflicts of interest
The authors declare there is no financial/competing interest regarding to this work.
Nomenclature
|
T
| Temperature of nanofluid (K) |
| Prnf | Prandtl number of the nanofluid (m2 s−1) |
| Prf | Prandtl number of the base fluid (m2 s−1) |
|
K
nf
| Thermal conductivity of the nanofluid (W (m−1 K−1)) |
|
K
f
| Thermal conductivity of the base fluid (W (m−1 K−1)) |
|
K
s
| Thermal conductivity of the nanoparticles (W (m−1 K−1)) |
|
u,v | Velocity components in x and y direction, respectively (m s−1) |
|
ρ
nf
| Effective density of the nanofluid (kg m−3) |
|
ρ
f
| Density of base fluid (kg m−3) |
|
ρ
s
| Density of the nanoparticles (kg m−3) |
|
μ
nf
| Effective dynamic viscosity of nanofluid (N s m−2) |
|
μ
f
| Dynamic viscosity of the base fluid (N s m−2) |
| (ρCp)nf | Heat capacitance of the fluid (J/K or J K−1) |
| Pr | Prandtl number (—) |
|
ϕ
| Nanoparticle volume fraction (—) |
| Ec | Eckert number (—) |
| Re | Reynolds number (—) |
Subscript
Acknowledgements
The authors appreciate the Deanship of Scientific Research at Imam Mohammad Ibn Saud Islamic University (IMSIU) for supporting and supervising this project. The authors extend their appreciation to the Deputyship for Research & Innovation, Ministry of Education in Saudi Arabia for funding this research through the project number IFP-IMSIU-2023049.
References
- G. B. Jeffery and L. Edinb, Dublin Philos. Mag. J. Sci., 2009, 29, 455–465 CrossRef
 .
.
- A. H. Ganie, Z. Mahmood, U. Khan and M. Y. Almusawa, Int. J. Mod. Phys. C, 2023 DOI:10.1142/S0129183124400011
 .
.
- B. Ullah, U. Khan, H. A. Wahab, I. Khan, D. Baleanu and K. S. Nisar, Comput. Mater. Contin., 2021, 66, 947–960 Search PubMed
 .
.
- U. Khan, B. Ullah, W. Khan and M. Fayz-Al-Asad, Math. Probl. Eng., 2021, 2021, 1–10 Search PubMed
 .
.
-
U. K. Adnan, B. Ullah, H. A. Wahab, I. Ullah, M. A. Almuqrin and I. Khan, Waves Random Complex Media., 2022, pp. 1–16 Search PubMed
 .
.
- W. Khan, U. Khan, B. Ullah, N. Ahmed, I. Khan, A. M. Alqahtani and M. Alam, Math. Probl. Eng., 2023, 103(9), e202200435 Search PubMed
 .
.
- B. Ullah, S. A. Al Qahtani, M. Dahshan, H. A. Wahab and U. Khan, Z. Angew. Math. Mech., 2023, e202200435 CrossRef
 .
.
-
R. Rehman, U. Khan, H. A. Wahab and B. Ullah, Waves Random Complex Media., 2022, pp. 1–16 Search PubMed
 .
.
- B. Ullah, U. Khan, H. A. Wahab, I. Khan and M. Alam, J. Nanomater., 2022, 2022, 8929985 Search PubMed
 .
.
- M. M. Rashidi, N. V. Ganesh, A. A. Hakeem, B. Ganga and G. Lorenzini, Int. J. Heat Mass Transf., 2016, 98, 616–623 CrossRef CAS
 .
.
- A. H. Ganie, Z. Mahmood, M. M. AlBaidani, N. S. Alharthi and U. Khan, Int. J. Mod. Phys. B, 2023, 2350320 CrossRef
 .
.
- U. Khan, N. Ahmed, B. Bin-Mohsen and S. T. Mohyud-Din, Int. J. Numer. Methods Heat Fluid Flow, 2017, 27, 48–63 CrossRef
 .
.
- S. K. Das, N. Putra, P. Thiesen and W. Roetzel, J. Heat Transfer, 2003, 125, 567–574 CrossRef CAS
 .
.
- J. C. Umavathi, A. J. Chamkha, A. Mateen and A. Al-Mudhaf, J. Heat Mass Transfer, 2005, 42, 81–90 CrossRef CAS
 .
.
- S. Parvin, R. Nasrin, M. A. Alim, N. F. Hossain and A. J. Chamkha, J. Heat Mass Transfer, 2012, 55, 5268–5274 CrossRef CAS
 .
.
- M. Turkyilmazoglu, Comput. Fluids, 2014, 100, 196–203 CrossRef
 .
.
- O. D. Makinde, F. Mabood, W. A. Khan and M. S. Tshehla, J. Mol. Liq., 2016, 219, 624–630 CrossRef CAS
 .
.
- S. Parvin, R. Nasrin, M. A. Alim, N. F. Hossain and A. J. Chamkha, J. Heat Mass Transfer, 2012, 55, 5268–5274 CrossRef CAS
 .
.
- J. P. Kumar, J. C. Umavathi, A. J. Chamkha and I. Pop, Appl. Math. Model., 2010, 34, 1175–1186 CrossRef
 .
.
- B. Ullah, B. M. Fadhl, B. M. Makhdoum, K. S. Nisar and U. Khan, Case Stud. Therm. Eng., 2022, 40, 102538 CrossRef
 .
.
- B. Ullah, H. A. Wahab, U. Khan and S. Bhatti, Proc. Inst. Mech. Eng., Part E, 2022, 09544089221112034 Search PubMed
 .
.
- A. J. Chamkha, Int. J. Heat Fluid Flow, 2000, 21, 740–746 CrossRef
 .
.
- S. Izadi, T. Armaghani, R. Ghasemiasl, A. J. Chamkha and M. Molana, Powder Technol., 2019, 343, 880–907 CrossRef CAS
 .
.
- K. A. M. Alharbi, U. Khan, N. A. Ahammad, B. Ullah, H. A. Wahab, M. Zaib and A. M. A. M. Galal, J. Indian Chem. Soc., 2022, 99, 100578 CrossRef CAS
 .
.
- M. Qadeer, U. Khan, S. Ahmad, B. Ullah, M. Mousa and I. Khan, Sci. Rep., 2022, 12, 10214 CrossRef CAS PubMed
 .
.
- A. J. Chamkha, Int. J. Heat Mass Transf., 2002, 45, 2509–2525 CrossRef
 .
.
- A. J. Chamkha, T. Groşan and I. Pop, Int. J. Heat Mass Transf., 2002, 29, 1119–1127 CrossRef
 .
.
- J. Raza, F. Mebarek-Oudina and A. J. Chamkha, Multidiscip. Model. Mater. Struct., 2019, 15, 737–757 CrossRef CAS
 .
.
|
| This journal is © The Royal Society of Chemistry 2023 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *e
*e
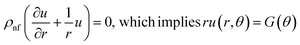
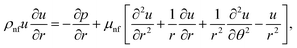
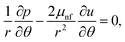
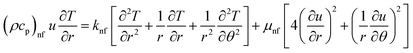
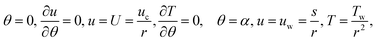
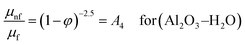
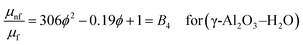
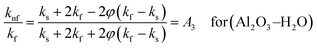
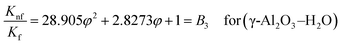
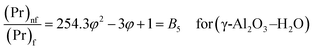
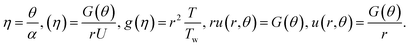
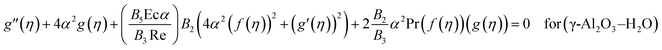
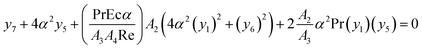
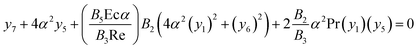
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.