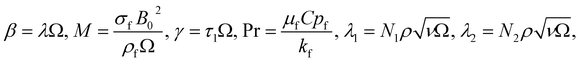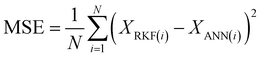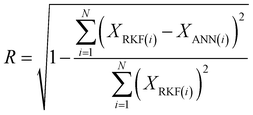Open Access Article
Open Access ArticleHeat transfer analysis in magnetohydrodynamic nanofluid flow induced by a rotating rough disk with non-Fourier heat flux: aspects of modified Maxwell–Bruggeman and Krieger–Dougherty models
Pudhari
Srilatha
a,
Madhu
J
 b,
Umair
Khan
b,
Umair
Khan
 *c,
R. Naveen
Kumar
*c,
R. Naveen
Kumar
 d,
R. J. Punith
Gowda
d,
R. J. Punith
Gowda
 e,
Samia
Ben Ahmed
f and
Raman
Kumar
g
e,
Samia
Ben Ahmed
f and
Raman
Kumar
g
aDepartment of Mathematics, Institute of Aeronautical Engineering, Hyderabad-500043, India. E-mail: pudhari.srilatha@gmail.com
bDepartment of Studies in Mathematics, Davangere University, Davangere, 577007, India. E-mail: madhuelemane09@gmail.com
cDepartment of Computer Science and Mathematics, Lebanese American University, Byblos, Lebanon. E-mail: umair.khan@lau.edu.lb
dDepartment of Mathematics, Amrita School of Engineering, Amrita Vishwa Vidyapeetham, Bengaluru, India. E-mail: nkrmaths@gmail.com
eDepartment of Mathematics, Bapuji Institute of Engineering & Technology, Davanagere 577004, India. E-mail: rjpunithgowda@gmail.com
fDepartment of Chemistry, College of Sciences, King Khalid University, P.O. Box 9004, Abha, Saudi Arabia. E-mail: sbahmad@kku.edu.sa
gDepartment of Mechanical Engineering, University Centre for Research & Development, Chandigarh University, Mohali-140413, Punjab, India. E-mail: raman.me@cumail.in
First published on 13th October 2023
Abstract
Non-Newtonian fluids have unique heat transfer properties compared to Newtonian fluids. The present study examines the flow of a Maxwell nanofluid across a rotating rough disk under the effect of a magnetic field. Furthermore, the Cattaneo–Christov heat flux model is adopted to explore heat transport features. In addition, a comparison of fluid flow without and with aggregation is performed. Using similarity variables, the governing partial differential equations are transformed into a system of ordinary differential equations, and this system is then solved by employing the Runge–Kutta Fehlberg fourth-fifth order method to obtain the numerical solution. Graphical depictions are used to examine the notable effects of various parameters on velocity and thermal profiles. The results reveal that an increase in the value of Deborah number decreases the velocity profile. An increase in the thermal relaxation time parameter decreases the thermal profile. An artificial neural network is employed to calculate the rate of heat transfer and surface drag force. The R values for skin friction and Nusselt number were computed. The results demonstrate that artificial neural networks accurately predicted skin friction and Nusselt number values.
1. Introduction
Non-Newtonian liquids (NNLs) are now receiving a lot of attention from investigators in the fluid dynamics research field. Such inspiration stems from using such materials in paper manufacture, oil recovery cosmetics, polymers, sustenance preparation, melting of plastics, coal slurries, clay mixtures, and beautifying agents. Furthermore, the varied features of NNLs cannot be managed by a single constitutive relation. In general, differential, integral, and rate-type classifications have been established in this manner. Also, stratification is essential in many manufacturing and engineering processes utilizing NNLs. The first viscoelastic rate-type model is the Maxwell model. The performance of numerous polymeric liquids has been predicted using this model with some success in recent years. However, the Maxwell model does not precisely capture the usual correlation between the shear rate and stress in a shear flow. Additionally, it has been specially employed for problems requiring a brief period of dimensionless relaxation. The heat transport mechanism in the flow of Maxwell fluid (MF) past a permeable stretchy sheet (SS) was described by Madhu et al.1 The magnetic dipole impact on the flow of MF via an SS was probed by Kumar et al.2 With the significance of diffusion impact, Shah et al.3 scrutinized the MF flow on a vertical sheet. Prasannakumara4 examined the MF flow via a permeable medium with the consequence of a magnetic dipole. Lie symmetry transformations were employed by Bhatti et al.5 to study the MF flow over an SS.Due to their superior qualities compared to conventional heat-transfer liquids, nanofluids have attracted the attention of many researchers. Nanofluids are composed of solid nanoparticles (NPs) that range in size from 1 to 100 nm. All substances with diameters smaller than 100 nm are considered as NPs. Numerous researchers have recently investigated how various nanofluids flow over various surfaces. Sarfraz and Khan6,7 explored the impact that nanoparticle suspensions have on the flow of numerous distinct base fluids across various kinds of surfaces by considering different factors that influence the flow and heat transport. Recently, numerous researchers examined the flow of different nanofluids past different surfaces along with a suspension of titania nanoparticles.8–10 It is possible to further improve heat-transfer efficiency and liquid stability by using NPs with a much larger surface and smaller size. NP aggregations affect both rheological and thermal properties. One of the main elements influencing the aggregation of nanoparticles is surface charge. Therefore, aggregation plays a significant role in the thermal applications of any nanofluid. The NP aggregation tends to build linear chains and percolating networks to provide a path with less heat resistance. Therefore, heat may be quickly transferred across the clusters as a result. This might enhance the nanofluid's thermal conductivity since the effective aggregation volume is greater than it is for NPs. The importance of NP aggregation on the nanoliquid flow via a flat surface was scrutinized by Sabu et al.11 Alsulami et al.12 inspected the influence of NP aggregation on the nanofluid flow on a spinning disk. The NP aggregation effect and thermal performance of nanofluid flow via a squeezing channel were debriefed by Adnan et al.13 Ali et al.14 described the significance of NP aggregation in nanofluid flow across a revolving surface. Makhdoum et al.15 studied the flow of nanoliquids past a SS with the impact of NP aggregation.
The impact of roughness on pressure losses in various geometries has been studied for many years, even though roughness is normally considered to be damaging to boundary layer flows. The basic transition processes of three-dimensional boundary layers have long been studied using the rotating-disk system's hydrodynamic instability. The continuous incompressible flow brought on by the rotation of an endless, smooth plane at a given angular velocity was the subject of ground-breaking research by Von Kármán. The heat transport of the fluid flow via a permeable rough rotating disk was described by Turkyilmazoglu and Senel.16 The flow of NNL between rotating disks using the Hall effect was analysed by Krishna and Chamkha.17 Mukherjee and Sahoo18 investigated the fluid flow across a rough spinning disk under slip conditions. Thermophysical attributes of fluids and gases over a rotating rough disk were studied by Khan et al.19 Pei et al.20 explored the nanofluid flow across a rough spinning disk in the presence of a magnetic field.
The use of a driving force, such as a magnetic field, can support the survivability of drug delivery systems after transduction and promote high transduction efficiency. By adjusting the magnetic field strength, this method may be utilized to adjust the effectiveness of delivery in addition to delivering the medications in a relatively short period. Nowadays, using an external magnetic field to control the welding process is a successful technique due to the magnetic control system's low cost and ease of implementation. The external magnetic field is used to regulate the molten metal flow and alter the element distribution. The magnetic field's influence on the fluid flow past a wedge and cone was scrutinized by Chamkha.21 The fluid flow over a permeable medium with the significance of a magnetic field was examined by Chamkha.22 Khan et al.23 described how the magnetic field affected the flow of Sisko fluid past a permeable surface. Takhar et al.24,25 discussed a magnetic field's influence on the flow of different fluids past a diverse surfaces with several influencing factors. Sarfraz et al.26 scrutinized the flow of fluid via a disk in the presence of a magnetic field. Krishna et al.27,28 investigated the effect that a magnetic field has on the flow of various fluids through different surfaces with several elements that affect the flow. The magnetic field impact on the flow of different fluids via diverse surfaces with several factors influencing the flow was examined by Chamkha and Rashad.29,30
Fourier is mainly responsible for the development of the law of heat conduction. It should be mentioned that the Fourier law of conduction for heat transfer and other classical laws have been used to analyze heat and mass transport. Cattaneo altered this relationship by considering thermal relaxation time. Christov explored the Oldroyd upper convective time derivative, a modified version of the Cattaneo model, commonly known as the Cattaneo–Christov (CC) model. Thermal and solutal relaxation durations are used to combat this inefficiency. CC mass and heat flux models are explored to examine the characteristics of the thermal and solvate aspects in mass and heat transport. The heat flux impact on the fluid flow through a surface was presented by Shilpa and Leela.31 The hybrid nanoliquid flow past a stretchy channel in the presence of CC heat flux was probed by Muhammad et al.32 The significance of CC heat flux in the fluid flow via a convectively heated surface was investigated by Sreelakshmi et al.33 Using the CC heat flux model, Gowda et al.34 studied the transport of heat in a flow of NNL via an SS. Using a numerical scheme, Sarfraz and Khan35 emphasized the flow of nanofluid via a moving plate in the presence of CC heat flux.
Very little attention has been given to studying this kind of problem, according to the literature that is currently available on the fluid flow over rough rotating disks. This study aims to close this research gap in the literature and investigate the magnetic field impact on the flow of Maxwell nanofluid over a rough rotating disk. By including the heat flux relaxation rate in the constitutive equation, the Cattaneo–Christov theory is applied to consider additional aspects of heat transport and avoid the restrictions of Fourier's laws. For transforming governing equations into nonlinear ordinary differential equations (ODEs), von Kármán's similarity approach is used. Runge–Kutta Fehlberg's fourth-fifth (RKF-45) order method is utilized to get the numerical solution. Artificial neural network models are developed to estimate the skin friction and Nusselt number.
2. Mathematical formulation
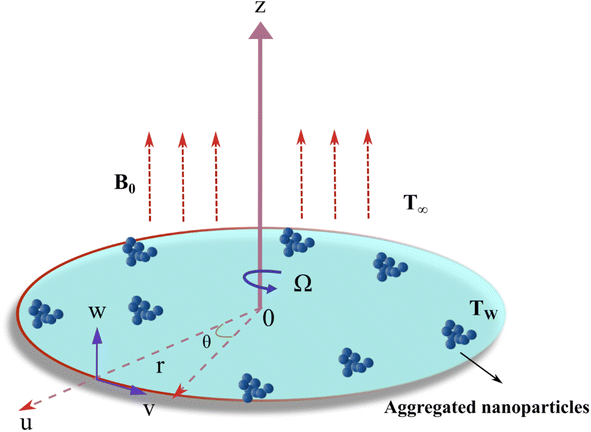
This analysis focuses on the characteristics of a laminar, axially symmetric, and electrically conducting viscous flow. The objective is to investigate the Maxwell nanofluid flow produced by an infinite disk that undergoes steady rotation with an angular velocity Ω around the axial axis z. The flow geometry is shown in Fig. 1. The inclusion of the Cattaneo–Christov heat flux theory characterizes the constitutive temperature equation.The governing equations can be expressed as follows based on the abovementioned assumptions.
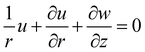 | (1) |
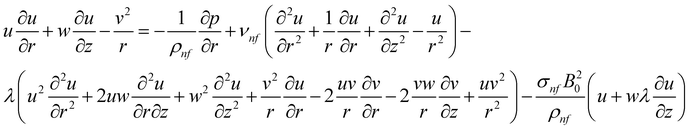 | (2) |
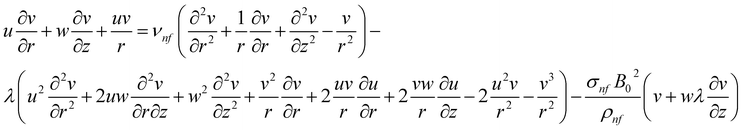 | (3) |
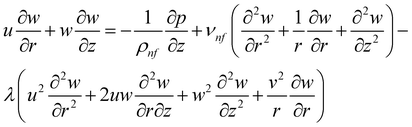 | (4) |
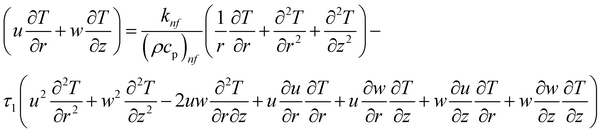 | (5) |
Along with the boundary conditions:
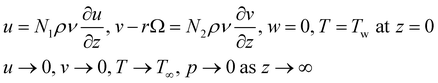 | (6) |
2.1. Thermal and physical features of the aggregation scheme
This study section demonstrates that nanoliquids have a high thermal conductivity (HTCN) as supported by the experimental data. To further enhance thermal characteristics, irregular NP movement or active galactic nuclei (AGNs) of NPs that result in natural drainage activity might be used. The Brownian random movement experiences a decline compared to AGN, leading to an increase in the total mass. However, the propensity towards total categorization may enhance heat conductivity. Therefore, in the case of non-primordial AGN, density, the effective absolute viscosity (EAV), heat capacitance, and thermal conductivity of the nanofluid are determined based on previous studies (see ref. 36–38).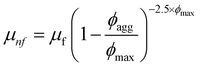 | (7) |
| ρnf = (1 − ϕagg)ρf + (ϕρ)agg | (8) |
| (ρCp)nf = (1 − ϕagg)(ρCp)f + ϕagg(ρCp)agg | (9) |
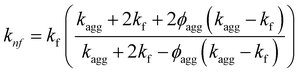 | (10) |
Aggregation of particles according to their thermal properties:
The mathematical equations representing the correlations for the EAV and TCN can be derived from established sources such as the modified Krieger model and, more specifically, the Dougherty model and the modified Maxwell model. These models provide a basis for understanding and analyzing the relationship between the EAV and TCN. which can be interpreted as
 | (11) |
| ρagg = ρf(1 − ϕint) + ρsϕint | (12) |
| (ρCp)agg = (ρCp)f(1 − ϕint) + (ρCp)sϕint | (13) |
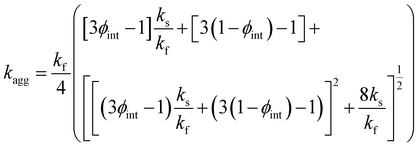 | (14) |
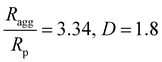 (see ref. 26–28).
(see ref. 26–28).
Considering the similarity transformation as follows
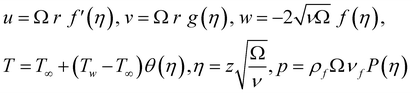 | (15) |
Simply by fitting eqn (15) into governing eqn (1)–(5), we can get the following reduced equations:
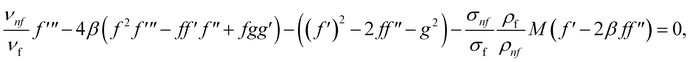 | (16) |
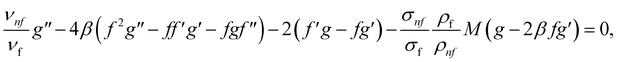 | (17) |
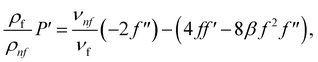 | (18) |
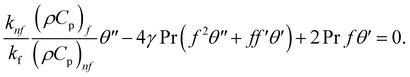 | (19) |
Along with the reduced boundary constraints:
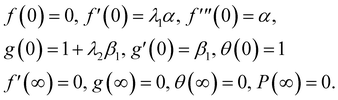 | (20) |
In the equations above, the non-dimensional parameters are defined as follows:
The expressions for the reduced skin-friction coefficient and the local Nusselt number are given as:
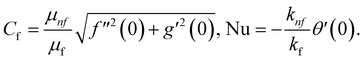 | (21) |
3. Results and discussion
The influence of several parameters such as λ1 (scaled radial slip co-efficient), γ (thermal relaxation parameter), β (Deborah number) and M (magnetic parameter) on various profiles was examined in this section. Nonlinear ODEs are numerically solved by the RKF-45 approach to better understand the problem's attributes. Graphs are used to analyze the effectiveness of the various constraints on the profiles involved. Two scenarios are considered in this study: (a) one with aggregation (ϕint ≠ 1)and (b) one without aggregation(ϕint = 1). The dashed lines represent the flow without aggregation of NPs, whereas the solid lines indicate the flow with aggregation of NPs. The thermophysical characteristics of base liquid and NPs are shown in Table 1. Table 2 represents the validation of the present model with published results.| μ (kg m−1 s−1) | C p (J kg−1 K−1) | k (W mK−1) | ρ (kg m−3) | |
|---|---|---|---|---|
| Ethylene glycol | 0.0157 | 2415 | 0.252 | 1114 |
| TiO2 | — | 686.2 | 8.9538 | 4250 |
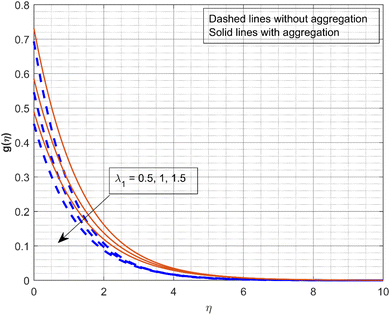
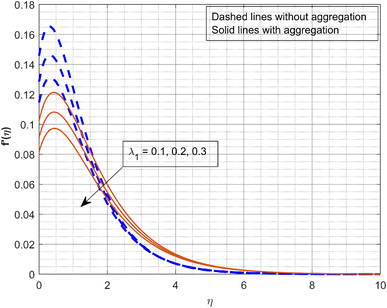
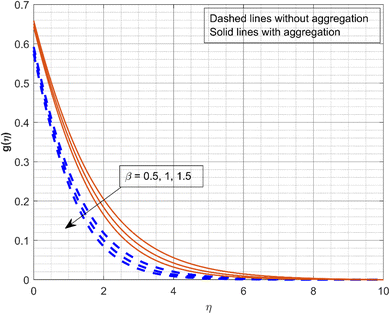
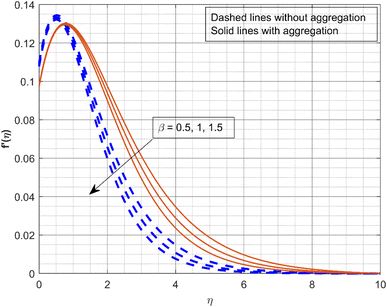
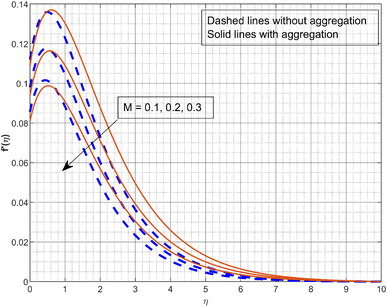
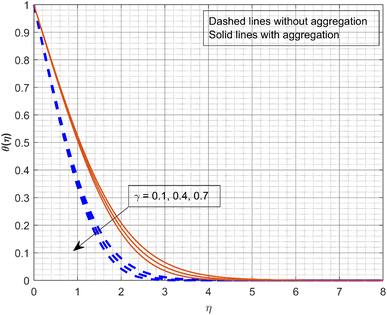
Fig. 2 and 3 illustrate the impact of the scaled radial slip co-efficient λ1 on g(η) and f′(η). As the values of λ1 increase, the velocity profiles are decreased. Centrifugal forces cause the induced radial velocity profile to start at zero, attain a maximum, and then decrease to zero without slipping. However, the maximum velocity decreases and moves closer to it as the disk slips. The significance of β on velocity profiles g(η) and f′(η) is displayed in Fig. 4 and 5. The Deborah number is a dimensionless quantity associated with the relaxation time or the amount of time the fluid needs to reach equilibrium after being subjected to stress. Fluids with a low Deborah number behave like liquids, while substances with a greater Deborah number behave like solids. When the β increases (0.5, 1, and 1.5), the fluid becomes more viscous, which increases the flow resistance and lowers velocity. Fig. 6 depicts the impact of M on f′(η). It is demonstrated that the f′(η) significantly declines as the M increases. As a consequence of the Lorentz force opposing motion in the system, as the values of M become greater, the velocity profiles declines. It appears from the figure that at greater values of M, the liquid velocity declines more quickly with NP aggregation. Fig. 7 portrays the consequence of γ on thermal profile. The rise in values of γ (0.1, 0.4, and 0.7) decreases the thermal profile as depicted in the figure. As the thermal relaxation parameter increases, the thermal boundary layer thickness and fluid temperature decrease. In fact, for increasing estimations of γ, liquid particles require a long time to transmit heat, resulting in a decrease in fluid temperature.
4. Artificial neural network modelling
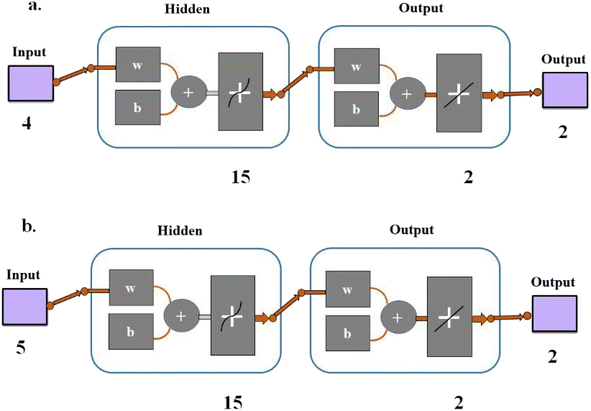
One of the methods with great performance in modelling nonlinear systems is artificial neural networks (ANNs), which were developed by taking inspiration from the structure of the human brain. The multi-layer perceptron (MLP) network is one of the often-employed ANN models.41–45 This ANN has an input layer, an output layer, and at least one hidden layer. A neuron is a computational component found in interconnected layers. In ANN training, feed-forward-back propagation (FF-BP) networks are common techniques. This algorithm's feed-forward phase from the input layer involves processing and dispersing data to the output layer. The errors between the target and predicted data are determined during the back-propagation process. The training procedure is carried out repeatedly until the number of errors is reduced, and it finishes at the lowest error rate.In this work, to calculate the skin friction (SF) and Nusselt number (Nu), ANN models were developed. The input for the SF model is given to the ANN training by varying the values of M, β, λ1, and λ2. The skin friction values achieved by using various values of M, β, λ1, and λ2 are taken as target data for the cases with aggregation and without aggregation of the nanoparticles. Furthermore, the equally divided data samples of M, β, γ, λ1, and λ2 are considered as the input whereas the heat transfer rate (Nu) obtained by varying the aforementioned parameter is treated as target values in the output layer for both cases of nanoparticle aggregation and without aggregation.
Three regions of the data sets were utilized to train the ANN models, 70% were used to train the model, 15% of the data were utilized for model validation, and 15% for testing. 15 neurons in its hidden layer, R values and mean square error (MSE) were used to assess the performance of an ANN.
The surface drag force and heat transfer rate for the Maxwell nanofluid are studied in this research work, and the established ANN model is indicated in the structure as displayed in Fig. 8a and b.
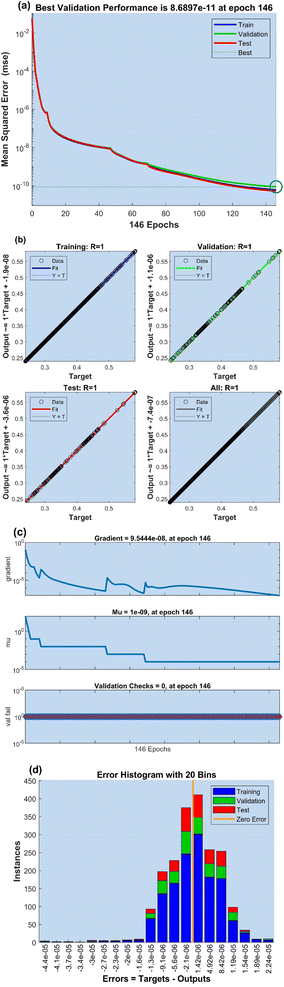
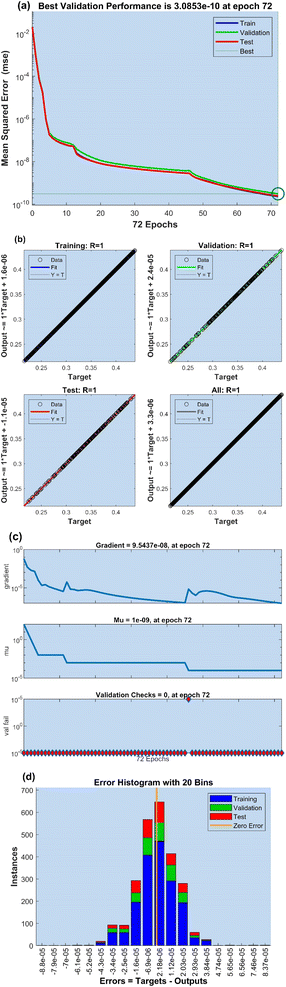
Fig. 9a and 10a display the validation performance of the developed ANN for SF and Nu models, respectively. Observing the graph, it can be noticed that values of MSE, which were large at the beginning of the ANN training phase, reduced as the training period progressed. For the SF model, the lowest MSE value of 8.6897 × 10−11 is attained in the 146th epoch, as shown in Fig. 9a, whereas at epoch 72, s MSE value of 3.0853 × 10−10 is achieved for the Nu model as portrayed in Fig. 10a. It is evident from the graphs that the ANN training phase is finished in the best possible way when the lines representing the training, validation, and test phases converge to the ideal (best) line.
Fig. 9b and 10b compare the data collected during the ANN training, validation, and test process with the target data for SF and Nu models, respectively. For the training, validation, and test phase, the dotted line, equality line, and R-value of 1 all show that the data points are near the zero-error line, indicating that the ANN's training, validation, and test phase is successfully performed with a very small error rate. All the data gathered during the three ANN steps are provided. The graph shows that the data points acquired using an ANN are on zero error and compatibility lines. The fact that the R-value is close to 1 and that the data points are in the right place proves that the ANN's training procedure is accurately presented.
The gradient, Mu and validation checks obtained from the training stages for SF and Nu models are shown in Fig. 9c and 10c, respectively. At epoch 146, a gradient value of 9.5444 × 10−8 with an Mu value of 1 × 10−9 is achieved for the SF model as shown in Fig. 9c. For the Nu model, in the 72nd epoch, a gradient value of 9.5437 × 10−8 is attained corresponding to Mu's value of 1 × 10−9 which can be seen in Fig. 10c.
Fig. 9d and 10d present the error histogram of developed ANN models for SF and Nu, respectively. When doing a performance study of the ANN training process, it is crucial to look at the error rates of the ANN's estimations. Using the difference between the output value and the target values as a measure of error, the figure presents the error amounts. The graph clearly shows that the lowest error rates are found at 1.42 × 10−6 and 2.18 × 10−6 for SF and Nu models, respectively, and are very close to the zero-error line. Another indication that the ANN has been trained accurately is low error rates.
5. Conclusion
In the current study, the flow of Maxwell nanofluid is investigated under the impact of a magnetic field and nanoparticle aggregation across a rough rotating disk. The Cattaneo–Christov heat flux models are adopted. Using suitable similarity transformations, the governing PDEs are transformed into ODEs. To solve the ODEs, the RKF-45 method is utilized. The visual representation shows how various nondimensional factors affect flow and heat transport. The ANN technique effectively predicted the surface drag force and heat transfer rate. The key findings of the current inquiry are as follows.❖ The velocity profiles decrease as the values of the scaled radial slip co-efficient increase.
❖ When the magnetic parameter increases, the velocity profile reduces.
❖ An increase in the thermal relaxation time parameter values decreases the temperature profile.
❖ The MSE value for the ANN model established to predict the values of the skin friction coefficients is 8.6897 × 10−11, and the R value is 1.
❖ The MSE value for the ANN model established to predict the values of the Nusselt number is 3.0853 × 10−10, and the R value is 1.
Nomenclature
| ν | Kinematic viscosity |
| k | Thermal conductivity |
| λ 1 | Scaled radial slip coefficient |
| N 1 and N2 | Slip coefficient |
| T | Temperature |
| T ∞ | |Ambient temperature |
| (u,v,w) | Velocity components |
| M | Magnetic parameter |
| Pr | Prandtl number |
| λ | Relaxation time |
| σ | Electrical conductivity |
| B 0 | Strength of the magnetic field |
| C f | Skin friction |
| nf | Nanofluid |
| agg | Aggregation |
| ρ | Density |
| ρC p | Heat capacitance |
| λ 2 | Scaled azimuthal slip coefficient |
| μ | Dynamic viscosity |
| η | Dimensionless similarity coordinate |
| β | Deborah number |
| f(η) | Non-dimensional velocity profile |
| Ω | Angular velocity |
| p | Pressure |
| τ 1 | Heat diffusion relaxation time |
| Nu | Local Nusselt number |
| ϕ | Solid volume fraction of nanoparticles |
| f | Fluid |
| int | Initial |
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University for funding this work through large group Research Project under grant number RGP2/3/44.References
- M. Madhu, N. Kishan and A. J. Chamkha, Unsteady flow of a Maxwell nanofluid over a stretching surface in the presence of magnetohydrodynamic and thermal radiation effects, Propuls. Power Res., 2017, 6(1), 31–40, DOI:10.1016/j.jppr.2017.01.002.
- R. Naveen Kumar, A. M. Jyothi, H. Alhumade, R. J. Punith Gowda, M. M. Alam, I. Ahmad, M. R. Gorji and B. C. Prasannakumara, Impact of magnetic dipole on thermophoretic particle deposition in the flow of Maxwell fluid over a stretching sheet, J. Mol. Liq., 2021, 334, 116494, DOI:10.1016/j.molliq.2021.116494.
- N. A. Shah, O. Tosin, R. Shah, B. Salah and J. D. Chung, Brownian motion and thermophoretic diffusion effects on the dynamics of MHD upper convected maxwell nanofluid flow past a vertical surface, Phys. Scr., 2021, 96, 125722, DOI:10.1088/1402-4896/ac36ea.
- B. C. Prasannakumara, Numerical simulation of heat transport in Maxwell nanofluid flow over a stretching sheet considering magnetic dipole effect, Partial Differ. Equ. Appl., 2021, 4, 100064 Search PubMed.
- M. M. Bhatti, A. Shahid, I. E. Sarris and O. Anwar Bég, Spectral relaxation computation of Maxwell fluid flow from a stretching surface with quadratic convection and non-Fourier heat flux using Lie symmetry transformations, Int. J. Mod. Phys. B, 2023, 37, 2350082, DOI:10.1142/S0217979223500820.
- M. Sarfraz and M. Khan, Thermodynamic irreversibility analysis of water conveying argentum and titania nanoparticles subject to inclined stretching surface, Phys. Scr., 2023, 98, 025205, DOI:10.1088/1402-4896/acab92.
- M. Sarfraz and M. Khan, Magnetized homann flow comprising GO and Co3O4 nanoparticles past a biaxially stretching surface, Phys. Scr., 2023, 98, 035218, DOI:10.1088/1402-4896/acba61.
- A. J. Chamkha, C. Issa and K. Khanafer, Natural convection from an inclined plate embedded in a variable porosity porous medium due to solar radiation, Int. J. Therm. Sci., 2002, 41, 73–81, DOI:10.1016/S1290-0729(01)01305-9.
- R. S. R. Gorla, A. J. Chamkha and A. M. Rashad, Mixed convective boundary layer flow over a vertical wedge embedded in a porous medium saturated with a nanofluid: Natural Convection Dominated Regime, Nanoscale Res. Lett., 2011, 6, 207, DOI:10.1186/1556-276X-6-207.
- M. V. Krishna and A. J. Chamkha, Hall and ion slip effects on Unsteady MHD Convective Rotating flow of Nanofluids—Application in Biomedical Engineering, J. Egypt. Math. Soc., 2020, 28, 1, DOI:10.1186/s42787-019-0065-2.
- A. Sabu, J. Mackolil, B. Mahanthesh and A. Mathew, Nanoparticle aggregation kinematics on the quadratic convective magnetohydrodynamic flow of nanomaterial past an inclined flat plate with sensitivity analysis, Proc. Inst. Mech. Eng., Part E, 2022, 236, 1056–1066, DOI:10.1177/09544089211056235.
- M. D. Alsulami, A. Abdulrahman, R. Naveen Kumar, R. J. Punith Gowda and B. C. Prasannakumara, Three-Dimensional Swirling Flow of Nanofluid with Nanoparticle Aggregation Kinematics Using Modified Krieger–Dougherty and Maxwell–Bruggeman Models: A Finite Element Solution, Mathematics, 2023, 11(9), 2081 CrossRef.
- Adnan, K. Abdulkhaliq, M. Alharbi, M. Z. Bani-Fwaz, S. M. Eldin and M. F. Yassen, Numerical heat performance of TiO2/Glycerin under nanoparticles aggregation and nonlinear radiative heat flux in dilating/squeezing channel, Case Stud. Therm. Eng., 2023, 41, 102568, DOI:10.1016/j.csite.2022.102568.
- B. Ali, I. Siddique, H. Ahmad and S. Askar, Influence of nanoparticles aggregation and Lorentz force on the dynamics of water-titanium dioxide nanoparticles on a rotating surface using finite element simulation, Sci. Rep., 2023, 13, 4702, DOI:10.1038/s41598-023-31771-w.
- B. M. Makhdoum, Z. Mahmood, B. M. Fadhl, M. S. Aldhabani, U. Khan and S. M. Eldin, Significance of entropy generation and nanoparticle aggregation on stagnation point flow of nanofluid over stretching sheet with inclined Lorentz force, Arabian J. Chem., 2023, 16, 104787, DOI:10.1016/j.arabjc.2023.104787.
- M. Turkyilmazoglu and P. Senel, Heat and mass transfer of the flow due to a rotating rough and porous disk, Int. J. Therm. Sci., 2013, 63, 146–158, DOI:10.1016/j.ijthermalsci.2012.07.013.
- M. V. Krishna and A. J. Chamkha, Hall effects on MHD squeezing flow of a water-based nanofluid between two parallel disks, J. Porous Media, 2019, 22(2), 209–223, DOI:10.1615/JPorMedia.2018028721.
- D. Mukherjee and B. Sahoo, The Effect of Slip on the Convective Instability Characteristics of the Stagnation Point Flow Over a Rough Rotating Disk, Kyungpook Math. J., 2021, 61, 831–843, DOI:10.5666/KMJ.2021.61.4.831.
- M. Khan, T. Salahuddin, M. Awais and B. Al Alwan, Thermo-physical properties of fluid and gases near a solar rough rotating disk, Waves Random Complex Media, 2022, pp. 1–16, DOI:10.1080/17455030.2022.2070685.
- Y.-X. Pei, X.-L. Zhang, L.-C. Zheng and X.-Z. Wang, Coupled flow and heat transfer of power-law nanofluids on non-isothermal rough rotary disk subjected to magnetic field, Chin. Phys. B, 2022, 31, 064402, DOI:10.1088/1674-1056/ac46bd.
- A. J. Chamkha, Non-Darcy hydromagnetic free convection from a cone and a wedge in porous media, Int. Commun. Heat Mass Transfer, 1996, 23, 875–887, DOI:10.1016/0735-1933(96)00070-X.
- A. J. Chamkha, MHD-free convection from a vertical plate embedded in a thermally stratified porous medium with Hall effects, Appl. Math. Model., 1997, 21, 603–609, DOI:10.1016/S0307-904X(97)00084-X.
- U. Khan, A. Zaib and A. Ishak, Magnetic Field Effect on Sisko Fluid Flow Containing Gold Nanoparticles through a Porous Curved Surface in the Presence of Radiation and Partial Slip, Mathematics, 2021, 9, 921, DOI:10.3390/math9090921.
- H. S. Takhar, A. J. Chamkha and G. Nath, Unsteady mixed convection flow from a rotating vertical cone with a magnetic field, Heat Mass Transfer, 2023, 39, 297–304, DOI:10.1007/s00231-002-0400-1.
- H. S. Takhar, A. J. Chamkha and G. Nath, MHD flow over a moving plate in a rotating fluid with magnetic field, Hall currents and free stream velocity, Int. J. Eng. Sci., 2002, 40, 1511–1527, DOI:10.1016/S0020-7225(02)00016-2.
- M. Sarfraz, M. Khan and M. Yasir, Dynamics of water conveying iron oxide and graphene nanoparticles subject to stretching/spiraling surface: an asymptotic approach, Ain Shams Eng., 2023, 14(8), 102021, DOI:10.1016/j.asej.2022.102021.
- M. V. Krishna, B. V. Swarnalathamma and A. J. Chamkha, Investigations of Soret, Joule and Hall effects on MHD rotating mixed convective flow past an infinite vertical porous plate, J. Ocean Eng. Sci., 2019, 4, 263–275, DOI:10.1016/j.joes.2019.05.002.
- M. V. Krishna, N. A. Ahammad and A. J. Chamkha, Radiative MHD flow of Casson hybrid nanofluid over an infinite exponentially accelerated vertical porous surface, Case Stud. Therm. Eng., 2021, 27, 101229, DOI:10.1016/j.csite.2021.101229.
- `A. J. Chamkha and A. M. Rashad, Unsteady heat and mass transfer by MHD mixed convection flow from a rotating vertical cone with chemical reaction and Soret and Dufour effects, Can. J. Chem. Eng., 2014, 92, 758–767, DOI:10.1002/cjce.21894.
- A. J. Chamkha and A. M. Rashad, Natural convection from a vertical permeable cone in a nanofluid saturated porous media for uniform heat and nanoparticles volume fraction fluxes, Int. J. Numer. Methods Heat Fluid Flow, 2012, 22, 1073–1085, DOI:10.1108/09615531211271871.
- B. Shilpa and V. Leela, Galerkin finite element analysis of heat and mass transfer of Jeffrey, Maxwell and Oldroyd-B nanofluids in a vertical annulus with an induced magnetic field and a non–uniform heat source/sink, Int. J. Ambient Energy, 2023, 1–17 Search PubMed.
- K. Muhammad, T. Hayat, S. Momani and S. Asghar, FDM analysis for squeezed flow of hybrid nanofluid in presence of Cattaneo-Christov (C-C) heat flux and convective boundary condition, Alexandria Eng. J., 2022, 61, 4719–4727, DOI:10.1016/j.aej.2021.10.027.
- T. K. Sreelakshmi, A. Abraham, A. S. Chethan, E. R. El-Zahar, C. S. K. Raju, B. T. Raju and N. A. Shah, Dynamics of ferromagnetic due to nonlinear thermal buoyancy when Cattaneo–Christov heat flux and magnetic dipole whose magnetic scalars are significant, Waves Random Complex Media, 2022, pp. 1–20, DOI:10.1080/17455030.2022.2028931.
- R. J. Punith Gowda, R. Naveen Kumar, R. Kumar and B. C. Prasannakumara, Three-dimensional coupled flow and heat transfer in non-newtonian magnetic nanofluid: an application of Cattaneo-Christov heat flux model, J. Magn. Magn. Mater., 2023, 567, 170329, DOI:10.1016/j.jmmm.2022.170329.
- M. Sarfraz and M. Khan, Cattaneo-Christov double diffusion-based heat transport analysis for nanofluid flows induced by a moving plate, Numer. Heat Transfer, Part A, 2023, 1–13, DOI:10.1080/10407782.2023.2186551.
- R. Ellahi, M. Hassan and A. Zeeshan, Aggregation effects on water base Al2O3—nanofluid over permeable wedge in mixed convection, Asia-Pac, J. Chem. Eng., 2016, 11, 179–186, DOI:10.1002/apj.1954.
- N. Acharya, K. Das and P. K. Kundu, Effects of aggregation kinetics on nanoscale colloidal solution inside a rotating channel, J. Therm. Anal. Calorim., 2019, 138, 461–477, DOI:10.1007/s10973-019-08126-7.
- L. Th. Benos, E. G. Karvelas and I. E. Sarris, Crucial effect of aggregations in CNT-water nanofluid magnetohydrodynamic natural convection, Therm. Sci. Eng. Prog., 2019, 11, 263–271, DOI:10.1016/j.tsep.2019.04.007.
- J. Mackolil and B. Mahanthesh, Sensitivity analysis of Marangoni convection in TiO2–EG nanoliquid with nanoparticle aggregation and temperature-dependent surface tension, J. Therm. Anal. Calorim., 2021, 143, 2085–2098, DOI:10.1007/s10973-020-09642-7.
- N. Kelson and A. Desseaux, Note on porous rotating disk flow, Anziam J., 2000, 42, C837eC855 CrossRef.
- B. Shilpa and V. Leela, An artificial intelligence model for heat and mass transfer in an inclined cylindrical annulus with heat generation/absorption and chemical reaction, Int. Commun. Heat Mass Transfer, 2023, 147, 106956, DOI:10.1016/j.icheatmasstransfer.2023.106956.
- B. Shilpa, V. Leela, B. C. Prasannakumara, and P. Nagabhushana, Soret and Dufour Effects on MHD Double-Diffusive Mixed Convective Heat and Mass Transfer of Couple Stress Fluid in a Channel Formed by Electrically Conducting and Non-conducting Walls', Waves Random Complex Media, 2022, pp. 1–22, DOI:10.1080/17455030.2022.2119491.
- R. S. V. Kumar, M. D. Alsulami, I. E. Sarris, G. Sowmya and F. Gamaoun., Stochastic Levenberg–Marquardt Neural Network Implementation for Analyzing the Convective Heat Transfer in a Wavy Fin, Mathematics, 2023, 11(10), 2401 CrossRef.
- R. S. Varun Kumar, M. D. Alsulami, I. E. Sarris, B. C. Prasannakumara and S. Rana., Backpropagated neural network modeling for the non-fourier thermal analysis of a moving plate, Mathematics, 2023, 11(2), 438 CrossRef.
- K. V. Nagaraja, et al., Heat and mass transfer analysis of assisting and opposing radiative flow conveying ternary hybrid nanofluid over an exponentially stretching surface, Sci. Rep., 2023, 13, 14795, DOI:10.1038/s41598-023-41916-6.
| This journal is © The Royal Society of Chemistry 2023 |