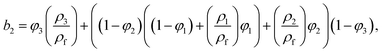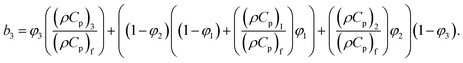Open Access Article
Open Access ArticleThermal performance of Fe3O4, SWCNT, MWCNT and H2O based on magnetohydrodynamic nanofluid flow across a wedge with significant impacts of Soret and Dufour
K.
Vinutha
a,
K. V.
Nagaraja
 b,
Kiran
Sajjan
b,
Kiran
Sajjan
 c,
Umair
Khan
c,
Umair
Khan
 *de,
J. K.
Madhukesh
*de,
J. K.
Madhukesh
 b,
Uma C.
Kolli
f and
Taseer
Muhammad
g
b,
Uma C.
Kolli
f and
Taseer
Muhammad
g
aDepartment of Studies in Mathematics, Davangere University, Davangere 577002, India. E-mail: vinuthavinu392@gmail.com
bDepartment of Mathematics, Amrita School of Engineering, Amrita Vishwa Vidyapeetham, Bengaluru, India. E-mail: kv_nagaraja@blr.amrita.edu; madhukeshjk@gmail.com
cDepartment of Mathematics, GITAM School of Science, GITAM Deemed to be University, Bangalore-Campus, India. E-mail: kiransajjan5@gmail.com
dDepartment of Computer Science and Mathematics, Lebanese American University, Byblos, Lebanon. E-mail: umair.khan@lau.edu.lb
eDepartment of Mathematical Sciences, Faculty of Science and Technology, Universiti Kebangsaan Malaysia (UKM), Bangi 43600, Selangor, Malaysia
fDepartment of Mathematics, SJT Government First Grade College, Mundargi, Karnataka, India. E-mail: umakolli@gmail.com
gDepartment of Mathematics, College of Science, King Khalid University, Abha, Saudi Arabia. E-mail: tasgher@kku.edu.sa
First published on 13th October 2023
Abstract
The Soret and Dufour effects have significant importance in several practical scenarios, especially in the domain of fluidic mass and temperature transfer. Nanofluidics, biological systems, and combustion processes are all areas where these consequences are crucial. Because of its distinct geometry, a wedge-shaped structure has aerodynamics, production, and engineering applications. Wedge shapes are used in aerodynamics for analyzing and improving airflow across various objects. Nanofluids increase thermal conductivity over traditional fluids making them ideal for cooling high-power electronics, boosting temperature transfer efficiencies, and boosting the solar energy system output. This work is of critical importance since it examines the consequences of a heat source/sink, the Soret impact and the Dufour impact, on the movement of a ternary nanofluid over a wedge. This work uses appropriate similarity constraints to reduce the complexity of the underlying governing equations, allowing for fast computational solutions with the Runge–Kutta–Fehlberg 4–5th order method (RKF-45). Analysis of these phenomena helps determine their possible real-world applications across various engineering fields, by presenting numerical results through plots. The results reveal that adjusting the moving wedge factor lessens the temperature profile, improving the magnetic constraint increases the velocity, and modifying the heat source/sink, Dufour, and Soret factors increases the temperature and concentration profiles. Dufour and heat source/sink constraints speed-up the heat transmission rate. In all cases, ternary nano liquids show significant performance over hybrid nano liquids.
1. Introduction
A mixture of nanoparticles and a base fluid is termed a “nanofluid”. Metals, carbides, oxides, and other substances are used as the nanoparticles in nanofluids; liquids such as oil, water, and ethylene glycol are often used as the base. The notion of “nanofluid” was proposed by Choi in 1995.1 The incorporation of particles at the nanoscale level enhances the thermal conductivity characteristics of conventional fluids. The use of this technology spans several disciplines, including but not limited to medical, engineering, and chemical sciences. Additionally, nanofluids find use in several industrial sectors such as biomedical, automotive, transportation, electrical, medication delivery, real-time monitoring of brain function, technological advancements, and tumour eradication. There is increasing interest among researchers on the use of nanofluids. Madhu et al.2 studied time-dependent circulation characteristics in a Maxwell nanofluid across a stretched surface, including the influence of magnetohydrodynamic and thermal radiation impacts. Prasannakumara et al.3 studied how nano liquids move through permeable surfaces that are stretched exponentially while being affected by thermophoretic particle deposition, bioconvection, and heat sources/sinks. Benos and Sarris4 studied the analytical solution of the laminar, two-dimensional magnetohydrodynamic natural convection of a deep cavity containing a nano liquid heated from inside and exposed to an external uniform perpendicular magnetic field. Alharbi et al.5 examined the time-dependent buoyancy resistance and heat transfer of alumina nanoparticles distributed in water, which behaves as a normal liquid, generated by a vertical cylinder. Gorla et al.6 explored the characteristics of the mixed convective boundary layer flow across a vertical wedge that is immersed in porous media filled with a nanofluid. There are numerous noticeable works on nanofluids. 7–9.To improve thermal efficiency, hybrid nanofluids have been created. Compared to nanofluids, hybrid nanofluids are better at exchanging heat. Hybrid nanofluids are formed by mixing two distinct nanoparticles in a base fluid. Significant primary works have been reported.10–13 A ternary nanofluid is an amalgam of three distinct nanoparticles: metal oxides, carbon nanotubes, and non-metallic particles in a base fluid. Compared to nanofluids and hybrid nanofluids, it is more capable of transmitting heat. There are several practical uses in various fields, including medicine, engineering, and chemistry. Nuclear reactor cooling, detergent production, automotive cooling, braking fluid, and military applications are just a few of the numerous industries where nanofluids are used. Ternary hybrid nanofluids and their heating efficiency have been reported: Madhukesh et al.14 examined the impact of essential limitations on the heat transfer properties of the tri-hybrid nanofluid, including porous medium, heat source/sink, and inclined geometry. Based on these results, a porous constraint would enhance heat dispersion while decreasing velocity. The use of a heat-source sink will enhance the thermal distribution. Yook et al.15 studied how different permeabilities and movable permeable walls exhibit the thermal and momentum diffusion of ternary hybrid nanoparticles. Ramzan et al.16 studied magnetohydrodynamic (MHD) tri-hybrid nanofluid movement across cone and wedge geometries. Animasaun et al.17 scrutinized convective and unstable acceleration effects on the Darcy motion of tri-hybrid nanofluids on horizontal surfaces. Das et al.18 scrutinized continuously fluctuating temperature on channel walls and the mixed convective motion of an ionic tri-hybrid nanofluid in a lengthy vertical nonconductive channel. Alanazi et al.19 examined the effect of tri-hybrid nanoparticles on the motion of nanofluids across an extended surface under varying gravity and noticed that increasing the magnetic parameter gave a decrease in the microrotation of tri-hybrid, hybrid, and mano nanofluids.
Electrical currents are produced when conductive fluid passes through a magnetic field to provide a mechanical force and regulate fluid flow. Because of its broad range of technical and scientific uses, MHDs is a crucial aspect in the areas of dynamics of fluids, biological and chemical technology, and medical research, including flow meters, power sources, motors, nuclear reactors using liquid metals, geothermal energy, solar energy absorbers, and metalworking. It is also used for filtering and purification. In the manufacturing, finance, heat exchanger, and mixing chamber industries, we also find evidence of the magnetic field effect. The MHD-free convection from a vertical plate immersed in a thermally stratified porous media, and the influence of Hall impacts on the convection process, was studied by Chamkha et al.20 Rauf et al.21 examined the thermal and mass transfer through an extending porous area using the two-dimensional (2D) mixed convective Maxwell hybrid nanofluid boundary layer with the provided exterior magnetic flux. Krishna et al.22 evaluated the influence of Soret, Joule, and Hall impacts on the characteristics of a MHD rotation mixed with convective flow across an infinitely long vertical porous plate. Madhukesh et al.23 studied the interaction between two fixed porous discs under the influence of a stable, incompressible, magnetized Casson–Maxwell non-Newtonian nanofluid. Takhar et al.24 examined the phenomenon of unsteady mixed convection circulation emanating from a vertically rotating cone, in the presence of a magnetic field. Ferdows et al.25 examined how flow between boundaries along a 3D extended surface is affected by MHD movement and hall current impacts. Takhar and Champka26 investigated MHD flow across a revolving plate using a magnetic field, Hall currents, and free flow velocity. Notable works on MHD flow over various geometries with different physical impacts have been reported. 27–30.
Heat generation and absorption applications in flowing fluids in a wide range of industrial and commercial systems, including cooling devices, freezers, heat pumps, combustion engines, and several more. With the help of the heat source and sink coefficient, we may examine the behavior of temperature distribution in nanofluids. The impact of the heat generation/absorption coefficient has been examined in several studies: Zeeshan et al.31 investigated the function of chemically magnetized nano liquid flow for the transition of energy across a permeable stretchable pipe with thermal generation and absorption and durability. Kumar et al.32 studied the machine learning strategy used to investigate the response surface methodology optimization of Lie group evaluation fluid solutions for an irregular radiated magnetized unstable wedge. Ramesh and Madhukesh et al.33 examined the hybrid carbon nanofluid activation energy mechanism and used heat sources and sinks to create magnetic slip movement. Kumar et al.34 studied the analytical solution on the impact of heat and mass transmission on a mixed convective motion field with a matrix of pores in a vertical channel. Alzahrani et al.35 inspected the existence of a heat source/sink and activation energy impacts of a third-grade liquid model upon heat and mass transfer in a chemically responding flow. Ramesh et al.36 examined the movement of an incompressible nanofluid caused by a non-uniform contracting cylinder.
When both heat and mass transmission events occur simultaneously, a more complicated driving potential results because energy flux can be generated by gradients. The movement of energy produced by a concentration gradient is known as the Dufour effect, while the mass transfer caused by temperature fluctuations is referred to as the Soret effect. The impacts of Soret and Dufour may also be observed in other areas, including solar collectors, fusion gases, building energy conservation, reactor safety, the oil and gas industry, environmental engineering and combustion flames. Using the application of an exterior magnetic field, the Dufour and Soret effects and thermal radiation impacts on mass and heat transport over a linearly increasing porous surface in a 2-D mixed convective hybrid nanofluid boundary layer, were studied by Rauf et al.37 Yogeesha et al.38 examined the Soret and Dufour impact across a stretched surface subjected to Stefan blowing (SB) in porous media, calculating the heat transfer and mass dispersal of a ternary unstable nanofluid flow. The impact of Soret (thermo-diffusion) and Dufour (diffusion-thermo) interactions upon a MHD second-grade nanofluid flow through a stretchy Riga surface, were examined by Shah et al.39 Hayat et al.40 examined the mixed convective Soret and Dufour movement of a stretched cylinder with a Reiner–Rivlin liquid undergoing ohmic heating, and viscous dissipation. Chamkha and Rashad41 investigated the phenomenon of time-dependent transfer of heat and mass during a combination of convection with MHDs from a revolving vertical cone. Yasir et al.42 studied the heat transmission mechanisms in a time-dependent axisymmetric flow generated by a deformable cylinder, including the effects of thermophoretic particle deposition and the Soret and Dufour impacts.
Considering the above literature, no work has examined the thermal performance of a ternary-based nano liquid (Fe3O4 + SWCNT + MWCNT/H2O) across a wedge with heat source/sink and Soret and Dufour impacts. The present study provides novel conclusions for thermal and concentration variations in the presence of a ternary-nano liquid flow. The confluence of wedge-shaped objects and nanofluids in many practical contexts highlights their profound influence on technological progress, including enhanced energy utilisation and breakthroughs in the field of medicine. The current study aims to address the following inquiries:
1. How the nature of a velocity profile varies upon changing magnetic field and moving wedge parameters.
2. What the changes observed are, in a temperature profile upon changing the heat source/sink and Dufour factors.
3. How the Soret, Dufour, heat source/sink and Schmidt factors affect the rate of heat and mass transfer.
2. Mathematical formulation
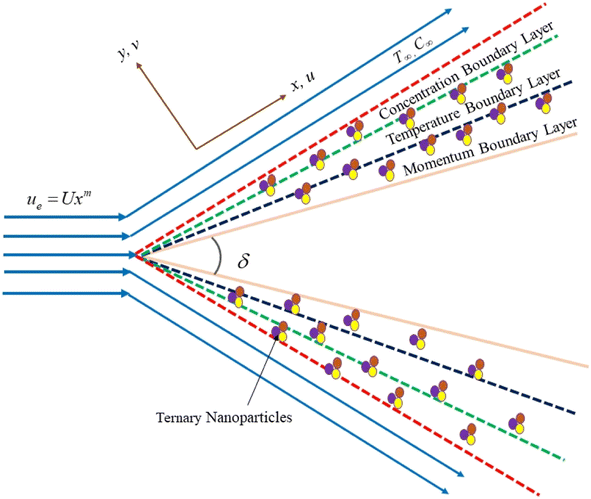
Consider a 2D, steady, incompressible flow with nanoparticles flowing through a wedge while also having a magnetic field. Additionally, heat and mass transportation occur due to the Soret and Dufour effect. Also, ue = A1xm1 and uw = A2xm1 are the external flow and uniform velocity of the wedge, respectively (Fig. 1). Here A1 and A2 are the constants, and m1 = (δ1/2 − δ1) is the Falkner–Skan power law parameter corresponding to πδ1. Therefore, δ is the wedge angle, and it is defined as δ = πδ1, where δ1 is the Hartree pressure parameter, Tw and T∞ correspondingly represent the wall and ambient temperatures. Similarly, Cw and C∞ denote the surface concentration and ambient concentration.Dimensional mass, velocity, temperature, and concentration equations are (see also ref. 43),
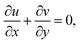 | (1) |
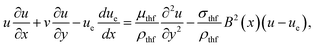 | (2) |
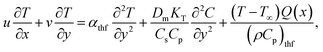 | (3) |
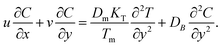 | (4) |
Comparable boundary conditions (BCs) are
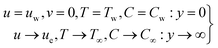 | (5) |
where, u and v are velocities in the x and y directions, respectively, μthf represents the dynamic viscosity, Dm is mass diffusivity, ρthf represents the density of the fluid, σthf represents the electrical conductivity, Cp represents the specific heat of the fluid, T represents the temperature, C is the concentration of the nanofluid, αthf is the thermal diffusivity of the nanofluid and is defined as 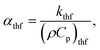 υthf represents the kinematic fluid viscosity and it is defined as
υthf represents the kinematic fluid viscosity and it is defined as 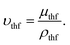
And the values of variable magnetic field B(x) and variable heat source/sink Q(x) are (see also ref. 44)
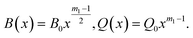 | (6) |
In eqn (6), B0 is the strength of the magnetic field and Q0 is the volumetric rate of the heat source/sink.
To convert the dimensional governing in eqn (1)–(4) into non-dimensional we use the following similarity variables (see ref. 43),
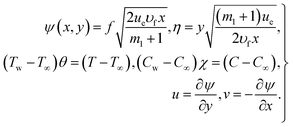 | (7) |
Using eqn (6) and (7), eqn (1) is identically satisfied and (2)–(4) are reduced to their non-dimensional form,
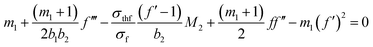 | (8) |
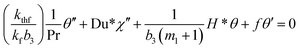 | (9) |
| χ′′ + Sc1fχ′ + Sr*Sc1θ′′ = 0. | (10) |
The corresponding reduced boundary conditions are
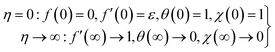 | (11) |
The non-dimensional parameters are: M2 represents the magnetic parameter 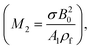 Pr represents the Prandtl number
Pr represents the Prandtl number 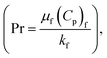 H* represents the heat source/sink parameter
H* represents the heat source/sink parameter 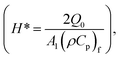 Du* represents the Dufour number
Du* represents the Dufour number 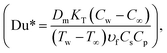 Sr* represents the Soret number
Sr* represents the Soret number 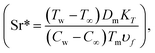 Sc1 represents the Schmidt number
Sc1 represents the Schmidt number 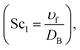 and
and 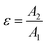 represents the moving wedge parameter.
represents the moving wedge parameter.
Here, b1 = (1 − φ1)2.5(1 − φ2)2.5(1 − φ3)2.5,
The thermophysical characteristics of the tri-hybrid nanofluid are (see also ref. 47 and Table 1),
| μthf = μf(1 − φ3)−2.5(1 − φ2)−2.5(1 − φ1)−2.5, | (12) |
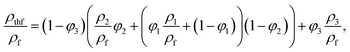 | (13) |
| (ρCp)thf = φ3(ρCp)3 + [(1 − φ2){(1 − φ1)(ρCp)f + φ1(ρCp)1} + φ2(ρCp)2](1 − φ3), | (14) |
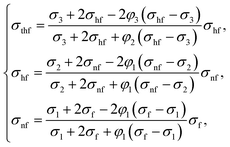 | (15) |
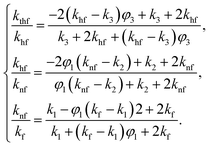 | (16) |
| Properties | ρ (kg m−3) | k (Wm−1 K−1) | σ (S m−1) | C p (J kg−1 K−1) |
|---|---|---|---|---|
| H2O | 997.1 | 0.613 | 0.05 | 4179 |
| Fe3O4 | 5180 | 9.7 | 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
670 |
| SWCNT | 2600 | 6600 | 106−107 | 425 |
| MWCNT | 1600 | 3000 | 1.9 × 10−4 | 796 |
Here, μ – dynamic viscosity, ρ – the density, k – thermal conductivity, σ – electrical conductivity, and Cp – specific heat, φ – volume fraction of a nanoparticle. In addition, the engineering physical quantities of interest are given in Table 2.
| Definition | Reduced form | |
|---|---|---|
a Where, local Reynolds number is 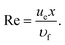
|
||
| Skin friction |
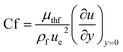
|
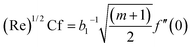
|
| Nusselt number |
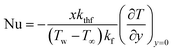
|

|
| Sherwood number |
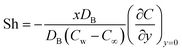
|
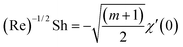
|
3. Numerical methodology
High order, coupling, and a two-point boundary make the equations and BCs produced in the previous part extremely challenging to solve. However, the provided system of equations can be transformed into a first-order system, which can then be solved. For that, we can take,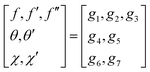 | (17) |
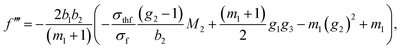 | (18) |
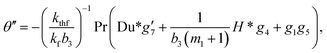 | (19) |
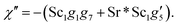 | (20) |
and
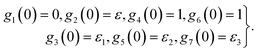 | (21) |
This study uses shooting strategies to discover the unknown boundary conditions in eqn (21), and the RKF-45 approach is used to obtain numerical solutions. For precision and efficiency, the computational software has an error tolerance of 10−6 and a step size of around 0.01. A complete validation process is carried out to confirm the numerical scheme's reliability and validity by limiting scenarios and comparing the findings with prior works (Table 3).48,49 The comparison shows that the generated values have a high level of agreement and are a near match to the previous study findings, proving the correctness and reliability of the current strategy.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b2
b2
4. Results and discussion
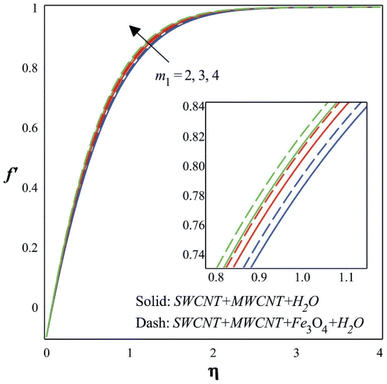
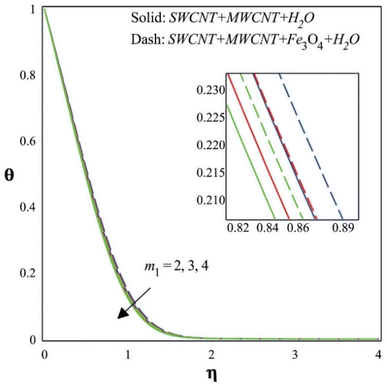
This section presents the detailed discussion of the results obtained by solving the resultant eqn (8)–(10) and BCs (11) using the numerical scheme explained above. The important dimensionless constraints and their impacts on the different profiles and essential engineering factors are discussed.Fig. 2–4 depict how the flow's velocity, temperature, and concentration profiles, respectively, are impacted by the Falkner–Skan power law parameter. Fig. 2 demonstrates that when the Falkner–Skan power law parameter rises, the velocity climbs as well. The Falkner–Skan equation describes the flow of a viscous fluid on a wedge-shaped surface. The behavior of the velocity profile within the boundary layer of the fluid flow is controlled by the power law parameter of the Falkner–Skan equation. The velocity profile and the rate at which velocity climbs away from the wedge surface are particularly influenced by the power law parameter, which is often denoted as “m1”. The properties of the velocity distribution near the wedge's surface are successfully changed by altering the value of the power law parameter (m1). The velocity profile within the boundary layer of a fluid flow is influenced by the equilibrium between viscous forces, pressure gradients, and inertial forces. Raising the power law value results in a steeper velocity profile that rises more rapidly away from the wedge's surface in the Falkner–Skan equation for a wedge-shaped surface.
Raising the power law parameter also decreases the relative impact of viscous forces. Fig. 3 illustrates how the temperature drops when the Falkner–Skan power law parameter rises. In the Falkner–Skan equation, which simulates laminar boundary layer flows, the power law parameter “m1” has an impact on the velocity profile across the surface. Larger values of “m1” (higher than 0) result in a slower velocity increase across the plate, which results in a thicker boundary layer, as was previously demonstrated. The link between the temperature profile, boundary layer thickness, and velocity profile is close. A thicker boundary layer might affect the temperature profile as there will be a slower heat transfer from the surface to the fluid. Nanoparticles may alter how a base fluid responds to temperature because of their thermal properties. Depending on the kind and number of nanoparticles, they may help or hinder the fluid's ability to transfer heat. If the nanoparticles mix to create thermal barriers or if they have a lower thermal conductivity than the base fluid, the temperature profile of the fluid may be changed. The interplay between the thermal behavior of the nanoparticles and the thicker boundary layer (produced by a bigger “m1” value) may combine with the power law parameter's effect on the power law parameter, and the presence of nanoparticles, to potentially reduce the overall heat transfer efficiency. The fluid's effective thermal conductivity may seem to decrease if the bigger boundary layer and the presence of nanoparticles prevent heat from transferring from the surface to the fluid.
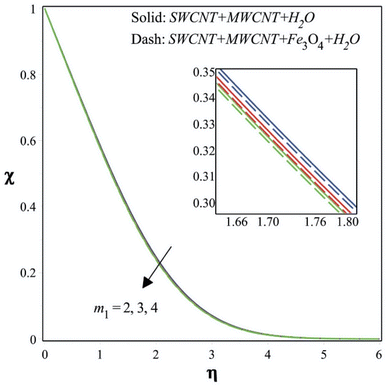
Additionally, it is evident from Fig. 4 that the concentration decreases as the Falkner–Skan power law parameter rises. An improved power law parameter in the setting of mass transfer might have an effect on the concentration profiles in the case of fluid flow with mass transfer over a wedge-shaped surface. If the power law parameter (m1) is raised, the flow velocity away from the surface might increase. The stronger convection brought on by this increased velocity may have an effect on the concentration profiles. By improving fluid mixing brought on by a greater flow velocity, concentration gradients at the surface may be minimized. This might lead to an even higher concentration profile.
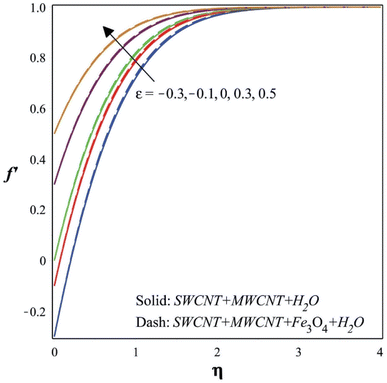
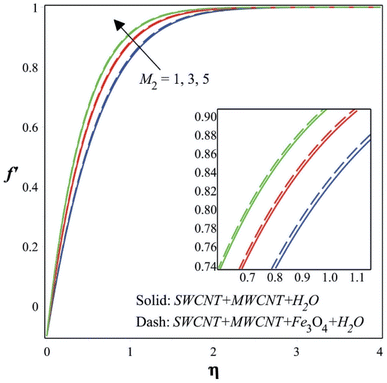
The moving wedge parameter's effects on the velocity, temperature, and concentration profiles of the flow are shown in Fig. 5–7, respectively. It is clear from Fig. 5 that increasing the moving wedge parameter raises the velocities. Better nanoparticle dispersion and diffusion within the base fluid could result from increasing the wedge parameter. By promoting more effective flow and reducing friction between fluid layers, this better dispersion may lead to higher velocity profiles. The effective viscosity of the nanofluid may change as nanoparticles are added. Higher velocities would result from a reduction in flow resistance if the wedge parameter somehow affects the effective viscosity in a manner that lessens internal friction within the fluid. The thickness of the boundary layer may be reduced, and fluid flow at greater speeds would be encouraged if the wedge parameter has an effect on the interaction between the boundary layer and the bulk fluid.
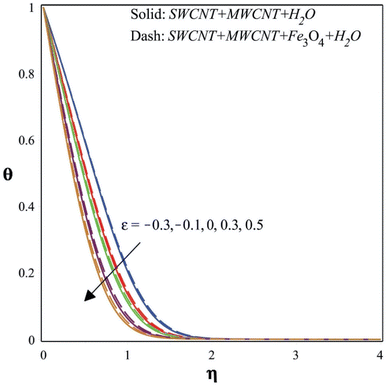
A rise in the moving wedge parameter results in a temperature decrease, as seen in Fig. 6. If the moving wedge parameter affects heat transfer or heat dissipation in the system, then raising its value could result in more effective heat transfer mechanisms. The increased surface area and thermal conductivity of the nanoparticles provide nanofluids an advantage over pure base fluids in terms of heat transfer. An increase in the moving wedge parameter may improve nanoparticle dispersion and boost heat transfer if it affects the flow rate inside the nanofluid. Consequently, the temperature throughout the nanofluid would be more uniform, resulting in a drop in temperature. Additionally, a decrease in local temperature gradients may result from effective heat transmission.
Likewise, it is clear from Fig. 7 that a reduction in the moving wedge parameter causes a drop in concentration. Increases in the moving wedge parameter value often signify improved fluid dispersion and movement. Together, these effects result in a more uniform distribution of the chemicals throughout the fluid, reducing concentration gradients and the profile's overall slope.
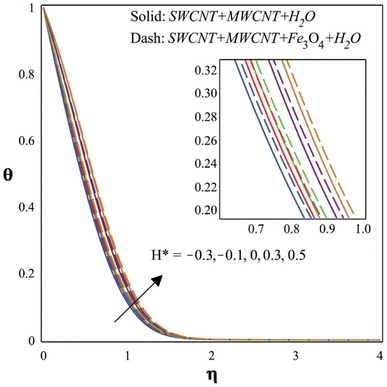
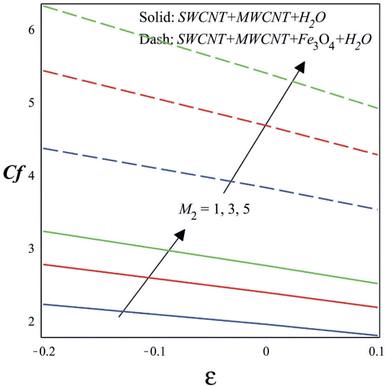
The rise in velocities that results from an increase in the magnetic parameter can be seen in Fig. 8. The application of a magnetic field that is oriented perpendicular to the direction of fluid flow results in the generation of a Lorentz force inside a conducting hybrid nanofluid. Depending on how the magnetic field and the flow are oriented, this force interacts with the fluid's motion and may either facilitate or hinder it. When the magnetic field interacts with the fluid flow, it produces a force known as the MHD drag force. In certain situations, the drag force may help the fluid motion by accelerating it. A heat source in the boundary layer may be identified when H* is positive. This heat source represents recombination in the boundary layer when Tw (wall temperature) < T∞ (free stream temperature), and it represents dissociation when Tw (wall temperature) > T∞. In all scenarios, heat transmission between the fluid and the wall happens even in the absence of a heat source. Heat transfer to the wall is enhanced when a heat source is present (H* > 0). This indicates that the extra heat provided by the heat source causes the heat transfer from the fluid to the wall to increase. A boundary layer heat sink is indicated by H* when it is negative (Q0). This heat sink is equivalent to combustion for Tw > T∞ and to endothermic chemical processes for Tw < T∞. Similar to the positive H* scenario, heat transmission between the fluid and the wall happens even in the absence of a heat sink. Heat transmission from the wall to the fluid is reduced when a heat sink is present (H* < 0). This is so that less heat flows to the wall, which is caused by the heat sink absorbing heat from the boundary layer. Fig. 9 illustrates how temperature-dependent heat sources and sinks effect temperature profiles. The heat sink effect manifests as a sharp temperature decrease brought on by the absorbed heat when Tw > T∞ with positive H*. The temperature of the boundary layer increases when Tw > T∞ with negative H*, which is caused by the heat source.
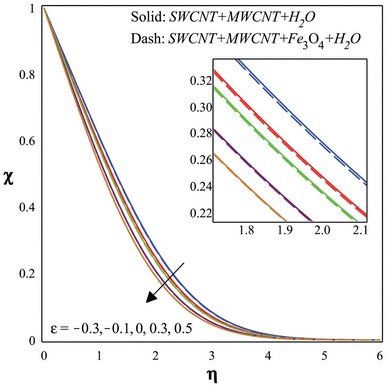
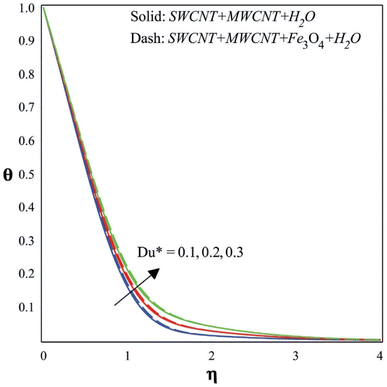
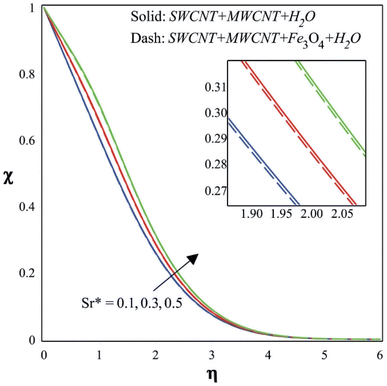
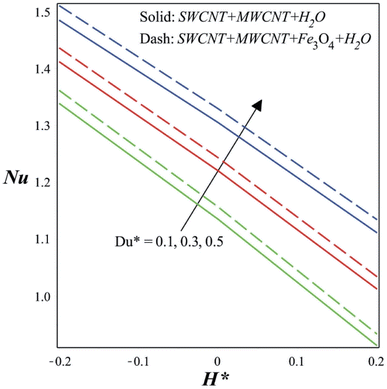
The temperature increases as the Dufour number increases, as seen in Fig. 10. As a result, the mass diffusion effect is overshadowed by the heat diffusion effect as the Dufour number increases. This implies that the process of mass diffusion gradually loses potency in favor of the process of heat diffusion. A higher Dufour number indicates that heat diffusion will have a greater impact on the overall transfer processes in a system where both heat and mass transfer are occurring. In the context of a temperature profile, an increased Dufour number indicates a change in the predominance of heat diffusion. The system's temperature gradient could grow steeper as a consequence because heat flows more rapidly than mass. Alterations in heat diffusion, in other words, increase the susceptibility of the temperature distribution. It is evident from Fig. 11 that the concentration increases as the Soret number increases. Indicators of temperature variation effects on mass diffusion include the Soret number, which is higher. Since there is a temperature differential within the mixture, species with higher Soret coefficients have a tendency to shift from hot to cold places. This could draw certain particles toward the cooler parts of the system. In a system with a greater Soret number, the temperature gradient's impact on the concentration gradient is more pronounced. This might lead to a concentration profile that is more dramatic, with the concentrations of specific species being substantially higher or lower in regions with significant temperature variations.
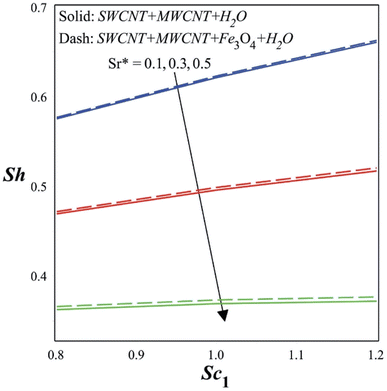
Fig. 12 shows how the moving wedge constraint and the magnetic constraint affect the skin friction coefficient along the wedge surface. Increasing the magnetic parameter would produce larger magnetic forces, which have the power to impede fluid motion. Greater skin friction might occur from the increased drag and resistance against the fluid flow. The interaction of a moving wedge with a magnetic field may result in more complex flow patterns than those of a stationary wedge. Depending on the wedge's orientation, motion speed, and magnetic field strength, the fluid flow may be altered or redirected in a variety of ways. Depending on the situation, this complex interaction may impact skin friction and produce variations. The Dufour number and the heat sink/source parameter both have an impact on the Nusselt number across the wedge surface, as illustrated in Fig. 13. A higher Dufour number indicates a greater thermal diffusion effect, which in turn strengthens the connection between the processes of heat and mass transfer within the fluid. As a consequence of this coupling, the interactions between the fluid flow, temperature distribution, and concentration profiles may become more challenging. This intricacy may cause variations in the local heat transfer rates, which might manifest as changes in the Nusselt number when a heat sink or source is present. Fig. 14 illustrates the influence of the Soret number and Schmidt number along the wedge surface. When the Soret number increases, it implies that the mass diffusion effect is no longer as significant as the influence of heat diffusion. As the fluid's temperature gradients become more noticeable, the concentration profiles might shift. The Sherwood number, which is often related to concentration gradients in a fluid flow, describes mass transfer. A higher Soret number may lead to magnified concentration variations because of the greater impact of thermal diffusion on mass transport. This may lead to a change in the Sherwood number. The Schmidt number determines the rate of momentum transmission relative to mass. When used to measure mass transfer, a lower Schmidt number often suggests that mass transfer occurs at a higher pace than momentum transmission. For instance, a fluid with a low Schmidt number would diffuse through it more quickly than it would advect through it. The mass transfer rate may fluctuate less notably than the momentum transfer rate in situations when the Soret number is low and concentration gradients change.
5. Conclusions
In this study, a solution to the Falkner–Skan issue for a wedge is presented that takes into account the impact of hybrid nanoparticle aggregation in the presence of the Soret and Dufour effects, the non-uniform heat source/sink, and the magnetic effect. This model was created by combining modified Maxwell and Bruggeman models for the inclusion of the hybrid nanoparticle aggregation influence in the flow of SWCNT/MWCNT/Fe3O4/H2O, which has already been tested experimentally, and we show that our model predicts the true values for properties of water-based ternary hybrid nanofluids. Using a numerical method known as RKF-45, the mathematical model is solved. By creating graphs, the properties of the flow were examined in-depth. The applications of wedge-based flow in several sectors, such as wire drawing, metal expulsion, and glass fiber manufacture, are covered in this paper. These industries often struggle with heat-related production issues that might degrade product quality. This study offers a method to guarantee constant flow and heat movement, improving the quality of final products and reducing manufacturing costs. It does this by adding hybrid nanoparticles and magnetic fields.The important results of this investigation are:
• The concentration profile increases with an increase in the Soret number.
• The temperature, as well as concentration, decreases with an increase in the moving wedge parameter and Falkner–Skan power law parameter.
• The temperature profile rises due to increments in the heat source/sink parameters and Dufour number.
• As the Dufour number is increased, the local Nusselt number increases while the local Sherwood number decreases with an increase in the Soret number.
• The Nusselt number and skin friction values are higher when ternary hybrid nanoparticle aggregation is taken into account.
• The numerical data are acquired and compared with previously reported examples found in the literature, and they are in excellent agreement.
The present study opens several exciting avenues for future research and applications. The outcomes of the present investigation will provide a path for the development of efficient cooling systems for high power electronic gadgets; the adoption of optimized architecture for heat dissipation in electronic equipment has been shown to significantly enhance their performance and durability.
Nomenclature
| A 1, A2 | Constants |
| B(x) | Variable magnetic field |
| B 0 | Strength of the magnetic field |
| C | Concentration |
| Cf | Skin friction |
| C s | Concentration susceptibility |
| C p | Specific heat |
| C w | Wall concentration |
| C ∞ | Ambient concentration |
| D | Diffusivity |
| Du* | Dufour number |
| H* | Heat source/sink parameter |
| k | Thermal conductivity |
| K T | Ratio of thermal diffusion |
| m 1 | Falkner–Skan power law parameter |
| M 2 | Magnetic parameter |
| Nu | Nusselt number |
| Pr | Prandtl number |
| Q(x) | Variable heat source/sink |
| Q 0 | Volumetric rate of heat source/sink |
| Rex | Local Reynolds number |
| Sr* | Soret number |
| Sc1 | Schmidt number |
| Sh | Sherwood number |
| T | Temperature |
| T w | Wall temperature |
| T ∞ | Ambient temperature |
| u e,uw | External flow and uniform velocities |
| u,v | Velocity components |
| x,y | Coordinates |
Greek symbols
| δ | Wedge angle |
| δ 1 | Hartree pressure parameter |
| μ | Dynamic viscosity |
| ρ | Density |
| σ | Electrical conductivity |
| υ | Kinematic viscosity |
| ψ | Stream function |
| η | Similarity variable |
| θ | Dimensionless temperature |
| χ | Dimensionless concentration |
| ε | Moving wedge parameter |
| φ | Solid volume fraction |
| α | Thermal diffusivity |
Subscripts
| f | Fluid |
| nf | Nanofluid |
| hf | Hybrid nanofluid |
| thf | Ternary nanofluid |
Author contributions
J. K. Madhukesh; K. Vinutha; conceptualization, methodology, software, formal analysis, writing – original draft. Kiran Sajjan: writing – original draft, resources, data curation, investigation, visualization, validation. Umair Khan; K. V. Nagaraja: conceptualization, project administration, funding, writing – original draft, writing – review & editing, supervision, resources. Uma C. Kolli: validation, investigation, writing – review & editing, formal analysis, validation, resources. Taseer Muhammad: provided significant feedback and assisted in the revised version of the manuscript.Conflicts of interest
It is declared that we have no conflict of interest.Acknowledgements
The authors extend their appreciation to the research unit at King Khalid University for funding this work through Project number 494 and the authors acknowledge the Research Center for Advanced Materials Science (RCAMS) at King Khalid University, Saudi Arabia for their valuable technical support.References
- S. U. S. Choi and J. A. Eastman, Enhancing Thermal Conductivity of Fluids with Nanoparticles, 1995 Search PubMed.
- M. Madhu, N. Kishan and A. J. Chamkha, Unsteady flow of a Maxwell nanofluid over a stretching surface in the presence of magnetohydrodynamic and thermal radiation effects, Propul. Power Res., 2017, 6, 31–40 CrossRef.
- B. C. Prasannakumara, J. K. Madhukesh and G. K. Ramesh, Bioconvective nanofluid flow over an exponential stretched sheet with thermophoretic particle deposition, Propul. Power Res., 2023 Search PubMed.
- L. Benos and I. E. Sarris, Analytical study of the magnetohydrodynamic natural convection of a nanofluid filled horizontal shallow cavity with internal heat generation, Int. J. Heat Mass Transfer, 2019, 130, 862–873, DOI:10.1016/j.ijheatmasstransfer.2018.11.004.
- S. O. Alharbi, U. Khan, A. Zaib, A. Ishak, Z. Raizah, S. M. Eldin and I. Pop, Heat transfer analysis of buoyancy opposing radiated flow of alumina nanoparticles scattered in water-based fluid past a vertical cylinder, Sci. Rep., 2023, 13, 10725 CrossRef CAS PubMed.
- R. S. R. Gorla, A. Chamkha and A. M. Rashad, Mixed convective boundary layer flow over a vertical wedge embedded in a porous medium saturated with a nanofluid, in 2010 3rd International Conference on Thermal Issues in Emerging Technologies Theory and Applications, 2010, pp. 445–451 Search PubMed.
- M. V. Krishna and A. J. Chamkha, Hall effects on mhd squeezing flow of a water-based nanofluid between two parallel disks, J. Porous Media, 2019, 22, 209 CrossRef.
- J. K. Madhukesh, V. Kalleshachar, C. Kumar, U. Khan, K. V. Nagaraja, I. E. Sarris, E.-S. M. Sherif, A. M. Hassan and J. S. Chohan, A model development for thermal and solutal transport analysis of non-newtonian nanofluid flow over a Riga surface driven by a waste discharge concentration, Water, 2023, 15, 2879 CrossRef CAS.
- H. S. Takhar, A. J. Chamkha and G. Nath, MHD flow over a moving plate in a rotating fluid with magnetic field, Hall currents and free stream velocity, Int. J. Eng. Sci., 2002, 40, 1511–1527 CrossRef.
- G. K. Ramesh, E. H. Aly, S. A. Shehzad and F. M. Abbasi, Bödewadt flow and heat transfer of hybrid nanomaterial, Int. J. Ambient Energy, 2022, 43, 3228–3236 CrossRef CAS.
- M. Dinesh Kumar, C. S. K. Raju, M. Alshehri, S. Alkarni, N. A. Shah, M. R. Ali and R. Sadat, Dual dynamical jumps on Lie group analysis of hydro-magnetic flow in a suspension of different shapes of water-based hybrid solid particles with Fourier flux, Arabian J. Chem., 2023, 16, 104889 CrossRef CAS.
- R. Girish, A. Salma, P. V. Ananth Subray, B. N. Hanumagowda, S. V. K. Varma, K. V. Nagaraja, J. singh chohan, U. Khan, A. M. Hassan and F. Gamaoun, Effect of temperature-dependent internal heat generation over exponential and dovetail convective-radiative porous fin wetted in hybrid nanofluid, Case Stud. Therm. Eng., 2023, 49, 103214 CrossRef.
- M. V. Krishna, N. A. Ahammad and A. J. Chamkha, Radiative MHD flow of Casson hybrid nanofluid over an infinite exponentially accelerated vertical porous surface, Case Stud. Therm. Eng., 2021, 27, 101229 CrossRef.
- J. K. Madhukesh, I. E. Sarris, K. Vinutha, B. C. Prasannakumara and A. Abdulrahman, Computational analysis of ternary nanofluid flow in a microchannel with nonuniform heat source/sink and waste discharge concentration, Numer. Heat Transfer, Part A, 2023, 1–18 Search PubMed.
- S.-J. Yook, C. S. K. Raju, B. Almutairi, S. U. Mamatha, N. A. Shah and S. M. Eldin, Heat and momentum diffusion of ternary hybrid nanoparticles in a channel with dissimilar permeability's and moving porous walls: a multi-linear regression, Case Stud. Therm. Eng., 2023, 47, 103133 CrossRef.
- M. Ramzan, P. Kumam, S. A. Lone, T. Seangwattana, A. Saeed and A. M. Galal, A theoretical analysis of the ternary hybrid nanofluid flows over a non-isothermal and non-isosolutal multiple geometries, Heliyon, 2023, 9, e14875 CrossRef PubMed.
- I. L. Animasaun, T. K. Kumar, F. A. Noah, S. S. Okoya, Q. M. Al-Mdallal and M. M. Bhatti, Insight into Darcy flow of ternary-hybrid nanofluid on horizontal surfaces: exploration of the effects of convective and unsteady acceleration, Z. Angew. Math. Mech., 2023, 103, e202200197 CrossRef.
- S. Das, A. Ali, R. N. Jana and O. D. Makinde, EDL impact on mixed magneto-convection in a vertical channel using ternary hybrid nanofluid, Chem. Eng. J. Adv., 2022, 12, 100412 CrossRef CAS.
- M. M. Alanazi, A. Ahmed Hendi, N. A. Ahammad, B. Ali, S. Majeed and N. A. Shah, Significance of ternary hybrid nanoparticles on the dynamics of nanofluids over a stretched surface subject to gravity modulation, Mathematics, 2023, 11, 809 CrossRef.
- A. J. Chamkha, MHD-free convection from a vertical plate embedded in a thermally stratified porous medium with Hall effects, Appl. Math. Modell., 1997, 21, 603–609 CrossRef.
- A. Rauf, F. Hussain, A. Mushtaq, N. Ali Shah and M. R. Ali, MHD mixed convection flow for Maxwell hybrid nanofluid with Soret, Dufour and morphology effects, Arabian J. Chem., 2023, 16, 104965 CrossRef CAS.
- M. V. Krishna, B. V. Swarnalathamma and A. J. Chamkha, Investigations of Soret, Joule and Hall effects on MHD rotating mixed convective flow past an infinite vertical porous plate, J. Ocean Eng. Sci., 2019, 4, 263–275 CrossRef.
- J. K. Madhukesh, G. K. Ramesh, S. A. Shehzad, S. Chapi and I. Prabhu Kushalappa, Thermal transport of MHD Casson–Maxwell nanofluid between two porous disks with Cattaneo–Christov theory, Numer. Heat Transfer, Part A, 2023, 1–16 Search PubMed.
- H. S. Takhar, A. J. Chamkha and G. Nath, Unsteady mixed convection flow from a rotating vertical cone with a magnetic field, Heat Mass Transfer, 2003, 39, 297–304 CrossRef.
- M. Ferdows, G. K. Ramesh and J. K. Madhukesh, Magnetohydrodynamic flow and Hall current effects on a boundary layer flow and heat transfer over a three-dimensional stretching surface, Int. J. Ambient Energy, 2023, 44, 938–946 CrossRef.
- H. S. Takhar, A. J. Chamkha and G. Nath, MHD flow over a moving plate in a rotating fluid with magnetic field, Hall currents and free stream velocity, Int. J. Eng. Sci., 2002, 40, 1511–1527 CrossRef.
- M. Waqas, U. Khan, A. Zaib, A. Ishak, M. D. Albaqami, I. Waini, R. G. Alotabi and I. Pop, Radiation effect on MHD three-dimensional stagnation-point flow comprising water-based graphene oxide nanofluid induced by a nonuniform heat source/sink over a horizontal plane surface, Int. J. Mod. Phys. B, 2023, 37, 2350146 CrossRef CAS.
- M. V. Krishna and A. J. Chamkha, Hall and ion slip effects on unsteady MHD convective rotating flow of nanofluids—application in biomedical engineering, J. Egpt. Math. Soc., 2020, 28, 1 CrossRef.
- M. F. Ahmed, A. Zaib, F. Ali, O. T. Bafakeeh, E. S. M. Tag-ElDin, K. Guedri, S. Elattar and M. I. Khan, Numerical computation for gyrotactic microorganisms in MHD radiative Eyring–Powell nanomaterial flow by a static/moving wedge with Darcy–Forchheimer relation, Micromachines, 2022, 13, 1768 CrossRef PubMed.
- A. J. Chamkha, Non-Darcy hydromagnetic free convection from a cone and a wedge in porous media, Int. Commun. Heat Mass Transfer, 1996, 23, 875–887 CrossRef CAS.
- A. Zeeshan, N. A. Ahammad, N. A. Shah, J. D. Chung and A. Ullah, Role of chemically magnetized nanofluid flow for energy transition over a porous stretching pipe with heat generation/absorption and its stability, Mathematics, 2023, 11, 1844 CrossRef.
- M. Dinesh Kumar, N. Ameer Ahammad, C. S. K. Raju, S.-J. Yook, N. A. Shah and S. M. Tag, Response surface methodology optimization of dynamical solutions of Lie group analysis for nonlinear radiated magnetized unsteady wedge: Machine learning approach (gradient descent), Alexandria Eng. J., 2023, 74, 29–50 CrossRef.
- G. K. Ramesh and J. K. Madhukesh, Activation energy process in hybrid CNTs and induced magnetic slip flow with heat source/sink, Chin. J. Phys., 2021, 73, 375–390 CrossRef CAS.
- K. Thanesh Kumar, S. Kalyan, M. Kandagal, J. V. Tawade, U. Khan, S. M. Eldin, J. Singh Chohan, S. Elattar and A. M. Abed, Influence of heat generation/absorption on mixed convection flow field with porous matrix in a vertical channel, Case Stud. Therm. Eng., 2023, 47, 103049 CrossRef.
- F. Alzahrani, R. N. Kumar, B. C. Prasannakumara, M. I. Khan and K. Guedri, Transportation of heat and mass in chemically reacted flow of third-grade model in the presence of heat generation/absorption and activation energy effects, Int. J. Mod. Phys. B, 2022, 36, 2250222 CrossRef CAS.
- G. K. Ramesh, K. Ganesh Kumar, B. J. Gireesha, S. A. Shehzad and F. M. Abbasi, Magnetohydrodynamic nanoliquid due to unsteady contracting cylinder with uniform heat generation/absorption and convective condition, Alexandria Eng. J., 2018, 57, 3333–3340 CrossRef.
- A. Rauf, F. Hussain, A. Mushtaq, N. Ali Shah and M. R. Ali, MHD mixed convection flow for Maxwell Hybrid nanofluid with Soret, Dufour and Morphology effects, Arabian J. Chem., 2023, 16, 104965 CrossRef CAS.
- K. M. Yogeesha, S. B. Megalamani, H. S. Gill, M. Umeshaiah and J. K. Madhukesh, The physical impact of blowing, Soret and Dufour over an unsteady stretching surface immersed in a porous medium in the presence of ternary nanofluid, Heat Transfer, 2022, 51, 6961–6976 CrossRef.
- F. Shah, T. Hayat and S. Momani, Non-similar analysis of the Cattaneo–Christov model in MHD second-grade nanofluid flow with Soret and Dufour effects, Alexandria Eng. J., 2023, 70, 25–35 CrossRef.
- T. Hayat, A. Razaq, S. A. Khan and S. Momani, Soret and Dufour impacts in entropy optimized mixed convective flow, Int. Commun. Heat Mass Transfer, 2023, 141, 106575 CrossRef CAS.
- A. J. Chamkha and A. M. Rashad, Unsteady heat and mass transfer by MHD mixed convection flow from a rotating vertical cone with chemical reaction and Soret and Dufour effects, Can. J. Chem. Eng., 2014, 92, 758–767 CrossRef CAS.
- M. Yasir, M. Khan and Z. U. Malik, Analysis of thermophoretic particle deposition with Soret-Dufour in a flow of fluid exhibit relaxation/retardation times effect, Int. Commun. Heat Mass Transfer, 2023, 141, 106577 CrossRef.
- U. Khan, A. Zaib, D. Baleanu, M. Sheikholeslami and A. Wakif, Exploration of dual solutions for an enhanced cross liquid flow past a moving wedge under the significant impacts of activation energy and chemical reaction, Heliyon, 2020, 6, e04565 CrossRef PubMed.
- U. Khan, A. Zaib and F. Mebarek-Oudina, Mixed convective magneto flow of SiO2–MoS2/C2H6O2 hybrid nanoliquids through a vertical stretching/shrinking wedge: stability analysis, Arabian J. Sci. Eng., 2020, 45, 9061–9073 CrossRef CAS.
- T. Hayat, S. A. Khan, A. Alsaedi and Q. M. Z. Zai, Computational analysis of heat transfer in mixed convective flow of CNTs with entropy optimization by a curved stretching sheet, Int. Commun. Heat Mass Transfer, 2020, 118, 104881 CrossRef CAS.
- A. Zaib, U. Khan, Z. Shah, P. Kumam and P. Thounthong, Optimization of entropy generation in flow of micropolar mixed convective magnetite (Fe3O4) ferroparticle over a vertical plate, Alexandria Eng. J., 2019, 58, 1461–1470 CrossRef.
- S. Li, V. Puneeth, A. M. Saeed, A. Singhal, F. A. M. Al-Yarimi, M. I. Khan and S. M. Eldin, Analysis of the Thomson and Troian velocity slip for the flow of ternary nanofluid past a stretching sheet, Sci. Rep., 2023, 13, 2340 CrossRef CAS PubMed.
- A. Asaithambi, A finite-difference method for the Falkner-Skan equation, Appl. Math. Comput., 1998, 92, 135–141 CrossRef.
- S. Nadeem, S. Ahmad and N. Muhammad, Computational study of Falkner-Skan problem for a static and moving wedge, Sens. Actuators, B, 2018, 263, 69–76 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2023 |