Growth pathways of Cu shells on Au and AuCu seeds: interdiffusion, shape transformations, strained shells and patchy surfaces

Abstract

The growth of AuCu nanoparticles obtained by depositing Cu atoms on starting seeds of pure Au and on mixed AuCu seeds is studied by molecular dynamics simulations. Depending on the shape of the seed, its composition and the growth temperature, different growth pathways are observed, in which several types of structural transformations take place. The final growth structures comprise Au@Cu core@shell arrangements as well as Janus-like structures with patchy surfaces. The results of the growth simulations are rationalized in terms of the activation of different diffusion processes, both on the surface and inside the growing clusters. These diffusion processes regulate structural transitions between different motifs and the occurrence of dewetting phenomena. The simulation results show that depositon of Cu atoms on pure Au or mixed AuCu seed can be an effective tool for producing clusters with uncommon surface atom arrangements of potential interest for catalysis.

---

1 Introduction

Owing to its high conductivity, low cost and abundance, copper has gained considerable popularity in several applications at the nanoscale.^1–4 The use of Cu nanoparticles (NPs) in several applications is hindered by the susceptibility of that metal to oxidation when exposed to air, which eradicates plasmonic properties and reduces catalytic activity. This major obstacle can be overtaken by using a robust metal as an additive to Cu NPs. To this end, several strategies have been attempted, mainly by forming alloys or core@shell structures with robust materials. In particular, gold has been proved to be a good candidate to mitigate the oxidation problems of copper NPs under harsh conditions.⁵ Alloying these two metals not only ameliorates the stability of copper but also pulls down the cost of gold.

AuCu NPs have been widely applied in heterogeneous catalysis for many chemical reactions including oxygen reduction reaction, oxidation of carbon monoxide and other oxidation reactions.⁶ The catalytic performance of AuCu NPs can be tuned to a significant extent by controlling their sizes, morphology, compositions, and elements distribution within the NPs. Many recent works showed that Au core and Cu shell is often the desired chemical arrangement of these bimetallic nanoparticles for several chemical reactions. In ref. 7, the authors have shown that Au@Cu core–shell nanoparticles is a good catalyst for the electrochemical reduction of carbon dioxide in a neutral medium. They observed that the activity and selectivity of Au@Cu catalyst can be adjusted by controlling the thickness of Cu shell. Clearly, Au@Cu with 7–8 copper layers presented higher selectivity towards the formation of hydrogen and ethylene, while Au@Cu with more than 14 copper layers were more selective towards the formation of hydrogen and methane. So far, (AuCu)@Cu core–shell with ultra thin Cu shell has shown higher selectivity and activity for nitrogen reduction reaction among other compositions.⁸ These different trends in reactivity and selectivity are linked to strain/electronic effects induced by the core–shell arrangement that can be tweaked by the composition of the shell.

AuCu system is highly miscible in bulk crystals⁹ with the formation of ordered phases at low temperatures, so that phase-separated configurations, such as the core@shell ones, may be expected to be out-of equilibrium. In addition, the large lattice mismatch between these metals (the Au lattice is larger by 12.5% than the Cu lattice) and the associated misfit strain can induce complex deformations in the shell.¹⁰ In fact, AuCu nanoparticles with different chemical ordering arrangements have been obtained in several experiments and simulations.^11–18

The growth of elemental nanoparticles and of nanocrystals is a quite complex phenomenon^19–21 whose explanation is often obtained by means of computer simulations.^22–26 Growth phenomena are even more complex in binary nanoparticles,^2,27 so that simulations are even more useful to predict the relevant growth pathways and understand the underlying atomic-level mechanisms.^28–34

In ref. 18, the growth of AuCu binary metallic clusters has been studied by Molecular Dynamics (MD) simulations in which Au atoms were deposited on pure Cu and mixed AuCu seeds of three geometric shapes (icosahedra (Ih), decahedra (Dh) and fcc truncated octahedra (TO)). The results of these simulations showed that the shape and composition of the starting seed have a significant effect on the growth pathways of the nanoparticles. While Cu@Au chemical ordering with pure Au surfaces was always obtained independently of the temperature and of the structure of the seeds, the final geometric shapes were quite different depending on whether the seed was pure Cu or intermixed AuCu, and on the specific shape of the seed. In particular a family of exotic structures was obtained when growing on pure TO and Dh seeds, while regular structures were obtained when growing on mixed seeds of different geometries.

In this paper, in contrast, we simulate using MD the growth by deposition of Cu atoms on pure Au and intermixed AuCu seeds in order to investigate the possibility of forming Au@Cu core@shell structures. It has been shown in several previous works^35–37 that in AuCu equilibrium structures the surface of the nanoparticles is very strongly enriched in Au; thus, the formation of a Cu outer shell may be prevented by the tendency of Au atoms to segregate to the surface. Our aim in this work is to determine whether kinetic phenomena may help the formation of the Au@Cu out-of-equilibrium core@shell arrangement, also unravelling the effect of shape and composition of the starting seeds on the final structures. To elucidate this aspect, we adopt the same growth procedure used in the previous work,¹⁸ in which an atomistic potential was used to model the interactions between the atoms. In this work we perform also Density Functional Theory (DFT) calculations to validate some important aspects of our model.

2 Computational details

In our MD simulations we deposit atoms one by one on a preformed seed according to the procedure adopted in ref. 18 and 25. Different types of initial seeds are chosen (see Fig. 1):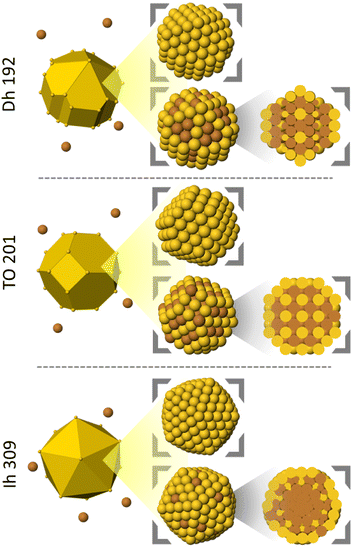

Fig. 1 Shapes and compositions of the considered seeds. For mixed seeds, also the cluster cross sections are shown.

• Truncated octahedron of 201 Au atoms.

• Truncated octahedron of 100 Au and 101 Cu atoms.

• Decahedron of 192 Au atoms.

• Decahedron of 96 Au and 96 Cu atoms.

• Icosahedron of 309 Au atoms.

• Icosahedron of 174 Au and 135 Cu atoms.

The composition of the mixed seeds has been chosen to be in a range close to 50–50% because it represents the lowest energy composition. The chemical ordering in mixed seeds corresponds to the optimal chemical arrangement obtained by global optimization runs with exchange moves (see Fig. S1 in ESI†). For all mixed seeds, the surface is strongly enriched in Au. In the inner part of Dh and TO seeds there is intermixing, while the central part of the Ih seed mostly contains Cu atoms to produce a sort of Cu@AuCu core@shell structure. In all structures, Cu atoms in surface prefer terrace sites on (111) facets.

Cu atoms are deposited on the seeds at time intervals of 10 ns, to reach the final size of 1000 atoms. The total duration of the simulations is therefore in the range 7–8 μs. The classical equations of motion are solved by the velocity Verlet algorithm with a time step of 5 fs. The simulations are made at constant temperature, which is kept constant by Andersen thermostat whose collision frequency is chosen in such a way that diffusive properties of atoms are not altered.³⁸ For each seed, we run 5 independent simulations at three different temperatures (300, 400 and 500 K), corresponding to a total of 90 simulations. We believe that our time scale is in general shorter than in experiments, but it is not very far from that of the experiments of gas-phase synthesis, in which the growth process takes place on total times that range from a fraction of millisecond to a few milliseconds. We note that our simulation protocol has been successfully used to interpret several growth experiments in the gas phase,^22,24,31 so that we believe that our simulations are informative.

The interaction between atoms are modeled by an atomistic potential based on the second-moment approximation to the tight-binding model (SMTB potentials, also known as Gupta potentials).^39,40 This potential for AuCu, whose form and parameters are given in ref. 18 and 36, has been previously tested against DFT calculations³⁶ obtaining a good agreement.

DFT calculations were carried out by using the pseudopotential method as implemented in the PWscf code of the QUANTUM ESPRESSO package.⁴¹ For all calculations, we use the generalized gradient approximation of Perdew–Burke–Ernzerhof (PBE)⁴² for exchange-correlation energy functional. The interactions between ions and core electrons for Au and Cu were described by the ultrasoft pseudopotentials.⁴³ The convergence thresholds for the total energy, total force, and for electronic calculations were set to 10⁻⁴ Ry, 10⁻³ Ry au⁻¹ and 5 × 10⁻⁶ Ry, respectively. For each calculation, we set the size of the cubic cell side to 30 Å, which is large enough to avoid the interaction between the cluster and its images. Furthermore, we used a cutoff of 45 Ry for plane-wave energy cutoff and 364 Ry for charge density.

3 Energetics of Cu impurities in Au seeds

In this section we discuss the preferential placement of Cu impurity in Au clusters. Two types of Au cluster are considered: truncated octahedron of 201 atoms and icosahedron of 147 atoms. For each cluster, we place Cu atom in different sites as shown in Fig. 2. In Table 1 we present the energies calculated by DFT and Gupta. The energy of the central site is set to zero in both structures.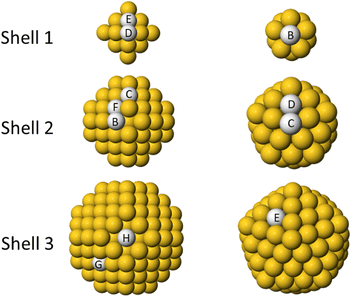

Fig. 2 Sites for placing single Cu impurities in Au clusters. Left column: shells of truncated octahedron of 201 atoms. Right column: shells of icosahedron of 147 atoms. The rows show the different shells for each geometry. For all clusters, site A is the central site of the cluster (not shown). The energies related to the different placement of the impurities are given in Table 1.

Table 1 Energies (in eV) for single Cu impurities in truncated octahedron and icosahedron Au clusters. The sites in which the impurities are placed are shown in Fig. 2. For all clusters, the zero of the energy is the cluster with the impurity placed in the central site A

Cluster geometry	Position	Gupta	DFT-PBE
	A center	0.000	0.000
	B subvertex	−0.055	−0.154
	C subedge	−0.044	−0.021
TO201	D subsubvertex	−0.078	−0.018
	E subsubedge	−0.027	0.051
	F subterrace	−0.054	0.057
	G (111) terrace	0.203	0.351
	H (100) terrace	0.240	0.414
	A center	0.000	0.000
	B subsubsurf	0.556	0.677
Ih147	C subvertex	0.760	0.665
	D subedge	0.834	0.858
	E terrace	1.236	1.429

---

The results of Gupta and PBE calculations are in good agreement. The worst sites for the placement of the Cu atoms are always those at the surface. As regards internal sites, there is a clear difference between the TO and the Ih. In the TO, the energy difference between internal sites are relatively small, and the best placement is not at the center, but in the subsurface layer or just below it. In the Ih, the central site is more favourable than any other site by large amounts of energy. This result is due to the advantage of placing the small Cu atom in the highly compressed central zone of the Ih to release the stress.⁴⁴

In summary, both Gupta and DFT results indicate that there is a driving force in favour of the incorporation of Cu atoms inside an Au cluster. Therefore, on sufficiently long time scale, deposited Cu atoms are expected to diffuse inside, with a tendency to stop in the subsurface region for the TO and a tendency to go towards the center in the Ih. The Dh is expected to behave qualitatively as the TO, since it does not present a highly compressed central region.⁴⁴ The tendency of Cu to migrate inside is thus expected to destabilize outer shells of Cu, unless temperature is sufficiently low to hinder migration.

4 Diffusion behaviour of a single Cu atom at constant temperature

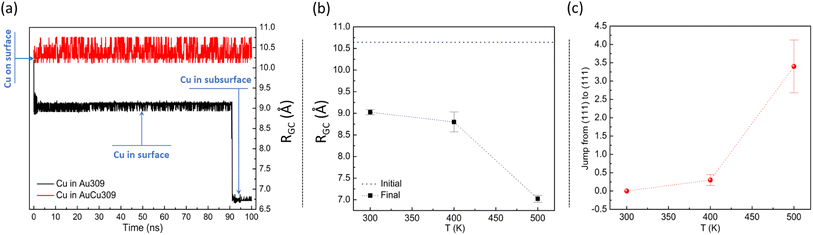
Before analysing the growth process on the considered seeds and the final outcomes of the growth simulations, we made some simulations at fixed temperatures and fixed cluster size. In these simulations, we aimed at understanding the evolution of a single Cu adatom on the considered starting TO and Ih seeds of sizes 201 and 309 atoms, respectively. For both structures, two different starting configurations were considered: Cu adatom on pure Au and Cu adatom on intermixed AuCu cluster. For each configuration, 10 independent simulations were performed. The results are given in Fig. 3 for Ih and Fig. 4 for TO.

Fig. 3 MD evolution of single Cu atom on Ih cluster of size 309 atoms with two different composition pure Au and mixed at equicomposition with lowest energy chemical ordering. (a) Migration behaviour of Cu atom on Au and AuCu Ih structures at 300 K during 100 ns (plot correspond to one simulation). (b) Distance between geometric center of cluster and single Cu atom on Au Ih R_GC for temperature range from 300 to 500 K. (c) Jump number from (111) to (111) facets of Cu adatom on mixed AuCu Ih structure for temperature range from 300 to 500 K. Values given in (b) and (c) are the average of all the 10 simulations. The errors correspond to the standard deviations of the averages. Blue dot line in (b) shows the distance in the initial configuration.

Fig. 4 Diffusion behavior of an isolated Cu atom which starts on the surface of TO seeds of pure Au and AuCu mixed compositions. First and second rows correspond to the diffusion of a Cu atom starting from sites on (100) and (111) facets, respectively. In (a) and (c) we report the distance R_GC between the geometric center of the cluster and the Cu atom on Au and AuCu seeds at 300 K during 100 ns. In (b) and (d) we report the ratio ξ of R_GC at the end of the simulation and at the beginning of the simulation in the temperature range from 300 to 500 K. Values given in (b) and (d) are averages over 10 simulations. Last column shows the initial position of Cu adatom on different facets.

In Fig. 3(a), we present the effect of composition of the icosahedral cluster on the migration behaviour of the Cu adatom at temperature 300 K during 100 ns. Specifically, we plot the evolution of the distance R_GC between the geometric center of the nanocluster and the Cu adatom at T = 300 K during 100 ns. The data show that the behaviour of the Cu adatom on pure Au and mixed AuCu Ih structures is different. On the pure Au cluster, the Cu adatom tends to incorporate deeply towards the inner part of the icosahedral matrix. On the contrary, on the intermixed AuCu cluster, the Cu adatom diffuses by jumps on the surface without incorporating in the cluster. This is due to the combined effect of the presence of Cu atoms on the surface and below the surface in the mixed Ih seed (vs.), which cause a contraction of the surface itself which renders incorporation much more difficult.

In Fig. 3(b) and (c), we show the effect of temperature on the diffusion of the Cu adatom in simulations of 10 ns. The considered temperature range is the same as in the growth simulations of the following chapters. The time of 10 ns corresponds to the interval between two successive depositions in the growth simulations. In order to quantify the volume diffusion of Cu inside Au₃₀₉, we calculate R_GC (see Fig. 3(b)) whereas, to analyse interfacet mobility for Cu on AuCu₃₀₉, we calculate the number of edge crossings between adjacent (111) facets (see Fig. 3(c)). For each temperature, we show the average value from 10 independent simulations. The effect of temperature on Cu migration is evident; i.e. both the volume diffusion for Cu incorporating in the Au seed and the surface diffusion for Cu on the AuCu seed become faster by increasing the temperature. On the time scale of 10 ns, interfacet mobility is truly activated only at 500 K. Only at 500 K, a fast enough volume diffusion achieved that allows the Cu atom to reach the center of the cluster.

From these results, we expect that the final outcomes of the growth process on icosahedral seeds can be strongly affected by the growth temperature and composition of the starting seed.

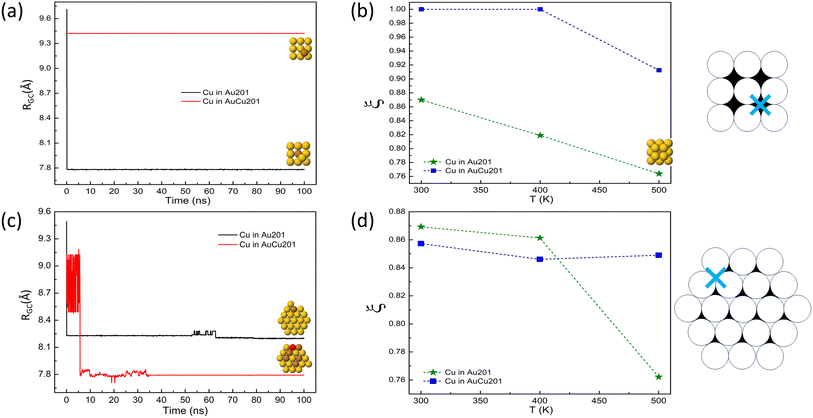
In Fig. 4, we show the results of the evolution of isolated Cu atoms on TO clusters. Truncated octahedra present both (100) and (111) facets, so it would be useful to understand the effect of the starting site of the Cu adatom on its diffusion behaviour. To this end, we performed different simulation series. The series differ according to the initial site of the Cu adatom which can be on (100) or (111) facets, and the composition of the TO support (pure Au or intermixed AuCu). The plots in the first column of Fig. 4 provide the distance between the geometric center of the cluster and the single Cu atom R_GC on both pure and intermixed TO clusters. The results are taken from simulations at temperature 300 K during 100 ns. For all cases, no interdiffusion of the Cu atom is observed and the diffusion is limited to the surface layer. All the diffusion processes occur by exchanges, by swapping the Cu adatom and a nearest neighbor surface atom. The analysis of R_GC shows the following:

• Cu on (100) facet of pure TO: no change in R_GC which means that there is no diffusion of the Cu atom.

• Cu on (100) facet of mixed TO: a sudden drop in R_GC at the beginning of the simulation meaning that the Cu adatom makes an exchange process with an atom of the (100) facet and stay in this site until the end of the simulation.

• Cu on (111) facet of pure TO: a sudden drop in R_GC at the beginning of the simulation signifying that the Cu adatom exchanges with a nearest neighbor atom of the edge between the (100) and (111) facets.

• Cu on (111) facet of mixed TO: R_GC presents two different values indicating that also in this case the Cu atom makes an exchange process with the edge atom of the TO mixed cluster.

The effect of temperature on Cu adatom diffusion on TO seeds are presented in the second column of Fig. 4. In this figure, we plot the ratio ξ of R_GC at the end and at the beginning of the simulations for the temperature range from 300 to 500 K. Each value corresponds to the average over 10 independent simulations. The plots show clearly that there is almost no mobility of the Cu adatom at temperatures of 300 and 400 K, whereas mobility is partially activated at 500 K, but it is limited to the surface for the mixed seed and the subsurface for the pure seed in this time scale of 10 ns.

Finally, comparing with the results of Cu on Ih clusters, we note that the diffusion of the Cu adatom to the center of the Au TO is almost absent. This result is understandable from the fact in the TO there is no icosahedral strain facilitating diffusion of Cu towards the center.

5 Growth on Ih preformed seeds

Fig. 5 summarizes the most common structures obtained at 300 and 500 K from the growth on the Ih starting seeds. Depending on temperature and composition of the seed, different structures are obtained. They can be classified into three classes: (a) decahedra obtained at 300 K on the pure Au seed, (b) icosahedra formed at 500 K again on the pure Au seed, icosahedra obtained at 300 K on the mixed seed and (d) poly-icosahedra grown at 500 K when starting from Ih mixed seed. In order to identify our structures, we use the common neighbor analysis which is a useful tool to discriminate different geometric structures.⁴⁵

Fig. 5 Final structures obtained during the growth of Cu atoms on Ih seeds. The structures are taken from simulations: (a) T = 300 K and deposition on pure Au seed; (b) T = 500 K and deposition on pure Au seed; (c) T = 300 K and deposition on mixed AuCu seed; (d) T = 500 K and deposition on mixed AuCu seed. The deposition rate is of 0.1/ns. Brown and yellow spheres represent copper and gold atoms, respectively.

The growth on pure Ih seed leads to the formation of decahedra at low temperatures and of icosahedra at high temperatures.

Even though the determination of equilibrium structures of clusters is often an open problem,¹⁹ there is a quite clear evidence that pure gold clusters in the gas phase are not expected to be Mackay icosahedra at equilibrium in our size range. Gupta and DFT calculations for the magic size 147 (ref. 46) show that decahedra are much more favourable than Mackay icosahedra, and icosahedra with rosette reconstruction stay in between. The stronger stability of decahedra compared to icosahedra is observed also in experiments on gas-phase clusters of magic sizes 561 and 923.^47,48 Icosahedra are energetically unfavourable due to the large strain and corresponding atomic-level compression in the innermost part of the structure.⁴⁹ Therefore, incorporation of small Cu atoms in the central sites may release stress and make the icosahedral structure more favorable. However, migration of Cu atoms towards the center is possible only if these atoms are highly mobile, which can happen only at sufficiently high temperatures. This means that the final shape of the nanoparticles can be strongly influenced by the mobility of Cu atoms throughout the volume of the icosahedral structure.

At T = 300 and 400 K, the transformation from icosahedra to the more energetically favourable decahedra is observed in all growth simulations. This transformation takes place at the initial stage of the growth; after depositing few tens of Cu atoms. The size at which this transformation occurs depends on temperature. Our analysis shows that, in the initial stages of the growth, the diffusion of Cu atoms to the inner part is partially activated but it is limited to the subsurface layers (see the discussion in Section 4). Therefore, Cu atoms are not able to reach the central sites of the icosahedron. As a consequence, the inner stress is not released and the clusters transform to decahedral shapes. The same results have been previously obtained by Toai et al.¹⁷ for smaller sizes.

On the other hand, at T = 500 K, the growth continues keeping the icosahedral shape till the end of the 5 simulations. At this temperature, the mobility of Cu atoms is fast enough to let them reach the central sites of the icosahedron, which helps in releasing stress and makes the icosahedron energetically favourable. Therefore, the driving force for the transformation to decahedral shapes is not active anymore.

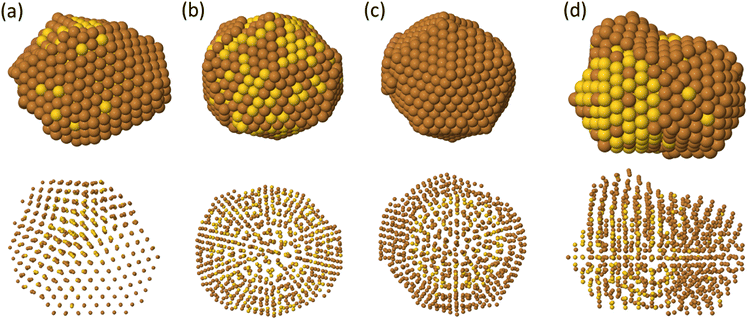
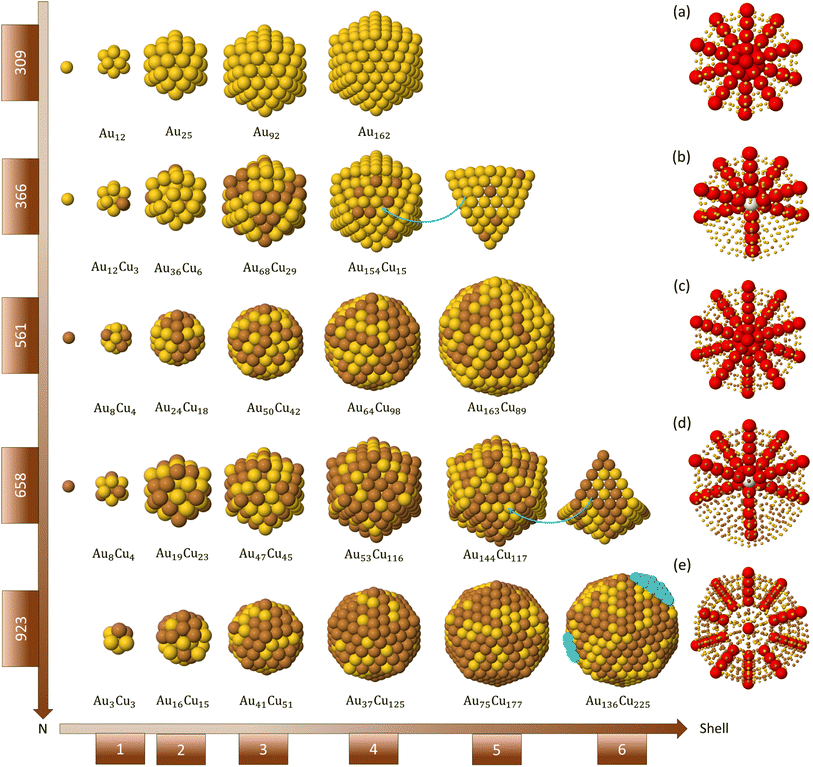
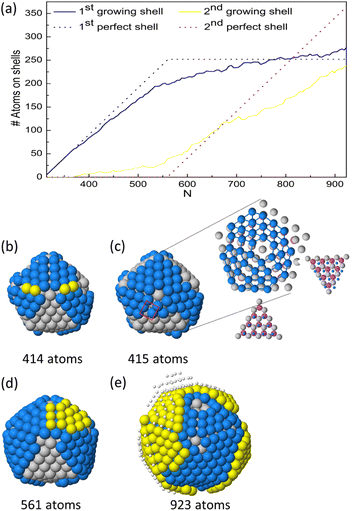
The representative growth mechanisms of these icosahedral shapes are presented in Fig. 6. Each row shows the composition of the different shells depending on the cluster size. At T = 500 K, a rather regular shell-by-shell growth within the icosahedral motif is observed up to size 923 atoms. The initial incorporation of Cu atoms causes disordering of the initial icosahedral structure by surface reconstruction, as shown in the second row of Fig. 6(b). In the reconstructed surface, some anti-Mackay patches appear. In anti-Mackay islands atoms are placed on hcp stacking on the surface of the icosahedron.⁵⁰ However, when Cu atoms succeed in reaching the central sites, the structure reorders to a good icosahedral shape with unreconstructed surface and then continues its growth towards the next magic icosahedron of size 561 atoms, as presented in third row of Fig. 6(c). The further growth towards the icosahedron of size 923 atoms takes place by the same mechanisms (see fourth and fifth rows of Fig. 6), passing through a surface reconstruction and then recovering the Mackay Ih symmetry. When analysing the inner part of the growing clusters, the formation of some atomic vacancies in the central site and in the innermost atomic shells is observed. The formation of these vacancies causes the ejection of a corresponding number of atoms on the cluster surface. Vacancy formation in central sites is a known stress release mechanism in icosahedra.⁵¹ It takes place by complex diffusion mechanisms involving the concerted displacement of many atoms at the same time,^32,34 and as such, is expected to be activated at high temperatures.

Fig. 6 Surface view and composition of the different shells during the growth on pure Au Ih seed at 500 K and deposition rate of 1 atom every 10 ns. Rows correspond the nanoparticle sizes from (a) 309 to (e) 923 atoms. Columns correspond the nanoparticle shells. Brown and yellow spheres represent copper and gold atoms, respectively. The atoms belonging to fivefold axes are coloured in red. Ejected atoms to the surface of the AuCu icosahedron of 923 atoms (a geometric magic number for the Ih) are shown by cyan spheres.

The main types of defects observed during the growth of these icosahedra are summarized in Fig. S3 in the ESI.† All these defects are generated due to the interdiffusion which can break the icosahedral symmetry.

Let us now discuss the shapes obtained in the growth on mixed Ih seeds, which takes place by quite different mechanisms than those observed for pure Au seeds and leads to different structures. In fact, depending on temperature, we observe the formation of icosahedral motifs at T = 300 K and of multiple icosahedra at 500 K.

In mixed icosahedral seeds, the surface is almost completely made of Au atoms. Some Au atoms are presented in the subsurface layer, but the core is fully occupied by the smaller Cu atoms to release the stress in the structure. As a result, the icosahedron is quite stable, for what concerns both shape and chemical ordering. Therefore, deposited Cu atoms do not incorporate easily in the seed, but keep on diffusing on its surface instead (see the discussion in Section 4). Surface diffusion of Cu atoms becomes faster and faster with increasing temperature.

At T = 300 and 400 K, we observe the growth of icosahedral shapes with pure Cu shell (Fig. 5(c)). The surface of these icosahedra is irregular and does not adopt the Mackay stacking of the initial seed. This may indicate that the nanoparticle does not grow in a layer-by-layer mode. In order to further characterise this growth pathway, we monitor the number of atoms in the first and second growing atomic layers during the growth process. The results are shown in Fig. 7 for one simulation over five at temperature 300 K (see Fig. S4 in the ESI† for the growth at 400 K). From Fig. 7(a), we observe that the evolution of atoms in the first and second shells is quite different from the ideal layer-by-layer growth. At size 561 atoms, the number of atoms in the first growing shell does not match the ideal one, since the second shell starts to grow before completing the formation of the first shell. Rather surprisingly, at size 923 atoms, the number of atoms in the first shell is higher than the ideal number.

Fig. 7 Growth pathway within the icosahedral motif starting from an AuCu mixed icosahedron, at temperature T = 300 K. (a) Number of atoms on the first and second growing shells on 309 AuCu seed. (b)–(e) Surface views of the growing cluster at different sizes. Gray, blue, and yellow spheres represent surface atoms of the seed, of the first growing shell and of the second growing shell, respectively. Inset snapshots show the stacking behavior of the first shell with respect of those of the initial seed.

To explore the mechanisms behind this growth pathway, we follow the growth process of the nanoparticle atom by atom. In Fig. 7, we present snapshots from growth simulations at 300 K. The snapshots show the main steps leading to this growth pathway. The first step of the growth takes place by nucleating faulted islands on different facets of the initial seed in order to form anti-Mackay islands (see blue atoms in Fig. 7(b)). The formation of several independent islands is due to the slow interfacet mobility of Cu atoms at these temperatures.

Indeed, in lattice mismatched bimetallic nanoalloy, anti-Mackay stacking is energetically favorable only at small sizes and when the shell lattice is larger than the core lattice.⁵⁰ In our case, we have the opposite, since the Cu shell lattice is smaller than the lattice of the seed by 6.25%. This highly destabilizes anti-Mackay arrangements, leading to a peculiar atomic pattern of the growing copper shell as presented in Fig. 7(c); some anti-Mackay facets transform to Mackay stacking and other stay in an anti-Mackay arrangement (see inset lattice).

This arrangement causes the formation of some fourfold adsorption sites on top of the growing Cu shell as shown by the red rectangle in Fig. 7(c). These sites may accommodate new atoms and start the formation of the second shell on the incomplete first one (yellow atoms in Fig. 7(d)). As a result, nanoparticle with an irregular surface is formed as represented in Fig. 7(e). As growth continues, Cu atoms can incorporate in the first growing shell to increase its density. The density increase is favored by the lattice mismatch, because the atoms of the growing Cu shell are on the average smaller than those of the underlying substrate.

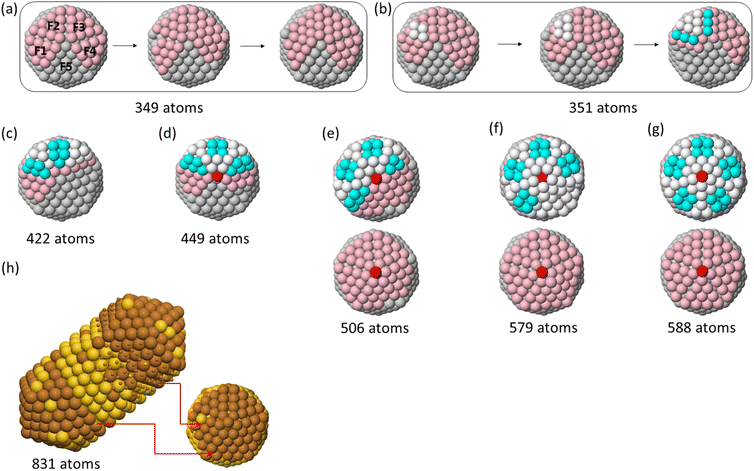
At T = 500 K, we observe that Cu atoms tend to accumulate on one side of the initial icosahedral seed, as presented in Fig. 5(d), which looks like a kind of strain-induced dewetting. To understand the mechanisms leading to this growth shape, we analyse the atomic displacements step by step. The results are reported in Fig. 8. In Section 4 we have shown that, at this temperature, interfacet mobility of Cu atoms is activated, so that Cu adatoms can quickly diffuse around the whole surface of the starting seed and meet each other to form a large island instead of the many small islands on different facets as observed in the low temperature growth.

Fig. 8 Growth pathway of Cu on Ih AuCu mixed seed. Snapshots are taken from simulation at T = 500 K and deposition rate of 0.1/ns. From (a) to (g): gray spheres represent atoms of the initial Ih seed; pink spheres show atoms of the first growing islands on the initial seed; atoms in (111) and (100) sites are shown by white and cyan spheres; the atoms of the newly formed fivefold axis are coloured in red. In the bottom row, the triple icosahedron obtained at 831 atoms is shown, with Au atoms in yellow and Cu atoms in brown. The surface of the triple icosahedron is patchy, with two Cu-rich patches at the extremities and an Au-rich patch in the middle.

As the island grows larger, it becomes more and more strained due to the lattice mismatch effect. Thus, ideal fcc (hcp) lattice sites are rarely observed (see Fig. 8(a) also Fig. S6 in ESI†). This complex off-lattice configuration may boost one or more Cu-island atoms to pop out the island layer as shown in Fig. 8(b) (white and cyan atoms) to release the stress. We note that this pop-up diffusion is not observed during the growth at T = 300 and 400 K, meaning that the frequency of pop-up events strongly depends on temperature. The popped atoms may stabilise the position of the lower layer atoms on hcp sites for several time steps. This leads to the creation of fourfold adsorption sites on top of the island, which act as traps for further adatoms,^24,25 which create further new adsorption sites in a kind of autocatalytic process.²⁴ This process leads to the growth of a new icosahedral part, finally to a double icosahedron, and of a triple icosahedron if two large islands are initially formed on opposite sides of the seed (see Fig. 8). The surface of these nanoparticles is patchy, since it alternates Cu-rich and Au-rich exposed regions.

Finally we note that, even though the structures grown at T = 500 K are quite elongated, they are lower in energy than those grown at lower temperatures because the latter are more irregular and strained.

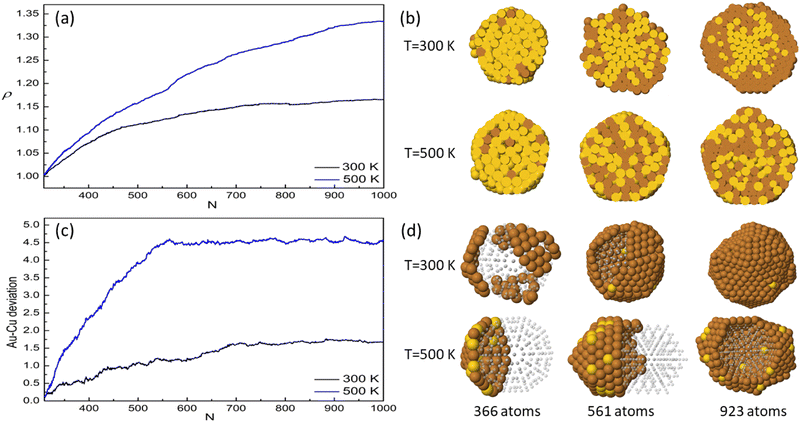
An analysis of the chemical arrangement in these clusters is given in Fig. 9. On pure Au seeds, the central part of the cluster is still rich in Au at 300 K and well intermixed at 500 K. The calculation of the gyration radius of the ensemble of Au atoms shows that they can diffuse towards the surface at 500 K, while they remain in the central zone at 300 K (Fig. 9(a) and (b)). For deposition on mixed seeds, we report in Fig. 9(c) the distances between the geometric centers of the Au and Cu parts at T = 300 and 500 K. While at 300 K the two parts are centered almost in the same position, at 500 K, they are displaced to form a Janus-like structure with patchy surface (Fig. 9(d)).

Fig. 9 (a) Evolution of gyration radius of Au atoms in the nanoparticle volume during the growth on pure Au seed. ρ is the ratio between the gyration radius at a given time and the gyration radius at the beginning of the simulation. (b) Representative cross sections of the clusters grown on pure Au seeds at different sizes. (c) Evolution of the difference (in Å) between the geometric centers of Au and Cu atoms deviation during the growth on a mixed AuCu Ih seed. In each graph, we show the results at two different temperatures T = 300 and 500 K. For each temperature we show the average over all performed simulations. (d) Representative cross sections of the clusters grown on mixed AuCu seeds at different sizes.

6 Growth on TO and Dh preformed seeds

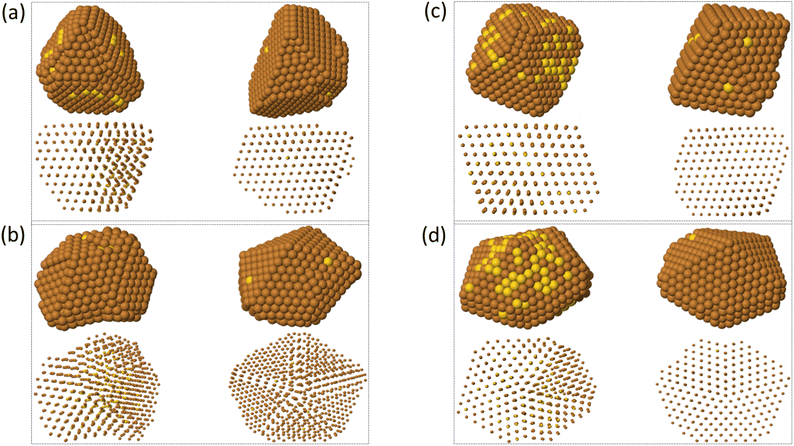
Here we analyze the outcomes of the growth on TO and Dh seeds.

In Fig. 10 we report representative snapshots of the final shapes obtained when growing on TO and Dh seeds, for both pure Au and mixed AuCu seeds. For TO seeds (snapshots in Fig. 10(a) and (c)), most clusters keep growing as fcc structures, comprising octahedra and tetrahedra (with different degrees of truncation), flat hexagons and triangles, as observed in simulations of other systems.^24,52 At T = 300 K, we observe the growth of some multi-twinned structures (see left column in Fig. 10(a)) in the same way as discussed in our previous work.¹⁸ Only one polydecahedron⁵³ is obtained, at T = 500 K.

Fig. 10 Final structures (at size 1000 atoms) obtained during the growth of Cu atoms on TO and Dh seeds. The structures are taken from simulations at temperatures T = 300 and 500 K and deposition rate of 0.1/ns. (a) and (b) show the representative snapshots of nanoparticles obtained from the growth on TO and Dh seeds at 300 K, respectively. (c) and (d) correspond the ones obtained at 500 K. For each temperature, the left column represents the structures obtained from pure seeds, whereas the right column shows the ones grown from mixed seeds. Brown and yellow spheres represent copper and gold atoms, respectively. In all cases, the same nanoparticle is shown in two different views. The first view shows the nanoparticle surface. In the second view, all atom types are shown as small spheres in order to better show the crystalline planes of the structures.

The growth on Dh seeds (snapshots in Fig. 10(b) and (d)) leads to the formation of Dh or polydecahedra in most cases. An icosahedral shape is grown in only one simulation, and also other complex structures are produced in some simulations.

In the deposition of Cu on pure Au seeds, all growing structures are irregular and strained. Their atomic rows present an arc-like bending, which is especially evident at low temperature. On the contrary, for Cu on AuCu, the structures are more regular and much less strained, exhibiting aligned atomic rows at any growth temperature.

The chemical ordering within the nanoparticle is core@shell: Au@Cu for pure starting seeds and (AuCu)@Cu for mixed seeds. However, in all simulations we observe the migration of some gold atoms to the surface of the cluster which prevents the formation of a perfect pure Cu outer shell.

Our results show that the degree of Au segregation and its distribution within the nanoparticle depend on three parameters – temperature, seed shape and composition. To characterise more deeply this effect, we calculate the number of Au atoms in the surface and subsurface layers. The results are given in ESI.† For each geometric shape of the starting seed, the amount of Au on the surface and its distribution within the nanoparticle depend both on the growth temperature and on the composition of the starting seed, being small for mixed seeds and for low temperatures, and larger for pure seeds or high temperatures. These results demonstrate that, at any temperature, the atomic mobility of Au atoms is somewhat higher in the case of Cu deposited on pure Au seeds than for deposition on AuCu seeds. There is also some difference between TO and Dh seeds, because the diffusion of Au towards the surface is easier in the former.

7 Conclusions

The growth of AuCu nanoparticles occurs through different pathways depending on the growth temperature, and on the shape and composition of the initial structure (the seed).

We note that the results presented in this work show completely opposite behaviours than those found in ref. 18, where Au atoms were deposited on pure Cu or AuCu seeds. In fact, when depositing Au atoms, growth on icosahedral seeds is found to be regular and without any shape transformation, while the transformations take place when growing on Dh or TO seeds. On the contrary, when depositing Cu atoms, it is the growth on Ih seeds that presents a more complex phenomenology. When starting from pure Au icosahedral seeds, we observe the formation of decahedra with Au@Cu core@shell arrangement at low temperatures and of icosahedra with intermixed chemical ordering at high temperature. Deposited Cu atoms tend to enter the Au seed at every simulation temperature. At low temperatures, the mobility of Cu atoms inside the Au seed is slow, so that they can incorporate only in the surface and subsurface layers. This incorporation is not sufficient to stabilize the icosahedral structures, which transforms into decahedra because they are more energetically favourable. At higher temperatures, Cu atoms are able to diffuse towards the center of the icosahedron, thus being able to release the atomic-level stress⁴⁴ and to stabilize the structure against the transformation into a decahedron. This behavior is an example of a rather counterintuitive effect: it shows that accelerating the diffusion kinetics helps to avoid cluster reshaping instead of promoting it. We note that icosahedral structures in this size range are not unstable but metastable, so that they can survive for long if temperature is sufficiently low and change their structure to Dh or fcc only after annealing.⁴⁸ Our simulations show that the transformation of Au icosahedra might be completely blocked by depositing Cu atoms on top of them, at a temperature at which the kinetics of Cu incorporation becomes comparable to that of the structural transformations.

When starting from intermixed AuCu icosahedral seeds, the diffusion of Cu atoms inside the seed is negligible. At low temperatures, interfacet mobility of Cu adatoms is difficult, so that several Cu islands are nucleated on the surface, on average in an isotropic way. As the number of deposited Cu atoms increases, the surface of the seed becomes fully covered by a Cu shell, which is rough due to the low atomic mobility and strained due to the lattice mismatch. At high temperatures, interfacet mobility of Cu adatoms is activated. This causes a sort of dewetting phenomenon in which Cu atoms accumulate in large islands on one side (or on opposite sides) of the seed, leading to the formation of elongated structures, i.e. of double or triple icosahedra, where the initial seed is only partially covered by the deposited Cu atoms. The surface of these nanoparticles is thus finally composed by alternating patches with Cu-rich and Au-rich compositions.

In TO and Dh seeds, the growth takes place within the initial structural motif. At low temperature, some multi-twinned structures are formed in the growth on the pure TO seed. In general, low-temperature growth shapes are irregular, with bending atomic columns for pure seeds, and regular with aligned atomic columns for mixed seeds. The Au@Cu core@shell arrangement is formed. In all cases, the purity of the surface layer is not perfect because of some surface migration of Au atoms. Au migration is somewhat stronger for pure seeds than for mixed ones, and for Dh seeds than for TO seeds. Correspondingly, the analysis of the internal arrangement of the nanoparticles indicates that in the growth process the mobility of Au atoms is higher for pure seeds than for mixed ones and for Dh seeds than for TO ones.

Our simulations therefore show that the deposition of Cu atoms on Au and AuCu seeds can produce a rich variety of nanoparticle shapes that very often presents strained shells and, in some cases, patchy surface arrangements. These surface arrangements can be of great interest for application to catalysis.

Author contributions

EE performed and analyzed the MD simulations and DFT calculations. RF assisted in the analysis of the simulations and supervised the work. All authors contributed to the drafting of the paper.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge support from the PRIN 2017 project UTFROM of the Italian MIUR and from the Progetto di Eccellenza of the Physics Department of the University of Genoa. The authors acknowledge networking support from the IRN Nanoalloys of CNRS. The authors thank Diana Nelli and Cesare Roncaglia for useful discussions.

Notes and references

1. C. L. Bracey, P. R. Ellis and G. J. Hutchings, Chem. Soc. Rev., 2009, 38, 2231–2243.
2. R. Ferrando, Structure and Properties of Nanoalloys, Elsevier, 2016.
3. N. Wang, Y. Han, Y. Xu, C. Gao and X. Cao, Anal. Chem., 2015, 87, 457–463.
4. C.-Y. Tai, J.-L. Chang, J.-F. Lee, T.-S. Chan and J.-M. Zen, Electrochim. Acta, 2011, 56, 3115–3121.
5. Y. Wang, Q. Zhang, Y. Wang, L. V. Besteiro, Y. Liu, H. Tan, Z. M. Wang, A. O. Govorov, J. Z. Zhang, J. K. Cooper, J. Zhao, G. Chen, M. Chaker and D. Ma, Chem. Mater., 2021, 33, 695–705.
6. S. Thota, Y. Wang and J. Zhao, Mater. Chem. Front., 2018, 2, 1074–1089.
7. J. Monzó, Y. Malewski, R. Kortlever, F. J. Vidal-Iglesias, J. Solla-Gullón, M. T. M. Koper and P. Rodriguez, J. Mater. Chem. A, 2015, 3, 23690–23698.
8. P. Wang, W. Nong, Y. Li, H. Cui and C. Wang, Appl. Catal., B, 2021, 288, 119999.
9. H. Okamoto, D. J. Chakrabarti, D. E. Laughlin and T. B. Massalski, J. Phase Equilib., 1987, 8, 454–474.
10. E. Panizon and R. Ferrando, Nanoscale, 2016, 8, 15911–15919.
11. J. A. Ascencio, H. B. Liu, U. Pal, A. Medina and Z. L. Wang, Microsc. Res. Tech., 2006, 69, 522–530.
12. H. Prunier, J. Nelayah, C. Ricolleau, G. Wang, S. Nowak, A.-F. Lamic-Humblot and D. Alloyeau, Phys. Chem. Chem. Phys., 2015, 17, 28339–28346.
13. L. Rout, A. Kumar, R. S. Dhaka, G. N. Reddy, S. Giri and P. Dash, Appl. Catal., A, 2017, 538, 107–122.
14. S. Thota, Y. Wang and J. Zhao, Mater. Chem. Front., 2018, 2, 1074–1089.
15. R. Mendoza-Cruz, L. Bazán-Diaz, J. J. Velázquez-Salazar, J. E. Samaniego-Benitez, F. M. Ascencio-Aguirre, R. Herrera-Becerra, M. José-Yacamán and G. Guisbiers, Nanoscale, 2017, 9, 9267–9274.
16. Y. Gafner, S. Gafner, L. Redel and I. Zamulin, J. Nanopart. Res., 2018, 20, 51.
17. T. J. Toai, G. Rossi and R. Ferrando, Faraday Discuss., 2008, 138, 49–58.
18. E. y. El koraychy and R. Ferrando, Nanoscale, 2023, 15, 2384–2393.
19. K. A. Fichthorn, Chem. Rev., 2023, 123, 4146–4183.
20. L. Marks and L. Peng, J. Phys.: Condens. Matter, 2016, 28, 053001.
21. M. Sun, Z. Cheng, W. Chen and M. Jones, ACS Nano, 2021, 15, 15953–15961.
22. D. M. Wells, G. Rossi, R. Ferrando and R. E. Palmer, Nanoscale, 2015, 7, 6498–6504.
23. J. Kim, J. Cui and K. A. Fichthorn, ACS Nano, 2021, 15, 18279–18288.
24. Y. Xia, D. Nelli, R. Ferrando, J. Yuan and Z. Y. Li, Nat. Commun., 2021, 12, 3019.
25. E. y. El koraychy, C. Roncaglia, D. Nelli, M. Cerbelaud and R. Ferrando, Nanoscale Horiz., 2022, 7, 883–889.
26. D. Nelli, V. Mastronardi, R. Brescia, P. P. Pompa, M. Moglianetti and R. Ferrando, Nano Lett., 2023, 23, 2644–2650.
27. B. Ni, J. Zhou, L. Stolz and H. Cölfen, Adv. Mater., 2023, 2209810.
28. F. Baletto, C. Mottet and R. Ferrando, Phys. Rev. Lett., 2003, 90, 135504.
29. I. Parsina and F. Baletto, J. Phys. Chem. C, 2010, 114, 1504–1511.
30. N. Ahmad, M. Bon, D. Passerone and R. Erni, ACS Nano, 2019, 13, 13333–13342.
31. D. Nelli, C. Roncaglia, S. Ahearn, M. Di Vece, R. Ferrando and C. Minnai, Catalysts, 2021, 11, 718.
32. D. Nelli, F. Pietrucci and R. Ferrando, J. Chem. Phys., 2021, 155, 144304.
33. I. V. Chepkasov, V. S. Baidyshev, A. A. Golubnichiy, I. S. Zamulin, A. G. Kvashnin and S. M. Kozlov, Aggregate, 2022, 3, e273.
34. D. Nelli, Eur. Phys. J.: Appl. Phys., 2022, 97, 18.
35. S. Lysgaard, J. S. G. Myrdal, H. A. Hansen and T. Vegge, Phys. Chem. Chem. Phys., 2015, 17, 28270–28276.
36. J.-Q. Goh, J. Akola and R. Ferrando, J. Phys. Chem. C, 2017, 121, 10809–10816.
37. D. Nelli, C. Mottet and R. Ferrando, Faraday Discuss., 2023, 242, 52–68.
38. F. Baletto, C. Mottet and R. Ferrando, Surf. Sci., 2000, 446, 31–45.
39. F. Cyrot-Lackmann and F. Ducastelle, Phys. Rev. B: Solid State, 1971, 4, 2406–2412.
40. R. P. Gupta, Phys. Rev. B: Condens. Matter Mater. Phys., 1981, 23, 6265.
41. P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. D. Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens.Matter, 2009, 21, 395502.
42. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
43. D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 7892–7895.
44. D. Nelli, C. Roncaglia and C. Minnai, Adv. Phys.: X, 2023, 8, 2127330.
45. C. Roncaglia and R. Ferrando, J. Chem. Inf. Model., 2023, 63, 459–473.
46. J.-P. Palomares-Baez, E. Panizon and R. Ferrando, Nano Lett., 2017, 17, 5394–5401.
47. D. Foster, T. Pavloudis, J. Kioseoglou and R. Palmer, Nat. Commun., 2019, 10, 2583.
48. Z. W. Wang and R. E. Palmer, Phys. Rev. Lett., 2012, 108, 245502.
49. D. M. Wells, G. Rossi, R. Ferrando and R. E. Palmer, Nanoscale, 2015, 7, 6498–6503.
50. D. Bochicchio and R. Ferrando, Nano Lett., 2010, 10, 4211–4216.
51. C. Mottet, G. Tréglia and B. Legrand, Surf. Sci., 1997, 383, L719–L727.
52. E. y. El koraychy, D. Nelli, C. Roncaglia, C. Minnai and R. Ferrando, Eur. Phys. J.: Appl. Phys., 2022, 97, 28.
53. G. Rossi and R. Ferrando, Nanotechnology, 2007, 18, 225706.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3na00714f

---