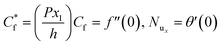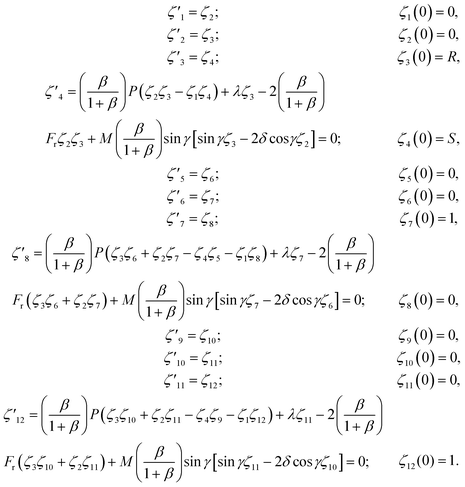Open Access Article
Open Access ArticleSqueezed Darcy–Forchheimer Casson nanofluid flow between horizontal plates under the effect of inclined magnetic field
M. Asif
Memon
 a,
Dur-e-Shehwar
Sagheer
b,
Mushrifah A. S.
Al-Malki
c,
Muhammad Sabeel
Khan
b,
Shafqat
Hussain
d,
Haseeb ur
Rehman
b and
Amsalu
Fenta
a,
Dur-e-Shehwar
Sagheer
b,
Mushrifah A. S.
Al-Malki
c,
Muhammad Sabeel
Khan
b,
Shafqat
Hussain
d,
Haseeb ur
Rehman
b and
Amsalu
Fenta
 *e
*e
aDepartment of Mathematics and Social Sciences, Sukkur IBA University, Sukkur, 65200, Sindh, Pakistan. E-mail: asif-memon@iba-suk.edu.pk
bDepartment of Mathematics, Capital University of Science and Technology, 44000 Islamabad, Pakistan. E-mail: d.e.shehwar@cust.edu.pk; muhammad.sabeel@cust.edu.pk; haseebchohan165@gmail.com
cDepartment of Mathematics and Statistics, College of Science, Taif University, P. O. Box 11099, Taif 21944, Saudi Arabia. E-mail: m.malky@tu.edu.sa
dDepartment of Mathematics, LS-III, Technical University Dortmund, Germany. E-mail: shafqat.hussain@math.tu-dortmund.de
eDepartment of Physics, Mizan Tepi University, PO Box 121, Tepi, Ethiopia. E-mail: amsalu.fenta09@gmail.com
First published on 8th November 2023
Abstract
This article explores the properties of heat and mass transport for MHD Casson nanofluid flow between two horizontal plates by considering the Darcy–Forchheimer medium. The effects of a uniform inclined magnetic field are discussed numerically. A Darcy–Forchheimer medium is considered in the x-direction between two plates. The features of Brownian diffusive motion, porosity, friction, viscous dissipation, chemical reaction, and thermophoresis are also considered. The governing equations of the model are a system of partial differential equations. This system is converted into non-linear ordinary differential equations using suitable similarity functions. The numerical shooting technique is used to solve the attained boundary value problem. This numerical technique is endowed with the Runge–Kutta order four method and the Newton method. Graphs and tables depict different significant effects. It is observed that the effect of a magnetic field is inversely related to the fluid flow. Moreover, the porosity factor (λ) and the magnetic inclination (γ) are inversely related to the surface drag force (Cf) and the Nusselt number (Nu).
1 Introduction
Physical scenarios containing viscous fluid involve the natural phenomenon of heat and mass convection. This phenomenon occurs naturally in many formations, including two parallel plates, stretched surfaces, and inside cylinders and spheres. The phenomenon of fluid moving between two surfaces is called squeezing flow. Researchers who investigated fluid flow, heat, and mass transport have given significant attention to squeezing flow because of its importance and applications in industry. Furthermore, in the last decade, many classical hydrodynamics flow problems obtained new consideration within the more general context of hydrodynamics. Many fields, such as chemical, mechanical, and biochemical engineering, food, and industrial processing, are emblematic examples of areas involving squeezing flow. Additionally, many applications can be seen in automobiles, lubricants, rolling elements, machine devices, and gears.Investigations have1–4 provided excellent information on steady, laminar, incompressible, free convection boundary-layer flow down a vertical plate immersed in a thermally stratified fluid-saturated porous media in the presence of a uniform normal magnetic field. The growing laminar free convection of a micropolar fluid in a vertical parallel plate channel with asymmetric heating is addressed numerically and analytically in ref. 5. The squeezing flow is first discussed by Stefan,6 which is well regarded by the scientific community with helpful remarks on the different profiles of fluid flow. After that, the squeezing flow was extensively addressed by many researchers. Rashidi et al.7 discussed the unsteady axisymmetric and 2D squeezing flows lying between two parallel plates. These authors found the solutions analytically by HAM and validated the effects of the squeezing parameter on skin friction and Nusselt number using the fourth-order Runge–Kutta method. In 2015, Hayat et al.8 revealed the different properties of 3D squeezing flow between two sheets using mixed convection. They found that with the rotation increase, the suction parameters are directly related to the magnitude of the drag force coefficient and the local Nusselt number. In another study, Hayat et al.9 demonstrated a flow in a rotating channel squeezed between two disks and discovered that the velocity profile increases with an enhancement in the squeezing parameter. Shahmohamadi and Rashidi10 reported some attractive verdicts on squeezing nanofluid flow within a rotating channel where the lower plate is porous. The obtained consequences showed that an increase of nanoparticles significantly affects the shear stress near the walls and the velocity profiles of the flow. Some recent studies11–13 are referred to for better understanding of the flows mentioned above. Nanofluids have more practical features14–16 in fluid mechanics due to technological advancements since the thermal properties of the nanofluid are better (see for instance ref. 17) than those of the fluids. These fluids have metallic nanoparticles dispersed in the base fluid. Nanofluids have provided considerable advances due to their thermal properties and dynamic suppleness in terms of irreversibility, entropy, and many other relevant features. The pioneering study in this area was conducted by Choi,18 illustrating nanoparticle effects on the underlying liquid’s thermo-physical properties. The research community appraised the idea practically by considering nanofluids in different flow problems. Later, Parvin and Chamkha19 analyzed nanofluid flow with entropy generation and free convection in an odd-shaped cavity. Zaraki et al.20 disclosed the convection properties within the boundary layer by considering additional properties of nanoparticles, e.g., size, type, and shape. Reddy and Chamkha21 accounted for the flow, heat, and mass transfer of MHD viscous, incompressible nanofluid flow with heat absorption/generation upon a homogeneously stretching sheet. Flow is considered in a porous medium with thermal radiation, chemical reaction, and thermal diffusion effects. Results of this article reveal that the increase in Rayleigh number is a reason for an increment in the average Nusselt number and the heat transport of entropy generation but a decrease in the viscous term. Chamkha et al.22 studied the entropy optimization and impact of magnetic parameters in a water-based nanofluid. Rasool et al.23 discussed the impacts of the porous medium on nanofluid flow over an expanding surface and demonstrated that skin friction increases significantly due to the porous medium, because of the high resistance of porosity. The heat and mass flux is decreased for a stronger porosity factor. This observation is crucial for industries where nanofluids are used. Ismael et al.24 analyzed nanofluid flow in a cavity filled with a porous media and studied entropy optimization. Many recent articles25–29 are focused on the analysis of the flow of nanofluids. Recently, Murtaza et al.11 addressed how the improved thermophysical properties of nanofluids have a substantial impact on how successful they are in convection processes. A few interesting studies on hybrid nanofluids can be found in the literature.15,30
The laws of Darcy are widely used to model and analyze the flows with fluid in a porous medium. If the Reynolds number is greater than one, then extra hydrodynamic head loss occurs due to inertial effects, making the flow non-Darcian. Forchheimer31 sum up the effects of inertia by introducing a non-linear term on the reduction of apparent permeability. This development is termed the Darcy–Forchheimer model. Muskat and Wyckoff32 presented homogeneous fluid flow through the Darcy medium. This classical study presents an analytical solution to the problem of combined seepage under a sheet piling cofferdam applied to dewatering systems. Seddeek33 considered the flow incorporating mixed convection to study the impacts of thermophoresis and viscous dissipation in Darcy-type fluid flow. The authors discovered that in this scenario, an increase in the thermophoretic parameter decreases the velocity and increases the boundary layer. Sadiq and Hayat34 considered Maxwell liquid to report the 2D, MHD flows over a surface expanding with linear velocity. Their findings reveal that the temperature profile is inversely associated with the thermal relaxation parameter and Prandtl number. Hayat et al.35 conducted a study of Darcy-type nanofluid flow with chemical reaction and heat generation. Rasool et al.36 considered a nanofluid flow in a Darcy–Forchheimer medium between two horizontal plates under the effect of a uniform magnetic field. The findings of this article reveal that the thermal profile decreases for increasing viscosity parameters; moreover, Brownian diffusion and thermophoresis increase for the said profile. An increase is observed in surface drag force for the elevated values of the porosity parameter.
This study presents an investigation of the inclined magnetic field on the Forchheimer porous Casson flow between horizontal plates. It extends the problem highlighted in ref. 36 by providing a numerical analysis of magneto-hydrodynamic Casson flow with porosity under the inclined magnetic field effects. The interaction of an inclined magnetic field in porous medium between plates can have different interesting applications, for instance, inclined magnetic fields can be utilized for improved efficiency in oil and gas reservoirs; in removal of contaminants from groundwater in aquifers; in heat exchangers and cooling systems, in measuring the magnetic response of porous formations; in electromagnetic braking in pipes; in filtration and separation processes and in microfluidic systems. From the primitive years, mass transfer has played an essential role in understanding the ocean’s vaporization, burning of oil pools, spray drying, leaching, and the abolition of a meteorite. Due to this critical role of mass transfer, we also considered the concentration equation in the flow model.
2 Mathematical modeling
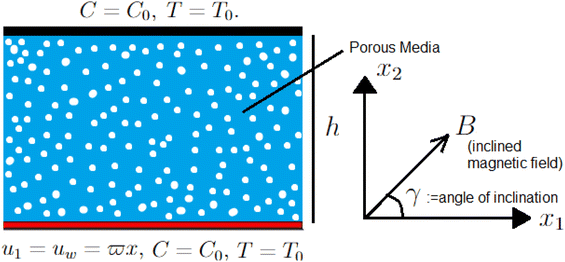
Consider a steady Casson fluid flow squeezed between two plates separated by distance h and adjusted horizontally. The lower plate is fixed at x2 = 0 and the upper plate at x2 = h Cartesian coordinates. The lower plate is stretching with velocity u1 = ϖx1, where ϖ is a positive integer. A magnetic field inclined at an angle γ with the horizontal x1-axis is considered to act uniformly in the flow. The flow is along the horizontal axis between the plates in the Darcy–Forchheimer medium with the additional effects of porosity and viscous dissipation. Moreover, the flow concentration is discussed using a concentration equation during a chemical reaction. The geometrical scenario of the flow problem is represented in Fig. 1.The governing equations for mass, momentum, energy, and concentration conservation in the presence of viscous dissipation, chemical reaction, thermophoretic motion and Brownian motion constitute the following mathematical model governing the flow (see ref. 37):
Equation of continuity:
| ∇·V = 0 | (1) |
Equation of momentum:
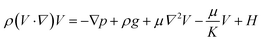 | (2) |
Energy equation:
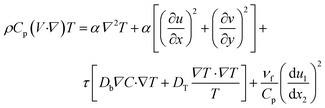 | (3) |
Concentration equation:
| (V·∇)C + Kc(C − Ch) = Db∇2C. | (4) |
The term H in eqn (2) is the current density times the velocity vector. Ohm’s law gives the form of the current density vector J = σ(V × B) = (0, 0, uB0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ − vB0
γ − vB0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ), in which σ is the electrical conductivity, and V = (u1, u2, 0) is the velocity vector. Hence, we obtain the Lorentz force:
γ), in which σ is the electrical conductivity, and V = (u1, u2, 0) is the velocity vector. Hence, we obtain the Lorentz force:
J × B = (σB02u2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ γ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ − σB02u1 γ − σB02u1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin2 sin2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ, σB02u1 γ, σB02u1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ γ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ − σB02u2 γ − σB02u2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ γ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos2 cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ,0). γ,0). |
In the above model description, thermal equilibrium between the fluid and porous media has been assumed in the present study. This is because the concept is applicable to many engineering and scientific applications. For instance, thermal equilibrium between the fluid and porous media is assumed in geothermal reservoirs, underground heat exchangers, and in many studies dealing with heat transfer through porous media in the literature. The component parts of the model (eqn (1)–(4)), now read:
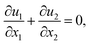 | (5) |
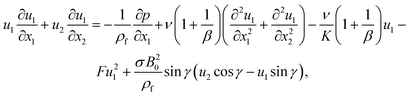 | (6) |
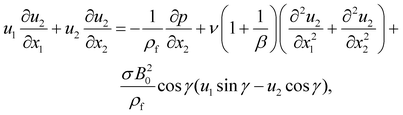 | (7) |
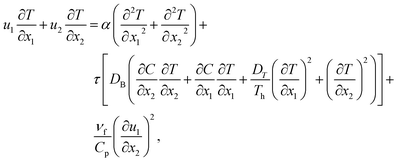 | (8) |
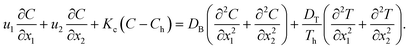 | (9) |
The components of velocity along the x1 and x2 directions are denoted by u1 and u2, respectively. The following conditions are associated with the boundaries:36,38
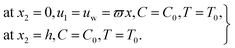 | (10) |
The following similarity transformation is used to convert partial differential equations eqn (5)–(10) into a boundary value problem:
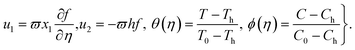 | (11) |
As a consequence of eqn (11), the governing equations acquire the following non-dimensional forms:
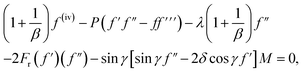 | (12) |
| θ′′ + Nbθ′ϕ′ + Ntθ′2 + Pr(Pfθ′ + Ecf′′2) = 0, | (13) |
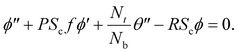 | (14) |
The associated boundary conditions given in eqn (10) have the following dimensionless form:
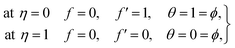 | (15) |
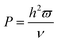 , porosity
, porosity 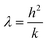 , Forchheimer number
, Forchheimer number 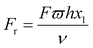 , Drag force coefficient
, Drag force coefficient 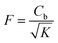 , magnetic parameter
, magnetic parameter 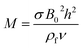 , Prandtl factor
, Prandtl factor 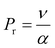 , Brownian coefficient
, Brownian coefficient 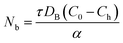 , thermophoresis coefficient
, thermophoresis coefficient 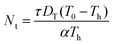 , Schmidt number
, Schmidt number 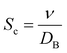 .
.
The skin friction coefficient Cf and the Nusselt number are defined as
3 Solution methodology
This section is dedicated to the implementation of the shooting method to solve the transformed ordinary differential equations eqn (12)–(14) along with the boundary conditions eqn (15). One can easily observe that eqn (12) is independent of θ, so the solution of eqn (12) will be worked out first and then will be used as a known function in eqn (13) and (14). For this purpose, the following notations are used:Denoting f = ζ1, f′ = ζ2, f′′ = ζ3 the resulting first order ODEs are:
The boundary conditions in eqn (15) have the following dimensionless form:
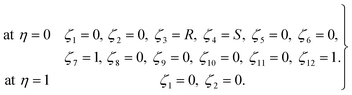 | (16) |
The Runge–Kutta method of order 4 solves the above system of 12 first-order differential equations with R and S missing initial conditions. These initial conditions are calculated by Newton’s method, which is used to solve algebraic equations: ζ1(η, R, S) = 0 and ζ2(η, R, S) = 0. The following iterative formula is used for this purpose:
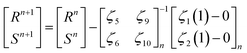 | (17) |
The iterative process is repeated until the criterion listed below is met:
| max[|ζ1(η,R,S)|,|ζ2(η,R,S)|] < ε, |
| F r | M | N b | λ | N t | Present | bvp4c |
|---|---|---|---|---|---|---|
| 0.1 | 1 | 0.1 | 0.2 | 0.1 | 3.5703852 | 3.5703849 |
| 1 | 2.8503317 | 2.8503313 | ||||
| 2 | 2.0831872 | 2.0831865 | ||||
| 1 | 3.5703852 | 3.5703850 | ||||
| 3 | 3.5838796 | 3.5838789 | ||||
| 5 | 3.5907478 | 3.5907468 | ||||
| 0.1 | 3.5703852 | 3.5703842 | ||||
| 0.3 | 2.1543236 | 2.1543236 | ||||
| 0.5 | 2.0533960 | 2.0533954 | ||||
| 0.2 | 4.2755563 | 4.2755556 | ||||
| 0.4 | 4.2205923 | 4.2205911 | ||||
| 0.6 | 4.1918619 | 4.1918610 | ||||
| 0.1 | 3.5703852 | 3.5703844 | ||||
| 0.3 | 4.2635093 | 4.2635089 | ||||
| 0.5 | 4.9829068 | 4.9829059 |
| F r | M | N b | λ | N t | Present | bvp4c |
|---|---|---|---|---|---|---|
| 0.1 | 1 | 0.1 | 0.2 | 0.1 | 1.5510276 | 1.5510262 |
| 1 | 1.5565799 | 1.5565783 | ||||
| 2 | 1.5623997 | 1.5623989 | ||||
| 1 | 1.5510276 | 1.5510271 | ||||
| 3 | 0.7990043 | 0.7990039 | ||||
| 5 | 0.4052419 | 0.4052411 | ||||
| 0.1 | 1.5510276 | 1.5510271 | ||||
| 0.3 | 0.9392732 | 0.9392729 | ||||
| 0.5 | 0.8955695 | 0.8955689 | ||||
| 0.2 | 1.5416834 | 1.5416831 | ||||
| 0.4 | 1.5419289 | 1.5419278 | ||||
| 0.6 | 1.5420601 | 1.5420599 | ||||
| 0.1 | 1.5510276 | 1.5510267 | ||||
| 0.3 | 1.8665458 | 1.8665445 | ||||
| 0.5 | 2.1915619 | 2.1915618 |
4 Representation of graphs
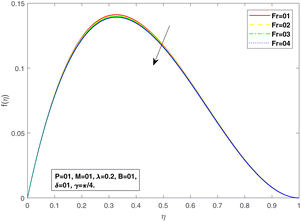
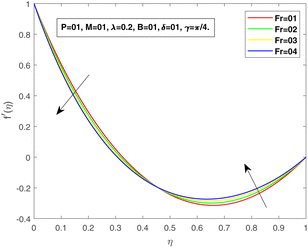
This section is dedicated to providing the physical reasoning for the three essential profiles – speed, temperature, and nanoparticle concentration – through graphs. Fig. 2–20 are sketched to expose the consequences of several fluid parameters disconcerted in the flow model.Fig. 2 and 3 are pictorial descriptions of f and f′ with changing Forchheimer number, respectively. A closer view highlights that the velocity region decreases with an increase in the Forchheimer number. The relation of the Forchheimer number with the skin friction coefficient is accountable for this trend in the velocity parameter. An exhaustive range is available for increasing Forchheimer number; hence, the drag stress constant produces more friction supplied to the fluid flow, which leads to a decline in the velocity profile.
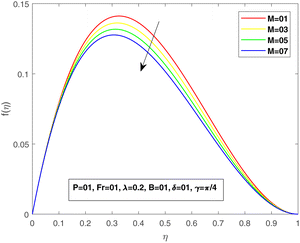
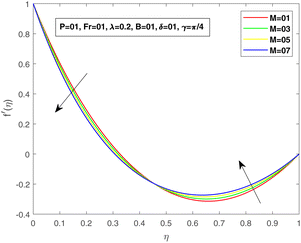
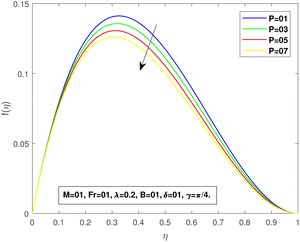
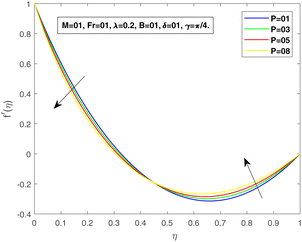
Fig. 4 and 5 indicate the influence of the magnetic parameter on fluid flow within a Darcy medium. An inverse relationship between the fluid flow and the magnetic number can be seen. A magnetic region acting at an angle γ to the surface produces certain collisions towards the fluid flow; therefore, a decrease is evidenced in each f and f′. The viscosity parameter P, impact on f and f′ is shown in Fig. 6 and 7. Physically, for bigger values of P, a decrease in the kinematic viscosity assures an increase in the dynamic viscosity, and consequently, a reduction in the velocity profile is observed.
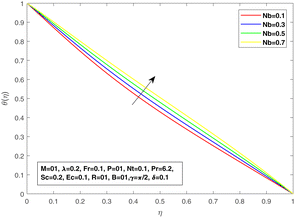
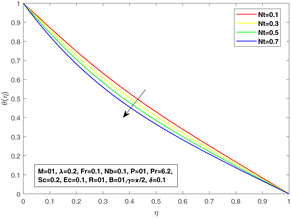
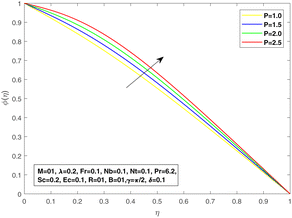
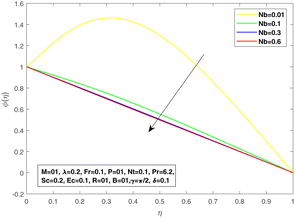
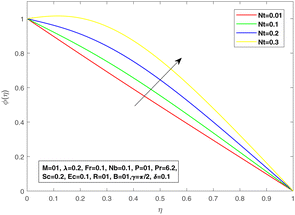
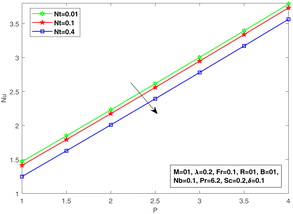
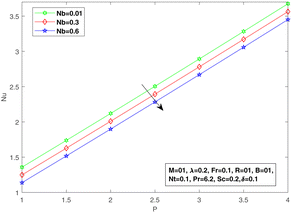
Fig. 8 suggests the impact of the viscosity constant on the temperature profile. The thermal boundary layer is reduced for increasing values of the viscosity constant. The effect of diffusive Brownian motion on the temperature distribution is shown in Fig. 9, while Fig. 10 is presented to reflect the impact of thermophoresis on the temperature distribution. The rapid and random movement of nanoparticles due to the Brownian motion raises the thermophoretic pressure, resulting in speedy fluid motion from the warm region to a lower temperature region. Therefore, an upward thrust in temperature distribution is discovered for each parameter. For multiplied values of the viscosity coefficient, we may see an augmentation in the concentration profile as proven in Fig. 11, which authorizes the mathematical formulation and physical significance of the viscosity parameter in the fluid flow. The concentration profile is reduced with increasing values of the Brownian diffusive movement parameter. The random movement reduces with enhanced Brownian motion, but the case is contrary to that of thermophoresis. At Nb = 0.01, an obvious effect of Brownian diffusion can be seen, but the impact is minimal with further increments in Nb. In addition, a linear increase is visible in the concentration profile with an improvement in Nt. Fig. 12 and 13 are plotted by taking Nu as a function of the viscosity parameter P for different values of Brownian diffusion parameter Nb and thermophoresis Nt, respectively. It can be seen in Fig. 14 that with an increase in P, Nu increases; and for a fixed value of P with increasing Nt, a decline in Nu can be seen. The same behavior can be seen in Fig. 15 for values of Nb.
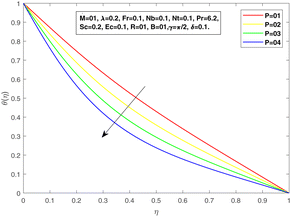
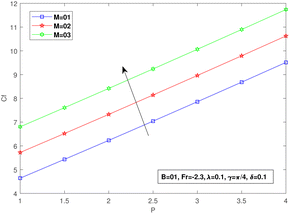
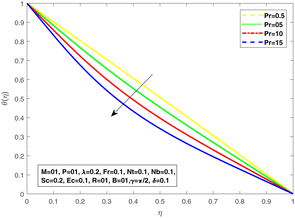
Fig. 16 and 17 are sketched to estimate the variation in skin friction as a function of the viscosity parameter by changing the values of λ and M, respectively. The larger friction is produced with the useful resource of Forchheimer medium and retardation provided through magnetic effect results in skin-friction enhancement. The effect of the Prandtl constant on the thermal boundary layer is demonstrated in Fig. 18 shows a decline in temperature profile for large values of Pr.
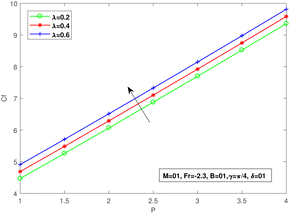
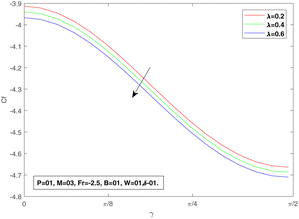
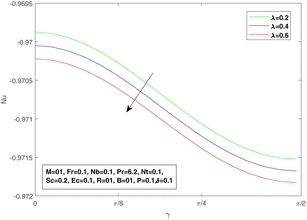
Fig. 19 is a plot of the skin friction as a function of inclination angle γ with changing porosity factor λ. We can see a decrease in Cf by increasing the value of λ. Fig. 20 is delineated to demonstrate the Nusselt number as a function of the angle of inclination γ by changing porosity factor λ values. We can see a decrease in the Nusselt number with increasing the value of λ.
5 Concluding remarks
In this article, the work of Rasool et al.36 is extended to the effect of the inclined magnetic field, Casson fluid, viscous dissipation, Brownian motion, thermophoresis diffusion, and chemical reaction. First, governing equations of the physical problem are transformed into ODEs via similarity transformations. Numerical solutions have been determined for the converted boundary value problem by incorporating the shooting technique. The numerical consequences are provided as graphs for temperature, momentum, and concentration profiles using various values of the governing physical parameters. The achievements of contemporary studies can be summarized below:• Velocity decreases for a large Forchheimer constant. The skin friction coefficient is responsible for such behavior.
• The effect of a magnetic parameter is reversely associated with the flow velocity. The depth of the momentum boundary layer is reduced.
• For increasing values of the viscosity parameter, a reduction in the velocity field is observed due to the inverse relation of kinematic viscosity with dynamic viscosity.
• The random motion of nanoparticles increases due to Brownian diffusion. This is because a stronger thermophoretic force ensures speedy transport from the warm region to the cold region.
• Augmentation in the concentration profile is observed for larger values of the viscosity parameter.
• The heat flux rate diminishes for diffusive Brownian motion and thermophoresis.
• The surface drag force is increased for accelerated porosity and magnetic parameters.
• For increasing porosity factor (λ) and the angle of magnetic inclination (γ), the skin friction (Cf) decreases and the Nusselt number (Nu) decreases. Moreover, skin friction and Nusselt number are decreasing functions with angle of inclination.
As an overall outlook, future studies can address the aforementioned problem by taking ion slip and Hall effects into consideration, see for instance ref. 39.
Nomenclature
| B 0 | Magnetic number [—] |
| C | Concentration of nanoparticles [mol m−3] |
| (cp)f | Specific heat of fluid [M L2 T−2 K−1] |
| D B | BDC [—] |
| D T | TDC [—] |
| E c | Eckert number [—] |
| f, h | Dimensionless velocity components [—] |
| K c | Constant rate of chemical reaction [—] |
| M | Dimensionless magnetic parameter [—] |
| ρ | Density [ML−3] |
| N b | Dimensionless BDC [—] |
| N t | Dimensionless TDC [—] |
| N u | Nusselt number [—] |
| P | Viscosity constant [—] |
| R | Thermal radiation parameter [—] |
| P r | Prandtl number [—] |
| S c | Schmidt number [—] |
| u 1, u2 | Velocity components [ms−1] |
| C f | Skin friction [—] |
| T | Temperature [K] |
| α | Thermal diffusivity of nanofluid [m2 s−1] |
| β | Casson fluid parameter [—] |
| γ | Chemical reaction parameter [—] |
| k | Thermal conductivity [W m−1 K−1] |
| δ | Heat generation/absorption [—] |
| ν | Kinematic viscosity [M L2 T−1] |
| μ | Dynamic viscosity [M L2 T−1] |
| ϕ | Nanoparticle volume fraction [—] |
| η | Similarity variable [—] |
| θ | Dimensionless temperature [—] |
| τ | Ratio of heat capacity [—] |
| x 1, x2 | Cartesian coordinates [—] |
Conflicts of interest
There are no conflicts to declare.References
- A. J. Chamkha, MHD-free convection from a vertical plate embedded in a thermally stratified porous medium with Hall effects, Appl. Math. Modell., 1997, 21(10), 603–609 CrossRef.
- A. J. Chamkha, Non-Darcy hydromagnetic free convection from a cone and a wedge in porous media, Int. Commun. Heat Mass Transfer, 1996, 23(6), 875–887 CrossRef CAS.
- M. V. Krishna, N. A. Ahammad and A. J. Chamkha, Radiative MHD flow of Casson hybrid nanofluid over an infinite exponentially accelerated vertical porous surface, Case Stud. Therm. Eng., 2021, 27, 101229 CrossRef.
- M. Keimanesh, M. M. Rashidi, A. J. Chamkha and R. Jafari, Study of a third grade non-Newtonian fluid flow between two parallel plates using the multi-step differential transform method, Comput. Math. Appl., 2011, 62(8), 2871–2891 CrossRef.
- A. J. Chamkha, T. Groşan and I. Pop, Fully developed free convection of a micropolar fluid in a vertical channel, Int. Commun. Heat Mass Transfer, 2002, 29(8), 1119–1127 CrossRef.
- M. Stefan, Versuchuber die scheinbare adhäsion, sitzungsber, Abt. II, Österr. Akad. Wiss. Math.-Naturwiss. Kl, 1874, vol. 69, pp. 713–721 Search PubMed.
- M. M. Rashidi, H. Shahmohamadi and S. Dinarvand, Analytic approximate solutions for unsteady two-dimensional and axisymmetric squeezing flows between parallel plates, Math. Probl. Eng., 2008, 2008, 935095 Search PubMed.
- T. Hayat, A. Qayyum and A. Alsaedi, Three-dimensional mixed convection squeezing flow, Appl. Math. Mech., 2015, 36(1), 47–60 CrossRef.
- T. Hayat, T. Muhammad, A. Qayyum, A. Alsaedi and M. Mustafa, On squeezing flow of nanofluid in the presence of magnetic field effects, J. Mol. Liq., 2016, 213, 179–185 CrossRef CAS.
- H. Shahmohamadi and M. M. Rashidi, Vim solution of squeezing MHD nanofluid flow in a rotating channel with lower stretching porous surface, Adv. Powder Technol., 2016, 27(1), 171–178 CrossRef CAS.
- S. Murtaza, P. Kumam, Z. Ahmad, M. Ramzan, I. Ali and A. Saeed, Computational Simulation of Unsteady Squeezing Hybrid Nanofluid Flow Through a Horizontal Channel Comprised of Metallic Nanoparticles, J. Nanofluids, 2023, 12(5), 1327–1334 CrossRef.
- A. Rostami, K. Hosseinzadeh, and D. Ganji, Hydrothermal analysis of ethylene glycol nanofluid in a porous enclosure with complex snowflake shaped inner wall, Waves in Random and Complex Media, 2022, vol. 32, issue 1, pp. 1–18 Search PubMed.
- Z. Shah, M. Sheikholeslami and P. Kumam, et al. , Influence of nanoparticles inclusion into water on convective magneto hydrodynamic flow with heat transfer and entropy generation through permeable domain, Case Stud. Therm. Eng., 2020, 21, 100732 CrossRef.
- S. Murtaza, P. Kumam, Z. Ahmad, K. Sitthithakerngkiet, and T. Sutthibutpong, Fractional Model of Brinkman-Type Nanofluid Flow with Fractional Order Fourier’s and Fick’s Laws, Fractals, 2023.
- S. Murtaza, P. Kumam, M. Bilal, T. Sutthibutpong, N. Rujisamphan and Z. Ahmad, Parametric simulation of hybrid nanofluid flow consisting of cobalt ferrite nanoparticles with second-order slip and variable viscosity over an extending surface, Nanotechnol. Rev., 2023, 12(1), 20220533 CrossRef CAS.
- S. Murtaza, P. Kumam, Z. Ahmad, T. Seangwattana and I. E. Ali, Numerical analysis of newly developed fractal-fractional model of Casson fluid with exponential memory, Fractals, 2022, 30(05), 2240151 CrossRef.
- M. S. Khan and T. Dil, Heat transfer enhancement of automobile radiator using h2o–cuo nanofluid, AIP Adv., 2017, 7(4), 045018 CrossRef.
- S. U. Choi and J. A. Eastman, Enhancing thermal conductivity of fluids with nanoparticles, Tech. Rep., Argonne National Lab.(ANL), Argonne, IL (United States), 1995 Search PubMed.
- S. Parvin and A. Chamkha, An analysis on free convection flow, heat transfer and entropy generation in an odd-shaped cavity filled with nanofluid, Int. Commun. Heat Mass Transfer, 2014, 54, 8–17 CrossRef CAS.
- A. Zaraki, M. Ghalambaz, A. J. Chamkha, M. Ghalambaz and D. De Rossi, Theoretical analysis of natural convection boundary layer heat and mass transfer of nanofluids: effects of size, shape and type of nanoparticles, type of base fluid and working temperature, Adv. Powder Technol., 2015, 26(3), 935–946 CrossRef CAS.
- P. S. Reddy and A. J. Chamkha, Soret and dufour effects on MHD convective flow of Al2O3–water and TiO2–water nanofluids past a stretching sheet in porous media with heat generation/absorption, Adv. Powder Technol., 2016, 27(4), 1207–1218 CrossRef CAS.
- A. Chamkha, M. Ismael, A. Kasaeipoor and T. Armaghani, Entropy generation and natural convection of CuO-water nanofluid in C-shaped cavity under magnetic field, Entropy, 2016, 18(2), 50 CrossRef.
- G. Rasool, A. Shafiq, C. M. Khalique and T. Zhang, Magnetohydrodynamic Darcy–Forchheimer nanofluid flow over a nonlinear stretching sheet, Phys. Scr., 2019, 94(10), 105221 CrossRef CAS.
- M. A. Ismael, T. Armaghani and A. J. Chamkha, Conjugate heat transfer and entropy generation in a cavity filled with a nanofluid-saturated porous media and heated by a triangular solid, J. Taiwan Inst. Chem. Eng., 2016, 59, 138–151 CrossRef CAS.
- M. Sohail and R. Naz, Modified heat and mass transmission models in the magnetohydrodynamic flow of sutterby nanofluid in stretching cylinder, Phys. A, 2020, 549, 124088 CrossRef CAS.
- I. Tlili, W. Khan and K. Ramadan, MHD flow of nanofluid flow across horizontal circular cylinder: steady forced convection, J. Nanofluids, 2019, 8(1), 179–186 CrossRef.
- A. Wakif, Z. Boulahia, A. Amine, I. Animasaun, M. Afridi, M. Qasimd and R. Sehaqui, Magneto-convection of alumina-water nanofluid within thin horizontal layers using the revised generalized buongiorno’s model, Front. Heat Mass Transfer, 2019, 12, 1–15 Search PubMed.
- K. Hosseinzadeh, A. Mogharrebi, A. Asadi, M. Sheikhshahrokhdehkordi, S. Mousavisani and D. Ganji, Entropy generation analysis of mixture nanofluid (H2O/c2H6O2)–Fe3O4 flow between two stretching rotating disks under the effect of MHD and nonlinear thermal radiation, Int. J. Ambient Energy, 2022, 43(1), 1045–1057 CrossRef CAS.
- Z. Shah, M. R. Hajizadeh, N. A. Alreshidi, W. Deebani and M. Shutaywi, et al. , Entropy optimization and heat transfer modeling for lorentz forces effect on solidification of NEPCM, Int. Commun. Heat Mass Transfer, 2020, 117, 104715 CrossRef.
- M. S. Khan and T. Dil, Numerical computation of heat transfer enhancement through cosserat hybrid nanofluids using continuous galerkin–petrov method, Eur. Phys. J. Plus, 2020, 135(2), 1–19 Search PubMed.
- P. Forchheimer, Wasserbewegung durch boden, Z. Ver. Deutsch Ing., 1901, 45, 1782–1788 Search PubMed.
- M. Muskat and R. Wyckoff, The Flow of Homogeneous Fluids through Porous Media, JW Edwards, Ann Arbor, Michigan, 1937 Search PubMed.
- M. Seddeek, Influence of viscous dissipation and thermophoresis on darcy–forchheimer mixed convection in a fluid saturated porous media, J. Colloid Interface Sci., 2006, 293(1), 137–142 CrossRef CAS PubMed.
- M. A. Sadiq and T. Hayat, Darcy–forchheimer flow of magneto maxwell liquid bounded by convectively heated sheet, Results Phys., 2016, 6, 884–890 CrossRef.
- T. Hayat, F. Shah, M. I. Khan and A. Alsaedi, Framing the performance of heat absorption/generation and thermal radiation in chemically reactive darcy-forchheimer flow, Results Phys., 2017, 7, 3390–3395 CrossRef.
- G. Rasool, W. A. Khan, S. M. Bilal and I. Khan, MHD squeezed Darcy–Forchheimer nanofluid flow between two h–distance apart horizontal plates, Open Phys., 2020, 18(1), 1100–1107 CAS.
- J. Buongiorno, Convective Transport in Nanofluids, 2006 Search PubMed.
- M. Sheikholeslami, M. Rashidi, D. M. Al Saad, F. Firouzi, H. B. Rokni and G. Domairry, Steady nanofluid flow between parallel plates considering thermophoresis and brownian effects, J. King Saud Univ., Sci., 2016, 28(4), 380–389 CrossRef.
- M. V. Krishna, B. Swarnalathamma and A. J. Chamkha, Investigations of Soret, Joule and Hall effects on MHD rotating mixed convective flow past an infinite vertical porous plate, J. Ocean Eng. Sci., 2019, 4(3), 263–275 CrossRef.
| This journal is © The Royal Society of Chemistry 2023 |