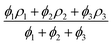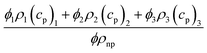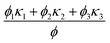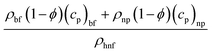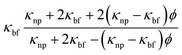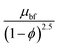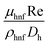Open Access Article
Open Access ArticleNumerical investigation of heat transfer and fluid flow characteristics of ternary nanofluids through convergent and divergent channels
M. M.
Alqarni
a,
Abid A.
Memon
b,
M. Asif
Memon
 bc,
Emad E.
Mahmoud
d and
Amsalu
Fenta
bc,
Emad E.
Mahmoud
d and
Amsalu
Fenta
 *e
*e
aDepartment of Mathematics, College of Sciences, King Khalid University, Abha 61413, Saudi Arabia. E-mail: Sair4466@gmail.com; malqrni@kku.edu.sa
bDepartment of Mathematics and Social Sciences, Sukkur IBA University, Sukkur 65200, Sindh, Pakistan. E-mail: abid.ali@iba-suk.edu.pk; asif-memon@iba-suk.edu.pk
cDepartment of Mathematics, Universiti Tun Hussein Onn Malaysia (UTHM), Parit Raja, Batu Pahat 86400, Johor, Malaysia
dDepartment of Mathematics and Statistics, College of Science, Taif University, PO Box 11099, Taif 21944, Saudi Arabia. E-mail: emad_eluan@yahoo.com
eDepartment of Physics, Mizan Tepi University, PO Box 121, Tepi, Ethiopia. E-mail: amsalu.fenta09@gmail.com
First published on 2nd November 2023
Abstract
The characteristics of nanomaterials have garnered significant attention in recent research on natural and forced convection. This study focuses on the forced convection characteristics of ternary nanofluids within convergent and divergent channels. The ternary nanofluid comprises titanium oxide (TiO2), zinc oxide (ZnO), and silver suspended in water, which serves as the base fluid. Using COMSOL Multiphysics 6.0, a reliable software for finite element analysis, numerical simulations were conducted for steady and incompressible two-dimensional flow. Reynolds numbers varying from 100 to 800 were employed to investigate forced convection. Additionally, we explored aspect ratios (channel height divided by the height of the convergent or divergent section) of −0.4, −0.2, 0, 0.2, and 0.4. Our findings revealed that only at aspect ratio a = 0.4 did the average outlet temperature increase as the Reynolds number rose, while other aspect ratios exhibited decreasing average temperatures with declining Reynolds numbers. Moreover, as the Reynolds number increased from 100 to 800 and the total volume fraction of the ternary nanofluids ranged from 0.003 to 0.15, there was a significant 100% enhancement in the average Nusselt number. For clarity, this article briefly presents essential information, such as the study's numerical nature, fluid properties (constant-property fluid), and the methodology (COMSOL Multiphysics 6.0, finite element analysis). Key conclusions are highlighted to enable readers to grasp the main outcomes at a glance. These details are also adequately covered in the manuscript to facilitate a comprehensive understanding of the research. The utilization of this emerging phenomenon holds immense potential in various applications, ranging from the development of highly efficient heat exchangers to the optimization of thermal energy systems. This phenomenon can be harnessed in scenarios in which effective cost management in thermal production is a critical consideration.
1. Introduction
The properties of thermal enhancement in mono-nanofluids are well understood by researchers and scientists, and numerous numerical and experimental observations have been made. Several research articles have also been written on this topic. Recently, it has been discovered through many experiments that when two different kinds of nanoparticles are added to a base fluid (such as water, oil, or glycols), a hybrid mixture is formed that is more powerful than mono-nanofluids. Both mono-nanofluids and hybrid mixtures have been extensively tested, and many research articles have stated that they are an excellent solution for improving thermal enhancement. Ternary nanofluids, which are mixtures of three different kinds of nanoparticles in base fluids or glycols, have just begun to be studied.1 Research has shown that the composition of ternary nanofluids is more powerful than that of mono-nanofluids and hybrid mixtures in terms of thermal enhancement.2,3 Natural metals whose nano-sized particles remain suspended in the base fluid and do not dissolve can be combined with the base fluid to create a powerful solution with high thermal conductivity. These mixtures are useful in enhancing heat transfer rates in thermochemical and automobile industries.4,5 They have many applications in efficient engine production, heat exchangers, and efficient solar collectors.The motivation behind this work is to understand the forced convection characteristics of ternary nanofluids through a convergent and divergent channel. Nanomaterials have unique properties, and they have been extensively studied in the past for their potential applications in various fields. In this study, the authors use titanium oxide, zinc oxide, and silver as nanomaterials in a ternary nanofluid and observe their behavior in a convergent and divergent channel. The application of this work lies in understanding the heat transfer and fluid flow characteristics of ternary nanofluids through a convergent and divergent channel. This understanding can help in the design of more efficient heat exchangers, which are widely used in various industries such as power generation, chemical processing, and electronics cooling. The findings of this study can also be used to optimize the use of nanofluids in other applications, such as lubrication and heat transfer fluids.
While keeping the usage and applications of nanofluids in mind, we here present a literature review of some articles that include numerical or experimental observations and suggestions based on them. A water and alumina mixing application was used in ref. 6 to identify a square hollow with a moving cylinder at its center. The researcher utilized an unusually thick meshing procedure to ensure accuracy because the challenge entailed forced convection. The research demonstrated that while the Nusselt number falls as the radius of the cylinder grows, the skin coefficient improves as the volume percent of nanoparticles grows. Further research revealed that the surface temperature and mass flow rate had opposing impacts on one another. Ref. 7 examines the application of water–alumina-based nanofluids in enhancing heat transfer in a three-dimensional annular geometry with the usage of κ − ε turbulence model. A heat source was positioned on the inner cylinder in this annular configuration. According to the study, while raising the Reynolds number and volume fraction enhances the rate of heat transfer at the channel outlet, increasing the particle concentration causes a drop in the average Nusselt number. Likewise, it was believed that a decrease in the temperature gradient at the exit of the annular geometry is caused by an increase in the volume fraction of nanofluids.
In another numerical investigation,8 the application of nanofluids was studied to note the heat transfer characteristics and their improvement in a three-dimensional annular geometry. The second time, the inner cylinder of the annulus was made moveable, and Comsol Multiphysics 5.6 was used throughout the simulation to construct it. The aspect ratio, volume percentage, and rotation speed of the inner cylinder were changed in this study to examine the heat transmission behavior. In addition, it was shown that skin friction has a favorable correlation with the rotation speed of the inner cylinder. Skin friction was discovered to be improved by increasing the volume percentage of nanoparticles. It was demonstrated in ref. 9 that using nanofluids to examine alternative plate heat exchanger (PHE) designs improved heat transmission more effectively than using traditional fluids. The article provides critical suggestions regarding nanoparticle size, base fluids, analytical approaches, pressure distribution, and flow regime to improve heat transfer. The statistical analysis in the article shows that nanofluids are significantly effective in PHE applications. Finally, it is stated that chevron and corrugated geometries are important for enhancing the heat transfer rate, and particularly for improving the Nusselt number.
The application of forced convection of hybrid nanofluids was shown to improve heat transmission in a three-dimensional rectangular channel with two moving perpendicular blocks positioned at its center.10 These nanofluids consisted of a mixture of Cu, alumina, and water, and the entire programming was done using computer code in COMSOL Multiphysics. The study concluded that the anticlockwise rotation of the perpendicular blocks is crucial for thermal enhancement, and the maximum average temperature can only be achieved when the temperature of copper and alumina is reduced to 0.001. Additionally, the study also concluded that an increase in the viscosity of the hybrid mixture initiates the cooling process inside the blocks. An analysis11 was conducted on the performance of a solar collector using hybrid nanofluids. These hybrid nanofluids consisted of combinations of water, copper, and alumina, and the entire simulation was developed using computer software. With more copper nanoparticles in the base fluid, the heat energy of the solar collector rises while receiving less direct sunlight, according to the simulation. Additionally, according to the article, the effectiveness of the solar collector is enhanced by boosting the copper and alumina content in the base fluid. Additionally, it was claimed that high permeability plays a crucial function in lowering friction, even if it has a negligible effect on the ability of the solar collector to generate heat.
To determine the convection properties of hybrid nanofluids in heated deep and shallow cavities, numerical research was carried out in ref. 12. This study employed the Corcione nanofluid model, which was developed using Comsol 5.6, a program that is based on the finite element method. Water, alumina, and copper were present in the nanofluids employed in the study. For the implementation of the program, the authors found numerical answers to the incompressible Navier–Stokes equations and the two-dimensional heat equation. According to the study, raising the copper volume percentage in the nanofluids causes the average temperature to rise. In addition, the Reynolds number and copper volume percentage are positively correlated with the average Nusselt number. However, when the cavity height is increased, the average Nusselt number declines, indicating improved conduction. An article13 discussed the use of nanofluids to observe the increase in heat transmission in a three-dimensional L-shaped conduit. The nanofluids used in this study were a mixture of aluminum oxide and copper, and a turbulent κ − ε model was used. The study showed that increasing the concentration of both nanomaterials in water is essential to increase heat transfer. Copper nanomaterials are more effective in increasing heat transfer rates compared to aluminum. It was also demonstrated that the temperature increment depends on the increase in thermal diffusivity, which is directly related to the volume fractions. Finally, the study emphasized the importance of the Reynolds number in increasing heat transfer rates.
An article14 was written in which the observation of convergent and divergent channel ternary nanofluids was carried out with the assumption that the flow is laminar. A wide range of parameters was used, and a finite element scheme was used to obtain numerical results. Cobalt, zinc, and silver nanoparticles were included in the ternary nanofluids, while the base fluid used was ethyl glycol. The article mentioned that the rate of heat transfer only increases significantly when cobalt, silver, and zinc are included in the base fluid in a 1/6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2/3
2/3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1/6 ratio. The article also mentioned that the enhancement of heat transport occurs only when the flow of particles is in the laminar direction. Furthermore, the article mentioned that ternary nanofluids are extremely useful for increasing the rate of heat transfer in convergent and divergent channels. A numerical investigation15 was conducted in which ternary nanofluids were used along with the effects of a magnetic field and thermal radiation. The channel used in this study was a stretching convergent and divergent channel, and Galerkin's finite element method was used to implement the program. The study revealed that heat generation, stronger dissipation, and thermal radiation play important roles in enhancing the heat transfer of ternary nanofluids. Furthermore, the study also indicated that having nanoparticle blades is crucial for increasing the Nusselt number.
1/6 ratio. The article also mentioned that the enhancement of heat transport occurs only when the flow of particles is in the laminar direction. Furthermore, the article mentioned that ternary nanofluids are extremely useful for increasing the rate of heat transfer in convergent and divergent channels. A numerical investigation15 was conducted in which ternary nanofluids were used along with the effects of a magnetic field and thermal radiation. The channel used in this study was a stretching convergent and divergent channel, and Galerkin's finite element method was used to implement the program. The study revealed that heat generation, stronger dissipation, and thermal radiation play important roles in enhancing the heat transfer of ternary nanofluids. Furthermore, the study also indicated that having nanoparticle blades is crucial for increasing the Nusselt number.
In study,16 the impact of aspect ratio was investigated using a numerical scheme by simulating 3D mixed convection around a cylinder. For this purpose, three Reynolds numbers (100, 500, and 1000) were utilized while maintaining fixed values of the Prandtl number (0.7) and the Grashof number (105). The study demonstrated that increasing the aspect ratio enhances the heat transfer rate, but only for a specific Reynolds number. The study also suggested that an artificial neural network can predict heat transfer rates for mixed convection using a limited dataset, providing a faster alternative to direct numerical simulation. A numerical approach,17 the incompressible smoothed particle hydrodynamics (ISPH) method, was utilized to investigate natural convection in the presence of a magnetic field through a porous annulus suspended in a wavy enclosure with non-equilibrium phase change material. The study examined nanoparticle concentration, fractional time derivative, Darcy parameter, thermal radiation, and Rayleigh number. The findings reveal that the initial influence is governed by the fractional time derivative, while the nanoparticle concentration impacts flow, thermal radiation affects heat capacity, and the Rayleigh number influences both flow strength in the annulus and temperature distribution in the domain. In another numerical study,18 a Carreau–Yasuda model of non-Newtonian fluid was utilized to investigate shear thinning behavior, in contrast to a shear-rate-dependent viscosity approach. In order to compare the findings to the Carreau–Yasuda model, the study examined both fluid flow and temperature behavior. As a result of ohmic dissipation, the results showed that wall shear stress in combination with the impact of a magnetic field increased heat transfer rates. Additionally, as compared to mono-nanofluids, hybrid nanofluids enabled faster heat transfer rates.
In one study,19 the flow of a hybrid nanofluid including copper and cobalt ferrite nanoparticles through a squeezing plate is investigated. Mathematical models take into consideration a number of variables, such as magnetic fields, chemical processes, heat sources, and suction. The results show that the hybrid nanoliquid outperforms conventional nanofluids in terms of velocity and energy transfer when compared to earlier investigations. Factors including squeezing, suction, heat absorption, heat creation, and plate stretching affect how well this transfer occurs. In order to find workable solutions, ref. 20 investigates fractal-fractional derivative operators, which are sophisticated mathematical techniques useful in physics and engineering. They make it possible to examine fractal dimension and fractional order at the same time. Graphs showing how physical factors influence nanofluid rheology can be seen in numerical solutions. Notably, adding cadmium telluride nanoparticles boosts transformer oil effectiveness by around 15.27%, while lowering fluid velocity and couple stress.
In ref. 21, the authors examine the interaction between natural convection on an expanding surface inside a porous medium and the dynamic flow of a novel hybrid nanofluid made up of cobalt ferrite (CoFe2O4) and copper (Cu) nanoparticles. The analysis takes into account a number of variables, including temperature-dependent viscosity, chemical processes, heat generation, second-order velocity slip conditions, and the Darcy–Forchheimer effect. According to the results, operations like aerodynamic plastic sheet extrusion and polymer sheet dye extrusion may be able to benefit from the use of Cu and Fe2O4 nanoparticles in conventional fluids. The analysis of the free convection Couette flow of Casson fluid between parallel plates in ref. 22 takes into account heat production and uses fractal-fractional derivatives. Using fractal-fractional derivatives with an exponential kernel, the research presents a novel methodology. The findings, which are displayed through velocity and temperature field profiles, emphasize the sizeable memory effect associated with the fractal-fractional order model, which is impacted by the fractal order parameter.
In a numerical study,23 a sinusoidal wavy channel was investigated for forced convection using alumina–water nanofluids with varying phase shifts. The flow was assumed to be laminar, and different parameters such as phase shift, nanoparticle concentration, Nusselt number, skin friction, and Reynolds number were analyzed through various parametric studies. The study revealed that optimal performance was achieved using a phase shift of 0°, while adjusting the Reynolds number and varying the nanoparticle concentration in the base fluid (ranging from 0% to 5%). In ref. 24, a square duct was tested to enhance the heat transfer rate by introducing surface roughness, and a mixture of ethylene glycol, zinc oxide, and water was used as the nanofluid. The objective of this study was to increase the heat transfer and friction factor by manipulating variables such as the volume fraction of nanoparticles in base fluids, flow attack angle, and Reynolds number. In this article, relationships for Nusselt number correlation and friction factor correlation were developed, showing deviations of 12.4% and 9.3%, respectively, when compared to results available in the literature.
The thermal performance of a parabolic solar collector was studied25 with the incorporation of mono- and hybrid nanofluids alongside various turbulence-promoting elements and setups. The investigation resulted in thermal performance enhancements of 69% and 79% using nanofluids and a converging–diverging receiver configuration, respectively. An experimental study26 was conducted to analyze thermal and hydraulic performance, considering a rectangular duct. In addition to using dimpled ribs in an arc pattern inside the duct, the research was conducted using nanofluids as the transport medium. The dimpled ribs of the arc pattern have been shown to improve both thermal and hydraulic performance. It was discovered that a 4.5% nanoparticle concentration, a 0.933 ratio of dimpled arc rib height to print diameter, a 4.64 relative dimpled arc rib height, and a 55° dimpled arc angle were the ideal conditions for achieving the greatest heat transfer rate. Ref. 27 investigates substituting nanofluids for water in an angled slot and ribbed square duct. With angled slot ribs and a constant temperature, the heated square conduit is square. 35 nm diameter silica nanoparticles were introduced at 3.5% of the total volume of water. After experimenting with various settings, it was found that an angled slot rib height of 0.08 doubled performance compared to a plain wall and provided the optimum heat transfer increase.
One investigation28 focused on the heating and cooling capabilities of annular fins in nucleate boiling, which has real-world implications in heat exchangers, vehicle radiators, and electronics cooling. The study examines the effects of a number of variables, such as magnetic fields, thermal radiation, nanomaterials, and heating species. According to the results, increasing the thermal conductivity coefficient in case 2 and the concentration in case 3 increase heat transmission. Furthermore, the inserted heating source (Q1) and directed radiation efficiently increase heat transfer to the environment. The study in ref. 29 highlights the crucial function of heat transmission in nanoliquids, especially in practical areas such as thermal, biological, mechanical, and chemical engineering. It offers a unique biohybrid nanofluid model (BHNF) created for a channel with expanding/constricting walls imitating blood flow. The model investigates the effect of several physical factors using the variational iteration method (VIM), combining graphene and CuO nanoparticles in a blood-based fluid. The results show that by modifying the wall permeation, thermal radiation, and temperature coefficients, the flow rate towards the channel ends is enhanced and the thermal performance is optimized.
In ref. 30, the investigation of heat transfer in convergent/divergent channels in a ternary nanofluid is the focus of the work. The effects of a magnetic field (Ha), thermal radiation (Rd), heat production (Q1), and stretching (S1) are taken into account. It produces results for heat transport using the Galerkin Finite Element Method. According to the results, the Nusselt number in the ternary nanofluid including blade-shaped nanoparticles noticeably increases as a result of efficient heat management provided by absorption and Joule heating. Another investigation reported in ref. 31 examines how hybrid nanoparticles may be used in a base fluid to improve the ability of conventional fluids to transport heat and address modern thermal issues. In particular, it evaluates hybrid nanofluids made of [(ZnO-MWCNTs)/water-EG (50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50)] and [(ZnO)/water-EG (50
50)] and [(ZnO)/water-EG (50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50)] on a Riga surface. Innovative thermal radiation effects and convective heat conditions are included in the model in the investigation. The heat capacity of the [(ZnO-MWCNTs)/water-EG(50
50)] on a Riga surface. Innovative thermal radiation effects and convective heat conditions are included in the model in the investigation. The heat capacity of the [(ZnO-MWCNTs)/water-EG(50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50)] hybrid nanofluid and the large temperature increase caused by convective heat situations are both clearly demonstrated by computational methods.
50)] hybrid nanofluid and the large temperature increase caused by convective heat situations are both clearly demonstrated by computational methods.
A tetra-nanofluid is used in the study in ref. 32 to examine heat transfer in converging/diverging channels. A depreciation function and other novel features are introduced in the study, which uses the Galerkin finite element method (GFEM) to evaluate the data. The results highlight the advantages of tetra-nanofluids over more traditional approaches and support the models that have been suggested for analyzing heat transfer dynamics in nanofluids comprising tetra-nanomaterials. In ref. 33, the Corcione concept is used to examine the effects of heating an Al2O3/H2O nanofluid. The impact of thermal radiation, internal heating, and important factors in case 1, case 2, and the modified Hartmann number are all given special consideration. According to the study, greater values of 1 and 2 result in less fluid motion, which might be useful in engineering settings. In high-viscosity nanofluids in particular, the modified Hartmann number has a significant effect on particle motion. For effective temperature management and efficient heat generation, heating sources and thermal radiation are included.
After an in-depth analysis of the reviewed literature, we reached the conclusion that nanomaterials prove to be highly effective for studying forced convection. It has also been substantiated that a combination of nanomaterials (hybrid nanofluids) is essential for augmenting the heat transfer rate. Moreover, the geometry under investigation holds significant importance. Up to this point, wavy channels have predominantly been utilized to explore heat transfer rates due to the ensuing increase in pressure within these channels. In wavy channels, the boundaries are curved, whereas, while the channel in our present investigation can be deemed to be a periodic or wavy channel, its boundaries remain linear rather than curved. This channel type is commonly denoted as a convergent and divergent channel (CADC). Research in this specific area remains scarce, which motivated us to select it for our investigation, thus highlighting a noticeable research gap, as wavy channels continue to dominate the field.
The importance and application of this work lie in its contributions to the understanding of forced convection characteristics in ternary nanofluids within convergent and divergent channels. The study addresses the intricate behavior of ternary nanofluids containing titanium oxide (TiO2), zinc oxide (ZnO), and silver suspended in water as a base fluid. This research provides insights into the effects of varying the Reynolds numbers and aspect ratios on the heat transfer performance within these channels.
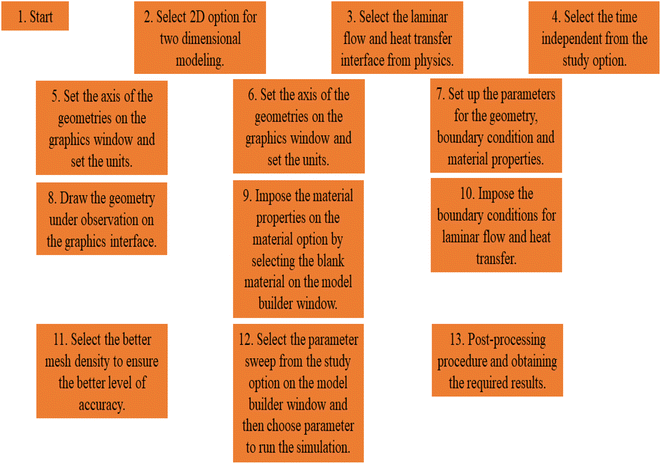
In this article, we have coupled the emerging software COMSOL 6.0, a finite element-based program, to craft numerical simulations. The principal focus of this article centers on scrutinizing forced convection in a convergent and divergent channel. The initial section delineates the problem formulation; it encompasses the construction and geometrical intricacies of this channel, the properties of the materials (nanofluids), their composition, empirical relationships, and the governing partial differential equations exploited to yield the numerical simulations. Furthermore, we delve into the mechanics of COMSOL within this section. The subsequent section is devoted to validation, and encompasses a mesh-independent study and validation via Nusselt-based correlations. The third section is dedicated to discussing the results, and the concluding section encapsulates the main insights drawn from this study.
2. Problem formulation
We present the design of convergent and divergent channels for fluid flow and energy transfer analysis in Fig. 1. The inlet and outlet heights of the channel are equal, as shown in Fig. 1. The slant lengths of the channel are referred to as L1 to L4. In Fig. 1, we have highlighted in orange color a section of the channel where fluid will move both upward and downward. This section has a length of aH, where ‘a’ represents the aspect ratio.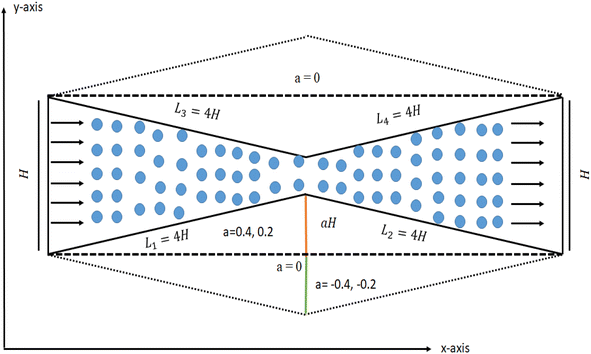 | ||
| Fig. 1 Schematic presentation of the convergent and divergent fluid channel and the assigned boundary conditions. | ||
If ‘a’ is positive, the channel will be convergent, causing the middle part and the section between L1 and L2 to move upwards. Conversely, if ‘a’ is negative, the middle section between L1 and L2 will move outward. These conditions also apply to the upper boundaries of the channel, which will move inside and outside for positive and negative values of ‘a’, respectively.
The portions with lengths L1, L2, L3, and L4 in Fig. 1 are referred to as the legs of the channel. In simpler terms, for a positive ‘a’, the channel will contract, while for a negative ‘a’, it will expand.
In this study, we have kept the inlet height to L ratio fixed at 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 and tested different values of ‘a’ (−0.4, −0.2, 0, 0.2, and 0.4). If ‘a’ is 0, the channel will become a rectangular channel. For ‘a’ values of −0.2 or −0.4, it will act as an expander, while for other ‘a’ values, it will behave as a contractor.
4 and tested different values of ‘a’ (−0.4, −0.2, 0, 0.2, and 0.4). If ‘a’ is 0, the channel will become a rectangular channel. For ‘a’ values of −0.2 or −0.4, it will act as an expander, while for other ‘a’ values, it will behave as a contractor.
We have not extensively observed forced convection of nanofluids in this specific channel design. For our simulations, we set the upper and lower boundaries of the channel to a hot temperature, as indicated in the boundary condition in eqn (7). The outlet pressure is maintained at zero, and a mixture of nanoparticles enters the channel at a certain velocity from the left entrance, which is calculated using the Reynolds number. The nanofluids function as coolants and possess an initial temperature, Tc, as specified in boundary condition in eqn (5). Additionally, we assume that the fluid is incompressible, and we are addressing a time-independent problem.
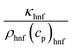
This channel is being tested for the characteristics of ternary nanofluids. Although it is widely known that nanofluids have excellent heat transfer characteristics, we are specifically testing water-based nanofluids containing three types of nanoparticles. These nanofluids consist of equal volume fractions of titanium oxide, zinc oxide, and silver nanoparticles mixed in water. We include the thermo-physical characteristics of the basic water and these nanoparticles in Table 1. The formulae for calculating the density, viscosity, heat capacity, and thermal conductivity of the nanofluids are also listed in the table. The goals of this research are the investigation of how the interaction of nanoparticles affects the rate of heat transfer and the determination of the volume fraction values that give the fastest heat transfer rates. We have reviewed many articles in which nanofluids are claimed to increase the heat transfer rate, and researchers can easily achieve their goals.
2.1 Governing equations and other post-processing parameters
To investigate the transport characteristics of ternary-based nanofluids in a forced convection problem, we developed a simulation using the two-dimensional heat equation and incompressible Navier–Stokes equation, which are given in eqn (1)–(4). The entire simulation was implemented on the finite element-based software Comsol Multiphysics 6.0, in which we utilized a non-isothermal interface to model the problem. Comsol 6.0 uses the finite element method and a Python code to obtain numerical solutions for the constitutive equation. Eqn (1)–(3) will be used to control the fluid flow, while eqn (4) will be used to control energy transport.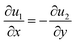 | (1) |
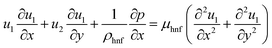 | (2) |
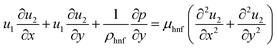 | (3) |
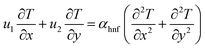 | (4) |
Subject to boundary conditions:
At inlet:
| u1 = uin, u2 = 0, T = Tc when x = 0 and 0 ≤ y ≤ H | (5) |
At outlet:
| p = 0 when x = 2L and 0 ≤ y ≤ H | (6) |
Along the other boundaries:
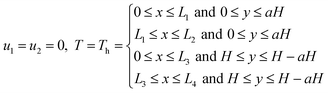 | (7) |
The finite element method is a simple and robust method that can easily deal with all kinds of boundaries and has a generalized code. In this process, the governing equations are first reduced to a weak form using the weighted residual procedure. Then, the weak form is transformed into a system of nonlinear equations by solving it on each element of the domain through an integral process. Finally, the system of nonlinear equations is solved using the generalized Newton–Raphson method. The results obtained from this method have the components of the velocity field, u1 and u2, along with the pressure p, which is included in the constitutive equations, and the temperature T. These are the basic variables that are obtained after the numerical solution. Then, a post-processing procedure is started to calculate the computational values given below:6–8,10,12,13
Heat flux along the domain:
| Q = −κhnfTy | (9) |
Heat transfer coefficient:
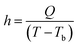 | (10) |
Bulk temperature:7
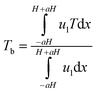 | (11) |
Average temperature:
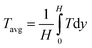 | (12) |
Local Nusselt number:
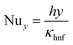 | (13) |
Average Nusselt number:
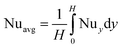 | (14) |
The working flow chart of the COMSOL 6.0 procedure is delineated in Fig. 2.
3. Meshing procedure and mesh independent study
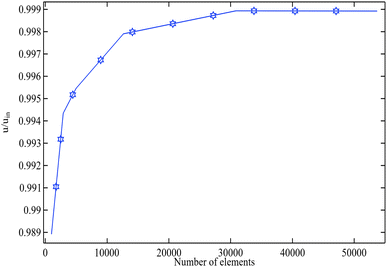
We have shown an example meshing procedure in Fig. 3(a) and (b). We refer to Fig. 3(a) as the divergent channel and Fig. 3(b) as the convergent channel. Different types of mesh elements were used in this domain. Irregular triangles and rectangles were included in the meshing procedure. The mesh density of any numerical approach determines how accurate the outcome will be; therefore, the more computational elements employed, the more accurate the findings will be. Comparatively speaking, the finite element approach is stable since it can handle any type of boundary with ease. A grid-independence test is essential to determine the correctness level of a numerical method, as we illustrate in the mesh-independent research in Fig. 4. In this calculation, we used an increasing number of components to determine u/uin. The answer improves as the number of components rises, as seen in Fig. 4. We can see in this figure that our numerical solution achieves mesh-independence after about 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 elements. However, to ensure reliable results, we need to increase the mesh density as much as possible, since we are discussing a domain involving ternary-based nanofluids, which has not been widely researched. Therefore, it is essential to have highly reliable numerical results. For this reason, we used approximately 55
000 elements. However, to ensure reliable results, we need to increase the mesh density as much as possible, since we are discussing a domain involving ternary-based nanofluids, which has not been widely researched. Therefore, it is essential to have highly reliable numerical results. For this reason, we used approximately 55![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 elements to obtain our numerical results.
000 elements to obtain our numerical results.
We calculated the average Nusselt number using the present numerical scheme, and it was computed at the outlet. A comparison has been made with the Nusselt number correlation provided in ref. 34. This is presented in Fig. 5(a) and (b), in which the present numerical results exhibit strong agreement with the available correlation. Furthermore, we maintained an aspect ratio of a = 0, representing a rectangular channel. This choice was due to the focus of the correlation on the local Nusselt number, while with the aid of COMSOL 6.0 software, we were capable of calculating the average Nusselt number, also at the outlet, given the fixed x-axis at that location. As is evident from Fig. 5(a) and (b), the data for both volume fraction values align well with the present work, demonstrating comparability with the correlation.
 | ||
| Fig. 5 Validation of the average Nusselt number at the outlet of the channel vs. the Reynolds number when a = 0 and (a) ϕ = 0.003 and (b) ϕ = 0.15. | ||
Finally, the error table is displayed below for the continuity equation at the end of the channel (Table 2).
| Re | ϕ | a = −0.4 | a = −0.2 | a = 0 | a = 0.2 | a = 0.4 |
|---|---|---|---|---|---|---|
| 100 | 0.15 | −1.12 × 10−17 | −1.59 × 10−17 | −1.75 × 10−17 | −2.39 × 10−17 | −4.92 × 10−17 |
| 300 | 0.15 | −1.46 × 10−17 | −4.64 × 10−17 | −6.37 × 10−17 | −8.29 × 10−17 | −6.83 × 10−16 |
| 500 | 0.15 | −3.53 × 10−17 | −8.94 × 10−17 | −1.24 × 10−16 | −1.57 × 10−16 | −2.93 × 10−15 |
| 700 | 0.15 | −8.40 × 10−17 | −1.50 × 10−16 | −1.98 × 10−16 | −2.40 × 10−16 | −4.80 × 10−15 |
| 800 | 0.15 | −1.23 × 10−16 | −1.88 × 10−16 | −2.39 × 10−16 | −2.82 × 10−16 | −5.53 × 10−15 |
4. Results and discussion
In the next section, we discuss the numerical findings from the analysis of the forced convection caused by the movement of ternary nanofluids in convergent and divergent channels. We examined the effects of average temperature, average Nusselt number, and temperature gradient at the outlet of the convergent and divergent channel (CADC) to emphasize the outcomes of these phenomena. Subsequently, we estimated the pressure at the middle of the channel, at which the width of the channel changes owing to the channel ‘a’ values changing or staying the same. This is the first time this channel is being examined for ternary-based nanofluid properties. It is certain that using nanofluids will speed heat transmission, but it is critical to quantify how much faster it will be and by what percentage. Another common quantity used to study forced convection is the Reynolds number. In order to ascertain the effect on the heat transfer rate, we are primarily interested in the ‘a’ values, which are the proportion of the overall height of the channel to the height of the convergent or diverging component.4.1 Average temperature at the outlet of the channel
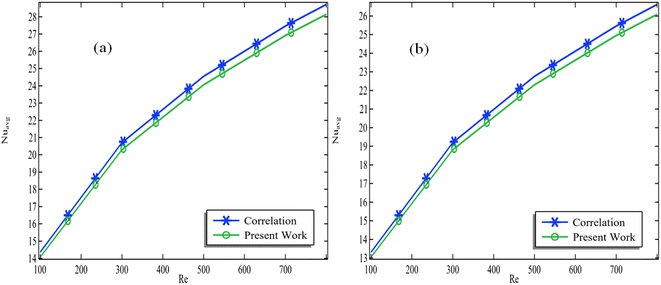
Fig. 6(a) shows the outlet temperature of the channel versus increasing Reynolds number for a fixed aspect ratio ‘a’ plotted on a graph. In Fig. 6(a) and (b), we reproduced the graphs by changing the total volume fraction of ternary nanofluids. In Fig. 6(a), it can be seen that when a = −0.4, the average temperature decreases continuously with an increase in Reynolds number. Similarly, in the case where a = 0, the outlet temperature decreases with an increase in Reynolds number. Additionally, it can be observed that as we increase the value of ‘a’ from −0.4 to 0.2, the outlet temperature increases with an increase in Reynolds number. However, a special instance happens when a = 0.4, at which the average temperature increases with an increase in Reynolds number. This physical phenomenon can be attributed to the middle portion becoming more conducive to heat transfer, resulting in an increase in the heat transfer rate.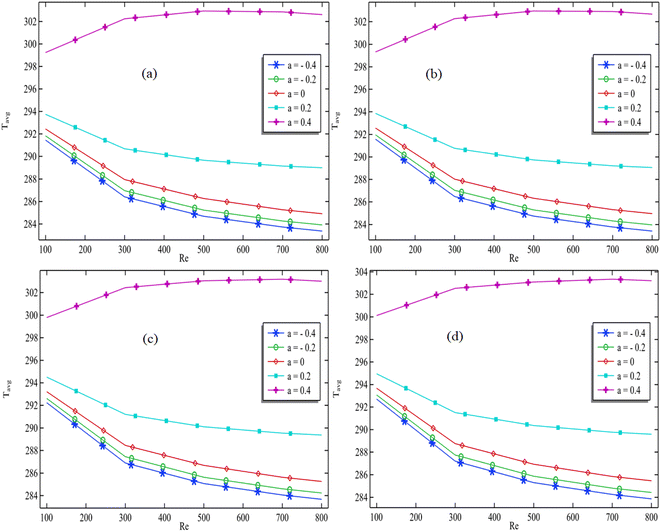 | ||
| Fig. 6 Average temperature vs. Reynolds number at exit of the CADC for all aspect ratios: (a) ϕ = 0.003; (b) ϕ = 0.015; (c) ϕ = 0.09; (d) ϕ = 0.15. | ||
In Fig. 6(b)–(d), we kept the same Reynolds number and volume fractions and changed the total volume fraction. However, we still observed the same pattern in which the average temperature decreases with an increase in Reynolds number for all aspect ratio cases where −0.4 < a < 0.2. However, a = 0.4 has a different pattern of average temperature against Reynolds number.
From these results, we can conclude that as the channel converges, the average temperature decreases with an increase in Reynolds number for all aspect ratio cases when −0.4 < a < 0.2. However, a = 0.4 has a different pattern of average temperature against the Reynolds number. In Fig. 6(a), it can be estimated that when Re = 800, the average temperature increases from 284 K to 290 K when ‘a’ varies from −0.4 to 0.2, which is approximately 2.06%. However, when ‘a’ varies from 0.2 to 0.4 for the same Re = 800 case, the average temperature increases from 290 K to 303 K, which is approximately 4.4%. We can see from Fig. 6(a)–(d) that changing the value of a leads to a change in the pattern of the average temperature against the Reynolds number, but thermal enhancement is still taking place. The underlying physical mechanism can be attributed to the aspect ratio value of 0.4, which leads to a substantial constriction in the channel. This narrowing of the channel effectively compresses the nanofluid molecules, bringing them into closer proximity. As a consequence of this molecular compression, the fluid exhibits heightened conductivity, which, in turn, results in a remarkable increase in the average temperature compared to other aspect ratios.
As shown in Fig. 7(a)–(d), we also focused on the average temperature against the increasing values of Reynolds number. However, here, we fixed the total volume fraction ϕ for the pattern of each graph. We changed the aspect ratio in each graph from Fig. 7(a)–(d). In Fig. 7(a), we can see that the average temperature at the outlet decreases parabolically with increasing Reynolds number. This pattern can clearly be observed in all the graphs. In Fig. 7(a), the aspect ratio is −0.4. We can also see in Fig. 7(a) that as we increase the total volume fraction of the nanofluids, the minimum temperature at Re = 800 increases. Specifically, when the volume fraction is 0.003, the minimum average temperature at Re = 800 is approximately 283 K, but this minimum temperature is 284 K at a volume fraction of 0.15, which is a change of approximately 1 K. In Fig. 7(b) and (c), we can see that as the Reynolds number increases, the average temperature decreases, but as the volume fraction increases, there is an improvement in the average temperature. In the two cases, the aspect ratio ‘a’ is 0 and 0.2, respectively. However, in this case, we were interested in the ratio in Fig. 7(d), where the aspect ratio is 0.4. Here, it is clearly apparent that as the Reynolds number increases, the average temperature also increases. However, we can also see that the average temperature only increases up to Re = 700 and then starts to decrease. This could be because as the aspect ratio increases, the convergent channel becomes so narrow that the fluid flows too fast, and the characteristics of the nanofluids cannot be detected.
 | ||
| Fig. 7 Average temperature vs. Reynolds number at the exit of the CADC for all total volume fractions: (a) a = −0.4; (b) a = 0; (c) a = 0.2; (d) a = 0.4. | ||
From Fig. 7(d), we can conclude that when the total volume of ternary nanofluids is 0.003, the maximum average temperature that exists at Re = 800 is approximately 302.5 K. When the total volume fraction reaches 0.15, the maximum temperature is 303.5 K. This is an increase of approximately 1 K.
4.2 Average Nusselt number at the outlet of the channel
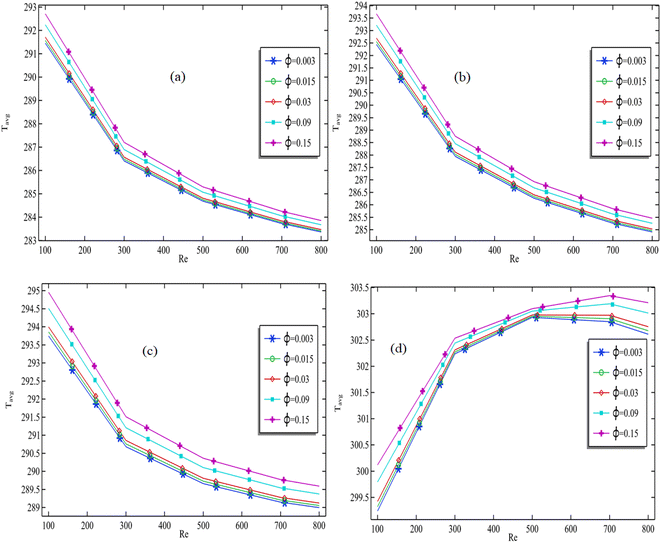
In Fig. 8(a)–(d), we have plotted the average Nusselt number against Reynolds number. For each graph in the figure, we fixed the total volume fraction and varied the aspect ratio to study the patterns of the different graphs with respect to aspect ratio. In Fig. 8(a), it can be observed that the Nusselt number improves continuously with an increase in Reynolds number. When the aspect ratio is −0.4, the value of the Nusselt number increases from approximately 12.5 to 25 as we increase the value of the Reynolds number from 100 to 800, representing an increase of approximately 100 percent. Similarly, when the aspect ratio is 0.4, the Nusselt number increases from 9 to 18.5, representing an increase of approximately 105 percent. We can conclude from this that when the channel goes from divergent to convergent, the convection procedure will be faster for a given aspect ratio, as well as when the Reynolds number increases. Additionally, in Fig. 8(a), we see that the average Nusselt number is maximum when Re = 800. When Re is fixed at 800, the average Nusselt number decreases from 25 to 18.5 as the aspect ratio is increased. We conclude from this that as the channel goes from divergent to convergent, and the aspect ratio increases, the Nusselt number decreases by approximately 26 percent. In Fig. 8(b)–(d), we also observe that the average Nusselt number improves as we increase the Reynolds number for a fixed aspect ratio. We can also conclude that for a fixed Reynolds number, the average Nusselt number decreases as the aspect ratio is changed from −0.4 to 0.4.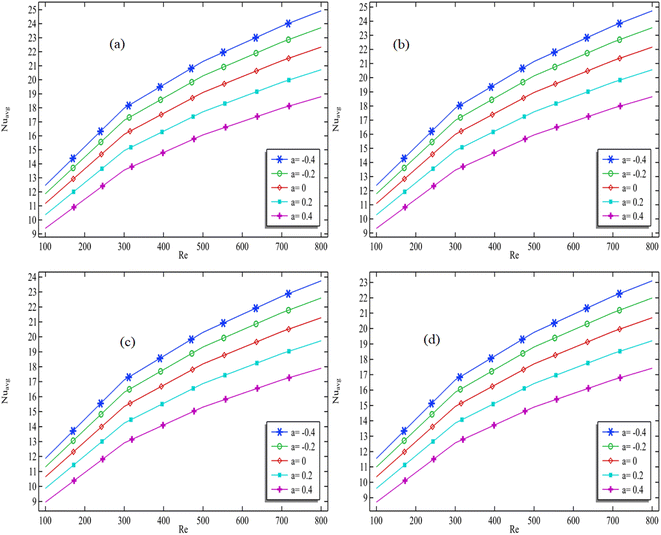 | ||
| Fig. 8 Average Nusselt number vs. Reynolds number at the exit of the CADC for all aspect ratios: (a) ϕ = 0.003; (b) ϕ = 0.015; (c) ϕ = 0.09; (d) ϕ = 0.15. | ||
In Fig. 9(a)–(d), we plotted the average Nusselt number against the increasing Reynolds number, while fixing the total volume fraction for each graph. We produced Fig. 9(a)–(d) to see the pattern with changing the aspect ratio ‘a’. In Fig. 9(a), it is evident that the average Nusselt number at the outlet increases as the Reynolds number increases, maintaining a constant total volume fraction. In Fig. 9(a), it can be seen that when the volume fraction is 0.003, the average Nusselt number at the outlet increases from 12.5 to 25, which is approximately a 100% increment. Similarly, in Fig. 9(a), it can be seen that when the volume fraction is 0.15, the average Nusselt number at the outlet increases from 11.5 to 23, which is also approximately a 100% increment. From this, we can conclude that the convection process increases by almost 100% for each volume fraction in both convergent and divergent channels as the Reynolds number increases from 100 to 800.
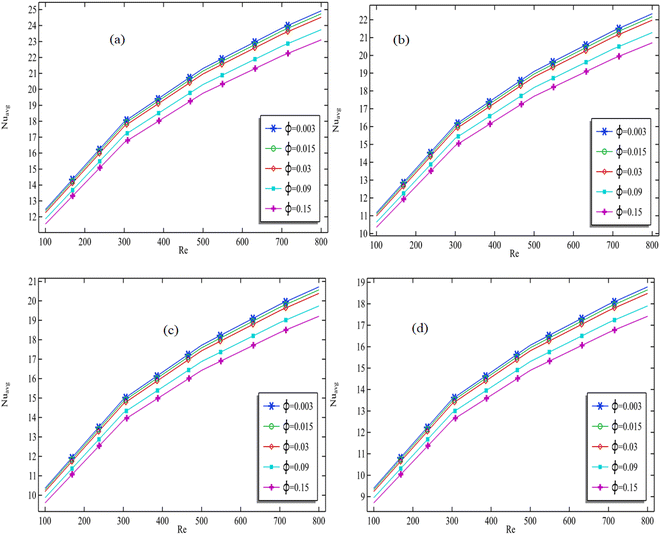 | ||
| Fig. 9 Average Nusselt number vs. Reynolds number at exit of CADC for all total volume fractions when (a) a = −0.4; (b) a = 0; (c) a = 0.2; (d) a = 0.4. | ||
In Fig. 9(a), it can be seen that when Re = 800, the average Nusselt number is at its maximum, and it exhibits the minimum value when Re = 100. When Re = 800 and the aspect ratio is fixed, the average Nusselt number decreases from approximately 25 to 23 in Fig. 9(a), which is approximately an 8% decrement. In Fig. 9(c) and (d), it can be seen that the average Nusselt number at the outlet increases for all the fixed total volume fractions with increasing the Reynolds number from 100 to 800. It can also be seen that the average Nusselt number is at its maximum when Re = 800 for all the cases.
It can be concluded that if we increase the volume fraction for any fixed aspect ratio or Reynolds number, the average Nusselt number decreases. This suggests that as we increase the volume fraction, the convection process becomes weaker, and the conduction process becomes stronger. In Fig. 9(a), it can be observed that when the volume fraction is 0.15, the average Nusselt number increases from 8.5 to 17.5, which is approximately a 100% increase.
4.3 Maximum temperature gradient at the outlet of the channel
In Fig. 10(a) and (b), we have plotted the maximum temperature gradient against Reynolds number. In both figures, we fixed the volume fraction and observed the patterns of the different graphs with increasing aspect ratio. As shown in Fig. 10(a), we found that an increase in Reynolds number leads to an increase in the maximum temperature gradient. For the point at which the volume fraction is 0.003, we can see that the maximum temperature gradient decreases with an increase in aspect ratio. This decrement is only possible when the aspect ratio is between −0.4 and 0.2. At a = 0.4, we see a special pattern in which the maximum temperature increases with Reynolds number. We can conclude that the convergent channel should have a moderate shape to decrease the temperature gradient. In an extremely convergent channel, the temperature gradient might increase, as we previously analyzed for the average temperature. In Fig. 10(b), we again observe that the maximum temperature increases with Reynolds number when the volume fraction is 0.15 and decreases with an increase in aspect ratio. Here again, we see a special case for a = 0.4.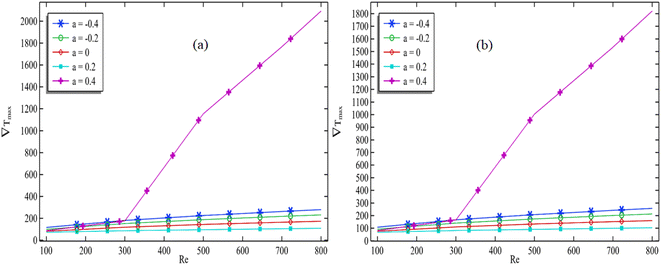 | ||
| Fig. 10 Maximum temperature gradient vs. the Reynolds number for all aspect ratios when (a) ϕ = 0.003 and (b) ϕ = 0.15. | ||
We plotted the maximum temperature gradient against the Reynolds number in Fig. 11(a) and (b) by fixing the aspect ratio in each graph and compared the patterns of different graphs with increasing the volume fraction of nanofluids. It can be seen in both Fig. 11(a) and (b) that for a fixed volume fraction, the maximum temperature gradient always increases as the Reynolds number increases. In Fig. 11(a), it can be seen that as the total concentration of nanofluids increases, the temperature gradient decreases significantly. In Fig. 11(a), it can also be seen that the maximum temperature gradient, which was 280 at Re = 800 for a volume fraction of 0.003, decreases to 258 when the volume fraction is increased to 0.15, which is approximately a 7% decrement. In Fig. 8(b), we kept the aspect ratio at 0.4 and also found that the maximum temperature gradient improves as the Reynolds number increases. This improvement is normal when Re is less than 300, but after Re exceeds 300, a significant increase in the maximum temperature gradient is observed.
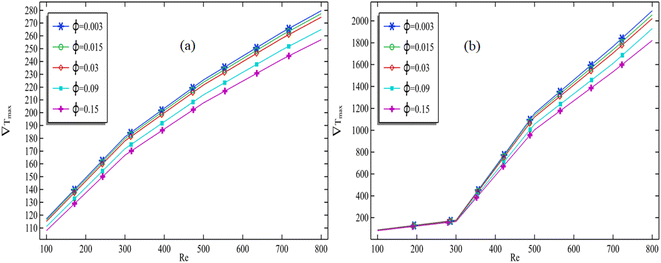 | ||
| Fig. 11 Maximum temperature gradient vs. the Reynolds number for all volume fractions when (a) a = −0.4 and (b) a = 0.4. | ||
When the Reynolds number increases, it indicates that the flow, initially in a laminar state, undergoes a transition into turbulence. This transformation results in alterations to the flow characteristics, leading to an increase in the mixing power and agitation of the nanofluids. Consequently, we observe an enhancement in the rate of heat transfer. Additionally, it is noteworthy that as the aspect ratio increases, transitioning from a divergent to a convergent channel, changes take place that contribute to a reduction in mixing and the transition to turbulence. From these observations, we can infer that an increase in the Reynolds number will correspond to an increase in the maximum temperature. Conversely, an increase in the aspect ratio will lead to a decrease in the maximum temperature.
4.4 Average pressure at the middle of the channel
The study presented in Fig. 12(a)–(e), examines the average pressure at the middle of the channel as the Reynolds number increases. Fig. 12(a)–(c) indicate that an increase in Reynolds number results in a corresponding increase in average pressure at the middle of the channel in a divergent channel. The aspect ratio in these figures ranges from −0.4 to 0. Therefore, it can be concluded that divergent channels experience an increase in average pressure with an increase in Reynolds number. Furthermore, Fig. 12(a)–(c) suggest that an increase in the total volume fraction of nanofluids leads to a decrease in average pressure, but this only applies to divergent channels. In contrast, Fig. 12(d) and (e) show that an increase in Reynolds number results in a decrease in average pressure at the middle of the channel in convergent channels. Consequently, it can be inferred that an increase in Reynolds number in convergent channels causes a reduction in average pressure at the middle of the channel. Additionally, Fig. 12(d) and (e) demonstrate that an increase in the total volume fraction of nanofluids leads to a decrease in average pressure.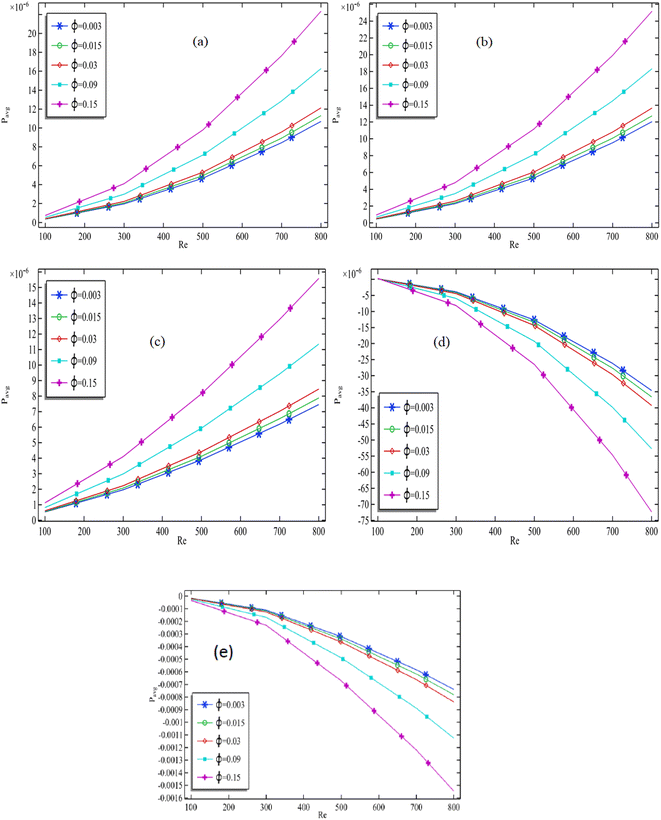 | ||
| Fig. 12 Average pressure calculated at the middle of the channel vs. the Reynolds number for all volume fractions when (a) a = −0.4, (b) a = −0.2, (c) a = 0, (d) a = 0.2, (e) a = 0.4. | ||
5. Conclusions
In this work, we tested a convergent and divergent channel using ternary nanofluids for their convectional heat transfer characteristics. The ternary nanofluid mixture consisted of titanium oxide, zinc oxide, and silver, mixed with water in equal volume fractions as the base fluid. The convergent and divergent channel was designed in such a way that its middle portion either contracted or expanded. We assumed that the inlet and outlet heights were equal, and the aspect ratio, represented by ‘a’ in Fig. 1, was the height between the contracting or expanding middle portion divided by the width of the channel. We kept the aspect ratio value between −0.4 and 0.4, where a negative value represented a divergent channel, and a positive value represented a convergent channel. We modeled the entire simulation and modeling process using finite-element-based software. We focused on the numerical results of Reynolds number, total volume fraction, and aspect ratio to understand the average temperature, average Nusselt number, average pressure at the middle line, and maximum gradient from a graphical point of view. Our main findings are presented below:• The average outlet temperature decreases continuously with an increase in Reynolds number for all values of ‘a’ from −0.4 to 0.2. A special case is observed when a = 0.4. In this case, the channel is highly convergent and an increase in Reynolds number leads to an increase in the average temperature.
• Increasing the aspect ratio leads to an increase in the average outlet temperature. When the value of ‘a’ is increased from −0.4 to 0.2, the average temperature increases by 2.06%. The outlet average temperature increases by 4.4%.
• It was found that for all fixed total volume fractions, the average temperature at the outlet decreases as the Reynolds number increases, except for the aspect ratio a = 0.4. An increase in the volume fraction of ternary nanofluids improves the thermal enhancement in the channel, and the minimum temperature at Re = 800 is improved by 1 K when the volume fraction is increased from 0.003 to 0.15.
• It was found that with a fixed volume fraction and aspect ratio, the average Nusselt number increased with an increase in Reynolds number, and was found to reach a maximum at Re = 800 for all cases. It was also observed that with increasing the Reynolds number from 100 to 800, the average Nusselt number improved by 100.
• Furthermore, it was concluded that increasing the total volume fraction of ternary nanofluids would improve the average Nusselt number. It was observed that the average Nusselt number improved almost 100% when the volume fraction was increased from 0.003 to 0.15.
• It was found that for a fixed volume fraction and aspect ratio, the temperature gradient increases with increasing Reynolds number. The maximum temperature gradient decreases as the aspect ratio increases from −0.4 to 0.2. However, we found the greatest increment in temperature gradient for a = 0.4. The maximum temperature gradient increases significantly when the Reynolds number exceeds 300 at a = 0.4.
• The addition of a concentration of ternary nanofluids will help decrease the maximum temperature gradient at the outlet of the channel. It was noted that by increasing the volume fraction of ternary nanofluids from 0.003 to 0.15, the maximum temperature gradient decreased from 280 K m−1 to 258 K m−1, representing a 7.8% decrease.
• It was found that for a fixed volume fraction of nanofluids and aspect ratios ranging from −0.4 to 0, the average pressure at the middle of the channel increases with an increase in Reynolds number. However, for all volume fractions and aspect ratios ranging from 0 to 0.4, the average pressure at the outlet decreases with an increase in Reynolds number.
• For a divergent channel, the average pressure at the middle of the channel increases with the addition of ternary nanofluids. On the other hand, for a convergent channel, the addition of nanofluids will decrease the average pressure at the middle line of the channel.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University for funding this work through large group Research Project under grant number RGP2/340/44.References
- M. Abbasi, M. M. Heyhat and A. Rajabpour, Study of the effects of particle shape and base fluid type on density of nanofluids using ternary mixture formula: a molecular dynamics simulation, J. Mol. Liquids, 2020, 305, 112831 CrossRef CAS.
- H. Adun, D. Kavaz and M. Dagbasi, Review of ternary hybrid nanofluid: synthesis, stability, thermophysical properties, heat transfer applications, and environmental effects, J. Clean. Prod., 2022, 328, 129525 CrossRef.
- W. Ashraf, Heat transfer mechanism in ternary nanofluid between parallel plates channel using modified hamilton-crossers model and thermal radiation effects, Geoenergy Sci. Eng., 2023, 225, 211732 CrossRef.
- S. Salari and S. M. Jafari, Application of nanofluids for thermal processing of food products, Trends Food Sci. Technol., 2022, 97, 100–113 CrossRef.
- S. Senthilraja, M. Karthikeyan and R. Gangadevi, Nanofluid applications in future automobiles: comprehensive review of existing data, Nano-Micro Lett., 2010, 2, 306–310 CrossRef.
- A. A. Memon, H. Anwaar, T. Muhammad, A. A. Alharbi, A. S. Alshomrani and Y. R. Aladwani, A forced convection of water-aluminum oxide nanofluids in a square cavity containing a circular rotating disk of unit speed with high Reynolds number: a Comsol Multiphysics study, Case Stud. Therm. Eng., 2021, 39, 102370 Search PubMed.
- M. S. Alqarni, A. A. Memon, H. Anwaar and T. Muhammad, The forced convection analysis of water alumina nanofluid flow through a 3D annulus with rotating cylinders via κ − ε turbulence model, Energies, 2022, 15(18), 6730 CrossRef CAS.
- M. M. Memon, M. Alghamdi and T. Muhammad, A forced convection of water aluminum oxide nanofluid flow and heat transfer study for a three-dimensional annular with inner rotated cylinder, Sci. Rep., 2022, 12(1), 16735 CrossRef PubMed.
- N. S. Pandya, H. Shah, M. Molana and A. K. Tiwari, Heat transfer enhancement with nanofluids in plate heat exchangers: a comprehensive review, Eur. J. Mech. B Fluids, 2022, 81, 173–190 CrossRef.
- S. H. Elhag, A. A. Memon, M. A. Memon, K. Bhatti, K. Jacob, S. Alzahrani and J. Seidu, Analysis of forced convection with hybrid Cu-Al2O3 nanofluids injected in a three- dimensional rectangular channel containing three perpendicular rotating blocks with turbulent modeling, J. Nanomater., 2022, 2446972 CAS.
- S. Samiezadeh, R. Khodaverdian, M. H. Doranehgard, H. Chehrmonavari and Q. Xiong, CFD simulation of thermal performance of hybrid oil-Cu-Al2O3 nanofluid flowing through the porous receiver tube inside a finned parabolic trough solar collector, Sustainable Energy Technol. Assess., 2022, 50, 101888 CrossRef.
- A. A. Memon, M. A. Memon and A. Fenta, A laminar forced convection via transport of water– copper–aluminum hybrid nanofluid through heated deep and shallow cavity with Corcione model, Sci. Rep., 2023, 13(1), 4915 CrossRef CAS PubMed.
- N. Akkurt, T. Shedd, A. A. Memon, M. R. Ali and M. Bouye, Analysis of the forced convection via the turbulence transport of the hybrid mixture in three-dimensional L-shaped channel, Case Stud. Therm. Eng., 2022, 41, 102558 CrossRef.
- I. Zahan, R. Nasrin and S. Khatun, Thermal performance of ternary-hybrid nanofluids through a convergent-divergent nozzle using distilled water-ethylene glycol mixtures, Int. Commun. Heat Mass Transfer, 2021, 137, 106254 CrossRef.
- W. A. Adnan, Joule heating and heat generation/absorption effects on the heat transfer mechanism in ternary nanofluid containing different shape factors in stretchable converging/diverging Channel, Waves Random Complex Media, 2023, 1–18, DOI:10.1080/17455030.2023.2198038.
- H. W. Cho, Y. M. Seo, Y. G. Park, S. Pandey and M. Y. Ha, Estimation of heat transfer performance on mixed convection in an enclosure with an inner cylinder using an artificial neural network, Case Stud. Therm. Eng., 2022, 28, 101595 CrossRef.
- W. Alhejaili and A. M. Aly, Thermal radiation impacts on natural convection of NEPCM in a porous annulus between two horizontal wavy cavities, Case Stud. Therm. Eng., 2022, 40, 102526 CrossRef.
- U. Nazir, N. H. Abu-Hamdeh, M. Nawaz, S. O. Alharbi and W. Khan, Numerical study of thermal and mass enhancement in the flow of Carreau-Yasuda fluid with hybrid nanoparticles, Case Stud. Therm. Eng., 2021, 27, 101256 CrossRef.
- S. Murtaza, P. Kumam, Z. Ahmad, M. Ramzan, I. Ali and A. Saeed, Computational simulation of unsteady squeezing hybrid nanofluid flow through a horizontal channel comprised of metallic nanoparticles, J. Nanofluids, 2023, 12(5), 1327–1334 CrossRef.
- S. Murtaza, Z. Ahmad, I. E. Ali, Z. Akhtar, F. Tchier, H. Ahmad and S. W. Yao, Analysis and numerical simulation of fractal-fractional order non-linear couple stress nanofluid with cadmium telluride nanoparticles, J. King Saud. Univ. Sci., 2023, 35(4), 102618 CrossRef.
- S. Murtaza, P. Kumam, M. Bilal, T. Sutthibutpong, N. Rujisamphan and Z. Ahmad, Parametric simulation of hybrid nanofluid flow consisting of cobalt ferrite nanoparticles with second-order slip and variable viscosity over an extending surface, Nanotechnol. Rev., 2023, 12(1), 20220533 CrossRef CAS.
- S. Murtaza, P. Kumam, Z. Ahmad, T. Seangwattana and I. E. Ali, Numerical analysis of newly developed fractal-fractional model of Casson fluid with exponential memory, Fractals, 2022, 30(05), 2240151 CrossRef.
- M. A. Ahmed, M. Z. Yusoff, K. C. Ng and N. H. Shuaib, The effects of wavy-wall phase shift on thermal-hydraulic performance of Al2O3–water nanofluid flow in sinusoidal-wavy channel, Case Stud. Therm. Eng., 2015, 4, 153–165 CrossRef.
- A. Kumar, Priyanka, S. Kumar and S. Kalia, Optimization and correlations development for heat transfer and fluid flow characteristics of ZnO/H2O-ethylene glycol-based nanofluid flow through an inclined ribbed square duct, Numer. Heat Transfer, Part A, 2023, 1–16 Search PubMed.
- Priyanka, S. Kumar and A. Kumar, Effect of mono/hybrid nanofluids and passive techniques on thermal performance of parabolic trough solar collector: a review, Energy Sources, Part A, 2023, 45(1), 1686–1709 CrossRef.
- A. Kumar, R. Maithani, S. Sharma, S. Kumar, M. Sharifpur, T. Alam, N. K. Gupta and S. M. Eldin, Effect of dimpled rib with arc pattern on hydrothermal characteristics of Al2O3-H2O nanofluid flow in a square duct, Sustainability, 2022, 14(22), 14675 CrossRef CAS.
- A. Kumar, R. Maithani, S. Sharma, S. Kumar and N. Rathour, Enhancement of heat transfer of SiO2-H2O based nanofluid flow through 45° angled slot ribbed square duct, Mater. Today: Proc., 2022, 69, 328–332 CAS.
- W. Aich, H. Almujibah, S. S. Abdullaevd, M. Z. Bani-Fwaz and A. M. Hassan, Thermal performance of radiated annular extended surface using advanced nanomaterials influenced by various physical controlling parameters for nucleate boiling case, Case Stud. Therm. Eng., 2023, 103524 CrossRef.
- N. K. Mishra, Adnan, K. U Rahman, S. M. Eldin and M. Z. Bani-Fwaz, Investigation of blood flow characteristics saturated by graphene/CuO hybrid nanoparticles under quadratic radiation using VIM: study for expanding/contracting channel, Sci. Rep., 2023, 13(1), 8503 CrossRef PubMed.
- Adnan and W. Ashraf, Joule heating and heat generation/absorption effects on the heat transfer mechanism in ternary nanofluids containing different shape factors in stretchable converging/diverging Channel, Waves Random Complex Media, 2023, 1–18 Search PubMed.
- Adnan, Heat transfer inspection in [(ZnO-MWCNTs)/water-EG (50: 50)] hnf with thermal radiation ray and convective condition over a Riga surface, Waves Random Complex Media, 2022, 1–15 CAS.
- Adnan and W. Ashraf, Heat transfer in tetra-nanofluid between converging/diverging channel under the influence of thermal radiations by using Galerkin finite element method, Waves Random Complex Media, 2023, 1–16 Search PubMed.
- N. K. Mishra, Adnan, G. Sarfraz, M. Z. Bani-Fwaz and S. M. Eldin, Dynamics of Corcione nanoliquid on a convectively radiated surface using Al2O3 nanoparticles, J. Therm. Anal. Calorim., 2023, 1–12 CAS.
- R. K. Shah, Thermal entry length solutions for the circular tube and parallel plates, in Proceedings of 3rd National Heat and Mass Transfer Conference, Indian Institute of Technology Bombay, Delhi, 1975, vol. 1, pp. 11–75 Search PubMed.
| This journal is © The Royal Society of Chemistry 2023 |