DOI:
10.1039/D2NJ04301G
(Paper)
New J. Chem., 2023,
47, 224-230
A QSAR model for predicting the corneal permeability of drugs – the application of the Monte Carlo optimization method†
Received
29th August 2022
, Accepted 15th November 2022
First published on 21st November 2022
Abstract
Direct implementation into the eye is the most commonly used method for applying drugs for the treatment of most ocular diseases. The preferred way for improving the bioavailability of ophthalmic drugs is by increasing their corneal permeability, but evaluation of this activity is a time-consuming and expensive process carried out on experimental animals. One solution to overcome these issues is developing a QSAR model to predict corneal permeability. For developing a QSAR model, the Monte Carlo optimization method was applied, using three splits of the initial molecular data set for training and test sets. The QSAR model was developed with the application of optimal molecular descriptors based on both SMILES notation and molecular graphs. Various statistical parameters, including the correlation coefficient, cross-validated correlation coefficient, standard error of estimation, mean absolute error, Fischer ratio, root-mean-square error, Rm2, MAE-based metrics, and index of ideality of correlation, were used to validate the developed QSAR model. The predictability potential and robustness of the developed QSAR model were proven to be very good by applying statistical methods. Molecular fragments, used as optimal descriptors in QSAR modeling, that have a positive and negative effect on corneal permeability were identified. The developed QSAR models for corneal permeability with the application of the Monte Carlo optimization method have very good predictivity potential. The identified molecular fragments could be useful when assessment of novel drugs' corneal permeability has to be performed.
1. Introduction
For the treatment of most ocular diseases and for the achievement of localized action of a used drug (on the surface or in the interior of the eye), direct implementation into the eye is the most commonly used method of application.1–4 Since less than 5% of the applied drug reaches the intraocular tissues, improvement of ocular absorption of ophthalmic drugs must be achieved, and it is carried out in two ways: by increasing corneal permeability and prolonging the contact time on the ocular surface. The preferred way for improving the bioavailability of ophthalmic drugs is by increasing their corneal permeability since a major part (50–100%) of the instilled dose is absorbed systemically and it may cause systemic side effects. Intraocular drug absorption occurs mainly across the cornea, where the corneal epithelium acts as the main barrier directing the drug penetration into the eye. Across the epithelium, drugs can penetrate in two ways: via the transcellular route for lipophilic drugs, and the paracellular route for hydrophilic drugs, in which either passive or altered diffusion through intercellular spaces is involved. The route and rate of corneal permeability are directed by physicochemical drug properties like molecular size, solubility, the degree of ionization, charge, lipophilicity, and pH 8.5–9 The lipoidal corneal epithelium is the rate-limiting barrier for highly hydrophilic drugs. Partitioning from the epithelium to the hydrophilic stroma is rate-limiting and, in most cases, determines the corneal permeability for highly lipophilic drugs.10
The determination of the permeability coefficient is necessary to determine corneal permeability. In vitro experiments are used for measuring permeability coefficients in an isolated rabbit cornea mounted in a perfusion chamber to maintain its integrity and viability throughout the experimental procedure. This experimental setup makes the determination of corneal permeability very time-consuming and expensive.11–13 For this reason, the development of theoretical models for the determination of the corneal permeability of drug candidates based on their physicochemical properties and other structural parameters is very appealing. Several quantitative structure–activity relationship (QSAR) models have been reported so far.14–18 Several QSAR models are based on the partition coefficient (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P) or the distribution coefficient (log
P) or the distribution coefficient (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D, for an ionizable compound) of the drug. However, some steroids could not be fit into the QSAR model developed for -blockers. Yoshida and Topliss developed a QSAR satisfying model that unified-blockers and steroids based on the difference between the octanol–water partition coefficient and the alkane–water partition coefficient (log
D, for an ionizable compound) of the drug. However, some steroids could not be fit into the QSAR model developed for -blockers. Yoshida and Topliss developed a QSAR satisfying model that unified-blockers and steroids based on the difference between the octanol–water partition coefficient and the alkane–water partition coefficient (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P) and the distribution coefficient (log
P) and the distribution coefficient (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D). The main drawback of this QSAR model is the complexity of log
D). The main drawback of this QSAR model is the complexity of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P values it requires. To overcome this problem, a QSAR model based on charge and solid parameters of compounds has been developed.17 Apart from “classic” QSAR models, membrane-interaction (MI)-QSAR analysis was applied to establish a QSAR model for measuring permeability coefficients. However, this method requires complex computational calculations to establish a satisfactory QSAR model. In light of the given facts, there is still a need to develop a reliable QSAR model that can be used to predict the corneal permeability coefficient. A Monte Carlo optimization method in which the studied activity is treated as a random event has emerged as a promising approach in QSAR modeling in recent years. This method is based on a conformation-independent approach with optimal descriptors based on topological molecular features and molecules in the Simplified Molecular Input Line Entry System (SMILES) notation.19–21 One of the primary advantages of the described method over more commonly used ones is its simplicity and efficiency. Also, this method can be used to determine molecular fragments (calculated as SMILES notation descriptors) that have an influence on the studied activity and that can be associated with the chemical structures of studied compounds. The main aim of this research is the development of a conformation-independent QSAR model based on the Monte Carlo optimization method for the corneal permeability of various organic compounds. Furthermore, one of the main aims of this research was to define SMILES notation descriptors associated with molecular fragments that have both positive and negative influences on corneal permeability.
P values it requires. To overcome this problem, a QSAR model based on charge and solid parameters of compounds has been developed.17 Apart from “classic” QSAR models, membrane-interaction (MI)-QSAR analysis was applied to establish a QSAR model for measuring permeability coefficients. However, this method requires complex computational calculations to establish a satisfactory QSAR model. In light of the given facts, there is still a need to develop a reliable QSAR model that can be used to predict the corneal permeability coefficient. A Monte Carlo optimization method in which the studied activity is treated as a random event has emerged as a promising approach in QSAR modeling in recent years. This method is based on a conformation-independent approach with optimal descriptors based on topological molecular features and molecules in the Simplified Molecular Input Line Entry System (SMILES) notation.19–21 One of the primary advantages of the described method over more commonly used ones is its simplicity and efficiency. Also, this method can be used to determine molecular fragments (calculated as SMILES notation descriptors) that have an influence on the studied activity and that can be associated with the chemical structures of studied compounds. The main aim of this research is the development of a conformation-independent QSAR model based on the Monte Carlo optimization method for the corneal permeability of various organic compounds. Furthermore, one of the main aims of this research was to define SMILES notation descriptors associated with molecular fragments that have both positive and negative influences on corneal permeability.
2. Methods
As the first step in developing appropriate QSAR models, molecules obtained from the literature18 were drawn using ACD/ChemSketch software v.11.0 and converted into the SMILES notation using the same software. Chemical structures of the compounds used for QSAR modeling with their SMILES notation are presented in the ESI.† The molecular weights of the studied molecules ranged from 18.02 to 468.37. As a dependent variable for the development of the QSAR model, we used the logarithm of the corneal permeability coefficient (P), log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P. P (cm−1) is calculated in vitro using the equation P = (7C)/(tAC0). In this equation, C/t is the change in concentration in dpm mL−1 sample per unit time, and 7 is the volume of the sampling chamber in mL. Therefore, the quantity 7C/t is the steady-state flux in dpm h−1. A is the surface area of the cornea (taken to be 1.087 cm2), and C0 is the initial concentration of the diffusing drug. It should be noted that we used all experimental values published to-date of log
P. P (cm−1) is calculated in vitro using the equation P = (7C)/(tAC0). In this equation, C/t is the change in concentration in dpm mL−1 sample per unit time, and 7 is the volume of the sampling chamber in mL. Therefore, the quantity 7C/t is the steady-state flux in dpm h−1. A is the surface area of the cornea (taken to be 1.087 cm2), and C0 is the initial concentration of the diffusing drug. It should be noted that we used all experimental values published to-date of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P to cover the range of −6.17 to −3.82. The experimental and calculated corneal permeability coefficient values are presented in Table S1 (ESI†). After we finished constructing the appropriate database, we made three different random splits of the main molecular database into two sets–the training set, which included 50 compounds (75%), and the test set with 17 compounds (25%), and we checked the normality of the activity distribution according to the published method.22 To establish conformation-independent QSAR models, in this study, we applied software called CORAL (CORrelation and Logic, https://www.insilico.eu/coral) based on the Monte Carlo method and its algorithm, which treats the pertinent activity as a random event. We took into consideration two types of molecular descriptors based on the molecular graph and SMILES notation. Based on molecular graphs, invariants were defined as local graph invariants: Morgan extended connectivity indices of increasing order (EC0), path numbers of length 2 and 3 (p2, p3), valence shells of range 2 and 3 (s2, s3), and the code of nearest neighbors (NNCk). In recent years, Simplified Molecular Input-Line Entry System (SMILES) notation has become one of the most convenient representations, and especially used in chemoinformatics because SMILES notation is considered as a very convenient alternative to the molecular graph. This fact is very appealing for medicinal chemistry since correlating molecular fragments with molecular graph-based descriptors can be quite challenging. For QSAR modeling, SMILES notation can be used to define molecular optimal descriptors (DCW), where DCW can be calculated as a function of SMILES notation according to eqn (1).
P to cover the range of −6.17 to −3.82. The experimental and calculated corneal permeability coefficient values are presented in Table S1 (ESI†). After we finished constructing the appropriate database, we made three different random splits of the main molecular database into two sets–the training set, which included 50 compounds (75%), and the test set with 17 compounds (25%), and we checked the normality of the activity distribution according to the published method.22 To establish conformation-independent QSAR models, in this study, we applied software called CORAL (CORrelation and Logic, https://www.insilico.eu/coral) based on the Monte Carlo method and its algorithm, which treats the pertinent activity as a random event. We took into consideration two types of molecular descriptors based on the molecular graph and SMILES notation. Based on molecular graphs, invariants were defined as local graph invariants: Morgan extended connectivity indices of increasing order (EC0), path numbers of length 2 and 3 (p2, p3), valence shells of range 2 and 3 (s2, s3), and the code of nearest neighbors (NNCk). In recent years, Simplified Molecular Input-Line Entry System (SMILES) notation has become one of the most convenient representations, and especially used in chemoinformatics because SMILES notation is considered as a very convenient alternative to the molecular graph. This fact is very appealing for medicinal chemistry since correlating molecular fragments with molecular graph-based descriptors can be quite challenging. For QSAR modeling, SMILES notation can be used to define molecular optimal descriptors (DCW), where DCW can be calculated as a function of SMILES notation according to eqn (1).| | | DCW(T,Nepoch) = ΣCW(Sk) + ΣCW(SSk) + ΣCW(SSSk) + ΣCW(EC0k) + ΣCW(PT2k) + ΣCW(PT3k) + ΣCW(VS2k) + ΣCW(VS3k) + ΣCW(NNCk) | (1) |
In this research, we used all SMILES notation based descriptors: local, global, and HARD-index. One of the main features of the developed QSAR model with the application of the Monte Carlo method is that we calculate the correlation weight (CW), a numerical value for each used optimal descriptor.21 The manner in which this task is achieved is based on generating suitable random numbers and observing how that fraction of numbers obeys some property or properties, in which CW values are randomly assigned to all used optimal descriptors, both molecular graph and SMILES notation based descriptors, in each independent Monte Carlo run. The Monte Carlo optimization process is applied further to calculate the numerical data for the correlation weights, which gives the maximal value of the correlation coefficient between the studied activity and used optimal descriptors. For this purpose, the Monte Carlo method uses two parameters: threshold (T) and the number of epochs (Nepoch). For the development of QSAR models, we used values of 0–10 for T and 0–70 for Nepoch, from which the search for the most predictive combination of T and Nepoch was concluded according to the published methodology.19–21 The development of a robust model capable of predicting the properties of new molecules in an objective, reliable, and precise manner is the main goal of any QSAR modeling process. We used the following methods to determine the goodness of the established QSAR models: internal validation using the training set, external validation using the validation set, and data randomization (Y-scrambling test). This was carried out by using statistical parameters such as the correlation coefficient (r2), cross-validated correlation coefficient (q2), standard error of estimation (s), mean absolute error (MAE), Fischer ratio (F), root-mean-square error (RMSE), Rm2, and MAE-based metrics.22–26 Recently, the so-called index of ideality of correlation (IIC) has been suggested as a novel criterion for the estimation of the predictive potential of QSAR models, considering not only the correlation coefficient but also the arrangement of the cluster of dots-images relative to the diagonal, in coordinates of observed–calculated values of the studied endpoint, and we calculated the IIC according to eqn (2)–(5) as the QSAR model final estimator.27–29| | | Δk = observedk − calculatedk | (2) |
Having data on all Δk for the test set, one can calculate sum of negative and positive values of Δk similar to the mean absolute error (MAE):| | 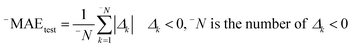 | (3) |
| | 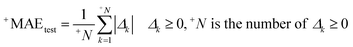 | (4) |
| | 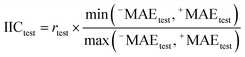 | (5) |
3. Results and discussion
The applicability domain (AD) is a fundamental characteristic based on which the selection of molecules is carried out.30–32 For defining AD we applied the published methodology and we determined that all molecules in this study were within the range of AD defined and we did not identify any outliers.21 The values of the statistical metrics that helped us to determine the quality of the developed QSAR models for corneal permeability are available in Table 1. They indicate that the applied method was capable of establishing a QSAR model with good reproducibility, which we tested using the concordance correlation coefficient. We evaluated the predictability of the developed QSAR model using values presented in Table 1, and the developed model was proved to be valid. In addition, the model was classified as valid using MAE-based metrics. We performed the final evaluation of the developed QSAR models both for the training and the test set using the index of ideality of correlation and obtained values that suggest that the developed QSAR models have a high predictive potential. Furthermore, we applied Y-randomization, which implied scrambling of Y values in 1000 trials in ten separate runs, to assess the sturdiness of the developed QSAR models. The obtained values presented in Table 2 indicate that there was no correlation by chance among the developed models.22 Concerning corneal permeability, we obtained the best QSAR model from the second split.
Table 1 Statistical quality of the developed QSAR models for corneal permeability
|
|
Training set |
Test set |
|
r
2
|
q
2
|
CCC |
IIC |
s
|
MAE |
F
|
r
22
|
q
2
|
CCC |
IIC |
s
|
MAE |
F
|
|
r
2 – correlation coefficient, q2 – cross-validated correlation coefficient, CCC – concordance correlation coefficient, IIC – index of ideality of correlation, s – standard error of estimation, MAE – mean absolute error, F – Fischer ratio, Av – average value for statistical parameters obtained from three independent Monte Carlo optimization runs. |
| Split 1 |
1 run |
0.9203 |
0.9585 |
0.9593 |
0.9134 |
0.172 |
0.134 |
554 |
0.8643 |
0.8813 |
0.9296 |
0.8293 |
0.328 |
0.214 |
96 |
| 2 run |
0.8407 |
0.9135 |
0.6113 |
0.8293 |
0.244 |
0.178 |
253 |
0.8978 |
0.8560 |
0.9475 |
0.8731 |
0.347 |
0.239 |
132 |
| 3 run |
0.8783 |
0.9352 |
0.8651 |
0.8690 |
0.213 |
0.157 |
347 |
0.8856 |
0.8822 |
0.9411 |
0.8589 |
0.324 |
0.228 |
116 |
| Av |
0.8798 |
0.9357 |
0.8119 |
0.8706 |
0.210 |
0.156 |
385 |
0.8826 |
0.8732 |
0.9394 |
0.8538 |
0.333 |
0.227 |
115 |
| Split 2 |
1 run |
0.9046 |
0.9499 |
0.5647 |
0.8980 |
0.217 |
0.157 |
464 |
0.9272 |
0.9418 |
0.9629 |
0.9045 |
0.181 |
0.153 |
178 |
| 2 run |
0.9222 |
0.9595 |
0.8536 |
0.9163 |
0.196 |
0.137 |
581 |
0.9148 |
0.9095 |
0.9564 |
0.8756 |
0.217 |
0.167 |
150 |
| 3 run |
0.9124 |
0.9542 |
0.9184 |
0.9067 |
0.208 |
0.147 |
510 |
0.9084 |
0.9173 |
0.9531 |
0.8471 |
0.211 |
0.174 |
139 |
| Av |
0.9131 |
0.9545 |
0.7789 |
0.9070 |
0.207 |
0.147 |
518 |
0.9168 |
0.9229 |
0.9575 |
0.8757 |
0.203 |
0.165 |
156 |
| Split 3 |
1 run |
0.8893 |
0.9413 |
0.8032 |
0.8801 |
0.213 |
0.154 |
385 |
0.8655 |
0.8974 |
0.9303 |
0.838 |
0.310 |
0.24 |
97 |
| 2 run |
0.8716 |
0.9314 |
0.7952 |
0.8612 |
0.230 |
0.171 |
326 |
0.8790 |
0.8889 |
0.9376 |
0.8532 |
0.317 |
0.243 |
109 |
| 3 run |
0.8891 |
0.9413 |
0.9429 |
0.8797 |
0.213 |
0.161 |
385 |
0.8483 |
0.8907 |
0.9210 |
0.8182 |
0.323 |
0.259 |
84 |
| Av |
0.8832 |
0.9380 |
0.8471 |
0.8737 |
0.219 |
0.162 |
365 |
0.8643 |
0.8923 |
0.9296 |
0.8365 |
0.317 |
0.247 |
97 |
Table 2 Y-randomization of the best QSAR models (best optimization run) for three independent splits
|
|
Split 1 |
Split 2 |
Split 3 |
| Training |
Test |
Training |
Test |
Training |
Test |
|
C
R
p
2 = R × (R2 − Rr2)1/2 should be >0.5. |
| 0 |
0.8407 |
0.8978 |
0.9046 |
0.9272 |
0.8716 |
0.879 |
| 1 |
0.0048 |
0.3684 |
0.0075 |
0.012 |
0.0303 |
0.0623 |
| 2 |
0.0346 |
0.0009 |
0.0004 |
0.0101 |
0.0478 |
0.1231 |
| 3 |
0.0008 |
0.0928 |
0 |
0.0286 |
0.0079 |
0.0074 |
| 4 |
0.0309 |
0.0059 |
0.0215 |
0.0619 |
0.0005 |
0.0535 |
| 5 |
0.0567 |
0.0189 |
0.0011 |
0.0663 |
0.0005 |
0.0917 |
| 6 |
0.0005 |
0.0413 |
0.0209 |
0.1078 |
0.0024 |
0 |
| 7 |
0.0384 |
0.1799 |
0.0442 |
0.0519 |
0.1054 |
0.0362 |
| 8 |
0.0029 |
0.0121 |
0.0081 |
0.0316 |
0.0028 |
0.0762 |
| 9 |
0.0171 |
0.0004 |
0.0035 |
0.0243 |
0.0155 |
0 |
| 10 |
0.07 |
0.0719 |
0.1405 |
0.168 |
0.0204 |
0.0131 |
|
R
r
2
|
0.0257 |
0.0792 |
0.0248 |
0.0562 |
0.0234 |
0.0464 |
|
C
R
p
2
|
0.8278 |
0.8572 |
0.8921 |
0.8987 |
0.8598 |
0.8555 |
Also, we observed that the best model was obtained with a T value of 1, whereas the best Nepoch value amounted to 20. The best Monte Carlo optimization runs (the highest value for r2) for the developed QSAR models for all splits are shown in Fig. 1 in the form of graphical representations. Using the Least squares method, the best developed QSAR models for the studied activity, regarding T and Nepoch values, are presented in the form of eqn (6)–(8).
| | Split 1: log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P = −6.0994(±0.0095) + 0.0235(±0.0002) × DCW(3,21) P = −6.0994(±0.0095) + 0.0235(±0.0002) × DCW(3,21) | (6) |
| | Split 2: log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P = −6.7242(±0.0100) + 0.0300(±0.0002) × DCW(1,20) P = −6.7242(±0.0100) + 0.0300(±0.0002) × DCW(1,20) | (7) |
| | Split 3: log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P = −6.3163(±0.0121) + 0.0241(±0.0002) × DCW(2,17) P = −6.3163(±0.0121) + 0.0241(±0.0002) × DCW(2,17) | (8) |
Chen and Yang developed a QSAR model on the basis of membrane-interaction (MI)-QSAR analysis and the calculated models had correlation coefficients ranging from 0.73 to 0.94.
33 We compared values for the correlation coefficient presented in this research and found that there is a similarity regarding predictivity potential. However, the complexity of MI-QSAR model development, in our opinion, makes Monte Carlo optimization-based QSAR models superior. Ghorbanzad’e
et al. developed QSAR models with the same data set as in the presented research study with multiple linear regression (MLR) and multilayer perceptron neural network (MLP-NN) as main algorithms.
18 The authors used eight molecular descriptors to develop QSAR models–four dragon based descriptors,
i.e., the hydrophilic factor, a total size of index/unweighted, Borto–Moreau autocorrelation of lag 1 weighted using van der Waals volume and property potential (mass weighted), maximum partial charge on an H atom (ıH(max)), count of H acceptor sites, molecular volume and average information content order 1. The authors reported the following statistical values for the external validation set used in MLP-NN modeling:
q2 = 0.938,
R2 = 0.982,
k = 0.972, and
R2m = 0.876. However, most of the descriptors used in the QSAR model stated above do not have physical meaning and cannot be associated with mechanistic interpretation. It has to be noted that QSAR models developed with the Monte Carlo optimization method are developed with SMILES notation based molecular descriptors that have mechanistic interpretation and could be associated with molecular fragments.
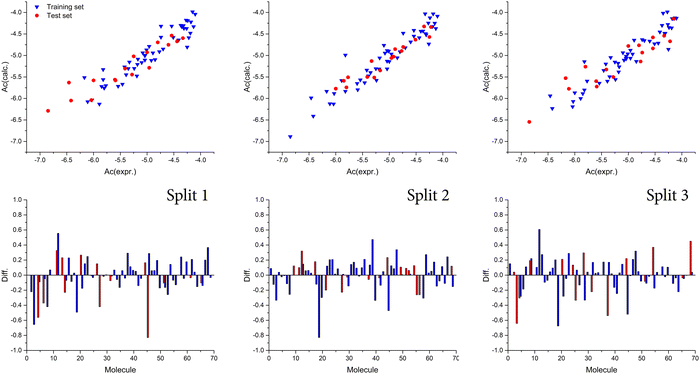 |
| | Fig. 1 Graphical presentation of the best Monte Carlo optimization runs (the highest value for r2) for the developed QSAR models. | |
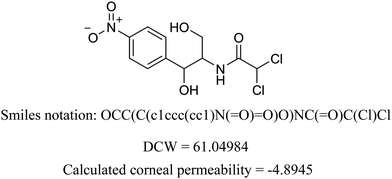
We present the calculation for chloramphenicol in Table 3 with omitted local graph invariant descriptors. In Table S2 (ESI†) we present a list of structural alerts (SAKs), all defined as SMILES notation-based molecular fragments for the three runs of the Monte Carlo optimization process of the best developed QSAR model.
Table 3 Example of DCW calculation
According to the published methodology we classified the obtained SAKs as promoters of the corneal permeability increase or decrease.19–21,34–36 In Table 4 we enlist selected SAKs with their mechanistic interpretation while the complete list is given in Table S2 (ESI†). We present the analysis of molecular fragments’ contribution to corneal permeability in Fig. 2 for molecule atenolol. In the presented figure, the green color indicates groups that have positive influence, while the red color indicate groups that have negative influence on corneal permeability. As already stated each SAK contributes with its CW value. The CW numerical value is the measurement of its contribution to the studied activity.
Table 4 Mechanistic interpretation of selected SAKs
| Increase |
| 1……….. |
Presence of one or two rings in molecule |
| 2……….. |
| C……….. |
Carbon atom |
| N…C……. |
Primary amino group |
O…![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) ……. ……. |
Oxygen atom with double bond |
| O…C…C… |
Ethoxy group |
| Decrease |
| (……….. |
Branching in molecule as such, branching in molecule on either carbon or nitrogen atom |
| (…C…(… |
| N…(……. |
| O……….. |
Oxygen atom |
| c…O……. |
Phenyl group |
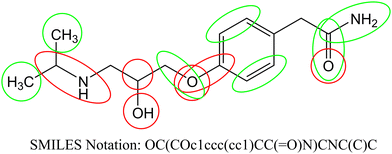 |
| | Fig. 2 Contribution of molecular fragments to corneal permeability (green – increase and red – decrease). | |
We observed different fragments in the same part of the molecule presented in Fig. 2. As exemplified in Fig. 2 carbon atoms have a positive influence, while branching has a negative influence. Also, all aromatic carbon atoms have a positive influence, while branching on the same atoms has a negative influence. Oxygen atoms (regardless of which group is present) have a negative effect, but carbonyl groups have a positive effect on the studied activity. For the above-stated reasons not only molecular fragments but also their CW values must be considered when predictions for corneal permeability are made.
4. Conclusion
The determination of the permeability coefficient is necessary to investigate corneal permeability, which has further application in drug development and design. We developed a very appealing QSAR model, with high predictability potential, based on Monte Carlo optimization. Furthermore, we identified molecular fragments that contribute both in a positive and negative manner to the studied activity. The presented QSAR models can be applied for easy, fast and accurate prediction of corneal permeability.
Data availability statement
Data is contained within the article and ESI.†
Conflicts of interest
The authors declare that there are no conflicts of interest in this study.
Acknowledgements
This work is supported by the Ministry of Education and Science, the Republic of Serbia and the Faculty of Medicine, University of Niš, Republic of Serbia (project no. 70). The authors would like to thank the Ministry of Education, Science and Technological Development of Republic of Serbia (grant no: 451-03-9/2021-14/200113) for financial support.
References
- S. Mishima, Invest. Ophthalmol. Visual Sci., 1981, 21, 504–541 CAS.
- C. Le Bourlais, L. Acar, H. Zia, P. A. Sado, T. Needham and R. Leverge, Prog. Retinal Eye Res., 1998, 17, 33–58 CrossRef CAS PubMed.
- N. M. Davies, Clin. Exp. Pharmacol. Physiol., 2000, 27, 558–562 CrossRef CAS.
- R. Suri, S. Beg and K. Kohli, J. Drug Delivery Sci. Technol., 2020, 55, 101389 CrossRef CAS.
- K. Järvinen, T. Järvinen and A. Urtti, Adv. Drug Delivery Rev., 1995, 16, 3–19 CrossRef.
- H. Sasaki, K. Yamamura, T. Mukai, K. Nishida, J. Nakamura, M. Nakashima and M. Ichikawa, Crit. Rev. Ther. Drug, 1999, 16, 85–146 CAS.
- R. T. Borchardt, Drug Dev. Ind. Pharm., 1990, 16, 2595–2612 CrossRef CAS.
- J. Liaw, Y. Rojanasakul and J. R. Robinson, Int. J. Pharm., 1992, 88, 111–124 CrossRef CAS.
- R. D. Schoenwald and H. S. Huang, J. Pharm. Sci., 1983, 72, 1266–1272 CrossRef CAS PubMed.
- R. L. Shih and V. H. L. Lee, J. Ocul. Pharmacol., 1990, 6, 329–336 CrossRef CAS.
- P. Agarwal and I. Rupenthal, Drug Delivery Transl. Res., 2016, 6, 634–647 CrossRef CAS PubMed.
- L. Ghemtio, H. Xhaard, A. Urtti and H. Kidron, Curr. Pharm. Des., 2016, 22, 6928–6934 CrossRef CAS PubMed.
- M. Balls, A. Bogni, S. Bremer, S. Casati, S. Coecke, C. Eskes, P. Prieto, E. Sabbioni, A. Worth, V. Zuang, M. Barratt, B. Blaauboer, P. Botham, R. Combes, J. Doehmer, J. Fentem, M. Liebsch and H. Spielmann, ATLA, Altern. Lab. Anim., 2002, 30, i–vi+1 Search PubMed.
- R. D. Schoenwald and R. L. Ward, J. Pharm. Sci., 1978, 67, 786–788 CrossRef CAS.
- G. M. Grass and J. R. Robinson, J. Pharm. Sci., 1988, 77, 3–14 CrossRef CAS.
- F. Yoshida and J. G. Topliss, J. Pharm. Sci., 1996, 85, 819–823 CrossRef CAS PubMed.
- X. C. Fu and W. Q. Liang, Int. J. Pharm., 2002, 232, 193–197 CrossRef CAS.
- M. Ghorbanzad‘e, M. H. Fatemi, M. Karimpoura and P. L. Anderssona, Talanta, 2011, 85, 2686–2694 CrossRef PubMed.
- M. A. Toropova, I. Raška Jr., A. A. Toropov and M. Raškova, Comb. Chem. High Throughput Screening, 2016, 19, 676–687 CrossRef CAS.
- A. P. Toropova and A. A. Toropov, Mini-Rev. Med. Chem., 2018, 18, 382–391 CrossRef CAS PubMed.
- A. M. Veselinović, J. B. Veselinović, J. V. Živković and G. M. Nikolić, Curr. Top. Med. Chem., 2015, 15, 1768–1779 CrossRef.
- P. K. Ojha and K. Roy, Chemom. Intell. Lab., 2011, 109, 146–161 CrossRef CAS.
- P. K. Ojha, I. Mitra, R. N. Das and K. Roy, Chemom. Intell. Lab., 2011, 107, 194–205 CrossRef CAS.
- P. P. Roy, J. T. Leonard and K. Roy, Chemom. Intell. Lab., 2008, 90, 31–42 CrossRef CAS.
- K. Roy, R. N. Das, P. Ambure and R. B. Aher, Chemom. Intell.
Lab., 2016, 152, 18–33 CrossRef CAS.
- L. I. Lin, Biometrics, 1989, 45, 255–268 CrossRef CAS.
- V. Stoičkov, D. Stojanović, I. Tasić, S. Šarić, D. Radenković, P. Babović, D. Sokolović and A. M. Veselinović, Struct. Chem., 2018, 29, 441–449 CrossRef.
- A. A. Toropov and A. P. Toropova, Mutat. Res., Genet. Toxicol. Environ., 2017, 819, 31–37 CrossRef CAS.
- A. M. Veselinović, A. Toropov, A. Toropova, D. Stanković-Dordević and J. B. Veselinović, New J. Chem., 2018, 42, 10976–10982 RSC.
- D. Gadaleta, G. F. Mangiatordi, M. Catto, A. Carotti and O. Nicolotti, IJQSPR, 2016, 1, 45–63 Search PubMed.
- P. Gramatica, QSAR Comb. Sci., 2007, 26, 694–701 CrossRef CAS.
- P. Gramatica and A. Sangion, J. Chem. Inf. Model., 2016, 56, 1127–1131 CrossRef CAS.
- C. Chen and J. Yang, Acta Pharmacol. Sin., 2006, 27, 193–204 CrossRef.
- S. Ahmadi, S. Lotfi and P. Kumar, Toxicol. Mech. Methods, 2022, 32, 302–312 CrossRef CAS PubMed.
- S. Ahmadi, S. Ketabi and M. Qomi, New J. Chem., 2022, 46, 8827–8837 RSC.
- S. Lotfi, S. Ahmadi and P. Kumar, RSC Adv., 2022, 12, 24988–24997 RSC.
|
| This journal is © The Royal Society of Chemistry and the Centre National de la Recherche Scientifique 2023 |
Click here to see how this site uses Cookies. View our privacy policy here.  *d
*d
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P) or the distribution coefficient (log
P) or the distribution coefficient (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D, for an ionizable compound) of the drug. However, some steroids could not be fit into the QSAR model developed for -blockers. Yoshida and Topliss developed a QSAR satisfying model that unified-blockers and steroids based on the difference between the octanol–water partition coefficient and the alkane–water partition coefficient (log
D, for an ionizable compound) of the drug. However, some steroids could not be fit into the QSAR model developed for -blockers. Yoshida and Topliss developed a QSAR satisfying model that unified-blockers and steroids based on the difference between the octanol–water partition coefficient and the alkane–water partition coefficient (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P) and the distribution coefficient (log
P) and the distribution coefficient (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D). The main drawback of this QSAR model is the complexity of log
D). The main drawback of this QSAR model is the complexity of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P values it requires. To overcome this problem, a QSAR model based on charge and solid parameters of compounds has been developed.17 Apart from “classic” QSAR models, membrane-interaction (MI)-QSAR analysis was applied to establish a QSAR model for measuring permeability coefficients. However, this method requires complex computational calculations to establish a satisfactory QSAR model. In light of the given facts, there is still a need to develop a reliable QSAR model that can be used to predict the corneal permeability coefficient. A Monte Carlo optimization method in which the studied activity is treated as a random event has emerged as a promising approach in QSAR modeling in recent years. This method is based on a conformation-independent approach with optimal descriptors based on topological molecular features and molecules in the Simplified Molecular Input Line Entry System (SMILES) notation.19–21 One of the primary advantages of the described method over more commonly used ones is its simplicity and efficiency. Also, this method can be used to determine molecular fragments (calculated as SMILES notation descriptors) that have an influence on the studied activity and that can be associated with the chemical structures of studied compounds. The main aim of this research is the development of a conformation-independent QSAR model based on the Monte Carlo optimization method for the corneal permeability of various organic compounds. Furthermore, one of the main aims of this research was to define SMILES notation descriptors associated with molecular fragments that have both positive and negative influences on corneal permeability.
P values it requires. To overcome this problem, a QSAR model based on charge and solid parameters of compounds has been developed.17 Apart from “classic” QSAR models, membrane-interaction (MI)-QSAR analysis was applied to establish a QSAR model for measuring permeability coefficients. However, this method requires complex computational calculations to establish a satisfactory QSAR model. In light of the given facts, there is still a need to develop a reliable QSAR model that can be used to predict the corneal permeability coefficient. A Monte Carlo optimization method in which the studied activity is treated as a random event has emerged as a promising approach in QSAR modeling in recent years. This method is based on a conformation-independent approach with optimal descriptors based on topological molecular features and molecules in the Simplified Molecular Input Line Entry System (SMILES) notation.19–21 One of the primary advantages of the described method over more commonly used ones is its simplicity and efficiency. Also, this method can be used to determine molecular fragments (calculated as SMILES notation descriptors) that have an influence on the studied activity and that can be associated with the chemical structures of studied compounds. The main aim of this research is the development of a conformation-independent QSAR model based on the Monte Carlo optimization method for the corneal permeability of various organic compounds. Furthermore, one of the main aims of this research was to define SMILES notation descriptors associated with molecular fragments that have both positive and negative influences on corneal permeability.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P. P (cm−1) is calculated in vitro using the equation P = (7C)/(tAC0). In this equation, C/t is the change in concentration in dpm mL−1 sample per unit time, and 7 is the volume of the sampling chamber in mL. Therefore, the quantity 7C/t is the steady-state flux in dpm h−1. A is the surface area of the cornea (taken to be 1.087 cm2), and C0 is the initial concentration of the diffusing drug. It should be noted that we used all experimental values published to-date of log
P. P (cm−1) is calculated in vitro using the equation P = (7C)/(tAC0). In this equation, C/t is the change in concentration in dpm mL−1 sample per unit time, and 7 is the volume of the sampling chamber in mL. Therefore, the quantity 7C/t is the steady-state flux in dpm h−1. A is the surface area of the cornea (taken to be 1.087 cm2), and C0 is the initial concentration of the diffusing drug. It should be noted that we used all experimental values published to-date of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P to cover the range of −6.17 to −3.82. The experimental and calculated corneal permeability coefficient values are presented in Table S1 (ESI†). After we finished constructing the appropriate database, we made three different random splits of the main molecular database into two sets–the training set, which included 50 compounds (75%), and the test set with 17 compounds (25%), and we checked the normality of the activity distribution according to the published method.22 To establish conformation-independent QSAR models, in this study, we applied software called CORAL (CORrelation and Logic, https://www.insilico.eu/coral) based on the Monte Carlo method and its algorithm, which treats the pertinent activity as a random event. We took into consideration two types of molecular descriptors based on the molecular graph and SMILES notation. Based on molecular graphs, invariants were defined as local graph invariants: Morgan extended connectivity indices of increasing order (EC0), path numbers of length 2 and 3 (p2, p3), valence shells of range 2 and 3 (s2, s3), and the code of nearest neighbors (NNCk). In recent years, Simplified Molecular Input-Line Entry System (SMILES) notation has become one of the most convenient representations, and especially used in chemoinformatics because SMILES notation is considered as a very convenient alternative to the molecular graph. This fact is very appealing for medicinal chemistry since correlating molecular fragments with molecular graph-based descriptors can be quite challenging. For QSAR modeling, SMILES notation can be used to define molecular optimal descriptors (DCW), where DCW can be calculated as a function of SMILES notation according to eqn (1).
P to cover the range of −6.17 to −3.82. The experimental and calculated corneal permeability coefficient values are presented in Table S1 (ESI†). After we finished constructing the appropriate database, we made three different random splits of the main molecular database into two sets–the training set, which included 50 compounds (75%), and the test set with 17 compounds (25%), and we checked the normality of the activity distribution according to the published method.22 To establish conformation-independent QSAR models, in this study, we applied software called CORAL (CORrelation and Logic, https://www.insilico.eu/coral) based on the Monte Carlo method and its algorithm, which treats the pertinent activity as a random event. We took into consideration two types of molecular descriptors based on the molecular graph and SMILES notation. Based on molecular graphs, invariants were defined as local graph invariants: Morgan extended connectivity indices of increasing order (EC0), path numbers of length 2 and 3 (p2, p3), valence shells of range 2 and 3 (s2, s3), and the code of nearest neighbors (NNCk). In recent years, Simplified Molecular Input-Line Entry System (SMILES) notation has become one of the most convenient representations, and especially used in chemoinformatics because SMILES notation is considered as a very convenient alternative to the molecular graph. This fact is very appealing for medicinal chemistry since correlating molecular fragments with molecular graph-based descriptors can be quite challenging. For QSAR modeling, SMILES notation can be used to define molecular optimal descriptors (DCW), where DCW can be calculated as a function of SMILES notation according to eqn (1).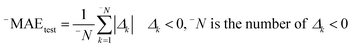
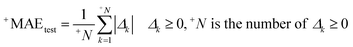
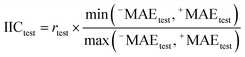
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P = −6.0994(±0.0095) + 0.0235(±0.0002) × DCW(3,21)
P = −6.0994(±0.0095) + 0.0235(±0.0002) × DCW(3,21)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P = −6.7242(±0.0100) + 0.0300(±0.0002) × DCW(1,20)
P = −6.7242(±0.0100) + 0.0300(±0.0002) × DCW(1,20)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P = −6.3163(±0.0121) + 0.0241(±0.0002) × DCW(2,17)
P = −6.3163(±0.0121) + 0.0241(±0.0002) × DCW(2,17)
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) …(…
…(…![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) …O…(…
…O…(…![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) …(…
…(…![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) …O…(…
…O…(…![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) …(…….
…(…….![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) …….
…….![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) …(…….
…(…….![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) ………..
………..![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) …….
…….![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) …
…![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) …(…
…(…![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) …O…(…
…O…(…![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) ………..
………..![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) …(…….
…(…….![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) …….
…….![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) ………..
………..![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif)
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif)
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif)
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif)
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif)
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif)
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif)
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif)
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif)
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif)
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif)
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif)
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif)
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif)
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif)
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) …….
…….