Crystal properties without crystallinity? Influence of surface hydroxylation on the structure and properties of small TiO₂ nanoparticles

Abstract

Titania (TiO₂) nanoparticles (NPs) are widely employed in applications that take advantage of their photochemical properties (e.g. pollutant degradation, photocatalysis). Here, we study the interrelation between crystallinity, surface hydroxylation and electronic structure in titania NPs with 1.4–2.3 nm diameters using all electron density functional theory-based calculations. We show how the distribution of local coordination environments of the atoms in thermally annealed quasi-spherical non-crystalline NPs converge to those in correspondingly sized faceted crystalline anatase NPs upon increasing hydroxylation. When highly hydroxylated, annealed NPs also possess electronic energy gaps with very similar energies and band edge orbital characters to those of the crystalline anatase NPs. We refer to the crystallite-mimicking non-crystalline annealed NPs as “crystalikes”. Small stable crystalike NPs could allow for photochemical applications of titania in the size range where crystalline anatase NPs tend to become thermodynamically unfavoured (<3–5 nm). Our work implies the anatase crystal structure may not be as essential as previously assumed for TiO₂ NP applications and generally suggests that crystalikes could be possible in other nanomaterials.

---

Introduction

Over five decades have passed since the breakthrough discovery that the anatase crystal polymorph of titania (TiO₂) is able to split water into hydrogen and oxygen under ultraviolet light.¹ Since then, the anatase TiO₂ + water system has become a benchmark for studying the fundamental physiochemical principles underlying a range of photocatalytic processes^2,3 with relevance to numerous practical applications⁴ (e.g. production of H₂ as green fuel,^5,6 polluted water remediation⁷). As an extended solid, titania is thermodynamically most stable in the rutile crystal phase, which shows a significantly lower photocatalytic activity than anatase. This polymorphic difference in performance has been discussed with respect to numerous possible factors but is often ascribed to the relative ease in which photo-generated excitons in anatase can reach the surface.⁸ Experiments on thin films show that up to a thickness of about 2.5 nm the photoactivity of anatase and rutile are comparable, but that further thickness increase (up to 15 nm) only improves the performance of the anatase films.⁹ This result demonstrates: (i) that the surface-accessible excitons in anatase can be formed further from the reactive surface than in rutile, and (ii) this difference only starts to be measurable for systems with surface-to-interior dimensions greater than 2.5 nm. In turn, this implies that the surface accessibility of excitons should not play a role in distinguishing the photoactivity of anatase and rutile nanoparticles (NPs) with diameters ≤5 nm. We note that titania NPs close to this size are often employed in photocatalytic experiments where the variation in observed photoactivity is thus most likely dependent on other factors. Herein, we study titania NPs within this size range (<2.5 nm diameters) and focus on two alternative properties of that are likely to significantly affect their photocatalytic performance: (1) surface hydroxyl (–OH) coverage and (2) crystallinity.

Nanoscale titania has a high surface to bulk ratio and possesses surface atoms with low coordination which readily react with water vapour under ambient conditions resulting in surface hydroxylation.¹⁰ Recently, combined computational and experimental efforts have been used to identify types and locations of the hydroxyl groups on anatase NPs.¹¹ Generally, the degree of surface hydroxylation can vary depending on TiO₂ system size and the environment (e.g. humidity, temperature).¹² For many years it has been known that the density of surface hydroxyls plays an important role in affecting the photoactivity of titania NPs.¹³ This effect is linked to the exciton-induced conversion of surface hydroxyls to hydroxyl radicals (˙OH) which subsequently play a role in photocatalytic oxidation reactions.^3,14,15 The observation that hydroxylated anatase NPs generate more mobile OH species than rutile NPs has even been proposed as a key factor to explain the relatively higher activity of anatase NPs for many photooxidative reactions.¹⁶ We note that surface hydroxyl groups can also facilitate the interaction of titania NPs with biosystems¹⁷ where the photocatalytic production of hydroxyl radicals may lead to bio-toxicity.¹⁸

Starting from the stable extended rutile crystal phase, decreasing the system size to the nanoscale decreases the relative thermodynamic stability of rutile with respect to anatase until a crossover is reached for titania NPs of approximately 14 nm diameter.¹⁹ The exact size at which the more photoactive anatase crystal phase becomes the most stable in NPs is largely determined by surface contributions to the free energy,²⁰ and can thus be significantly affected by adsorbed species.^21,22 Generally, it is known that strongly bound water (e.g. surface hydroxyl groups) plays an essential role in determining the stability of TiO₂ NPs.²³ In the bare case, the anatase crystal phase persists in NPs down to a diameter ∼2–3 nm, whereupon titania NPs are predicted to energetically favour non-crystalline structures due to the extended influence surface reconstruction from the high proportion of undercoordinated surface atoms.^24,25 In such small amorphous NPs for other materials, the effect of water strongly interacting with the surface has been shown to induce crystallinity by lowering the interfacial energy.²⁶ For TiO₂ NPs, water adsorption is more exothermic on rutile crystal surfaces than on anatase surfaces.²³ For small crystalline TiO₂ NPs it has been predicted that a high surface coverage of strongly bound water could make rutile NPs thermodynamically competitive with anatase NPs.²⁷

For experimental studies on NPs, it is difficult to disentangle the intimate interrelation between the type and degree of crystallinity, the nature of their surfaces and their resulting physicochemical properties. Here we employ accurate and detailed computational models to understand how these interacting factors play out for two families of TiO₂ NPs (i.e., crystalline faceted NPs and non-crystalline thermally annealed NPs). We focus on titania NPs with diameters ranging between 1.4–2.3 nm which is close to the non-crystalline/crystalline anatase crossover size for bare NPs.²⁴ The structure of NPs in this size regime is thus likely to be highly sensitive to surface adsorption. We consider both facetted crystalline anatase NPs, and thermally annealed NPs which can explore potentially lower energy non-crystalline structures. Simultaneously, we probe the effect of systematically increasing the degree of surface hydroxylation from the bare case to high –OH coverages for both types of NP. For the resulting two sets of NPs, we then compare the energetic, structural, and electronic properties. To enable a rigorous comparison, we employ the same NP size and degrees of hydroxylation for both NP types. The unique perspective provided by our controlled study allows us to discern numerous differences and similarities between crystalline and non-crystalline titania NPs with corresponding varying degrees of hydroxylation. For low and intermediate hydroxylation the two types of NP have distinct atomistic structures and electronic gaps which respond in different ways to varying hydroxylation. For higher degrees of hydroxylation, we find that the electronic energy gap of both types of NP converges to a very similar value. We also find that the distribution of local atomic coordination environments for both types of NPs become very similar at high hydroxyl coverages. However, this hydroxylation-induced electronic and local structural convergence does not appear to coincide with an increase in crystallinity in the thermally annealed NPs. Our results show that degree of surface hydroxylation can determine the electronic energy gap in nanotitania via induced modifications of local structural (i.e. coordination environments). At high –OH coverages, our results also suggest that this induced local structural effect leads to a convergence in the electronic structure, regardless of the degree of crystallinity of the NPs. This surprising result indicates that it may be possible to employ hydroxylation to induce electronic properties associated with crystalline anatase NPs in non-crystalline nanotitania.

Crystallite-mimicking non-crystalline NPs (or “crystalike” NPs) could have important implications for photochemical applications of small hydroxylated titania NPs. Synthesis of small crystalline anatase NPs is hampered by their low thermodynamic stability.²⁸ As crystallinity may no longer be a requirement to access the characteristic electronic structure of crystalline anatase NPs, small hydroxylated crystalike NPs may offer new opportunities for photochemical applications arising from: higher surface areas, higher energy excitons from quantum confinement (QC), lower radiationless photon transfer from quantization.²⁹ Overall, our study highlights the possibility of crystalike nanomaterials as a potential means to obtain the desirable properties of crystalline systems without the requirement of long-range crystalline order.

Models and computational methodology

Our study models the progressive and systematic hydroxylation of realistically structured model (TiO₂)₃₅ NPs. This size allows us to employ structurally stable crystalline reference NP models with a morphology and atomic ordering characteristic of larger anatase NPs, while also allowing for a computationally tractable study. We assume that hydroxylation occurs from the interaction of these initially anhydrous species with water molecules up to highly hydroxylated NPs with a (TiO₂)₃₅(H₂O)₂₅ chemical composition. We consider two types of NPs during this process: (i) crystalline anatase NPs with a faceted bipyramidal morphology, (ii) thermally annealed NPs with no fixed morphology (see Fig. 1).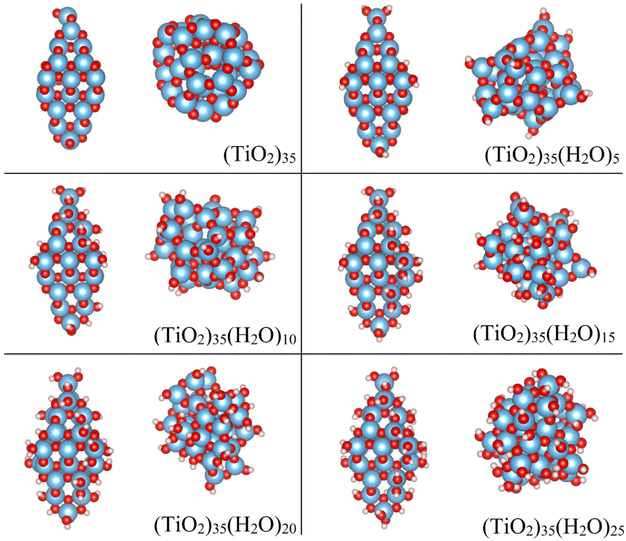

Fig. 1 DFT-optimized structures of the crystalline anatase (left) and annealed (right) (TiO₂)₃₅(H₂O)_m NPs for m = 0, 5, 10, 15, 20, 25. Atom colour key: Ti – blue, O – red, H – white.

As for all NPs, the properties of all our model NPs will be affected by the presence of undercoordinated atoms at their surfaces and by intrinsic QC. The effects of undercoordination are most pronounced for small anhydrous NPs which tend to energetically favour resconstructed non-crystalline structures.^24,25 Even for small faceted NPs cut from crystal structures, as used as model reference systems herein, surface relaxation can lead to a measurable decrease in the degree of atomic ordering.³⁰ However, hydroxylation tends to recover the bulk like coordination of surface atoms which reduces the tendency for structural reconstruction/relaxation. Thus, for increasing hydroxylation, the main size-related effect is likely to be a electronic energy gap increase (with respect to the bulk band gap) due to QC. As QC is primarily dependent on NP size, its effect is likely to result in an almost a constant electronic gap increase for all our considered NPs. We thus expect small, hydroxylated NPs to reflect most of the properties of larger hydroxylated NPs (e.g. bonding, structure, morphology) but with a somewhat larger electronic energy gap.

Crystalline anatase NP models

The initial anhydrous crystalline (TiO₂)₃₅ NP was derived from a top-down cut from the bulk anatase crystal structure following the Wulff construction, as described in previous works.^24,31,32 This procedure results in bipyramidal NPs which exhibit the thermodynamically stable (101) surface on all facets in line with experimental observations for larger anatase NPs.³³ From collaborative experimental and computational work, it is known that water molecules interact in a dissociative way with the surfaces of bipyramidal anatase NPs.¹¹ The resultant –H and –OH species are bound to O and Ti atoms, respectively where the energetic stability of hydroxylation depends on the coordination environment of the surface atoms (i.e. apical > equatorial > edge > facet).^11,27 Here we followed this energetically-determined order to progressively hydroxylate the initial faceted anatase (TiO₂)₃₅ NP and produce a set of crystalline anatase NPs with the composition (TiO₂)₃₅(H₂O)_m with m = 0–25 (see selected NPs in Fig. 1).

Initial crystalline NP structures were pre-optimised using the NanoTiO interatomic potential (IP) which has been shown to accurately describe the structures and relative energetics of nano-titania systems with high computational efficiency.^12,31,32 The final DFT-optimised anatase NPs have maximum diameters ranging between 2.1–2.3 nm depending on the degree of hydroxylation. These optimisations lead to local energy minima NP structures in which the internal crystalline structure of the NP is largely unperturbed. We note that these anatase NPs are used only as size-appropriate reference systems to assess how crystalline the more stable thermally annealed NPs (described below) are with respect to their calculated structural and electronic properties.

Thermally annealed NP models

To compare with the hydroxylation of an anhydrous faceted crystalline NP, we also started from a non-crystalline anhydrous (TiO₂)₃₅ NP. This initial NP was generated by using a molecular dynamics (MD) based method to thermally anneal the internal structure and morphology of a spherical cut (TiO₂)₃₅ NP from the anatase crystal structure (see details below). In previous work we have shown that thermally annealed anhydrous NPs of this size lose their internal crystalline atomic ordering and also adopt quasi-spherical morphologies.^31,32 The purpose of the thermal annealing is to search for low energy NP structures. Indeed, bare annealed (TiO₂)₃₅ NPs are significantly more energetically stable than bare faceted crystalline anatase NPs of the same size.^24,31 To an initially bare annealed NP structure, we first added a dissociated water molecule by binding one H and one –OH species to low coordinated surface O and Ti atoms, respectively. The interaction of NPs with water can strongly affect surface energies and overall NP stability^21,22 and even induce internal crystallisation.²⁶ As such, for every step of hydroxylation by a single water the NP was again thermally annealed to search for low energy (TiO₂)₃₅(H₂O)_m NP structures with m = 1–25, generally leading to significant changes in all atomic positions and the NP morphology. This implies that every NP in the series of progressively hydroxylated thermally annealed NPs is structurally independent of each other, unlike in the case of the crystalline anatase NPs. In other words, the structural framework of the annealed NPs changes as hydroxylation increases due to the thermal annealing process, whereas it is relatively unaltered in the (non-annealed) locally optimised crystalline faceted counterparts. The final DFT-optimised thermally annealed NPs have maximum diameters ranging between 1.4–1.8 nm depending on the degree of hydroxylation. Structures of selected annealed NPs are shown in Fig. 1.

MD-based thermal annealing

Global optimisation searches have been previously employed to search for the lowest energy structure (global minimum) for relatively small, hydroxylated NPs.^12,34,35 As NPs get larger and more chemically complex the corresponding energy landscapes tend to have a very rapidly increasing number of low energy minima. In such cases, the global minimum structure is likely to be one of many characteristic low energy minima inhabited by the system. For our chemically complex (TiO₂)₃₅(H₂O)_m systems with three atom types and up to 180 atoms we use a physically motivated simulated annealing (SA)³⁶ approach to guide us to characteristic low energy structures. Generally, SA involves controlled cycles of heating and cooling to guide the system into regions of energetic stability. Here, we use classical MD in the canonical NVT ensemble to control the temperature of our NPs. Specifically, we use MD runs starting at 300 K with an equilibration of 600 ps. The temperature is then increased gradually for 3500 ps with a step of 0.5 K ps⁻¹, thus reaching ∼1750 K. This latter temperature is then maintained for 800 ps, after which the system is then cooled down by 300 K over a period of 1250 ps and, again, maintained for 800 ps. This stepwise cooling process is repeated till the initial temperature of 300 K is reached again, in which the system remains for the final 8000 ps. Five (TiO₂)₃₅(H₂O)_m structures were selected from each MD-SA run for each NP composition (i.e. degree of hydroxylation) for further DFT-based refinement (see below). Fig. S1 in the ESI† illustrates the stepwise MD-SA procedure.

The interactions between atoms in the NPs during the MD-SA calculations were modelling using the NanoTiO IP.^12,31,32 We note that the internal structure of the NP (including the locations and interactions between –OH groups) and its overall morphology can freely adapt to the degree of hydroxylation during our MD-SA runs while exploring progressively lower energy states. The General Utility Lattice Program (GULP)³⁷ was used for all IP-based MD-SA calculations. Classical MD simulations have also been employed in other work for studying how the size of spherically cut crystalline anatase NPs affects their surface reactive response to water solvation.³⁸ In this latter study the anatase crystalline structure and spherical morphology of the studied NPs was relatively unperturbed and the degree of hydroxylation was determined by the solvation. In contrast, thermally annealing via a MD-SA approach allows us to search for low energy NP structures in a much more extensive and unbiased manner, helping us to avoid higher energy parts of the potential energy landscape. In this way, we can follow the interplay of NP crystallinity/morphology and hydroxylation by systematically comparing and varying both aspects.

DFT calculations

To obtain the electronic structure for all (TiO₂)₃₅(H₂O)_m compositions the selected low energy annealed NPs and all faceted NPs were further optimised using relativistic all-electron DFT-based calculations as implemented in the FHI-aims code.³⁹ Structural optimisations were performed using Perdew–Burke–Ernzerhof (PBE) exchange–correlation functional⁴⁰ and electronic energy gaps were calculated using a hybrid PBEx (12.5% Fock exchange) which has been tailored to well reproduce the electronic structure of various titania systems.^41,42 All calculations employed a light tier-1 numerical atom-centred orbital basis set, which has an accuracy comparable to a TZVP Gaussian-type orbital basis set for TiO₂.⁴³ The convergence thresholds for atomic forces and total energy during the relaxation of the structure of the NPs were set to 10⁻⁵ eV Å⁻¹ and 10⁻⁶ eV, respectively. Relativistic effects were included using the zero order regular approximation.⁴⁴

Results and discussion

Below, we report the calculated energetic, structural and electronic properties of our (TiO₂)₃₅(H₂O)_m NPs. In particular, we compare how these characteristics are affected by the degree of hydroxylation and by the underlying crystallinity of the respective NP.

NP energetics with respect to hydroxylation

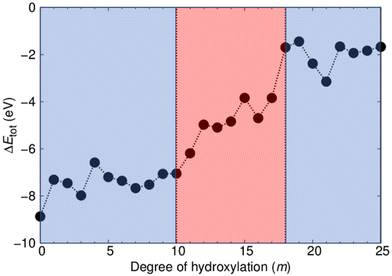
As our two types of NP have the same range of compositions, we can directly compare their respective energetic stabilities for all degrees of hydroxylation. In Fig. 2 we show how the difference in total energy between faceted and annealed (TiO₂)₃₅(H₂O)_m NPs (ΔE_tot(m) = E_tot-anneal(m) − E_tot-cryst(m)) varies with m. The plot shows that ΔE_tot is always negative, showing that annealed (TiO₂)₃₅(H₂O)_m NPs are more energetically stable than crystalline faceted NPs for the full range of hydroxylation considered. The largest magnitude of ΔE_tot occurs for the anhydrous case. This observation is in line with previous work, where we show that for small NP sizes anhydrous non-crystalline NPs are energetically more favourable than faceted crystalline NPs.^24,31 Upon increasing hydroxylation, the magnitude of ΔE_tot remains fairly constant and high (|ΔE_tot| = 7.5 ± 1.4 eV) for m ≤ 10. When increasing hydroxylation beyond this point in the range 11 ≤ m ≤ 17, the annealed NPs are progressively destabilized with respect to the faceted anatase NPs by approximately 5 eV. For the highest considered hydroxylations (17 < m ≤ 25) the magnitude of ΔE_tot is relatively low and again fairly constant (|ΔE_tot| = 2.0 ± 1.1 eV). We note that this energy difference translates to 0.06 ± 0.03 eV per TiO₂ unit, which is comparable to typical energy differences between crystalline bulk titania polymorphs.⁴⁵ The convergence of the energetic stability of faceted anatase NPs and thermally annealed NPs with increasing m suggests that hydroxylation could be inducing a structural homogenisation.

Fig. 2 Total energy difference (ΔE_tot) between the faceted and annealed (TiO₂)₃₅(H₂O)_m NPs with respect to degree of hydroxylation induced by the number of dissociatively adsorbed water molecules (m). The coloured regions indicate two regions of relatively constant energetic stability (blue) and a transitional region (light red).

It is important to note that this stability convergence is rather asymmetric with respect to crystallinity. The faceted crystalline NPs are used as a reference system in which the degree of crystallinity is relatively fixed. Increasing hydroxylation only acts to reduce the undercoordination of the surface atoms of these NPs, which, in a sense, only increases the crystallinity. In fact, for their size, our crystalline NPs can be taken as maximally crystalline reference NPs for their size.^24,31 In contrast, the annealed NPs are free to adopt a new energy-lowering structure and morphology for each degree of hydroxylation. As such any convergence of properties in the two NP types implies that the annealed NPs are becoming more like the reference crystalline NPs rather than the other way around.

To follow the induced energetic changes due to gradually increasing the degree of hydroxylation for each of our two types of (TiO₂)₃₅(H₂O)_m NP, we use two quantities:

(1) the total hydration energy:

E_hyd(m) = E_tot(m) − (E_tot(0) + m·E_H2O)

and

(2) the incremental hydration energy:

ΔE_hyd(m) = E_tot(m) − (E_tot(m − 1) + E_H2O)

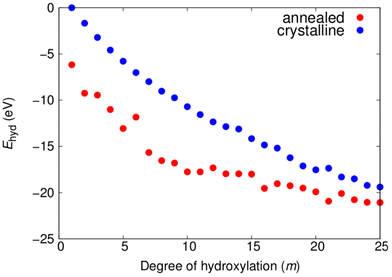
where E_tot(m) is the total energy of a NP with m dissociatively adsorbed water molecules and E_H2O is the total energy of a water molecule. As such, E_tot(0) is the total energy of a bare titania NP. In Fig. 3 the plot of E_hyd(m) versus m shows a tendency to become progressively more negative for both NP types with increasing hydroxylation. Here, we use a common reference E_tot(0) value for the bare crystalline NP in both curves. Overall, the E_hyd(m) plot shows that dissociative reaction with water molecules is energetically stabilising for all –OH coverages considered for both crystalline and annealed NPs. We note that the stabilising effect of water addition is slightly less effective for the annealed NPs than for the crystalline NPs for higher degrees of hydroxylation. This tendency is in line with the energetics of hydroxylation for smaller globally optimised titania nanoclusters.¹²

Fig. 3 Variation of E_hyd(m) with the number of water molecules (m) for increasingly hydroxylated crystalline and annealed (TiO₂)₃₅(H₂O)_m NPs. The E_tot(0) reference energy is taken to be that of the anhydrous crystalline NP in both cases leading to a corresponding energetic stabilisation downshift in the data for the annealed NPs.

In Fig. 4 we show the evolution of ΔE_hyd(m) with respect to the degree of hydroxylation for both NP types. Here, the E_tot(0) value in each case is taken to be that of the corresponding NP type. For the crystalline NPs with their structurally persistent anatase NP core, the resulting series of energies indicates how the dissociative reaction energy of adding each successive H₂O water molecule varies with –OH coverage. Here, we see that our chosen sequence of anatase NP hydration, depending on increasing surface coordination of adsorption sites (i.e. apical > equatorial > edge > facet), results in nearly every individual H₂O addition reaction being exothermic. Only for m = 21 do we see a small endothermic adsorption energy for incremental hydroxylation. This is likely to be simply due to the specific adsorption sequence chosen, of which there are a huge number, and does not imply that there is anything unusual for this degree of hydroxylation. Overall, the magnitude of ΔE_hyd(m) is highest for the lowest hydroxylation (approx. −2.0 eV) and then steadily decreases until about m = 14. This reflects the progressive adsorption of surface sites with increasing coordination. For the highest hydroxylation, ΔE_hyd(m) fluctuates around a value of about −0.5 eV.

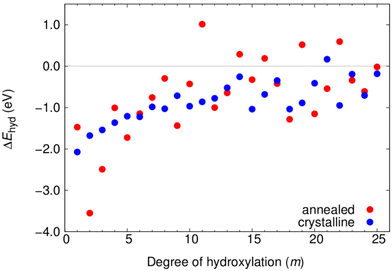Fig. 4 Variation of ΔE_hyd(m) with the number of water molecules (m) for increasingly hydroxylated crystalline (blue) and annealed (red) (TiO₂)₃₅(H₂O)_m NPs.

For the annealed NPs, ΔE_hyd(m) is not open to such a simple interpretation (i.e. sequential H₂O adsorption reaction energy) as for the crystalline anatase NPs. For each degree of hydroxylation, each annealed NP is produced from a new MD-based stochastic search and all such NPs are thus structurally independent from each other. Going from m to m + 1, for example, typically involves a change in the both underlying (TiO₂)₃₅ NP structure and the locations of the m –OH groups. In general, the trend of ΔE_hyd(m) for the annealed NPs with increasing m, is quite similar to that for the anatase NP, but with significantly larger fluctuations. These large changes in ΔE_hyd(m) for small changes in m reflects the corresponding larger structural changes for the annealed NPs. The positive values of ΔE_hyd(m) for some values of m could indicate the difficulty of finding low energy NPs for these degrees of hydroxylation using our MD-SA approach. We note that these positive incremental changes do not affect the fact that the corresponding degrees of hydroxylation are energetically stabilising overall, as shown in Fig. 3. Such behaviour could indicate that energetically costly changes in NP structure are necessary to dissociatively adsorb water in the most energetically favourable way with increasing hydroxylation. Below we analyse the change in NP structure with increasing hydroxylation.

Structure of hydroxylated (TiO₂)₃₅ NPs

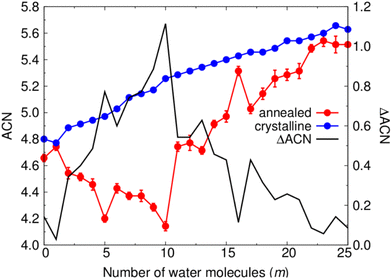
To compare the local structure of each type of NP throughout the considered hydroxylation range we follow the change in the local bonding coordination of Ti atoms. To do so we count the number of O atoms around each Ti centre in each NP within a maximum Ti–O cut-off distance of 2.4 Å. Summing the coordination values of each Ti centre within a given NP and then dividing by the total number of Ti centres gives the average coordination number (ACN). Fig. 5 shows the variation in the ACN for crystalline anatase NPs and thermally annealed NPs with respect to hydroxylation, and the respective difference in ACN between both NP types (ΔACN). We note that the ACN values for the annealed NPs for each degree of hydroxylation are averaged from values obtained for the five low energy NPs from the respective thermal annealing run.

Fig. 5 Average coordination number (ACN) of Ti centres for the annealed and crystalline anatase NPs with respect to hydroxylation (left hand axis). The “error bars” for the annealed NP data indicate the maximum and minimum ACN values found in a sample of five low energy NPs from each respective annealing run. The black line follows the difference between the ACN values of the annealed and crystalline NPs (ΔACN) with respect to m (right hand axis).

For the crystalline anatase NPs, the ACN tends to steadily increase with increasing hydroxylation from 4.8 for the bare case to 5.6 for the highest hydroxylation considered. This increasing tendency is due to new Ti–OH bonds being formed the surface. The small observed fluctuations in the ACN are the result of surface relaxation upon hydroxylation which can sometimes lead to a localised reduction in Ti coordination. In the case of the annealed NPs, the bare NP has a relatively lower ACN value of 4.65. Unlike for the anatase NPs, increasing the degree of hydroxylation of the annealed NPs from this point initially tends decrease the ACN until a minimum of about 4.15 is reached at m = 10. Afterwards, for m ≥ 11, the ACN tends to increase and approach the ACN of the respective hydroxylated anatase NPs. This rate of ACN increase with respect to m is fastest in the range 11 ≤ m ≤ 17. This range of hydroxylation coincides with that in which rapid energetic destabilisation of the annealed NPs occurs with respect to the anatase crystalline NPs (see Fig. 2). In the range 17 < m ≤ 25, the ACN values are very similar for both annealed and crystalline NPs. This is also the hydroxylation regime for which the energetic stabilities of annealed and crystalline NPs are found to be most similar (see Fig. 2). The correspondence between the hydroxylation dependence of both ACN and ΔE_tot values suggests that annealed NPs become structurally more anatase-like with increasing hydroxylation.

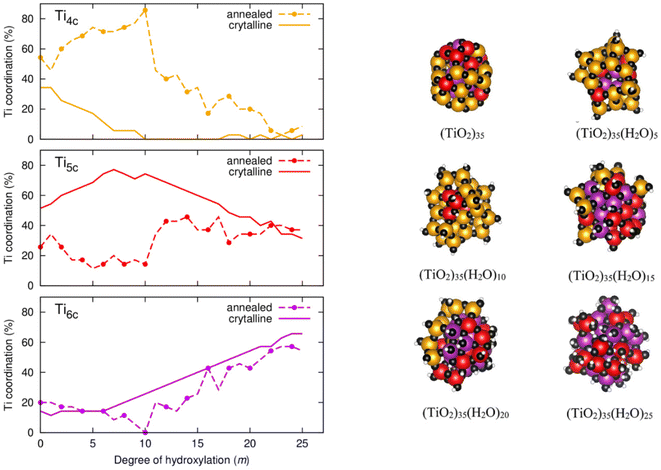
To better understand the m-dependent ACN trends and differences we follow a more detailed analysis whereby we breakdown the ACN values into contributing proportions of 4-, 5-, and 6-coordinated Ti atoms (denoted as Ti_4c, Ti_5c, and Ti_6c). Fig. 6 (left) displays the evolution of the proportion of Ti_4c, Ti_5c, and Ti_6c centres with respect to hydroxylation. Starting with the Ti_6c centres, we see that they follow a very similar m-dependence for both annealed and crystalline anatase NPs. In the hydroxylation range 0 ≤ m ≤ 6 for both NP types, Ti_6c centres make up 15–20% of the total number of Ti centres. In the anatase NP, for m > 6 the number of these centres increases at steady rate with further hydroxylation until they constitute ∼65% of the total number of Ti centres for m = 25. For this progressively OH-covered crystalline NP this two-stage m-dependence can be understood by: (i) the initial energetic preference to hydroxylate low coordinated Ti_4c centres for small m (reducing the number of Ti_4c centres and increasing the number of Ti_5c centres), and (ii) after the exhaustion of Ti_4c centres, the gradual hydroxylation of Ti_5c centres for larger m producing Ti_6c centres. This explanation is corroborated by following the corresponding tendencies in the proportions of Ti_4c, Ti_5c and Ti_6c centres in the anatase NPs in Fig. 6 (left).

Fig. 6 Left: Evolution of the distribution of 4-, 5- and 6-fold local atomic coordination environments of Ti centres (Ti_4c, Ti_5c, and Ti_6c) with respect to the degree of hydroxylation (m) of both crystalline and annealed (TiO₂)₃₅ NPs. Right: location of Ti_4c, Ti_5c, and Ti_6c centres depicted by dark yellow, red, and purple spheres respectively in the thermally annealed NPs for m = 0, 5, 10, 15, 20 and 25.

For the annealed NPs, after initially possessing a similarly constant proportion of Ti_6c centres as for the anatase NPs for low hydroxylation, this value then drops to 0% going from m = 7–10. Thereafter, for m = 11–25, the proportion of Ti_6c centres progressively increases in a very similar way as for the crystalline anatase NPs towards a maximum of ∼60% at the highest hydroxylation. In this later range of hydroxylation the proportions of Ti_4c and Ti_5c centres in the annealed NPs also gradually approach those found in the anatase NPs in line with the corresponding change in ACN. Although we see a convergence for the ACN and its individual components for both types of NP we find no evidence of significant increases in crystallinity or faceting in the annealed NPs with increasing hydroxylation. In the case of highest hydroxylation, we extract the pair distribution function for Ti–O distances for each type of NP (see Fig. S2 in the ESI†) to provide an approximate measure of crystallinity.^24,25 This shows that the local Ti–O distance distribution is similarly sharp in both types of highly hydroxylated NPs, but for larger Ti–O distances the distributions are broader for the annealed NPs, indicating less longer range order (i.e. lower crystallinity). Generally, the highly hydroxylated annealed NPs tend to structurally mimic the highly hydroxylated anatase NPs on a local scale, but both have distinct overall NP structures and morphologies.

For the initial stages of hydroxylation from m = 0–10, where we see distinct tendencies in the ACN for both NP types, the proportions of Ti_4c and Ti_5c centres are correspondingly also very different. Overall, the proportion of Ti_5c centres in the annealed NPs is fairly constant and relatively low (approx. 10–30%) in this initial range of hydroxylation low. This is in contrast to the corresponding high and increasing proportions of Ti_5c centres in the crystalline anatase NPs. In the same hydroxylation range, we also find a high (approx. 50–90%) and increasing proportion of Ti_4c centres. Considering that the m = 0–10 range is where the annealed NPs are most energetically stable with respect to the anatase NPs, it thus appears that Ti_4c centres are helping to stabilise the annealed NPs for low/moderate hydroxylation. NPs have a high proportion of surface atoms and, as noted above, their energetic stability is highly sensitive to changes in surface stress.^20,21 Ti_4c centres have a tetrahedral structure which tend to lead to more open lower density networks with respect to the octahedral Ti_6c centres. We suggest that the density-lowering effect of Ti_4c centres helps to lower the surface stress in the annealed NPs. Inspecting the structure of a low energy annealed (TiO₂)₃₅(H₂O)₁₀ NP, we indeed see that the Ti_4c centres are associated with surface hydroxyls (i.e. ≡Ti–OH), see Fig. 6 (right). With the increasing number of oxygen atoms in the system due to hydroxylation it appears that the stabilising effect of these surface Ti_4c species reaches a limit at around m = 10. After this degree of hydroxylation, we see is a sudden significant decrease in the proportion of surface Ti_4c centres (see Fig. 6). We note that Ti_4c species have also been found near the surface of relatively large anhydrous TiO₂ NPs after simulated annealing. Here, the centres were not hydroxylated, and their main observed effect was to reduce the band gap of the NP.³¹ Below, we examine the effect of hydroxylation and the associated structural changes on the electronic structure of both annealed and crystalline NPs.

Electronic structure of hydroxylated (TiO₂)₃₅ NPs

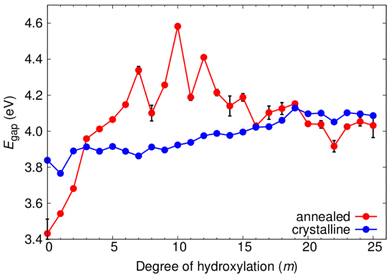
In Fig. 7 we show the evolution of the electronic energy gap (E_gap), as estimated by the difference in the highest occupied and lowest unoccupied orbital energies, of both annealed and crystalline NPs with respect to hydroxylation. A hybrid density functional that contains 12.5% Fock exchange and which accurately reproduces the band gap of stoichiometric and reduced anatase and rutile bulk crystals⁴¹ was used to calculate the electronic structure. We note that the E_gap in both systems is higher than that for the bulk anatase phase due to the effect of QC in our small NPs.^43,46 From previous work on smaller titania nanoclusters, it is expected that increasing hydroxylation would tend to only slightly and gradually increase the magnitude of E_gap.¹² This tendency is in line with the overall effect of hydroxylation to stabilise low coordinated surface sites. For the crystalline anatase NPs we indeed see this type of behaviour, whereby increasing hydroxylation from the anhydrous state to the highest hydroxylation tends to progressively raise the E_gap value by ∼0.25 eV from 3.84 eV to 4.11 eV. However, for the annealed NPs we observe a stark contrast in the hydroxylation dependent E_gap behaviour. Initially, the anhydrous annealed NP has a E_gap of 3.45 eV, which is ∼0.4 eV lower than that of the corresponding anatase NP. With increasing hydroxylation up to m = 10 the value of E_gap rises by 1 eV to a maximum of 4.6 eV. Thereafter, for further increases in m, the value of E_gap falls towards that of the highly hydroxylated anatase NPs. We note that in the region 7 ≤ m ≤ 13 the E_gap value exhibits its largest fluctuations (4.3 ± 0.3 eV). This hydroxylation range overlaps with that at which the ACN and local coordination environments (see Fig. 5 and 6) show their largest change with respect to hydroxylation. These competing structural variations in the annealed NPs in this transitional hydroxylation range will significantly affect the electronic structure and are thus the likely reason for the observed larger fluctuations in E_gap. In contrast, for the highest degrees of hydroxylation considered the E_gap values for the crystalline anatase and annealed NPs are relatively stable and almost identical. In this converged E_gap value range for m ≥ 19 the electronically perturbing effects of low-coordinated surface sites is minimal and we can assume that the E_gap value of ∼4.05 eV (i.e. +0.85 eV with respect to the bulk anatase band gap) is mainly influenced by QC.

Fig. 7 Evolution of E_gap with respect to degree of hydroxylation for crystalline and annealed (TiO₂)₃₅(H₂O)_m NPs. For the annealed NPs, the data points indicate a mean value of E_gap from considering five low energy NPs. The “error bars” indicate the range of E_gap values for five low energy NPs from the respective MD-SA run.

To help understand the overall E_gap trends we have extracted the projected density of states (pDOS) with respect to the coordination of the atoms making up the NPs (see Fig. 8 and 9). Generally, in bulk titania the valence band maximum (VBM) is dominated by contributions from O centres, while the conduction band minimum (CBM) is dominated by contributions from Ti centres. Although reference to electronic bands is only strictly valid for extended systems, for convenience we also use VBM and CBM when describing the electronic structure of our NPs below. For anhydrous NPs and very low degrees of hydroxylation the relatively smaller E_gap values found for the annealed NPs is due to surface 2-coordinated oxygen (O_2c) 2p contributions to the VBM, as found in previous work on anhydrous NPs.³⁰ For increasing hydroxylation of the surface of the annealed NPs this O_2c-induced E_gap decrease is rapidly quenched.

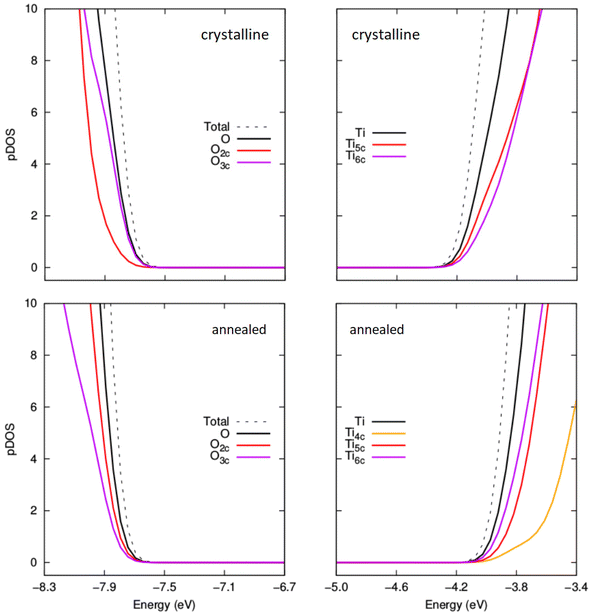Fig. 8 Comparison of projected density of states (pDOS) for the VBM and CBM for crystalline anatase NPs (upper) and thermally annealed NPs (lower) with composition (TiO₂)₃₅(H₂O)₁₁.

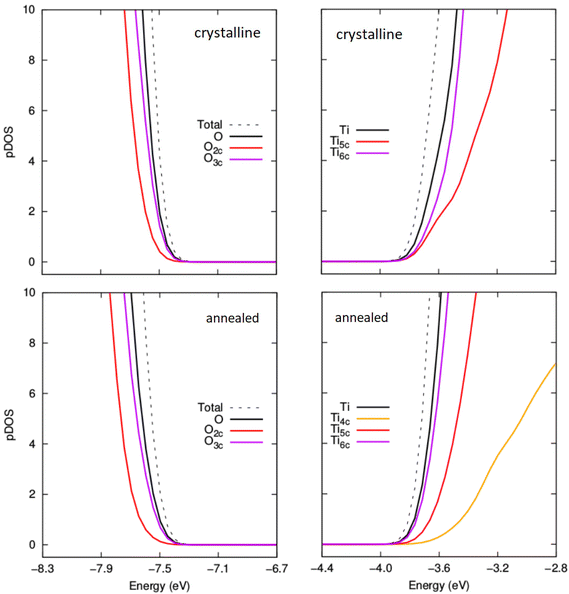Fig. 9 Comparison of projected density of states (pDOS) for the VBM and CBM for crystalline anatase NPs (upper) and thermally annealed NPs (lower) with composition (TiO₂)₃₅(H₂O)₂₀.

In Fig. 8, we compare the pDOS for both types of NP for m = 11, where the E_gap value for the annealed NP is larger than the corresponding anatase NP. Here we see that both NPs have a VBM with main contributions from O_2c and O_3c centres and a CBM made up from contributions from Ti_5c and Ti_6c centres. The Ti_4c centres in the annealed NP contribute to the pDOS only at higher energies. We note that the anatase NP for m = 11 has no Ti_4c centres. The VBM in both these cases is found at a similar energy. However, the CBM for the crystalline anatase NP is found at a lower energy than in the annealed NP indicating an electronic destabilisation of the Ti 3d states in its Ti_5c and Ti_6c centres. This destabilisation could be due to the relatively high proportion of Ti_4c centres which tend to disrupt higher density structures made from highly coordinated centres. The relative difference in the energy of the CBM seems to be the main contributing factor for the observed difference in the E_gap value for annealed and crystalline anatase NPs at this degree of hydroxylation. We note that this link between E_gap differences and the stability of Ti 3d states in Ti_5c/Ti_6c centres seems to be reflected in the difference in the proportion of Ti_6c centres in each type of NP (see Fig. S3 in the ESI†).

In Fig. 9 we show the pDOS for both types of NP for m = 20. Here, it seems that the unoccupied 3d states associated with the increasing number of Ti_5c and Ti_6c centres contributing to the CBM tend to become energetically similar in both types of NP with increasing m. In fact, we now see that both the character and energies of the VBM and CBM are very similar for both annealed and anatase NPs. For higher degrees of hydroxylation, the convergence in E_gap values between annealed and crystalline NPs is also found to follow a convergence of the VBM and CBM. This implies that annealed and crystalline NPs should become electronically very similar with higher degrees of hydroxylation, in spite of the evident differences in atomic structure.

In summary, the above results show that the gap/edge electronic structure of small hydroxylated anatase NPs can be accurately mimicked by NPs of the same chemical composition and the same distribution of local atomic coordination environments but with a different overall (non-crystalline) structure and morphology. In particular, such crystalike NPs could be electronically indistinguishable from anatase NPs. Considering that surface accessibility of photogenerated excitons is unlikely to vary significantly in small NPs (i.e. ≤5 nm diameter),⁹ it would be interesting to examine photoactivity of crystalike NPs with respect to that of small hydroxylated anatase NPs. Generally, smaller NPs offer potential photochemical performance improvements over larger NPs due to their higher surface areas, higher energy photo-generated carriers due to QC and lower radiationless photon transfer due to increased quantization of electronic levels.²⁹ However, the anatase-like electronic structure of small crystalike NPs does not necessarily imply a corresponding anatase-like photoactivity as there could be differences in the nature of the photoactivated reactions at crystalike and anatase NP surfaces. Nevertheless, our results suggest that, as far as small unsupported and undoped titania NPs are concerned, the anatase crystal structure may not be as important as previously thought for achieving an electronic structure that could be favourable for NP-based photocatalytic applications. The highly sensitive response of such crystalike NPs to hydroxylation could also offer more tunability with respect to crystalline titania NP applications.

Conclusions

We have employed DFT-based calculations to analyse and compare the effect of hydroxylation by dissociative water addition on the on the properties of thermally annealed and crystalline (TiO₂)₃₅ NPs with diameters between 1.4–2.3 nm. In both cases the hydroxylation is energetically favourable for (TiO₂)₃₅(H₂O)_m NPs up to the considered upper limit with m = 25. For lower values of m in this range, the thermally annealed NPs are significantly more energetically stable than the crystalline NPs. With increasing m there is a rapid convergence in the stability of both types of NP resulting in annealed and crystalline NPs having comparable energetic stabilities for high hydroxylation. This hydroxylation-induced convergence in stability in not reflected in a convergence of NP morphology or crystallinity. However, for high hydroxylation both quasi-spherical non-crystalline NPs and faceted crystalline anatase NPs are found to converge with respect to their local structure. Specifically, the distributions of local atom coordination environments are found to become almost the same in both types of NP for high hydroxylation. This local structural similarity for high hydroxylation is found to also be accompanied with a convergence in the electronic properties of both NP types. Here, we find that both the magnitude of the electronic energy gap and the energies and orbital character of the band edges become almost the same in both types of highly hydroxylated NP.

Overall, we show that, for small NPs, one can use hydroxylation to induce the characteristic electronic structure of faceted crystalline NPs in compositionally equivalent but non-faceted non-crystalline NPs (i.e. crystalike NPs). The key to this effect is the surface-induced change in the distribution of local atom coordination environments throughout the annealed hydroxylated crystalike NP structures. Our study thus suggests that the anatase crystal structure may not be as essential as previously assumed for obtaining an electronic structure that could be favourable for NP-based photocatalytic applications. In turn, this opens the possibility to employ highly tunable crystalike NPs in a size range where obtaining anatase crystalline samples becomes thermodynamically disfavoured (i.e. diameters <3–5 nm). As the realisation of crystalike NPs in titania appears to rely only on mimicking the local coordination environment distribution of a correspondingly crystalline NP, we speculate that it may also be possible to form crystalike NPs of other materials.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We acknowledge financial support from MCIN/AEI/10.13039/501100011033 through projects PID2020-115293RJ-I00, PID2021-126076NB-I00, TED2021-129506B-C22, TED2021-132550B-C21 and the María de Maeztu CEX2021-001202-M projects; the fund from FEDER Una manera de hacer Europa also supports the former project. The reported research is involved in the COST Action CA18234 (CompNanoEnergy), supported by European Cooperation in Science and Technology (COST). S. T. B. acknowledge support from grant 2021SGR00354 funded by the Generalitat de Catalunya. M. R.-P. acknowledges the Ministerio de Ciencia e Innovación for a Formación Personal Investigador (FPI) fellowship (PRE2019-087627). We also acknowledge the Red Espanola de Supercomputación (RES) for the provision of supercomputing time.

References

1. A. Fujishima and K. Honda, Nature, 1972, 238, 37–38.
2. J. Schneider, M. Matsuoka, M. Takeuchi, J. Zhang, Y. Horiuchi, M. Anpo and D. W. Bahnemann, Chem. Rev., 2014, 114, 9919–9986.
3. A. Fujishima, X. Zhang and D. A. Tryk, Surf. Sci. Rep., 2008, 63, 515–582.
4. X. Chen and S. S. Mao, Chem. Rev., 2007, 107, 2891–2959.
5. A. Kudo and Y. Miseki, Chem. Soc. Rev., 2009, 38, 253–278.
6. H. Idriss, Curr. Opin. Chem. Eng., 2020, 29, 74–82.
7. J. Ryu and W. Choi, Environ. Sci. Technol., 2008, 42, 294–300.
8. B. Samanta, Á. Morales-García, F. Illas, N. Goga, J. A. Anta, S. Calero, A. Bieberle-Hütter, F. Libisch, A. B. Muñoz-García, M. Pavone and M. C. Toroker, Chem. Soc. Rev., 2022, 51, 3794–3818.
9. T. Luttrell, S. Halpegamage, J. Tao, A. Kramer, E. Sutter and M. Batzill, Sci. Rep., 2014, 4, 4043.
10. C. Deiana, E. Fois, S. Coluccia and G. Martra, J. Phys. Chem., 2010, 114, 21531–21538.
11. L. Mino, Á. Morales-García, S. T. Bromley and F. Illas, Nanoscale, 2021, 13, 6577–6585.
12. A. Cuko, A. M. Escatllar, M. Calatayud and S. T. Bromley, Nanoscale, 2018, 10, 21518–21532.
13. K. Kobayakawa, Y. Nakazawa, M. Ikeda, Y. Sato and A. Fujishima, Ber. Bilnsenges. Phys. Chern., 1990, 94, 1439–1443.
14. A. Di Paola, M. Bellardita, L. Palmisanoa, Z. Barbierikovác and V. Brezovác, J. Photochem. Photobiol., A, 2014, 273, 59–67.
15. J. Wang, X. Liu, R. Li, P. Qiao, L. Xiao and J. Fan, Catal. Commun., 2012, 19, 96–99.
16. W. Kim, T. Tachikawa, G.-H. Moon, T. Majima and W. Choi, Angew. Chem., Int. Ed., 2014, 53, 14036–14041.
17. M. J. Limo, A. Sola-Rababa, E. Boix, V. Thota, Z. C. Westcott, V. Puddu and C. C. Perry, Chem. Rev., 2018, 118, 11118–11193.
18. Y. Tanga, R. Caia, D. Caob, X. Konga and Y. Luc, Toxicology, 2018, 406–407, 1–8.
19. H. Zhang and J. F. Banfield, Chem. Rev., 2014, 114, 9613–9644.
20. H. Zhang and J. F. Banfield, J. Mater. Chem., 1998, 8, 2073–2076.
21. A. S. Barnard and P. Zapol, Phys. Rev. B: Condens. Matter., 2004, 70, 235403.
22. M. P. Finnegan, H. Zhang and J. F. Banfield, J. Phys. Chem. C, 2007, 111(5), 1962–1968.
23. A. A. Levchenko, G. Li, J. Boerio-Goates, B. F. Woodfield and A. Navrotsky, Chem. Mater., 2006, 18, 6324–6332.
24. O. Lamiel-García, A. Cuko, M. Calatayud, F. Illas and S. T. Bromley, Nanoscale, 2017, 9, 1049–1058.
25. H. Zhang, B. Chen, J. F. Banfield and G. A. Waychunas, Phys. Rev. B: Condens. Matter, 2008, 78, 214106.
26. H. Zhang, B. Gilbert, F. Huang and J. F. Banfield, Nature, 2003, 424, 1025–1029.
27. D. R. Hummer, J. D. Kubicki, P. R. C. Kent and P. J. Heaney, J. Phys. Chem. C, 2013, 117, 26084–26090.
28. E. Scolan and C. Sanchez, Chem. Mater., 1998, 10, 3217–3223.
29. M. Anpo, T. Shima, S. Kodama and Y. Kubokawa, J. Phys. Chem., 1987, 91, 4305–4310.
30. L. Zamirri, A. Macia Escatller, J. Mariñoso Guiu, P. Ugliengo and S. T. Bromley, ACS Earth Space Chem., 2019, 3, 2323–2338.
31. Á. Morales, A. Macia-Escatllar, F. Illas and S. T. Bromley, Nanoscale, 2019, 11, 9032–9041.
32. A. Macia Escatllar, Á. Morales-García, F. Illas and S. T. Bromley, J. Chem. Phys., 2019, 150, 214305.
33. S. Pigeot-Rémy, F. Dufour, A. Herissan, V. Ruaux, F. Maugé, R. Hazime, C. Foronato, C. Guillard, C. Chaneac, O. Durupthy, C. Colbeau-Justin and S. Cassaignon, Appl. Catal., B, 2017, 203, 324–334.
34. K. E. Jelfs, E. Flikkema and S. T. Bromley, Phys. Chem. Chem. Phys., 2013, 15, 20438–20443.
35. A. Cuko, A. Macià, M. Calatayud and S. T. Bromley, Comput. Theor. Chem., 2017, 1102, 38–43.
36. S. Kirkpatrick, C. D. Gelatt and M. P. Vecchi, Science, 1983, 220, 671–680.
37. J. D. Gale and A. L. Rohl, Mol. Simul., 2003, 29, 291–341.
38. F. A. Soria and C. Di Valentin, Nanoscale, 2021, 13, 4151–4166.
39. V. Blum, R. Gehre, F. Hanke, P. Havu, V. Havu, X. Ren, K. Reuter and M. Scheffler, Comput. Phys. Commun., 2009, 180, 2175–2196.
40. J. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
41. K. C. Ko, O. Lamiel-García, J. Y. Lee and F. Illas, Phys. Chem. Chem. Phys., 2016, 18, 12357–12367.
42. Á. Morales-García, R. Valero and F. Illas, Phys. Chem. Chem. Phys., 2018, 20, 18907.
43. O. Lamiel-García, K. C. Ko, J. Y. Lee, S. T. Bromley and F. Illas, J. Chem. Theory Comput., 2017, 13, 1785–1793.
44. E. van Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1993, 99, 4597–4610.
45. T. Zhu and S.-P. Gao, J. Phys. Chem. C, 2014, 118(21), 11385.
46. K. C. Ko, S. T. Bromley, J. Y. Lee, F. Illas and J. Phys, Chem. Lett., 2017, 8, 5593–5598.

---

Footnote

† Electronic supplementary information (ESI) available: MD-SA temperature profile, difference in proportion of Ti_6c centres and E_gap for crystalline and annealed NPs, comparison of the pair distribution function for Ti–O distances in highly hydroxylated crystalline and annealed NPs. See DOI: https://doi.org/10.1039/d3nr00141e

---