Highly anisotropic and ultra-diffusive vacancies in α-antimonene

Abstract

α-Antimonene has recently been successfully fabricated in experiment; hence, it is timely to examine how various types of point defects in α-antimonene can affect its novel electronic properties. Herein, we present a comprehensive investigation of a total of nine possible types of point defects in α-antimonene via first-principles calculations. Particular attention is placed on the structural stability of the point defects and the effects of point defects on the electronic properties of α-antimonene. Compared with its structural analogs, such as phosphorene, graphene, and silicene, we find that most defects in α-antimonene can be more easily generated, and that among the nine types of point defects, the single vacancy SV-(5|9) is likely the most stable one while its presence can be orders of magnitude higher in concentration than that in phosphorene. Moreover, we find that the vacancy exhibits anisotropic and low diffusion barriers, of merely 0.10/0.30 eV in the zigzag/armchair direction. Notably, at room temperature, the migration of SV-(5|9) in the zigzag direction of α-antimonene is estimated to be three orders faster than that along the armchair direction, and also three orders faster than that of phosphorene in the same direction. Overall, the point defects in α-antimonene can significantly affect the electronic properties of the host two-dimensional (2D) semiconductor and thus the light absorption capability. The anisotropic, ultra-diffusive, and charge tunable single vacancies, along with the high oxidation resistance, render the α-antimonene sheet a unique 2D semiconductor (beyond the phosphorene) for developing vacancy-enabled nanoelectronics.

---

Introduction

Owing to their anisotropic structures and novel functional properties, group-V elemental nanomaterials have attracted intense interests.^1–6 In particular, phosphorene, a single-layer black phosphorous, possesses an intrinsically tunable direct bandgap (∼1.56 eV),⁷ high carrier mobility (1.0–2.6 × 10⁴ cm² V⁻¹ s⁻¹),⁸ flexible mechanical properties, and anisotropic electrical, optical, and thermal transport properties, thereby having potential for various applications, e.g., flexible nano-devices in nanoelectronics, optoelectronics, thermoelectrics, and photocatalysts, etc.^9–12 However, due to the poor chemical stability, phosphorene can be easily oxidized and degraded in open air.^13,14 Thus, coating protection of phosphorene should be required for its application in various devices. A structural analog of phosphorene with higher chemical stability would be highly desired. Recently, stable BP-like α-antimonene was successfully synthesized on different substrates, such as T_d-WTe₂, T_d-MoTe₂, SnSe, etc.^15–18Compared with phosphorene, the α-antimonene not only possesses similar anisotropic mechanical, electrical and transport properties, along with a strain-tunable band gap (0.2 eV) and high ZT values, but also exhibits a two orders higher carrier mobility (1.4 × 10⁶ cm² V⁻¹ s⁻¹) and a higher electrical conductivity, as well as excellent chemical stability in air.^19–23

Like bulk materials, intrinsic point defects can be also present in 2D materials. Hence, the defect-dependent structural, physical, and chemical properties can be exploited for various applications, e.g., electrocatalytic hydrogen evolution, gas sensors, spintronics, multiferroics, memristive devices, etc.^24–36 For 2D elemental materials (e.g., phosphorene, graphene, and silicene) with honeycomb-like structures, known point defects include the Stone–Wales (SW), single vacancy (SV), and double vacancy (DV) defects, which have been extensively investigated.^{24,25,37–40} Among them, the SW defect has been viewed as the most popular defect in 2D elemental sheets because it generally entails the lowest formation energy (E_f).⁴¹ In graphene and silicene, the DV can be much more easily generated than SV, whereas in phosphorene, the opposite trend prevails. Moreover, the concentration of all three types of point defects is much higher in phosphorene than in silicene and graphene, again due to the significantly lower vacancy formation energy (E_f) in the former. For example, E_f of SV is 1.63 eV (phosphorene)⁴¹ <3.77 eV (graphene)²⁴ <7.80 eV (silicene).²⁵

Note that the diffusion of SV in phosphorene is 16 orders of magnitude faster than that in graphene at room temperature due to the much lower diffusion barrier of E_b = 0.4 eV for phosphorene (vs. 1.39 eV for graphene). In addition, the diffusion barriers are strikingly adjustable (by ∼0.2 eV) through in-plane strain, allowing strain engineering of defect motion.²⁹ Indeed, owing to its highly mobile SV, phosphorene has been considered as a promising candidate for vacancy-enabled nanodevices, e.g., memristive devices, via strain engineering and defect manipulation.²⁹ For α-antimonene, its point defects have been indirectly measured in experiment once the defects can be clasped by adsorbates.¹⁵ However, the structural properties of various point defects in α-antimonene, their likelihood of occurrence, and their diffusivity at room temperature are still largely unexplored.⁴²

In this work, the structural properties and thermal stability of typical point defects in α-antimonene, as well as the influence of defects on the electronic structure and on the light absorption are systematically studied by using first-principles computation and ab initio molecular dynamics simulations. Compared with phosphorene, graphene, and silicene, we find that the same type of point defects can be more easily generated in α-antimonene. The point defects can be mostly distinguished through simulated scanning tunneling microscopy (STM) imaging. Notably, we find that the defects can have a marked influence on the electronic and optical properties of α-antimonene. Among the point defects, the SV-(5|9) defect is predicted to be the most stable and it has the lowest formation energy, hence the highest concentration. Furthermore, the diffusion of the SV-(5|9) defect appears to be anisotropic and ultra-mobile as the diffusion barrier of SV-(5|9) is merely 0.10–0.30 eV. The charge injection is an alternative means to enhance the controllability of the vacancies via an electric field and to develop vacancy-enabled electronics applications.

Results and discussion

Geometric structure of α-antimonene and stability of point defects

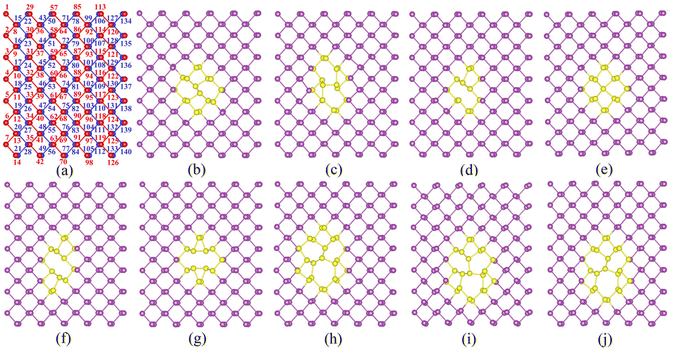
The structure of α-antimonene (5 × 7 × 1 supercell) is shown in Fig. 1a and Fig. S1 (ESI).† The lattice constants are a = 4.36 Å and b = 4.74 Å, in agreement with those reported in a previous study (a = 4.36 Å, b = 4.73 Å).⁴³ In Fig. 1a, all Sb atoms are marked with numbers, where the red and blue balls represent the Sb atoms in the upper and lower layers, respectively. Structures of nine types of defects in α-antimonene are illustrated in Fig. 1b–j, including two types of SW (denoted as SW-1 and SW-2), two types of SV (denoted as SV-(5|9) and SV-(55|66)), and five types of double-vacancy DV-(555|777) (denoted as DV-(5|8|5), DV-(4|10|4), DV-(555|777)-1, DV-(555|777)-2, and DV-(555|777)-3) defects after structure optimization. Compared with graphene and silicene, the low symmetry α-antimonene entails more varieties of point defects like phosphorene (as similar defective structures have been created in the previous study⁴¹). In Fig. 1b and c, SW-1 and SW-2 defects are generated via rotating Sb₍₆₇₎–Sb₍₇₄₎ and Sb₍₆₀₎–Sb₍₆₇₎ pairs by 90°, respectively. In Fig. 1c and d, both SV defects are generated by removing Sb₍₆₇₎ atoms but within different reconstructions; namely, inclined Sb₍₇₄₎ to generate the SV-(5|9) defect and central Sb₍₇₄₎ to generate the SV-(55|66) defect. Among the five DV defects in α-antimonene, as shown in Fig. 1f and g, the DV-(5|8|5) defect is generated by removing the Sb₍₆₁₎–Sb₍₆₇₎ pair, and the DV-(4|10|4) defect is produced by removing the Sb₍₆₇₎–Sb₍₇₄₎ pair. The three other DV structures all belong to DV-(555|777), which are more complicated. As shown in Fig. 1h–j, different from DV-(5|8|5) and DV-(4|10|4), DV-(555|777)-1, DV-(555|777)-2 and DV-(555|777)-3 defects are generated by removing two non-bonding Sb atoms, Sb₍₅₄₎ and Sb₍₆₀₎, or Sb₍₆₇₎ and Sb₍₆₈₎, or Sb₍₆₁₎ and Sb₍₇₅₎, respectively.

Fig. 1 The optimized geometry of α-antimonene without or with defects in 5 × 7 supercells: (a) perfect structure without defects, (b) SW-1, (c) SW-2, (d) SV-(5|9), (e) SV-(55|66), (f) DV-(5|8|5), (g) DV-(4|10|4), (h) DV-(555|777)-1, (i) DV-(555|777)-2, and (j) DV-(555|777)-3 defects. In panel a, all Sb atoms are labeled by numbers and the red and blue balls denote the Sb atoms in upper and lower layers of α-antimonene, respectively. In panels b–j, the violet and yellow balls denote unmoved and relocated Sb atoms, respectively.

To evaluate the stability of various defects in α-antimonene, the formation energy of defects is calculated according to the formula:

E_f = E_tot − N_Sb × E_Sb

where E_tot is the total energy of the supercell of the defective α-antimonene monolayer, E_Sb represents the energy of a single Sb atom in the perfect α-antimonene monolayer, and N_Sb is the number of antimonene atoms within the supercell of the defective α-antimonene monolayer. For perfect α-antimonene, E_f (α-antimonene) = 0 eV. The formation energies of different defects in α-antimonene are summarized in Table 1. Among all nine types of point defects, the SV-(5|9) defect has the lowest formation energy of 0.97 eV, indicating that it is likely the easiest to form in α-antimonene. This defect trend is different from that in phosphorene,⁴¹ graphene,²⁴ and silicene,²⁵ for which the SW defects have the lowest formation energy. Among all five DV defects, the DV-(4|10|4) defect has the lowest formation energy, whereas the three DV-(555|777) defects have the highest formation energies of 2.33–2.65 eV, indicating that they are harder to form. As shown in Table S1,† the cohesive energy of the intrinsic (perfect) α-antimonene is 2.62 eV per atom, much smaller than that of graphene (7.90 eV per atom),⁴⁴ and somewhat smaller than phosphorene (3.48 eV per atom)⁴¹ and silicene (3.96 eV per atom),²⁵ indicating that, overall, the point defects are much easier to form in α-antimonene, compared with phosphorene, graphene, and silicene.

Table 1 Calculated formation energy (E_f (eV)), and electronic band gap (E_g (eV)) of perfect and defective α-antimonene

	E f	E g
Perfect	0.00	0.20
SW-1	1.12	0.12
SW-2	1.61	0.16 (Indirect)
SV-(5|9)	0.97	Metal
SV-(55|66)	0.99	Metal
DV-(5|8|5)	1.16	0.11
DV-(4|10|4)	1.07	0.11
DV-(555|777)-1	2.33	0.11
DV-(555|777)-2	2.65	0.11
DV-(555|777)-3	2.34	0.07

---

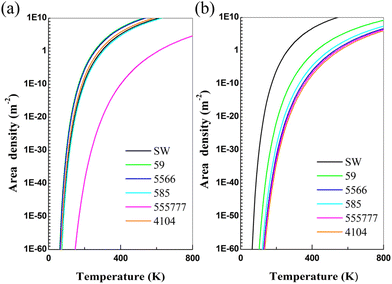
The thermal stability of defective α-antimonene is investigated by using ab initio molecular dynamics (AIMD) simulations with the temperature being controlled at 300 K, 400 K, and 800 K, respectively. As shown in Fig. S2–S4 (ESI),† at 300 K and 400 K, the SW-1 and SW-2 defects can spontaneously transform into the perfect α-antimonene structure. SV-(55|66) can transform into SV-(5|9) after 5 ps MD simulation, while the SV-(5|9) can be stable after 5 ps AIMD simulation. For DV defects, all defective structures except the DV-(555|777)-3 defect appear to be thermally stable after 5 ps simulation. At a much higher temperature of 800 K, the SW-1 defect still spontaneously transforms into the perfect α-antimonene. SV-(5|9) and DV-(5|8|5) can survive after 5 ps AIMD simulation at 800 K, while other defective structures undergo considerable reconstruction after 5 ps simulation. Thus, the SV-(5|9) defect is likely a stable configuration at room temperature, which may be detectable in experiment.

For the perfect α-antimonene and phosphorene, the areal densities of the number of the atoms are N_perfect(antimonene) = 1.94 × 10¹⁹ atom per m² and N_perfect(phosphorene) = 2.62 × 10¹⁹ atom per m², respectively.⁴¹ At a finite temperature, the areal density of the number of atoms of defects (N_defect) in a 2D material can be estimated via the Arrhenius equation:

N_defect = N_perfectexp(−E_f/k_BT)

where N_perfect is the areal density of atoms in the perfect 2D material, E_f is the defect formation energy, T is the temperature, and k_B is the Boltzmann constant. The temperature-dependent areal densities of the defects in α-antimonene and phosphorene are shown in Fig. 2. For phosphorene, the SW point defects exhibit a higher areal density than other defects (Fig. 2b). Except DV-(555|777), most point defects in α-antimonene have similar areal density, significantly higher than those in phosphorene, indicating that these defects should be more easily formed in α-antimonene than in phosphorene. For instance, at 300 K, the areal density of the SV-(5|9) defect in α-antimonene and phosphorene is 9.83 × 10² m⁻² and 1.27 × 10⁻⁸ m⁻², respectively, which differ by ten orders of magnitude. At 400 K, they differ by eight orders of magnitude. These results indicate that the SV-(5|9) defect in α-antimonene would be easier to be detected, compared with phosphorene. Combined with the corresponding results for graphene and silicene (see Fig. S5, ESI†), a general conclusion can be drawn that the areal density of the various defects in the four 2D materials is in the order of α-antimonene > phosphorene > silicene > graphene (see further areal density comparison in Table S2†).

Fig. 2 The areal density of various defects versus temperature for (a) α-antimonene and (b) phosphorene. The defects considered include SW, SV-(5|9), SV-(55|66), DV-(5|8|5), DV-(555|777) and DV-(4|10|4).

Diffusion barrier of SV in α-antimonene

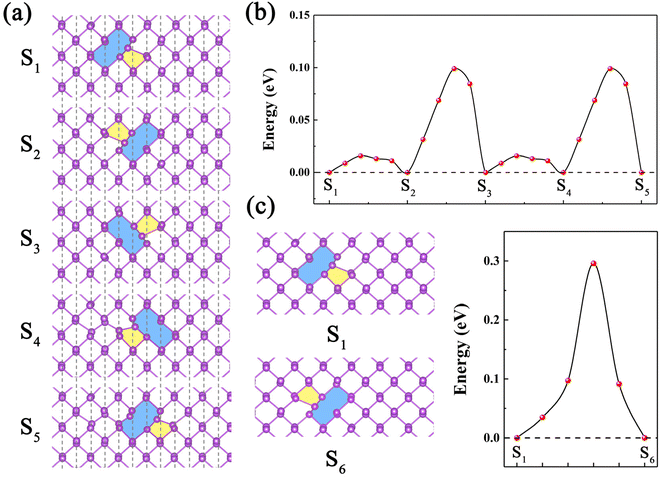
The defects can migrate or transform among one another at finite temperatures. Thus, it is important to investigate temperature-dependent diffusion behavior of the defects. Here, the diffusion behavior of the most stable SV-(5|9) defect is investigated. Due to the anisotropic structure of α-antimonene, two possible diffusion paths of SV-(5|9) are considered, including the intrachain diffusion path (along the zigzag direction) and the interchain diffusion path (along the armchair direction). The combination of the two paths allows an analysis of the diffusion behavior of SV in any direction within the sheet. For the intrachain diffusion of SV-(5|9) along the zigzag direction, the sequential steps (S1 → S2 → … → S5) and the corresponding energy landscapes are plotted in Fig. 3a and b. For the diffusion steps of S1 → S2 and S3 → S4, the energy barrier is 0.02 eV. For S2 → S3 and S4 → S5, the energy barrier of the rate-limiting step is only 0.10 eV. For the interchain diffusion of SV-(5|9), the energy barrier of the rate-limiting step (S1 → S6) is 0.30 eV, as shown in Fig. 3c. Thus, the diffusion of SV-(5|9) in α-antimonene is anisotropic, with a 0.10 eV energy barrier in the zigzag direction vs. a 0.30 eV energy barrier in the armchair direction (referred to as the 0.10/0.30 eV energy barrier in the zigzag/armchair direction).

Fig. 3 (a) Intermediates states (S1–S5) for the SV-(5|9) defect diffusion along the zigzag direction between neighboring equivalent sites. (b) Energetic profiles for the diffusion of the vacancy from S1 to S5. (c) Computed energy barrier for interchain vacancy diffusion from S1 to S6.

The diffusion energy barrier of SV-(5|9) for α-antimonene (0.10/0.30 eV energy barrier in the zigzag/armchair direction) is lower than that for phosphorene (0.3/0.4 eV energy barrier in the zigzag/armchair direction),²⁹ and much lower than that for graphene (1.39 eV), MoS₂ (V_S, 2.27 eV), and BN (V_B, 2.60 eV). The hopping rate can be calculated from the Arrhenius formula v = v_s exp(−E_b/k_BT), where v_s is the characteristic frequency, normally around 10¹³ Hz, k_B is the Boltzmann constant, and T is the temperature.²⁹ At room temperature, the migration of SV-(5|9) in α-antimonene and in the zigzag direction is estimated to be three orders faster than that in the armchair direction, and exhibits high anisotropy. In addition, the migration of SV-(5|9) in α-antimonene and in the zigzag direction is estimated to be three orders of magnitude faster than that of phosphorene in the same direction at room temperature (RT). Moreover, the migration of SV-(5|9) in α-antimonene and in the armchair direction is estimated to be one order of magnitude faster than that in phosphorene, and 18 orders of magnitude faster than that in graphene and in the same direction at RT. These results indicate that SV-(5|9) in α-antimonene is more feasible for vacancy migration, compared with phosphorene. Further AIMD simulation of SV-(5|9) at 300 K confirms that a number of hopping events occurred in the zigzag direction within 5 ps (see Movie S1 and Fig. S6, ESI†), consistent with the low diffusion energy barrier in the zigzag direction. Therefore, SV-(5|9) in α-antimonene exhibits highly anisotropic diffusivity and mobile motion.

In addition to strain engineering mentioned in the previous study,²⁹ finding more ways to manipulate the motion of point defects is very important for practical applications. The mobile defects with dipoles or with local charge are directionally migratable under an external electric field. For example, in memristive materials,^33,36 an electric field can be exploited as an effective manipulation method to control point defect behavior. According to our calculation under charge-neutral conditions, the total charge of Sb atoms around the SV-(5|9) defect is 0.07e per vacancy (involving 14 Sb atoms), where the highest charge of a neighboring Sb atom is 0.06e, as shown in Fig. S7 (ESI).† The vacancies with few charges may be detectable and drivable in an electric field for vacancy-enabled nanoelectronics applications. Moreover, the defect possesses an intrinsic electric dipole due to its specific shape so that the defect can be manipulated by an external electric field. Furthermore, charge injection can be used as a way to enhance the capability of electric field manipulation of the defects. For instance, under the condition of negative charge injection with a concentration of 1e per SV-(5|9), the extra charge tends to locate around the SV-(5|9) defect. As a result, the local charge can rise to 0.19e per vacancy, and the highest charge associated with a neighboring Sb atom can amount to 0.09e. On the other hand, for positive charge injection, the total charge around the defect is reduced to −0.01e per vacancy. Thus, the negative charge injection can be useful to strengthen the controllability of defect motion.

Influence of point defects on electronic and optical properties of α-antimonene

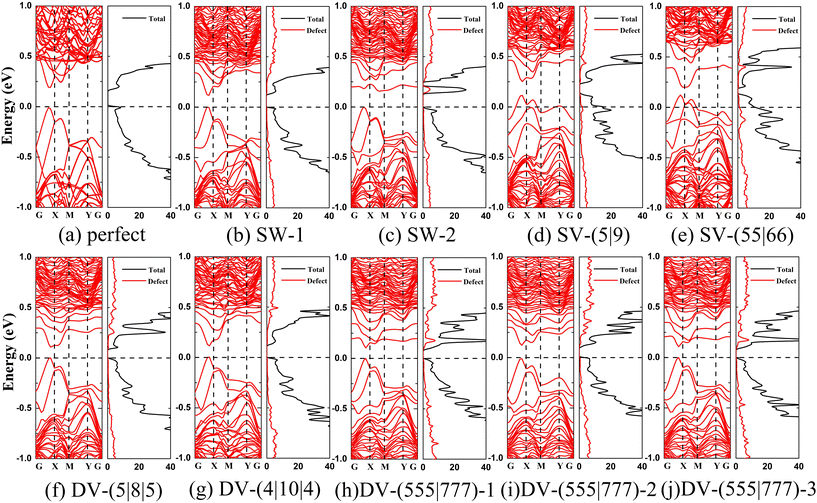
The computed electronic structures of α-antimonene with or without point defects are shown in Fig. 4a–j, respectively. As shown in Fig. 4a, the band structure of the perfect α-antimonene exhibits a direct band gap of 0.2 eV, consistent with the previous theoretical study⁴³ and the experimental value of 0.17 eV.¹⁷ Like the perfect α-antimonene, α-antimonene with the SW-1 defects is predicted to be the direct band gap semiconductor (Fig. 4b) with a reduced band gap of 0.12 eV (see Table 1). For the α-antimonene with SW-2 defects, the band gap becomes an indirect one with a value of 0.16 eV (Fig. 4c). Fig. 4d and e shows that the α-antimonene with SV-(5|9) or SV-(55|66) point defects exhibits metallic characters with hole doping due to the odd number of electrons in the system. These distinctly different electronic structures are helpful for applications, e.g., to distinguish different areas with a different density of vacancies.

Fig. 4 Computed electronic band structure and density of states of various α-antimonenes without or with defects: (a) perfect; α-antimonene with defects of (b) SW-1; (c) SW-2; (d) SV-(5|9); (e) SV-(55|66); (f) DV-(5|8|5); (g) DV-(4|10|4); (h) DV-(555|777)-1; (i) DV-(555|777)-2; and (j) DV-(555|777)-3.

As shown in Fig. 4f–j, the DV defects result in direct band gap semiconductors for α-antimonene, but the band gap is significantly reduced to ∼0.1 eV. Among them, α-antimonenes with DV-(5|8|5), DV-(4|10|4), DV-(555|777)-1, or DV-(555|777)-2 defects all have a band gap of ∼0.11 eV, while that with DV-(555|777)-3 defects has an even smaller band gap of 0.07 eV. Therefore, the presence of the point defects can markedly affect the electronic properties of α-antimonene.

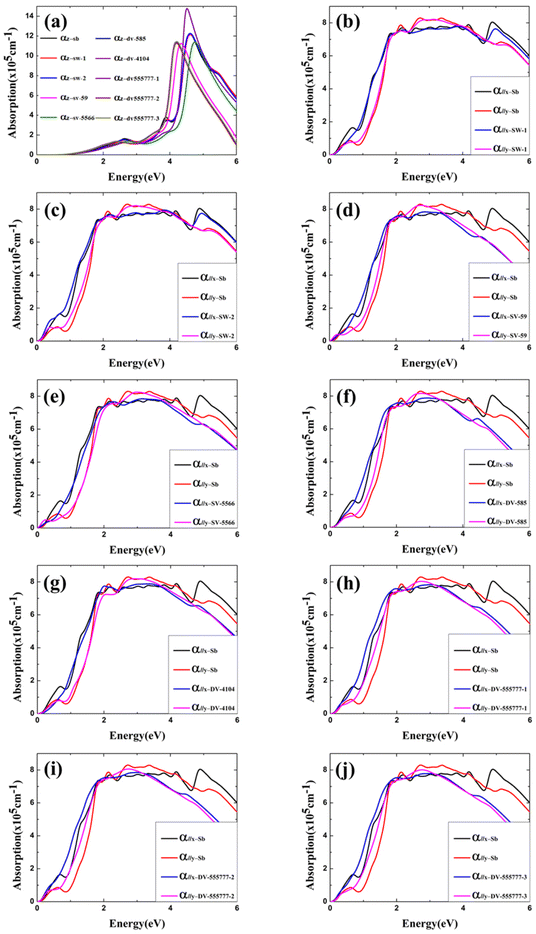
Optical properties of α-antimonene without and with point defects are also computed (see detailed results in ESI†). As shown in Fig. 5a, for incident light polarized along the z-axis (α//z), the optical absorption coefficient (α) of both the perfect α-antimonene and the defective α-antimonene exhibits strong light absorption in the ultraviolet region. As shown in Fig. 5b–j, for incident light polarized along the x-axis (α//x) and y-axis (α//y), both the perfect α-antimonene and the defective α-antimonene exhibit strong light absorption properties in the visible light region. Fig. 5b and c shows that the optical absorption of α-antimonene with SW-1 and SW-2 defects is similar to that of perfect α-antimonene. The absorption edge for α-antimonene with SV-(5|9) and SV-(55|66) appears red-shifted due to the semiconductor-to-metal transition (Fig. 5d and e). For DV defects, the absorption of ultraviolet light in the 4–6 eV range is generally weakened. However, α-antimonene with DV-(5|8|5) and DV-(555|777) class of defects results in stronger absorption of near-infrared light in the 0–2 eV range.

Fig. 5 (a) Computed optical absorption coefficient in the z direction (perpendicular to the plane) of the perfect α-antimonene; absorption coefficient in the x and y direction (parallel to the plane) of α-antimonene with defects: (b) SW-1; (c) SW-2; (d) SV-(5|9); (e) SV-(55|66); (f) DV-(5|8|5); (g) DV-(4|10|4); (h) DV-(555| 777)-1; (i) DV-(555|777)-2; and (j) DV-(555|777)-3.

Simulated STM images of α-antimonene point defects

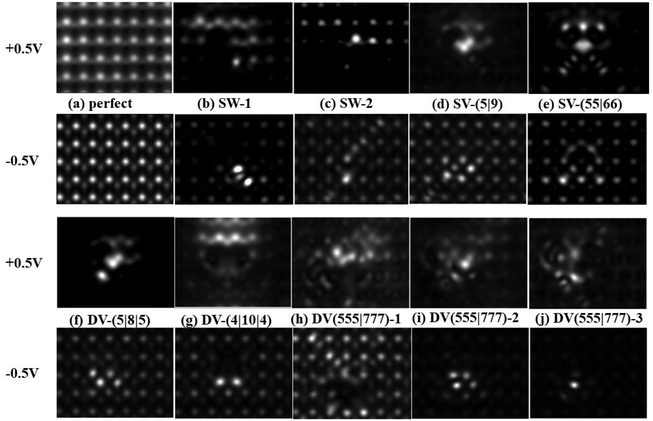
To assist experimental identification of different types of point defects in future experiments, the simulated scanning tunneling microscopy (STM) images of the perfect and defective α-antimonene under +0.5 V and −0.5 V bias are shown in Fig. 6. As shown in the upper panels of Fig. 6c–g, the SW-2, SV-(5|9), SV-(55|66), DV-(5|8|5), and DV-(4|10|4) defects can be distinguished more easily under a positive bias (+0.5 V). Specifically, the STM images of SW-2, SV-(5|9), and DV-(5|8|5) exhibit one large and one small bright spot, a small group of bright spots, and two small bright spots on the same diagonal, respectively. The SV-(55|66) defect gives rise to a symmetric bright spot pattern, corresponding to the structure of the defect. The DV-(4|10|4) defect gives rise to a light spot surrounding a black area with two wide ends and a narrow middle, highly similar to its defective structure. As shown in the lower part of Fig. 6b and h–j, SW-1, DV-(555|777)-2, and DV-(555|777)-3 defects can be distinguished more easily under a negative bias (−0.5 V). The STM image of SW-1, DV-(555|777)-2, and DV-(555|777)-3 defects is displayed as two bright spots, four bright spots, and one bright spot, respectively.

Fig. 6 Simulated STM image of the perfect α-antimonene (a) and defective α-antimonene with defect: (b) SW-1; (c) SW-2; (d) SV-(5|9); (e) SV-(55|66); (f) DV-(5|8|5); (g) DV-(4|10|4); (h) DV-(555|777)-1; (i) DV-(555|777)-2; (j) the simulated STM image of DV-(555|777)-3 at a distance of 2 Å from the surface.

Conclusions

Nine types of point defects in α-antimonene are systematically studied by using density functional theory and ab initio molecular dynamics simulation. These point defects include SW-1, SW-2, SV-(5|9), SV-(55|66), DV-(5|8|5), DV-(555|777)-1, DV-(555|777)-2, DV-(555|777)-3, and DV-(4|10|4). Among the nine defects, the formation energy of the SV-(5|9) defect is the lowest. Moreover, α-antimonene appears to have an areal density of the SV-(5|9) defects orders higher than that of phosphorene at same temperature. AIMD simulations indicate that SW-1, SW-2, and SV-(55|66) defects are unstable at room temperature, while the other defective structures are thermally stable at room temperature. The diffusion of SV-(5|9) exhibits strong anisotropic character with the diffusion barrier of 0.10/0.30 eV along the zigzag/armchair direction, notably lower than that (0.3/0.4 eV) for phosphorene. The charge injection can be a useful means to strengthen the controllability of the defect motion and manipulation via an electric field. The presence of the defects also has a marked effect on the electronic and optical properties of α-antimonene. In particular, the SV-(5|9) defect results in the metallic character of hole doping for α-antimonene, making the SV-(5|9) defect easier to be detected in experiments and manipulated, compared with phosphorene. Furthermore, most point defects of different types can be easily distinguished from one another through scanning tunneling microscopy measurements. Our study provides helpful guidance in the identification of various point defects in α-antimonene, and new insights into defect formation, defect diffusion behavior, as well as the effect of various defects on the electronic and optical properties. Overall, the novel defect-related properties of α-antimonene, including anisotropic, ultra-diffusive, and charge adjustable vacancies, render α-antimonene a potential 2D semiconductor for designing vacancy-enabled low-dimensional electronic devices.

Computational details

All calculations are performed within the framework of density-functional theory (DFT), implemented in the Vienna ab initio simulation package (VASP 5.4).^45,46 Among them, the exchange correlation functional is the PBE method of generalized gradient approximation,⁴⁷ which has previously proven to describe the electronic structure of 2D α-antimonene, phosphorene,⁴⁸ graphene²⁴ and silicene²⁵ well. By using the conjugate gradient algorithm, all atomic coordinates are fully relaxed until the total energy and atomic force converge to 10⁻⁵ eV and 10⁻² eV Å⁻¹, respectively. To study the influence of various point defects in α-antimonene, a 5 × 7 α-antimonene (140 antimony (Sb) atoms) superlattice is used, and a 15 Å vacuum layer is added in the Z direction to eliminate the influence between the crystal layer and its image layers. In the calculations, a plane-wave basis with a cutoff energy of 500 eV is selected to expand the electronic wave function, and the k-point sampling is carefully examined to assure that the calculation results are converged. To examine the thermal stability of the 2D α-antimonene structure, ab initio molecular dynamics (AIMD) simulations are performed on the selected system. The AIMD simulations are carried out in the canonic ensemble, and the total simulation time is 5.0 ps, while the time step is set to 1.0 fs. The temperature is controlled at 300 K, 400 K and 800K, respectively. The diffusion energy barriers are calculated based on the climbing image nudged elastic band (CI-NEB) method.⁴⁹

Conflicts of interest

The authors declare no competing financial interest.

Acknowledgements

NL and ZZ were supported by the Anhui Provincial Natural Science Foundation (No. 2208085QA11 and No. 2008085QA33), the University Annual Scientific Research Plan of Anhui Province (No. 2022AH010013) and the Hefei Advanced Computing Center. GZZ was supported by the National Natural Science Foundation of China (No. 11775261). XCZ acknowledges the support by the Hong Kong Global STEM Professorship Scheme.

References

1. T. Niu, J. Zhang and W. Chen, ChemNanoMat, 2019, 5, 6–23.
2. S. Zhang, M. Xie, F. Li, Z. Yan, Y. Li, E. Kan, W. Liu, Z. Chen and H. Zeng, Angew. Chem., Int. Ed., 2016, 55, 1666–1669.
3. P. Ares, J. J. Palacios, G. Abellán, J. Gómez-Herrero and F. Zamora, Adv. Mater., 2018, 30, 1703771.
4. A. A. Kistanov, D. R. Kripalani, Y. Cai, S. V. Dmitriev, K. Zhou and Y.-W. Zhang, J. Mater. Chem. A, 2019, 7, 2901–2907.
5. D. R. Kripalani, A. A. Kistanov, Y. Cai, M. Xue and K. Zhou, Phys. Rev. B, 2018, 98, 085410.
6. M. Pumera and Z. Sofer, Adv. Mater., 2017, 29, 1605299.
7. V. Wang, Y. Kawazoe and W. T. Geng, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 045433.
8. J. Qiao, X. Kong, Z.-X. Hu, F. Yang and W. Ji, Nat. Commun., 2014, 5, 4475.
9. L. Li, Y. Yu, G. J. Ye, Q. Ge, X. Ou, H. Wu, D. Feng, X. H. Chen and Y. Zhang, Nat. Nanotechnol., 2014, 9, 372–377.
10. S. Lin, S. Liu, Z. Yang, Y. Li, T. W. Ng, Z. Xu, Q. BaO, J. Hao, C. S. Lee and C. Surya, Adv. Funct. Mater., 2016, 26, 864–871.
11. G. Long, D. Maryenko, J. Shen, S. Xu, J. Hou, Z. Wu, W. K. Wong, T. Han, J. Lin and Y. Cai, Nano Lett., 2016, 16, 7768–7773.
12. S. Zhang, S. Guo, Z. Chen, Y. Wang, H. Gao, J. Gómez-Herrero, P. Ares, F. Zamora, Z. Zhu and H. Zeng, Chem. Soc. Rev., 2018, 47, 982–1021.
13. J. D. Wood, S. A. Wells, D. Jariwala, K.-S. Chen, E. Cho, V. K. Sangwan, X. Liu, L. J. Lauhon, T. J. Marks and M. C. Hersam, Nano Lett., 2014, 14, 6964–6970.
14. Z. Hu, Q. Li, B. Lei, Q. Zhou, D. Xiang, Z. Lyu, F. Hu, J. Wang, Y. Ren, R. Guo, E. Goki, L. Wang, C. Han, J. Wang and W. Chen, Angew. Chem., Int. Ed., 2017, 56, 9131–9135.
15. Z.-Q. Shi, H. Li, Q.-Q. Yuan, Y.-H. Song, Y.-Y. Lv, W. Shi, Z.-Y. Jia, L. Gao, Y.-B. Chen, W. Zhu and S.-C. Li, Adv. Mater., 2019, 31, 1806130.
16. Z.-Q. Shi, H. Li, Q.-Q. Yuan, C.-L. Xue, Y.-J. Xu, Y.-Y. Lv, Z.-Y. Jia, Y. Chen, W. Zhu and S.-C. Li, ACS Nano, 2020, 14, 16755–16760.
17. Z.-Q. Shi, H. Li, C.-L. Xue, Q.-Q. Yuan, Y.-Y. Lv, Y.-J. Xu, Z.-Y. Jia, L. Gao, Y. Chen, W. Zhu and S.-C. Li, Nano Lett., 2020, 20, 8408–8414.
18. C. Hogan, K. Holtgrewe, F. Ronci, S. Colonna, S. Sanna, P. Moras, P. M. Sheverdyaeva, S. Mahatha, M. Papagno, Z. S. Aliev, M. Babanly, E. V. Chulkov, C. Carbone and R. Flammini, ACS Nano, 2019, 13, 10481–10489.
19. D. Singh, S. K. Gupta, T. Hussain, Y. Sonvane, P. N. Gajjar and R. Ahuja, Energy Fuels, 2021, 35, 9001–9009.
20. T. Bo, Y. Liu, J. Yuan, P. Wu and W. Zhou, Appl. Surf. Sci., 2020, 507, 145194.
21. Y. Guo, H. Zhu and Q. Wang, J. Phys. Chem. C, 2020, 124, 5506–5513.
22. G. Wang, R. Pandey and S. P. Karna, ACS Appl. Mater. Interfaces, 2015, 7, 11490–11496.
23. Y. Wu, K. Xu, C. Ma, Y. Chen, Z. Lu, H. Zhang, Z. Fang and R. Zhang, Nano Energy, 2019, 63, 103870.
24. F. Banhart, J. Kotakoski and A. V. Krasheninnikov, ACS Nano, 2011, 5, 26–41.
25. J. Gao, J. Zhang, H. Liu, Q. Zhang and J. Zhao, Nanoscale, 2013, 5, 9785–9792.
26. O. Leenaerts, B. Partoens and F. M. Peeters, Appl. Phys. Lett., 2008, 93, 193107.
27. W. Hu, X. Wu, Z. Li and J. Yang, Nanoscale, 2013, 5, 9062–9066.
28. W. Hu, X. Wu, Z. Li and J. Yang, Phys. Chem. Chem. Phys., 2013, 15, 5753–5757.
29. Y. Cai, Q. Ke, G. Zhang, B. I. Yakobson and Y.-W. Zhang, J. Am. Chem. Soc., 2016, 138, 10199–10206.
30. T. Hu and J. Dong, Nanotechnology, 2015, 26, 065705.
31. R. Babar and M. Kabir, J. Phys. Chem. C, 2016, 120, 14991–15000.
32. J. Kerski, P. Lochner, A. Ludwig, A. D. Wieck, A. Kurzmann, A. Lorke and M. Geller, Phys. Rev. Appl., 2021, 15, 024029.
33. M. Lübben, F. Cüppers, J. Mohr, M. von Witzleben, U. Breuer, R. Waser, C. Neumann and I. Valov, Sci. Adv., 2020, 6, eaaz9079.
34. X. Tong, Y. Zhao, Z. Zhuo, Z. Yang, S. Wang, Y. Liu, N. Lu, H. Li and T. Zhai, Angew. Chem., Int. Ed., 2022, 61, e202112953.
35. Q. Yang, W. Xiong, L. Zhu, G. Gao and M. Wu, J. Am. Chem. Soc., 2017, 139, 11506–11512.
36. K. C. Kwon, J. H. Baek, K. Hong, S. Y. Kim and H. W. Jang, Nano-Micro Lett., 2022, 14, 58.
37. A. Hashimoto, K. Suenaga, A. Gloter, K. Urita and S. Iijima, Nature, 2004, 430, 870–873.
38. R. G. Amorim, A. Fazzio, A. Antonelli, F. D. Novaes and A. Silva, Nano Lett., 2007, 7, 2459–2462.
39. L. Kou, C. Tang, W. Guo and C. Chen, ACS Nano, 2011, 5, 1012–1017.
40. H. Sahin, J. Sivek, S. Li, B. Partoens and F. M. Peeters, Phys. Rev. B: Condens. Matter Mater. Phys, 2013, 88, 7795–7799.
41. W. Hu and J. Yang, J. Phys. Chem. C, 2015, 119, 20474–20480.
42. Y. Liu, F. Xu, Z. Zhang, E. S. Penev and B. I. Yakobson, Nano Lett., 2014, 14, 6782–6786.
43. Y. Xu, B. Peng, H. Zhang, H. Shao, R. Zhang, H. Lu, D. W. Zhang and H. Zhu, Ann. Phys., 2017, 529, 1600152.
44. J. M. H. Kroes, M. A. Akhukov, J. H. Los, N. Pineau and A. Fasolino, Phys. Rev. B: Condens. Matter Mater. Phys, 2011, 83, 165411.
45. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys, 1996, 54, 11169–11186.
46. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys, 1999, 59, 1758–1775.
47. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
48. H. Guo, N. Lu, J. Dai, X. Wu and X. C. Zeng, Physics, 2014, 118, 14051–14059.
49. G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3nr00194f

---