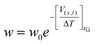Open Access Article
Open Access ArticleMetadynamics simulations for the investigation of drug loading on functionalized inorganic nanoparticles†
Stefano
Motta
 a,
Paulo
Siani
a,
Paulo
Siani
 b,
Edoardo
Donadoni
b,
Edoardo
Donadoni
 b,
Giulia
Frigerio
b,
Giulia
Frigerio
 b,
Laura
Bonati
b,
Laura
Bonati
 a and
Cristiana
Di Valentin
a and
Cristiana
Di Valentin
 *bc
*bc
aDipartimento di Scienze dell'Ambiente e del Territorio, Università di Milano Bicocca, Piazza della Scienza 1, 20126 Milano, Italy
bDipartimento di Scienza dei Materiali, Università di Milano Bicocca, via R. Cozzi 55, 20125 Milano, Italy. E-mail: cristiana.divalentin@unimib.it
cBioNanoMedicine Center NANOMIB, University of Milano-Bicocca, Italy
First published on 31st March 2023
Abstract
Inorganic nanoparticles show promising properties that allow them to be efficiently used as drug carriers. The main limitation in this type of application is currently the drug loading capacity, which can be overcome with a proper functionalization of the nanoparticle surface. In this study, we present, for the first time, a computational approach based on metadynamics to estimate the binding free energy of the doxorubicin drug (DOX) to a functionalized TiO2 nanoparticle under different pH conditions. On a thermodynamic basis, we demonstrate the robustness of our approach to capture the overall mechanism behind the pH-triggered release of DOX due to environmental pH changes. Notably, binding free energy estimations align well with what is expected for a pH-sensitive drug delivery system. Based on our results, we envision the use of metadynamics as a promising computational tool for the rational design and in silico optimization of organic ligands with improved drug carrier properties.
1. Introduction
In recent years, nanoparticles (NPs) of different compositions have greatly contributed to the field of biomedicine. Researchers have been developing novel nanoparticles for both (i) diagnosis, using imaging technologies, and (ii) treatment purposes, through drug delivery technologies. Nanostructured materials, indeed, have unique features and capabilities that make them suitable for specific interactions with biosystems (proteins, lipids, or other metabolites) that, in turn, can influence the properties and the biological reactivity of the nanomaterials.1 In particular, NPs have been studied as drug carriers for targeted drug delivery towards tumor cells. Often, when it comes to antitumoral therapeutic agents, the selectivity of the treatments does not meet expectations: the tumor cells cannot be completely killed, and the side effects cannot be prevented.2 For this reason, NPs can be rationally designed to discriminate between normal and tumor sites and to release the therapeutic agents at the tumor sites3,4 selectively. A crucial role in the efficacy of the NP system is played by its dimensions: NPs of small sizes and spherical shape5,6 are frequently preferred because of their ability to remain in the blood circulatory system for a prolonged period of time, resulting in an increase in their penetration into tumor blood vessels and, in the end, in a facilitated drug uptake by tumor cells.7Currently, several targeted drug release strategies are used based on the different growth, proliferation and metabolism of tumoral tissues. Such unique characteristics allow drug delivery systems to attack the tumor selectively and effectively, based either on biochemical (pH, redox potential, enzymatic activity, and hypoxia) or pathological (abnormal vascular structure and overexpression of receptors) differences.8,9 The pH value of tumor cells’ microenvironment is one of the most widely investigated features. Due to their faster growth rate, tumoral cells produce a large amount of lactic acid from glucose to provide enough energy for tumor growth. The acidic extracellular pH is a universal characteristic of solid tumors.10 For this reason, many novel pH-responsive nanosystems have been developed in the last few decades. Some of them can change their physical properties (shape, size or rigidity), chemical properties (hydrophilicity/hydrophobicity, isomerization, or surface charge) or even conduct chemical reactions under pH variation.11–15 The mechanism of pH-triggered drug delivery mainly includes pH-sensitive bond cleavage and proton transfers, which should be better exploited to design smart and responsive drug delivery systems.
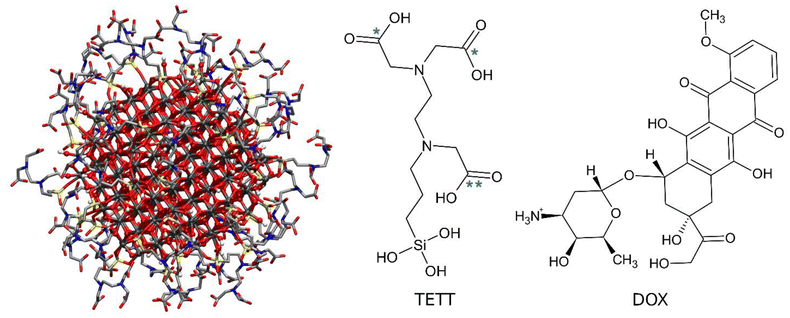
In recent years, inorganic NPs have shown great potential as drug delivery systems.16 They are small particles with special and enhanced physical and chemical properties depending on their particle size. The advantages of using inorganic nanoparticles rely on their very low toxicity profile, biocompatibility, and hydrophilic nature; they are not subject to microbial attack and are extremely stable. Among the most common inorganic NP materials are silver, gold, calcium phosphates, silica, iron oxide, titanium dioxide, and fullerenes.1,5,17 Among them, titanium dioxide (TiO2) NPs stand out because they are cheap, easy to prepare and can be functionalized with anchoring ligands, and they act as highly efficient photosensitizers.18 An example of TiO2 NPs’ application as drug delivery systems is provided by the work of Wang et al., where folate ions were covalently bonded to polyethylenimine-functionalized TiO2 NPs to obtain a targeting anticancer drug carrier for paclitaxel.19 In particular, folate molecules enhance the selective delivery to tumor cells, as folate receptors are overexpressed in cancer cells. Moreover, Zhang et al. found that daunorubicin, a molecule with a broad spectrum of anti-tumor activity, can be loaded on TiO2 NPs and that its release is faster at pH 5.0 and 6.0 than at pH 7.4.20 In addition, Wu et al. used TiO2 NPs functionalized with flavin mononucleotides for the delivery of the anticancer drug doxorubicin (DOX).21 DOX is a conventional chemotherapy drug that belongs to the anthracycline family that intercalates in the DNA double helix, thereby preventing DNA replication and cell division processes.22 The loading of DOX on the NPs functionalized with flavin mononucleotides allowed NPs’ internalization in BT-20 cells and led to cell death. DOX was also successfully loaded by Qin et al. on TiO2 NPs functionalized with TETT (N-(trimethoxysilylpropyl)ethylenediamine triacetic acid trisodium salt) ligands.23 TETT ligands induce NPs’ water dispersibility and allow non-covalent drug loading, therefore preserving the biological and pharmaceutical activities of DOX.
Computational nanomedicine is a growing field, with the need for theoretical models capable of simulating more and more realistic nanodevices in terms of both their dimensions and the conditions of the surrounding environment. Nowadays, the affinity of a drug for its target protein is routinely tackled by molecular docking or more advanced molecular dynamics (MD) techniques. However, only a few studies addressed the problem of drug-loading mechanisms on or into NPs. Regarding drug binding to a target protein, methods based on MD have gained increasing attention for their higher accuracy in considering the protein conformational flexibility.24–26 These methods can be classified into two categories:27 those mainly focused on the bound and unbound states for estimation of the binding free energy28–31 and those aimed at reproducing the physical pathway (PP) of drug binding.32–40 This last category of methods simulates the complete binding and/or unbinding events, and, in principle, they can lead to the calculation of both thermodynamic and kinetic properties41 and the characterization of relevant states along the pathways. In particular, metadynamics (MetaD) is a widely used method for the investigation of drug binding to its target.42–51 The critical aspect of MetaD is the choice of a suitable set of collective variables (CVs) that describe the event under investigation. Neglecting a relevant CV may lead to a non-converged value of the free energy.52–55
Here, we used the MetaD approach to study the binding mechanism of DOX to a TiO2 NP functionalized with TETT molecules. Despite the wide use of MetaD in protein–drug studies, to the best of our knowledge, this is the first attempt at its application on an NP–drug system. For this reason, part of the work was devoted to developing an accurate MetaD protocol. The principal difference with protein–drug studies lies in the presence of multiple, similar, but not identical, binding spots on the functionalized NP surface, which may establish different interactions with the drug. MetaD accelerates the simulation of binding and unbinding processes, allowing one to sample most of these interaction sites, collecting the average free energy of binding. Moreover, given the importance of modeling pH conditions, which influence the strength of the interaction, we performed MetaD calculations at different protonation states of the TETT ligands. The MetaD protocol developed herein turned out to be robust, providing similar binding free energies using different sets of CVs, and captured the decrease of DOX affinity that follows the reduction of pH. The obtained results are in line with what is expected for a pH-sensitive drug delivery system and are promising for the development of a computationally driven design of NP functionalization that optimizes the selective drug release under certain pH conditions.
2. Computational details
2.1 System preparation
The starting point geometry of the TETT functionalized anatase TiO2 NP (Fig. 1) is a result of previous works.56–58 The TiO2 spherical NP model was carved from a large bulk anatase supercell with a diameter of 2.2 nm. Only atoms within that sphere were considered. The 3-fold and some 4-fold coordinated Ti atoms or mono-coordinated O atoms were either removed or saturated with OH groups or H atoms, respectively. In other words, we used a small number of dissociated water molecules to achieve the chemical stability of the nanoparticles, with a resulting stoichiometry of (TiO2)223·10H2O (699 atoms). This model then underwent simulated annealing at 700 K at the DFTB level of theory and full atomic relaxation at the hybrid DFT level.57 In a following work,58 this NP model was fully decorated with forty TETT linkers anchored in a monodentate, bidentate or tridentate fashion through the formation of Si–O–Ti bonds between the silanol group of TETT and 4-fold and 5-fold coordinated Ti atoms and simulated through DFTB-molecular dynamics at 300 K.56–59The same starting point geometry was used in a previous MD work by some of us.60 The protonation state of TETT ionizable groups was assigned to model specific pH conditions. According to the pKa values for the ionizable groups of TETT, we either removed one or two protons from the three carboxylic groups of each TETT ligand to mimic acidic or neutral pH conditions, respectively. Protons were removed from the carboxylic groups that lie at the furthest extremity of the TETT chain tail since they are more exposed to the solvent and, therefore, are expected to be the most acidic (labelled with one star in Fig. 1). In this work, we used some very recently developed parameters for TiO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 61 that were reported to improve previous ones by the same group62 and others by Matsui and Akaogi.63 TETT (in the different protonation states), and DOX molecules were parametrized using the GAFF2 force field with atomic partial charges obtained following the standard restrained electrostatic potential fitting protocol64 (RESP) on the single molecules using the 6-31G* basis set at the Hartree–Fock (HF) level of theory. The system was then immersed in a large octahedral box (boundaries at 20 Å from the solute) of TIP3P65 water molecules and neutralized with Na+ ions using the GROMACS preparation tools.66 All the subsequent energy minimization calculations and MD simulations were performed using the GROMACS MD engine.66
61 that were reported to improve previous ones by the same group62 and others by Matsui and Akaogi.63 TETT (in the different protonation states), and DOX molecules were parametrized using the GAFF2 force field with atomic partial charges obtained following the standard restrained electrostatic potential fitting protocol64 (RESP) on the single molecules using the 6-31G* basis set at the Hartree–Fock (HF) level of theory. The system was then immersed in a large octahedral box (boundaries at 20 Å from the solute) of TIP3P65 water molecules and neutralized with Na+ ions using the GROMACS preparation tools.66 All the subsequent energy minimization calculations and MD simulations were performed using the GROMACS MD engine.66
2.2 Equilibration protocol
The solvated system was subjected to 2000 steps of the steepest descent energy minimization, followed by a Berendsen NVT dynamics that heated the system from 0 to 300 K in 500 ps. During this simulation phase, all TETT and DOX heavy atoms were restrained to their initial position with a force constant of 1000 kJ mol−1 nm−2. The Particle Mesh Ewald method67 was used to treat long-range electrostatic interactions with the cutoff distance set at 12 Å. Short-range repulsive and attractive dispersion interactions were simultaneously described by a Lennard-Jones potential, with a cutoff at 12 Å. A time step of 2.0 fs was used, together with the SHAKE algorithm, to constrain H-involving covalent bonds. During the production phase (NPT in water), the restraints were removed, the thermostat was switched to the V-rescale,68 and the pressure was set to 1 bar with the Parrinello–Rahman barostat69 (coupling constant of 2.0 ps). To avoid deviation from the QM-optimized conformation of the NP, we also restrained the NP oxygen and titanium atoms during all the equilibration steps and the following MetaD simulations with a force constant of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 kJ mol−1 nm−2. The same approach was applied in previous works.70,71
000 kJ mol−1 nm−2. The same approach was applied in previous works.70,71
2.3 Metadynamics simulations
In MetaD33,54 a system is biased along a set of CVs using a history-dependent potential. To achieve this, a Gaussian-shaped potential is added to bias the system at the current position of the CVs, at regular time intervals. This allows the system to escape from any local minimum and to visit new regions in the space of CVs. In Standard MetaD (St-MetaD), the Gaussian-shaped potential has a constant height to push the system to visit even high free energy regions. While, in the Well-Tempered MetaD72 (WT-MetaD) approach, the height of the Gaussian is decreased with the amount of bias already deposited according to:where w0 is an initial Gaussian height, ΔT an input parameter with the dimension of a temperature, and τG is the time interval at which Gaussians are deposited.72 In this work, we performed both St-MetaD and WT-MetaD, biasing a different set of CVs that are designed to describe different properties of the system during the binding process. They are shown in Fig. 2 and can be described as follows:
1. d: the distance between the DOX nitrogen atom, and the closest NP atom;
2. Φ: the angle formed by the center of the NP, the DOX nitrogen atom, and the carbon on the opposite side of the anthraquinone ring;
3. C: the number of carboxylic groups H-bonded to the DOX amino group (coordination number).
The first two CVs were considered in a previous work in terms of interesting parameters for a fair representation of the distribution of the DOX states sampled during the unbiased MD simulations.60 The third CV is selected in this work to describe the interaction of the (positively charged) DOX amino group with the carboxylic tails of TETT, which we expect to be critical for the investigation of the pH effect on the drug binding. We are aware that the chosen set of CVs does not describe the relative position of the drug with respect to the nanoparticle. This type of description would require two additional CVs related to the drug's polar coordinates with respect to the NP center. However, since we want to keep the number of CVs at most two, for an efficient MetaD run, and since we expect the drug to sample spontaneously different regions of the NP surface, we decided not to include these two additional CVs.
In all the simulations we used a height of the gaussian hills of 0.5 kJ mol−1. Biasing only one CV, we increased the pace of the deposition from 1 ps to 3 ps. The bias factor used in WT-MetaD was set to 10. The width of the gaussian hills was set to about one-third of the standard deviation of the CV during previous unbiased MD simulations of a DOX bound to the functionalized NP. An upper wall at a d value of 33 Å was applied. A summary of the MetaD parameters of all the simulations is provided in Table S1 in the ESI.† Similar parameters were used in protein–ligand or RNA-ligand MetaD simulations.42,73–76 The convergence of the simulations was assessed by estimating the free energy difference between the bound state (d between 2 Å and 18 Å) and the unbound state (d greater than 25 Å). For the CV describing the coordination of DOX nitrogen by the TETT carboxylic group, we used a switching function with an R_0 value of 5.0 Å.
2.4 Self-organizing maps
A self-organizing map (SOM) is an unsupervised learning method that allows the visualization of multidimensional data in a low-dimensional representation and their clustering by keeping similar input data close to each other in the map.77–79 Several applications of SOMs to the analysis of biomolecular simulations can be found in the literature ranging from the clustering of ligand poses in virtual screening80 to the clustering of protein conformations from MD trajectories77,81 and analysis of pathways in enhanced sampling MD simulations.82–84 In this work, we used the PathDetect-SOM tool85 to investigate molecular features of the sampled bound states and recognize differences in the configurations sampled during the MetaD simulations. For the SOM training, we used a 10 × 10 toroidal SOM (with periodicity across the boundaries) with a hexagonal lattice shape. The input features to train the SOM were computed on St-MetaD biasing only d, and they are the intermolecular distances between the DOX N1, O4, O8 and C26 atoms (see Fig. S1 in the ESI†) and:• the four closest NP oxygen atoms
• the two closest NP titanium atoms
• the six closest TETT deprotonated carboxy-groups
• the six closest TETT protonated carboxy-groups
• the two closest TETT nitrogen atoms
• the three closest TETT silicate oxygen atoms
Measuring the distances with the closest atom instead of a specific atom allowed us to account for the change of the DOX position around the NP system. A capping value of 12 Å was applied to all distances. This set of distances was optimized to obtain a good description of the interaction of both the sugar ring and the anthraquinone ring of DOX with the functionalized NP. After training, each frame of the simulations was assigned to a neuron on the map, with each neuron representing a protein–ligand conformational microstate. In the second step, the neurons were further grouped in a small, but representative, number of clusters by agglomerative hierarchical clustering using Euclidean distance and complete linkage. The visualization of the map was optimized by reconstructing boundaries based on the similarity between neurons. The optimal number of clusters, N, was selected based on the Silhouette profiles (Fig. S2†). All the analyses were performed in the R statistical environment using the kohonen package.86,87
2.5 Preliminary analysis and choice of TiO2 force field parameters
The system consisting of NPs functionalized with TETT and DOX has already been studied through unbiased MD simulations and simulated annealing by some of us.60 In that work, we used the set of TiO2 parameters developed by Brandt et al.62 and we noticed an overestimation of the interaction between the NP and the DOX molecule (states at low distance values, Fig. S3a and c†). Recently, the same group61 proposed an improved version of the latter FF in which a more accurate description of intermolecular interactions between TiO2 NPs and small biomolecules in an aqueous solution was achieved. Thus, we started our investigation by comparing the results obtained with the old TiO2 parameters with the ones obtained with the most recent set of FF parameters. Starting from DOX in the bulk solvent, we performed two cycles of simulated annealing and compared the distributions of DOX state probabilities in the subspace of two selected variables. The details regarding this type of simulation can be found in our precedent work.60 The results with the new force-field are presented in Fig. S3b and d† and they show that with the new set of FF parameters61 the DOX molecules tend to interact more with the TETT ligands and less with the NP surface (more states were visited at high distance values). This is consistent with the fact that a change in the pH (and in turn protonation of TETTs) leads to a change in the affinity of the ligand. The few configurations near the NP surface that are still present with the new force-field may be an artifact or may represent configurations of DOX molecules that are not released following a pH change mechanism. For this reason, the most recent TiO2 parameters have been used in the present work.3. Results and discussion
3.1 Setup of the metadynamics protocol: choice of the collective variables
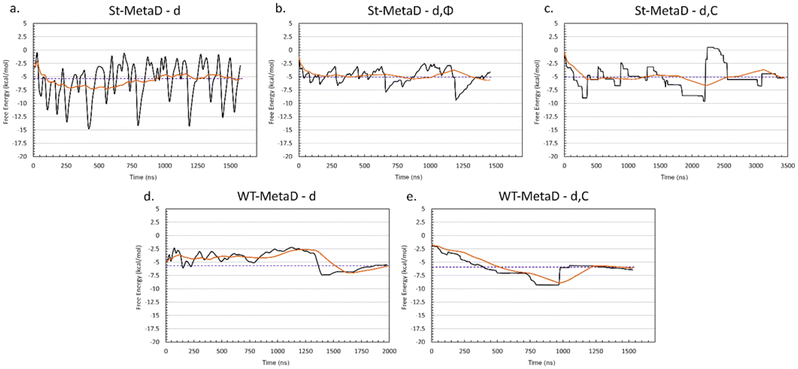
To perform meaningful MetaD simulations, it is crucial to define appropriate CVs, which can capture the slow degrees of freedom of the system and discriminate among its relevant states. At the same time, the number of CVs should be kept as small as possible (ideally not more than two) to maintain a reasonable computational cost. For this reason, we investigated the optimal choice of CVs able to describe the DOX binding to TiO2 nanoparticles functionalized with TETT ligands (see Fig. 1). The selected CVs are described in section 2.3 and represent the distance between the DOX nitrogen atom and the closest NP atom (d); the angle formed by the center of the NP, the DOX nitrogen atom, and the carbon on the opposite side of the anthraquinone ring (Φ); the number of carboxylic groups H-bonded to the DOX amino group (coordination number, C).To find the best CVs among the three selected above and to identify an efficient protocol that describes the binding process, we then performed a set of simulations. In all of them, we decided to include the d CV, as it is a good descriptor of the distance of the drug with respect to the NP surface, and, therefore, of the binding/unbinding process. Moreover, we also considered the possibility of performing well-tempered (WT) or standard (St) MetaD simulations. Slightly acidic conditions were investigated, with only one deprotonated carboxylic group per TETT ligand, as discussed in section 2.1 and below. Simulations were run for about 1.5 μs each, although some were extended until they reached convergence. The simulation parameters are reported in Table 1.
| CV | MetaD approach | Simulation length (μs) | Deposition rate (ps) | Binding free energy (kcal mol−1) | |
|---|---|---|---|---|---|
| 1 | d | St | 1.6 | 3 | −5.34 ± 0.4 |
| 2 | d, Φ | St | 1.5 | 1 | −5.10 ± 0.4 |
| 3 | d, C | St | 3.4 | 1 | −5.09 ± 0.5 |
| 4 | d | WT | 2.0 | 3 | −5.67 ± 0.2 |
| 5 | d, C | WT | 1.5 | 1 | −5.93 ± 0.3 |
The time evolutions of the biased CVs are reported in Fig. S4† and they show that a good level of diffusion was attained in all the simulations. Interestingly, for all the simulations the computed binding free energy values are in the range of −5.1/−5.9 kcal mol−1. This fair agreement suggests that all the approaches are equally valid. However, the values computed with WT-MetaD are systematically more negative than those obtained with St-MetaD. We have investigated the possible reason for this discrepancy, and we found that, during the WT-MetaD, DOX only explored some regions on the NP surface (around one-third of the total surface), while in St-MetaD the molecule explored almost the whole NP surface (Fig. 3).
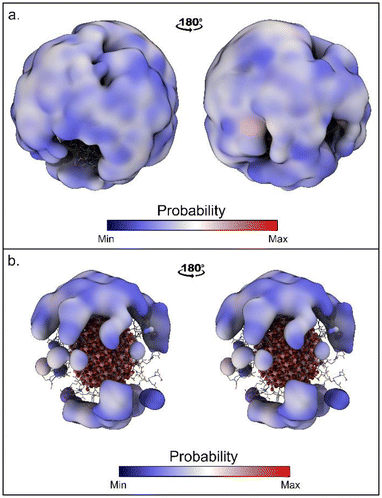 | ||
| Fig. 3 Region of the NP surfaces visited during (a) St-MetaD biasing only d and (b) WT-MetaD biasing only d. Surface shows regions within 17 Å from the NP surface sampled by DOX. | ||
In WT-MedaD, indeed, after the first part of the simulation, where the hill height is still relatively high, DOX binding/unbinding sampling proceeds at a slower rate. This is reasonable as the height of the hills decreases during the WT-MetaD simulation and, at a certain point, it becomes harder to observe the unbinding events (due to a small hysteresis effect). Usually, this is not a problem, as the simulation reaches a converged value for the free energy and does not need to sample further binding/unbinding events. In the present case, however, the continuous sampling of DOX binding and unbinding is necessary to compensate for the lack of CVs describing the DOX position around the NP. WT-MetaD simulations using a higher starting hills height or a higher bias factor may mitigate this problem and help in reaching the convergence of the simulation.
Based on the above, we decided that St-MetaD is better suited for more efficient exploration of the phase space, and therefore, we adopted it for the subsequent simulations. A comparison of different CV combinations revealed that the use of d alone is sufficient to describe the binding process, as also evidenced by the same converged values of the free energy obtained with all the St-MetaD simulations (Fig. 4a–c). During this simulation, we observed a large oscillation of the free energy value, probably due to hysteresis and the rapid filling of the free energy wells. In the second half of the simulation, however, the average of the free energy converged at around a value of −5.3 kcal mol−1. The block analysis also corroborates the convergence of this simulation (Fig. S5†). Here, the average free energy across blocks and the error as a function of the block size are computed. The converged value of the error in correspondence with a block dimension that exceeds the correlation between data points is an indicator of the convergence of the calculation.
Including additional CVs leads to similar values for the converged binding free energy (Table 1). However, looking at the bidimensional free energy surface (Fig. 5), it is evident that no relevant energetic barrier exists along the Φ CV (Fig. 5a and Fig. S4†). For this reason, the inclusion of the Φ CV was not considered in the subsequent simulations. St-MetaD simulations, where an additional bias on the number of TETT carboxylic groups interacting with the DOX-charged amino group (C) is applied, show that, surprisingly, the deepest minimum is found with a zero-coordination number (C), although other relevant states can be observed at higher coordination numbers. These other states could play a key role at neutral pH, where more deprotonated TETT carboxylic groups are expected. For the reasons explained above, in the next section, we have investigated the effect of pH through St-MetaD simulation where either only the d parameter is biased or both the d and C parameters are biased.
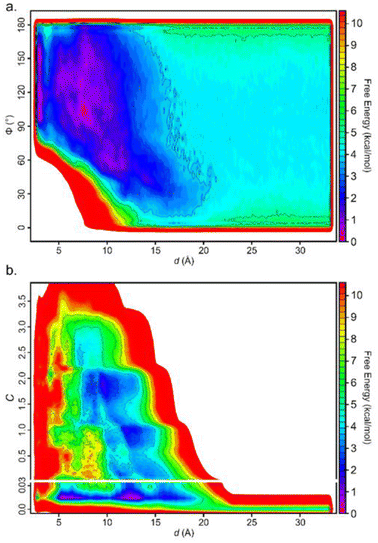 | ||
| Fig. 5 Free energy surface for the simulation biasing (a) d and Φ; (b) d and C. In (b), the y-scale is modified to enlarge the region around the values of C near 0. | ||
3.3 Effect of pH
To clarify the pH effect on the DOX binding to TETT-functionalized TiO2 NPs, we compared St-MetaD simulations with different TETT protonation states. Since pKa values for TETT are not available in the literature, we used those reported for hydroxyethylethylenediaminetriacetic acid (HEDTA), an organic compound similar to TETT, where the silanol group is substituted by a hydroxyl group. The three reported pKa values for HEDTA are 2.51, 5.31 and 9.86.88,89 This implies that, under neutral pH conditions, two of the three carboxylic groups in each TETT ligand are expected to be deprotonated, leaving only one protonated carboxylic group per TETT ligand (overall charge: −2). Differently, at slightly acidic pH, only one of the three carboxylic groups is deprotonated (overall charge −1). For this reason, in the following, using the St-MetaD approach we will compare the DOX binding process to a TETT-functionalized NP presenting either two or one deprotonated carboxylic groups per TETT ligand, corresponding to neutral or slightly acidic pH conditions, respectively. We want to clarify that simulations at acidic pH are the same as that presented in the previous section.In all St-MetaD simulations, considering only a bias on d or on both d and C, we attained a converged value for the free energy difference between the DOX/NP bound and unbound states (Fig. 4 and Fig. S6†). Moreover, also during simulations at neutral pH we obtained a good level of diffusion for the biased CVs (Fig. S7†). The values of converged binding free energy are summarized in Table 2.
| CV | pH | Simulation length (μs) | Binding free energy (kcal mol−1) |
|---|---|---|---|
| d | Acidic | 1.6 | −5.34 ± 0.4 |
| d, C | Acidic | 3.4 | −5.09 ± 0.5 |
| d | Neutral | 1.8 | −8.09 ± 0.5 |
| d, C | Neutral | 4.5 | −7.86 ± 0.5 |
It can be noted that the change in pH from neutral to acidic causes a reduction of about 2.75 kcal mol−1 (about 30%) in the binding affinity. Interestingly, the simulations with a bias on both d and C showed a slightly less negative binding free energy (about 0.25 kcal mol−1) than those with only a bias on d. However, the results are highly consistent, supporting the reliability of the employed protocol.
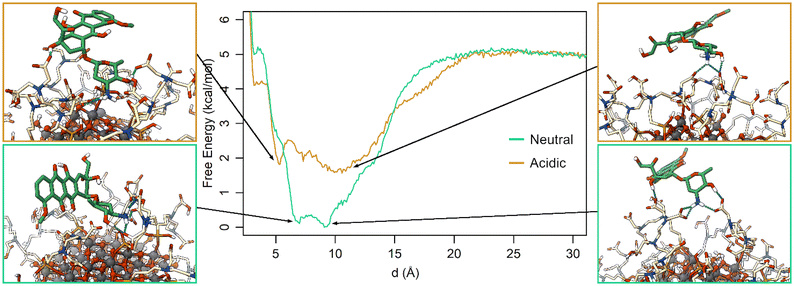
The free energy profiles along d (Fig. 6) show that at neutral pH the most favorable DOX binding modes are located between 7 and 9 Å, indicating a specific and strong interaction with the TETT molecules. On the other side, the bound minimum is wider at acidic pH and comprises configurations between 5 and 14 Å. In particular, the configurations at 5 Å present a specific minimum that can be interpreted as DOX also interacting with the O atoms at the NP surface. “It is interesting to note that no stable minima were identified for values of d below 5 Å, whereas these configurations frequently appeared in previous simulated annealing runs (Fig. S3†). To rationalize this apparent discrepancy, one should note that the two simulations were performed under different conditions: in the simulated annealing 10 DOX molecules were simultaneously put in the bulk solvent and, then, allowed to bind the TETT-functionalized NP, whereas during MetaD only one DOX molecule was present along all the simulations. The number of DOX molecules may affect the behavior of the overall system, leading, for instance, to a larger number of TETTs in a bent conformation in the simulated annealing case (Fig. S8†). Moreover, due to the high temperature during the simulated annealing, one can notice that TETT chains become very mobile and, thus, unable to establish stable interactions with the DOX amino groups, which, consequently, penetrate more deeply towards the NP surface. As a result, configurations of DOX near the NP surface appear more frequently after the simulated annealing protocol than in MetaD calculations.
The free energy surface in St-MetaD simulations with a bias on both d and C variables reveals that at acidic pH (Fig. S8a†) the favorite coordination number of the DOX amino group by TETT carboxylic groups is around 0, at values of d between 5 and 14 Å. Interestingly, at neutral pH (Fig. S8b†), the deepest minimum is found at values of C between 1 and 2, indicating the presence of one or even two carboxylic groups coordinating the DOX amino group. This minimum is found at a value of d within the range of 6–9 Å, consistent with results obtained by biasing only d (Fig. 6). Additional minima are found in correspondence of a C value of three, while a significantly higher energy is found at low C values.
Together, the MetaD simulations highlight a strong effect of the TETT protonation state on the DOX binding affinity for the functionalized NP. At neutral pH, the highest number of deprotonated TETT carboxylic groups contribute to stabilizing the charged DOX amino group, increasing the NP-DOX affinity of about 2.75 kcal mol−1.
3.4 Self-organizing maps
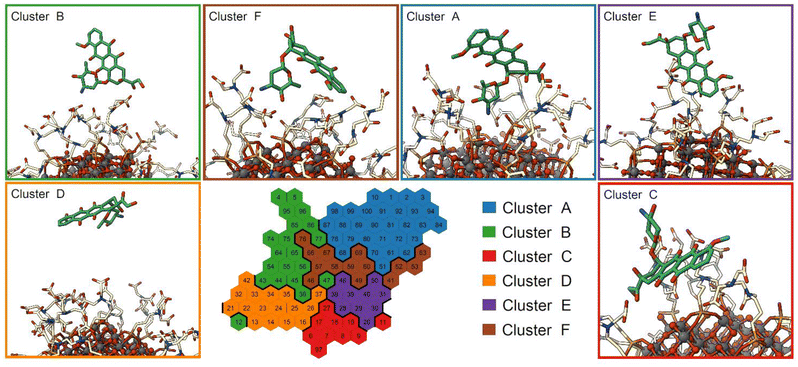
To investigate the structural binding features of DOX on the NP surface, we used a self-organizing map (SOM), an unsupervised machine learning method for visualizing multidimensional data in a low-dimensional representation and for their clustering.77–79,90 Here, we trained a SOM with a set of selected distances that describe the binding feature of the DOX molecule computed on the St-MetaD simulations biasing only d (see the Computational details section). During the training, the map is optimized to describe input conformations, each of which is finally assigned to a particular neuron (hexagon on the map). Thus, each neuron of the SOM represents a conformational microstate of the system, and neurons close to each other represent similar configurations. The neurons are further grouped into small but representative numbers of clusters representing the macrostates of the system.The trained SOM is presented in Fig. 7. The unbound state is included in cluster D, while the bound state closer to the NP surface is included in cluster A, as shown in Fig. S9a.† The latter is characterized by DOX molecules with the charged amino group near the NP surface and interacting both with the O atoms at the NP surface and with the TETT chains. Clusters B, C, E and F are intermediate configurations with the DOX molecules forming contacts with the TETT chains. In particular, the DOX molecule turns the amino group towards the solvent in clusters C and E, whereas the anthraquinone ring is immersed in the TETT chains (cluster E) or in contact with the NP surface (Cluster C). In clusters B and F, conversely, the charged amino group interacts with the carboxylic group of the TETT chains but, while in cluster B the anthraquinone ring is immersed in the solvent, in cluster F it also forms contacts with the TETT chains.
A representation of the per-neuron average values of the three CVs used in the present work (d, Φ and C) is reported in Fig. S9.† Interestingly, some neurons within cluster A displayed very low coordination C values, despite the short distance from the NP. These are configurations in which DOX can reach the NP surface, but its amino group does not interact with the TETT carboxylic groups.
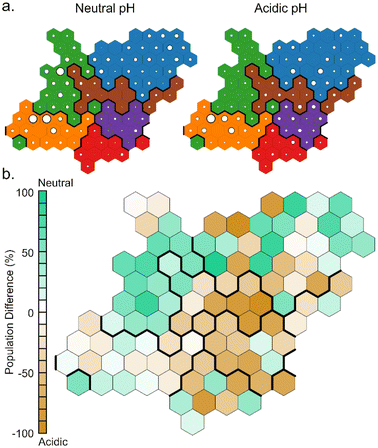
Comparing the population of the neurons in the simulations at different pH (Fig. 8), it can be noted that clusters A and B are more populated during the simulations at neutral pH, while clusters C, E and most of F are more populated during the simulations at acidic pH. This finds an explanation in the different hydrophilicity of the layer around the NP caused by the different protonation states of TETTs. At neutral pH, where a greater number of negative charges makes the layer more hydrophilic, the polar side of DOX is most frequently found to interact with TETT ligands. On the other hand, the lower number of charges at acidic pH increases the hydrophobicity of the TETT chains and enhances their interaction with the DOX anthraquinone ring.
The analysis with SOM highlighted the features of the binding configurations under different pH conditions that were not captured by the representative states of the minima presented in Fig. 6. This was possible because SOM considers a wide set of intermolecular distances that well describes the binding configuration and creates a large number of microstates that represent all the possible DOX binding modes.
4. Conclusions
In the present study, we have developed a successful MetaD protocol for the computational investigation of drug binding to functionalized NPs. The work benefits from previous efforts that allowed us to obtain chemically stable structures of a TETT-functionalized TiO2 NP of realistic size.56–58Our first concern, here, was to investigate the effect of neglecting some descriptors of the system in the selected biased CVs during the MetaD calculations. We found that the distance between the positively charged amino group of the drug and the surface of the NP is a good descriptor for the binding event in St-MetaD. On the one hand, additional CVs did not significantly change the computed binding free energy. On the other hand, the use of WT-MetaD suffers particularly from the lack of CVs describing the position of DOX around the NP, leading to slightly different and less statistically meaningful results. We want to underline that in all the MetaD calculations performed in this study, the binding free energy converged to values that lie within 0.3 kcal mol−1 for St-MetaD and 1 kcal mol−1 for WT-MetaD.
Then, we investigated the pH effect by performing the calculation at two different TETT protonation states. Given that the second carboxylic group of TETT is expected to present a pKa value that falls within the pH range of healthy and tumoral cells, we performed St-MetaD calculations in which each of the TETT molecules has either one or two deprotonated carboxylic groups. These calculations led to a difference of about 2.75 kcal mol−1 in the DOX binding affinity, which corresponds to a 100-fold increase in the probability of finding DOX in the solvent under acidic conditions compared to that at neutral pH, according to the Boltzmann distribution. The increased propensity of the molecule to stay in solution at acidic pH explains the efficient release mechanism of DOX under acidic conditions.
The MetaD simulations were then analyzed to identify the typical binding configurations using a SOM, i.e., an unsupervised machine learning method. This analysis revealed that DOX strongly interacts with the TETT negatively charged chains under neutral conditions through its positively charged amino group. The pH change alters the electrostatic properties of the layer around the NP and DOX tends to interact more through its anthraquinone ring, leaving the amino group exposed to the solvent. The lack of a complete stabilization of the charged moiety of DOX by the nanocarrier is the main reason for the reduced stability of the interaction.
To conclude, the outcomes of our study provide a solid basis for the rationalization of a pH-triggered release mechanism of DOX by functionalized inorganic NPs and are promising for the future computationally-driven optimization of NP-coated ligands to enhance the selective release of drugs under certain pH conditions.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The research leading to these results has received funding from the European Union – NextGenerationEU through the Italian Ministry of University and Research under PNRR – M4C2-I1.3 Project PE_00000019 “HEAL ITALIA” to Prof. Cristiana Di Valentin CUP H43C22000830006 of University of Milano Bicocca.References
- W. Paul and C. P. Sharma, in Biointegration of Medical Implant Materials, Elsevier, 2020, pp. 333–373 Search PubMed.
- Z. Shi, Y. Zhou, T. Fan, Y. Lin, H. Zhang and L. Mei, Smart Mater. Med., 2020, 1, 32–47 CrossRef.
- C. Li, J. Wang, Y. Wang, H. Gao, G. Wei, Y. Huang, H. Yu, Y. Gan, Y. Wang, L. Mei, H. Chen, H. Hu, Z. Zhang and Y. Jin, Acta Pharm. Sin. B, 2019, 9, 1145–1162 CrossRef PubMed.
- Y. Dang and J. Guan, Smart Mater. Med., 2020, 1, 10–19 CrossRef PubMed.
- C. P. Sharma, Drug delivery nanosystems for biomedical applications, Elsevier, 2018 Search PubMed.
- O. C. Farokhzad and R. Langer, ACS Nano, 2009, 3, 16–20 CrossRef CAS PubMed.
- J. K. Patra, G. Das, L. F. Fraceto, E. V. R. Campos, M. D. P. Rodriguez-Torres, L. S. Acosta-Torres, L. A. Diaz-Torres, R. Grillo, M. K. Swamy, S. Sharma, S. Habtemariam and H. S. Shin, J. Nanobiotechnol., 2018, 16, 71 CrossRef PubMed.
- N. N. Pavlova and C. B. Thompson, Cell Metab., 2016, 23, 27–47 CrossRef CAS PubMed.
- J. D. Martin, H. Cabral, T. Stylianopoulos and R. K. Jain, Nat. Rev. Clin Oncol., 2020, 17, 251–266 CrossRef PubMed.
- X. Wang, X. Wang, S. Jin, N. Muhammad and Z. Guo, Chem. Rev., 2019, 119, 1138–1192 CrossRef CAS PubMed.
- M. Kanamala, W. R. Wilson, M. Yang, B. D. Palmer and Z. Wu, Biomaterials, 2016, 85, 152–167 CrossRef CAS PubMed.
- J. Liu, Y. Huang, A. Kumar, A. Tan, S. Jin, A. Mozhi and X.-J. Liang, Biotechnol. Adv., 2014, 32, 693–710 CrossRef CAS PubMed.
- M.-X. Wu and Y.-W. Yang, Adv. Mater., 2017, 29, 1606134 CrossRef PubMed.
- K. M. Huh, H. C. Kang, Y. J. Lee and Y. H. Bae, Macromol. Res., 2012, 20, 224–233 CrossRef CAS.
- Z. Dong, L. Feng, W. Zhu, X. Sun, M. Gao, H. Zhao, Y. Chao and Z. Liu, Biomaterials, 2016, 110, 60–70 CrossRef CAS PubMed.
- Z. P. Xu, Q. H. Zeng, G. Q. Lu and A. B. Yu, Chem. Eng. Sci., 2006, 61, 1027–1040 CrossRef CAS.
- J. Xie, S. Lee and X. Chen, Adv. Drug Delivery Rev., 2010, 62, 1064–1079 CrossRef CAS PubMed.
- T. Rajh, N. M. Dimitrijevic, M. Bissonnette, T. Koritarov and V. Konda, Chem. Rev., 2014, 114, 10177–10216 CrossRef CAS PubMed.
- T. Wang, H. Jiang, L. Wan, Q. Zhao, T. Jiang, B. Wang and S. Wang, Acta Biomater., 2015, 13, 354–363 CrossRef CAS PubMed.
- H. Zhang and B.-A. Chen, Blood, 2011, 118, 3479–3479 CrossRef.
- K. C. W. Wu, Y. Yamauchi, C. Y. Hong, Y. H. Yang, Y. H. Liang, T. Funatsu and M. Tsunoda, Chem. Commun., 2011, 47, 5232–5234 RSC.
- C. M. Perou, T. Sørile, M. B. Eisen, M. van de Rijn, S. S. Jeffrey, C. A. Ress, J. R. Pollack, D. T. Ross, H. Johnsen, L. A. Akslen, Ø. Fluge, A. Pergammenschlkov, C. Williams, S. X. Zhu, P. E. Lønning, A. L. Børresen-Dale, P. O. Brown and D. Botstein, Nature, 2000, 406, 747–752 CrossRef CAS PubMed.
- Y. Qin, L. Sun, X. Li, Q. Cao, H. Wang, X. Tang and L. Ye, J. Mater. Chem., 2011, 21, 18003–18010 RSC.
- A. Basciu, L. Callea, S. Motta, A. M. J. J. Bonvin, L. Bonati and A. v. Vargiu, Annu. Rep. Med. Chem., 2022, 59, 43–97 Search PubMed.
- D. Gioia, M. Bertazzo, M. Recanatini, M. Masetti and A. Cavalli, Molecules, 2017, 22, 1–21 CrossRef PubMed.
- M. de Vivo, M. Masetti, G. Bottegoni and A. Cavalli, J. Med. Chem., 2016, 59, 4035–4061 CrossRef CAS PubMed.
- V. Limongelli, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2020, 10, 1–32 Search PubMed.
- J. Aqvist, C. Medina and J. E. Samuelsson, A new method for predicting binding affinity in computer-aided drug design, Protein Eng., 1994, 7, 385–391 CrossRef CAS PubMed.
- N. Homeyer and H. Gohlke, Mol. Inf., 2012, 31, 114–122 CrossRef CAS PubMed.
- J. G. Kirkwood, J. Chem. Phys., 1935, 3, 300 CrossRef CAS.
- R. W. Zwanzig, J. Chem. Phys., 1954, 22, 1420 CrossRef CAS.
- B. Isralewitz, M. Gao and K. Schulten, Curr. Opin. Struct. Biol., 2001, 11, 224–230 CrossRef CAS PubMed.
- A. Laio and M. Parrinello, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 12562–12566 CrossRef CAS PubMed.
- S. Raniolo and V. Limongelli, Nat. Protoc., 2020, 15, 2837–2866 CrossRef CAS PubMed.
- P. Tiwary and M. Parrinello, Phys. Rev. Lett., 2013, 111, 1–5 CrossRef PubMed.
- R. Capelli, P. Carloni and M. Parrinello, J. Phys. Chem. Lett., 2019, 10, 3495–3499 CrossRef CAS PubMed.
- Y. Miao, A. Bhattarai and J. Wang, J. Chem. Theory Comput., 2020, 16, 5526–5547 CrossRef CAS PubMed.
- L. Mollica, S. Decherchi, S. R. Zia, R. Gaspari, A. Cavalli and W. Rocchia, Sci. Rep., 2015, 5, 11539 CrossRef PubMed.
- S. Motta, L. Callea, S. G. Tagliabue and L. Bonati, Sci. Rep., 2018, 8, 16207 CrossRef PubMed.
- J. Rydzewski, Comput. Phys. Commun., 2020, 247, 106865 CrossRef CAS.
- A. Nunes-Alves, D. B. Kokh and R. C. Wade, Curr. Opin. Struct. Biol., 2020, 64, 126–133 CrossRef CAS PubMed.
- L. Callea, L. Bonati and S. Motta, J. Chem. Theory Comput., 2021, 17, 3841–3851 CrossRef CAS PubMed.
- V. Limongelli, M. Bonomi and M. Parrinello, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 6358–6363 CrossRef CAS PubMed.
- F. Comitani, V. Limongelli and C. Molteni, J. Chem. Theory Comput., 2016, 12, 1–25 CrossRef PubMed.
- P. Tiwary, V. Limongelli, M. Salvalaglio and M. Parrinello, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, E386–E391 CAS.
- R. Casasnovas, V. Limongelli, P. Tiwary, P. Carloni and M. Parrinello, J. Am. Chem. Soc., 2017, 139, 4780–4788 CrossRef CAS PubMed.
- F. L. Gervasio, A. Laio and M. Parrinello, J. Am. Chem. Soc., 2005, 127, 2600–2607 CrossRef CAS PubMed.
- M. Masetti, A. Cavalli, M. Recanatini and F. L. Gervasio, J. Phys. Chem. B, 2009, 113, 4807–4816 CrossRef CAS PubMed.
- A. Cavalli, A. Spitaleri, G. Saladino and F. L. Gervasio, Acc. Chem. Res., 2015, 48, 277–285 CrossRef CAS PubMed.
- N. Saleh, P. Ibrahim, G. Saladino, F. L. Gervasio and T. Clark, J. Chem. Inf. Model., 2017, 57, 1210–1217 CrossRef CAS PubMed.
- D. Provasi, A. Bortolato and M. Filizola, Biochemistry, 2009, 48, 10020–10029 CrossRef CAS PubMed.
- D. Provasi, Biomolecular Simulations, Methods in Molecular Biology, 2019, vol. 2022, pp. 233–253 Search PubMed.
- G. Bussi and D. Branduardi, Reviews in Computational Chemistry, 2015, pp. 28, 1–49 Search PubMed.
- A. Laio and F. L. Gervasio, Rep. Prog. Phys., 2008, 71, 126601 CrossRef.
- G. Bussi and A. Laio, Nat. Rev. Phys., 2020, 2, 200–212 CrossRef.
- G. Fazio, L. Ferrighi and C. Di Valentin, J. Phys. Chem. C, 2015, 119, 20735–20746 CrossRef CAS.
- D. Selli, G. Fazio and C. Di Valentin, J. Chem. Phys., 2017, 147, 164701 CrossRef PubMed.
- M. Datteo, L. Ferraro, G. Seifert and C. Di Valentin, Nanoscale Adv., 2020, 2, 2774–2784 RSC.
- C. Ronchi, M. Datteo, M. Kaviani, D. Selli and C. di Valentin, J. Phys. Chem. C, 2019, 123, 10130–10144 CrossRef CAS.
- S. Motta, P. Siani, A. Levy and C. Di Valentin, Nanoscale, 2021, 13, 13000–13013 RSC.
- I. Rouse, D. Power, E. G. Brandt, M. Schneemilch, K. Kotsis, N. Quirke, A. P. Lyubartsev and V. Lobaskin, Phys. Chem. Chem. Phys., 2021, 23, 13473–13482 RSC.
- E. G. Brandt and A. P. Lyubartsev, J. Phys. Chem. C, 2015, 119, 18110–18125 CrossRef CAS.
- M. Matsui and M. Akaogi, Mol. Simul., 1991, 6, 239–244 CrossRef.
- C. I. Bayly, P. Cieplak, W. D. Cornell and P. A. Kollman, J. Phys. Chem., 1993, 97, 10269–10280 CrossRef CAS.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935 CrossRef CAS.
- M. J. Abraham, T. Murtola, R. Schulz, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 2, 19–25 CrossRef.
- A. Toukmaji, C. Sagui, J. Board and T. Darden, J. Chem. Phys., 2000, 113, 10913 CrossRef CAS.
- G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 014101 CrossRef PubMed.
- M. Parrinello and A. Rahman, J. Appl. Phys., 1981, 52, 7182–7190 CrossRef CAS.
- D. Selli, S. Motta and C. di Valentin, J. Colloid Interface Sci., 2019, 555, 519–531 CrossRef CAS PubMed.
- D. Selli, M. Tawfilas, M. Mauri, R. Simonutti and C. di Valentin, Chem. Mater., 2019, 31, 7531–7546 CrossRef CAS PubMed.
- A. Barducci, G. Bussi and M. Parrinello, Phys. Rev. Lett., 2008, 100, 1–4 CrossRef PubMed.
- F. Moraca, J. Amato, F. Ortuso, A. Artese, B. Pagano, E. Novellino, S. Alcaro, M. Parrinello and V. Limongelli, Ligand binding to telomeric G-quadruplex DNA investigated by funnel-metadynamics simulations, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, E2136–E2145 CrossRef CAS PubMed.
- V. Mlýnský and G. Bussi, J. Phys. Chem. Lett., 2018, 9, 313–318 CrossRef PubMed.
- Y. Wang, S. Parmar, J. S. Schneekloth and P. Tiwary, ACS Cent. Sci., 2022, 8, 741–748 CrossRef CAS PubMed.
- R. Evans, L. Hovan, G. A. Tribello, B. P. Cossins, C. Estarellas and F. L. Gervasio, J. Chem. Theory Comput., 2020, 16, 4641–4654 CrossRef CAS PubMed.
- A. Pandini, D. Fraccalvieri and L. Bonati, Curr. Top. Med. Chem., 2013, 13, 642–651 CrossRef CAS PubMed.
- D. Miljković, MIPRO, 2017, 1061–1066 Search PubMed.
- T. Kohonen, Neural Networks, 2013, 37, 52–65 CrossRef PubMed.
- A. B. Mantsyzov, G. Bouvier, N. Evrard-Todeschi and G. Bertho, Adv. Appl. Bioinf. Chem., 2012, 5, 61–79 CAS.
- D. Fraccalvieri, A. Pandini, F. Stella and L. Bonati, BMC Bioinf., 2011, 12, 158 CrossRef PubMed.
- S. Motta, A. Pandini, A. Fornili and L. Bonati, J. Chem. Theory Comput., 2021, 17, 2080–2089 CrossRef CAS PubMed.
- T. Li, S. Motta, A. O. Stevens, S. Song, E. Hendrix, A. Pandini and Y. He, JACS Au, 2022, 2, 1935–1945 CrossRef CAS PubMed.
- E. Hendrix, S. Motta, R. F. Gahl and Y. He, J. Phys. Chem. B, 2022, 126, 7934–7942 CrossRef CAS PubMed.
- S. Motta, L. Callea, L. Bonati and A. Pandini, J. Chem. Theory Comput., 2022, 18, 1957–1968 CrossRef CAS PubMed.
- R. Wehrens, JSS Journal of Statistical Software Search PubMed.
- R. Wehrens and J. Kruisselbrink, J. Stat. Softw., 2018, 87, 1–18 Search PubMed.
- M. C. Bruzzoniti, C. Sarzanini, A. M. Torchia, M. Teodoro, F. Testa, A. Virga and B. Onida, J. Mater. Chem., 2011, 21, 369–376 RSC.
- K. L. Cheng, K. Ueno and T. Imamura, CRC Handbook of Organic Analytical Reagents, CRC Press, Boca Raton, 1982 Search PubMed.
- G. Bouvier, N. Desdouits, M. Ferber, A. Blondel and M. Nilges, Bioinformatics, 2015, 31, 1490–1492 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3nr00397c |
| This journal is © The Royal Society of Chemistry 2023 |