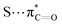Impacts of noncovalent interactions involving sulfur atoms on protein stability, structure, folding, and bioactivity
Volga
Kojasoy
 and
Dean J.
Tantillo
and
Dean J.
Tantillo
 *
*
Department of Chemistry, University of California, Davis, 1 Shields Avenue, Davis, CA 95616, USA. E-mail: djtantillo@ucdavis.edu
First published on 4th November 2022
Abstract
This review discusses the various types of noncovalent interactions in which sulfur atoms participate and their effects on protein stability, structure, folding and bioactivity. Current approaches and recommendations for modelling these noncovalent interactions (in terms of both geometries and interaction energies) are highlighted.
1. Introduction
How does the presence of sulfur atoms in proteins affect structure, stability, and bioactivity? The conformational stability of a protein is characterized as the free energy change between its folded and unfolded states, which generally amounts to 5–15 kcal mol−1.1–5 A balance (sometimes compromise) between many individual (but often interdependent) noncovalent interactions generates each unique folded structure.2,4,6,7 Noncovalent interactions involving sulfur atoms (S), although generally receiving less attention than those involving oxygen and nitrogen, play essential roles in protein structure and, as a result, stability, and function.8–11Many examples of interactions involving sulfur have been shown to have important biological consequences. For example, the attractive electrostatic interaction between sulfur and oxygen atoms in thiazole nucleoside analogues was found to be important for their antitumor activity.12 Sulfur, being a highly polarizable atom, is able to participate in strong dispersion interactions that allow the sulfur containing amino acids methionine (Met) and cysteine (Cys) to make large contributions to the overall 3-dimensional structure and function of membrane proteins.13 While the formation of disulfide bonds between Cys residues is a key means of stabilizing the tertiary structure of a protein, Brandt et al. revealed that the cleavage of disulfide bonds promoted by sulfur–oxygen interactions can play a critical role in receptor activation.14 It also was suggested that the reduction of disulfide bonds to thiols—a reaction that modifies that types of noncovalent interactions available for the Cys residues involved—impairs the binding affinity of SARS-CoV/CoV-2 spike protein to the angiotensin-converting enzyme 2, which is the receptor that enables entering the host cells.15
There have been many excellent reviews on the importance of noncovalent interactions in biological systems, for example, those by Diederich,10,16,17 Meanwell,18 Stahl,19 Schreiner,9 and Raines.11 Of particular note is Meanwell and co-workers’ review on applications of noncovalent interactions involving sulfur in drug design. Here we provide a catalog of types of noncovalent interactions involving sulfur atoms, along with details of from computational studies on their physical nature and examples of their occurrence specifically in proteins. On the basis of this data, we also provide recommendations for computational chemists modelling systems containing such interactions.
2. Computational approaches for modelling noncovalent interactions
2.1. Geometries
The initial step of a computational study on noncovalent interactions generally involves determining a reasonable geometry for the system of interest. Strengths of noncovalent interactions, and contributions to these strengths from different physical factors, are geometry (distance, angle, etc.) dependent.20,21 In general, one is interested in the lowest energy conformer on a multidimensional potential energy surface (PES). While the lowest energy conformers often correspond to bioactive conformers, one should keep in mind that that need not always be the case. There are many conformational sampling algorithms that vary in accuracy and required computational time (cost).22–29 A systematic search would explore the whole potential energy surface for each degree of freedom; that completeness comes at a high computational cost, however. In contrast, a knowledge-based approach would be faster, since it would cover only a portion of the conformational space, but if it covers the relevant portion then all is well. Random searches (e.g., Monte Carlo) and simulated annealing (artificially applying a high temperature to get over barriers) can be used to attempt to sample multiple regions of a PES. Molecular dynamics (MD) can be used to sample conformational changes over time. If one is interested in aqueous solution, then implicit or explicit solvent must be included as well. Detailed descriptions of these (and many other) techniques are beyond the scope of this review, but ref. 24–31 provide good starting points for interested readers. Sometimes the validity of a computed structure is assessed through comparison with experimental data (crystallography, NMR, circular dichroism, etc.).29 However, the limits of these experimental methods should always be kept in mind, e.g., NMR shifts could represent contributions from several interconverting conformers, the geometric parameters obtained from an X-ray crystal structure may be influenced by crystal packing forces, etc.2.2. Interaction energies
Prediction of protein–ligand binding affinity is an indispensable tool in drug discovery.32–42 Here we are concerned, however, with the strengths of interactions between two protein substructures. Estimating such interaction energies is difficult. Often, what is done is to “cut” the groups of interest out of the protein context to arrive at a complex of two small molecules whose interaction energy can then be evaluated by comparing the energy of the complex with the energy of the two separate molecules. Such an estimate, of course, comes with caveats, the most significant being that the effects of the surrounding protein environment are not taken into account. That is okay, though, if one wishes to assess the inherent strength of an interaction.2.3. Origins of attraction
The 3-dimensional structure of a protein is maintained through the interplay of multiple noncovalent interactions. Here we describe the commonly used theoretical approaches for assessing the origins of attraction (and repulsion) in noncovalent interactions. Note that these tools may provide numbers, but the results should be treated as qualitative in nature, given the issues described below.32Noncovalent interaction (NCI) analysis33 is a popular method for visualizing the noncovalent interaction regions in molecules. Users can generate color-coded reduced density gradient isosurfaces (NCI plots) in which blue, green and red represent strong attraction, weak (typically, van der Waals) attraction, and strong repulsion, respectively (Fig. 1). For large, complex systems, it is not convenient to use routine NCI analysis. One solution is to apply NCI analysis based on promolecular density in which predetermined electron density of the atoms in their free-states is used. Alternatively, independent gradient model (IGM) analysis based on promolecular density can also be applied to large systems at a reduced computational time and cost.34 Also, with the IGM method, one can visualize interactions at a specific region of interest rather than visualizing all the interactions present within the system. Program packages such as Multiwfn support these types of wavefunction analysis.35
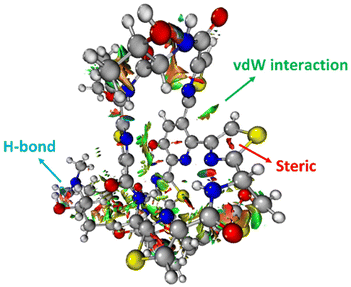 | ||
| Fig. 1 An NCI plot for glycothiohexide α.46 | ||
Another approach, the quantum theory of atoms in molecules (QTAIM),36,37 is used to characterize the properties of chemical bonds via a topological analysis of electron density. In QTAIM, the presence of a bond critical point (BCP) is often used to argue for bonding between atoms. It has been argued that at a BCP, for some cases, the sign of the energy density may correspond to the nature of the bond, positive and negative values representing noncovalent and covalent interactions, respectively.38 This argument has been extended to a point where a positive value of energy density per unit electron at a BCP (also defined as bond degree) represents a noncovalent bond and hence, a weak interaction.39 While the exact connections between the quantities computed with QTAIM and the bonding concepts used by organic and bioorganic chemists are still argued about, this tool can still prove useful for comparing interactions to each other.
Natural bond orbital (NBO)40 calculations allow for the computation of orbital interaction energies between NBOs that correspond to localized (2-center 2-electron, Lewis-like) bonds. Second-order perturbation NBO energies provide estimates of contributions from donor–acceptor (filled-empty) and donor-donor (filled-filled) orbital interactions.
Another approach is energy decomposition analysis (EDA).41 This widely used tool partitions interaction energies between two moieties into physically meaningful components such as exchange-repulsion, electrostatics, polarization and charge-transfer. Since there are many possible ways of partitioning energy, there exist different types of EDA approaches that can be classified into two main groups: variational and perturbation-based methods. Variational methods such as Kitaura–Morokuma analysis,42,43 and absolutely localized molecular orbital EDA (ALMO EDA)44 use intermediate wavefunctions (which provide expression for the monomers) to decompose interaction energy. On the other hand, in perturbation-based methods such as symmetry-adapted perturbation theory (SAPT),45 the interaction energy is constructed as perturbative corrections to the isolated fragments. We direct our readers to Phipps et al.'s review for detailed descriptions and comments on limitations of the EDA methods used in biomolecular systems.41
3. Noncovalent interactions involving sulfur atoms
We catalogue different types of sulfur noncovalent interactions present in biological systems below. Both experimental and computational studies that address energetic and geometric contributions of sulfur-based noncovalent interactions to stability and bioactivity are reviewed.3.1. Hydrogen bonds involving sulfur atoms
Whereas the thioether-containing Met sidechain can accept hydrogen bonds, the thiol-containing Cys can both accept and donate hydrogen bonds.47 Furthermore, the sulfur atoms in disulfide bonds can form bifurcated hydrogen bonds, i.e., hydrogen bonding motifs that include both sulfur atoms acting as hydrogen bond acceptors.48,49 While the majority of hydrogen bond lengths observed in proteins range from 2.7 to 3.3 Å,50 sulfur containing hydrogen bonds are longer compared to hydrogen bonds where oxygen and nitrogen atoms are involved, since sulfur is a highly polarizable atom with a comparatively large atomic radius. In addition, electronegativity is key to the strength of hydrogen bonds, and sulfur is less electronegative (2.58 on the Pauling scale) than oxygen (3.44) and nitrogen (3.04), suggesting that its hydrogens bonds might be weaker. Nonetheless, these weak interactions can be important contributors to the overall shapes of proteins.51,52While O⋯H–O type hydrogen bonds are generally dominated by electrostatic effects, which are smaller for S⋯H–O type hydrogen bonds, the contribution of dispersion interactions is larger in S⋯H–O type hydrogen bonds due to the high polarizability of sulfur.47,53 Biswal et al. used complexes between thioethers and para-cresol to mimic S⋯H–O interactions between Met and tyrosine (Tyr). Their experimental and computational results show that O⋯H–O hydrogen bonding is stronger than that of S⋯H–O hydrogen bonding, but, for S⋯H–O interactions, the longer the alkyl chain in the acceptor, stronger the binding of the complex,47 hinting at effects beyond direct hydrogen bonding. A representative example of an S⋯H–O type hydrogen bond in a protein, here a Met–Tyr interaction of the type examined by Biswal et al., is shown in Fig. 2.47,54
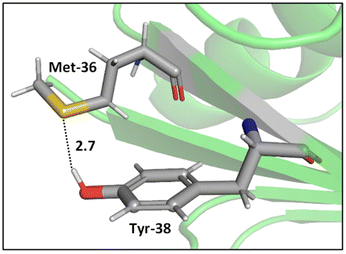 | ||
| Fig. 2 S⋯H–O hydrogen bonding interaction between the S of Met-36 and O–H of Tyr-38 (PDB ID: 1A2Z54). Distances shown in Å. | ||
Gregoret et al. surveyed 85 protein structures for hydrogen bonds involving sulfur atoms.48 They found that hydrogen bonding is not common for Met residues, which could be attributed to the hydrophobic nature of Met. On the other hand, they observed that deprotonated Cys can act as an acceptor of hydrogen bonds from hydroxyl groups. Their study revealed that Cys residues participate in hydrogen bonding more abundantly. Thus, they suggest that Cys's propensity for participating in hydrogen bonding between the thiol group of a Cys (i) and the carbonyl oxygen of residue i-4 may have a direct influence helical conformational preferences.48
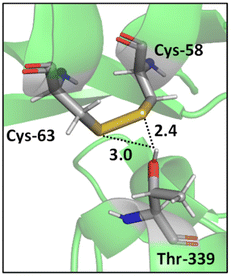
In addition, a statistical analysis conducted on >500 protein structures by Zhou et al. suggested that bifurcated hydrogen bonds involving sulfur contacts are prevalent in proteins.49 For instance, Fig. 3 shows a bifurcated hydrogen bond between two sulfur atoms of a disulfide bond (Cys-58 and Cys-63 residues) acting as acceptors and Thr-339 acting as donor. This interaction unites two α helices.55
Mons and co-workers reported a combined gas-phase spectroscopy and quantum chemistry study on S⋯H–Nbackbone hydrogen bonds in N-acetyl-L-phenylalaninyl-L-methionine-amide and N-acetyl-L-methioninyl-L-phenylalanine-amide dipeptides in solvent-free environments created using a supersonic expansion.57 Both systems showed a local folding of the Met side-chains associated with hydrogen bonds between the sulfur and the neighboring NH(i) or NH(i + 1) amides of the backbone. At 300 K the stability brought by the Met side-chain folding was predicted to be ∼2 kcal mol−1 (at the RI-B97-D/QZVPP level). An example of the local folding of Met residues via hydrogen bonding in the context of a protein is shown in Fig. 4.58
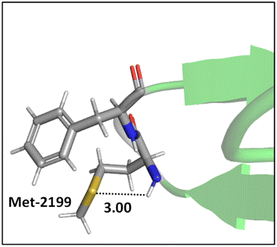 | ||
| Fig. 4 The local folding of Met-2199 via S⋯H–N hydrogen bonding interaction (PDB ID: 1D7P58). Distances shown in Å. | ||
Lampkin and VanVeller, studied the influence of geometry and dielectric properties on the strength of S⋯H–N hydrogen bonding in thioamides and showed that hydrogen bonds involving thioamides as hydrogen bond donors range in strength from 1.0–1.5 kcal mol−1.59 They reported that hydrogen bonding contact angle (Table 1) is strongly affected by the nature of the hydrogen bond donor and acceptor. For instance, they calculated an optimized hydrogen bonding contact angle of 116° when the thioamide and amide are hydrogen bond donor and acceptor, respectively (Table 1, entry 2). However, an optimized hydrogen bonding contact angle of 97° was found when the hydrogen bond acceptor and donor are thioamide and amide, respectively (Table 1, entry 3), which is consistent with the involvement of a σ-hole in the thioamide electrostatic potential map (Table 1, top right). Overall, they showed that the thioamides act as good hydrogen bond acceptors when the hydrogen bond contact angle is between 90° and 100, whereas amides can tolerate different angles.59 The geometry of these hydrogen bonds appears to be determined mainly by dipole–dipole interactions.60
| Entry | X | Y | Geometry | Interaction energy (ΔH, kcal mol−1) | ||
|---|---|---|---|---|---|---|
| d (Å) | θ (°) | Gas phase | Water (SMD) | |||
| a Numbers in parentheses are the relative energies with respect to entry 1. Interaction energies are calculated at CCSD(T)-SMD/aug-ccpVDZ//ωB97XD-SMD/aug-cc-pVDZ level of theory. Electrostatic potential maps generated at B3LYP/6-311+g(d,p) with an isovalue of 0.04. Adapted with permission from B. J. Lampkin and B. VanVeller, J. Org. Chem., 2021, 86, 18287–18291. Copyright 2021 American Chemical Society | ||||||
| 1 | O | O | 1.92 | 116 | −7.27 | −3.06 |
| 2 | S | O | 1.89 | 116 | −8.86 (−1.58)a | −4.00 (−0.93)a |
| 3 | O | S | 2.45 | 97 | −6.89 (+0.38)a | −3.30 (−0.23)a |
The energy associated with hydrogen bonds is sensitive to the environment. Hydrogen bonds in vacuum and hydrophobic environments are generally much stronger than hydrogen bonds in polar environments like water. This reduction in the strength can be attributed in part to screening of attractive electrostatic interactions and to entropic effects. Lampkin and VanVeller's study exemplifies the effect of solvent as well.59 They tested the strength of S⋯H–N hydrogen bonds in implicit water solvent and found weaker interactions than in the gas phase. Moreover, they found that thioamides are slightly stronger hydrogen bond acceptors compared to amides in polar media. With regard to entropy, in vacuum, peptide side-chains fold back to form internal hydrogen bonds, whereas in water they have other options.60–62
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1).49 Paul and Thomas studied S–H⋯O hydrogen bonds using local energy decomposition (LED)63 analysis on different thiol–water complexes and showed that the binding energy of the resulting hydrogen bonds ranges from −2.1 to −3.6 kcal mol−1 and the dominant source of stabilization in these complexes was electrostatic attraction.64 NBO analysis on these systems also pointed to the importance of
1).49 Paul and Thomas studied S–H⋯O hydrogen bonds using local energy decomposition (LED)63 analysis on different thiol–water complexes and showed that the binding energy of the resulting hydrogen bonds ranges from −2.1 to −3.6 kcal mol−1 and the dominant source of stabilization in these complexes was electrostatic attraction.64 NBO analysis on these systems also pointed to the importance of 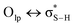 orbital interactions (the natural orbital interaction energies for selected thiol–water complexes varied from ∼3–5.5 kcal mol−1 at the B3LYP/cc-pVTZ level of theory).
orbital interactions (the natural orbital interaction energies for selected thiol–water complexes varied from ∼3–5.5 kcal mol−1 at the B3LYP/cc-pVTZ level of theory).
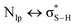 ), electrostatic and dispersion interactions are also important contributors.
), electrostatic and dispersion interactions are also important contributors.
3.2. S⋯O and S⋯N interactions
Although sometimes overlooked, S⋯O and S⋯N interactions are common in biological systems. For example, more than two decades ago, Nagao et al. revealed that an S⋯O interaction (∼2.5 Å) was present in the (acylimino)thiadiazoline moiety of a class of angiotensin II receptor antagonists.67 In general, an interatomic S⋯O distance shorter than the sum of sulfur and oxygen van der Waals radii (3.32 Å) is taken as an indication of the presence of a favorable S⋯O interaction. While there is some debate over the origins of close S⋯O and S⋯N contacts,68 both electrostatic and dispersion interactions are known to contribute and these can be comparable in strength.69 The electrostatic stabilization comes from attraction between partially positively charged sulfur (note that sulfur is not very electronegative and is frequently found near to electron-withdrawing groups in biological settings) and partially negatively charged oxygen or nitrogen.12 In addition to electrostatic and dispersion interactions, donor–acceptor orbital interactions (e.g.,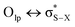 ) also are significant for the directional preference of S⋯O and S⋯N contacts,70 even if these are counterbalanced by S lone pair/O or N lone pair repulsion.68 Recently, Biswal et al. found that interaction energies associated with donor–acceptor orbital interactions (
) also are significant for the directional preference of S⋯O and S⋯N contacts,70 even if these are counterbalanced by S lone pair/O or N lone pair repulsion.68 Recently, Biswal et al. found that interaction energies associated with donor–acceptor orbital interactions (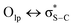 ) are typically ∼2 kcal mol−1 and ∼1 kcal mol−1 for small molecules obtained from the Cambridge Structural Database (CSD) and the Protein Data Bank (PDB), respectively.71
) are typically ∼2 kcal mol−1 and ∼1 kcal mol−1 for small molecules obtained from the Cambridge Structural Database (CSD) and the Protein Data Bank (PDB), respectively.71
3.3. Interactions involving π-systems
A statistical analysis on sulfur–aromatic interactions was carried out by Zauhar et al. by collecting all crystal structures that contain at least one divalent sulfur atom and a phenyl ring from the Cambridge Crystallographic Database.72 The results suggest that, for an ideal interaction the sulfur–aromatic distance should be ∼5 Å and the sulfur should be placed in the plane of the ring as opposed to the trend observed for proteins, which places sulfur above the ring plane. This contradiction may be attributed to the stacking interactions present in small planar molecules that favor edge-on interactions or to the crystal packing forces that play crucial roles in controlling overall geometries, especially when weak interactions are involved. Energy analysis showed that a single sulfur–aromatic interaction contributes ∼1–2 kcal mol−1 to the stability of a protein and involves both van der Waals and electrostatic components, with their relative contributions varying with structure. There are several common structural motifs in which sulfur atoms are ∼5 Å away from aromatic rings, differing by which, if any, groups shield the sulfur atom from the π-electrons of the aromatic system.Pranata investigated dimethyl sulfide (DMS)–benzene complexes, models of a Met sidechain and an aromatic residue, in detail.78 Three different orientations of DMS–benzene complexes were studied (Fig. 5). Ab initio calculations based on isolated molecules (not necessarily PES minima) predicted that complex I (Fig. 5) had the largest interaction energy (−2.9 kcal mol−1 at the MP2/6-31G* level) and the shortest contact distance from the sulfur atom to the center of the benzene ring (4.9 Å) (compared to complex II and complex III). Note that upon full optimization of complex II at the MP2/6-31G* level, a structure similar to complex I, but with the DMS horizontally displaced, was generated, which also was predicted to have an interaction energy of −2.9 kcal mol−1. This study also suggested that the molecular mechanics force fields AMBER95 and OPLS-AA can reproduce the MP2/6-31G* results.
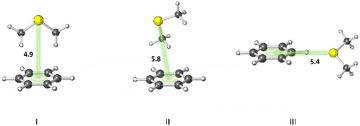 | ||
| Fig. 5 Three different orientations of DMS–benzene complexes. (I) The sulfur atom is placed on the symmetry axis of the benzene ring and the two methyl groups are directed towards the face of the benzene ring. (II) One of the methyl groups is oriented towards the face of the benzene ring. (III) The sulfur atom is pointed towards the edge of the benzene ring. Distances shown in Å.78 | ||
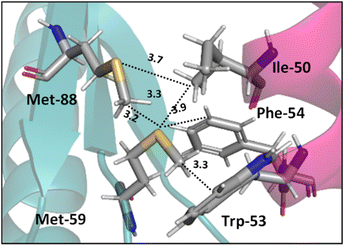
Interactions analogous to those in complex II (Fig. 5) are found in protein structures. For example, Di Lello et al. determined the structure of a complex formed by the interaction between the amino-terminal transactivation domain of p53 and the pleckstrin homology domain of transcription factor b1 (Tfb1) by high-resolution NMR.79 In the Tfb1/p53 binding interface (shown in Fig. 6) the Met-59 residue participates in sulfur–π interactions with Trp-53. Additional contacts present between the isoleucine (Ile) and phenylalanine (Phe) residues of p53 and the Met residues of Tfb1 contribute to the overall stability of the complex.
The S–H⋯π interactions in indole·H2S (IND·H2S) and 3-methylindole·H2S (3-MI·H2S) complexes, models of Cys interacting with the sidechain of tryptophan (Trp), were studied by Biswal and Wategaonkar.80 Both σ-type (O–H⋯S and N–H⋯S; see sections 3.1.1–2) and π-type (S–H⋯π; Fig. 7) complexes were investigated. Computations at the MP2/aug-cc-pVDZ level of theory suggested that the binding energies for π-type and σ-type IND·H2S complexes are −4.9 and −2.7 kcal mol−1, respectively. Similarly, the binding energies for π-type and σ-type 3-MI·H2S complexes are −5.2 and −2.7 kcal mol−1, respectively. In contrast, for IND·H2O and 3-MI·H2O complexes, σ-type complexes are preferred. Moreover, they found that the S–H⋯π interaction was stronger than other X–H⋯π (X = C, N, O) interactions.
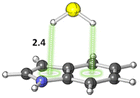 | ||
| Fig. 7 π-type IND·H2S complex. Distances shown in Å.80 | ||
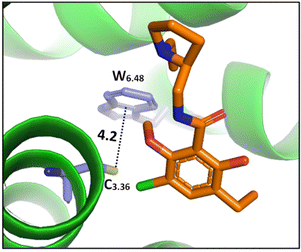 | ||
| Fig. 8 The cocrystal structure (PDB ID: 3PBL) of the dopamine D3 receptor bound to antagonist eticlopride (in orange). Distances shown in Å.82 | ||
To compare the strengths of direct interactions between the π-faces of aromatic rings with oxygen and sulfur, Motherwell et al. prepared the series of oxathiolanes shown in Fig. 9 (and others), which can adopt conformations with either an oxygen or sulfur atom proximal to an aromatic ring.83 Based on their results, it appears that (a) oxygen atoms do not like to be near the π-faces of electron-rich aromatics, (b) sulfur atoms do not mind being near the π-faces of electron-rich aromatics, (c) oxygen atoms do not mind being near the π-faces of electron-poor aromatics. While it is difficult to pin down the relative contributions of attraction and repulsion in such systems, it is clear that sulfur can reside near the π-face of aromatics, even electron-rich ones, likely a consequence of its polarizability.
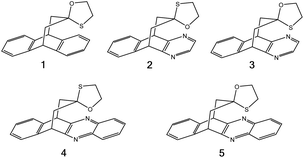 | ||
| Fig. 9 π systems studied by Motherwell et al. to compare S⋯π versus O⋯π noncovalent interactions.83 | ||
Viguera and Serrano's work on sidechain interactions between sulfur containing amino acids (Cys and Met) and phenylalanine (Phe) residues—the first experimental analysis probing helix stability mediated by Phe and Cys/Met interactions—showed that these interactions are related directly to the stability of α helices.84,85 The origins of this α helix stability appears to come from both the hydrophobic nature of the aromatic rings and the electrostatic interactions between the S and the aromatic ring (primarily dispersion).
Two tumor necrosis factor (TNF) ligand–receptor complexes TRAIL-DR5 and LTα-TNFR1 were examined both experimentally via vitro cellular experiments and computationally to probe the role of the Met–aromatic binding motif.76 DR5-Met/TRAIL-Tyr (left) and TNFR1-Trp/LTα-Met (right) interactions are shown in Fig. 10. Molecular dynamics simulations were used to obtain bioactive conformers that match with those in the Protein Data Bank (PDB). The results from quantum mechanical calculations suggested that dispersive sulfur–aromatic interactions at around 5 Å separation provide extra stability (∼1–1.5 kcal mol−1) to the protein compared to interactions within their analogues where sulfur was replaced with CH2. Note that SC–H⋯π interactions (section 3.3.1) may also contribute here (and in the following cases).
 | ||
| Fig. 10 Crystal structures of TRAIL-DR5 showing DR5-Met/TRAIL-Tyr interaction (left, PDB ID: 1d0g) and LTα-TNFR1 showing TNFR1-Trp/LTα-Met interaction (right, PDB ID: 1tnr). Both Met–aromatic contacts are at around 5 Å separation. Distances shown in Å.76 | ||
Tatko and Waters investigated the nature of sulfur-π interactions in a β-hairpin by putting a Met residue diagonal to an aromatic ring (Trp or Phe) (Fig. 11).86 The proximity between Met and the aromatic ring provides a suitable geometry for sulfur-π contacts to occur. They found that the Met significantly contributes to β-hairpin stability with a hydrophobic driving force (for instance, as determined by double-mutant cycles, Met–Phe interaction contributes −0.31 kcal mol−1).
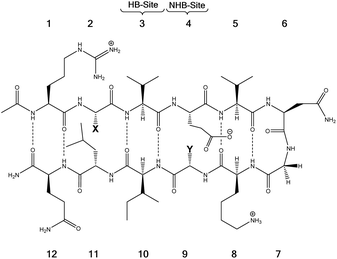 | ||
| Fig. 11 The model system consisting of 12 amino acids. X (= Phe, Trp, Cha) and Y (= Lys, Nle, Met) are the diagonal interacting residues. The hydrogen bonded and nonhydrogen-bonded sites are abbreviated as HB-site and NHB-site, respectively.86 | ||
Albanese and Waters examined the role of sulfur in the Met residues in the binding of a gene expression regulator trimethyllysine (Kme3).87 They probed the recognition of Kme3 by the Met containing aromatic cage in the reader proteins DIDO1 and TAF3 by systematic mutational studies (Fig. 12). For both systems, they observed a change in the NMR chemical shifts of the Met residue upon binding histone 3 K4me3 (H3K4me3), which indicated the presence of a binding interaction. Linear free energy relationships suggested that the origin of this Met–Kme3 binding was dispersive, which again could be attributed to the high polarizability of sulfur. They also found that the charge on Kme3 did not alter the interaction with the Met, which suggested that the electrostatic interactions (sulfur–cation) do not contribute significantly to binding.87
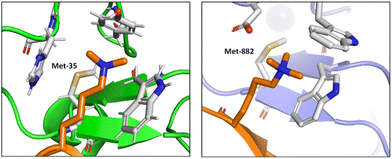 | ||
| Fig. 12 The molecular recognition of H3K4me3 (in orange) by DIDO1 (in green, PDB ID: 4L7X) and TAF3 (in purple, PDB ID: 5WXH).87 | ||
A study on a cisplatin–(1,3-GTG) cross-link within DNA polymerase η revealed that the Met residue in the DNA polymerase η participates in sulfur–arene interactions, which helps maintain the folded geometry of the protein complex and blocks the movement of the polymerase along the DNA strand (Fig. 13).88 In this complex, both S⋯π and SC–H⋯π interactions are present.
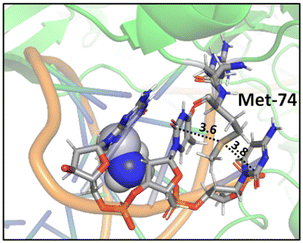 | ||
| Fig. 13 Crystal structure of cisplatin–(1,3-GTG) lesion in complex with DNA polymerase η (PDB ID: 2WTF). The Met residue surrounded by nucleobases blocks the movement of the polymerase along the DNA strand. Distances shown in Å.88 | ||
Recently, Waters and coworkers compared the strength of the sulfonium⋯π, S⋯π and ammonium⋯π interactions in a β-hairpin peptide model system via a combination of computational studies and analysis of structures in the PDB.89 They found that, presumably due to sulfur's higher polarizability, sulfonium⋯π interactions are stronger than ammonium⋯π interactions. Further comparison of sulfonium⋯π and S⋯π interaction energies by the analysis of S-adenosylmethionine (SAM) and S-adenosylhomocysteine (SAH)-bound proteins in the PDB highlighted the importance of charge. They found similar aromatic interactions between SAM and SAH except for the methyl⋯π interaction that is only present in SAM, which highly influences the bioactivity of SAM-dependent methyltransferases (Fig. 14).89 This interaction is an example of a SC–H⋯π interaction (section 3.3.1) enhanced by charge.
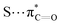 interactions.
n → π* interactions resulting from the overlap of lone pairs (n) and π* antibonding orbitals along the Bürgi–Dunitz trajectory play an important role in maintaining the conformational stability of proteins (Fig. 15).90,91 Similar to the observations of Bürgi and Dunitz for other lone pair donors (Fig. 15B, θ angle), Chakrabarti and Pal found that the preferred S⋯C–O angle for the
interactions.
n → π* interactions resulting from the overlap of lone pairs (n) and π* antibonding orbitals along the Bürgi–Dunitz trajectory play an important role in maintaining the conformational stability of proteins (Fig. 15).90,91 Similar to the observations of Bürgi and Dunitz for other lone pair donors (Fig. 15B, θ angle), Chakrabarti and Pal found that the preferred S⋯C–O angle for the 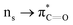 interaction is 109° (± 15°).92
interaction is 109° (± 15°).92
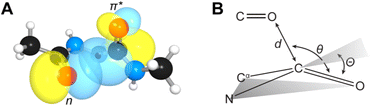 | ||
| Fig. 15 (A) n → π* orbital interaction in the backbone of bitter gourd trypsin inhibitor (PDB: 1vbw), residues 5–7. (B) Geometric parameters characterizing n → π* interaction (d: distance between the nucleophile and carbonyl; θ: angle of the nucleophilic attack; Θ: degree of pyramidalization). Adapted with permission from R. W. Newberry, G. J. Bartlett, B. VanVeller, D. N. Woolfson and R. T. Raines, Protein Sci., 2014, 23, 284–288. Copyright 2014 John Wiley & Sons, Inc. | ||
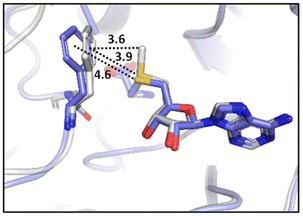
Many experimental and computational studies by Raines and co-workers have revealed the intricacies of stereoelectronic effects in tuning the secondary structures of proteins, including the importance of n → π* interactions.11,93–100 For instance, Choudhary et al. explored the origin of carbonyl–carbonyl interaction in proteins and found that thioamides are better electron-pair donors compared to their amide counterparts.93 Newberry et al. reported that the n → π* interaction between amide carbonyl groups in proteins contributes ≥0.27 kcal mol−1, and this magnitude triples when the interaction is between two thioamides due to better orbital overlap and a lower energy gap between donor and acceptor orbitals.95 They also observed an increase in the pyramidalization of the acceptor C atom as the n → π* interaction strengthens, consistent with work on related systems.93,95,100–102 The stability of the collagen triple helix – which is highly affected by hydrogen bonds and n → π* interactions103 – was also shown to be increased upon replacement of backbone amides with thioamides.94 Later, Kilgore at al. probed the importance of 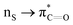 interactions in Cys residues and disulfide bonds in proteins.98 They found that nS → π* interactions provided enhanced stability and led to lowered pKa values of N-terminal Cys residues of the CXXC motifs104 (shown in Fig. 16), which are critical for redox functions. In addition, the strong
interactions in Cys residues and disulfide bonds in proteins.98 They found that nS → π* interactions provided enhanced stability and led to lowered pKa values of N-terminal Cys residues of the CXXC motifs104 (shown in Fig. 16), which are critical for redox functions. In addition, the strong 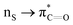 interactions present in vicinal disulfide bonds led to an electropositive (and hydrophobic site) for ligand binding.98
interactions present in vicinal disulfide bonds led to an electropositive (and hydrophobic site) for ligand binding.98
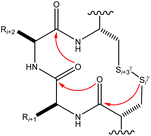 | ||
| Fig. 16 The map of n → π* interactions inside the CXXC motif.98 | ||
3.4. Generalizations
Table 2 represents the typical magnitudes and the major sources of stabilization for the sulfur noncovalent interactions reviewed here. However, we would like to warn our readers that the magnitude of stabilization may vary, since it highly depends on the system of interest and its environment.4. Recommendations for modelers
Computational chemistry is an indispensable tool to study noncovalent interactions in biological systems. With the aid of quantum chemical calculations, one can investigate these interactions both qualitatively and quantitatively. Nowadays, most computational studies on noncovalent interactions are carried out using density functional theory (DFT),105 a versatile computational modelling method for calculating the electronic structure of atoms and molecules. However, the choice of which method to use – DFT or a more expensive but more accurate method – depends on the system of interest. One generally faces a compromise between accuracy and computational cost (i.e., time for calculations to finish with available computer resources). Here, we recommend a few methods that have been found useful for studying noncovalent interactions involving sulfur atoms. The DFT functionals that account for dispersion correction such as ωB97X-D,106 M06-2X,107–109 PBE0-D3,110,111 B3LYP-D3(BJ)105,112–114 have been commonly used in geometry optimizations and provided reasonable results.53,56,64,71,115–118 Due to issues with DFT in describing dispersion interactions, many have chosen second-order Møller–Plesset perturbation theory (i.e., MP2) or coupled cluster (CC) theory with single, double and perturbative triple excitations (i.e. CCSD(T)).47,53,65,66,77,116,117,119–121,122 For small systems, these methods can be affordable. A study by Rothlisberger and co-workers showed that dispersion corrected atom centered potentials (DCACPs)123,124 significantly improve the DFT description of the weak interactions of sulfur-containing molecules and the resulting DFT method correctly reproduces MP2 or CCSD(T) binding energies.120 For basis sets, double-ζ or triple-ζ Pople type basis sets that include diffuse and polarization functions, Weigend's def2-TZVP125,126 basis set, and Dunning's correlation-consistent cc-pVnZ or augmented correlation-consistent aug-cc-pVnZ (where n = D, T, or Q) basis sets127–131 are commonly used in calculations on sulfur-based noncovalent interactions.53,56,64–66,71,77,115–117,119–121 To obtain reliable interaction energies, the counterpoise correction for basis set superposition error (BSSE)132 and corrections for zero-point vibrational energies are recommended, especially when small basis sets are used.133–135If one wishes to include solvent in one's modelling, there are three general approaches: implicit solvation, explicit solvation, and a hybrid of the two. In implicit solvation, the solvent is treated as a continuum with a certain dielectric constant (and other properties). In explicit solvation, the solvent is treated as discrete molecules. Hybrid solvation modelling involves using a few explicit solvent molecules with an implicit solvent model on top. Using an implicit model is the most affordable approach, but a hybrid approach can be used as a balancing act between a realistic and a cost-efficient treatment of solvent, especially if noncovalent interactions between solute and solvent are important.136–138
If one wishes to include a whole protein in one's modelling, the Quantum Mechanics/Molecular Mechanics (QM/MM) approach is the way to go. This approach was introduced by Warshel and Levitt in the 1970s.139,140 The QM/MM method is an efficient way of studying large systems in which a small region of the system—that where the key chemical processes take place—is treated quantum-mechanically, while the remainder of the system is treated classically, e.g., using molecular mechanics or a force field. Recently, Jorgensen and co-workers developed a new force field that improved the representation of sulfur charge anisotropy and directional noncovalent interactions via the addition of off-atom charged sites,141 a welcome development for those modelling systems with sulfur-based noncovalent interactions. In the popular multilayer approach known as ONIOM, a large biomolecule is divided into “n” number of layers and each layer is treated with a different model chemistry (i.e, ab initio, semi-empirical and molecular mechanics) at a reduced cost.142,143 We recommend a careful consideration in choosing suitable QM and MM methods, how one partitions a system into QM and MM regions, and how one treats the interactions between QM and MM regions. Along these lines, we direct readers to recent reviews for a deeper dive into QM/MM modelling.144,145
5. Conclusion and outlook
While sulfur may not receive the same attention as carbon, hydrogen, nitrogen, and oxygen, it plays many important roles in biology. Here we have summarized the variety of types of noncovalent interactions in which it participates, illustrated with examples from protein structures and accompanied by accounts of theoretical studies on preferred geometries and interaction energies. We hope that bringing these examples together will inspire readers not only to consider noncovalent interactions involving sulfur when examining structures of biological molecules that have captured their interest, but also to make use of them in designing new molecules of biological relevance.Author contributions
Both authors wrote and edited the text.Conflicts of interest
The authors have no conflicts of interest to report.Acknowledgements
We gratefully acknowledge continued financial and computational support from the US National Science Foundation.References
- K. A. Dill, Biochemistry, 1990, 29, 7133–7155 CrossRef CAS.
- C. N. Pace, Trends Biotechnol., 1990, 8, 93–98 CrossRef CAS.
- C. N. Pace, Trends Biochem. Sci., 1990, 15, 14–17 CrossRef CAS.
- S. R. Trevino, S. Schaefer, J. M. Scholtz and C. N. Pace, J. Mol. Biol., 2007, 373, 211 CrossRef CAS.
- M. C. Deller, L. Kong and B. Rupp, Acta Crystallogr., Sect. F: Struct. Biol. Commun., 2016, 72, 72 CrossRef CAS.
- M. L. Waters, Pept. Sci., 2004, 76, 435–445 CrossRef CAS.
- S. Jena, J. Dutta, K. D. Tulsiyan, A. K. Sahu, S. S. Choudhury and H. S. Biswal, Chem. Soc. Rev., 2022, 51, 4261–4286 RSC.
- S. L. Cockroft and C. A. Hunter, Chem. Soc. Rev., 2007, 36, 172 RSC.
- J. P. Wagner and P. R. Schreiner, Angew. Chem., Int. Ed., 2015, 54, 12274–12296 CrossRef CAS.
- E. Persch, O. Dumele and F. Diederich, Angew. Chem., Int. Ed. Engl., 2015, 54, 3290–3327 CrossRef CAS PubMed.
- R. W. Newberry and R. T. Raines, ACS Chem. Biol., 2019, 14, 1677–1686 CrossRef CAS.
- F. T. Burling and B. M. Goldstein, J. Am. Chem. Soc., 1992, 114, 2313–2320 CrossRef CAS.
- J. C. Gómez-Tamayo, A. Cordomí, M. Olivella, E. Mayol, D. Fourmy and L. Pardo, Protein Sci., 2016, 25, 1517–1524 CrossRef PubMed.
- W. Brandt, A. Golbraikh, M. Täger and U. Lendeckel, Eur. J. Biochem., 1999, 261, 89–97 CrossRef CAS.
- S. Hati and S. Bhattacharyya, ACS Omega, 2020, 5, 16292–16298 CrossRef CAS PubMed.
- E. A. Meyer, R. K. Castellano and F. Diederich, Angew. Chem., Int. Ed., 2003, 42, 1210–1250 CrossRef CAS.
- L. M. Salonen, M. Ellermann and F. Diederich, Angew. Chem., Int. Ed., 2011, 50, 4808–4842 CrossRef CAS.
- B. R. Beno, K. S. Yeung, M. D. Bartberger, L. D. Pennington and N. A. Meanwell, J. Med. Chem., 2015, 58, 4383–4438 CrossRef CAS.
- C. Bissantz, B. Kuhn and M. Stahl, J. Med. Chem., 2010, 53, 5061–5084 CrossRef CAS PubMed.
- A. K. Vitek, T. M. E. Jugovic and P. M. Zimmerman, ACS Catal., 2020, 10, 7136–7145 CrossRef CAS.
- A. V. Brethomé, S. P. Fletcher and R. S. Paton, ACS Catal., 2019, 9, 2313–2323 CrossRef.
- G. Olanders, H. Alogheli, P. Brandt and A. Karlén, J. Comput.-Aided Mol. Des., 2020, 34, 231–252 CrossRef CAS.
- T. Lewis-Atwell, P. A. Townsend and M. N. Grayson, Tetrahedron, 2021, 79, 131865 CrossRef CAS.
- J. C. Cole, O. Korb, P. McCabe, M. G. Read and R. Taylor, J. Chem. Inf. Model., 2018, 58, 615–629 CrossRef CAS.
- G. Klebe, Perspect. Drug Discovery Des., 1995, 3, 85–105 CrossRef CAS.
- G. Sliwoski, S. Kothiwale, J. Meiler and E. W. Lowe, Pharmacol. Rev., 2014, 66, 334 CrossRef.
- C. Liao, M. Sitzmann, A. Pugliese and M. C. Nicklaus, Future Med. Chem., 2011, 3, 1057 CrossRef CAS.
- A. Liwo, C. Czaplewski, S. Ołdziej and H. A. Scheraga, Curr. Opin. Struct. Biol., 2008, 18, 134 CrossRef CAS PubMed.
- N. Foloppe and I.-J. Chen, Curr. Med. Chem., 2009, 16, 3381–3413 CrossRef CAS.
- K. N. Houk, A. G. Leach, S. P. Kim and X. Zhang, Angew. Chem., Int. Ed., 2003, 42, 4872–4897 CrossRef CAS PubMed.
- D. H. Williams, E. Stephens, D. P. O'Brien and M. Zhou, Angew. Chem., Int. Ed., 2004, 43, 6596–6616 CrossRef CAS PubMed.
- S. Scheiner, J. Comput. Chem., 2022, 43, 1814–1824 CrossRef CAS PubMed.
- E. R. Johnson, S. Keinan, P. Mori-Sánchez, J. Contreras-García, A. J. Cohen and W. Yang, J. Am. Chem. Soc., 2010, 132, 6498–6506 CrossRef CAS.
- C. Lefebvre, H. Khartabil, J. C. Boisson, J. Contreras-García, J. P. Piquemal and E. Hénon, ChemPhysChem, 2018, 19, 724–735 CrossRef CAS PubMed.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- R. F. W. Bader, Chem. Rev., 1991, 91, 893–928 CrossRef CAS.
- R. F. W. Bader, Acc. Chem. Res., 1985, 18, 9–15 CrossRef CAS.
- D. Cremer and E. Kraka, Angew. Chem., Int. Ed. Engl., 1984, 23, 627–628 CrossRef.
- E. Espinosa, I. Alkorta, J. Elguero and E. Molins, J. Chem. Phys., 2002, 117, 5529 CrossRef CAS.
- F. Weinhold, C. R. Landis and E. D. Glendening, Int. Rev. Phys. Chem., 2016, 35, 399–440 Search PubMed.
- M. J. S. Phipps, T. Fox, C. S. Tautermann and C. K. Skylaris, Chem. Soc. Rev., 2015, 44, 3177–3211 RSC.
- K. Kitaura and K. Morokuma, Int. J. Quantum Chem., 1976, 10, 325–340 CrossRef CAS.
- K. Morokuma, Acc. Chem. Res., 1977, 10, 294–300 CrossRef CAS.
- R. Z. Khaliullin, E. A. Cobar, R. C. Lochan, A. T. Bell and M. Head-Gordon, J. Phys. Chem. A, 2007, 111, 8753–8765 CrossRef CAS.
- B. Jeziorski, R. Moszynski and K. Szalewicz, Chem. Rev., 1994, 94, 1887–1930 CrossRef CAS.
- V. Kojasoy and D. J. Tantillo, unpublished work.
- H. S. Biswal, Challenges Adv. Comput. Chem. Phys, 2015, vol. 19, pp. 15–45 Search PubMed.
- L. M. Gregoret, S. D. Rader, R. J. Fletterick and F. E. Cohen, Proteins: Struct., Funct., Bioinf., 1991, 9, 99–107 CrossRef CAS.
- P. Zhou, F. Tian, F. Lv and Z. Shang, Proteins: Struct., Funct., Bioinf., 2009, 76, 151–163 CrossRef CAS PubMed.
- D. F. Sticke, L. G. Presta, K. A. Dill and G. D. Rose, J. Mol. Biol., 1992, 226, 1143–1159 CrossRef.
- I. G. Kamphuis, J. Drenth and E. N. Baker, J. Mol. Biol., 1985, 182, 317–329 CrossRef CAS PubMed.
- J. F. Bazan and R. J. Fletterick, Proc. Natl. Acad. Sci. U. S. A., 1988, 85, 7872 CrossRef CAS PubMed.
- F. Wennmohs, V. Staemmler and M. Schindler, J. Chem. Phys., 2003, 119, 3208–3218 CrossRef CAS.
- M. Singleton, M. Isupov and J. Littlechild, Structure, 1999, 7, 237–244 CrossRef CAS PubMed.
- P. A. Karplus and G. E. Schulz, J. Mol. Biol., 1987, 195, 701–729 CrossRef CAS PubMed.
- C. L. Andersen, C. S. Jensen, K. Mackeprang, L. Du, S. Jørgensen and H. G. Kjaergaard, J. Phys. Chem. A, 2014, 118, 11074–11082 CrossRef CAS PubMed.
- H. S. Biswal, E. Gloaguen, Y. Loquais, B. Tardivel and M. Mons, J. Phys. Chem. Lett., 2012, 3, 755–759 CrossRef CAS PubMed.
- K. P. Pratt, B. W. Shen, K. Takeshima, E. W. Davie, K. Fujikawat and B. L. Stoddard, Nature, 1999, 402, 439–442 CrossRef CAS PubMed.
- B. J. Lampkin and B. VanVeller, J. Org. Chem., 2021, 86, 18287–18291 CrossRef CAS PubMed.
- E. S. Feldblum and I. T. Arkin, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 4085–4090 CrossRef CAS.
- S. Y. Sheu, D. Y. Yang, H. L. Selzle and E. W. Schlag, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 12683–12687 CrossRef CAS.
- J. Gao, D. A. Bosco, E. T. Powers and J. W. Kelly, Nat. Struct. Mol. Biol., 2009, 16, 684–690 CrossRef CAS PubMed.
- W. B. Schneider, G. Bistoni, M. Sparta, M. Saitow, C. Riplinger, A. A. Auer and F. Neese, J. Chem. Theory Comput., 2016, 12, 4778–4792 CrossRef CAS PubMed.
- A. Paul and R. Thomas, J. Mol. Liq., 2021, 118078 Search PubMed.
- K. Grzechnik, K. Rutkowski and Z. Mielke, J. Mol. Struct., 2012, 1009, 96–102 CrossRef CAS.
- K. Jaju, D. Pal, A. Chakraborty and S. Chakraborty, Chem. Phys. Lett.: X, 2019, 4, 100031 CrossRef CAS.
- Y. Nagao, T. Hirata, S. Goto, S. Sano, A. Kakehi, K. Iizuka and M. Shiro, J. Am. Chem. Soc., 1998, 120, 3104–3110 CrossRef CAS.
- B. M. Hudson, E. Nguyen and D. J. Tantillo, Org. Biomol. Chem., 2016, 14, 3975–3980 RSC.
- F. Zhou, R. Liu, P. Li and H. Zhang, New J. Chem., 2015, 39, 1611–1618 RSC.
- Y. N. Xiao and C. X. Zhang, Bull. Chem. Soc. Jpn., 2002, 75, 1611–1625 CrossRef.
- H. S. Biswal, A. K. Sahu, B. Galmés, A. Frontera and D. Chopra, ChemBioChem, 2022, 23, e202100498 CrossRef CAS PubMed.
- R. J. Zauhar, C. L. Colbert, R. S. Morgan and W. J. Welsh, Biopolymers, 2000, 53, 233–248 CrossRef CAS PubMed.
- A. L. Ringer, A. Senenko and C. D. Sherrill, Protein Sci., 2007, 16, 2216 CrossRef CAS PubMed.
- R. S. Morgan, C. E. Tatsch, R. H. Gushard and P. K. Warme, Int. J. Pept. Protein Res., 1978, 11, 209–217 CrossRef CAS PubMed.
- C. Reid, P. F. Lindley and J. M. Thornton, FEBS Lett., 1985, 190, 209–213 CrossRef.
- C. C. Valley, A. Cembran, J. D. Perlmutter, A. K. Lewis, N. P. Labello, J. Gao and J. N. Sachs, J. Biol. Chem., 2012, 287, 34979–34991 CrossRef CAS PubMed.
- T. P. Tauer, M. E. Derrick and C. D. Sherrill, J. Phys. Chem. A, 2005, 109, 191–196 CrossRef CAS PubMed.
- J. Pranata, Bioorg. Chem., 1997, 25, 213–219 CrossRef CAS.
- P. Di Lello, L. M. M. Jenkins, T. N. Jones, B. D. Nguyen, T. Hara, H. Yamaguchi, J. D. Dikeakos, E. Appella, P. Legault and J. G. Omichinski, Mol. Cell, 2006, 22, 731–740 CrossRef CAS PubMed.
- H. S. Biswal and S. Wategaonkar, J. Phys. Chem. A, 2009, 113, 12774–12782 CrossRef CAS PubMed.
- K. N. M. Daeffler, H. A. Lester and D. A. Dougherty, J. Am. Chem. Soc., 2012, 134, 14890–14896 CrossRef CAS PubMed.
- E. Y. T. Chien, W. Liu, Q. Zhao, V. Katritch, G. W. Han, M. A. Hanson, L. Shi, A. H. Newman, J. A. Javitch, V. Cherezov and R. C. Stevens, Science, 2010, 330, 1091–1095 CrossRef CAS PubMed.
- W. B. Motherwell, R. B. Moreno, I. Pavlakos, J. R. T. Arendorf, T. Arif, G. J. Tizzard, S. J. Coles and A. E. Aliev, Angew. Chem., 2018, 130, 1207–1212 CrossRef.
- G. Némethy and H. A. Scheraga, Biochem. Biophys. Res. Commun., 1981, 98, 482–487 CrossRef PubMed.
- A. R. Viguera and L. Serrano, Biochemistry, 1995, 34, 8771–8779 CrossRef CAS PubMed.
- C. D. Tatko and M. L. Waters, Protein Sci., 2004, 13, 2515–2522 CrossRef CAS PubMed.
- K. I. Albanese and M. L. Waters, Chem. Sci., 2021, 12, 8900–8908 RSC.
- T. Reißner, S. Schneider, S. Schorr and T. Carell, Angew. Chem. Int. Ed., 2010, 49, 3077–3080 CrossRef PubMed.
- K. I. Albanese, A. Leaver-Fay, J. W. Treacy, R. Park, K. N. Houk, B. Kuhlman and M. L. Waters, J. Am. Chem. Soc., 2022, 144, 2535–2545 CrossRef CAS PubMed.
- H. B. Biirgi, J. D. Dunitz and E. Shefter, J. Am. Chem. Soc., 1973, 95, 5065–5067 CrossRef.
- C. Fufezan, Proteins: Struct., Funct., Bioinf., 2010, 78, 2831–2838 CrossRef CAS PubMed.
- P. Chakrabarti and D. Pal, Protein Sci., 1997, 6, 851–859 CrossRef CAS PubMed.
- A. Choudhary, D. Gandla, G. R. Krow and R. T. Raines, J. Am. Chem. Soc., 2009, 131, 7244–7246 CrossRef CAS PubMed.
- R. W. Newberry, B. VanVeller and R. T. Raines, Chem. Commun., 2015, 51, 9624–9627 RSC.
- R. W. Newberry, B. Vanveller, I. A. Guzei and R. T. Raines, J. Am. Chem. Soc., 2013, 135, 7843 CrossRef CAS PubMed.
- R. W. Newberry and R. T. Raines, Acc. Chem. Res., 2017, 50, 1838–1846 CrossRef CAS PubMed.
- G. J. Bartlett, R. W. Newberry, B. Vanveller, R. T. Raines and D. N. Woolfson, J. Am. Chem. Soc., 2013, 135, 18682–18688 CrossRef CAS PubMed.
- H. R. Kilgore and R. T. Raines, J. Am. Chem. Soc., 2018, 140, 17606–17611 CrossRef CAS PubMed.
- G. J. Bartlett, A. Choudhary, R. T. Raines and D. N. Woolfson, Nat. Chem. Biol., 2010, 6, 615–620 CrossRef CAS PubMed.
- R. W. Newberry, G. J. Bartlett, B. VanVeller, D. N. Woolfson and R. T. Raines, Protein Sci., 2014, 23, 284–288 CrossRef CAS PubMed.
- G. A. Jeffrey, J. Mitra, K. N. Houk, N. G. Rondan and M. N. Paddon-Row, J. Am. Chem. Soc., 1985, 107, 321–326 CrossRef CAS.
- L. Esposito, L. Vitagliano, A. Zagari and L. Mazzarella, Protein Sci., 2000, 9, 2038 CrossRef CAS PubMed.
- M. D. Shoulders and R. T. Raines, Annu. Rev. Biochem., 2009, 78, 929–958 CrossRef CAS PubMed.
- D. E. Fomenko and V. N. Gladyshev, Biochemistry, 2003, 42, 11214–11225 CrossRef CAS PubMed.
- A. D. Becke, J. Chem. Phys., 1998, 98, 5648 CrossRef.
- J. Da Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- Y. Zhao, D. G. Truhlar, Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2007, 120, 215–241 Search PubMed.
- Y. Zhao and D. G. Truhlar, Acc. Chem. Res., 2008, 41, 157–167 CrossRef CAS PubMed.
- N. Mardirossian and M. Head-Gordon, J. Chem. Theory Comput., 2016, 12, 4303–4325 CrossRef CAS PubMed.
- A. V. Vorontsov and P. G. Smirniotis, J. Mol. Model., 2017, 23, 223 CrossRef PubMed.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158 CrossRef CAS.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- S. Tsuzuki and T. Uchimaru, Phys. Chem. Chem. Phys., 2020, 22, 22508–22519 RSC.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. Nikoo, Ph.D. thesis, University of Windsor, 2019.
- H. S. Biswal, S. Bhattacharyya, A. Bhattacherjee and S. Wategaonkar, Int. Rev. Phys. Chem., 2015, 34, 99–160 Search PubMed.
- C. A. Morgado, J. P. McNamara, I. H. Hillier, N. A. Burton and M. A. Vincent, J. Chem. Theory Comput., 2007, 3, 1656–1664 CrossRef CAS PubMed.
- J. Sharma and P. A. Champagne, J. Comput. Chem., 2022, 1 DOI:10.1002/jcc.27007.
- B. J. Mintz and J. M. Parks, J. Phys. Chem. A, 2012, 116, 46 CrossRef PubMed.
- P. C. Aeberhard, J. S. Arey, I.-C. C. Lin and U. Rothlisberger, J. Chem. Theory Comput., 2009, 5, 23–28 CrossRef CAS PubMed.
- K. E. Riley and P. Hobza, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 3–17 CAS.
- K. Raghavachari, G. W. Trucks, J. A. Pople and M. Head-Gordon, Chem. Phys. Lett., 1989, 157, 479–483 CrossRef CAS.
- O. A. Von Lilienfeld, I. Tavernelli, U. Rothlisberger and D. Sebastiani, Phys. Rev. Lett., 2004, 93, 153004 CrossRef PubMed.
- I. C. Lin, M. D. Coutinho-Neto, C. Felsenheimer, O. A. Von Lilienfeld, I. Tavernelli and U. Rothlisberger, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 205131 CrossRef.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065 RSC.
- T. H. Dunning, J. Chem. Phys., 1998, 90, 1007 CrossRef.
- R. A. Kendall, T. H. Dunning and R. J. Harrison, J. Chem. Phys., 1998, 96, 6796 CrossRef.
- J. Dunning, K. A. Peterson and A. K. Wilson, J. Chem. Phys., 2001, 114, 9244–9253 CrossRef.
- A. K. Wilson and T. H. Dunning, J. Phys. Chem. A, 2004, 108, 3129–3133 CrossRef CAS.
- R. D. Bell and A. K. Wilson, Chem. Phys. Lett., 2004, 394, 105–109 CrossRef CAS.
- S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–566 CrossRef CAS.
- A. L. Garden, J. R. Lane and H. G. Kjaergaard, J. Chem. Phys., 2006, 125, 144317 CrossRef PubMed.
- J. A. Plumley and J. J. Dannenberg, J. Comput. Chem., 2011, 32, 1519–1527 CrossRef CAS PubMed.
- G. Pohl, J. A. Plumley and J. J. Dannenberg, J. Chem. Phys., 2013, 138, 245102 CrossRef PubMed.
- W. Wu and J. Kieffer, J. Chem. Theory Comput., 2019, 15, 371–381 CrossRef CAS PubMed.
- J. Zhang, H. Zhang, T. Wu, Q. Wang and D. Van Der Spoel, J. Chem. Theory Comput., 2017, 13, 1034–1043 CrossRef CAS PubMed.
- R. Sure, M. el Mahdali, A. Plajer and P. Deglmann, J. Comput.-Aided Mol. Des., 2021, 35, 473–492 CrossRef CAS PubMed.
- A. Warshel and M. Levitt, J. Mol. Biol., 1976, 103, 227–249 CrossRef CAS PubMed.
- R. Estrada-Tejedor, L. Ros-Blanco and J. T. Closa, Afinidad, 2014, 71, 89–94 CAS.
- X. C. Yan, M. J. Robertson, J. Tirado-Rives and W. L. Jorgensen, J. Phys. Chem. B, 2017, 121, 6626–6636 CrossRef CAS PubMed.
- M. Svensson, S. Humbel, R. D. J. Froese, T. Matsubara, S. Sieber and K. Morokuma, J. Phys. Chem., 1996, 100, 19357–19363 CrossRef CAS.
- L. W. Chung, W. M. C. Sameera, R. Ramozzi, A. J. Page, M. Hatanaka, G. P. Petrova, T. V. Harris, X. Li, Z. Ke, F. Liu, H. B. Li, L. Ding and K. Morokuma, Chem. Rev., 2015, 115, 5678–5796 CrossRef CAS PubMed.
- S. Ahmadi, L. Barrios Herrera, M. Chehelamirani, J. Hostaš, S. Jalife and D. R. Salahub, Int. J. Quantum Chem., 2018, 118, e25558 CrossRef.
- R. P. Magalhães, H. S. Fernandes and S. F. Sousa, Isr. J. Chem., 2020, 60, 655–666 CrossRef.
| This journal is © The Royal Society of Chemistry 2023 |