Open Access Article
Open Access ArticleStrengthened cooperativity of DNA-based cyclic hydrogen-bonded rosettes by subtle functionalization†
David
Almacellas
a,
Célia
Fonseca Guerra
 *b and
Jordi
Poater
*b and
Jordi
Poater
 *ac
*ac
aDepartament de Química Inorgànica i Orgànica & IQTCUB, Universitat de Barcelona, Martí i Franquès 1-11, 08028 Barcelona, Spain. E-mail: c.fonsecaguerra@vu.nl; jordi.poater@ub.edu
bDepartment of Chemistry and Pharmaceutical Sciences, AIMMS, Vrije Universiteit Amsterdam, De Boelelaan 1108, 1081 HZ Amsterdam, The Netherlands
cICREA, Passeig Lluís Companys 23, 08010 Barcelona, Spain
First published on 5th October 2023
Abstract
Cooperative effects cause extra stabilization of hydrogen-bonded supramolecular systems. In this work we have designed hydrogen-bonded rosettes derived from a guanine–cytosine Janus-type motif with the aim of finding a monomer that enhances the synergy of supramolecular systems. For this, relativistic dispersion-corrected density functional theory computations have been performed. Our proposal involves a monomer with three hydrogen-bonds pointing in the same direction, which translates into shorter bonds, stronger donor–acceptor interactions, and more attractive electrostatic interactions, thus giving rise to rosettes with strengthened cooperativity. This newly designed rosette has triple the cooperativity found for the naturally occurring guanine quadruplex.
Introduction
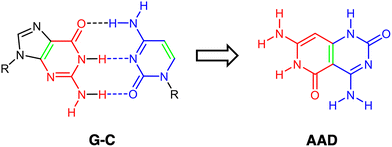
Supramolecular chemistry is growing considerably due to its promising role and applications in materials science, specifically focusing on novel nanostructures and nanoelectronics. The selection and design of appropriate building blocks by considering their molecular recognition capabilities, self-assembly and self-organization becomes a determinant step. An interesting functionalization at the supramolecular level is the capability of cooperativity between hydrogen-bonded structures.1–5Taking into consideration the spatial disposition of cooperative molecules, mainly there are two different kinds of studied hydrogen-bonded systems with specific capabilities or properties related to their arrangement, thus being either linearly6–10 or cyclically cooperative.1,11–13 With respect to the latter, lately the so-called rosette structures or cyclic hexamers have gained interest.14–16 These are hydrogen-bonded cyclic complexes of relatively small organic compounds, or even derived or inspired from DNA nucleobases. In particular, the guanine (G) nucleobase has become an important building block both experimentally and theoretically, like in guanine quartet structures (G4) that are of high significance in quadruplex structures of DNA.17–19 G4 has been proven to experience a large synergistic effect due to charge separation through donor–acceptor interactions in the σ-electron system.14–16
Of high importance is the Janus-type molecule, i.e., presenting two different hydrogen-bond patterns, synthesized and characterized by Lehn and coworkers,20,21 designed to self-assemble uniquely into a supramolecular cyclic entity. This was derived from the guanine–cytosine (G–C) base pair, with the ability to hydrogen bond to G and C simultaneously (Scheme 1). In addition, with G4 in mind and inspired by guanine and cytosine structures, some hydrogen-bonded cyclic rosettes have been recently synthesized with significant stability, as complexes with Janus-type rigid monomer molecules where two six-membered heterocycles are fused together and oriented at a 60° angle with low conformational freedom (Fig. 1).14,15,22,23 Importantly, in this kind of hydrogen-bonded system, cooperativity becomes a determinant for the adequate thermodynamic stability of the supramolecular system.14,15,22,23
In this work, the G–C Janus-type motif for rosettes will be further analyzed and used as a departing structure for the design of other monomeric structures with the aim of synthesizing hexamers with strengthened synergy. Thus, by means of a quantitative Kohn–Sham molecular orbital analysis combined with an energy decomposition analysis, we have unveiled how a slightly modified monomer derived from initial AAD (Fig. 1) can largely improve cooperativity in the corresponding rosette. In particular, the three hydrogen-bonds must point in the same direction, instead of two hydrogen-bond acceptors and one hydrogen-bond donor as in the previously synthesized AAD. Having all hydrogen bonds pointing in the same direction translates into shorter bonds, stronger donor–acceptor interactions, and more attractive electrostatic interactions, thus giving rise to rosettes with strengthened cooperativity.
Computational methods
All geometry optimizations and energies were computed using the Amsterdam Density Functional (ADF2021.101) program at the dispersion-corrected relativistic density functional theory (DFT) ZORA-BLYP-D3(BJ)/TZ2P level of theory.24 Previous studies have proved the reliability of this level of theory for the evaluation of the hydrogen bonding interaction mechanism within weakly-bound complexes.25–27The bonding energies of the hexamers, as well as their subunits, i.e., dimers, trimers, tetramers and pentamers, were computed using eqn (1):
| ΔEnbond = Emn − n × Em | (1) |
| ΔEbond = Erosette − 6 × Emonomer | (2) |
And this overall bond energy can be split as shown in eqn (3):
| ΔEbond = ΔEstrain + ΔEint | (3) |
| ΔEint = ΔEPauli + ΔVelstat + ΔEoi + ΔEdisp | (4) |
| ΔEoi = ΔEσoi + ΔEπoi | (5) |
The electron charge distribution has been analyzed within the Voronoi Deformation Density (VDD) analysis.4,30
Results and discussion
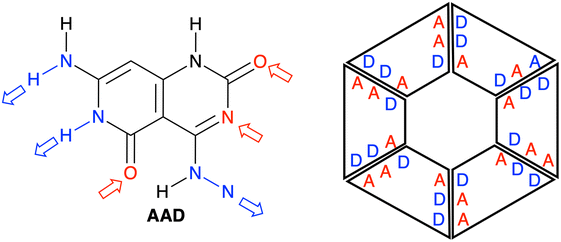
We have studied four systems that can form hydrogen-bonded rosettes derived from a G–C Janus-type monomer,20,21 with two proton acceptor and one proton donor groups. The three new monomers maintain the overall structure of the original monomer (Fig. 1), while different subtle functional modifications have been introduced with the aim of strengthening the cooperativity of the formed rosettes. From the AAD system, with two hydrogen bond acceptors (A, red arrow in Fig. 2) and one hydrogen bond donor (D, blue arrow in Fig. 2), we have systematically analyzed AA, AAA and AAAOH monomers (Cartesian coordinates of the systems under study are given in Tables S2–S7 of the ESI†). AA is introduced to understand the effect of one hydrogen-bond donor in AAD, that is, the effect of one hydrogen bond pointing in the opposite direction. Next, AAA involves changing the hydrogen bond donor (D) in AAD into a hydrogen bond acceptor (A), such that all hydrogen bonds point in the same direction. AAAOH is proposed to improve the synergy further. The hexamers formed by these monomers have different hydrogen bond interactions (Fig. 2): the hydrogen bond donor can be an amine group or a secondary amine group (N–H) and the hydrogen bond acceptor can be an endocyclic N atom or the oxygen atom of a carbonyl or hydroxyl group.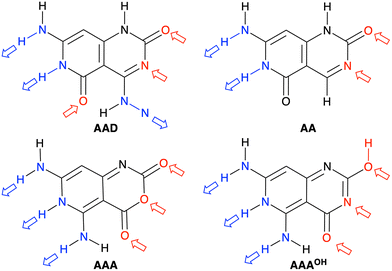 | ||
| Fig. 2 Structures of AAD, AA, AAA, and AAAOH monomers. Red and blue arrows indicate the hydrogen bond acceptors and donors, respectively. | ||
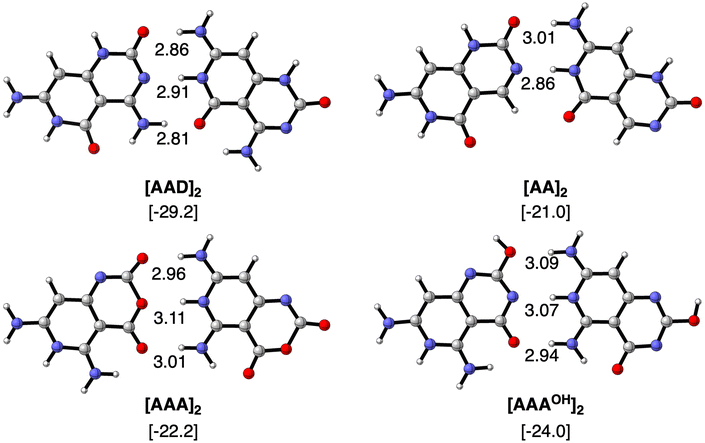
We first focus on the geometries and energies of the dimers formed from the four monomers. Optimized geometries of the dimers with Cs symmetry are shown in Fig. 3 with their hydrogen bond lengths and bonding energies. The reference AAD system presents the strongest stabilization energy (−29.2 kcal mol−1) and also the shortest O⋯N distances of the two outer hydrogen bonds (2.81 and 2.86 Å). The N⋯N distance amounts to 2.91 Å in the case of [AAD]2 and is shorter only for the [AA]2 dimer (2.86 Å). The bond energy is less stabilizing when only hydrogen-bond donor groups are present on one monomer and hydrogen-bond acceptors on the other monomer to form the interaction. ΔE increases only slightly from [AA]2 to [AAA]2 and to [AAAOH]2 (from −21.0 to −22.2 and to −24.0 kcal mol−1, respectively). As AAAOH has the possibility of tautomerization, we have also investigated by substituting –OCH3 instead of –OH (see Fig. S1 in the ESI†), which showed almost identical hydrogen bond lengths and bonding energies.
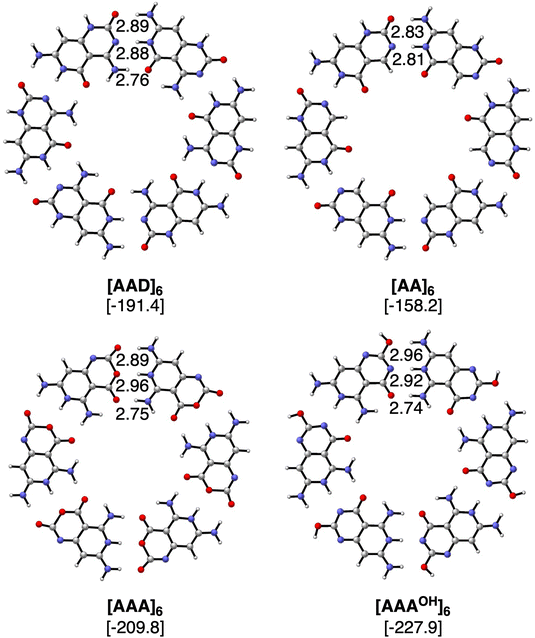
The geometries and hydrogen bond energies of the rosettes [AAD]6, [AA]6, [AAA]6 and [AAAOH]6 are shown in Fig. 4. We have focused our analyses on the Cs symmetry structures, as experimentally these systems are either on the surface or stacked on top of each other.31–33 Nonetheless the non-planar dimers and rosettes have also been computed (Tables S2–S7 in the ESI†), which are only up to −1.6 and −2.7 kcal mol−1 more stable than their Cs counterparts, mainly due to the pyramidalization of the amino groups. The strongest bound rosettes are [AAA]6 and [AAAOH]6 with three hydrogen bonds pointing in the same direction (−209.8 kcal mol−1 and −227.9 kcal mol−1, respectively). The bonding energy for [AAD]6 only amounts to −191.4 kcal mol−1 despite that in the case of the dimer [AAD]2 is the strongest.
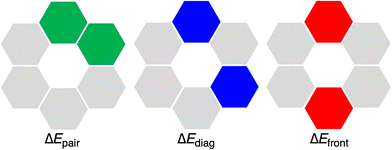
The hexamers with all hydrogen bonds pointing in the same direction have been shown to experience cooperativity.1,12,16 This cooperativity or synergy, ΔEsyn, can be computed by comparing the interaction energy ΔEint of the rosette with the summation ΔEsum of the individual pairwise interactions for all possible pairs of units in the rosettes (eqn (6)). In particular, ΔEsum includes the interaction energy between the two hydrogen-bonded molecules (ΔEpair, green in Fig. 5), the interaction energy between the two mutually diagonally oriented molecules (ΔEdiag, blue in Fig. 5), and the interaction energy between the two frontal molecules (ΔEfront, red in Fig. 5). In the case of the rosette, we have 6 pairwise-, 6 diagonal-, and 3 frontal-interaction energies (eqn (7)).
| ΔEsyn = ΔEint − ΔEsum | (6) |
| ΔEsum = 6·ΔEpair + 6·ΔEdiag + 3·ΔEfront | (7) |
Then, if |ΔEint| > |ΔEsum| in eqn (6) we have positive cooperativity, which means that the average energy of the hydrogen bonds in the rosette is reinforced with respect to their isolated counterparts.1,12,16
Table 1 includes the bond energy, the interaction energy, the sum of pairwise interactions and the synergy for the four rosettes. ΔEsyn clearly increases from [ADD]6 to [AA]6 to [AAA]6 and to [AAAOH]6 from −12.7 to −32.1 to −61.2 and to −66.2 kcal mol−1. Thus, our goal of designing a macromolecular hexamer with strengthened cooperativity is achieved. It should be noted that the synergy of either AAA or AAAOH hexamers is almost triple the value previously obtained for G4, which amounted to −20.9 kcal mol−1.1 This strengthening of the hydrogen bonds due to cooperativity effects is also verified from the comparison of the dimerization energies between the hexamers and the dimers. For instance, in the case of ADD, ΔEbond increases from −29.2 to −31.9 kcal mol−1 from the optimized dimer to the equivalent average dimer within the rosette (computed as ΔEbond/6, Table 1). More importantly, such an increase due to cooperativity is much more pronounced for AAA (ΔEbond increases from −22.2 to −35.0 kcal mol−1 from the dimer to the hexamer) than for AA (from −21.0 to −26.4 kcal mol−1) because of the third hydrogen bond in the former. Thus, from these data, it is shown how stronger hydrogen bonds also give rise to more cooperativity. Furthermore, as stated above, the strongest reinforcement by cooperativity is found for AAAOH with ΔEbond increasing from −24.0 to −38.0 kcal mol−1, which means that the pair of hydrogen bonds within the rosette becomes 58% stronger than the isolated interactions. Such synergy arising from the formation of the hexamer causes the hydrogen-bond lengths to be clearly shortened (Fig. 4), a trend that is more pronounced when all hydrogen bonds point in the same direction. For instance, in the case of AAAOH, hydrogen-bond lengths in the dimer, 3.09 (O⋯N), 3.07 (O⋯N), and 2.94 Å (O⋯N), are shortened to 2.96, 2.92, and 2.74 Å, respectively.
| Hexamer | ΔEbond | ΔEbond/6 | ΔEint | ΔEsum | ΔEsyn |
|---|---|---|---|---|---|
| AAD | −191.4 | −31.9 | −218.5 | −205.8 | −12.7 |
| AA | −158.2 | −26.4 | −179.9 | −147.8 | −32.1 |
| AAA | −209.8 | −35.0 | −239.9 | −178.7 | −61.2 |
| AAAOH | −227.9 | −38.0 | −260.5 | −194.3 | −66.2 |
Now that we have demonstrated that the hydrogen bonds in these series of rosettes can be strengthened by synergy, we will analyze how this synergy develops when we go from initial AAD to AA, with only two hydrogen-bonds pointing in the same direction, and then to the strongest cooperative AAA and AAAOH systems, with three hydrogen-bonds pointing in the same direction. For this, we will analyze the construction of the hydrogen-bonded rosette by adding one monomer at a time, that is, a stepwise procedure in which an incoming monomer is added to the former one until the hexamer is formed (Fig. 6).12,16 For each step the interaction energy is decomposed by means of an energy decomposition analysis (see eqn (4)), and the synergy of the EDA components (either interaction, electrostatic, Pauli, orbital or dispersion) within the hexamers is also computed.28,29,34 These are computed as follows:
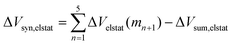 | (8) |
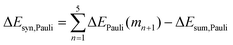 | (9) |
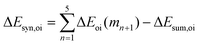 | (10) |
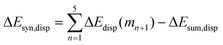 | (11) |
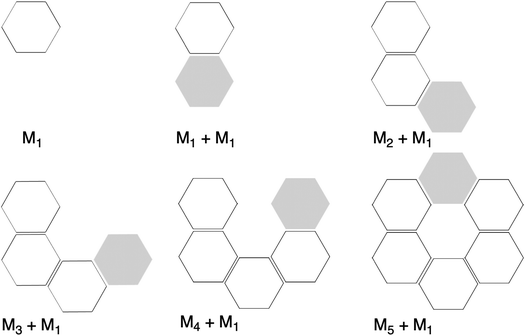 | ||
| Fig. 6 Representation of molecular fragments in the formation of the rosette structures by a stepwise addition of monomers in a one-way direction. Grey hexagons represent the incoming monomer. | ||
It is the difference between the sum over the gradual formation of the hexamer and the sum of the pairwise interactions. The acquisition of the EDA components for the formation of the hexamer by the addition of a monomer to the previously formed complex is shown in Fig. 7. The sum of pairwise interactions, ΔVsum,elstat, ΔEsum,Pauli, ΔEsum,oi, and ΔEsum,disp, is computed using eqn (7), for each component, that is, for the electrostatic, Pauli, orbital interaction and dispersion component, respectively (see all data in Table S1 in the ESI†).
 | ||
| Fig. 7 Schematic representation of the energy decomposition analysis (in kcal mol−1) for the formation of AAD, AA, AAA, and AAAOH rosettes in a stepwise one-way direction, computed at the ZORA-BLYP-D3(BJ)/TZ2P level. See also Fig. S2 and S3 in the ESI for further data.† | ||
First, the removal of one hydrogen-bond from AAD to AA causes weakening of the interaction ΔEint, as observed above for the dimers, but there is an increase in cooperativity in the AA rosette compared to the AAD rosette (see the larger slope of ΔEint for AA in Fig. 7). Although for AAD the interaction energy amounts to −33.6 kcal mol−1 for M1 + M1 (that is, the formation of M2) and −35.7 kcal mol−1 for M2 + M (that is, the formation of M3), the increase of the interaction energy from M2 to M3 is twice as large as that for AA (from −24.2 kcal mol−1 for M2 and −28.2 kcal mol−1 for M3). The stabilization of 2.1 kcal mol−1 for AAD from M2 to M3 can be attributed mainly to 1.1 kcal mol−1 of electrostatic and 0.6 kcal mol−1 of orbital interactions, whereas the stabilization of 4.0 kcal mol−1 for AA from M2 to M3 can be attributed to 2.0 kcal mol−1 of ΔVelstat and 1.5 kcal mol−1 of ΔEoi.
The addition of an extra hydrogen bond to the AA rosette in the same direction as that of the other two hydrogen bonds forming the AAA and AAAOH rosettes shows an even steeper increase of the interaction energy (see Fig. 7). In particular, for AAA, ΔEint increases from −26.7 to −35.9 kcal mol−1 from M2 to M3, i.e., a 9.2 kcal mol−1 difference! This increase can be mainly attributed to the electrostatic interaction (5.3 kcal mol−1) and the orbital interaction (2.8 kcal mol−1).
Further insight into the cooperativity in the hydrogen bonds of the rosettes can be gained if we analyze the synergy in different energy terms of the EDA (Table 2). Already from ADD to AA, synergy is almost tripled from −12.7 to −32.1 kcal mol−1 due to more attractive σ and π orbital interactions as well as electrostatic interactions, whereas Pauli repulsion remains constant. But more noticeably, from AA to either AAA or AAAOH the synergy is almost doubled (from −32.1 to −61.2 or −66.2 kcal mol−1). In all cases, the largest contribution to the synergy comes from the electrostatic and orbital interactions. And, with respect to the latter, the σ electronic system contributes more than the π electronic system. For instance, for AAA ΔEσsyn,oi amounts to −17.1 and ΔEπsyn,oi to −12.0 kcal mol−1 (Table 2).
| Synergy | [AAD]6 | [AA]6 | [AAA]6 | [AAAOH]6 |
|---|---|---|---|---|
| a See eqn (8)–(11) for the definition of the terms. | ||||
| ΔEsyn | −12.7 | −32.1 | −61.2 | −66.2 |
| ΔVsyn,elstat | −5.2 | −13.7 | −27.0 | −28.6 |
| ΔEsyn,Pauli | −1.0 | −1.8 | −4.1 | −4.7 |
| ΔEsyn,oi | −6.5 | −16.6 | −30.1 | −32.9 |
| ΔEσsyn,oi | −3.7 | −9.4 | −17.1 | −20.6 |
| ΔEπsyn,oi | −2.8 | −7.2 | −12.0 | −12.3 |
| ΔEsyn,disp | 0.0 | 0.0 | 0.0 | 0.0 |
More insight can be obtained by analyzing the charge distribution by means of the computed Voronoi deformation density (VDD) charges. In Fig. 8, we see that in all cases the charge separation gradually increases throughout the stepwise addition of monomers. Thus, the monomers with hydrogen-bond acceptor atoms become more negatively charged in each step (blue hexagons in Fig. 8), whereas the opposite happens for those with hydrogen-bond donor atoms (red hexagons in Fig. 8). In ADD the monomer with hydrogen acceptor atoms experiences only a small gain of −11 milli-electrons from M2 to M3 (that is, from −121 to −132 me−). However, the largest increase was obtained for AAAOH, from −312 to −325 me− from M2 to M3, due to having all hydrogen bonds pointing in the same direction. This is in line with our previous work on guanine quadruplexes,1 which showed that the cooperativity originates from the charge separation in the σ electronic systems due to the covalent component in the hydrogen bonds. The charge transfer within the hydrogen bonds then leads to charge separation within the dimer, which enhances the electrostatic interactions and the orbital interactions between the dimer and the third monomer. However, this charge separation converges, i.e., it does not increase much further from M3 to M4 to M5. For instance, for AAAOH we go from −325 to −352 to −359 me−. This convergency of the charge separation was less in the case of G4.1
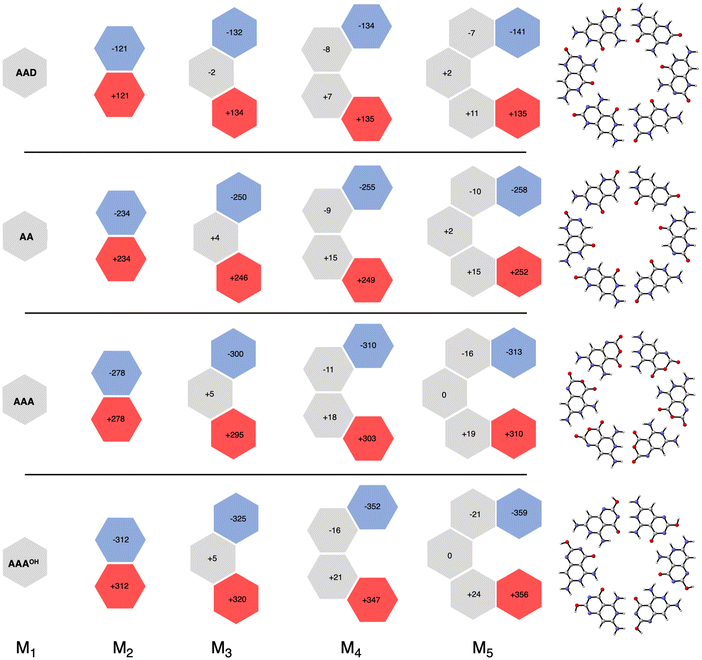 | ||
| Fig. 8 VDD charges (in milli-electrons) in the formation of cyclic structures. Values in black are the sum of the atomic charges of the monomer (see also Fig. S4 in the ESI for the changes in the atomic charges of the front atoms†). | ||
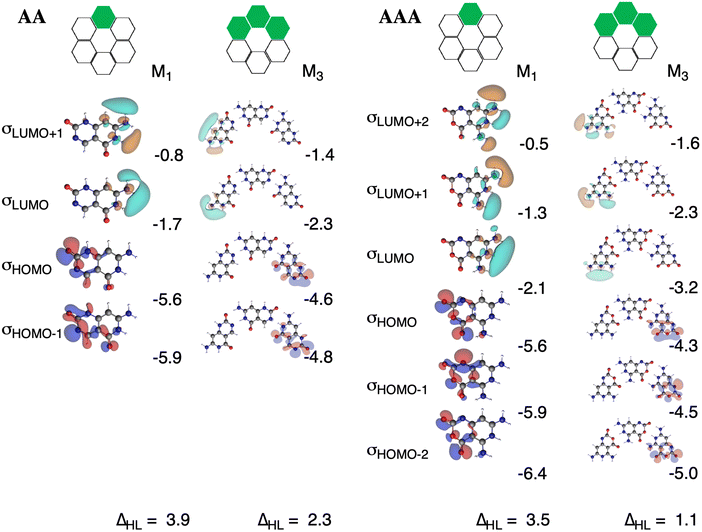
The charge separation within the formed complexes also enhances the cooperativity within the orbital interactions. The reason is found in the destabilization of lone pair HOMO orbitals of the hydrogen-bond accepting monomer as the monomer becomes slightly negatively charged when it forms a dimer. At the same time, the antibonding LUMOs of the hydrogen-bond donating monomer are stabilized because the monomer becomes slightly positively charged when it forms a dimer. This gives rise to stronger donor–acceptor interactions as the HOMO–LUMO gap of the interacting moieties decreases upon the gradual formation of the rosette. The effect is even more pronounced for AAA with three hydrogen bonds than for AA with two hydrogen bonds. The HOMO–LUMO gap in AA amounts to 3.9 eV and in [AA]3 to 2.3 eV, whereas in AAA it amounts to 3.5 eV and in [AAA]3 to 1.1 eV (Fig. 9). The gap decreases for AAAOH even to 0.6 eV in the trimer (Fig. S5–S7 in the ESI†).
Thus, the comparison of AA with AAD and AAA shows that for making dimers it is better to have the third hydrogen bond pointing in the opposite direction (see Fig. 3) as that will lead to the strongest dimer, i.e., [AAD]2 has a bond energy of −29.2 kcal mol−1 compared to [AAA]2 with −22.2 kcal mol−1. However, if the goal is to obtain stronger rosettes, the additional hydrogen bond should point in the same direction as that of the other two hydrogen bonds. This will lead to stronger donor–acceptor interactions due to more charge transfer within the σ electron system, as observed above.
Conclusions
In this work we have designed hydrogen-bonded supramolecular rosettes with strengthened cooperativity. Our dispersion-corrected DFT computations reveal that stronger cooperativity in rosettes can be achieved by having all hydrogen-bond donors on one side and all hydrogen-bond acceptors on the other side of the hydrogen bonding interaction. This translates into shorter hydrogen-bond lengths between the monomers, with stronger donor–acceptor interactions, and thus more charge transfer within the σ electron system. The overall result is an enhancement of cooperativity due to more pronounced electrostatic attraction and stronger donor–acceptor orbital interactions as proven by our Kohn–Sham molecular orbital analysis together with the quantitative energy decomposition analysis. Noticeably, the two rosettes with all three hydrogen-bonds pointing in the same direction, i.e., AAA and AAAOH, achieve a cooperative interaction that is triple that previously obtained for the guanine quadruplex (G4). Overall, the present study opens the door for the design of hydrogen-bonded supramolecular systems with extra gain of cooperativity by modeling the frontal functional groups involved in these interactions.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank the Netherlands Organization for Scientific Research (NWO), the Spanish MINECO (PID-2019-106830GB-I00, PID2022-138861NB-I00 and CEX2021-001202-M) and the Catalan Government (2021SGR442) for financial support.References
- C. Fonseca Guerra, H. Zijlstra, G. Paragi and F. M. Bickelhaupt, Telomere Structure and Stability: Covalency in Hydrogen Bonds, Not Resonance Assistance, Causes Cooperativity in Guanine Quartets, Chem. – Eur. J., 2011, 17, 12612–12622 CrossRef CAS PubMed.
- C. A. Hunter and H. L. Anderson, What is Cooperativity?, Angew. Chem., Int. Ed., 2009, 48, 7488–7499 CrossRef CAS.
- A. S. Mahadevi and G. N. Sastry, Cooperativity in Noncovalent Interactions, Chem. Rev., 2016, 116, 2775–2825 CrossRef CAS.
- C. Nieuwland, S. Lekanne Deprez, C. de Vries and C. Fonseca Guerra, Chalcogen Atom Size Dictates Stability of Benzene-1,3,5-triamide Polymers: Overlooked Role of Geometrical Fit for Enhanced Hydrogen Bonding, Chem. – Eur. J., 2023, 29, e202300850 CrossRef CAS PubMed.
- L. Tebben, C. Muck-Lichtenfeld, G. Fernandez, S. Grimme and A. Studer, From Additivity to Cooperativity in Chemistry: Can Cooperativity Be Measured?, Chem. – Eur. J., 2017, 23, 5864–5873 CrossRef CAS.
- L. de Azevedo Santos, D. Cesario, P. Vermeeren, S. C. C. van der Lubbe, F. Nunzi and C. Fonseca Guerra, σ-Electrons Responsible for Cooperativity and Ring Equalization in Hydrogen-Bonded Supramolecular Polymers, ChemPlusChem, 2022, 87, e202100436 CrossRef CAS PubMed.
- I. A. W. Filot, A. R. A. Palmans, P. A. J. Hilbers, R. A. van Santen, E. A. Pidko and T. F. A. de Greef, Understanding Cooperativity in Hydrogen-Bond-Induced Supramolecular Polymerization: A Density Functional Theory Study, J. Phys. Chem. B, 2010, 114, 13667–13674 CrossRef CAS PubMed.
- J. Nochebuena, C. Cuautli and J. Ireta, Origin of cooperativity in hydrogen bonding, Phys. Chem. Chem. Phys., 2017, 19, 15256–15263 RSC.
- G. Paragi and C. Fonseca Guerra, Cooperativity in the Self-Assembly of the Guanine Nucleobase into Quartet and Ribbon Structures on Surfaces, Chem. – Eur. J., 2017, 23, 3042–3050 CrossRef CAS.
- P. Vermeeren, L. P. Wolters, G. Paragi and C. Fonseca Guerra, Cooperative Self-Assembly in Linear Chains Based on Halogen Bonds, ChemPlusChem, 2021, 86, 812–819 CrossRef CAS.
- A. N. Petelski and C. Fonseca Guerra, Designing Self-Assembled Rosettes: Why Ammeline is a Superior Building Block to Melamine, ChemistryOpen, 2019, 8, 135–142 CrossRef CAS.
- A. N. Petelski and C. Fonseca Guerra, Hydrogen-Bonded Rosettes of Aminotriazines for Selective-Ion Recognition, J. Phys. Chem. C, 2020, 124, 3352–3363 CrossRef CAS.
- L. P. Wolters, N. W. G. Smits and C. Fonseca Guerra, Covalency in resonance-assisted halogen bonds demonstrated with cooperativity in N-halo-guanine quartets, Phys. Chem. Chem. Phys., 2015, 17, 1585–1592 RSC.
- F. Aparicio, M. J. Mayoral, C. Montoro-Garcia and D. González-Rodríguez, Guidelines for the assembly of hydrogen-bonded macrocycles, Chem. Commun., 2019, 55, 7277–7299 RSC.
- A. del Prado, D. González-Rodríguez and Y. L. Wu, Functional Systems Derived from Nucleobase Self-assembly, ChemistryOpen, 2020, 9, 409–430 CrossRef CAS.
- A. N. Petelski and C. Fonseca Guerra, Understanding the influence of alkali cations and halogen anions on the cooperativity of cyclic hydrogen-bonded rosettes in supramolecular stacks, Chem. – Asian J., 2022, 17, e202201010 CrossRef CAS.
- S. Balasubramanian, L. H. Hurley and S. Neidle, Targeting G-quadruplexes in gene promoters: a novel anticancer strategy?, Nat. Rev. Drug Discovery, 2011, 10, 261–275 CrossRef CAS.
- G. N. Parkinson, M. P. H. Lee and S. Neidle, Crystal structure of parallel quadruplexes from human telomeric DNA, Nature, 2002, 417, 876–880 CrossRef CAS.
- C. Fonseca Guerra, T. van der Wijst, J. Poater, M. Swart and F. M. Bickelhaupt, Adenine versus guanine quartets in aqueous solution: dispersion-corrected DFT study on the differences in pi-stacking and hydrogen-bonding behavior, Theor. Chem. Acc., 2010, 125, 245–252 Search PubMed.
- H. Fenniri, M. Packiarajan, K. L. Vidale, D. M. Sherman, K. Hallenga, K. V. Wood and J. G. Stowell, Helical rosette nanotubes: Design, self-assembly, and characterization, J. Am. Chem. Soc., 2001, 123, 3854–3855 CrossRef CAS PubMed.
- A. Marsh, M. Silvestri and J. M. Lehn, Self-complementary hydrogen bonding heterocycles designed for the enforced self-assembly into supramolecular macrocycles, Chem. Commun., 1996, 1527–1528 RSC.
- C. Montoro-Garcia, N. Bilbao, I. M. Tsagri, F. Zaccaria, M. J. Mayoral, C. Fonseca Guerra and D. González-Rodríguez, Impact of Conformational Effects on the Ring-Chain Equilibrium of Hydrogen-Bonded Dinucleosides, Chem. – Eur. J., 2018, 24, 11983–11991 CrossRef CAS.
- C. Montoro-Garcia, J. Camacho-Garcia, A. M. Lopez-Perez, M. J. Mayoral, N. Bilbao and D. González-Rodríguez, Role of the Symmetry of Multipoint Hydrogen Bonding on Chelate Cooperativity in Supramolecular Macrocyclization Processes, Angew. Chem., Int. Ed., 2016, 55, 223–227 CrossRef CAS PubMed.
- G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. A. Van Gisbergen, J. G. Snijders and T. Ziegler, Chemistry with ADF, J. Comput. Chem., 2001, 22, 931–967 CrossRef CAS.
- C. Nieuwland and C. Fonseca Guerra, How the Chalcogen Atom Size Dictates the Hydrogen-Bond Donor Capability of Carboxamides, Thioamides, and Selenoamides, Chem. – Eur. J., 2022, 28, e202200755 CrossRef CAS PubMed.
- S. C. C. van der Lubbe and C. Fonseca Guerra, Hydrogen-Bond Strength of CC and GG Pairs Determined by Steric Repulsion: Electrostatics and Charge Transfer Overruled, Chem. – Eur. J., 2017, 23, 10249–10253 CrossRef CAS PubMed.
- S. C. C. van der Lubbe, F. Zaccaria, X. B. Sun and C. Fonseca Guerra, Secondary Electrostatic Interaction Model Revised: Prediction Comes Mainly from Measuring Charge Accumulation in Hydrogen-Bonded Monomers, J. Am. Chem. Soc., 2019, 141, 4878–4885 CrossRef CAS.
- F. M. Bickelhaupt and E. J. Baerends, in Reviews in Computational Chemistry, ed. K. B. Lipkowitz and D. B. Boyd, Wiley-VCH, New York, 2000, vol. 15, pp. 1–86 Search PubMed.
- P. Vermeeren, S. C. C. van der Lubbe, C. Fonseca Guerra, F. M. Bickelhaupt and T. A. Hamlin, Understanding chemical reactivity using the activation strain model, Nat. Protoc., 2020, 15, 649–667 CrossRef CAS.
- C. Fonseca Guerra, J. W. Handgraaf, E. J. Baerends and F. M. Bickelhaupt, Voronoi deformation density (VDD) charges: Assessment of the Mulliken, Bader, Hirshfeld, Weinhold, and VDD methods for charge analysis, J. Comput. Chem., 2004, 25, 189–210 CrossRef.
- B. Adhikari, X. Lin, M. Yamauchi, H. Ouchi, K. Aratsua and S. Yagai, Hydrogen-bonded rosettes comprising pi-conjugated systems as building blocks for functional one-dimensional assemblies, Chem. Commun., 2017, 53, 9663–9683 RSC.
- Y. H. Chen, C. Chen, P. C. Ding, G. Q. Shi, Y. Sun, L. N. Kantorovich, F. Besenbacher and M. Yu, Molecular recognition and homochirality preservation of guanine tetrads in the presence of melamine, Nano Res., 2020, 13, 2427–2430 CrossRef CAS.
- D. L. Li, Y. Q. Ding, X. Y. Wang and W. Xu, On-Surface Fabrication of Bimetallic Metal-Organic Frameworks through the Synergy and Competition among Noncovalent Interactions, J. Phys. Chem. Lett., 2021, 12, 5228–5232 CrossRef CAS.
- T. A. Hamlin, P. Vermeeren, C. Fonseca Guerra and F. M. Bickelhaupt, in Complementary Bonding Analyses, ed. S. Grabowski, De Gruyter, Berlin, 2021, pp. 199–212 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ob01391j |
| This journal is © The Royal Society of Chemistry 2023 |