Insights into the mechanism and selectivity of the Rh(I)-catalyzed cycloisomerization reaction of benzylallene-alkynes involving C–H bond activation†
Ying
Ren
 *a,
Tilong
Yang
*a,
Tilong
Yang
 b and
Zhenyang
Lin
b and
Zhenyang
Lin
 *b
*b
aKey Laboratory of Magnetic Molecules & Magnetic Information Materials Ministry of Education, The School of Chemistry and Material Science, Shanxi Normal University, Taiyuan, China. E-mail: ren.ying1991@163.com
bDepartment of Chemistry, The Hong Kong University of Science and Technology, Clear Water Bay, Kowloon, Hong Kong, China. E-mail: chzlin@ust.hk
First published on 14th November 2022
Abstract
A systematic theoretical study has been carried out with the aid of density functional theory (DFT) calculations on the mechanism of the Rh-catalyzed cycloisomerization of benzylallene-alkynes involving Csp2–H bond activation on the benzyl phenyl ring. Experimentally, it was found that the substituent on the allene moiety has a drastic effect on the cycloisomerization selectivity and the terminal substituent on the alkyne moiety also shows an effect on the product selectivity. In this work, through our detailed mechanistic calculations, we found that when the terminal substituent on the alkyne moiety is a hydrogen, regardless of the substituent Y on the allene moiety is an EDG or EWG, the pathway involving β-elimination of this hydrogen in an intermediate (derived from an olefin insertion step following oxidative coupling and σ-bond metathesis) is always favorable. When the terminal substituent on the alkyne moiety is an alkyl, two scenarios were found depending on whether the substituent Y on the allene moiety is an EWG or EDG.
Introduction
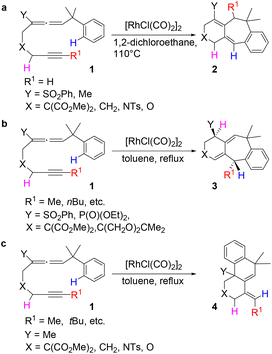
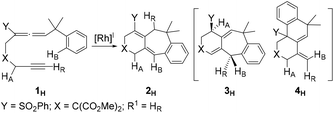
Transition metal-catalyzed cyclization of unsaturated systems involving the activation of C–H and/or C–C bonds has become one of the powerful and effective methods to construct complex cyclic frameworks in organic synthesis.1 Allenes, which have a cumulated diene structure with an sp-hybridized central carbon, are widely used in the construction of cyclic compounds. Actually, allenes have been discovered in many natural products with biological activities.2 They can react with various unsaturated hydrocarbons, such as alkenes and alkynes. With different substituents, allenes show different interesting reactivities and reaction modes.3 Rhodium-catalyzed cyclizations of allenes with other multiple bonds have attracted much attention over the last few decades for the construction of complex polycyclic skeletons.4–6Recently, Mukai and co-workers reported [RhCl(CO)2]2-catalyzed cycloisomerization of benzylallene-alkynes via C–H bond activation to form tricyclic compounds (Scheme 1).7–9 The reactions shown in Scheme 1 indicate that the terminal substituent R1 on the alkyne moiety and the internal substituent Y on the allene moiety play significant roles in the product selectivity. When the terminal substituent R1 on the alkyne moiety is a hydrogen, product 2 is produced (Scheme 1a). When the terminal substituent R1 on the alkyne moiety is non-hydrogen, product 3 (Scheme 1b) or 4 (Scheme 1c) was observed, depending on whether the substituent Y on the allene moiety is SO2Ph/PO(OEt)2 or Me.
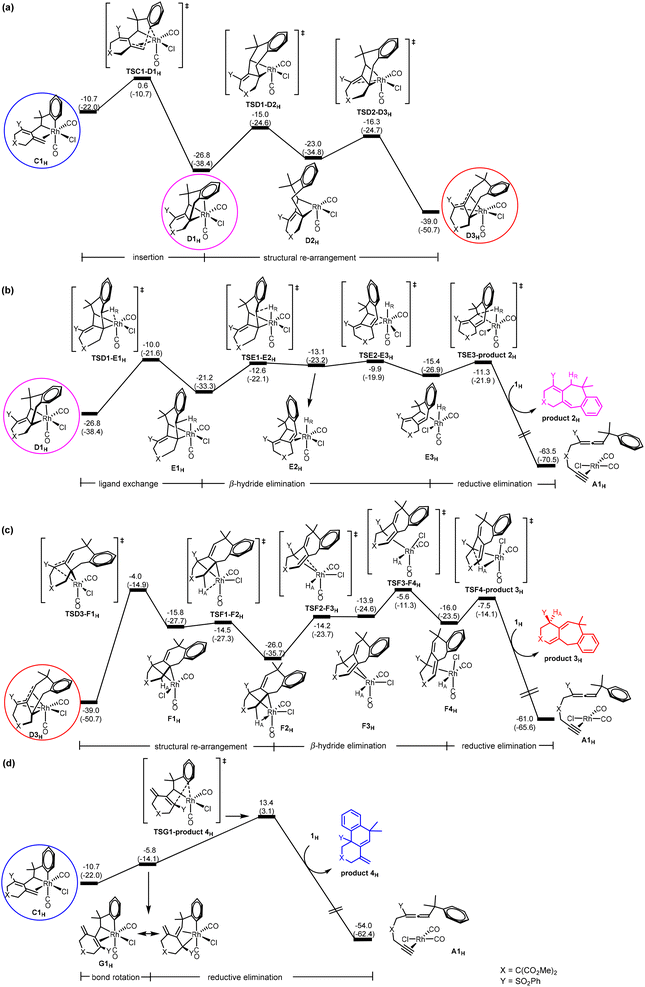
On the basis of their experimental findings, Mukai and co-workers proposed a plausible mechanism (Scheme 2) to describe the formation of the experimentally observed products shown in Scheme 1.7–9 As shown in Scheme 2, the coordination complex A of [Rh(I)] with the substrate 1 undergoes oxidative coupling to give the rhodabicyclic intermediate B, which would form the arylrhodium intermediate C through σ-bond metathesis between an ortho Csp2–H bond on the phenyl ring and the Csp2–Rh bond. Then, insertion of the exocyclic double bond unit into the Csp2–Rh(III) bond in C would produce the tricyclic intermediate D. When R1 = H, D undergoes β-hydride (R1) elimination to form the σ-allylrhodium intermediate E, which undergoes reductive elimination to give the six/seven/six tricyclic product 2. When R1 = alkyl (using Me as the representative in Scheme 2), D undergoes an alternative β-hydride (HA) elimination followed by reductive elimination to give a different six/seven/six tricyclic product 3. When Y = alkyl (instead of an electron-withdrawing group (EWG); again using Me as the representative in Scheme 2), the intermediate C should be in equilibrium via a 1,3-Rh shift with another σ-allylrhodium intermediate G, which undergoes reductive elimination to give the six/six/six tricyclic product 4.
 | ||
| Scheme 2 A plausible mechanism to account for the formation of the experimentally observed products shown in Scheme 1. | ||
The proposed mechanism (Scheme 2) nicely links and describes the experimentally observed reaction products with different reaction pathways. However, the understanding of the substituent effect, which is crucially important in the rational design of new pharmaceutical compounds, is particularly lacking. In this work, by taking advantage of the insightful mechanism, we carried out DFT calculations to understand how the above-mentioned different substituents affect the preference of one reaction pathway over the other. We hope that the insights obtained through our DFT calculations will contribute to the development of new synthetic methods for building complex polycyclic frameworks.
Computational methods
Molecular geometries of all the structures studied in this work were optimized without constraints via DFT calculations at the M06 level.10 Frequency analysis was performed at the same level of theory for all of the obtained stationary points to characterize them as transition states (one imaginary frequency) and minima (no imaginary frequency). The 6-31G(d,p) basis set11 was chosen to describe C, H, and O atoms. The effective core potentials of Hay and Wadt with double-ζ valence basis sets (LANL2DZ)12 were employed for Rh, Cl, and S atoms. Polarization functions were also added to Rh (ζf = 1.350), Cl (ζd = 0.640), and S (ζd = 0.503) atoms.13 The M06 method has been confirmed to be appropriate for Rh-catalyzed reactions in a number of recent theoretical studies.14 Intrinsic reaction coordinate (IRC) calculations15 were carried out on transition state structures to further verify that such structures connect two relevant minimum species. To match with the experimental conditions given in ref. 7–9, all the thermodynamic data reported in this work were calculated under an actual reaction temperature of 383.15 K. Natural bond orbital (NBO)16 analysis was performed on selected optimized structures. Single-point energy calculations with a better basis set at the level of M06/6-311+G(d,p)17 (using LANL2DZ+f for the Rh atom and LANL2DZ+d for Cl and S atoms) were conducted with the SMD solvation model (solvent = toluene)18 for all the structures optimized at the M06/6-31G(d,p) level. In all of the Gibbs energy profiles discussed, basis-set- and solvation-corrected relative Gibbs energies (kcal mol−1) were employed. The selected key structures of the optimized intermediates were visualized using the XYZviewer software developed by de Marothy.19 All of the calculations were performed with the Gaussian 09 software package.20Results and discussion
Scheme 1 clearly shows that if the benzylallene-alkyne substrates contain a terminal alkyne moiety, no matter what the linker X and the internal substituent Y on the allene moiety are, product 2 was always produced. For non-terminal alkyne substrates, the internal substituent Y affects the reaction outcome depending on whether it is an electron-withdrawing group (EWG) such as SO2Ph or PO(OEt)2 or an electron-donating group (EDG) such as Me. Among the reactions shown in Scheme 1, the linker X clearly had no effect on the reaction outcome. In view of this, we considered models having X = C(CO2Me)2 for our calculations.Reactions of benzylallene-alkyne substrates having an EWG internal substituent Y on the allene moiety
 | (1) |
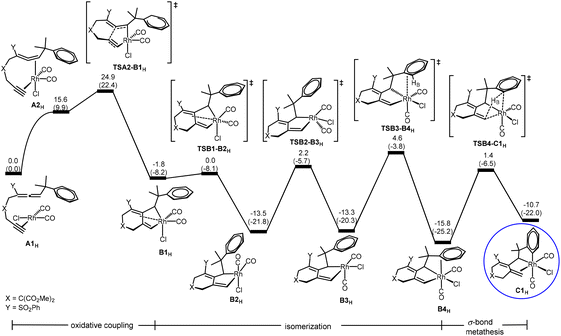
Oxidative coupling followed by σ-bond metathesis (A → B → C) in the central cycle of Scheme 2. According to Scheme 2, the first step of the reaction is oxidative coupling. A closely related oxidative coupling step has been theoretically thoroughly studied in our recent work on Rh-catalyzed cycloisomerization of homopropargylallene-alkynes,21 which was also developed by Mukai and co-workers.4g Therefore, we will only give a brief account of this step calculated for substrate 1H without a detailed discussion of other possible structural isomers involved. Furthermore, pathways related to other structural isomers show higher barriers (Fig. S1 and S2 in the ESI†). Fig. 1 shows the Gibbs energy profile calculated for the favorable oxidative coupling process (A → B). The oxidative coupling starts with a square planar complex containing metal fragment Rh(CO)2Cl6d,e and the substrate molecule as a ligand. The oxidative coupling initially gives a pseudo-octahedral complex (B1H) containing a weakly coordinated alkene moiety in the newly-formed six-membered ring. Then, a series of structural re-organizations (isomerization) occurs to release the ring strain and achieve optimal coordination, giving the most stable oxidative coupling species B4H that contains phenyl π coordination to the Rh(III) metal center.
 | ||
| Fig. 1 Gibbs energy profile calculated for the oxidative coupling process (A → B) (oxidative coupling followed by structural rearrangement in the organic ligand (isomerization)) and the followed σ-bond metathesis process (B → C) shown in Scheme 2. Relative Gibbs energies and electronic energies (in parentheses) are given in kcal mol−1. | ||
As also shown in Fig. 1, from B4H, σ-bond metathesis takes place involving a Csp2–H bond activation giving the alkene-coordinated intermediate C1H. The corresponding transition state TSB4-C1H is a four-center species, with a moderate Gibbs energy barrier of 17.2 kcal mol−1.
C → D insertion process in the central cycle of Scheme 2. C is a bifurcation point in the reaction mechanism proposed in Scheme 2. Let us discuss the C → D insertion process in the central cycle first. Fig. 2(a) shows the Gibbs energy profile calculated for the C → D insertion process. The insertion of the alkene unit into the Csp2–RhIII bond in C1H occurs via the transition state TSC1-D1H to produce intermediate D1H. Intermediate D1H then undergoes a very facile stepwise structural re-arrangement, which turns off the weaker Rh–arene interaction and switches to the stronger Rh–alkene interaction to generate a much more stable species D3H containing allyl coordination. D3H is an η4-coordinated species in which the Rh metal center coordinates with four carbon atoms of the organic ligand in an η4 mode.
D → E β-hydride elimination process in the central cycle of Scheme 2. Here, we discuss D → E β-hydride elimination proposed in the central cycle of Scheme 2. Our calculation results indicate that D → E starts with D1H (Fig. 2(b)), instead of the more stable η4-coordinated species D3H, although D3H should be considered as a resting state for this pathway. Then, a simple configurational change in the organic ligand of D1H easily leads to an agostic interaction between C–HR and the metal center (E1H in Fig. 2(b)), a species ready for the desired β-hydride (HR) elimination. From E1H, β-hydride elimination forms σ-allylrhodium intermediate E3H. In E2H, a double bond moiety and a carbon atom of the seven-membered ring both coordinate with the rhodium metal center. The ring strain results in the instability of E2H, which easily dissociates the olefinic unit from the metal center to form the more stable intermediate E3H. Finally, reductive elimination followed by a ligand exchange of substrate 1H takes place to produce product 2H and regenerates A1H to complete the catalytic cycle. It can be seen that the process (D → E) requires a Gibbs energy barrier of 29.1 kcal mol−1 relative to intermediate D3H.
D → F β-hydride elimination process in the left cycle of Scheme 2. Next, we discuss the D → F process shown in the left cycle of Scheme 2, leading to the six/seven/six tricyclic product 3H. Fig. 2(c) shows that the η4-coordinated species D3H undergoes a stepwise structural rearrangement, leading to intermediate F2H with an agostic interaction between C–HA and the Rh center. The barrier calculated for this rearrangement is significantly high (35.0 kcal mol−1). From F2H, β-hydride elimination followed by the first reductive elimination and then a ligand exchange produces product 3H and regenerates the initial species A1H.
C → G 1,3-Rh shift process in the right cycle of Scheme 2. Finally, we discuss the C → G process proposed in the right cycle of Scheme 2, leading to the six/six/six tricyclic product 4H. According to Scheme 2, C → G involves the 1,3-Rh shift. However, we found that the bond rotation in C easily leads to a species ready for reductive elimination to give the product. Fig. 2(d) shows the calculated Gibbs energy profile. From intermediate C1H, a rotation of approximately 180 degrees of the heterocyclic ring along the Csp2–Csp3 bond affords intermediate G1H, which undergoes reductive elimination followed by a ligand exchange to give the final product 4H and regenerates the initial species A1H. The reductive elimination transition state TSG1-product 4H is rate-determining for this pathway. The barrier from C1H to TSG1-product 4H was only 24.1 kcal mol−1, which is considered easily accessible. However, since the Gibbs energy of insertion transition state TSC1-D1H (from C1H) is much lower (by 12.8 kcal mol−1) than that of TSG1-product 4H, D3H becomes a thermodynamic sink for this pathway. Thus, we saw a prohibitively high overall Gibbs energy barrier of 52.4 kcal mol−1 (with respect to the η4-coordinated species D3H) for the pathway leading to product 4H.
Brief summary. Combining all the calculated Gibbs energy profiles shown in Fig. 1 and 2, we have the following findings: (1) the oxidative coupling A → B is an irreversible process; (2) the η4-coordinated species D3H, derived from the insertion process C → D, is the resting state for all of the three catalytic cycles; (3) TSD1-E1H or TSE2-E3H (Fig. 2(b)), TSD3-F1H (Fig. 2(c)) and TSG1-product 4H (Fig. 2(d)) are the rate-determining transition states, respectively, for the formation of products 2H, 3H and 4H.
On the basis of the findings given above, the overall barriers for the formation of products 2H, 3H and 4H were calculated to be 29.1, 35.0 and 52.4 kcal mol−1, respectively, corresponding to the energy differences between the rate-determining transition states and the η4-coordinated resting state D3H. These results suggest that only product 2 is kinetically possible when R1 = H, completely in agreement with the experimental observation shown in Scheme 1a.
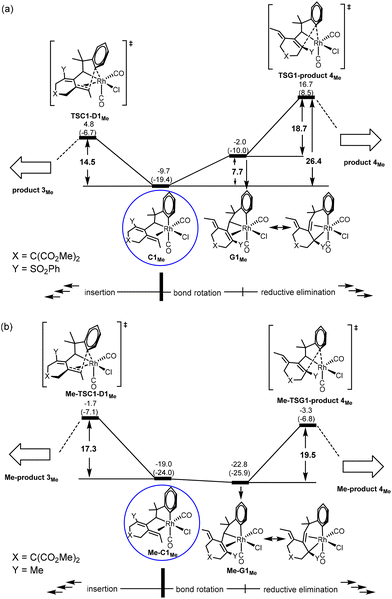
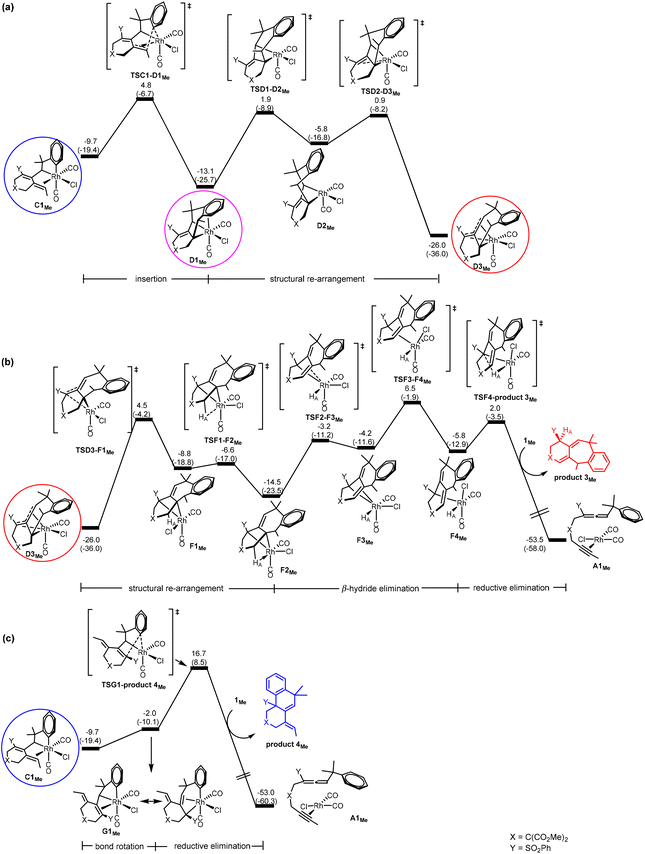
DFT results. Our calculations using the model benzylallene-alkyne substrate with R1 = Me, X = C(CO2Me)2 and Y = SO2Ph confirm that the Gibbs energy profiles (Fig. 3) for the two possible pathways resemble in general what we have obtained for the model reaction with R1 = H, in which the corresponding η4-coordinated species D3Me is also the resting state, and the overall barrier with respect to D3Me for the formation of product 3Me was calculated to be 32.5 kcal mol−1 (versus 35.0 kcal mol−1 when R1 = H). Although this barrier is relatively high, this pathway should be feasible in view of the experimental conditions with an actual reaction temperature of 110 °C. D3Me is also a thermodynamic sink for the pathway leading to product 4Me whose overall barrier (with respect to D3Me) was 42.7 kcal mol−1 (versus 52.4 kcal mol−1 when R1 = H). These results are consistent with the experimental observation showing that only product 3 was produced (Scheme 1b).
 | ||
| Fig. 3 Gibbs energy profiles calculated for (a) C → D (insertion), (b) D → F (β-hydride elimination) followed by F → A (reductive elimination) to give product 3Me, and (c) C → G (bond rotation) followed by G → A (reductive elimination) to give product 4Me, according to Scheme 2. Relative Gibbs energies and electronic energies (in parentheses) are given in kcal mol−1. | ||
Comparing Fig. 2(a) and 3(a), we found that changing from R1 = H to R1 = Me, the C1 → D3 transformation becomes less exergonic (−28.3 versus −16.3 kcal mol−1, a noticeable, significant difference of 12.0 kcal mol−1). Clearly, the introduction of a methyl group significantly destabilizes the insertion “products” D1, D2 and D3 relatively much more than C1, and at the same time hinders the structural re-arrangement from D1 to D3. Examining the structures of the insertion “products”, we found that the C–C(Ar) bond formation as a result of the insertion makes the methyl group to repulsively interact with the nearest H on the aryl ring (having a very close contact of 2.121 Å in D1Me). In other words, an alkyl substituent on the terminal alkynyl moiety of the substrate molecule significantly reduces the exergonicity of the insertion process leading to the above-mentioned C–C(Ar) bond formation.
Comparing Fig. 2(c) and 3(b) (pathway leading to product 3), we found that the two Gibbs energy profiles look very similar to each other, where the only difference between them is that the profile calculated for R1 = Me is energetically relatively higher than that calculated for R1 = H by approximately 10 ± 3 kcal mol−1. Clearly, this levelling up is a result of destabilization related to the insertion “product” D3 discussed in the last paragraph.
Comparing Fig. 2(d) and 3(c) (pathway leading to product 4), we found that the two profiles also look very similar to each other where the profile calculated for R1 = Me is energetically relatively higher than that calculated for R1 = H in a range of only 1–4 kcal mol−1. We assume that this levelling up is a result of relatively less stable C1Me when compared with C1H.
Combining all the subtle changes from R1 = H to Me discussed here, we can understand the changes related to the overall barriers leading to products 3 and 4 mentioned above.
Reactions of benzylallene-alkyne substrates having an EDG internal substituent Y on the allene moiety
Scheme 1c indicates that when the substituent Y is an electron-donating alkyl group (EDG) (instead of an electron-withdrawing group (EWG)), the six/six/six tricyclic product 4 instead of the six/seven/six tricyclic product 3 becomes favorable. In Scheme 1c, R1 is also an alkyl substituent. Thus, it is expected that the pathway leading to product 2 is also turned off. To understand the origin behind the interesting selectivity of products 3versus4, we examined the two possible pathways leading to products 3 and 4, considering two other substrates having Y = Me (EDG) and R1 = Me, and Y = Me (EDG) and R1 = tBu.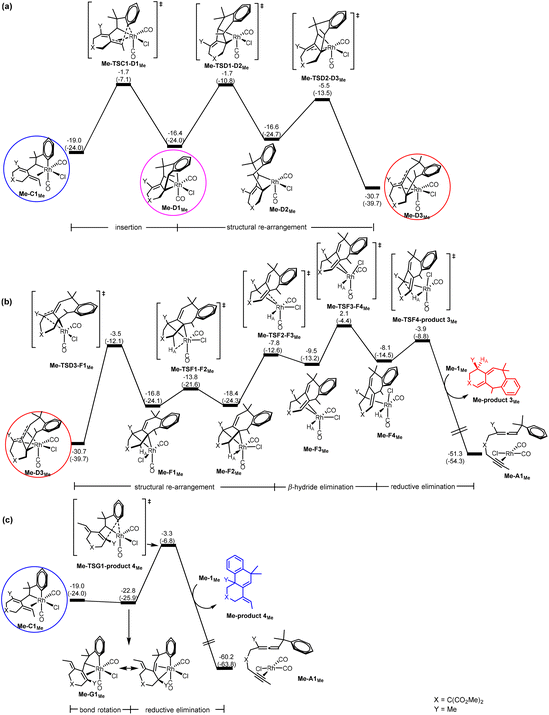 | ||
| Fig. 4 Gibbs energy profiles calculated for (a) C → D (insertion), (b) D → F (β-hydride elimination) followed by F → A (reductive elimination) to give Me-product 3Me, and (c) C → G (bond rotation) followed by G → A (reductive elimination) to give Me-product 4Me, according to Scheme 2. Relative Gibbs energies and electronic energies (in parentheses) are given in kcal mol−1. | ||
For the pathway leading to Me-product 4Me from Me-C1Me (Fig. 4(c)), we see the most significant effect as a result of the change from Y = SOPh2 (EWG) to Y = Me (EDG). The barrier from Me-C1Me to Me-TSG1-product 4Me was reduced to 15.7 kcal mol−1 (versus 26.4 kcal mol−1 in Fig. 3(c) for Y = SO2Ph). Furthermore, the relative Gibbs energy of Me-TSG1-product 4Me (Fig. 4(c)) is now lower than that of Me-TSC1-D1Me. This switch in the stability order of the two competing transition states has far-reaching impact on the reaction mechanism, indicating that the reaction will favorably proceed directly through G and then produce Me-product 4MeviaMe-TSG1-product 4Me once the metathesis (B → C) step is completed, without falling into the corresponding thermodynamic sink Me-D3MeviaMe-TSC1-D1Me (Fig. 4(a)) and then producing Me-product 3Me (Fig. 4(b)). In other words, for the reaction of a benzylallene-alkyne substrate having Y = Me (EDG) and R1 = Me, the pathway leading to Me-product 4Me from Me-C1Me (Fig. 4(c)) is the most favorable. Indeed, as indicated in Scheme 1, when Y = Me, product 4 was experimentally produced. The bond rotation step from Me-C1Me to Me-G1Me involves a series of conformational changes with accessible barriers as shown in the ESI (Fig. S3†).
Understanding how an EDG Y promotes the pathway leading to product 4viaG
In order to understand how an EDG Y promotes the pathway leading to product 4viaG, we show the two competing transition states starting from C, which is a bifurcation point for the two pathways, for both Y = SO2Ph (EWG) and Y = Me (EDG) cases. Comparing the structures of Me-C1Me and C1Me, we found that the olefinic moiety in the former is more strongly bonded to the Rh(III) metal center than that in the latter (2.495 versus 2.545 Å in their average bond distances (Fig. 5)). We clearly see from Fig. 6 that from Y = SO2Ph (EWG) to Y = Me (EDG), the olefin insertion in the pathway for product 3 becomes less favored. An EDG Y makes the olefinic moiety π-electron richer, leading to a stronger metal–olefin bonding interaction. It is understandable that stronger metal–olefin bonding interactions impede the insertion process.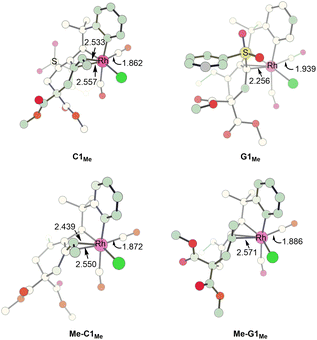 | ||
| Fig. 5 Structures calculated for C1Me, G1Me, Me-C1Me and Me-G1Me. Bond lengths are given in angstroms (Å). | ||
For the pathway leading to product 4viaG, we found that from Y = SO2Ph (EWG) to Y = Me (EDG), the overall barrier decreases significantly (from 26.4 to 19.5 kcal mol−1, Fig. 6). However, the decrease in the overall barrier does not come from the reductive elimination step starting from G, as we can clearly see that the two reductive elimination barriers (18.7 and 19.5 kcal mol−1, Fig. 6) for both cases were almost the same. Clearly, the reductive elimination barrier is not sensitive to the substituent effect. This is true in the first case when Y = SO2Ph and R1 = H discussed above and the case when Y = Me and R1 = tBu where the corresponding reductive elimination barriers were 19.2 kcal mol−1 (Fig. 2(d)) and 19.6 kcal mol−1 (Fig. S4(c)†), respectively. Instead, a decrease in the overall barrier is due to the bond rotation step. In the case when Y = SO2Ph (EWG), the bond rotation leads to a much less stable isomer G1Me (Fig. 6(a)), while in the case when Y = Me (EDG), it leads to a more stable isomer Me-G1Me (Fig. 6(b)). The bond rotation isomer G1 contains an allyl ligand. In the early studies22 on how different substituents X affect the relative stability of the trans and cis isomers in the square planar palladium(II) complexes Pd(I)(PPh3)(η3-XCHC(Ph)CH2), it was demonstrated that an EWG X results in a strong trans-influence Pd–C(X) bond. Thus, we see a scenario that in G1Me, two strong trans-influence ligands, Rh–C(SO2Ph) (2.256 Å) and CO, are arranged in trans to each other, significantly destabilizing the structure. In Me-G1Me, Rh–C(Me) (2.571 Å) is not strong trans-influencing, and therefore the destabilizing scenario is absent. Examining the calculated structures involved, we found that the Rh–CO (trans) bond distance changed from 1.862 (C1Me) to 1.939 Å (G1Me) and from 1.872 (Me-C1Me) to 1.886 Å (Me-G1Me) (Fig. 5). The NBO analysis shows that the C atom of Rh–C(Me) in Me-G1Me reveals a much more positive charge than that the C atom of Rh–C(SO2Ph) in G1Me (+0.130e vs. −0.307e). The calculated results support the trans-influence argument above.
Conclusions
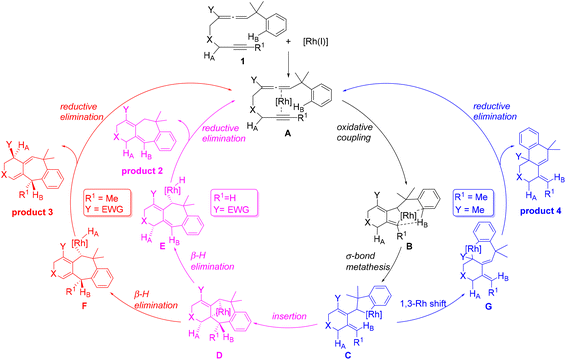
The cycloisomerization of benzylallene-terminal alkynes involving Csp2–H bond activation on the benzyl phenyl ring catalyzed by [RhCl(CO)2]2 has been theoretically investigated with the aid of DFT calculations. Scheme 3 summarizes the mechanisms we have found on the basis of our DFT calculations.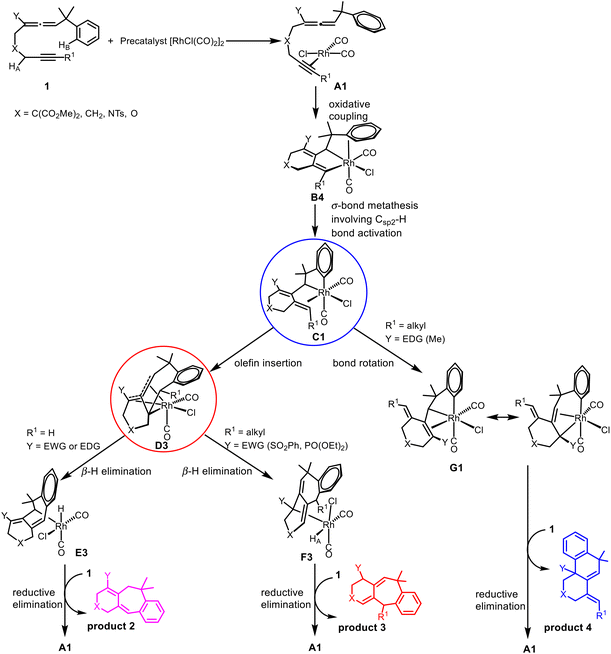 | ||
| Scheme 3 Mechanisms of [RhCl(CO)2]2-catalyzed cycloisomerization of benzylallene-alkynes through DFT calculations. | ||
The reaction is initiated by oxidative coupling to form a rhodacyclopentane intermediate B, which undergoes σ-bond metathesis involving Csp2–H bond activation to form arylrhodium intermediate C.
When the terminal substituent R1 on the alkyne moiety is a hydrogen, regardless of the substituent Y on the allene moiety is an EDG or EWG, the exocyclic olefin in C inserts into the Csp2–RhIII bond producing the tricyclic intermediate D, which undergoes β-hydride (R1) elimination to form the metal hydride intermediate E, reductive elimination of which gives the six/seven/six tricyclic product 2.
When the terminal substituent R1 on the alkyne moiety is non-hydrogen, there are two scenarios depending on whether the substituent Y on the allene moiety is an EDG or EWG. We found that an electron-donating alkyl group Y significantly promotes a Csp2–Csp3(Rh) bond rotation step transforming C to G, which undergoes reductive elimination to give the six/six/six tricyclic product 4. G contains an allyl ligand, where the Rh–C(Y) σ bond is significantly weak due to the EDG substituent Y on the allyl ligand. A significantly weak Rh–C(Y) σ bond benefits the structure G in terms of its stability considering that the ligand trans to Rh–C(Y) is a very strong trans-influencing carbonyl CO ligand. When Y is an electron-withdrawing group, the Csp2–Csp3(Rh) bond rotation is significantly less favored because the Rh–C(Y) σ bond here is significantly strengthened, significantly destabilizing the bonding interaction between the metal center and the carbonyl CO which is trans to it. Thus, the reaction also proceeds to form D, followed by β-hydride elimination to produce F, which undergoes reductive elimination to give the six/seven/six product 3.
Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
This work is supported by the National Natural Science Foundation of China (21501115), the Fund Program for the Scientific Activities of Selected Returned Overseas Professionals in Shanxi Province (20210044) and the Research Grants Council of Hong Kong (HKUST 16300620).References
- (a) R. G. Bergman, Organometallic chemistry: C–H activation, Nature, 2007, 446, 391–393 CrossRef CAS PubMed; (b) J. F. Hartwig, Carbon-heteroatom bond formation catalyzed by organometallic complexes, Nature, 2008, 455, 314–322 CrossRef CAS; (c) C. S. Yeung and V. M. Dong, Catalytic dehydrogenative cross-coupling: forming carbon-carbon bonds by oxidizing two carbon-hydrogen bonds, Chem. Rev., 2011, 111, 1215–1292 CrossRef CAS PubMed; (d) J. Yamaguchi, A. D. Yamaguchi and K. Itami, C–H bond functionalization: emerging synthetic tools for natural products and pharmaceuticals, Angew. Chem., Int. Ed., 2012, 51, 8960–9009 CrossRef CAS; (e) J. Wencel-Delord and F. Glorius, C–H bond activation enables the rapid construction and late-stage diversification of functional molecules, Nat. Chem., 2013, 5, 369–375 CrossRef CAS; (f) M. Gulías and J. L. Mascareñas, Metal-catalyzed annulations through activation and cleavage of C–H bonds, Angew. Chem., Int. Ed., 2016, 55, 11000–11019 CrossRef PubMed; (g) T. K. Achar, S. Maiti, S. Jana and D. Maiti, Transition metal catalyzed enantioselective C(sp2)–H bond functionalization, ACS Catal., 2020, 10, 13748–13793 CrossRef CAS.
- A. Hoffmann-Röder and N. Krause, Synthesis and properties of allenic natural products and pharmaceuticals, Angew. Chem., Int. Ed., 2004, 43, 1196–1216 CrossRef.
- (a) R. Zimmer, C. U. Dinesh, E. Nandanan and F. A. Khan, Palladium-catalyzed reactions of allenes, Chem. Rev., 2000, 100, 3067–3126 CrossRef CAS; (b) S. Ma, Transition metal-catalyzed/mediated reaction of allenes with a nucleophilic functionality connected to the α-carbon atom, Acc. Chem. Res., 2003, 36, 701–712 CrossRef CAS PubMed; (c) A. Hoffmann-Röder and N. Krause, Synthesis and properties of allenic natural products and pharmaceuticals, Angew. Chem., Int. Ed., 2004, 43, 1196–1216 CrossRef; (d) S. Ma, Some typical advances in the synthetic applications of allenes, Chem. Rev., 2005, 105, 2829–2872 CrossRef; (e) T. Bai, S. Ma and G. Jia, Insertion reactions of allenes with transition metal complexes, Coord. Chem. Rev., 2009, 253, 423–448 CrossRef CAS.
- For selected examples of Rh-catalyzed cycloaddition reactions of allenes by Mukai's group, see: (a) F. Inagaki, S. Narita, T. Hasegawa, S. Kitagaki and C. Mukai, Rhodium(I)-catalyzed intramolecular carbonylative [2 + 2 + 1] cycloaddition of bis(allene)s: bicyclo [6.3.0] undecadienones and bicyclo [5.3.0] decadienones, Angew. Chem., Int. Ed., 2009, 48, 2007–2011 CrossRef CAS; (b) F. Inagaki, K. Sugikubo, Y. Miyashita and C. Mukai, Rhodium(I)-catalyzed intramolecular [5 + 2] cycloaddition reactions of alkynes and allenylcyclopropanes: construction of bicyclo [5.4.0] undecatrienes and bicyclo [5.5.0] dodecatrienes, Angew. Chem., Int. Ed., 2010, 49, 2206–2210 CrossRef CAS; (c) F. Inagaki, K. Sugikubo, Y. Oura and C. Mukai, RhI-catalyzed [6 + 2] cycloaddition of alkyne-allenylcyclobutanes: a new entry for the synthesis of bicyclo [6.m.0] skeletons, Chem. – Eur. J., 2011, 17, 9062–9065 CrossRef CAS PubMed; (d) F. Inagaki, S. Kitagaki and C. Mukai, Construction of diverse ring systems based on allene-multiple bond cycloaddition, Synlett, 2011, 594–614 CAS; (e) C. Mukai, Y. Ohta, Y. Oura, Y. Kawaguchi and F. Inagaki, Csp3–Csp3 and Csp3–H bond activation of 1,1-disubstituted cyclopentane, J. Am. Chem. Soc., 2012, 134, 19580–19583 CrossRef CAS; (f) T. Kawamura, Y. Kawaguchi, K. Sugikubo, F. Inagaki and C. Mukai, Rhodium(I)-catalyzed cycloisomerization of allene-allenylcyclopropanes, Eur. J. Org. Chem., 2015, 719–722 CrossRef CAS; (g) T. Kawaguchi, K. Yabushita and C. Mukai, Rhodium(I)-catalyzed cycloisomerization of homopropargylallene-alkynes through C(sp3)–C(sp) bond activation, Angew. Chem., Int. Ed., 2018, 57, 4707–4711 CrossRef.
- For selected examples of Rh-catalyzed cycloaddition reactions of allenes by other groups, see: (a) X. Jiang and S. Ma, trans-RhCl(CO)(PPh3)2-catalyzed monomeric and dimeric cycloisomerization of propargylic 2,3-dienoates. Establishment of α,β-unsaturated δ-lactone rings by cyclometallation, J. Am. Chem. Soc., 2007, 129, 11600–11607 CrossRef CAS PubMed; (b) Y. Oonishi, A. Hosotani and Y. Sato, Rh(I)-catalyzed formal [6 + 2] cycloaddition of 4-allenals with alkynes or alkenes in a tether, J. Am. Chem. Soc., 2011, 133, 10386–10389 CrossRef CAS PubMed; (c) Y. Oonishi, Y. Kitano and Y. Sato, Csp3–H bond activation triggered by formation of metallacycles: rhodium(I)-catalyzed cyclopropanation/cyclization of allenynes, Angew. Chem., Int. Ed., 2012, 51, 1–5 CrossRef; (d) Y. Oonishi, T. Yokoe, A. Hosotani and Y. Sato, Rhodium(I)-catalyzed cyclization of allenynes with a carbonyl group through unusual insertion of a C=O bond into a rhodacycle intermediate, Angew. Chem., Int. Ed., 2014, 53, 1135–1139 CrossRef CAS; (e) O. Torres, M. Solà, A. Roglans and A. Pla-Quintana, Unusual reactivity of rhodium carbenes with allenes: an efficient asymmetric synthesis of methylenetetrahydropyran scaffolds, Chem. Commun., 2017, 53, 9922–9925 RSC; (f) D. Cassú, T. Parella, M. Solà, A. Pla-Quintana and A. Roglans, Rhodium-catalyzed [2 + 2 + 2] cycloaddition reactions of linear allene-ene-ynes to afford fused tricyclic scaffolds: insights into the mechanism, Chem. – Eur. J., 2017, 23, 14889–14899 CrossRef.
- For selected examples of theoretical studies, see: (a) G. Huang, Mechanism and selectivity in rhodium-catalyzed [7 + 2] cycloaddition and cyclopropanation/cyclization of allenylcyclopentane-alkynes: metallacycle-directed C(sp3)–C(sp3) vs C(sp3)–H activation, J. Org. Chem., 2015, 80, 7564–7571 CrossRef CAS PubMed; (b) G. Huang, Mechanism of rhodium-catalyzed cyclopropanation/cyclization of allenynes, Org. Lett., 2015, 17, 1994–1997 CrossRef CAS PubMed; (c) T. Liu, L. Han, S. Han and S. Bi, Theoretical investigation on Rhodium(I)-catalyzed cycloisomerizations of 4-allenal species with linked alkyne: ketone vs alcohol products, Organometallics, 2015, 34, 280–288 CrossRef CAS; (d) Y. Wang, W. Liao, Y. Wang, L. Jiao and Z. Yu, Mechanism and stereochemistry of Rhodium-catalyzed [5 + 2 + 1] cycloaddition of ene–vinylcyclopropanes and carbon monoxide revealed by visual kinetic analysis and quantum chemical calculations, J. Am. Chem. Soc., 2022, 144, 2624–2636 CrossRef CAS PubMed; (e) Y. Yang, Z. Tian, C. Li and Z. Yu, Why [4 + 2 + 1] but Not [2 + 2 + 1]? Why Allenes? A mechanistic study of the Rhodium-catalyzed [4 + 2 + 1] cycloaddition of in situ generated ene–ene–allenes and carbon monoxide, J. Org. Chem., 2022, 87, 10576–10591 CrossRef CAS.
- Y. Kawaguchi, S. Yasuda, A. Kaneko, Y. Oura and C. Mukai, Rhodium(I)-catalyzed cycloisomerization of benzylallene-alkynes through C–H activation, Angew. Chem., Int. Ed., 2014, 53, 7608–7612 CrossRef CAS PubMed.
- Y. Kawaguchi, S. Yasuda and C. Mukai, Mechanistic Investigation of RhI-catalyzed cycloisomerization of benzylallene-internal alkynes via C–H activation, J. Org. Chem., 2017, 82, 7666–7674 CrossRef CAS.
- Y. Kawaguchi, S. Yasuda and C. Mukai, Construction of Hexahydrophenanthrenes By Rhodium(I)-catalyzed cycloisomerization of benzylallene-substituted internal alkynes through C–H activation, Angew. Chem., Int. Ed., 2016, 55, 10473–10477 CrossRef CAS PubMed.
- (a) Y. Zhao and D. G. Truhlar, Density functionals with broad applicability in chemistry, Acc. Chem. Res., 2008, 41, 157–167 CrossRef CAS PubMed; (b) Y. Zhao and D. G. Truhlar, The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: two new functionals and systematic testing of four M06-class functionals and 12 other functionals, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed; (c) D. G. Truhlar, Molecular modeling of complex chemical systems, J. Am. Chem. Soc., 2008, 130, 16824–16827 CrossRef CAS.
- (a) W. J. Hehre, R. Ditchfield and J. A. Pople, Self-consistent molecular orbital methods. XII. Further extensions of Gaussian-type basis sets for use in molecular orbital studies of organic molecules, J. Chem. Phys., 1972, 56, 2257–2261 CrossRef CAS; (b) P. C. Hariharan and J. A. Pople, The influence of polarization functions on molecular orbital hydrogenation energies, Theor. Chim. Acta, 1973, 28, 213–222 CrossRef CAS.
- (a) W. R. Wadt and P. J. Hay, Ab initio effective core potentials for molecular calculations. Potentials for the transition metal atoms Sc to Hg, J. Chem. Phys., 1985, 82, 270–283 CrossRef; (b) P. J. Hay and W. R. Wadt, Ab initio effective core potentials for molecular calculations. Potentials for potassium to gold including the outermost core orbitals, J. Chem. Phys., 1985, 82, 299–310 CrossRef CAS.
- (a) A. W. Ehlers, M. Böhme, S. Dapprich, A. Gobbi, A. Höllwarth, V. Jonas, K. F. Köhler, R. Stegmenn and G. Frenking, A set of f-polarization functions for pseudo-potential basis sets of the transition metals Sc-Cu, Y-Ag and La-Au, Chem. Phys. Lett., 1993, 208, 111–114 CrossRef CAS; (b) A. Höllwarth, M. Böhme, S. Dapprich, A. W. Ehlers, A. Gobbi, V. Jonas, K. F. Köhler, R. Stegmenn and G. Frenking, A set of d-polarization functions for pseudo-potential basis sets of the main group elements Al-Bi and f-type polarization functions for Zn, Cd, Hg, Chem. Phys. Lett., 1993, 208, 237–240 CrossRef.
- (a) G. Lu, C. Fang, T. Xu, G. Dong and P. Liu, Computational study of Rh-catalyzed carboacylation of olefins: ligand-promoted rhodacycle isomerization enables regioselective C–C bond functionalization of benzocyclobutenones, J. Am. Chem. Soc., 2015, 137, 8274–8283 CrossRef CAS; (b) Z. Zhang, S. Yang, J. Li and X. Liao, DFT mechanistic study of Rh(III)-catalyzed [3 + 2]/[5 + 2] annulation of 4-aryl-1,2,3-triazoles and alkynes unveils the dual C–H activation atrategy, J. Org. Chem., 2016, 81, 9639–9646 CrossRef CAS; (c) P. Dai, A. A. Ogunlana and X. Bao, Mechanistic insights into cyclopropenes-involved carbonylative carbocyclization catalyzed by Rh(I) catalyst: a DFT study, J. Org. Chem., 2018, 83, 12734–12743 CrossRef CAS.
- (a) K. Fukui, A formulation of the reaction coordinate, J. Phys. Chem., 1970, 74, 4161–4163 CrossRef CAS; (b) K. Fukui, The path of chemical reactions - the IRC approach, Acc. Chem. Res., 1981, 14, 363–368 CrossRef CAS.
- A. E. Reed, L. A. Curtiss and F. Weinhold, Intermolecular interactions from a natural bond orbital, donor-acceptor viewpoint, Chem. Rev., 1988, 88, 899–926 CrossRef CAS.
- R. Krishnan, J. Binkley, R. Seeger and J. A. Pople, Self-consistent molecular orbital methods. XX. A basis set for correlated wave functions, J. Chem. Phys., 1980, 72, 650–654 CrossRef CAS.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, Universal solvation model based on solute electron density and on a continuum model of the solvent defined by the bulk dielectric constant and atomic surface tensions, J. Phys. Chem. B, 2009, 113, 6378–6396 CrossRef CAS PubMed.
- S. A. de Marothy, XYZviewer, version 0.97, Stockolm, Sweden, 2010 Search PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, revision D.01, Gaussian, Inc., Wallingford, CT, 2009 Search PubMed.
- Y. Ren and Z. Lin, Theoretical studies on Rh-catalyzed cycloisomerization of homopropargylallene-alkynes through C(sp3)–C(sp) bond activation, ACS Catal., 2020, 10, 1828–1837 CrossRef CAS.
- (a) L. Xue, G. Jia and Z. Lin, DFT studies on the stability of the trans and cis isomers in the square planar palladium(II) complexes Pd(I)(PPh3)(η3-XCHC(Ph)CHR) (X = CMe3, CO2Me, P(O)(OMe)2, and SO2H; R = H, Me), J. Theor. Comput. Chem., 2008, 7, 505–515 CrossRef CAS; (b) T. Bai, L. Xue, P. Xue, J. Zhu, H. H.-Y. Sung, S. Ma, I. D. Williams, Z. Lin and G. Jia, Insertion reactions of allenes with palladium aryl complexes [PdI(Ph)(PPh3)]2 and PdI(Ph)(dppe), Organometallics, 2008, 27, 2614–2626 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2qo01503j |
| This journal is © the Partner Organisations 2023 |