(Pre)association as a crucial step for computational prediction and analysis of the catalytic activity of σ-hole donating organocatalysts†
Denis A.
Polonnikov
 a,
Mikhail V.
Il'in
a,
Mikhail V.
Il'in
 a,
Yana V.
Safinskaya
a,
Yana V.
Safinskaya
 a,
Irina S.
Aliyarova
a,
Irina S.
Aliyarova
 a,
Alexander S.
Novikov
a,
Alexander S.
Novikov
 ab and
Dmitrii S.
Bolotin
ab and
Dmitrii S.
Bolotin
 *a
*a
aInstitute of Chemistry, Saint Petersburg State University, Universitetskaya Nab. 7/9, Saint Petersburg, 199034, Russian Federation. E-mail: d.s.bolotin@spbu.ru
bPeoples’ Friendship University of Russia (RUDN University), Miklukho-Maklaya St. 6, Moscow, 117198, Russian Federation
First published on 22nd November 2022
Abstract
Based upon the experimentally obtained kinetic data on iodonium salt catalyzed nucleophilic addition of isocyanide to imine leading to imidazopyridine species, a reliable model for DFT calculations has been suggested. It was shown that preassociation of the catalysts with the reaction species might significantly affect the total energy profile of the reaction obtained by DFT. The associates of the organocatalysts featuring the solvent molecules ligated to its σ-holes should be used as a starting point for calculations. Taking these reaction steps into consideration during the calculations leads to significantly more reliable theoretical results, which can be applied either for prediction of the catalytic activity of yet untested species or for justification of the catalytic paths based upon the experimental kinetic data as well.
Introduction
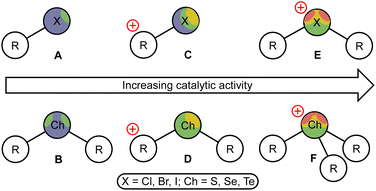
Over the last decade, σ-hole donating species have been successfully engaged in the field of homogeneous organocatalysis, as they exhibit high catalytic activity with negligible sensitivity to oxygen and water, which favorably distinguishes them from many metal-containing Lewis acids.1,2 Among the σ-hole donating catalysts, halogen (XB)3–5 and chalcogen (ChB)6–8 bond donors featuring iodine- and tellurium-based σ-hole carriers were shown to exhibit the highest catalytic activity, which, at least in a few comparative studies,9,10 turned out to be higher than that of well-proven (thio)urea-based organocatalysts.11,12 These results may indicate that the transition from traditional hydrogen bond-donating organocatalysts2,13–15 to XB and ChB donors can provide the next step in the evolution of sustainable catalysis.It has been unambiguously shown that the catalytic activity of XB and ChB donors has similar trends, namely the increase of the catalytic activity from the lighter to heavier halogen or chalcogen σ-hole carriers,16 and a significantly higher activity for the cationic species (Fig. 1, C–D) compared to the uncharged catalysts A and B.10,17–24 Moreover, the catalytic activity of the XB and ChB species featuring the halogen(III) or chalcogen(IV) atoms (E and F, respectively) is remarkably higher than that of halogen(I)- and chalcogen(II)-containing species C and D, correspondingly. Thus, cationic iodine(I)-based catalysts C (in particular, iodoazolium salts9,25–33) effectively catalyze a wide range of organic reactions, whereas cationic iodine(III) derivatives (iodonium salts E, X = I) featuring two σ-holes at the iodine atom possess even a higher catalytic activity.34–47 Similarly, tellurium(IV) derivatives (telluronium salts F, Ch = Te) exhibit a higher catalytic activity than that of tellurium(II) derivatives D and lighter chalcogen(IV)-derived species.48,49
A rational design of new noncovalent organocatalysts based on preliminary prediction of their activity by computational studies and computer modeling seems to be an attractive and sustainable way to progress in the field, minimizing efforts to synthesize a wide spectrum of test substrates potentially exhibiting catalytic activity. Considering this, a research on reliable models of catalytic routes giving experimentally consistent results is a challenging task. In our previous work,33 it was shown that a simple analysis of electrostatic potential on the σ-hole is able to give a rough estimation of the relative catalytic activity within a series of organocatalytic species, but it is hardly applicable for the estimation of a catalytic effect relatively to non-catalyzed processes.
In this work, we experimentally study the catalytic activity of a series of iodonium salts and suggest a suitable model for computational study, which correlates with the experimental data and gives a reliable estimation of the catalytic effect compared with the non-catalyzed transformations.
Results and discussion
Selected catalysts and their catalytic activity in the model reaction
Recent progress in the study of diaryliodonium-based noncovalent organocatalysts has focused on functionalization of the aryl rings in the cation,4,36,37 as well as changing the aryl to heteroaryl moieties;38 and, to a lesser extent, the preparation of chelating dinuclear iodine(III)-species.34,39 In particular, Nachtsheim and co-workers have shown that pyrazolyl-containing iodolium salts exhibit higher catalytic activity than the dibenziodolium analogue in the reaction of solvolysis of benzhydryl halides.50 In this work those substrates, as well as referent dibenziodolium salt (Fig. 2), were chosen as model substrates for study of their catalytic activity in the multicomponent Groebke–Blackburn–Bienaymé reaction, since it is a powerful tool for the synthesis of biologically active compounds,51–53 and thus the application of organocatalysts for its promotion will avoid the contamination of the target products with trace metals from metal-complex catalysts.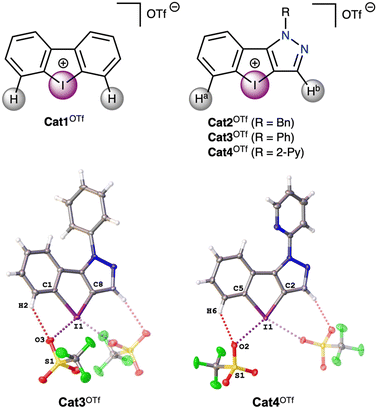 | ||
| Fig. 2 Iodonium salts Cat1OTf–Cat4OTf chosen as a model and the molecular structures of Cat3OTf and Cat4OTf. | ||
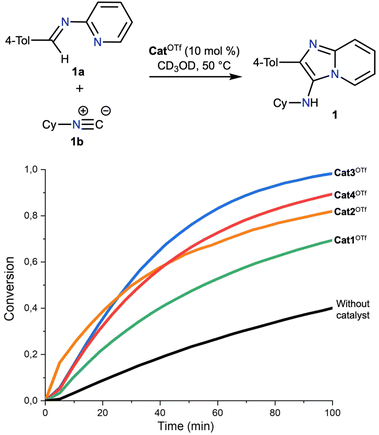
In our previous works,47,54 it was shown that the rate-limiting step of the chosen Groebke–Blackburn–Bienaymé reaction is nucleophilic attack of the isocyanide 1b to the imine 1a (Fig. 3), which is reversibly generated during the first step of reaction. Considering this, the catalytic activity of Cat1OTf–Cat4OTf was studied for the second step of reaction. 1H NMR monitoring in CD3OD at 50 °C for 100 min indicated that the dibenziodolium triflate Cat1OTf exhibited the lowest catalytic activity among the series of catalysts, whereas Cat3OTf provided the highest acceleration of the reaction. Nevertheless, all studied iodonium salts have shown a significant acceleration of the studied reaction.
To confirm practical applicability of the organocatalysts based on pyrazole-containing iodonium salts for acceleration of the Groebke–Blackburn–Bienaymé reaction, the species Cat3OTf has been applied for the catalysis of the reaction with a series of aldehydes and isocyanides (Scheme 1). The obtained results clearly indicate that Cat3OTf effectively catalyzes this reaction for a wide range of the starting substrates leading to 1–14, which were isolated in 60–96% yields of the products.
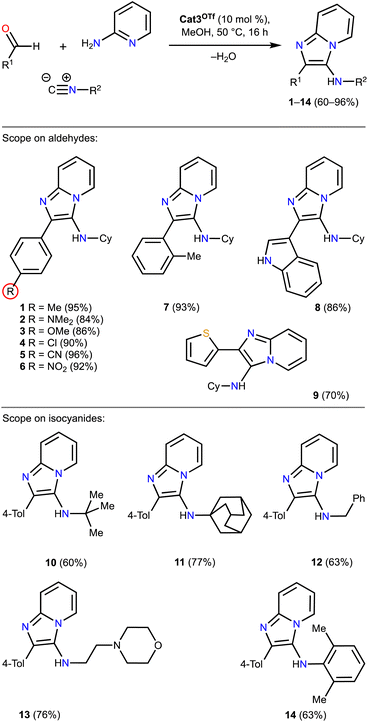 | ||
| Scheme 1 Application of Cat3OTf for a preparation of a series of imidazopyridines 1–14. Isolated yields are represented. | ||
Quantitative kinetic study of the reaction progress
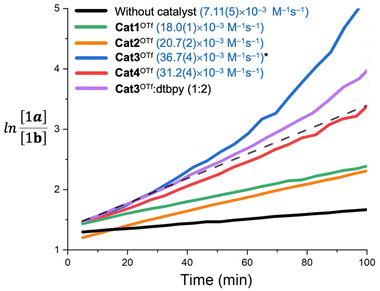
In order to obtain more accurate experimental reference points for further theoretical study, linearized plots for the kinetics have been created (Fig. 4). The kinetics expectedly exhibited a second-order either for the non-catalyzed or Cat1OTf- and Cat2OTf-catalyzed modes.47 The rate constants were calculated according to eqn (1):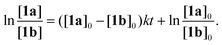 | (1) |
The graph for Cat3OTf indicated significant deviation from a straight line after the first 30 min from the beginning of the reaction, which correlates with the partial unselective decomposition of the catalyst (ca. 10–12% after 100 min) observable by 1H NMR. Carrying out the reaction in the presence of 20 mol% of 2,6-di-tert-butylpyridine (2 equiv. relatively to Cat3OTf) exhibited lesser deviation of the curve but did not completely exclude it. Considering that only ca. 10 mol% of the catalyst decompose within 100 min after the start of the reaction, these observations may indicate either formation of yet undefined highly catalytically active organic species, whose catalytic effect is not provided by donation of H+, or availability of some chain processes leading to multiplication of quantity of Brønsted acid when compared to the quantity of decomposed Cat3OTf. It is worth mentioning that the kinetic data for Cat4OTf also show low but observable deviation from the straight line (Fig. 4), which also agrees well with the 1H NMR monitoring data showing decomposition of ca. 3 mol% of Cat4OTf within the first 100 min of the reaction. Taking these observations into account, one can conclude that the calculated reaction rate constants obtained for Cat3OTf and Cat4OTf might be overestimated.
Electrostatic surface potential distribution analysis
The quantum chemical calculations (see Computational details section) show that the electrostatic potentials on the surfaces of the cations are entirely positive, but anisotropic. Dibenziodolium cation Cat1+ possesses a symmetrical structure with similar σ-holes on the I atom, whereas the pyrazolyl-containing cations Cat2+–Cat4+ feature two types of the σ-holes, namely from the side of Ha (abbreviated I⋯Ha) and Hb (abbreviated I⋯Hb) (Fig. 2). The obtained values of the highest electrostatic potential on the σ-holes I⋯Ha of Cat2+–Cat4+ equaled to 663–675 kJ mol−1, whereas the values for the σ-holes I⋯Hb lay in the interval of 610–621 kJ mol−1 (Table 1). Considering that in the solution coordination sites of the iodonium cations Cat1+–Cat4+ should be occupied by the solvent molecules, the highest electrostatic potential values on the σ-holes (Vs(max)) were also calculated for the case of the ligated MeOH molecule (Table 1). The obtained data indicated that in all the cases involving one ligated MeOH molecule, Vs(max) values decrease by 28–33 kJ mol−1, which does not significantly affect their relative values among Cat1+–Cat4+ when compared to the model with unoccupied σ-holes, but reduces it by 5% in an absolute scale. On the one hand, this observation indicates that the ligated solvent molecules can be omitted for the rough estimation of relative catalytic activity of the σ-hole-donating organic species, but, on the other hand, it proves that the comparison of absolute values of this parameter should be used with great care due to its dependence on a chosen model.| σ-Hole | Cat1+ | Cat2+ | Cat3+ | Cat4+ |
|---|---|---|---|---|
| The distribution of electrostatic potential was calculated on the 0.001 a.u. molecular surface for the optimized equilibrium model structures using the Multiwfn program.55 | ||||
| I⋯Ha (unoccupied I⋯Hb) | 628 | 663 | 670 | 675 |
| I⋯Hb (unoccupied I⋯Ha) | 610 | 621 | 619 | |
| I⋯Ha (I⋯Hb occupied by MeOH) | 600 | 633 | 639 | 642 |
| I⋯Hb (I⋯Ha occupied by MeOH) | 579 | 588 | 586 | |
Examination of the model for DFT calculations of catalyst behavior
Based upon the experimental data on kinetics of the model reaction, DFT calculations of its plausible route have been done (Scheme 2). The non-catalyzed route includes the nucleophilic attack of CyNC to the imine A leading to Cvia transition state B, whereas the catalyzed routes involve the nucleophilic attack of CyNC to the associate D giving Fvia transition state E. For the catalyzed route, the ligations of the imine to σ-hole I⋯Ha and I⋯Hb were taken into account.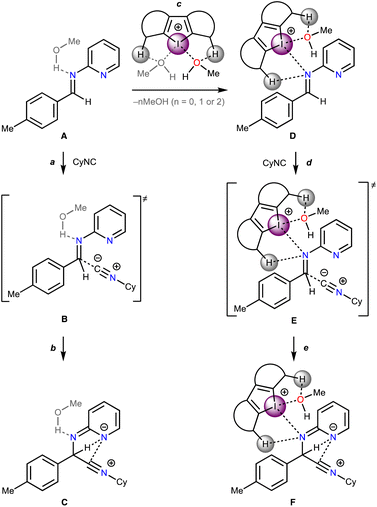 | ||
| Scheme 2 Plausible mechanism of the rate-limiting step of the studied multicomponent reaction in the absence of catalysts and in the presence of Cat1+–Cat4+. | ||
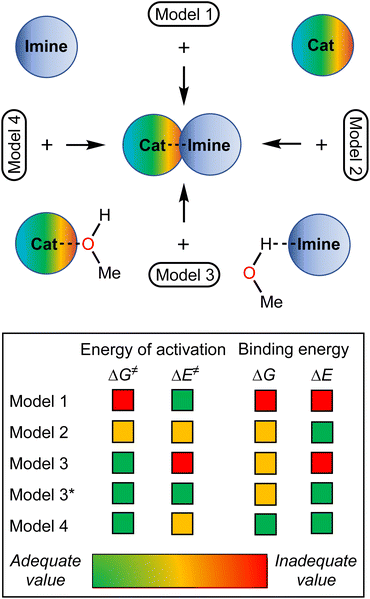
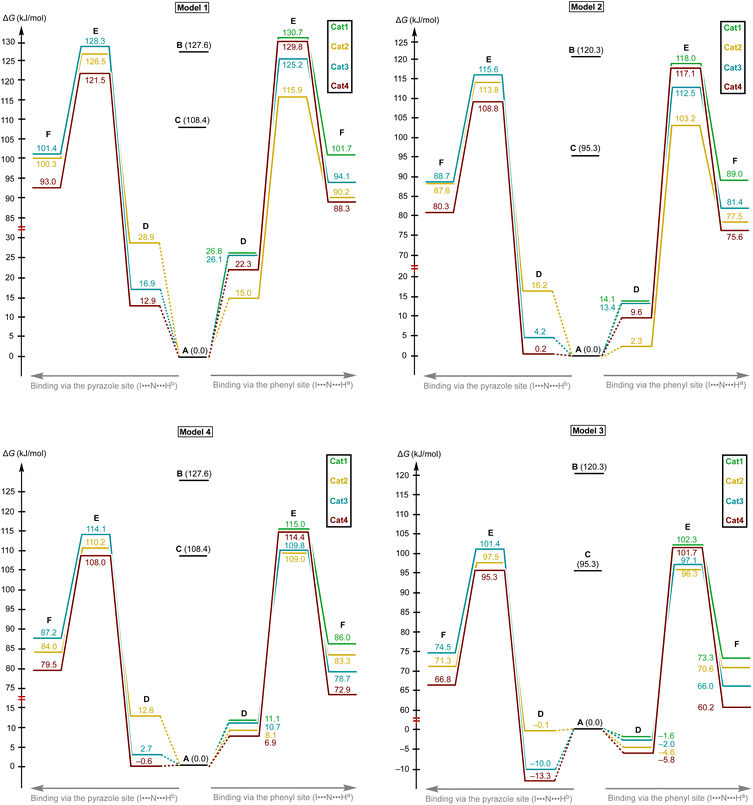
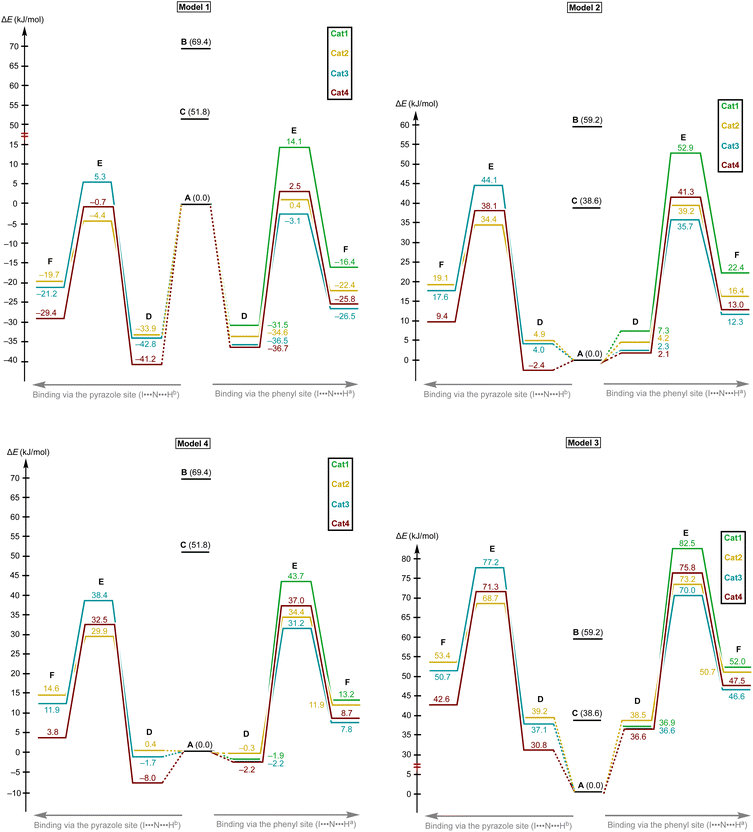
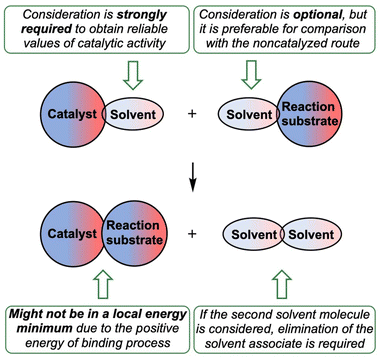
Considering the relative weakness of binding energy between the organocatalysts and organic species, which is realized via coordination of the imine to the iodine-centered σ-holes, the involvement of the solvent molecules to the consideration of the association process might have a significant impact on the total energy profile of the reaction.56 To examine the most plausible model of calculation, four cases were compared with each other and their relevance to the experimental data has been evaluated (Fig. 5). In this study, Model 1 included direct binding of Cat+ species with the imine. This simplest model of association has been previously considered by us,33,46,47 as well as by other authors,19,41,57 for a wide range of structurally different σ-hole-donating organic species including iodonium salts. Model 2 involved the ligation of the solvent molecule to the electrophilic species and, thus, considered the formation of the Cat+⋯reaction substrate associate as a substitution process instead of addition. This model was utilized by us previously for the same model reaction catalyzed by sulfonium and selenonium salts, and the comparison of this model with Model 1 previously did not give any unambiguous evidence of which model is better.54Model 3 considered the interaction of Cat+⋯solvent and substrate⋯solvent associates giving Cat+⋯substrate species and two independent solvent molecules. As it was previously found by us, this model is the best one correlated with the experimentally obtained binding energies between the catalysts species and the reaction substrates, but no data has been obtained for the prediction of the acceleration of the studied reaction.45 Finally, Model 4 described the imine coordination via substitution of the ligated solvent molecule to the organocatalyst.
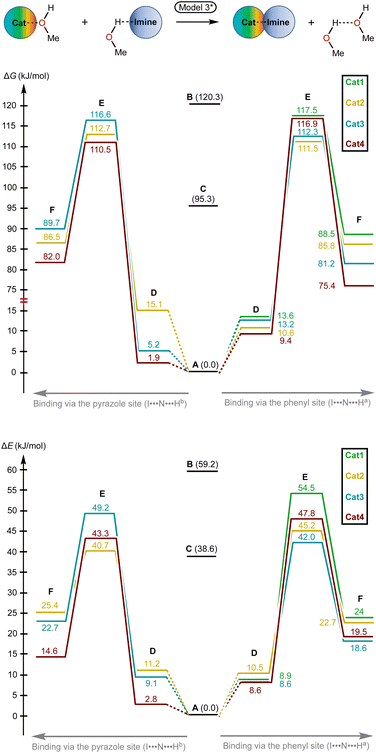
For the examination of the models, four parameters have been considered, namely Gibbs free energy of activation, total electronic energy of activation, Gibbs free energy of Cat+–imine binding, and total electronic energy of Cat+–imine binding (Fig. 5). The adequacy of the calculated parameters was assessed based on the analysis of their relative and absolute values and their comparison with the experimental data obtained in this work and previously obtained data.45,47
Model 1 gave inadequately high positive values of the Gibbs free energy of binding (12.9–26.8 kJ mol−1 for the most favorable binding mode) and, consequently, too high values of the energy of activation (Fig. 6 and 7), which might be explained in terms of overestimated loss in entropy due to the formation of one associate from two species. Very negative total electronic energy of binding may indicate that these values were also overestimated, because they include the coordination of the imine to the naked σ-hole of the catalysts, whose positive charge is not compensated by the solvent molecule. Nevertheless, this model gives adequate values of the total electronic energy of activation for the series of catalysts Cat1+–Cat4+ when compared with the non-catalyzed process (29.5–48.1 kJ mol−1vs. 69.4 kJ mol−1 for the catalyzed and non-catalyzed routes, respectively).
Model 2 gave better ΔG values of binding (0.2–14.1 kJ mol−1)—which are expected by us to range from −10 to 10 kJ mol−1 for coordination of noncharged species to iodonium salts45,47—and adequate ΔE values of binding. Although all studied species are predicted by this model to provide the catalytic effect, ΔG‡ for Cat1+ is very close to the value of the non-catalyzed process, which somehow contradicts the experimental data exhibiting observable acceleration of the reaction by Cat1+, but ΔE‡ represents adequate relative values. The experimentally observed difference in the reaction rates (2–2.5-fold increase from the non-catalyzed process to the catalyzed by Cat1+ or Cat2+, and potential 2-fold increase from Cat1+–Cat2+ to Cat3+–Cat4+) indicates that the differences in ΔG‡ for the range of Cat1+–Cat4+ should be comparable with the overall difference in ΔG‡ between the non-catalyzed and catalyzed routes. This model gives only 2.3 kJ mol−1 difference between the non-catalyzed reaction and the less catalytically active Cat1+, whereas a variation of this parameter equals 14.8 kJ mol−1 within a series of Cat1+–Cat4+, which indicates a non-reliable character of the data obtained by this model.
Model 3 involving liberation of two solvent molecules during complexation of the imine by the iodonium cations gave reasonable values in the ΔG scale both for binding process (from −0.1 kJ mol−1 to −13.3 mol−1) and transition state energy (97.6–111.4 kJ mol−1vs. 120.3 kJ mol−1 for the catalyzed and non-catalyzed paths, respectively), whereas the calculated values of ΔE of binding turned out to be too positive, which resulted in the overestimated ΔE‡ values. Thus, ΔE‡ values for the catalyzed reaction routes turned out to be even higher than those of the non-catalyzed reaction.
Model 4 considering the substitution of the solvent molecule at the iodine σ-hole by the imine gave similar but more reasonable binding energies compared to Model 2 in ΔG scale and showed adequate values of ΔG‡ of the reaction (108.6–115.0 kJ mol−1vs. 127.6 kJ mol−1 for the catalyzed and non-catalyzed reactions, respectively). In addition, ΔE values obtained by this model lay in the expected range, although the ΔE‡ for the catalyzed routes are more energetically favorable than it was expected from the experimental data.
Generally, the obtained data indicates that overall energy profile obtained by DFT calculations significantly depend on the model of complexation of the electrophilic species, which have not previously drawn any special attention. The computational results indicate that it is strongly required to consider the solvent molecules in the explicit form during the calculations when catalyzed reaction routes are compared with the non-catalyzed paths, or otherwise binding constants are theoretically predicted. Moreover, the explicit form of the solvent molecule bound to the organocatalyst gives narrower ranges of all studied parameters (ΔG and ΔE of binding as well as ΔG‡ and ΔE‡ values) than those obtained for organocatalysts featuring naked σ-hole. Thus, comparing the catalytic activity of organocatalysts featuring unoccupied σ-holes may give overestimated range of catalytic activity differences within a series of species.
The models implying the change in the quantity of bonds during the species association (Models 1 and 3) may introduce uncertainty to the energy profile. Thus, Model 1 involving formation of one additional bond showed extreme negative total electronic energy of binding, whereas Model 3 involving the decrease of bonds quantity gave highly positive values of ΔE. The change in the quantity of independent species during the studied process may also provide a significant impact on the energy profile. In ΔG scale, the binding energy is inadequately highly positive, which might be explained in terms of entropy loss during the formation of the associate. For Model 3, which gave the results very close to those obtained experimentally,45 uncertainties caused by the decrease of quantity of bonds and stemming from the increase in quantity of formed species seem to cancel each other out. To avoid the described unwanted influence on the energy profile, the best model for calculations should retain the total number of bonds and species during the catalyst-to-substrate association. Models 2 and 4 meet this requirement, but occupation of the organocatalyst σ-hole by the solvent molecule seems to lead to more plausible results in ΔG scale than its ligation to the reaction substrate.
Considering these observations, Model 3 was modified by us in order to retain the quantity of bonds and independent species during the catalyst-to-substrate association by binding of two eliminated solvent molecules to one H-bonded associate (Model 3*; Fig. 5 and 8). This model gave reasonable ΔG and ΔE values for the binding process (1.9–13.6 kJ mol−1 for ΔG) and exhibited the expectable experimental data values of ΔG‡ (110.5–117.5 kJ mol−1vs. 120.3 kJ mol−1 for the catalyzed and non-catalyzed paths).
 | ||
| Fig. 8 The energy profiles (in Gibbs free energy and total electronic energy scales) for the studied reaction paths for Model 3*. | ||
The obtained results indicate that consideration of preassociation of the catalysts with the solvent molecules and further association of the catalysts with the reaction species can significantly affect the total energy profiles for the processes studied by DFT calculations. Although direct estimation of the energy values of catalyst⋯transition state gives qualitatively reliable results when compared with the energy value of either starting species taken separately or catalyst⋯substrate associates, it might lead to significant overestimation of energy range of relative catalytic activity within a series of studied organocatalysts species. In addition, it cannot be applied for the credible comparison with the energy of non-catalyzed reaction paths.
Conclusion
In this work, it was shown that consideration of preassociation of organocatalysts with the solvent molecules as well as the process of coordination of the reaction substrates to the catalyst σ-holes significantly affect an overall energy profile of the modelled reaction, and, thus, it should be taken into account during theoretical calculations of the catalytic activity. The most common models for theoretical estimation and justification of the experimentally observed catalytic effect of σ-hole-donating organocatalysts typically omit both these processes.Based upon the obtained results, the reliable model for computational analysis and prediction of catalytic activity of σ-hole-donating organocatalytic species is suggested in this work (Fig. 9). Preassociation of the organocatalyst with the solvent molecule should be taken as a starting point. If the studied process proceeds in a weakly coordinating but undried solvent, H2O molecules may be considered as ligands. Starting from these complexes gives significantly more reliable results compared with the experimental data. Electrophilic reaction substrates optionally can be taken as associates with the solvent molecule. Such complication of the studied system might give more correct relative energies of activation for the catalyzed processes and non-catalyzed route. If the second solvent molecule is considered in the model, solvent associate should be taken as an eliminating species.
Since the catalyst with the occupied σ-hole is considered as a starting point, the reversibly forming catalyst⋯reaction substrate associate might not be in a local energy minimum and, thus, the estimation of the energy of activation should be done from the catalyst⋯solvent associate, which might significantly affect the overall activation energy.
In addition, in this work it was experimentally shown that a remarkably higher catalytic activity50 of the pyrazole-containing iodonium salts compared to the dibenziodolium analogue may be associated with unselective degradation of the heterocyclic species with the consequent acceleration of the reaction by the decomposition products. This observation shows the importance of examination of the catalyst's stability under the reaction conditions and the requirement to check its activity in complex model reactions.
Experimental section
Materials and instrumentation
All solvents, aldehydes, isocyanides, and 2-aminopyridine were obtained from commercial sources and used as received. The iodonium salts Cat1OTf–Cat4OTf were synthesized according to published procedures.45,50 All syntheses were conducted in air. The chromatographic separation was carried out using Macherey-Nagel silica gel 60 M (0.063–0.2 mm). The analytical TLC was performed on unmodified Merck ready-to-use plates (TLC silica gel 60 F254) with UV detection. The melting points were measured on a Stuart SMP30 apparatus in capillaries and are not corrected. The electrospray ionization mass-spectra were obtained on a Bruker maXis and Shimadzu LCMS-9030 spectrometers equipped with an electrospray ionization (ESI) source. The instrument was operated in a positive ion mode using an m/z range 50–1200. The nebulizer gas flow was 1.0 bar and the drying gas flow 4.0 L min−1. For HRESI+, the studied compounds were dissolved in MeOH. 1H- and 13C{1H} NMR spectra were measured on a Bruker Avance 400 spectrometer in CDCl3 and (CD3)2SO at 295 K; the residual solvent signal was used as the internal standard. The NMR monitoring kinetic experiments were carried out by measuring the 1H NMR spectra every 5 min (four scans; repetition time = 4 s) following the initial equilibration period of 5 min on a Bruker Avance III 500 spectrometer in CD3OD at 50 °C; the residual solvent signal was used as the internal standard.X-ray structure determinations
For single-crystal XRD experiments, the crystals of Cat3OTf and Cat4OTf were fixed on a micro mount and placed on SuperNova, single source at offset/far, HyPix3000 and XtaLAB Synergy, single source at home/near, HyPix diffractometers and measured at 100 K using CuKα monochromated radiation. The structures were solved by the Superflip58–60 and the ShelXT61 structure solution programs using Charge Flipping and Intrinsic Phasing and refined by means of the ShelXL program61 incorporated in the OLEX2 program package.62 The crystal data and details of structure refinements for Cat3OTf and Cat4OTf are shown in Table S1.†1H NMR monitoring of the imine-isocyanide coupling
The imine (86 mg, 0.439 mmol) and cyclohexyl isocyanide (13.6 μL, 0.110 mmol) were added to the CD3OD solution of any of Cat1OTf–Cat4OTf (18.3 mM, 600 μL, 0.011 mmol) and placed in an NMR tube. For the experiment with 2,6-di-tert-butylpyridine, 0.022 mmol of the reagent was added to the reaction mixture containing Cat3OTf. For the non-catalyzed reaction, the same quantities of the reactants were added to the CD3OD (600 μL) and placed in an NMR tube. The NMR tube was sealed, and the obtained homogeneous solution was maintained at 50 °C for 100 min in an NMR spectrometer. The reaction was monitored by measuring the time-dependent integral density of the ipso-cyclohexyl proton group signals in isocyanide and in the product of the reaction.Computational details
The full geometry optimization of all model structures in methanol solution was carried out at the DFT level of theory using the M06-2X functional63 with the help of the Gaussian-09 program package.64 The quasi-relativistic MWB46 pseudopotentials,65 which described 46 core electrons, and the appropriate contracted basis sets were used for iodine atoms, while the standard 6-31G* basis sets were used for other atoms. No symmetry restrictions were applied during the geometry optimizations. The solvent effects were taken into account using the SMD (Solvation Model based on Density) continuum solvation model suggested by Truhlar and coworkers.66 The Hessian matrices were calculated analytically for all optimized model structures to prove the location of the correct minimum or saddle point on the potential energy surface (no imaginary frequencies or only one imaginary frequency, respectively). The calculations of molecular surface electrostatic potentials were performed using Multiwfn program (version 3.7).55 The Chemcraft program (https://www.chemcraftprog.com/) was used for the visualization of the molecular surface electrostatic potential distribution. The Cartesian atomic coordinates for all model structures are presented in the attached xyz-files (Tables S2 and S3†).Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Russian Science Foundation (grant 20-73-10013 – experimental studies) and RUDN University Strategic Academic Leadership Program (computational studies). Physicochemical studies were performed at the Center for Magnetic Resonance, Center for X-ray Diffraction Studies, Chemistry Educational Centre, and Center for Chemical Analysis and Materials Research (all at Saint Petersburg State University).References
- V. Oliveira, M. Cardoso and L. Forezi, Organocatalysis: A Brief Overview on Its Evolution and Applications, Catalysts, 2018, 8, 605 CrossRef.
- Y. Qin, L. Zhu and S. Luo, Organocatalysis in Inert C-H Bond Functionalization, Chem. Rev., 2017, 117, 9433–9520 CrossRef CAS.
- D. Bulfield and S. M. Huber, Halogen Bonding in Organic Synthesis and Organocatalysis, Chem. – Eur. J., 2016, 22, 14434–14450 CrossRef CAS PubMed.
- F. Heinen, E. Engelage, A. Dreger, R. Weiss and S. M. Huber, Iodine(III) Derivatives as Halogen Bonding Organocatalysts, Angew. Chem., Int. Ed., 2018, 57, 3830–3833 CrossRef CAS.
- R. L. Sutar and S. M. Huber, Catalysis of Organic Reactions through Halogen Bonding, ACS Catal., 2019, 9, 9622–9639 CrossRef CAS.
- L. Vogel, P. Wonner and S. M. Huber, Chalcogen Bonding: An Overview, Angew. Chem., Int. Ed., 2019, 58, 1880–1891 CrossRef CAS.
- S. Kolb, G. A. Oliver and D. B. Werz, Chemistry Evolves, Terms Evolve, but Phenomena Do Not Evolve: From Chalcogen-Chalcogen Interactions to Chalcogen Bonding, Angew. Chem., Int. Ed., 2020, 59, 22306–22310 CrossRef CAS.
- J. Y. C. Lim and P. D. Beer, Sigma-Hole Interactions in Anion Recognition, Chem, 2018, 4, 731–783 CAS.
- K. Takagi, H. Murakata and T. Hasegawa, Application of Thiourea/Halogen Bond Donor Cocatalysis in Metal-Free Cationic Polymerization of Isobutyl Vinyl Ether and Styrene Derivatives, Macromolecules, 2022, 55, 5756–5765 CrossRef CAS.
- P. Wonner, A. Dreger, L. Vogel, E. Engelage and S. M. Huber, Chalcogen Bonding Catalysis of a Nitro-Michael Reaction, Angew. Chem., Int. Ed., 2019, 58, 16923–16927 CrossRef CAS PubMed.
- C. M. Volla, I. Atodiresei and M. Rueping, Catalytic C-C bond-forming multi-component cascade or domino reactions: pushing the boundaries of complexity in asymmetric organocatalysis, Chem. Rev., 2014, 114, 2390–2431 CrossRef CAS PubMed.
- F. E. Held and S. B. Tsogoeva, Asymmetric cycloaddition reactions catalyzed by bifunctional thiourea and squaramide organocatalysts: recent advances, Catal. Sci. Technol., 2016, 6, 645–667 RSC.
- X. Han, H. B. Zhou and C. Dong, Applications of Chiral Squaramides: From Asymmetric Organocatalysis to Biologically Active Compounds, Chem. Rec., 2016, 16, 897–906 CrossRef CAS.
- T. James, M. van Gemmeren and B. List, Development and Applications of Disulfonimides in Enantioselective Organocatalysis, Chem. Rev., 2015, 115, 9388–9409 CrossRef CAS.
- B. Han, X. H. He, Y. Q. Liu, G. He, C. Peng and J. L. Li, Asymmetric organocatalysis: an enabling technology for medicinal chemistry, Chem. Soc. Rev., 2021, 50, 1522–1586 RSC.
- A. S. Novikov and D. S. Bolotin, Halonium, chalconium, and pnictonium salts as noncovalent organocatalysts: a computational study on relative catalytic activity, Org. Biomol. Chem., 2022, 20, 7632–7639 RSC.
- K. Strakova, L. Assies, A. Goujon, F. Piazzolla, H. V. Humeniuk and S. Matile, Dithienothiophenes at Work: Access to Mechanosensitive Fluorescent Probes, Chalcogen-Bonding Catalysis, and Beyond, Chem. Rev., 2019, 119, 10977–11005 CrossRef.
- S. Benz, J. Mareda, C. Besnard, N. Sakai and S. Matile, Catalysis with chalcogen bonds: neutral benzodiselenazole scaffolds with high-precision selenium donors of variable strength, Chem. Sci., 2017, 8, 8164–8169 RSC.
- N. Tarannam, M. H. H. Voelkel, S. M. Huber and S. Kozuch, Chalcogen vs Halogen Bonding Catalysis in a Water-Bridge-Cocatalyzed Nitro-Michael Reaction, J. Org. Chem., 2022, 87, 1661–1668 CrossRef CAS PubMed.
- P. Wonner, T. Steinke, L. Vogel and S. M. Huber, Carbonyl Activation by Selenium- and Tellurium-Based Chalcogen Bonding in a Michael Addition Reaction, Chem. – Eur. J., 2020, 26, 1258–1262 CrossRef CAS.
- N. Biot and D. Bonifazi, Chalcogen-bond driven molecular recognition at work, Coord. Chem. Rev., 2020, 413, 213243 CrossRef CAS.
- K. T. Mahmudov, M. N. Kopylovich, M. F. C. Guedes da Silva and A. J. L. Pombeiro, Chalcogen bonding in synthesis, catalysis and design of materials, Dalton Trans., 2017, 46, 10121–10138 RSC.
- T. Steinke, P. Wonner, R. M. Gauld, S. Heinrich and S. M. Huber, Catalytic Activation of Imines by Chalcogen Bond Donors in a Povarov [4+2] Cycloaddition Reaction, Chem. – Eur. J., 2022, 28, e202200917 CrossRef CAS.
- H. Zhu, P. P. Zhou and Y. Wang, Cooperative chalcogen bonding interactions in confined sites activate aziridines, Nat. Commun., 2022, 13, 3563 CrossRef CAS.
- Y. Takeda, D. Hisakuni, C. H. Lin and S. Minakata, 2-Halogenoimidazolium salt catalyzed aza-Diels-Alder reaction through halogen-bond formation, Org. Lett., 2015, 17, 318–321 CrossRef CAS PubMed.
- S. H. Jungbauer, S. M. Walter, S. Schindler, L. Rout, F. Kniep and S. M. Huber, Activation of a carbonyl compound by halogen bonding, Chem. Commun., 2014, 50, 6281–6284 RSC.
- J. P. Gliese, S. H. Jungbauer and S. M. Huber, A halogen-bonding-catalyzed Michael addition reaction, Chem. Commun., 2017, 53, 12052–12055 RSC.
- M. Kaasik, A. Metsala, S. Kaabel, K. Kriis, I. Jarving and T. Kanger, Halo-1,2,3-triazolium Salts as Halogen Bond Donors for the Activation of Imines in Dihydropyridinone Synthesis, J. Org. Chem., 2019, 84, 4294–4303 CrossRef CAS.
- A. Dreger, E. Engelage, B. Mallick, P. D. Beer and S. M. Huber, The role of charge in 1,2,3-triazol(ium)-based halogen bonding activators, Chem. Commun., 2018, 54, 4013–4016 RSC.
- R. Haraguchi, S. Hoshino, M. Sakai, S. G. Tanazawa, Y. Morita, T. Komatsu and S. I. Fukuzawa, Bulky iodotriazolium tetrafluoroborates as highly active halogen-bonding-donor catalysts, Chem. Commun., 2018, 54, 10320–10323 RSC.
- K. Torita, R. Haraguchi, Y. Morita, S. Kemmochi, T. Komatsu and S. I. Fukuzawa, Lewis acid-base synergistic catalysis of cationic halogen-bonding-donors with nucleophilic counter anions, Chem. Commun., 2020, 56, 9715–9718 RSC.
- R. A. Squitieri, K. P. Fitzpatrick, A. A. Jaworski and K. A. Scheidt, Synthesis and Evaluation of Azolium-Based Halogen-Bond Donors, Chem. – Eur. J., 2019, 25, 10069–10073 CrossRef CAS PubMed.
- A. A. Sysoeva, A. S. Novikov, M. V. Il'in, V. V. Suslonov and D. S. Bolotin, Predicting the catalytic activity of azolium-based halogen bond donors: an experimentally-verified theoretical study, Org. Biomol. Chem., 2021, 19, 7611–7620 RSC.
- S. Portela, J. J. Cabrera-Trujillo and I. Fernandez, Catalysis by Bidentate Iodine(III)-Based Halogen Donors: Surpassing the Activity of Strong Lewis Acids, J. Org. Chem., 2021, 86, 5317–5326 CrossRef CAS.
- R. Robidas, D. L. Reinhard, C. Y. Legault and S. M. Huber, Iodine(III)-Based Halogen Bond Donors: Properties and Applications, Chem. Rec., 2021, 21, 1912–1927 CrossRef CAS.
- F. Heinen, E. Engelage, C. J. Cramer and S. M. Huber, Hypervalent Iodine(III) Compounds as Biaxial Halogen Bond Donors, J. Am. Chem. Soc., 2020, 142, 8633–8640 CrossRef CAS.
- D. L. Reinhard, F. Heinen, J. Stoesser, E. Engelage and S. M. Huber, Tuning the Halogen Bonding Strength of Cyclic Diaryliodonium Salts, Helv. Chim. Acta, 2021, 104, e2000221 CrossRef CAS.
- A. Boelke, T. J. Kuczmera, E. Lork and B. J. Nachtsheim, N-Heterocyclic Iod(az)olium Salts - Potent Halogen-Bond Donors in Organocatalysis, Chem. – Eur. J., 2021, 27, 13128–13134 CrossRef CAS.
- F. Heinen, D. L. Reinhard, E. Engelage and S. M. Huber, A Bidentate Iodine(III)-Based Halogen-Bond Donor as a Powerful Organocatalyst, Angew. Chem., Int. Ed., 2021, 60, 5069–5073 CrossRef CAS PubMed.
- R. J. Mayer, A. R. Ofial, H. Mayr and C. Y. Legault, Lewis Acidity Scale of Diaryliodonium Ions toward Oxygen, Nitrogen, and Halogen Lewis Bases, J. Am. Chem. Soc., 2020, 142, 5221–5233 CrossRef CAS.
- A. Labattut, P. L. Tremblay, O. Moutounet and C. Y. Legault, Experimental and Theoretical Quantification of the Lewis Acidity of Iodine(III) Species, J. Org. Chem., 2017, 82, 11891–11896 CrossRef CAS PubMed.
- Y. Nishida, T. Suzuki, Y. Takagi, E. Amma, R. Tajima, S. Kuwano and T. Arai, A Hypervalent Cyclic Dibenzoiodolium Salt as a Halogen-Bond-Donor Catalyst for the [4+2] Cycloaddition of 2-Alkenylindoles, ChemPlusChem, 2021, 86, 741–744 CrossRef CAS PubMed.
- Y. Zhang, J. Han and Z.-J. Liu, Diaryliodonium salts as efficient Lewis acid catalysts for direct three component Mannich reactions, RSC Adv., 2015, 5, 25485–25488 RSC.
- R. Haraguchi, T. Nishikawa, A. Kanazawa and S. Aoshima, Metal-Free Living Cationic Polymerization Using Diaryliodonium Salts as Organic Lewis Acid Catalysts, Macromolecules, 2020, 53, 4185–4192 CrossRef CAS.
- S. N. Yunusova, A. S. Novikov, N. S. Soldatova, M. A. Vovk and D. S. Bolotin, Iodonium salts as efficient iodine(III)-based noncovalent organocatalysts for Knorr-type reactions, RSC Adv., 2021, 11, 4574–4583 RSC.
- A. S. Novikov and D. S. Bolotin, Xenon Derivatives as Aerogen Bond-Donating Catalysts for Organic Transformations: A Theoretical Study on the Metaphorical “Spherical Cow in a Vacuum” Provides Insights into Noncovalent Organocatalysis, J. Org. Chem., 2022 DOI:10.1021/acs.joc.2c00680 , in press.
- M. V. Il'in, A. A. Sysoeva, A. S. Novikov and D. S. Bolotin, Diaryliodoniums as Hybrid Hydrogen- and Halogen-Bond-Donating Organocatalysts for the Groebke-Blackburn-Bienayme Reaction, J. Org. Chem., 2022, 87, 4569–4579 CrossRef.
- B. Zhou and F. P. Gabbai, Anion Chelation via Double Chalcogen Bonding: The Case of a Bis-telluronium Dication and Its Application in Electrophilic Catalysis via Metal-Chloride Bond Activation, J. Am. Chem. Soc., 2021, 143, 8625–8630 CrossRef CAS.
- R. Weiss, E. Aubert, P. Pale and V. Mamane, Chalcogen-Bonding Catalysis with Telluronium Cations, Angew. Chem., Int. Ed., 2021, 60, 19281–19286 CrossRef CAS.
- A. Boelke, T. J. Kuczmera, L. D. Caspers, E. Lork and B. J. Nachtsheim, Iodolopyrazolium Salts: Synthesis, Derivatizations, and Applications, Org. Lett., 2020, 22, 7261–7266 CrossRef CAS.
- A. Boltjes and A. Domling, The Groebke-Blackburn-Bienayme Reaction, Eur. J. Org. Chem., 2019, 7007–7049 CrossRef CAS PubMed.
- S. Zhi, X. Ma and W. Zhang, Consecutive multicomponent reactions for the synthesis of complex molecules, Org. Biomol. Chem., 2019, 17, 7632–7650 RSC.
- J. C. Flores-Reyes, A. Islas-Jácome and E. González-Zamora, The Ugi three-component reaction and its variants, Org. Chem. Front., 2021, 8, 5460–5515 RSC.
- M. V. Il'in, A. S. Novikov and D. S. Bolotin, Sulfonium and Selenonium Salts as Noncovalent Organocatalysts for the Multicomponent Groebke-Blackburn-Bienayme Reaction, J. Org. Chem., 2022, 87, 10199–10207 CrossRef.
- T. Lu and F. Chen, Multiwfn: a multifunctional wavefunction analyzer, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- L. L. Han, S. J. Li and D. C. Fang, Theoretical estimation of kinetic parameters for nucleophilic substitution reactions in solution: an application of a solution translational entropy model, Phys. Chem. Chem. Phys., 2016, 18, 6182–6190 RSC.
- M. Breugst, E. Detmar and D. von der Heiden, Origin of the Catalytic Effects of Molecular Iodine: A Computational Analysis, ACS Catal., 2016, 6, 3203–3212 CrossRef CAS.
- L. Palatinus and G. Chapuis, SUPERFLIP - A Computer Program for the Solution of Crystal Structures by Charge Flipping in Arbitrary Dimensions, J. Appl. Crystallogr., 2007, 40, 786–790 CrossRef CAS.
- L. Palatinus and A. van der Lee, Symmetry Determination Following Structure Solution in P1, J. Appl. Crystallogr., 2008, 41, 975–984 CrossRef CAS.
- L. Palatinus, S. J. Prathapa and S. van Smaalen, EDMA: A Computer Program for Topological Analysis of Discrete Electron Densities, J. Appl. Crystallogr., 2012, 45, 575–580 CrossRef CAS.
- G. M. Sheldrick, SHELXT – Integrated Space-group and Crystal Structure Determination, Acta Crystallogr., Sect. A: Found. Adv., 2015, 71, 3–8 CrossRef.
- O. V. Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. K. Howard and H. Puschmann, OLEX2: a Complete Structure Solution, Refinement and Analysis Program, J. Appl. Crystallogr., 2009, 42, 339–341 CrossRef CAS.
- Y. Zhao and D. G. Truhlar, The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: two new functionals and systematic testing of four M06-class functionals and 12 other functionals, Theor. Chem. Acc., 2007, 120, 215–241 Search PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision C.01, 2010 Search PubMed.
- A. Bergner, M. Dolg, W. Küchle, H. Stoll and H. Preuß, Ab initio energy-adjusted pseudopotentials for elements of groups 13–17, Mol. Phys., 1993, 80, 1431–1441 CrossRef CAS.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, Universal Solvation Model Based on Solute Electron Density and on a Continuum Model of the Solvent Defined by the Bulk Dielectric Constant and Atomic Surface Tensions, J. Phys. Chem. B, 2009, 113, 6378–6396 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: 1H NMR monitoring of the Groebke–Blackburn–Bienaymé reaction; synthesis of the imine 1a; synthesis and characterization of Cat2OTf–Cat4OTf; synthesis of dibenziodolium triflate Cat1OTf; synthesis and characterization of 1–14; spectra of 1a, Cat1OTf–Cat4OTf, and 1–14; Table S1. Crystal data for Cat3OTf and Cat4OTf; Table S2. Calculated total electronic energies (E, in Hartree), enthalpies (H, in Hartree), Gibbs free energies (G, in Hartree), and entropies (S, cal mol−1 K−1) for optimized equilibrium model structures; Table S3. Calculated values of total electronic energies, enthalpies, and Gibbs free energies of activation and reaction (ΔE‡, ΔH‡, ΔG‡, ΔE, ΔH, and ΔG in kJ mol−1) for model processes. CCDC 2212224 and 2212225. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d2qo01648f |
| This journal is © the Partner Organisations 2023 |