Computational insights for predicting the binding and selectivity of peptidomimetic plasmepsin IV inhibitors against cathepsin D

Abstract

Plasmepsins (Plms) are aspartic proteases involved in the degradation of human hemoglobin by P. falciparum and are essential for the survival and growth of the parasite. Therefore, Plm enzymes are reported as an important antimalarial drug target. Herein, we have applied molecular docking, molecular dynamics (MD) simulations, and binding free energy with the Linear Interaction Energy (LIE) approach to investigate the binding of peptidomimetic PlmIV inhibitors with a particular focus on understanding their selectivity against the human Asp protease cathepsin D (CatD). The residual decomposition analysis results suggest that amino acid differences in the subsite S3 of PlmIV and CatD are responsible for the higher selectivity of the 5a inhibitor. These findings yield excellent agreement with experimental binding data and provide new details regarding van der Waals and electrostatic interactions of subsite residues as well as structural properties of the PlmIV and CatD systems.

---

Introduction

Malaria is a disease caused by parasites of the genus Plasmodium.¹ This disease is transmitted to the human host by the female mosquitoes belonging to the genus Anopheles.² A large part of the world's population lives in endemic areas of malaria, mainly in tropical countries, making this disease a global health problem.³ The progress against this disease remains stagnant, especially in endemic countries.³ In 2019, the global malaria cases corresponded to 229 million, an annual estimate that has remained virtually unchanged over the past 4 years, with the disease claiming around 409 000 lives in the same year.³ These numbers may be aggravated as the COVID-19 pandemic affects the fight against this disease.⁴ In addition, malaria remains a primary cause of childhood illness and death in sub-Saharan Africa. More than 260 000 African children under the age of five die annually from malaria. Recently, the World Health Organization (WHO) recommends widespread use of the RTS,S/AS01 (RTS,S) malaria vaccine among children in sub-Saharan Africa and other regions with moderate to high P. falciparum malaria transmission. However, RTS,S/AS01 provides incomplete and only short-term protection.⁵

Particularly, artemisinin (ATS) is a frontline drug used for the treatment of malaria disease and ATS combination therapies (ACTs) is used to treat P. falciparum and P. vivax. However, resistance to frontline artemisinin and partner drugs is now causing the failure of P. falciparum ACTs in Southeast Asia.⁶ Thus, it is evident that further development of new antimalarial drugs with new modes of action are warranted.

After the complete sequencing of the genome of P. falciparum, several new drugs with different forms of action were proposed, for example, respiratory chain enzymes in the parasite's mitochondria,⁷ transport proteins^8,9 and proteases.^10,11 In particular, aspartic protease Plms are important targets for developing drugs against malaria.^12–14

Sequencing of the P. falciparum genome has led to the identification of ten different genes that encode the Plms, these enzymes are numbered from I to X.¹⁵ Plms I–IV are located in the acid food vacuole and are active during the intro-erythrocytic stage of the life cycle by providing nutrients for the parasite's growth.^16–18 Since Plms are involved in degrading the host hemoglobin, they are attractive targets for designing new drugs against malaria.¹⁷

The successful development of Plms inhibitors as drugs requires optimization of on-target potency and minimization of undesirable off-target activity, particularly against related host proteases.¹² Noteworthy, vacuolar Plms (PlmsI–IV) are highly homologous, sharing 50–79% amino acid sequence identity,¹⁹ but are only ∼35% homologous to mammalian enzymes renin and cathepsin D (CatD).²⁰ Particularly, CatD is an enzyme responsible for protein digestion and is involved in a range of physiological processes.^21–23 These involve critical roles in protein catabolism and retinal function.^24,25 Therefore, inhibition of CatD by PlmIV inhibitors may result in pathophysiological conditions as well as a decrease in antimalarial efficacy.

Previous studies have suggested that PlmII/CatD selectivity is dependent on the substituents reaching the S3–S4 subsites.²⁶ According to Johansson et al., the S2 subsite in CatD is smaller than in PlmII.²⁷ Recently, Zogota et al.¹² proposed a set of peptidomimetic PmlV inhibitors with antimalarial activity at nanomolar concentrations and selectivity against CatD,¹² where some inhibitor substituents occupy the non-prime sub-pockets (S′ part). Therefore, steric and energetical features can be related to increasing antimalarial activity and selectivity of peptidomimetic PmlV inhibitors.

As a successful strategy for the process of structure-based drug design (SDBB), we have applied powerful computational approaches to investigate a myriad of enzymatic reactions and binding inhibition mechanisms.^29–34 Herein, we used molecular docking in combination with molecular dynamics (MD) simulations^35,36 and subsequent binding free energy calculations applying the Linear Interaction Energy (LIE) method³⁷ to investigate the structural and energetic features that contribute to the binding of peptidomimetic inhibitors of PlmIV that was previously reported,¹² as well as their selectivity against CatD. We demonstrated that the computational approach applied here accurately predicts the binding free energy of inhibitors of PlmIV and CatD that agree with experimental results.¹² Overall, we explain at the molecular level the reason for the selectivity between PlmIV and CatD and provide insight for rationally designing new antimalarial drugs.

Materials and methods

PlmIV/CatD and inhibitors preparation and molecular docking

The initial coordinates for PlmIV and CatD were taken from Protein Data Bank (PDB) under codes 2ANL³⁸ and 4OD9,³⁹ respectively. As the starting point for inhibitor structures (Table 1), 5a was in silico constructed into catalytic site of enzymes and then optimized with Gaussian09 ⁴⁰ at QM level using PM6 semi-empirical method.⁴¹ The AutoDockTools 1.5.6 (ADT)^42,43 package was used to prepare all PDBQT files to carry molecular docking simulations into AutoDock Vina v.1.2.0,⁴⁴ where only ligands were considered flexibles.

Table 1 Inhibitors and its IC₅₀ experimental values (μM) for PlmIV and CatD

Inhibitor	R1	R2	R3	IC50 PlmIV^a	IC50 CatD^a	S^b
a Data obtained from ref. 12 and 28.b Selectivity factor between CatD and PlmIV, IC50 “non target”/IC50 “target”.
1a	n-Pr	n-Pr		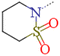0.029	0.043	1.48
1b	n-Pr	n-Pr		0.024	0.042	1.75
1c	n-Pr	n-Pr	Ph	0.006	0.054	9.00
1d	H	n-Pr		0.038	0.11	2.90
2a	Et	Et		0.014	0.250	17.86
2b	Me	Me		0.087	0.500	5.74
2c	HOCH2CH2	HOCH2CH2		0.068	0.270	3.97
2d	MeOCH2CH2	MeOCH2CH2		0.037	0.100	2.70
2e	CF3CH2CH2	CF3CH2CH2		0.210	0.120	0.57
3a	H	MeOC(CH3)2CH2		0.048	2.100	43.75
4a	n-Pr	n-Pr	Me	0.023	0.210	9.13
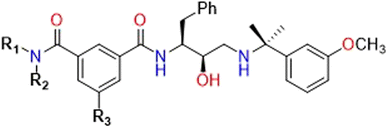
5a	H	t-BuCH2	H	0.076	3.800	50.00
5b	H	CF3CH2CH2	H	0.150	4.900	32.66

---

The AutoDock Vina v.1.2.0 ⁴⁴ software was used to examine the binding of the PlmIV inhibitors to the target proteins: PlmIV and CatD. All the receptors were placed inside the grid box and all the grid information was described in the script file (number of modes = 10, exhaustiveness = 50 and energy range = 3 kcal mol⁻¹). The grid (Å) that was used to run PlmIV was center-X = 56.69, center-Y = 10.68, center-Z = 18.84, size-X = 40.00, size-Y = 40.00, size-Z = 40.00. The grid box information for CatD was center-X = 0.53, center-Y = 11.96, center-Z = −33.72, size-X = 40.00, size-Y = 40.00, size-Z = 40.00. The grid box was chosen carefully to be sure that the whole receptors are fitted inside the box. It should be highlighted that all studied molecules (see Table 1) used here were initially proposed by GlaxoSmithKline (GSK) group⁴⁵ and later studied by Zogota et al.¹² (Fig. 1).

Fig. 1 Starting structure for antimalarial HTS-based on the GSK group.⁴⁵

Molecular dynamics (MD) simulations

The complexes obtained from molecular docking calculations were used as starting points for MD simulations performed using the program Q (version 6).^46,47 The OPLS-AA force field⁴⁸ and TIP3P water model⁴⁹ were used as a set of classical parameters for the solute (enzymes and inhibitors) and solvent (water), respectively. Particularly, classical parameters for the inhibitors were obtained through an automatic parametrization carried out by the MACROMODEL version 10.8.⁵⁰ Initially, pK_a values of all titratable residues were computed using the PROPKA method⁵¹ as implemented in the PDB2PQR server⁵² at neutral pH. It should be noted that the protonation state of the catalytic aspartates was initially retrieved from a previous study carried out by ref. 53, where QM/MM MD and potential of mean force simulations suggest that the proton is located on the carboxylic group of Asp214 (hereafter referred to as AspH214) for PlmIV system, while Asp34 was considered into its charged state. Similarly, the same procedure was adopted for the CatD system (Asp33 and AspH231). Besides, this protonation model of PlmIV was applied by Gutiérrez-de-Terán and Åqvist.⁵⁴

A simulation sphere of 20 Å radius was considered in simulated systems, centered on the center of mass of each inhibitor. The sphere was solvated with TIP3P water molecules⁴⁹ and subjected to polarization and radial constraints according to the surface-constrained all-atom solvent (SCAAS) model⁵⁵ at the sphere surface to describe appropriately the properties of bulk water. Titratable amino acid residues closer than 3–5 Å to the boundary, as well as those outside the solvent sphere, were modeled into their neutral state due to the lack of dielectric screening.

Initially, each complexed system (bound state) was slowly heated up to 300 K during 150 ps, which was followed by 1000 ps for the equilibration stage, in which initial positional restrains on all solute heavy atoms were gradually released. The subsequent production phase for data collection consists of 12 ns of MD simulations from 3 randomized replicas of 4 ns each for each simulated system.

Nonbonded interactions were calculated explicitly up to a 10 Å cut-off, except for the atoms of ligands, for which no cutoff was used. In addition, long-range electrostatics were computed by the local reaction field (LRF) multipole expansion method.^56,57 A time step of 1.0 fs was set up and the SHAKE algorithm⁵⁸ was applied to restrain all solvent bonds and angles. Nonbonded pair lists and the ligand-surrounding interaction energies were saved every 25 steps. To estimate binding free energies by the LIE method,³⁷ in the water (free state) simulations a weak harmonic restraint was applied to the center of mass of the ligands to keep them centered in the water simulation sphere following the same conditions as for the bound state.

Linear interaction energy (LIE) for binding free energy calculations

Binding free energies of every PlmIV/CatD system were calculated using the LIE method³⁷ as:

ΔG_LIE = α(〈V_vdW〉_bound − 〈V_vdW〉_free) + β(〈V_ele〉_bound − 〈V_ele〉_free) + γ (1)

The α and β parameters are empirically derived from nonpolar and polar contributions, respectively.⁵⁹ The brackets “〈 〉” refers to the average of van der Waals and electrostatic (V_ele) interaction energies for the “bound” and “free” states of each inhibitor.³⁷ Particularly, the empirical parameters (α and β) are usually taken from the literature (α = 0.181 and β = 0.33–0.50)^59,60 or can be appropriately obtained by linear fitting the ligand-surrounding interaction energies versus experimental binding affinities. Finally, the last parameter γ is a constant related to the protein environment that does not change the relative binding free energies⁶¹ but is used to equalize the calculated energies to the experimental binding affinity values (ΔG^exp_bind), which is calculated from IC₅₀ values as:

ΔG^exp_bind = RT ln IC₅₀ (2)

Results and discussion

Molecular docking calculations

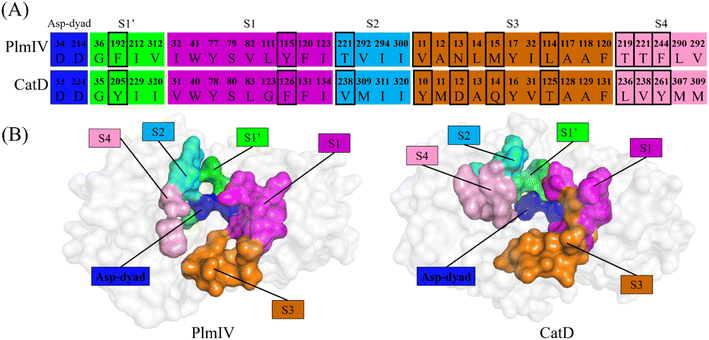
Initially, to evaluate differences in inhibitor recognition for PlmIV and CatD proteins, we plotted a sequence alignment based on the structure of each protein (Fig. 2A) highlighting all prime and non-prime sub-pockets (Fig. 2B). As shown in Fig. 2, the S3 subsite contains the greatest polarity difference in amino acid sequence composition between PlmIV and CatD, followed by the S4 subsite. Furthermore, the S3 subsite of PlmIV was more hydrophobic than the S3 of CatD, which can allow us to expect that the occupation and interactions of inhibitors in the region of the S3 subsite are essential for the selectivity between these two proteins. A previous study performed by Rasina et al.⁶² revealed that a set of non-peptidomimetic Plm inhibitors showed inhibitory potency at the nanomolar range with remarkable selectivity against CatD followed by decreasing lipophilicity and increasing solubility.

Fig. 2 (A) Sequence alignment based on the structure of the amino acid residues that belong to the Asp-dyad, S1′ and S1–S4 subsites of PlmIV and CatD. The residues that most differ according to the chain polarity side are highlighted in a box. (B) Surface representation of the Asp-dyad, S1′ and S1–S4 subsites in PlmIV and CatD.

The binding modes of the 5a, 3a and 5b, depict the highest selectivity factors (50.0, 43.75, and 32.66, respectively), in the models of PlmIV and CatD, which were obtained by the molecular docking calculations as illustrated in Fig. 3 and their respective affinity scoring values are summarized in Table 2. Our docking studies indicated that the selected PlmIV inhibitors (Tables 1 and 2) are bound into CatD binding pocket in a similar mode to PlmIV (Fig. 3). Besides, by comparing binding affinity values for both systems, no suitable structural differences could be found between 5a, 3a and 5b into PlmIV/CatD binding pockets. In general, the sub-pocket S3 accommodates R₁ and R₂ substituents of PlmIV inhibitors while the R₃ group occupies the sub-pocket S4 in the PlmIV model. In the CatD model, R₁ and R₂ substituents occupy the same sub-pocket S3. Particularly, for 3a, the R₃ is positioned to sub-pocket S2.

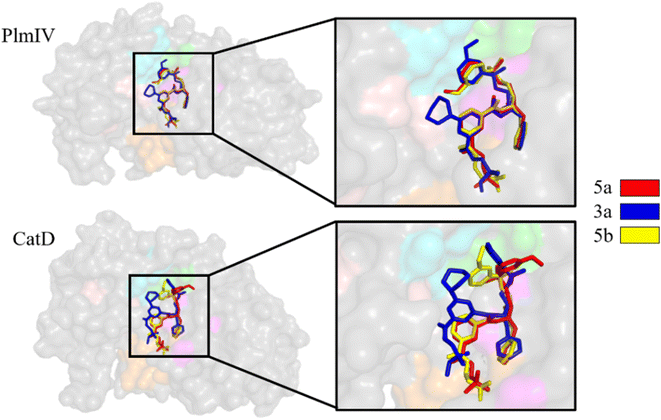Fig. 3 Molecular docking overlapping for 5a, 3a and 5b inhibitors into catalytic site of PlmIV and CatD enzymes. The 3D structures of the docked complexes are provided as ESI.†

Table 2 Molecular docking binding affinity values (kcal mol⁻¹) for 5a, 3a and 5b inhibitors

Inhibitor	PlmIV	CatD
5a	−9.2	−8.6
3a	−9.2	−9.1
5b	−9.1	−9.1

---

MD simulations and structural analysis

Plms systems have shown great enzymatic flexibility in all reported crystal structures.^63,64 So, MD simulations was used to avail the structural flexibility of Plm-peptidomimetic systems. In this study, each Plm system was submitted to a total of 12 ns of classical MD simulations. Previous computational studies demonstrated that peptidomimetic inhibitors promote interactions which stabilize the flap loop of Plm complexes.^63,65–67 Whereas, nonpeptidomimetic compounds greatly affect the flap loop dynamics, requesting a larger MD scale.⁶³ The time-evolution of RMSD values of the inhibitor atoms complexed to PlmIV and CatD is shown in Table 3. In all systems (a total of 26), the RMSD values are smaller than 2.0 Å, which indicates that these systems are quite stable during the production phase of MD simulations for data collection, as expected for Plm-peptidomimetic systems.^13,68

Table 3 Root-Mean-Square Deviation (RMSD) values (in Å) of inhibitor structure during the production phase of MD simulations. The RMSD plots for all systems are provided as ESI (Fig. S1 and S2)

Inhibitor	RMSD (Å)
	PlmIV	CatD
1a	0.52 ± 0.09	0.74 ± 0.27
1b	0.68 ± 0.18	0.92 ± 0.32
1c	0.78 ± 0.18	0.74 ± 0.24
1d	0.84 ± 0.16	0.59 ± 0.13
2a	0.72 ± 0.14	0.75 ± 0.19
2b	0.75 ± 0.18	0.72 ± 0.20
2c	0.58 ± 0.20	0.71 ± 0.24
2d	0.90 ± 0.13	0.56 ± 0.15
2e	1.15 ± 0.24	0.70 ± 0.16
3a	0.57 ± 0.14	0.73 ± 0.21
4a	0.55 ± 0.17	0.56 ± 0.23
5a	0.90 ± 0.22	1.49 ± 0.41
5b	0.74 ± 0.17	0.97 ± 0.40

---

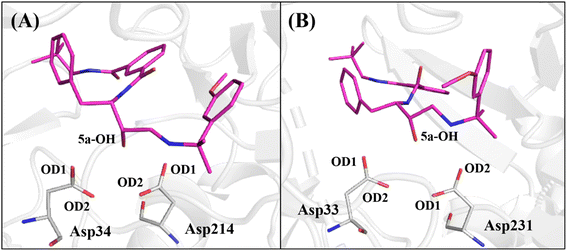
The protonation state of the catalytic aspartates in aspartic proteases is still an unsolved and challenging question. Some different computational^53,69–74 and experimental^75–78 techniques have addressed this question. Then, we could conclude that the position of the proton(s) into the carboxylic groups of catalytic Asp can be changed by the presence and chemical nature of the ligand-bound and that more than one model could occur. Here, we chose to consider the model proposed by Silva et al.⁵³ obtained by QM/MM⁷⁹ and umbrella sampling⁸⁰ methods which suggest the carboxylic group of Asp214 as neutral (containing a proton in the oxygen atom, named as AspH214) while Asp34 has its carboxylic group charged (without proton and formal charge equal to −1). A similar procedure was adopted for the CatD system (Asp33 and AspH231).

Therefore, to avail the inhibitors' stability at each protein's binding site, their interactions with catalytic aspartates (aspartic acid dyad) were monitored during the production phase of MD simulations (Fig. 4). To this end, the averages of the distances between the hydroxyl group of the base structure of the inhibitors and the oxygen atoms of the carboxylic group of the catalytic Asp on each protein are summarized in Table 4.

Fig. 4 A representative snapshot from MD simulations of 5a (C atoms in pink color) into the binding site of (A) PlmIV and (B) CatD systems highlighting their respective aspartic acid dyad (hydrogen atoms were omitted).

Table 4 Average distances (in Å) from MD simulations between the hydroxyl group of inhibitors (1a–5b) and oxygen atoms of carboxylic groups of the aspartic acid dyad of PlmIV and CatD systems

Inhibitor	PlmIV				CatD
	Asp34 (OD1)	Asp34 (OD2)	Asp214 (OD1)	Asp214 (OD2)	Asp33 (OD1)	Asp33 (OD2)	Asp231 (OD1)	Asp231 (OD2)
1a-(OH)	3.64 ± 0.24	2.66 ± 0.18	4.33 ± 0.51	5.27 ± 0.59	4.37 ± 0.31	3.81 ± 0.31	4.18 ± 0.60	2.87 ± 0.81
1b-(OH)	3.02 ± 0.32	3.27 ± 0.41	3.22 ± 0.32	4.92 ± 0.38	3.80 ± 0.81	2.81 ± 0.92	4.19 ± 0.59	3.08 ± 0.51
1c-(OH)	3.69 ± 0.21	2.81 ± 0.22	3.59 ± 0.33	3.15 ± 0.20	3.22 ± 0.40	3.01 ± 0.34	2.80 ± 0.33	3.36 ± 0.22
1d-(OH)	3.80 ± 0.21	2.70 ± 0.11	3.83 ± 0.23	3.25 ± 0.29	3.51 ± 0.25	2.49 ± 0.24	2.73 ± 0.10	3.19 ± 0.10
2a-(OH)	2.96 ± 0.32	3.37 ± 0.40	3.17 ± 0.36	3.08 ± 0.34	3.93 ± 0.56	2.64 ± 0.46	3.72 ± 0.52	3.03 ± 0.35
2b-(OH)	3.95 ± 0.63	4.52 ± 0.30	5.74 ± 0.70	3.74 ± 0.35	3.79 ± 0.28	2.62 ± 0.22	3.47 ± 0.25	3.03 ± 0.10
2c-(OH)	3.23 ± 0.33	2.80 ± 0.22	2.97 ± 0.39	3.23 ± 0.26	4.65 ± 0.43	4.52 ± 0.52	4.16 ± 0.50	2.88 ± 0.87
2d-(OH)	3.71 ± 0.22	2.71 ± 0.15	3.69 ± 0.36	3.42 ± 0.37	3.11 ± 0.32	3.02 ± 0.33	4.05 ± 0.57	2.99 ± 0.55
2e-(OH)	3.23 ± 0.50	2.98 ± 0.25	3.33 ± 0.59	3.20 ± 0.28	3.73 ± 0.21	2.74 ± 0.38	3.85 ± 0.50	2.83 ± 0.36
3a-(OH)	3.74 ± 0.21	2.66 ± 0.14	3.86 ± 0.37	5.03 ± 0.38	2.77 ± 0.42	3.16 ± 0.34	4.19 ± 0.25	4.07 ± 0.33
4a-(OH)	3.32 ± 0.33	3.08 ± 0.26	4.07 ± 0.46	3.09 ± 0.21	3.25 ± 0.11	2.86 ± 0.25	3.25 ± 0.25	3.45 ± 0.10
5a-(OH)	4.15 ± 0.34	2.75 ± 0.15	3.82 ± 0.33	3.38 ± 0.31	2.94 ± 0.28	3.00 ± 0.27	3.23 ± 0.22	3.61 ± 0.22
5b-(OH)	3.65 ± 0.51	3.26 ± 0.63	3.58 ± 0.42	3.21 ± 0.31	4.37 ± 0.20	2.88 ± 0.22	3.99 ± 0.31	2.96 ± 0.27

---

As observed in Table 4, the average distances between the hydroxyl group of 1a, 1b, 1c, 1d, 2a, 2c, 2d, 2e, 3a and 5a inhibitors show that they are positioned to form a hydrogen bond with catalytic Asp34 in PlmIV (Table 4), where this residue was considered in its anionic form.^53,54 On the other hand, it was found that inhibitors 1b, 1c, 1d, 2a, 2b, 2e, 3a, 4a, 5a and 5b tend to hydrogen bond with the Asp33 in the active site of CatD.

Binding free energy by LIE method

Molecular docking is a computationally fast, efficient, and low-cost technique,³⁵ however, its predictions of binding poses and, mainly, binding affinity energies as measured by docking scores do not have high accuracy^81–83 and it has difficulty to distinguish compounds with similar binding affinities. Some computational alternatives to overcome these limitations are the use of Alchemical Free Energy (AFE) methods^84,85 such as Free Energy Perturbation (FEP)^86,87 and Thermodynamic Integration (TI)^88,89 that can be used to predict the binding free energy involving biochemical systems, however, they require extensive sampling of several non-physical intermediate states and then their applications into high-throughput scenarios may not be useful.⁹⁰ Therefore, a suitable alternative in terms of efficacy and efficiency to compute the binding free energy are end-point free energy (EPFE) methods,⁹¹ which are based on the configurations of the final states of a system, and therefore, computationally less expensive than AFE methods and more accurate than most docking scoring functions.^91,92 Among the most popular EPFE methods, we chose the Linear Interaction Energy (LIE)³⁷ which offers advantages to AFE methods (in terms of efficiency) and docking scoring functions (in terms of accuracy).^93,94 Furthermore, it has been successfully used for PlmIV systems.^54,73

Herein, all peptidomimetic inhibitors were thermodynamically evaluated by computing their respective binding free energy (ΔG_LIE) by applying the LIE method. The sampling for each state of the computed system was obtained through the average of the production phase of MD simulations, as described previously. Table 5 shows the ΔG_LIE values (in kcal mol⁻¹) for each PlmIV/CatD system considering their respective averages of electrostatic (ΔV_ele) and van der Waals (ΔV_vdW) contributions, as well as the experimental binding free energy (ΔG_EXP) values according to eqn (2), by using experimental data from the literature.^12,28 The empirical parameters α and β of the LIE equation (eqn (1)) were obtained directly from the literature (α = 0.181 and β = 0.5, 0.43, 0.37 and 0.33),⁵⁹ while γ parameter was set to zero,⁹⁵ as proposed by Gutiérrez-de-Terán and Åqvist.⁵⁴ The empirical LIE parameters used for each system are better described in Table S1 of ESI.†

Table 5 Calculated (ΔG_LIE, from eqn (1)) and experimental (ΔG_EXP, from eqn (2)) binding free energy for PlmIV and CatD systems

Inhibitor	PlmIV				CatD
	ΔVvdW (kcal mol^−1)	ΔVele (kcal mol^−1)	ΔGLIE (kcal mol^−1)	ΔGEXP (kcal mol^−1)	ΔVvdW (kcal mol^−1)	ΔVele (kcal mol^−1)	ΔGLIE (kcal mol^−1)	ΔGEXP (kcal mol^−1)
1a	−31.75 ± 0.34	−12.41 ± 1.08	−10.30 ± 0.39	−10.30	−41.27 ± 0.52	−7.63 ± 0.42	−10.24 ± 0.15	−10.07
1b	−30.99 ± 0.61	−13.49 ± 0.98	−10.56 ± 0.99	−10.42	−39.12 ± 0.40	−8.46 ± 0.21	−10.16 ± 0.23	−10.08
1c	−32.48 ± 0.89	−14.51 ± 1.09	−11.21 ± 0.54	−11.24	−39.40 ± 0.16	−7.27 ± 0.35	−9.78 ± 0.08	−9.94
1d	−27.10 ± 0.82	−13.85 ± 0.57	−10.00 ± 0.29	−10.14	−34.37 ± 0.69	−8.53 ± 0.37	−9.34 ± 0.08	−9.51
2a	−34.90 ± 0.27	−11.64 ± 0.21	−10.65 ± 0.19	−10.74	−36.65 ± 0.47	−6.44 ± 0.11	−8.98 ± 0.14	−9.02
2b	−31.26 ± 0.57	−10.82 ± 1.04	−9.63 ± 0.74	−9.65	−30.97 ± 0.14	−7.93 ± 0.37	−8.50 ± 0.12	−8.61
2c	−29.43 ± 0.47	−13.40 ± 0.63	−9.72 ± 0.12	−9.80	−40.64 ± 0.11	−4.54 ± 1.89	−8.82 ± 0.44	−8.98
2d	−31.55 ± 0.66	−11.85 ± 0.97	−10.07 ± 0.91	−10.16	−37.01 ± 1.05	−7.49 ± 1.79	−9.44 ± 0.90	−9.57
2e	−30.78 ± 0.32	−9.08 ± 0.89	−8.90 ± 0.68	−9.13	−36.92 ± 0.55	−8.94 ± 0.50	−8.95 ± 0.31	−9.46
3a	−30.54 ± 0.27	−12.17 ± 1.04	−10.00 ± 0.70	−10.01	−31.82 ± 0.89	−6.65 ± 0.70	−8.17 ± 0.65	−7.76
4a	−32.38 ± 0.74	−11.88 ± 0.99	−10.23 ± 0.54	−10.44	−35.59 ± 1.22	−6.86 ± 1.00	−8.94 ± 0.24	−9.13
5a	−23.16 ± 0.21	−13.23 ± 0.70	−9.07 ± 0.52	−9.73	−28.14 ± 0.23	−7.00 ± 0.33	−7.65 ± 0.50	−7.41
5b	−31.71 ± 0.33	−9.12 ± 0.40	−9.08 ± 0.37	−9.33	−26.42 ± 1.01	−7.64 ± 1.21	−7.58 ± 0.91	−7.26

---

Interestingly, in all systems, an unusually high contribution from the van der Waals (non-polar) component of the binding free energy was observed. In other words, the electrostatic interactions are not the most important contributions to the binding process of peptidomimetic inhibitors into the binding site of PlmIV and CatD proteins. This can be explained because both proteins' S1–S4 and S1′ pockets are predominantly hydrophobic.^12,28 These results are in concordance with the experimental proposal of Zogota et al.¹² and the computational evidence from Gutiérrez-de-Terán.⁵⁴

By comparing ΔG_LIE and ΔG_EXP values (Table 5), we obtain the coefficients of determination (r²) equal to 0.93 (Fig. 5) and 0.94 (Fig. 6) for PlmIV and CatD systems, respectively; demonstrating that our results are in agreement with experimental data reported in previous studies.^12,28 Particularly, ΔG_LIE for 1a in the PlmIV corresponds exactly to the ΔG_EXP value (−10.30 kcal mol⁻¹). In general, all inhibitors calculated here were also in excellent agreement between ΔG_EXP and ΔG_LIE, which reflect the strong correlation coefficients, as it is assumed that the typical precision of the method shows the root mean square errors (RMS) of the experimental binding free energies of less than 1 kcal mol⁻¹,^13,96 which is better than the average performance of the scoring functions (2–2.5 kcal mol⁻¹).⁹⁷

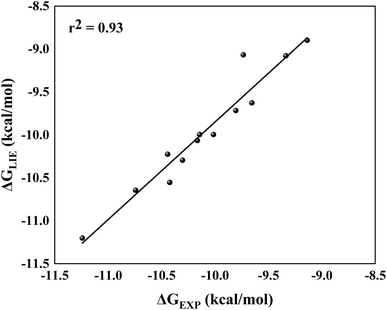Fig. 5 Linear regression model between the calculated (ΔG_LIE) and experimental (ΔG_EXP) binding free energy (in kcal mol⁻¹) for the selected peptidomimetic inhibitors bound to PlmIV.

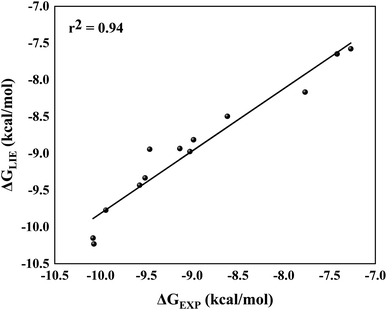Fig. 6 Linear regression model between the calculated (ΔG_LIE) and experimental (ΔG_EXP) binding free energy (in kcal mol⁻¹) for the selected peptidomimetic inhibitors bound to CatD.

Initially, for molecular docking procedures, we choose 5a as a starting point to design other inhibitors, the reason for that is due to its highest selectivity factor value (S = 50.00, Table 1). Interestingly, it showed an excellent concordance between ΔG_LIE and ΔG_EXP values for PlmIV (−9.07 and −9.73 kcal mol⁻¹, respectively) and CatD (−7.65 and −7.41 kcal mol⁻¹, respectively). The same conclusion can be observed in 2e, which has the lowest selectivity factor value (S = 0.57, Table 1), where ΔG_LIE and ΔG_EXP values for PlmIV are −8.90 and −9.13 kcal mol⁻¹, respectively, and CatD for −8.95 and −9.46 kcal mol⁻¹, respectively. Overall, both inhibitors with high selectivity and low selectivity factors have ΔG_LIE in excellent agreement with the ΔG_EXP values. Also, it was possible to obtain the calculated (S_CALC) and experimental (S_EXP) selectivity factor for each of the inhibitors (Table S2, ESI†), the r² value found is equal to 0.90 (Fig. 7). All results demonstrate that the LIE parameterization used for both models is a robust method that reproduces the experimental affinities of inhibitors in complex with PlmIV and CatD as well as their selectivity factors.

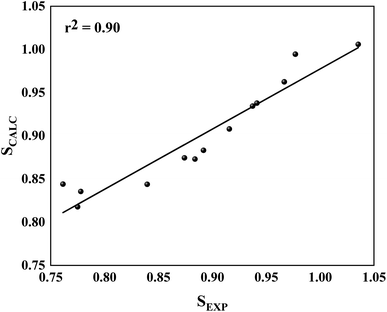Fig. 7 Linear regression model between the calculated for S_CALC and S_EXP involving all simulated systems.

Per-residue decomposition analysis

A computational study performed by Valiente et al.⁶⁶ identified by structural analysis seven important amino acid residues: Tyr17, Val105, Thr108, Leu191, Leu242, Gln275 and Thr298 (according to PlmII numbering). For PlmIV system, their results demonstrated a smaller fluctuaions in the flap loop region when compared with PlmII system. Here, to further quantify the contribution of amino acids from prime and non-prime sub-pockets towards selectivity between PlmIV and CatD, the electrostatic and van der Waals contributions for 5a and 2e complexed with PlmIV and CatD were computed to identify which residues are important for binding as well as how they can explain each selectivity factor. Therefore, only energetic contributions for 5a and 2e at the binding site of both proteins will be presented.

Initially, by considering the interaction between each inhibitor and aspartic protease dyad for PlmIV and CatD (Fig. 8), respectively, the electrostatic contribution of Asp34 from PlmIV and Asp33 from the CatD system is the most evident component of binding free energy. For 5a, a decrease of electrostatic of Asp34 from PlmIV (−10.09 kcal mol⁻¹) to Asp33 from CatD (−13.01 kcal mol⁻¹) is observed, resulting in a change of about −2.92 kcal mol⁻¹. Similar behavior can be observed for 2e, where the electrostatic energy decreases by 1.48 kcal mol⁻¹ from PlmIV to CatD. On other hand, the protonated Asp of PlmIV and CatD system does not contribute significantly to the binding free energy of 5a or 2e.

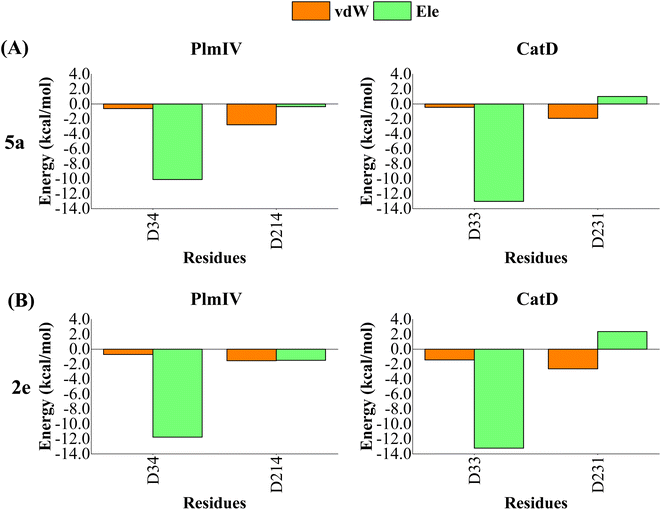Fig. 8 Per-residue decomposition of the binding free energy into contributions from electrostatic (Ele) and van der Waals (vdW) interactions for (A) 5a bound to PlmIV (left) and CatD (right) and (B) 2e bound to PlmIV (left) and CatD (right). The detailed contribution values for each residue are in ESI.†

When we consider each prime and non-prime sub-pockets for 5a and 2e into PlmIV and CatD, the most important contributions are provided by vdW interactions (Fig. 9 and 10). For 5a bound to PlmIV, the vdW contributions for subsites S1′, S1, S2, S3 and S4 are −3.55, −15.33, −6.25, −7.41 and −5.32 kcal mol⁻¹, respectively. Whereas for CatD, the values of vdW contributions are −6.75, −18.71, −7.46, −9.27 and −4.43 kcal mol⁻¹, respectively. Then, a suitable change can be observed for subsites S1′ and S1 where vdW contributions decrease by about 3.00 kcal mol⁻¹ for each subsite from PlmIV to CatD. Particularly, for subsite S1′ the decreasing of vdW contribution can be related replacement of Val312 (0.01 kcal mol⁻¹, in PlmIV) by Leu320 (−2.44 kcal mol⁻¹, in CatD). Interestingly, for subsite S3 the replacement of Leu14, Met15 and Leu114 (in PlmIV) by Ala13, Gln14 and Thr125 (in CatD), respectively, promotes suitable changes in the vdW interactions (from −0.11, −0.69 and −3.32 kcal mol⁻¹ to −1.42, −2.28 and −1.30 kcal mol⁻¹, respectively).

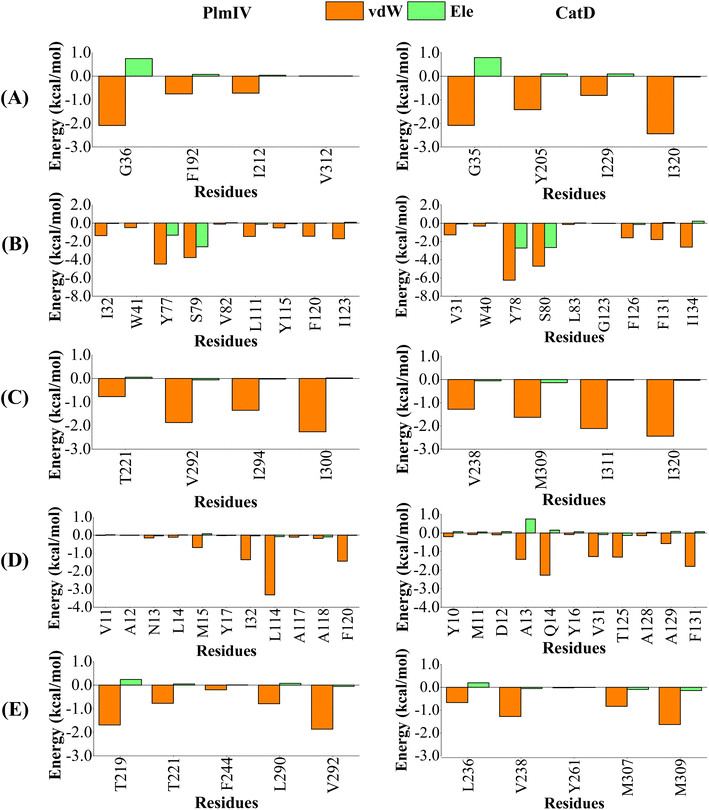Fig. 9 Per-residue decomposition of the binding free energy into contributions from electrostatic (Ele) and van der Waals (vdW) interactions for 5a compound bound to PlmIV (left) and CatD (right) considering only (A) subsite S1′, (B) subsite S1, (C) subsite S2, (D) subsite S3, (E) subsite S4. The full contribution values for each residue are in ESI (see Tables S3 and S4).†

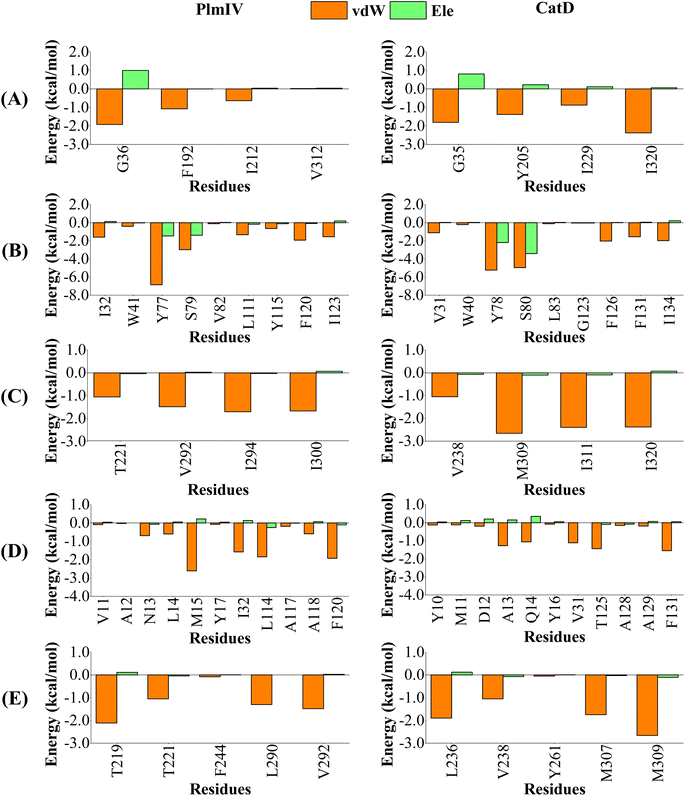Fig. 10 Per-residue decomposition of the binding free energy into contributions from electrostatic (Ele) and van der Waals (vdW) interactions for 2e compound bound to PlmIV (Left) and CatD (Right) considering only (A) subsite S1′, (B) subsite S1, (C) subsite S2, (D) subsite S3, (E) subsite S4. The full contribution values for each residue are in ESI (see Tables S5 and S6).†

On the other hand, for 2e inhibitor bound to PlmIV the same subsites have vdW contributions equal to −3.62, −17.33, −5.90, −10.22 and −6.02 kcal mol⁻¹, for subsites S1′, S1, S2, S3 and S4, respectively. Whereas for CatD, these values are −6.45, −17.21, −8.49, −7.28 and −7.41 kcal mol⁻¹, respectively. Here, the most relevant changes can be observed for subsite S1′, where the vdW contribution decreases by 2.83 kcal mol⁻¹, and subsite S3, where the vdW interaction increases by 2.94 kcal mol⁻¹, from PlmIV to CatD. In the subsite S1′, the replacement of Val312 (in PlmIV) by Ile320 (in CatD) promote a vdW interaction decreasing about 2.35 kcal mol⁻¹ (which means 65% of total S1′ interaction). In the subsite S3, the replacement of Leu14 and Met15 (in PlmIV) by Ala13 and Gln14 (in CatD), respectively, show more relevant changes into vdW interactions (from −0.60 and −2.61 kcal mol⁻¹ to −1.27 and −1.06 kcal mol⁻¹).

Therefore, our results suggest that vdW interactions driven by subsite S3 can differentiate between the highest and lowest selective factor of 5a and 2e inhibitors into the binding site of PlmIV and CatD, where the decreasing of vdW interactions favors the high selectivity factor, while its increasing favors the low selectivity factor. Particularly, the selectivity could be related to replacement of Leu114 (in PlmIV) by Thr125 (in CatD), due to its larger vdW changes be observed only for 5a inhibitor. These findings agree with the experimental proposal of Zogota et al.¹²

Conclusion

The structural and energetic investigation for the selectivity of non-peptidomimetic PlmIV over CatD provided binding models for both enzymes that quantitatively describe the main interactions at the active sites, which were improved by MD simulations followed by binding free energy calculations applying the LIE approach. All computed models were supported by the availability of the experimental data of inhibition for both PlmIV and CatD systems. Utilizing the energetic information, our results suggest that vdW interactions are the most important term to differentiate the highest and lowest selective factor of non-peptidomimetic inhibitors into the binding site of PlmIV and CatD. Particularly, the selectivity difference found for 5a and 2e inhibitors can be related to the increasing vdW contributions promoted by the replacement of Leu114 (in PlmIV) by Thr125 (in CatD) into subsite S3 of both enzymes. The enzyme–inhibitor interactions, largely non-polar, highlight the main role of the hydrophobic interactions in the recognition of inhibitors into subsites of both aspartic proteases. Therefore, our results may contribute to the development of novel potent and selective PlmIV inhibitors.

Author contributions

Conceptualization, L. S. M., J. L. and J. R. A. S.; methodology, J. L. and J. R. A. S.; software, L. S. M. and J. R. A. S.; validation, J. L., H. G. K. and J. R. A. S.; formal analysis, J. L., H. G. K., T. N. and J. R. A. S.; writing—original draft preparation, L. S. M., H. G. K., T. N., J. L., C. N. A. and J. R. A. S.; writing—review and editing, L. S. M., H. G. K., T. N., J. L. and J. R. A. S.; visualization, J. L. and J. R. A. S.; supervision, J. L., C. N. A. and J. R. A. S.; project administration, J. R. A. S.; funding acquisition, J. L., C. N. A. and J. R. A. S. All authors have read and agreed to the published version of the manuscript.

Conflicts of interest

The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.

Acknowledgements

This research was funded by the National Council for Scientific and Technological Development (CNPQ). L. S. M. thanks to Training of Higher Education Personnel (CAPES) for providing PhD scholarship (process #88882.445391/2019-01). This study was granted access to the computational resources of the Centro de Computação de Alto Desempenho (https://www.ccad.ufpa.br/) at the Federal University of Pará, South African Centre for High-Performance Computing (https://www.chpc.ac.za/) and Hippo (https://astro.ukzn.ac.za/%7Ehippo/) at the University of KwaZulu-Natal. The authors thank PROPESP/UFPA for the financial support.

References

1. J. Talapko, I. Škrlec, T. Alebić, M. Jukić and A. Včev, Microorganisms, 2019, 7, 179.
2. A. Rossati, O. Bargiacchi, V. Kroumova, M. Zaramella, A. Caputo and P. L. Garavelli, Infez. Med., 2016, 24, 93–104.
3. WHO, World Malaria Report 2021, 2021.
4. S. Rogerson, J. Beeson, M. Laman, J. Poespoprodjo, T. William, J. Simpson, R. Price and I. ACREME, BMC Med., 2020, 18, 239.
5. L. von Seidlein, B. Hanboonkunupakarn, P. Jittamala, P. Pongsuwan, K. Chotivanich, J. Tarning, R. M. Hoglund, M. Winterberg, M. Mukaka, P. Peerawaranun, P. Sirithiranont, Z. Doran, C. F. Ockenhouse, K. Ivinson, C. Lee, A. J. Birkett, D. C. Kaslow, P. Singhasivanon, N. P. J. Day, A. M. Dondorp, N. J. White and S. Pukrittayakamee, Hum. Vaccines Immunother., 2020, 16, 33–41.
6. K. Haldar, S. Bhattacharjee and I. Safeukui, Nat. Rev. Microbiol., 2018, 16, 156–170.
7. G. A. Biagini, P. Viriyavejakul, P. M. O'Neill, P. G. Bray and S. A. Ward, Antimicrob. Agents Chemother., 2006, 50, 1841–1851.
8. E. Beitz, Biol. Cell, 2005, 97, 373–383.
9. R. M. Reguera, B. L. Tekwani and R. Balaña-Fouce, Comp. Biochem. Physiol., Part C: Toxicol. Pharmacol., 2005, 140, 151–164.
10. A. Coppi, M. Cabinian, D. Mirelman and P. Sinnis, Antimicrob. Agents Chemother., 2006, 50, 1731–1737.
11. N. Micale, A. P. Kozikowski, R. Ettari, S. Grasso, M. Zappalà, J. J. Jeong, A. Kumar, M. Hanspal and A. H. Chishti, J. Med. Chem., 2006, 49, 3064–3067.
12. R. Zogota, L. Kinena, C. Withers-Martinez, M. J. Blackman, R. Bobrovs, T. Pantelejevs, I. Kanepe-Lapsa, V. Ozola, K. Jaudzems, E. Suna and A. Jirgensons, Eur. J. Med. Chem., 2019, 163, 344–352.
13. S. Bjelic, M. Nervall, H. Gutiérrez-de-Terán, K. Ersmark, A. Hallberg and J. Åqvist, Cell. Mol. Life Sci., 2007, 64, 2285–2305.
14. P. Sittikul, N. Songtawee, N. Kongkathip and N. Boonyalai, Biochimie, 2018, 152, 159–173.
15. G. H. Coombs, D. E. Goldberg, M. Klemba, C. Berry, J. Kay and J. C. Mottram, Trends Parasitol., 2001, 17, 532–537.
16. R. Banerjee, J. Liu, W. Beatty, L. Pelosof, M. Klemba and D. E. Goldberg, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 990–995.
17. P. Bhaumik, A. Gustchina and A. Wlodawer, Biochim. Biophys. Acta, 2012, 1824, 207–223.
18. I. Russo, S. Babbitt, V. Muralidharan, T. Butler, A. Oksman and D. E. Goldberg, Nature, 2010, 463, 632–636.
19. P. Bhaumik, H. Xiao, C. L. Parr, Y. Kiso, A. Gustchina, R. Y. Yada and A. Wlodawer, J. Mol. Biol., 2009, 388, 520–540.
20. S. E. Francis, R. Banerjee and D. E. Goldberg, J. Biol. Chem., 1997, 272, 14961–14968.
21. L. Qiao, S. Hamamichi, K. A. Caldwell, G. A. Caldwell, T. A. Yacoubian, S. Wilson, Z.-L. Xie, L. D. Speake, R. Parks, D. Crabtree, Q. Liang, S. Crimmins, L. Schneider, Y. Uchiyama, T. Iwatsubo, Y. Zhou, L. Peng, Y. Lu, D. G. Standaert, K. C. Walls, J. J. Shacka, K. A. Roth and J. Zhang, Mol. Brain, 2008, 1, 17.
22. M. Fusek and V. Větvička, Biomed. Pap., 2005, 149, 43–50.
23. P. Saftig, M. Hetman, W. Schmahl, K. Weber, L. Heine, H. Mossmann, A. Köster, B. Hess, M. Evers and K. von Figura, EMBO J., 1995, 14, 3599–3608.
24. L. Myllykangas, J. Tyynelä, A. Page-McCaw, G. M. Rubin, M. J. Haltia and M. B. Feany, Neurobiol. Dis., 2005, 19, 194–199.
25. R. Steinfeld, K. Reinhardt, K. Schreiber, M. Hillebrand, R. Kraetzner, W. Brück, P. Saftig and J. Gärtner, Am. J. Hum. Genet., 2006, 78, 988–998.
26. C. D. Carroll, T. O. Johnson, S. Tao, G. Lauri, M. Orlowski, I. Y. Gluzman, D. E. Goldberg and R. E. Dolle, Bioorg. Med. Chem. Lett., 1998, 8, 3203–3206.
27. P.-O. Johansson, J. Lindberg, M. J. Blackman, I. Kvarnström, L. Vrang, E. Hamelink, A. Hallberg, Å. Rosenquist and B. Samuelsson, J. Med. Chem., 2005, 48, 4400–4409.
28. K. Jaudzems, K. Tars, G. Maurops, N. Ivdra, M. Otikovs, J. Leitans, I. Kanepe-Lapsa, I. Domraceva, I. Mutule, P. Trapencieris, M. J. Blackman and A. Jirgensons, ACS Med. Chem. Lett., 2014, 5, 373–377.
29. J. D. O. Araújo, A. M. dos Santos, J. Lameira, C. N. Alves and A. H. Lima, Molecules, 2019, 24, 2370.
30. J. Lameira, V. Bonatto, L. Cianni, F. Dos Reis Rocho, A. Leitão and C. A. Montanari, Phys. Chem. Chem. Phys., 2019, 21, 24723–24730.
31. L. S. Martins, J. Lameira, H. G. Kruger, C. N. Alves and J. R. A. Silva, Int. J. Mol. Sci., 2020, 21, 4783.
32. J. R. A. Silva, J. Urban, E. Araújo, J. Lameira, V. Moliner and C. N. Alves, Int. J. Mol. Sci., 2021, 23, 300.
33. C. H. S. Costa, A. M. Santos, C. N. Alves, S. Martí, V. Moliner, K. Santana and J. Lameira, Proteins: Struct., Funct., Bioinf., 2021, 89, 1340–1352.
34. J. R. A. Silva, A. E. Roitberg and C. N. Alves, J. Phys. Chem. B, 2015, 119, 1468–1473.
35. B. Honarparvar, T. Govender, G. E. M. Maguire, M. E. S. Soliman and H. G. Kruger, Chem. Rev., 2014, 114, 493–537.
36. V. T. Sabe, T. Ntombela, L. A. Jhamba, G. E. M. Maguire, T. Govender, T. Naicker and H. G. Kruger, Eur. J. Med. Chem., 2021, 224, 113705.
37. J. Åqvist, C. Medina and J. E. Samuelsson, Protein Eng., 1994, 7, 385–391.
38. J. C. Clemente, L. Govindasamy, A. Madabushi, S. Z. Fisher, R. E. Moose, C. A. Yowell, K. Hidaka, T. Kimura, Y. Hayashi, Y. Kiso, M. Agbandje-McKenna, J. B. Dame, B. M. Dunn and R. McKenna, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2006, 62, 246–252.
39. U. Grädler, P. Czodrowski, C. Tsaklakidis, M. Klein, D. Werkmann, S. Lindemann, K. Maskos and B. Leuthner, Bioorg. Med. Chem. Lett., 2014, 24, 4141–4150.
40. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 9 Revision C.01, Gaussian, Inc., Wallingford, CT, 2009.
41. J. J. P. Stewart, J. Mol. Model., 2007, 13, 1173–1213.
42. G. M. Morris, D. S. Goodsell, R. S. Halliday, R. Huey, W. E. Hart, R. K. Belew and A. J. Olson, J. Comput. Chem., 1998, 19, 1639–1662.
43. G. M. Morris, R. Huey, W. Lindstrom, M. F. Sanner, R. K. Belew, D. S. Goodsell and A. J. Olson, J. Comput. Chem., 2009, 16, 2785–2791.
44. O. Trott and A. J. Olson, J. Comput. Chem., 2010, 31, 455.
45. F.-J. Gamo, L. M. Sanz, J. Vidal, C. de Cozar, E. Alvarez, J.-L. Lavandera, D. E. Vanderwall, D. V. S. Green, V. Kumar, S. Hasan, J. R. Brown, C. E. Peishoff, L. R. Cardon and J. F. Garcia-Bustos, Nature, 2010, 465, 305–310.
46. J. Marelius, K. Kolmodin, I. Feierberg and J. Åqvist, J. Mol. Graphics Modell., 1998, 16, 213–225.
47. P. Bauer, A. Barrozo, M. Purg, B. A. Amrein, M. Esguerra, P. B. Wilson, D. T. Major, J. Åqvist and S. C. L. Kamerlin, SoftwareX, 2018, 7, 388–395.
48. W. Jorgensen, D. Maxwell and J. Tirado-rives, J. Am. Chem. Soc., 1996, 118, 11225–11236.
49. W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935.
50. F. Mohamadi, N. G. J. Richards, W. C. Guida, R. Liskamp, M. Lipton, C. Caufield, G. Chang, T. Hendrickson and W. C. Still, J. Comput. Chem., 1990, 11, 440–467.
51. H. Li, A. D. Robertson and J. H. Jensen, Proteins, 2005, 61, 704–721.
52. T. J. Dolinsky, J. E. Nielsen, J. A. McCammon and N. A. Baker, Nucleic Acids Res., 2004, 32, W665.
53. N. de F. Silva, J. Lameira and C. N. Alves, Chem. Phys. Lett., 2011, 509, 169–174.
54. H. Gutiérrez-de-Terán and J. Åqvist, Methods Mol. Biol., 2012, 305–323.
55. G. King and A. Warshel, J. Chem. Phys., 1989, 91, 3647–3661.
56. L. Diaz, J. Bujons, A. Delgado, H. Gutierrez-de-Terán and J. Aqvist, J. Chem. Inf. Model., 2011, 51, 601–611.
57. f. S. Lee and A. Warshel, J. Chem. Phys., 1992, 97, 3100–3107.
58. J.-P. Ryckaert, G. Ciccotti and H. J. C. Berendsen, J. Comput. Phys., 1977, 23, 327–341.
59. T. Hansson, J. Marelius and J. Åqvist, J. Comput.-Aided Mol. Des., 1998, 27–35.
60. M. Almlöf, J. Carlsson and J. Åqvist, J. Chem. Theory Comput., 2007, 3, 2162–2175.
61. M. Almlöf, B. O. Brandsdal and J. Åqvist, J. Comput. Chem., 2004, 25, 1242–1254.
62. D. Rasina, G. Stakanovs, O. V. Borysov, T. Pantelejevs, R. Bobrovs, I. Kanepe-Lapsa, K. Tars, K. Jaudzems and A. Jirgensons, Bioorg. Med. Chem., 2018, 26, 2488–2500.
63. R. Bobrovs, K. Jaudzems and A. Jirgensons, J. Med. Chem., 2019, 62, 8931–8950.
64. D. E. Goldberg, in Malaria: Drugs, Disease and Post-genomic Biology, ed. R. W. Compans, M. D. Cooper, T. Honjo, H. Koprowski, F. Melchers, M. B. A. Oldstone, S. Olsnes, M. Potter, P. K. Vogt, H. Wagner, D. J. Sullivan and S. Krishna, Springer-Verlag, Berlin/Heidelberg, 2005, pp. 275–291.
65. M. S. Valdés-Tresanco, M. E. Valdés-Tresanco, M. Rubio-Carrasquilla, P. A. Valiente and E. Moreno, ACS Omega, 2021, 6, 29525–29536.
66. P. A. Valiente, P. R. Batista, A. Pupo, T. Pons, A. Valencia and P. G. Pascutti, Proteins: Struct., Funct., Bioinf., 2008, 73, 440–457.
67. L. McGillewie and M. E. Soliman, Proteins: Struct., Funct., Bioinf., 2015, 83, 1693–1705.
68. H. Gutiérrez-de-Terán, M. Nervall, B. M. Dunn, J. C. Clemente and J. Åqvist, FEBS Lett., 2006, 580, 5910–5916.
69. H. Park and S. Lee, J. Am. Chem. Soc., 2003, 125, 16416–16422.
70. S. Piana, D. Sebastiani, P. Carloni and M. Parrinello, J. Am. Chem. Soc., 2001, 123, 8730–8737.
71. T. Polgár and G. M. Keserü, J. Med. Chem., 2005, 48, 3749–3755.
72. R. Rajamani and C. H. Reynolds, J. Med. Chem., 2004, 47, 5159–5166.
73. H. Gutiérrez-de-Terán, M. Nervall, B. M. Dunn, J. C. Clemente and J. Åqvist, FEBS Lett., 2006, 580, 5910–5916.
74. F. Hofer, J. Kraml, U. Kahler, A. S. Kamenik and K. R. Liedl, J. Chem. Inf. Model., 2020, 60, 3030–3042.
75. Y.-X. Wang, D. I. Freedberg, T. Yamazaki, P. T. Wingfield, S. J. Stahl, J. D. Kaufman, Y. Kiso and D. A. Torchia, Biochemistry, 1996, 35, 9945–9950.
76. K. K. Reiling, N. F. Endres, D. S. Dauber, C. S. Craik and R. M. Stroud, Biochemistry, 2002, 41, 4582–4594.
77. J. Brynda, P. Rezacova, M. Fabry, M. Horejsi, R. Stouracova, J. Sedlacek, M. Soucek, M. Hradilek, M. Lepsik and J. Konvalinka, J. Med. Chem., 2004, 47, 2030–2036.
78. V. Y. Torbeev, H. Raghuraman, D. Hamelberg, M. Tonelli, W. M. Westler, E. Perozo and S. B. H. Kent, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 20982–20987.
79. A. Warshel and M. Levitt, J. Mol. Biol., 1976, 103, 227–249.
80. B. Roux, Comput. Phys. Commun., 1995, 91, 275–282.
81. Y. Li, J. Shen, X. Sun, W. Li, G. Liu and Y. Tang, J. Chem. Inf. Model., 2010, 50, 1134–1146.
82. E. Yuriev, J. Holien and P. A. Ramsland, J. Mol. Recognit., 2015, 28, 581–604.
83. Z. Wang, H. Sun, X. Yao, D. Li, L. Xu, Y. Li, S. Tian and T. Hou, Phys. Chem. Chem. Phys., 2016, 18, 12964–12975.
84. J. D. Chodera, D. L. Mobley, M. R. Shirts, R. W. Dixon, K. Branson and V. S. Pande, Curr. Opin. Struct. Biol., 2011, 21, 150–160.
85. R. Abel, L. Wang, D. L. Mobley and R. A. Friesner, Curr. Top. Med. Chem., 2017, 17, 2577–2585.
86. R. W. Zwanzig, J. Chem. Phys., 1954, 22, 1420–1426.
87. Z. Cournia, B. Allen and W. Sherman, J. Chem. Inf. Model., 2017, 57, 2911–2937.
88. J. G. Kirkwood, J. Chem. Phys., 1935, 3, 300–313.
89. M. R. Shirts and V. S. Pande, J. Chem. Phys., 2005, 122, 144107.
90. R. E. Amaro, R. Baron and J. A. McCammon, J. Comput.-Aided Mol. Des., 2008, 22, 693–705.
91. E. Wang, H. Sun, J. Wang, Z. Wang, H. Liu, J. Z. H. Zhang and T. Hou, Chem. Rev., 2019, 119, 9478–9508.
92. S. Genheden and U. Ryde, Proteins: Struct., Funct., Bioinf., 2012, 80, 1326–1342.
93. C. D. Christ, A. E. Mark and W. F. Van Gunsteren, J. Comput. Chem., 2010, 31, 1569–1582.
94. N. Hansen and W. F. Van Gunsteren, J. Chem. Theory Comput., 2014, 10, 2632–2647.
95. J. Åqvist and T. Hansson, J. Phys. Chem., 1996, 100, 9512–9521.
96. J. Aqvist and J. Marelius, Comb. Chem. High Throughput Screening, 2001, 4, 613–626.
97. R. Wang, L. Lai and S. Wang, J. Comput.-Aided Mol. Des., 2002, 16, 11–26.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2ra06246a

---