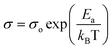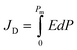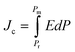DOI:
10.1039/D2RA06640H
(Paper)
RSC Adv., 2023,
13, 5293-5306
Fabrication of La3+ doped Ba1−xLaxTiO3 ceramics with improved dielectric and ferroelectric properties using a composite-hydroxide-mediated method†
Received
20th October 2022
, Accepted 5th February 2023
First published on 10th February 2023
Abstract
Lanthanum (La3+) doped Ba1−xLaxTiO3 (x = 0.0, 0.0025, 0.005, 0.0075) ceramics were synthesized by the composite-hydroxide-mediated method. Rietveld refinement of the XRD patterns confirmed the formation of a perovskite crystal structure that transforms from tetragonal to pseudo-cubic with La3+ doping content (x). Scanning electron microscopy displayed a dense and homogeneous microstructure with reduced grain size on La3+ doping. The frequency and temperature-dependent dielectric measurements showed an improvement in the dielectric permittivity, a decrease in the ferroelectric–paraelectric transition temperature, and an increase in the dielectric diffusivity with increasing La3+ doping content. Complex impedance analysis indicated the semiconducting behavior with a positive temperature coefficient of resistance effect, which could be explained in terms of a charge compensation mechanism in the donor doped BaTiO3. The ferroelectric hysteresis loops revealed that these ceramics are ferroelectric in nature, while an improvement in the energy storage density and energy storage efficiency was observed for the doped samples due to reduced grain size on La3+ doping. Here, the sample with x = 0.005 has a high dielectric permittivity, a low dielectric tangent loss, and the highest energy storage efficiency. This makes this composition interesting for energy storage applications.
1. Introduction
Multilayer ceramic capacitors have seen tremendous development in recent years to meet the rising demands for miniaturization. Typically, multilayer ceramic capacitors are built up of individual dielectric layers that are 1 μm or thinner. To achieve this, it is necessary to employ ultrafine (nano- or submicron-sized) powders as raw materials, while also maintaining proper control over particle size and uniformity.1,2 Lead-free ferroelectric ceramics have received much interest over the past few decades because of their non-toxic nature and exceptional electrical characteristics.3 Among different lead-free ferroelectrics, barium titanate (BaTiO3) is found to be a promising material for multilayer ceramic capacitors because of its exceptional dielectric characteristics, including a high dielectric constant (>103) and reduced dielectric loss.4 However, these characteristics can only be achieved within a small temperature range close to the ferroelectric phase transition. Therefore, to resolve this shortcoming, doping with a suitable element at Ba-, Ti-, or both sites has been frequently used to fabricate BaTiO3-based materials for more viable multilayer ceramic capacitors.5,6
Trivalent rare-earth (RE3+) ions are typically utilized to tune the electrical characteristics of ferroelectric perovskite BaTiO3 ceramics because of their intermediate size and charge relative to Ba2+ and Ti4+ ions.7 In general, depending on ionic size, small-sized RE3+ ions (like Yb3+) dope only on the Ti-site with charge compensation by oxygen vacancies, intermediate-sized RE3+ ions (such as Gd3+, Er3+) may dope equally on each Ba- and Ti-sites, and large-sized RE3+ ions (such as La3+, Pr3+) dope exclusively on the Ba-site.8 However, among different doping mechanisms, the Ba-site doping of RE3+ ions is a subject of discussion for a long time, as the dc resistivity of ceramics at ambient temperature can exhibit either semiconducting and/or insulating behavior, depending on the dopant concentration and/or processing parameters.9–12 Since, the pure BaTiO3 is a good insulator with a resistive value of ∼1010 Ωcm at room temperature and a large energy gap Eg = 3.5 eV. When BaTiO3 is doped with extremely low concentrations (<0.5 at%) of higher valence foreign ions as La3+, Gd3+, Dy3+ on the Ba-site, it usually exhibits semiconducting behavior, implying compensation via an electronic mechanism.13,14 However, for higher dopant contents (>1 at%), the compensation occurs through an ionic mechanism resulting in the formation of cation vacancies and insulating behavior.9,15 Among different trivalent rare-earth ions, lanthanum (La3+) is found to be one of the most investigated RE3+ dopant which behaves as a donor dopant and usually replaces Ba2+ ions in the crystal lattice of BaTiO3 at smaller amount of La3+ doping content (<1 at%), because La3+ ions are too large to replace Ti4+ ions on the Ti-site. Moreover, La3+ ions have a different valence than Ba2+, causing a charge imbalance that produces n-type semiconductivity. Thus, the charge compensation involves the formation of electrons, electron holes, or titanium (VTi) and oxygen (Vo) vacancies in the ceramic materials, resulting in a variation of their electrical characteristics.16 Morrison et al. reported the semiconducting character in La3+ doped BaTiO3 ceramics, which is attributed to the loss of oxygen during sintering at high temperatures (≥1350 °C) in air.17 Ganguly et al. obtained a compositional induced phase transition from tetragonal to cubic symmetry with the increase in La3+ doping content in BaTiO3 ceramics.18 They also found an increase in the dielectric permittivity along with the broadening of dielectric peak. Wang et al. showed that increasing the La3+ doping content in BaTiO3 ceramics inhibits the grain growth and that both the room and maximum dielectric constants diminish monotonously.19 Puli et al. explored the effect of La3+ doping on the dielectric and ferroelectric properties of Ba1−xLaxTiO3 (x = 0.0–0.003) semiconducting ceramics.20 The dielectric constant and recoverable energy storage density are found to be improved by La3+ doping. However, due to high hysteresis loss, a small decrease of 12% in the energy storage efficiency is obtained for the doped samples. Moreover, for both undoped and doped samples, room temperature semiconducting behavior is observed with positive temperature coefficient of resistivity (PTCR) behavior at Curie temperature (Tc) due to the electron compensation mechanism. Recently, Kumar et al. reported a significant enhancement in the dielectric and energy storage properties of La3+ doped Ba1−zLazTi0.95Sn0.05O3 (z = 0.0–0.035) ceramics.21 The highest value of energy storage efficiency (63%) for a z = 0.035 sample is found to be 8.4 times higher than that of an undoped sample. According to them, the observed improvement in the dielectric constant and energy storage density along with a reduction in hysteresis loss is attributed to reduced grain size due to La3+ doping. Hence, in light of the aforementioned studies, it follows that the effects of dopant concentration and grain size may be optimized in order to modify the dielectric and energy storage characteristics of BaTiO3 ceramics.
During the past decade, with the requirement of size reduction in electronic devices, a lot of research work has been put in the processing of nanomaterials of different shapes and sizes with the aim of enhancing their electronic, optical, and structural properties. The conventional approach for fabricating BaTiO3 ceramics is a solid-state reaction followed by a ball milling and high-temperature sintering process.22 However, in recent years, different low-temperature chemical routes have been developed, including the hydrothermal,23 sol–gel,24 solvothermal,25 and microwave processing technique.26 For all of these chemical routes, various synthesis parameters (like reaction temperature and time, sintering temperature, pressure, surfactant, etc.) are required to optimize and control for synthesizing nanostructured BaTiO3 ceramics. However, the composite-hydroxide-mediated (CHM) method is found to be an environmentally friendly, cost-effective, fast, mass-productive, and one-step process to produce a wide range of nanostructures. The BaTiO3 nanostructures have been prepared using the CHM method, wherein the influence of different reaction times and temperatures on the morphological structures of prepared particles has been explored.27,28 It is found that the particle size, surface smoothness, and crystal structure of these CHM-prepared nanostructures strongly depend on the processing conditions. Xie et al. also reported the synthesis of fine-grained tetragonal BaTiO3 nanoparticles by the CHM method.29 The obtained powder was then compacted and sintered at relatively lower temperature of 1200 °C for 4 h, which presented a high value of dielectric constant due to much higher density (∼99%) than that of commercially available BaTiO3 powder. To the best of our knowledge, very limited work has been found on the dielectric properties of BaTiO3 ceramics prepared by the CHM method. Furthermore, no attempt has been made to prepare doped BaTiO3 ceramics using the CHM method, as well as to investigate the ferroelectric and energy storage properties of the CHM prepared BaTiO3 ceramics. Therefore, in this work, we prepared different compositions of La3+ doped Ba1−xLaxTiO3 ceramics (x = 0.0, 0.0025, 0.005, 0.0075) using a composite-hydroxide-mediated method under optimum conditions. The influence of La3+ doping on the microstructure, dielectric, ferroelectric, and energy storage properties, along with the sintering of resulting powders to produce dense, La3+ doped Ba1−xLaxTiO3 ceramics was investigated. Moreover, the La3+ doped prepared ceramics are also explored in terms of their semiconducting properties with a PTCR effect.
2. Experimental
La3+ doped Ba1−xLaxTiO3 (x = 0.0, 0.0025, 0.005, 0.0075) ceramics were prepared using the composite-hydroxide-mediated (CHM) method. A mixture of 20 g of mixed hydroxides (NaOH/KOH = 51.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 48.5) was put into a 50 ml Teflon vessel. Afterward, a mixture of barium nitrate [Ba(NO3)2, Sigma-Aldrich, ≥99%], lanthanum nitrate [La(NO3)2·6H2O, Sigma-Aldrich, ≥99%], and titanium oxide [TiO2, Sigma-Aldrich, ≥99%] at 10 mmol each was added to the vessel as per their stoichiometric ratio. The vessel was then put in a heating oven at 200 °C for 72 h. After the chemical reaction, the vessel was taken out of the oven and cooled down to room temperature. To eliminate hydroxides on the surface of the particles, the product was filtered and washed many times with deionized water. Finally, the obtained powders were dried overnight at 100 °C in an oven and annealed in the furnace at 700 °C for 3 h under ambient conditions. The calcined powders were mixed with 5 wt% binder (polyvinyl alcohol) and then uniaxially pressed by applying a compaction pressure of 5 ton per cm2. The pelletized samples were then sintered at 1200 °C for 4 h in a conventional furnace with a heating/cooling rate of 5 °C min−1.
48.5) was put into a 50 ml Teflon vessel. Afterward, a mixture of barium nitrate [Ba(NO3)2, Sigma-Aldrich, ≥99%], lanthanum nitrate [La(NO3)2·6H2O, Sigma-Aldrich, ≥99%], and titanium oxide [TiO2, Sigma-Aldrich, ≥99%] at 10 mmol each was added to the vessel as per their stoichiometric ratio. The vessel was then put in a heating oven at 200 °C for 72 h. After the chemical reaction, the vessel was taken out of the oven and cooled down to room temperature. To eliminate hydroxides on the surface of the particles, the product was filtered and washed many times with deionized water. Finally, the obtained powders were dried overnight at 100 °C in an oven and annealed in the furnace at 700 °C for 3 h under ambient conditions. The calcined powders were mixed with 5 wt% binder (polyvinyl alcohol) and then uniaxially pressed by applying a compaction pressure of 5 ton per cm2. The pelletized samples were then sintered at 1200 °C for 4 h in a conventional furnace with a heating/cooling rate of 5 °C min−1.
The structural characterization of the prepared Ba1−xLaxTiO3 samples was examined with an X-ray diffractometer (ARL EQUINOX 3000). Rietveld refinement was carried out with the help of Fullprof software for a more precise analysis. The surface morphology of the prepared samples was studied using a field-emission scanning electron microscope (FESEM, TESCAN MAIA3). Before electrical measurements, both sides of the sintered pellets were polished and coated with silver paste. Afterwards, the silver-coated pellets were dried at 100 °C for 2 h in a heating oven. Impedance spectroscopy was carried out using an Impedance analyzer (Agilent 4294A, USA) at different temperatures (303–463 K) within the frequency range of 40–107 Hz. The room temperature ferroelectric measurements were performed by a Precision Multiferroic II ferroelectric tester (Radiant Technology Inc., USA).
3. Results and discussion
3.1. XRD analysis
Fig. 1(a–d) shows the X-ray diffraction (XRD) patterns of La3+ doped Ba1−xLaxTiO3 (x = 0.0, 0.0025, 0.005, 0.0075) samples sintered at 1200 °C for 4 h. The XRD peaks for the pure BaTiO3 sample (i.e., x = 0.0) belong to a tetragonal perovskite phase in accordance with the JCPDS file no. 05-0626.30 As seen from Fig. 1(a), no un-indexed peak is observed in the XRD pattern of a pure sample, which indicates the formation of a pure single-phase sample. Here, the splitting of (002)/(200) and (112)/(211) diffraction peaks at 2θ = 45° and 56°, respectively, confirmed the presence of tetragonal phase for the pure sample. With the doping of La3+ ions in place of Ba2+ in BaTiO3 lattice, we found that all peaks correspond to tetragonal phase and the XRD peaks shift towards the higher 2θ values with increasing La3+ doping content (x). This behavior of peak shifting is attributed to the difference between the ionic radii of dopant (La3+ = 1.16 Å) and host (Ba2+ = 1.42 Å) ions. To estimate the structural parameters, Rietveld refinement on the XRD patterns of pure BaTiO3 and La3+ doped Ba1−xLaxTiO3 samples was employed using the Fullprof program. The figure demonstrates that the calculated XRD patterns provide the best match to the experimental data, with a goodness-of-fit value (χ2 = 1.08–1.62) that is close to the value obtained from the experiment. The estimated values of lattice constants (a, c), cell volume (V), and goodness of fit (χ2) are presented in Table 1. We observed that as La3+ doping content (x) increases, the value of lattice constant a increases while the values of c and V decrease slightly due to the smaller ionic radii of La3+ compared to Ba2+ ions. Further, with increasing La3+ doping content, it can be seen that the value of tetragonality ratio (c/a) approaches to 1 suggesting a probable change in the unit cell symmetry from tetragonal to pseudo-cubic structural phase.31
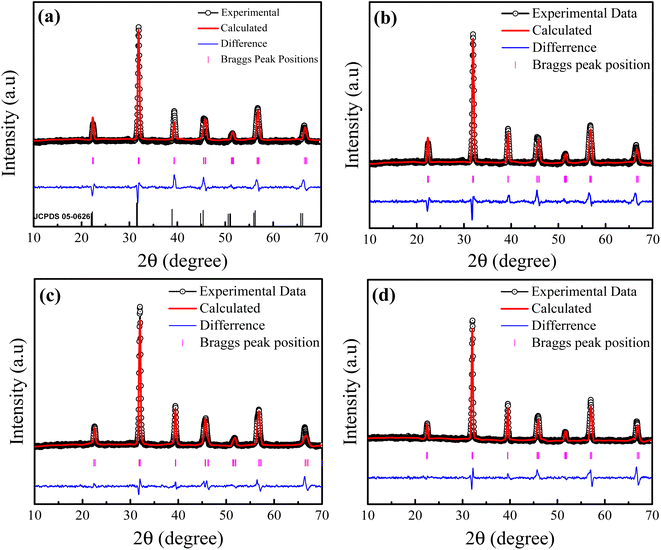 |
| | Fig. 1 Rietveld refinement of the XRD data of La3+ doped Ba1−xLaxTiO3 ceramics with (a) x = 0.0, (b) x = 0.0025, (c) x = 0.005, and (d) x = 0.0075. Here, the experimental data are depicted by the black circle, the estimated intensities by the red line, the difference between both intensities by the blue baseline, and the allowed Bragg's position by the magenta vertical lines. | |
Table 1 Compositional variation of lattice constant (a, c), tetragonality ratio (c/a), cell volume (V), goodness of fit (χ2), average grain size (D), sintered density (ρs), relative density (ρ), Curie temperature (Tc), and degree of diffuseness (γ) for the La3+ doped Ba1−xLaxTiO3 ceramics
| Sample (x) |
a (Å) |
c (Å) |
c/a |
V (Å3) |
χ2 |
D (μm) |
ρs (g cm−3) |
ρ (%) |
Tc (K) |
γ |
| 0.00 |
3.967 |
3.998 |
1.0078 |
62.92 |
1.08 |
3.06 |
5.77 |
96 |
409 |
1.18 |
| 0.0025 |
3.968 |
3.994 |
1.0065 |
62.90 |
1.10 |
1.10 |
5.60 |
93 |
405 |
1.26 |
| 0.005 |
3.971 |
3.982 |
1.0027 |
62.76 |
1.82 |
0.98 |
5.66 |
94 |
398 |
1.33 |
| 0.0075 |
3.972 |
3.978 |
1.0015 |
62.75 |
1.43 |
0.89 |
5.54 |
92 |
393 |
1.49 |
Since, the ionic radius of La3+ ions lies between the respective ionic radii of Ba2+ and Ti4+ ions.32 Thus, to find out the probability of whether La3+ ions occupy the Ba-site or Ti-site in the BaTiO3 lattice, we used the Goldschmidt tolerance factor (t) which indicates the stability and distortion in the perovskite structure (ABO3) and is given by:33
| |
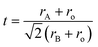 | (1) |
where
rA,
rB, and
ro are the ionic radii of A cation (Ba
2+), B cation (Ti
4+), and oxygen anion (O
2−). Generally, the value of the tolerance factor for a stable perovskite structure is between 0.88 and 1.06.
34 Here, we have calculated the tolerance factor of La
3+ ions to occupy completely Ba- and Ti-sites, and the obtained values are found to be 0.995 and 0.871 for the Ba- and Ti-sites, respectively. Since the value of the tolerance factor to occupy Ti-site is less than 0.88, which excludes the possibility of La
3+ replacing the Ti
4+ ions at Ti-site. Hence, La
3+ ions have a greater probability of replacing Ba
2+ ions at the Ba-site.
3.2. SEM analysis
Fig. 2(a–d) displays the field-emission scanning electron microscopy (FE-SEM) images of the prepared Ba1−xLaxTiO3 (x = 0.0, 0.0025, 0.005, 0.0075) samples. All of these images were taken from the fractured surfaces of pelletized samples. As seen from Fig. 2(a), the pure BaTiO3 sample (i.e., x = 0.0) shows a dense microstructure consisting of bigger grains wherein a few smaller grains and grains with terraced surfaces are also visible among them. Here, the presence of discontinuous grain growth and terraced surfaces could be attributed to the enhanced mass transport phenomenon due to formation of oxygen vacancies at higher sintering temperatures.21 Therefore, to estimate the average grain size (D) in a pure sample, the grain size distribution was estimated from the SEM image using ImageJ software and found to be ∼3 μm (see inset of Fig. 2(a)). With the addition of La3+ ions, there is a considerable reduction in grain sizes along with uniform and denser microstructures for the La3+ doped Ba1−xLaxTiO3 samples, as shown in Fig. 2(b–d). Further, the insets of Fig. 2(b–d) show the distribution of grain size in the doped samples, and the estimated average grain sizes (D) are presented in Table 1. Here, it is observed that the average grain size of the x = 0.005 sample is reduced by ∼70% as compared with the pure sample. This apparent decline in grain size due to La3+ doping is attributed to an overall decrease in the diffusion rate during the sintering process which might suppress the formation of oxygen vacancies. Similar variation in the grain sizes have been reported for small values of La3+ doping in BaTiO3 and Pb(Zr1−xTix)O3.18,35 Moreover, the relative density (ρ) was estimated using the theoretical density of BaTiO3 (ρth = 6.02 g cm−3) and the sintered density (ρs) of the pelletized samples calculated by the Archimedes method. The values of ρ for the prepared samples are ≥92% (see Table 1), which indicates better densification in the microstructures of sintered samples prepared by the CHM method. These values also showed that pure BaTiO3 had a higher density than La3+-doped samples. The observed decrease in the value of ρ with La3+ doping content is attributed to the fact that, when La3+ occupies the Ba-site as a donor, cation vacancies and radius discrepancies between La3+ and Ba2+ deform the lattice. This could hinder densification by making mass mobility more difficult in compact structures.19,26
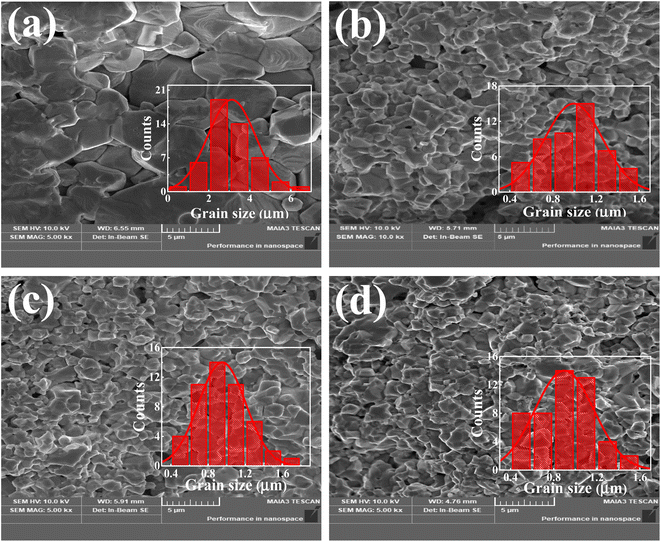 |
| | Fig. 2 SEM micrographs of La3+ doped Ba1−xLaxTiO3 ceramics with (a) x = 0.0, (b) x = 0.0025, (c) x = 0.005, and (d) x = 0.0075. Insets of (a–d) show the grain size distribution. | |
3.3. Dielectric properties
Fig. 3(a–d) shows the temperature-dependent behavior of real part of dielectric permittivity (ε′) and dielectric tangent loss (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ) for the La3+ doped Ba1−xLaxTiO3 (x = 0.0, 0.0025, 0.005, 0.0075) samples measured at different frequencies (1 kHz to 1 MHz) between the temperature range of 303 K to 463 K. It can be seen that, for the pure BaTiO3 sample (x = 0.0), the ε′ value begins to increase gradually with increasing temperature and reaches a maximum value at 409 K and then decreases smoothly with further increase in temperature (Fig. 3(a)). Here, the increasing trend of ε′ with temperature is accredited to the orientational polarization which is associated with the thermal motion of dipoles. The specific temperature at which ε′ has a maximum value is defined as the Curie temperature (Tc). At this temperature, the ferroelectric phase transforms into the paraelectric phase, followed by a structural transition from tetragonal symmetry to cubic. A similar transition temperature was also found in the literature for BaTiO3.19,21 However, a small difference in the values of ε′ and Tc might be caused by the grain size effect. Further, the Curie temperature (Tc) of a pure sample is observed to continually decrease from 409 K to 393 K with increasing La3+ doping content (x) in Ba1−xLaxTiO3 (see Table 1). While, the value of ε′ is found to increase by La3+ doping at the Ba2+ site, when compared with a pure sample. Here, the observed trend of Tc and ε′ with La3+ doping might be associated with the reduction in grain size and smaller ionic dopant. Also, the replacement of Ba2+ by the higher valence La3+ ions generates cation vacancies on the Ti4+ site to maintain charge neutrality, which in turn introduces distortion in the TiO6 octahedra.21,36 Thus, these distorted TiO6 octahedra break the long-range ordering and assist in the reorientation of ferroelectric domains, which results in the improved ε′ value of BaTiO3 with La3+ doping. Here, the observed ε′ value at room temperature for the pure BaTiO3 and La3+ doped BaTiO3 samples is relatively higher than the values reported for similar systems,13,19,26,34 which might be related to the grain size effect. It is well known that the maximum value of ε′ in the BaTiO3 ceramics is obtained at a grain size of 1.0 μm as a result of the optimum density and mobility of 90° domain walls in the prepared sample.37 Since the average grain size of prepared BaTiO3 and La3+ doped BaTiO3 samples are 3 μm (>1.0 μm) and 0.89–1.1 μm (∼1.0 μm), respectively (see Fig. 2). Thus, the La3+ doped BaTiO3 samples exhibit higher values of ε′ in comparison to pure BaTiO3 sample. However, among the doped samples, the sample with x = 0.005 sample provides the highest value of ε′ due to the dominant effect of fine grains (0.98 μm) with uniform distribution and enhanced charge carrier concentration. Moreover, the figure reveals that the ε′ value decreases slightly with increasing frequency over the entire temperature range, and the ε′ peak is found to be temperature independent for all prepared samples. While, a visible broadening of the dielectric peaks can be seen, suggesting that the observed phase transition is of the diffuse-type. Typically, such broadening of the dielectric peak results from compositional fluctuation, merging of micro to macro polar regions, and/or doping induced disorder in the crystal lattice.38 Moreover, the low values of dielectric tangent loss (tan
δ) for the La3+ doped Ba1−xLaxTiO3 (x = 0.0, 0.0025, 0.005, 0.0075) samples measured at different frequencies (1 kHz to 1 MHz) between the temperature range of 303 K to 463 K. It can be seen that, for the pure BaTiO3 sample (x = 0.0), the ε′ value begins to increase gradually with increasing temperature and reaches a maximum value at 409 K and then decreases smoothly with further increase in temperature (Fig. 3(a)). Here, the increasing trend of ε′ with temperature is accredited to the orientational polarization which is associated with the thermal motion of dipoles. The specific temperature at which ε′ has a maximum value is defined as the Curie temperature (Tc). At this temperature, the ferroelectric phase transforms into the paraelectric phase, followed by a structural transition from tetragonal symmetry to cubic. A similar transition temperature was also found in the literature for BaTiO3.19,21 However, a small difference in the values of ε′ and Tc might be caused by the grain size effect. Further, the Curie temperature (Tc) of a pure sample is observed to continually decrease from 409 K to 393 K with increasing La3+ doping content (x) in Ba1−xLaxTiO3 (see Table 1). While, the value of ε′ is found to increase by La3+ doping at the Ba2+ site, when compared with a pure sample. Here, the observed trend of Tc and ε′ with La3+ doping might be associated with the reduction in grain size and smaller ionic dopant. Also, the replacement of Ba2+ by the higher valence La3+ ions generates cation vacancies on the Ti4+ site to maintain charge neutrality, which in turn introduces distortion in the TiO6 octahedra.21,36 Thus, these distorted TiO6 octahedra break the long-range ordering and assist in the reorientation of ferroelectric domains, which results in the improved ε′ value of BaTiO3 with La3+ doping. Here, the observed ε′ value at room temperature for the pure BaTiO3 and La3+ doped BaTiO3 samples is relatively higher than the values reported for similar systems,13,19,26,34 which might be related to the grain size effect. It is well known that the maximum value of ε′ in the BaTiO3 ceramics is obtained at a grain size of 1.0 μm as a result of the optimum density and mobility of 90° domain walls in the prepared sample.37 Since the average grain size of prepared BaTiO3 and La3+ doped BaTiO3 samples are 3 μm (>1.0 μm) and 0.89–1.1 μm (∼1.0 μm), respectively (see Fig. 2). Thus, the La3+ doped BaTiO3 samples exhibit higher values of ε′ in comparison to pure BaTiO3 sample. However, among the doped samples, the sample with x = 0.005 sample provides the highest value of ε′ due to the dominant effect of fine grains (0.98 μm) with uniform distribution and enhanced charge carrier concentration. Moreover, the figure reveals that the ε′ value decreases slightly with increasing frequency over the entire temperature range, and the ε′ peak is found to be temperature independent for all prepared samples. While, a visible broadening of the dielectric peaks can be seen, suggesting that the observed phase transition is of the diffuse-type. Typically, such broadening of the dielectric peak results from compositional fluctuation, merging of micro to macro polar regions, and/or doping induced disorder in the crystal lattice.38 Moreover, the low values of dielectric tangent loss (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ) between 0.036 and 0.55 are observed in the prepared Ba1−xLaxTiO3 samples, and the values of tan
δ) between 0.036 and 0.55 are observed in the prepared Ba1−xLaxTiO3 samples, and the values of tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ are found to slightly increase with La3+ doping compared to pure BaTiO3 sample (see Fig. 2(a–d)). However, above the Curie temperature, there is an abrupt increase in tan
δ are found to slightly increase with La3+ doping compared to pure BaTiO3 sample (see Fig. 2(a–d)). However, above the Curie temperature, there is an abrupt increase in tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ value with increasing temperature, which would be the direct consequence of higher electrical conductivity.21
δ value with increasing temperature, which would be the direct consequence of higher electrical conductivity.21
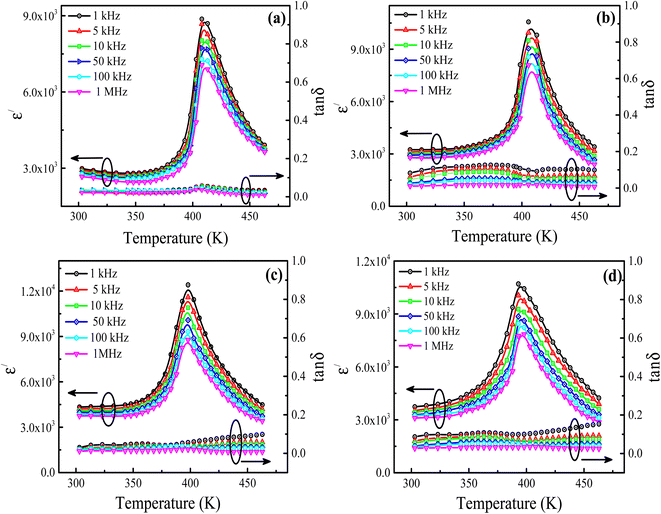 |
| | Fig. 3 Temperature-dependent behavior of the real part of dielectric permittivity (ε′) and dielectric tangent loss (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ) for the La3+ doped Ba1−xLaxTiO3 ceramics (a) x = 0.0, (b) x = 0.0025, (c) x = 0.005, and (d) x = 0.0075 measured at different frequencies (1 kHz to 1 MHz) between the temperature range of 303 K to 463 K. δ) for the La3+ doped Ba1−xLaxTiO3 ceramics (a) x = 0.0, (b) x = 0.0025, (c) x = 0.005, and (d) x = 0.0075 measured at different frequencies (1 kHz to 1 MHz) between the temperature range of 303 K to 463 K. | |
To further investigate the dielectric dispersion and diffusiveness for the prepared Ba1−xLaxTiO3 samples, the temperature dependence of the inverse of ε′ is plotted for the prepared samples at a particular frequency of 1 kHz as presented in Fig. 4(a–d). As seen in the figure, all samples exhibit a deviation from the Curie–Weiss law because of a small discrepancy among the maximum ε′ temperature (T) and the temperature at which ε′ starts to depart from the Curie–Weiss law (Tm). To describe this deviation, a modified version of the Curie–Weiss law might be used:39
| |
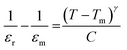 | (2) |
where
εr is the dielectric permittivity at
T,
εm is the dielectric permittivity at
Tm,
C is the constant, and
γ is the degree of diffuseness whose value may vary from 1 (normal ferroelectric) to 2 (relaxor ferroelectric). Insets of
Fig. 4(a–d) display the graphs of ln(1/
εr − 1/
εm) as a function of ln(
T −
Tm) for the prepared samples at 1 kHz. It is obvious that these graphs display a linear relationship and by fitting with
eqn (2), the values of diffuseness degree (
γ) are obtained from the slopes of these graphs, which are presented in
Table 1. Here, the value of
γ = 1.18 for the pure BaTiO
3 sample (
x = 0.0) reveals the normal ferroelectric behavior while the value of
γ gradually increases from 1.18 to 1.49 with increasing La
3+ doping in BaTiO
3, which indicates that the diffuseness in the phase transition increases with La
3+ doping. Here, the observed increase in the diffuseness is due to cation disordering effect and the difference between the ionic radii of dopant and host ions. This phenomenon plays an important role in increasing the compositional fluctuation, which leads to diffused phase transition.
40,41
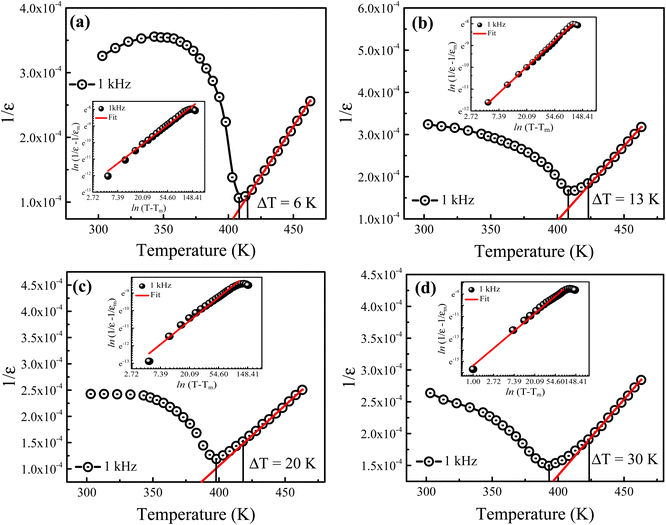 |
| | Fig. 4 Temperature dependence of the inverse of dielectric permittivity (ε′) for the La3+ doped Ba1−xLaxTiO3 ceramics with (a) x = 0.0, (b) x = 0.0025, (c) x = 0.005, and (d) x = 0.0075 measured at a representative frequency of 1 kHz. Insets of (a–d) display the graphs of ln(1/εr − 1/εm) versus ln(T − Tm) for the prepared samples. | |
3.4. Impedance analysis
Impedance spectroscopy (IS) is a technique that may be utilized to investigate the electrical homogeneity within ceramic materials. It is well known that ceramic materials have an electrically heterogeneous structure, consisting of semiconducting grains (Gs) that are isolated by an insulating grain boundary (GBs), particularly when doping is included. Consequently, impedance analysis was used to analyze and extract the contributions of the Gs and GBs resistance from the material's overall resistance.42 Fig. 5(a–d) depicts the complex impedance plane plots (Z/ vs. Z//) of Ba1−xLaxTiO3 (x = 0.0, 0.0025, 0.005, 0.0075) samples measured at various temperatures. As seen in the figure, pure BaTiO3 and La3+ doped BaTiO3 samples exhibit two overlapping semicircular arcs at each temperature. Here, the appearance of two semicircular arcs indicates distinct electroactive regions resulting from the presence of Gs and GBs with different relaxation times.42 Typically, the conductive bulk region exhibits relaxation at higher frequencies; hence, the semicircular arc's reduced diameter that forms on the higher frequency region and passes through the origin, is termed as the electroactive region's Gs. Similarly, the GBs relate to the region defined by the semicircular arc's large diameter at lower frequencies and a more resistive electroactive region. In general, the x-intercept of these semicircular arcs gives the expected values of sample resistance for GBs and Gs. It can be observed in the figure, both the size and shape of the semicircular arcs vary with the increase in temperature and La3+ doping concentration in the prepared ceramics, showing an overall changes in the resistive characteristics. Thus, to estimate the expected variations in the resistance and to assign distinct electroactive regions, we have used the ZView software to fit an equivalent circuit model of (R1 − C1)(R2 − CPE) to our experimental data. Here, the resistance R, capacitance C, and constant phase element CPE are the components of this circuit. CPE is typically a deviation from the real capacitance behavior, suggesting the presence of dissimilar relaxations that have a similar relaxation time. Usually, the following expression is used to compute the capacitance of CPE:43| |
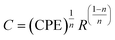 | (3) |
where n represents the dispersion parameter and takes on the value 1 for an ideal capacitor and the value 0 for an ideal resistor. On the basis of the fitting parameters given in the ESI (Table S1†) for each temperature and La3+ doping content (x), the capacitance values (C1) derived from the first circuit are comparable to the geometric values for Gs (10−11 to 10−13 Fcm−1).44 However, the capacitance values (C2) derived from the second circuit are equivalent to the geometric value for GBs (10−8 to 10−10 Fcm−1).44 Here, the C2 values for all samples at each temperature were calculated using eqn (3). Thus, we determined that GBs and Gs conduction are responsible for the semicircular arcs seen at lower and higher frequencies, respectively. Usually, the resistance of GBs (RGBs) is found to be much higher than the Gs resistance (RGs). However, compared to an undoped sample, no significant variation of the RGs is observed while a significant decrease in the value of RGBs is observed with a small doping of La3+ in BaTiO3. As seen from Table S1,† the values of RGs and RGBs initially decrease up to x = 0.005 and then slowly increase for x = 0.0075 sample. Here, the smallest value of resistance obtained for the x = 0.005 sample is probably attributed to more uniform incorporation of dopant in the BaTiO3 lattice and a high concentration of free charge carriers, which will be discussed in detail in the next paragraph.
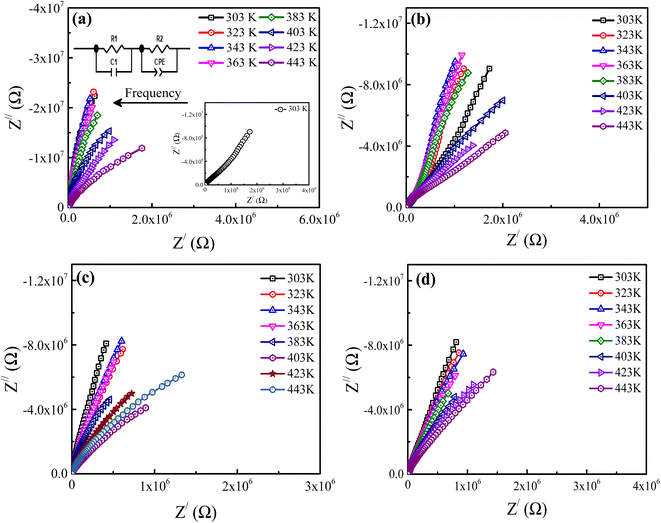 |
| | Fig. 5 Complex impedance plane plots (Z/ vs. Z//) of Ba1−xLaxTiO3 ceramics with (a) x = 0.0, (b) x = 0.0025, (c) x = 0.005, and (d) x = 0.0075 measured at various temperatures. Insets of (a) show the enlarged Insets of (a) show the impedance plane plot measured at 303 K and the equivalent circuit model. Here, the arrow shows the direction of the applied frequency. | |
To further explore the temperature dependence of total resistance (RT) in the prepared Ba1−xLaxTiO3 (x = 0.0, 0.0025, 0.005, 0.0075) samples, we have plotted the total resistance (RT = RGs + RGBs) of all prepared samples measured from the Z/ vs. Z// plots as a function of temperature (T) in Fig. 6(a–d). Generally, the pure BaTiO3 sample exhibits insulating behavior rather than semiconducting behavior, when sintered in air. Here, contrary to the common understanding regarding pure BaTiO3: an insulator and ferroelectric at room temperature, the doping of La3+ ions in Ba1−xLaxTiO3 samples sintered in air at 1200 °C results in a decline in the overall resistance with a weak positive temperature coefficient of resistance (PTCR) effect. Similar results are also reported in some of the donor doped BaTiO3 samples sintered at >1200 °C in air.9,13,45 Since, in most of the PTCR ceramics, the GBs has higher electrical resistivity than the Gs interior. Thus, the ceramics with larger Gs size (i.e., less GBs density) should exhibit lower resistance value. However, the inset of Fig. 6(a) reveals that, at room temperature, the value of RT initially decreases with the La3+ doping content (x) in BaTiO3, reaching a minimum at x = 0.005, and then begins to increase, despite the smaller grain size. Therefore, the observed variation in RT with La3+ doping content (x) in Ba1−xLaxTiO3 samples can be explained by the chemical defect compensation mechanism. Typically, there are two types of compensation mechanisms possible in the donor doped BaTiO3 when La3+ ions replace Ba2+ ions at the A-sites of ABO3 type perovskite crystal and are given by the following defect reactions:16
| |
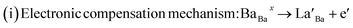 | (4) |
| |
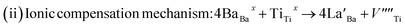 | (5) |
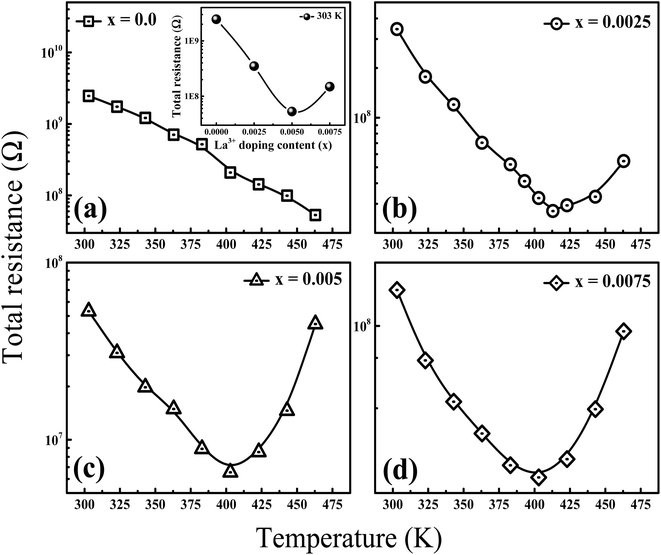 |
| | Fig. 6 Temperature dependence of the total resistance (RT) in the prepared Ba1−xLaxTiO3 ceramics with (a) x = 0.0, (b) x = 0.0025, (c) x = 0.005, and (d) x = 0.0075. Inset of (a) shows the variation in the magnitude of RT with increasing La3+ doping content (x) at room temperature. | |
At low La3+ doping content (x), free electrons are usually released due to the incorporation of La3+ ions at the Ba2+ site as presented in eqn (4). These free electrons are loosely bonded and can be thermally triggered to jump from the donor level to the conduction band in a semiconductor. This results in an increase in the concentration of charge carriers and a reduction in resistance. However, the minimum resistance is observed for La3+ doping content of x = 0.005, which is attributed to a change in the doping mechanism, i.e., a transformation from electronic compensation to ionic (cation vacancies) compensation. Thus, with the further increase in La3+ doping content, cation vacancies may be produced for the defect reactions as presented in eqn (5), which results in the occurrence of electronic holes. This leads to a decrease in the electronic charger carrier's concentration and an increase in resistance for x > 0.005. Moreover, one can also see from the figure that the value of RT decreases as the temperature increases, indicating the existence of thermally stimulated conduction mechanism and confirming the semiconducting nature. However, a discontinuity is observed above the Curie temperature (T > Tc) where we observed an increasing trend of RT with increasing temperature in the La3+ doped samples. This behavior indicates a weak positive temperature coefficient of resistance (PTCR) effect in the doped samples, which is typically a GBs phenomena in the donor-doped BaTiO3 samples.46 Here, the observed PTCR effect is attributed to the fact that, above the Curie temperature (Tc), BaTiO3 transforms from the ferroelectric phase (where spontaneous polarization occurs near GBs) to the paraelectric phase (where spontaneous polarization disappears) resulting in an increase in resistance due to the potential barrier increasing because of the lack of compensation for polarization induced charge.
3.5. AC conductivity
Fig. 7 depicts the temperature-dependent ac conductivity (σac) behavior of the prepared Ba1−xLaxTiO3 (x = 0.0, 0.0025, 0.005, 0.0075) samples at different frequencies (1–100 kHz). As seen from the figure, the prepared samples exhibit semiconducting behavior because the value of σac initially increases with the increase in temperature up to the Curie temperature (Tc). While, above the Curie temperature (T > Tc), the σac value begins to decrease sharply with temperature due to their insulating behavior, as discussed earlier. Moreover, we observed that these plots can be distinguished into three different regions: two regions (R-I and R-II) at T < Tc and one region (R-III) at T > Tc, characterized by dissimilar slopes indicating distinct conduction processes with different activation energies (Ea) values. The notable change in the slopes of the prepared samples is observed between the regions R-I and R-II for T < Tc which is likely due to a difference in the rearrangement of the lattice during the transition of ferroelectric-paraelectric crystalline phase.47 This verifies the diffuse nature of the transition along with the dominance of GBs observed earlier in Fig. 4 for the prepared samples. However, a straight line is observed in the region R-III at T > Tc revealing a sharp decrease in σac. The activation energies (Ea) were calculated from the slopes of the linear regions of plots between ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) σ and 1000/T of all prepared samples in different regions using the Arrhenius law given below:
σ and 1000/T of all prepared samples in different regions using the Arrhenius law given below:| |
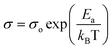 | (6) |
where σo is the pre-exponential factor, Ea is the activation energy, kB is the Boltzmann constant and T is the absolute temperature.48 Table 2 shows the calculated values of Ea′s for the prepared samples in different regions at a representative frequencies of 1 kHz, 10 kHz and 100 kHz. We found that the BaTiO3 sample has a large values of Ea due to bigger grain size. While, for La3+ doped samples, a significant decrease in the values of Ea is observed as a result of reduced grain sizes in comparison to pure sample. Here the values of Ea are observed to increase with temperature, which shows that the conduction mechanism is a thermally activated process. While, in all doped samples, the values of Ea for R-II are bit higher than that for other regions, indicating that the GBs have a dominant effect in the total conduction of samples. Further, the values of Ea for all regions are found to decrease sharply with La3+ doping content (x) suggesting better conductivity of semiconducting Gs and the appearance of less conductive GBs with increasing La3+ doping content in the prepared Ba1−xLaxTiO3 ceramics.
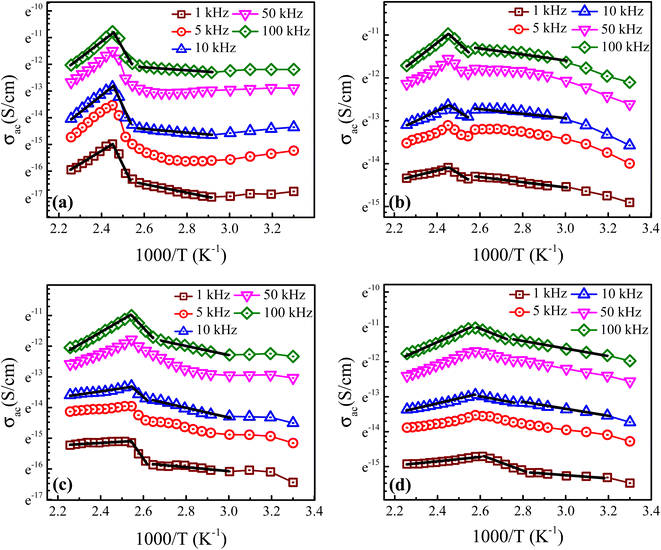 |
| | Fig. 7 Temperature-dependent ac conductivity (σac) behavior of the prepared Ba1−xLaxTiO3 ceramics with (a) x = 0.0, (b) x = 0.0025, (c) x = 0.005, and (d) x = 0.0075 at different frequencies (1 kHz–100 kHz). Solid lines show the fit to the experimental data using eqn (6) at different frequency regions. | |
Table 2 Calculated values of activation energies (Ea′s) for the prepared La3+ doped Ba1−xLaxTiO3 ceramics in different regions at a representative frequencies of 1 kHz, 10 kHz and 100 kHz
| Samples (x) |
Frequency (kHz) |
Region-I |
Region-II |
Region-III |
| Ea (eV) |
Ea (eV) |
Ea (eV) |
| 0.0 |
1 |
0.195 |
1.035 |
0.306 |
| 10 |
0.185 |
1.072 |
0.356 |
| 100 |
0.166 |
0.902 |
0.381 |
| 0.0025 |
1 |
0.039 |
0.168 |
0.065 |
| 10 |
0.024 |
0.169 |
0.125 |
| 100 |
0.031 |
0.269 |
0.199 |
| 0.005 |
1 |
0.012 |
0.224 |
0.009 |
| 10 |
0.046 |
0.145 |
0.016 |
| 100 |
0.057 |
0.194 |
0.114 |
| 0.0075 |
1 |
0.008 |
0.032 |
0.013 |
| 10 |
0.022 |
0.024 |
0.029 |
| 100 |
0.026 |
0.057 |
0.058 |
3.6. Ferroelectric analysis
Fig. 8(a–d) shows the ferroelectric polarization versus electric field (P–E) hysteresis loops of Ba1−xLaxTiO3 (x = 0.0, 0.0025, 0.005, 0.0075) samples, which were measured by applying an electric field of ±10 kV cm−1 at room temperature. Here, the development of hysteresis loops confirms the ferroelectric nature of La3+ doped BaTiO3 samples. With increasing La3+ doping content, the hysteresis loops become slimmer, which might be attributed to the donor doping and the presence of pinned polar nanoregions along with a low dielectric loss.49,50 Moreover, it is observed that there is a slight increase in the maximum polarization (Pm) value along with a decrease in the values of remnant polarization (Pr) and coercive field (Ec) with increasing La3+ doping content up to x = 0.0025 compared to a pure x = 0.0 sample. With a further increase in the La3+ doping content (x > 0.0025), the value of Pm begins to decrease and becomes more or less similar to the value for pure sample. While, the values of remnant polarization (Pr) and coercive field (Ec) further decrease with increasing La3+ doping content and become unchanged for x ≥0.005. These variations in the ferroelectric parameters could be understood in terms of the competing effects of the domain wall motion ability and the overall change in the crystal structure of BaTiO3 on La3+ doping.26 However, for x ≥0.005 samples, the relatively unchanged ferroelectric parameters suggest a critical point of La3+ doping content in which BaTiO3 maintain the initial value of Pm along with reduced values of Pr and Ec which may be responsible for the enhancement in the energy storage density in these samples. The ferroelectric hysteresis loops were further utilized to estimate the discharge (Jd) and charge (Jc) energy storage densities of the prepared samples using the following formulas:51| |
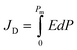 | (7) |
| |
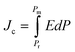 | (8) |
where E and P are the applied electric field and polarization, respectively. Table 3 presents the calculated values of JD and Jc for the prepared samples. With increasing La3+ doping concentration, it is found that JD and Jc values initially increase until x = 0.0025, after which they begin to decrease. However, the maximum values of JD for La3+ doped samples are found to be 2–3 times higher than that of pure x = 0.0 sample, which is accredited to the reduced grain size and remnant polarization by La3+ doping. Moreover, the energy storage efficiency (η) of the prepared samples was also calculated using the formula: η = JD/Jc.51 The calculated values of η are presented in Table 3, where a significant improvement in the energy storage efficiency is observed for La3+ doped BaTiO3 samples in comparison to the reported values.20,21 Here, the observed increase in the η values is accredited to the decrease in the slope of the hysteresis loop, the large difference in the values of Pm and Pr, high dielectric permittivity, low dielectric tangent loss, and reduced grain size. Among the prepared samples, the sample with x = 0.005 shows the highest energy storage efficiency of 78% at ∼10 kV cm−1, which is found to be 2.3 times higher than that of x = 0.0 sample. So, the improved energy storage properties and high dielectric value of this composition make it attractive for energy storage applications.
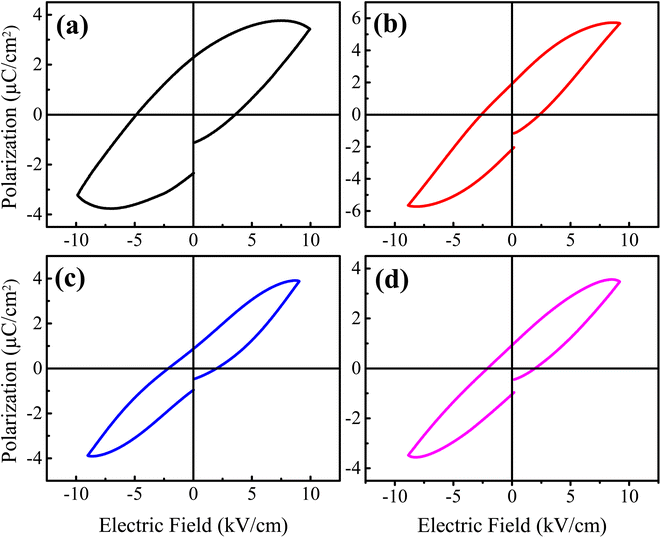 |
| | Fig. 8 Ferroelectric hysteresis loops of the prepared Ba1−xLaxTiO3 ceramics with (a) x = 0.0, (b) x = 0.0025, (c) x = 0.005, and (d) x = 0.0075 measured at room temperature. | |
Table 3 Saturation polarization (Pm), remnant polarization (Pr), coercive field (Hc), difference between the saturation and remnant polarization (Pm − Pr), discharge energy density (Jd), charge energy density (Jc), and energy storage efficiency (η) of the La3+ doped Ba1−xLaxTiO3 ceramics
| Sample (x) |
Pm (μC cm−2) |
Pr (μC cm−2) |
Hc (kV cm−1) |
Pm − Pr (μC cm−2) |
Jd (J cm−3) |
Jc (J cm−3) |
η (%) |
| 0.00 |
3.44 |
2.29 |
4.88 |
1.14 |
0.011 |
0.034 |
34 |
| 0.0025 |
5.66 |
1.87 |
2.63 |
3.79 |
0.035 |
0.052 |
66 |
| 0.005 |
3.90 |
0.83 |
2.19 |
3.06 |
0.027 |
0.035 |
78 |
| 0.0075 |
3.48 |
0.90 |
2.08 |
2.57 |
0.023 |
0.031 |
74 |
4. Conclusions
La3+ doped Ba1−xLaxTiO3 (x = 0.0, 0.0025, 0.005, 0.0075) were successfully prepared by the composite-hydroxide-mediated method and their structural, dielectric, and ferroelectric properties were investigated using different analytical techniques. Rietveld refinement on the XRD patterns confirmed the formation of pure perovskite structure, while a systematic decrease in the tetragonality ratio (c/a) indicated a transformation from the tetragonal phase to a pseudo-cubic phase with La3+ doping content. SEM analysis showed that the La3+ doping inhibited the grain growth. The dielectric and impedance analysis revealed that the La3+ doped samples exhibit: (i) increase in the dielectric permittivity; (ii) ferroelectric–paraelectric transition around the Curie temperature; (iii) decrease in Tc towards the lower temperatures; (iv) increase in the dielectric diffusivity; and (v) the semiconducting behavior with PTCR behavior. These observed behaviors are explained in terms of a decrease in the grain size and charge compensation mechanism. While the PTCR effect results from both Gs and GBs effects, but the GBs contribution is more dominant. The P–E loops confirmed the ferroelectric behavior with a decrease in the remnant polarization and coercive field due to La3+ doping. Moreover, the doped samples exhibited an improvement in energy storage density and energy storage efficiency compared to that of pure undoped sample. Such a significant improvement in energy storage properties could be attributed to the reduced grain size due to La3+ doping. In conclusion, we found that the proposed composite-hydroxide-mediated method allowed us to fabricate dense and homogeneous microstructures with a submicron grain size (∼1 μm). Among the prepared ceramics, the sample with x = 0.005 exhibits significantly enhanced dielectric permittivity (4381), low dielectric tangent loss (0.02), and the highest energy storage efficiency (78%) at room temperature, which makes this composition interesting for energy storage applications.
Author contributions
U. Younas: investigation, visualization, writing—original draft. M. Atif: conceptualization, supervision, writing—review & editing. A. Anjum: investigation, formal analysis. M. Nadeem: methodology, validation. T. Ali: resources, formal analysis. R. Shaheen: resources, formal analysis. W. Khalid: software, validation. Z. Ali: writing—review & editing.
Conflicts of interest
There are no conflicts to declare.
References
- W. H. Lee and C. Y. Su, Improvement in the temperature stability of a BaTiO3-based multilayer ceramic capacitor by constrained sintering, J. Am. Ceram. Soc., 2007, 90, 3345–3348 CrossRef CAS.
- C. H. Kim, K. J. Park, Y. J. Yoon, M. H. Hong, J. O. Hong and K. H. Hur, Role of yttrium and magnesium in the formation of core-shell structure of BaTiO3 grains in MLCC, J. Eur. Ceram. Soc., 2008, 28, 1213–1219 CrossRef CAS.
- Z. Yang, F. Gao, H. Dua, L. Jin, L. Yan, Q. Hu, Y. Yu, S. Qu, X. Wei, Z. Xu and Y.-J. Wang, Grain size engineered lead-free ceramics with both large energy storage density and ultrahigh mechanical properties, Nano Energy, 2019, 58, 768–777 CrossRef CAS.
- M. M. Vijatovic, History and Challenges of Barium Titanate Part II, J. Sci. Sinter., 2008, 40, 235–244 CrossRef CAS.
- A. Rached, M. A. Wederni, A. Belkahla, J. Dhahri, K. Khirouni, S. Alaya and R. J. Martín-Palma, Effect of doping in the physico-chemical properties of BaTiO3 ceramics, Physica B, 2020, 596, 412343 CrossRef CAS.
- D. Y. Lu, S. Z. Cui, Q. L. Liu and X. Y. Sun, Dielectric properties and defect chemistry of barium titanate ceramics co-doped R and Dy ions (R = Eu, Gd, Tb), Ceram. Int., 2016, 42, 14364–14373 CrossRef CAS.
- C. L. Freeman, J. A. Dawson, H.-Ru. Chen, L. Ben, J. H. Harding, F. D. Morrison, D. C. Sinclair and A. R. West, Energetics of Donor-Doping, Metal Vacancies, and Oxygen-Loss in A-Site Rare Earth-Doped BaTiO3, Adv. Funct. Mater., 2013, 23, 3925–3928 CrossRef CAS.
- Y. Tsur, T. D. Dunbar and C. A. Randall, Crystal and Defect Chemistry of Rare Earth Cations in BaTiO3, J. Electroceram., 2001, 7, 25–34 CrossRef CAS.
- F. D. Morrison, A. M. Coats, D. C. Sinclair and A. R. West, Charge Compensation Mechanisms in La-Doped BaTiO3, J. Electroceram., 2001, 6, 219–232 CrossRef CAS.
- C. L. Freeman, J. A. Dawson, H.-R. Chen, J. H. Harding, L.-B. Ben and D. C. Sinclair, A new potential model for barium titanate and its implications for rare-earth doping, J. Mater. Chem., 2011, 21, 4861–4868 RSC.
- S. Chatterjee, B. D. Stojanovic and H. S. Maiti, Effect of additives and powder preparation techniques on PTCR properties of barium titanate, Mater. Chem. Phys., 2003, 28, 702–710 CrossRef.
- Y. L. Chen and S. F. Yang, PTCR effect in donor doped barium titanate: review of compositions, microstructures, processing and properties, Adv. Appl. Ceram., 2011, 110(5), 257–269 CrossRef CAS.
- A. Ianculescu, Z. V. Mocanu, L. P. Curecheriu, L. Mitoseriu, L. Padurariu and R. Truşcă, Dielectric and tunability properties of La-doped BaTiO3 ceramics, J. Alloys Compd., 2011, 509, 10040–10049 CrossRef CAS.
- D.-Y. Lu and S.-Z. Cui, Defects characterization of Dy-doped BaTiO3 ceramics via electron paramagnetic resonance, J. Eur. Ceram. Soc., 2014, 34, 2217–2227 CrossRef CAS.
- D. Makovec, N. Ule and M. Drofenik, Positive Temperature Coefficient of Resistivity Effect in Highly Donor-Doped Barium Titanate, J. Am. Ceram. Soc., 2001, 84, 1273–1280 CrossRef CAS.
- M. M. Vijatović Petrović, J. D. Bobić, R. Grigalaitis, B. D. Stojanović and J. Banys, La-doped and La/Mn-co-doped Barium Titanate Ceramics, Acta Phys. Pol., A, 2013, 124, 155–160 CrossRef.
- F. D. Morrison, D. C. Sinclair and A. R. West, An Alternative Explanation for the Origin of the Resistivity Anomaly in La-Doped BaTiO3, J. Am. Ceram. Soc., 2001, 84(2), 474–476 CrossRef CAS.
- M. Ganguly, S. K. Rout, T. P. Sinha, S. K. Sharma, H. Y. Park, C. W. Ahn and I. W. Kim, Characterization and Rietveld Refinement of A-site deficient Lanthanum doped Barium Titanate, J. Alloys Compd., 2013, 579, 473–484 CrossRef CAS.
- Y. Wang, K. Miao, W. Wang and Y. Qin, Fabrication of lanthanum doped BaTiO3 fine-grained ceramics with a high dielectric constant and temperature-stable dielectric properties using hydro-phase method at atmospheric pressure, J. Eur. Ceram. Soc., 2017, 37, 2385–2390 CrossRef.
- V. S. Puli, P. Li, S. Adireddy and D. B. Chrisey, Crystal structure, dielectric, ferroelectric and energy storage properties of La-doped BaTiO3 semiconducting ceramics, J. Adv. Dielectr., 2015, 5, 1550027 CrossRef CAS.
- R. Kumar, I. Singh, R. Meena, K. Asokan, B. Birajdar and S. Patnaik, Effect of La-doping on dielectric properties and energy storage density of lead-free Ba(Ti0.95Sn0.05)O3 ceramics, Mater. Res. Bull., 2020, 123, 110694 CrossRef CAS.
- T. Badapanda, V. Senthil, S. Panigrahi and S. Anwar, Diffuse phase transition behavior of dysprosium doped barium titanate ceramic, J. Electroceram., 2013, 31, 55–60 CrossRef CAS.
- H.-J. Chen and Y.-W. Chen, Hydrothermal Synthesis of Barium Titanate, Ind. Eng. Chem. Res., 2003, 42(3), 473–483 CrossRef CAS.
- R. Ashiri, A. Nemati, M. S. Ghamsari, S. Sanjabi and M. Aalipour, A modified method for barium titanate nanoparticles synthesis, Mater, Res. Bull., 2011, 46, 2291–2295 CrossRef CAS.
- D. Chen and X. Jiao, Solvothermal Synthesis and Characterization of Barium Titanate Powders, J. Am. Ceram. Soc., 2000, 83, 2637–2639 CrossRef CAS.
- S. Sharma, R. K. Patel, C. Prakash and P. Kumar, Structural, dielectric and ferroelectric study of microwave sintered lanthanum substituted BaTiO3 ceramics, Mater. Chem. Phys., 2011, 130, 191–195 CrossRef CAS.
- M. Borah and D. Mohanta, Composite-Hydroxide-Mediated Formation of Barium Titanate Nanocubes and Their Optical Emission Response, Chin. J. Phys., 2015, 53, 020804 Search PubMed.
- T. M. Khan, M. Zakria, R. I. Shakoor and S. Hussain, Composite-hydroxide-mediated approach an effective synthesis route for BaTiO3 functional nanomaterials, Appl. Phys. A, 2016, 122, 274 CrossRef.
- Y. Xie, S. Yin, T. Hashimoto, Y. Tokano, A. Sasaki and T. Sato, Low temperature synthesis of tetragonal BaTiO3 by a novel composite-hydroxide-mediated approach and its dielectric properties, J. Eur. Ceram. Soc., 2010, 30, 699–704 CrossRef CAS.
- Joint Committee on Powder Diffraction Standards, Powder Diffraction Files no. 05-0626.
- A. E. Ghandouri, S. Sayouri, T. Lamcharfi and A. Elbasset, Structural, microstructural and dielectric properties of Ba1−xLaxTi(1−x/4)O3 prepared by sol gel method, J. Adv. Dielectr., 2019, 9, 1950026 CrossRef.
- R. D. Shannon, Revised effective ionic radii in halides and chalcogenides, Acta Crystallogr., Sect. A: Found. Crystallogr., 1976, 32, 751–767 CrossRef.
- X. Liu, R. Hong and C. Tian, Tolerance factor and the stability discussion of ABO3-type ilmenite, J. Mater. Sci.: Mater. Electron., 2009, 20, 323–327 CrossRef CAS.
- Z. Lv, J. Wei, T. Yang, Z. Sun and Z. Xu, Manipulation of Curie temperature and ferroelectric polarization for large electrocaloric strength in BaTiO3-based ceramics, Ceram. Int., 2020, 46, 14978–14984 CrossRef CAS.
- L. Pdungsap, N. Udomkan, S. Boonyuen and P. Winotai, Optimized conditions for fabrication of La-dopant in PZT ceramics, Sens. Actuators, A, 2005, 122, 250–256 CrossRef CAS.
- S. M. Bobade, D. D. Gulwade, A. R. Kulkarni and P. Gopalan, Dielectric properties of A- and B-site-doped BaTiO3 (I): La- and Al-doped solid solutions, J. Appl. Phys., 2005, 97, 074105 CrossRef.
- Y. Tan, J. Zhang, Y. Wu, C. Wang, V. Koval, B. Shi, H. Ye, R. McKinnon, G. Viola and H. Yan, Unfolding grain size effects in barium titanate ferroelectric ceramics, Sci. Rep., 2015, 5, 9953 CrossRef CAS PubMed.
- Z. Raddaoui, S. El Kossi, J. Dhahri, N. Abdelmoula and K. Taibi, Study of diffuse phase transition and relaxor ferroelectric behavior of Ba0.97Bi0.02Ti0.9Zr0.05Nb0.04O3 ceramic, RSC Adv., 2019, 9, 2412–2425 RSC.
- K. Uchino and S. Nomura, Critical exponents of the dielectric constants in diffused-phase-transition crystals, Ferroelectrics, 1982, 44, 55–61 CrossRef CAS.
- X.-G. Tang and H. L.-W. Chan, Effect of grain size on the electrical properties of (Ba,Ca)(Zr,Ti)O3 relaxor ferroelectric ceramics, J. Appl. Phys., 2005, 97(3), 034109 CrossRef.
- Y. Wang, Y. Pu, X. Li and H. Zheng, Structural evolution, relaxation behaviors and dielectric properties of BaTiO3–BiAlO3 perovskite solid solutions, J. Mater. Sci.: Mater. Electron., 2016, 27, 11565–11571 CrossRef CAS.
- E. Barsoukov and J. R. Macdonald, Impedance Spectroscopy Theory, Experiments and Applications, Wiley, New York, 2005 Search PubMed.
- M. Younas, M. Nadeem, M. Atif and R. Grossinger, Metal-semiconductor transition in NiFe2O4 nanoparticles due to reverse cationic distribution by impedance spectroscopy, J. Appl. Phys., 2011, 109, 093704 CrossRef.
- J. T. S. Irvine, D. C. Sinclair and A. R. West, Electroceramics: Characterization by Impedance Spectroscopy, Adv. Mater., 1990, 2, 132 CrossRef CAS.
- K. Matsuura, T. Hoshina, H. Takeda, Y. Sakabe and T. Tsurumi, Effects of Ca substitution on room temperature resistivity of donor-doped barium titanate based PTCR ceramics, J. Ceram. Soc. Jpn., 2014, 122(6), 402–405 CrossRef.
- J. Nowotny and M. Rekas, Positive Temperature Coefficient of Resistivity for BaTiO3-based Materials, Ceram. Int., 1991, 17, 227 CrossRef CAS.
- S. Ben Moumen, A. Neqali, B. Asbani, D. Mezzane, M. Amjoud, E. Choukri, Y. Gagou, M. El Marssi and I. Lukyanchuk, Impedance spectroscopy studies on lead free Ba1−xMgx(Ti0.9Zr0.1)O3 ceramics, Superlattices Microstruct., 2018, 118, 45–54 CrossRef CAS.
- Atta Ur Rehman, M. Atif, M. Younas, T. Rafique, H. Wahab, A. Ul-Hamid, N. Iqbal, Z. Ali, W. Khalid and M. Nadeem, Unusual semiconductor–metal–semiconductor transitions in magnetite Fe3O4 nanoparticles, RSC Adv., 2022, 12, 12344 RSC.
- Y. H. Huang, Y. J. Wu, W. J. Qiu, J. Li and X. M. Chen, Enhanced energy storage density of Ba0.4Sr0.6TiO3–MgO composite prepared by spark plasma sintering, J. Eur. Ceram. Soc., 2015, 35, 1469–1476 CrossRef CAS.
- W. Kleemann, The relaxor enigma–charge disorder and random fields in ferroelectrics, J. Mater. Sci., 2006, 41, 129–136 CrossRef CAS.
- Y. Lin, D. Li, M. Zhang, S. Zhan, Y. Yang, H. Yang and Q. Yuan, Excellent Energy-Storage Properties Achieved in BaTiO3-Based Lead-Free Relaxor Ferroelectric Ceramics via Domain Engineering on the Nanoscale, ACS Appl. Mater. Interfaces, 2019, 11, 36824–36830 CrossRef CAS PubMed.
|
| This journal is © The Royal Society of Chemistry 2023 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a,
A. Anjuma,
M. Nadeemb,
T. Alic,
R. Shaheenc,
W. Khalida and
Z. Alia
*a,
A. Anjuma,
M. Nadeemb,
T. Alic,
R. Shaheenc,
W. Khalida and
Z. Alia
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 48.5) was put into a 50 ml Teflon vessel. Afterward, a mixture of barium nitrate [Ba(NO3)2, Sigma-Aldrich, ≥99%], lanthanum nitrate [La(NO3)2·6H2O, Sigma-Aldrich, ≥99%], and titanium oxide [TiO2, Sigma-Aldrich, ≥99%] at 10 mmol each was added to the vessel as per their stoichiometric ratio. The vessel was then put in a heating oven at 200 °C for 72 h. After the chemical reaction, the vessel was taken out of the oven and cooled down to room temperature. To eliminate hydroxides on the surface of the particles, the product was filtered and washed many times with deionized water. Finally, the obtained powders were dried overnight at 100 °C in an oven and annealed in the furnace at 700 °C for 3 h under ambient conditions. The calcined powders were mixed with 5 wt% binder (polyvinyl alcohol) and then uniaxially pressed by applying a compaction pressure of 5 ton per cm2. The pelletized samples were then sintered at 1200 °C for 4 h in a conventional furnace with a heating/cooling rate of 5 °C min−1.
48.5) was put into a 50 ml Teflon vessel. Afterward, a mixture of barium nitrate [Ba(NO3)2, Sigma-Aldrich, ≥99%], lanthanum nitrate [La(NO3)2·6H2O, Sigma-Aldrich, ≥99%], and titanium oxide [TiO2, Sigma-Aldrich, ≥99%] at 10 mmol each was added to the vessel as per their stoichiometric ratio. The vessel was then put in a heating oven at 200 °C for 72 h. After the chemical reaction, the vessel was taken out of the oven and cooled down to room temperature. To eliminate hydroxides on the surface of the particles, the product was filtered and washed many times with deionized water. Finally, the obtained powders were dried overnight at 100 °C in an oven and annealed in the furnace at 700 °C for 3 h under ambient conditions. The calcined powders were mixed with 5 wt% binder (polyvinyl alcohol) and then uniaxially pressed by applying a compaction pressure of 5 ton per cm2. The pelletized samples were then sintered at 1200 °C for 4 h in a conventional furnace with a heating/cooling rate of 5 °C min−1.
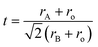

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ) for the La3+ doped Ba1−xLaxTiO3 (x = 0.0, 0.0025, 0.005, 0.0075) samples measured at different frequencies (1 kHz to 1 MHz) between the temperature range of 303 K to 463 K. It can be seen that, for the pure BaTiO3 sample (x = 0.0), the ε′ value begins to increase gradually with increasing temperature and reaches a maximum value at 409 K and then decreases smoothly with further increase in temperature (Fig. 3(a)). Here, the increasing trend of ε′ with temperature is accredited to the orientational polarization which is associated with the thermal motion of dipoles. The specific temperature at which ε′ has a maximum value is defined as the Curie temperature (Tc). At this temperature, the ferroelectric phase transforms into the paraelectric phase, followed by a structural transition from tetragonal symmetry to cubic. A similar transition temperature was also found in the literature for BaTiO3.19,21 However, a small difference in the values of ε′ and Tc might be caused by the grain size effect. Further, the Curie temperature (Tc) of a pure sample is observed to continually decrease from 409 K to 393 K with increasing La3+ doping content (x) in Ba1−xLaxTiO3 (see Table 1). While, the value of ε′ is found to increase by La3+ doping at the Ba2+ site, when compared with a pure sample. Here, the observed trend of Tc and ε′ with La3+ doping might be associated with the reduction in grain size and smaller ionic dopant. Also, the replacement of Ba2+ by the higher valence La3+ ions generates cation vacancies on the Ti4+ site to maintain charge neutrality, which in turn introduces distortion in the TiO6 octahedra.21,36 Thus, these distorted TiO6 octahedra break the long-range ordering and assist in the reorientation of ferroelectric domains, which results in the improved ε′ value of BaTiO3 with La3+ doping. Here, the observed ε′ value at room temperature for the pure BaTiO3 and La3+ doped BaTiO3 samples is relatively higher than the values reported for similar systems,13,19,26,34 which might be related to the grain size effect. It is well known that the maximum value of ε′ in the BaTiO3 ceramics is obtained at a grain size of 1.0 μm as a result of the optimum density and mobility of 90° domain walls in the prepared sample.37 Since the average grain size of prepared BaTiO3 and La3+ doped BaTiO3 samples are 3 μm (>1.0 μm) and 0.89–1.1 μm (∼1.0 μm), respectively (see Fig. 2). Thus, the La3+ doped BaTiO3 samples exhibit higher values of ε′ in comparison to pure BaTiO3 sample. However, among the doped samples, the sample with x = 0.005 sample provides the highest value of ε′ due to the dominant effect of fine grains (0.98 μm) with uniform distribution and enhanced charge carrier concentration. Moreover, the figure reveals that the ε′ value decreases slightly with increasing frequency over the entire temperature range, and the ε′ peak is found to be temperature independent for all prepared samples. While, a visible broadening of the dielectric peaks can be seen, suggesting that the observed phase transition is of the diffuse-type. Typically, such broadening of the dielectric peak results from compositional fluctuation, merging of micro to macro polar regions, and/or doping induced disorder in the crystal lattice.38 Moreover, the low values of dielectric tangent loss (tan
δ) for the La3+ doped Ba1−xLaxTiO3 (x = 0.0, 0.0025, 0.005, 0.0075) samples measured at different frequencies (1 kHz to 1 MHz) between the temperature range of 303 K to 463 K. It can be seen that, for the pure BaTiO3 sample (x = 0.0), the ε′ value begins to increase gradually with increasing temperature and reaches a maximum value at 409 K and then decreases smoothly with further increase in temperature (Fig. 3(a)). Here, the increasing trend of ε′ with temperature is accredited to the orientational polarization which is associated with the thermal motion of dipoles. The specific temperature at which ε′ has a maximum value is defined as the Curie temperature (Tc). At this temperature, the ferroelectric phase transforms into the paraelectric phase, followed by a structural transition from tetragonal symmetry to cubic. A similar transition temperature was also found in the literature for BaTiO3.19,21 However, a small difference in the values of ε′ and Tc might be caused by the grain size effect. Further, the Curie temperature (Tc) of a pure sample is observed to continually decrease from 409 K to 393 K with increasing La3+ doping content (x) in Ba1−xLaxTiO3 (see Table 1). While, the value of ε′ is found to increase by La3+ doping at the Ba2+ site, when compared with a pure sample. Here, the observed trend of Tc and ε′ with La3+ doping might be associated with the reduction in grain size and smaller ionic dopant. Also, the replacement of Ba2+ by the higher valence La3+ ions generates cation vacancies on the Ti4+ site to maintain charge neutrality, which in turn introduces distortion in the TiO6 octahedra.21,36 Thus, these distorted TiO6 octahedra break the long-range ordering and assist in the reorientation of ferroelectric domains, which results in the improved ε′ value of BaTiO3 with La3+ doping. Here, the observed ε′ value at room temperature for the pure BaTiO3 and La3+ doped BaTiO3 samples is relatively higher than the values reported for similar systems,13,19,26,34 which might be related to the grain size effect. It is well known that the maximum value of ε′ in the BaTiO3 ceramics is obtained at a grain size of 1.0 μm as a result of the optimum density and mobility of 90° domain walls in the prepared sample.37 Since the average grain size of prepared BaTiO3 and La3+ doped BaTiO3 samples are 3 μm (>1.0 μm) and 0.89–1.1 μm (∼1.0 μm), respectively (see Fig. 2). Thus, the La3+ doped BaTiO3 samples exhibit higher values of ε′ in comparison to pure BaTiO3 sample. However, among the doped samples, the sample with x = 0.005 sample provides the highest value of ε′ due to the dominant effect of fine grains (0.98 μm) with uniform distribution and enhanced charge carrier concentration. Moreover, the figure reveals that the ε′ value decreases slightly with increasing frequency over the entire temperature range, and the ε′ peak is found to be temperature independent for all prepared samples. While, a visible broadening of the dielectric peaks can be seen, suggesting that the observed phase transition is of the diffuse-type. Typically, such broadening of the dielectric peak results from compositional fluctuation, merging of micro to macro polar regions, and/or doping induced disorder in the crystal lattice.38 Moreover, the low values of dielectric tangent loss (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ) between 0.036 and 0.55 are observed in the prepared Ba1−xLaxTiO3 samples, and the values of tan
δ) between 0.036 and 0.55 are observed in the prepared Ba1−xLaxTiO3 samples, and the values of tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ are found to slightly increase with La3+ doping compared to pure BaTiO3 sample (see Fig. 2(a–d)). However, above the Curie temperature, there is an abrupt increase in tan
δ are found to slightly increase with La3+ doping compared to pure BaTiO3 sample (see Fig. 2(a–d)). However, above the Curie temperature, there is an abrupt increase in tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ value with increasing temperature, which would be the direct consequence of higher electrical conductivity.21
δ value with increasing temperature, which would be the direct consequence of higher electrical conductivity.21
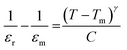
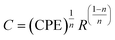
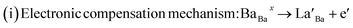
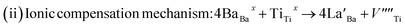
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) σ and 1000/T of all prepared samples in different regions using the Arrhenius law given below:
σ and 1000/T of all prepared samples in different regions using the Arrhenius law given below: