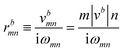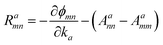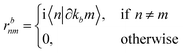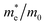DOI:
10.1039/D2RA06860E
(Paper)
RSC Adv., 2023,
13, 1955-1963
Insights into the relationship between ferroelectric and photovoltaic properties in CsGeI3 for solar energy conversion
Received
30th October 2022
, Accepted 3rd January 2023
First published on 11th January 2023
Abstract
Materials such as oxide and halide perovskites that simultaneously exhibit spontaneous polarization and absorption of visible light are called photoferroelectrics. They hold great promise for the development of applications in optoelectronics, information storage, and energy conversion. Devices based on ferroelectric photovoltaic materials yield an open-circuit voltage that is much higher than the band gap of the corresponding active material owing to a strong internal electric field. Their efficiency has been proposed to exceed the Shockley–Queisser limit for ideal solar cells. In this paper, we present theoretical calculations of the photovoltaic properties of the ferroelectric phase of the inorganic germanium halide perovskite (CsGeI3). Firstly, the electronic, optical and ferroelectric properties were calculated using the FP-LAPW method based on density functional theory, and the modern theory of polarization based on the Berry phase approach, respectively. The photovoltaic performance was evaluated using the Spectroscopic Limited Maximum Efficiency (SLME) model based on the results of first-principles calculations, in which the power conversion efficiency and the photocurrent density–voltage (J–V) characteristics were estimated. The calculated results show that the valence band maximum (VBM) of CsGeI3 is mainly contributed by the I-5p and Ge-4s orbitals, whereas the conduction band is predominantly derived from Ge-4p orbitals. It can be seen that CsGeI3 exhibits a direct bandgap semiconductor at the symmetric point of Z with a value of 1.53 eV, which is in good agreement with previous experimental results. The ferroelectric properties were therefore investigated. With a switching energy barrier of 19.83 meV per atom, CsGeI3 has a higher theoretical ferroelectric polarization strength of 15.82 μC cm−2. The SLME calculation also shows that CsGeI3 has a high photoelectric conversion efficiency of over 28%. In addition to confirming their established favorable band gap and strong absorption, we demonstrate that CsGeI3 exhibits a large shift current bulk photovoltaic effect of up to 40 μA V−2 in the visible region. Thus, this material is a potential ferroelectric photovoltaic absorbed layer with high efficiency.
Introduction
Solar energy technology has been continuously improved as part of renewable energy technology. A solar cell, commonly known as a photovoltaic cell, is the most widely used device that converts sunlight directly into electricity. The important accomplishments of halide perovskites in photovoltaics and other optoelectronic applications result from a great advantageous combination of optical and electronic properties and their simple fabrication processes. This distinguishes them as an entirely new class of semiconductors that can approach or exceed the performance of the typical III–V and II–IV semiconductor classes that still rule the applied optoelectronic industry.1–7 The emerging halide perovskites with exceptional semiconducting properties also have the potential to be ferroelectric. Recently, it was suggested that the high performance of photovoltaic cells based on the use of halide perovskites originates from the presence of ferroelectricity in these perovskites. Some theoretical works have shown that ferroelectricity in halide perovskites reduces the recombination of electron–hole pairs excited by light, and also extends the charge carrier lifetimes to several nanoseconds.4 Consequently, ferroelectricity is a good approach to increase photovoltaic performance beyond the Shockley–Queisser limit. The photovoltaic response in ferroelectric materials is called “the bulk photovoltaic effect” (BPVE). The photocurrent of the ferroelectric–photovoltaic device is governed by the light-absorption process, exciton dissociation efficiency, the lifetime of the photogenerated nonequilibrium charges, and charge carrier mobility. The Shift current which is the dominant photocurrent response in the bulk photovoltaic effect (BPVE) may be calculated using the first-principles method, which uses perturbation theory to estimate the transition intensity and shift vector.8–12 The measurements conducted on the tetragonal methylammonium lead triiodide (CH3NH3PbI3) confirm its excellent light-absorbing and charge-transporting properties, which make it ideal to give crucial insight into the design and working mechanism of perovskite solar cells. At low temperatures, Cahen et al. reported experimental findings of ferroelectric hysteresis in tetragonal CH3NH3PbI3 single crystals,13 and they express all of the necessary ferroelectricity-related features: lack of inversion symmetry, spontaneous polarization, and presence of polar domains. In addition, Huang et al. showed the existence of ferro-elastic domains in polycrystalline CH3NH3PbI3 films and single crystals.14 Frost et al. calculated the polarization magnitude of CH3NH3PbI3 perovskite up to 38 μC cm−2 (similar to that of the ferroelectric oxide perovskite KNbO3).1 The electric polarization present in the ferroelectric CH3NH3PbI3 has been shown to effectively separate the photoexcited carriers, leading to novel ferroelectric PV materials with potentially enhanced energy conversion efficiency. Lead toxicity which has hazardous effects on the environment and the human body has drawn considerable attention to emerging halide perovskite solar cells. To address this toxicity issue, intensive research efforts have recently been made to replace lead with non-toxic elements without compromising the photovoltaic properties. So far, various metal cations such as tin or germanium have been explored as alternatives for the development of lead-free halide perovskites. High-throughput computational methods based on density functional theory (DFT) have been proposed to search for a suitable replacement for lead in halide perovskite materials, drawing attention to their computed band gap values and their potential solar cell applications. Krishnamoorthy et al.15 investigated a series of AMX3 chemical compositions with A1+ and X1− ions selected from {K, Rb, and Cs} alkali metals and {Cl, Br, and I} halogen elements, respectively, in combination with various divalent candidates M site cations. The inorganic germanium perovskite compound CsGeI3 was identified among these compounds as the energetically most stable. The first synthesis and properties of CsGeI3 were reported by Stoumpos et al.,16 and through the X-ray diffraction characterization, the compound has been indexed to a rhombohedral crystal structure (with a R3m space group symmetry), which shows intriguing ferroelectric properties. The theoretical power conversion efficiency (PCE) of CsGeI3 in photovoltaic perovskite solar cells has increased rapidly, from around 18% to more than 31%.17–19 Because of its suitable charge mobility and low hole-effective mass, it has been proposed as an efficient hole transport material that can enhance the efficiency. The experimental findings of CsGeI3 were also published by Chen et al.,20 who examined its power conversion efficiency (PCE), which reached 4.92% under AM1.5G. Similarly, Krishnamoorthy et al.15 evaluated its PCE to be 11%. Understanding the linear and nonlinear optical (NLO) responses of the ferroelectric phase of CsGeI3 is critical for its effective use in solar applications. Therefore, in this paper, the FP-LAPW method based on density functional theory and the modern theory of polarization based on the Berry phase approach were used to calculate the optical and ferroelectric properties of CsGeI3, respectively. Secondly, based on these computed findings, the photoresponse and photovoltaic properties were investigated using the Spectroscopic Limited Maximum Efficiency (SLME) model, in which the power conversion efficiency and the photocurrent density–voltage (J–V) characteristics were evaluated. We will demonstrate that the ferroelectric phase of CsGeI3 can exhibit suitable nonlinear optical responses in the visible region, which is a potential mechanism for the high photovoltaic efficiency of next-generation solar cells.
Computational methodology
The calculations reported in this work have been performed using the full-potential linear-augmented plane waves plus local orbitals (FP-LAPW) method, within the generalized gradient approximation (GGA) as implemented in the Wien2k code.21,22 The Tran-Blaha modified Becke-Johnson (TB-mBJ) potential was used to find out the suitability for the study of electronic and optical properties of the CsGeI3 compound.23–27 LAPW sphere radii of 2.4, 2.3, and 2.4 bohr were employed for Cs, Ge, and I, respectively. The geometric structure was relaxed until the total energy change was less than 10−5 eV, and the forces acting on the atoms were relaxed to less than 0.001 eV Å−1. One of the most important properties of ferroelectric materials is spontaneous polarization. It is defined as the shift in polarization that happens when a crystal transforms from a centrosymmetric structure to a structure lacking inversion symmetry. For our study, we employed the program BerryPI28 to calculate polarization using the Berry phase method.29,30 A form of photovoltaic effect that occurs in certain semiconductors and insulators is the bulk photovoltaic effect (BPVE). Shift current is an intriguing concept for BPVE. This is a second-order process involving electron wavefunctions that have been excited twice by light. The first-principles method may be used to compute the transition intensity and shift vector based on perturbation theory in order to derive short-circuit current. Wannier90, which is based on maximally localized Wannier functions (MLWFs),31 was used to perform the shift current, which is closely related to the Wannier interpolation method. The MLWFs were calculated by projecting a series of Bloch energy bands into s-like and p-like orbitals on Ge and I atoms. The photovoltaic performance was evaluated using the Spectroscopic Limited Maximum Efficiency (SLME) model based on the results of first-principles calculations.32 It can be used for an initial screening based only on intrinsic properties. This means that greater theoretical efficiency can be obtained within this approach simply by calculating the J–V characteristic with an absorption spectrum.33–36
Results and discussion
Crystal structure and electronic band structure
Firstly, we perform the full geometry optimization to determine the crystal parameters in the rhombohedral phase of CsGeI3. The optimized unit-cell parameters and bond lengths are summarized in Table 1. According to the optimized geometry, we have performed the electronic structure calculations of the rhombohedral phase of CsGeI3 based on the FP-LAPW method21 and by using Tran and Blaha's23 modified Becke-Johnson potential functional, denoted TB-mBJ. Unlike standard GGA functionals, which are optimized to reproduce total energies, these potential delivers band gaps that are consistent with experiments for many basic semiconductors and insulators.24–26,37–39
Table 1 The calculated lattice constants and coordinates of the rhombohedral phase of CsGeI3 (space group R3m). Hole and electron effective masses (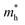 and
and 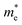 ) along different directions for CsGeI3 (m0 is the electron rest mass). The VBM and the CBM are both located at the Z point
) along different directions for CsGeI3 (m0 is the electron rest mass). The VBM and the CBM are both located at the Z point
| |
a (Å) |
G–I bond-length (Å) |
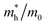
|
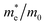
|
| Short |
Long |
Z–L |
Z–Γ |
Z–L |
Z–Γ |
| Ref. 16. Ref. 17. |
| Our work |
8.34 |
2.78 |
3.35 |
0.26 |
0.24 |
0.43 |
0.347 |
| Others |
8.34a |
2.75a |
3.26a |
0.22b |
0.21b |
0.42b |
0.21b |
Fig. 1 and 2 show the density of states and the energy band structure of this compound along the high symmetry points in the first Brillouin zone, respectively. From Fig. 1, the valence band maximum (VBM) of CsGeI3 is mainly contributed by the I-5p and Ge-4s orbitals, whereas the conduction band is predominantly derived from Ge-4p orbitals. The states of Cs atom are far from the Fermi level and do not contribute to any of the band edge states. From Fig. 2, it can be seen that CsGeI3 is a direct bandgap semiconductor at the symmetric point of Z with a value of 1.53 eV, which is in good agreement with previous experimental results.15–17 The optoelectronic properties significantly depend on carrier mobilities, which are closely related to the effective masses of carriers. We, therefore, calculate the effective masses of CsGeI3 by fitting the energy dispersions of VBM and CBM to parabolic functions along different k directions in the vicinity of the direct bandgap edges according to the following equation.40
| |
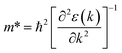 | (1) |
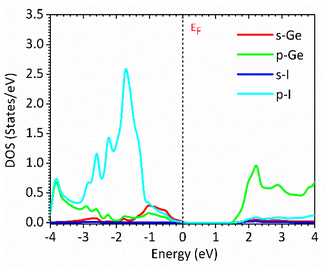 |
| | Fig. 1 Partial density of states (DOSs) of the rhombohedral phase of CsGeI3 based on FP-LAPW within TB-mBJ with the Fermi levels at 0 eV. | |
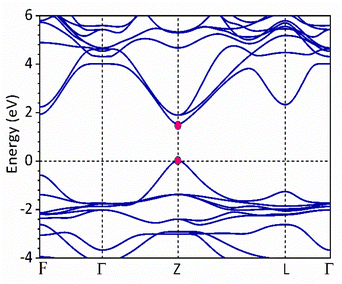 |
| | Fig. 2 The band structure of the rhombohedral phase of CsGeI3 along the high symmetry directions in the Brillouin zone based on FP-LAPW within TB-mBJ. | |
The k is the wave vector along different directions. The symbol ħ and ε(k) represent the Planck constant and eigenvalues of the energy band, respectively.
The calculated effective masses for holes in x, z directions are about 0.26, which shows weak anisotropy in hole effective masses. As for the electron effective masses, the anisotropy is obvious. The electron effective masses along [100] and [001] directions are 0.43 and 0.347, respectively. The calculated effective masses for both electrons and holes (∼0.25–0.4), indicate the good transport properties of the rhombohedral phase of CsGeI3.
Optical properties
The investigation of the optical properties of CsGeI3 provides useful information regarding its application in optoelectronic devices. The optical response of the medium is determined by its dielectric function ε(ω) = ε1(ω) + iε2(ω) at all photon energies. Since the imaginary part of the dielectric function ε2(ω), which is an important quantity for the optical transitions between energy bands, is directly related to the electronic band structure of a material, it can therefore be calculated using the information from wave functions and energies approximated from solutions of the Kohn–Sham equation:41| |
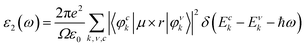 | (2) |
where ε0 is the vacuum dielectric constant, Ω is the volume, ν and c represents the valence and conduction bands, respectively, ħω is the energy of the incident photon, u is the vector defining the polarization of the incident electric field, u × r is the momentum operator, and φck and φνk are the wave functions of the conduction band and the valence band at the k point, respectively. In this equation, the integration is done in the first Brillouin zone. The Kramers–Kronig relations can be used to establish relationship between the dispersions of the real and imaginary parts of the dielectric function:| |
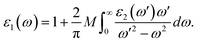 | (3) |
The elements of the dipole momentum Mcv(k) = φck|δ·∇|φνk are the elements of the direct transition matrix between the valence band φνk and the conduction band φck, in which δ is the potential vector describing the electric field. The absorption spectrum indicates the light-gathering ability of a material. The absorption coefficient is calculated by the following relation;42
| |
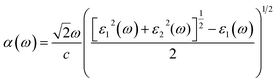 | (4) |
or, in term of energy (
E)
| |
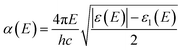 | (5) |
with
h is the Planck constant and
c is the speed of light.
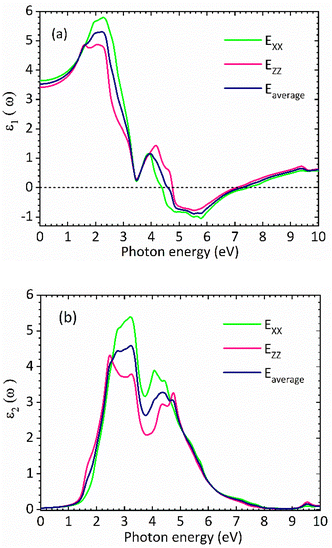
Fig. 3(a) and (b) show the real and the imaginary parts of the dielectric function spectra for rhombohedral phase of CsGeI3, respectively. The maximum value for the real part of dielectric function ε1 is achieved at around 2.27 eV. The higher value of ε1 shows a greater ability for the polarization of low incident photon energy. Moving towards higher incident photon energy, an inflection point is observed around 5.78 eV, where ε1 takes on negative values. Above 5.78 eV, its intensity increases from negative to positive values. The imaginary part of the dielectric function, ε2, is shown in Fig. 3(b). This component is related to the transitions between the valence and conduction bands, and therefore to the electronic structure of CsGeI3 and the absorption of the incident photons.
 |
| | Fig. 3 Calculated (a) real part and (b) imaginary part of the dielectric function of the rhombohedral phase of CsGeI3. | |
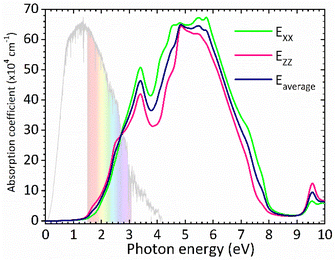
The optical band gap of CsGeI3 can then be estimated from ε2 to a value of 1.53 eV comparable to the electronic band gap energy obtained from the electronic structure. Above the optical band gap energy, a sharp rise in the intensity ε2 is observed, with two successive strongest peaks appearing at 3.22 eV and 4.07 eV, which mainly originated from the electron transitions between the Ge 4s valence band to the Ge 4p conduction band, as indicated by the density of states of CsGeI3 (Fig. 1). Fig. 4 shows the calculated absorption spectrum for rhombohedral phase of CsGeI3. The optical absorption records a strong onset of direct transitions at ∼2.9 eV, which can demonstrate that the rhombohedral phase of CsGeI3 shows a great sunlight absorption in the visible region.
 |
| | Fig. 4 Calculated absorption spectrum for rhombohedral phase of CsGeI3. | |
Spectroscopic limited maximum efficiency (SLME)
An effective way to evaluate the maximum efficiency of a photovoltaic cell using a single p–n junction is by using the Shockley–Queisser limit.43 The Shockley–Queisser limit is calculated by examining the amount of electrical energy that is extracted per photon of incoming sunlight. It offers a relationship between the bandgap of a material and its maximum efficiency. Yu and Zunger32 have recently extended the work of Shockley and Queisser by employing the Spectroscopic Limited Maximum Efficiency (SLME) and including the absorption spectrum and the absorber layer thickness in the efficiency assessment. The SLME has been successfully applied to a wide range of solar absorber materials, including perovskites,44–47 chalcogenides,48,49 and other materials.50–55 Theoretically, the maximum solar cell efficiency is defined as56,57| |
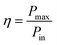 | (6) |
where Pmax is the maximum power density and Pin is the total incident power density from the solar spectrum. The maximum power density is derived using the J–V characteristic of the solar cell:| |
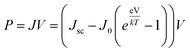 | (7) |
with J the total current density, V the potential over the absorber layer, k Boltzmann's constant, T the temperature of the device and e the elementary charge. The short circuit current density Jsc and the reverse saturation current density J0 are calculated from the absorbance A(E) of the material, as well as the AM1.5G solar spectrum Isun(E) and the black-body spectrum Ibb(E,T):| |
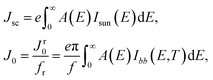 | (8) |
where Jr0 is the radiative recombination current density. The absorbance A(E) for an absorber layer of thickness L with a reflecting back surface is defined as:21
The absorption coefficient α(E) is given by eqn (5). The absorbance A(E) in eqn (9) increases with the thickness L because there is an increasing chance to be absorbed when light travels further inside the material. The fraction of radiative recombination fr is modeled using a Boltzmann factor:
| |
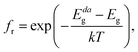 | (10) |
where
Eg and
Edag are respectively the fundamental and direct allowed band gaps.
The open-circuit voltage Voc which corresponds to the maximum voltage available from a solar cell, and this occurs under zero current density condition, is determined as follows,
| |
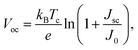 | (11) |
The fill factor (FF) is essentially a measure of the quality of the solar cell. It is calculated by comparing the maximum power that would be delivered from or to a device at both open circuit voltage and short circuit current combined.
| |
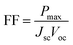 | (12) |
After we calculate the band gap and dielectric function for the rhombohedral phase of CsGeI3 compound, we have all the required information to calculate its SLME.
Because we find a direct allowed fundamental band gap for CsGeI3, we only have to consider cases where the non-radiative recombination is negligible (fr = 1, see eqn (10)).
In Fig. 5(a) we show the calculated J–V characteristic of the rhombohedral phase of CsGeI3. These results clearly show an increasing Jsc with absorber thickness and decreasing Voc (Fig. 5(b)). The total current density J remains close to Jsc up to a certain voltage Vm that maximizes the power density. The maximum solar cell efficiency η and the fill factor are plotted as a function of the film thickness in Fig. 5(c). We can see that for CsGeI3, the fill factor remains almost constant around the value of 0.89. The efficiency rises quickly for an increasing thickness. For an infinitely thick absorption layer the curve becomes a step function. This curve indicates that at a thickness of 70 μm or greater, the cell efficiency maintains its highest value ηmax of around 28.7% due to maximum absorption of light as evidenced from constant Jsc (Fig. 5(b)). This highlights the potential of the rhombohedral phase of CsGeI3 as absorber layers in thin-film solar cells.
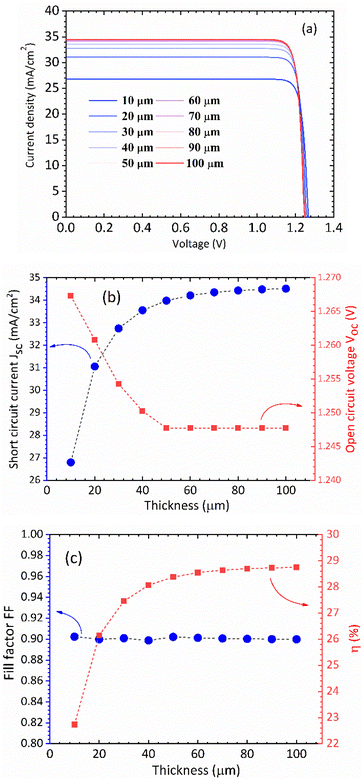 |
| | Fig. 5 (a) Calculated J–V characteristic as a function of absorber layer thickness of the rhombohedral phase of CsGeI3 at T = 300 K. Effect of absorber layer thickness on (b) Jsc and Voc, and (c) fill factor and power conversion efficiency. | |
We present the calculated efficiency values in Table 2, in order to compare our results with those of Yu and Zunger, all efficiencies were evaluated using thickness L = 50 μm. These results clearly show that the rhombohedral phase of CsGeI3 has a favourable optical gap for solar light absorption in which the absorber thickness of 600–700 nm is suitable. Therefore, there is no benefit in using thicker (>700 nm) films.
Table 2 Calculated solar cell parameters for CsGeI3, compared with other compounds from literature, all efficiencies were evaluated using thickness L = 50 μm
| Cells |
PCE (%) |
Voc (V) |
Jsc (mA cm−2) |
FF |
Eg (eV) |
| Ref. 56. Ref. 57. |
| CsGeI3 |
28.37 |
1.24 |
33.98 |
0.899 |
1.53 |
| Sia |
26.70 |
0.738 |
42.65 |
0.849 |
1.12 |
| GaAsa |
29.10 |
1.127 |
29.78 |
0.867 |
1.42 |
| PSCsa |
25.20 |
1.181 |
25.14 |
0.848 |
1.56 |
| AgGaSe2b |
27.00 |
— |
— |
— |
1.41 |
| CuGaSe2b |
27.80 |
— |
— |
— |
1.19 |
| CuGaTe2b |
28.90 |
— |
— |
— |
1.06 |
| AgGaTe2b |
28.90 |
— |
— |
— |
0.95 |
| CuInS2b |
27.90 |
— |
— |
— |
0.94 |
| CuInSe2b |
20.70 |
— |
— |
— |
0.58 |
Ferroelectric properties
The mechanism of ferroelectricity in CsGeI3 has not yet been described in detail. CsGeI3 is one of the all-inorganic metal halide perovskite materials in which the presence of Ge lone pairs could lead to lattice instabilities that trigger the breaking of inversion symmetry and allow the appearance of permanent electric dipoles. Hence, it shows a rhombohedral structure that is slightly deformed from the cubic perovskite structure along its diagonal direction. Therefore, symmetry breaking in the CsGeI3 ferroelectric phase (polar phase) is driven by zone-center lattice instability of the centrosymmetric (paraelectric, non-polar) phase, which shows collective displacement of Ge ions away from the GeI6 octahedral centers. The amplitude of the displacement is an important factor in determining the ferroelectric properties. Fig. 6 presents the symmetric double-well depth curve indicating the change of total energy as a function of the relative location of the Ge2+ ion within the halides (I) octahedral cage. This curve is a quantitative indicator of the energetic stability of the polar (ferroelectric) phase over the non-polar (paraelectric) phase with an energy barrier (ΔE) of 19.83 meV per atom. Similar representation has been reported by Chen et al.58 and Zhang et al.59 for the polar tetragonal BaTiO3. The low energy barrier of CsGeI3 may support the fast ferroelectric switching in experiments. The faster switching side states can be manipulated by applying an electric field in a specific direction. Further investigations are needed to confirm the fast ferroelectric switching of CsGeI3 in a way that makes it a viable candidate for low-power computing and electronics. In the absence of external applied electric field, ferroelectric materials exhibit spontaneous polarization that can be reversed by such a field. In the context of the modern theory of polarization, Berry phase calculations have been used to determine the magnitude of spontaneous polarization (Ps).60,61 The theoretical value of Ps in CsGeI3 is predicted to be around 15.82 μC cm−2, which is obtained from the value of polarization corresponding to the minimum of the double well potential. Our calculation result is smaller than the experimental measurement 20 μC cm−2.62 In general, the anomaly in measured polarization values can be attributed to the quality of sample, sample orientation during measurement and defect chemistry. In addition, the difference between the two results may possibly be explained by the fact that our ab initio calculations were performed at 0 K whereas the experimental data were obtained at room temperature.
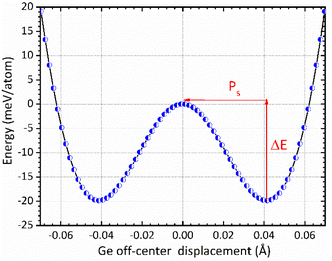 |
| | Fig. 6 The change of total energy as a function of the relative location of the Ge2+ ion within the halides (I) octahedral cage in the rhombohedral phase of CsGeI3. The centrosymmetric phase is taken as energy reference. | |
Nonlinear photocurrent (bulk photovoltaic effect)
Recent studies have shown that ferroelectric materials exhibit promising features for photovoltaic devices. However, the primary mechanism proposed to explain experimental observations in the literature, is the bulk photovoltaic effect (BPVE), which is associated to the ferroelectricity of material that lack inversion symmetry, and it appears to be independent of any internal fields within the material. In addition, the voltages that the material can sustain exceed conventional limits (i.e., those imposed by the material's bandgap).63–65 In this section, we discuss the bulk photovoltaic effect (BPVE) and put more emphasis on the so-called shift current mechanism, which offers some advantages over traditional p–n junction-based solar cells. Von Baltz and Kraut66 presented the shift current theory as an explanation for the BPVE in BaTiO3, and it was later developed within the framework of Green's functions67 and nonlinear optics.68 Young and Rappe reformulated the shift current theory and have derived an adaptive formula for efficient first-principles calculation, and they offered the first comparison of experimental BPVE data with shift current theory.69 A more useful formulation for shift current can be found using response functions. If we define Eb(ω) as an electric field with frequency ω this is linearly polarized in the b direction, the shift current takes the form| |
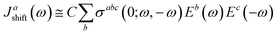 | (13) |
where a,b,c are Cartesian indices, and σabc is a third-rank tensor giving current density J as a response to monochromatic electromagnetic field E, which in a D-dimension is given by| |
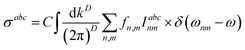 | (14) |
where 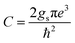 and gs = 2 accounts for spin degeneracy. n,m are the band indices, fnm = fn − fm is the Fermi–Dirac occupations number of bands n and m, and ħωnm = Em − En is the band energy difference. The integral is over the first Brillouin zone (BZ).
and gs = 2 accounts for spin degeneracy. n,m are the band indices, fnm = fn − fm is the Fermi–Dirac occupations number of bands n and m, and ħωnm = Em − En is the band energy difference. The integral is over the first Brillouin zone (BZ).| | |
Iabcnm = rbmnrcnm;aRamn
| (15) |
The Iabcnm expression is composed of the effective position matrix elements rbmn and the so-called “shift vector” Ramn:
| |
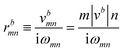 | (16) |
| |
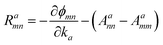 | (17) |
Here,
vbmn are velocity matrix elements,
Aamm are Berry connections for the band
m, and
ϕmn is the phase of the momentum matrix element between bands
m and
n.
rbnm are the inter-band matrix elements of the position operator called inter-band Berry connections,
70 which are defined as:
| |
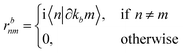 | (18) |
and
rcnm;a =
∂karcnm − i(
ξann −
ξamm)
rcnm are generalized derivatives of the berry connections. In the last expression
ξann = i〈
n∣∂
kan〉 is the diagonal berry connection for the band
n. These berry connections are closely related to Berry phases. The calculations for CsGeI
3 were performed using its optimized geometry in the ferroelectric phase, which belongs to a polar space group of
R3
m with point group 3
m that only allows eight nonzero tensor elements for its BPVE responses, which can be obtained from first principles calculations using the shift current theory. The wave functions and eigenvalues were generated using the plane-wave density functional theory (DFT) package FP-LAPW in the TB-mBJ approximation of the exchange correlation functional. Due to the symmetry of CsGeI
3, only four independents
σxzX =
σyzY,
σxxY = −
σyyY =
σxyX,
σxxZ =
σyyZ and,
σzzZ tensorial components of
σabc(0;
ω;−
ω) are nonzero. Where the uppercase letter represents the direction of shift current response and the first two lower case letters represent light polarization. For a monochromatic light linearly polarized along a particular direction, we calculate longitudinal (
σzzZ,
σyyY) and transversal (
σxzX,
σxxZ) tensorial components of
σabc(0;
ω;−
ω) of the shift current responses. The longitudinal component
σzzZ (
σyyY) represents the shift current response along the
Z(
Y) axis,
i.e., along the direction of out-of-plane (in-plane) polarization due to
zz (
yy) polarized light, respectively. Whereas the transversal component
σxzX (
σxxZ) represents the shift current response along the
X(
Z) axis due to
xz (
xx) polarized light, respectively.
In Fig. 7 we plot both the longitudinal and transversal shift current responses as a function of photon energy for the CsGeI3 compound. A scissor correction was applied to the calculated spectra in Fig. 7 to eliminate the underestimation of the gap and to facilitate its comparison with the electronic band structure. The spectral quantities were rigidly shifted by 0.362 eV. Accordingly, all shift current responses are zero below the bandgap, the dominating current responses are σzzZ and σyyZ, and they all attain a maximum absolute value of about 40 μA V−2 above the band edge within the photon energy of 2.9 eV in the visible spectrum, which is highly desired for efficient solar energy conversion. Interestingly, the reported shift current in CsGeI3 is comparable to the most studied ferroelectric perovskite oxides such as BaTiO3 (30 μA V−2) and PbTiO3 (50 μA V−2).69 On the basis of the shift current result, we can control the direction and the magnitude of the shift current in CsGeI3 by tuning the applied light.
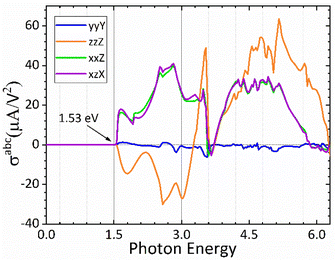 |
| | Fig. 7 Calculated shift current tensor elements for the rhombohedral phase of CsGeI3. | |
Conclusions
First principles-based density functional theory (DFT) calculations reveal that CsGeI3 in its rhombohedral structure (ferroelectric phase) exhibits excellent optoelectronic properties. Specifically, the calculated results indicate that the valence band maximum (VBM) of CsGeI3 is mainly contributed by the I-5p and Ge-4s orbitals, whereas the conduction band is predominantly derived from Ge-4p orbitals. CsGeI3 exhibits a direct bandgap semiconductor with a value of 1.53 eV. The ferroelectric properties were therefore investigated. CsGeI3 has a higher theoretical ferroelectric polarization strength of 15.82 μC cm−2 related to its switching energy barrier of 19.83 meV per atom. The performance of CsGeI3 in photoconversion devices is analysed. Using the spectroscopic limited maximum efficiency (SLME) model, the best efficiencies of over 28% is achieved for the rhombohedral structure of CsGeI3, which demonstrates that lead-free germanium iodide perovskite is very good candidate for highly efficient solar energy conversion. We also apply the Wannier interpolation method to evaluate photocurrent generation in CsGeI3 through the bulk photovoltaic effect (BPVE). Strong absorption of visible light at ∼2.9 eV and a large shift current bulk photovoltaic effect of ∼40 μA V−2 is obtained in the visible region. Our findings highlight the potential of the ferroelectric structure of germanium iodide perovskite for developing third-generation solar cells with high efficiency beyond the fundamental S–Q limit.
Author contributions
The authors confirm contribution to the paper as follows: conceptualization: N. C. and R. L.; data curation: N. C. and Z. B.; investigation: M. S. and N. C.; visualisation: Z. B.; writing – original draft: M. S., S. M. E. and N. C. All authors reviewed the results and approved the final version of the manuscript.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
This research work was supported by the DGRSDT (MESRS), Algeria, under PRFU program.
Notes and references
- J. M. Frost, K. T. Butler, F. Brivio, C. H. Hendon, M. Van Schilfgaarde and A. Walsh, Nano Lett., 2014, 14(5), 2584–2590 CrossRef CAS PubMed.
- S. Liu, F. Zheng, N. Z. Koocher, H. Takenaka, F. Wang and A. M. Rappe, J. Phys. Chem. Lett., 2015, 6(4), 693–699 CrossRef CAS PubMed.
- J. Wei, Y. Zhao, H. Li, G. Li, J. Pan, D. Xu, Q. Zhao and D. Yu, J. Phys. Chem. Lett., 2014, 5(21), 3937–3945 CrossRef CAS PubMed.
- Y. Zhang, W. Jie, P. Chen, W. Liu and J. Hao, Adv. Mater., 2018, 30(34), 1707007 CrossRef PubMed.
- M. Ikram, R. Murray, M. Imran, S. Ali and S. I. Shah, Mater. Res. Bull., 2016, 75, 35–40 CrossRef CAS.
- M. Imran, M. Ikram, A. Shahzadi, S. Dilpazir, H. Khan, I. Shahzadi, S. A. Yusaf, S. Ali, J. Geng and Y. Huang, RSC Adv., 2018, 8(32), 18051 RSC.
- M. Ikram, R. Murray, A. Hussain, S. Ali and S. I. Shah, Mater. Sci. Eng., C, 2014, 189, 64–69 CrossRef CAS.
- D. Xiao, M. C. Chang and Q. Niu, Rev. Mod. Phys., 2010, 82(3), 1959 CrossRef CAS.
- Y. Zhang, T. Holder, H. Ishizuka, F. de Juan, N. Nagaosa, C. Felser and B. Yan, Nat. Commun., 2019, 10(1), 1–7 CrossRef PubMed.
- M. Nakamura, S. Horiuchi, F. Kagawa, N. Ogawa, T. Kurumaji, Y. Tokura and M. Kawasaki, Nat. Commun., 2017, 8(1), 1–6 CrossRef CAS PubMed.
- L. Qiao, W. H. Fang and R. Long, J. Phys. Chem. Lett., 2019, 10(22), 7237–7244 CrossRef CAS PubMed.
- C. Wehrenfennig, G. E. Eperon, M. B. Johnston, H. J. Snaith and L. M. Herz, Adv. Mater., 2014, 26, 1584–1589 CrossRef CAS PubMed.
- Y. Rakita, O. Bar-Elli, E. Meirzadeh, H. Kaslasi, Y. Peleg, G. Hodes, I. Lubomirsky, D. Oron, D. Ehre and D. Cahen, Proc. Natl. Acad. Sci. U. S. A., 2017, 114(28), E5504–E5512 CrossRef CAS PubMed.
- E. Strelcov, Q. Dong, T. Li, J. Chae, Y. Shao, Y. Deng, A. Gruverman, J. Huang and A. Centrone, Sci. Adv., 2017, 3(4), e1602165 CrossRef PubMed.
- T. Krishnamoorthy, H. Ding, C. Yan, W. L. Leong, T. Baikie, Z. Zhang, M. Sherburne, S. Li, M. Asta, N. Mathews and S. G. Mhaisalkar, J. Mater. Chem. A, 2015, 3(47), 23829–23832 RSC.
- C. C. Stoumpos, L. Frazer, D. J. Clark, Y. S. Kim, S. H. Rhim, A. J. Freeman, J. B. Ketterson, J. I. Jang and M. G. Kanatzidis, J. Am. Chem. Soc., 2015, 137(21), 6804–6819 CrossRef CAS PubMed.
- W. Ming, H. Shi and M. H. Du, J. Mater.
Chem. A, 2016, 4(36), 13852–13858 RSC.
- A. Raj, M. Kumar, H. Bherwani, A. Gupta and A. Anshul, J. Vac. Sci. Technol., B: Nanotechnol. Microelectron.: Mater., Process., Meas., Phenom., 2021, 39(1), 012401 CAS.
- J. Qian, B. Xu and W. Tian, Org. Electron., 2016, 37, 61–73 CrossRef CAS.
- L. J. Chen, RSC Adv., 2018, 8(33), 18396–18399 RSC.
- P. Blaha, K. Schwarz, G. K. Madsen, D. Kvasnicka, J. Luitz, WIEN2k: An augmented plane wave+ local orbitals program for calculating crystal properties, 2001, vol. 60 Search PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77(18), 3865 CrossRef CAS PubMed.
- F. Tran and P. Blaha, Phys. Rev. Lett., 2009, 102(22), 226401 CrossRef PubMed.
- D. J. Singh, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82(20), 205102 CrossRef.
- D. Koller, F. Tran and P. Blaha, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83(19), 195134 CrossRef.
- D. J. Singh, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82(15), 155145 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77(18), 3865 CrossRef CAS PubMed.
- S. J. Ahmed, J. Kivinen, B. Zaporzan, L. Curiel, S. Pichardo and O. Rubel, Comput. Phys. Commun., 2013, 184(3), 647–651 CrossRef CAS.
- R. D. King-Smith and D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47(3), 1651 CrossRef CAS PubMed.
- R. Resta and D. Vanderbilt, Theory of polarization: a modern approach, Physics of Ferroelectrics, Springer, Berlin, Heidelberg, 2007, pp. 31–68 Search PubMed.
- N. Marzari, A. A. Mostofi, J. R. Yates, I. Souza and D. Vanderbilt, Rev. Mod. Phys., 2012, 84(4), 1419 CrossRef CAS.
- L. Yu and A. Zunger, Phys. Rev. Lett., 2012, 108(6), 068701 CrossRef PubMed.
- L. H. Wong, A. Zakutayev, J. D. Major, X. Hao, A. Walsh, T. K. Todorov and E. Saucedo, J. Phys.: Energy, 2019, 1(3), 032001 CAS.
- X. G. Zhao, D. Yang, Y. Sun, T. Li, L. Zhang, L. Yu and A. Zunger, J. Am. Chem. Soc., 2017, 139(19), 6718–6725 CrossRef CAS PubMed.
- V. Tuyikeze, F. Fraija, L. H. Omari, S. Tariq, I. Abdelrhafor, M. Bouhbou, M. Abid and E. K. Hlil, Mater. Sci. Eng., C, 2022, 282, 115794 CrossRef CAS.
- C. Lan, S. Yang, Y. Wang and S. Zhao, Chem. Phys. Lett., 2022, 140049 CrossRef CAS.
- Y. S. Kim, M. Marsman, G. Kresse, F. Tran and P. Blaha, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82(20), 205212 CrossRef.
- L. Kang, D. M. Ramo, Z. Lin, P. D. Bristowe, J. Qin and C. Chen, J. Mater. Chem. C, 2013, 1(44), 7363–7370 RSC.
- L. Y. Huang and W. R. Lambrecht, Phys. Rev. B, 2016, 93(19), 195211 CrossRef.
- M. O. Ali, Elementary solid-state physics: principles and applications, Addison-Wesley Publishing Company, 1993 Search PubMed.
- C. Chen, T. Sasaki, R. Li, Y. Wu, Z. Lin, Y. Mori, Z. Hu, J. Wang, G. Aka, M. Yoshimura and Y. Kaneda, Nonlinear optical borate crystals: Principals and applications, John Wiley and Sons, 2012 Search PubMed.
- S. Saha, T. P. Sinha and A. Mookerjee, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62(13), 8828 CrossRef CAS.
- W. Shockley and H. J. Queisser, J. Appl. Phys., 1961, 32(3), 510–519 CrossRef CAS.
- W. J. Yin, T. Shi and Y. Yan, Adv. Mater., 2014, 26(27), 4653–4658 CrossRef CAS PubMed.
- W. J. Yin, J. H. Yang, J. Kang, Y. Yan and S. H. Wei, J. Mater. Chem. A, 2015, 3(17), 8926–8942 RSC.
- W. J. Yin, T. Shi and Y. Yan, J. Phys. Chem. C, 2015, 119(10), 5253–5264 CrossRef CAS.
- W. Meng, B. Saparov, F. Hong, J. Wang, D. B. Mitzi and Y. Yan, Chem. Mater., 2016, 28(3), 821–829 CrossRef CAS.
- F. Hong, W. Lin, W. Meng and Y. Yan, Phys. Chem. Chem. Phys., 2016, 18(6), 4828–4834 RSC.
- N. Sarmadian, R. Saniz, B. Partoens and D. Lamoen, J. Appl. Phys., 2016, 120(8), 085707 CrossRef.
- I. H. Lee, J. Lee, Y. J. Oh, S. Kim and K. J. Chang, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90(11), 115209 CrossRef.
- Y. J. Oh, I. H. Lee, S. Kim, J. Lee and K. J. Chang, Sci. Rep., 2015, 5(1), 1–11 Search PubMed.
- L. Yu, R. S. Kokenyesi, D. A. Keszler and A. Zunger, Adv. Energy Mater., 2013, 3(1), 43–48 CrossRef CAS.
- T. Yokoyama, F. Oba, A. Seko, H. Hayashi, Y. Nose and I. Tanaka, Appl. Phys. Express, 2013, 6(6), 061201 CrossRef.
- J. Heo, R. Ravichandran, C. F. Reidy, J. Tate, J. F. Wager and D. A. Keszler, Adv. Energy Mater., 2015, 5(7), 1401506 CrossRef.
- X. Huang, T. R. Paudel, S. Dong and E. Y. Tsymbal, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92(12), 125201 CrossRef.
- M. A. Green and K. Emery, Solar cell efficiency tables, Prog. Photovoltaics, 1993, 1(1), 25–29 CAS.
- M. Bercx, N. Sarmadian, R. Saniz, B. Partoens and D. Lamoen, Phys. Chem. Chem. Phys., 2016, 18(30), 20542–20549 RSC.
- Z. X. Chen, Y. Chen and Y. S. Jiang, J. Phys. Chem. B, 2001, 105(24), 5766–5771 CrossRef CAS.
- Y. Zhang, J. Sun, J. P. Perdew and X. Wu, Phys. Rev. B, 2017, 96(3), 035143 CrossRef.
- R. D. King-Smith and D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47(3), 1651 CrossRef CAS PubMed.
- N. A. Spaldin, J. Solid State Chem., 2012, 195, 2–10 CrossRef CAS.
- Y. Zhang, E. Parsonnet, A. Fernandez, S. M. Griffin, H. Huyan, C. K. Lin, T. Lei, J. Jin, E. S. Barnard, A. Raja and P. Behera, Sci. Adv., 2022, 8(6), 5881 CrossRef PubMed.
- D. H. Auston, A. M. Glass and A. A. Ballman, Phys. Rev. Lett., 1972, 28(14), 897 CrossRef CAS.
- A. M. Glass, D. Von der Linde and T. J. Negran, Appl. Phys. Lett., 1974, 25(4), 233–235 CrossRef CAS.
- V. M. Fridkin, Crystallogr. Rep., 2001, 46(4), 654–658 CrossRef.
- W. Kraut and R. von Baltz, Phys. Rev. B: Condens. Matter Mater. Phys., 1979, 19(3), 1548 CrossRef CAS.
- P. Král, J. Phys.: Condens. Matter, 2000, 12(22), 4851 CrossRef.
- J. E. Sipe and A. I. Shkrebtii, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 61(8), 5337 CrossRef CAS.
- S. M. Young and A. M. Rappe, Phys. Rev. Lett., 2012, 109(11), 116601 CrossRef PubMed.
- G. Pizzi, V. Vitale, R. Arita, S. Blügel, F. Freimuth, G. Géranton, M. Gibertini, D. Gresch, C. Johnson, T. Koretsune and J. Ibañez-Azpiroz, J. Phys.: Condens. Matter, 2020, 32(16), 165902 CrossRef CAS PubMed.
|
| This journal is © The Royal Society of Chemistry 2023 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a,
Z. Benhalimaa,
R. Larbia and
Sayed M. Eldinb
*a,
Z. Benhalimaa,
R. Larbia and
Sayed M. Eldinb
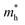 and
and 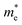 ) along different directions for CsGeI3 (m0 is the electron rest mass). The VBM and the CBM are both located at the Z point
) along different directions for CsGeI3 (m0 is the electron rest mass). The VBM and the CBM are both located at the Z point
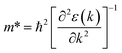


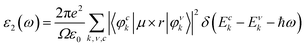
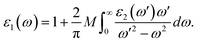
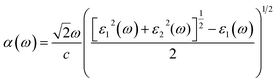
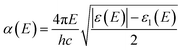

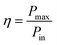
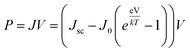
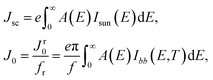
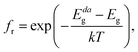
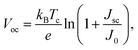
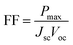
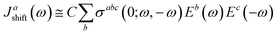
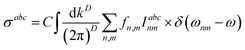
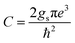 and gs = 2 accounts for spin degeneracy. n,m are the band indices, fnm = fn − fm is the Fermi–Dirac occupations number of bands n and m, and ħωnm = Em − En is the band energy difference. The integral is over the first Brillouin zone (BZ).
and gs = 2 accounts for spin degeneracy. n,m are the band indices, fnm = fn − fm is the Fermi–Dirac occupations number of bands n and m, and ħωnm = Em − En is the band energy difference. The integral is over the first Brillouin zone (BZ).