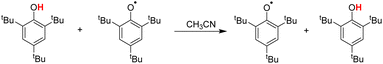Open Access Article
Open Access ArticleQuantitative evaluation of the actual hydrogen atom donating activities of O–H bonds in phenols: structure–activity relationship†
Yan-Hua Fu *a,
Yanwei Zhanga,
Fang Wanga,
Ling Zhaoa,
Guang-Bin Shen
*a,
Yanwei Zhanga,
Fang Wanga,
Ling Zhaoa,
Guang-Bin Shen b and
Xiao-Qing Zhuc
b and
Xiao-Qing Zhuc
aCollege of Chemistry and Environmental Engineering, Anyang Institute of Technology, Anyang, Henan 455000, China. E-mail: 20180031@ayit.edu.cn
bSchool of Medical Engineering, Jining Medical University, Jining, Shandong 272000, P. R. China
cDepartment of Chemistry, Nankai University, Tianjin, 300071, China
First published on 23rd January 2023
Abstract
The H-donating activity of phenol and the H-abstraction activity of phenol radicals have been extensively studied. In this article, the second-order rate constants of 25 hydrogen atom transfer (HAT) reactions between phenols and PINO and DPPH radicals in acetonitrile at 298 K were studied. Thermo-kinetic parameters ΔG≠o(XH) were obtained using a kinetic equation [ΔG≠XH/Y = ΔG≠o(XH) + ΔG≠o(Y)]. Bond dissociation free energies ΔGo(XH) were calculated by the iBonD HM method, whose details are available at https://pka.luoszgroup.com/bde_prediction. Intrinsic resistance energies ΔG≠XH/X and ΔG≠o(X) were determined as ΔG≠o(XH) and ΔGo(XH) were available. ΔGo(XH), ΔG≠XH/X, ΔG≠o(XH) and ΔG≠o(X) were used to assess the H-donating abilities of the studied phenols and the H-abstraction abilities of phenol radicals in thermodynamics, kinetics and actual HAT reactions. The effect of structures on these four parameters was discussed. The reliabilities of ΔG≠o(XH) and ΔG≠o(X) were examined. The difference between the method of determining ΔG≠XH/X mentioned in this study and the dynamic nuclear magnetic method mentioned in the literature was studied. Via this study, not only ΔGo(XH), ΔG≠XH/X, ΔG≠o(XH) and ΔG≠o(X) of phenols could be quantitatively evaluated, but also the structure–activity relationship of phenols is clearly demonstrated. Moreover, it lays the foundation for designing and synthesizing more antioxidants and radicals.
Introduction
Hydrogen atom transfer (HAT) reactions (eqn (1)) play important roles in a variety of chemical and biological processes and are therefore actively investigated.1–3 Research on HAT from a wide variety of substrates, XH (1,4-dihydropyridine,4,5 alkanes,6 amines and amides,7,8 and phenols9,10), by a number of radicals, Y (N-oxyl radicals,10 C-oxyl radicals,11 and 2,2-diphenyl-1-picrylhydrazyl (DPPH˙)12), has drawn intense attention from chemists. In particular, phenols can not only act as hydrogen atom donors (H-donors) in HAT reactions with free radicals9 but also act as hydrogen atom acceptors (H-acceptors) to oxidize many antioxidants13 such as 5,6-isopropylidene ascorbate (iAscH−).14| X–H + Y → X + Y–H | (1) |
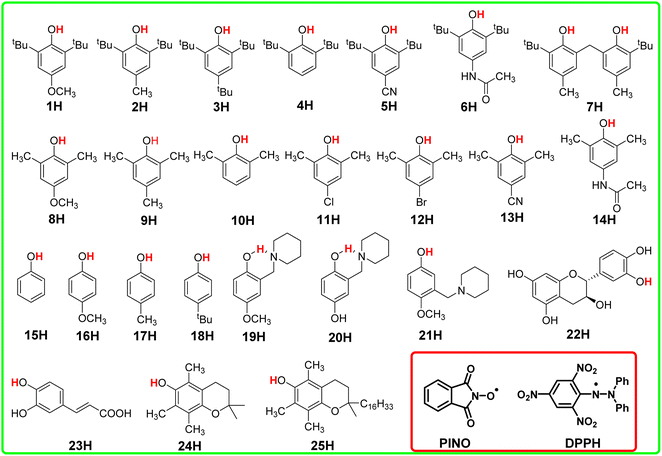
In this article, the HAT reaction between 25 phenols XH and phthalimide-N-oxyl radical (PINO˙) and DPPH˙ was researched; parent structures and marks of phenols and radicals examined in this work are shown in Scheme 1. The time-resolved kinetic studies in CH3CN of the HAT reactions of activated phenols including natural phenols (2,6-dimethyl-, 2,6-di-tert-butyl-4-substituted15,16 and 4-substituted phenols)17 (1H–18H), hydrogen-bonded phenols18 (19H–23H) including (+)-catechin (22H) and caffeic acid (23H), 2,2,5,7,8-pentamethylchroman-6-ol (PMC, 24H)16 and α-tocopherol (α-TocOH, 25H)19 with radicals were carried out.
In previous works,8,20–24 four physical parameters of H-donor XH, bond dissociation free energy ΔGo(XH), kinetic intrinsic resistance energy ΔG≠XH/X, thermo-kinetic parameter ΔG≠o(XH) and ΔG≠o(X), have been used to evaluate the H-donating and H-abstraction activities of XH and the corresponding radical X in thermodynamics, kinetics and actual HAT reactions, respectively. ΔGo(XH) is the thermodynamic factor and usually used to assess the potential H-donating capacity of XH and H-abstraction capacity of X. ΔG≠XH/X is the activation free energy of the self-exchange HAT reaction for XH (XH + X → X + XH). It is the kinetic resistance of the HAT reaction as the thermodynamic driving force is zero, which means the kinetic intrinsic resistance barrier of XH in HAT reaction. It is also called intrinsic resistance energy. The thermo-kinetic parameter ΔG≠o is proposed by a new kinetic model in previous works25,26 and consists of both the thermodynamic force and kinetic intrinsic barrier and can be used not only to describe the actual H-donating ability of XH and the H-abstraction ability of X in a chemical reaction during a certain reaction time but also to predict the rate of the HAT reaction (eqn (1)) by kinetic eqn (2). The definitions of ΔG≠o are listed in eqn (3) and (4). In this work, ΔGo(XH), ΔG≠XH/X, ΔG≠o(XH) and ΔG≠o(X) were investigated to study the H-donating abilities of phenols XH in Scheme 1 and the H-abstraction abilities of the corresponding phenol radicals X.
| ΔG≠XH/Y = ΔG≠o(XH) + ΔG≠o(Y) | (2) |
| ΔG≠o(XH) ≡ 1/2[ΔG≠XH/X + ΔGo(XH)] | (3) |
| ΔG≠o(Y) ≡ 1/2[ΔG≠YH/Y − ΔGo(YH)] | (4) |
Results and discussion
Determination of the “ΔGo(XH), ΔG≠XH/X, ΔG≠o(XH), and ΔG≠o(X)” values of phenols XH and phenol radicals X
The kinetic studies of the HAT reactions from O–H bonds of phenols to the PINO and DPPH radicals are listed in ESI.†15–19,27 The second-order rate constants k2 and activation free energies ΔG≠XH/Y of HAT reactions, which were obtained using the Eyring equation [k2 = (kBT/h)exp(−ΔG≠/RT)], are listed in Table S1.† As the thermo-kinetic parameters of the PINO radical [ΔG≠o(PINO) = −34.94 kcal mol−1] and DPPH radical [ΔG≠o(DPPH) = −29.67 kcal mol−1] were already available in our previous work,22 the thermo-kinetic parameters of phenols ΔG≠o(XH) = ΔG≠XH/Y − ΔG≠o(Y) can be determined using eqn (2). According to the definition of ΔG≠o(XH), as long as the bond dissociation free energies ΔGo(XH) of XH are available, the intrinsic resistance energies ΔG≠XH/X can be obtained by eqn (3). In this work, the bond dissociation energies (BDE) of O–H bonds of phenols in acetonitrile were calculated by the iBonD HM method developed by Luo and Zhang in 2020, whose details are available at https://pka.luoszgroup.com/bde_prediction.28,29 It is a holistic BDE prediction model (HM) based on the iBonD experimental dataset.30 Many methods such as quantum chemistry (QC), molecular dynamics (MD), and Monte Carlo (MC) simulation methods reported in the literature for the theoretical calculation of BDE were used to calculate the reaction sites and hydrogen dissociation energy of HTPB propellant antioxidants.31 The iBonD HM model has provided so far the best accuracy in prediction non-aqueous BDE and is equally applied for aqueous and micro-BDE prediction. ΔGo(XH) can be obtained by subtracting 4.9 kcal mol−1 from the BDE values.32 Subsequently, ΔG≠XH/X can be obtained using eqn (3). At the same time, ΔG≠o(X) of phenol radicals can be determined as long as ΔG≠XH/X and ΔGo(XH) of XH are available according to eqn (4). These four physical parameters of the studied phenols and phenol radicals are listed in Table 1.| XH | Structure | kcal mol−1 | |||
|---|---|---|---|---|---|
| ΔGo(XH)a | ΔG≠XH/Xb | ΔG≠o(XH)c | ΔG≠o(X)d | ||
| a ΔGo(XH) values are obtained by the iBonD HM method in this work.b ΔG≠XH/X values are derived from eqn (3).c ΔG≠o(XH) values are derived from eqn (2).d ΔG≠o(X) values are derived from eqn (4). | |||||
| 1H | 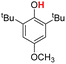 |
72.70 | 17.88 | 45.29 | −27.41 |
| 2H | 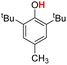 |
75.30 | 18.25 | 46.78 | −28.52 |
| 3H | 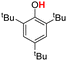 |
76.70 | 18.03 | 47.37 | −29.33 |
| 4H | 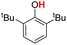 |
78.00 | 18.11 | 48.05 | −29.95 |
| 5H | 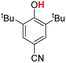 |
79.50 | 18.28 | 48.89 | −30.61 |
| 6H | 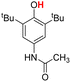 |
73.30 | 19.04 | 46.17 | −27.13 |
| 7H | 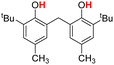 |
76.50 | 6.34 | 41.42 | −35.08 |
| 8H | 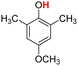 |
73.10 | 13.31 | 43.20 | −29.90 |
| 9H | 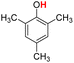 |
77.20 | 12.67 | 44.94 | −32.26 |
| 10H | 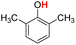 |
79.50 | 12.98 | 46.24 | −33.26 |
| 11H | 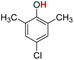 |
79.20 | 17.94 | 48.57 | −30.63 |
| 12H | 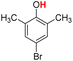 |
79.00 | 14.04 | 46.52 | −32.48 |
| 13H | 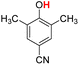 |
79.60 | 19.97 | 49.79 | −29.81 |
| 14H | 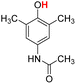 |
79.40 | 7.97 | 43.68 | −35.72 |
| 15H | 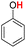 |
81.90 | 17.03 | 49.46 | −32.44 |
| 16H |  |
78.70 | 13.62 | 46.16 | −32.54 |
| 17H |  |
83.00 | 14.49 | 48.74 | −34.26 |
| 18H |  |
81.10 | 17.14 | 49.12 | −31.98 |
| 19H | 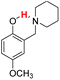 |
75.60 | 10.23 | 42.92 | −32.68 |
| 20H | 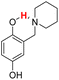 |
76.20 | 8.84 | 42.52 | −33.68 |
| 21H | 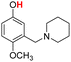 |
75.90 | 11.66 | 43.78 | −32.12 |
| 22H | 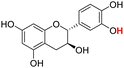 |
76.60 | 14.32 | 45.46 | −31.14 |
| 23H | 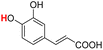 |
75.20 | 16.17 | 45.68 | −29.52 |
| 24H | 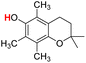 |
72.70 | 9.17 | 40.93 | −31.77 |
| 25H | 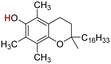 |
74.30 | 12.59 | 43.45 | −30.85 |
Potential H-donating capacities of phenols ΔGo(XH)
As well known, the bond dissociation free energies ΔGo(XH) of O–H bonds in phenols are the thermodynamics parameters, and can be used to assess the potential H-donating capacities of O–H bonds with different structures. The bigger the ΔGo(XH) value is, the weaker the potential H-donating capacity of XH is. In order to discover the relationship of ΔGo(XH) on the structures of XH, the direct vision dependence of ΔGo(XH) on the structures of XH is shown in Scheme 2. From Scheme 2, it is clear that the ΔGo(XH) values of these phenols in CH3CN at 298 K range from 72.70 kcal mol−1 for PMC (24H) and 2,6-di-tert-butyl-4-methoxyphenol (1H) to 83.00 kcal mol−1 for 2-methylphenol (17H), and the structures of XH have great effect on the ΔGo(XH) values.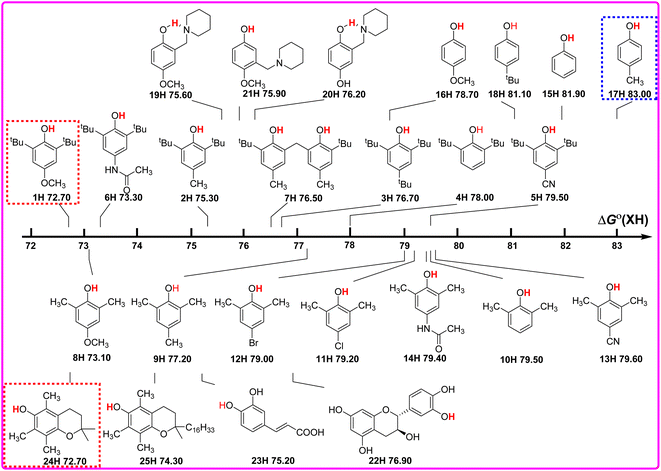 | ||
| Scheme 2 Visual comparison of ΔGo(XH) among the 25 phenols of O–H bonds in CH3CN at 298 K, the unit is kcal mol−1. | ||
For 2,6-di-tert-butylphenol series (1H–7H), 2,6-di-methylphenol series (8H–14H) and 4-substituted phenols (15H–18H), combined with the electronic effect of substituents on ΔGo(XH), the order of ΔGo(XH) of three types of phenols is 2,6-di-tert-butylphenol series > 2,6-di-methylphenol series > 4-substituted phenols. In the same series, for example, 2,6-di-tert-butylphenol series (1H–7H), with the different electronic effects of substituents at position 4, the ΔGo(XH) values of O–H bonds increase from the electron-donating groups to the electron-withdrawing groups (OCH3 > CH3CONH > CH3 > tBu > H > CN), and the H-donating capacities decrease gradually. In order to obtain the electronic effects of the substituents at position 4, the changes in bond dissociation free energy ΔΔGo between H-substituted phenols (4H, 10H and 15H) and other substituents in the 2,6-di-tert-butylphenol series, 2,6-di-methylphenol series and 4-substituted phenols respectively, are compared in Table 2. As can be seen from Table 2, in these three different phenol series, the ΔΔGo values caused by the electronic effect of the substituent at position 4 are not the same. Therefore, the electronic effect of the substituent at position 4 of phenol cannot be obtained simply by comparing the changes in ΔGo(XH). Since ΔGo(XH) represents the homolytic bond dissociation free energy of the O–H bond in phenol, the electronic effects of substituent at position 4 on ΔGo(XH) of different phenol series are not uniform.
| –R | ΔΔGoa (kcal mol−1) | ||
|---|---|---|---|
a ΔΔGo values are given by ΔGo(R![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) H) minus ΔGo(R).b ΔGo(XH) determined by the iBonD HM method in this work are listed in Table S2. H) minus ΔGo(R).b ΔGo(XH) determined by the iBonD HM method in this work are listed in Table S2. |
|||
| OCH3 | 5.30 | 6.40 | 3.20 |
| CH3CONH | 4.70 | 0.10 | 1.00b |
| CH3 | 2.70 | 2.30 | −1.10 |
| tBu | 1.30 | 0.90b | 0.80 |
| H | 0.00 | 0.00 | 0.00 |
| Cl | 0.50b | 0.30 | −3.50b |
| Br | 1.30b | 0.50 | −1.80b |
| CN | −1.50 | −0.10 | −5.90b |
Similarly, by comparing the two series of 2,6-disubstituted-4-methoxyphenol and 2,6-disubstituted-4-methylphenol, it can be seen that the ΔΔGo values obtained by the substitution of positions 2 and 6 with CH3 and tBu are not the same in these two series. For different structures of 2,6-disubstituted phenols, the ΔΔGo values caused by the substitution of position 4 from CH3 to OCH3 are also different, as shown in Scheme 3. When there are groups in the o-position of phenol that can form intramolecular hydrogen bonds with the phenolic hydroxyl group, the ΔGo(XH) values decrease and are concentrated between 75–77 kcal mol−1, such as 19H–20H and 22H–23H.
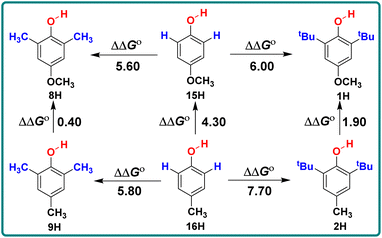 | ||
| Scheme 3 Energy changes ΔΔGo for 2,6-disubstituted-4-methoxyphenol series and 2,6-disubstituted-4-methylphenol in CH3CN at 298 K, the unit is kcal mol−1. | ||
Kinetic H-donating abilities of phenols ΔG≠XH/X
The intrinsic resistance energies ΔG≠XH/X of O–H bonds in phenols are the kinetic parameters and used to characterize the kinetic resistance caused by the steric effect of the compound itself, which can generally be used to evaluate the kinetic H-donating abilities of O–H bonds with different structures. The bigger the ΔG≠XH/X value is, the weaker the kinetic H-donating ability of XH is. In order to discover the dependence of ΔG≠XH/X on the structures of XH, the direct vision dependence of ΔG≠XH/X on the structures of XH is shown in Scheme 4. From Scheme 4, it is clear that the ΔG≠XH/X values of 25 XH in CH3CN at 298 K range from 6.34 kcal mol−1 for 6, 6′-methylenebis(2-(tert-butyl)-4-methylphenol) (7H) to 19.97 kcal mol−1 for 2,6-dimethyl-4-cyanophenol (13H), and the order of ΔG≠XH/X is different from the order of ΔGo(XH).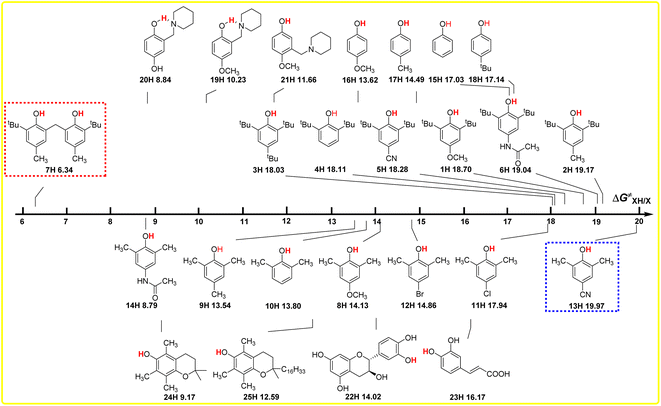 | ||
| Scheme 4 Visual comparison of ΔG≠XH/X among the 25 phenols of O–H bonds in CH3CN at 298 K, the unit is kcal mol−1. | ||
From Scheme 4, it can be seen that the order of ΔG≠XH/X is 2,6-di-tert-butylphenol series > 2,6-di-methylphenol series ≈ 4-substituted phenols, as the steric effect of tBu is bigger than that of CH3. For the 2,6-di-tert-butylphenol series, the ΔG≠XH/X values are concentrated between 18 and 19 kcal mol−1, indicating that the steric hindrance of different substituents at position 4 have little influence on the reaction centre O–H. However, for 2,6-di-methylphenol series, the ΔG≠XH/X values are scattered, ranging from 8.79 to 19.79 kcal mol−1, indicating that the hindrance of different substituents at position 4 has great influence on the reaction centre. Compared with the 2,6-di-tert-butyl phenol series, the different phenomenon also shows that the steric effect of tert-butyl group is far greater than that of the methyl group, so the steric effect of other groups at position 4 can be basically ignored in 2,6-di-tert-butyl phenol series, while the steric effect of methyl group is not prominent compared with other groups, so the ΔG≠XH/X values of 2,6-dimethyl phenol series are relatively dispersed.
For 6,6′-methylenebis(2-(tert-butyl)-4-methylphenol) (7H), apparently, the steric hindrance of the compound is large, but because there are two reaction sites in the compound, and the two benzene rings are connected by the methylene group, the actual steric hindrance of the reaction centre is not large, and its kinetic H-donating ability is the strongest among these phenols. Compared with PMC (24H), the steric effect of the long-chain alkyl group at the far end of the reaction centre in α-tocopherol (25H) leads to an increase in ΔG≠XH/X by 3.42 kcal mol−1. At the same time, it can be seen from Scheme 2 that this long-chain alkyl group increases the ΔGo(XH) value of O–H bond by 1.60 kcal mol−1.
In addition to the method of determining the intrinsic resistance energy ΔG≠XH/X mentioned in this paper, a dynamic nuclear magnetic method is also mentioned in the literature, which is obtained from ΔG≠XH/X by measuring the reaction rate of the pseudo-self-exchange HAT reaction.33 The self-exchange rate constant for tBu3PhOH was determined by studying the pseudo-self-exchange reaction of tBu3PhO˙ + 2,6-di-tert-butyl-4-methylphenol.33a In Table 3, the ΔG≠XH/X values determined by eqn (3) in this work and by pseudo-self-exchange HAT reaction 2,6-tBu2-4-CH3Ph/tBu3PhO˙ using dynamic 1H NMR are listed. There is a certain deviation (2.36 kcal mol−1) between the ΔG≠XH/X values measured by the two methods. The possible reasons may be that there is a deviation between the pseudo-self-exchange HAT reaction and the real self-exchange HAT reaction. The ΔG≠XH/X values of 2,6-di-tert-butylphenol substituted at position 4 obtained by this method are all equal, which cannot reflect the influence of the substituent at position 4 on the ΔG≠XH/X. There is also an error in the reaction rate measured by dynamic 1H NMR. However, the ΔG≠XH/X value determined by eqn (3) in this work was calculated by the cross-HAT reaction method. The accuracy of the reaction rate constant kH (ΔG≠XH/Y) measurement and the accuracy of the bond dissociation free energy [ΔGo(XH)] will affect the accuracy of the ΔG≠XH/X value. All the above-mentioned factors may lead to a difference in the ΔG≠XH/X values obtained by the two methods.
Actual H-donating activities of phenols ΔG≠o(XH)
According to the definition of thermo-kinetic parameter ΔG≠o(XH) (eqn (3)), it consists of both the thermodynamic parameter ΔGo(XH) and the kinetic parameter ΔG≠XH/X. Therefore, it is a comprehensive parameter that can well characterize the H-donating activity of the compound in HAT reactions. The bigger the value of ΔG≠o(XH) is, the weaker the actual H-donating activity of XH is. Considering the above-mentioned thermodynamic and kinetic analyses, the structure–activity relationship of thermo-kinetic parameters is shown in Scheme 5. The ΔG≠o(XH) values range from 40.93 kcal mol−1 for PMC (24H) to 49.79 kcal mol−1 for 2,6-dimethyl-4-cyanophenol (13H). The scale of ΔG≠o(XH) is 8.85 kcal mol−1, from which it can be seen that the structures of phenols have a great influence on their actual H-donating activities.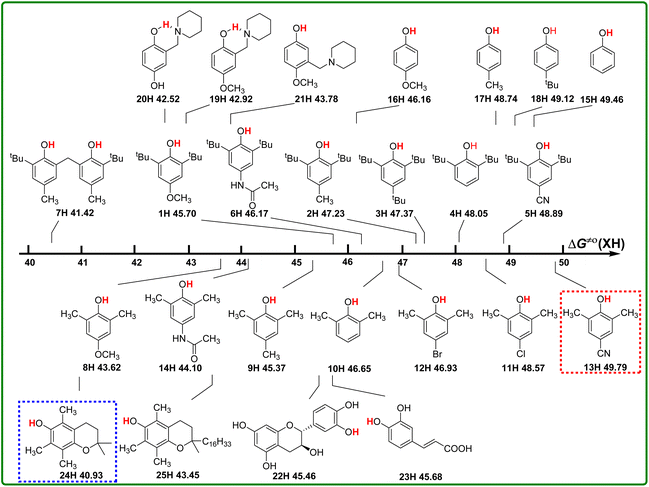 | ||
| Scheme 5 Visual comparison of ΔG≠o(XH) among the 25 phenols of O–H bonds in CH3CN at 298 K, the unit is kcal mol−1. | ||
From Scheme 5, the actual H-donating activities of 2,6-di-tert-butyl-4-substituted phenols and 2,6-dimethyl-4-substituted phenols are in the same orders for the substituent at 4 position.
Although phenols 20, 22, and 23 have two phenolic OH groups (see Scheme 6), the labeled OH groups will react first, because they have a smaller bond dissociation free energy ΔΔGo(XH) than that of the other OH groups. Therefore, we focus on the more reactive hydrogen atom of the molecule. The ΔGo(XH) values of phenolic OH groups in phenols 20, 22, and 23 are listed in the following Scheme 6, which were obtained by the iBonD HM method. After the departure of the target hydrogen atom, the phenol radical forms an intramolecular hydrogen bond with the adjacent hydroxyl group or N atom. For example, phenol 23 is caffeic acid. After the target hydrogen atom leaves, the oxygen radical forms an intramolecular hydrogen bond with the adjacent OH groups, which stabilizes the radical to a certain extent, as shown in Scheme 6.
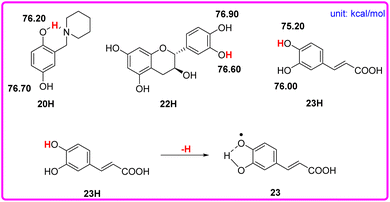 | ||
| Scheme 6 Visual comparison of ΔGo(XH) among the three phenols of O–H bonds that have 2 phenolic OH groups in CH3CN at 298 K, and the effect of the structure of phenol 23 for the abstraction of H. | ||
The thermo-kinetic parameter ΔG≠o(XH) can be used not only to compare the H-donating activities of different phenols qualitatively and quantitatively, but also to provide data support for the accurate selection of appropriate antioxidants in scientific research and chemical production. Alkyl peroxyl radicals (ROO˙) such as CumOO˙ [PhC(CH3)2OO˙] are important oxygen-centred radicals that are involved in a variety of chemical and biological processes.19 In order to reduce the free radical CumOO˙, we need to choose suitable antioxidants XH. In general, the selection of antioxidants should satisfy the following principles: first, the thermodynamic feasibility is satisfied; second, the rate constant of HAT reaction is easy to measure (k2's magnitude is among 10–105 M−1 s−1). As ΔGo(CumOO˙) = −81.90 kcal mol−1 and ΔG≠o(CumOO˙) = −33.72 kcal mol−1 were available in our previous work,22 the value of ΔG≠o(XH) for antioxidants should be within the scope of 44.35–49.80 kcal mol−1. The calculation process is provided in ESI† according to eqn (2). Considering the thermodynamic feasibility and the rate constant of the HAT reaction, 2,6-di-tert-butyl-4-substituted phenols (1H–6H) and 2,6-dimethyl-4-substituted phenols (9H–13H) except for 4-CH3 and 4-NHCOCH3, (+)-catechin (22H) and caffeic acid (23H) can be selected as antioxidants for the reduction of CumOO˙.
Actual H-abstraction activities of phenol radicals ΔG≠o(X)
Phenols are not only one kind of H-donors, but also phenol radicals are important free radicals, which play an important role in the study of the kinetics and mechanism of the HAT reaction.14,15 In this part, the actual H-abstraction abilities of these phenol radicals are discussed using thermo-kinetic parameters ΔG≠o(X) in detail. According to the definition of ΔG≠o(X) (eqn (4)), ΔG≠o(X) is composed of one half of the difference between ΔG≠XH/X and ΔGo(XH), and the value is negative. The higher the negative value of ΔG≠o(X) is, the stronger the oxidation ability of free radical X is, and the stronger the actual H-abstraction activity of X is. The visual comparison of ΔG≠o(X) for these phenol radicals is shown in Scheme 7. The ΔG≠o(X) values range from −27.00 kcal mol−1 for 1 to −35.30 kcal mol−1 for 14.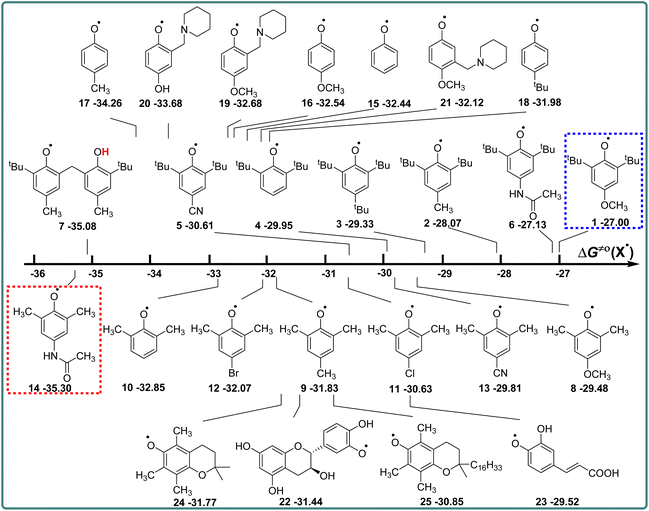 | ||
| Scheme 7 Visual comparison of ΔG≠o(X) among the 25 phenols of O–H bonds in CH3CN at 298 K, the unit is kcal mol−1. | ||
From Scheme 7, it can be observed that the H-abstraction activities ΔG≠o(X) of X and the H-donating activities ΔG≠o(XH) of XH are not in the same order. The phenol molecule has a strong H-donating activity, and its corresponding phenol radical may not have strong H-abstraction activity. For 2,6-di-tert-butyl-4-substituted phenols, the H-abstraction activities are in the order of CN > H > tBu > CH3 > CH3CONH > OCH3, which is in the opposite order of H-donating activities of XH. However, for 2,6-dimethyl-4-substituted phenols, the order of H-abstraction activities of X and the order of H-donating activities of XH are no obvious pattern.
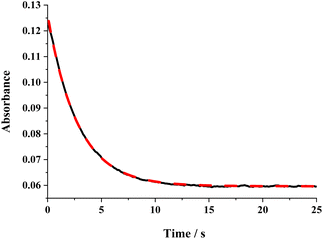
The ΔG≠o(X) values of phenolic radicals are very important for the selection of free radicals and the judgment of reaction rate in HAT reactions. In our previous work, the thermo-kinetic parameter ΔG≠o(BNAH) = 44.35 kcal mol−1 of BNAH, the nicotinamide coenzyme analogue (NADH), has been obtained.26 In this work, ΔG≠o(tBu3PhO˙) = −29.33 kcal mol−1 was obtained. According to eqn (2), as long as ΔG≠o(BNAH) and ΔG≠o(tBu3PhO˙) are available, the activation free energy 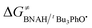 of the HAT reaction between BNAH and tBu3PhO˙ can be evaluated. The
of the HAT reaction between BNAH and tBu3PhO˙ can be evaluated. The 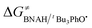 value is 44.35–29.33 = 15.02 kcal mol−1. In order to verify the accuracy of the thermo-kinetic parameters obtained in this paper and verify the accuracy of the prediction of the HAT reaction rate by using the thermo-kinetic parameters, the HAT reaction between BNAH and tBu3PhO˙ was studied by a kinetic method. The absorbance decay of tBu3PhO˙ (1.0 mM) in acetonitrile at Δλmax = 631 nm following the addition of BNAH (20 mM) in deaerated anhydrous acetonitrile at 298 K (black line) and the fit (red line) using pseudo-first-order kinetic model is shown in Fig. 1. The comparison of the activation free energies ΔG≠calc. and ΔG≠exp. for the HAT reaction BNAH/tBu3PhO˙ and the difference between these two values [ΔΔG≠ = ΔG≠calc. − ΔG≠exp.] are listed in Table 4. The differences (0.23 kcal mol−1) between the experimental and the calculated values of the activation free energies ΔΔG≠ are quite small.
value is 44.35–29.33 = 15.02 kcal mol−1. In order to verify the accuracy of the thermo-kinetic parameters obtained in this paper and verify the accuracy of the prediction of the HAT reaction rate by using the thermo-kinetic parameters, the HAT reaction between BNAH and tBu3PhO˙ was studied by a kinetic method. The absorbance decay of tBu3PhO˙ (1.0 mM) in acetonitrile at Δλmax = 631 nm following the addition of BNAH (20 mM) in deaerated anhydrous acetonitrile at 298 K (black line) and the fit (red line) using pseudo-first-order kinetic model is shown in Fig. 1. The comparison of the activation free energies ΔG≠calc. and ΔG≠exp. for the HAT reaction BNAH/tBu3PhO˙ and the difference between these two values [ΔΔG≠ = ΔG≠calc. − ΔG≠exp.] are listed in Table 4. The differences (0.23 kcal mol−1) between the experimental and the calculated values of the activation free energies ΔΔG≠ are quite small.
Conclusions
In this article, the H-donating abilities of 25 well-known phenols and the H-abstraction abilities of the corresponding phenol radicals have been studied by using the bond dissociation free energy ΔGo(XH), kinetic intrinsic resistance energy ΔG≠XH/X and thermo-kinetic parameters ΔG≠o(XH) and ΔG≠o(X) in thermodynamics, kinetics and actual HAT reactions. The ΔGo(XH) values have been determined by the iBonD HM method. The ΔG≠XH/X, ΔG≠o(XH) and ΔG≠o(X) values of phenols and phenol radicals in acetonitrile at 298 K have been determined according to eqn (2)–(4). The following conclusions could be drawn:(1) The order of ΔGo(XH) of three types of phenols is 2,6-di-tert-butylphenol series > 2,6-di-methylphenol series > 4-substituted phenols. The presence of a substituent at position 4 has different effects on ΔGo(XH) of 2,6-di-tert-butylphenol, 2,6-dimethyl phenol and 4-substituted phenol series. The bond dissociation free energy changes ΔΔGo caused by substituent change at position 4 are also different.
(2) If the group steric effect at positions 2 and 6 of phenol is large (as tBu), ΔG≠XH/X of phenol in the HAT reaction mainly depends on the group at positions 2 and 6, and the steric effect at position 4 has a small effect on ΔG≠XH/X; however, if the steric effect at position 2 and 6 is not significant (as CH3), the hindrance at position 4 has a large effect on ΔG≠XH/X. The differences between the method of determining ΔG≠XH/X mentioned in this paper and the dynamic nuclear magnetic method mentioned in the literature are compared.
(3) The actual H-donating and H-abstraction activities of phenols and phenol radicals are compared using ΔG≠o(XH) and ΔG≠o(X). The accuracy of ΔG≠o and the accuracy of the prediction of the HAT reaction rate by using ΔG≠o are verified.
These parameters not only provide data support for the selection of antioxidants and free radicals in scientific research and practical production, but also provide new ideas for the design and synthesis of more efficient antioxidants and free radicals.
Experiment section
Kinetic measurements
The kinetics of the HAT reactions were conveniently monitored using an Applied Photophysics SX.18MV-R stopped-flow, which were thermostated at 298 K under strict anaerobic conditions in dry acetonitrile. The method of the kinetic measurement was a pseudo-first-order method. The concentration of the antioxidant was maintained at more than 20-fold excess of the oxidant to attain the pseudo-first-order condition. The second-order rate constants (k2) were derived from the plots of the pseudo-first-order rate constants versus the concentrations of the excessive reactants. In each case, it was confirmed that the rate constants derived from three to five independent measurements agreed within an experimental error of ±5%.Thermodynamic measurements
The bond dissociation free energies ΔGo(XH) are determined by the iBonD HM prediction methods: light GBM and SPOC descriptors with RMSE = 1.82, r2 = 0.980 and mean absolute errors (MAEs) = 1.03 (95![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 train test split).28,29
5 train test split).28,29
Conflicts of interest
The authors declare no competing financial interests.Acknowledgements
Financial support from PhD Research Startup Foundation of Anyang Institute of Technology (BSJ2019032).References
- (a) K. Murakami, S. Yamada, T. Kaneda and K. Itami, Chem. Rev., 2017, 117, 9302–9332 CrossRef CAS PubMed; (b) L. Valgimigli and D. A. Pratt, Acc. Chem. Res., 2015, 48, 966–975 CrossRef CAS PubMed; (c) K. U. Ingold and D. A. Pratt, Chem. Rev., 2014, 114, 9022–9046 CrossRef CAS PubMed.
- (a) N. Holmberg-Douglas and D. A. Nicewicz, Chem. Rev., 2022, 122, 1925–2016 CrossRef CAS PubMed; (b) Y. Qin, L. Zhu and S. Luo, Chem. Rev., 2017, 117, 9433–9520 CrossRef CAS PubMed.
- (a) Y. Shang, X. Li, Z. Li, L. Shen, J. Zhou, R. Hu and K. Chen, J. Mol. Struct., 2022, 1260, 132830–132836 CrossRef CAS; (b) M. R. Antonijević, E. H. Avdović, D. M. Simijonović, Ž. B. Milanović, A. D. Amić and Z. S. Marković, Int. J. Mol. Sci., 2022, 23, 490–505 CrossRef PubMed.
- (a) S. Immanuel, R. Sivasubramanian, R. Gul and M. Ahmad Dar, Chem.–Asian J., 2020, 15, 4256–4270 CrossRef CAS PubMed; (b) S. Zhang, J. Shi, Y. Chen, Q. Huo, W. Li, Y. Wu, Y. Sun, Y. Zhang, X. Wang and Z. Jiang, ACS Catal., 2020, 10, 4967–4972 CrossRef CAS.
- (a) J.-D. Yang, B.-L. Chen and X.-Q. Zhu, J. Phys. Chem. B, 2018, 122, 6888–6898 CrossRef CAS PubMed; (b) X.-Q. Zhu, Y. Tan and C.-T. Cao, J. Phys. Chem. B, 2010, 114, 2058–2075 CrossRef CAS PubMed; (c) X.-Q. Zhu, J.-Y. Zhang and J.-P. Cheng, J. Org. Chem., 2006, 71, 7007–7015 CrossRef CAS PubMed.
- (a) M. Salamone, M. Galeotti, E. Romero-Montalvo, J. A. v. Santen, B. D. Groff, J. M. Mayer, G. A. DiLabio and M. Bietti, J. Am. Chem. Soc., 2021, 143, 11759–11776 CrossRef CAS PubMed; (b) M. Salamone, G. A. DiLabio and M. Bietti, J. Org. Chem., 2012, 77, 10479–10487 CrossRef CAS PubMed; (c) M. Finn, R. Friedline, N. K. Suleman, C. J. Wohl and J. M. Tanko, J. Am. Chem. Soc., 2004, 126, 7578–7584 CrossRef CAS PubMed.
- (a) M. Salamone and M. Bietti, Acc. Chem. Res., 2015, 48, 2895–2903 CrossRef CAS PubMed; (b) M. Salamone, M. Milan, G. A. DiLabio and M. Bietti, J. Org. Chem., 2014, 79, 7179–7184 CrossRef CAS PubMed.
- Y.-H. Fu, Z. Wang, Y. Zhang, G.-B. Shen and X.-Q. Zhu, ChemistrySelect, 2022, 7, e202202625 CAS.
- (a) J. J. Warren, T. A. Tronic and J. M. Mayer, Chem. Rev., 2010, 110, 6961–7001 CrossRef CAS PubMed; (b) R. Amorati, S. Menichetti, C. Viglianisib and M. C. Foti, Chem. Commun., 2012, 48, 11904–11906 RSC.
- (a) A. Coniglio, C. Galli, P. Gentili and R. Vadal`a, Org. Biomol. Chem., 2009, 7, 155–160 RSC; (b) H. Zhang, Z. Shi, R. Bai, D. Wang, F. Cui, J. Zhang and T. J. Strathmann, Environ. Sci. Technol., 2021, 55, 7681–7689 CrossRef CAS PubMed.
- (a) M. Salamone, R. Amorati, S. Menichetti, C. Viglianisi and M. Bietti, J. Org. Chem., 2014, 79, 6196–6205 CrossRef CAS PubMed; (b) M. Finn, R. Friedline, N. Suleman, C. J. Wohl and J. M. Tanko, J. Am. Chem. Soc., 2004, 126, 7578–7584 CrossRef CAS PubMed.
- (a) R. Amorati, S. Menichetti, C. Viglianisi and M. C. Foti, Chem. Commun., 2012, 48, 11904–11906 RSC; (b) M. C. Foti, R. Amorati, G. F. Pedulli, C. Daquino, D. A. Pratt and K. U. Ingold, J. Org. Chem., 2010, 75, 4434–4440 CrossRef CAS PubMed; (c) M. C. Foti, C. Daquino, I. D. Mackie, G. A. DiLabio and K. U. Ingold, J. Org. Chem., 2008, 73, 9270–9282 CrossRef CAS PubMed.
- (a) V. W. Manner, T. F. Markle, J. H. Freudenthal, J. P. Roth and J. M. Mayer, Chem. Commun., 2008, 256–258 RSC; (b) S. C. Remke, T. H. Bürgin, L. Ludvíková, D. Heger, O. S. Wenger, U. Gunten and S. Canonica, Water Res., 2022, 213, 118095–118107 CrossRef CAS PubMed.
- J. J. Warren and J. M. Mayer, J. Am. Chem. Soc., 2008, 130, 7546–7547 CrossRef CAS PubMed.
- C. D'Alfonso, M. Bietti, G. A. DiLabio, O. Lanzalunga and M. Salamone, J. Org. Chem., 2013, 78, 1026–1037 CrossRef PubMed.
- M. Mazzonna, M. Bietti, G. A. DiLabio, O. Lanzalunga and M. Salamone, J. Org. Chem., 2014, 79, 5209–5218 CrossRef CAS PubMed.
- G. Litwinienko and K. U. Ingold, J. Org. Chem., 2003, 68, 3433–3438 CrossRef CAS PubMed.
- R. Amorati, S. Menichetti, C. Viglianisib and M. C. Foti, Chem. Commun., 2012, 48, 11904–11906 RSC.
- L. Valgimigli, J. T. Banks, J. Lusztyk and K. U. Ingold, J. Org. Chem., 1999, 64, 3381–3383 CrossRef CAS PubMed.
- Y.-H. Fu, G.-B. Shen, K. Wang and X.-Q. Zhu, ChemistrySelect, 2021, 6, 8007–8010 CrossRef CAS.
- Y.-H. Fu, K. Wang, G.-B. Shen and X.-Q. Zhu, J. Phys. Org. Chem., 2022, e4358 CAS.
- Y.-H. Fu, G.-B. Shen, K. Wang and X.-Q. Zhu, ACS Omega, 2022, 7, 25555–25564 CrossRef CAS PubMed.
- Y.-H. Fu, C. Geng, G.-B. Shen, K. Wang and X.-Q. Zhu, ACS Omega, 2022, 7, 26416–26424 CrossRef CAS PubMed.
- Y.-H. Fu, Z. Wang, K. Wang, G.-B. Shen and X.-Q. Zhu, RSC Adv., 2022, 12, 27389–27395 RSC.
- X.-Q. Zhu, F.-H. Deng, J.-D. Yang, X.-T. Li, Q. Chen, N.-P. Lei, F.-K. Meng, X.-P. Zhao, S.-H. Han, E.-J. Hao and Y.-Y. Mu, Org. Biomol. Chem., 2013, 11, 6071–6089 RSC.
- Y.-H. Fu, G.-B. Shen, Y. Li, L. Yuan, J.-L. Li, L. Li, A.-K. Fu, J.-T. Chen, B.-L. Chen, L. Zhu and X.-Q. Zhu, ChemistrySelect, 2017, 2, 904–925 CrossRef CAS.
- G. Litwinienko and K. U. Ingold, J. Org. Chem., 2005, 70, 8982–8990 CrossRef CAS PubMed.
- https://pka.luoszgroup.com/bde_prediction.
- Q. Yang, Y. Li, J. D. Yang, Y. Liu, L. Zhang, S. Luo and J. P. Cheng, Angew. Chem., Int. Ed., 2020, 59, 19282–19291 CrossRef CAS PubMed.
- https://ibond.nankai.edu.cn/.
- L. Konga, K. Donga, G. Lia, C. Yang, S. Lai and Y. Qu, FirePhysChem, 2022, 2, 4–13 CrossRef.
- X.-Q. Zhu, J. Zhou, C.-H. Wang, X.-T. Li and S. Jing, J. Phys. Chem. B, 2011, 115(13), 3588–3603 CrossRef CAS PubMed.
- (a) J. J. Warren and J. M. Mayer, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 5282–5287 CrossRef CAS PubMed; (b) A. Wu, E. A. Mader, A. Datta, D. A. Hrovat, W. T. Borden and J. M. Mayer, J. Am. Chem. Soc., 2009, 131, 11985–11997 CrossRef CAS PubMed; (c) J. C. Yoder, J. P. Roth, E. M. Gussenhoven, A. S. Larsen and J. M. Mayer, J. Am. Chem. Soc., 2003, 125, 2629–2640 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: The second-order rate constants k2 and activation free energies ΔG≠XH/Y of HAT reactions from phenols to radicals in acetonitrile at 298 K, and the ΔGo(XH) values determined by theoretical calculation in this work are shown. See DOI: https://doi.org/10.1039/d2ra06877j |
| This journal is © The Royal Society of Chemistry 2023 |