Open Access Article
Open Access ArticleTheoretical design of porous dodecagonal germanium carbide (d-GeC) monolayer
Yusuf Zuntu Abdullahi†
 *a and
Fatih Ersan†
*a and
Fatih Ersan† b
b
aDepartment of Physics, Faculty of Science, Kaduna State University, P.M.B. 2339, Kaduna State, Nigeria. E-mail: yusufzuntu@gmail.com
bDepartment of Physics, Aydin Adnan Menderes University, Aydin 09010, Turkey. E-mail: fatih.ersan@adu.edu.tr
First published on 23rd January 2023
Abstract
Porous nanosheet materials have recently emerged as attractive candidates to serve as nanofiltration membranes. Through first-principles calculations based on density functional theory (DFT) calculations, we propose a new porous dodecagonal GeC (d-GeC) monolayer. We show that the d-GeC monolayer exhibits excellent energetic, mechanical, dynamic, and thermal stabilities. The d-GeC monolayer shows semiconducting properties with an indirect band gap of 1.73 eV (2.53 eV) PBE(HSE06). We also show that the d-GeC monolayer can serve as a good membrane for molecular and atomic permeation due to its low value of estimated diffusion energy barriers. Our results demonstrate the potential of the d-GeC monolayer for the design of nanofiltration membrane technology.
1 Introduction
In recent years, graphitic porous monolayers have attracted much research interest due to their numerous industrial advantages over non-porous graphitic monolayer materials. So far, the synthesized porous monolayers can be grouped into non-metal containing (e.g. carbon nitride1 and graphene oxide layer2) and metal-containing (pore sites created in two-dimensional (2D) transition metal chalcogenide3–5) materials. These reported porous monolayers inherently exhibit highly reactive dangling bonds at the pore edge, which have a significant impact on their properties. In practice, the atoms at the edge of the pore are usually passivated by hydrogen atoms, resulting in a reduction of the pore size. This means that the performance of these porous materials in any application is controlled by the edge atom at the pore site. Consequently, this issue severely limits the development of these types of porous materials where a reasonably less reactive pore site is needed. The issue offers a new research opportunity to design a porous monolayer with a non-dangling bond at the pore site. If found, it is expected to consolidate the potential prospects of porous materials for gas separation,6,7 water purification8–14 and15–17 related applications.Here we design a new porous d-GeC monolayer with non-dangling bonds at the pore site. To our knowledge, the porous d-GeC monolayer has not been previously predicted. However, we are aware that recently the porous Ge3N4 monolayer with a non-dangling bond at the pore site has been theoretically predicted and shown to exhibit indirect bandgap semiconducting properties.18 In addition, it was shown that the band gap of the Ge3N4 monolayer can be tuned by mechanical strain, while the indirect band gap remained unchanged across the strain ranges. In a separate study, a direct bandgap of 5.2 eV has been observed for d-BN monolayer while an octagonal porous BN monolayer exhibits an indirect bandgap of 5.20 eV.19 It should be emphasized that such a porous d-GeC monolayer with semiconducting property is rarely found. However, the structure exists in the form of purely carbon-based structures called biphenylene carbons20 or graphenylenes.22 These structures occur in various allotropes with a well-ordered ring composed of 8, 10, or 12 atoms. They are generally non-magnetic semiconductors and have been synthesized.23 A previous report has also suggested inorganic forms of these structures.19,21,24,25 We expect that the d-GeC monolayer will provide a suitable layer thickness and pore electron density for gas mixture separation and related applications. In this study, we investigate the stability and electronic properties of the d-GeC monolayer by first-principle calculations based on DFT.26 We also estimate the diffusion barrier of some selected (H2, O2, CH2) molecules and (He, Na, Cl) atoms.
2 Computational method
The ground state monolayer of d-GeC has been obtained by carrying out DFT26 calculations using the Vienna ab initio Simulation Package (VASP).27 The generalized gradient approximation (GGA) of Perdew–Burke–Ernzerhof (PBE)28 exchange-correlation parametrization has been used to treat strongly orbitals of all atoms. The projected augmented wave (PAW) pseudopotentials method28 has been used for all atoms to describe the core and valence electrons. The DFT-D2 method of the Grimme van der Waals (vdW) correction29 has been used. The Brillouin zone is sampled using a Γ-centered k-point meshes and (12 × 12 × 1) and (20 × 20 × 1) meshes have been used for self-consistency and total density of state computations respectively.30 The cut-off energy for the plane-wave basis set was set to 500 eV. A vacuum space of at least 16 Å perpendicular to the d-GeC monolayer was set in simulation cells to minimize interactions between the adjacent layers. All the structures have been fully relaxed until the remaining force on each atom and the energy were smaller than 0.01 eV Å−1 and 10−5 eV respectively. To determine the minimum energy diffusion pathways for the considered molecules and atoms passing through the pore site of the d-GeC monolayer, we carried out the climbing-image nudged elastic band (CI-NEB) scheme.31 Quantum ESPRESSO (QE) code32 was used for the CI-NEB calculations. A total of 9 images have been used between the initial and final positions. To produce results with negligible error, we make sure that similar computational parameters, such as PAW PPs, are used for both VASP and QE computations. As a check for the thermal stability of the d-GeC monolayer, we performed ab initio molecular dynamics (AIMD) simulations with a time step of 4.0 ps. The temperature was controlled using the Nosé–Hoover thermostat.333 Results and discussions
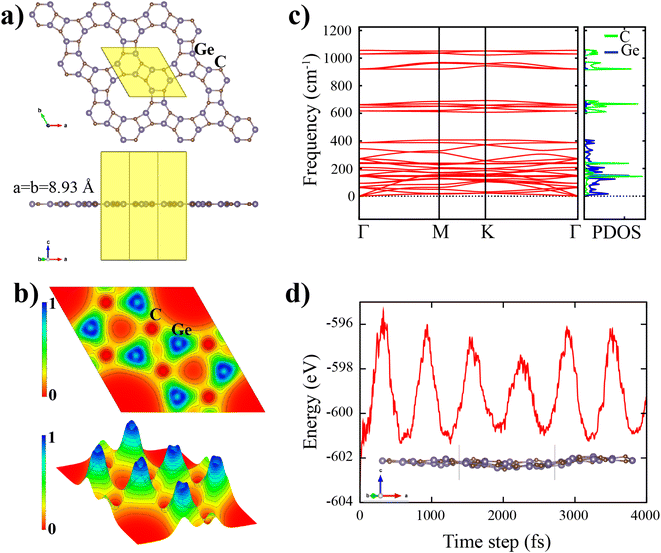
The top and side view of the d-GeC monolayer is illustrated in Fig. 1(a), which is similar to the porous d-BN and d-ZnO sheets.19,25 It has hexagonal symmetry (C16h) with the space group of P6/m. In Fig. 1(a), the black rhombohedral line displays the geometric structure of the d-GeC unit cell. The unit cell consists of a total of six Ge and six C atoms and each atom in the d-GeC is bonded by three neighboring atoms. As clearly displayed in Fig. 1(a), the d-GeC crystal structure is formed by two Ge3C3 hexagonal rings that are chemically bonded side by side through Ge–C bond. Between the two Ge3C3 rings, the Ge–C bond forms a square structure that leaves no dangling bonds at the edge of the pore site. There are two kinds of Ge and C atoms according to the angle formed with their bonded atoms. It is also noted that both Ge and C atoms contribute equally to the pore site. The smallest optimized distance between the two symmetrically opposite atoms in the pore is 7.27 Å (the diameter of the pore). The pore size of the d-GeC is expected to be sufficient to function as a membrane for certain applications where large pore size is required.After full structural optimization, the side view of the d-GeC monolayer is planar without any obvious buckling tendencies (see Fig. 1(a)). The obtained equilibrium lattice constant (a = b) of the d-GeC monolayer is 8.93 Å The estimated Ge–C bond lengths are in the range of 1.840–1.95 Å. The ranges of values do not deviate that much, indicating a robust bonding network in the d-GeC structure. Consequently, it is expected that the d-GeC structure will be stable. To investigate the chemical bonding nature of the d-GeC structure, we calculated the electron localization functions (ELF). As illustrated in Fig. 1(b), the ELF takes the values in the range of 0 to 1e− Å−3. It is evident from Fig. 1(b) that both ionic and non-polar covalent bonds exist in the d-GeC structure due to the accumulation and depletion of the charge density. These bonding properties are attributed to the difference in electronegativity between the C(2.55) atom and the Ge(2.01) atom. The Bader charge analysis34 was used to estimate the charge transfers in the d-GeC structure. About 2.58e− charge transfer occurs from the Ge atom to the C atom. The net charge transfer of electrons from Ge to C indicates ionic bonding, while the nonpolar covalent bonding is caused by the difference in electronegativity between the two bonded Ge and C atoms being less than 0.5.
Next, we evaluate the stability of the d-GeC monolayer. Firstly, we estimate both the cohesive energy (Ecoh) and formation energy (EFE) per atom. The Ecoh is determined from the expression given as;
| Ecoh = (6EGe + 6EC − Ed-GeC)/12 | (1) |
| EFE = (Ed-GeC − 6μGe − 6μC)/12 | (2) |
We then evaluate the mechanical stability of the d-GeC by computing the in-plane stiffness (Y) and Poisson's ratio (ν) of the d-GeC monolayer using the previously reported36–38 strain-energy method. The calculated Y and ν along the a or b strain directions are 98.90 N m−1 and 0.33, respectively. The Y and ν values are both positive and isotropic, which means that they satisfy the minimum born criteria for elastic stability of hexagonal 2D materials.39 The obtained Y and ν values ascertain the good mechanical stability of the d-GeC monolayer. In comparison, the Y value is comparable to WSTe (100 N m−1) monolayer.40
We assess both the dynamic and thermal stability of the d-GeC monolayer using phonon dispersion and AIMD calculations as further verification of its stability. Fig. 1(c) shows no imaginary phonon modes throughout the first Brillouin zone. The absence of imaginary modes confirms the dynamic stability of the d-GeC monolayer. As shown in Fig. 1(c), the lowest three phonon dispersion curves i.e. longitudinal acoustic (LA) and transverse acoustic (TA) branches show linear dispersion while the transverse acoustic (ZA) branch has a quadratic form in the vicinity of the Γ-point. The lattice thermal conductivity and the group velocity are driven by these acoustic phonon modes. The highest frequency of the d-GeC monolayer goes above 1000 cm−1, comparable to most of the well-known 2D materials. Alongside the phonon band structure, we provide the phonon projected density of states (phDOS) plot. It is evident that the atomic vibration contribution in the porous d-GeC structure varies according to the atom weights, i.e. the highest vibration frequency originates from the lighter C atom which confirms that frequency is proportional to the square root of atomic mass. It can be concluded that the porous d-GeC monolayer is robust material owing to its high optical vibration modes. With regard to the thermal stability of the d-GeC monolayer, we performed AIMD at 300 K using a (3 × 3) supercell of d-GeC. There is no structural deformation in the d-GeC monolayer and only negligible atomic height deviation as displayed in Fig. 1(d). Moreover, the oscillation range for the total energy against the time step is provided. The obtained energies are of the order of meV for each atom in the considered (3 × 3) supercell of d-GeC without obvious variations.
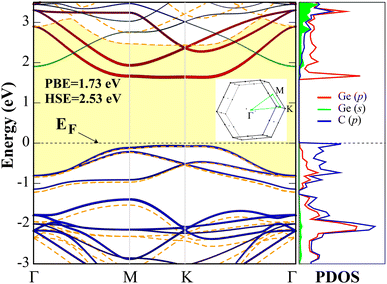
After ensuring that the d-GeC monolayer is stable, the electronic property is then calculated. The PBE and PBE + HSE06 band structures and the corresponding PBE projected density of states (PDOS) of the d-GeC monolayer are displayed in Fig. 2. The plots show nonmagnetic semiconducting structure with indirect band gaps of 1.73 eV (PBE) and 2.53 eV (HSE06). The obtained HSE06 hybrid functional calculation band gap value clearly shows improvement over the PBE results. In addition, the obtained HSE06 band gap of the d-GeC monolayer will allow exploitation of the visible region of the solar spectrum, making it a suitable material for photocatalysis and related applications. As displayed in the plot, the increase in band gap for the HSE06 calculation is due to the shift of conduction band minimum (CBM) to the region of higher energy. The valence band maximum (VBM) is situated at the M high symmetry point while the CBM is between M–K in the band structure. The dominant orbital contribution to the VBM comes from the p orbitals of both C and Ge atoms while these orbitals become delocalized at the CBM. The presence of nearly flat bands at the VBM is an important feature that could lead to large effective masses of electrons due to the wide radius of curvature. We expect large correlation effects41–43 from the large localization of holes. This may result in unusual phenomena like the fractional quantum Hall effect44,45 and room temperature ferromagnetism/anti-ferromagnetism.46,47
To demonstrate the permeability of the d-GeC monolayer for some (H2, O2, CH2) molecules and (He, Na, Cl) atoms, we estimate the minimum diffusion energy barrier (Ebarrier). For these calculations, we use the climbing image nudged elastic band (CI-NEB) method to evaluate the diffusion of these molecules and atoms passing through the pore site of the d-GeC monolayer. We choose initial and final images which are the top and the bottom of the center of the porous site of the d-GeC structure both of them are fully optimized, and then seven intermediate images with equal intervals are linearly chosen between them. At the end of calculations, energy versus diffusion path curves is plotted as illustrated in Fig. 3. We also summarised these deduced Ebarrier values in Table 1. The calculated Ebarrier values for molecules are lower than those obtained for atoms. The Ebarrier decrease in the order of He < H2‖ < H2⊥ < H2O < CH4 < Na < Cl. The larger Ebarrier for Cl@GeC/Na@GeC systems indicate an interaction between Na+ ion/Cl− ions and Ge/C atoms along the edge of the pore. In general, these Ebarrier values show that H2O, H2‖, and He will experience weak interaction by the edge Ge or C atoms when passing through the pore of d-GeC monolayer.
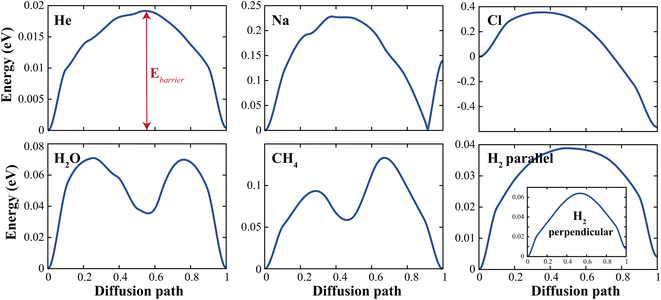 | ||
| Fig. 3 The estimated diffusion energy profiles for molecules and atoms passing through the pore site of the d-GeC monolayer. | ||
| Mol–atom | He | Na | Cl | H2‖ | H2⊥ | H2O | CH4 |
| Ebarrier (eV) | 0.019 | 0.228 | 0.920 | 0.039 | 0.064 | 0.071 | 0.133 |
4 Summary
In brief, we studied the ground-state properties of the d-GeC monolayer as a newly theoretically found porous membrane material based on the PBE method. Stability tests show that the d-GeC monolayer is energetically, mechanically, dynamically, and thermally stable based on formation energy, in-plane stiffness, phonon dispersion and AIMD simulations. The d-GeC monolayer exhibits semiconducting property with an indirect band gap of 1.73 eV (2.53 eV) PBE(HSE06). As a further investigation, we show that the d-GeC monolayer can serve as a good membrane for the permeation of molecules and atoms due to its estimated diffusion energy barriers. We believe that the novel d-GeC monolayer will be a potential candidate for true experimental synthesis in the field of nanomembranes for gas mixture and water purification.Author contributions
Yusuf Zuntu Abdullahi: formal analysis, investigation, visualization, validation, writing-reviewing and editing. Fatih Ersan: conceptualization, software, writing-reviewing and editing, supervision, project administration.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the BAGEP Award of the Science Academy, so, Fatih Ersan thanks to the Science Academy. The calculations were performed at TUBITAK ULAKBIM, High Performance and Grid Computing Center (TR-Grid e-Infrastructure) and the National Center for High Performance Computing of Turkey (UHEM) under Grant No. 5007092019. Y. Z. A acknowledges the TUBITAK for the financial support under the project number: 121F270 calculations done in this paper.Notes and references
- D. Vaya, B. Kaushik and P. K. Surolia, Mater. Sci. Semicond. Process., 2022, 137, 106181 CrossRef CAS.
- W. Hooch Antink, Y. Choi, K.-d. Seong, J. M. Kim and Y. Piao, Adv. Mater. Interfaces, 2018, 5, 1701212 CrossRef.
- N. Hassani, M. Ghorbani-Asl, B. Radha, M. Drndic, A. V. Krasheninnikov and M. Neek-Amal, J. Phys. Chem. C, 2021, 125, 25055–25066 CrossRef CAS.
- Z. Cui, K. Yang, Y. Shen, Z. Yuan, Y. Dong, P. Yuan and E. Li, Appl. Surf. Sci., 2022, 155978 Search PubMed.
- C. Lee, B. G. Jeong, S. H. Kim, D. H. Kim, S. J. Yun, W. Choi, S.-J. An, D. Lee, Y.-M. Kim and K. K. Kim, et al., npj 2D Mater. Appl., 2022, 6, 1–9 CrossRef CAS.
- T. Ashirov and A. Coskun, Chem, 2021, 7, 2385–2394 CAS.
- H. Qiu, M. Xue, C. Shen, Z. Zhang and W. Guo, Adv. Mater., 2019, 31, 1803772 CrossRef CAS PubMed.
- S. Remanan, N. Padmavathy, S. Ghosh, S. Mondal, S. Bose and N. C. Das, Sep. Purif. Rev., 2021, 50, 262–282 CrossRef CAS.
- S. P. Surwade, S. N. Smirnov, I. V. Vlassiouk, R. R. Unocic, G. M. Veith, S. Dai and S. M. Mahurin, Nat. Nanotechnol., 2015, 10, 459–464 CrossRef CAS PubMed.
- J. S. Lim and G. Kim, J. Colloid Interface Sci., 2019, 538, 367–376 CrossRef CAS PubMed.
- D. Cohen-Tanugi and J. C. Grossman, Nano Lett., 2012, 12, 3602–3608 CrossRef CAS PubMed.
- T. Wu, F. Moghadam and K. Li, J. Membr. Sci., 2022, 645, 120216 CrossRef CAS.
- T. A. Tabish, F. A. Memon, D. E. Gomez, D. W. Horsell and S. Zhang, Sci. Rep., 2018, 8, 1–14 CAS.
- J. Park, P. Bazylewski and G. Fanchini, Nanoscale, 2016, 8, 9563–9571 RSC.
- Z. Cui, H. Wu, K. Bai, X. Chen, E. Li, Y. Shen and M. Wang, Phys. E, 2022, 144, 115361 CrossRef CAS.
- Z. Cui, K. Yang, K. Ren, S. Zhang and L. Wang, Mater. Sci. Semicond. Process., 2022, 152, 107072 CrossRef CAS.
- Z. Cui, S. Zhang, L. Wang and K. Yang, Micro Nanostruct., 2022, 207260 CrossRef CAS.
- Y. Yayak, Y. Sozen, F. Tan, D. Gungen, Q. Gao, J. Kang, M. Yagmurcukardes and H. Sahin, Appl. Surf. Sci., 2022, 572, 151361 CrossRef CAS.
- H. Suzuki, I. Miyazato, T. Hussain, F. Ersan, S. Maeda and K. Takahashi, CrystEngComm, 2022, 24, 471–474 RSC.
- T. Gorkan, Ş. Çallıoğlu, S. Demirci, E. Aktürk and S. Ciraci, ACS Appl. Electron. Mater., 2022, 4(6), 3056–3070 CrossRef CAS.
- S. Demirci, S. Çallıoglu, T. Görkan, E. Aktürk and S. Ciraci, Phys. Rev. B, 2022, 105, 035408 CrossRef CAS.
- R. Baughman, H. Eckhardt and M. Kertesz, J. Chem. Phys., 1987, 87, 6687–6699 CrossRef CAS.
- Q. Fan, L. Yan, M. W. Tripp, O. Krejčí, S. Dimosthenous, S. R. Kachel, M. Chen, A. S. Foster, U. Koert and P. Liljeroth, et al., Science, 2021, 372, 852–856 CrossRef CAS PubMed.
- E. Perim, R. Paupitz, P. Autreto and D. Galvao, J. Phys. Chem. C, 2014, 118, 23670–23674 CrossRef CAS.
- Y. Z. Abdullahi and F. Ersan, Phys. Rev. Appl., 2023, 19, 014019 CrossRef.
- P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864 CrossRef.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188 CrossRef.
- G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904 CrossRef CAS.
- P. Giannozzi, S. Baroni and N. Bonini, et al., J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed.
- G. J. Martyna, M. L. Klein and M. Tuckerman, J. Chem. Phys., 1992, 97, 2635–2643 CrossRef.
- R. F. Bader, Acc. Chem. Res., 1985, 18, 9–15 CrossRef CAS.
- Y. Z. Abdullahi, F. Ersan, Z. D. Vatansever, E. Aktürk and O. Ü. Aktürk, J. Appl. Phys., 2020, 128, 113903 CrossRef CAS.
- M. Topsakal, S. Cahangirov and S. Ciraci, Appl. Phys. Lett., 2010, 96, 091912 CrossRef.
- H. Şahin, S. Cahangirov, M. Topsakal, E. Bekaroglu, E. Akturk, R. T. Senger and S. Ciraci, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 155453 CrossRef.
- Y. Z. Abdullahi, Comput. Condens. Matter, 2022, 30, e00619 CrossRef.
- F. Mouhat and F.-X. Coudert, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 224104 CrossRef.
- X. Duan, J.-C. Ren, X. Zhang, S. Li and W. Liu, Cell Rep. Phys. Sci., 2021, 2, 100284 CrossRef CAS.
- H. Henck, J. Avila, Z. B. Aziza, D. Pierucci, J. Baima, B. Pamuk, J. Chaste, D. Utt, M. Bartos and K. Nogajewski, et al., Phys. Rev. B, 2018, 97, 245421 CrossRef CAS.
- A. V. Kuklin, S. A. Shostak and A. A. Kuzubov, J. Phys. Chem. Lett., 2018, 9, 1422–1428 CrossRef CAS PubMed.
- T. Bilitewski and R. Moessner, Phys. Rev. B, 2018, 98, 235109 CrossRef.
- S. Park, S. Kang, H. Kim, K. H. Lee, P. Kim, S. Sim, N. Lee, B. Karuppannan, J. Kim and J. Kim, et al., Sci. Rep., 2020, 10, 1–8 CrossRef PubMed.
- D. L. Bergman, C. Wu and L. Balents, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 125104 CrossRef.
- J.-Y. You, B. Gu and G. Su, Sci. Rep., 2019, 9, 1–7 CrossRef PubMed.
- Y. Z. Abdullahi, Z. D. Vatansever, F. Ersan, U. Akinci, O. U. Akturk and E. Akturk, Phys. Chem. Chem. Phys., 2021, 23, 6107–6115 RSC.
Footnote |
| † These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2023 |