DFT insights into Nb-based 211 MAX phase carbides: Nb₂AC (A = Ga, Ge, Tl, Zn, P, In, and Cd)

Abstract

In this study, we performed the first-principles calculations to study the 211 MAX phase carbides: Nb₂AC (A = Ga, Ge, Tl, Zn, P, In, Cd, and Al). The structural characteristics are in good agreement with those of the prior studies. The mechanical behavior has been explored by calculating the stiffness constants, elastic moduli, and Vickers hardness. The stiffness constants and phonon dispersion curves were used to check the structural stability of the selected compounds. 2D and 3D plotting of elastic moduli and calculated anisotropy indices disclosed the anisotropy of the elastic properties. We utilized the Mulliken atomic and bond overlap population to explain the mixture of ionic and covalent bonding among these carbides. The metallic behavior has been confirmed by calculating the band structure and density of states (DOS). Partial DOS was also used to discuss the bonding nature and strength among the different states. The optical properties of these phases have also been computed and analyzed to reveal possible relevance in diverse fields. The Debye temperature (Θ_D), Grüneisen parameter (γ), melting temperature (T_m), and minimum thermal conductivity (K_min) were studied to bring out their possible relevance in high-temperature technology. The outcomes of this research indicate that the titled carbides are suitable for use as solar radiation-protecting coating and thermal barrier coating (TBC) materials.

---

1 Introduction

Many ternary compounds such as carbides, nitrides, and borides have been included in the MAX phase materials family and can be expressed as M_n+1AX_n, where M belongs to the early transition metal group, A is the element that exists within the groups 12–16, and X can only be C, N, and B, and n is a positive integer with a value of 1–3.^1–4 The MAX phase was first revealed in the 1960s by Nowotny et al.^1–4 In the 1990s, Barsoum et al.^5,6 renewed the interest by revealing their remarkable characteristics. They have remarkable mechanical strength, machinability, electronic conductivity, and thermal conductivity. They are also machinable, similar to metals, have better mechanical properties at high temperatures, and have superior corrosion and oxidation resistance including ceramics.⁷ The MAX phase family has become a significant materials group from both research and application points of view. Owing to the magnificent fusing of metallic and ceramic properties, the number of published articles is increasing day by day.⁸

Use of C and N as X elements was confined for a long time^9–11 and has been extended recently, where B has been used as an X element. The extension has opened a new platform for the MAX phase materials, owing to the interesting properties and potential applications of B and B-containing compounds.^12,13 To date, only a few of the MAX phase borides have been synthesized so far in spite of a large number of predicted phases.¹⁴ On the contrary, a significant number of MAX phase carbides have already been synthesized and characterized, revealing their prospective applications. In parallel to the experimental study, a large number of computational approaches^15,16 have also already been performed throughout the last decades. Cover et al.¹⁷ performed the first-principles calculation of the elastic properties of 240 elemental combinations, revealing the role of A elements and their interaction with M elements. Keast et al.¹⁸ computed the total energies of competing phases to check the stability of five different schemes (Cr_n+1-Al-C_n, Ti_n+1-Al-C_n, Ti_n+1-Si-N_n, Ti_n+1-Al-N_n, and Ti_n+1-Si-C_n, where n is a positive integer with a value of 1 ∼ 4). Aryal et al.¹⁹ studied 792 MAX phases, and 665 phases were found to be thermodynamically and elastically stable. 10 314 solid solutions and 216 possible M₂AX phases were revealed by Ashton et al.²⁰ Khaledialidusti et al.²¹ explored a large group of MAX phases, where M is taken as Sc, Ti, Y, Zr, V, Cr, Nb, Hf, Ta, Mo, and W and A is taken as P, S, Al, Si, Zn, Cu, Ga, As, Ge, Sn, Cd, In, Bi, Ir, Tl, Au, and Pb, and revealed their possibility of exfoliation to produce 2D systems. More than 80 MAX phases have been synthesized, most of which are 211 phases (58 prominent members).²² These studies have inspired us to think about Nb-based 211 MAX phases.

Nb-based 211 MAX phases have also attracted attention in recent years. For example, Nb₂AC (A = Al, Ge, Ga, Sn, In, As, P, S, and Cu) MAX phases were studied by Hadi et al.²³ to explore the elastic behavior and radiation tolerant behavior. Superconducting nature has been found in the Nb₂SnC, Nb₂InC, Nb₂AsC, and Nb₂SC phases²³ with the lowest superconducting temperature for Nb₂AsC.²² Bouhemadou et al.^24,25 performed first-principles calculations to study the structural and elastic properties of Nb₂InC and Nb₂GeC. The Nb₂InC phase was first synthesized by Jeitschko et al.²⁶ Nb₂AlC has attracted much attention as a viable material because of its better mechanical and thermal properties.^27,28 When compared with several MAX phases, it has been seen that Nb₂PC has higher elastic constants.¹⁷ The exfoliation possibility of Nb₂GaC and Nb₂InC into 2D MXene systems has been reported.²⁹ The electrochemical properties of Nb₂SnC have been investigated for use in a Li-ion electrolyte.³⁰ The noble transition metal Cu has also been selected as an A element in Nb₂CuC.³¹ Shein et al.³² explored the structural, electrical, and elastic properties of M₂GaC (M = Mo, V, and Nb). Cover et al.¹⁷ studied only the elastic and structural properties of Nb₂SiC, whereas some fundamental properties need to be investigated. Bouhemadou et al.³³ carried out a theoretical study to calculate the structural, elastic, electronic, and thermal properties of Nb₂SiC.

Moreover, so far, we know only the electronic and mechanical characteristics of Nb₂AC (A = Ga, Ge, P, and In) phases have been investigated, whereas Nb₂AC (A = Tl, Zn, and Cd) phases have been predicted to be stable via the calculation of formation energy,²¹ and the physical properties are not disclosed yet. Exploration of the physical properties of new materials carries the same significance as prediction of new materials: it is impossible to take any advantage of new materials unless their physical properties are brought out. Several essential physical aspects, important optical properties, mechanical anisotropy, Vickers hardness including Mulliken populations, and thermal properties of Nb₂AC (A = Ga, Ge, P, and In) are still unexplored. Mechanical anisotropy is critical for structural materials since it is linked to important mechanisms such as crack formation (and propagation), plastic deformation, and elastic instability, all of which limit their utility. The Vickers hardness describes the total strength properties of a solid's particular bonds. Mulliken population analysis is important to prove the existence of the combination of the ceramic and metallic nature. Understanding the thermal properties is important to forecast their appropriateness for use in extreme conditions. The optical characteristics of standard MAX phase compounds are necessary to predict their possible applications, for instance, as coating materials for protection from solar heating. These are the motivations behind this study, which demonstrates the significance of in-depth research on MAX phase carbides Nb₂AC (A = Ga, Ge, Tl, Zn, P, In, and Cd).

Therefore, we aimed to provide a theoretical insight into the MAX phase carbides Nb₂AC (A = Ga, Ge, Tl, Zn, P, In, and Cd), in which we will consider the first-time investigation of Nb₂AC (A = Tl, Zn, and Cd) and some important unexplored properties of Nb₂AC (A = Ga, Ge, P, and In) phases. Last of all, the calculated parameters of the titled phases are compared with those of the most known Nb-based phase, Nb₂AlC, to make this research a systematic one.

2 Computational methodology

The Nb₂AC (A = Ga, Ge, Tl, Zn, P, In, and Cd) carbides' physical properties have been calculated using the pseudopotential-based DFT, implemented in CASTEP (CAmbridge Serial Total Energy Package).^34,35 For the term of exchange-correlation, the GGA (generalized gradient approximation) of the PBE (Perdew–Burke–Ernzerhof)³⁶ and PBEsol (Perdew–Burke–Ernzerhof for solids)³⁷ were used. The PBE has been widely used for DFT calculations, whereas PBEsol gives a more accurate lattice constant for solids.³⁸ Recently, the effect of different functionals on the calculated values of the parameters has been reported, in which it is seen that the PBEsol gives more accurate results of the lattice parameters compared with other functionals for solids. The more accurate values of the lattice parameters give more accurate results, especially the mechanical behavior characterizing parameters. Thus, we have selected PBEsol in association with the mostly used GGA-PBE functional for this study.^39,40 The electronic structure was optimized by density mixing, and the atomic configuration was relaxed using BFGS (Broyden Fletcher Goldfarb Shanno).⁴¹ The electronic orbitals of Nb- 4d⁴ 5s¹, C- 2s² 2p², Ga- 4s² 4p¹, Ge- 3d¹⁰ 4s² 4p², Tl- 5d¹⁰ 6s² 6p¹, Zn- 3d¹⁰ 4s², P- 3s² 3p³, In- 4d¹⁰ 5s² 5p¹ and Cd- 4d¹⁰ 5s² were accomplished for pseudo-atomic calculations. The cutoff energy was set to 500 eV, and the convergence was assured using a k-point mesh of 9 × 9 × 2.⁴² The total energy self-consistent convergence was carried out using 5 × 10⁻⁶ eV per atom, with 0.01 eV Å as the maximum force on the atom. Again, 5 × 10⁻⁴ Å is used for an ionic displacement, which is the maximum range, with a maximum stress of 0.02 GPa. The phonon dispersion curves were calculated using the Density Functional Perturbation Theory (DFPT) linear-response method.⁴³ Most of our data have been compared to those of ref. 23 (and ²⁵), where the calculations were performed using the following inputs: exchange-correlation – GGA-PBE (LDA-CA), cut-off energy- 550 (350) eV, k-points-10 × 10 × 2 (9 × 9 × 2).

3 Results and discussion

3.1 Structural properties and phase stability

3.1.1 Structural properties. As shown in Fig. 1, the unit cell of Nb₂AC (A = Ga, Ge, Tl, Zn, P, In, Cd, and Al) compounds belongs to the hexagonal system wherein the space group is P6₃/mmc (No. 194).⁶ Two formula units are there in the unit cell. Each formula unit cell has four atoms. The atomic positions in the unit cell are as follows: Nb atoms at (1/3, 2/3, z_M), A atoms at (2/3, 1/3, 1/4) and the C atoms at (0, 0, 0). Additionally, z_M is an internal parameter; its value is listed in Table 1.

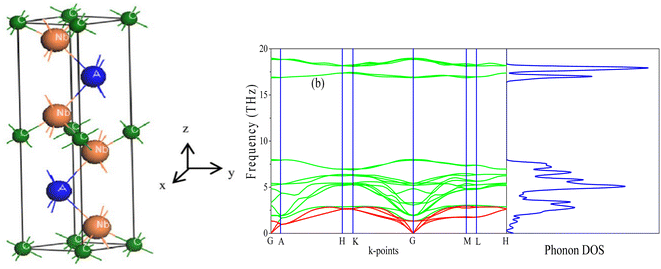Fig. 1 (a) The unit cell of Nb₂AC (A = Ga, Ge, Tl, Zn, P, In, Cd, and Al); (b) phonon dispersion curve and DOS of Nb₂GaC calculated using GGA PBEsol.

Table 1 Calculated lattice parameters (a and c), c/a ratio, internal parameter (Z_m), density (ρ), volume (Å), and distortion parameters of octahedral (O_d) and trigonal prisms (P_d) of Nb₂AC (A = Ga, Ge, Tl, Zn, P, In, Cd, and Al) MAX phases

Phases	a (Å)	c (Å)	Zm	c/a	Density (ρ)	Volume (Å^3)	Od	Pd	Ref.
a Calculated values using GGA PBE.^36b Calculated values using GGAPBEsol^37 and *calculated values using reported data.
Nb2GaC	3.145	13.73	0.0896	4.366	7.59	^a116.97	1.039	0.689	^aThis
	3.115	13.51		4.337		^b113.53	1.044	0.834	^bThis
	3.143	13.64		4.340		116.66	*1.044	*0.834	23
	3.13	13.56		4.332		115.05	*1.046	*0.836	6
Nb2GeC	3.244	12.69	0.095	3.914	7.76	115.75	1.086	0.904	^aThis
	3.194	12.77		3.998		112.83	1.066	0.890	^bThis
	3.255	12.59		3.868			*1.097	*0.912	32
	3.237	12.35		3.815			*1.109	*0.959	25
	3.228	12.76		3.953		115.10	*1.076	*0.898	23
Nb2TlC	3.229	12.74	0.0795	3.944	10.18	131.11	1.254	0.891	^aThis
	3.199	14.27		4.461		126.46	1.131	0.781	^bThis
Nb2ZnC	3.145	13.73	0.0875	4.366	7.43	117.58	1.060	0.829	^aThis
	3.117	13.53		4.341		113.83	1.066	0.833	^bThis
Nb2PC	3.299	11.59	0.0999	3.515	8.28	109.33	1.149	0.978	^aThis
	3.267	11.52		3.526		106.48	1.146	0.976	^bThis
	3.292	11.578		3.517		108.68	*1.139	*0.978	23
	3.28	11.5		3.506		107.15	*1.152	*0.979	6
Nb2InC	3.185	14.54	0.0821	4.563	11.49	127.69	1.103	0.799	^aThis
	3.152	14.37		4.559		123.67	1.079	0.799	^bThis
	3.186	14.528		4.560		127.72	*1.079	*0.799	23
	3.172	14.37		4.530		125.21	*1.085	*0.804	47
Nb2CdC	3.172	14.68	0.0830	4.628	8.06	127.87	1.055	0.790	^aThis
	3.140	14.45		4.602		123.37	1.060	0.794	^bThis
Nb2AlC	3.245	12.69	0.0897	3.911	6.34	115.74	1.142	0.902	^aThis
	3.102	13.79		4.446		114.99	1.021	0.819	^bThis
	3.12	13.93		4.463		117.41	*1.017	*0.817	23

---

Table 1 shows the lattice constants (a, c) for an optimized cell, internal parameters, and the hexagonal ratio (c/a) ratio of Nb₂AC (A = Ga, Ge, Tl, Zn, P, In, Cd, and Al). The fundamental polyhedrons of Nb₂AC (A = Ga, Ge, Tl, Zn, P, In, Cd, and Al) are studied using Hug's distortion indexes (DIs).^44,45 Two parameters- the distortion of octahedral (O_d) and trigonal prism (P_d) of the M₆X octahedrons and M₆A trigonal prisms, respectively, are used to describe the distortions in the structure of the 211 MAX phases using the following equations:⁴⁶

O_d = √3/2{4z_M²(c/a)² + 1/12}^1/2

P_d = 1/{1/3 + (1/4 − z_M)²(c/a)²}^1/2

The polyhedron would be ideal when both the octahedron and the trigonal parameters are equal to 1.⁴⁶ The distortion of the polyhedron is measured by the deviation from 1, where a low distortion value indicates a more stable structure.⁴⁶ Table 1 shows the value of the O_d and P_d of Nb₂AC (A = Ga, Ge, Tl, Zn, P, In, Cd, and Al). Table 1 also contains the O_d and P_d of Nb₂AC (A = Ga, Ge, P, In, and Al) as calculated from the reported lattice parameters. A very good consistency is observed for the previously studied phases, indicating the reliability of our present calculations. The comparison is not possible for Nb₂AC (A = Tl, Zn, and Cd) phases because of their first-time calculation. The accuracy of the present calculations is also revealed by the close agreement of the values of a and c [Table 1] of Nb₂AC (A = Ga, Ge, P, In, and Al) phases with previously reported values.^23,25,32

3.1.2 The dynamical stability. To check the dynamical stability of the titled phases, we have computed the phonon dispersion curves (PDC) and phonon density of states (PHDOS) of Nb₂AC (A = Ga, Ge, Tl, Zn, P, In, and Cd), displayed in Fig. 1(b) for Nb₂GaC and Fig. S1(a–f) [in the ESI file†] for the rest of the six compounds. The phonon frequency across the entire BZ is used to determine whether a compound is stable or not: positive frequencies indicate stability, whereas any negative frequencies indicate the instability of the compounds. As evident from Fig. 1(b) and S1(a–f),† the studied phases are dynamically stable owing to the non-existence of the negative frequency. In addition, one can obtain some more information from the PDCs. The PDCs have 24 vibrational modes that are caused by the eight atoms in the unit cell. There are only three acoustic modes, whereas the rest 21 are called optical modes. The dispersion curve for the lower three modes is of the form ω = νk at small k values, and it illustrates the sound wave's ω(k) relations. These modes are the part of the acoustic branch. The upper vibrational modes create the optical branch. The optical phonons are produced due to the atom's out-of-phase oscillations caused by photon-induced excitation. Acoustic modes have zero frequency just at the G point. No phononic band gap is found due to the overlap of the optical branches and acoustic modes. Furthermore, the PHDOS is presented alongside the PDCs, wherein the PDC's flat modes lead the sharp peaks. Peaks are diminished when the dispersion changes, either upward or downward. We have presented only the results for GGA PBEsol; GGA PBE results are not shown because of similarity in nature (Fig. 2).

Fig. 2 Comparison of (a) stiffness constants and (b) elastic moduli of Nb₂AC (A = Ga, Ge, Tl, Zn, P, In, Cd, and Al) MAX phases calculated using GGA PBEsol.

3.2 Mechanical properties

3.2.1 Stiffness constants and elastic moduli. We have calculated the elastic stiffness constants and the polycrystalline elastic moduli using the strain–stress method⁴⁸ to bring out the mechanical behavior of Nb₂AC (A = Ga, Ge, Tl, Zn, P, In, Cd, and Al). Checking mechanical stability is a must for solids before studying the mechanical properties. The Nb₂AC (A = Ga, Ge, Tl, Zn, P, In, Cd, and Al) phases belong to the hexagonal system, which need to satisfy the following requirements: C₁₁ > 0, C₃₃ > 0, C₄₄ > 0, C₁₁ − C₁₂ > 0, (C₁₁ + C₁₂)C₃₃ − 2(C₁₃)² > 0.^49,50 We have calculated the elastic constants and presented them in Table 2, revealing that the requirements mentioned earlier have been satisfied by the selected carbides. Thus, Nb₂AC (A = Ga, Ge, Tl, Zn, P, In, Cd, and Al) phases are considered to be mechanically stable. We may use the calculated stiffness constants to get some additional information. For instance, C₁₁ and C₃₃ measure the stiffness of the solid along the a-axis and c-axis when pressure is applied along [100] and [001] directions, respectively. Here, C₁₁ > C₃₃ for Nb₂AC (A = Ga, Ge, Tl, Zn, P, In, Cd, and Al) compounds, revealing the requirement of more pressure along the a-axis for deformation compared to the c-axis, whereas for Nb₂PC C₃₃ > C₁₁. Moreover, the inequality of C₁₁ and C₃₃ also indicates the anisotropic bonding strength. The hexagonal structure contains different atomic arrangements along the a- and c-axis, which is assumed to be responsible for the difference in the bonding strength along the a- and c-axis. One of the stiffness constants, C₄₄, is considered to be a better hardness predictor⁵¹ in comparison with other elastic constants. Thus, Nb₂PC is expected to be the hardest one with the highest C₄₄ (194 GPa), while Nb₂TlC is the softest one with the lowest C₄₄ (71 GPa). The C₁₁, C₃₃, and C₄₄ of Nb₂AC (A = Ga, Ge, Tl, Zn, In, and Cd) are lower than those of the most known Nb-based Nb₂AlC phase, but the values are greater for Nb₂PC. Better visualization of the differences among the values of the stiffness constants is done by presenting them in Fig. 2(a) for the GGA-PBEsol functional. Fig. S2(a)† shows the values calculated using GGA-PBE.

Table 2 Calculated stiffness constant (C_ij), bulk modulus (B), shear modulus (G), Young's modulus (Y), machinability index (B/C₄₄), Cauchy pressure (CP), Poisson^'s ratio (ν), and Pugh ratio (G/B)

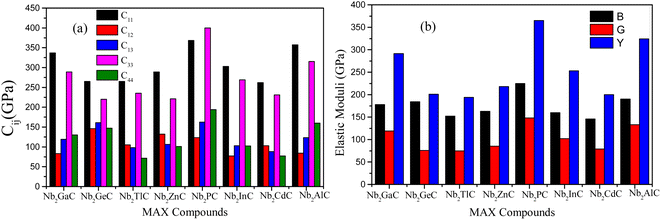
Parameters	Nb2GaC	Nb2GeC	Nb2TlC	Nb2ZnC	Nb2PC	Nb2InC	Nb2CdC	Nb2AlC	Ref.
a Calculated values using GGA PBE.^36b Calculated values using GGA PBEsol^37 and *calculated values using reported data.
C11 (GPa)	337	265	265	289	368	303	262	357	^aThis
	363	306	283	294	394	331	282	368	^bThis
	323	284			373	280		333	23
		308							25
C33 (GPa)	289	220	235	221	400	269	231	315	^aThis
	313	295	258	225	423	295	258	314	^bThis
	281	275			407	266		284	23
		306							25
C44 (GPa)	130	147	71	101	194	102	77	160	^aThis
	141	151	86	113	212	112	89	164	^bThis
	126	152			193	104		138	23
		177							25
C12 (GPa)	83	146	105	132	123	77	103	98	^aThis
	92	137	106	137	132	85	123	84	^bThis
	77	136			114	80		84	23
		133							25
C13 (GPa)	119	161	98	106	162	103	88	123	^aThis
	131	161	118	122	179	112	102	119	^bThis
	130	161			172	113		117	23
		168							25
CP (GPa)	−47	−1	34	31	−71	−25	26	−62	^aThis
	−49	−14	20	24	−80	−27	34	−80	^bThis
	*−49	*−16			*−79	*−24		*−54	23
		*−44							25
B (GPa)	178	184	152	163	225	160	146	190	^aThis
	194	203	168	173	242	175	163	188	^bThis
	178	195			230	160		176	23
		206							25
G (GPa)	119	76	75	85	148	102	79	133	^aThis
	128	101	84	88	153	112	85	140	^bThis
	114	101			150	96		122	23
		109							25
Y (GPa)	291	201	194	218	365	253	200	324	^aThis
	314	261	215	225	379	277	216	337	^bThis
	282	258			369	240		298	23
		279							25
ν	0.23	0.32	0.29	0.28	0.23	0.24	0.27	0.22	^aThis
	0.23	0.29	0.29	0.28	0.24	0.23	0.28	0.20	^bThis
	*0.24	*0.28			*0.23	*0.25		*0.22	23
		*0.28							25
G/B	0.67	0.41	0.49	0.52	0.65	0.63	0.54	0.70	^aThis
	0.66	0.49	0.50	0.51	0.63	0.64	0.52	0.74	^bThis
	*0.64	*0.52			*0.65	*0.60		*0.69	23
		*0.53							25
B/C44	1.36	1.25	2.14	1.61	1.15	1.56	1.89	1.18	^aThis
	1.38	1.34	1.95	1.53	1.14	1.56	1.83	1.15	^bThis
	*1.41	*1.28			*1.19	*1.54		*1.28	23
		*1.16							25

---

Furthermore, the stiffness constants are used to predict the ductile/brittle behavior of Nb₂AC (A = Ga, Ge, Tl, P, Zn, In, Cd, and Al) phases by computing the Cauchy pressure (CP). The difference between C₁₁ and C₄₄ is defined as the CP;⁵² a negative and positive value represents the brittle and ductile nature, respectively. Negative and positive values also indicate the directional covalent and ionic bonds, respectively. As evident from Table 2, Nb₂GaC, Nb₂GeC, Nb₂PC, Nb₂InC, and Nb₂AlC have directional covalent bonds and behave as brittle solids. On the contrary, Nb₂TlC, Nb₂ZnC, and Nb₂CdC phases behave as ductile solids with a positive CP. Though most MAX phases are brittle, a few of them, such as Zr₃CdB₄, Ti₂CdC, and Ti₂ZnX (X = C and N), have already been reported to be ductile.^53–55

Finally, the stiffness constants were used to calculate the polycrystalline elastic moduli. Hill's approximation⁵⁶ was used to compute the bulk modulus (B) and shear modulus (G), which is the average of the Voight⁵⁷ and the Reuss⁵⁸ models as follows: [B = (B_V + B_R)/2]; here, B_V = [2 (C₁₁ + C₁₂) + C₃₃ + 4C₁₃]/9 and B_R = C²/M, where C² = C₁₁ + C₁₂C₃₃ − 2C₁₃²; M = C₁₁ + C₁₂ + 2C₃₃ − 4C₁₃. B_V and B_R are expressed as the upper (Voight) and lower limit (Reuss) of B, respectively. Again, [G = (G_V + G_R)/2]; here, G_V = [12C₄₄ + 12C₆₆]/30 and G_R = (5/2) [C²C₄₄C₆₆]/[3B_VC₄₄C₆₆ + C²(C₄₄ + C₆₆)], where C₆₆ = (C₁₁ − C₁₂)/2. Here, like B, G_V and G_R are also expressed as the upper (Voight) and lower limit (Reuss) of G, respectively. The Poisson's ratio (υ) and Young's modulus (Y) are also computed from B and G by using these relations: Y = 9BG/(3B + G) and υ = (3B − Y)/(6B).^59,60

As known, the pure deformations (volume and shape) are studied by the bulk modulus (mostly known for the study of elastic response against pressure) and the shear modulus (mostly known for the study of rigidity of solids against pressure). It is seen from Table 2 that Nb₂PC (Nb₂CdC) has the highest (lowest) resistance against hydrostatic pressure, whereas the lowest resistance to plastic deformation is noted for Nb₂TlC among the studied compounds. However, the compounds can be ranked based on the values of B (calculated using GGA-PBEsol) as follows: Nb₂PC > Nb₂GeC > Nb₂GaC > Nb₂AlC > Nb₂InC > Nb₂ZnC > Nb₂TlC > Nb₂CdC, whereas the ranking for G will be as follows: Nb₂PC > Nb₂AlC > Nb₂GaC > Nb₂InC > Nb₂GeC > Nb₂ZnC > Nb₂CdC > Nb₂TlC. For Young's modulus, Y is the measure of the stiffness of solids that relates the stiffness with the thermal shock resistance (inverse relationship) of solids. Therefore, a solid with a high Y value indicates high stiffness and low thermal shock resistance (TSR).⁶¹ The Y-based ranking of the phases also follows the G-based ranking. Table 2 implies that Nb₂TlC exhibits high TSR, while Nb₂PC has the lowest TSR, followed by the Y-based reverse ranking among the herein-studied phases. Although these moduli do not indicate hardness, they are usually higher for harder materials.⁶² Compared to Y, B and G have a close relationship with the material's hardness. In some cases, these parameters are used to predict the hardness of solids using the following formulae: ,⁶³ and ,⁶⁴ Table 2 also includes the previously reported values.²³ As evident from Table 2, the obtained values are in good accord with reported values, ensuring the accuracy of the present calculation that helps other researchers to consider our calculated values as a reference for both application and research purposes. A comparison of the elastic moduli for the studied compounds is shown in Fig. 2(b).

3.2.2 The brittleness of Nb₂AC (A = Ga, Ge, Tl, Zn, P, In, Cd, and Al). The remarkable combination of metal and ceramic characteristics is the most excellent feature of MAX phases.⁶⁵ They are machinable, just like metals, as stated in the preceding section, and brittle, just like ceramic materials. But, some of them are also ductile,^53,55,66 making them more machinable and, consequently, more useful owing to easy shaping. By using the Pugh ratio (G/B)⁶⁷ and Poisson's ratio (υ),⁶⁸ the ductile/brittle characteristics of Nb₂AC (A = Ga, Ge, Tl, Zn, P, In, Cd, and Al) have been evaluated and are presented in Table 2. Pugh proposed a critical value of G/B ratio (0.571) for ductile (less than 0.571) and brittle (greater than 0.571) classification, whereas υ is used to separate the brittle (less than 0.26) and ductile (greater than 0.26) solids with a critical value of 0.26. As evident, Nb₂GaC, Nb₂PC, Nb₂InC, and Nb₂AlC are brittle, while Nb₂GeC, Nb₂TlC, Nb₂ZnC, and Nb₂CdC are ductile; the results are in good agreement with the CP results presented above and the previously reported results.^23,25

The Machinability Index (MI) is commonly used in the tribological sector to forecast a solid's performance and is defined as the B/C₄₄ ratio. The MI index is presented in Table 2. As evident, the MI of Nb₂TlC, Nb₂ZnC, and Nb₂CdC is higher than that of other studied phases owing to their ductile nature. Though Nb₂GeC is ductile, its C₄₄ is comparatively higher, which results in a lower MI value. Based on the values [Table 2], the titled phases are expected to be more machinable than the widely known Nb₂AlC phase except for Nb₂PC. The lowest MI is found for Nb₂PC, as expected, due to its highest C₄₄. In addition, a good relationship between machinability and ductility is observed as expected. The MI values are also different for PBE and PBEsol functions because of the different values of B and C₄₄. However, the obtained values of MI are comparable with those of some other 211 MAX phases, like Ti₂AlC, whose machinability index is 1.23.⁶⁹ Though some 211 phases exhibit a very high value of MI, such as W₂SnC (MI = 33.3) and Mo₂PbC (MI = 15.8),^17,70 it should be noted that their C₄₄ values are much lower (W₂SnC, 6 GPa, and Mo₂PbC, 10 GPa).¹⁷

3.2.3 Theoretical values of Vickers hardness. The Vickers hardness, due to the atomic bonds present within the solids, is the solid's ability to resist deformation under extreme conditions. Different factors, such as the strength of the atomic bonds, atomic arrangement, the structure of the solids, crystal defects, etc., determine the hardness of solids. The Vickers hardness of the Nb₂AC (A = Ga, Ge, Tl, Zn, P, In, Cd, and Al) MAX phases is calculated using Mulliken bond population based on Gou et al.,^71,72 which is mostly suitable for partial metallic systems like MAX phases. The relevant hardness formula is H^μ_v= 740(P^μ − P^μ′) (v^μ_b)^−5/3; here, P^μ indicates the μ type bond's Mulliken overlap population and , E_p indicates the energy of the pseudogap and E_F indicates the energy of the Fermi level. The volume of the μ-type bond is denoted by v^μ_b, which is calculated in the following way: . At last, the equation for Vickers hardness is as follows: ; n^μ = μ-type bond number. Table 3 shows the computed Vickers hardness of Nb₂AC (A = Ga, Ge, Tl, Zn, P, In, Cd, and Al). As shown in Table 3, Nb₂PC has higher Vickers hardness than other studied compounds, wherein Nb₂TlC possesses the lowest value of H_v, in agreement with mechanical parameters such as C₄₄ and G, which are assumed to be more related to the hardness of solids. The H_v values of Nb₂AC (A = Ga, Ge, Tl, Zn, In, Cd, and Al) are comparable with the exception of Nb₂PC, which has a much higher value of H_v. This can be explained on the basis of the bond overlap population (P^μ). As seen in Table 3, the P^μ of Nb₂PC is 1.01 and 0.98 for C–Nb and P–Nb bonds, respectively, which indicates that strong covalent bonding is found between both Nb–C and Nb–P atoms, whereas for Nb₂AC (A = Ga, Ge, Tl, Zn, In, Cd, and Al), P^μ is found only for Nb–C atoms, and no other significant covalent bond is noticed for these phases. Thus, both significant covalent bonding among Nb–C and Nb–P atoms is assumed to be responsible for such higher hardness. However, the variation in H_v of Nb₂AC (A = Ga, Ge, Tl, Zn, In, Cd, and Al) phases is due to the combined effect of the variation in both bond population P^μ and bond length d^μ.

Table 3 Calculated Mulliken bond number n^μ, bond length d^μ, bond overlap population P^μ, metallic population P^μ′, bond volume v^μ_b, bond hardness H^μ_vof the μ-type bond and Vickers hardness H_v

Compounds	Bond	n^μ	d^μ (Å)	P^μ	P^μ′	v^μb (Å^3)	H^μv (GPa)	Hv (GPa)	Ref.
a Calculated values using GGA PBE.^36b Calculated values using GGA PBEsol.^37
Nb2GaC	C–Nb	4	2.177	0.93	0.0223	0.0036	2.418	2.418	^aThis
			2.167	0.93	0.0209	0.0037	2.55	2.55	^bThis
Nb2GeC	C–Nb	4	2.208	0.99	0.0443	0.0037	1.498	1.498	^aThis
			2.183	1.02	0.0100	0.0038	2.86	2.86	^bThis
Nb2TlC	C–Nb	4	2.194	0.94	0.0358	0.0029	1.994	1.994	^aThis
			2.176	0.96	0.0207	0.0031	2.19	2.19	^bThis
Nb2ZnC	C–Nb	4	2.177	0.92	0.0504	0.0036	2.297	2.297	^aThis
			2.160	0.91	0.0741	0.0037	2.33	2.33	^bThis
Nb2PC	C–Nb	4	2.229	1.01	0.0195	0.0187	13.706	9.312	^aThis
	P–Nb	4	2.580	0.98		0.0089	6.326		^aThis
	C–Nb	4	2.211	1.00	0.0166	0.0200	14.56	10.02	^bThis
	P–Nb	4	2.557	0.98		0.0096	6.89		^bThis
Nb2InC	C–Nb	4	2.193	0.96	0.0184	0.0031	2.160	2.160	^aThis
			2.174	0.95	0.0105	0.0032	2.82	2.82	^bThis
Nb2CdC	C–Nb	4	2.177	0.99	0.0206	0.0031	2.224	2.224	^aThis
			2.160	0.93	0.0648	0.0032	2.11	2.11	^bThis
Nb2AlC	C–Nb	4	2.165	0.98	0.0179	0.0037	2.63	2.63	^aThis
			2.166	1.00	0.0112	0.0037	2.71	2.71	^bThis

---

3.3 Electronic properties, and Mulliken atomic and bond population analysis

3.3.1 Electronic properties. The electronic conductivity, contribution from different states, and nature of atomic bonding can be revealed by studying the electronic band structure, total and partial density of states (DOS), and Mulliken's population analysis. We have calculated the electronic band structure to predict the metallic nature of the titled MAX compounds. Fig. 3(a), (b) and S3† [calculated using PBEsol] show the calculated electronic band structure of Nb₂AC (A = Ga, Ge, Tl, Zn, P, In, Cd, and Al), in which the Fermi level (E_F) is represented by a horizontal dashed line. The green curves indicate the Fermi level crossing bands and blue curves denote the bands in the valence and conduction bands. As seen from Fig. 3(a), (b) and S3(a)–(f),† due to the overlapping of the conduction and valence bands, there is no band gap at the Fermi level; thus, the Nb₂AC (A = Ga, Ge, Tl, Zn, P, In, Cd, and Al) phases are considered to be metallic solids. The pathways Γ-A, H-K, and M-L show the energy dispersion for the c-direction. On the other hand, the pathways A-H, K-Γ, Γ-M, and L-H show energy dispersion in the basal planes. It has been seen from Fig. 3(a), (b) and S3(a)–(f)† that the energy dispersion is smaller in the c-direction than that of the basal plane (ab-plane); thus, the electronic conductivity in the basal plane is higher than that of the c-direction.⁷³ The effective mass tensor is assumed to be higher in the c-direction than that of the basal plane, which is responsible for smaller dispersion in the c-direction.⁷⁴ Consequently, the anisotropic nature of electronic conductivity is observed in the herein-studied phases, a common feature of the MAX phases, including Nb₂AlC.^25,72

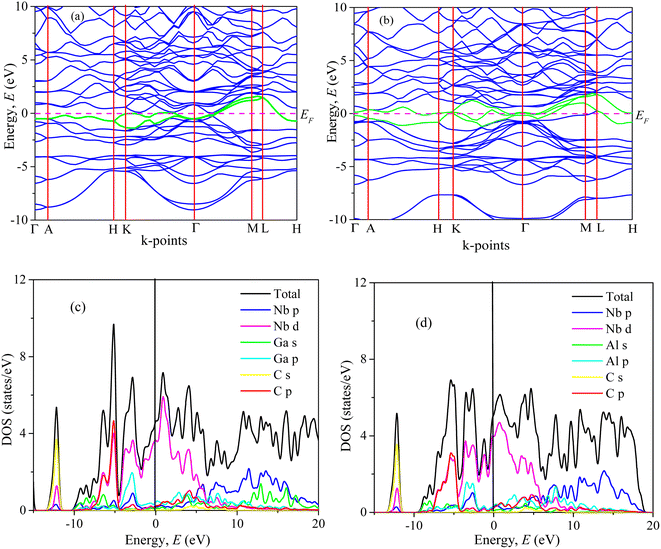Fig. 3 Band structure, and total and partial DOS of (a, c) Nb₂GaC and (b, d) Nb₂AlC calculated using GGA PBEsol.

We have also computed the total and partial density of states (DOS) of Nb₂AC (A = Ga, Ge, Tl, Zn, P, In, Cd, and Al), which are also shown in Fig. 3(c), (d) and S4(a)–(f)† [calculated using PBEsol]. Here, E_F is the Fermi level, where the DOS values are 3.2, 3.3, 4.0, 3.5, 3.0, 3.1, 2.8, and 3.0 for Nb₂GaC, Nb₂GeC, Nb₂TlC, Nb₂ZnC, Nb₂PC, Nb₂InC, Nb₂CdC, and Nb₂AlC, respectively. The computed compound's DOSs of the studied phases are found to be similar to those of reported MAX phases^25,72 and Nb₂AlC, which is presented here for comparison.

We have also computed the partial density of states (PDOS) to understand better the chemical bonding of Nb₂AC (A = Ga, Ge, Tl, Zn, P, In, Cd, and Al). Fig. 3(c), (d), and S4(a)–(f)† [calculated using PBEsol] show the PDOS for Nb₂AC. As seen, C-2s is not involved in the DOS at E_F. As a result, the conduction properties are not attributed to carbon. On the other hand, at the Fermi level, Nb-d electrons contribute significantly to the DOS; therefore, the conduction properties ought to be involved in Nb. The A-p (A = Ga, Ge, Tl, Zn, P, In, and Cd) electrons are also involved in the conduction mechanism, with a much lower level of contribution. C-p states also slightly contribute to the conduction properties. This outcome is in line with an earlier MAX phase reported.⁶⁸ The degenerate states concerning both lattice sites and angular momentum indicate that a covalent interaction exists between the atoms of the compounds. Hybridized states include C-p and Nb-d and A (A = Ga, Ge, Tl, Zn, P, In, Cd, and Al) p and Nb d states. Moreover, some ionic characteristics can be anticipated because of the disparity in electro-negativity between the constituent atoms. There is a covalent–ionic combination in the bonding character, which has been explained in Section 3.3.2. When compared to Nb-d and A-p states, the hybridization peak of Nb-d and C-p lies in the lower energy side, as seen in the PDOS; consequently, covalent bonding due to hybridization between Nd-d and C-p states is stronger than that of Nb-d and A p states (A = Ga, Ge, Tl, Zn, P, In, and Cd). The peak position of hybridization between Nb-X and Nb and A states is also responsible for the variation in the hardness of the studied phases. For example, the hybridization among Nb-d, P-p and C-p states is observed in the lowest energy side (below – 5 eV), which results in strong hybridization among them, and a higher bond overlap population is found, which results in the hardest phase of Nb₂PC among the considered phases. The same hybridization peak for other phases is found to appear at an energy scale of above −5 eV. Similar results are also reported for the MAX phases.^25,72 Additionally, we demonstrated the PDOS of Nb₂AlC, which is similar to those of Nb₂AC (A = Ga, Ge, Tl, Zn, P, In, Cd, and Al).

3.3.2 Mulliken's atomic and bond population analysis. The charge transfer mechanism can be understood by analyzing the atomic population. Mulliken's atomic populations are presented in Table 4 [calculated using GGA PBEsol] and Table S1† [calculated using GGA PBE]. As seen, C possesses a negative charge for each phase, whereas Nb and A (A = Ga, Ge, Tl, Zn, P, In, Cd, and Al) have positive charges, which indicates that the charges are transferred from A (A = Ga, Ge, Tl, and Zn) and Nb to the C atoms. The charge transfer mechanism in these phases indicates the existence of ionic bonding within them. The BOP (bond overlap population) study quantitatively provides bonding and anti-bonding strength.⁷⁵ A positive BOP stands for covalent bonds, and a negative BOP value certifies ionic bonds. As evident from Table 4, a strong covalent bond is formed between Nb and C atoms for each of the titled phases. For Nb₂PC, a strong covalent bond is also expected to be formed in association with the Nb–C bonds, which is responsible for a much higher hardness value compared to other phases presented here. Thus, electronic charge transfer ensured the presence of ionic bonding. In contrast, the high positive value of BOP revealed the existence of covalent bonding, a common characteristic of the MAX phase materials.

Table 4 Mulliken atomic and bond overlap population (BOP) calculated using GGA PBEsol

Phases	Atoms	s	p	d	Total	Charge (e)	Bond	Bond number n^μ	Bond overlap population P^μ
Nb2GaC	C	1.43	3.22	0.00	4.65	−0.65	C–Nb	4	0.93
	Ga	0.88	1.84	9.99	12.71	0.29
	Nb	2.27	6.62	3.94	12.82	0.18
Nb2GeC	C	1.45	3.23	0.00	4.67	−0.67	C–Nb	4	1.02
	Ge	0.99	2.53	0.00	3.52	0.48
	Nb	2.35	6.56	3.99	12.90	0.10
Nb2TlC	C	1.43	3.22	0.00	4.65	−0.65	C–Nb	4	0.96
	Tl	3.11	7.84	9.92	20.87	0.13
	Nb	2.25	6.58	3.92	12.74	0.26
Nb2ZnC	C	1.43	3.23	0.00	4.66	−0.66	C–Nb	4	0.91
	Zn	0.53	1.32	9.93	11.78	0.22
	Nb	2.28	6.63	3.87	12.78	0.22
Nb2PC	C	1.44	3.20	0.00	4.63	−0.63	C–Nb	4	1.00
	P	1.57	3.45	0.00	5.02	0.04	P–Nb	4	0.98
	Nb	2.24	6.45	3.98	12.67	0.33
Nb2InC	C	1.43	3.22	0.00	4.65	−0.65	C–Nb	4	0.95
	In	0.99	1.81	9.97	12.77	0.23
	Nb	2.22	6.63	3.94	12.79	0.21
Nb2CdC	C	1.43	3.23	0.00	4.66	−0.66	C–Nb	4	0.93
	Cd	0.55	1.28	9.91	11.73	0.27
	Nb	2.29	6.65	3.87	12.81	0.19
Nb2AlC	C	1.45	3.22	0.00	4.67	−0.67	C–Nb	4	1.00
	Al	0.97	1.83	0.00	2.80	0.20
	Nb	2.22	6.57	3.98	12.76	0.24

---

3.4 The elastic anisotropy

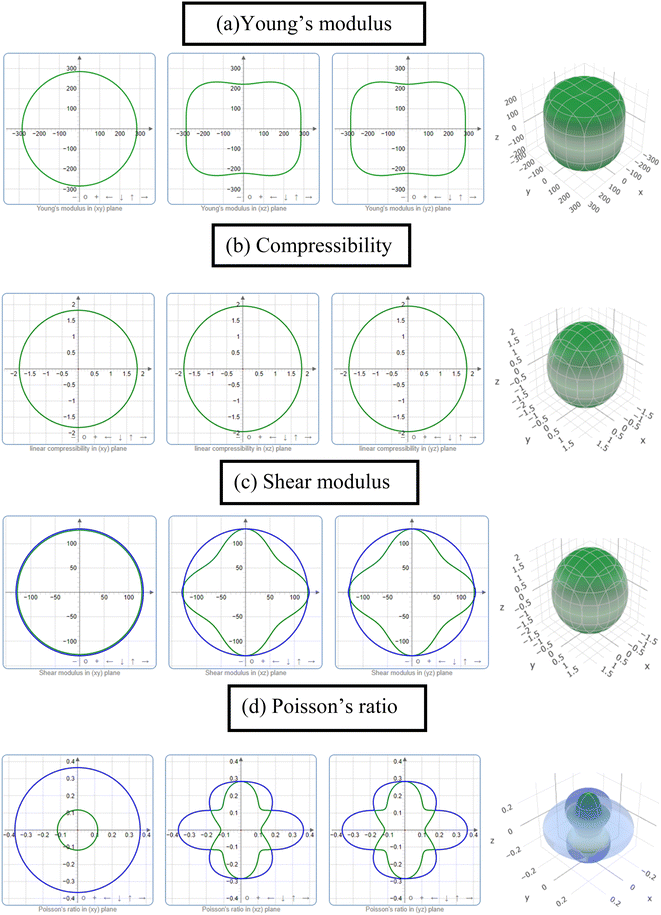
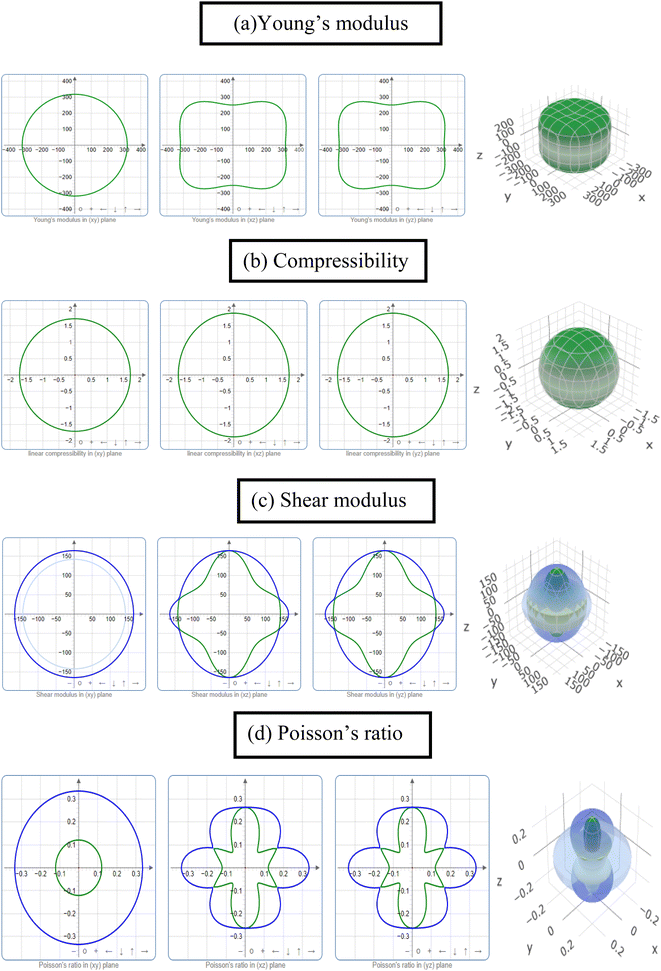
The study of the elastic anisotropy of the MAX phases is essential because of their potential use in practical applications. Some important physical processes, such as plastic deformation, unusual phonon modes, dislocation dynamics, crack behavior, etc., are caused by mechanical anisotropy in solids.^76,77 Since the values of C₁₁ and C₃₃ are unequal [Table 2], other elastic moduli are calculated using these elastic constants. Thus anisotropic nature of the elastic properties is expected for these compounds. These facts encourage us to study the mechanical anisotropy of the titled carbides in the 211 MAX phases. It is possible to demonstrate the level of anisotropy by plotting the elastic moduli in different directions. In this manner, we used the ELATE code⁷⁸ to compute the values of Young's modulus, compressibility, shear modulus, and Poisson's ratio, which are presented in Fig. 4(a–d) for Nb₂GaC, 5(a–d) for Nb₂AlC, S5(a–d) for Nb₂GeC, S6(a–d) for Nb₂TlC, S7(a–d) for Nb₂ZnC, S8(a–d) for Nb₂PC, S9(a–d) for Nb₂InC and S10(a–d)† for Nb₂CdC. The 3D and 2D plots will help to explain the anisotropic nature. The isotropic nature of solids is represented by the sphere in 3D plots and the circle in 2D plots. In contrast, the anisotropy is indicated by a departure from a perfect circle or sphere, and the degree depends on the departure level. Young's modulus (Y) is anisotropic in the xz and yz planes but isotropic in the xy planes, as seen in Fig. 4(a), 5(a), S5(a), S6(a), S7(a), S8(a), S9(a), and S10(a).† Y has minimum values at the vertical axis of the xz and yz planes and a maximum value at an intermediate angle of 45° of those axes. Fig. 4(b), 5(b), S5(b), S6(b), S7(b), S8(b), S9(b), and S10(b)† depict the compressibility (K), which exhibits a similar anisotropic character to Y. The compressibility (K) is isotropic in the xy plane but anisotropic in the xz and yz planes, where K has maximum values on the axes of the xz and yz planes and a minimum value at an angle of 45° to those axes. For the considered compounds presented in Fig. 4(c), 5(c), S5(c), S6(c), S7(c), S8(c), S9(c), and S10(c),† the shear modulus (G) displays two surfaces for both 2D and 3D representations. The green line shows the minimum values for a 45° angle, while the blue line shows the maximum values for the same angle. In the xy and yz planes, G is maximum along both axes, with the minimum value found at an angle of 45° between the axes. In the xy plane, it is seen to be isotropic. In Fig. 4(d), 5(d), S5(d), S6(d), S7(d), S8(d), S9(d), and S10(d),† a different anisotropic characteristic is seen for Poisson's ratio. Like G, there are two surfaces for both 2D and 3D representations, except Nb₂GeC. The blue line indicates maximum values at a 45° angle, whereas the green line indicates minimum values at the same angle for all compounds except Nb₂GeC. For Nb₂GeC, the green line indicates positive values, where the values are maximum at an angle of 45°, and the red line indicates maximum negative values for the same angle. Poisson's ratio is also shown to be anisotropic, with the minimum values found within the vertical axes in the xz and yz planes. In contrast, the maximum values are found within the horizontal axes for both compounds. In the xy plane, Poisson's ratio is found to be isotropic.

Fig. 4 The 2D and 3D plots of (a) Y, (b) K, (c) G and (d) υ of Nb₂GaC for GGA PBEsol.

Fig. 5 The 2D and 3D plots of (a) Y, (b) K, (c) G and (d) υ of Nb₂AlC for GGA PBEsol.

Other important anisotropic indices have also been calculated. Using the following relationships, the three shear anisotropic factors A_i (i = 1, 2, and 3) are computed: 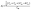, , and A₃ = A₁. 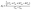,⁷⁹ for the {100}, {011}, and {001}, respectively. Using the following relations, the elastic anisotropy for the bulk modulus (B_a and B_c) across both the a and c-axes is computed:⁸⁰ and 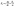, where A = 2(C₁₁ + C₁₂) + 4C_13α + C₃₃α², where . Additionally, the elastic anisotropy for the ratio of the linear compressibility coefficients (k_c/k_a) [k_a for a and k_c for c-directions] is computed using the following relation:⁸¹ . Table 5 and S2† show the value of the obtained anisotropy factors. The value of A_i = 1 implies isotropy, otherwise anisotropic nature; thus, the Nb₂AC (A = Ga, Ge, Tl, Zn, P, In, Cd, and Al) compounds are anisotropic owing to their non-unit (1) value. The equality of k_c and k_a, and B_a and B_c also implies the isotropic nature. As evident, these parameters also suggest the anisotropic nature of the studied compounds. Furthermore, the percentage anisotropies of compressibility and shear modulus were computed as follows:⁸² and , also certifying the anisotropic nature.

Table 5 Anisotropy factors A_1, A_2, A_3, k_c/k_a, B_a, and B_c, percentage anisotropy factors A_G and A_B and universal anisotropic index A^u, calculated values using GGA PBESOL^{37 a}

Phase	A1	A2	A3	Ba	Bc	Kc/ka	AB	AG	A^u	Ref.
a *Calculated values using reported data.
Nb2GaC	0.658	1.041	0.685	491.61	1130.96	1.06	0.001	0.013	0.130	This
	*0.585	*1.024	*0.599	*505.19	*1483.25	0.93	*0.001	*0.022	*0.224	23
Nb2GeC	0.429	1.787	0.767	475.71	1792.77	0.90	0.003	0.057	0.607	This
	*0.358	*2.054	*0.734	*448.88	*1317.91	0.86	*0.004	*0.085	*0.932	23
	*0.359	*2.023	*0.723	*470.79	*2125.46	*0.76	*0.001	*0.084	*0.922	*^25
Nb2TlC	0.839	0.972	0.816	420.78	1034.08	1.09	0.002	0.003	0.031	This
Nb2ZnC	0.579	1.439	0.833	468.84	869.98	1.82	0.012	0.027	0.296	This
Nb2PC	0.515	1.618	0.833	563.72	2019.99	0.69	0.004	0.038	0.407	This
	*0.529	*1.490	*0.789	*520.15	*2105.85	0.61	*0.007	*0.033	*0.358	*^23
Nb2InC	0.830	0.911	0.756	448.67	951.08	1.05	0.006	0.005	0.051	This
	*0.705	*1.037	*0.731	*387.65	*1095.07	0.88	*0.005	*0.008	*0.095	25
Nb2CdC	0.960	1.119	1.074	437.09	782.85	1.29	0.003	0.002	0.023	This
Nb2AlC	0.614	1.155	0.709	487.51	986.40	1.09	0.003	0.016	0.165	This
	0.656	1.074	0.704	*438.87	*1042.45	0.95	0.006	0.012	0.129	23

---

Finally, we have calculated the universal anisotropy index A^U based on the Voight, V (upper limit), and Reuss, R (lower limit), models using the following relation:⁸³ If the value of A^U is zero, it implies isotropic behavior, whereas a non-zero value reveals anisotropic behavior; the non-zero values of A^U reveal the anisotropic behavior of the studied compounds. In summary, we have found the anisotropic nature of Nb₂AC (A = Ga, Ge, Tl, Zn, P, In, Cd, and Al) compounds.

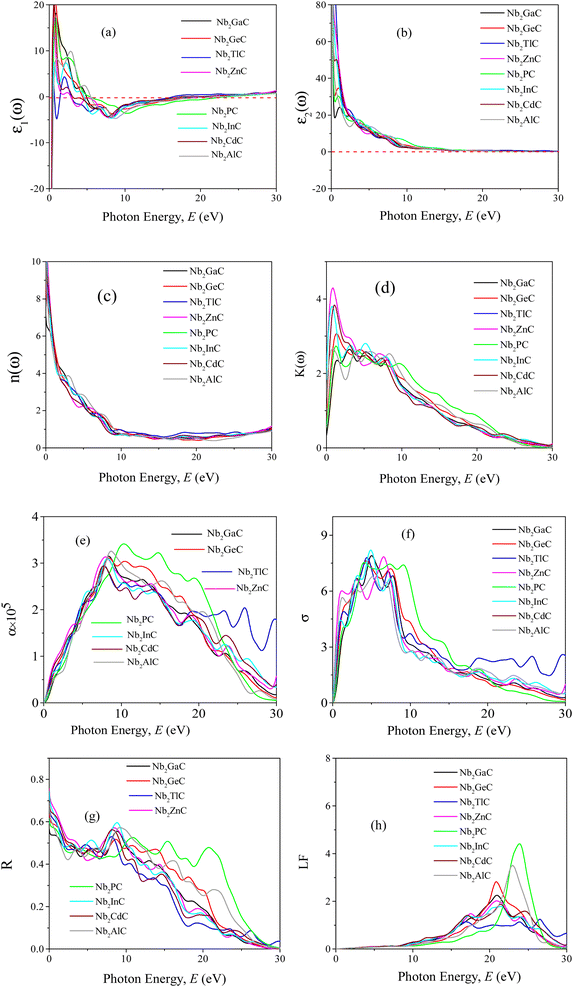
3.5 Optical properties

The MAX phase materials have already been identified as prospective candidates for use as a coating layer to lessen solar heating.⁸⁴ They have also been used in other sectors, such as optical systems.⁸⁴ Therefore, it is also hoped that the studied carbides will also be appropriate for the above mentioned ones. We have computed a variety of optical constants in an approach to reveal the optical response of these carbides when electromagnetic radiation is incident upon them.

To estimate the optical properties, it is essential to use the equation ε(ω) = ε₁(ω)+iε₂(ω). Based on the electronic states of each momentum matrix element's occupied and unoccupied states, it is possible to state that ε₂(ω) is the imaginary portion of the related dielectric function and fully calculated by CASTEP using the formula below:

where the vector u designates how the incident electric field is polarized, ω represents the frequency of light, e stands for the electronic charge, ψ^c_k represents the conduction band wave function and ψ^v_k indicates the valence band wave function. By using the Kramers–Kronig transform, the real part (ε₁) is obtained from the imaginary part ε₂ (ω). The refractive index (n), extinction coefficient (k), absorption coefficient (α), reflectivity (R), photoconductivity (σ) and loss function (LF) were calculated by the following equations:^85–87

A Drude correction must be made for the study of the dielectric function of metallic materials, which is usually done by adding the plasma frequency and a broadening factor during first-principles calculations.^88,89 Because of the metallic nature of the studied carbides, a damping of 0.05 eV and plasma frequency of 3 eV were used to enhance the computed spectra lower energy side. Moreover, a Gaussian smearing value of 0.5 eV was also used to smear out the k-points around the Fermi level. The calculated optical constants of the titled phases are presented in Fig. 6, along with those of Nb₂AlC for comparison. The real part ε₂(ω) of the dielectric function, where the low energy peaks are attributed to electron intra-band transitions,⁹⁰ is shown in Fig. 6(a). Because of the electron intra-band transitions, the assigned value for each peak is less than 1 eV. The materials exhibit Drude-like behavior, as indicated by the massive negative values of ε₁(ω), whereas inter-band transitions occur at higher energies. Fig. 6(b) shows the imaginary part of the dielectric function ε₂(ω). At around 16 eV, it has been seen that the values of ε₂(ω) pass through zero from above. This is another example of the compound's metallic nature. A similar nature of the real and imaginary parts of the dielectric function was reported for the most studied MAX phase Ti₃SiC₂ (ref. 84) and widely used 211 MAX phase Ti₂AlC.⁹¹ The refractive index, n(ω), of Nb₂AC (A = Ga, Ge, Tl, Zn, P, In, Cd, and Al) is depicted in Fig. 6(c). This significant optical constant contributes to the design of optical systems like photonic crystals and wave guides. As shown in Fig. 6(c), the static value of n (0) for Nb₂AC (A = Ga, Ge, Tl, Zn, P, In, Cd, and Al) is 7.0, 8.9, 9.4, 11, 8.3, 10.9, 9.5 and 8.9, respectively. Fig. 6(d) shows the extinction coefficient, k(ω), for the Nb₂AC (A = Ga, Ge, Tl, Zn, P, In, Cd, and Al) MAX phases. The extinction coefficient, k(ω), is used for measuring the loss of electromagnetic radiation due to absorption and is found to vary similarly to ε₂(ω), like other MAX phases.^89,90 In Fig. 6(e), the absorption coefficient of Nb₂AC (A = Ga, Ge, Tl, Zn, P, In, Cd, and Al) MAX phases is illustrated, where the spectra are shown to increase from zero photon energy due to the metallic behavior of the researched compounds. The spectra are seen to increase as incident energy increases. It showed the strongest absorption region in the spectral range of 7–10 eV; it decreases with a further increase in photon energy. Because of the high absorption coefficients in the high energy range (7–10 eV), Nb₂AC (A = Ga, Ge, Tl, Zn, P, In, Cd, and Al) MAX phases can be considered potential absorbing materials in this energy range. The photoconductivity of Nb₂AC (A = Ga, Ge, Tl, Zn, P, In, Cd, and Al) is shown in Fig. 6(f), which is also found to start at the beginning from zero photon energy because of the metallic behavior of the selected phases. The band structure and electronic DOS results are well consistent with the absorption coefficient and photoconductivity results.

Fig. 6 (a) Real part (ε₁) and (b) imaginary part (ε₂) of dielectric function (ε), (c) refractive index (n), (d) extinction coefficient (k), (e) absorption coefficient (α), (f) photoconductivity (σ), (g) reflectivity (R), and (h) loss function (LF) of Nb₂AC (A = Ga, Ge, Tl, Zn, P, In, Cd, and Al) MAX phases as a function of photon energy calculated using GGA PBEsol.

MAX phases are used as coating materials to reduce solar heating, which is one of their most significant applications. The reflectivity of the target materials has been investigated to disclose this possibility, shown in Fig. 6(g). It was reported by Li et al.^84,92 that if a MAX compound has a reflectivity of 44% in the visible range, it will be able to reduce solar heating. The reflectivity spectrum for Nb₂GaC begins with a value of 0.569 (56.9%), the minimum value among the studied phases. Nb₂TlC has the highest value, which is 0.982 (98.2%). For Ti₃SiC₂, the spectrum has an initial value of ∼0.75 (75%), going down at around 1 eV, and then remaining almost constant up to 6 eV, whereas for Nb₂AlC, it starts with an initial value of 0.68 (68%), which is down to below 44% at around 2.1 eV. Though Nb₂AC (A = Ga, Ge, and P) has a lower initial value of R than Nb₂AlC, neither of their spectra are down to less than 44% up to the visible light range. However, each spectrum of the titled compounds exhibits average higher values (also higher than 44% up to the visible light range) than that of Nb₂AlC. Thus, in comparison with Ti₃SiC₂ and Nb₂AlC, it can be concluded that Nb₂AC (A = Ga, Ge, Tl, Zn, P, In, and Cd) compounds are candidates for use as cover materials to lessen solar heating. In the energy range of 5.5 to 11 eV, there are a few sharp peaks in the reflectivity spectra, and around 30 eV, reflectivity finally approaches zero.

When electrons move through materials, they lose their energy. An optical constant called the loss function is used to evaluate this type of energy loss. Fig. 6(h) displays the calculated loss functions for the aforementioned MAX phase compounds. The loss function's peak frequency is referred to as the plasma frequency (ω_p), which is observed at 20.89, 20.92, 16.38, 17.50, 23.91, 20.54, 17.21 and 23.11 for Nb₂GaC, Nb₂GeC, Nb₂TlC, Nb₂ZnC, Nb₂PC, Nb₂InC, Nb₂CdC, and Nb₂AlC, respectively. In a loss function, this energy is determined by its characteristic frequency when ε₁(ω) and ε₂(ω) both pass through zero from below and above, respectively. Reflectivity also identifies the falling edges. This is the critical value that is established by the plasma frequency when the materials are transformed into transparent dielectrics from the metallic system. We have also calculated the optical constant using GGA PBE, but not been shown due to their similar nature.

3.6 Thermal properties

MAX phases are excellent candidates for applications at high-temperature because of their excellent mechanical properties at high temperatures. Therefore, the study of the basic parameters required to predict their application carries significant interest. The Debye temperature (Θ_D), minimum thermal conductivity (K_min), Grüneisen parameter (γ), melting temperature (T_m), etc. of the researched compounds have been calculated for predicting their high temperature applications.

The Debye temperature (Θ_D), one of the key characteristic parameters of solids, is closely related to the material's bonding strength, melting temperature, thermal expansion, thermal conductivity, etc. The Θ_D of studied phases has been calculated using sound velocity following Anderson's method.⁹³ The relevant formulae are as follows:

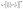where M is the molar mass; n is the number of atoms in the molecules; ρ is the mass density; h is Planck's constant; k_B is the Boltzmann constant; N_A is Avogadro's number; and v_m is the average sound velocity. In an isotropic material, the v_m can be computed from the longitudinal sound velocities (v_l) and transverse sound velocities (v_t) using the given relationship: ; v_l and v_t can be obtained from their relationships with the polycrystalline bulk modulus (B) and shear modulus (G): v_l = [(3B + 4G)/3ρ]^1/2 and v_t = [G/ρ]^1/2. The calculated Θ_D of Nb₂AC (A = Ga, Ge, Tl, Zn, P, In, Cd, and Al) is presented in Table 6 for GGA PBEsol and Table S3† for GGA PBE.

Table 6 Calculated density (ρ), longitudinal, transverse and average sound velocities (v_l, v_l, and v_m, respectively), Debye temperature (Θ_D), minimum thermal conductivity (K_min) and Grüneisen parameter (γ) of Nb₂AC (A = Ga, Ge, Tl, Zn, P, In, Cd, and Al)^a

Phases	ρ (g cm^−3)	vl (m s^−1)	vt (m s^−1)	vm (m s^−1)	ΘD (K)	Kmin (W mK^−1)	Γ	Tm (K)	Ref.
a Calculated values using GGA PBESOL^37 and *calculated values using reported data.
Nb2GaC	7.59	6931	4106	4547	548	1.05	1.41	1913	This
Nb2GeC	7.76	6596	3607	4022	485	0.93	1.71	1715	This
		6632	3695	4114	508	*0.95	*1.66	*1737	25
Nb2TlC	10.18	5244	2872	3202	372	0.68	1.71	1590	This
Nb2ZnC	7.43	6248	3440	3834	461	0.88	1.66	1574	This
Nb2PC	8.28	7337	4297	4764	640	1.29	1.45	2171	This
Nb2InC	11.49	5311	3121	3459	483	0.95	1.41	1790	This
Nb2CdC	8.06	5855	3247	3616	424	0.79	1.65	1587	This
Nb2AlC	6.34	7315	4405	4871	592	1.46	*1.37	1800	94

---

As shown in Table 6, Θ_D is highest for Nb₂PC and lowest for Nb₂TlC. The ranking of the compounds roughly followed the hardness-based ranking, which fairly agrees with the hardness and Debye temperature relationship.⁹⁵ The Θ_D of the titled compounds is lower than that of Nb₂AlC, except Nb₂PC. Recently, Hadi et al.⁹⁶ reported a MAX (V₂SnC) phase as a TBC material with a Θ_D value of 472 K. Among the studied compounds, a much lower Θ_D is found for only Nb₂TlC (372 K) and Nb₂CdC (424 K); others have Θ_D either comparable to or higher than that of V₂SnC. In addition, the Θ_D of Y₄Al₂O₉, a well-known TBC material, is 564 K.⁹⁷ Thus, Θ_D values of Nb₂AC (A = P, Al, Ga, and Ge) phases [Table 6] are comparable with that of Y₄Al₂O₉.⁹⁷

The minimum thermal conductivity (K_min) is defined as the constant value of thermal conductivity at high temperature. As its name suggests, this conductivity is minimum owing to the breaking of the pairing of phonons at high temperature. Calculation of minimum thermal conductivity is essential for predicting the use of solids at high temperature. It has already been established that the MAX phases are suitable for use in high temperature technology as a coating layer (TBC). Thus, calculation of K_min is also required for the titled phases. We have calculated the K_min of Nb₂AC (A = Ga, Ge, Tl, Zn, P, In, Cd, and Al) compounds using the following equation:⁹⁸ , where k_B is the Boltzmann constant, v_m is the average phonon velocity, N_A is Avogadro's number, and ρ is the crystal's density, respectively, as listed in Table 6. The order of the K_min value is expected to be as follows: Nb₂AlC > Nb₂PC > Nb₂GaC > Nb₂InC > Nb₂GeC > Nb₂ZnC > Nb₂CdC > Nb₂TlC; that is, the K_min values of the studied compounds are lower than that of Nb₂AlC, indicating more suitability of the phases as the smaller the K_min is, the more suitable as TBC materials. It should be noted that the K_min of V₂SnC is 1.20 Wm⁻¹ K⁻¹ and Y₄Al₂O₉ is 1.13 Wm⁻¹ K⁻¹.^96,98 Thus, it is expected that the K_min value suggests the studied compounds as suitable TBC materials.

An essential thermal parameter that helps to explain the anharmonic effects of lattice dynamics is the Grüneisen parameter (γ); lower anharmonic effects are expected for the solids used at high temperature. Therefore, we have calculated γ of Nb₂AC (A = Ga, Ge, Tl, Zn, P, In, Cd, and Al) compounds using the following equation:⁹⁹ . According to Table 6, the obtained values of γ are lying in between 0.85 and 3.53, which is in line with what is predicted for the polycrystalline materials with ν values in the range of 0.05–0.46.¹⁰⁰ Besides, the low values of γ confirm the lower anharmonic effects in the selected compounds, like other MAX phase materials.⁹⁹

Finally, we have calculated the melting temperature (T_m) of the studied compounds using the following equation: ,¹⁰¹ and listed it in Table 6. The melting temperature of the solids mainly depends on atomic bonding strength; the stronger the atomic bonding, the higher the T_m. Thus, a close relationship between T_m and Y is expected,^94,97 and the order of T_m for the titled phases is found to be following the Y-based ranking of the phases. It is seen from Table 6 that T_m of Nb₂AC (A = Ge, Tl, Zn, In, and Cd) is lower than that of the Nb₂AlC, but still higher than that of the V₂SnC (1533 K) MAX phase, a known TBC material.⁹⁶ In addition, the T_m of Nb₂AC (A = Ga and P) is not only higher than that of Nb₂AlC⁹⁴ but also comparable to that of Y₄Al₂O₉ (2000 K). T_m values of Nb₂AC (A = Ge, Tl, Zn, In, and Cd) are lower than that of Y₄Al₂O₉ (2000 K) but still reasonably high. Thus, based on the values of Θ_D, k_min, and T_m of the studied phases, in comparison with those of Y₄Al₂O₉ and some other MAX phases that have already been reported as TBC materials, we conclude that the titled phases can be considered as potential TBC materials.

4 Conclusion

A DFT investigation of 211 Nb₂AC (A = Ga, Ge, Tl, Zn, P, In, and Cd) carbides has been carried out in this research. The studied phases are dynamically and mechanically stable. Among the studied phases, Nb₂PC exhibits the best combination of mechanical properties, while Nb₂TlC exhibits the lowest. The Nb₂GaC, Nb₂PC, and Nb₂InC are brittle, whereas Nb₂GeC, Nb₂TlC, Nb₂ZnC, and Nb₂CdC are ductile. The Vickers hardness of Nb₂PC is also higher than that of others considered here, while the lowest Vickers hardness is found for Nb₂TlC, in good agreement with elastic moduli. The calculated direction-dependent (2D and 3D) elastic moduli and anisotropic indices confirm the anisotropic character of the studied phases. The electronic band structure and DOS confirm the metallic nature with a dominating contribution from Nb-3d states. Partial DOS discloses strong hybridization between Nb-d and C-2p states. Mulliken's population analysis reveals the existence of both ionic bonds and covalent bonds within the studied compounds. The optical constants, such as real and imaginary parts of the dielectric function, absorption coefficient, and photoconductivity spectra, are in good accord with band structure results. The reflectivity spectra reveal the possibility of their use as coating materials to diminish solar heating. The obtained values of the Grüneisen parameter (γ) show a lower anharmonic effect within the title carbides. The low value of K_min and comparatively higher melting temperature with reasonable Debye temperature suggest the studied compounds as TBC materials. The results found in this study are encouraging and hoped to attract attention from the scientific community for further investigation of new MAX phase materials.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors are grateful to the Ministry of Science and Technology (MOST), Bangladesh, for providing the financial support to complete this work (Physical Science-626, 2021–2022 Special Research Grant Project). Prima Das is also grateful to the Chittagong University of Engineering and Technology (CUET) for the financial support.

References

1. W. Jeitschko, H. Nowotny and F. Benesovsky, Carbides of formula T₂MC, J. Less-Common Met., 1964, 7, 133–138.
2. H. Wolfsgruber, H. Nowotny and F. Benesovsky, Die kristallstruktur von Ti₃GeC₂, Monatsh. Chem., 1967, 98, 2403–2405.
3. H. Nowotny, Struktur chemieeiniger verbindungen der ubergangsmetalemit den elementen C, Si, Ge, Sn, Prog. Solid State Chem., 1970, 2, 27–70.
4. H. Nowotny, J. C. Schuster and P. Rogl, Structural chemistry of complex carbides and related compounds, J. Solid State Chem., 1982, 44, 126–133.
5. M. W. Barsoum and T. El-Raghy, Synthesis and characterization of a remarkable ceramic: Ti₃SiC₂, J. Am. Ceram. Soc., 1996, 79, 1953–1956.
6. M. W. Barsoum, The M_n+1AX_n phases: a new class of solids: thermodynamically stable nanolaminates, Prog. Solid State Chem., 2000, 28, 201–281.
7. M. W. Barsoum, MAX phases: properties of machinable ternary carbides and nitrides, Wiley VCH Verlag GmbH & Co. KGaA, 2013.
8. P. Chakraborty, A. Chakrabarty, A. Dutta and T. Saha-Das gupta, Soft MAX phases with boron substitution: a computational prediction, Phys. Rev. Mater., 2018, 2, 103605.
9. M. Sokol, V. Natu, S. Kota and M. W. Barsoum, On the chemical diversity of the MAX phases, Trends Chem., 2019, 1, 210–223.
10. M. S. Ali, M. A. Rayhan, M. A. Ali, R. Parvin and A. K. M. A. Islam, New MAX phase compound Mo₂TiAlC₂: first-principles study, J. Sci. Res., 2016, 8, 109–117.
11. M. A. Ali, M. M. Hossain, M. A. Hossain, M. T. Nasir, M. M. Uddin, M. Z. Hasan, A. K. M. A. Islam and S. H. Naqib, Recently synthesized (Zr_1-xTi_x)₂AlC (0 ≤ x ≤ 1) solid solutions: theoretical study of the effects of M mixing on physical properties, J. Alloys Compd., 2018, 743, 146–154.
12. P. Li, R. Zhou and X. C. Zeng, Computational analysis of stable hard structures in the Ti-B system, ACS Appl. Mater. Interface., 2015, 7, 15607–15617.
13. B. Feng, J. Zhang, Q. Zhong, W. Li, S. Li, H. Li, P. Cheng, S. Meng, L. Chen and K. Wu, Experimental realization of two-dimensional boron sheets, Nat. Chem., 2016, 8, 563–568.
14. M. S. Hossain, N. Jahan, M. M. Hossain, M. M. Uddin and M. A. Ali, High pressure mediated physical properties of Hf₂AB (A = Pb, Bi) via DFT calculations, Mater. Today Commun., 2023, 34, 105147.
15. A. Jain, G. Hautier, C. J. Moore, S. P. Ong, C. C. Fischer, T. Mueller, K. A. Persson and G. Ceder, A high-throughput infrastructure for density functional theory calculations, Comput. Mater. Sci., 2011, 50, 2295–2310.
16. S. Curtarolo, G. Hart, M. B. Nardelli, N. Mingo, S. Sanvito and O. Levy, The high-throughput highway to computational materials design, Nat. Mater., 2013, 12, 191–201.
17. M. F. Cover, O. Warschkow, M. M. M. Bilek and D. R. McKenzie, A comprehensive survey of M₂AX phase elastic properties, J. Phys.: Condens. Matter, 2009, 21, 305403.
18. V. J. Keast, S. Harris and D. K. Smith, Prediction of the stability of the Mn₊₁AX_n phases from first principles, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 214113.
19. S. Aryal, R. Sakidja, M. W. Barsoum and W. Y. Ching, A genomic approach to the stability, elastic, and electronic properties of the MAX phases, Phys. Status Solidi B, 2014, 251, 1480–1497.
20. M. Ashton, R. G. Hennig, S. R. Broderick, K. Rajan and S. B. Sinnott, Computational discovery of stable M₂AX phases, Phys. Rev. B, 2016, 94, 054116.
21. R. Khaledialidusti, M. Khazaei, S. Khazaei and K. Ohno, High-throughput computational discovery of ternary-layered MAX phases and prediction of their exfoliation for formation of 2D MXenes, Nanoscale, 2021, 13, 7294–7307.
22. M. A. Hadi, Superconducting phases in a remarkable class of metallic ceramics, J. Phys. Chem. Solids, 2020, 138, 109275.
23. M. A. Hadi, S. R. G. Christopoulos, A. Chroneos, S. H. Naqib and A. K. M. A. Islam, Elastic behaviour and radiation tolerance in Nb-based 211 MAX phases, Mater. Today Commun., 2020, 25, 101499.
24. A. Bouhemadou, Calculated structural and elastic properties of M₂InC (M = Sc, Ti, V, Zr, Nb, Hf, Ta), Mod. Phys. Lett. B, 2008, 22, 2063–2076.
25. A. Bouhemadou, Calculated structural, electronic and elastic properties of M₂GeC (M = Ti, V, Cr, Zr, Nb, Mo, Hf, Ta and W), Appl. Phys. A, 2009, 96, 959–967.
26. W. Jeitschko, H. Nowotny and F. Benesovsky, Die H-Phasen Ti₂TiC, Ti₂PbC, Nb₂InC, Nb₂SnC and Ta₂GaC, Monatsh. fur Chem., 1964, 95, 431–435.
27. I. Salama, T. El-Raghy and M. W. Barsoum, Synthesis and mechanical properties of Nb2AlC and (Ti, Nb)2AlC, J. Alloys Compd., 2002, 347, 271–278.
28. W. Zhang, N. Travitzky, C. F. Hu, Y. C. Zhou and P. Greil, Reactive hot pressing and properties of Nb₂AlC, J. Am. Ceram. Soc., 2009, 92, 2396–2399.
29. M. Khazaei, A. Ranjbar, K. Esfarjani, D. Bogdanovski, R. Dronskowski and S. Yunoki, Insights into exfoliation possibility of MAX phases to MXenes, Phys. Chem. Chem. Phys., 2018, 20, 8579–8592.
30. S. Zhao, Y. Dall'Agnese, X. Chu, X. Zhao, Y. Gogotsi and Y. Gao, Electrochemical interaction of Sn-containing MAX phase (Nb2SnC) with Li-ions, ACS Energy Lett., 2019, 4, 2452–2457.
31. H. Dinga, Y. Li, J. Lu, K. Luo, K. Chen, M. Li, P. O. A. Persson, L. Hultman, P. Eklund, S. Du, Z. Huang, Z. Chai, H. Wang, P. Huang and Q. Huang, Synthesis of MAX phases Nb2CuC and Ti2(Al0.1Cu0.9) N by A-site replacement reaction in molten salts, Mater. Res. Lett., 2019, 7, 510–516.
32. I. R. Shein and A. L. Ivanovskii, Structural, elastic, electronic properties and Fermi surface for superconducting Mo₂GaC in comparison with V₂GaC and Nb₂GaC from first principles, Physica C, 2010, 470, 533–537.
33. M. A. Ghebouli, B. Ghebouli, A. Bouhemadou and M. Fatmi, Theoretical study of the structural, elastic, electronic and thermal properties of the MAX phase Nb₂SiC, Solid State Commun., 2011, 151, 382–387.
34. M. D. Segall, P. J. D. Lindan, M. J. Probert, C. J. Pickard, P. J. Hasnip, S. J. Clark and M. C. Payne, First principles simulation: ideas, illustrations and the CASTEP code, J. Phys.: Condens. Matter, 2002, 14, 2717–2744.
35. S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. I. J. Probert, K. Refson and M. C. Payne, First principles methods using CASTEP, ZeitschriftFürKrist. – Cryst. Mater., 2005, 220, 567–570.
36. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77, 3865.
37. J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Restoring the density-gradient expansion for exchange in solids and surfaces, Phys. Rev. Lett., 2008, 100, 136406.
38. O. Beckstein, J. E. Klepeis, G. L. W. Hart and O. Pankratov, First-principles elastic constants and electronic structure of α-Pt2Si and PtSi, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 134112.
39. J. Islam, S. K. Mitro, M. M. Hossain, M. M. Uddin, N. Jahan, A. K. M. A. Islam, S. H. Naqib and M. A. Ali, Exploration of the physical properties of the newly synthesized kagome superconductor LaIr₃Ga₂ using different exchange–correlation functionals, Phys. Chem. Chem. Phys., 2022, 24, 29640.
40. S. Masys and V. Jonausaks, A first-principles study of structural and elastic properties of bulk SrRuO₃, J. Chem. Phys., 2013, 139, 224705.
41. T. H. Fischer and J. Almlof, General methods for geometry and wave function optimizatin, J. Phys. Chem., 1992, 96, 9768.
42. H. J. Monkhorst and J. D. Pack, Special points for Brillouin-zone integrations, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188.
43. E. I. Isaev, QHA project, https://qe-forge.org/qha, accessed May 25, 2013.
44. G. Hug, M. Jaouen and M. W. Barsoum, X-ray absorption spectroscopy, EELS, and full-potential augmented plane wave study of the electronic structure of Ti₂Al₃, Ti₂AlN, Nb₂AlC and (Ti_0.5Nb_0.5)₂AlC, Phys. Rev. B: Condens. Matter, 2005, 71, 024105.
45. G. Hug, Electronic structures of and composition gaps among the ternary carbides Ti₂MC, Phys. Rev. B: Condens. Matter, 2006, 74, 184113.
46. M. B. Kanoun, S. Gourmi-said and M. Jaouen, Steric effect on the M site of nanolaminate compounds M₂SnC (M = Ti, Zr, Hf and Nb), Phys. Condens. Matter, 2009, 21, 045404.
47. A. D. Bortolozo, Z. Fisk, O. H. Sant' Anna, C. A. M. dos Santos and A. J. S. Machado, Superconductivity in Nb₂InC, Physica C, 2009, 469, 57.
48. M. A. Ali and A. K. M. A. Islam, Sn_1-xBi_xO₂ and Sn_1-xTa_xO₂ (0≤x≤0.75): A first-principles study, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 407, 1020–1026.
49. M. Born, On the stability of crystal lattices. I, Math. Proc. Cambridge Philos. Soc., 1940, 36, 160–172.
50. Z. Sun, D. Music, R. Ahuja and J. M. Schneider, Theoretical investigation of the bonding and elastic properties of nanolayered ternary nitrides, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 193402.
51. S. H. jhi, J. Ihm, S. G. Louie and M. L. Cohen, Electronic mechanism of hardness enhancement in transition-metal carbonitrides, Nature, 1999, 399, 132–134.
52. D. G. Pettifor, Theoretical predictions of structure and related properties of intermetallics, J. Mater. Sci. Tech., 1992, 8, 345–349.
53. M. W. Qureshi, M. A. Ali and X. Ma, Screen the thermomechanical and optical properties of the new ductile 314 MAX phase boride Zr₃CdB₄: A DFT insight, J. Alloys Compd., 2021, 877, 160248.
54. M. Roknuzzaman, M. A. Hadi, M. J. Abden, M. T. Nasir, A. K. M. A. Islam, M. S. Ali, K. Ostrikov and S. H. Naqib, Physical properties of predicted Ti₂CdN versus existing Ti₂CdC MAX phase: An ab initio study, Comput. Mater. Sci., 2016, 113, 148–153.
55. M. W. Qureshi, M. A. Ali, X. Ma, G. Tang, M. U. Javed and D. Paudyal, Verification of stability and unraveling the electronic and physical properties of bulk and (001)-surfaces of newly synthesized Ti₂ZnX (X = C, N) MAX phases, Surf. Interfaces, 2022, 31, 102032.
56. R. Hill, The elastic behaviour of a crystalline aggregate, Proc. Phys. Soc., London, Sect. A, 1952, 65, 349–354.
57. W. Voigt, Lehrbuch der Kristallphysik, Teubner, Leipzig, 1928.
58. A. Reuss, Berechnung der fließgrenze von mischkristallen auf grund der plastizitätsbedingungfüreinkristalle, J. Appl. Math. Mech., 1929, 9, 49–58.
59. M. A. Ali, M. Roknuzzaman, M. T. Nasir, A. K. M. A. Islam and S. H. Naqib, Structural, elastic, electronic and optical properties of Cu₃MTe₄ (M = Nb, Ta) sulvanites —An ab initio study, Int. J. Mod. Phys. B, 2016, 30, 1650089.
60. M. A. Ali, M. A. Hossain, M. A. Rayhan, M. M. Hossain, M. M. Uddin, M. Roknuzzaman, K. Ostrikov, A. K. M. A. Islam and S. H. Naqib, First-principles study of elastic, electronic, optical and thermoelectric properties of newly synthesized K₂Cu₂GeS₄chalcogenide, J. Alloys Compd., 2018, 781, 37–46.
61. X. Wang, H. Xiang, X. Sun, J. Liu, F. Hou and Y. Zhou, Mechanical properties and damage tolerance of bulk Yb₃Al₅O₁₂ ceramic, J. Mater. Sci. Technol., 2015, 31, 369–374.
62. M. A. Ali, A. K. M. A. Islam, N. Jahan and S. Karimunnesa, First-principles study of SnO under high pressure, Int. J. Mod. Phys. B, 2016, 30, 1650228.
63. X. Q. Chen, H. Niu, D. Li and Y. Li, Modeling hardness of polycrystalline materials and bulk metallic glasses, Intermetallics, 2011, 19, 1275–1281.
64. N. Miao, B. Sa, J. Zhou and Z. Sun, Theoretical investigation on the transition-metal borides with Ta3B4-type structure: A class of hard and refractory materials, Comput. Mater. Sci., 2011, 50, 1559–1566.
65. M. Radovic and M. W. Barsoum, MAX phases: Bridging the gap between metals and ceramics, Am. Ceram. Soc. Bull., 2013, 92, 20–27.
66. M. Mebrek, A. Mokaddem, B. Doumi, A. Yakoubi and A. Mir, A novel theoretical study of elastic and electronic properties of M₂CdC (M = Zr, Hf, and Ta) MAX phases, Acta Phys. Pol. A, 2018, 133, 76–81.
67. S. F. Pugh, Relations between the elastic moduli and the plastic properties of polycrystalline pure metals, Philos. Mag. J. Sci., 1954, 45, 823–843.
68. M. Roknuzzaman, M. A. Hadi, M. A. Ali, M. M. Hossain, N. Jahan, M. M. Uddin, J. A. Alarco and K. Ostrikov, First hafnium-based MAX phase in the 312 family, Hf₃AlC₂: A first-principles study, J. Alloys Compd., 2017, 727, 616–626.
69. I. R. Shein and A. L. Ivanovskii, Graphene-like titanium carbides and nitrides Ti_n+1C_n, Ti_n+1N_n (n = 1, 2, and 3) from de-intercalated MAX phases: First-principles probing of their structural, electronic properties and relative stability, Comput. Mater. Sci., 2012, 65, 104.
70. I. R. Shein and A. L. Ivanovskii, Elastic properties of superconducting MAX phases from first-principles calculations, Phys. Status Solidi B, 2011, 248, 228–232.
71. H. Gou, L. Hou, J. Zhang and F. Gao, Pressure-induced incompressibility of ReC and effect of metallic bonding on its hardness, Appl. Phys. Lett., 2008, 92, 2419.
72. P. Barua, M. M. Hossain, M. A. Ali, M. M. Uddin, S. H. Naqib and A. K. M. A. Islam, Effects of transition metals on physical properties of M₂BC (M = V, Nb, Mo and Ta): a DFT calculation, J. Alloy. Compd., 2018, 770, 523–534.
73. Y. Zhou and Z. Sun, Electronic structure and bonding properties of layered machinable and ceramics, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 61, 12570–12573.
74. M. A. Ali and S. H. Naqib, Recently synthesized (Ti_1-xMo_x)₂AlC (0 ≤ x ≤ 0.20) solid solutions: deciphering the structural, electronic, mechanical and thermodynamic properties via ab initio simulations, RSC Adv., 2020, 10, 31535–31546.
75. A. Chowdhury, M. A. Ali, M. M. Hossain, S. H. Naqib and A. K. M. A. Islam, Predicted MAX phase Sc₂InC: dynamical stability, vibrational and optical properties, Phys. Status Solidi B, 2018, 255, 1700235.
76. H. M. Ledbetter and A. Migliori, A general elastic-anisotropy measure, J. Appl. Phys., 2006, 100, 063516.
77. J. Chang, G. P. Zhao, X. L. Zhou, K. Liu and L. Y. Lu, Structure and mechanical properties of tantalum mononitride under high pressure: a first-principles study, J. Appl. Phys., 2012, 112, 083519.
78. R. Gaillac, P. Pullumbi and F. X. Coudert, ELATE: an open-source online application for analysis and visualization of elastic tensors, J. Phys.: Condens. Matter, 2016, 28, 275201.
79. H. M. Ledbetter, Elastic properties of zinc: a compilation and a review, J. Phys. Chem. Ref. Data, 1977, 6, 1181–1203.
80. A. K. M. A. Islam, A. S. Sikder and F. N. Islam, NbB₂: a density functional study, Phys. Lett. A, 2006, 350, 288–292.
81. J. Wang, Y. Zhou, T. Liao and Z. Lin, First-principles prediction of low shear-strain resistance of Al₃BC₃: a metal borocarbide containing short linear BC₂ units, Appl. Phys. Lett., 2006, 89, 021917.
82. Anisotropy in single crystal refractory compound, ed. D. H. Chung, W. R. Buessem, F. W. Vahldiek and S. A. Mersol, Plenum Press, New York, 1968, vol. 2.
83. S. I. Ranganathan and M. Ostoja-Starzewski, Universal elastic anisotropy index, Phys. Rev. Lett., 2008, 101, 055504.
84. S. Li, R. Ahuja, M. W. Barsoum, P. Jena and B. Johansson, Optical properties of Ti₃SiC₂ and Ti₄AlN₃, Appl. Phys. Lett., 2008, 92, 221907.
85. M. F. Li, Physics of Semiconductor, Science Press, Beijing, 1991.
86. R. C. Fang, Solid Spectroscopy, Chinese Science Technology University Press, Hefei, 2003.
87. Y. Zhang and W. M. Shen, Basic of Solid Electronics, Zhe Jiang University Press, Hangzhou, 2005.
88. M. T. Nasir, M. A. Hadi, M. A. Rayhan, M. A. Ali, M. M. Hossain and M. Roknuzzaman, et al., First-principles study of superconducting ScRhP and ScIrP pnictides, Phys. Status Solidi B, 2017, 254, 1700336.
89. F. Sultana, M. M. Uddin, M. A. Ali, M. M. Hossain, S. H. Naqib and A. K. M. A. Islam, First principles study of M₂InC (M = Zr, Hf and Ta) MAX phases: the effect of M atomic species, Results Phys, 2018, 11, 869–876.
90. K. Akter, F. Parvin, M. A. Hadi and A. K. M. A. Islam, Insights into the predicted Hf₂SN in comparison with the synthesized MAX phase Hf₂SC: a comprehensive study, Comput. Condens. Matter., 2020, 24, e00485.
91. N. Haddad, E. G. Caurel, L. Hultman, M. W. Barsoum and G. Hug, Dielectric Properties of Ti2AlC and Ti2AlN MAX Phases: The Conductivity Anisotropy, J. Appl. Phys., 2008, 104, 023531.
92. M. A. Ali and M. W. Qureshi, Newly synthesized MAX phase Zr₂SeC: DFT insights into physical properties towards possible applications, RSC Adv., 2021, 11, 16892.
93. O. L. Anderson, A simplified method for calculating in the Debye temperature from elastic constants, J. Phys. Chem. Solids, 1963, 24, 909–917.
94. M. A. Hadi, N. Kelaidis, S. H. Naqib, A. K. M. A. Islam, A. Chroneos and R. V. Vovk, Insights into the physical properties of a new 211 MAX phase Nb₂CuC, J. Phys. Chem. Solids, 2020, 149, 109759.
95. M. A. Ali, M. M. Hossain, M. M. Uddin, M. A. Hossain, A. K. M. A. Islam and S. H. Naqib, Physical properties of new MAX phase borides M₂SB (M = Zr, Hf and Nb) in comparison with conventional MAX phase carbides M₂SC (M = Zr, Hf and Nb): Comprehensive insights, J. Mater. Res. Tech., 2021, 11, 1000–1018.
96. M. A. Hadi, M. Dahlqvist, S. R. G. Christopoulos, S. H. Naqib, A. Chroneos and A. K. M. A. Islam, Chemically stable new MAX phase V2SnC: a damage and radiation tolerant TBC material, RSC Adv., 2020, 10, 43783–43798.
97. Y. Zhou, X. Lu, H. Xiang, Z. Feng and Z. Li, Theoretical prediction on mechanical and thermal properties of a promising thermal barrier material: Y₄Al₂O₉, J. Adv. Ceram., 2015, 4, 83–93.
98. G. A. Slack, The thermal conductivity of nonmetallic crystals, Solid State Phys., 1979, 34, 1–71.
99. V. N. Belomestnykh and E. P. Tesleva, Interrelation between anharmonicity and lateral strain in quasi-isotropic polycrystalline solids, Tech. Phys., 2004, 49, 1098–1100.
100. S. I. Mikitishin, Interrelationship of Poisson's ratio with other characteristics of pure metals, Sov. Mater. Sci., 1982, 18, 262–265.
101. M. E. Fine, L. D. Brown and H. L. Marcus, Elastic constants versus melting temperature in metals, Scr. Metall., 1984, 18, 951–956.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2ra07468k

---