Open Access Article
Open Access ArticleNew C2h phase of group III monochalcogenide monolayers AlX (X = S, Se, and Te) with anisotropic crystal structure: first-principles study
Tuan-Anh Tran a,
Le S. Haia,
Cuong Q. Nguyen
a,
Le S. Haia,
Cuong Q. Nguyen bc,
Vo T. T. Vi
bc,
Vo T. T. Vi d,
Tran P. T. Linh
d,
Tran P. T. Linh e and
Nguyen N. Hieu
e and
Nguyen N. Hieu *bc
*bc
aFaculty of Applied Sciences, Ho Chi Minh City University of Technology and Education, Ho Chi Minh City, Vietnam. E-mail: anhtt@hcmute.edu.vn
bInstitute of Research and Development, Duy Tan University, Da Nang, Vietnam. E-mail: hieunn@duytan.edu.vn
cFaculty of Natural Sciences, Duy Tan University, Da Nang, Vietnam
dFaculty of Basic Sciences, University of Medicine and Pharmacy, Hue University, Hue, Vietnam
eFaculty of Physics, Hanoi National University of Education, Ha Noi, Vietnam
First published on 28th February 2023
Abstract
In this paper, we introduce a new phase of two-dimensional aluminum monochalcogenide, namely C2h-AlX (X = S, Se, and Te). With the C2h space group, C2h-AlX possesses a large unit cell containing 8 atoms. The C2h phase of AlX monolayers is found to be dynamically and elastically stable based on the evaluation of its phonon dispersions and elastic constants. The anisotropic atomic structure of C2h-AlX leads to a strong anisotropy in its mechanical properties with Young's modulus and Poisson's ratio strongly dependent on the directions examined in the two-dimensional plane. All three monolayers of C2h-AlX are found to be direct band gap semiconductors, which are compared with the indirect band gap semiconductors of available D3h-AlX. Particularly, the transition from direct to indirect band gap is observed in C2h-AlX when a compressive biaxial strain is applied. Our calculated results indicate that C2h-AlX exhibits anisotropic optical characteristics and its absorption coefficient is high. Our findings suggest that C2h-AlX monolayers are suitable for applications in next-generation electro-mechanical and anisotropic opto-electronic nanodevices.
1 Introduction
Since the invention of graphene in 2004,1 intense research in the field of two-dimensional (2D) nanostructures has been carried out by both theoretical and experimental studies.2–5 2D layered-structures, such as silicene,6 germanene,2 or metal chalcogenide compounds7 possess many novel physical features that cannot be found in their bulk phases. Among those interesting candidates, group III–VI post-transition metal chalcogenides have appeared recently as a promising family due to their intriguing physical properties.8,9 Group III metal chalcogenide monolayers can serve as catalysts in photocatalytic applications due to their large band gap and suitable band alignment.10 With strong absorption of light in the UV-visible region, group III metal chalcogenide are expected to be suitable for applications in photodetectors.112D layered nanosheets can stably exist in different polymorphs. For example, both the α and γ phases of germanium monochalcogenides have been experimentally fabricated recently.12,13 More interestingly, the physical properties of these polymorphs are significantly different from each other.14,15 Therefore, from our point of view, along with the discovery of new materials, the search for new stable polymorphs of available 2D structures is also a necessary work that deserves attention. This will contribute to clarifying the full picture of these materials. In this manuscript, we study a new phase of 2D aluminum monochalcogenide with C2h space group, namely C2h-AlX (X = S, Se, and Te). We knew that the α phase of group III monochalcogenides MX (M is the group III metal) has been experimentally fabricated and widely theoretically studied.8,16 While the structure of γ-MX monolayers has a graphene-like hexagonal lattice with non-centrosymmetric D3h space group,8 the atomic structure of C2h-MX It has lower symmetry with larger unit-cell. It is noted that C2h polymorph of bulk group III monochalcogenide InSe has been fabricated17 and also experimentally investigated previously.18 Besides, different polytypes of InSe and also C2h phase of GaS, GaSe, InS, and InSe monolayers have been studied theoretically recently by the first-principles method.19,20 This supports the expectation that 2D C2h-MX sheets can be synthesized soon in the future.
In this study, we investigate the characteristics of the crystal structure, electronic properties, and fundamental optical features of C2h phase of aluminum monochalcogenide monolayers C2h-AlX (X = S, Se, and Te) using first-principles techniques. The structural stabilities of the studied materials are carefully examined based on the evaluation of cohesive energy, phonon dispersion, and analysis of their elastic constants. Since the structural stabilities are confirmed, we examine the electronic and optical features of the studied materials. The effects of applied strains and electric field on electronic characteristics of C2h-AlX are also reported in the present paper.
2 Computational method
We perform the first-principles simulations based on the density functional theory (DFT) as implemented in the QUANTUM ESPRESSO package.21 The projector-augmented wave pseudo-potential method22 with an energy cutoff of 70 Ry is selected to consider the electronic-ion core interactions. The exchange-correlation functions are approximated by generalized gradient approximation with the Perdew, Burke, and Ernzerhof (PBE) parameterization. Besides, the hybrid functional proposed by Heyd, Scuseria, and Ernzerhof (HSE06)23 is adopted to correct the bandgaps by using the Vienna ab initio simulation package.24,25 Besides, the corrected DFT-D2 approach suggested by Grimme26 is also included to consider the van der Waals forces. The Brillouin zone is sampled by (15 × 15 × 1) k-grid mesh based on the Monkhorst–Pack scheme.27 The convergence criteria for energy is selected to be 10−6 eV. To reduce interactions between periodic images in adjacent cells, we insert a vacuum spacing of 25 Å along the vertical direction of the investigated materials. We evaluate the phonon dispersion through the density functional perturbation approximation.28 The thermodynamic stability is tested based on ab initio molecular dynamics (AIMD) calculations using the NVT ensemble with a 6 × 6 × 1 supercell within 8 ps (time step of 1 fs).29 Born's criterion is used to confirm mechanical stability through the evaluation of elastic coefficients.30 We used a biaxial strain and external electric field to turn bandgaps of the studied monolayers. The electric field is applied perpendicularly to the 2D plane of the material with the positive direction of the electric field along the z-axis.3 Calculated results and discussion
3.1 Crystal structure and structural stability
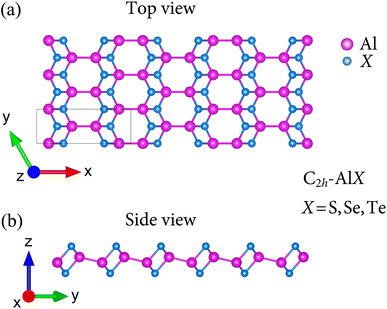
We first optimized the structures of binary AlX (X = S, Se, Te). Apart from previous studies8 in which the geometry of group III monochalcogenides AlX belong to D3h point group, the current polymorph of AlX monolayers possess the geometry of monoclinic lamellae phase with respect to C2h point group. Fig. 1 presents the atomic structures AlX monolayers viewed along a and b directions in which the unit cell contains eight atoms. It also can be seen that in C2h point group, there are four sublayers X–Al–Al–X held together with polar covalent bonds.The fully optimized lattice constants are predicted by the Quantum Espresso package and tabulated in Table 1. The lattice parameters a and b increase in the order of AlS, AlSe, and AlTe, namely, their structural parameters increase with increasing the atomic radius of the chalcogen atoms. The trend of two lattice parameters a and b are attributed to the bond lengths of Al–Al and Al–X in the interlayers and intralayers of these lamellae. However, there are neither theoretical nor experimental results related to the C2h-AlX monolayers so far. Hence, in order to have a qualitative explanation, the obtained bond lengths of In–X8 are used and similar trends for lattice parameters are found. The monolayer thicknesses Δh are also calculated and increase when moving down a group. These reasonable results are expected since the monolayer thicknesses are proportional to both Al–Al and Al–X. It is noted that the atomic structure of C2h-AlX exhibits high directionally anisotropic along the armchair and zigzag axes with the anisotropic ratio τ = a/b up to 2.75 (for AlS monolayer).
| a | b | Δh | Ecoh | C11 | C12 | C22 | C66 | |
|---|---|---|---|---|---|---|---|---|
| AlS | 9.80 | 3.57 | 2.97 | −4.86 | 48.11 | 3.85 | 48.38 | 10.62 |
| AlSe | 9.94 | 3.75 | 3.24 | −4.41 | 38.54 | 2.96 | 45.14 | 8.40 |
| AlTe | 10.10 | 4.06 | 3.64 | −3.91 | 23.90 | 1.75 | 40.09 | 4.72 |
In order to investigate the stability of the crystal structure of these proposed systems AlX, we next test the strength of chemical bonding based on the evaluation of cohesive energies, as defined as
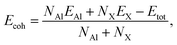 | (1) |
Additionally, to examine the dynamical stabilities of AlX monolayers, the phonon dispersions along the high symmetry line Γ–X–S–Y–Γ are investigated and shown in Fig. 2(a). It is found that the phonon dispersion of AlX monolayers contains 24 vibrational branches due to the unit-cell containing eight atoms as depicted in Fig. 1(a). The phonon spectrum contains three acoustic branches and 21 optical branches. No negative frequencies are available in the whole Brillouin zones that confirm the dynamically stable characteristic of these AlX structures. Besides, the AIMD calculations for the energy fluctuation to time of AlX materials are carried out as shown in Fig. 2(b). Obtained calculations demonstrate that the fluctuations of the total energy of the studied materials are small, only about 0.5 eV. The chemical bonds in all structures are still robust and no significant structural transitions occur during the 8 ps AIMD simulation, suggesting the thermodynamic stabilities of AlX monolayers.
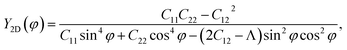 | (2) |
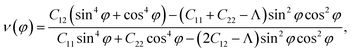 | (3) |
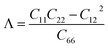 and φ is determined by the angle between the x axis and considered direction.
and φ is determined by the angle between the x axis and considered direction.
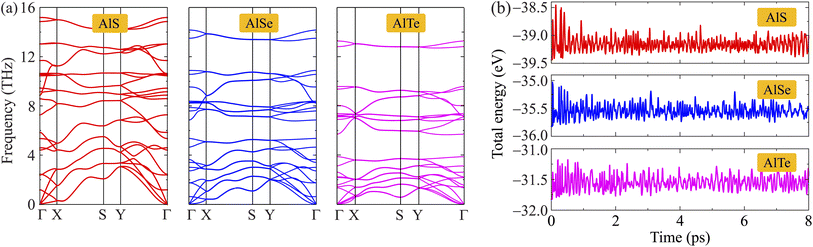 | ||
| Fig. 2 Phonon dispersions (a) and AIMD calculations for energy fluctuations to time (b) of C2h-AlX monolayers. | ||
We first calculate the elastic constants Cij of the studied 2D structures based on the fitting in the polynomial function of their uniaxial strain-dependent energy.33 There are four constants, including C11, C22, C12, and C66 (using Voigt's notation), that need to be evaluated for 2D materials. The evaluated results for the Cij of the C2h-AlX are listed in Table 1. It is found that C2h-AlX monolayers exhibit small stiffness constants. All four stiffness constants share a common trend of change, that the Cij decreases with the increasing of the atomic size of the chalcogen element. This is consistent with the statement that the smaller the lattice constant, the greater the in-plane stiffness.8 Importantly, the elastic constants listed in Table 1 satisfy the corresponding criteria for elastic stability according to Born–Huang's lattice dynamical theory (C11C12 − C122 > 0, C11 > 0, C22 > 0, C66 > 0).34 These calculated results suggest that all three C2h-AlX monolayers are mechanically stable.
Due to the anisotropy in the atomic structure, the elastic characteristics of the investigated materials will also be anisotropic accordingly. The directional dependent Y2D(φ) and ν(φ) of C2h-AlX structures are presented in Fig. 3. At first glance, it is revealed the AlX lamella have strong mechanical anisotropy since both Y2D and ν are changed with different in-plane angles. These results are in good agreement with the anisotropy of the structure of these AlX monolayers. From Fig. 1, we can see that Y2D(φ) of C2h-AlX structures depends strongly on the investigated direction, namely the in-plane angle φ. It is calculated that Young's modulus gets the maximum value corresponding to φ = 90°. The maximum value of Young's modulus Y2D (90°) is evaluated to be 48.07, 44.91, and 39.97 N m−1 for AlS, AlSe, and AlTe, respectively. The Young's modulus along the [100] direction (φ = 0°) is also large, especially in the case of AlS (47.80 N m−1). However, the difference in Y2D(φ) along φ = 0° and φ = 90° directions is progressively larger with increasing atomic radii of the chalcogen elements. At φ = 0°, Young's modulus of AlTe is only 23.82 N m−1, which is much smaller than that along the φ = 90° direction as above-mentioned. From Fig. 3, we found that the C2h-AlX material was the softest along the φ = 45° or φ = 135° directions with Young's modulus of 30.18, 24.38, and 14.58 N m−1 for AlS, AlSe, and AlTe, respectively. Young's modulus of the AlTe monolayer is found to be the smallest, indicating that the AlTe monolayer is the most stretchable, flexible, and promising for flexible material applications. Besides, when going down in this group (S, Se, and Te), Poisson's ratio is increasing, i.e., that of laminated AlTe is the highest, hence, AlTe monolayer has the lowest in-plane stiffness. This result is in accordance with the obtained result of Young's modulus mentioned above and could be attributed to the highest lattice parameters of AlTe (Table 1) in which the bonding between elemental sites becomes weaker. The polar diagram of Poisson's ratio of the studied monolayers is also shown in Fig. 3(b), which provides us with the dependence of the Poisson's ratio on the investigated direction in the 2D plane of the material.
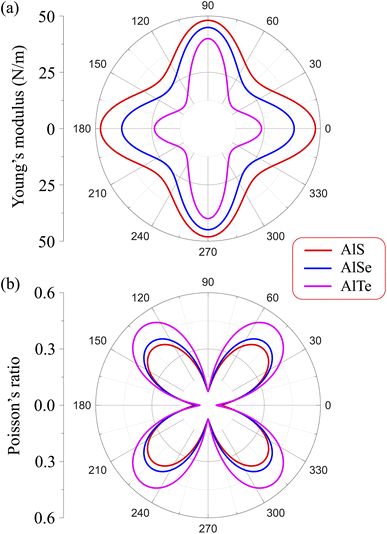 | ||
| Fig. 3 Dependence of (a) Young's modulus and (b) Poisson's ratio on angular φ of C2h-AlX m0-dependent Y2D(φ) and Poisson's ratio ν(φ) are expressed as follows.31,32 | ||
3.2 Electronic properties
The structural and dynamical stabilities are confirmed. Next, the electronic structures are considered by investigating the electronic band dispersions along the high symmetry line Γ–X–S–Y–Γ. Since the DFT techniques parameterized the PBE often underestimate the bandgap, additionally, the HSE06 method is used to correct the band diagram and overcome the underestimation of the bandgap issue. The examined PBE and HSE06 bandgaps for C2h-AlX monolayers are presented in Fig. 3. It can be seen that these three monolayers exhibit semiconducting characteristics with direct band gap energies due to the alignment of the conduction band minimums (CBM) and the valence band maximums (VBM) at Γ point. The band gap energies obtained by the PBE and HSE06 functionals are tabulated in Table 2. As predicted, the energy gap in the PBE level of C2h-AlX is narrower than that in the HSE06 level. The band gaps are decreasing in order of AlS, AlSe, and AlTe in both PBE and HSE06 functionals calculations. It is also noted that D3h-AlX is an indirect semiconducting material8 with a wider energy gap compared with corresponding C2h-AlX.| EPBEg | EHSE06g | EF | Evac | Φ | |
|---|---|---|---|---|---|
| AlS | 1.94 | 2.75 | −3.25 | 2.12 | 5.37 |
| AlSe | 1.66 | 2.43 | −3.00 | 2.07 | 5.07 |
| AlTe | 1.56 | 2.21 | −2.20 | 2.55 | 4.75 |
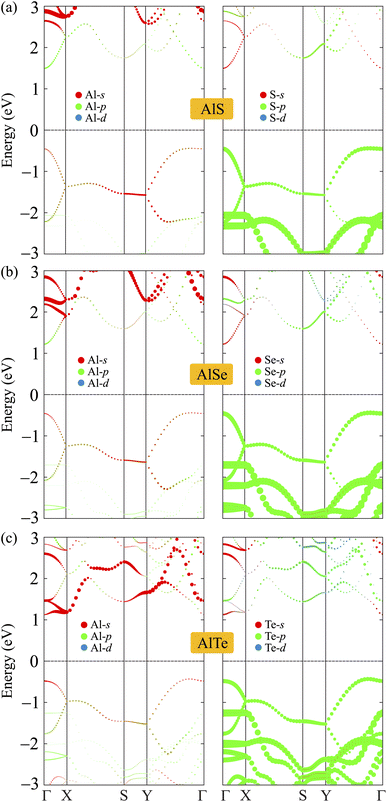
To analyze the formation of electronic bands, we calculate the weighted bands of AlX as shown in Fig. 5. It is found that the VBM of AlX is mainly dominated by the p orbitals of the chalcogen element X. Meanwhile, both X-s and Al-p orbitals have significant contributions to the CBM. Besides, the contribution of the Al-s orbitals to the conduction band is significant.
Next, we evaluate the ability of the electrons to escape from the surface by calculating the work function of the materials. The work function Φ of materials can be evaluated from the vacuum level Φvac and Fermi level ΦF as follows:
| Φ = Φvac − ΦF | (4) |
The values of Φvac and ΦF can be obtained based on the analysis of the electrostatic potentials of materials as presented in Fig. 6. Monolayers AlX have vertical symmetric structures, therefore, there is no vacuum level difference between the sides. Obtained results for Φvac, ΦF, and corresponding Φ are presented in Table 2. It is found that the AlTe has the smallest work function being 4.75 eV, implying that the electrons can more easily escape from the surface of AlTe than other structures.
Finding ways to modulate physical properties, especially electronic characteristics, has always been a topic of interest to the scientific community. Several methods for modifying electronic properties have been introduced, including doping,35 placing materials on semiconductor substrates or forming heterostructures,36,37 surface functionalization,38 etc. Recent studies have shown that mechanical strain is one of the simple and effective approaches in tuning the properties of 2D materials.3,39 Here, we consider the effect of a biaxial strain on the energy band diagrams of C2h-AlX structures at the PBE level. The biaxial strain εb is quantitatively introduced as εb = (l − l0)/l0. Here, l0 and l are the lengths of the computed cell of C2h-AlX material before and after strain, respectively.
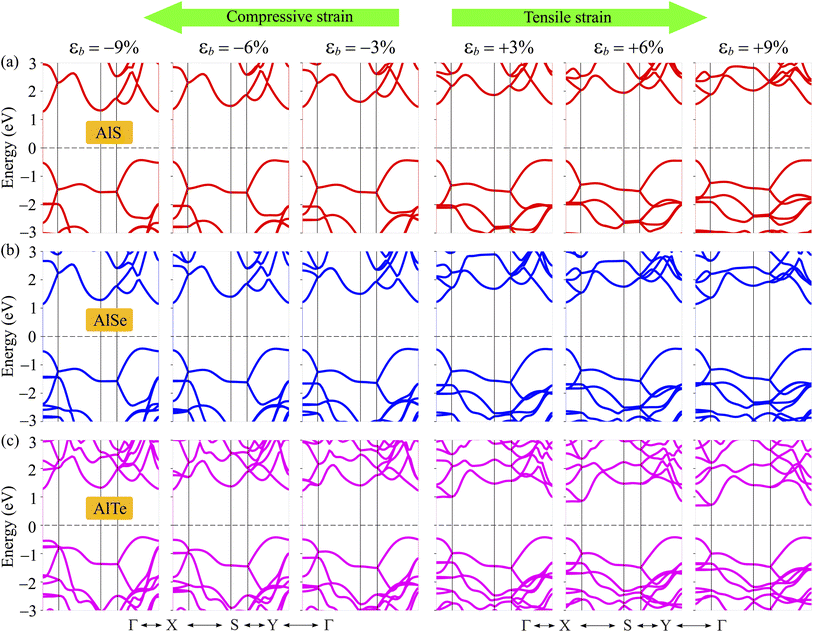
The electronic band dispersions of C2h-AlX under the biaxial strains are depicted in Fig. 7 It is demonstrated that the effect of the strains on the electronic band dispersions of C2h-AlX is significant. While the tensile strain is a significant change in the band gap, the compressive strain tends to change the position of the VBM. From Fig. 7, we can see that, in the presence of the compressive strain, the VBM tends to move away from the Γ point and lies on the YΓ path. It implies that the compressive strain can lead to phase transition from direct-to-indirect bandgap in AlX materials. The dependence of the band gap of AlX on the applied biaxial strains is depicted in Fig. 8(a). It is shown that the energy gap of AlTe decreases rapidly under tensile strain. In the examined range of the strain, the graph showing the strain-dependent energy for AlS and AlSe is quite similar. The energy gap of AlS increases slightly and then tends to decrease in the presence of tensile strain. For AlSe, the strain reduces its energy gap in both the tensile and compression strains. When the biaxial strain is introduced, there is a significant difference in the bandgaps of AlTe and other structures, namely AlS and AlSe. This may be because the lattice constant difference (and also other structural parameters) between AlTe and AlS/AlSe is larger than that between AlS and AlSe monolayers.
In parallel with the investigation of the change in the physical properties of the material when it is deformed, the investigation of the electronic properties of the material in the presence of an electric field is also a concern of scientists. This is due to the practical significance of this problem in the fabrication and design of nanoelectronic devices. When an electric field was introduced, the effective charge polarization in valence/conduction bands will react to the electric field. As a result, the energy of the electrons in the electronic bands can be significantly modulated accordingly. Besides, the electronic characteristics can be changed due to the redistribution of charge in the studied structures. Ke and co-workers recently showed that electric fields can lead to indirect–direct energy gap phase transitions in the hexagonal 2D structure GaSe.40 Besides, the effects of electric field on electronic characteristics of asymmetric structure group III Ga2SeTe is also significant, especially in the energy gap.41 In some 2D structures, however, the effect of the external field on the electronic features is insignificant, particularly in the case of the low-applied electric field.42,43 Wang and co-worker indicated that the energy gap of 2D tellurium structure is almost unchanged under electric fields up to 9 V nm−1.42 Also, there was no significant change in the energy gap of the γ phase of group IV–VI binary materials when the electric field up to 8 V nm−1 was applied.43 The electronic structures can be significantly altered with the higher applied electric fields. In the present study, we examine the influences of the electric field E on the electronic properties of AlX structures. The field E from 0 to 4 V nm−1 is applied perpendicularly to the 2D plane of materials. This value of the electric field is close to that of recent experimental works on 2D structures (3 V nm−1).44 Our calculated results demonstrate that the influences of E on the electronic characteristics of the C2h-AlX is insignificant. No significant change in the band diagrams of AlX monolayers when E up to 4 V nm−1 is applied (not shown). The dependence of the band gap on the applied electric field is shown in Fig. 8(b). It is observed that the band gap of AlX is only slightly reduced by about 3–8% when the electric field is introduced.
3.3 Optical properties
The basic optical features of material can be described via its photon frequency-dependence of the dielectric constant ε(ω) written as ε(ω) = ε1(ω) + iε2(ω). It is well-known that we usually calculated ε2(ω) first by summing the filled–empty state transitions and ε1(ω) can be delivered later via Kramers–Kronig relationship.45,46 The imaginary part ε2(ω) is given by:45,46
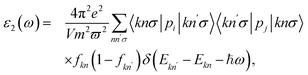 | (5) |
We here calculate the optical spectra with the electric field along the crystallographic axes, namely parallel to the 2D plane x (E∥xx and E∥y) and perpendicular to the 2D plane (E⊥zz), corresponding to the electric field vector polarized along the three principal axes x, y, and z. We can evaluate the absorption spectrum A(ω) based on the calculated dielectric constant parts as follows:47
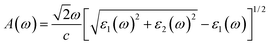 | (6) |
The optical spectra, including ε2(ω) and A(ω), are closely related to the band structures of the investigated materials. In the optical spectra, the basic peaks can be explained based on the interband transitions that cause these peaks. The absorption spectra A(ω) of AlX are depicted in Fig. 9. It is found that the absorption spectra of AlX structures are all activated in the visible light domain which is consistent with their direct energy gaps as presented in Fig. 4. Focusing on the absorption spectrum of each investigated structure, we can see that the absorption coefficient of AlX exhibits strong anisotropy in different polarization directions of the electric field. This is due to the anisotropy in the atomic structure of the investigated structures. In the low photon energy domain, the absorption coefficient in the cases of E∥xx and E∥y is slightly larger than in the case of E⊥zz. However, in the higher photon energy domain, the absorption coefficient in the case of E⊥zz increases rapidly and reaches its maximum value. From Fig. 9, it is revealed that the main peak of AlS for E⊥zz is located at 7.99 eV with the value of A(ω) up to 112 × 104 cm−1. With high absorption, the monolayers AlX are suitable for optoelectronic device applications.
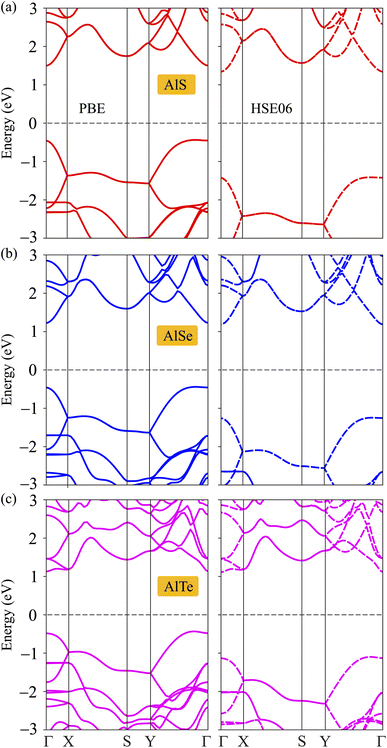 | ||
| Fig. 4 Calculated band dispersions of monolayers AlS (a), AlSe (b), and AlTe (c) using PBE/HSE06 functional. | ||
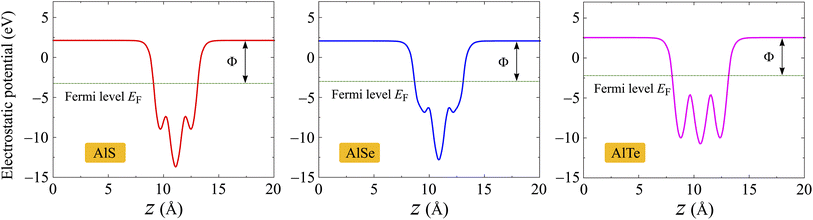 | ||
| Fig. 6 Electrostatic potentials of AlX monolayers. The horizontal dashed line indicates the Fermi level EF. | ||
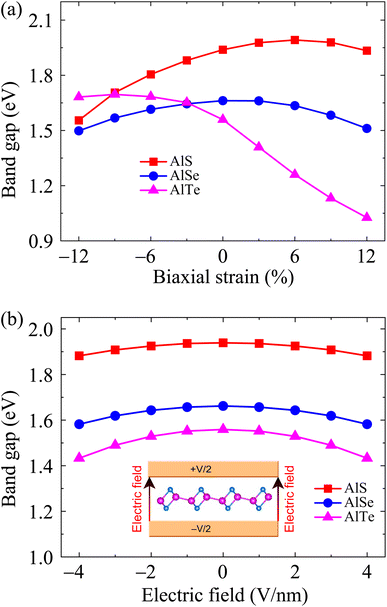 | ||
| Fig. 8 Dependence of band energy gaps of AlX monolayers on biaxial strain (a) and electric field (b). | ||
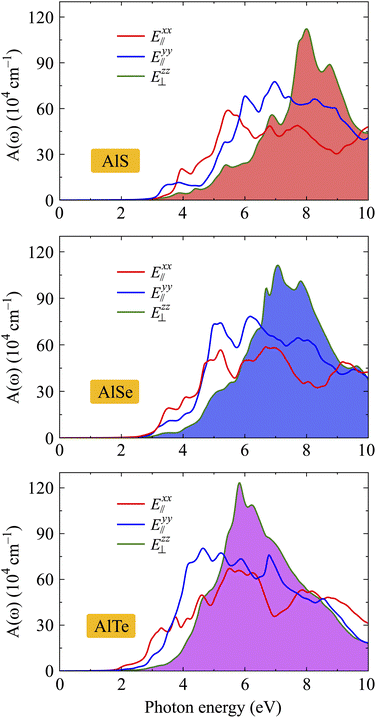 | ||
| Fig. 9 Dependence of band energy gaps of AlX monolayers on biaxial strain (a) and electric field (b). | ||
4 Conclusion
In conclusion, we systematically examined the structural, electronic, and optical properties of C2h phase of aluminum monochalcogenides AlX using the DFT simulations. The obtained results indicated that C2h-AlX materials are structurally stable. Unlike the available D3h-AlX structures (indirect semiconductors), C2h phase of aluminum monochalcogenides AlX are semiconductors with direct band energy gap with the HSE06 energy gap values from 2.21 to 2.75 eV. The band gaps of C2h-AlX depend strongly on the applied strain, especially tensile strain. Also, the phase transition from the direct band gap to the indirect band gap was found in C2h-AlX when the compressive strain was introduced. The mechanical and optical properties exhibit marked anisotropy due to the monolayers having an anisotropic atomic structure. Our calculated results indicated that C2h-AlX possesses many novel characteristics that do not exist in other polymorphs of aluminum monochalcogenides. These findings support the view that in parallel with the efforts on the discovery of new materials, the search for new polymorphs of existing nanomaterials is also an approach that needs more attention.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This work belongs to the project grant No: T2022-23 funded by Ho Chi Minh City University of Technology and Education (Viet Nam).References
- K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666 CrossRef CAS PubMed.
- A. Acun, L. Zhang, P. Bampoulis, M. Farmanbar, A. van Houselt, A. N. Rudenko, M. Lingenfelder, G. Brocks, B. Poelsema, M. I. Katsnelson and H. J. W. Zandvliet, J. Phys.: Condens. Matter., 2015, 27, 443002 CrossRef CAS PubMed.
- T. V. Vu, C. V. Nguyen, H. V. Phuc, A. A. Lavrentyev, O. Y. Khyzhun, N. V. Hieu, M. M. Obeid, D. P. Rai, H. D. Tong and N. N. Hieu, Phys. Rev. B, 2021, 103, 085422 CrossRef CAS.
- N. D. Hien, C. V. Nguyen, N. N. Hieu, S. S. Kubakaddi, C. A. Duque, M. E. Mora-Ramos, L. Dinh, T. N. Bich and H. V. Phuc, Phys. Rev. B, 2020, 101, 045424 CrossRef.
- D. Muoi, N. N. Hieu, C. V. Nguyen, B. D. Hoi, H. V. Nguyen, N. D. Hien, N. A. Poklonski, S. S. Kubakaddi and H. V. Phuc, Phys. Rev. B, 2020, 101, 205408 CrossRef CAS.
- B. Lalmi, H. Oughaddou, H. Enriquez, A. Kara, S. Vizzini, B. Ealet and B. Aufray, Appl. Phys. Lett., 2010, 97, 223109 CrossRef.
- H. S. S. Ramakrishna Matte, A. Gomathi, A. K. Manna, D. J. Late, R. Datta, S. K. Pati and C. N. R. Rao, Angew. Chem., Int. Ed., 2010, 49, 4059–4062 CrossRef PubMed.
- S. Demirci, N. Avazli, E. Durgun and S. Cahangirov, Phys. Rev. B, 2017, 95, 115409 CrossRef.
- N. N. Hieu, H. V. Phuc, A. I. Kartamyshev and T. V. Vu, Phys. Rev. B, 2022, 105, 075402 CrossRef CAS.
- H. L. Zhuang and R. G. Hennig, Chem. Mater., 2013, 25, 3232 CrossRef CAS.
- P. Hu, Z. Wen, L. Wang, P. Tan and K. Xiao, ACS Nano, 2012, 6, 5988 CrossRef CAS PubMed.
- D. D. Vaughn, R. J. Patel, M. A. Hickner and R. E. Schaak, J. Am. Chem. Soc., 2010, 132, 15170 CrossRef CAS PubMed.
- S. Lee, J.-E. Jung, H. gyu Kim, Y. Lee, J. M. Park, J. Jang, S. Yoon, A. Ghosh, M. Kim, J. Kim, W. Na, J. Kim, H. J. Choi, H. Cheong and K. Kim, Nano Lett., 2021, 21, 4305–4313 CrossRef CAS PubMed.
- N. Luo, W. Duan, B. I. Yakobson and X. Zou, Adv. Funct. Mater., 2020, 30, 2000533 CrossRef CAS.
- T. V. Vu, H. V. Phuc, A. I. Kartamyshev and N. N. Hieu, Appl. Phys. Lett., 2023, 122, 061601 CrossRef CAS.
- S. Acharya, M. Dutta, S. Sarkar, D. Basak, S. Chakraborty and N. Pradhan, Chem. Mater., 2012, 24, 1779–1785 CrossRef CAS.
- G. Vezzoli, Mater. Res. Bull., 1971, 6, 1201–1204 CrossRef CAS.
- D. Errandonea, D. Martínez-García, A. Segura, A. Chevy, G. Tobias, E. Canadell and P. Ordejon, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 235202 CrossRef.
- L. Ghalouci, F. Taibi, F. Ghalouci and M. Bensaid, Comput. Mater. Sci., 2016, 124, 62–77 CrossRef CAS.
- T. Hu, C. Xu, A. Zhang and P. Yu, Mater. Adv., 2022, 3, 2213–2221 RSC.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. D. Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B, 1996, 54, 11169–11186 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787 CrossRef CAS PubMed.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188–5192 CrossRef.
- T. Sohier, M. Calandra and F. Mauri, Phys. Rev. B, 2017, 96, 075448 CrossRef.
- S. Nosé, J. Chem. Phys., 1984, 81, 511 CrossRef.
- M. Born and K. Huang, Am. J. Phys., 1955, 23, 474 CrossRef.
- N. T. Hung, A. R. T. Nugraha and R. Saito, J. Phys. D: Appl. Phys., 2018, 51, 075306 CrossRef.
- P. Xiang, S. Sharma, Z. M. Wang, J. Wu and U. Schwingenschlögl, ACS Appl. Mater. Interfaces, 2020, 12, 30731 CrossRef CAS PubMed.
- K.-A. N. Duerloo, M. T. Ong and E. J. Reed, J. Phys. Chem. Lett., 2012, 3, 2871–2876 CrossRef CAS.
- F. Mouhat and F.-X. Coudert, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 224104 CrossRef.
- Y.-C. Lin, J. Karthikeyan, Y.-P. Chang, S. Li, S. Kretschmer, H.-P. Komsa, P.-W. Chiu, A. V. Krasheninnikov and K. Suenaga, Adv. Mater., 2021, 33, 2007819 CrossRef CAS PubMed.
- H. V. Phuc, N. N. Hieu, B. D. Hoi, L. T. T. Phuong and C. V. Nguyen, Surf. Sci., 2018, 668, 23–28 CrossRef CAS.
- C. V. Nguyen, M. Idrees, H. V. Phuc, N. N. Hieu, N. T. T. Binh, B. Amin and T. V. Vu, Phys. Rev. B, 2020, 101, 235419 CrossRef CAS.
- V. T. T. Vi, C. Q. Nguyen, B. D. Hoi, H. V. Phuc, C. V. Nguyen and N. N. Hieu, J. Phys. D: Appl. Phys., 2022, 55, 505302 CrossRef.
- T. V. Vu, V. T. T. Vi, H. V. Phuc, C. V. Nguyen, N. A. Poklonski, C. A. Duque, D. P. Rai, B. D. Hoi and N. N. Hieu, J. Phys.: Conden. Matter, 2021, 33, 225503 CrossRef CAS PubMed.
- C. Ke, Y. Wu, G.-Y. Guo, W. Lin, Z. Wu, C. Zhou and J. Kang, Phys. Rev. Appl., 2018, 9, 044029 CrossRef CAS.
- T. V. Vu, V. T. T. Vi, C. V. Nguyen, H. V. Phuc and N. N. Hieu, J. Phys. D: Appl. Phys., 2020, 53, 455302 CrossRef CAS.
- J. Wang, H. Shen, Z. Yu, S. Wang, Y.-Y. Chen, B.-R. Wu and W.-S. Su, ACS Omega, 2020, 5, 18213–18217 CrossRef CAS PubMed.
- V. V. Thanh, N. D. Van, D. V. Truong and N. T. Hung, Appl. Surf. Sci., 2022, 582, 152321 CrossRef.
- K. F. Mak, C. H. Lui, J. Shan and T. F. Heinz, Phys. Rev. Lett., 2009, 102, 256405 CrossRef PubMed.
- A. Delin, P. Ravindran, O. Eriksson and J. Wills, Int. J. Quantum Chem., 1998, 69, 349 CrossRef CAS.
- S. Z. Karazhanov, P. Ravindran, A. Kjekshus, H. Fjellvag and B. G. Svensson, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 155104 CrossRef.
- P. Ravindran, A. Delin, B. Johansson, O. Eriksson and J. M. Wills, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1776–1785 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2023 |