DOI:
10.1039/D2RA08077J
(Paper)
RSC Adv., 2023,
13, 5753-5761
Investigating the magnetic and magnetocaloric behaviors of LiSm(PO3)4
Received
18th December 2022
, Accepted 10th February 2023
First published on 15th February 2023
Abstract
We report a detailed study on the magnetic behaviors and magnetocaloric (MC) effect of a single crystal of lithium samarium tetraphosphate, LiSm(PO3)4. The analyses of temperature-dependent magnetization data have revealed magnetic ordering established with decreasing temperature below Tp, where Tp is the minimum of a dM/dT vs. T curve and varies as a linear function of the applied field H. The Curie temperature has been extrapolated from Tp(H) data, as H → 0, to be about 0.51 K. The establishment of magnetic-ordering causes a substantial change in the heat capacity Cp. Above Tp, the crystal exhibits paramagnetic behavior. Using the Curie–Weiss (CW) law and Arrott plots, we have found the crystal to have a CW temperature θCW ≈ −36 K, and short-range magnetic order associated with a coexistence of antiferromagnetic and ferromagnetic interactions ascribed to the couplings of magnetic dipoles and octupoles at the Γ7 and Γ8 states. An assessment of the MC effect has shown increases in value of the absolute magnetic-entropy change (|ΔSm|) and adiabatic-temperature change (ΔTad) when lowering the temperature to 2 K, and increasing the magnetic-field H magnitude. Around 2 K, the maximum value of |ΔSm| is about 3.6 J kg−1 K−1 for the field H = 50 kOe, and ΔTad is about 5.8 K for H = 20 kOe, with the relative cooling power (RCP) of ∼82.5 J kg−1. In spite of a low MC effect in comparison to Li(Gd,Tb,Ho)(PO3)4, the absence of magnetic hysteresis reflects that LiSm(PO3)4 is also a candidate for low-temperature MC applications below 25 K.
1. Introduction
The magnetocaloric (MC) effect is an intrinsic property of any magnetic material. It is related to a temperature change of a magnetic material under an adiabatic process when an external magnetic field is applied. This phenomenon is generated from a decreased magnetic entropy that is compensated by the lattice-entropy change because the total entropy of the system under an isentropic process is unchanged. Together with the isentropic process, an adiabatic process also takes place irreversibly, after in the entropy–temperature (S–T) diagram.1 In other words, the isentropic change of the material leads to an adiabatic temperature change (ΔTad), and when the magnetization is isothermally carried out, a magnetic-entropy change (ΔSm) causes an isothermal total entropy change.1–3 Using the adiabatic demagnetization and paramagnetic (PM) salts, typically Gd2(SO4)3·8H2O, (Dy,Ce)(C2O5SO4)3·9H2O and (NH4)2SO4MnSO4·6H2O, one has been given the birth of cryogenic and sub-Kelvin cooling.1,4,5 The successful fabrication of adiabatic demagnetization refrigerators can somewhat solve the shortage and high price of 3He helium isotope.6
Comparing with the vapor-compression refrigeration cycle, the MC-based refrigeration has been proven to gain a higher efficiency,7 and does not cause environmental challenges because of using recyclable solid refrigerants composed of non-toxic elements.1,8 Apart from using PM salts, it has been seeking for H2O-free MC materials applicable for sub-Kelvin/cryogenic cooling devices1,4,5 and space technology,9 particularly for the liquefaction of hydrogen and helium isotopes at below 20 and 4.2 K, respectively. These materials need to ensure some application requirements, such as low magnetic-ordering temperature, large |ΔSm| and ΔTad values, no thermal hysteresis phenomenon, and no degrading at high temperatures and ultra-high vacuum. Until now, it has been introduced many materials with magnetic-ordering temperatures below 20 K satisfying with the above requirements, such as Re(V, P)O4 zircon-type oxides (Re is a rare-earth element),9–12 ReMO3 perovskite-type oxides (M is a transition metal),13–16 EuRe2O4 spinel-type oxides,17,18 Re3CrGa4O12 garnets,19,20 KBaYb(BO3)2,21 and many alloys (including ErMn2Si2,22 Er2Ni1.5Ga2.5,23 Er3Ni6Al2,24 Ho2Ni0.95Si2.95,25 and YbPt2Sn26), in which YbPt2Sn26 could work from 2 K down to 0.2 K. Recently, Petrov et al.27 have found a large MC effect in LiRe(PO3)4 single crystals (Re = Gd, Tb, and Dy), a material system has been widely used for optoelectronic applications.28–30 Intriguing optical and magnetic properties of these LiRe(PO3)4 materials are related to Re3+ ions confined in the ReO8 dodecahedral crystal field. In crystallography, along the b axis, edge-shared ReO8 dodecahedra and LiO4 tetrahedra in turn arrange, while PO4 tetrahedra form helical chains. Additionally, the ReO8 and LiO4 chains share their corners with the helical PO4 chains that constitute a 3D framework.31,32 Together with the 3D framework, a large nearest Re–Re distance (∼5.6 Å31,33) is thought to obstruct exchange interactions between Re ions, leading to a large MC effect of LiRe(PO3)4 at low temperatures. Investigating LiRe(PO3)4 materials with Re = Gd, Tb, Dy and Pr, Petrov et al.27,32 found their |ΔSm| and ΔTad values at 2 K are about 9.8–27.6 J kg−1 K−1 for the field H = 50 kOe and 3–13 K for H = 20 kOe, respectively.
To learn more about this LiRe(PO3)4 material system, we have prepared a single crystal of lithium samarium tetraphosphate, LiSm(PO3)4, and investigated in detail its structural characterization, magnetic behaviors and MC effect. To the best of our knowledge, no previous work on the magnetocaloric behaviors of LiSm(PO3)4, though its electronic and optical properties have been widely studied.34–36 Herein, the magnetic behaviors have studied through the magnetization (M) and heat-capacity (Cp) measurements versus the temperature and magnetic field. Based on these M and Cp data, and thermodynamic relations, the characteristic parameters of the MC effect (|ΔSm| and ΔTad) have been evaluated in comparison to the previous works on low-temperature MC materials.
2. Experimental details
A single crystal (SC) of LiSm(PO3)4 was grown by using the flux method.37 After fabrication, its crystal structure was analyzed by using an X-ray diffractometer in Bragg–Brentano geometry (Malvern Panalytical) equipped with an X-ray wavelength of 1.5406 Å. To record the magnetization and heat-capacity data dependent on the temperature and magnetic field, M(T, H) and Cp(T, H), respectively, we used a Quantum Design Physical Properties Measurement System (PPMS-9). Specifically, M(T, H) data were recorded at temperatures T = 2–300 K and magnetic fields H = 0–50 kOe, while Cp(T, H) data were recorded at T = 2–300 K and H = 0–20 kOe. After collecting M(T, H) and Cp(T, H) data, |ΔSm(T, H)| and ΔTad were calculated by using Maxwell's relations and thermodynamic equations.
3. Results and discussion
The LiSm(PO3)4 SC after fabricated has pale yellow (see the inset of Fig. 1), which was roughly ground to examine the structural properties by using the X-ray diffraction (XRD) method. The X-ray data analysis based on the profile matching mode (Le Bail fit) belonging to the FullProf structural refinement software38 has revealed that the diffraction peaks can be fitted successfully only with a monoclinic phase with the C2/c symmetry, indicating a single-phase nature of our sample. The refined lattice parameters, a = 16.3784(7) Å, b = 7.0373(6) Å, c = 9.6895(5) Å, and β = 126.071(3)°, are well consistent with those obtained from previous works on LiSm(PO3)4.39,40
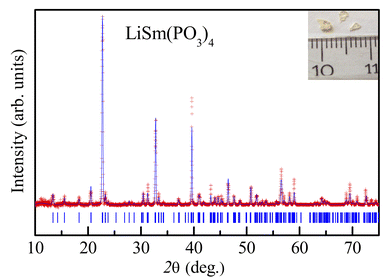 |
| | Fig. 1 Room-temperature XRD pattern of LiSm(PO3)4. Experimental data (red symbols) and calculated profile (blue lines) are shown. Vertical blue ticks denote the nuclear reflections of the monoclinic C2/c phase. The inset shows an image of LiSm(PO3)4 single crystals studied in this work. | |
Following the structural characterization, we have studied the magnetic behaviors of LiSm(PO3)4 upon analyzing M(T, H) and Cp(T, H) data. In Fig. 2, it graphs M(T) data measured for the sample in powder according to the increasing and decreasing directions of temperature for an applied field H = 1 kOe. Similar to Li[Gd,Tb,Dy](PO3)4 (ref. 27) and (Er,Yb)VO4 (ref. 9) materials, we have also observed a gradual decrease in M when T increases from 2 to ∼300 K. Though T reached 2 K, no trace of magnetic-ordering transition temperatures (Néel/Curie temperatures, TN/TC) was observed. The performance of the magnetic susceptibility (χ−1 = H/M) from these M(T) data, and the extrapolation of the high-temperature Curie–Weiss (CW) law would obtain the CW temperature (θCW) of about −36 K, as shown in Fig. 2. A negative θCW value reflects that antiferromagnetic (anti-FM) super-exchange interactions take place between Sm3+ ions in SmO8 chains of monoclinic LiSm(PO3)4 mediated by O and P ions. In other words, LiSm(PO3)4 is anti-FM with the Néel temperature (TN) lower than 2 K. Measuring a full M(H) loop at 2 K, we have found no magnetic hysteresis. M tends to saturate as H > 10 kOe, with a saturation value (Ms) of ∼22.4 emu g−1 (or ∼1.97 μB/f.u.), see the inset of Fig. 2. This effective moment value is fairly greater than the theoretical value of gJ[J(J + 1)]1/2 = 0.85μB for a free Sm3+ ion in the ground state (4f5, 6H5/2, with S = 5/2, L = 5 and J = L − S), and experimental values obtained for Sm3+ in van-Vleck-paramagnetic compounds of Sm3Sb3Zn2O14 (ref. 41) and SmZnAl11O19.42 Such differences could be due to the fact that Sm3+ is a Kramers ion and occupies in various crystal fields. In the SmO8 dodecahedral field, there could be a degenerate ground state with several types of degrees of freedom. After the ground term 6H5/2, the next higher order term, J = L − S + 1 (6H7/2), has a moment value of 3.32μB. Energy levels of these terms seem close to each other, and can mix as a function of T and H. Additionally, due to the crystalline-electric-field effect, a J = 5/2 ground state can split into a Γ7 doublet and a Γ8 quartet. The Γ7 state has a magnetic dipole while the Γ8 state has a magnetic dipole, electric quadrupoles and magnetic octupoles.43 The interactions of magnetic dipoles and octupoles could result in a large value of magnetic moment of LiSm(PO3)4. As studying the materials having strongly-correlated electron states via hybridization with electrons, it has also been found large magnetic moments of 1.2–1.7μB.43 Measuring a series of M(T) curves at higher fields H = 2–50 kOe and T = 2–50 K, as shown in Fig. 3(a), we have found a gradual increase of paramagnetic background signals, and M becomes saturated at Ms ∼ 22.4 emu g−1 as H ≥ 10 kOe. There is a temperature range (named a saturation region) from 2 K that M is less changed and approximately equal to Ms. It broadens towards high temperatures when H increases above 30 kOe, see a dashed rectangle plotted in Fig. 3(a). After the saturation region, M would gradually decrease with increasing T. Interestingly, having performed dM(T)/dT data, we have observed the minimum that starts appearing as H ≈ 5 kOe at the so-called Tp temperature. Tp tends to shift towards higher temperatures as increasing H, see Fig. 3(b) and its inset. This proves an H-dependent ferromagnetic–paramagnetic (FM–PM) separation at Tp. These Tp(H) data can be described a linear function of Tp = 0.51 + 0.48 × H, as shown in Fig. 4. The zero-field extrapolation, H → 0, would obtain the Curie temperature (TC) of LiSm(PO3)4 at 0.51 K. A negative θCW value together with these results suggest a coexistence of FM and anti-FM interactions induced by Sm3+ ions (probably associated with interactions between magnetic dipoles and octupoles of the Γ7 and Γ8 states) in LiSm(PO3)4 at low temperatures and fields. The high-field application promotes FM-ordering establishment, leading to the FM–PM transition at Tp. It is necessary to measure M(T, H) data at lower temperatures (<2 K) to identify exactly LiSm(PO3)4 being a ferromagnet and/or antiferromagnet.
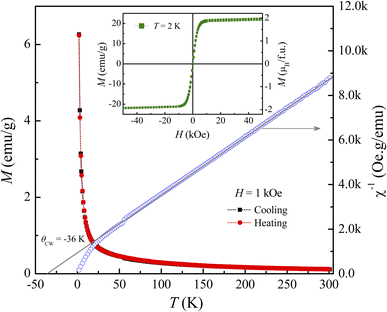 |
| | Fig. 2 M(T) and χ−1(T) curves of LiSm(PO3)4 in the field H = 1 kOe, and the straight line is plotted according to the CW law. The inset is an M(H) loop recorded at T = 2 K. | |
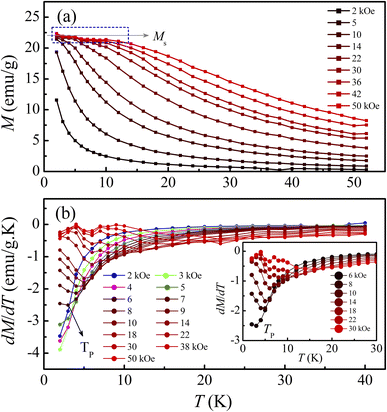 |
| | Fig. 3 (a) M(T) and (b) dM(T)/dT data of LiSm(PO3)4 in different applied fields of H = 2–50 kOe. The inset plots an enlarged view of the dM(T)/dT data for H = 6–30 kOe showing the minima at Tp. | |
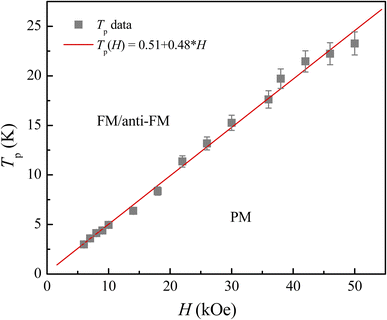 |
| | Fig. 4 H-Dependent Tp data of LiSm(PO3)4 showing a FM–PM phase separation. | |
The FM-ordering establishment in the LiSm(PO3)4 sample can be further confirmed upon Cp(T) measurement at different applied fields for a bulk sample. The Cp(T, H) data for H = 0–20 kOe graphed in Fig. 5 indicate a gradual decrease of Cp as decreasing T from 300 K to Tm, which is defined as the point that a decrease in temperature below it will enhance Cp. Tm is about 3.7 K for H = 0 and increases to ∼6.7 K for H = 20 kOe. An enhancement of Cp as lowering T below Tm is assigned to the magnetic contribution to heat capacity,44 demonstrating the establishment of magnetic ordering in this material. Due to the limit of low-temperature measurement, we could not obtain the onset of magnetic ordering (i.e., TN or TC) corresponding to a (Schottky) peak in the Cp(T, H) curves such as phenomena observed in materials GdVO4,9, (Tb,Dy,Ho)3CrGa4O12,19 Li(Gd,Tb,Dy)(PO3)4,27 and ErRuSi.44 It should be noticed that the magnetic contribution to Cp is mainly at temperatures below Tm. Above Tm, the phonon contribution (Cph) to Cp plays a dominant role, consequently Cp is less dependent on H. We have found that the Cp(T) data for H = 0 and T = 2–100 K can be described by the combination of one Debye and one Einstein terms for phonons:45
| |
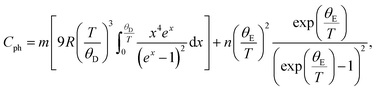 | (1) |
see the inset of
Fig. 5, where
θD is the Debye temperature,
θE is the Einstein temperature, and
m and
n are the fit parameters. The sum
m +
n was fixed to the total number of atoms in the formula unit of LiSm(PO
3)
4. Herein, the obtained values of
θD and
θE are about 217.6 and 439.4 K, respectively.
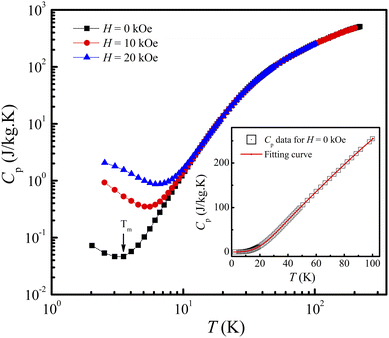 |
| | Fig. 5 Cp(T) data of LiSm(PO3)4 in the log–log scale for H = 0, 10, and 20 kOe. The insets plots Cp(T) data for H = 0 fitted to a combination of Debye–Einstein functions, eqn (1). | |
Magnetic behaviors of LiSm(PO3)4 can be further understood as considering M(H) isotherms recorded at T = 2–50 K. Typical M(H) curves shown in Fig. 6(a) indicate the change in their curvature when T increases from 2 to 40 K, particularly at fields H = 0–20 kOe. In other words, low-temperature nonlinear M(H) curves become linear as increasing T above 30 K. This indicates the collapse of magnetic ordering, and the material becomes paramagnetic at high temperatures. Similar to M(T) data shown in Fig. 3(a), below 8 K, M goes to saturate as raising H above 30 kOe. As performing M2(H/M) plots, see Fig. 6(b), it comes to our attention that these curves have positive slopes, and are not parallel straight lines. These features reflect that LiSm(PO3)4 undergoes a second-order nature in the investigating temperature range (according to Banerjee's criteria46) and exhibiting short-range magnetic order (according to Arrott and Noakes47,48). Short-range magnetic order in LiSm(PO3)4 is ascribed to a coexistence of FM and anti-FM interactions between Sm3+ ions via O and P atoms. Additionally, under the impacts of the crystal and magnetic fields, Kramers doublet on Sm3+ ions could have more (2J + 1)-fold degeneracy, leading to multiplets.32 The jj-coupling and/or spin population on these multiplets could also cause short-range magnetic order in LiSm(PO3)4.
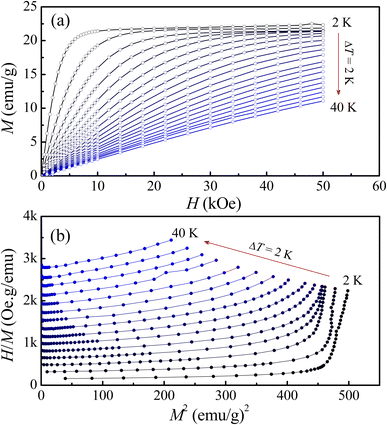 |
| | Fig. 6 (a) Representative M(H) and (b) M2(H/M) data of LiSm(PO3)4 at temperatures T = 2–40 K, where temperature increments are maintained at 2 K. | |
Together with the magnetic behaviors, we have also studied the MC effect through the parameters |ΔSm| and ΔTad calculated by the following expressions:1
| |
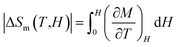 | (2) |
| |
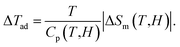 | (3) |
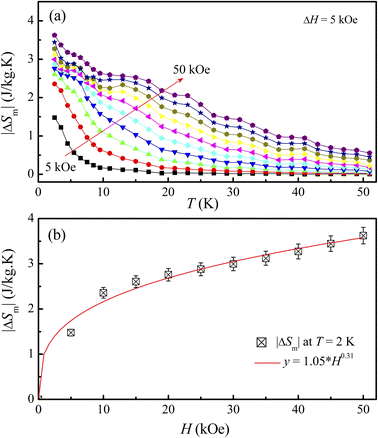
Fig. 7(a) shows |ΔSm| data of LiSm(PO3)4 at temperatures T = 2–50 kOe in magnetic fields H = 5–50 kOe, with magnetic-field increments (ΔH) fixed at 5 kOe. One can see that |ΔSm(T)| increases with increasing H, particularly at T < 25 K. Due to magnetic saturation, |ΔSm(T)| less changes at high fields (>30 kOe). At T = 2 K, |ΔSm| is largest (|ΔSmax|) of ∼3.6 J kg−1 K−1 for H = 50 kOe. This value is fairly smaller than the |ΔSm| values (9.8–27.6 J kg−1 K−1, H = 50 kOe) obtained for Li(Gd,Tb,Dy,Pr)(PO3)4 single crystals.27,32 It is reasonable because magnetic moment of Sm3+ is lower than that of Gd3+, Tb3+, Dy3+, and Pr3+.49 Considering |ΔSm(H)| data at T = 2 K, we have found that these data could be described by a power law of y = a × Hn, with a = 1.05 and n = 0.31. This n value falls in the range of Li(Gd,Tb,Dy)(PO3)4 materials with n = 0.12–0.64,27 but smaller than the value of mean-field theory (MFT) n = 0.67.8 According to Franco et al.,8 n has a relationship with another parameter N(T, H) characteristic for magnetic ordering, which is calculated as follows:
| |
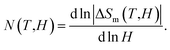 | (4) |
 |
| | Fig. 7 (a) |ΔSm(T)| data of LiSm(PO3)4, and (b) |ΔSm(H)| data at T = 2 K fitted to a function y = a × Hn. | |
For ferromagnets obeying the MFT (long-range ferromagnets), N goes to 1 and 2 as T ≪ TC and T ≫ TC, respectively. It achieves the minimum at T = TC, and n = N(TC) = 0.67, which is independent of H.8 In our work, though N tends to 2 at high temperatures (corresponding to the paramagnetic region), the minima of N(T, H) are about 0.1–0.2 and strongly dependent on H, which are much lower than the MFT value, as shown in Fig. 8.
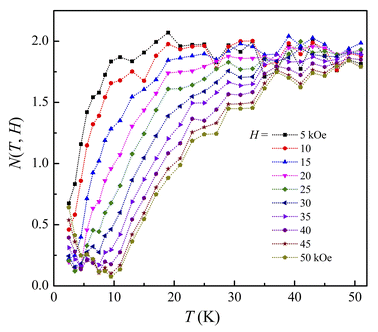 |
| | Fig. 8 N(T, H) data of LiSm(PO3)4 for H = 5–50 kOe calculated by using eqn (4). | |
This deviation is ascribed to (i) |ΔSm(H)| and N(T, H) values calculated at temperatures higher than TN/TC, and (ii) the absence of long-range magnetic order in LiSm(PO3)4. If combining |ΔSm(T)| and Cp(T) data for H = 0–20 kOe, we would evaluate ΔTad(T) values upon eqn (3). As seen in Fig. 9, ΔTad increases gradually when T decreases below 12 K. The maximum ΔTad for LiSm(PO3)4 are about 4 and 5.8 K at 2 K, for applied fields of 10 and 20 kOe, respectively, which is higher than the maximum ΔTad (∼2.8 K) of LiPr(PO3)4 (ref. 32) at the same conditions. For Li(Gd,Tb,Dy)(PO3)4, they have fairly higher maximum ΔTad values of 11.9–12.9 K at 2 K and H = 20 kOe.27 These differences are mainly related to the ground-state degeneracy of RE ions due to spin–orbit coupling and impacts of crystal and magnetic fields, depending on each rare-earth ion type.
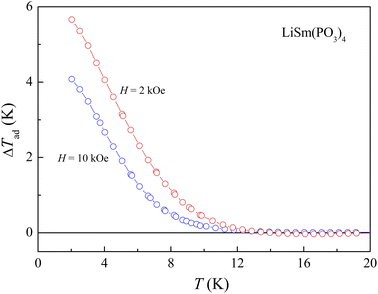 |
| | Fig. 9 ΔTad(T) calculated from Cp(T, H) data of LiSm(PO3)4 for H = 10 and 20 kOe, using eqn (3). | |
Together with |ΔSm| and ΔTad, it is also additionally assessed the relative cooling power (RCP) and/or the refrigeration capacity (RC) by using the following expressions:1,8
| |
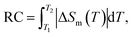 | (6) |
where
δT is the full-width-at-half maximum of a |Δ
Sm(
T)| curve. Meanwhile,
T1 and
T2 are defined as the cold and hot ends, respectively, of an ideal thermodynamic cycle that are usually selected at the middle points of a |Δ
Sm(
T)| curve. With |Δ
Sm(
T)| curves shown in
Fig. 7(a), one can see their linewidth (
δT) increases with increasing
H, and
δT ≈ 23 K for
H = 50 kOe, see
Fig. 10(a). In the investigating
H range,
δT(
H) dependence is almost linear (described by a function
y ≈ 0.5 ×
H0.98). An enhanced
δT is expected to increase RCP and RC with respect to
H. As shown in
Fig. 10(b), both RCP and RC increases according to power functions of
H (
y =
b ×
Hm, with
m = 1.31 and 1.24 for RC and RCP, respectively), in which RCP is about 1.2–1.4 time higher than that of RC. For
H = 50 kOe, RCP (RC) is about 82.4 (57.4) J kg
−1.
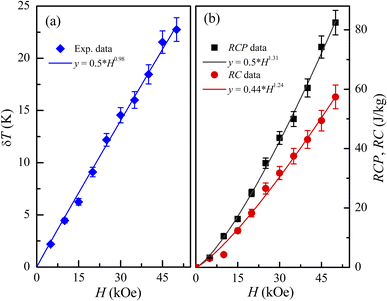 |
| | Fig. 10 (a) δT(H) and (b) RCP(H) and RC(H) data of LiSm(PO3)4 for H = 0–50 kOe fitted to a power law of y = b × Hm, with the values of b and m labeled in the figures. | |
For comparison, we have summarized the MC behaviors (|ΔSmax| and RCP/RC values) of LiSm(PO3)4 compared with those of some typical materials with TN (TC) < 10 K, for the field H = 50 kOe. These materials are potential magnetic coolants useable for liquefying helium and hydrogen gases. The data shown in Table 1 reveals that LiSm(PO3)4 has MC values of |ΔSmax| = 3.6 J kg−1 K−1 and RCP (RC) = 82.4 (57.4) J kg−1. Belonging to the same family, Li(Gd,Tb,Dy)(PO3)4 have larger MC values, with |ΔSmax| = 11.7–27.6 J kg−1 K−1 and RCP (RC) = 174–334 (133–254) J kg−1,27 which are comparable to MC behaviors of DyVO4 (ΔSmax| = 19.8 J kg−1 K−1 and RCP ≈ 300 J kg−1)51 and ErRu2Si2 (ΔSmax| = 17.6 J kg−1 K−1 and RCP = 278 J kg−1).53 It has been found large MC values as studying NaGdF4 (|ΔSmax| = 51.2 J kg−1 K−1 and RCP (RC) = 331 (250) J kg−1),50 and EuTiO3 (|ΔSmax| = 40.4–42.2 J kg−1 K−1 and RCP = 300–353 J kg−1).14 Studying EuSe, it has found its MC values being very large with |ΔSmax| = 37.5 J kg−1 K−1 and RCP = 580 J kg−1.53 Though Sm3+-related MC materials have been less studied, it is clear that LiSm(PO3)4 has fairly humble MC values. We think that spin–orbit interaction (L–S coupling) and the J = 5/2 ground-state degeneracy into the Γ7 and Γ8 states lead to a competition of FM and anti-FM interactions between Sm3+ ions, meaning short-range magnetic order, consequently low MC effect in LiSm(PO3)4.
Table 1 MC behaviors of LiSm(PO3)4 and typical MC materials with TN (TC) < 10 K at H = 50 kOe
| Compound |
TN/TC (K) |
|ΔSmax| (J kg−1 K−1) |
RCP/RC (J kg−1) |
Ref. |
| LiSm(PO3)4 |
/0.51 |
3.6 |
82.4/57.4 |
This work |
| LiGd(PO3)4 |
— |
27.6 |
174/133 |
27 |
| LiTb(PO3)4 |
— |
15.9 |
334/254 |
27 |
| LiDy(PO3)4 |
— |
11.7 |
236/193 |
27 |
| NaGdF4 |
2.3 |
51.2 |
331/250 |
50 |
| DyVO4 |
3.5 |
19.8 |
∼300 |
51 |
| EuSe |
4.6 |
37.5 |
580 |
52 |
| EuTiO3 |
4.4–5.6 |
40.4–42.2 |
300–353 |
14 |
| ErRu2Si2 |
5.5 |
17.6 |
278 |
53 |
4. Conclusion
We recorded XRD, dc magnetization M(T, H), and heat capacity Cp(T, H) data to investigate the magnetic and MC behaviors of LiSm(PO3)4. Rietveld refinement demonstrated a single phase in the C2/c monoclinic structure of LiSm(PO3)4. The analyses of M(T), M(H) and Cp(T, H) data demonstrated the magnetic-ordering establishment at low temperatures, and a coexistence of FM and anti-FM interactions with θCW ≈ −36 K and TC ≈ 0.51 K. The FM phase tends to widen towards high temperatures as increasing H. MC assessments based on |ΔSm| and ΔTad indicated an increase of these parameters as lowering T down to 2 K, and increasing the H magnitude. At 2 K, the maximum values of |ΔSm|, and ΔTad are about 3.6 J kg−1 K−1 for H = 50 kOe, and 5.8 K for H = 20 kOe. Thus, the corresponding values of RCP and RC are about 82.5 and 57.4 J kg−1 for H = 50 kOe, respectively. It should be noticed that the MC effect of LiSm(PO3)4 is fairly smaller than that of Li(Gd,Tb,Dy)(PO3)4 having the same structure. Strong L–S coupling, the J = 5/2 ground-state degeneracy into the Γ7 and Γ8 states, and the competition of FM and anti-FM interactions between Sm3+ ions, causing short-range magnetic ordering, are thought to lead to low MC effect of LiSm(PO3)4.
Author statement
T. A. Tran, Dimitar N. Petrov, N. T. Dang, and T. L. Phan: conceptualization, methodology and writing; T. P. Hoang, H. C. Tran, B. D. Tu, Yu S. Koshkid'ko, B. Weise, and V. M. Tien: investigation and data analyses; and J. Ćwik, and H. N. Nhat: reviewing and editing.
Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgements
This work belongs to the project grant no: T2022-17 funded by Ho Chi Minh City University of Technology and Education (Vietnam).
References
- A. M. Tishin and Y. I. Spichkin, The Magnetocaloric Effect and its Applications, CRC Press, 2003, DOI:10.1201/9781420033373
 .
. - V. K. Pecharsky and K. A. Gschneidner, Magnetocaloric effect and magnetic refrigeration, J. Magn. Magn. Mater., 1999, 200, 44–56, DOI:10.1016/S0304-8853(99)00397-2
 .
. - A. Kitanovski, Energy Applications of Magnetocaloric Materials, Adv. Energy Mater., 2020, 10, 1903741, DOI:10.1002/aenm.201903741
 .
. - W. F. Giauque, A thermodynamic treatment of certain magnetic effects. A proposed method of producing temperatures considerably below 1° absolute, J. Am. Chem. Soc., 1927, 49, 1864–1870, DOI:10.1021/ja01407a003
 .
. - W. F. Giauque and D. P. MacDougall, Attainment of temperatures below 1° absolute by demagnetization of Gd2(SO4)3·8H2O, Phys. Rev., 1933, 43, 768, DOI:10.1103/PhysRev.43.768
 .
. - R. T. Kouzes and J. H. Ely, PNNL-19360: Status Summary of 3He and Neutron Detection Alternatives for Homeland Security, Richland, WA (United States), 2010, DOI:10.2172/981573
 .
. - J. Lyubina, Magnetocaloric materials for energy efficient cooling, J. Phys. D: Appl. Phys., 2017, 50, 053002, DOI:10.1088/1361-6463/50/5/053002
 .
. - V. Franco, J. S. Blázquez, J. J. Ipus, J. Y. Law, L. M. Moreno-Ramírez and A. Conde, Magnetocaloric effect: From materials research to refrigeration devices, Prog. Mater. Sci., 2018, 93, 112–232, DOI:10.1016/j.pmatsci.2017.10.005
 .
. - K. Dey, A. Indra, S. Majumdar and S. Giri, Cryogenic magnetocaloric effect in zircon-type RVO4 (R = Gd, Ho, Er, and Yb), J. Mater. Chem. C, 2017, 5, 1646–1650, 10.1039/c6tc05182k
 .
. - Y. Y. Yu, D. N. Petrov, P. T. Long, K. C. Park, J. Ćwik, P. T. Phong and B. T. Huy, Electronic structure and large magnetocaloric effect in GdVO4 nanocrystals, J. Alloys Compd., 2021, 885, 161002, DOI:10.1016/j.jallcom.2021.161002
 .
. - E. Palacios, M. Evangelisti, R. Sáez-Puche, A. J. Dos Santos-García, F. Fernández-Martínez, C. Cascales, M. Castro, R. Burriel, O. Fabelo and J. A. Rodríguez-Velamazán, Magnetic structures and magnetocaloric effect in RVO4 (R = Gd, Nd), Phys. Rev. B, 2018, 97, 214401, DOI:10.1103/PhysRevB.97.214401
 .
. - Y. Y. Yu, D. N. Petrov, K. C. Park, B. T. Huy and P. T. Long, Magnetic and cryogenic magnetocaloric properties of GdPO4 nanorods, J. Magn. Magn. Mater., 2021, 519, 167452, DOI:10.1016/j.jmmm.2020.167452
 .
. - S. Mahana, U. Manju and D. Topwal, Giant magnetocaloric effect in GdAlO3 and a comparative study with GdMnO3, J. Phys. D: Appl. Phys., 2017, 50, 035002, DOI:10.1088/1361-6463/50/3/035002
 .
. - A. Midya, P. Mandal, K. Rubi, R. Chen, J. S. Wang, R. Mahendiran, G. Lorusso and M. Evangelisti, Large adiabatic temperature and magnetic entropy changes in EuTiO3, Phys. Rev. B, 2016, 93, 094422, DOI:10.1103/PhysRevB.93.094422
 .
. - J. H. Jia, Y. J. Ke, X. X. Zhang, J. F. Wang, L. Su, Y. D. Wu and Z. C. Xia, Giant magnetocaloric effect in the antiferromagnet GdScO3 single crystal, J. Alloys Compd., 2019, 803, 992–997, DOI:10.1016/j.jallcom.2019.06.361
 .
. - M. Balli, B. Roberge, J. Vermette, S. Jandl, P. Fournier and M. M. Gospodinov, Magnetocaloric properties of the hexagonal HoMnO3 single crystal revisited, Phys. B, 2015, 478, 77–83, DOI:10.1016/j.physb.2015.08.063
 .
. - E. Palacios, R. Sáez-Puche, J. Romero, Y. Doi, Y. Hinatsu and M. Evangelisti, Large magnetocaloric effect in EuGd2O4 and EuDy2O4, J. Alloys Compd., 2022, 890, 161847, DOI:10.1016/j.jallcom.2021.161847
 .
. - A. Midya, N. Khan, D. Bhoi and P. Mandal, Giant magnetocaloric effect in magnetically frustrated EuHo2O4 and EuDy2O4 compounds, Appl. Phys. Lett., 2012, 101, 132415, DOI:10.1063/1.4754849
 .
. - P. Mukherjee and S. E. Dutton, Enhanced Magnetocaloric Effect from Cr Substitution in Ising Lanthanide Gallium Garnets Ln3CrGa4O12 (Ln = Tb, Dy, Ho), Adv. Funct. Mater., 2017, 27, 1701950, DOI:10.1002/adfm.201701950
 .
. - N. K. Chogondahalli Muniraju, R. Baral, Y. Tian, R. Li, N. Poudel, K. Gofryk, N. Barišić, B. Kiefer, J. H. Ross and H. S. Nair, Magnetocaloric Effect in a Frustrated Gd-Garnet with No Long-Range Magnetic Order, Inorg. Chem., 2020, 59, 15144–15153, DOI:10.1021/acs.inorgchem.0c02074
 .
. - Y. Tokiwa, S. Bachus, K. Kavita, A. Jesche, A. A. Tsirlin and P. Gegenwart, Frustrated magnet for adiabatic demagnetization cooling to milli-Kelvin temperatures, Commun. Mater., 2021, 2, 42, DOI:10.1038/s43246-021-00142-1
 .
. - L. Li, K. Nishimura, W. D. Hutchison, Z. Qian, D. Huo and T. Namiki, Giant reversible magnetocaloric effect in ErMn2Si2 compound with a second order magnetic phase transition, Appl. Phys. Lett., 2012, 100, 152403, DOI:10.1063/1.4704155
 .
. - D. Guo, Y. Zhang, B. Wu, H. Wang, R. Guan, X. Li and Z. Ren, Structural, magnetic and magnetocaloric properties in RE2Ni1.5Ga2.5 (RE = Dy, Ho, Er and Tm) compounds, J. Alloys Compd., 2020, 830, 154666, DOI:10.1016/j.jallcom.2020.154666
 .
. - J. W. Xu, X. Q. Zheng, S. X. Yang, L. Xi, D. S. Wang, C. F. Liu, J. Y. Zhang, Y. F. Wu, J. X. Shen, S. G. Wang and B. G. Shen, Large reversible magnetic entropy change of R3Ni6Al2 (R = Dy, Ho and Er) compounds, J. Alloys Compd., 2021, 879, 160468, DOI:10.1016/j.jallcom.2021.160468
 .
. - S. Pakhira, C. Mazumdar, R. Ranganathan and M. Avdeev, Magnetic frustration induced large magnetocaloric effect in the absence of long range magnetic order, Sci. Rep., 2017, 7, 7367, DOI:10.1038/s41598-017-07459-3
 .
. - D. Jang, T. Gruner, A. Steppke, K. Mitsumoto, C. Geibel and M. Brando, Large magnetocaloric effect and adiabatic demagnetization refrigeration with YbPt2Sn, Nat. Commun., 2015, 6, 8680, DOI:10.1038/ncomms9680
 .
. - D. N. Petrov, P. T. Long, Y. S. Koshkid'Ko, J. Ćwik and K. Nenkov, Large magnetocaloric effect in LiLnP4O12 (Ln = Gd, Tb, Dy) single crystals, J. Phys. D: Appl. Phys., 2020, 53, 495005, DOI:10.1088/1361-6463/abb26f
 .
. - A. Lukowiak, M. Stefanski, M. Ferrari and W. Strek, Nanocrystalline lanthanide tetraphosphates: energy transfer processes in samples co-doped with Pr3+/Yb3+ and Tm3+/Yb3+, Opt. Mater., 2017, 74, 159–165, DOI:10.1016/j.optmat.2017.03.025
 .
. - N. Ben Hassen, M. Ferhi, K. Horchani-Naifer and M. Férid, Synthesis, characterization and optical properties of LiSm(PO3)4 phosphor, Opt. Mater., 2015, 46, 355–360, DOI:10.1016/j.optmat.2015.04.045
 .
. - B. Han, H. Liang, Y. Huang, Y. Tao and Q. Su, Luminescence of LiTb(PO3)4:Sm3+ and energy transfer from Tb3+ to Sm3+ under vacuum ultraviolet-ultraviolet excitation, Appl. Phys. B: Lasers Opt., 2011, 104, 241–246, DOI:10.1007/s00340-011-4580-6
 .
. - H. Ettis, H. Naïli and T. Mhiri, The crystal structure, thermal behaviour and ionic conductivity of a novel lithium gadolinium polyphosphate LiGd(PO3)4, J. Solid State Chem., 2006, 179, 3107–3113, DOI:10.1016/j.jssc.2006.06.003
 .
. - D. N. Petrov, N. T. Dang, T. L. Phan, B. W. Lee, J. Ćwik, Y. S. Koshkid'ko, T. V. Manh, H. R. Park and S. C. Yu, Metamagnetism and Magnetocaloric Effect of LiPr(PO3)4 Crystal, J. Electron. Mater., 2022, 51, 4479–4485, DOI:10.1007/s11664-022-09655-y
 .
. - D. Petrov, B. Angelov and V. Lovchinov, Magnetic and XPS studies of lithium lanthanide tetraphosphates LiLnP4O12 (Ln=Nd, Gd, Er), J. Rare Earths, 2013, 31, 485–489, DOI:10.1016/S1002-0721(12)60307-X
 .
. - C.-G. Ma, M. G. Brik, W. Ryba-Romanowski, H. C. Swart and M. A. Gusowski, Spectroscopy and Calculations for 4fN → 4fN–15d Transitions of Lanthanide Ions in K3YF6, J. Phys. Chem. A, 2012, 116, 9158–9180, DOI:10.1021/jp306409p
 .
. - D. N. Petrov and B. M. Angelov, Fluorescence of UV-excited single crystals of LiSmP4O12 and LiDyP4O12, Optik, 2018, 169, 291–296, DOI:10.1016/j.ijleo.2018.05.080
 .
. - N. Ben Hassen, M. Ferhi, K. Horchani-Naifer and M. Férid, Synthesis, characterization and optical properties of LiSm(PO3)4 phosphor, Opt. Mater., 2015, 46, 355–360, DOI:10.1016/j.optmat.2015.04.045
 .
. - B. M. Anghelov and B. M. Wanklyn, Flux growth of lithium rare-earth tetraphosphates, J. Mater. Sci. Lett., 1986, 5, 1067–1069, DOI:10.1007/BF01730286
 .
. - J. Rodríguez-Carvajal, Recent advances in magnetic structure determination by neutron powder diffraction, Phys. B, 1993, 192, 55–69, DOI:10.1016/0921-4526(93)90108-I
 .
. - D. Zhao, F. Li, W. Cheng and H. Zhang, Lithium samarium polyphosphate, LiSm(PO3)4, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2010, 66, i3, DOI:10.1107/S1600536809055822
 .
. - S. Sebai, S. Hammami, A. Megriche, D. Zambon and R. Mahiou, Synthesis, structural characterization and VUV excited luminescence properties of LixNa(1−x)Sm(PO3)4 polyphosphates, Opt. Mater., 2016, 62, 578–583, DOI:10.1016/j.optmat.2016.11.015
 .
. - M. B. Sanders, J. W. Krizan and R. J. Cava, RE3Sb3Zn2O14 (RE = La, Pr, Nd, Sm, Eu, Gd): a new family of pyrochlore derivatives with rare earth ions on a 2D Kagome lattice, J. Mater. Chem. C, 2016, 4, 541–550, 10.1039/C5TC03798K
 .
. - M. Ashtar, M. A. Marwat, Y. X. Gao, Z. T. Zhang, L. Pi, S. L. Yuan and Z. M. Tian, REZnAl11O19 (RE = Pr, Nd, Sm–Tb): a new family of ideal 2D triangular lattice frustrated magnets, J. Mater. Chem. C, 2019, 7, 10073–10081, 10.1039/C9TC02643F
 .
. - R. Higashinaka, A. Yamada, T. D. Matsuda and Y. Aoki, Relationship between specific heat, valence and effective magnetic moment of Sm ions in strongly correlated Sm compounds, AIP Adv., 2018, 8, 125017, DOI:10.1063/1.5043120
 .
. - S. Gupta, A. Das, K. G. Suresh, A. Hoser, Y. V. Knyazev, Y. I. Kuz'Min and A. V. Lukoyanov, Experimental and theoretical investigations on magnetic and related properties of ErRuSi, Mater. Res. Express, 2015, 2, 046101, DOI:10.1088/2053-1591/2/4/046101
 .
. - E. Gamsjäger and M. Wiessner, Low temperature heat capacities and thermodynamic functions described by Debye–Einstein integrals, Monatsh. Chem., 2018, 149, 357–368, DOI:10.1007/s00706-017-2117-3
 .
. - B. K. Banerjee, On a generalised approach to first and second order magnetic transitions, Phys. Lett., 1964, 12, 16–17, DOI:10.1016/0031-9163(64)91158-8
 .
. - A. Arrott and J. E. Noakes, Approximate Equation of State For Nickel Near its Critical Temperature, Phys. Rev. Lett., 1967, 19, 786–789, DOI:10.1103/PhysRevLett.19.786
 .
. - A. Arrott, Criterion for ferromagnetism from observations of magnetic isotherms, Phys. Rev., 1957, 108, 1394–1396, DOI:10.1103/PhysRev.108.1394
 .
. - J. Zhou and G. A. Fiete, Rare earths in a nutshell, Phys. Today, 2020, 73, 66–67, DOI:10.1063/PT.3.4397
 .
. - D. N. Petrov, V. Lovchinov, B. The Huy, P. The Long, N. T. Dang and D. S. Yang, Magnetic and cryogenic magnetocaloric properties of NaGdF4 nanocrystals, J. Appl. Phys., 2019, 126, 135101, DOI:10.1063/1.5114993
 .
. - A. Midya, N. Khan, D. Bhoi and P. Mandal, Giant magnetocaloric effect in antiferromagnetic DyVO4 compound, Phys. B, 2014, 448, 43–45, DOI:10.1016/j.physb.2014.03.019
 .
. - D. X. Li, T. Yamamura, S. Nimori, Y. Homma, F. Honda and D. Aoki, Giant and isotropic low temperature magnetocaloric effect in magnetic semiconductor EuSe, Appl. Phys. Lett., 2013, 102, 152409, DOI:10.1063/1.4802260
 .
. - T. Samanta, I. Das and S. Banerjee, Giant magnetocaloric effect in antiferromagnetic ErRu2Si2 compound, Appl. Phys. Lett., 2007, 91, 152506, DOI:10.1063/1.2798594
 .
.
|
| This journal is © The Royal Society of Chemistry 2023 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article a,
Dimitar N. Petrovb,
T. L. Phan*cd,
B. D. Tuc,
H. N. Nhatc,
H. C. Trana,
B. Weise
a,
Dimitar N. Petrovb,
T. L. Phan*cd,
B. D. Tuc,
H. N. Nhatc,
H. C. Trana,
B. Weise e,
J. Cwikf,
Yu S. Koshkid'ko
e,
J. Cwikf,
Yu S. Koshkid'ko f,
T. V. Manh
f,
T. V. Manh g,
T. P. Hoanghi and
N. T. Dang
g,
T. P. Hoanghi and
N. T. Dang *hj
*hj


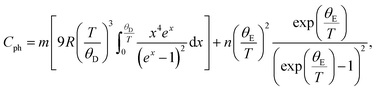


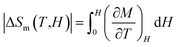
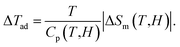
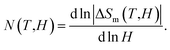



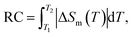

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.


