Open Access Article
Open Access ArticleStrain and magnetic field effects on the electronic and transport properties of γ-graphyne
H. Rezania *a,
E. Nourianb,
M. Abdi
*a,
E. Nourianb,
M. Abdi b and
B. Astinchap
b and
B. Astinchap bc
bc
aDepartment of Physics, Razi University, Kermanshah, Iran. E-mail: rezania.hamed@gmail.com; Fax: +98 831 427 4569; Tel: +98 831 427 4569
bDepartment of Physics, Faculty of Science, University of Kurdistan, 66177-15175 Sanandaj, Kurdistan, Iran
cResearch Center for Nanotechnology, University of Kurdistan, 66177-15175 Sanandaj, Kurdistan, Iran
First published on 10th March 2023
Abstract
In this paper, we apply a tightly binding Hamiltonian model in the presence of a magnetic field for investigating the electronic and transport properties of γ-graphyne layers. We also consider the effects of in-plane biaxial strain on the electronic behavior of γ-graphyne layers. Moreover the impact of strain on magnetic susceptibility and specific heat of the structure is also studied. In particular, the temperature dependence of static thermal conductivity of γ-graphyne layers due to magnetic field and strain effects is studied. We exploit the linear response theory and Green's function approach to obtain the temperature behavior of thermal conductivity, electrical conductivity and the Seebeck coefficient. Our numerical results indicate that thermal conductivity increases upon increasing temperature temperatures. This effect comes from the increasing thermal energy of charge carriers and their excitation to the conduction bands. The temperature dependence of Seebeck coefficient shows that the thermopower of an undoped γ-graphyne layer is positive on the whole range of temperatures in the absence of strain effects. The effects of both electron doping and magnetic field factors on temperature behavior of the electrical conductivity of γ-graphyne are investigated in detail. Moreover the effects of biaxial strain on thermal conductivity of single layer γ-graphyne have been addressed.
1 Introduction
Carbon is the most abundant element in the atmosphere and the Earth's crust. In the past decades, many carbon allotropes with special properties have been reported, the most well-known are 0 dimensional fullerene,1 one dimensional nanotube,2 and two dimensional graphene.3 Graphene consists of a honeycomb network of carbon atoms that has attracted a lot of attention due to its properties of high thermal conductivity, high charge carrier mobility and Young's modulus.4,5 These amazing properties of graphene have led to its application in the electronics, photonics and sensors fields.6,7 However, researchers have made many efforts to control the properties of graphene via strain, defects, and dopants.8,9 Moreover, the properties of graphene have not been optimized enough to be used in practical applications, so graphene-like structures such as graphyne have been examined.10,11 Baughman et al. theoretically presented the structure of graphyne in 1987.12 Haley et al. were able to synthesize 2D graphyne in 1997.13 Graphyne is a new family of allotropes of carbon, constructed by the arrangement of an acetylenic bond between two carbon bonds in graphene. A carbon material’s dimensionality depends on its hybridization.14 For example, sp2 hybridization leads to 2D graphene, while sp and sp3 hybridization forms one dimensional and three dimensional carbon materials, respectively.15,16 However, graphyne is found to be the only two dimensional carbon material so far that has both sp and sp2 hybridization,17 which gives rise to its versatile and flexible crystal structure. The amazing features of acetylenic bonds with sp hybridization, and also possible alterations in the bonds, allow for the construction of various structures called α-, β-, γ- and (6,6,12)-graphynes.18 These carbon allotropes exhibit interesting mechanical, chemical, thermal, and electrical properties that have been identified as strong competitors for graphene.19,20 Xing et al. examined the thermoelectric properties of β-graphyne nanoribbons employing the non-equilibrium Green's function.21 Their results indicated that the thermoelectric properties of β-graphyne nanoribbons are improved by defects. Perkgoz et al. studied the vibrational, thermal expansion coefficient, and Gibbs free energy of α-, β-, γ- and (6,6,12)-graphyne through first-principles calculations.22 It is well-known that a simple π-electronic tight binding model clearly shows the linear dispersive nature of low-energy graphene electrons and has been used extensively to analyze their electronic behavior. The coexistence of the sp2 and sp carbon atoms in graphynes makes atomic orbital hybridization more complicated and thus it is not easy to develop a tight binding model for graphynes. In theoretical work,18 the possibility of establishing a tight binding model for graphyne structures has been studied. A simple tight binding model composed of the pz atomic orbital is developed, which works to describe the band structures of the graphyne allotrope.18γ-Graphyne has the largest negative cohesive energy and thus the most stable structure, while the β-graphyne comes second.23 Both β-graphyne and γ-graphyne have sp–sp, sp–sp2 and sp2–sp2 hybridization bonds, of which γ-graphyne has shorter bond lengths and thus larger Young's modulus.23 They showed that Gruneisen parameters and thermal expansion coefficients for these allotropes are lower than graphene, and allotropes have relatively lower phase stability in contrast to graphene. Liu, et al. were able to manage the zigzag β-graphyne nanoribbons band gap in the tight-binding model utilizing the Coulomb repulsion and the transverse electric field.24 Also, Han et al. investigated the stability, optical, elastic, and thermal conductivity of γ-graphyne using density functional theory.23 It has been demonstrated that the electronic band structure of graphene-like structures can be tuned by the in-plane25,26 or out-of-plane strains.27 The crystal structure of these nanostructures exhibits considerable flexibility for elastic planar strain.25 A high compressive strain can induce a structural phase transition with Dirac-like cones.25 Along both zigzag and armchair directions, there is a large strain up to around 30 percent.26,28 Some theoretical studies of in-plane uniaxial strain effects on the band gap in graphene-like structures have demonstrated changing the electronic,29 thermoelectric30 and optical properties31 of this nanolattice structure.
The purpose of this paper is to provide a tight binding model for studying electronic heat capacity, magnetic susceptibility, and thermal conductivity of γ-graphyne layers in the presence of a magnetic field perpendicular to the plane. Also, the γ-graphyne plane has been considered under simple tensile and compressive strain conditions. Such strain will greatly enhance the thermoelectric performance of the structure. The effects of biaxial in-plane strains on the thermoelectric and transport properties of the γ-graphyne layer are investigated using linear response theory. Using the suitable hopping integral and on-site parameter values, the band dispersion of electrons in the structure has been calculated. For calculating the transport coefficients we have exploited the linear response theory in the context of the Kubo formula. Based on Green's function approach, we have obtained the density of states, thermal conductivity and Seebeck coefficient of γ-graphyne layer. Also, we discuss and analyze how electron doping, longitudinal magnetic field and strain values affect the temperature behavior of specific heat, magnetic susceptibility and transport properties of γ-graphyne.
2 Model Hamiltonian and formalism
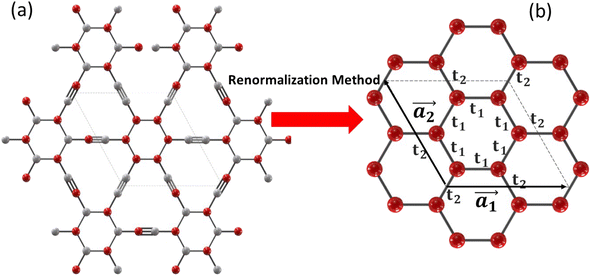
We consider the γ-graphyne lattice structure shown in Fig. 1. Such type of graphyne has no Dirac-cone-like band structure exhibition around the Fermi level. Hence, we apply a tight binding model to describe the electron dynamics of this type of graphyne. Density functional theory (DFT) calculations indicate that we can establish a π-electronic tight-binding model for this type of graphyne, which is composed of the pz atomic orbital.18 In order to apply a tight-binding Hamiltonian model, we need to evaluate the corresponding hopping energies. For γ-graphyne, we need three hopping energies. According to the crystal structure of γ-graphyne and DFT calculations, the two different renormalized hopping parameters are given as t1 = −2.73 eV, t2 = 1.50 eV.18We begin with γ-graphyne subjected to a perpendicular longitudinal magnetic field. The unit cell of γ-graphyne structure is depicted in Fig. 1. The primitive unit cell vectors of honeycomb lattice are shown by a1 = ai and 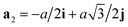 where a describes the length of each unit cell vector. According to Fig. 1, i and j denote the unit vectors along the zigzag and armchair directions, respectively. Considering nearest-neighbor hopping, the tight binding part and the Zeeman part of the model Hamiltonian on γ-graphyne are given by
where a describes the length of each unit cell vector. According to Fig. 1, i and j denote the unit vectors along the zigzag and armchair directions, respectively. Considering nearest-neighbor hopping, the tight binding part and the Zeeman part of the model Hamiltonian on γ-graphyne are given by
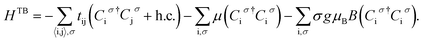 | (1) |
The first term in the Hamiltonian is the nearest-neighbor hopping with Ciσ†(Ciσ) being the electron creation (annihilation) operator on site i with spin index σ = ↑ or ↓. 〈i, j〉 refers to nearest neighbor lattice sites i and j. The nearest-neighbor hopping integrals tij are denoted as t1, t2 as shown in Fig. 1. g implies the gyromagnetic constant and μB denotes the Bohr magneton constant. Also B denotes the magnetic field strength. The chemical potential is introduced by μ in eqn (1). The operators fulfil the fermionic standard anticommunication relations {Ciσ, Ciσ′†} = δijδσσ′. Based on Fig. 1, the translational vectors 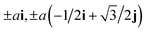 connect the nearest neighbor unit cells. Using these connecting vectors between nearest neighbor unit cells, we can rewrite the model Hamiltonian in eqn (1) in terms of Fourier transformations of fermionic operators. The following Fourier transformation for fermionic operator C†l,α is given by
connect the nearest neighbor unit cells. Using these connecting vectors between nearest neighbor unit cells, we can rewrite the model Hamiltonian in eqn (1) in terms of Fourier transformations of fermionic operators. The following Fourier transformation for fermionic operator C†l,α is given by
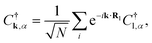 | (2) |
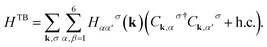 | (3) |
Using parameters Hαα′σ(k), the matrix form of the model Hamiltonian of γ-graphyne from eqn (3) can be given by
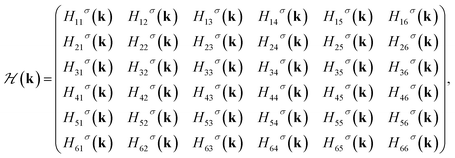 | (4) |
The matrix elements of Hαα′σ(k) can be expressed based on renormalized hopping amplitude parameters t1, t2, magnetic field strength and chemical potential. The diagonal elements of matrix 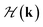 in eqn (4) arise from the magnetic field and chemical potential. Also, the off diagonal matrix elements
in eqn (4) arise from the magnetic field and chemical potential. Also, the off diagonal matrix elements 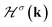 originate from the hopping amplitude of electrons between nearest neighbor atoms on the different sublattices. These matrix elements are obtained as
originate from the hopping amplitude of electrons between nearest neighbor atoms on the different sublattices. These matrix elements are obtained as
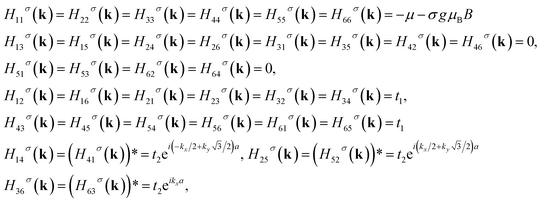 | (5) |
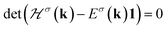 where 1 denotes a 6 × 6 unit matrix. The final results for electronic band structures are lengthy and are not given here. The band structures of electrons with spin σ have been presented by Eησ(k). Using the band energy spectrum, the Hamiltonian in eqn (1) can be rewritten by
where 1 denotes a 6 × 6 unit matrix. The final results for electronic band structures are lengthy and are not given here. The band structures of electrons with spin σ have been presented by Eησ(k). Using the band energy spectrum, the Hamiltonian in eqn (1) can be rewritten by
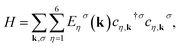 | (6) |
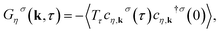 | (7) |
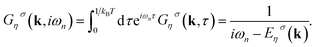 | (8) |
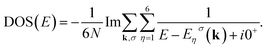 | (9) |
Summation over wave vectors is performed in the first Brillouin zone of the γ-graphyne lattice. The density of states includes prominent asymmetric peaks due to the band edge of parabolic sub-bands. The peak positions arise from the band edge state energies and the density of states heights are proportional to the inverse square root of the sub-band curvature and band degeneracy. For determining the chemical potential, μ, we use the relation between concentration of electrons (ne) and chemical potential. This relation is given by
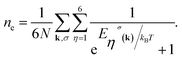 | (10) |
Based on the values of electronic concentration ne, the chemical potential, μ, can be obtained using eqn (10).
3 Mechanical strain effects in γ-graphyne
In this section, we consider the lattice deformation, like strain. Hence the effect of strain is driven by the dependence of tight-binding amplitudes on the interatomic distance. Under compressive and tensile mechanical strain we have found changes in the bond length, bond angle, and hopping energy of graphyne layers.32,33 The Harrison law has been applied to relate the hopping amplitudes to the inverse square of the atomic distance. When strain is applied to γ-graphyne, the deformed ith bond vector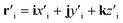 can be expanded in terms of the non-deformed bond vector, ri = ixi + jyi + kzi, as follows
can be expanded in terms of the non-deformed bond vector, ri = ixi + jyi + kzi, as follows
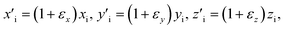 | (11) |
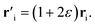 | (12) |
Under the biaxial strain effect and based on eqn (12), hopping amplitudes 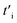 with i = 1, 2 are obtained by using the Harrison law as34
with i = 1, 2 are obtained by using the Harrison law as34
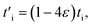 | (13) |
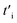 determines the modified hopping energies of the deformed system, and ti describes the hopping energies in the deformed structure with the values given in the previous section. Under substitution of
determines the modified hopping energies of the deformed system, and ti describes the hopping energies in the deformed structure with the values given in the previous section. Under substitution of 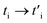 according to eqn (13), in the matrix elements of the Hamiltonian in eqn (5), we obtain the effects of strain on the electronic properties of γ-graphyne.
according to eqn (13), in the matrix elements of the Hamiltonian in eqn (5), we obtain the effects of strain on the electronic properties of γ-graphyne.
4 Transport and thermodynamic properties
Transport properties such as electrical, thermal conductivities and thermoelectric coefficient can be obtained using the electron band structure. In the presence of a temperature gradient (∇T) and in an open circuit situation with zero electrical current, heat current is related to the temperature gradient via JQ = κ∇T where κ is the thermal conductivity and is obtained using the transport coefficients as35
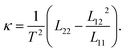 | (14) |
Based on spectral function, i.e. the imaginary part of the retarded Green's function, one can calculate the static transport coefficients of single layer γ-graphyne along the x direction as
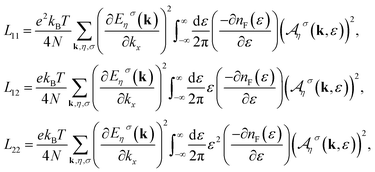 | (15) |
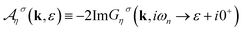 denotes the electric spectral function. Substituting the electronic Green's function into eqn (15) and performing the numerical integration over the wave vector through the first Brillouin zone, the results of transport coefficients are obtained. The ratio of the measured voltage to the temperature gradient applied across the sample is known as the Seebeck coefficient (or the thermopower) and is given by S = ∇V/∇T, where ∇V is the potential difference between two points of the sample.35 The Seebeck coefficient, S, is related to the transport coefficients as
denotes the electric spectral function. Substituting the electronic Green's function into eqn (15) and performing the numerical integration over the wave vector through the first Brillouin zone, the results of transport coefficients are obtained. The ratio of the measured voltage to the temperature gradient applied across the sample is known as the Seebeck coefficient (or the thermopower) and is given by S = ∇V/∇T, where ∇V is the potential difference between two points of the sample.35 The Seebeck coefficient, S, is related to the transport coefficients as
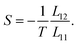 | (16) |
The sign of S determines the sign of the majority carriers of thermal transport in the γ-graphyne. The static electrical conductivity along the x direction for monolayer γ-graphyne in the presence of a magnetic field and biaxial strain, is related to the spectral function as
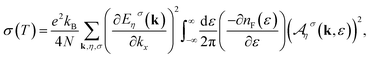 | (17) |
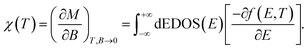 | (18) |
After substituting eqn (9) into eqn (18), the static susceptibility, χ(T), is found with the following expression in terms of Green's function
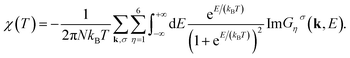 | (19) |
The electronic specific heat could be obtained by means of Green's function as
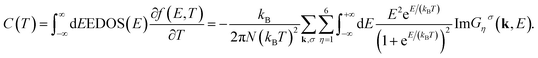 | (20) |
In the next section, the numerical results of electronic properties of single layer γ-graphyne are presented.
5 Numerical results and discussion
In this section our numerical results for the electronic and transport properties of the γ-graphyne monolayer due to a perpendicular magnetic field and biaxial strain effects, are presented. We investigate the electrical conductivity, thermal conductivity and Seebeck coefficient. Also, the behaviors of specific heat and Pauli paramagnetic susceptibility are investigated. The amount of hopping amplitudes of strained γ-graphyne, i.e.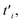 have been expressed in Section 3. Based on the substitution of hopping amplitudes of strained γ-graphyne, i.e.
have been expressed in Section 3. Based on the substitution of hopping amplitudes of strained γ-graphyne, i.e. 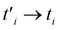 with i = 1, 2, into eqn (5), we can obtain the matrix elements of the model Hamiltonian in the presence of strain effects. The band structure of γ-graphyne has been numerically found in the presence of strain and magnetic field effects. Using the band structure of the electron, we can obtain the electronic Green's function in eqn (8). Afterwards transport coefficients are found by substitution of Green's function into eqn (15), respectively. The static electrical conductivity, thermal conductivity and thermopower are readily calculated based on eqn (14), (16) and (17). Also Green's function of electrons has been exploited to find the Pauli paramagnetic susceptibility and specific heat, obtained using eqn (19) and (20). Both inter and intra band transitions contribute to the results of electronic properties of the γ-graphyne monolayer. It should be noted that the transport properties of the γ-graphyne layer have been studied in a zigzag direction according to Fig. 1: the optimized atomic structure of the γ-graphyne layer with primitive unit cell vector length a = 1 is shown in Fig. 1. The unit cell of γ-graphyne includes six sublattices.
with i = 1, 2, into eqn (5), we can obtain the matrix elements of the model Hamiltonian in the presence of strain effects. The band structure of γ-graphyne has been numerically found in the presence of strain and magnetic field effects. Using the band structure of the electron, we can obtain the electronic Green's function in eqn (8). Afterwards transport coefficients are found by substitution of Green's function into eqn (15), respectively. The static electrical conductivity, thermal conductivity and thermopower are readily calculated based on eqn (14), (16) and (17). Also Green's function of electrons has been exploited to find the Pauli paramagnetic susceptibility and specific heat, obtained using eqn (19) and (20). Both inter and intra band transitions contribute to the results of electronic properties of the γ-graphyne monolayer. It should be noted that the transport properties of the γ-graphyne layer have been studied in a zigzag direction according to Fig. 1: the optimized atomic structure of the γ-graphyne layer with primitive unit cell vector length a = 1 is shown in Fig. 1. The unit cell of γ-graphyne includes six sublattices.
We have plotted the electronic band structure of the γ-graphyne structure in the absence of magnetic field and strain effects in Fig. 2, using the tight binding model Hamiltonian. Our results are consistent with the results obtained in the DFT model.37–39 Fig. 2 shows the γ-graphyne structure behaving as a semiconductor.
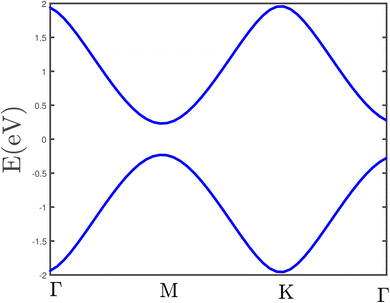 | ||
| Fig. 2 The band structure of the γ-graphyne layer in the absence of an external magnetic field and strain effects. | ||
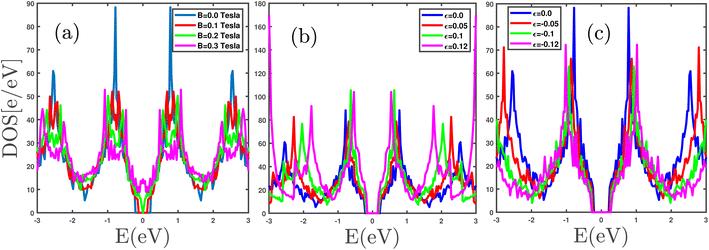
The total density of states (DOS(E)) of a single layer of undoped γ-graphyne are presented in panels in Fig. 3. The effects of magnetic field and strain parameter on the density of states curves shows the symmetry around E = 0.0 eV according to the panels in Fig. 3. This arises from the fact that the model Hamiltonian preserves its particle–hole symmetry in the presence of strain parameter and magnetic field. In panel (a) of Fig. 3, we have plotted the energy dependence of the density of states for various magnetic fields in the absence of any strain parameter, i.e. ε = 0.0. It is clearly observed that the band gap width reduces with magnetic field value so that this band gap vanishes at magnetic field value B = 0.3 tesla. Under such fact, the sample presents the metallic behavior at B = 0.3 tesla. On the contrary, the area under each curve of density of states is proportional to the charge carrier concentration. According to the curves of density of states in panel (a) of Fig. 2 it can be understood that the area under each DOS curve does not change in the absence and presence of a magnetic field. This issue arises from the fact that applying the magnetic field does not add/remove any particle, neither electron nor hole, to/from the system. Consequently, the area under the density of states curves for different magnetic fields is the same, as shown in panel (a) of Fig. 3. The behavior of density of states for different tensile biaxial strain parameters ε in the absence of a magnetic field are depicted in panel (b) of Fig. 3. The band gap width in the density of states curves slightly decreases with increase of tensile strain parameter. Thus the semiconducting behavior of the sample decreases with tensile strain parameter ε. In panel (c), the increase of in-plane biaxial compressive strain values ε leads to an enhanced band gap in the density of states of the γ-graphyne layer. As shown in panel (c) of Fig. 3, there is a band gap in the density of states in the absence of compressive strain parameter and magnetic field. Upon increasing ε further, the band gap width in the density of states increases, improving the insulating behavior of the γ-graphyne layer. Since the variation of strain parameters has no effect on charge carrier concentrations, the area under the density of states curves remains unchanged due to the strain parameter variation as shown in panels (b) and (c).
Fig. 4 presents the temperature behavior of electronic specific heat of undoped γ-graphyne for various normalized magnetic fields B, in the absence of a biaxial strain parameter. For temperatures below 125 K, thermal energy is insufficient for exciting the electrons from the valence to conduction band. Consequently, the specific heat gets a zero value at temperatures T < 125 K for all values of magnetic field. Upon further increase of temperature above 125 K, the thermal transition rate of electrons rises so that the electron population in the conduction band is increased. Thus, the specific heat exhibits an increasing behavior in the temperature region T > 125 K for all magnetic fields. Another novel feature shown in Fig. 4 is that the specific heat increases with magnetic field at fixed temperature above 125 K. The increasing behavior of specific heat with magnetic field at fixed temperature in the region T > 125 K can be justified based on decreasing band gap width in electronic density of states with B as shown in panel (a) of Fig. 3.
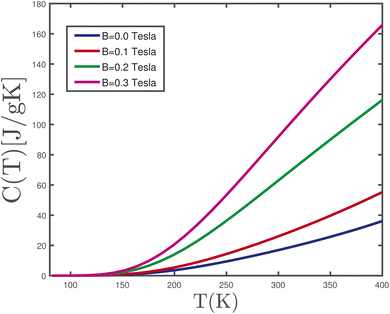 | ||
| Fig. 4 Specific heat of undoped γ-graphyne as a function of temperature, T, for different values of magnetic field, namely B = 0.0, 0.1, 0.2, 0.3 tesla, in the absence of a strain parameter. | ||
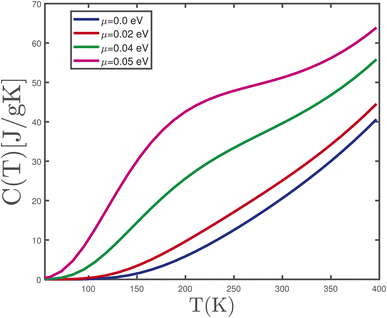
The effects of electronic concentration on temperature dependence of specific heat have also been studied. The electronic concentration for each value of chemical potential in γ-graphyne is obtained based on eqn (10). With increasing positive chemical potential, the concentration of electrons increases. In Fig. 5, we show the electronic specific heat of doped γ-graphyne as a function of temperature for different values of chemical potential, namely μ = 0.0 eV, 0.02 eV, 0.04 eV, 0.05 eV for zero biaxial strain parameter ε = 0.0 in the absence of a magnetic field. All curves of specific heat for each value of chemical potential show an increasing behavior in terms of temperature according to Fig. 5. There is a finite temperature region where specific heat vanishes for chemical potentials, μ = 0.0 eV, 0.02 eV, 0.04 eV. This temperature region comes from the finite band gap in density of states of the γ-graphyne layer at B = 0.0 tesla (see panel (a) of Fig. 3) so that electronic transition rate from valence to conduction band vanishes for chemical potential values μ = 0.0 eV, 0.02 eV, 0.04 eV. The width of this temperature region decreases with chemical potential so that specific heat reaches the finite non-zero value for all temperatures T > 0 K at chemical potential μ = 0.05 eV. On the other hand, the increase of chemical potential leads to an increased electronic concentration which enhances the transition rate of electrons between energy levels. Thus, specific heat increases with chemical potential at a fixed temperature value.
We studied the temperature dependence of the electronic specific heat of γ-graphyne due to variation of the biaxial tensile strain parameters. In Fig. 6, we depict the temperature dependence of specific heat of the undoped γ-graphyne plane for different values of tensile strain parameter, namely ε = 0.00, 0.05, 0.10, 0.12, in the absence of magnetic field. For each value of ε, this figure shows that specific heat increases with temperature in the temperature region T > 130 K. The specific heat goes to zero at temperatures below 130 K for all values of strain parameter. The electronic transition rate from valence to conduction band has no considerable values compared to the band gap for T < 130 K so that specific heat gets the zero value in this temperature region. In addition, at a fixed temperature above 130 K, a higher strain parameter causes a smaller band gap width between energy bands (see panel (b) of Fig. 3) and consequently higher values in specific heat.
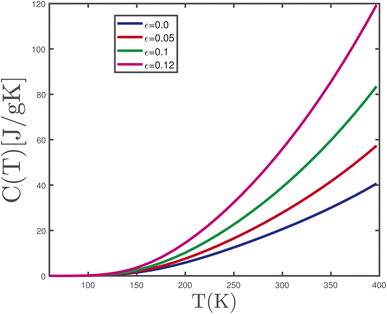 | ||
| Fig. 6 Specific heat of undoped γ-graphyne as a function of temperature, T, for different values of tensile strain, namely ε = 0.0, 0.05, 0.1, 0.12, in the absence of magnetic field. | ||
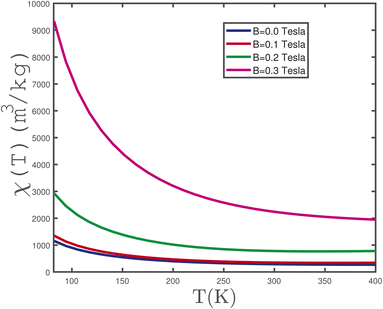
We also studied the temperature dependence of paramagnetic spin susceptibility of γ-graphyne due to variation of biaxial strain, magnetic field and chemical potential. The effect of magnetic field on temperature dependence of paramagnetic spin susceptibility, χ, of undoped γ-graphyne at zero biaxial strain is shown in Fig. 7. A monotonic decreasing behavior for temperature dependence of paramagnetic spin susceptibility has been clearly observed for all values of magnetic field. On the other hand, the low temperature behavior of paramagnetic spin susceptibility arises from the quantum property of electrons, so that spin susceptibility obeys the Pauli paramagnetic susceptibility rule.40 Based on this rule the susceptibility corresponds to the electronic density of states value at zero energy. As is shown in panel (a) of Fig. 3, the density of states at zero energy enhances with magnetic field strength. Thus, the zero temperature limit of spin susceptibility enhances with magnetic field as shown in Fig. 7. Upon increasing temperature, paramagnetic susceptibility reduces with temperature for all values of magnetic field. This behavior of susceptibility at high temperatures is in agreement with the Curie law of paramagnetism. This law states paramagnetic spin susceptibility decays as a function of the inverse of temperature at high values of temperature. Moreover this law is valid only at high temperatures where electrons behave as classical objects. Another feature in Fig. 7 is that the curves specifically for B = 0.0 tesla and B = 0.1 tesla, overlay each other along the whole range of temperature.
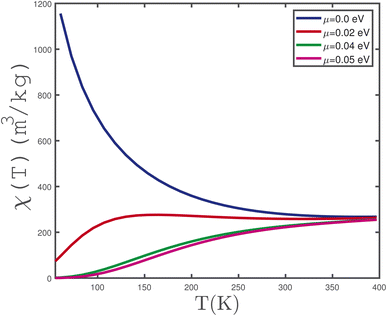
We have also studied the temperature dependence of the paramagnetic spin susceptibility of γ-graphyne for various electronic concentrations. In Fig. 8, paramagnetic spin susceptibility of doped γ-graphyne in the absence of magnetic field and a strain parameter has been plotted as a function of temperature. This figure shows that spin susceptibility is independent of chemical potential for normalized temperatures above 330 K and all curves fall on each other in this temperature region. It is clearly observed that the zero temperature limit of paramagnetic spin susceptibility tends to lower values with chemical potential. It can be understood from this fact that the density of states at chemical potential decreases with μ. Also, it can be understood that the metallic property of γ-graphyne rises with the increase of μ. A considerable value for spin susceptibility of undoped γ-graphyne with μ = 0.0 eV at zero temperature limit, is found. There is an increasing behavior for temperature dependence of spin susceptibility at finite chemical potential values μ = 0.02 eV, 0.04 eV, 0.05 eV. However, Pauli paramagnetic spin susceptibility shows a monotonic decreasing behavior for the undoped case μ = 0.0 eV. In addition, at fixed temperature, spin susceptibility decreases with chemical potential. Based on Fig. 8, the results of spin susceptibility is independent of chemical potential values μ = 0.04 eV, 0.05 eV.
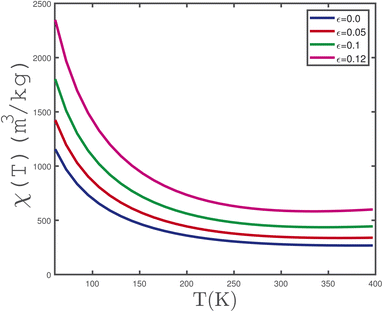
The results of spin susceptibility of undoped γ-graphyne as a function of temperature in the absence of magnetic field for various biaxial tensile strain parameters ε = 0.0, 0.05, 0.1, 0.12 are shown in Fig. 9. The increase of temperature reduces χ, moreover at a fixed temperature the increase of biaxial strain parameter leads to an increase of paramagnetic spin susceptibility. In fact the increase of ε leads to a reduced band gap in density of states and thus electronic transition increases so that χ rises with ε at fixed temperature.
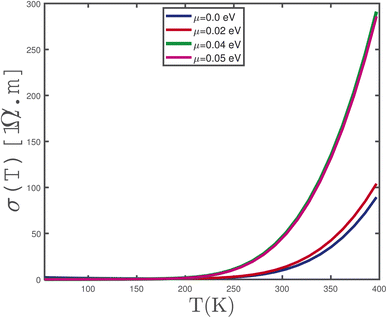
In Fig. 10, results for the electrical conductivity (σ) of an undoped γ-graphyne layer are presented versus temperature T for several values of the longitudinal magnetic field, namely B = 0.0 tesla, 0.1 tesla, 0.2 tesla, 0.3 tesla, under the half filling constraint in the absence of any type of strain. Several features are remarkable. The curve for B = 0.2 tesla shows increasing behavior in terms of temperature which manifests the presence of a finite-energy gap in the energy spectrum. Also Fig. 10 implies electrical conductivity for B = 0.2 tesla is zero for temperatures below 150 K. For temperatures above 150 K, the enhancement of temperature leads to an increase in the transition rate of electrons to the excited state. Therefore we see an increase of electrical conductivity at magnetic field B = 0.2 tesla. This feature of electrical conductivity at B = 0.2 tesla can be justified based on the semiconducting property of the structure under the magnetic field. The behavior of electrical conductivity at B = 0.0 tesla, 0.1 tesla, 0.2 tesla can be justified based on the band gap in the density of states of γ-graphyne as shown in panel (a) of Fig. 3. However the electrical conductivity of γ-graphyne at B = 0.3 tesla, monotonically decreases with temperature. This behavior of electrical conductivity at B = 0.3 tesla comes from the metallic property of the structure in which there is no gap in density of states as expected in panel (a) of Fig. 3. In fact the electrons of the metallic phase suffer from scattering effects on each other which reduces the electrical conductivity.
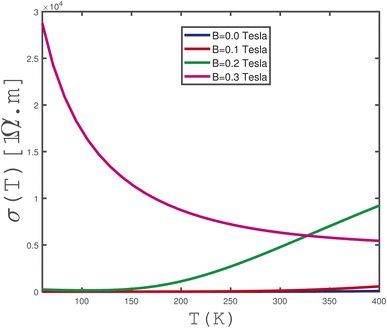 | ||
| Fig. 10 Electrical conductivity of undoped γ-graphyne as a function of temperature, T, for different values of magnetic field, namely B = 0.0, 0.1, 0.2, 0.3 tesla, in the absence of strain. | ||
Fig. 11 presents the temperature behavior of electrical conductivity as a function of temperature for various amounts of chemical potential in the absence of strain parameter and magnetic field. The existence of a band gap in the density of states (see panel (a) of Fig. 3) leads to a zero value for electrical conductivity in the temperature region below 230 K. For temperatures above 230 K, the thermal excitation of electrons from the valence band to the conduction band causes increasing electrical conductivity. Fig. 11 implies that electrical conductivity results for chemical potentials μ = 0.04 eV, 0.02 eV are considerably different. On the other hand the curves for μ = 0.04 eV, 0.05 eV overlay each other along the whole range of temperature. This electronic property is clearly observed for electrical conductivity curves for μ = 0.0 eV, 0.02 eV.
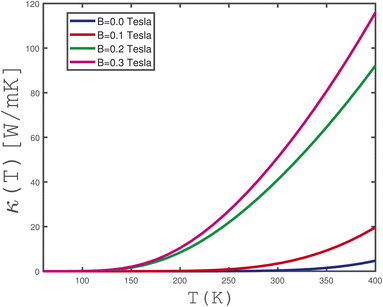
The effects of magnetic field on the temperature dependence of thermal conductivity for an undoped γ-graphyne layer in the absence of strain parameter are plotted in Fig. 12. Thermal conductivity for each magnetic field shows an increasing dependence on temperature, however there is a finite temperature region where thermal conductivity reaches zero. The width of this temperature region reduces with magnetic field as shown in Fig. 12. In addition, at fixed temperature above 150 K, thermal conductivity enhances with an increase of magnetic field which can be understood based on the reduction of the band gap with B.
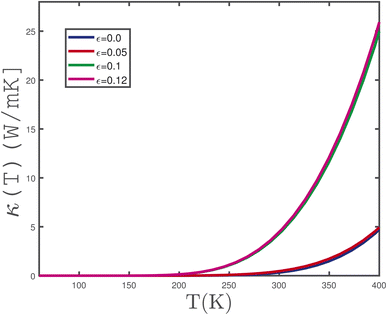
Also, we studied the thermal conductivity of the γ-graphyne plane in terms of temperature due to the variation of biaxial strain parameter ε. In Fig. 13, we plot the curves of thermal conductivity as a function of temperature for different values of strain in the absence of magnetic field and electron doping in the half filling case. This figure implies that thermal conductivity obtains a non-zero value at temperatures above 210 K for ε = 0.1, 0.12 while κ has finite values in the temperature region T > 290 K for ε = 0.0, 0.05. In other words, thermal conductivity curves overlay each other for strain values ε = 0.1, 0.12, and for ε = 0.0, 0.05.
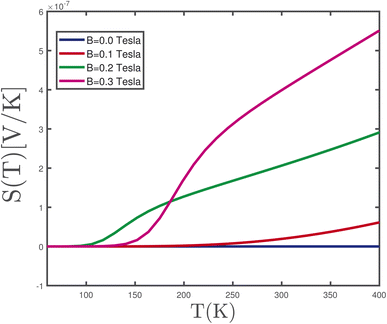
Considering magnetothermal effects, we look at the Seebeck coefficient, S, under zero electrical current Je = 0 for ballistic transport. In Fig. 14, we plot the Seebeck coefficient, S, of an undoped γ-graphyne monolayer as a function of temperature T for several values of magnetic field B in the absence of biaxial strain. We note that the Seebeck coefficient of the γ-graphyne layer increases with B at temperature higher than 200 K. The sign of S along the whole range of temperature for magnetic field values B = 0.1 tesla, 0.2 tesla, 0.3 tesla is positive. In ref. 41, it was suggested that the sign of S is a criterion to clarify the type of carriers; a positive (negative) S implies that the charge and heat are dominantly carried by electrons (holes). In the absence of magnetic field, the Seebeck coefficient reaches zero on the whole range of temperature as shown in Fig. 14. Also, the Seebeck coefficient for magnetic fields B = 0.2 tesla and 0.3 tesla shows increasing behavior at temperature T > 100 K.
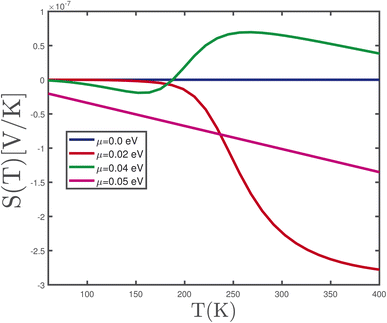
We have also considered the electron doping effects on the behavior of the Seebeck coefficient of γ-graphyne monolayers. In Fig. 15, we plot the temperature dependence of Seebeck coefficient, S, in the absence of magnetic field for different values of chemical potential, namely μ = 0.0 eV, 0.02 eV, 0.04 eV, 0.05 eV. As we have mentioned, the sign of S determines the type of majority carrier for transport properties. Based on Fig. 15, thermopower has a negative sign across the whole range of temperature for chemical potentials μ = 0.02 eV, 0.05 eV and consequently the majority of carriers are electrons. However, the sign of S for μ = 0.04 eV is negative for T < 200 K so the majority of carriers are electrons; but positive in the temperature region T > 200 K, as shown in Fig. 15.
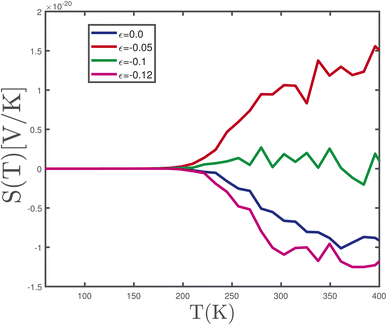
We plotted the temperature dependence of the Seebeck coefficient of undoped γ-graphyne in the absence of magnetic field for different values of compressive biaxial strain parameter ε in Fig. 16. Based on this figure, thermopower obtains a negative sign at T > 200 K in the absence of magnetic field at ε = 0.0, −0.12 and consequently the majority of carriers are electrons. Moreover it is clearly observed that the Seebeck coefficient has positive sign in the temperature region T > 100 K for ε = −0.05 and thus the majority of carriers are holes. There is no value for Seebeck coefficient at T < 200 K for all biaxial tensile strain parameters. In addition, there are no considerable amounts for S at biaxial strain parameter ε = −0.1 according to Fig. 16.
Finally, we studied the temperature dependence of the Seebeck coefficient of the undoped γ-graphyne monolayer at zero magnetic field for various tensile strain parameters, Fig. 17. At temperatures above 150 K, it is clearly observed that the Seebeck coefficient of γ-graphyne is positive for strain parameters ε = 0.1, 0.12. Consequently the holes contribute the majority transport properties of the structure. On the other hand, Fig. 17 implies that the S has negative sign at T > 150 K for biaxial strain parameters ε = 0.0, 0.05, so that electrons become the majority carriers in the structure.
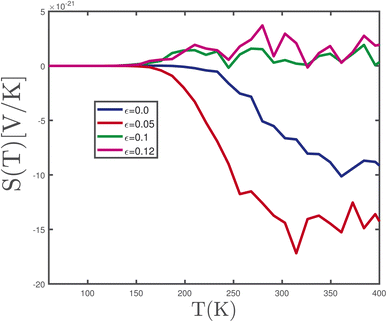 | ||
| Fig. 17 Seebeck coefficient of undoped γ-graphyne as a function of temperature, T, for different values of tensile strain parameter, namely ε = 0.0, 0.05, 0.1, 0.12, in the absence of magnetic field. | ||
It is worth adding a few comments about the dynamic stability and synthesis of these 2D compounds from phonon spectra calculations. The breakthrough in the research of graphdiyne accelerates the study of other kinds of graphdiyne. Among the members of the graphynes family, γ-graphyne has the advantages of high stability and semiconductor characteristics.42,43 Its structure can be viewed as modified graphene (sp2-hybridized carbon) inserted by ethynyl linkages (sp-hybridized carbon).44 The theoretical research on γ-graphyne has been booming recently.38,39,45 For example, Srinivasu et al. calculated the electronic structure of γ-graphyne by density functional theory (DFT), and calculated the band gap energy of γ-graphyne to be 2.23 eV.46 Although the theoretical and computational research of γ-graphyne is inspiring, studies on the synthesis and characterization of γ-graphyne have also been reported.47–49
We have not considered the electron–phonon scattering for the calculation of electrical and thermal conductivities. As we know, at temperatures lower than room temperature, the contribution of phonon vibrations is negligible. Therefore, electron–phonon scattering does not have a significant contribution to thermal properties. In the calculations we performed, the electrical and thermal conductivity properties were in the low temperature range where the contribution of phonon vibrations is negligible. For this reason, in this work, we have not calculated the thermal and electrical phonon conductivity calculations. During the studies we conducted, the phonon thermal properties of γ-graphyne at temperatures higher than room temperature were performed using first-principles calculations combined with the Boltzmann transport equations.43 Their results showed that the γ-graphyne structure has significant thermoelectric properties compared to other graphyne allotropes. Therefore, we intend to calculate the thermoelectric properties of γ-graphyne at temperatures higher than room temperature using the Holstein model and compare our results with the works that have already been done.
Also, γ-graphyne has attracted the attention of researchers in recent years due to its interesting physical properties. γ-Graphyne has been synthesized using different methods.47–49 As far as we know, thermoelectric and thermodynamic properties of the γ-graphyne structure have not been studied experimentally yet. But a series of theoretical studies on its thermoelectric properties have been carried out using DFT and first principles calculations.37,43–52
Finally, we calculated the electronic band structure of γ-graphyne using the tight binding model and added it to the manuscript, and the obtained results are completely consistent with the DFT calculations.37–39 As far as we know, the thermoelectric and thermodynamic properties of γ-graphyne have not been reported using the tight binding model and Green's function approach. Also, our goal in this article was to use the tight binding method because this method has advantages such as simplicity and low cost. But, we confirm your comment and agree with your opinion that the DFT method is more reliable, for this reason we will try to use that method in our future research.
6 Conclusions
In this work, we have proposed the tight binding model for γ-graphyne structures, which includes the effects of the biaxial strain, doping, and external magnetic field on electronic and transport properties. Also, the effects of biaxial strain and external magnetic field on heat capacity and magnetic susceptibility have been investigated. In addition, by applying the linear response theory and Green's function approach, we obtained the behavior of thermal conductivity, electrical conductivity, and the Seebeck coefficient with temperature. Our results show that the application of an external magnetic field and biaxial tensile strain reduces the band gap, while biaxial compressive strain increases the band gap. Moreover, thermal conductivity, heat capacity, and magnetic susceptibility increase with the application of an external magnetic field and tensile biaxial strain. The Seebeck coefficient of the γ-graphene structure is positive in the entire temperature range, which indicates that γ-graphene structure is a p-type semiconductor. By applying strain and electron doping, the sign of the Seebeck coefficient changes from positive to negative. The results offered here exhibit that the γ-graphyne structure is appropriate for use in spintronic, thermoelectric and valleytronics devices.Conflicts of interest
There are no conflicts to declare.References
- H. W. Kroto, J. R. Heath, S. C. O. Brien, R. F. Curl and R. E. Smalley, C60: buckminsterfullerene, Nature, 1985, 318, 162 CrossRef CAS.
- S. Iijima, Helical microtubules of graphitic carbon, Nature, 1991, 354, 56 CrossRef CAS.
- K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666 CrossRef CAS PubMed.
- A. H. C. Neto, F. Guinea, N. M. R. Peres, K. S. Novoselov and A. K. Geim, Rev. Mod. Phys., 2009, 81, 109 CrossRef.
- C. Soldano, A. Mahmood and E. Dujardin, Carbon, 2010, 48, 2127 CrossRef CAS.
- F. Bonaccorso, Z. Sun, T. Hasan and A. C. Ferrari, Nat. Photonics, 2010, 4, 611 CrossRef CAS.
- F. Schwierz, Nat. Nanotechnol., 2010, 5, 487 CrossRef CAS PubMed.
- D. W. Boukhvalov and M. I. Katsnelson, Nano Lett., 2008, 8, 4373 CrossRef CAS PubMed.
- K. Wakabayashi, K. Sasaki, T. Nakanishi and T. Enoki, Sci. Technol. Adv. Mater., 2010, 11, 54504 CrossRef PubMed.
- X Han, H. Zho, X. Nie, G. Wang and X. Zeng, Creation of graphene allotropes using patterned defects, Carbon, 2009, 47, 2226 CrossRef.
- A. N. Enyashin and A. L. Ivanovskii, Graphene allotropes, Phys. Status Solidi B, 2011, 248, 1879–1883 CrossRef CAS.
- R. H. Baughman, H. Eckhardt and M. Kertesz, Structure-property predictions for new planar forms of carbon: layered phases containing sp2 and sp atoms, J. Chem. Phys., 1987, 87, 6687–6699 CrossRef CAS.
- M. M. Haley, S. C. Brand and J. J. Pak, Carbon Networks Based on Dehydrobenzoannulenes: Synthesis of Graphdiyne Substructures, Angew. Chem., Int. Ed. Engl., 1997, 36, 836–838 CrossRef CAS.
- B. Yang, H. C. Zhou, X. M. Zhang, X. B. Liu and M. W. Zhao, Carbon, 2017, 113, 40 CrossRef CAS.
- M. Hu, M. Ma and Z. Zhao, AIP Adv., 2016, 6, 055020 CrossRef.
- C. He, L. Sun, C. Zhang and J. Zhong, Phys. Chem. Chem. Phys., 2013, 15, 680 RSC.
- H. Zhang, X. he, M. Zhao, M. Zhang, L. Zhao, X. Feng and Y. Lou, J. Phys. Chem. C, 2012, 116, 16634 CrossRef CAS.
- Z. Liu, G. Yu, H. yao, L. Liu, L. Jiang and Y. Zheng, New J. Phys., 2012, 14, 113007 CrossRef.
- A. R. Puigdollers, G. Alonso and P. Gamallo, First-principles study of structural, elastic and electronic properties of α− ,β− and γ-graphyne, Carbon, 2016, 96, 879 CrossRef CAS.
- Y. Xue, Y. Li, J. Zhang, Z. Liu and Y. Zhao, 2D graphdiyne materials: challenges and opportunities in energy field, Sci. China: Chem., 2018, 61, 765 CrossRef CAS.
- W.-X. Zhou and K.-Q. Chen, Enhancement of thermoelectric performance in β-graphyne nanoribbons by suppressing phononic thermal conductance, Carbon, 2015, 85, 24 CrossRef CAS.
- N. K. Perkgoz and C. Sevik, Vibrational and thermodynamic properties of α− , β− , γ− , and 6, 6, 12− graphyne structures, Nanotechnology, 2014, 25, 185701 CrossRef PubMed.
- X. Hou, Z. Xie, C. Li, G. Li and Z. Chen, Materials, 2018, 11, 392 CrossRef PubMed.
- Y.-Q. Liu, L. Xu and J. Zhang, Energy gaps and half-metallicity in β-graphyne nanoribbons, Phys. Lett. A, 2019, 383, 1498 CrossRef CAS.
- R. Fei and L. Yang, Nano Lett., 2014, 14, 2884 CrossRef CAS PubMed.
- X. Peng, A. Copple and Q. Wei, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 085402 CrossRef CAS.
- A. S. Rodin, A. Carvalho and A. H. C. Neto, Phys. Rev. Lett., 2014, 112, 176801 CrossRef CAS PubMed.
- Q. Wei and X. Peng, Appl. Phys. Lett., 2014, 104, 251915 CrossRef.
- M. Tahir, P. Vasilopoulos and F. M. Peeters, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 045420 CrossRef.
- V. Tran, R. Soklaski, Y. Liang and L. Yang, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 235319 CrossRef.
- H. Y. Lv, W. J. Lu, D. F. Shao and Y. P. Sun, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 085433 CrossRef CAS.
- C. Wang, Q. Xia, Y. Nie and G. Guo, Strain-induced gap transition and anisotropic Dirac like cones in monolayer and bilayer phosphorene, J. Appl. Phys., 2015, 117, 124302 CrossRef.
- B. Sa, Y.-L. Li, J. Qi, R. Ahuja and Z. Sun, Strain engineering for phosphorene: the potential application as a photocatalyst, J. Phys. Chem. C, 2014, 118, 26560 CrossRef CAS.
- G. Gui, J. Li and J. X. Zhong, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 075435 CrossRef.
- G. Grosso and G. P. Parravicini, Solid State Physics, Academic Press, Singapore, 2000 Search PubMed.
- W. Nolthing and A. Ramakanth, Quantum Theory of Magnetism, Springer, New York, 2009 Search PubMed.
- Z. Liu, G. Yu, H. Yao, L. Liu, L. Jiang and Y. Zheng, A simple tight-binding model for typical graphyne structures, New J. Phys., 2012, 14, 113007 CrossRef.
- P.-P. Liu, H. Zhang, X.-L. Cheng and Y.-J. Tang, External electric field: an effective way to prevent aggregation of Mg atoms on γ-graphyne for high hydrogen storage capacity, Appl. Surf. Sci., 2016, 371, 44 CrossRef CAS.
- H. Sevincli and C. Sevik, Electronic, phononic, and thermoelectric properties of graphyne sheets, Appl. Phys. Lett., 2014, 105, 223108 CrossRef.
- R. K. Pathria, Statistical Mechanics, Oxford Press, New York, 2008 Search PubMed.
- S. Furukawa, D. Ikeda and K. Sakai, J. Phys. Soc. Jpn., 2005, 74, 3241 CrossRef CAS.
- A. R. Puigdollers, G. Alonso and P. Gamallo, Carbon, 2016, 96, 879 CrossRef CAS.
- P. H. Jiang, H. J. Liu, L. Cheng, D. D. Fan, J. Zhang, J. Wei, J. H. Liang and J. Shi, Thermoelectric properties of γ-graphyne from first-principles calculations, Carbon, 2017, 113, 108 CrossRef CAS.
- S. Ajori, R. Ansari and M. Mirnezhad, Mater. Sci. Eng., A, 2013, 561, 34 CrossRef CAS.
- Z.-G. Shao and Z.-L. Sun, Phys. E., 2015, 74, 438 CrossRef CAS.
- K. Srinivasu and S. K. Ghosh, J. Phys. Chem. C, 2012, 116, 5951 CrossRef CAS.
- Q. Li, Y. Li, Y. Chen, L. Wu, C. Yang and X. Cui, Carbon, 2018, 136, 248 CrossRef CAS.
- C. Yang, Y. Li, Y. Chen, Q. Li, L. Wu and X. Cui, Small, 2019, 15, 1804710 CrossRef PubMed.
- Y. Hu, C. Wu, Q. Pan, Y. Jin, R. Lyu, V. Martinez, S. Huang, J. Wu, L. J. Wayment and N. A. Clark, Nat. Synth., 2022, 5, 1 Search PubMed.
- C. Wang, T. Ouyang, Y. Chen and J. Zhong, Eur. Phys. J. B, 2015, 88, 1 CAS.
- X. Hou, Z. Xie, C. Li, G. Li and Z. Chen, Materials, 2018, 11, 1 CAS.
- Z. Yang, Y.-L. Ji, G. Lan, L.-C. Xu, H. Wang, X. Liu and B. Xu, J. Phys. D: Appl. Phys., 2016, 49, 145102 CrossRef.
| This journal is © The Royal Society of Chemistry 2023 |