Time–temperature superposition for kinetic mapping of solventless autocatalytic addition of diisocyanates and macrodiols

Abstract

The migration of chemicals from polyurethane (PUR) is a concern in many applications, such as adhesives for food packaging. Low molecular weight catalysts, which are prone to migration, need to be eliminated from PUR, in particular those containing Sn or other metals. This is difficult partly due to many uncertainties of autocatalytic polyaddition between isocyanates and polyols. Hexamethylene and tolylene diisocyanates, HDI and TDI, are often reacted with macrodiols to produce prepolymers for PUR. This study measures isocyanate contents during the polyaddition of HDI and TDI with excess macrodiols. Ester-based macrodiols were reacted between 60 °C and 90 °C using 1 : 0.3 and 1 : 0.5 molar ratios to form OH-terminated prepolymers. Time–temperature superposition (TTS) was used to process the values of unreacted isocyanate fractions from several temperatures. Presumed activation energies and kinetic data scatter implied that polymerization has a distinct initial phase of conversion of unreacted diisocyanate into monofunctional adducts by addition to macrodiols, followed by more complex processes. Utilization of the activation energy from the initial phase and TTS application might allow the prediction of kinetic trends without the need for a large volume of accurate data. Such kinetic mapping should be useful for developing catalyst-free PUR with low levels of migrating chemicals.

---

1. Introduction

The migration of chemicals from packaging or plastics is among the top concerns when introducing new materials to consumers. While polymer chains are not sufficiently mobile to leach out from the plastic substrate, components of smaller molecular size, such as plasticizers, inhibitors, or catalysts, are quite prone to migration. Polyurethane (PUR) is a broadly used polymer, widespread in plastics, coatings, rigid foam, cushioning, and elsewhere. It is also used in sensitive areas such as lamination adhesive in multilayer films, which are a packaging material of choice in a rapidly growing number of applications with very few recycling options.¹ The final PUR products are often manufactured by reacting prepolymers with hydroxyl and isocyanate functionalities. These prepolymers are frequently produced from long-chain difunctional alcohols, also known as macrodiols, which are reacted with diisocyanates. The prepolymers can be OH- or NCO- terminated depending on the molar ratio between the two. In the case of OH-terminated prepolymers, macrodiol is used in excess, see Scheme 1.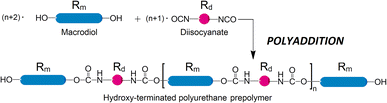

Scheme 1 A typical polyaddition reaction to produce a linear OH-terminated prepolymer from diisocyanate (short molecules) and excess macrodiol (long molecules). Linker sizes are not to scale.

Structurally, macrodiols are much more diverse than diisocyanates and can be categorized as ether-based or ester-based. Ester-based macrodiols may have a variety of molecular architectures, such as dibasic acid esters with various glycols as linkers, or PCL chains, esterified from a glycol anchor, or castor oil derivatives, or similar. The molecular weight of individual macrodiols is often above 1000 g mol⁻¹ because otherwise they can lead to migration problems themselves. During prepolymer formation, these macrodiols are reacted with diisocyanates leading to a product with better adhesion and faster curing in the final application. Unfortunately, many formulators utilize catalysts to accelerate curing, tin-based organometallics in particular. The catalysts have a relatively small molecular size, so they migrate through the plastics much easier than PUR polymers and might produce leaching or contamination problems.

A poor understanding of the kinetics of the prepolymer formation represents one of the main reasons, why catalysts are used. Many researchers report that isocyanate addition to alcohols might involve complex mechanisms, which would be difficult to interpret in kinetic models even for linear PUR.^2–4 Various uncertainties make it problematic to derive reaction rate constants for every step of the mechanism even for monofunctional alcohols. Higher homologs, such as diisocyanates and macrodiols would result in further complexity, because of several NCO groups, which would react with several OH functionalities. Nevertheless, researchers still pursue exact kinetic studies of polyaddition between diisocyanates and macrodiols due to their technological significance.

Among industrially widespread diisocyanates, 1,6-hexamethylene diisocyanate (HDI) is the simplest one. Other industrial diisocyanates, such as tolylene diisocyanate (TDI) are more problematic for exact kinetic studies because they contain isomers or functional groups of different reactivity. As a result, building accurate kinetic models with industrial macrodiols and diisocyanates might be challenging even for catalyst-free solventless reactions, thus simplified systems are sometimes chosen. Kinetics and activation energies (E_a) of solventless autocatalytic polyaddition of HDI to 1-hexanol and 1-hexadecanol were investigated at 80 °C to 120 °C,³ obtaining E_a of 59.1 and 43.6 kJ mol⁻¹ respectively. The addition of isophorone diisocyanate to polybutylene glycols of 1000 and 2000 g mol⁻¹ was also studied.⁵ The reactions were carried out at 110 °C and 80 °C respectively in equimolar ratios. The second-order kinetics was assumed and seven reaction rate constants were needed to arrive at a good correlation of experimental data. Polyaddition of TDI to hydroxy-terminated poly-butadiene with or without butane catalysts was reported⁶ to proceed through several mechanisms of the second-order kinetics with activation energies ranging from 12.3 to 90.8 kJ mol⁻¹. The authors admitted the complexity of comparing their “apparent E_a” to activation energies established by other authors for similar reactions. Consequently, for a given set of reactants, some generalizations are needed to compile an overall kinetic outline of their prepolymer formation process. If established, the general kinetic trends might enable the users to forecast temperatures and durations, needed for specific components to achieve a required degree of polymerization and the needed distribution of polyaddition products.

In this study, a PCL adduct and two adipate copolymers were selected as the macrodiols for studying their addition kinetics with diisocyanates. Diisocyanates HDI and TDI, employed for this study, are broadly used in the industry for producing prepolymers from macrodiols. Excess macrodiols were selected for the reaction by utilizing 1 : 0.3 mol or 1 : 0.5 mol ratios between OH- and NCO- functional groups. Such concentration interval is often employed in the industry when OH-terminated prepolymers are manufactured.

2. Experimental

Original descriptions of materials and methods have already been provided in the literature.⁷ In this section, they are summarized only briefly. Most investigated new methods are described below in detail.

2.1 Materials

Two widely used diisocyanates were employed for polyaddition. Hexamethylene 1,6-diisocyanate (HDI) was provided by Covestro Deutschland AG and titrated periodically to assure 51.5 ± 0.5 %NCO. Tolylene diisocyanate (TDI) was also provided by Covestro and represented a mixture of 2,4-TDI and 2,6-TDI isomers at a 4 : 1 mol ratio. Again, its purity was periodically validated by titration to assure 48.7 ± 0.2 %NCO.

Three highly linear macrodiols were acquired as representatives of ester-based OH-components, which are widely used for adhesives in food packaging, Scheme 2.

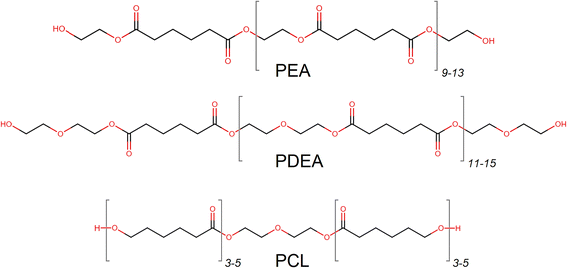Scheme 2 Molecular structures of investigated ester-based macrodiols with an approximate number of monomers.

A polycaprolactone adduct (PCL) of 2000 g mol⁻¹, was acquired from Sigma-Aldrich. Polyethylene adipate (PEA) of 2050 g mol⁻¹ was provided by Covestro. Poly-diethylene glycol adipate (PDEA) of 2700 g mol⁻¹ was also supplied by Covestro as a hybrid-type macrodiol with both ether and ester functionalities. Both PEA and PDEA contained adipate moieties, esterified with ethylene glycol (EG) or diethylene glycol (DEG) respectively. The structural details of the macrodiols and their main properties are provided in Table 1.

Table 1 List of macrodiols, tested in this study along with their compositional moieties and key properties

Code	CAS number	Monomer I	Monomer II	Center unit	Mol. wt, g mol^−1	OH value, mg KOH g^−1	Acidity, mg KOH g^−1
PEA	24 937-05-1	Adipate	EG	n.a	2050	55	0.75 ± 0.05
PDEA	25 036-49-1	Adipate	DEG	n.a	2700	36	1.1 ± 0.1
PCL	36 890-68-3	Caprolactone	n.a	DEG	2000	56	0.9 ± 0.05

---

Molecular weights and OH values are listed in Table 1 as specified by the suppliers. Caution was exercised during the sample preparation, reaction procedures, and titration to avoid any entrainment of humidity or moisture. Such risks were minimized by opening containers only for as short as possible and purging them with dry N₂ every time before capping.

2.2 Procedures of polyaddition and analysis

A measured amount of macrodiol was poured into a 3-neck flask, which was set up in a thermostat and a reflux condenser was attached. The flask was purged with dry nitrogen and heated to the required temperature ±1 °C while agitated with a mechanical stirrer. A respective amount of HDI or TDI per Table 2 was preheated and poured into the flask. The flask continued stirring at the established temperature with small samples of 0.1–0.9 mL being periodically withdrawn for the titrations with dibutyl amine. When titration showed the absence of isocyanates, the flask was removed from the thermostat to stop the reaction.

Table 2 List of polyaddition reactions, studied in this report, with the reactant amounts and the theoretically calculated initial %NCO concentrations (wt/wt)

Reaction	Polyol, amount	Diisocyanate, amount	NCO0 before reaction, theor.
PEA : HDI 1 : 0.3 mol	10 g	0.252 g	1.256%
PEA : HDI 1 : 0.5 mol	10 g	0.420 g	2.059%
PDEA : HDI 1 : 0.3 mol	10 g	0.187 g	0.938%
PDEA : HDI 1 : 0.5 mol	10 g	0.311 g	1.541%
PCL : TDI 1 : 0.3 mol	10 g	0.261 g	1.237%

---

The titration procedure to determine the amount of isocyanates as %NCO involved withdrawing a small sample from the reaction flask with a disposable pipette at specified duration and weighing the pipette on a precision balance before and after dropping the sample into 10 mL of acetone solution of 0.1 M dibutyl amine. The tightly capped titration flask with the solution was placed into an oven at 40 °C for 30–40 min and then cooled to room temperature. After that 2–3 drops of bromophenol blue were added and the solution was titrated with aqueous 0.1 M HCl until blue color faded into yellow. A blank 10 mL sample of 0.1 M dibutyl amine was concurrently heated and titrated as well. The %NCO was calculated as 0.42·(V_B − V_S)/m_S, where V_B is the volume in mL of the 0.1 M HCl solution, used up for the titration of the blank, and V_S is that of the sample, whose weight is m_S (in grams). The molar mass of NCO functionality at 42 g per eq is reflected by the 0.42 multiplier in the calculation. In essence, %NCO represents the weight percentage of unreacted NCO functional groups in the test sample. Kinetic calculations were performed on the MS Excel spreadsheet, which automatically computes the exponential trendlines and coefficients of determination as R².

Acidity values were measured by titration using adapted procedures of standard EN 14104. Briefly, the macrodiol was diluted in isopropanol and titrated using a 0.01 M solution of KOH and a phenolphthalein indicator as described previously.^8,9

3. Results and discussion

Before presenting the experimental results, the main assumptions are explained for mapping the kinetic data. Afterward, the acquired data is processed and described separately for the reactions of TDI and HDI. In the last subchapter, further generalizations are proposed based on the observed kinetic tendencies.

3.1 Time–temperature superposition (TTS) for kinetics of diisocyanate addition

The purpose of this study is to compare kinetic data from polyaddition reactions at several temperatures with different reactant concentrations. Monitoring the variation of %NCO provides some indication of how the reaction proceeds at that particular ratio of the reactants. However, %NCO makes it complicated to compare the kinetic data from reactions, which involve different concentrations of the same macrodiol and diisocyanate. There are reports that the polyaddition mechanism could change depending on the concentration of PUR components.^10,11 Such transitions of the reaction mechanisms could be easier to detect when superimposing the kinetic data from various concentrations as a dimensionless value, instead of %NCO. Therefore, fractions of unreacted isocyanates are employed, as it is frequently used by other PUR researchers.⁵ These fractions can be expressed as NCO_t/NCO₀, where NCO_t and NCO₀ are respectively the %NCO at a given reaction time and the initial %NCO before the reaction, which is calculated theoretically as listed in Table 2.

In addition to aggregating as NCO_t/NCO₀ values from reactions at different concentrations, a tool is utilized to combine them from reactions at several temperatures. Time–temperature superposition (TTS) is widespread in dynamic mechanical analysis of polymers and viscoelasticity studies.¹² It turns out that TTS can also be occasionally applied to map the kinetics of PUR polyaddition,^13,14 epoxy curing,¹⁵ oxypolymerization,¹⁶ oxidation¹⁷ and other reactions. A simplified version of TTS can be introduced, which disregards the effects of frequency since no oscillations are involved. Then the actual duration of the reaction can be replaced with its normalized value after multiplication by a shift factor based on the Arrhenius law:

t_TTS = t·exp[(−E_a/R)·(1/T₀ − 1/T_TTS)]

where E_a is the presumed activation energy, J mol⁻¹ R is universal gas constant, i.e. 8.3145 J (mol⁻¹ K) T₀ is the actual test temperature, K T_TTS is an arbitrary temperature as the reference for the normalized duration, i.e. 343.16 K, t is the actual duration of the reaction at a specific test temperature, hrs t_TTS is the normalized duration at the reference temperature, hrs at 70 °C.

In this report, the arbitrary temperature for the normalization of reaction durations is selected as 70 °C, or 343.16 K. Any other temperature can also be selected, the only reason to prefer 70 °C might be the fact that more specimens from reactions at this temperature were titrated compared to those at 60 °C, 80 °C or 90 °C.

Application of TTS for one particular reaction segment should be more successful if the reaction order stays the same, activation energies of involved processes are similar and the kinetic factors are the only ones, which affect the reaction progress. TTS might not be appropriate if reactants and/or products rapidly vaporize, especially in films,¹⁸ form colloidal particles, undergo solvation, or engage at a significant extent in other processes, which are not governed by the Arrhenius law. There are reports of similar E_a values for isocyanate addition to hydroxyls.^3,11,14 This makes it likely that kinetic mapping using TTS can successfully integrate the NCO_t/NCO₀ values from different temperatures into one master curve. Therefore, the data from HDI and TDI polyaddition to the macrodiols from Table 1 is processed using TTS in the below sub-chapters.

In this report, an attempt is made to determine an apparent E_a for each combination of diisocyanates and macrodiols. Some authors propose that polyaddition follows second-order kinetics.⁵ Since the macrodiols are used in excess, the OH concentration is much higher than that of NCO and the latter drops down much faster with respect to the initial concentration during the course of polyaddition. Therefore, an approximation can be made by assuming that the OH concentration is constant. Then it becomes possible to apply the first-order kinetics, i.e.

NCO_t/NCO₀ = exp(−k × t)

where t is the actual duration of the reaction at a specific test temperature, hrs NCO_t/NCO₀ is the fraction of unreacted isocyanates at reaction time t, k is the reaction rate constant, which is specific to the reaction temperature.

Consequently, the exponential dependence between NCO_t/NCO₀ and the reaction duration can be correlated by a linear trendline on the logarithmic scale. When the fraction of unreacted NCO is aggregated against the TTS-normalized durations, the established trendline results in a respective coefficient of determination R². Assuming the reaction rate constant k is governed by Arrhenius law as a function of activation energy, different E_a values can be plugged into TTS during the normalization until the highest R² value is achieved, establishing the optimum E_a. It should be noted that TTS can be used to process data from second-order or other types of kinetics, just in those cases it might not be possible to employ exponential correlations.

When correlating the data in this report, the %NCO values of 0 were not included. Since many of the %NCO = 0 values were determined well after the addition reaction was completed, the recorded durations might not reflect the actual time when the reaction was about to end. Some titrations did record %NCO = 0 during the study, however, the isocyanates are sensitive to hydrolysis and other side reactions, therefore, the detection limits can be achieved faster due to the latter processes than because of the polyaddition alone. Therefore, the zero values were not processed with TTS, and neither they were included in correlations. The values of %NCO at t = 0 are shown in the concentration vs. time charts for reference, although they were not measured but calculated theoretically. Also, all the trendlines were forced to cross through NCO_t/NCO₀ = 1 at t = 0, which reduced the coefficients of determination somewhat in most correlations.

It was assumed that isocyanates were added to hydroxyls only, not to carboxyls, whose traces were detectable in the macrodiols, see Table 1. Some oxidation of primary OH groups into carboxyls does happen during the manufacture and storage of macrodiols. Since the macrodiols were used in excess, the reaction between isocyanates and carboxyls should have been rather slow¹⁹ and the formation of carbamic carboxylic anhydrides²⁰ was considered negligible in this investigation.

Two mainstream industrial diisocyanates were used in this study. Their depletion trends with different macrodiols are presented in the following subchapters for aromatic TDI and aliphatic HDI respectively. Kinetic maps of their depletion during the polyaddition are produced based on the fractions of unreacted NCO, plotted against the normalized TTS durations, keeping 70 °C as the baseline temperature. The actual titration results, recorded as %NCO values, are displayed in separate charts before normalizing the durations with TTS.

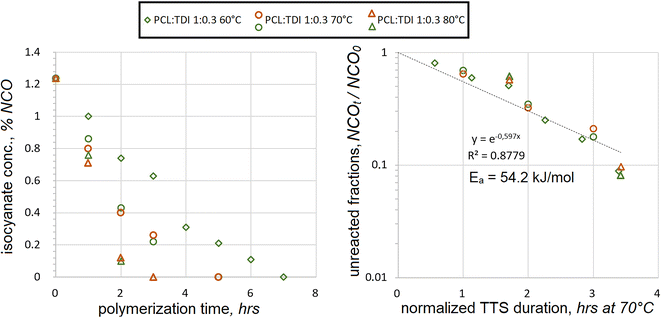
3.2 TDI addition

Aromatic diisocyanate TDI was reacted with the PCL macrodiol at temperatures from 60 °C to 80 °C. Measured %NCO concentrations were plotted against the reaction durations, Fig. 1.

Fig. 1 Decrease in isocyanate contents (as %NCO) with ongoing TDI polyaddition to PCL using 1 : 0.3 mol ratio at different temperatures (left) and superposition of the unreacted NCO fractions after processing polyaddition durations with TTS using E_a = 54.2 kJ mol⁻¹ (right).

During the reaction, isocyanate concentrations went down quite steadily at all temperatures. As expected, their consumption was the fastest at 80 °C and the slowest at 60 °C. The theoretical initial NCO concentration was calculated at %NCO₀ = 1.237% wt. All measured values were lower during the course of polyaddition, recording below 1.0. Utilizing TTS the fractions of unreacted NCO were overlaid at different temperatures. When plotted on the semilog scale, an exponential dependence was used to correlate the NCO consumption to the duration, assuming the first-order kinetics. Its trendline appears as a straight line on the semilog chart in Fig. 1. The values of activation energy were iterated in the TTS expression until the best coefficient of determination was achieved at R² = 0.8779, yielding E_a = 54.2 kJ mol⁻¹. The correlation was not perfect, because the actual NCO values appeared lower when NCO_t/NCO₀ < 0.1, while most of those were underpredicted during the earlier stages of polyaddition. These tendencies seem to suggest that there might be a cross-over period during the reactions at all three temperatures, when reaction rates start changing. Such cross-over is not evident if TTS is not applied, but on the other hand, this might just be a deviation from first-order kinetics.

It should also be noted that the value of E_a = 54.2 kJ mol⁻¹ was not established as actual activation energy in its thermodynamic sense. It might rather be viewed as an empirically established value, which could relate the kinetic trends of TDI polyaddition at different temperatures. Despite these reservations, such an assumption can be tolerated in some applications, where isocyanate polyaddition takes place. Utilization of TTS, based on the first-order kinetics and individually established E_a values, can make it easier to control the polyaddition reactions with TDI when unexpected temperature variations take place and possibly under other circumstances.

3.3 HDI addition

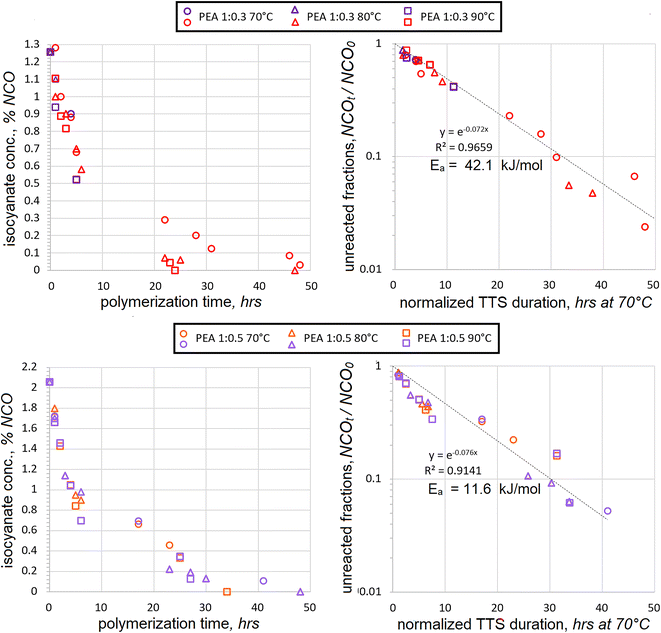
Since HDI is aliphatic, its addition proceeds slower than that of aromatic TDI. Therefore, somewhat higher temperatures of 70 °C, 80 °C and 90 °C were selected for its polyaddition. The excess of two macrodiols, PEA and PDEA, reacted with HDI. Two different molar ratios were used at 1 : 0.3 mol and 1 : 0.5 mol. The consumption of HDI during polyaddition with PEA is plotted in Fig. 2. In order to evaluate the accuracy of polyaddition and titration procedures, several samples were rerun at the same conditions, such as 4 h at 70 °C and 1 : 0.3 mol or 6 h at 70 °C and 1 : 0.5 mol. It must be admitted that the data scatter does exist, but it is well within ±10%. It should still be relatively safe to expect that most data is accurate to ±5%, with the exception of %NCO = 0, as discussed above. As in the case of TDI addition, the titration values show that isocyanate contents continually drop due to progressing polyaddition of HDI as well as due to the increasing temperature.

Fig. 2 Decrease in isocyanate contents (as %NCO) with ongoing HDI polyaddition to PEA using 1 : 0.3 mol (upper charts) and 1 : 0.5 mol (lower charts) ratios at different temperatures (left) and superposition of the unreacted NCO fractions after processing polyaddition durations with TTS using E_a of 42.1 and 11.6 kJ mol⁻¹ respectively (right).

After normalizing the actual reaction times using TTS, the apparent E_a was established and the data from different temperatures was combined into separate charts for 1 : 0.3 and 1 : 0.5 mol, Fig. 2 (right). The data from several temperatures at both ratios of the PEA : HDI appeared to converge better than in the case of TDI. The relationship followed the exponential trend at 1 : 0.3 mol ratio quite closely all the way until the fractions of unreacted NCO fractions dropped below NCO_t/NCO₀ < 0.1. After the presumed activation energy value of E_a = 41.4 kJ mol⁻¹ was plugged into the TTS, the coefficient of determination achieved the highest value of R² = 0.9673.

When the isocyanates were titrated during the polyaddition at a 1 : 0.5 mol ratio, the correlation was less perfect. Still, the trendline was quite linear on the semilog scale during the early stages when the fractions of unreacted isocyanates exceeded NCO_t/NCO₀ > 0.34. Below this value, a cross-over period seems to begin, as can be discerned in both charts. However, the presence of such a cross-over is more evident in the chart with TTS. Both the cross-over and the increased data scatter during the later stages of the HDI polyaddition suggest significant changes in NCO consumption mechanisms. The best coefficient of determination was achieved at R² = 0.9141 when the presumed activation energy value of E_a = 11.6 kJ mol⁻¹ was used. This value is several times lower than 42.1 kJ mol⁻¹, which was obtained in the case of 1 : 0.3 mol polyaddition.

The difference in actual HDI concentrations between 1 : 0.3 mol and 1 : 0.5 mol is significant, but not dramatic. Hence, it seems quite counterintuitive that activation energy values might be so different. Since E_a was established based on the highest R² values, it would make sense to assess the data scatter trends. Most data scatter seems to occur during the late stages of polyaddition, and these data points might have a major bearing in determining the E_a value. Consequently, the activation energy value of E_a = 11.6 kJ mol⁻¹ should be taken with caution and additional generalizations might be helpful to explain the disparity in activation energies between the two molar ratios.

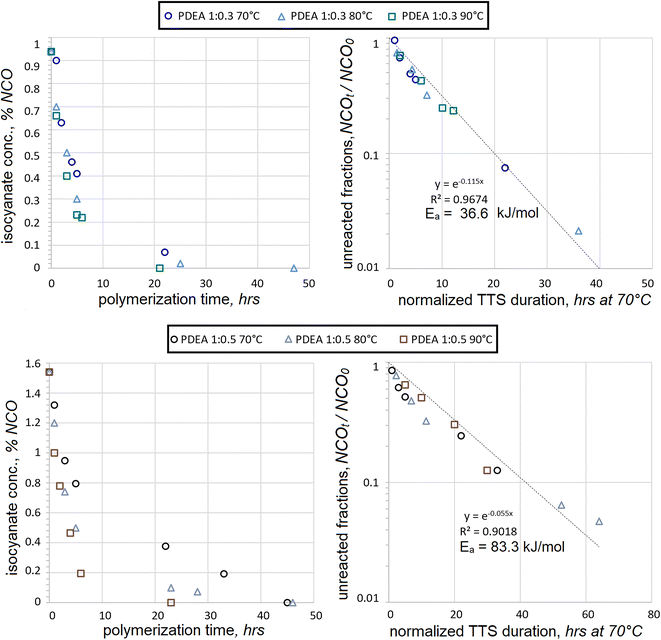
Consumption of HDI was also tested with another macrodiol, PDEA, under the same conditions, see Fig. 3. As in the case with PEA, the consumption of fractions of unreacted NCO followed the trendline quite closely for PDEA : HDI at 1 : 0.3 mol. Iterations of activation energies produced the best fit at E_a = 36.6 kJ mol⁻¹ with R² = 0.9674. This E_a value is not too distant from that of PEA at E_a = 42.1 kJ mol⁻¹, which suggests that both reactions might engage similar mechanisms of first-order kinetics. The molecules of PEA and PDEA are highly linear, contain many adipate moieties, are much larger in molecular size than HDI, and share many more common features of molecular architecture. Therefore, it is not too surprising that the E_a values are similar for their polyaddition reactions when macrodiols are in significant excess. Yet another similarity was the increase of data scatter during the late stages of polyaddition, in particular for NCO_t/NCO₀ < 0.3.

Fig. 3 Decrease in isocyanate contents (as %NCO) with ongoing HDI polyaddition to PDEA using 1 : 0.3 and 1 : 0.5 mol ratios at different temperatures (left) and superposition of the unreacted NCO fractions after processing polyaddition durations with TTS using E_a of 36.6 and 83.3 kJ mol⁻¹ respectively.

When macrodiol excess is less significant, the kinetic trends of PEA and PDEA reactions are not so similar. In the case of PDEA : HDI at 1 : 0.5 mol, the correlation to the first-order kinetics was less evident and iterations produced E_a = 83.3 kJ mol⁻¹ with R² = 0.9018. The data scatter became evident much earlier into the polyaddition and the lack of convergence was very noticeable even at NCO_t/NCO₀ = 0.7. The presumed activation energy is again very different compared to E_a = 36.6 kJ mol⁻¹, which was extracted from the PDEA : HDI reactions at a 1 : 0.3 mol ratio. As opposed to the polyaddition with PEA, in the case of PDEA, the presumed activation energy at 1 : 0.5 mol was more than twice as high as that of 1 : 0.3 mol.

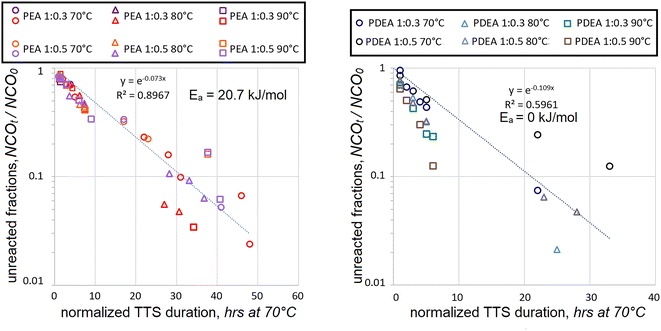
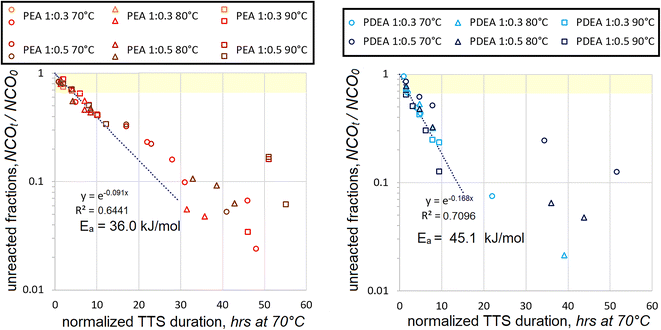
When HDI data was combined for both concentrations and polyaddition durations normalized using TTS, the following kinetic maps were obtained, see Fig. 4.

Fig. 4 Decrease in fractions of unreacted isocyanate (as NCO_t/NCO₀) with ongoing HDI polyaddition to PEA at different temperatures (left) and PDEA (right) per reaction durations, normalized by TTS at different temperatures. Data from 1 : 0.3 mol and 1 : 0.5 mol ratios is combined for the whole conversion range.

In the case of polyaddition between PEA and HDI, the E_a = 20.7 kJ mol⁻¹ value turned out to be in between those, established separately for the 1 : 0.3 and 1 : 0.5 mol reactions, i.e. 42.1 and 11.6 kJ mol⁻¹ respectively. The coefficient of determination was noticeably lower, but not too far from acceptable reliability. The merger of PDEA polyaddition data was quite different. The data could not correlate using the first-order kinetics, R² never exceeded 0.6 when using various positive E_a values. The best fit was obtained when no temperature dependence was assumed. Such lack of convergence suggests that the mechanism of PDEA polyaddition at 1 : 0.3 mol might be quite different from that at 1 : 0.5 mol. Such suspicion might be applied to PEA polyaddition as well since the R² value went down somewhat. It should also be noted that both in PEA and in PDEA cases the data scatter became progressively higher when the fraction of unreacted isocyanates was dropping below NCO_t/NCO₀ < 0.3. Such propagation of the data scatter and the establishment of unrealistic E_a values suggests that more assumptions might be necessary in order to simplify the interpretation of the findings.

3.4 Generalization of kinetic trends

Acquired data shows significant variations in kinetic trends under different molar ratios. With temperature changes, unexpected variations of presumed activation energies are observed if the first-order kinetics is assumed. These findings imply that polyaddition between the same reactants might follow rather different kinetic trends when the molar ratio is changed. It should be noted that the addition of isocyanates and hydroxyls does not have to be the only process, which takes place. The blend of macrodiols, diisocyanates, and their reaction products might engage in agglomeration or colloidal processes. Their mechanisms might be overly complex and proceed very differently from the first-order kinetics. Such supposition might explain the observation that the data scatter becomes more significant in the late stages of polyaddition, because the increasing amount of polyaddition products are more likely to make such side processes more influential.

Early stages of polyaddition might be suited for yet another assumption. Bearing in mind that both diisocyanates and macrodiols are difunctional and the two reactants have very different molecular sizes, a new generalization can be proposed. Macrodiols are much larger than TDI or HDI and their mobility is more restricted in the reaction media. So it would be reasonable to assume that the first NCO group in a diisocyanate should react much faster than the second one due to the small molecular size of the initial diisocyanate. After the initial addition reaction, when one NCO functionality forms a carbamate bond with a macrodiol, the molecular size of the newly formed adduct becomes much larger, see Scheme 3.

Scheme 3 Two stages of the polyaddition of diisocyanates to the excess macrodiols. Top: initial addition as the very first reaction to form a monofunctional adduct of large molecular size. Bottom: adduct addition as the second reaction, which prevails due to macrodiol excess. Further polyaddition is not shown.

Intermolecular movements of the larger adduct are much more restricted and the reaction rate should be significantly lower for the residual NCO group. So it can be expected that at the beginning of addition the predominant reaction is between the unreacted diisocyanate and a macrodiol. Therefore, when considering activation energies, the distinction can be made for the initial stage of polyaddition. Such an approach was reported by other researchers for 1,3-xylylene diisocyanate with simple primary alcohols from 1-propanol to 1-hexanol,²¹ yielding E_a of 26.9 to 36.6 kJ mol⁻¹ respectively for the initial addition reaction. Combining the whole range of NCO_t/NCO₀ values into one plot after transforming the durations with TTS might be successful when E_a for the slow and fast reactions are similar. However, if the two activation energies are significantly different, major discrepancies could be observed after TTS transformations. Even if the E_a values were similar, an occurrence of aggregation or colloidal processes between reactants and products might lead to data scatter anyway.

The possibility of the latter processes aside, more attention can be devoted to these two major mechanisms that govern the polyaddition: (1) fast addition of the unreacted diisocyanate and (2) slow addition of the monofunctional adduct. Statistically, when the polyaddition reaches the value NCO_t/NCO₀ = 0.67, the reaction between the unreacted diisocyanate and the macrodiol should prevail as 2 : 1 against that involving the adduct, assuming that both reaction rates are the same. Since larger molecules most likely react much slower, at NCO_t/NCO₀ = 0.67 the prevalence of the diisocyanate reactions should be significantly higher than just 2 : 1. Therefore, the deviation from the actual rates of NCO addition should not be excessive under the assumption that all reactions with NCO_t/NCO₀ > 0.67 take place due to the addition of the unreacted diisocyanate.

A reciprocal assumption might be proposed for the slow reaction of the larger adducts, which contain only one unreacted NCO group. Once the polyaddition passes below NCO_t/NCO₀ = 0.34 the concentration of the unreacted diisocyanates becomes much lower than that of the larger adducts. Since the first NCO group in diisocyanates reacts much faster than the second one, it would be relatively safe to assume that the slow reaction of the adduct predominates when NCO_t/NCO₀ < 0.34. However, the abundance of polyaddition products during the late stages might have a much more significant effect on the reaction mechanisms. A rapidly increasing number of possible reactions would make it very difficult to establish their reaction rates, activation energies, or other kinetic parameters.

Since the TTS method, which is employed in this study, uses a single E_a value for normalizing the reaction duration, only the concentration interval from the beginning of the addition was selected for establishing the activation energy. The results from the HDI polyaddition at 1 : 0.3 mol and 1 : 0.5 mol ratios were combined into one set and presumed E_a values were determined for several NCO_t/NCO₀ intervals. The results from the progressively narrower intervals of 1.0 to 0.01, to 0.34, and to 0.67 are presented in Table 3.

Table 3 Presumed activation energies E_a (kJ mol⁻¹) and coefficients of determination R² of the correlations within specific intervals of unreacted isocyanate fractions NCO_t/NCO₀. The parentheses indicate the smallest number of data points, used in correlations

NCOt/NCO0 range →	0.01–1.0		0.34–1.0		0.67–1.0
↓ Molar ratio ↓	Ea	R^2	Ea	R^2	Ea	R^2 (# of points)
PEA : HDI 1 : 0.3	42.1	0.9673	28.3	0.9402	39.4	0.776 (9)
PEA : HDI 1 : 0.5	11.6	0.9141	17.1	0.9375	3.1	0.9485 (8)
PEA : HDI all	20.7	0.8943	25.8	0.9345	36.0	0.6441 (17)
PDEA : HDI 1 : 0.3	36.6	0.9674	27.7	0.9604	38.7	0.8386 (4)
PDEA : HDI 1 : 0.5	83.3	0.9018	48.7	0.9708	48.3	1.0 (2)
PDEA : HDI all	0	0.5961	18.1	0.6421	45.1	0.7096 (6)
PCL : TDI 1 : 0.3	54.2	0.8779	41.4	0.8608	50.9	1.0 (2)

---

The presumed activation energies, which were established for the narrower ranges of isocyanate conversion, show even more unexpected values. It should be kept in mind that fewer data points were used when establishing E_a for the narrower conversion ranges. Less data increases the probability of discrepancies, therefore, the activation energies for the reactions at solely 1 : 0.3 mol ratio or solely 1 : 0.5 mol ratio should be viewed with great caution. In the case of PCL or PDEA polyaddition at 1 : 0.3 mol ratio and the latter at 1 : 0.5, when the data from NCO_t/NCO₀ > 0.67 was utilized, only 4 or fewer data points were employed for every correlation. Despite occasional R² = 1 values, listed E_a should not be considered as an indication of actual activation energy.

On the other hand, the data, which combines both molar ratios, is more significant statistically. Even during the early stages, when mostly unreacted HDI is added to the macrodiol, quite a sufficient number of data points are employed for the correlations. Kinetic maps, which utilize E_a values, which were established using the data only from NCO_t/NCO₀ > 0.67 range, are presented in Fig. 5.

Fig. 5 Decrease in fractions of unreacted isocyanate (as NCO_t/NCO₀) with ongoing HDI polyaddition to PEA at different temperatures (left) and PDEA (right) per reaction durations, normalized by TTS at different temperatures. Data from reactions at 1 : 0.3 mol and 1 : 0.5 mol ratios is combined. Trendlines show only the best fit for the NCO_t/NCO₀ range of 0.67 to 1.0, as shaded in yellow on the charts.

As expected, the trendlines seem to fit the data during the early stages of polyaddition much better than during the late stages. This is in line with the generalization that the polyaddition proceeds in two stages, first the initial addition and then the adduct polyaddition. Most data points below NCO_t/NCO₀ = 0.67 appear above the trendlines. This shows that the reaction rates become lower with progressing polyaddition. Such tendency strongly supports the expectation that due to their large molecular size the monofunctional isocyanate adducts react much slower than unreacted diisocyanates of relatively small molecular size.

The obtained E_a values are not very distant from the activation energies, reported by other researchers for similar isocyanates and hydroxyl compounds. Measurements of HDI consumption during equimolar polyaddition to carbonate macrodiol at 90 °C to 140 °C¹⁴ yielded E_a = 43.5 ± 1.5 kJ mol⁻¹. Other isocyanates also demonstrate not-too-distant activation energies, as discussed by other researchers.¹¹ In just one polyaddition reaction the values of 35 to 55 kJ mol⁻¹ were reported with a strong dependence on the degree of conversion. The addition of TDI to phenol and its halogenated derivatives was reported²² to proceed with activation energies within a relatively wide range of 32 to 76 kJ mol⁻¹.

As mentioned previously, this report does not attempt to establish accurate activation energies for each step of the polyaddition mechanism. This investigation aims to provide the approach to interpret the mechanisms of a relatively complex reaction, whose kinetic data was collected at different temperatures and molar ratios. Assumption of reaction order (quite often the first order kinetics), utilization of TTS, and extraction of E_a values from the early stages of the addition might provide a useful protocol to overview the main processes during the reaction without a need for high accuracy or abundance of data points. Such kinetic maps might be instrumental not only in establishing the apparent E_a, but also in identifying cross-over periods, deviations from first-order kinetics, and other aspects of process mechanisms. These approaches might prove useful in PUR manufacture, especially when prolonged heating or cooling are needed to achieve required temperature, or unexpected temperature variations take place. Also, the ester-based macrodiols receive a lot of attention from PUR industry due to their excellent rates of enzymatic degradation.²³ Better control of the kinetic processes can make it easier to produce catalyst-free PUR with extremely low levels of migrating chemicals and good potential for biodegradation. This would not only increase the safety, but will also assure better user-friendliness and sustainability of PUR plastics.

4. Conclusions

The experimental data of NCO depletion during addition reactions between several diisocyanates and macrodiols was collected at different concentrations and temperatures. It was processed using TTS, the assumption of the first-order kinetics, and the segregation of the data from the conversion of unreacted diisocyanates into monofunctional adducts. Several conclusions can be drawn from these observations.

• First-order kinetics can be used to correlate the concentrations to the reaction duration from the early stages of autocatalytic addition of TDI or HDI to excess macrodiols.

• Time–temperature superposition (TTS) based on the Arrhenius equation can make it possible to combine the concentration values from various temperatures and molar ratios.

• Kinetic maps show that NCO depletion proceeds faster until most unreacted diisocyanates are converted into monofunctional adducts by addition to the macrodiols. Afterward, the polyaddition rates become slower.

• The deviations from the first-order kinetics become progressively more apparent with proceeding polyaddition. This implies that the increasing amount of reaction products might lead to new processes, such as aggregation or colloidal transitions, which are not governed by first-order kinetics.

• Application of TTS can yield kinetic maps, which display reaction trends without the need for a large volume of high-accuracy data points.

• Better understanding of the addition kinetics of diisocyanates can be instrumental in eliminating the usage of catalysts and significantly reducing the chemical migration from PUR plastics.

Conflicts of interest

There are no research-related conflicts to declare. The experimentally determined values, utilized in this investigation, constitute a part of a publicly available Dataset.²⁴

Acknowledgements

Experimental contributions from Julija Bekiš, Goda Andrijaitytė, Lukas Adomaitis (Vilnius University), Antanas Strakšys and Sandra Mačiulytė (FTMC) are acknowledged. The technical concept and advice of Joerg Buechner and Thomas Fait (Covestro Deutschland AG), who also donated the reactants, are cordially appreciated. This study was carried out under project TERMINUS, funded by the European Union under Horizon 2020. Call: H2020-NMBP-ST-IND-2018. Grant Agreement: 814400.

Notes and references

1. K. Vadoudi, P. Deckers, C. Demuytere, H. Askanian and V. Verney, Sustain. Prod. Consum., 2022, 33, 820–830,  DOI:10.1016/j.spc.2022.08.004.
2. M. L. Polo, M. E. Spontón, F. Jaramillo, D. A. Estenoz and G. R. Meira, J. Appl. Polym. Sci., 2018, 135(4), 45747,  DOI:10.1002/app.45747.
3. P. Król, J. Appl. Polym. Sci., 1995, 57(6), 739–749,  DOI:10.1002/app.1995.070570609.
4. H. Al-ri, L. Jaf and G. J. Suppes, RSC Adv., 2017, 7(43), 26583–26592,  10.1039/C7RA01242J.
5. M. Rochery, I. Vroman and T. M. Lam, J. Macromol. Sci., Part A: Pure Appl.Chem., 2000, 259–275,  DOI:10.1081/MA-100101092.
6. B. Lucio and J. L. de la Fuente, Polymer, 2018, 140, 290–303,  DOI:10.1016/j.polymer.2018.02.058.
7. P. Nemaniutė, T. Matijošius, D. Bražinskienė and S. J. Asadauskas, in Proc. 24th Conf. “Advanced Materials and Technologies”, 2022, p. 137,  DOI:10.5281/zenodo.7146381.
8. I. Liascukiene, D. Brazinskiene, A. Griguceviciene, A. Straksys and S. J. Asadauskas, Fuel Process. Technol., 2018, 180, 87–95,  DOI:10.1016/j.fuproc.2018.08.009.
9. J.-L. Dubois, J.-L. Couturier, S. J. Asadauskas, L. Labanauskas, D. Bražinskienė and R. Blauuw, RSC Adv., 2021, 11, 31030,  10.1039/d1ra04045f.
10. C. Gertig, E. Erdkamp, A. Ernst, C. Hemprich, L. C. Kröger, J. Langanke, A. Bardow and K. Leonhard, ChemistryOpen, 2021, 10(5), 534–544,  DOI:10.1002/open.202000150.
11. A. Olejnik, K. Gosz and Ł. Piszczyk, Thermochim. Acta, 2020, 683, 178435,  DOI:10.1016/j.tca.2019.178435.
12. L. I. Palade, V. Verney and P. Attane, Macromolecules, 1995, 28(21), 7051–7057,  DOI:10.1021/ma00125a003.
13. S. Li, R. Vatanparast, E. Vuorimaa and H. Lemmetyinen, J. Polym. Sci., Part B: Polym. Phys., 2000, 38(17), 2213–2220,  DOI:10.1002/1099-0488(20000901)38:17<2113::AID-POLB10>3.0.CO;2-K.
14. B. F. d'Arlas, L. Rueda, P. M. Stefani, K. De la Caba, I. Mondragon and A. Eceiza, Thermochim. Acta, 2007, 459(1–2), 94–103,  DOI:10.1016/j.tca.2007.03.021.
15. J. Gonzalez-Benito, D. Olmos, P. G. Sanchez, A. J. Aznar and J. Baselga, J. Mater. Process. Technol., 2003, 143, 153–157,  DOI:10.1016/S0924-0136(03)00397-2.
16. S. Asadauskas, J. M. Perez and S. Z. Erhan, Tribol. Trans., 1999, 42(4), 860–866,  DOI:10.1080/10402009908982293.
17. A. Wolfberger, M. Zehl, A. Hausberger, M. Tockner, S. Schlögl, M. Hołyńska and C. Semprimoschnig, Tribol. Lett., 2021, 69(1), 1–13,  DOI:10.1007/s11249-020-01372-z.
18. A. Stoncius, I. Liascukiene, S. Jankauskas and S. J. Asadauskas, Ind. Lubr. Tribol., 2013, 65(3), 209–215,  DOI:10.1108/00368791311311213.
19. C. Gürtler and K. Danielmeier, Tetrahedron Lett., 2004, 45(12), 2515–2521,  DOI:10.1016/j.tetlet.2004.02.012.
20. P. Babusiaux, R. Longeray and J. Dreux, Justus Liebigs Ann. Chem., 1976, 1976(3), 487–495,  DOI:10.1002/jlac.197619760313.
21. L. Nagy, A. Juhász, M. Zsuga and S. Kéki, eXPRESS Polym. Lett., 2020, 14(4), 336–347,  DOI:10.3144/expresspolymlett.2020.28.
22. S. Kalaimani, B. M. Ali and A. S. Nasar, RSC Adv., 2016, 6(108), 106990–107000,  10.1039/C6RA24409B.
23. A. Rosato, A. Romano, G. Totaro, A. Celli, F. Fava, G. Zanaroli and L. Sisti, Polymers, 2022, 14(9), 1850,  DOI:10.3390/polym14091850.
24. S. J. Asadauskas, S. Mačiulytė and P. Nemaniutė, “TERMINUS WP5: Chain Extension Kinetics for Solvent-Free Adhesive Components”, Zenodo Dataset, 2022,  DOI:10.5281/zenodo.6406174.

---

Footnote

† This report reflects only the views of the authors. European Commission, Research Executive Agency, CNRS (French National Centre for Scientific Research), and FTMC (Center for Physical Sciences and Technology) are not responsible for any use that may be made of the information it contains, see §29.5 of “H2020 General Model Grant Agreement” for details.

---