The electronic and mechanical properties of (U, Th)O₂ compounds: a first-principles study

Abstract

Alloying is widely acknowledged as an effective strategy for enhancing the performance of UO₂ nuclear fuel. Herein, the thermodynamic stability and kinetic stability of U–Th–O ternary compounds are used to clarify the hidden stable structures. The calculation results of the total and the partial density of states indicated that there is significant orbital hybridization between the added Th and O atoms at −5 eV. Furthermore, the mechanical anisotropy was evaluated by means of the three-dimensional Young's modulus, revealing that the U–Th–O ternary compound exhibits a high degree of isotropy, with the Young's modulus reaching approximately 200 GPa in all three directions. In our upcoming work, our focus will be on studying the changes in properties, such as thermal conductivity of the U–Th–O ternary compound, which may provide a data basis for the application of ternary U–Th–O fuel in reactors.

---

1. Introduction

The most efficient, economical and environmentally friendly commercial light-water reactor fuel currently used is UO₂, which is the world's main source of electricity.^1–3 Traditional UO₂ fuel has very high melting point and good water corrosion resistance, however, its thermal conductivity is not high enough to meet industrial demand.^4,5 After the Fukushima nuclear accident in 2011, one of the focuses on the fault-tolerant fuel system is to modify UO₂ fuel or to find new fuels in place of UO₂ to ensure that the improved fuel has higher thermal conductivity and mechanical stability at high temperatures.⁵ Among them, it is an effective solution to improve the overall performance by adding other elements to form new configurations.⁶

Various properties of U–O–X compounds have been studied extensively in recent years. Rittman D. R. et al.⁷ studied the phase behavior of ternary compounds formed by doping UO₂ with different concentrations of lanthanides (La, Nd) under high-pressure conditions of 0–50 GPa. The results show that the pressure of phase transformations increases with the doping concentration, while the volume modulus changes in inversely proportional to the radius and concentration of doped atoms. S. C. Finkeldei et al.⁸ explored the preparation of monolithic UO₂ and UO₂–Mo composite materials using molybdenum metal powder and UO₃ spheres as raw materials. The results prove that by adding 10% Mo as the second phase to UO₂ will increase the thermal conductivity by 30%, and different sizes of molybdenum raw materials will lead to different microstructures, which will affect the thermal conductivity of the composite material. Be element was introduced into the system to form the UO₂–Mo–Be system, the thermal conductivity of the system increased by 128.65 percent and 157.71 percent at the temperature of 298 K and 1273 K, respectively, made it become one of the accident fault tolerance candidate materials.⁹ Rahman M.¹⁰ performed the classical molecular dynamics (MD) simulation method to prove that the number of residual defects in (U_0.5Th_0.5)O₂ are significantly higher than the number of residual defects in UO₂ and ThO₂. The research results of Evitts L. et al. showed the existence of Th can increase the ratio of 242 Pu/239 Pu by 3.5% when UO₂ is low fuel consumption.¹¹

Various studies have shown that adding other elements to UO₂ fuel can significantly improve its overall performance. Thorium fuel has the advantages of abundant reserves, less waste, and anti-nuclear proliferation.¹² Thorium-based materials has excellent properties as viable nuclear fuel candidates in fourth-generation nuclear reactors, and are considered to be one of the most easily commercialized reactor types.¹³ So far, researchers have done a series of work on UO₂ and Th-based nuclear fuels, while the research on (Th, U)O ternary nuclear fuels has not yet been fully developed. More intriguingly, a mixture of ThO₂ and U in recent article demonstrated that (Th, U)O ternary nuclear fuels can be comparable in energy generation with existing UO₂ fuels while own long-term cost effectiveness than UO₂ fuels.¹⁴ In addition, K. Rickert et al. found that by tune the content of Th in the (U, Th)O₂ solid solution, the oxidation of UO₂ to U₃O₈ can be completely inhibited which originated from the fact that Th has a stable oxidation state of 4⁺.¹⁵ Therefore, this work is to systematically study the electronic and mechanical properties of Th element as a dopant and UO₂ basis to form a new thorium–uranium–oxygen ternary compound based on the first-principles method. The research results may be helpful for the design and application of Th-doped UO₂-based modified nuclear fuel to new A generation of commercial reactors provides reference.

2. Method

The theoretical calculations in this part of the work are based on density functional theory,^16,17 using the Vienna ab initio calculation package for first-principles calculations.^18,19 In the calculation process, the projected enhanced wave electric potential (PAW) method is used.²⁰ The exchange-correlation functional uses the generalized gradient approximation (GGA) function combined with the PBE functional²¹ and the local density approximation (LDA). The PBE + U approximation method is proven to effectively improve the accuracy of the performance calculation of actinide materials.^22,23 Therefore, U = 3.0 is used as a calculation parameter considering the strong correlation effect of 5f orbital, which is consistent with the calculation parameters of Torres and Pegg et al.^24–26 The calculation uses the Monkhorst–Pack method to divide the simple Briyuan area by 5 × 3 × 3 K points.²⁷ The truncation can be 500 eV, and when the atomic energy volume converges to 1.0 × 10⁻⁵ eV per atom, and the atomic force converges below 0.01 eV s⁻¹, the structural relaxation optimization is completed. All calculations are done under periodic boundary conditions. Considering the computational cost, a supercell of size 2 × 2 × 1 is used to calculate properties such as energy and electrons.

3. Results and discussion

3.1. Structure optimization and design

UO₂ belongs to the cubic crystal system, with a space group of Fm3̄m, contains three atoms (including two O atoms and one U atom) in a unit cell. The specific structure is shown in Fig. 1(a) (some models used in calculations are based on this structure, as shown in Fig. 1(b), but due to the requirements of this work, the lattice structure shown in Fig. 1(a) is adopted). To eliminate the boundary effect, all calculations are performed in the 2 × 2 × 1 supercell. In the optimization process of the initial structure, we considered the strong correlation effect of the 5f orbital of U atoms, and the DFT + U method was used through the calculations. For the U atom, U = 3.0 and J = 0 were used as the calculation parameters, which is tested by the simulation research of Torres and Pegg et al.^24–26 and has been proved to be reliable. For Th atoms, Wang²⁸ et al. verified through research that the 5f orbitals in thorium atoms are empty, so it is reasonable to set the U value of thorium atoms to 0 in our calculations. At the same time, considering that the U atom itself has a certain degree of magnetism, we will consider the spin in the following calculations. It should be pointed out that the lattice parameter of UO₂ calculated in this work is 5.462 Å (Table 1), which is consistent with previous experimental value 5.474 (ref. 29) and 5.468 Å.³⁰

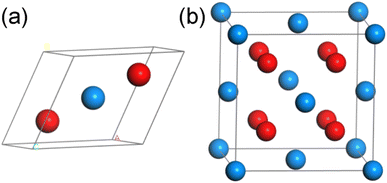Fig. 1 The schematic diagrams for the (a) unit cell and (b) supercell of UO₂ (blue atom: U, red atom: O).

Table 1 The lattice parameter of UO₂, U₄O₇Th, U₃O₈Th, U₂O₈Th₂ and UO₈Th₃

Phase	Lattice parameter (Å)
UO2	5.462
U3O8Th	5.473
U2O8Th2	5.539
UO8Th3	5.550

---

Based on the above optimized primitive cell, we designed four configurations of Th–U–O ternary compounds in the 2 × 2 × 1 supercell by substituting the U and O with Th element. As shown in Fig. 2, they are named U₄O₇Th, U₃O₈Th, U₂O₈Th₂ and UO₈Th₃, and their structures are optimized respectively. Furthermore, as can be seen from Table 1, the lattice constants change very little after alloying and therefore structural distortions are not considered. In the next step, we will calculate and analyze their thermodynamic stability and kinetic stability.

Fig. 2 Crystal structure of (a) U₃O₈Th, (b) U₂O₈Th₂ and (c) UO₈Th₃ (blue atom: U; red atom: O; pink atom: Th).

3.2. Thermodynamic stability

To judge whether the designed four ternary compounds are thermodynamically stable, the cohesive energy are used to evaluate. The calculation formula of cohesive energy is as follows:¹²

E_f = E_tot − E_U4O8 + nE_Th − nE_U/O

where E_f denotes the energy of formation, E_tot denotes the Gibbs energy of the compound, E_U4O8 represents the energy of U₄O₈, E_Th signifies the Gibbs energy of one Th atom, E_U/O is the Gibbs energy of one U atom or O atom, and N represents the number of U atoms or O atoms replaced by Th atoms.

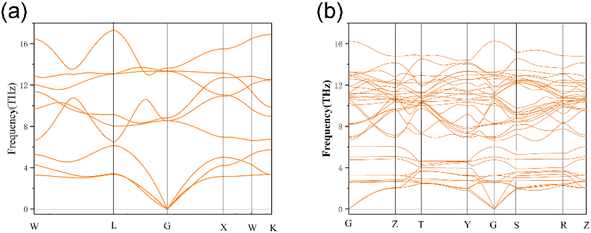
Generally speaking, the cohesive energy of a compound turns to be negative should indicate that the structure is thermodynamically stable under 0 K. While the formation can be positive, indicating this compound is thermodynamically unstable. At the same time, the smaller the negative value is, the more stability the structure possess, and the total energy and cohesive energy of the Th–U–O ternary compounds are listed in Table 1. From the calculation results shown in Table 2, it can be concluded that the cohesive energy of the compound formed by the replacement of the Th atom with one O atom is 4.36 eV, indicates that U₄O₇Th possesses a thermodynamically unstable structure. Other constructions are thermodynamically stable at 0 K, and as the number of substituted uranium atoms increases, the structural stability is further improved, and the formation energies are −7.50, −9.2 and −11.14 eV, respectively. To further understand their dynamic stability, we calculated the phonon dispersion curves of three thermodynamically stable structures and UO₂.

Table 2 The structures of total energy, and cohesive energy ΔH of U₄O₇Th, U₃O₈Th, U₂O₈Th₂ and UO₈Th₃

Phase	Etotal (eV)	ΔH
U4O7Th	−115.58	4.36
U3O8Th	−121.51	−7.50
U2O8Th2	−119.52	−9.21
UO8Th3	−117.75	−11.14

---

3.3. Dynamic stability

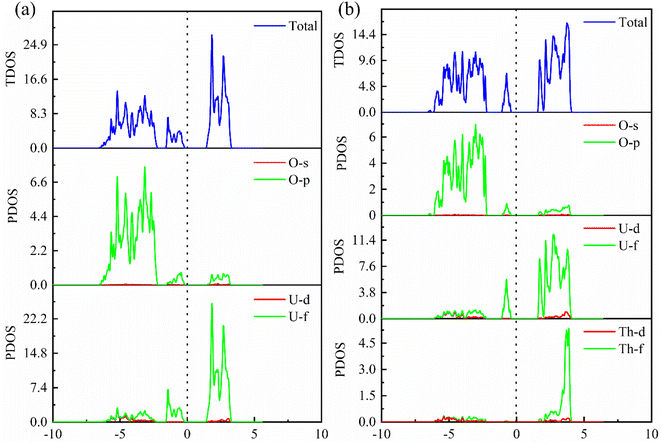
The phonon dispersion curves of three thermodynamically stable structures are calculated, among which U₃O₈Th is a dynamically stable structure, U₂O₈Th₂ and UO₈Th₃ are dynamically unstable structures, they reach negative frequencies of −0.5 and −2.6 in the K-path and Y-path, respectively. The calculation results of U₃O₈Th are shown in Fig. 3(b). If the phonon dispersion curve appears in the Brillouin region with a frequency lower than 0 THz, that is, “imaginary frequency”, it means that the structure is dynamically unstable.³¹ By calculating the phonon spectra of UO₂ and U–Th–O ternary compounds, it is found that the structures of U₂O₈Th₂ and UO₈Th₃ have obvious imaginary frequencies. Therefore, we believe that these structures are relatively dynamically unstable. Under the slight influence, the atoms in these structures may shift, that is, the structures may undergo phase changes. Therefore, these dynamically unstable structures will not be considered in the following calculations. The phonon spectrum of U₃O₈Th do not show any imaginary frequencies, indicating that this structure occupies the lowest point of the energy curve of the compound, so it is the focus of the next calculation.

Fig. 3 Phonon dispersion curve of (a) UO₂ and (b) U₃O₈Th.

3.4. The density of states including the total (TDOS) and partial (PDOS) parts

In order to further explore the charge distribution and bonding characteristics of U₃O₈Th, we calculated the total density of states (TDOS) and partial density of states (PDOS) of UO₂ and U₃O₈Th, and the calculation results are displayed in Fig. 4. From the TDOS of UO₂ and U₃O₈Th in Fig. 4, it can be seen that all curves of UO₂ and U₃O₈Th cross the Fermi level, which may be inferred that these two uranium fuels have a certain degree of metallicity. At the same time, the TDOS diagrams of UO₂ and U₃O₈Th show a slight upward and downward asymmetry, indicating that these two structures have certain magnetic properties. The magnetic moment of the uranium atom itself is asymmetrical, hence both structures exhibit a certain degree of magnetism.

Fig. 4 The TDOS and PDOS curves of (a) UO₂ and (b) U₃O₈Th.

The main peak of UO₂ is mainly determined by the 5f orbital of the U atom above the Fermi level, while the contribution of the O element can be ignored; in addition, the main peak of the TDOS of U₃O₈Th is contributed by the 3p orbital of the O element and the 5f orbital of the uranium element while the contribution from Th element is very small. The density of states around the Fermi level of U₃O₈Th is mainly contributed by the 5f orbital of U atom, the 3p orbital of O atom while the 6d orbital of Th atom contribute a small amount, the density of states around the Fermi level of UO₂ is mainly contributed by the 5f orbital of U atom, while the 3p orbital of O atom contributes a small amount. In addition, the TDOS of UO₂ shows that the s-, p-orbitals of O atoms and the 5f orbitals of U atoms have peaks at −3 eV at the same time, indicating that O atoms have obvious hybrid bonding effects, while in U₃O₈Th at −5 eV, all three kinds of atoms have peaks, which proves that Th atoms form new bonds with O atoms.

3.5. Mechanical properties

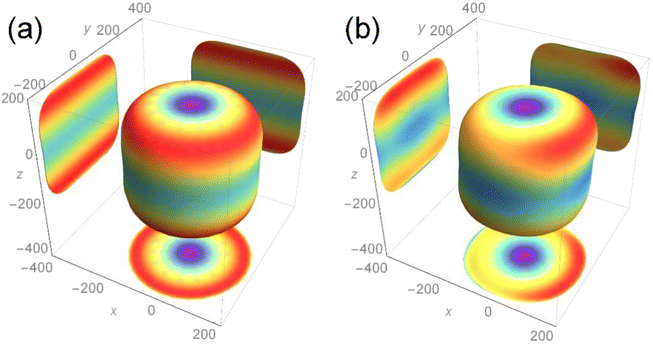
The condition stability of nuclear fuel is very important, and the material may appear fracture failure with the action of the mechanical and thermal stresses. Therefore, there are certain requirements for mechanical anisotropy. To further understand the changes in the mechanical anisotropy of the compound after the addition of Th atoms, we use the three-dimensional Young's modulus diagram to more intuitively show the anisotropic changes in elasticity. For cubic crystal form and orthorhombic crystal form, the calculation formula of the three-dimensional Young's modulus diagram is as follows:³²

E_o = 1/(l₁⁴S₁₁+2l₁²l₂²S₁₂+2l₁²l₃²S₁₃ + l₂⁴S₂₂+2l₂²l₃²S₂₃ + l₃⁴S₃₃ + l₂²l₃²S₄₄ + l₁²l₃²S₅₅ + l₁²l₂²S₆₆)

The calculation result is shown in Fig. 5, and the two-dimensional projection of the three-dimensional Young's modulus diagram in the three directions of (100), (010) and (001) is also added. For the length of each axial direction of the Young's modulus for the nuclear fuel, the more its shape tends to be circular, the more mechanical isotropy turns up, and vice versa. From the overall point of view, the two compounds are cylindrical, indicating that the addition of Th almost has no effect on the overall Young's modulus of UO₂ and maintains its mechanical properties to a certain extent.

Fig. 5 The three-dimensional Young's modulus for (a) UO₂ and (b) U₃O₈Th.

It can be seen from the projection diagram that the projections of the two compounds on the x–y plane are circular, but U₃O₈Th is slightly elliptical compared to UO₂, indicating that Young's modulus of U₃O₈Th in the 001 direction is A slight change. At the same time, the projections of the two compounds upon the x–z and y–z planes are square, in addition, the maximum Young's modulus of the two configurations appears in the (011) and (101) directions. The maximum Young's modulus of U₃O₈Th reaches 200 GPa, which is almost equal to that of UO₂, and the calculated results show that the formation of U–Th–O compound formed with the Th element doped in the U–O compound will not reduce Young's modulus for the fuel. Hence, we can conclude that the U–Th–O compound designed in this work behaves good mechanical behavior and isotropy of the mechanical property.

4. Conclusion

In this work, the thermodynamic stability and kinetic stability of U–Th–O ternary compounds were carried out to screen the promising new stable configurations. The calculation results of the density of states including total and partial parts indicated that obvious orbital hybridization emerges between the addition of Th and O atoms at −5 eV. The three-dimensional Young's modulus of the U–Th–O ternary compound demonstrates that the mechanical properties of the Th-doped compound remain highly isotropic, reaching around 200 GPa in all three directions. In the future work, we will focus on the changes in properties such as the thermal conductivity of the U–Th–O ternary compound, hoping to provide a data basis for the application of ternary U–Th–O fuel to the light water reactor.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge the financial support from the National Key Research and Development Program of China (no. 2019YFB1901003), National Natural Science Foundation of China (grant no. 21875271 and U20B2021), the Entrepreneurship Program of Foshan National Hi-tech Industrial Development Zone and Zhejiang Province Key Research and Development Program (no. 2019C01060), “Pioneer” and “Leading Goose” R&D Program of Zhejiang (grant no. 2022C01236), Leading Innovative and Entrepreneur Team Introduction Program of Zhejiang (grant no. 2019R01003), and Research Foundation for Talented Scholars of Zhejiang Ocean University (no. 11185091722).

References

1. J. Roleček, Š. Foral and K. Katovský, et al., A feasibility study of using CeO₂ as a surrogate material during the investigation of UO₂ thermal conductivity enhancement, Adv. Appl. Ceram., 2017, 116(3), 123–131.
2. T. Wiss, J.-P. Hiernaut and D. Roudil, et al., Evolution of spent nuclear fuel in dry storage conditions for millennia and beyond, J. Nucl. Mater., 2014, 451(1–3), 198–206.
3. S. J. Zinkle and G. Was, Materials challenges in nuclear energy, Acta Mater., 2013, 61(3), 735–758.
4. X. Chen, Y. Qin and D. Shi, et al., First-principles investigations on the anisotropic elasticity and thermodynamic properties of U₃Si₂–Al, RSC Adv., 2020, 10(58), 35049–35056.
5. X. Chen, Y. Qin and D. Shi, et al., Investigations of the stability and electronic structures of U₃Si₂–Al: A first-principles study, Chem. Phys., 2021, 543, 111088.
6. E. Wu, N. Qiu and K. Luo, et al., The studies of electronic structure, mechanical properties and ideal fracture behavior of U₃Si_1.75Al_0.25: first-principle investigations, J. Mater. Res. Technol., 2021, 15, 1356–1369.
7. D. R. Rittman, S. Park and C. L. Tracy, et al., Structure and bulk modulus of Ln-doped UO₂ (Ln = La, Nd) at high pressure, J. Nucl. Mater., 2017, 490, 28–33.
8. S. C. Finkeldei, J. Kiggans and R. D. Hunt, et al., Fabrication of UO₂-Mo composite fuel with enhanced thermal conductivity from sol-gel feedstock, J. Nucl. Mater., 2019, 520, 56–64.
9. L. Cheng, R. Gao and Q. Xu, et al., UO₂–Mo–Be composites for Accident Tolerant Fuel: SPS fabrication, microcracks-free in as-fabricated state and superior thermal conductivity, Ceram. Int., 2020, 46(18), 28939–28948.
10. M. Rahman, M. W. D. Cooper and B. Szpunar, et al., Primary radiation damage on displacement cascades in UO₂, ThO₂ and (U_0.5Th_0.5)O₂, Comput. Mater. Sci., 2018, 154, 508–516.
11. L. Evitts, M. Gilbert and S. Middleburgh, et al., Utilizing neutronics modelling to predict changing Pu ratios in UO₂ in the presence of Th, Prog. Nucl. Energy, 2021, 137, 103762.
12. D. Shi, Y. Guo and Y. Qin, et al., The mechanical and thermal properties of (Th, U)Si compounds: A systematic density functional theory research, Comput. Mater. Sci., 2021, 188, 110148.
13. A. Alemberti, K. Tuček and T. Obara, et al., Status of Generation-IV Lead Fast Reactor Activities, 2017.
14. J. S. Herring, P. E. Macdonald and K. D. Weaver, et al., Low cost, proliferation resistant, uranium–thorium dioxide fuels for light water reactors, Nucl. Eng. Des., 2001, 203(1), 65–85.
15. K. Rickert, T. A. Prusnick and E. Hunt, et al., Inhibiting laser oxidation of UO₂ via Th substitution, J. Nucl. Mater., 2019, 517, 254–262.
16. A. D. Becke, Density-functional thermochemistry I. The effect of the exchange-only gradient correction, J. Chem. Phys., 1992, 96(3), 2155–2160.
17. D. R. Kripalani, A. A. Kistanov and Y. Cai, et al., Strain engineering of antimonene by a first-principles study: mechanical and electronic properties, Phys. Rev. B, 2018, 98(8), 085410.
18. G. Kresse and D. Joubert, From ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59(3), 1758.
19. D. R. Kripalani, P.-P. Sun and P. Lin, et al., Strain-driven superplasticity of ultrathin tin (II) oxide films and the modulation of their electronic properties: a first-principles study, Phys. Rev. B, 2019, 100(21), 214112.
20. P. E. Blöchl, Projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50(24), 17953.
21. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77(18), 3865.
22. J. T. Pegg, X. Aparicio-Angles and M. Storr, et al., DFT + U study of the structures and properties of the actinide dioxides, J. Nucl. Mater., 2017, 492, 269–278.
23. B. Ao, R. Qiu and S.-X. Hu, Plutonium oxidation states in complex molecular solids, J. Phys. Chem. C, 2019, 123(19), 12096–12103.
24. E. Torres, I. Cheiknjifon and T. Kaloni, et al., A comparative analysis of the phonon properties in UO₂ using the Boltzmann transport equation coupled with DFT + U and empirical potentials, Comput. Mater. Sci., 2020, 177, 109594.
25. J. T. Pegg, A. E. Shields and M. T. Storr, et al., Magnetic structure of UO₂ and NpO₂ by first-principle methods, Phys. Chem. Chem. Phys., 2019, 21(2), 760–771.
26. E. Torres and T. Kaloni, Thermal conductivity and diffusion mechanisms of noble gases in uranium dioxide: a DFT + U study, J. Nucl. Mater., 2019, 521, 137–145.
27. H. J. Monkhorst and J. D. Pack, Special points for Brillouin-zone integrations, Phys. Rev. B: Solid State, 1976, 13(12), 5188.
28. B.-T. Wang, H. Shi and W.-D. Li, et al., First-principles study of ground-state properties and high pressure behavior of ThO₂, J. Nucl. Mater., 2010, 399(2–3), 181–188.
29. B. Frazer, G. Shirane and D. Cox, et al., Neutron-Diffraction Study of Antiferromagnetism in UO₂, Phys. Rev., 1965, 140(4A), A1448.
30. A. Padel and C. De Novion, Constantes elastiques des carbures, nitrures et oxydes d'uranium et de plutonium, J. Nucl. Mater., 1969, 33(1), 40–51.
31. M. Born, K. Huang and M. Lax, Dynamical theory of crystal lattices, Am. J. Phys., 1955, 23(7), 474.
32. D. Shi, J. Song and Z. Liu, et al., Defective structures in FeCrAl alloys from first principles calculations, Jpn. J. Appl. Phys., 2020, 59(4), 046003.

---