Open Access Article
Open Access ArticleTiO2/graphitic carbon nitride nanosheet composite with enhanced sensitivity to atmospheric water†
Tosapol Maluangnont *a,
Phieraya Pulpholb,
Satana Pongampaic,
Thawanrat Kobkeatthawind,
Siwaporn Meejoo Smith
*a,
Phieraya Pulpholb,
Satana Pongampaic,
Thawanrat Kobkeatthawind,
Siwaporn Meejoo Smith d and
Naratip Vittayakornc
d and
Naratip Vittayakornc
aElectroceramics Research Laboratory, College of Materials Innovation and Technology, King Mongkut's Institute of Technology Ladkrabang, Bangkok 10520, Thailand. E-mail: tosapol.ma@kmitl.ac.th
bDepartment of Materials Science, Faculty of Science, Srinakharinwirot University, Bangkok 10110, Thailand
cAdvanced Materials Research Unit and Department of Chemistry, School of Science, King Mongkut's Institute of Technology Ladkrabang, Bangkok 10520, Thailand
dCenter of Sustainable Energy and Green Materials and Department of Chemistry, Faculty of Science, Mahidol University, Nakhon Pathom 73170, Thailand
First published on 20th February 2023
Abstract
Understanding the fundamentals of transport properties in two-dimensional (2D) materials is essential for their applications in devices, sensors, and so on. Herein, we report the impedance spectroscopic study of carbon nitride nanosheets (CNNS) and the composite with anatase (TiO2/CNNS, 20 atom% Ti), including their interaction with atmospheric water. The samples were characterized by X-ray diffraction, N2 adsorption/desorption, solid state 1H nuclear magnetic resonance spectroscopy, thermogravimetric analysis, and transmission electron microscopy. It is found that CNNS is highly insulating (resistivity ρ ∼ 1010 Ω cm) and its impedance barely changes during a 20 min-measurement at room temperature and 70% relative humidity. Meanwhile, incorporating the semiconducting TiO2 nanoparticles (∼10 nm) reduces ρ by one order of magnitude, and the decreased ρ is proportional to the exposure time to atmospheric water. Sorbed water shows up at low frequency (<102 Hz) with relaxation time in milliseconds, but the response intrinsic to CNNS and TiO2/CNNS is evident at higher frequency (>104 Hz) with relaxation time in microseconds. These two signals apparently correlate to the endothermic peak at ≤110 °C and >250 °C, respectively, in differential scanning calorimetry experiments. Universal power law analysis suggests charge hopping across the 3D conduction pathways, consistent with the capacitance in picofarad typical of grain response. Our work demonstrates that the use of various formalisms (i.e., impedance, permittivity, conductivity, and modulus) combined with a simple universal power law analysis provides insights into water-induced transport of the TiO2/CNNS composite without complicated curve fitting procedure or dedicated humidity control.
Introduction
Graphitic carbon nitrides (g-C3N4) are defect-rich, polymeric aromatic layered materials consisting mainly of C and N atoms bonded in sp2 fashion. The parallel chains of tri-s-triazine units organize in layers with A–B stacking, together with a misalignment to decrease the repulsive π–π interactions.1 Moreover, stacks of graphitic layers can be separated into carbon nitride nanosheets (CNNS) by a facile thermal exfoliation.2 These nanosheets can be further modified by compositing with metals3,4 or metal oxides,5 leading to potential applications in photocatalysis,2,6,7 thermal catalysis,4 optical sensing,8 nanocomposites,9 to name but a few.While the electronics properties of g-C3N4-based materials are widely investigated, the fundamentals of their electrical properties are less well known, contrasting with closely related materials such as amorphous carbon10 or amorphous carbon nitride.11–13 The studies on g-C3N4 and/or CNNS focus on thin film devices14–20 including diode, double dielectric, metal–insulator–semiconductor, typically prepared by sophisticated vacuum techniques. It is known that the electrical conductivity of g-C3N4 along the basal plane (i.e. in plane) is approximately two orders of magnitude smaller than that through the stacked layers (out of plane).21 A few authors explored the properties of g-C3N4-based composites with metal oxides or polymers,22–25 where the tested specimens can be easily prepared by pelletizing the powder. It was found that the dielectric permittivity ε′ of g-C3N4 varies from 7 in thin film13,18 to ∼60 in bulk.23,24 Pareek and Quamara24 showed the decreasing ε′ with increasing TiO2 content in the TiO2/g-C3N4 composite, despite of the intrinsic dielectric nature of TiO2. Moreover, ε′ of BaTiO3/g-C3N4 composite is even lower than the individual components.23 Meanwhile, Liu et al.25 reported that the addition of g-C3N4 increased ε′ of the composite based on poly(vinylidene fluoride).
Specifically, TiO2/CNNS composite is widely studied for organic disinfection in water because the heterojunction tailors band structure and charge separation.2,26,27 In this regard, water adsorption on surface is an important microscopic process in e.g., photocatalysis, sensors, and separation membranes.28 The sensitivity to atmospheric water leads to such applications, but it also complicates fundamental understanding of charge transport. Examples of materials exhibiting proton conduction are layered double hydroxides,29 titanate nanowires/nanotubes,30,31 illitic clay,32 and TiO2.33,34 For g-C3N4, water dissociates at the defect site and forms a mixed adsorption structure including a hydroxy group.35 A single layer of CNNS is an indirect semiconductor with the calculated band gap energy of 1.15–2.72 eV.36 Upon water adsorption, the sheet becomes buckled, and the band gap is direct with the band gap energy increasing to 1.79–3.05 eV. The calculated adsorption energy36 is larger than that on graphene and comparable to that on metal oxides, suggesting favorable water adsorption. Such water-induced charge transport explains the use of g-C3N4- or CNNS-based devices for humidity detection,14,15,22,37,38 where the resistance/impedance, capacitance, optical transmitted power, current, etc., were measured at varying relative humidity. However, the scarcity of studies on water-induced electrical properties of the TiO2/CNNS composite contrasts with the known surface protonic conduction and surface–water interactions in TiO2 (ref. 33, 34 and 39) or g-C3N4 and CNNS.35,36
Impedance spectroscopy is an important tool to elucidate the nature of charge transport in materials ranging from ionic to insulator, from crystalline to amorphous, from organic to inorganic, and so on.40,41 The alternating current (AC) responses are described in four basic formalisms including complex impedance Z*, complex admittance Y* (or conductivity σ*), complex permittivity ε*, and complex electric modulus M*. In particular, the frequency dependence of σ* and ε* follows the universal power law proposed by Jonscher,42–44 which provide further insights into effective dimensionality of charge transport. Herein, we report the impedance study of TiO2/CNNS composite and CNNS, supplemented by the direct current–voltage (I–V) measurement, in a simple time-dependent experimental set up and sample pretreatments without the need for dedicated humidity control. The samples were characterized by X-ray diffraction (XRD), N2 adsorption/desorption, solid state 1H nuclear magnetic resonance spectroscopy (1H NMR), thermogravimetric analysis (TGA), differential scanning calorimetry (DSC), and transmission electron microscopy (TEM). Our work contributes to the understanding of fundamental AC electrical properties in TiO2/CNNS or CNNS, including those induced by atmospheric water, such as dielectric permittivity, effective dimensionality of charge carriers, and relaxation time.
Experimental
Synthesis
Bulk graphitic carbon nitride was prepared by a direct heating of urea powder (125 g) in an alumina crucible with a cover at 600 °C (heating rate 10 °C min−1) for 4 h.2 After cooling down to room temperature (RT), the pale-yellow product was collected and ground into powder. The nanosheets analog (carbon nitride nanosheets, CNNS) was produced by immersing the bulk powder (2.5 g) in 100 mL of HNO3 (65%) for 12 h. The obtained sample was filtered and washed with deionized water, and further heated at 500 °C for 4 h.To prepare the TiO2/CNNS composite, an amount of 1 g of TiOSO4 was stirred in 100 mL of deionized water for 15 min and sonicated for 20 min.2 Then, 4 g of CNNS (dispersed in water) was added into this solution. The slurry was further sonicated at RT for 30 min to obtain the homogeneous mixing. The solution was transferred to a Teflon-lined stainless-steel autoclave and heated at 180 °C for 4 h. The product was collected via centrifugation, washed with water, and dried at 65 °C for 24 h.
Characterization
XRD was performed using Cu Kα radiation at 2θ = 10°–60° (Bruker model D2 PHASER). The specific surface area SBET was measured via N2 adsorption/desorption using an Autosorb-1C instrument (Quantachrome) after degassing at 300 °C. 1H solid state NMR spectra were acquired using a JEOL 400YH operating at 400 MHz. TGA was performed under the flow of N2 gas (20 mL min−1) from RT to 800 °C (10 °C min−1) using a PerkinElmer, Pyris-1 instrument. DSC measurements were conducted using a Netzsch DSC 3500 instrument with the sample (≤10 mg) packed inside an Al crucible with pierced lid and an empty Al crucible as a reference, from RT to 400 °C using two heating rates (0.5 and 25 °C min−1). The morphology of the samples was characterized by transmission electron microscopy at 200 kV (JEOL, JEM 2010).Electrical properties measurements
An amount of ∼30 mg of TiO2/CNNS powder was pressed without a binder into a pellet with thickness of ∼0.15 mm and diameter of ∼0.5 mm (apparent density of 1.16 g cm−3). On the other hand, the CNNS pellet could be prepared only with at least ∼60 mg of the powder, leading to a thicker (∼0.3 mm) specimen with an apparent density of 1.04 g cm−3. For comparison, the theoretical density of g-C3N4 is 2.34 g cm−3, suggesting porosity in both specimens.The pellet was gold-sputtered on both sides to form electrical contacts. All measurements were conducted using a precision LCR meter (HP-4284A, Hewlett-Packard, Palo Alto, CA) covering the frequency f = 20 to 106 Hz. The data were collected under a typical laboratory atmosphere at 25 °C and the relative humidity of ∼70% following one or more of these pretreatments/conditions:
(i) “Dry”: the pellet was dried at 60 °C for 3 days prior to the immediate impedance measurement at RT. The sample removal from the oven to the start of the measurement typically took less than one minute.
(ii) “Air exposed”: the pellet was left under ambient for 2 days prior to the remeasurement at RT, and.
(iii) “400 °C”: the air exposed pellet was heated up from 25 to 400 °C (2 °C min−1), stabilized at 400 °C for 15 min, after which the sample impedance was recorded.
In all conditions, up to 8 cycles were repeated during a total time of 20 min. Note that we observed the artefact in our setup at ∼105 Hz which is removed from all frequency-dependent plots presented herein.
The direct current–voltage (I–V) characteristics was measured only under condition (i) using an LCR meter (Agilent, E4980A model) and a 0.5 V interval from −10 to 10 V.
Results and discussion
Sample characteristics
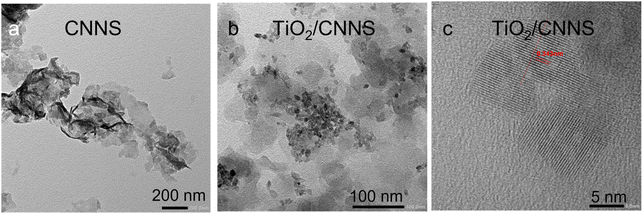
Fig. 1a shows the XRD patterns of the two samples. All are typical of g-C3N4 (JCPDS 87-1526) with two prominent peaks at ∼27.5° and 13.0° due to the stacking of the graphitic carbon nitride sheet and the constituting aromatic tri-s-triazine unit.1,2 The broad reflections indicate the small number of coherent length along the c-direction (i.e., thickness of the stacked sheets) due to the HNO3-assisted thermal exfoliation.2 The lack of any TiO2 reflections in the composite suggests that the metal oxide must be extremely small. Fig. 1b show the N2 adsorption/desorption isotherms of the samples. They are classified as type IV characteristics of monolayer adsorption and capillary condensation as evident by the hysteresis at P/P0 > 0.5.45 The specific surface SBET is similar at 118 m2 g−1 for CNNS, and 113 m2 g−1 for TiO2/CNNS. The 1H NMR spectra in Fig. 1c comprise of three signals at ∼10.9, 5.8–6.2, and 2.3–2.7 ppm. These chemical shifts are due to H attached to N atom (Hamine), H2O (HW), and H attached to C atom (Haliphatic), respectively.46,47 Accordingly, the presence of water in both samples is suggested spectroscopically.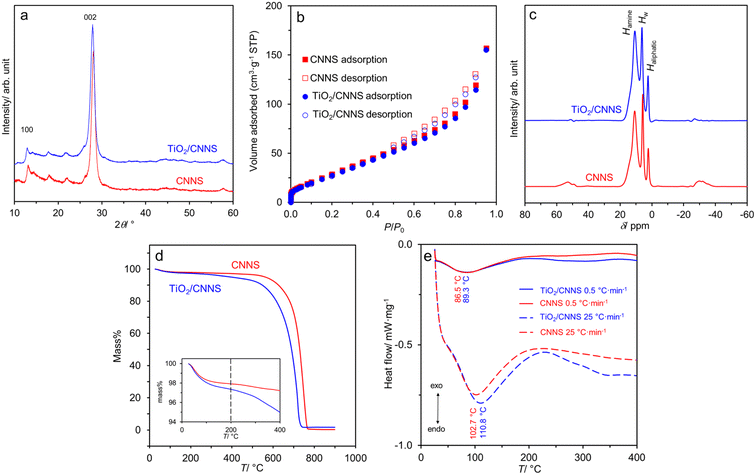 | ||
| Fig. 1 Some characteristics of CNNS and TiO2/CNNS composite: (a) XRD patterns, (b) N2 adsorption/desorption isotherms, (c) 1H NMR spectra, (d) mass loss curves, and (e) heat flow curves. | ||
In addition, Fig. 1d shows that the samples undergo a mass loss as soon as the temperature is raised, presumably due to the removal of loosely bound, physisorbed water. The loss at T < 200 °C (inset) translates to the water content of 2.1 and 2.7 wt% for CNNS and TiO2/CNNS, respectively. This finding hints at the enhanced hydrophilic nature of the composite. At T > 400 °C, a significant mass loss is observed in both samples, which limits the temperature for electrical properties investigation. Meanwhile, DSC in Fig. 1e shows endothermic peak at ∼87–89 °C (at the heating rate 0.5 °C min−1) or ∼103–111 °C (at the heating rate 25 °C min−1), ascribed to the removal of physisorbed water. Another broad, endothermic peak is at >250 °C in both samples which is independent of the heating rate. Notably, the heat flow (i.e., peak area) and peak temperature of TiO2/CNNS are consistently larger than those of CNNS, suggesting a stronger water–surface interaction in the former.
Lastly, morphology of the samples was examined by TEM. Thin sheets with faint contrast as typical with nanosheets are observed for CNNS in Fig. 2a. This feature is preserved in the TiO2/CNNS composite (Fig. 2b and c), which also contains particles of ∼10 nm on top. The lattice fringe of the nanoparticle corresponding to 0.34 nm agrees with the (101) plane of anatase-type TiO2. Formation of the (101) facet of TiO2 on g-C3N4 has been frequently observed.48,49 This is because the (101) facet has the lower surface energy (0.44 J m−2) than other surfaces, such as the (001) with the surface energy of 0.90 J m−2.50 An energy dispersive X-ray analysis (Fig. S1†) indicates 20 atom% Ti in the composite.
Impedance and direct current measurements
The complex impedance Z* is described by| Z* = Z′ + iZ″ | (1) |
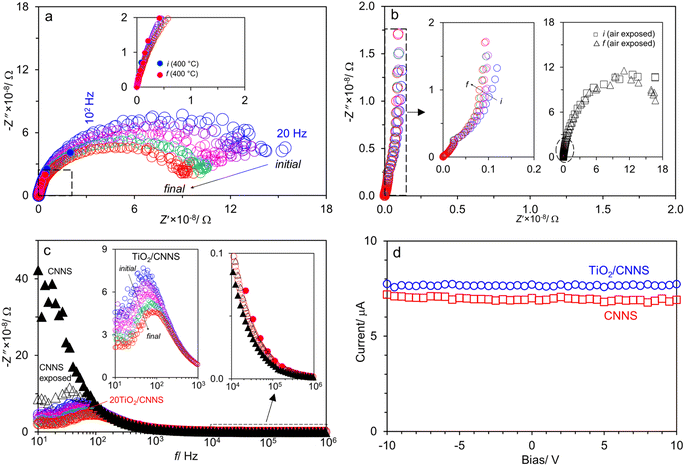
Fig. 3b shows that the Nyquist plots of CNNS appear almost as a straight line, indicating that it is highly insulating which is consistent with others.15,18,22,33 Unlike TiO2/CNNS, CNNS shows relatively constant impedance which just slightly moves throughout 20 min (left inset of Fig. 3b), suggesting that CNNS is not as sensitive to atmospheric water as TiO2/CNNS (the direct comparison of impedance in absolute value is not straightforward, however, because the CNNS pellet is thicker).
In another experiment, the CNNS sample was left under ambient for 2 days for exposure to atmospheric water prior to the impedance measurements. The “air exposed” sample now shows a clear semicircle (right inset of Fig. 3b) which remains constant throughout the 20 min-measurement. Meanwhile, the data at high f (left circle on the right inset of Fig. 3b) overlap with those from the dry CNNS. Accordingly, air exposure for a few days (instead of merely 20 min) sufficiently generates water-induced charge carriers in CNNS, thereby decreasing its impedance.
Fig. 3c shows the spectroscopic plots −Z″(f) at the final repetition. In all cases, there is a broad and asymmetric peak with varies in the maximum impedance 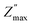 and the frequency fmax especially on the low frequency side. Otherwise, the data at high f are very similar (see the right inset of Fig. 3c). This finding indicates that the response due to adsorbed water (or water–surface interaction) dominates at low f, while that of materials dominates at high f. Specifically,
and the frequency fmax especially on the low frequency side. Otherwise, the data at high f are very similar (see the right inset of Fig. 3c). This finding indicates that the response due to adsorbed water (or water–surface interaction) dominates at low f, while that of materials dominates at high f. Specifically, 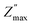 of TiO2/CNNS systematically shifts to the higher f and shows the lower
of TiO2/CNNS systematically shifts to the higher f and shows the lower 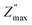 with increasing repetition. The magnitude of
with increasing repetition. The magnitude of 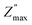 in the order CNNS > CNNS (air exposed) > TiO2/CNNS is inversely proportional to the extent of water-induced conduction.
in the order CNNS > CNNS (air exposed) > TiO2/CNNS is inversely proportional to the extent of water-induced conduction.
The resistance R (Ω) and resistivity ρ (Ω cm) can be calculated from 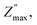 following eqn (2):
following eqn (2):
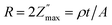 | (2) |
| Sample | Pretreatment or condition | ρ/Ω cm [RLF/GΩ] | CLF/pF | CMF/pF | CHF/pF | τLF/ms | τMF/µs | τHF/µs |
|---|---|---|---|---|---|---|---|---|
a ρ and R calculated from −Z″, C calculated from the M′ vs. M″ plot. The relaxation time before comma is τ(tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ), and that after comma is τ(Z″).b The subscript LF, MF, and HF refer to low-, medium-, and high-frequency, respectively.c The symbol — means not detected. δ), and that after comma is τ(Z″).b The subscript LF, MF, and HF refer to low-, medium-, and high-frequency, respectively.c The symbol — means not detected. |
||||||||
| CNNS | Initial, RT | 7.7 × 109 [9.8] | — | 5.30 | 4.19 | —, 6.9 | 78.4, — | 9.7, — |
| Final, RT | 7.7 × 109 [9.8] | — | 5.81 | 4.12 | —, 13.8 | 59.4, — | 8.4, — | |
| Initial, RT (air exposed) | 1.7 × 109 [2.2] | 3.28 | — | 4.53 | 10.5, 5.2 | —, — | 4.8, — | |
| Final, RT (air exposed) | 1.8 × 109 [2.3] | 3.28 | — | 4.50 | 10.5, 4.5 | —, — | 4.2, — | |
| TiO2/CNNS | Initial, RT | 1.9 × 109 [1.5] | 2.29 | —c | 4.05 | 13.1, 3.3 | —, — | 8.7, — |
| Final, RT | 1.1 × 109 [0.9] | 2.31 | — | 4.02 | 10.8, 2.3 | —, — | 7.9, — | |
| Initial, 400 °C | — | — | — | — | —, — | —, — | 1.4, — | |
| Final, 400 °C | — | — | — | — | —, — | —, — | 1.4, — | |
Fig. 3d compares the I–V plots performed right after the pellet was removed from the oven. Considering that the measurement was quickly accomplished in 5 min, we assume that the interference by atmospheric water is minimal. The two samples display a relatively constant direct current I over the bias from −10 to 10 V. It is found that I is 7.66(4) µA for TiO2/CNNS, and 6.95(9) µA for CNNS, where the number in parenthesis is the standard deviation to the last digit. Using geometrical surface area of each specimen, the current density is 34.7(2) µA cm−2 for TiO2/CNNS and 32.7(4) µA cm−2 for CNNS. Recently, Urakami et al.16,17 reported the direct current on the order of pA (in plane) vs. µA (out of plane) in g-C3N4 thin films. It was explained that carriers are confined around the N atom for the in-plane direction, leading to low conductivity in the pA range. In contrast, delocalized hopping occurs more easily along stacks of sheets, leading to a higher current on the µA range for the out of plane direction.17,21 The electrical properties reported herein for TiO2/CNNS and CNNS pellets are likely dominated by conduction across the plane, because the graphitic layers were uniaxially pressed to be parallel to others prior to gold sputtering on the opposite faces of the pellet.
Dielectric properties, conductivity, and electric modulus
The complex dielectric permittivity ε* [eqn (3)] can be calculated from Z′ and −Z″ following eqn (4) and (5)| ε* = ε′ + iε″ | (3) |
| ε′ = (t/ωAε0)[Z″/(Z′2 + Z″2)] | (4) |
| ε″ = (t/ωAε0)[Z′/(Z′2 + Z″2)] | (5) |
Fig. 4a compares ε′ at the end of the 20 min-measurement, showing two parts. Firstly, ε′ very strongly decreases with increasing f (<80 Hz). It is known that water shows high ε′ at low f (5 × 105 at ∼80 Hz) which rapidly decreases with increasing f (79 at 106 Hz).52 Accordingly, the dielectric response at low f is attributed to sorbed water interacting with the surface, presumably in combination with electrode polarization. This may be correlated to the dominating peak of −Z″(f) in Fig. 3c. Secondly, the variation of ε′ becomes modest up to 106 Hz and this could be characteristics of water-free materials. The decrease of ε′ with increasing f in both regions is expected (see, e.g., ref. 42, 53 and 54) because dipoles cannot effectively reorient themselves with the increasing alternating field.
 | ||
Fig. 4 The frequency dependence of (a) ε′, (b) tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ, (c) δ, (c)  and (d) the complex plane plot of the electric modulus M′ vs. M″, all taken from the final repetition of the 20 min-measurement. The lines in (c) are fit to the Bfs term in eqn (7). The inset in (c) shows and (d) the complex plane plot of the electric modulus M′ vs. M″, all taken from the final repetition of the 20 min-measurement. The lines in (c) are fit to the Bfs term in eqn (7). The inset in (c) shows  at low f for TiO2/CNNS from the initial to final measurements. at low f for TiO2/CNNS from the initial to final measurements. | ||
At f = 106 Hz, ε′ for CNNS, TiO2/CNNS (both at RT) and TiO2/CNNS (400 °C) is practically similar at 10–15, which are smaller than that of the air exposed, water-sorbed CNNS (21). These values might be compared to ε′ of 7–8 in graphitic carbon nitride thin films.13,18 Accordingly, TiO2 promotes only the rate of water uptake, but does not contribute to magnitude of ε′, especially when the atmospheric water uptake is already saturated (i.e., at 20 min). The similar ε′ without or with added TiO2 was earlier reported in TiO2/g-C3N4 (ref. 24) and BaTiO3/g-C3N4 (ref. 23) composites. This finding was earlier explained by the altered band gap which affects the electronic polarization and consequently ε′.23,24 Additionally, ε′ of the TiO2/CNNS composite at 400 °C (filled circles in Fig. 3a) is smaller than that at RT (open circles) due to the lack of water-induced charge carriers. The data at RT and 400 °C overlap only at f > 105 Hz, indicating that the water–surface interaction persists even at 400 °C.
Fig. 4b shows that tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ (=ε″/ε′) decreases with increasing f as is common.42,53,54 At low f, the loss tangent is up to 4 for TiO2/CNNS, and 2 for air exposed CNNS. Otherwise, tan
δ (=ε″/ε′) decreases with increasing f as is common.42,53,54 At low f, the loss tangent is up to 4 for TiO2/CNNS, and 2 for air exposed CNNS. Otherwise, tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ is ∼0.2 at higher f, which is comparable to carbon nitride films on Si by Konofaos et al.13 The high tan
δ is ∼0.2 at higher f, which is comparable to carbon nitride films on Si by Konofaos et al.13 The high tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ at low f indicates that they behave more like a conductor than a dielectric, while the rapid increase at low f suggests the onset of direct current conduction.41 It is postulated that water sorption leads to a conducting hydrolyzed entity on each grain, forming macroscopic dipoles which interact strongly with each other. On the other hand, CNNS exhibit low tan
δ at low f indicates that they behave more like a conductor than a dielectric, while the rapid increase at low f suggests the onset of direct current conduction.41 It is postulated that water sorption leads to a conducting hydrolyzed entity on each grain, forming macroscopic dipoles which interact strongly with each other. On the other hand, CNNS exhibit low tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ throughout because it is less hydrophilic than TiO2/CNNS.
δ throughout because it is less hydrophilic than TiO2/CNNS.
We calculated the AC conductivity 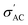 (i.e., the real part of complex admittance) using eqn (6) and the results are shown in Fig. 4c:
(i.e., the real part of complex admittance) using eqn (6) and the results are shown in Fig. 4c:
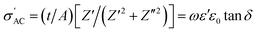 | (6) |
It is found that σ′ is relatively constant at low f, but increases at high f. This behavior is typical of the phenomenal universal power law as proposed by Jonscher, ascribed to interacting charges/dipoles:42–44
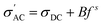 | (7) |
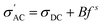 [eqn (7)]
[eqn (7)]
| Sample | Pretreatment or condition | σDC/S cm−1 | B | s |
|---|---|---|---|---|
| CNNS | Initial, RT | Not observed | 7.2 × 10−12 | 0.80 |
| Final, RT | Not observed | 4.2 × 10−12 | 0.86 | |
| Initial, RT (air exposed) | 9.9 × 10−10 | 2.0 × 10−11 | 0.79 | |
| Final, RT (air exposed) | 9.9 × 10−10 | 3.9 × 10−11 | 0.73 | |
| TiO2/CNNS | Initial, RT | 6.0 × 10−10 | 1.3 × 10−11 | 0.76 |
| Final, RT | 1.0 × 10−9 | 2.0 × 10−11 | 0.73 | |
| Initial, 400 °C | Not observed | 1.6 × 10−11 | 0.65 | |
| Final, 400 °C | Not observed | 1.1 × 10−11 | 0.68 |
Next, we have calculated the complex electric modulus M* which is the inverse of the complex dielectric permittivity with the real part M′ and imaginary part M″ as follows:
| M* = (1/ε*) = M′ + iM″ | (8) |
| M′ = ε′/(ε′2 + ε″2) | (9) |
| M″ = ε″/(ε′2+ ε″2) | (10) |
Fig. 4d shows the complex plane plots of M′–M″ analogous to the Nyquist plots of the impedance. (We deliberately show the unequal x- and y-axis to clearly depict the semicircle.) Two semicircles are evident which contrast with the single semicircle in the Z′ vs. Z″ plots. Meanwhile, the electric modulus is dominated by electrical components of the smallest capacitance where the maximum value on the y-axis 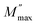 relates to the capacitance C by eqn (11)
relates to the capacitance C by eqn (11)
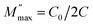 | (11) |
The calculated capacitance is also shown in Table 1. The CLF, CMF, and CHF correspond to the calculated capacitance at low, middle, and high frequency, respectively. It is found that C varies very slightly (2.3–4.5 pF) despite of the difference in frequency. The capacitances are independent of pretreatment or measurement temperature, and in the order of 10−12 F typical of the grain response.40 The result suggests that adsorbed water covering the grain is bulk-like (but not as the thin/grain boundary-like layer) and consistent with the 3D conduction as deduced from the exponent s of eqn (7) discussed above.
Relaxation time
A relaxation peak is apparent in the frequency-dependent Z″ (Fig. 3c) and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ (Fig. 4b), enabling the calculation of the relaxation time τ as:
δ (Fig. 4b), enabling the calculation of the relaxation time τ as:| τ = 1/(2πfmax) | (12) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ) as also summarized in Table 1. The τ(tan
δ) as also summarized in Table 1. The τ(tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ) is typically larger than τ(Z″), consistent with the theoretical explanation.41
δ) is typically larger than τ(Z″), consistent with the theoretical explanation.41
It is found that τ does not vary appreciably among different samples. At the low-frequency (LF, f < 80 Hz), τLF is ∼2–14 ms. While power law analysis indicates a local 3D-hopping, the millisecond-range τ is typical of the relaxation of surface water57 as opposed to femtoseconds for bulk water.58 Two other relaxations are observed at middle-frequency (MF, ∼103 Hz; τMF = 59–78 µs) and high-frequency (HF, ∼104 Hz; τHF = 1–9 µs). It is reasonable assuming that they are characteristics of TiO2/CNNS or CNNS with a minor contribution from adsorbed water. The relaxation time on the µs scale has been reported (or can be deduced) in a closely related amorphous carbon10 or carbon nitride12,13 thin films. The two types of relaxation at LF and MF/HF could be linked to the low- and high-temperature endothermic peak in DSC, respectively. The direct comparison between the f-scan experiment and T-scan experiment is not straightforward, however.
Charge conduction pathway
We consider four pathways28 of water-induced charge transport as schematically depicted in Fig. 5 for TiO2/CNNS. Firstly, the transport at the bulk (I) should be minimal (due to the highly insulating nature15,18,22,33) and concentrated mostly in the direction perpendicular to the sheet (i.e., out of plane)16,17,21 as discussed in the I–V results. On the other hand, the transport along the grain boundary (II) and on the open pores surfaces (III) is possible considering that the samples were simply pressed into pellet, leaving residual porosities. We propose that the adsorbed water in this region is bulk-like, as deduced from the exponent s typical of 3D conduction.55,56 Lastly, charges could be enriched right below the pore/material interface (IV) presumably as a surface layer. If so, this corresponds to τLF in milliseconds typical of surface water,57 as deduced from the relaxation peak in Fig. 3c and 4b.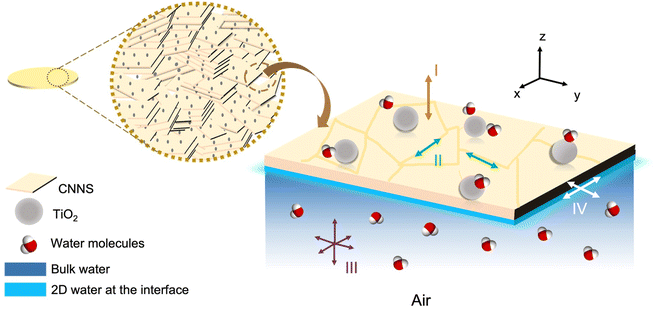 | ||
| Fig. 5 Schematic diagram of proton conduction in TiO2/CNNS, depicting four charge transport pathways (I to IV). | ||
The protonic conduction of TiO2 is well known, leading to its application as a humidity sensor.33,34,39 Water molecules accumulated on the surface into different layers which are chemisorbed, ice-like, liquid-like, etc.33 Among different facets, proton conduction on (101) of anatase33 has a low activation enthalpy because water is loosely bound, as compared to that on (001) and (100) with higher activation enthalpy. As suggested from the time-dependent Nyquist plots of TiO2/CNNS (Fig. 3a), it is likely that water is preliminarily adsorbed first on the (101) facet of TiO2 nanoparticles which are distributed throughout the composite. The adsorbed water (or proton) then transports to other parts, thereby demonstrating the increased sensitivity to water, presumably via the synergistic effect of TiO2.
Conclusions
(1) The TiO2/CNNS composite shows decreasing Z′ (and increasing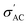 ) with repetition across the 20 min-measurement at RT and 70% RH, indicating the increased sensitivity to atmospheric water. Simultaneously, −Z″ and tan
) with repetition across the 20 min-measurement at RT and 70% RH, indicating the increased sensitivity to atmospheric water. Simultaneously, −Z″ and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ show a peak with increasing f (i.e., a decreasing τ). Altogether, proton conduction due to water adsorption and dissociation can be inferred. On the other hand, these signals are not observed at 400 °C and consistent with water loss at elevated temperature deduced from TGA and DSC.
δ show a peak with increasing f (i.e., a decreasing τ). Altogether, proton conduction due to water adsorption and dissociation can be inferred. On the other hand, these signals are not observed at 400 °C and consistent with water loss at elevated temperature deduced from TGA and DSC.
(2) CNNS is highly insulating, but it allows detectable proton conduction given sufficient equilibration to atmospheric water as demonstrated for air exposed CNNS. The ε′ of CNNS and TiO2/CNNS (at 106 Hz) of ∼10–15 is reasonably close to 7 in the previously reported thin film.
(3) The universal power law fitting of 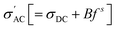 suggests the 3D hopping of charges (i.e., proton conduction), likely reflecting the transport along the grain boundary and the open pores surfaces. Meanwhile, two ranges of the relaxation times are deduced from the frequency dependence of −Z″ and tan
suggests the 3D hopping of charges (i.e., proton conduction), likely reflecting the transport along the grain boundary and the open pores surfaces. Meanwhile, two ranges of the relaxation times are deduced from the frequency dependence of −Z″ and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ. The first is τLF (ms) ascribed to surface water presumably accumulated right below the pore/material interface. The next is τMF and τHF (both in µs) ascribed to water-free materials.
δ. The first is τLF (ms) ascribed to surface water presumably accumulated right below the pore/material interface. The next is τMF and τHF (both in µs) ascribed to water-free materials.
Author contributions
Tosapol Maluangnont: conceptualization; writing, review, and editing; funding acquisition; and project administration. Phieraya Pulphol, Satana Pongampai, and Thawanrat Kobkeatthawin: investigation. Siwaporn Meejoo Smith and Naratip Vittayakorn: supervision. All authors have reviewed and approved of the manuscript.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This work is supported by King Mongkut’s Institute of Technology Ladkrabang (2565-02-09-003). The work of N. Vittayakorn is funded by KMITL under Grant No. 2565-02-05-025 and KREF116501; of S. Pongampai by KMITL under Grant No. KREF146411; of S. M. Smith and T. Kobkeatthawin by Mahidol University (Basic Research Fund: fiscal year 2022) under Grant No. BRF1-046/2565. We thank Mahidol University-Frontier Research Facility (MU-FRF) for instrument support, and the MU-FRF scientists, Nawapol Udpuay and Suwilai Chaveanghong, for their assistance in XRD measurements. We also acknowledge the facilities and technical assistance from Nanotechnology and Materials Analytical Instrument Service Unit (NMIS) of College of Materials Innovation and Technology, KMITL.References
- F. Fina, S. K. Callear, G. M. Carins and J. T. S. Irvine, Structural investigation of graphitic carbon nitride via XRD and neutron diffraction, Chem. Mater., 2015, 27, 2612–2618 CrossRef CAS.
- T. Kobkeatthawin, J. Trakulmututa, T. Amornsakchai, P. Kajitvichyanukul and S. M. Smith, Identification of active species in photodegradation of aqueous imidacloprid over g-C3N4/TiO2 Nanocomposites, Catalysts, 2022, 12, 120 CrossRef CAS.
- X. Wang, X. Chen, A. Thomas, X. Fu and M. Antonietti, Metal‐containing carbon nitride compounds: a new functional organic–metal hybrid material, Adv. Mater., 2009, 21, 1609–1612 CrossRef CAS.
- Z. Chen, S. Mitchell, E. Vorobyeva, R. K. Leary, R. Hauert, T. Furnival, Q. M. Ramasse, J. M. Thomas, P. A. Midgley and D. Dontsova, et al., Stabilization of single metal atoms on graphitic carbon nitride, Adv. Funct. Mater., 2017, 27, 1605785 CrossRef.
- R. Mohini and N. Lakshminarasimhan, Coupled semiconductor nanocomposite g-C3N4/TiO2 with enhanced visible light photocatalytic activity, Mater. Res. Bull., 2016, 76, 370–375 CrossRef CAS.
- X. Wang, S. Blechert and M. Antonietti, Polymeric graphitic carbon nitride for heterogeneous photocatalytsis, ACS Catal., 2012, 2, 1596–1606 CrossRef CAS.
- D. J. Martin, K. Qiu, S. A. Shevlin, A. D. Handoko, X. Chen, Z. Guo and J. Tang, Highly efficient photocatalytic H2 evolution from water using visible light and structure-controlled graphitic carbon nitride, Angew. Chem., Int. Ed., 2014, 53, 9240–9245 CrossRef CAS PubMed.
- Y. Dong, Q. Wang, H. Wu, Y. Chen, C.-H. Lu, Y. Chi and H.-H. Yang, Graphitic carbon nitride materials: sensing, imaging and therapy, Small, 2016, 12, 5376–5393 CrossRef CAS PubMed.
- S. K. Gaddam, R. Pothu and R. Boddula, Graphitic carbon nitride (g-C3N4) reinforced polymer nanocomposite systems—a review, Polym. Compos., 2020, 41, 430–442 CrossRef CAS.
- N. Konofaos, C. T. Angelis, E. K. Evangelou, C. A. Dimitriadis and S. Logothetidis, Charge carrier response time in sputtered a-C/n-Si heterojunctions, Appl. Phys. Lett., 2001, 79, 2381–2383 CrossRef CAS.
- C. Godet, J. P. Kleider and A. S. Gudovskikh, Frequency scaling of ac hopping transport in amorphous carbon nitride, Diamond Relat. Mater., 2007, 16, 1799–1805 CrossRef CAS.
- J. P. Kleider, A. S. Gudovskikh and C. Godet, DC and AC hopping transport in metal/amorphous carbon nitride/metal devices, J. Non-Cryst. Solids, 2006, 352, 1323–1326 CrossRef CAS.
- N. Konofaos, E. K. Evangelou, S. Logothetidis and M. Gioti, Electrical properties of carbon nitride films on silicon, J. Appl. Phys., 2002, 91, 9915–9918 CrossRef CAS.
- L. M. Zambov, C. Popov, M. F. Plass, A. Bock, M. Jelinek, J. Lancok, K. Masseli and W. Kulisch, Capacitance humidity sensor with carbon nitride detecting element, Appl. Phys. A, 2000, 70, 603–606 CrossRef CAS.
- Z. Zhang, J. Huang, Q. Yuan and B. Dong, Intercalated graphitic carbon nitride: a fascinating two-dimensional nanomaterial for an ultra-sensitive humidity nanosensor, Nanoscale, 2014, 6, 9250–9256 RSC.
- N. Urakami, K. Ogihara, H. Futamura, K. Takashima and Y. Hashimoto, Demonstration of electronic devices in graphitic carbon nitride crystalline film, AIP Adv., 2021, 11, 075204 CrossRef CAS.
- K. Takashima, N. Urakami and Y. Hashimoto, Electronic transport and device application of crystalline graphitic carbon nitride film, Mater. Lett., 2020, 281, 128600 CrossRef CAS.
- P. C. Patra and Y. N. Mohapatra, Dielectric constant of thin film graphitic carbon nitride (g-C3N4) and double dielectric Al2O3/g-C3N4, Appl. Phys. Lett., 2021, 118, 103501 CrossRef CAS.
- P. C. Patra and Y. N. Mohapatra, Graphitic carbon nitride (g-C3N4)/Al2O3 heterostructure as double dielectric: a comparative study in MIS based on a-IGZO, IEEE J. Electron Devices Soc., 2021, 9, 618–622 CAS.
- M. Aono and S. Nitta, High resistivity and low dielectric constant amorphous carbon nitride films: application to low-k materials for ULSI, Diamond Relat. Mater., 2002, 11, 1219–1222 CrossRef CAS.
- Y. Noda, C. Merschjann, J. Tarábek, P. Amsalem, N. Koch and M. J. Bojdys, Directional charge transport in layered two-dimensional triazine-based graphitic carbon nitride, Angew. Chem., Int. Ed., 2019, 58, 9394–9398 CrossRef CAS PubMed.
- X. Guo, D. Kuang, Z. Zhu, Y. Ding, L. Ge, Z. Wu, B. Du, C. Liang, G. Meng and Y. He, Humidity sensing by graphitic carbon nitride nanosheet/TiO2 nanoparticle/Ti3C2Tx nanosheet composites for monitoring respiration and evaluating the waxing of fruits, ACS Appl. Nano. Mater., 2021, 4, 11159–11167 CrossRef CAS.
- S. Pareek, M. Sharma, S. Lai and J. K. Quamara, Polymeric graphitic carbon nitride-barium titanate nanocomposites with different content ratios: a comparative investigation on dielectric and optical properties, J. Mater. Sci.: Mater. Electron., 2018, 29, 13043–13051 CrossRef CAS.
- S. Pareek and J. K. Quamara, Dielectric and optical properties of graphitic carbon nitride-titanium dioxide nanocomposite with enhanced charge separation, J. Mater. Sci., 2018, 53, 604–612 CrossRef CAS.
- S. Liu, T. Ye, Y. Liu, H. Cheng and X. Liu, Graphitic-carbon nitride nanosheets as a new inorganic filler for improving energy storage density of PVDF-based dielectric composites, J. Mater. Sci.: Mater. Electron., 2020, 31, 13063–13069 CrossRef CAS.
- R. Ratshiedana, A. T. Kuvarega and A. K. Mishra, Titanium dioxide and graphitic carbon nitride-based nanocomposites and nanofibers for the degradation of organic pollutants in water: a review, Environ. Sci. Pollut. Res., 2021, 28, 10357–10374 CrossRef CAS PubMed.
- Y. Xiao, S. Guo, G. Tian, B. Jiang, Z. Ren, C. Tian, W. Li and H. Fu, Synergistic enhancement of surface reactions and charge separation over holey C3N4/TiO2 2D heterojunctions, Sci. Bull., 2021, 66, 275–283 CrossRef CAS PubMed.
- Y. Meng, J. Gao, Z. Zhao, J. Amoroso, J. Tong and K. S. Brinkman, Review: recent progress in low-temperature proton-conducting ceramics, J. Mater. Sci., 2019, 54, 9291–9312 CrossRef CAS.
- V. Bugris, H. Haspel, Á. Kukovecz, Z. Kónya, M. Sipiczki, P. Sipos and I. Pálinkó, Water types and their relaxation behavior in partially rehydrated CaFe-mixed binary oxide obtained from CaFe-layered double hydroxide in the 155–298 K temperature range, Langmuir, 2013, 29, 13315–13321 CrossRef CAS PubMed.
- H. Haspel, V. Bugris and Á. Kukovecz, Water sorption induced dielectric changes in titanate nanowires, J. Phys. Chem. C, 2013, 117, 16686–16697 CrossRef CAS.
- W. Hu, L. Li, W. Tong and G. Li, Water-titanate intercalated nanotubes: Fabrication, polarization, and giant dielectric property, Phys. Chem. Chem. Phys., 2010, 12, 12638–12646 RSC.
- Š. Csáki, J. Ondruška, V. Trnovcová, I. Štubňa, P. Dobroň and L. Vozár, Temperature dependence of the AC conductivity of illitic clay, Appl. Clay Sci., 2018, 157, 19–23 CrossRef.
- X. Kang, A. Chatzitakis, T. Aarholt, X. Sun, C. Negri and T. Norby, Facet-engineered TiO2 nanomaterials reveal the role of water-oxide interactions in surface protonic conduction, J. Mater. Chem. A, 2022, 10, 218–227 RSC.
- G. Garcia-Belmonte, V. Kytin, T. Dittrich and J. Bisquert, Effect of humidity on the ac conductivity of nanoporous TiO2, J. Appl. Phys., 2003, 94, 5261–5264 CrossRef CAS.
- H.-Z. Wu, L.-M. Liu and S.-J. Zhao, The role of the defect on the adsorption and dissociation of water on graphitic carbon nitride, Appl. Surf. Sci., 2015, 358, 363–369 CrossRef CAS.
- H.-Z. Wu, L.-M. Liu and S.-J. Zhao, The effect of water on the structural, electronic and photocatalytic properties of graphitic carbon nitride, Phys. Chem. Chem. Phys., 2014, 16, 3299–3304 RSC.
- W. Meng, S. Wu, X. Wang and D. Zhang, High-sensitivity resistive humidity sensor based on graphitic carbon nitride nanosheets and its application, Sens. Actuators, B, 2020, 315, 128058 CrossRef CAS.
- Z. Yan, C. Wang, R. Yu, Z. Hu and L. Xiao, Graphitic carbon nitride for enhancing humidity sensing of microfibers, J. Lightwave Technol., 2021, 39, 3896–3902 CAS.
- Y.-C. Yeh, T.-Y. Tseng and D.-A. Chang, Electrical properties of porous titania ceramic humidity sensors, J. Am. Ceram. Soc., 1989, 72, 1472–1475 CrossRef CAS.
- J. T. S. Irvine, D. C. Sinclair and A. R. West, Electroceramics: characterization by impedance spectroscopy, Adv. Mater., 1990, 2, 132–138 CrossRef CAS.
- R. Gerhardt, Impedance and dielectric spectroscopy revisited: distinguishing localized relaxation from long-range conductivity, J. Phys. Chem. Solids, 1994, 55, 1491–1506 CrossRef CAS.
- S. Sriphan, P. Pulphol, T. Charoonsuk, T. Maluangnont and N. Vittayakorn, Effect of adsorbed water and temperature on the universal power law behavior of lepidocrocite-type alkali titanate ceramics, J. Phys. Chem. C, 2021, 125, 12910–12920 CrossRef CAS.
- A. K. Jonscher, Dielectric relaxation in solids, J. Phys. D: Appl. Phys., 1999, 32, R57–R70 CrossRef CAS.
- A. K. Jonscher, The 'universal' dielectric response, Nature, 1977, 267, 673–679 CrossRef CAS.
- M. D. Donohue and G. L. Aranovich, Classification of Gibbs adsorption isotherms, Adv. Colloid Interface Sci., 1988, 76–77, 137–152 Search PubMed.
- P. Zhang, Y. Tong, Y. Liu, J. J. M. Vequizo, H. Sun, C. Yang, A. Yamakata, F. Fan, W. Lin and X. Wang, et al., Heteroatom dopants promote two-electron O2 reduction for photocatalytic production of H2O2 on polymeric carbon nitride, Angew. Chem., Int. Ed., 2020, 59, 16209–16217 CrossRef CAS PubMed.
- W. Li, Z. Guo, L. Jiang, L. Zhong, G. Li, J. Zhang, K. Fan, S. Gonzalez-Cortes, K. Jin and C. Xu, et al., Facile in situ reductive synthesis of both nitrogen deficient and protonated g-C3N4 nanosheets for the synergistic enhancement of visible-light H2 evolution, Chem. Sci., 2020, 11, 2716–2728 RSC.
- R. Guo, D. Zeng, Y. Xie, Y. Ling, D. Zhou, L. Jiang, W. Jiao, J. Zhao and S. Li, Carbon nitride quantum dots (CNQDs)/TiO2 nanoparticle heterojunction photocatalysts for enhanced ultraviolet-visible-light-driven bisphenol a degradation and H2 production, Int. J. Hydrogen Energy, 2020, 45, 22534–22544 CrossRef CAS.
- D. Vidyasagar, A. Balapure, S. G. Ghugal, A. G. Shende and S. S. Umare, Template-free macro-mesoporous TiO2/carbon nitride interface for visible-light-driven photocatalysis, Phys. Status Solidi A, 2019, 216, 1900212 CrossRef CAS.
- M. Lazzeri, A. Vittadini and A. Selloni, Structure and energetics of stoichiometric TiO2 anatase surfaces, Phys. Rev. B, 2001, 63, 155409 CrossRef.
- B. Zhu, B. Cheng, L. Zhang and J. Yu, Review on DFT calculation of s-triazine-based carbon nitride, Carbon Energy, 2019, 1, 32–56 CrossRef CAS.
- K. Gelin, A. Bodin, P. Gatenholm, A. Mihranya, K. Edwards and M. Strømme, Characterization of water in bacterial cellulose using dielectric spectroscopy and electron microscopy, Polymer, 2007, 48, 7623–7631 CrossRef CAS.
- T. Charoonsuk, S. Sriphan, P. Pulphol, W. Vittayakorn, N. Vittayakorn and T. Maluangnont, AC conductivity and dielectric properties of lepidocrocite-type alkali titanate tunable by interlayer cation and intralayer metal, Inorg. Chem., 2020, 59, 15813–15823 CrossRef CAS PubMed.
- T. Maluangnont, S. Sriphan, T. Charoonsuk and N. Vittayakorn, Dielectric spectroscopy and electric modulus analyses of Ti0.8O2 nanosheets-Ag nanoparticles-cellulose filter paper composites, Integr. Ferroelectr., 2022, 224, 214–224 CrossRef CAS.
- J. C. Dyre, P. Maass, B. Roling and D. L. Sidebottom, Fundamental questions relating to ion conduction in disordered solids, Rep. Prog. Phys., 2009, 72, 046501 CrossRef.
- D. L. Sidebottom, Dimensionality dependence of the conductivity dispersion in ionic materials, Phys. Rev. Lett., 1999, 83, 983–986 CrossRef CAS.
- M. Liu, J. K. Beattie and A. Gray-Weale, The surface relaxation of water, J. Phys. Chem. B, 2012, 116, 8981–8988 CrossRef CAS PubMed.
- S. T. van der Post, C.-S. Hsieh, M. Okuno, Y. Nagata, H. J. Bakker, M. Bonn and J. Hunger, Strong frequency dependence of vibrational relaxation in bulk and surface water reveals sub-picosecond structural heterogeneity, Nat. Commun., 2015, 6, 8384 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ra00045a |
| This journal is © The Royal Society of Chemistry 2023 |