Open Access Article
Open Access ArticleA reliable QSPR model for predicting drug release rate from metal–organic frameworks: a simple and robust drug delivery approach†
Leila Tayebi,
Rahmatollah Rahimi ,
Ali Reza Akbarzadeh
,
Ali Reza Akbarzadeh * and
Ali Maleki
* and
Ali Maleki
Department of Chemistry, Iran University of Science and Technology, P. O. Box: 16846-13114, Tehran, Islamic Republic of Iran. E-mail: a_akbarzadeh@iust.ac.ir
First published on 17th August 2023
Abstract
During the drug release process, the drug is transferred from the starting point in the drug delivery system to the surface, and then to the release medium. Metal–organic frameworks (MOFs) potentially have unique features to be utilized as promising carriers for drug delivery, due to their suitable pore size, high surface area, and structural flexibility. The loading and release of various therapeutic drugs through the MOFs are effectively accomplished due to their tunable inorganic clusters and organic ligands. Since the drug release rate percentage (RES%) is a significant concern, a quantitative structure–property relationship (QSPR) method was applied to achieve an accurate model predicting the drug release rate from MOFs. Structure-based descriptors, including the number of nitrogen and oxygen atoms, along with two other adjusted descriptors, were applied for obtaining the best multilinear regression (BMLR) model. Drug release rates from 67 MOFs were applied to provide a precise model. The coefficients of determination (R2) for the training and test sets obtained were both 0.9999. The root mean square error for prediction (RMSEP) of the RES% values for the training and test sets were 0.006 and 0.005, respectively. To examine the precision of the model, external validation was performed through a set of new observations, which demonstrated that the model works to a satisfactory degree.
1. Introduction
Cancer is one of the major diseases affecting human health, and morbidity has increased gradually.1 Although the remedies for cancer have progressed and survival rates have increased in recent years, the heterogeneity of cancer necessitates further effective treatment strategies.2 Cancer involves uncontrolled cell division and tissue invasion (metastasis) caused by a series of mutations in the genes of proteins that regulate the cell cycle.3 These mutations typically involve either promotion of cell division or the inactivation of cell cycle suppression.4 With our changing daily lifestyle and social environment, noncommunicable diseases have become the leading cause of death.5 Cancer is caused by significant changes in and damage to genes,6 which may be accidental or via exposure to carcinogens. A carcinogen includes chemical substances, such as arsenic and asbestos,7,8 or environmental, viral, or genetic factors.9 Cancer risk factors are classified into four main classes: (a) biological factors, such as age, gender, and genetic diseases; (b) carcinogen exposure, for instance, to radioactive radiation, many chemicals, and some particulate materials; and (c) lifestyle-related factors such as tobacco, alcohol, and exposure to UV radiation in sunlight.10Ways to treat cancer include surgery, chemotherapy, radiation therapy, targeted therapy, immunotherapy, stem cell or bone marrow transplant, and hormone therapy.11 Generally, cancer drugs destroy the RNA or DNA responsible for replication in cell division; therefore, the cancer cells are unable to divide and die.12 Chemotherapy drugs kill cancer cells by stopping them from growing and multiplying.13 If the cells can't grow and multiply, they usually die. Some chemotherapy drugs target a specific stage of the cell cycle.14 The fluoropyrimidine 5-fluorouracil (5-FU) is an effective antimetabolite drug that is widely used for the treatment of cancer, especially colorectal cancer. The action of 5-FU is through the inhibition of thymidylate synthase (TS) and incorporation of its metabolites into RNA and DNA.15
Unfortunately, chemotherapeutic drugs in free formation always lead to adverse effects on healthy tissues and even the immune system. Nanocarriers have been intensively engineered as stimuli-responsive drug delivery systems to load and intelligently release various drug molecules. To achieve superior efficacy, the drugs need to be loaded into nanocarriers with high loading content and released at the target site in a controllable and specific-responsive manner.16 Further, various nanoparticle-based systems have been studied for drug delivery, such as liposomes, micelles, dendrimers, microbubbles, and solid particles.17 Due to their suitable pore size and diverse functional groups, as well as great loading of drugs, metal–organic frameworks (MOFs) are potentially beneficial to encapsulate drug products.18 Furthermore, MOFs show several outstanding advantages, such as facile modification of physical and chemical properties through inorganic clusters and/or organic ligands.19
The quantitative structure–activity relationship (QSAR) model is a regression model in which the relationship between chemical structure and biological action is quantitatively investigated.20 The basis of QSAR methods is the dependence on action and structure.21 Quantitative dependence on action and structure is one of the most fundamental methods of intra-computer study for biological and chemical modeling, especially in drug design, drug targeting, and drug discovery.22 The quantitative structure–property relationship (QSPR) method applies structural features of molecules to create an accurate and fast model that correlates structure-based properties of materials to their quantitative functions. Generally, there are two common categories for QSPR models, based on the type of descriptors used in modeling: theory- and experiment-based modeling. To build a theory-based QSPR model, various molecular descriptors, such as geometric, quantum mechanical, and thermodynamic quantities are used, and experiment-based QSPR models are mainly presented using experimental descriptors that express the physicochemical properties related to the structure of molecules.23 QSPR investigations on drug release from hydroxypropyl methylcellulose compounds have been conducted using structural descriptors; these have confirmed that the aqueous solubility of drugs and the size of the drug molecules are appropriate descriptors that can influence drug release from these polymers.24 Also, penetration enhancement activities of some compounds towards different drugs have been investigated, employing a QSPR study.25 This QSPR technique was developed using the molecular descriptors created by the COSMIC force field and the molecular mechanical descriptors by the NEMESIS software; which helps to better understand the mechanisms of penetration enhancement.25 A prediction of the volume of distribution has been created by Ghafourian et al. using some structural descriptors, including partitioning, quantum mechanical, molecular mechanical, and connectivity parameters.26 Selection of the proper variable was made using a genetic algorithm, and stepwise regression analyses and many models were created for acidic and basic drugs. Furthermore, QSPR analysis of many MOFs has been developed by researchers to correlate their structural features and their physical, chemical, and biological properties.27–29 To develop a QSPR/QSAR model, several mathematical methods have been applied. Multiple linear regression (MLR), partial least squares (PLS), principal component analysis (PCA), and artificial neural network (ANN) are four commonly used methods.23
In this research, based on structural variables—such as ligand fragments and metal secondary building units (SBUs)—as the adjusted parameters, we obtained the most appropriate drug release model from MOFs through the QSPR method, which was performed using 5-FU drug release. The presented procedure here investigated the relationships between the release of drugs from a large class of MOFs and their structures. This work indicates a simple computational method for the rapid calculation of drug release from MOF drug delivery systems with suitable results. Considering that 5-FU is widely used for cancer treatment, the model was specifically created for this drug. One of the challenges we face in modeling drug release from drug delivery systems is that the desired software is not available to everyone. In addition, the determination of quantum descriptors is a complex process. The advantage of the presented work is that (a) the model is performed without special software, and (b) modeling is carried out using simple and knowledge-based descriptors.
2. Materials and methods
The studied dataset of MOFs containing different metal SBUs and various organic linkers, as drug delivery systems, was collected from different scientific research studies. The experimental data of the drug release rate of different MOFs were gathered and tested for the delivery of 5-fluorouracil (5-FU) in several cancer cell lines. Drug delivery data for 5-FU were collected because 5-FU has a small size and is widely used as an anticancer chemotherapy drug for the treatment of several cancers. The measured drug release rate is expressed as a percentage (RES%). The RES% for 67 metal–organic frameworks were collected from the literature. Table 1 lists the MOFs together with the experimental RES% for 5-FU collected from the literature. The best multilinear regression (BMLR) model was created using a set of 54 MOFs as a training set (80% of all data), which was then applied to 13 MOFs as a test set (20% of all data) to evaluate the predictive ability of the model. External validation is a validation strategy to ensure that the BMLR model is accurate for the prediction of dependent variables, using external data that was not used to develop the model. After the regression model has been obtained from the original dataset, the new data points investigate the model's validity. Hereupon, eight observations were used to form the external test set. The molecular structures of organic linkers for the training and test sets are illustrated in Table S1 (ESI).†| No. | MOF | nN | nO | RES+ | RES− | Exp. RES%a | IM–L | Ref. | Pred. RES%b | Dev.c | Std. dev.d | L.B. 95%e | U.B. 95%f |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a Exp. RES%: experimental value of RES%.b Pred. RES%: predicted value of RES%.c Dev.: deviation.d Std. dev.: standard deviation.e L.B.: lower bound.f U.B.: upper bound. | |||||||||||||
| Training set (54 entries) | |||||||||||||
| 1 | NTU-Z11 | 0.00 | 16.00 | 1.377 | 2.550 | 64.00 | −5.91 | 32 | 28.991 | 0.009 | −0.026 | 63.991 | 64.009 |
| 2 | CPON-1 | 1.00 | 5.00 | −0.220 | 2.811 | 25.00 | −3.27 | 33 | 23.994 | 0.006 | 0.556 | 24.989 | 25.006 |
| 3 | [(CH3)2NH2]2[Zn(TATAT)2/3]·3DMF | 9.00 | 12.00 | −7.698 | 4.739 | 44.00 | −9.95 | 34 | 51.994 | 0.006 | 1.055 | 43.987 | 44.004 |
| 4 | fa-IRMOF3 | 3.00 | 13.00 | −2.189 | 3.300 | 45.00 | −5.09 | 35 | 14.999 | 0.001 | 2.116 | 44.983 | 45.000 |
| 5 | [(Me2NH2)4Zn2(FDC)4]n | 4.00 | 20.00 | −5.491 | 3.664 | 29.00 | −7.70 | 36 | 25.993 | 0.007 | −1.934 | 29.000 | 29.017 |
| 6 | [Zn3(BTC)2(Me)(H2O)2](MeOH)13 | 0.00 | 33.00 | −4.982 | 2.627 | 18.00 | −9.95 | 37 | 31.003 | −0.003 | 0.149 | 17.991 | 18.008 |
| 7 | [Zn3(bdcNH2)2(dfp)2]·DMF | 4.00 | 12.00 | 0.227 | 3.712 | 89.00 | −13.05 | 38 | 51.999 | 0.001 | −1.332 | 88.997 | 89.015 |
| 8 | NH2(CH3)2[Zn3(L)2·3.5DMF] | 0.00 | 16.00 | −0.596 | 4.440 | 22.00 | −9.60 | 39 | 42.999 | 0.001 | 1.293 | 21.986 | 22.003 |
| 9 | IRMC-1 | 12.00 | 1.00 | −5.553 | 5.521 | 85.00 | −7.27 | 40 | 11.993 | 0.007 | −0.200 | 84.991 | 85.010 |
| 10 | [Zn2(ad)2(hmdb)(H2O)](DMF)2 | 15.00 | 12.00 | −17.118 | 2.995 | 13.00 | −19.86 | 41 | 19.992 | 0.008 | −0.216 | 12.992 | 13.010 |
| 11 | [Zn(FDC)]·H2O | 0.00 | 5.00 | 1.375 | 2.624 | 34.00 | −1.09 | 42 | 51.999 | 0.001 | −1.981 | 34.000 | 34.017 |
| 12 | [Zn(BTC)(HME)]·(DMAc)(H2O) | 7.00 | 8.00 | −6.494 | 3.260 | 31.00 | −8.48 | 43 | 22.996 | 0.004 | 1.757 | 30.984 | 31.001 |
| 13 | [Zn2(ad)2(fmdb)(H2O)](DMF)3 | 10.00 | 15.00 | −11.880 | 4.244 | 11.00 | −14.79 | 44 | 23.991 | 0.009 | −0.969 | 10.995 | 11.013 |
| 14 | [Zn3(OH)2(H2tccp)2(bpy)2](H2O)3(DMF)3 | 6.00 | 18.00 | −6.142 | 5.810 | 29.00 | −14.22 | 45 | 63.998 | 0.002 | 0.412 | 28.989 | 29.007 |
| 15 | [Zn8(O)2(CDDB)6(DMF)4(H2O)] | 10.00 | 31.00 | −13.260 | 3.020 | 43.00 | −17.87 | 46 | 45.991 | 0.009 | −2.038 | 43.000 | 43.017 |
| 16 | [Zn2(ad)2(AMDB)(H2O)](DMF)3 | 17.00 | 10.00 | −18.100 | 3.533 | 20.00 | −20.87 | 47 | 47.995 | 0.005 | 0.245 | 19.990 | 20.008 |
| 17 | [Zn2(bptc)(H2O)]·(DMAc)3(H2O)4 | 3.00 | 16.00 | −4.027 | 3.400 | 26.00 | −7.02 | 48 | 9.998 | 0.002 | −0.741 | 25.995 | 26.012 |
| 18 | [Zn(4,4-bipy)(formic acid)2(NO3)2] | 1.00 | 4.00 | −0.836 | 2.334 | 17.00 | −8.83 | 49 | 56.199 | 0.001 | 0.266 | 16.990 | 17.008 |
| 19 | ([Zn4O(dmcapz)3] | 6.00 | 7.00 | −2.396 | 5.965 | 52.00 | −5.40 | 50 | 39.991 | 0.009 | 0.540 | 51.989 | 52.007 |
| 20 | [Zn7L2(HL)2(OH–)4(H2O)2]·2H2O | 4.00 | 40.00 | −10.174 | 3.465 | 17.00 | −12.62 | 51 | 83.997 | 0.003 | −0.433 | 16.993 | 17.011 |
| 21 | [Zn2(fer)2] | 0.00 | 8.00 | 0.449 | 1.088 | 40.00 | −8.23 | 52 | 95.001 | −0.001 | −0.697 | 39.994 | 40.012 |
| 22 | [Zn2(abtc)(DMA)(H2O)2]·(DMA)4 | 3.00 | 11.00 | −1.637 | 4.194 | 41.00 | −9.12 | 53 | 78.991 | 0.009 | −0.070 | 40.992 | 41.009 |
| 23 | [(Me2NH2)2Zn3(fdc)4]n·DMA | 2.00 | 20.00 | −0.153 | 3.664 | 75.00 | −5.35 | 54 | 28.991 | 0.009 | −0.378 | 74.993 | 75.010 |
| 24 | ZIF-NP | 5.00 | 4.00 | −2.293 | 1.896 | 60.00 | −4.65 | 55 | 23.994 | 0.006 | 0.907 | 59.987 | 60.005 |
| 25 | ZIF-90 | 2.00 | 0.00 | 0.552 | 2.375 | 41.00 | −7.57 | 56 | 51.994 | 0.006 | −0.218 | 40.992 | 41.010 |
| 26 | Cu-BTC | 0.00 | 12.00 | 1.356 | 2.550 | 53.00 | −13.30 | 57 | 14.999 | 0.001 | −0.151 | 52.992 | 53.009 |
| 27 | [Cu(L)(4,4′-bipy)(H2O)]n·1.5nCH3CN | 3.50 | 5.00 | −3.353 | 3.235 | 15.00 | −26.65 | 58 | 25.993 | 0.007 | −1.176 | 14.996 | 15.014 |
| 28 | [(Cu2(L2)(H2O)2]·2.22DMA | 3.22 | 12.20 | −3.335 | 4.095 | 24.00 | −19.77 | 59 | 31.003 | −0.003 | 0.473 | 23.989 | 24.007 |
| 29 | GDMU-2 | 0.00 | 14.00 | −0.794 | 5.100 | 9.00 | −20.12 | 60 | 51.999 | 0.001 | 1.042 | 8.987 | 9.004 |
| 30 | [Cu(BTTA)]n | 6.00 | 4.00 | −4.745 | 5.334 | 15.00 | −6.93 | 61 | 42.999 | 0.001 | 0.446 | 14.989 | 15.007 |
| 31 | [NH2(CH3)][Cu6(L)3(OAc)(H2O)4]·xsolvent | 10.00 | 30.00 | −13.703 | 5.211 | 18.00 | −28.52 | 62 | 11.993 | 0.007 | −0.953 | 17.995 | 18.013 |
| 32 | [H3O][Cu6(tpta)3(DMA)4(COO)]·12H2O·7DMA | 4.00 | 30.00 | −7.078 | 3.400 | 35.00 | −26.73 | 63 | 19.992 | 0.008 | 1.097 | 34.987 | 35.004 |
| 33 | [Cu2(OH)bcb](DMF)2(H2O)3 | 0.00 | 9.00 | 0.993 | 4.028 | 29.00 | −20.22 | 64 | 51.999 | 0.001 | 1.010 | 28.987 | 29.004 |
| 34 | [Dy(BTC)(H2O)]·(H2O)(DMF) | 0.00 | 6.00 | 0.450 | 2.550 | 24.00 | −9.85 | 65 | 22.996 | 0.004 | 0.174 | 23.991 | 24.008 |
| 35 | [Dy(HABA)(ABA)](DMA)4] | 27.00 | 6.00 | −26.397 | 2.198 | 52.00 | −67.28 | 66 | 23.991 | 0.009 | 0.657 | 51.987 | 52.007 |
| 36 | [Gd(BCB)(DMF)](H2O)2 | 1.00 | 10.00 | −1.050 | 4.386 | 15.00 | −47.01 | 67 | 63.998 | 0.002 | −1.063 | 14.996 | 15.013 |
| 37 | [Gd2(H2O)3(SDBA)3](DMA)3] | 3.00 | 15.00 | −3.987 | 3.114 | 26.00 | −48.84 | 68 | 45.991 | 0.009 | 0.422 | 25.990 | 26.007 |
| 38 | [In(Hpbic)(pbic)](DMF)2 | 6.00 | 4.00 | −4.715 | 3.200 | 31.00 | −15.35 | 69 | 47.995 | 0.005 | −1.747 | 30.999 | 31.016 |
| 39 | [Co(SDB)(bpdh)0.5]n | 2.00 | 6.00 | 2.064 | 6.027 | 52.00 | −19.06 | 70 | 9.998 | 0.002 | −0.637 | 51.994 | 52.012 |
| 40 | [Ca3(TATAB)2(H2O)(MeOH)](DMF)3 | 12.00 | 14.00 | −12.910 | 1.630 | 43.00 | −18.70 | 71 | 56.199 | 0.001 | −0.814 | 42.995 | 43.012 |
| 41 | Mg(H2TBAPy)(H2O)3·C4H8O2 | 0.00 | 13.00 | −1.265 | 3.400 | 12.00 | −9.40 | 72 | 39.991 | 0.009 | 0.258 | 11.990 | 12.008 |
| 42 | [Co2(L)(4,4′-Bipy)2]·CH3CN | 6.00 | 10.00 | −5.475 | 5.418 | 20.00 | −13.87 | 73 | 83.997 | 0.003 | 0.620 | 19.989 | 20.006 |
| 43 | [Sr(HTATB)(H2O)2](DMF)4 | 3.00 | 7.00 | −0.290 | 3.860 | 52.00 | −9.77 | 74 | 95.001 | −0.001 | −0.585 | 51.994 | 52.011 |
| 44 | [Ba(HTATB)(H2O)2](DMF)4 | 7.00 | 12.00 | −7.495 | 3.860 | 23.00 | −15.84 | 75 | 78.991 | 0.009 | −0.162 | 22.992 | 23.009 |
| 45 | MIL-100 (Fe) | 0.00 | 24.00 | −2.918 | 2.550 | 24.00 | −7.88 | 76 | 28.991 | 0.009 | 0.988 | 23.987 | 24.005 |
| 46 | UiO-66 | 0.00 | 20.00 | 0.195 | 1.700 | 64.00 | −7.78 | 77 | 23.994 | 0.006 | −0.289 | 63.992 | 64.010 |
| 47 | MIL-101-NH2-Fe | 4.00 | 16.00 | −4.873 | 1.082 | 46.00 | −10.54 | 78 | 51.994 | 0.006 | 1.168 | 45.986 | 46.004 |
| 48 | MIL-88B | 0.00 | 24.00 | −0.211 | 4.564 | 48.00 | −7.44 | 79 | 14.999 | 0.001 | 0.237 | 47.990 | 48.008 |
| 49 | UiO-66-COOH | 1.00 | 4.00 | −1.025 | 2.922 | 10.00 | −6.36 | 80 | 25.993 | 0.007 | −0.932 | 9.995 | 10.013 |
| 50 | CP5-capped UiO-66-NH-Q | 7.00 | 62.00 | −14.774 | 3.377 | 56.20 | −20.31 | 81 | 31.003 | −0.003 | −0.442 | 56.192 | 56.212 |
| 51 | MOF-In1 | 0.00 | 20.00 | −0.646 | 3.342 | 40.00 | −8.55 | 82 | 51.999 | 0.001 | 1.074 | 39.987 | 40.004 |
| 52 | Mn-ZIF-90 | 4.00 | 2.00 | 1.068 | 2.380 | 84.00 | −2.09 | 83 | 42.999 | 0.001 | 0.036 | 83.991 | 84.009 |
| 53 | UiO-67-(NH2)2 | 12.00 | 32.00 | −13.236 | 0.464 | 95.00 | −20.00 | 84 | 11.993 | 0.007 | −0.570 | 94.993 | 95.012 |
| 54 | DCA-UiO-DTDP-FA | 14.00 | 36.00 | −17.144 | 0.622 | 79.00 | −22.83 | 85 | 19.992 | 0.008 | 1.759 | 78.983 | 79.002 |
| RMSEP | 0.006 | ||||||||||||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||||||||
| Test set (13 entries) | |||||||||||||
| 55 | [Zn3(μ3-O)(BTC)2(DMF)]·2NH2(CH3)2·4H2O | 3.00 | 18.00 | −3.087 | 2.550 | 51.00 | −10.32 | 32 | 50.999 | 0.001 | −0.559 | 50.993 | 51.011 |
| 56 | [Zn(bptc)(H2O)]·(DMA)4 | 4.00 | 13.00 | −4.317 | 3.400 | 29.00 | −10.09 | 86 | 28.991 | 0.009 | 1.206 | 28.986 | 29.005 |
| 57 | [Zn2(L)(H2O)1.5]·5H2O | 1.00 | 9.50 | −0.476 | 4.095 | 24.00 | −7.09 | 87 | 23.995 | 0.005 | 0.405 | 23.988 | 24.009 |
| 58 | [Zn3(bdc)2(dfp)2]·2DMF | 2.00 | 12.00 | 0.844 | 4.330 | 63.00 | −13.64 | 38 | 62.996 | 0.004 | 0.236 | 62.988 | 63.010 |
| 59 | [Zn(H2O)6K2(H2BTC)2(H2O)4](H2BTC)2·2H2O | 0.00 | 36.00 | −3.904 | 2.550 | 42.00 | −8.06 | 88 | 41.993 | 0.007 | 0.819 | 41.986 | 42.008 |
| 60 | ZIF-8 | 5.00 | 4.00 | −3.831 | 1.896 | 38.00 | −6.19 | 89 | 37.998 | 0.002 | −0.325 | 37.991 | 38.011 |
| 61 | [(Zn2(L1)(DMA)]·1.75DMA | 3.75 | 10.75 | −3.975 | 4.095 | 19.00 | −7.04 | 59 | 18.998 | 0.002 | −0.830 | 18.993 | 19.013 |
| 62 | ZIF-90 | 2.00 | 0.00 | 0.482 | 2.375 | 40.00 | −7.64 | 90 | 39.996 | 0.004 | 0.744 | 39.988 | 40.007 |
| 63 | [Zn10(OH)O(BTC)5(HBTC)(DMA)2(H2O)4]·11DMA | 13.00 | 55.00 | −21.242 | 2.550 | 42.00 | −27.15 | 91 | 41.991 | 0.009 | −0.330 | 41.989 | 42.013 |
| 64 | [Dy2(L)2(H2O)2]n | 0.00 | 14.00 | 0.912 | 2.550 | 52.00 | −10.18 | 92 | 51.999 | 0.001 | −0.058 | 51.991 | 52.010 |
| 65 | FA-MOF-808 | 0.00 | 12.00 | 0.797 | 2.550 | 45.00 | −5.48 | 93 | 45.005 | −0.005 | −1.695 | 44.997 | 45.016 |
| 66 | FA-NH2-UiO-66 | 4.00 | 20.00 | −5.901 | 1.082 | 42.00 | −13.01 | 93 | 41.994 | 0.006 | 0.877 | 41.987 | 42.007 |
| 67 | MIL-88B | 0.00 | 20.00 | −2.743 | 1.700 | 22.00 | −38.24 | 94 | 21.999 | 0.001 | −0.492 | 21.991 | 22.012 |
| RMSEP | 0.0052 | ||||||||||||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||||||||
| External validation test set (8 entries) | |||||||||||||
| 68 | Zn6(L)3(DMA)4]·5DMA | 9.00 | 33.00 | −10.35 | 3.400 | 72.00 | −13.61 | 95 | 71.998 | 0.002 | −0.931 | 71.986 | 72.022 |
| 69 | [Zn3(BTC)2(Aml)(H2O)2](MeOH)6 | 6.00 | 14.00 | −7.12 | 2.296 | 30.00 | −12.12 | 96 | 29.997 | 0.003 | −0.519 | 29.985 | 30.019 |
| 70 | [[Dy2(H2O)3(SDBA)3](DMA)6] | 0.00 | 21.00 | −1.72 | 3.114 | 29.00 | −12.00 | 97 | 28.990 | 0.010 | 0.551 | 28.980 | 29.015 |
| 71 | [Gd2(TATAB)2]·6DMF | 12.00 | 12.00 | −11.28 | 1.630 | 61.00 | −49.29 | 98 | 60.997 | 0.003 | 0.090 | 60.982 | 61.017 |
| 72 | [Mg3(H2O)4(5-aip)2(5-Haip)2]·4DMA | 8.00 | 24.00 | −9.00 | 1.082 | 69.00 | −13.89 | 99 | 68.991 | 0.009 | 0.869 | 68.979 | 69.014 |
| 73 | [Ca3(TATB)2(H2O)](DMF)4(H2O) | 6.00 | 13.00 | −2.78 | 3.860 | 78.00 | −12.06 | 100 | 77.994 | 0.006 | 0.671 | 77.979 | 78.015 |
| 74 | NanoHKUST-1 | 0.00 | 12.00 | 2.06 | 2.550 | 63.00 | −3.65 | 101 | 62.996 | 0.004 | −0.167 | 62.985 | 63.017 |
| 75 | Fe-MIL-53-NH2 | 1.00 | 4.00 | 2.37 | 1.082 | 72.00 | −3.70 | 102 | 71.999 | 0.001 | −0.565 | 71.985 | 72.020 |
| RMSEP | 0.0054 | ||||||||||||
The statistical coefficients, R2 (coefficient of determination) and Radj2 (the adjusted R-squared), were calculated as follows (eqn (1) and (2)):
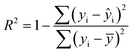 | (1) |
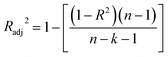 | (2) |
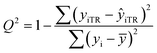 | (3) |
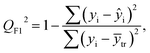 | (4) |
 | (5) |
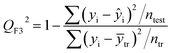 | (6) |
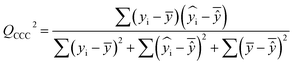 | (7) |
After the BMLR model has been developed with the original dataset, the new observations (the new set of compounds) investigate the model's validity by computing Q(Ext)2, Q(Ext)F12, Q(Ext)F22, Q(Ext)F32, and Q(Ext)CCC2.
3. Results and discussion
A reliable correlation for the prediction of drug release rate from MOFs containing different metal SBUs and various organic linkers was obtained in this research. The QSPR modeling for the abovementioned dataset was performed using SPSS software (version: 1.0.0.1406). The number of nitrogen and oxygen atoms, as well as the two adjustable parameters, comprise four variables employed to build the correlation by multiple linear regression model (eqn (8)). These descriptors were created based on our knowledge of chemistry, without using the software. The mentioned descriptors are knowledge-based and obtained through advanced inorganic chemistry theories with tedious work. The descriptors were selected in such a way that, on the one hand, they are related to the chemical structure of the MOF, and on the other hand, they can have a reasonable impact on the drug release rate (RES%). Several descriptors were examined for this purpose, and finally, these four descriptors were selected, which created the maximum R2 and minimum RMSE; also, they do not have a high correlation coefficient with each other.| RES% = 20.135 + 15.157nN + 2.675nO − 7.300RES− + 14.296RES+ | (8) |
According to our previous works,30,31 to estimate the important properties of materials, simple group-contribution methods can be employed, and the values of RES− were determined based on this technique. This study found a reliable contribution between various particular molecular fragments of the linker and the drug release rate from MOFs, RES%. Table 2 lists different RES− values; these values have been determined for several molecular fragments of linkers, which are the result of the core correlation. In Table 2, for the substituents containing nitrogen or oxygen attached to one or more rings, the ring symbol is used for simplicity.
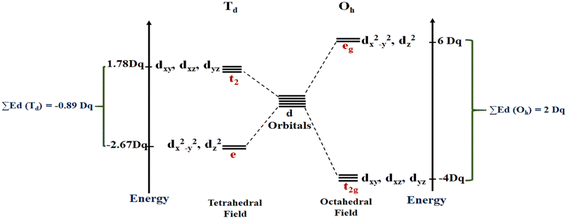
As mentioned above, RES+ represents one of the descriptors that increase the RES%. It is obtained from eqn (9) and consists of two parts: RESM and IM–L. The RESM results from eqn (10) and is calculated by considering the molecular weight of MOF and the atomic mass of oxygen and nitrogen, as well as the impact of d-orbitals of the metal center. IM–L describes the interaction between the d-orbitals of the metal center and the valence orbitals of heteroatoms of linkers. The IM–L value resulted from our experimental inorganic chemistry knowledge and can be applied to a variety of interactions. Fig. 1 represents the molecular orbital diagram resulting from the interaction of metal d-orbitals and the heteroatoms of linkers for an octahedral geometry of SBU, as an example.
| RES+ = RESM + IM–L | (9) |
| RESM = [(MOFMw)/(nOmO + nNmN)] × ∑Ed(SBU) | (10) |
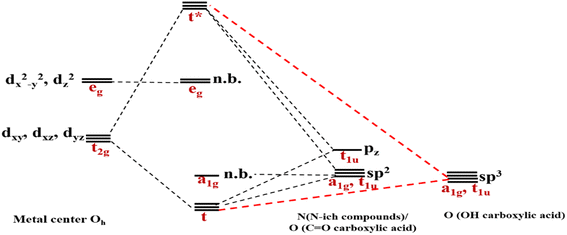 | ||
| Fig. 1 Molecular orbital diagram indicating the interaction of metal d-orbitals and the heteroatoms of linkers. | ||
The energies of the d-orbitals for the metal center are considered through the Krishnamurthy and Schaap findings.103 Hence, the relative energies of d orbitals in crystal fields of different metal center geometries were calculated based on Krishnamurthy and Schaap's approach (Table 3).
| Coordination number | Metal center configuration | Relative energy of d-orbitals in units of Dq | ||||
|---|---|---|---|---|---|---|
| dz2 | dx2–y2 | dxy | dxz | dyz | ||
| 1 | ML (z) | 5.14 | −3.14 | −3.14 | 0.57 | 0.57 |
| 2 | ML2 (XY) | −2.41 | 6.14 | 1.14 | −2.57 | −2.57 |
| 4 | ML4 (Td) | −2.67 | −2.67 | 1.78 | 1.78 | 1.78 |
In other words, first, RESM is calculated by considering the total energies of d-orbitals of metal SBUs using Krishnamurthy and Schaap's approach, then the corresponding interaction between metal and linker heteroatom (IM–L value) is added to the result in the RES+. The values of RES+ and IM–L for the training and test sets are listed in Table 1.
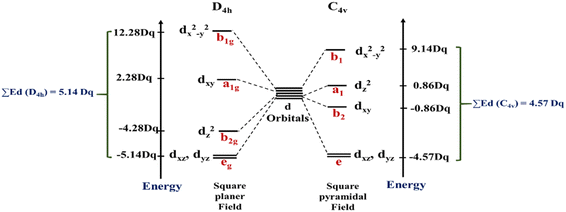
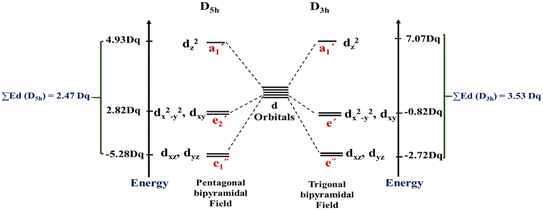
In this work, the geometries of the metal centers (SBUs) of MOFs were diverse, including octahedral, trigonal bipyramid, tetrahedral, square planar, square pyramidal, pentagonal bipyramid, square antiprism, and triangular dodecahedral. If the metal center is six-coordinated in octahedral coordination geometry, the d orbitals split into two sets, as shown in Table 4, first row. According to Table 3, the field for ML6 will be ML6 (Oh) = 2ML2(XY) + 2ML(Z), and the total energies of the d-orbitals for octahedral geometry are obtained as ∑Ed(Oh) = 2 Dq. The d-orbitals of the metal center under a tetrahedral crystal field are split in e and t2 orbitals (dz2, dx2–y2) (dxy, dxz, dyz). Regarding Table 3, the summation of d-orbital energies for tetrahedral geometry is ∑Ed(Td) = −0.89 Dq (Table 4, first row). Whenever the metal SBU is connected to five adjacent ligands to afford the square pyramidal environment, it causes the d orbitals to split into four groups with different energies, as listed in Table 4, second row. Considering Table 3, a square pyramidal field with C4V symmetry is considered as ML5 (C4V) = 2ML2(XY) + ML(Z), then the sum of d-orbital energies for square pyramidal configuration is derived by ∑Ed(C4V) = 4.57 Dq. The square planar geometry of metal centers with D4h symmetry creates a d-orbital splitting, shown in Table 4, second row. Its corresponding field is twice that of the ML2(XY) field, ML4(S.P.) = 2ML2(XY), and the sum of d-orbital energies is equal to 5.14 Dq. The metal d-orbital splitting diagram for trigonal bipyramidal metal SBU geometry is illustrated in Table 4, third row. For T.B.Py. with symmetry D3h, the respective field is 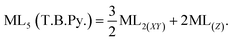 The total energy of d-orbitals for trigonal bipyramidal geometry is ∑Ed(D3h) = 3.53 Dq, and the corresponding RES+ variables are calculated. For metal SBUs having pentagonal bipyramidal (D5h), the crystal field splitting is displayed in Table 4, third row, and its field is considered as
The total energy of d-orbitals for trigonal bipyramidal geometry is ∑Ed(D3h) = 3.53 Dq, and the corresponding RES+ variables are calculated. For metal SBUs having pentagonal bipyramidal (D5h), the crystal field splitting is displayed in Table 4, third row, and its field is considered as 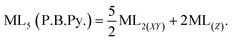 The consequent energies of the d orbitals is ∑Ed = −2.47 Dq. When the metal center is eight-coordinate, it can form square antiprism geometry with D4d symmetry. The d-orbital splitting is considered in Table 4, fourth row, and concerning Table 3, its field results from ML8 = 2ML4 (Td), but considering that in a cube, four ligands in the upper plate rotate 45°; the energy value of the dxy and dx2–y2 orbitals equal the average energy of the two orbitals in the cube configuration. Afterward, the resultant energies of the d orbitals are obtained by ∑Ed(D4d) = −2.67 Dq. The last studied metal SBU has triangular dodecahedral geometry with D2d symmetry. The metal d-orbital splitting diagram for this type of metal center geometry is exhibited in Table 4, fourth row. Its field is considered as
The consequent energies of the d orbitals is ∑Ed = −2.47 Dq. When the metal center is eight-coordinate, it can form square antiprism geometry with D4d symmetry. The d-orbital splitting is considered in Table 4, fourth row, and concerning Table 3, its field results from ML8 = 2ML4 (Td), but considering that in a cube, four ligands in the upper plate rotate 45°; the energy value of the dxy and dx2–y2 orbitals equal the average energy of the two orbitals in the cube configuration. Afterward, the resultant energies of the d orbitals are obtained by ∑Ed(D4d) = −2.67 Dq. The last studied metal SBU has triangular dodecahedral geometry with D2d symmetry. The metal d-orbital splitting diagram for this type of metal center geometry is exhibited in Table 4, fourth row. Its field is considered as 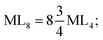 therefore, according to Table 3, the total energy of the d orbitals is ∑Ed = −10.68. As mentioned above, the respective RES+ is acquired from eqn (9), and Table 1 presents the corresponding RES+ values.
therefore, according to Table 3, the total energy of the d orbitals is ∑Ed = −10.68. As mentioned above, the respective RES+ is acquired from eqn (9), and Table 1 presents the corresponding RES+ values.
To validate the proposed QSPR model, an external validation method was employed using new data points and the statistical parameters obtained from the model for the external set, proving the accuracy and reliability of the proposed model. From the resulting BMLR model (eqn (8)), R2 and adjusted R2 values both are 0.9999 for the training and test sets. As shown in Table 5, correlation parameters for the test set, including QF12, QF22, QF32, and QCCC2 of the model yielded 0.9999. These correlation parameters for the external validation test set were acquired at 0.9999 as well, which demonstrated that the model is very credible and robust.
| R2 and Q2 tests | ||||||||
|---|---|---|---|---|---|---|---|---|
| Method | Sets | R2 | Radj2 | Q2 | QF12 | QF22 | QF32 | QCCC2 |
| Eqn (8) | Training set | 0.9999 | 0.9999 | — | — | — | — | — |
| Test set | 0.9999 | 0.9999 | 0.9999 | 0.9999 | 0.9999 | 0.9999 | 0.9999 | |
| External validation test set | 0.9999 | 0.9999 | 0.9999 | 0.9999 | 0.9999 | 0.9999 | 0.9999 | |
The root mean square error for prediction (RMSEP) values were 0.006, 0.0052, and 0.0054 for the training, test, and external validation test sets, respectively. Also, the mean absolute percentage errors (MAPE) were 0.012, 0.0073, and 0.0044 as shown in Table 6, which are low values for RMSEP and MAPE; thus, the model is suitable to estimate the drug release rate values from MOF materials.
| Eqn (8) | No. of MOFs | RMSEP | MSE | MAPE | F statistic | Significance F |
|---|---|---|---|---|---|---|
| Training set | 54 | 0.0063 | 0.000 | 0.012 | 373![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 493 493![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 505.6 505.6 |
1.109 × 10−182 |
| Test set | 13 | 0.0052 | 0.000 | 0.0073 | 35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 334 334![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 456.7 456.7 |
5.1323 × 10−29 |
| External validation test set | 8 | 0.0054 | 0.000 | 0.0044 | 34![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 571 571![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 821.9 821.9 |
7.988 × 10−12 |
The predicted and experimental values of drug release rate percentage for the training and test sets are shown in Fig. 2. It well proves that the predicted values of drug release rate percentage are fitted on the experimental values.
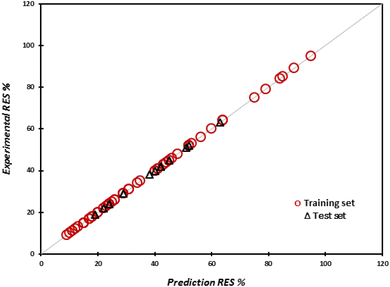 | ||
| Fig. 2 Predicted values of drug release rate for the training and test sets versus the experimental values of drug release rate. | ||
As can be observed from Table 7, the standard error (SE) for all descriptors are low values, which confirms that the proposed model is appropriate and robust. The probability values (p-values) of the descriptors are very small, confirming that the data could have occurred under the null hypothesis. Other parameters, such as t-test, significance level, and lower and upper bound values for descriptors are presented in Table 7. It can be concluded from Table 7 that all variables in eqn (8) have large effects on the resulting model. The VIF and tolerance for these descriptors are near 1, showing that there is no intercorrelation among the variables.
| Equation | Des.a | Coef.b | S.E.c | P-Value | t-Test | Sig.d | L.B.e (95%) | U.B.f (95%) |
|---|---|---|---|---|---|---|---|---|
| a Descriptor.b Coefficients.c Standard error.d Significance level.e Lower bound.f Upper bound.g Intercept. | ||||||||
| Eqn (8) | Int.g | 20.135 | 0.0021 | 1.563 × 10−155 | 9662.987 | <0.0001 | 20.139 | 20.130 |
| nN | 15.157 | 0.0004 | 5.7733 × 10−184 | 36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 759.32 759.32 |
<0.0001 | 15.158 | 15.156 | |
| nO | 2.675 | 0.0001 | 2.76 × 10−180 | 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 922.6 922.6 |
<0.0001 | 2.675 | 2.675 | |
| RES+ | −7.301 | 0.0005 | 1.4903 × 10−166 | −16219 | <0.0001 | −7.300 | −7.302 | |
| RES− | 14.296 | 0.0004 | 9.219 × 10−184 | 36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 409.89 409.89 |
<0.0001 | 14.297 | 14.296 | |
MOF design and RES calculation are accomplished through the descriptors in eqn (8) and also by considering the “mean effect”. Two parameters are involved the “mean effect”: (a) the coefficient of descriptors and (b) the nature of descriptors. The value assigned to the nature of descriptors may be positive or negative (Table 1); the coefficient of descriptors can also be positive or negative (the coefficients that appear in eqn (8)). After putting the values of the descriptors in eqn (8), the MOF design can be performed.104
For further assessment, the cross-validation method was used to make sure overfitting did not occur in modeling.105 Therefore, leave-one-out (LOO) and y-randomization (yrand) procedures were employed as cross-validation techniques. The values of RLOO2 and Ryrand2 were obtained at 0.999 and 0.206, respectively. The resulting values confirm the model's accuracy in predicting the release rate percentage (RES%) from MOFs. Also, Ryrand2 > 0.5 indicated that there is no chance correlation in the model. Moreover, the Durbin–Watson (DW) statistic of the proposed model was obtained at 2.453, which indicates that there is no autocorrelation in the residuals from the BMLR model. The acceptable range of DW is 1.50–2.50.
4. Conclusion
In this work, a straightforward and robust MLR model has been established, for the first time, to estimate the drug release rate from a set of 67 MOF materials containing different metal SBUs and various organic linkers. The QSPR model was based on four variables, which include the number of nitrogen and oxygen atoms calculated from MOF structures, as well as RES+ and RES−, new descriptors that play increaser and decreaser roles. These descriptors were not calculated using software or any complex method, but were computed using a simple and fast procedure. The R2 value was 0.9999 for both training and test sets. Also, other statistical parameters, including RMSEP, MSE, and MAPE, were satisfactory and confirmed the suitable reliability of eqn (8). The external validation proved that the model is valid for data beyond the dataset used to fit the model. Thus, the present QSPR model enables us to build a straightforward method for predicting drug release rates from MOFs using their structural configuration. As a view towards the future, we are developing QSPR models of MOF-based DDS for other important drugs.Data and software availability
This QSPR method—applying the number of atoms and adjusted descriptors (computed through chemistry knowledge and tedious work as increaser and decreaser parameters)—is considered proprietary; moreover, it can be used without any complex software and quantum methods. Therefore, this work has unique scientific value, and we share in Table S1 (ESI)† the metal center geometries as a decreaser descriptor, and in Table 4 the ligand fragments as a decreaser descriptor. Finally, the free version of Microsoft Excel 365, with no download needed, was utilized for calculating statistical parameters.Conflicts of interest
The authors declare that they have no known competition for financial interests or personal relationships that could have influenced the work reported in this paper. The corresponding author states that there is no conflict of interest.Acknowledgements
The authors gratefully acknowledge from the Iran University of Science and Technology.References
- S. Maman and I. P. Witz, Nat. Rev. Cancer, 2018, 18, 359–376 CrossRef CAS PubMed.
- A. C. Garrido-Castro, N. U. Lin and K. Polyak, Cancer Discovery, 2019, 9, 176–198 CrossRef CAS PubMed.
- V. Krishnamoorthy and R. Vilwanathan, Genomics, 2020, 112, 3703–3712 CrossRef CAS PubMed.
- S. Suryavanshi, A. Choudhari, P. Raina and R. Kaul-Ghanekar, J. Ethnopharmacol., 2019, 242, 112022 CrossRef CAS PubMed.
- A. P. Mishra, B. Salehi, M. Sharifi-Rad, R. Pezzani, F. Kobarfard, J. Sharifi-Rad and M. Nigam, Mol. Diagn. Ther., 2018, 22, 281–295 CrossRef CAS PubMed.
- A. Yimit, O. Adebali, A. Sancar and Y. Jiang, Nat. Commun., 2019, 10, 1–11 CrossRef CAS PubMed.
- K. Szyfter, M. Napierala, E. Florek, B. J. Braakhuis, R. P. Takes, J. P. Rodrigo, A. Rinaldo, C. E. Silver and A. Ferlito, Int. J. Cancer, 2019, 144, 2635–2643 CrossRef CAS PubMed.
- D. C. Wolf, S. M. Cohen, A. R. Boobis, V. L. Dellarco, P. A. Fenner-Crisp, A. Moretto, T. P. Pastoor, R. S. Schoeny, J. G. Seed and J. E. Doe, Regul. Toxicol. Pharmacol., 2019, 103, 86–92 CrossRef CAS PubMed.
- M. Fiore, G. Oliveri Conti, R. Caltabiano, A. Buffone, P. Zuccarello, L. Cormaci, M. A. Cannizzaro and M. Ferrante, Int. J. Environ. Res., 2019, 16, 1185 CAS.
- P. Rawla and A. Barsouk, Przegl. Gastroenterol., 2019, 14, 26 CAS.
- B. Singh and S. Mitragotri, Biotechnol. Adv., 2019, 42, 107339 CrossRef PubMed.
- E. M. Michalak, M. L. Burr, A. J. Bannister and M. A. Dawson, Nat. Rev. Mol. Cell Biol., 2019, 20, 573–589 CrossRef CAS PubMed.
- R. Oun, Y. E. Moussa and N. J. Wheate, Dalton Trans., 2018, 47, 6645–6653 RSC.
- G. Spengler, M. Gajdács, M. A. Marć, E. Domínguez-Álvarez and C. Sanmartín, Molecules, 2019, 24, 336 CrossRef PubMed.
- J. Kanduri, L. A. More, A. Godishala and A. Asnani, Cardiol. Clin., 2019, 37, 399–405 CrossRef PubMed.
- A. Montazerabadi, J. Beik, R. Irajirad, N. Attaran, S. Khaledi, H. Ghaznavi and A. Shakeri-Zadeh, Artif. Cells, Nanomed., Biotechnol., 2019, 47, 330–340 CrossRef CAS PubMed.
- Q. Zhou, L. Zhang, T. Yang and H. Wu, Int. J. Nanomed., 2018, 13, 2921 CrossRef CAS PubMed.
- H. Guo, Y. Xia, K. Feng, X. Qu, C. Zhang and F. Wan, Int. J. Nanomed., 2020, 15, 3235 CrossRef CAS PubMed.
- M. Y. Masoomi, A. Morsali, A. Dhakshinamoorthy and H. Garcia, Angew. Chem., Int. Ed., 2019, 58, 15188–15205 CrossRef CAS PubMed.
- B. J. Neves, R. C. Braga, C. C. Melo-Filho, J. T. Moreira-Filho, E. N. Muratov and C. H. Andrade, Front. Pharmacol., 2018, 9, 1275 CrossRef CAS PubMed.
- L. Bouarab-Chibane, V. Forquet, P. Lantéri, Y. Clément, L. Léonard-Akkari, N. Oulahal, P. Degraeve and C. Bordes, Front. Microbiol., 2019, 10, 829 CrossRef PubMed.
- S. Kwon, H. Bae, J. Jo and S. Yoon, BMC Bioinf., 2019, 20, 1–12 CrossRef CAS PubMed.
- T. N. Borhani, S. García-Muñoz, C. V. Luciani, A. Galindo and C. S. Adjiman, Phys. Chem. Chem. Phys., 2019, 21, 13706–13720 RSC.
- T. Gafourian, A. Safari, K. Adibkia, F. Parviz and A. Nokhodchi, J. Pharm. Sci., 2007, 96, 3334–3351 CrossRef CAS PubMed.
- T. Ghafourian, P. Zandasrar, H. Hamishekar and A. Nokhodchi, J. Controlled Release, 2004, 99, 113–125 CrossRef CAS PubMed.
- T. Ghafourian, M. Barzegar-Jalali, S. Dastmalchi, T. Khavari-Khorasani, N. Hakimiha and A. Nokhodchi, Int. J. Pharm., 2006, 319, 82–97 CrossRef CAS PubMed.
- I. Tsamardinos, G. S. Fanourgakis, E. Greasidou, E. Klontzas, K. Gkagkas and G. E. Froudakis, Microporous Mesoporous Mater., 2020, 300, 110160 CrossRef CAS.
- J. Burner, L. Schwiedrzik, M. Krykunov, J. Luo, P. G. Boyd and T. K. Woo, J. Phys. Chem. C, 2020, 124, 27996 CrossRef CAS.
- C. Altintas, O. F. Altundal, S. Keskin and R. Yildirim, J. Chem. Inf. Model., 2021, 61, 5 CrossRef PubMed.
- M. Keshavarz and A. Akbarzadeh, SAR QSAR Environ. Res., 2019, 30, 347–361 CrossRef CAS PubMed.
- A. Akbarzadeh, M. Nekoeifard, R. Rahmatollah and M. Keshavarz, SAR QSAR Environ. Res., 2020, 31, 347–371 CrossRef CAS PubMed.
- J. Wang, J. Jin, F. Li, B. Li, J. Liu, J. Jin, C. Wang, Y. Zeng and Y. Wang, RSC Adv., 2015, 5, 85606–85612 RSC.
- K. Xing, R. Fan, F. Wang, H. Nie, X. Du, S. Gai, P. Wang and Y. Yang, ACS Appl. Mater. Interfaces, 2018, 10, 22746–22756 CrossRef CAS PubMed.
- C. Y. Sun, C. Qin, C. G. Wang, Z. M. Su, S. Wang, X. L. Wang, G. S. Yang, K. Z. Shao, Y. Q. Lan and E. B. Wang, Adv. Mater., 2011, 23, 5629–5632 CrossRef CAS PubMed.
- B. Yang, M. Shen, J. Liu and F. Ren, Pharm. Res., 2017, 34, 2440–2450 CrossRef CAS PubMed.
- Y. Zhang and J. Wang, Inorg. Chim. Acta, 2018, 477, 8–14 CrossRef CAS.
- Y. Cai, Z. Sheng and J. Wang, Z. Anorg. Allg. Chem., 2018, 644, 877–882 CrossRef CAS.
- F. Li, C. Gu, H. Li, J. Xu and J. Liu, J. Inorg. Organomet. Polym. Mater., 2017, 27, 334–341 CrossRef CAS.
- Q. L. Li, J. P. Wang, W. C. Liu, X. Y. Zhuang, J. Q. Liu, G.-L. Fan, B.-H. Li, W.-N. Lin and J.-H. Man, Inorg. Chem. Commun., 2015, 55, 8–10 CrossRef CAS.
- J. S. Qin, D. Y. Du, W. L. Li, J. P. Zhang, S. L. Li, Z. M. Su, X. L. Wang, Q. Xu, K. Z. Shao and Y. Q. Lan, Chem. Sci., 2012, 3, 2114–2118 RSC.
- W. Zhang, Y. B. Ma, Y. A. Li and H. P. Wang, J. Iran. Chem. Soc., 2019, 16, 65–71 CrossRef CAS.
- D. Y. Ma, J. Xie, Z. Zhu, H. Huang, Y. Chen, R. Su and H. Zhu, Inorg. Chem. Commun., 2017, 86, 128–132 CrossRef CAS.
- X.-T. Xin and J.-Z. Cheng, J. Coord. Chem., 2018, 71, 3565–3574 CrossRef CAS.
- Z. C. Wang, Y. Zhang and Z. Y. Li, J. Cluster Sci., 2018, 29, 1285–1290 CrossRef CAS.
- Z. Yan, X. Li, Q. Fan, H. Bai, S. Wu, Z. F. Zhang and L. Pan, J. Mol. Struct., 2020, 1204, 127477 CrossRef CAS.
- P. P. Bag, D. Wang, Z. Chen and R. Cao, Chem. Commun., 2016, 52, 3669–3672 RSC.
- B. Yan, H. Li, W. Jiang and L. Mu, Aust. J. Chem., 2018, 71, 978–982 CrossRef CAS.
- Z. Y. Lv, X. R. Zhao and L. Zhao, J. Iran. Chem. Soc., 2019, 16, 757–763 CrossRef CAS.
- D. Wang, X. Liu, X. Ye, K. Yuan, X. Xing, Y. Xie, Z. Chen, B. Li, C. Huang and T. Kuang, Mater. Express, 2020, 10, 934–941 CrossRef CAS.
- S. A. Noorian, N. Hemmatinejad and J. A. Navarro, Microporous Mesoporous Mater., 2020, 302, 110199 CrossRef CAS.
- D. C. Zhang and X. Li, CrystEngComm, 2017, 19, 6673–6680 RSC.
- F. Li, B. Li, C. Wang, Y. Zeng, J. Liu, C. Y. Gu, P. Lu and L. Mei, RSC Adv., 2016, 6, 47959–47965 RSC.
- B. H. Song, X. Ding, C. Li and G. F. An, Z. Anorg. Allg. Chem., 2018, 644, 472–476 CrossRef CAS.
- J. Wang, D. Ma, W. Liao, S. Li, M. Huang, H. Liu, Y. Wang, R. Xie and J. Xu, CrystEngComm, 2017, 19, 5244–5250 RSC.
- S. Li, K. Wang, Y. Shi, Y. Cui, B. Chen, B. He, W. Dai, H. Zhang, X. Wang and C. Zhong, Adv. Funct. Mater., 2016, 26, 2715–2727 CrossRef CAS.
- F. M. Zhang, H. Dong, X. Zhang, X. J. Sun, M. Liu, D. D. Yang, X. Liu and J. Z. Wei, ACS Appl. Mater. Interfaces, 2017, 9, 27332–27337 CrossRef CAS PubMed.
- F. R. S. Lucena, L. C. de Araújo, M. d. D. Rodrigues, T. G. da Silva, V. R. Pereira, G. C. Militão, D. A. Fontes, P. J. Rolim-Neto, F. F. da Silva and S. C. Nascimento, Biomed. Pharmacother., 2013, 67, 707–713 CrossRef CAS PubMed.
- J. Q. Liu, J. Wu, Z. B. Jia, H. L. Chen, Q. L. Li, H. Sakiyama, T. Soares, R. Fei, C. Daiguebonne and O. Guillou, Dalton Trans., 2014, 43, 17265–17273 RSC.
- J. Q. Liu, X. F. Li, C. Y. Gu, J. C. da Silva, A. L. Barros, S. Alves Jr, B. H. Li, F. Ren, S. R. Batten and T. A. Soares, Dalton Trans., 2015, 44, 19370–19382 RSC.
- C. Gu, F. Li, B. Li, J. Xu, S. Yang, M. Luo, J. Liu and G. Liu, Inorg. Chem. Commun., 2016, 73, 26–29 CrossRef CAS.
- W. Liu, Y. Zhong, X. Wang, C. Zhuang, J. Chen, D. Liu, W. Xiao, Y. Pan, J. Huang and J. Liu, Inorg. Chem. Commun., 2020, 111, 107675 CrossRef CAS.
- J. Wu, J. W. Xu, W. C. Liu, S. Z. Yang, M. M. Luo, Y. Y. Han, J. Q. Liu and S. R. Batten, Inorg. Chem. Commun., 2016, 71, 32–34 CrossRef CAS.
- E. H. Zhou, R. Wang, J. Wu, S. W. Qiu, J. Q. Liu, H. R. Zhong, H. D. Zeng, J. W. Xu and J. C. Jin, Bull. Chem. Soc. Ethiop., 2017, 31, 457–463 CrossRef CAS.
- R. Li, S. Liu, Q. Tang, T. Wang, Y. Xie and R. Zhai, Z. Anorg. Allg. Chem., 2018, 644, 317–321 CrossRef CAS.
- L. Chen, H. Yu, Y. Li, X. Zhang and Y. Du, Struct. Chem., 2018, 29, 1885–1891 CrossRef CAS.
- Y. Guo, B. Yan, Y. Cheng and L. Mu, J. Coord. Chem., 2019, 72, 262–271 CrossRef CAS.
- L. L. Sun, Y. H. Li and H. Shi, J. Cluster Sci., 2019, 30, 251–258 CrossRef CAS.
- M. Ren, H. Li, H. Liu, L. Wang, H. Xiang, X. Zhang and B. Yu, Aust. J. Chem., 2018, 72, 233–239 CrossRef.
- H. T. Li, S. J. Song, X. R. Pei and D. B. Lu, Z. Anorg. Allg. Chem., 2019, 645, 801–809 CrossRef CAS.
- Q. Q. Wang, Z. P. Yang, Z. T. Cui, X. H. Wang and Y. Lin, J. Coord. Chem., 2020, 73, 1436–1449 CrossRef CAS.
- D. Li, L. F. Li, Z. F. Zhang, D. Xue, L. Pan and Y. Liu, J. Coord. Chem., 2020, 73, 266–281 CrossRef CAS.
- Z. Hu, C. Qiao, Z. Xia, F. Li, J. Han, Q. Wei, Q. Yang, G. Xie, S. Chen and S. Gao, ACS Appl. Mater. Interfaces, 2020, 12, 14914–14923 CrossRef CAS PubMed.
- F. Wang, J. Wang, S. Yang, C. Gu, X. Wu, J. Liu, H. Sakiyama, J. Xu, M. Luo and W. Liu, Russ. J. Coord. Chem., 2017, 43, 133–137 CrossRef.
- X. E. Feng and T. T. Zhu, Inorg. Nano-Met. Chem., 2020, 50, 1302–1307 CrossRef CAS.
- Q. Zhang, J. Zhao, Y. Li, X. Wu, L. Ma and Z. Ding, Russ. J. Coord. Chem., 2020, 46, 584–591 CrossRef CAS.
- B. E. Souza and J.-C. Tan, CrystEngComm, 2020, 22, 4526–4530 RSC.
- S. Tai, W. Zhang, J. Zhang, G. Luo, Y. Jia, M. Deng and Y. Ling, Microporous Mesoporous Mater., 2016, 220, 148–154 CrossRef CAS.
- B. Miri, N. Motakef-Kazemi, S. A. Shojaosadati and A. Morsali, Iran. J. Pharm. Res., 2018, 17, 1164 Search PubMed.
- L. Li, S. Han, C. Yang, L. Liu, S. Zhao, X. Wang, B. Liu, H. Pan and Y. Liu, Nanotechnology, 2020, 31, 325602 CrossRef CAS PubMed.
- X. Gao, Y. Wang, G. Ji, R. Cui and Z. Liu, CrystEngComm, 2018, 20, 1087–1093 RSC.
- L. L. Tan, H. Li, Y. Zhou, Y. Zhang, X. Feng, B. Wang and Y. W. Yang, Small, 2015, 11, 3807–3813 CrossRef CAS PubMed.
- X. Du, R. Fan, L. Qiang, K. Xing, H. Ye, X. Ran, Y. Song, P. Wang and Y. Yang, ACS Appl. Mater. Interfaces, 2017, 9, 28939–28948 CrossRef CAS PubMed.
- Z. Jiang, B. Yuan, N. Qiu, Y. Wang, L. Sun, Z. Wei, Y. Li, J. Zheng, Y. Jin and Y. Li, Nano-Micro Lett., 2019, 11, 1–17 CAS.
- W. Liu, Y. Pan, Y. Zhong, B. Li, Q. Ding, H. Xu, Y. Qiu, F. Ren, B. Li and M. Muddassir, Chem. Eng. J., 2021, 412, 127899 CrossRef CAS.
- C. Liu, X. Xu, J. Zhou, J. Yan, D. Wang and H. Zhang, BMC Materials, 2020, 2, 1–11 CrossRef.
- C. Zou, Z. Wang, X. Ren, R. Li, S. Zhang and B. Sheng, Inorg. Chem. Commun., 2018, 91, 91–94 CrossRef CAS.
- Z. Luo, R. Wang, C. Gu, F. Li, Y. Han, B. Li and J. Liu, Inorg. Chem. Commun., 2017, 76, 91–94 CrossRef CAS.
- M. Rezaei, A. Abbasi, R. Dinarvand, M. Jeddi-Tehrani and J. Janczak, ACS Appl. Mater. Interfaces, 2018, 10, 17594–17604 CrossRef CAS PubMed.
- C. Y. Sun, C. Qin, X. L. Wang, G. S. Yang, K. Z. Shao, Y. Q. Lan, Z. M. Su, P. Huang, C. G. Wang and E. B. Wang, Dalton Trans., 2012, 41, 6906–6909 RSC.
- X. Xiao, S. Liang, Y. Zhao, D. Huang, B. Xing, Z. Cheng and J. Lin, Nanoscale, 2020, 12, 3846–3854 RSC.
- H. N. Wang, G. S. Yang, X. L. Wang and Z. M. Su, Dalton Trans., 2013, 42, 6294–6297 RSC.
- F. J. Liu and B. M. Xu, Z. Anorg. Allg. Chem., 2018, 644, 821–826 CrossRef CAS.
- H. Dong, G. X. Yang, X. Zhang, X. B. Meng, J. L. Sheng, X. J. Sun, Y. J. Feng and F. M. Zhang, Chem.–Eur. J., 2018, 24, 17148–17154 CrossRef CAS PubMed.
- X. G. Wang, L. Xu, M. J. Li and X. Z. Zhang, Angew. Chem., Int. Ed., 2020, 59, 18078–18086 CrossRef CAS PubMed.
- A. Ma, Z. Luo, C. Gu, B. Li and J. Liu, Inorg. Chem. Commun., 2017, 77, 68–71 CrossRef CAS.
- B. H. Song, X. Ding, Z. F. Zhang and G. F. An, J. Iran. Chem. Soc., 2019, 16, 333–340 CrossRef CAS.
- L. C. Zhao, M. Tang, Q. H. Zhang, Z. Y. Hu, H. W. Gao, X. Y. Liao, G. Wang and J. Leng, J. Chem., 2018, 2018, 1–7 Search PubMed.
- D. Wei, Y. Xin, Y. Rong, Y. Li, C. Zhang, Q. Chen, S. Qin, W. Wang and Y. Hao, J. Inorg. Organomet. Polym. Mater., 2020, 30, 1121–1131 CrossRef CAS.
- H. N. Wang, X. Meng, X. L. Wang, G. S. Yang and Z. M. Su, Dalton Trans., 2012, 41, 2231–2233 RSC.
- Y. Liu, L. W. Shen and M. X. Song, Main Group Chem., 2019, 18, 427–436 CAS.
- Y. Li, X. Li, Q. Guan, C. Zhang, T. Xu, Y. Dong, X. Bai and W. Zhang, Int. J. Nanomed., 2017, 12, 1465 CrossRef CAS PubMed.
- X. Gao, M. Zhai, W. Guan, J. Liu, Z. Liu and A. Damirin, ACS Appl. Mater. Interfaces, 2017, 9, 3455–3462 CrossRef CAS PubMed.
- R. Krishnamurthy and W. B. Schaap, J. Chem. Educ., 1969, 46, 799 CrossRef CAS.
- M. Moharramnejad, L. Tayebi, A. R. Akbarzadeh and A. Maleki, Microporous Mesoporous Mater., 2022, 336, 111815 CrossRef CAS.
- X. Ying, J. Phys.: Conf. Ser., 2019, 1168, 022022 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ra00070b |
| This journal is © The Royal Society of Chemistry 2023 |

![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O
O