First-principles study on electronic states of In₂Se₃/Au heterostructure controlled by strain engineering

Abstract

The development of low-dimensional multifunctional devices has become increasingly important as the size of field-effect transistors decreases. In recent years, the two-dimensional (2D) semiconductor In₂Se₃ has emerged as a promising candidate for applications in the fields of electronics and optoelectronics owing to its remarkable spontaneous polarization properties. Through first-principles calculations, the effects of the polarization direction and biaxial tensile strain on the electronic and contact properties of In₂Se₃/Au heterostructures are investigated. The contact type of In₂Se₃/Au heterostructures depends on the polarization direction of In₂Se₃. The more charge transfers from the metal to the space charge region, the biaxial tensile strain increases. Moreover, the upward polarized In₂Se₃ in contact with Au maintains a constant n-type Schottky contact as the biaxial tensile strain increases, with a barrier height Φ_SB,n of only 0.086 eV at 6% strain, which is close to ohmic contact. On the other hand, the downward polarized In₂Se₃ in contact with Au can be transformed from p-type to n-type by applying a biaxial tensile strain. Our calculation results can provide a reference for the design and fabrication of In₂Se₃-based field effect transistors.

---

1. Introduction

As the miniaturization of silicon-based field-effect transistors (FETs) progresses, their scalability is approaching its limit, and a critical factor limiting this scalability is the short-channel effect. Therefore, an alternative material to silicon should be developed to avoid those scaling issues in future logic transistor applications. Two-dimensional (2D) materials, such as transition metal dichalcogenides (TMDs) and black phosphorus (BP), with atomic thickness, dangling-bond-free surface, and a moderate band gap of E_g ∼ 1–2 eV, are active candidates for application in logic transistors.^1–4 However, TMDs suffer from a low carrier mobility (∼200 cm² V⁻¹ s⁻¹), and BP easily decomposes in air, and thus they are unsuitable for high-performance applications.^5,6 In recent years, In₂Se₃ has attracted much attention as an emerging 2D III-VI semiconductor material. This material exhibits several phases: α, β, γ, δ, and κ, depending on the temperature and preparation conditions.^7,8 Among them, α-In₂Se₃, which belongs to the R3m group (rhombohedral structure), is stable at room temperature.⁹ From bulk to monolayer, α-In₂Se₃ has a direct band gap of 1.45 eV to 2.8 eV, comparable to BP.¹⁰ It is theoretically predicted that the electron (hole) carrier mobility of monolayer α-In₂Se₃ is as high as 920–960 (510–560) cm² V⁻¹ s⁻¹.¹¹ In 2D In₂Se₃-based FET, a high on-off ratio exceeding 10⁸ and on-state current of 671 μA μm⁻¹ have been observed.¹² In addition, Ding et al.¹³ have theoretically predicted the existence of in-plane and out-of-plane ferroelectricity of the monolayer In₂Se₃ at room temperature and subsequently demonstrated the ferroelectricity of the material experimentally.^14,15 Xue et al. observed ferroelectric polarization switching and hysteresis loop sown to the bilayer and monolayer In₂Se₃ at room temperature, indicating that ferroelectricity of the thinnest layer can be realized in 2D materials.¹⁶ More recently, Wan et al. successfully fabricated a 2D ferroelectric FET consisting of graphene and layered In₂Se₃, demonstrating nonvolatile memory after repeated writing of more than 10⁵ cycles.¹⁷ Wang et al. observed the abnormal bipolar resistive switching phenomenon in In₂Se₃-based FET, which was rationalized on the basis of Schottky barrier (SB) modulation by in-plane ferroelectric switching.¹⁸ Thus, the presence of out-of-plane and in-plane piezoelectricity in α-In₂Se₃ flakes offers an opportunity for the development of both directed and non-directed piezoelectric devices, including optoelectronic devices,^19–21 ferroelectric diodes, and nonvolatile memories.²²

In 2D FET devices with 2D semiconductor as the channel materials, contacts with metal electrodes are absolutely necessary, where SB is usually formed. The SB can induce an extra contact resistance and thus decrease the carrier transfer efficiency between the 2D semiconductor and metal electrodes, which often significantly reduces the performance of the FETs.^23,24 Yang et al. theoretically predicted the formation of lateral p-type Schottky contact in monolayer In₂Se₃/Au heterostructure with Schottky barrier height (SBH) of 0.35 eV and 0.31 eV, respectively, using the work function approximation and quantum transport simulation methods.²⁵ Unfortunately, the average pinning factor calculated for monolayer In₂Se₃ is about 0.09, which implies strong Fermi level pinning (FLP) effects.²⁶ The robust FLP is influenced by the interplay between the metal and In₂Se₃ while being insensitive to the metal work function. Therefore, tuning SBH is difficult with different metal electrodes. In recent years, many methods have been proposed to tune the interfacial SBH, such as passivating the metal surface with external atoms or inserting an h-BN insulating layer between MoS₂ and metal to reduce FLP, while the electron injection is impeded by a significant tunneling barrier due to the weak interaction between the 2D material and the metal layer.^27–29 Strain engineering is one of the most feasible ways to tune the electronic properties of 2D heterostructures. For example, Dai et al. reported that biaxial strain could induce the band alignment of PtS₂/MoTe₂ and GaN/WS₂ heterostructures transition from type-II to type-I but also can realize semiconductor–metal transition.^30,31 The calculated carrier mobility of the CdS/SiI₂ heterostructure is up to 10³ cm² V⁻¹ s⁻¹ by applying a biaxial strain, implying an excellent photocatalyst performance.³² Feng et al. achieved a strain sensor made of patterned α-In₂Se₃ films with high sensitivity (gauge factor ∼237 in −0.39% to 0.39% uniaxial strain range along the device channel length) and high spatial resolution of the strain distribution.³³ Hou et al. deposited Au electrodes on α-In₂Se₃ nanosheets to prepare a flexible transistor, and they modulated the photoresponse characteristics of the transistor by applying plane strain and found that the optimized photoresponsiveness was improved by 200% at a compressive strain of −0.15%.³⁴ However, the influence of strain on the electronic structures and contact properties of In₂Se₃/metal heterostructures are still veiled.

In this paper, the effect of biaxial strain on the interfacial electronic states and contact properties of monolayer In₂Se₃/Au heterostructures are investigated by first-principles calculations. Both polarization directions (upward and downward, defined by the built-in electric field) are considered. It is found that the type of contact between In₂Se₃ and Au depends on the polarization direction of In₂Se₃ contacted with Au, potentially leading to a transition from n-type to p-type behavior. Furthermore, biaxial strain engineering is a valuable method to modulate the electronic structure and contact properties of the In₂Se₃/Au heterostructure. This investigation offers a deeper comprehension of the interplay between strain engineering and polarization direction dependence on the interfacial properties of In₂Se₃/Au, presenting guidance for future In₂Se₃-based transistors.

2. Computational details

All calculations are performed using the Vienna ab initio simulation package (VASP) based on density functional theory.^35,36 The electron-ion core interaction is described by projector augmented wave potentials, which is more precise than ultra-soft pseudo-potentials.³⁷ For the generalized gradient approximation (GGA), not only the spatial distribution of the charge density but also the effect of the charge density gradient on the exchange correlation energy is taken into account. As we all know, the GGA approximation often underestimates the band gap of the semiconductor. However, considering the consistency of the resulting trend between the different methods, the GGA method is used in this work. The Perdew–Burke–Ernzerhof (PBE) formulation of the GGA is used to describe the exchange–correlation interaction.³⁸ The DFT-D2 method in the Grimme scheme is employed to include the contribution of van der Waals interaction between layers.³⁹ The cutoff energy of the plane wave is chosen to be 400 eV, and the Gaussian trailing method with an energy spread of 0.05 eV is used. The K points in the first Brillouin zone are optimized for geometry structure and static calculation using 5 × 5 × 1 and 11 × 11 × 1 grids, respectively. The ions are relaxed to the ground state using a conjugate gradient algorithm with an energy convergence rate of 1.0 × 10⁻⁵ eV and a force convergence rate of 0.02 eV Å⁻¹ for each ion. A vacuum layer of 15 Å thickness is added in the z-direction of the lattice to avoid interactions between adjacent plates.

The crystal structure of monolayer In₂Se₃ consists of five triangular atomic planes stacked in a sequence of Se–In–Se–In–Se. The optimized lattice constants of In₂Se₃ is 3.986 Å, in agreement with the experimental value of 4.0 Å.⁴⁰ The polarization direction of In₂Se₃ is defined by the direction of the inducted built-in electric field. Both upward (left, Up-In₂Se₃/Au) and downward directions (right, Dw-In₂Se₃/Au) are studied interfacial systems, as presented in Fig. 1(a). Previous studies have demonstrated that even a few percentage modification of the in-plane lattice constants of closely aligned metal surfaces results in negligible changes in their electronic properties.^41–43 However, modifying the lattice constant of In₂Se₃ can lead to significant changes in its electronic properties.⁴⁴ Hence, in order to preserve the intrinsic properties of In₂Se₃, we kept the lattice size constant and followed the method described in the literature⁴⁵ for our modeling. In this paper, the In₂Se₃/Au heterostructure is constructed by stretching the 4 × 4 supercell of Au (111) surface and matching the 3 × 3 supercell of the monolayer In₂Se₃ with a lattice mismatch rate of 2.610%. We maintained the minimum unit lattice constant of In₂Se₃ at a value of 3.9954 Å and the initial minimum unit lattice constant of Au at a value of 2.884 Å to ensure the desired structure. During the ionic relaxation of the interface structure, all atoms are completely relaxed. To investigate the effect of strain on the electronic properties of In₂Se₃/Au heterostructure, the In₂Se₃/Au heterostructure under biaxial tensile strain in the xy-plane is investigated. The biaxial tensile strain is applied along the xy-plane by varying the lattice constant of the heterostructure and can be defined as ε = (a − a₀)/a₀, where a₀ and a are the in-plane lattice constants of the equilibrium and strained lattice constant, respectively, as shown in Fig. 1(b).

Fig. 1 (a) The initial configuration of the monolayer In₂Se₃/metal heterostructure system in both the upward and downward directions of In₂Se₃ (Up-In₂Se₃/Au and Dw-In₂Se₃/Au). (b) In-plane biaxial tensile strain is depicted.

3. Results and discussion

As shown in Table 1, the interlayer distance (d_z) is the average distance between the closest layer of In₂Se₃ and metal in the vertical direction. d_Se–Au is set as the minimum distance between the selenium atoms in the In₂Se₃ layer and the atoms in the metal layer. The binding energy (E_b) is defined to evaluate the thermodynamic stability of the In₂Se₃/Au heterostructure as follows:

E_b = (E_In2Se3 + E_Au − E_In2Se3–Au)/N, (1)

where E_In2Se3, E_Au and E_In2Se3–Au are the total energies of the pristine In₂Se₃, metal, and In₂Se₃–Au interfacial systems, respectively. N represents the total number of In₂Se₃ unit cells in the system. When E_b is positive, the system is stable. The larger the absolute value of E_b, the stronger the heterostructure binding.

Table 1 Optimized interlayer distance d_z (Å) and d_Se–Au (Å), binding energy E_b (eV), and charge transfer value Δρ (e) of Up- and Dw-In₂Se₃/Au heterostructures under a biaxial strain

		0%	2%	4%	6%	7%
Up-In2Se3/Au	dz (Å)	2.523	2.478	2.416	2.348	2.352
		2.760 (ref. 25)
		2.275 (ref. 46)
	dSe–Au (Å)	2.643	2.595	2.552	2.524	2.512
		3.340 (ref. 25)
	Eb (eV)	0.962	0.852	0.548	0.131	−0.102
		0.510 (ref. 25)
	Δρ (e)	0.637	0.786	0.868	0.940	0.966
Dw-In2Se3/Au	dz (Å)	2.665	2.614	2.551	2.490	2.464
		2.920 (ref. 25)
		2.485 (ref. 46)
	dSe–Au (Å)	2.697	2.649	2.611	2.567	2.552
		3.400 (ref. 25)
	Eb (eV)	0.822	0.704	0.388	0.052	−0.297
		0.350 (ref. 25)
	Δρ (e)	0.503	0.590	0.674	0.755	0.791

---

For Up-In₂Se₃/Au heterostructure, d_z (d_Se–Au) is smaller than that of the Dw-In₂Se₃/Au heterostructure without strain, indicating the stronger interaction between In₂Se₃ and Au in Up-In₂Se₃/Au heterostructure, which is consistent with the literature results.²⁵ By applying the biaxial tensile strain from 1% to 7%, the d_z (d_Se–Au) in both Up-In₂Se₃/Au and Dw-In₂Se₃/Au heterostructures gradually decreased, indicating a gradually enhanced interaction between In₂Se₃ and Au. The binding energy of the Up-In₂Se₃/Au heterostructure is larger than that of the Dw-In₂Se₃/Au heterostructure without strain. For the Up-In₂Se₃/Au and Dw-In₂Se₃/Au heterostructures, E_b gradually decreases as the biaxial tensile strain increases from 1% to 7%, reaching negative values at 7% strain, and the heterostructure changes from a stable to an unstable structure. Therefore, the later section focuses on the interfacial properties of In₂Se₃/Au stable structures at 1–6% strain.

To gain further insight into bonding properties and interlayer interactions, the plane-averaged charge density difference is calculated as follows:

Δρ = ρ_In2Se3–Au − ρ_Au − ρ_In2Se3, (2)

where ρ_In2Se3–Au, ρ_In2Se3, and ρ_Au are the charge densities of the In₂Se₃–Au heterostructure, monolayer In₂Se₃, and the metal, respectively. Fig. 2 displays the charge density difference of (a) Up-In₂Se₃/Au and (b) Dw-In₂Se₃/Au heterostructures under biaxial strain. The red and blue-filled areas represent the charge accumulation and consumption, respectively. In general, the charge depletion and accumulation lead to electron wave function polarization, that is, the formation of interface electric dipoles, which will modify the band alignment.⁴⁷ Apparently, the charge transfer occurs at the interface between In₂Se₃ and Au. Bader charge analysis shows that the Up-In₂Se₃/Au heterostructure exhibits a larger charge transfer of 0.637e compared to the 0.503e observed for the Dw-In₂Se₃/Au heterostructure, indicating a stronger interaction for Up-In₂Se₃/Au heterostructure, as listed in Table 1. By increasing the biaxial tensile strain, the charge accumulation in the first layer of Au gradually decreases but gradually increases in the space charge region for the Up-In₂Se₃/Au and Dw-In₂Se₃/Au heterostructures.

Fig. 2 Planar average charge density difference Δρ along the z-direction of (a) Up-In₂Se₃/Au and (b) Dw-In₂Se₃/Au heterostructures under biaxial strain. Red and blue represent the accumulation and depletion of electrons, respectively.

The tunneling barrier is an important factor in determining the performance of the semiconductor/metal contact. The strong interaction not only leads to high orbital overlap but also promotes the electron injection between the metal and the semiconductor, leading to the tunneling and Schottky barriers being lowered. To evaluate the tunneling barrier, the effective potential energy of In₂Se₃–Au with the biaxial tensile strain is calculated. The barrier width d is defined as the width of the vdW gap between Au and In₂Se₃, and as shown in Fig. 3, is equal to the interlayer distance d_Se-M in the above-mentioned structural optimization structure. The tunneling barrier height (Φ_TB,eff) is defined as the minimum barrier height that electrons need to overcome upon injection between the metal and semiconductor. According to the method in the literature,⁴⁸ we can obtain:

where Φ_In2Se3, Φ_gap, andΦ_Au,min are the maximum value of In₂Se₃, value of the van der Waals gap between In₂Se₃ and Au, and the minimum value of the metal of the effective potential (V_eff) of the entire device, respectively. From Fig. 3(b), it can be seen that the tunneling barrier Φ_TB,eff is 0.102 eV for the Dw-In₂Se₃/Au heterostructure without strain. When the biaxial tensile strain is applied, the tunneling barrier Φ_TB,eff vanishes for the Dw-In₂Se₃/Au heterostructure. While for the Up-In₂Se₃/Au heterostructure, the effective potential of In₂Se₃ (Φ_In2Se3) is all higher than that of the vdW gap (Φ_gap) between the Au and In₂Se₃ layers with or without strain, indicating no tunneling barrier exists.

Fig. 3 Effective potential (V_eff) along the z direction (direction perpendicular to the interface) at the interface of (a) Up-In₂Se₃/Au and (b) Dw-In₂Se₃/Au contact under biaxial tensile strain. Φ_In2Se3, Φ_gap and Φ_Au,min are the V_eff of In₂Se₃, the vdW gap between Au and In₂Se₃ layers, and the minimum V_eff of Au, respectively. Φ_TB,eff is the height of the tunnel barrier, and d is the width of the vdW gap between Au and In₂Se₃.

The unconstrained monolayer In₂Se₃ has an indirect band gap of 0.843 eV, with the valence band maximum (VBM) located between the Γ point and the M point, while the conduction band minimum (CBM) is located at the Γ point in the first Brillouin zone, which is consistent with previous theoretical results,²⁵ as shown in Fig. S1.† Fig. 4 presents the energy band structures of (a) Up-In₂Se₃/Au and (b) Dw-In₂Se₃/Au heterostructures under biaxial tensile strain. Compared to pristine In₂Se₃, the energy bands of In₂Se₃ hybridize to some extent with Au metal, but most of the In₂Se₃ energy bands and Au energy bands can still be distinguished by their different colors. Blue and gray colors indicate the contributions from the In₂Se₃ and Au layers, respectively. It can be found that the Up-In₂Se₃ energy band structure is significantly more hybridized than Dw-In₂Se₃, and the energy band exhibits more hybridization intensity with increasing tensile strain, consistent with the strong interfacial forces discussed previously. In addition, the dispersion of CBM becomes larger with increasing tensile strain, leading to a decrease in the effective mass that is beneficial for device application.

Fig. 4 Band structure of In₂Se₃ in (a) Up-In₂Se₃/Au and (b) Dw-In₂Se₃/Au contact systems under biaxial tensile strain. The gray line indicates the energy band structure of the interfacial system. The blue line indicates the energy band structure of the ML In₂Se₃ projection, whose weight is represented by the size of the dot. The Fermi level is set to zero energy and is denoted by the dashed line.

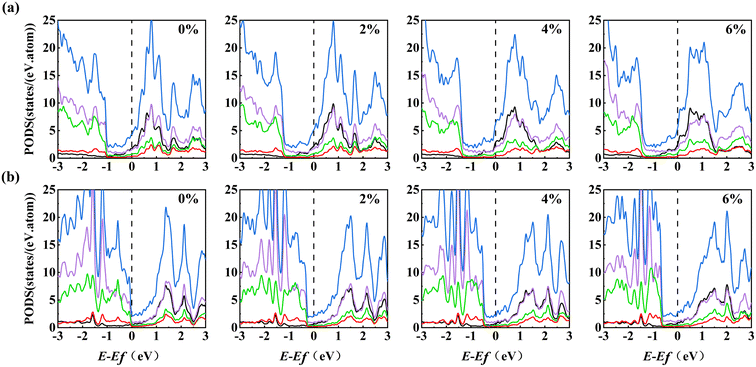
Fig. 5 shows the partial density of states (PDOS) of (a) Up-In₂Se₃/Au and (b) Dw-In₂Se₃/Au heterostructures under biaxial tensile strain. The conduction band portion of bulk In₂Se₃ is mainly contributed by In s and In p, while the valence band portion is mainly contributed by In p and Se s. Compared with pristine In₂Se₃, the E_F of the free Up-In₂Se₃/Au heterostructure is shifted in the direction of the conduction band, but the E_F of the free Dw-In₂Se₃/Au heterostructure is shifted in the direction of the valence band. Under biaxial stretching at 6% strain, the conduction band of pristine In₂Se₃ approaches the Fermi level while retaining its semiconductor properties, as shown in Fig. S2.† Similarly, the semiconductor properties of both Up- and Dw-In₂Se₃/Au heterostructures remain unchanged under biaxial stretching. Meanwhile, under biaxial tensile strain, the total electronic states of the Up-/Dw-In₂Se₃/Au heterostructure are gradually shifted to the left, indicating that the relative height between the CBM and the Fermi level in the In₂Se₃ layer can be continuously changed.

Fig. 5 Partial density of states (PDOS) of In₂Se₃ in (a) Up-In₂Se₃/Au and (b) Dw-In₂Se₃/Au contact systems under biaxial tensile strain. The black, purple, green, red, and blue lines represent the In s, In p, Se s, Se p, and the total density of states, respectively. The black vertical dashed line represents the Fermi level.

The In₂Se₃/Au heterostructure acts as a metal–semiconductor contact heterostructure, and the Fermi level of the combined system is located in the In₂Se₃ band gap region, resulting in the formation of a Schottky barrier at the interface. There are two ways to calculate SBH, one is Mott–Schottky estimation, and the other is first-principles calculation. The Mott–Schottky estimation is based on ignoring the interaction between the metal and semiconductor, defining n-type SBH as the difference between the metal work function Φ_M and the electron affinity of In₂Se₃ χ_In2Se3, where Φ_M is the difference between the vacuum potential and the Fermi level, and χ_In2Se3 is the free energy difference between the conduction band minimum (CBM) level and the vacuum electron level. The work function of Au (111) is calculated to be 5.152 eV. Owing to the asymmetric structure of In₂Se₃ and the built-in electric field caused by spontaneous ferroelectric polarization along the vertical direction, the work functions on its two sides are different. The calculated χ_In2Se3 of Up-In₂Se₃ is 5.111 eV, while the χ_In2Se3 of Dw-In₂Se₃ is 4.613 eV. It can be found that an n-type Schottky contact is formed between Au and Up-In₂Se₃ with an electronic SBH of 0.041 eV. It forms a lateral p-type Schottky barrier for Dw-In₂Se₃ contacted with Au and the SBH of 0.251 eV. In first-principles calculations, the n-type Schottky barrier (Φ_SB,n) is indeed the energy difference of the conduction band minimum (CBM) with respect to E_F, while the p-type Schottky barrier (Φ_SB,p) is indeed the energy difference of the valence band maximum (VBM) with respect to E_F. It can be found that the polarization direction of In₂Se₃ is upward, and the In₂Se₃/Au heterostructure presents an n-type Schottky contact with Φ_SB,n = 0.410 eV under no strain. On the contrary, when the polarization direction of In₂Se₃ is downward, the contact type between Au and In₂Se₃ becomes a p-type Schottky contact with Φ_SB,p = 0.093 eV. The large difference in the values of SBH calculated by the two methods reflects the possible existence of Fermi level pinning (FLP) behavior at the interface.

Fig. 6 displays the SBH results of Schottky–Mott estimates and first-principles calculations. The strain dependence of SBH estimated by the Schottky–Mott limit is determined by the strain dependence of intrinsic properties of Au and In₂Se₃. The SBH of In₂Se₃/Au heterostructure is found to decrease as the work function of Au decreases, and the electron affinity of In₂Se₃ increases under tensile strain. The contribution of interfacial atomic and electronic rearrangements to the SBH is completely ignored. However, when the tensile strain reaches 6%, the SBH of the Up-In₂Se₃/Au heterostructure becomes 0.086 eV by using the first-principles calculations, which is close to ohmic contact. The electrons in the Au layer can freely flow to the In₂Se₃ layer through the In₂Se₃/Au contact. However, the VBM of Dw-In₂Se₃/Au heterostructure is gradually moved away from the Fermi level under the action of biaxial tensile strain, resulting in a gradual increase of the SBH at the interface. Until 6% tensile strain, Dw-In₂Se₃/Au heterostructure changes from p-type to n-type Schottky barrier. Our findings suggest that strain-tunable SBHs of In₂Se₃/Au heterostructures can be used in the design and fabrication of future In₂Se₃-based field effect transistors.

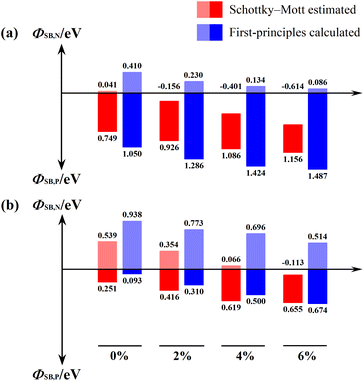Fig. 6 Schottky barriers of (a) Up-In₂Se₃Au and (b) Dw-In₂Se₃/Au contact systems under biaxial tensile strain.

4. Conclusions

In summary, the effects of the polarization direction and biaxial tensile strain on the electronic properties and Schottky barrier of In₂Se₃/Au heterostructures are comprehensively investigated by first-principles calculations. The interaction force between Up-In₂Se₃ and Au is stronger than that of Dw-In₂Se₃, and the interfacial force gradually increases with increasing tensile strain. In₂Se₃/Au heterostructure can switch from n-type to p-type when the polarization direction of In₂Se₃ changes. When the biaxial tensile strain is 6%, the Φ_SB,n of the Up-In₂Se₃/Au heterostructure is only 0.086 eV, which is close to ohmic contact, while the Dw-In₂Se₃/Au heterostructure changes from p-type to n-type Schottky contact. Our study provides a detailed biaxial tensile strain of the SBH of In₂Se₃/Au heterostructures, providing theoretical guidance for more efficient applications.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was jointly supported by the Doctoral Program of Xi'an Polytechnic University (Grant No. 107020519 and 107020534), the Project of Xi’an Science and Technology Bureau (Grant No. 21XJZZ0009), and the Natural Science Foundation of Shaanxi Province (Grant No. 2020JQ-823).

References

1. W. Cao, J. Jiang, X. Xie, A. Pal, J. H. Chu, J. Kang and K. Banerjee, IEEE Trans. Electron Devices, 2018, 65, 4109.
2. C. Tan, X. Cao, X. J. Wu, Q. He, J. Yang, X. Zhang, J. Chen, W. Zhao, S. Han, G. H. Nam, M. Sindoro and H. Zhang, Chem. Rev., 2017, 117, 6225.
3. S. Das, J. A. Robinson, M. Dubey, H. Terrones and M. Terrones, Annu. Rev. Mater. Res., 2015, 45, 1.
4. S. J. Kim, K. Choi, B. Lee, Y. Kim and B. H. Hong, Annu. Rev. Mater. Res., 2015, 45, 63.
5. M. Tosun, S. Chuang, H. Fang, A. B. Sachid, M. Hettick, Y. Lin, Y. Zeng and A. Javey, ACS Nano, 2014, 8, 4948.
6. M. Z. Rahman, C. W. Kwong, K. Davey and S. Z. Qiao, Energy Environ. Sci., 2016, 9, 709.
7. G. Han, Z. G. Chen, J. Drennan and J. Zou, Small, 2014, 10, 2747.
8. L. Debbichi, O. Eriksson and S. Lebègue, J. Phys. Chem. Lett., 2015, 6, 3098.
9. M. Küpers, P. M. Konze, A. Meledin, J. Mayer, U. Englert, M. Wuttig and R. Dronskowski, Inorg. Chem., 2018, 57, 11775.
10. J. Quereda, R. Biele, G. Rubio-Bollinger, N. Agraït, R. DÁgosta and A. Castellanos-Gomez, Adv. Opt. Mater., 2016, 4, 1939.
11. P. Zhao, Y. Ma, X. Lv, M. Li, B. Huang and Y. Dai, Nano Energy, 2018, 51, 533.
12. M. Si, A. K. Saha, S. Gao, G. Qiu, J. Qin, Y. Duan, J. Jian, C. Niu, H. Wang, W. Wu, S. K. Gupta and P. D. Ye, Nat. Electron., 2019, 2, 580.
13. W. Ding, J. Zhu, Z. Wang, Y. Gao, D. Xiao, Y. Gu, Z. Zhang and W. Zhu, Nat. Commun., 2017, 8, 1.
14. C. Cui, W. J. Hu, X. Yan, C. Addiego, W. Gao, Y. Wang, Z. Wang, L. Li, Y. Cheng, P. Li, X. Zhang, H. N. Alshareef, T. Wu, W. Zhu, X. Pan and L. J. Li, Nano Lett., 2018, 18, 1253.
15. F. Xue, W. Hu, K. C. Lee, L. S. Lu, J. Zhang, H. L. Tang, A. Han, W. T. Hsu, S. Tu, W. H. Chang, C. H. Lien, J. H. He, Z. Zhang, L. J. Li and X. Zhang, Adv. Funct. Mater., 2018, 28, 1803738.
16. F. Xue, J. Zhang, W. Hu, W. T. Hsu, A. Han, S. F. Leung, J. K. Huang, Y. Wan, S. Liu, J. Zhang, J. H. He, W. H. Chang, Z. L. Wang, X. Zhang and L. J. Li, ACS Nano, 2018, 12, 4976.
17. S. Wan, Y. Li, W. Li, X. Mao, C. Wang, C. Chen, J. Dong, A. Nie, J. Xiang, Z. Liu, W. Zhu and H. Zeng, Adv. Funct. Mater., 2019, 29, 1808606.
18. L. Wang, X. Wang, Y. Zhang, R. Li, T. Ma, K. Leng, Z. Chen, I. Abdelwahab and K. P. Loh, Adv. Funct. Mater., 2020, 30, 2004609.
19. J. Igo, M. Gabel, Z. G. Yu, L. Yang and Y. Gu, ACS Appl. Nano Mater., 2019, 2, 6774.
20. J. O. Island, S. I. Blanter, M. Buscema, H. S. J. van der Zant and A. Castellanos-Gomez, Nano Lett., 2015, 15, 7853.
21. Z. Q. Zheng, J. D. Yao and G. W. Yang, J. Mater. Chem. C, 2016, 4, 8094.
22. S. Wan, Y. Li, W. Li, X. Mao, W. Zhu and H. Zeng, Nanoscale, 2018, 10, 14885.
23. N. Jiang, Y. Xie, S. Wang, Y. Song, L. Chen, W. Han, X. Jin, Z. Zhou and Z. Yan, Appl. Surf. Sci., 2023, 623, 157007.
24. H. Liu, Y. Du, Y. Deng and P. D. Ye, Chem. Soc. Rev., 2015, 44, 2732.
25. C. Yang, X. Zhang, X. Sun, H. Zhang, H. Tang, B. Shi, H. Pang, L. Xu, S. Liu, J. Yang, J. Yan, L. Xu, Z. Zhang, J. Yang, D. Yu and J. Lu, Phys. Status Solidi B, 2019, 257, 1900198.
26. B. Liu, F. Lyu, B. Tang, X. Li, J. Liao and Q. Chen, ACS Appl. Electron. Mater., 2021, 3, 4604.
27. K. A. Min, J. Park, R. M. Wallace, K. Cho and S. Hong, 2D Mater., 2016, 4, 015019.
28. P. Ou, X. Zhou, C. Chen, F. Meng, Y. Chen and J. Song, Nanoscale, 2019, 11, 11569.
29. M. Farmanbar and G. Brocks, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 161304.
30. S. Yin, Q. Luo, D. Wei, G. Guo, X. Sun and Y. Tang, Results Phys., 2022, 33, 105172.
31. S. Yin, Q. Luo, D. Wei, G. Guo, X. Sun, Y. Li, Y. Tang, Z. Feng and X. Dai, Phys. E, 2022, 142, 115258.
32. X. Sun, S. Yin, Q. Luo, D. Wei, Y. Ma and X. Dai, Results Phys., 2022, 38, 105636.
33. W. Feng, W. Zheng, F. Gao, X. S. Chen, G. Liu, T. Hasan, W. W. Cao and P. A. Hu, Chem. Mater., 2016, 28, 4278.
34. P. Hou, Y. Lv, Y. Chen, Y. Liu, C. Wang, P. Zhou, X. Zhong, J. Wang and X. Ouyang, ACS Appl. Electron. Mater., 2019, 2, 140.
35. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251.
36. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558.
37. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953.
38. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
39. S. Grimme, J. Comput. Chem., 2006, 27, 1787.
40. J. Y. J. Ye, S. S. S. Soeda, Y. N. Y. Nakamura and O. N. O. Nittono, Jpn. J. Appl. Phys., 1998, 37, 4264.
41. G. Giovannetti, P. A. Khomyakov, G. Brocks, V. M. Karpan, J. van den Brink and P. J. Kelly, Phys. Rev. Lett., 2008, 101, 026803.
42. P. A. Khomyakov, G. Giovannetti, P. C. Rusu, G. Brocks, J. van den Brink and P. J. Kelly, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 195425.
43. H. P. Komsa and A. V. Krasheninnikov, J. Phys. Chem. C, 2012, 116, 8983.
44. E. F. Procopio, R. N. Pedrosa, F. A. L. de Souza, W. S. Paz and W. L. Scopel, Phys. Chem. Chem. Phys., 2020, 22, 3520–3526.
45. M. Farmanbar and G. Brocks, Phys. Rev. B, 2016, 93, 085304.
46. L. Kang, P. Jiang, H. Hao, Y. Zhou, X. Zheng, L. Zhang and Z. Zeng, Phys. Rev. B, 2021, 103, 125414.
47. R. T. Tung, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 205310.
48. J. H. Kang, W. Liu, D. Sarkar, D. Jena and K. Banerjee, Phys. Rev. X, 2014, 4, 031005.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ra00134b

---