 Open Access Article
Open Access ArticleStructures, band gaps, and formation energies of highly stable phases of inorganic ABX3 halides: A = Li, Na, K, Rb, Cs, Tl; B = Be, Mg, Ca, Ge, Sr, Sn, Pb; and X = F, Cl, Br, I†‡
Saad M. Alqahtania,
Abduljabar Q. Alsayoudbc and
Fahhad H. Alharbi *de
*de
aElectrical Engineering Department, Alasala Colleges, Dammam, Saudi Arabia
bMaterial Sciences and Engineering Department, King Fahd University of Petroleum & Minerals, Dhahran, Saudi Arabia
cInterdisciplinary Research Center for Advanced Materials, King Fahd University of Petroleum & Minerals (KFUPM), Dhahran, Saudi Arabia
dElectrical Engineering Department, King Fahd University of Petroleum & Minerals, Dhahran, Saudi Arabia. E-mail: fahhad.alharbi@kfupm.edu.sa
eSDAIA-KFUPM Joint Research Center for Artificial Intelligence, Dhahran, Saudi Arabia
First published on 20th March 2023
Abstract
Recently, halide perovskites have attracted a substantial attention. Although the focus was mostly on hybrid ones with organic polyatomic cations and with inadequate stability, there is a sizable inorganic halide space that is not well explored and may be more stable than hybrid perovskites. In this work, a robust automated framework is used to calculate the essential properties of the highly stable phases of 168 inorganic halide perovskites. The considered space of ABX3 compounds consists of A = Li, Na, K, Rb, Cs, Tl, B = Be, Mg, Ca, Ge, Sr, Sn, Pb, and X = F, Cl, Br, I. The targeted properties are the structure, the formation energy to assess stability, and the energy gap for potential applicability. The calculations are carried out using the density functional theory (DFT) integrated with the precision library of Standard Solid-State Pseudopotentials (SSSP) for structure relaxation and PseudoDojo for energy gap calculation. Furthermore, we adopted a very sufficient and robust random sampling to identify the highly stable phases. The results illustrated that only 118 of the possible 168 compounds are formidable and have reliable results. The remaining 50 compounds are either not formidable or suffer from computational inconsistencies.
1 Introduction
Arguably, one of the main factors that has led to the current technological advancement is the ability to produce, engineer, and deploy materials in almost all aspects of life.1–3 Any technological development depends on using a suitable set of materials within different systems, device concepts, and device designs. Seemingly, this materials/advancement correlation is expected to continue and it could be one of the determinant factors for sustainable future.4,5 Till recently, experimentally known materials were the main source for materials selection. Despite the rich experimental data, there is certainly a limitation in the selection space. However, advances in computational capabilities and techniques have paved the way for computational materials discovery as an alternative way to explore and to design new materials much beyond the rich experimental data.2,6–8Computational materials discovery (CMD) is currently one of the main pillars in the modern materials science. This is reflected in the large number of immense international CMD initiatives such as the Materials Genome Initiative (MGI),9 the Novel Materials Discovery (NOMAD),10 Materials Projects,11 and the Automatic FLOW for Materials Discovery (AFLOW).12 In general, there are two classes of CMD approaches. The first one is the forward CMD in which a material space (large or small) is predefined and then a variety of atomic scale calculation methods are used to calculate a set of targeted properties. Finally, the generated data are explored for specific applications. In the second class, a desired functionality is initially specified. Then by using some atomistic design keys, the properties of some starting materials are tuned to provide the desired functionality. The former approach is the commonly used one and it is the one adopted in this work.
The targeted material space – in this work – is the inorganic halide perovskites (IHP). In the past decade, perovskites have attracted a substantial attention. This is started with the emergence of methylammonium lead iodide (CH3NH3PbI3) solar cells. One of the main limitations of these hybrid perovskite solar cells is their marginal stability due to many internal and external factors, including thermal stability. On the other hand, IHP are known to have high intrinsic thermal stability. IHP space is reasonably large and it takes the chemical composition of ABX3; where A+ is a monovalent cation, B2+ is a divalent cation, and X− is a halide ion (X = F, Cl, Br, I). By considering the common oxidation states, the materials space can have 720 possible compounds. This is significantly extendable to more than 9000 possibilities if non-common oxidation states are considered. The considered monovalent and divalent cations – in this work – are A = Li, Na, K, Rb, Cs, Tl and B = Be, Mg, Ca, Ge, Sr, Sn, Pb. With the four considered halogens, the resulted materials space has 168 possible materials. The thorough calculations indicated that only 118 of them are formidable and have robust and reliable results. The remaining 50 compounds are either not formidable or suffer from computational inconsistencies.
CMD search for perovskites is not new as many related high-throughput calculations based on the density functional theory (DFT) have been conducted for several applications such as photovoltaic, transparent contacts, light emitting diode (LED), water-splitting, piezoelectrics, magnetoelectrics, etc.13,14 For example, for water-splitting applications, 5329 cubic and distorted perovskite metal oxides were screened and 138 compounds were proposed as new candidates for thermochemical water splitting.15 It is very important to mention that these new materials were not known experimentally beforehand. Furthermore, many of these efforts focus on inorganic halide perovskites; but with different screened spaces and diverse levels of computational robustness.16–18
In this paper, we present the structures, energy gaps, and formation energies of highly stable phases (probably the most stable ones) of 118 inorganic ABX3 halides. The properties are calculated through an automated framework to determine the highly stable structures using the density functional theory (DFT) integrated with the precision library of Standard Solid-State Pseudopotentials (SSSP)19 for structure relaxation and PseudoDojo20 for energy gap calculation. To identify the highly stable phases, we adopted a very sufficient and robust random sampling.6 SSSP library establishes the most suitable pseudopotential, cutoff energy, and dual for each element either for precision or efficiency. In this work, we focused on precision. On the other hand, PseudoDojo framework provides optimized norm-conserving pseudopotentials for more accurate energy gap calculation.
2 Methods
The screening of a subset of ABX3 compounds was carried out starting from the selection of elements till bandgap energy calculation automatically as depicted in Fig. 1. The considered elements are A = Li+, Na+, K+, Rb+, Cs+, Tl+; B = Be2+, Mg2+, Ca2+, Ge2+, Sr2+, Sn2+, Pb2+; and X = F−, Cl−, Br−, I−. The materials space of constituent elements was generated based on their common oxidation states, which are A+, B2+ and X−. The total number of generated ABX3 compounds is 168. Then, supercells of ABX3 compounds were generated following the recipe explained in a previous paper6 and using an improved estimations for ionic radii.21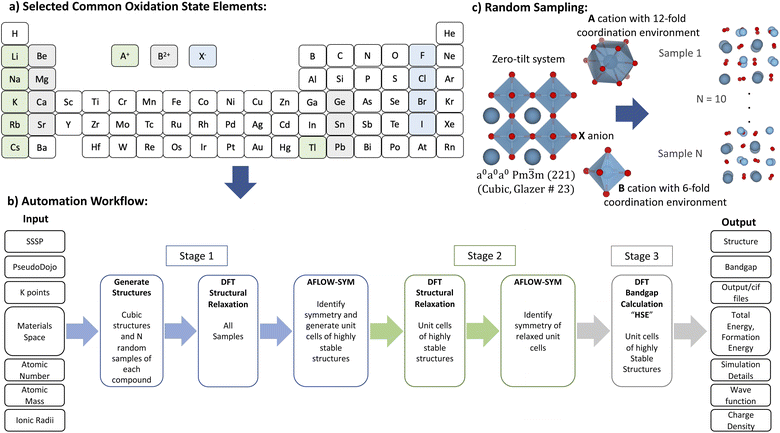 | ||
| Fig. 1 Materials screening methodology: (a) building the ABX3 compounds space from elements with suitable common oxidation state elements; (b) using automation workflow to obtain highly stable structures and their corresponding structural and electronic properties; and (c) adopting random sampling approach for ABX3 to identify the highly stable phases.6 | ||
In this work, we used plane-wave DFT as implemented in Quantum Espresso for all the calculations.22 For structural prediction (Stage 1), the exchange–correlation interactions were approximated by the generalized gradient approximation (GGA) of Perdew, Burke and Ernzerhof (PBE) method.23 The SSSP library optimized for precision was the source for all the compounds' pseudopotentials.19 The used highest kinetic cutoff energy (Ec), corresponding duals, and type of pseudopotentials are tabulated in Tables 1 and 2. Then AFLOW-SYM24 is used to identify the crystal symmetry and produce the unit cells of ABX3 compounds. The unit cell allows reducing the computational cost. Then, in Stage 2, these obtained unit cells are further relaxed to be used later in Stage 3 for bandgap energy calculations.
| Materials | Ec [Ry] | Dual |
|---|---|---|
| (Li,Rb,Cs)B(I3) | 45 | 8 |
| (K)B(I3) | 60 | 8 |
| (Tl)B(I3) | 70 | 8 |
| (Li,K,Rb,Cs,Tl)B(F3) | 90 | 4 |
| (Li,K,Rb,Cs,Tl)B(Br3) | 90 | 8 |
| (Na)B(F3,Br3,I3) | 100 | 4 |
| AB(Cl3) | 100 | 8 |
| Pseudopotential type | Elements |
|---|---|
| Projector-augmented wave (PAW) | K+, Pb2+, I− |
| Ultrasoft (US) | Li+, Cs+, Tl+, Mg2+, Ca2+, Ge2+, Sr2+, Sn2+, Cl−, Br− |
| Norm-conserving (NC) | Na+, Rb+, Be2+, F− |
Finally, the thermodynamical stability of the predicted structures were assessed based on their formation energy:
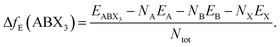 | (1) |
For bandgap energy calculation (Stage 3), the hybrid functional HSE25 is used as it is adequately accurate for this purpose and is known to be more computationally efficient in comparison with GW approximation. The PseudoDojo library20 was used to conduct bandgap calculation with PBE norm-conserving (NC) fully-relativistic pseudopotentials and highest stringent Ec,Eg parameters as shown in Table 3. In Ec,Eg subscript corresponds to bandgap calculations and they are different from those used for the geometry (i.e. Ec). The duals are set to the default value, which is 4. The spin–orbit coupling (SOC) was activated during the calculation of the bandgap energies. This is done as the importance of SOC is well established in halide perovskites.26,27 However, in a recent interesting work by Das et al.,28 it was demonstrated that SOC should be used with caution as it may lead to over-correction. The K points of Stage 2 and Stage 3 are provided in the ESI† for each compound.
| Materials | Ec,Eg [Ry] |
|---|---|
| (Rb)(Sr)(Cl3) | 72 |
| (Rb,Cs)(Ca)(Cl3) | 76 |
| (Li)(Ca)(Cl3) | 82 |
| (K)(Ca,Sr)(Cl3) | 86 |
| (Li,K,Rb,Cs)(Ca,Sr)(Br3,I3) | 88 |
| (Li,K,Rb,Cs)Ge(Br3,Cl3) | 90 |
| Na(Mg,Ca,Ge,Sr)X3, (Li,K,Rb,Cs)(Mg)X3, (Li,K,Rb,Cs)(Ca,Ge,Sr)(F3) | 96 |
| Tl(Mg,Ca,Ge,Sr)X3, A(Pb)X3 | 100 |
| A(Sn)X3 | 114 |
| A(Be)X3 | 118 |
The previously reported in-house automated workflow in ref. 6 was further developed to calculate the structural relaxation of obtained unit cells and bandgap energies using the aforementioned method. Eventually, structures, bandgap energies, energy of structures, simulation details, wavefunctions and charge densities are obtained. These results would be useful for post-processing and further analysis.
3 Results and discussion
As aforementioned, there are 168 ABX3 compounds in the considered materials space. The used random sampling optimization required a total of 1848 structures calculations (11 per compound). Only 141 ABX3 compounds passed Stage 1, whereas the other 27 compounds failed either due to divergence issues or due to an insufficient number of succeeded structural relaxation samples to draw conclusions about the highly stable structures. The obtained unit cells are relaxed for further verification of the symmetry. Furthermore, 23 other compounds suffer from computational inconsistencies and hence do not pass Stage 3. Here, only compounds that successfully passed Stage 3 are reported, which are 118 ABX3 compounds.To verify the obtained results, some of the considered ABX3 compounds are known and hence the corresponding obtained results are compared with these in literature. Table 4 shows the calculated and previously reported bandgap and formation energy for CsCaCl3, CsPbCBr3, CsPbI3, CsSnCl3, and CsSnI3. The agreement is clear. Nonetheless, the verification is certainly not comprehensive and it is not meant to be. The purpose is to demonstrate the reliability of the calculations on known materials (this is why the used 5 ones are Cs based perovskites).
| Materials | Eg [eV] | ΔfE [eV per atom] | ||
|---|---|---|---|---|
| This work | Other reports | This work | Other reports | |
| CsCaCl3 | 6.684 | 7.08 (ref. 16) | −2.325 | −2.290 (ref. 16) |
| CsPbBr3 | 1.797 | 1.52–2.00 (ref. 29 and 30) | −1.353 | −1.323 (ref. 16) |
| CsPbI3 | 1.329 | 1.25 (ref. 31) | −1.062 | −1.021 (ref. 16) |
| CsSnCl3 | 2.660 | 2.8 (ref. 32 and 33) | −1.490 | −1.460 (ref. 16) |
| CsSnI3 | 1.292 | 1.27–1.31 (ref. 32–34) | −0.989 | −0.960 (ref. 16) |
The converged crystal structures and space groups counts are summarized in Fig. 2 as classified by AFLOW-SYM.24 It suggests that there are 46 triclinic, 10 monoclinic, 39 orthorhombic, 1 tetragonal, 11 trigonal and, 11 cubic crystals. It is very clear that there is a high percentage of highly stable structures identified as triclinic. As per this classification, the total number of perovskite structures35 is 51 while the remaining ones are non-perovskite (please see the following discussion). However, it should be pointed that such classification depends highly on the considered demarcations, tolerances, and convergence criteria. To illustrate this important point, the effects of the tolerances on CsSnCl3 and CsSrF3 are analyzed. For CsSnCl3, the lattice parameters a, b, & c are 11.400, 11.440, and 11.458 Å ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) respectively and the angles α, β, & γ are 89.479°, 89.801°, and 89.912° respectively. Those for CsSrF3 are 9.670 Å, 9.579 Å, 9.581 Å, 89.985°, 89.914°, and 90.013° respectively. According to the default tolerances of AFLOW-SYM, they are classified as triclinic crystals. When the angle tolerance is set to 0.2°, CsSnCl3 would be monoclinic while CsSrF3 would be orthorhombic. If this is even further relaxed to 1°, they would be both orthorhombic. If one further makes the lattice tolerance to 0.1 Å, both would be then cubic. So clearly, the space group classification is not conclusive and somehow subjective. This is also applicable to many other compounds in the consider materials space.
respectively and the angles α, β, & γ are 89.479°, 89.801°, and 89.912° respectively. Those for CsSrF3 are 9.670 Å, 9.579 Å, 9.581 Å, 89.985°, 89.914°, and 90.013° respectively. According to the default tolerances of AFLOW-SYM, they are classified as triclinic crystals. When the angle tolerance is set to 0.2°, CsSnCl3 would be monoclinic while CsSrF3 would be orthorhombic. If this is even further relaxed to 1°, they would be both orthorhombic. If one further makes the lattice tolerance to 0.1 Å, both would be then cubic. So clearly, the space group classification is not conclusive and somehow subjective. This is also applicable to many other compounds in the consider materials space.
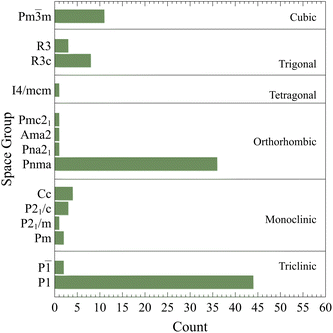 | ||
| Fig. 2 The converged crystal structures and space groups counts as classified by AFLOW-SYM.24 | ||
Fig. 3 represents the bandgap energy, space group and formation energy of the highly stable phases of the formidable 118 compounds which have reliable results (arranged based on the A sites). The enumerated bandgaps and formation energies are presented in the ESI†. Furthermore, the full cif files of the optimized structures are made accessible through https://github.com/cmd-l/ComputationalMaterialsScreening.
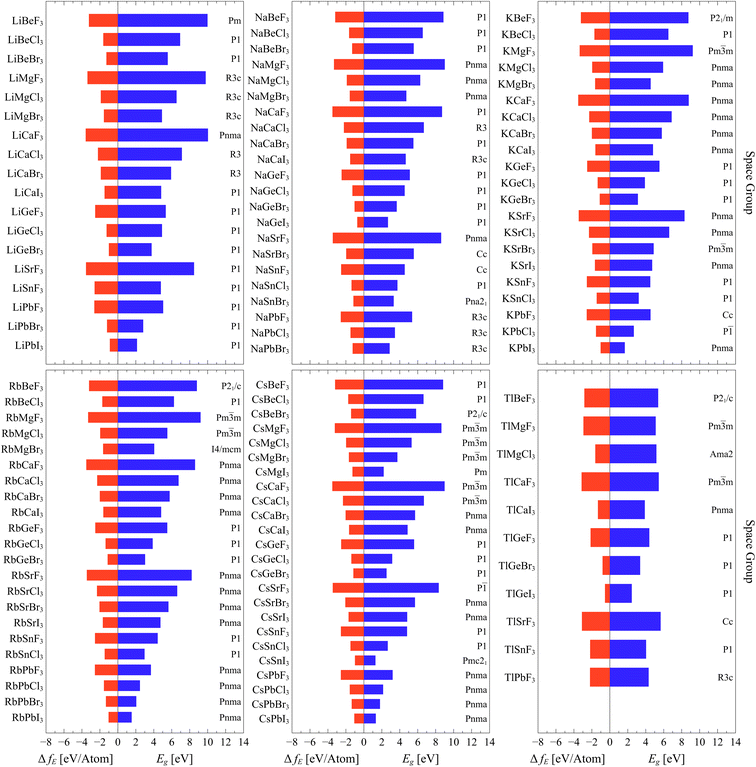 | ||
| Fig. 3 Bandgap energy Eg, space group and formation energy ΔfE of the highly stable phases of the formidable 118 compounds which have reliable results. | ||
For band gap, it is clear that the gap is mostly affected by the halogen. Evidently, the gap decreases by going down the halogen group where the highest gaps are associated with fluorides and the lowest ones are the iodides. This is expected and it is attributed to the fact that coulombic interactions, where distances are crucial and dictating the energy. So, the bandgap decreases with increasing ionic radius of the halide ion. This results from the fact these halides dominate the valence band maximum (VBM). As the ionic radius of the halide ion becomes larger, the VBM gets elevated to higher values (smaller ionization energies) resulting in a reduction in the bandgap.36,37 On the other hand, the bandgap is not strongly affected by varying A and B sites within the same group. Similar trends are observed for formation energy. As the energy becomes more negative, the stability of the compound increases. The stability of the compounds increases as we go from I to F in the X site. Both A and B sites within the same group have minimal effects on the formation energy.
The resulted number of (Li)BX3 compounds is 18 out of 28 possibilities. According to AFLOW-SYM, they all converged to non-perovskite structures except LiCaF3, which is identified to be orthorhombic perovskite with space group (Pnma,62). Most of them have bandgaps above 3 eV while only LiPbBr3 and LiPbI3 possess bandgap energies below 3 eV (semiconductor range). LiCaF3 exhibits the highest bandgap of 10.035 eV and the highest stability with a formation energy of −3.583 eV per atom. On the other hand, LiPbI3 has the lowest bandgap of 2.137 eV and its formation energy of −0.894 eV per atom.
For (Na)BX3 compounds, the resulted number of compounds is 22 out of the 28 possibilities. The majority of their highly stable phases are identified not to be perovskites except NaMg(F,Cl,Br)3 and NaSrF3, which are classified as perovskites with orthorhombic crystallography and space group (Pnma,62). As in the case of (Li)BX3 compounds, most of (Na)BX3 compounds have bandgaps above 3 eV except NaGeI3 and NaPbBr3. The perovskite NaMgF3 has the highest bandgap energy of 9.01 eV and the non-perovskite triagonal NaCaF3 is the most stable compound with formation energy of −3.583 eV per atom. On the other side, NaGeI3 has lowest bandgap of 2.685 eV as well as the least formation energy of −0.737 eV per atom.
The third subset of compounds are (K)BX3 ones. The resulted number of compounds is 21, where most of the obtained highly stable phases are orthorhombic perovskites with space group (Pnma,62). Again, there are only two compounds that have bandgap energies below 3 eV. In comparison to other (K)BX3, KMgF3 has the highest bandgap of 9.233 eV whereas KPbI3 has the lowest bandgap of 1.667 eV as well as the least stability with a formation energy of −1.026 eV per atom. KCaF3 is the most stable compound compared to other K-based compounds with a formation energy of −3.522 eV per atom.
Similar to (K)BX3 compounds, the highly stable phases of (Rb)BX3 compounds converged to perovskite structures and the majority of them are orthorhombic with space group (Pnma,62). The resulted number of compounds is 22. In terms of energy gap, in this case (and for Cs base coumpounds), there are more compounds (4 in total) with gaps below 3 eV. RbPbI3 has the lowest bandgap of 1.534 eV and the lowest formation energy of −1.037 eV per atom. On the other hand, RbMgI3 exhibits the highest energy of 9.213 eV while RbCaF3 is the most stable compound with a formation energy of −3.511 eV per atom.
For (Cs)BX3 compounds, the resulted number of compounds is the highest with 24 out of 28 possibilities. Most of them are perovskites which are either orthorhombic with space group (Pnma,62) or cubic with space group (Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m – 221). There are six compounds with a bandgap below 3 eV. CsSnI3 has the lowest bandgap energy of 1.292 eV among all resulted ABX3 compounds. On the other hand, CsCaF3 has the highest bandgap of 8.994 eV and the highest formation energy of −3.513 eV per atom.
m – 221). There are six compounds with a bandgap below 3 eV. CsSnI3 has the lowest bandgap energy of 1.292 eV among all resulted ABX3 compounds. On the other hand, CsCaF3 has the highest bandgap of 8.994 eV and the highest formation energy of −3.513 eV per atom.
Finally, for (Tl)BX3 compounds, the resulted number of compounds is the lowest, which is only 11. Most of them are classified as non-perovskite. Also, only one compound (TlGeI3) has a gap below 3 eV. On the other side, TlSrF3 has the highest bandgap of 5.657 eV while TlCaF3 exhibits the highest stability with formation energy of −3.150 eV per atom.
4 Conclusions
In this paper, a robust automated framework is used to calculate the essential properties of highly stable phases of many inorganic halide perovskites. The considered space of ABX3 compounds consists of A = Li, Na, K, Rb, Cs, Tl, B = Be, Mg, Ca, Ge, Sr, Sn, Pb, and X = F, Cl, Br, I. So, the space consists of 168 possible materials. The calculations show that only 118 of them are formidable and have reliable results. It turned out that the remaining 50 other compounds are either not formidable or suffer from computational inconsistencies. The targeted properties are the structure, the formation energy to assess stability, and the energy gap for evaluating optoelectronic applicability. The used automated framework is robust and very reliable. The core of the work is based on the density functional theory (DFT) integrated with the precision library of Standard Solid-State Pseudopotentials (SSSP) for structure relaxation and PseudoDojo for energy gap calculation. Furthermore, a very sufficient and robust random sampling is used to determine the highly stable phases. The work was driven by the fact that halide perovskites have attracted recently a substantial attention. However, we believe that the focus on the hybrid halides with organic polyatomic cations and with inadequate stability might shadow other possibilities. There is a sizable inorganic halide space that is not well explored and may be more stable than hybrid perovskites.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors would like to thank the Supercomputing Laboratory at King Abdullah University of Science & Technology (KAUST), Thuwal, Kingdom of Saudi Arabia for the support and the computing time. Also, FH Alharbi would like to acknowledge the support provided from the Saudi Data and AI Authority (SDAIA) and King Fahd University of Petroleum and Minerals (KFUPM) under SDAIA-KFUPM Joint Research Center for Artificial Intelligence Grant no JRC-AI-RFP-02.Notes and references
- K. T. Butler, D. W. Davies, H. Cartwright, O. Isayev and A. Walsh, Nature, 2018, 559, 547–555 CrossRef CAS PubMed.
- S. Curtarolo, G. L. Hart, M. B. Nardelli, N. Mingo, S. Sanvito and O. Levy, Nat. Mater., 2013, 12, 191–201 CrossRef CAS PubMed.
- F. Giustino, J. H. Lee, F. Trier, M. Bibes, S. M. Winter, R. Valentí, Y.-W. Son, L. Taillefer, C. Heil and A. I. Figueroa, et al., J. Phys.: Mater., 2021, 3, 042006 Search PubMed.
- J. L. Cann, A. De Luca, D. C. Dunand, D. Dye, D. B. Miracle, H. S. Oh, E. A. Olivetti, T. M. Pollock, W. J. Poole and R. Yang, et al., Prog. Mater. Sci., 2021, 117, 100722 CrossRef CAS.
- E. Sanchez-Rexach, T. G. Johnston, C. Jehanno, H. Sardon and A. Nelson, Chem. Mater., 2020, 32, 7105–7119 CrossRef CAS.
- S. M. Alqahtani, A. Q. Alsayoud and F. H. Alharbi, Comput. Mater. Sci., 2021, 192, 110304 CrossRef CAS.
- A. Mannodi-Kanakkithodi and M. K. Chan, Trends Chem., 2021, 3, 79–82 CrossRef CAS.
- P. Friederich, F. Häse, J. Proppe and A. Aspuru-Guzik, Nat. Mater., 2021, 20, 750–761 CrossRef CAS PubMed.
- J. J. de Pablo, N. E. Jackson, M. A. Webb, L.-Q. Chen, J. E. Moore, D. Morgan, R. Jacobs, T. Pollock, D. G. Schlom and E. S. Toberer, et al., npj Comput. Mater., 2019, 5, 1–23 CrossRef.
- C. Draxl and M. Scheffler, MRS Bull., 2018, 43, 676–682 CrossRef.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner and G. Ceder, et al., APL Mater., 2013, 1, 011002 CrossRef.
- S. Curtarolo, W. Setyawan, G. L. Hart, M. Jahnatek, R. V. Chepulskii, R. H. Taylor, S. Wang, J. Xue, K. Yang and O. Levy, et al., Comput. Mater. Sci., 2012, 58, 218–226 CrossRef CAS.
- A. Dey, J. Ye, A. De, E. Debroye, S. K. Ha, E. Bladt, A. S. Kshirsagar, Z. Wang, J. Yin and Y. Wang, et al., ACS Nano, 2021, 15, 10775–10981 CrossRef CAS PubMed.
- A. K. Jena, A. Kulkarni and T. Miyasaka, Chem. Rev., 2019, 119, 3036–3103 CrossRef CAS PubMed.
- A. A. Emery, J. E. Saal, S. Kirklin, V. I. Hegde and C. Wolverton, Chem. Mater., 2016, 28, 5621–5634 CrossRef CAS.
- S. Körbel, M. A. Marques and S. Botti, J. Mater. Chem. C, 2016, 4, 3157–3167 RSC.
- S. Hayat, R. A. Khalil, M. I. Hussain, A. M. Rana and F. Hussain, Solid State Commun., 2022, 344, 114674 CrossRef CAS.
- A. Zia, G. Murtaza, K. Ismail, R. A. Khalil and M. I. Hussain, Comput. Condens. Matter, 2022, 33, e00737 CrossRef.
- G. Prandini, A. Marrazzo, I. E. Castelli, N. Mounet and N. Marzari, npj Comput. Mater., 2018, 4, 1–13 CrossRef.
- M. J. van Setten, M. Giantomassi, E. Bousquet, M. J. Verstraete, D. R. Hamann, X. Gonze and G.-M. Rignanese, Comput. Phys. Commun., 2018, 226, 39–54 CrossRef CAS.
- A. A. Baloch, S. M. Alqahtani, F. Mumtaz, A. H. Muqaibel, S. N. Rashkeev and F. H. Alharbi, Phys. Rev. Mater., 2021, 5, 043804 CrossRef CAS.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni and I. Dabo, et al., J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- D. Hicks, C. Oses, E. Gossett, G. Gomez, R. H. Taylor, C. Toher, M. J. Mehl, O. Levy and S. Curtarolo, Acta Crystallogr., Sect. A: Found. Adv., 2018, 74, 184–203 CrossRef CAS PubMed.
- J. Heyd and G. E. Scuseria, J. Chem. Phys., 2004, 121, 1187–1192 CrossRef CAS PubMed.
- J. Even, L. Pedesseau, J.-M. Jancu and C. Katan, J. Phys. Chem. Lett., 2013, 4, 2999–3005 CrossRef CAS.
- A. Amat, E. Mosconi, E. Ronca, C. Quarti, P. Umari, M. K. Nazeeruddin, M. Gratzel and F. De Angelis, Nano Lett., 2014, 14, 3608–3616 CrossRef CAS PubMed.
- T. Das, G. Di Liberto and G. Pacchioni, J. Phys. Chem. C, 2022, 126, 2184–2198 CrossRef CAS.
- H. Joshi, R. Thapa, A. Laref, W. Sukkabot, L. Pachuau, L. Vanchhawng, P. Grima-Gallardo, M. M. S. HE and D. Rai, Surf. Interfaces, 2022, 30, 101829 CrossRef CAS.
- E. Cao, J. Qiu, D. Zhou, Y. Yang, Q. Wang and Y. Wen, Chem. Commun., 2020, 56, 4460–4463 RSC.
- C. Vona, D. Nabok and C. Draxl, Adv. Theory Simul., 2022, 5, 2100496 CrossRef CAS.
- S. F. Hoefler, G. Trimmel and T. Rath, Monatshefte für Chemie, 2017, 148, 795–826 CrossRef CAS PubMed.
- L. Peedikakkandy and P. Bhargava, RSC Adv., 2016, 6, 19857–19860 RSC.
- D. Sabba, H. K. Mulmudi, R. R. Prabhakar, T. Krishnamoorthy, T. Baikie, P. P. Boix, S. Mhaisalkar and N. Mathews, J. Phys. Chem. C, 2015, 119, 1763–1767 CrossRef CAS.
- A. M. Glazer, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1972, 28, 3384–3392 CrossRef CAS.
- H. Park, F. H. Alharbi, S. Sanvito, N. Tabet and F. El-Mellouhi, ChemPhysChem, 2018, 19, 703–714 CrossRef CAS PubMed.
- M. Legesse, H. Park, F. El Mellouhi, S. N. Rashkeev, S. Kais and F. H. Alharbi, ChemPhysChem, 2018, 19, 943–953 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ra00185g |
| ‡ All the data and the optimized cif files of the presented materials are accessible through https://github.com/cmd-l/ComputationalMaterialsScreening. |
| This journal is © The Royal Society of Chemistry 2023 |
