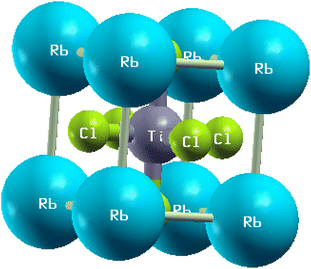Open Access Article
Open Access ArticleInvestigation of structural, opto-electronic and thermoelectric properties of titanium based chloro-perovskites XTiCl3 (X = Rb, Cs): a first-principles calculations
Naimat Ullah Khana,
Abdullah*b,
Umar Ayaz Khanb,
Vineet Tirth cd,
Jehan Y. Al-Humaidi
cd,
Jehan Y. Al-Humaidi e,
Moamen S. Refatf,
Ali Algahtanicd and
Abid Zaman
e,
Moamen S. Refatf,
Ali Algahtanicd and
Abid Zaman *g
*g
aDepartment of Physics, University of Science and Technology Bannu, 28100 Pakistan
bDepartment of Physics, Government Post Graduate College Karak, 27200 Pakistan. E-mail: ktkshoraim@gmail.com
cMechanical Engineering Department, College of Engineering, King Khalid University, Abha 61421, Asir, Kingdom of Saudi Arabia
dResearch Center for Advanced Materials Science (RCAMS), King Khalid University, Guraiger, P. O. Box 9004, Abha-61413, Asir, Kingdom of Saudi Arabia
eDepartment of Chemistry, College of Science, Princess Nourah bint Abdulrahman University, P. O. Box 84428, Riyadh 11671, Saudi Arabia
fDepartment of Chemistry, College of Science, Taif University, P. O. Box 11099, Taif 21944, Saudi Arabia
gDepartment of Physics, Riphah International University, Islamabad 44000, Pakistan. E-mail: zaman.abid87@gmail.com
First published on 21st February 2023
Abstract
Perovskites are a significant class of materials with diverse uses in modern technology. The structural, electronic, elastic, thermoelectric, and optical properties of RbTiCl3 and CsTiCl3 perovskites were estimated using the FP-LAPW method within the framework of density functional theory. The exchange–correlation energy of both analyzed systems was calculated using the Generalized Gradient Approximation (GGA) functional. The structures are optimized and lattice constants of 5.08 Å and 5.13 Å are found for XTiCl3 (X = Rb, Cs), respectively. The structural analysis reveals that they have cubic symmetry. Their half metallic nature was proved by their metallic nature in one spin channel and semiconducting nature in the opposing spin channel. Densities of states are calculated to predict the interaction of orbitals of distinct atoms in the compounds. From the results of optical response, it is found that these compounds show high optical absorption in the visible region of light. Moreover, thermoelectric properties of the studied materials are calculated as a function of chemical potential at different temperatures using the theory of semi-classical Boltzmann transport within BoltzTrap code. The thermoelectric response shows that the investigated compounds as p-type can be beneficial in overcoming the global warming issue.
Introduction
Researchers are looking for materials that may exhibit potential applications and fulfill the need of modern technology. Literature reveals that perovskites have been investigated frequently due to their remarkable physical and chemical features such as piezoelectricity, ferro-electricity, superconductivity, thermoelectricity, catalytic activity, ferromagnetism, half-metallic and magneto-resistance, and thermoelectric properties.1–3Perovskites can be described in terms of the general formula ABX3, where A & B are cations and X is an anion. Halide perovskites refers to perovskites in which X belongs to halide anions. A literature study reveals that halide perovskites have been studied for a number of device applications, including solar-cells, topological insulators, superconductors and spintronics.4,5
Spintronic applications are based on half-metallicity. It is an emerging phenomenon that refers to compounds exhibiting a metallic nature for one spin channel and insulating or semiconducting for the opposite spin channel.6 Half metallic (HM) compounds were found in 1980 and have been extensively researched for spin injection both theoretically and experimentally over the last decade.7–12 This is a widespread phenomenon that has been observed in a variety of other materials, including Heusler alloys, transition metal oxides, and dilute magnetic semiconductors13–19 The spin dependent unique property of HM allows for an opportunity to construct novel devices such as magnetic sensors and non-volatile magnetic random access memory that operate under the combined effect of spin-polarization and microelectronics.20,21
Among the oxide perovskites, MgMnO3 is a semiconductor at ambient temperature and has an insulating response at low temperatures.22 Thota and his research group further investigated MgMnO3 experimentally using the sol–gel method and discovered that MgMnO3 is stable in cubic phase at low temperatures.23 The same research group further investigated Manganese oxide perovskite GaMnO3 for magnetic and thermoelectric properties.24
Recently, halide perovskites have been studied to find more suitable HM materials. In the literature we found that complex alkali metals fluorides are widely explored by scientists owing to their vast applications as fluorinating agents and as catalysts in organo-fluorochemical chemistry.25,26
The thallium based chloroperovskite TlXCl3 (X = Ca and Cd) compounds have been reported by Shams U. Zaman et al.27 They suggested that these can be used as scintillating materials. Ternary chloride perovskites have a broad range of applications among halide perovskite compounds due to wide bandgap and maximum valued optical absorption coefficients and having bright photoluminescence of narrow band, low exciton binding energies, and long-range carrier diffusion. Due to these properties, such materials are widely examined theoretically as well as experimentally.28–31
Moreover, fluoro-perovskites have considerable applications in photoluminescence, high temperature superconductors, colossal magneto-resistivity and piezoelectricity. Motivated by the literature review, we presented a detailed simulation-based analysis on the structural, electronics, thermoelectric, and optical properties of CsTiCl3 and RbTiCl3 halide perovskites in this paper. To carry out our calculations, we employed Tran–Blaha modified Becke–Johnson (Tb-mbj) approximation to find the exchange–correlation energy and full-potential linearized augmented plane wave (FP-LAPW) method to treat nuclei–electrons interaction within the framework of density functional theory (DFT). It is hoped that the present study would motivate the experimentalists to conduct experiments and further explore this field.
Computational details
To perform the present study, we have employed Wien2k code under the frame work of DFT.15,32 Wien2K works on the principle of pull potential leading to FP-LAPW method.33 Tb-mbj approximation is selected to estimate the exchange–correlation energy.34 The cut-off energy of 500 eV was employed with taking titanium (Ti) as center of the first Brillouin zone of both the compounds.The structural parameters and volume versus energy curve are calculated with the help of Birch–Murnaghan equation. Various elastic parameters are calculated from the elastic constants which are determined by using IR-Elastic package.35 Optical properties are determined from the real and imaginary part of dielectric function ε(ω) = ε1(ω) + iε2(ω). The real part ε1(ω) is calculated from the momentum matrix of occupied and unoccupied energy states, while the imaginary part is determined from the real part using Kramers–Kronig relations. Thermal properties are calculated using BoltzTrap code.36 To achieve the best results, the cut-off value of 1 max was set to 10, RKmax was set to 2.5, and 2000 K-points were chosen.
Structural properties
In this subsection, we investigated the structural properties of chloro-perovskites XTiCl3 (X = Cs or Rb). Both compounds have an ideal cubic structure with the same unit formula having space group Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (221). In its unit cell X = Cs or Rb atom lies at the corner of the unit cell with positions (0,0,0) and titanium atom occupies the center of the unit cell with the position (0.5,0.5,0.5) to which six chlorine atoms are attached at center positions (0,0.5,0.5). Fig. 1 depicts the crystallographic unit cell of these compounds. For the verification of structural stability of these perovskite, we use Goldschmidt tolerance factor having formula;37
m (221). In its unit cell X = Cs or Rb atom lies at the corner of the unit cell with positions (0,0,0) and titanium atom occupies the center of the unit cell with the position (0.5,0.5,0.5) to which six chlorine atoms are attached at center positions (0,0.5,0.5). Fig. 1 depicts the crystallographic unit cell of these compounds. For the verification of structural stability of these perovskite, we use Goldschmidt tolerance factor having formula;37
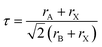 | (1) |
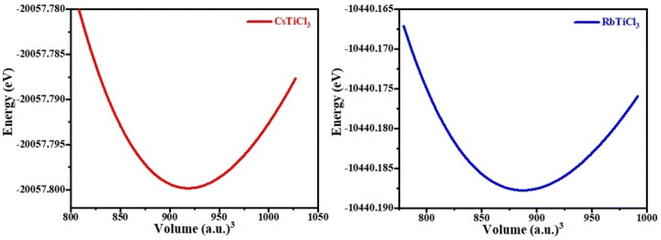
In the above formula, rA, rB and rX represents the ionic radii of A, B and X atoms respectively. The literature shows that if 0.7 < τ < 1, then material will possess stable structure and the structure of material will be more stable if the tolerance factor is close to 1. The tolerance factor values for CsTiCl3 and RbTiCl3 are found to be 0.98 and 0.97 respectively, indicating that both crystal structures are stable, however CsTiCl3 has a more stable crystal structure than RbTiCl3. Moreover, the octahedral factor is also evaluated for both compounds and presented in Table 1, which indicates the stability of these compound.38 The stability of this structure is also checked by plotting the changes in total energy as a function of volume has been shown in Fig. 2. The goodness of fit (R2) is also evaluated and presented in Table 1.
| Structural parameters | RbTiCl3 | CsTiCl3 |
|---|---|---|
| Equilibrium lattice constant (ao) | 5.08 | 5.13 |
| Bulk modulus (B0) | 35.49 | 34.48 |
| Ground state volume (V0) | 887.21 | 918.56 |
| Bulk modulus first derivative B′ | 5.04 | 4.66 |
| Energy at ground state (E0) | −10440.18 | −20057.79 |
| Tolerance factor | 0.97 | 0.98 |
| Octahedral factor | 0.83 | 0.88 |
| Goodness of fit (R2) | 0.952 | 0.961 |
Electronic properties
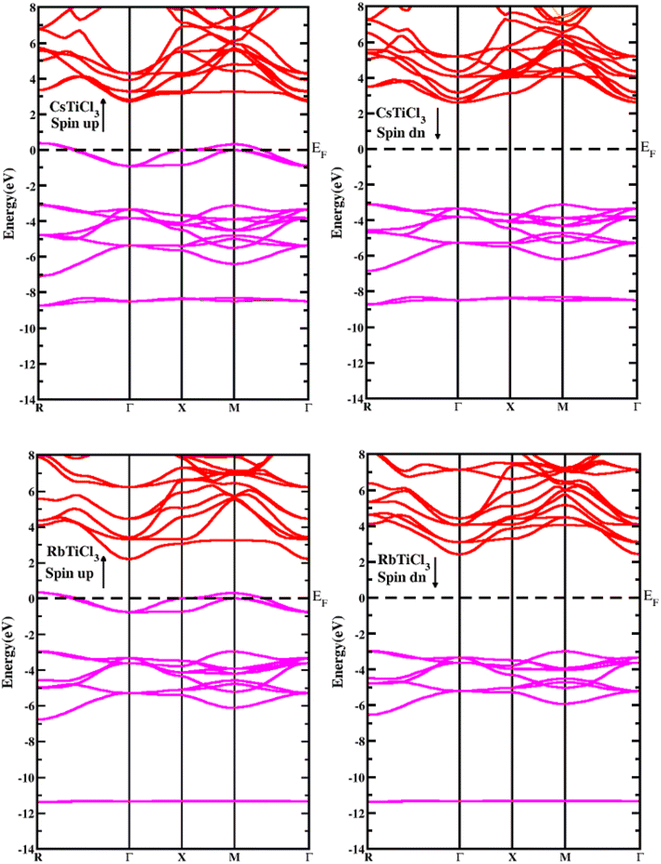
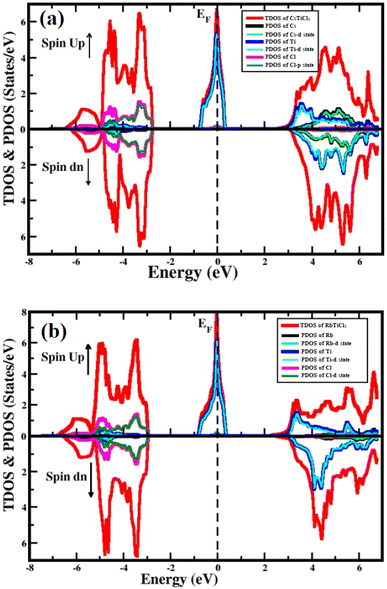
To study the semiconducting nature of materials we calculate their electronic properties. The electronic band structure and density of states are calculated for both compounds in spin up and spin down directions using the generalized gradient approximation of Tran–Blaha modified Becke–Johnson (Tb-mbj). The electronic band structures for the investigated systems are depicted in Fig. 3. The band structure analysis shows that both understudy perovskites exhibited indirect band gap semiconductors in spin down channel. In case of spin dn channel, their estimated energy band gap values are found 5.2 eV and 5.5 eV for RbTiCl3 and CsTiCl3, respectively. However, in case of spin up direction, both the compounds are found metallic as their valence and conduction bands overlap; hence the materials are half metallic compounds.39 To further investigate the contribution of each valence orbital of every constituent atom of the compound to the valence and conduction bands, we calculate their total density of states (TDOS) and projected density of states (PDOS). The density of states also conform the half metallic behavior of the studied compounds. The plots of calculated density of states for RbTiCl3 and CsTiCl3 are presented Fig. 4 respectively. The PDOS graphs show that in the case of RbTiCl3, the d-states of Ti and Cl contribute significantly to the valence band while only the Ti-d state contributes significantly to the conduction band. However, in case of CsTiCl3, Ti-d and Cl-p sates principally form the valence band while Ti-d and Cs-d states play a major rule in the conduction band near the Fermi level. Further, it can also be noticed from the study of PDOS that hybridization between the d-states of Ti and Cl atoms and Ti-d and Cl-p sates take place in the valence bands of XTiCl3 (X = Rb, Cs), respectively. However, in case of CsTiCl3, there is occurrence of hybridization between the d sates of Ti and Cs atoms in conduction, while no overlapping of orbitals are observed in conduction band of RbTiCl3.Optical properties
The well known dielectric function ε(ω) = ε1(ω) + iε2(ω) describes the optical response of the medium at all photon energies. The imaginary part explains the compound's absorptive behavior and is directly related to the electronic band structure of a material. The Imaginary part of the dielectric function ε2(ω) is represented by:40
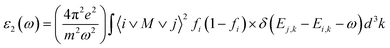 | (2) |
 | ||
| Fig. 5 The curve of obtained (a) real part and (b) imaginary part of dielectric function for XTiCl3 (X = Cs, Rb). | ||
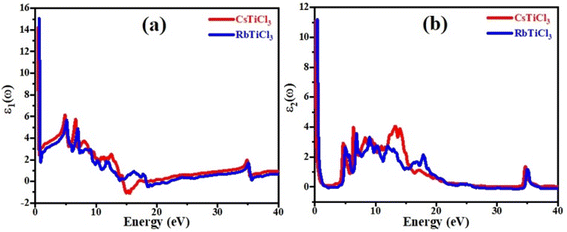
Fig. 6(a) depicts the relationship between refractive index and incident photon energy. The figure clearly shows that the value of n(0) for CsTiCl3 is 3.94 and for RbTiCl3 is 4.01. Figure indicates that the refractive index increases and eventually reaches a maximum value of 2.5 for CsTiCl3 at 4 eV and 2.4 for RbTiCl3 at 5 eV energy, after which the refractive index drops to 0.4 and 0.3 for CsTiCl3 and RbTiCl3, respectively. Both compounds have refractive index values larger than one, indicating that incident photons lose energy when they interact with the electrons of the compound. Fig. 6(b) shows the absorption coefficient of CsTiCl3 and RbTiCl3 and it is clear that CsTiCl3 has a threshold absorption 0.001 and RbTiCl3 has threshold absorption 0.0011 and a maximum absorption 250 at 35 eV energy in the visible region and 249.5 at 35 eV in the visible region energy for CsTiCl3 and RbTiCl3, respectively. Fig. 6(c) depicts the optical conductivity of CsTiCl3 and RbTiCl3 as a function of incident photon energy. From the figure we can see that CsTiCl3 has high optical conductivity of 7590 in the visible region and RbTiCl3 has a high optical conductivity of 6500 in the visible region.
 | ||
| Fig. 6 The curve of (a) refractive index, (b) absorption coefficient, (c) reflectivity, and (d) conductivity of XTiCl3 (X = Cs, Rb). | ||
Fig. 6(d) shows the reflectivity curve of both compounds. From the figure it is clear that both compounds have a transmitting nature in the energy range of 0 to 11 eV and an excellent reflectivity in the energy range of 11 to 22 eV. From figure it is also clear that CsTiCl3 has maximum reflectivity of 0.44 at 15 eV energy and RbTiCl3 has maximum reflectivity of 0.26 at 22 eV energy, which justifies that CsTiCl3 is better reflector than RbTiCl3.
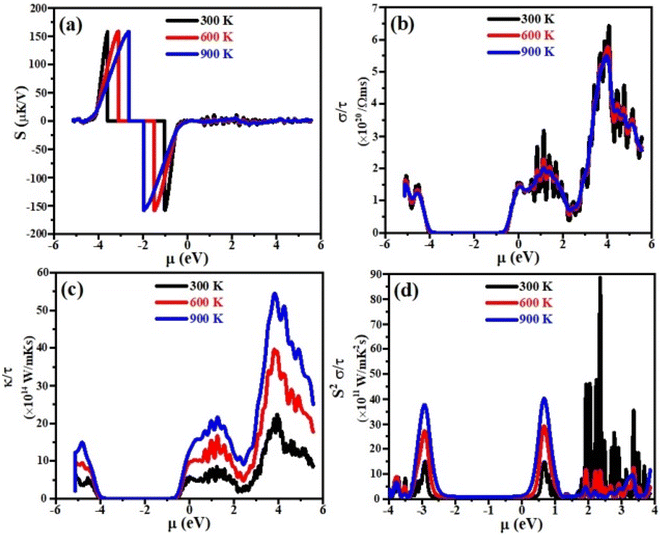
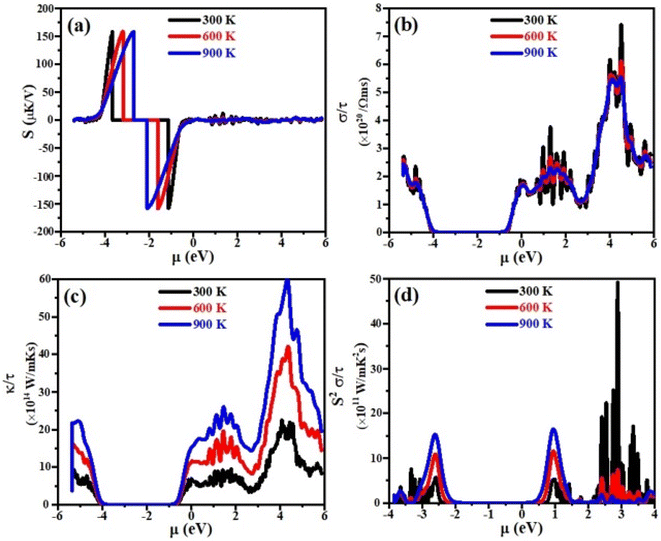
Thermoelectric properties
Currently, the world is facing the issue of energy crises. It has been estimated that more than half of the energy from primary energy sources is lost as waste heat during their use. This has badly affected the GDP of the world.42–44 Scientists across the world have focused their research to discover smart thermoelectric materials. Thermoelectricity is a phenomenon in which the waste heat can be converted into useable clean and green energy and vice versa and materials with these properties are referred to as thermoelectric materials.45,46 The thermoelectric performance of a material can be estimated in terms of figure of merit, abbreviated as ZT. Mathematically it can be written as;47 ZT = S2σT/κe where σ, S, T and κe represent the electrical conductivity, Seebeck coefficient, absolute temperature and thermal conductivity at which the thermoelectric properties are measured, respectively. Aiming that, we have for the first time calculated the electrical conductivity (σ), Seebeck coefficient (S), power factor (PF) and thermal conductivity (κe) for XTiCl3 (X= Cs, Rb) compounds for different temperatures as a function of chemical potential (μ) and are presented in Fig. 7 and 8.Seebeck coefficient is measured in terms of voltage induced at the cost of temperature gradient across a conductor. The sign of S refers to the type of dominant charge carriers. Positive S means p-type (holes as dominant charge carriers), while negative S refers to n-type semiconductor (electrons as main charge carriers). The room temperature S values for XTiCl3 (X= Cs, Rb) as a function of μ for different temperatures are plotted and shown in Fig. 7(a) and 8(a).
The figures indicate that both compounds have significant Seebeck coefficient values both in the positive and negative range which shows that both type of charge carriers are present in the systems. It is also worth noting that S exhibits its maximum values at small chemical potential values. Both the materials exhibit significant values of S ∼ 160 μK V−1 at 300 K. However, when temperature in increased from 300 K to 900 K no significant change have been noticed in S for both the investigated materials.
Electrical conductivity (σ) is an important thermoelectric parameter that describes how the movement of charge carriers from a higher temperature region to a lower temperature region causes an electric current.
For good thermoelectric performance, a compound should exhibit higher value of electrical conductivity. The plots of electrical conductivity as a function chemical potentials at different temperatures are displayed in Fig. 7(b) and 8(b).
It can be noticed from the plots that the value of σ is higher at positive chemical potential than in the negative μ region. This result implicates that electron doping in these XTiCl3 (X= Cs, Rb) materials will be more beneficial for thermoelectric applications than hole doping.
At 300 K, the maximum value of σ for CsTiCl3 and RbTiCl3 is found to be ∼6.5 × 1020 Ωms−1 (4 eV) and ∼7.5 × 1020 Ωms−1 (4.8 eV), respectively. However, when temperature is increased from 300 K to 900 K, σ are decreased and attain their lowest values (∼5.5 × 1020 Ωms−1 and ∼5.5 × 1020 Ωms−1) for CsTiCl3 and RbTiCl3, respectively. The slight decrease in the electrical conductivity with temperature rising may be attributed to the increasing charge carrier concentration plus collision and scattering phenomenon as well.
The phenomenon of heat conduction in a material by moment of free electrons and lattice vibration is termed as thermal conductivity κe. Fig. 7(c) & 8(c) illustrate the variation of electronic thermal conductivity versus chemical potential at 300 K, 600 K and 900 K.
It can be noticed from the figures that both the compounds exhibited higher thermal conductivity for positive chemical potential and their thermal conductivity is found to be ∼22 × 1014 W Ωms−1 (4 eV) at 300 K. However, in contrast to electrical conductivity, electronic thermal conductivity is increased drastically when temperature goes from 300 K to 900 K and achieve their maximum peaks (∼5.5 × 1014 W Ωms−1 for CsTiCl3∧60.0 × 1014 W Ωms−1 for RbTiCl3). It can also be noticed from the plots that both electrical and thermal conductivities show similar profile and their ratio bears a constant value, hence the results follow the Wiedemann–Franz law: k = σLT.
The efficiency of a material can be estimated in term of power factor (PF). PF can be determined from Seebeck coefficient and electrical conductivity (PF = S2σ).48 The graphs of power factor versus chemical potential at temperatures 300 K, 600 K and 900 K are shown in Fig. 7(d) and 8(d).
Both the compounds exhibited their maximum PF (90.0 × 1011 W mK−2 s−1 (2.4 eV) for CsTiCl3 and 50.0 × 1011 W mK−2 s−1 (2.9 eV) for RbTiCl3) at 300 K. However, at elevated temperature, their Pf decrease and attain minimum values at 900 K. It is also interesting to note that the power factor for p-type region is higher of the studied systems than n-type region. The thermoelectric study of the under investigated compounds reveals that these materials can be employed for the construction of thermoelectric applications at ambient temperature.
Elastics properties
Elastic properties of material have important applications in engineering and medical fields, using the material with best elastic properties are too much important. The mechanical and dynamical characteristics of material depend upon elasticity of material and related with each other through elastic constants. Elastic constant takes a crucial role in shaping the properties of material and shows its reaction to external applied forces. Three elastic constants C11, C12 and C44 are sufficient to completely describe the mechanical properties of cubic compounds. Elastic constant values are computed and correlated with the literature. The calculated values of all the elastic parameters are shown in Table 2.| Compounds | C11 | C12 | C44 | B | A | G | E | B/G |
|---|---|---|---|---|---|---|---|---|
| RbTiCl3 | 59.5 | 29.2 | 8.5 | 36.8 | 0.40 | 18.5 | 42.2 | 2.04 |
| CsTiCl3 | 55.9 | 24.8 | 6.84 | 34.9 | 0.14 | 15.2 | 46.40 | 2.29 |
To ensure the mechanical stability of cubic perovskites, the Born–Huang criteria C11 > 0, C44 > 0, (C11–C12) > 0 and C12 < B < C11 are determined for all the understudy compounds indicating their stability. Specific mechanical properties such as bulk modulus, young modulus, anisotropy factor and shear modulus can be estimated by using the following formulas:49
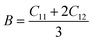 | (3) |
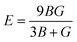 | (4) |
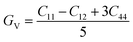 | (5) |
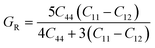 | (6) |
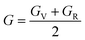 | (7) |
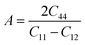 | (8) |
The computed result listed in Table 2 shows that the value of B (bulk modulus) for RbTiCl3 (36.8) is greater than that for CsTiCl3 (34.9), concluding that if both compounds are compressed from all sides RbTiF3 withstand more with respect to CsTiCl3.
The shear modulus (G) represents the toughness of the system. The computed data calculated for shear modulus is listed in Table 2. It is clear from the table values that shear modulus (G) for RbTiCl3 is greater than CsTiCl3. It determines that RbTiCl3 is harder than CsTiCl3. So, RbTiCl3 will show greater opposition to deformation than CsTiCl3.
The stiffness of the material can be represented by parameter known as young modulus (E). From Table 2 the computed values for the young modulus indicate that CsTiCl3 is stiffer than RbTiCl3. Ductility and brittleness are of much importance in an engineering point of view. Ductility and brittleness of a compound can be indicated by using Pugh ratio (B/G). According to criteria of high Pugh ratio material will be ductile if B/G > 1.75 and brittle if B/G < 1.75. Thus B/G values for these compounds from Table 2 indicates that both compound have ductile nature.
Anisotropic factor (A) is the parameter that indicates whether or not the material structural properties remain the same in all directions. For the medium to be isotropic, value of A is equal to 1 else, anisotropic. From Table 2 the computed values indicate the anisotropic nature.
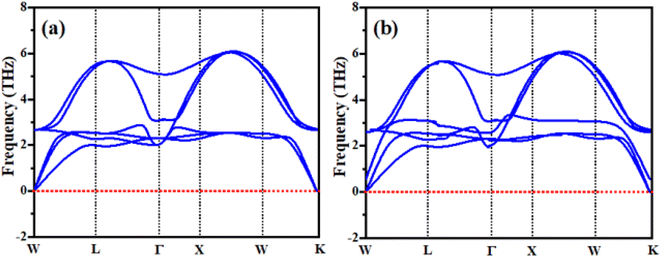
Phonopy spectra
Phonons are a crucial component of dynamic behaviors and thermal characteristics, which are the main aspects of the fundamental problems of materials science. The phonon dispersion band structure of cubic ternary RbTiCl3 and CsTiCl3 are investigated using the WIEN2K package as depicted in Fig. 9. It can be seen from Fig. 9 that the phonon dispersion curves for both materials are positive and there are no negative values of dispersion curves (imaginary phonon frequencies). The positive dispersion curves confirm the phonon dynamical stability of both compounds. Our result are analogy to BaMCl3 (M = Ag, Cu).50Conclusion
Shortly, in this research work, we have calculated the structural, electronic, elastic, optical and thermoelectric properties of XTiCl3 (X = Rb, Cs) perovskites using FP-LAPW numerical method in Wien2K under the umbrella of DFT. The structures of both the compounds were found in cubic phase. The lattice constant were optimized and found 5.08 and 5.13 for XTiCl3 (X = Rb, Cs), respectively. The compound shows 100% of spin polarization for electronic studies, with spin up states conducting and spin down states semi-conducting. Moreover, the optical response of these compounds like optical absorption, reflectivity and refractive index show that these materials can be used as a UV absorbers. The mechanical properties reveals that XTiCl3 (X = Rb, Cs) satisfy the stability criteria in cubic structure. The dynamical stability of the corresponding compounds is conformed from phonon spectra. Thermoelectric properties like electrical conductivity, thermal conductivity, Seebeck coefficient, and power factor were estimated using BoltzTrape code, based on the semi-classical Boltzmann transport theory. The thermoelectric study indicates that both compounds are the promising candidates for thermoelectric applications when used as p-type semiconductor.Conflicts of interest
The authors have no conflict of interest.Acknowledgements
The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University Abha 61421, Asir, Kingdom of Saudi Arabia for funding this work through the Small Groups Project under grant number RGP.1/123/43. Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2023R24), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.References
- B. Amin, F. Majid, M. B. Saddique, B. U. Haq, A. Laref, T. A. Alrebdi and M. Rashid, Physical properties of half-metallic AMnO3 (A= Mg, Ca) oxides via ab initio calculations, Comput. Mater. Sci., 2018, 146, 248–254 CrossRef CAS.
- N. Kumar, H. Kishan, A. Rao and V. P. Awana, Fe ion doping effect on electrical and magnetic properties of La0. 7Ca0. 3Mn1− xFexO3 (0≤ x≤ 1), J. Alloys Compd., 2010, 502(2), 283–288 CrossRef CAS.
- Y. Wang, Y. Sui, P. Ren, L. Wang, X. Wang, W. Su and H. J. Fan, Correlation between the structural distortions and thermoelectric characteristics in La1− x A x CoO3 (A= Ca and Sr), Inorg. Chem., 2010, 49(7), 3216–3223 CrossRef CAS PubMed.
- B. Kang, Q. Feng and K. Biswas, Comparative study of perovskite-type scintillator materials CsCaI3 and KCaI3 via first-principles calculations, J. Phys. D: Appl. Phys., 2018, 51(6), 065303 CrossRef.
- K. Ephraim Babu, N. Murali, K. Vijaya Babu, P. Taddesse Shibeshi and V. Veeraiah, Structural, Elastic, Electronic, and Optical Properties of Cubic Perovskite CsCaCl_3 Compound: An ab initio Study, Acta Phys. Pol., A, 2014, 125(5), 1179–1185 CrossRef.
- R. A. De Groot, F. M. Mueller, P. V. van Engen and K. H. Buschow, New class of materials: half-metallic ferromagnets, Phys. Rev. Lett., 1983, 50(25), 2024 CrossRef CAS.
- X. Dai, G. Liu, G. H. Fecher, C. Felser, Y. Li and H. Liu, New quaternary half metallic material CoFeMnSi, J. Appl. Phys., 2009, 105(7), 07E901 CrossRef.
- G. D. Liu, X. F. Dai, H. Y. Liu, J. L. Chen, Y. X. Li, G. Xiao and G. H. Wu, Mn 2 co z (z= al, ga, in, si, ge, sn, sb) compounds: Structural, electronic, and magnetic properties, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77(1), 014424 CrossRef.
- A. Abbad, W. Benstaali, H. A. Bentounes, S. Bentata and Y. Benmalem, Search for half-metallic ferromagnetism in orthorhombic Ce (Fe/Cr) O3 perovskites, Solid State Commun., 2016, 228, 36–42 CrossRef CAS.
- M. Benkabou, H. Rached, A. Abdellaoui, D. Rached, R. Khenata, M. H. Elahmar, B. Abidri, N. Benkhettou and S. Bin-Omran, Electronic structure and magnetic properties of quaternary Heusler alloys CoRhMnZ (Z= Al, Ga, Ge and Si) via first-principle calculations, J. Alloys Compd., 2015, 647, 276–286 CrossRef CAS.
- X. P. Wei, J. B. Deng, S. B. Chu, G. Y. Mao, L. B. Hu, M. K. Yang and X. R. Hu, A first principles study on the full-Heusler compound Mn2CuSb, Comput. Mater. Sci., 2011, 50(3), 1175–1178 CrossRef CAS.
- H. H. Xie, Q. Gao, L. Li, G. Lei, G. Y. Mao, X. R. Hu and J. B. Deng, First-principles study of four quaternary Heusler alloys ZrMnVZ and ZrCoFeZ (Z= Si, Ge), Comput. Mater. Sci., 2015, 103, 52–55 CrossRef CAS.
- S. Yousuf and D. C. Gupta, Insight into half-metallicity, spin-polarization and mechanical properties of L21 structured MnY2Z (Z= Al, Si, Ga, Ge, Sn, Sb) Heusler alloys, J. Alloys Compd., 2018, 735, 1245–1252 CrossRef CAS.
- A. Q. Seh and D. C. Gupta, Exploration of highly correlated Co-based quaternary Heusler alloys for spintronics and thermoelectric applications, Int. J. Energy Res., 2019, 43(14), 8864–8877 CAS.
- A. Missoum, T. Seddik, G. Murtaza, R. Khenata, A. Bouhemadou, Y. Al-Douri, A. Abdiche, H. Meradji and H. Baltache, Ab initio study of the structural and optoelectronic properties of the half-Heusler CoCr Z (Z= Al, Ga), Can. J. Phys., 2014, 92(10), 1105–1112 CrossRef CAS.
- L. H. Ye, A. J. Freeman and B. Delley, Half-metallic ferromagnetism in Cu-doped ZnO: density functional calculations, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73(3), 033203 CrossRef.
- S. Feng, S. Li, X. Li and H. Fu, Doping-dependent thermoelectric properties of BiSb3Te6 from first-principle calculations, Comput. Mater. Sci., 2014, 95, 563–567 CrossRef CAS.
- S. Balasubramanian, D. S. Priyanka, M. Srinivasan and P. Ramasamy, Ab-initio method to investigate perovskites BiXO3 (X= Be, Ca, Mg, Na, K, Li) for spintronics applications, Solid State Sci., 2022, 126, 106839 CrossRef CAS.
- Y. Al-Douri, U. Hashim, R. Khenata, A. H. Reshak, M. Ameri, A. Bouhemadou, A. R. Ruslinda and M. M. Arshad, Ab initio method of optical investigations of CdS1− xTex alloys under quantum dots diameter effect, Sol. Energy, 2015, 115, 33–39 CrossRef CAS.
- S. A. Wolf, D. D. Awschalom, R. A. Buhrman, J. M. Daughton, V. S. von Molnár, M. L. Roukes, A. Y. Chtchelkanova and D. M. Treger, Spintronics: a spin-based electronics vision for the future, science, 2001, 294(5546), 1488–1495 CrossRef CAS PubMed.
- F. Sher and J. P. Attfield, Synthesis, structure and magnetic properties of Ba2CrMoO6, Solid State Sci., 2006, 8(3–4), 277–279 CrossRef CAS.
- L. Bocher, M. H. Aguirre, R. Robert, D. Logvinovich, S. Bakardjieva, J. Hejtmanek and A. Weidenkaff, High-temperature stability, structure and thermoelectric properties of CaMn1-xNbxO3 phases, Acta Mater., 2009, 57(19), 5667–5680 CrossRef CAS.
- S. Thota, K. Singh, B. Prasad, J. Kumar, C. Simon and W. Prellier, Formation mechanism, optical and magneto-dielectric studies of new cubic spinel MgMnO3, AIP Adv., 2012, 2(3), 032140 CrossRef.
- Y. Wang, Y. Sui, P. Ren, L. Wang, X. Wang, W. Su and H. J. Fan, Correlation between the structural distortions and thermoelectric characteristics in La1− x A x CoO3 (A= Ca and Sr), Inorg. Chem., 2010, 49(7), 3216–3223 CrossRef CAS PubMed.
- G. G. Yakobson and N. E. Akhmetova, Alkali metal fluorides in organic synthesis, Synthesis, 1983, 1983(03), 169–184 CrossRef.
- M. Sahnoun, M. Zbiri, C. Daul, R. Khenata, H. Baltache and M. Driz, Full potential calculation of structural, electronic and optical properties of KMgF3, Mater. Chem. Phys., 2005, 91(1), 185–191 CrossRef CAS.
- S. U. Zaman, N. Rahman, M. Arif, M. Saqib, M. Husain, E. Bonyah, Z. Shah, S. Zulfiqar and A. Khan, Ab initio investigation of the physical properties of Tl based chloroperovskites TlXCl3 (X= Ca and Cd), AIP Adv., 2021, 11(1), 015204 CrossRef CAS.
- K. Shimamura, H. Sato, A. Bensalah, V. Sudesh, H. Machida, N. Sarukura and T. Fukuda, Crystal growth of fluorides for optical applications, Cryst. Res. Technol., 2001, 36(8–10), 801–813 CrossRef CAS.
- M. Lal and S. Kapila, Structural, electronic, optical and mechanical properties of CsCaCl3 and KCdF3 cubic perovskites, Int. J. Mater. Sci., 2017, 12, 137–147 Search PubMed.
- A. Voloshynovskii, P. Savchyn, I. Karbovnyk, S. Myagkota, M. C. Guidi, M. Piccinini and A. I. Popov, CsPbCl3 nanocrystals dispersed in the Rb0, 8Cs0, 2Cl matrix studied by far-infrared spectroscopy, Solid State Commun., 2009, 149(15–16), 593–597 CrossRef CAS.
- M. Tyagi, M. Zhuravleva and C. L. Melcher, Theoretical and experimental characterization of promising new scintillators: Eu2+ doped CsCaCl3 and CsCaI3, J. Appl. Phys., 2013, 113(20), 203504 CrossRef.
- P. Hohenberg and W. Kohn, Inhomogeneous electron gas, Phys. Rev., 1964, 136(3B), B864 CrossRef.
- E. Sjöstedt, L. Nordström and D. J. Singh, An alternative way of linearizing the augmented plane-wave method, Solid State Commun., 2000, 114(1), 15–20 CrossRef.
- F. Tran and P. Blaha, Accurate band gaps of semiconductors and insulators with a semilocal exchange-correlation potential, Phys. Rev. Lett., 2009, 102(22), 226401 CrossRef PubMed.
- F. D. Murnaghan, The compressibility of media under extreme pressures, Proc. Natl. Acad. Sci., 1944, 30(9), 244–247 CrossRef CAS PubMed.
- G. K. Madsen and D. J. Singh, BoltzTraP. A code for calculating band-structure dependent quantities, Comput. Phys. Commun., 2006, 175(1), 67–71 CrossRef CAS.
- G. Kieslich, S. Sun and A. K. Cheetham, An extended tolerance factor approach for organic–inorganic perovskites, Chem. Sci., 2015, 6(6), 3430–3433 RSC.
- C. J. Bartel, C. Sutton, B. R. Goldsmith, R. Ouyang, C. B. Musgrave, L. M. Ghiringhelli and M. Scheffler, New tolerance factor to predict the stability of perovskite oxides and halides, Sci. Adv., 2019, 5(2), eaav0693 CrossRef CAS PubMed.
- S. A. Dar, V. Srivastava, U. K. Sakalle, A. Rashid and G. Pagare, First-principles investigation on electronic structure, magnetic, mechanical and thermodynamic properties of SrPuO3 perovskite oxide, Mater. Res. Express, 2018, 5(2), 026106 CrossRef.
- A. Amudhavalli, R. Rajeswarapalanichamy, K. Iyakutti and A. K. Kushwaha, First principles study of structural and optoelectronic properties of Li based half Heusler alloys, Comput. Condens. Matter, 2018, 14, 55–66 CrossRef.
- F. Hamioud, G. S. AlGhamdi, S. Al-Omari and A. A. Mubarak, Ab initio investigation of the structural, electronic, magnetic and optical properties of the perovskite TlMnX3 (X= F, Cl) compounds, Int. J. Mod. Phys. B, 2016, 30(7), 1650031 CrossRef CAS.
- C. J. Bartel, C. Sutton, B. R. Goldsmith, R. Ouyang, C. B. Musgrave, L. M. Ghiringhelli and M. Scheffler, New tolerance factor to predict the stability of perovskite oxides and halides, Sci. Adv., 2019, 5(2), eaav0693 CrossRef CAS PubMed.
- C. Ambrosch-Draxl and J. O. Sofo, Linear optical properties of solids within the full-potential linearized augmented planewave method, Comput. Phys. Commun., 2006, 175(1), 1–14 CrossRef CAS.
- H. C. Kandpal, C. Felser and R. Seshadri, Covalent bonding and the nature of band gaps in some half-Heusler compounds, J. Phys. D: Appl. Phys., 2006, 39(5), 776 CrossRef CAS.
- S. Kacimi, H. Mehnane and A. Zaoui, I–II–V and I–III–IV half-Heusler compounds for optoelectronic applications: Comparative ab initio study, J. Alloys Compd., 2014, 587, 451–458 CrossRef CAS.
- F. Casper, T. Graf, S. Chadov, B. Balke and C. Felser, Half-Heusler compounds: novel materials for energy and spintronic applications, Semicond. Sci. Technol., 2012, 27(6), 063001 CrossRef.
- T. Fang, S. Zheng, T. Zhou, L. Yan and P. Zhang, Computational prediction of high thermoelectric performance in p-type half-Heusler compounds with low band effective mass, Phys. Chem. Chem. Phys., 2017, 19(6), 4411–4417 RSC.
- U. A. Khan, I. Ullah, V. Tirth, A. Algahtani and A. Zaman, DFT study of the structural, elastic and optoelectronic properties of Cu-based cubic halide-perovskites ACuF3 (A= Mg and Ca), Phys. Scr., 2022, 97(8), 085819 CrossRef.
- M. Saeed, I. U. Haq, S. U. Rehman, A. Ali, W. A. Shah, Z. Ali, Q. Khan and I. Khan, Optoelectronic and elastic properties of metal halides double perovskites Cs 2 InBiX 6 (X= F, Cl, Br, I), Chin. Opt. Lett., 2021, 19(3), 030004 CrossRef.
- M. Husain, A. Ullah, A. Algahtani, V. Tirth, T. Al-Mughanam, A. H. Alghtani, N. Sfina, K. Briki, H. Albalawi, M. A. Amin and A. Azzouz-Rached, Insight into the Structural, Mechanical and Optoelectronic Properties of Ternary Cubic Barium-Based BaMCl3 (M= Ag, Cu) Chloroperovskites Compounds, Crystals, 2023, 13(1), 140 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2023 |