Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Investigating the role of phonons in the phase stability of uranium-based Laves phases†‡
Erik Nykwest *,
Ashley E. Shields
*,
Ashley E. Shields *,
Z. E. Brubaker
*,
Z. E. Brubaker ,
J. L. Niedziela
,
J. L. Niedziela ,
S. B. Isbill
,
S. B. Isbill and
Andrew Miskowiec
and
Andrew Miskowiec
Nuclear Nonproliferation Division, Oak Ridge National Laboratory, USA. E-mail: nykwestec@ornl.gov; shieldsae@ornl.gov
First published on 15th March 2023
Abstract
Laves phase alloys possess unique thermal and electrical conduction properties, yet the factors governing phase stability in these systems remain an open question. The influence of phonons in particular has been broadly overlooked. Here, we investigate the UCo2xNi2(1−x) chemical space using density functional theory, which offers a unique opportunity to explore the factors influencing Laves phase stability as all three primary Laves phases (C14, C15, C36) can be stabilized by changing the ratio of Co to Ni. Calculations of the thermodynamic and dynamical stability of pure UCo2 and UNi2 in each of three primary Laves phases confirm the stability of experimentally known Laves phases for UNi2 and UCo2. A decrease in bonding strength is identified in UNi2 compared to UCo2, aligned with redshifts observed in the UNi2 phonon density of states and a decoupling of the U and Ni vibrational modes. Phonon calculations of C14 UCo2 reveal dynamical instabilities. Efforts to remove the unstable mode at the Γ point in UCo2 via atomic displacements break the symmetry of the C14 phase, revealing a lower energy P2/c structure. Vibrational contributions to the free energy were calculated and did not change the thermodynamically stable Laves phase below 1000 K. The temperature-dependent free energies of single phase UCo2 and UNi2 were used to interpolate the relative stability of ternary UCo2xNi2(1−x) in each of the three Laves phases at varying temperatures and stoichiometries. The ternary C36 phase is only predicted to be thermodynamically stable over a narrow stoichiometric range below 600 K.
Introduction
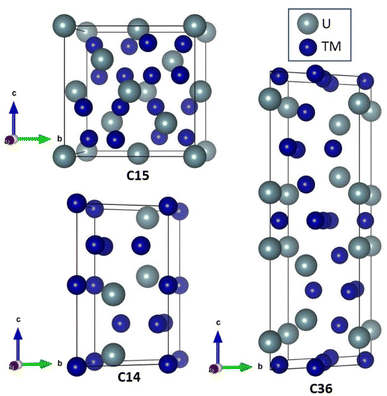
Because of the United States' commitment to reduce net greenhouse gas emissions by 2030,1 there is increased interest in using uranium alloys as fuel for nuclear reactors. Metallic fuels naturally transport heat more easily than ceramic fuels and can be shaped to allow more water to flow across the fuel rod's surface, further increasing heat transfer and electricity generation. Higher surface areas also promise an increased margin of safety to the reactor core.2,3 With the increasing interest of using uranium alloys in the nuclear fuel cycle, understanding the influence of alloy formation in these materials is critical.When uranium combines with a steel constituent (e.g., transition metal elements) a Laves phase is a common by-product. Laves phases account for more than 1400 materials and are formed by elements in all regions of the periodic table.4,5 Laves phases form three crystal structures, shown in Fig. 1, denoted as C14 (hexagonal, P63/mmc), C15 (cubic, Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m), and C36 (hexagonal, P63/mmc), and only differ by the stacking arrangement of the individual layers.5 Longer, more complex stacking patterns are possible but uncommon.6,7 Laves phases possess AB2 stoichiometry and exhibit novel thermophysical properties because of their interconnected network of tetrahedral structures, which facilitates high electrical and thermal conductivity. Owing to their high melting point, controlled precipitation of Laves phases can strengthen steels and superalloys.5,8 Laves phases are also the most frequently found intermetallic phase in high-entropy alloys.9 A significant amount of experimental, computational, and theoretical work has been performed on Laves phases; however, the factors dictating their structural stability remain an open question.10,11 Part of the difficulty stems from the vast number of Laves phases. This difficulty is exacerbated by the insufficient reliability of many phase diagrams due to experimental difficulties associated with the necessary measurements.11 Nonetheless, the stability of some Laves phase structures appear to be correlated with the valence electron configuration,12–14 relative atomic sizes,12,14 and electronegativity.15–20 Unfortunately, none of the developed models have been able to provide a general description of the relative stability between the different Laves phase structures across the large class of Laves phase-forming compounds.10,21 Surprisingly, the role of phonon interactions has been widely overlooked, despite studies linking phonon instabilities to structural transitions in other materials.22–25
m), and C36 (hexagonal, P63/mmc), and only differ by the stacking arrangement of the individual layers.5 Longer, more complex stacking patterns are possible but uncommon.6,7 Laves phases possess AB2 stoichiometry and exhibit novel thermophysical properties because of their interconnected network of tetrahedral structures, which facilitates high electrical and thermal conductivity. Owing to their high melting point, controlled precipitation of Laves phases can strengthen steels and superalloys.5,8 Laves phases are also the most frequently found intermetallic phase in high-entropy alloys.9 A significant amount of experimental, computational, and theoretical work has been performed on Laves phases; however, the factors dictating their structural stability remain an open question.10,11 Part of the difficulty stems from the vast number of Laves phases. This difficulty is exacerbated by the insufficient reliability of many phase diagrams due to experimental difficulties associated with the necessary measurements.11 Nonetheless, the stability of some Laves phase structures appear to be correlated with the valence electron configuration,12–14 relative atomic sizes,12,14 and electronegativity.15–20 Unfortunately, none of the developed models have been able to provide a general description of the relative stability between the different Laves phase structures across the large class of Laves phase-forming compounds.10,21 Surprisingly, the role of phonon interactions has been widely overlooked, despite studies linking phonon instabilities to structural transitions in other materials.22–25
In this study we attempt to gain insight into the factors affecting the structural preferences of uranium-based Laves phase systems by calculating and comparing the free energy, phonon density of states (phDOS), and electronic density of states (eDOS) of pure UCo2 and UNi2 in each of the three main Laves phases.11 The ternary U–Co–Ni system offers a promising subset of structures to investigate structural stability. To our knowledge, UNi2 is the only Ni-containing binary compound that forms in the C14 structure,26 and UCo2 forms the C15 structure.27 Experimental measurements of UCo2xNi2(1−x) claim that at small concentrations of Co (x < 0.12) the system stabilizes in the hexagonal C14 phase, at moderate concentrations (0.40 < x < 1.0) the cubic C15 phase is dominant, and in between these concentrations a mixture of phases is found, including the C36 phase.28,29 Currently there are only six different U-bearing alloys (U–Al, U–Al–Co, U–Ir–Al, U–Al–Ni, U–Os–Al, U–Co–Ni) with stable C36 phases reported in the Inorganic Crystal Structure Database,29–34 three of which (U–Al–Co, U–Os–Al, U–Ir–Al) are the subject of some dispute as to whether they truly form a stable C36 structure or not.35–37 The fourth structure (UAl2) is only stable at high pressures, and the fifth (U–Al–Ni) has the U atom on the B site instead of the A site. Therefore, ternary U–Co–Ni may be the only uranium-based C36 Laves phase that is stable under atmospheric conditions.
Although recent research has been performed on uranium-transition metal Laves phases,38,39 most was conducted before the 1990s and heavily focused on the magnetic properties and not phase stability. Most of this past research was experimental,40–48 with few theoretical studies.47,49,50 Because of computational limitations, past investigations were restricted to a small number of atoms, rather than the complete unit cell. The combination of improvements in high-performance computing systems and the underlying theory, particularly development of the local density and generalized gradient approximations in density functional theory (DFT), now allow more complete investigation of the electronic structure of complex materials, including the symmetry-breaking displaced structures required for calculating phonon band structures. To specifically address the role of phonon interactions in phase stability, we have computationally investigated pure UCo2 and UNi2 in each of three Laves phases using DFT.
Methodology
To model the C15 phase, the standard cubic unit cell was used. To reduce computational complexity, the hexagonal C14 and C36 phases were transformed to equivalent orthorhombic unit cells using the transform in eqn (1).
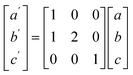 | (1) |
In terms of representing the crystal structure, the larger orthorhombic unit cell is equivalent to the traditional hexagonal unit cell but contains more atoms, similar to using a super cell, and does not change the underlying symmetry. Herein, the C14 and C36 will continue to be referred to as hexagonal phases.
Spin-polarized DFT calculations were performed in the Vienna ab initio simulation package (VASP) 5.4.4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 51 using the generalized gradient approximation PBEsol52 exchange–correlation functional, projector augmented wave pseudopotentials,53 periodic boundary conditions, and Γ-centered Monkhorst–Pack k point meshes.54 To achieve energy predictions converged to <1 meV per atom, a 3 × 3 × 5 k point mesh was used for the C14 structure, a 7 × 7 × 7 mesh for the C15 structure, and a 5 × 3 × 2 mesh for the C36 structure. All calculations were performed with a plane wave cutoff of 400 eV.
51 using the generalized gradient approximation PBEsol52 exchange–correlation functional, projector augmented wave pseudopotentials,53 periodic boundary conditions, and Γ-centered Monkhorst–Pack k point meshes.54 To achieve energy predictions converged to <1 meV per atom, a 3 × 3 × 5 k point mesh was used for the C14 structure, a 7 × 7 × 7 mesh for the C15 structure, and a 5 × 3 × 2 mesh for the C36 structure. All calculations were performed with a plane wave cutoff of 400 eV.
Structural relaxations were performed using the conjugant gradient method while allowing cell volume, shape, and ionic positions to relax simultaneously until atomic forces were less than 1 meV Å−1 with a 0.1 eV Methfessel–Paxton smearing55 of first order applied to the electron occupations at the Fermi level. Single point electronic density of states calculations (eDOS) utilized the tetrahedron method with Blöchl corrections.56 To determine how each element contributes to the eDOS, the calculated wavefunctions were projected onto spherical harmonics centered on each atom in the simulation cell. Magnetic moments were initialized on all atoms using a ferromagnetic ordering with a magnitude of 1 bohr-magneton, which is the default initialization condition in VASP.
The phonon band structure was calculated via the finite displacement method, where Phonopy57 was used to generate symmetrically inequivalent displacements of atoms in the unit cells, and VASP was used to calculate the internal energies of the perturbed systems. Postprocessing in Phonopy determined the force constants, phonon band structure, atom-projected density of states, heat capacity, entropy, and entropic contributions to the free energy for the system. The Python module Sumo58 was used to determine the symmetry group of the relaxed structures using a tolerance of 0.01 Å and to generate q-point paths through reciprocal space consistent with Bradley and Cracknell.59
From calculated phonon properties, we can extract thermal properties for these Laves phases. The thermodynamically stable phase of a system minimizes the relevant energy function for that system; for solids this is typically the Helmholtz free energy (F):
| F = Us + U0 − TS, | (2) |
The free energy of the mixed UCo2xNi2(1−x) system can be written as
| Fϕ(x) = xFϕ(UCo2) + (1 − x)Fϕ(UNi2) + δFm(x,ϕ), | (3) |
| Fseg = xFmin(UCo2) + (1 − x)Fmin(UNi2) + δFgb(x,ϕ1,ϕ2), | (4) |
| δF ≡ (δFgb(x) − δFm(x)) | (5) |
Results and discussion
Relaxed structures and unstable phonons in UCo2–C14
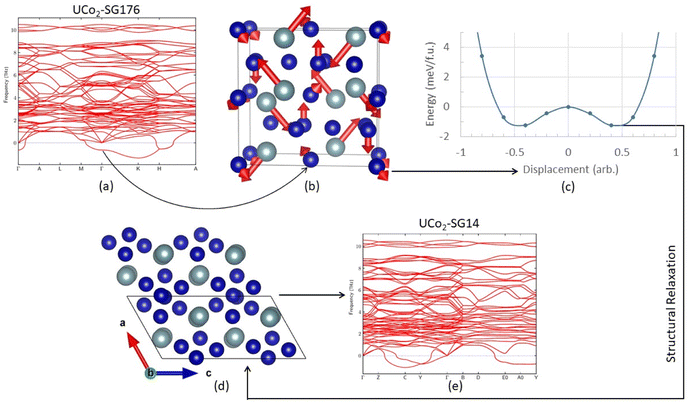
Before discussing results across structure classes, we make an observation about a dynamic instability identified in the UCo2 investigations. During atomic relaxation, the UCo2–C14 structure underwent spontaneous symmetry breaking, reducing the space group from 194 to 176 in the DFT optimized structure. From here on the relaxed UCo2–C14 structure will be referred to as SG176. Examination of the phonon band structure of UCo2-SG176, Fig. 2a, revealed vibrational modes with imaginary frequencies, indicating this structure is dynamically unstable. To determine if these unstable modes were an artifact of our methodology, we applied several different techniques such as using density functional perturbation theory instead of finite differences to calculate the phonon modes and performing phonon calculations on a super cell of the relaxed structure, neither of which successfully eliminated all imaginary frequencies. The resilience of these imaginary frequencies suggests they are not simply computational artifacts but real dynamic instabilities.To probe this hypothesis, the atoms of the relaxed structure were displaced along the eigenvectors of the unstable vibrational mode. The eigenvector components associated with the unstable mode at the Γ point are shown in Fig. 2b. To remove the unstable mode at the Γ point from the band structure, the atoms of UCo2-SG176 were displaced along their associated vibrational paths (indicated by red arrows), and single point energy calculations were performed at various displacement amplitudes. The energy surface associated with the displacement magnitude is shown in Fig. 2c. These calculations reveal there is no energy barrier between the SG176 structure and a lower energy, lower symmetry structure. This lower energy intermediate structure was relaxed using VASP, and the relaxed structure is referenced herein as SG14, as the symmetry belongs to the monoclinic space group number 14. The SG14 structure is shown in Fig. 2e and is 2.7 meV f.u.−1 lower in energy than SG176. Note that the eigenvector displacement successfully removed the unstable optical mode from the SG14 band structure at the Γ point (Fig. 2d), but imaginary frequency modes are present off the Γ point. The eigenvector displacement method previously described was also applied to the imaginary frequency modes at C, Y, E0, and A0, but the corresponding energy surfaces were concave parabolas and did not reveal any nearby minima. Nevertheless, this analysis shows that, at this level of theory, UCo2 is dynamically unstable in the C14 structure as there is no energy barrier to overcome during the C14 to SG14 transition.
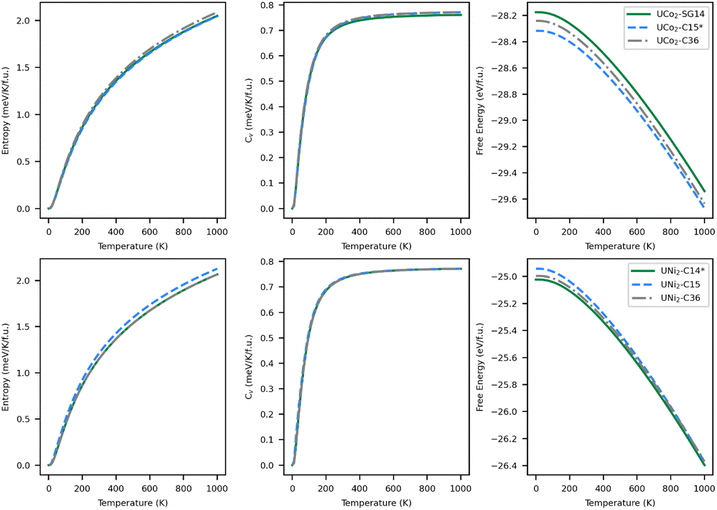
The lattice constants and internal energy of all systems investigated in this work, including the newly identified UCo2-SG14, are listed in Table 1. The structural parameters for the known ground states of UCo2 and UNi2 are in good agreement with experiment and the energetic predictions correctly identify the experimentally known stable structures28 (C15 for UCo2 and C14 for UNi2) as having the lowest internal energy. Note, the most stable phase for UCo2 is the least stable phase for UNi2, and vice versa. The supposed appearance of the C36 phase in the ternary system may be an attempt to balance the energetic structural preferences of Co and Ni, as the calculated internal energy of the C36 phase sits between the C14/SG14 and C15 phases for both the Co and Ni systems.28
| (a) UCo2 | SG14 | C15* | C36 | Exp*27 |
|---|---|---|---|---|
| Internal energy (eV f.u.−1) | −28.2614 | −28.4085 | −28.3286 | — |
| Spin moment (μB f.u.−1) | 0.00 | 0.59 | 0.54 | — |
| Space group number | 14 | 227 | 194 | 227 |
| a (Å) | 4.743 | 6.805 | 4.789 | 6.992 |
| b (Å) | 8.04933 | — | — | — |
| c (Å) | 9.520 | — | 15.878 | — |
| α (°) | 90 | 90 | 90 | — |
| β (°) | 119.41 | — | 90 | — |
| γ (°) | 90 | — | 120 | — |
| (b) UNi2 | C14* | C15 | C36 | Exp*26 |
|---|---|---|---|---|
| Internal energy (eV f.u.−1) | −25.1095 | −25.0249 | −25.0819 | — |
| Spin moment (μB f.u.−1) | 1.17 | 1.20 | 1.20 | — |
| Space group number | 194 | 227 | 194 | 194 |
| a (Å) | 4.830 | 6.901 | 4.847 | 4.9701(4) |
| b (Å) | — | — | — | — |
| c (Å) | 8.125 | — | 16.149 | 8.2527(8) |
| α (°) | 90 | 90 | 90 | — |
| β (°) | 90 | — | 90 | — |
| γ (°) | 120 | — | 120 | — |
Electronic density of states
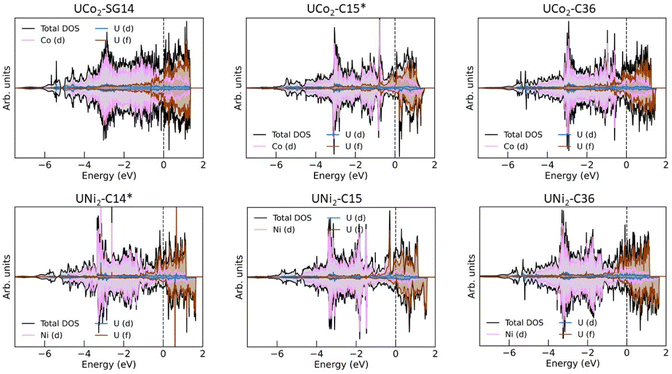
Much work has already been performed investigating the magnetic properties of uranium alloys,40,42,49,60–62 and a detailed study of the magnetic properties of UCo2 and UNi2 are beyond the scope of this work. However, some comments about the eDOS can still be made. Fig. 3 shows the eDOS for UCo2 and UNi2 decomposed into their atomic and orbital contributions.The majority of the conduction band is formed from the transition metal (TM) 3d states and the uranium 5f states, consistent with past calculations.49,60 Broadly, the eDOS can be understood as having a narrow U 5f band above the Fermi level and a broad TM 3d band below the Fermi level, with significant hybridization between these orbitals within 1 eV of the Fermi level. A nontrivial number of states display a U 6d-like character that spans the entire width of the valence band. Not shown is the band edge near −6 eV, which primarily comprises hybridized TM 4s and U 6d states.
There is little to no spin splitting (exchange splitting) of the TM 3d orbitals, evident from the near-mirror symmetry between the spin up (majority spin channel) and spin down (minority spin channel) states. This lack of spin splitting also holds for the U 5f states of UCo2-SG14. For each of the other structures, we observe exchange splitting of the U 5f states causing the spin down states to shift higher in energy compared to their corresponding spin up states. This spin splitting causes an asymmetric occupation of the eDOS creating a polarized ground state and a net spin magnetic moment attributable to the uranium 5f electrons. This outcome is consistent with previous DFT studies and neutron diffraction measurements that found UNi2–C14 to exhibit itinerant ferromagnetism,40,60 and polarized neutron diffraction studies of UNi2–C14 found it to have a low Curie temperature (TC) of 21 K.40 The net spin magnetic moment for each system is listed in Table 1. Based on the eDOS and their net spin magnetic moment, it would not be surprising if all the UNi2 Laves phases displayed itinerant ferromagnetism.
UCo2–C15 is thought to be paramagnetic.49,63 Our calculations predict a spin-polarized ground state with a spin magnetic moment of 0.59 μB per uranium atom. Examining the eDOS for UCo2–C15, we see there is an unpaired spin down peak in the eDOS just above the Fermi level near 0.2 eV. It is possible that, near 0 K, UCo2–C15 displays magnetic ordering, but at finite temperatures (i.e., above the TC) this spin splitting is reduced or overcome by thermal fluctuations. This conclusion is consistent with past experimental magnetic a.c. susceptibility studies that found UCo2 to have a TC of about 7 K and concluded that magnetic clusters exist in UCo2.63 Another possibility is that UCo2–C15 behaves like UFe2, and the orbital and spin magnetic moments from the U atoms cancel out, leading to paramagnetic behavior.48,64–66 As a reminder, the DFT calculations performed in this work do not account for the orbital angular momentum of the electrons. The spin magnetic moment and eDOS for UCo2–C36 is like that of UCo2–C15, and thus is also expected to be paramagnetic or have a low TC.
Some studies have linked the total number of electronic states at the Fermi level to the structural stability,67–69 with stability decreasing as the number of states increases. The total number of spin up and spin down states at the Fermi level (NEF) are given in Table 2; this relationship seems to hold for UNi2. However, UCo2 only partially agrees with this idea. Although the stable C15 phase has the lowest number of states at the Fermi level, the dynamically unstable and energetically unfavorable SG14 phase has the next lowest number of states.
| NEF (spin up) | NEF (spin down) | Total | |
|---|---|---|---|
| (a) UCo2 | |||
| SG14 | 2.51(13) | 2.69(06) | 5.20 |
| C15* | 2.37(30) | 1.49(02) | 3.86 |
| C36 | 4.28(41) | 1.48(09) | 5.76 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| (b) UNi2 | |||
| C14* | 2.12(11) | 1.88(10) | 4.00 |
| C15 | 4.80(02) | 1.99(05) | 6.78 |
| C36 | 3.16(23) | 1.31(06) | 4.48 |
Phonon density of states
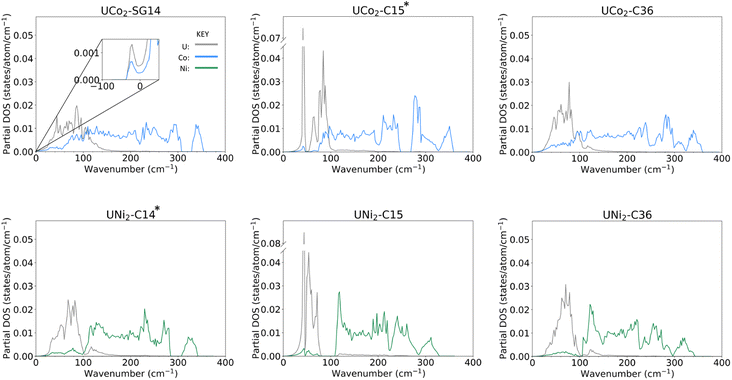
Examining the phonon density of states (phDOS) shown in Fig. 4, we see that the higher energy vibrational modes are primarily ascribed to Co/Ni vibrations, and the lower energy phonons are attributed to U atoms, which are consistent with the difference in masses of the contributing atoms. Fig. 4a shows the unstable phonon modes in the UCo2-SG14 phDOS as negative vibration frequencies, plotted in the inset. These unstable modes were discussed previously and shown in Fig. 2d. Note, none of the other Laves phases examined in this work exhibit unstable vibrational modes, including those that have not been explicitly experimentally determined. All phDOS terminate above ∼320 cm−1 for Ni phases and ∼350 cm−1 for Co phases.The phDOS predicted for the experimentally observed UCo2–C15 phase shows a very sharp peak at low wave numbers, dominated by modes of uranium character. Fig. 4b shows a prominent uranium peak that goes off the scale, followed by an apparent quadruplet of states with nonzero density, which begin mixing with Co near 75 cm−1. The remaining uranium bands are largely positioned under 100 cm−1, with a very small contribution of the uranium atoms between 100 and 200 cm−1. In contrast, the UNi2–C15 phase shown in Fig. 4e also possess strong contributions of uranium character that go off the scale below 100 cm−1. Investigation of the band structure for both cases (see ESI Fig. 1‡) reveals these states in both the Co and Ni C15 structures to be nearly dispersionless, potentially suggesting a rattling-type mode may exist in these systems. In the C15 Ni system, the Ni dominated phonon bands are shifted to start above 100 cm−1, leaving a phonon band gap in the UNi2 phase between 70 and 110 cm−1. No low energy phonon gap exists in the C15 UCo2 phase.
For both C15 systems, the phonon spectra greater than 100 cm−1 are dominated by TM modes, as might be expected, though each display a long residual tail of low uranium involvement that terminates at ∼200 cm−1 for Co and ∼220 cm−1 for Ni, each termination of which is accompanied by a sharp drop in the contribution of the TM vibrations. For the C15 UCo2 phase, the experimentally stable configuration, there is a phonon band gap near 250 cm−1, and a phonon “pseudogap”, where the phonon contributions are nearly zero, near 320 cm−1. For the C15 UNi2 phase, there is a similar pseudogap near 290 cm−1.
Comparing the C14 analogues, in UCo2-SG14, Fig. 4a, there is a phonon band gap near 320 cm−1. This gap also exists in UNi2–C14, Fig. 4d, but it starts at ∼290 cm−1 extending to 310 cm−1. Similar to the C15 case for the Co system, the region of U–Co modes extends to higher energy compared to the U–Ni system, although the tail for continued uranium involvement extends to higher overall energy.
In the C36 phases, the low energy modes follow the same trend where the uranium motions are better separated from the TM contributions at low energy for the case of Ni compared to Co. There is the continued presence of a phonon pseudogap near 325 cm−1 for C36 UCo2 and near 290 cm−1 for C36 UNi2. Total phDOS for all phases are shown in ESI Fig. 2.‡
Thermodynamic stability
The thermodynamically stable phase of a system minimizes the relevant energy function for that system; for solids this is typically the Helmholtz free energy (eqn (2)). Within the harmonic approximation, the entropic portion of the free energy may be estimated from the ground state vibrational properties. The accuracy of this method decreases with temperature but typically remains useful up to 1000 K.70 The entropy, specific heat at constant volume, and free energy are plotted in Fig. 5 as a function of temperature.The entropy curves, and thus also the specific heats, of all the structures are similar. The specific heat saturates to about 0.77 meV K−1 f.u.−1 at high temperatures. Although entropy has a large effect on the free energy of the systems, generating a decrease in energy in excess of 1.4 eV f.u.−1, there is no change in the most stable structure as a function of temperature over the range modeled. Although the C14 phase remains the lowest energy phase for UNi2 and the C15 phase remains the lowest energy phase for UCo2, the energetic differences between the phases do get smaller with increasing temperature. For UCo2, the energetic ordering remains the same over the full range of 0–1000 K, with the C15 phase remaining the most stable phase and the SG14 phase the least stable. At 1000 K, UCo2–C15 is 37.1 meV f.u.−1 lower in energy than the C36 phase and 132.0 meV f.u.−1 lower than the SG14 phase. For UNi2, the energetic ordering does change, with the C15 phase becoming more stable than the C36 near 850 K. At 1000 K, UNi2–C14 is more stable than the C15 phase by just 22.7 meV f.u.−1 and 27.0 meV f.u.−1 lower in energy than the C36 phase. This energy difference is just less than 2% of the total free energy change due to entropic effects. Accordingly, it is worth investigating the phase stability of UNi2 Laves phases with higher accuracy methods or via experiment.
Thermodynamic stability of ternary UCo2xNi2(1−x)
The phase stability of ternary UCo2xNi2(1−x) may be estimated by comparing the free energy of a single phase ternary system in each of the three Laves phase, predicted with eqn (3), with the free energy of the segregated multiphase system xUCo2 + (1 − x)UNi2, given by eqn (4).We first examine ternary phase stability without vibrational effects by setting the zero-point energy and temperature–entropy contributions to zero. If we assume δFgb and δFm are phase independent, it can be shown that for δF ≤ 0 eV f.u.−1 (i.e., the energetic penalty for mixing is greater than or equal to the penalty for creating grain boundaries in eqn (5)), it is always energetically favorable for the system to segregate into pure UCo2–C15 and UNi2–C14. For 0 < δF < 42.3 meV f.u.−1, (i.e., the penalty for creating grain boundaries is larger than the energy of mixing), it is possible to find ratios of Co to Ni that stabilize ternary C14–SG14 and C15, but not C36. As δF increases from 42.3 meV f.u.−1 the ratio where it is possible to stabilize the C36 increases until 49.3 meV f.u.−1, above which there are no further changes to the phase stability regions and the ternary system is not predicted to segregate into pure phases. Using this maximum difference in energetic penalty, the ternary C14–SG14 phase is stable for 0 < x < 0.28, the C36 phase is stable for 0.28 < x < 0.42, and the C15 phase is stable for 0.42 < x < 1.0. The C36 to C15 boundary at x = 0.42 is in good agreement with experiments by Zeleny et al.29 who found a boundary near x = 0.38. The C14 to C36 boundary of x = 0.12 measured by Zeleny et al., however, is much lower than we predict using structural energy alone.
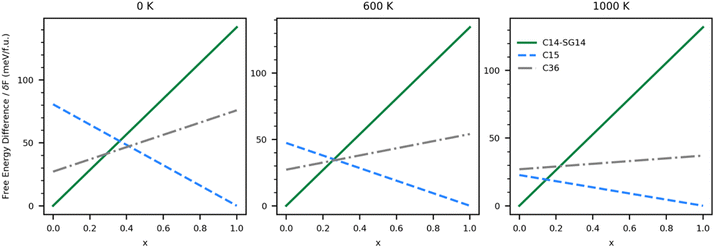
This same analysis can be applied to the system with vibrational effects by using the free energies shown in Fig. 5; however, the predictions become a function of temperature. Fig. 6 shows the free energy differences of each ternary single-phase system relative to a segregated system at three different temperatures. In the absence of an energetic penalty to segregation (e.g., grain boundary energy), the ternary system is not stable at any temperature, indicated by all of the relative free energies being greater than zero. The minimum energetic penalty predicted to stabilize the lowest energy single phase at any given value of x is shown as the free energy difference relative to the segregated system.
As expected, the 0 K system is predicted to behave similarly to the vibration-free system. As δF grows, it becomes possible to stabilize the C14 phase at low Co (high Ni) concentrations and C15 at high Co (low Ni) concentrations, but at intermediate values of x, the system thermodynamically favors segregation. As δF increases from 41 to 47 meV f.u.−1, it becomes possible to stabilize the C36 phase. As temperature increases, the x range over which the C36 phase is thermodynamically stable shrinks until around 600 K. Above 600 K our calculations predict the C36 phase is no longer thermodynamically stable at any value of x, and the C14 phase yields thermodynamic stability to the C15 phase directly when x > 0.28. The values of δF over which the stability regions change are listed in Table 3. Energetic penalties larger than those listed in the table will also stabilize the ternary single phases, but the stability regions will remain unchanged.
| C14 | C15 | C36 | |
|---|---|---|---|
| 0 K | 0–41 | 41–47 | 0–47 |
| 600 K | 0–34 | 0–34 | — |
| 1000 K | 0–19 | 0–19 | — |
Assuming the δF is large enough to stabilize the C36 phase, we can again determine what ranges of x stabilize each of the three Laves phases investigated, although experimentally Zeleny et al.29 report that the single phase regions are separated by narrow two phase domains. These ranges are shown in Table 4. At 0 K, the C36 phase is predicted to be stable in the stoichiometric region between the C14 and C15 phases. Further experimental and computational efforts may find C36 is an intermediate phase in the transition between C14 and C15 in the ternary system.
| C14 | C15 | C36 | |
|---|---|---|---|
| 0 K | 0 < x < 0.29 | 0.41 < x < 1 | 0.29 < x < 0.41 |
| 600 K | 0 < x < 0.28 | 0.28 < x < 1 | — |
| 1000 K | 0 < x < 0.17 | 0.17 < x < 1 | — |
As temperature increases, changes in the phase diagram are driven primarily by changes in the relative free energy of UNi2 Laves phases. As can be seen from Fig. 5, the free energy difference between the C15 phase of UNi2 and the other phases decreases with temperature, with the C15 phase becoming more stable than the C36 phase above 850 K. This increase in relative stability of the UNi2 in the C15 phase flattens the ternary C15 energy curve in Fig. 6, creating large changes in the C15 phase stability region as a function of temperature. This effect both increases the uncertainty in any reported C15 phase stability interval due to its high sensitivity to temperature and could also explain the discrepancy between our predicted C15 stability region and experiment. Using the free energies calculated at 270 K, we find a C36 to C15 transition at x = 0.37 in excellent agreement with Zeleny et al.,29 who report the transition at x = 0.38. However, at 270 K we find the C14 to C36 transition occurs at x = 0.29, which is barely different from the vibration free transition and still disagrees with the 0.12 < x < 0.17 range reported in their manuscript.
Conclusions
Currently, there is not one unifying theory for predicting relative phase stability that works across the large class of Laves phase-forming compounds and the effects of phonon contributions to the relative stability have largely been overlooked. Here, DFT was used to predict the structural, vibrational, energetic, magnetic, and electronic properties of UCo2 and UNi2 in each of the three main Laves phases. DFT confirmed the experimentally determined stable phases for each chemistry are the lowest energy phases, C14 for UNi2 and C15 for UCo2. DFT calculations also predict stable phonon structures for all but the UCo2 SG14 phase.The interatomic distances of UNi2 were typically larger than those seen in the corresponding UCo2 phases, suggestive of a decrease in bond strength. The proposed decrease in bond strength also aligned with observations of the phDOS, in which the UNi2 phDOS was redshifted compared to UCo2. In addition, the phDOS displayed a decoupling of the U and Ni vibrational modes. We have identified a modification to UCo2–C14, which we refer to as SG14, that lowers the internal energy of the structure and removes the unstable phonon mode at the Γ point. Other imaginary modes exist off Γ, but the SG14 structure can serve as a starting point for future research. There is no energetic barrier between the C14 structure and the SG14 structure.
Although the relative free energies change, vibrational contributions did not change the thermodynamically stable Laves phase below 1000 K. There may be a phase transition above 1000 K as the harmonic approximation breaks down at elevated temperatures, and the predicted energy differences decrease with increasing temperature, especially for UNi2. Accordingly, it is worth investigating the phase stability of UNi2 Laves phases with higher accuracy methods or via experiment.
Finally, the ternary C36 phase was found to only be thermodynamically stable below 600 K and over a narrow stoichiometric range. Agreement with experiment was mixed, as the stability region for ternary C15 was in excellent agreement, whereas the stability region for the C14 phase was in poor agreement, possibly because the dynamic instability of UCo2 in the C14 phase or entropic factors not considered by this simple linear interpolation. Further research is needed to elucidate ternary phase stability.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was sponsored by the Department of Energy, National Nuclear Security Administration Office. This research used resources of the Compute and Data Environment for Science (CADES) at the Oak Ridge National Laboratory, which is supported by the Office of Science of the U.S. Department of Energy under Contract No. DE-AC05-00OR22725.References
- US Department of State and US Executive Office of the President, The Long-Term Strategy of the United States: Pathways to Net-Zero Greenhouse Gas Emissions by 2050, 2021 Search PubMed.
- Y.-I. Chang, Technical Rationale for Metal Fuel in Fast Reactors, Nucl. Eng. Technol., 2007, 39, 161 CrossRef CAS.
- C. E. Till and Y. Il Chang, Plentiful Energy, CreateSpace Independent Publishing Platform, 2011 Search PubMed.
- I. Ansara, T. Chart, F. Guillermet, F. Hayes, U. Kattner, D. Pettifor, N. Saunders and K. Zeng, Workshop on Thermodynamic Modelling of Solutions and Alloys, Calphad, 1997, 21, 171 CrossRef CAS.
- F. Stein and A. Leineweber, Laves Phases: A Review of Their Functional and Structural Applications and an Improved Fundamental Understanding of Stability and Properties, J. Mater. Sci., 2021, 56, 5321 CrossRef CAS.
- Y. Komura and Y. Kitano, Long-Period Stacking Variants and Their Electron-Concentration Dependence in the Mg-Base Friauf–Laves Phases, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1977, 33, 2496 CrossRef.
- Y. Komura and K. Tokunaga, Structural Studies of Stacking Variants in Mg-Base Friauf–Laves Phases, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1980, 36, 1548 CrossRef.
- J. D. Livingston, Laves-Phase Superalloys?, Phys. Status Solidi A, 1992, 131, 415 CrossRef CAS.
- M.-H. Tsai, R.-C. Tsai, T. Chang and W.-F. Huang, Intermetallic Phases in High-Entropy Alloys: Statistical Analysis of Their Prevalence and Structural Inheritance, Metals, 2019, 9, 247 CrossRef CAS.
- F. Stein, M. Palm and G. Sauthoff, Structure and Stability of Laves Phases. Part I. Critical Assessment of Factors Controlling Laves Phase Stability, Intermetallics, 2004, 12, 713 CrossRef CAS.
- F. Stein, M. Palm and G. Sauthoff, Structure and Stability of Laves Phases Part II - Structure Type Variations in Binary and Ternary Systems, Intermetallics, 2005, 13, 1056 CrossRef CAS.
- G. Leitner and G. E. R. Schulze, Crystal Chemical Stability Conditions for Intermetallic Compounds (I) Frequency Distributions of Laves-Phases, Krist. Tech., 1971, 6, 449 CrossRef CAS.
- F. Laves and H. Witte, The Influence of Valence Electrons on the Crystal Structure of Ternary Magnesium Alloys, Metallwirtschaft, 1936, 15, 840 CAS.
- Y. Ohta and D. G. Pettifor, Size versus Electronic Factors in Transition Metal Laves Phase Stability, J. Phys.: Condens. Matter, 1990, 2, 8189 CrossRef CAS.
- J. Hafner, F. Hulliger, W. B. Jensen, J. A. Majewski, K. Mathis, P. Villars and P. Vogl, The Structures of Binary Compounds, Elsevier, Amsterdam, 1989 Search PubMed.
- R. Edwards, The Lattice Dimensions of the AB2 Laves Phases, Metall. Trans., 1972, 3, 1365 CrossRef.
- J. H. Zhu, C. T. Liu, L. M. Pike and P. K. Liaw, A Thermodynamic Interpretation of the Size-Ratio Limits for Laves Phase Formation, Metall. Mater. Trans. A, 1999, 30, 1449 CrossRef.
- J. H. Zhu, C. T. Liu, L. M. Pike and P. K. Liaw, Enthalpies of Formation of Binary Laves Phases, Intermetallics, 2002, 10, 579 CrossRef CAS.
- R. Miedema, Simple Model for Alloys, Philips Tech. Rev., 1973, 33, 149 Search PubMed.
- R. Miedema, Simple Model for Alloys. Pt. 2. Influence of Ionicity on the Stability and Other Physical Properties of Alloys, Philips Tech. Rev., 1973, 33, 196 Search PubMed.
- P. Eckerlin and W. B. Pearson, The Crystal Chemistry and Physics of Metals and Alloys, Wiley-Interscience, John Wiley & Sons, New York, 1972 Search PubMed.
- J. D. Budai, et al., Metallization of Vanadium Dioxide Driven by Large Phonon Entropy, Nature, 2014, 515, 535 CrossRef CAS PubMed.
- J. Łażewski, P. Piekarz, J. Toboła, B. Wiendlocha, P. T. Jochym, M. Sternik and K. Parlinski, Phonon Mechanism of the Magnetostructural Phase Transition in MnAs, Phys. Rev. Lett., 2010, 104, 147205 CrossRef PubMed.
- P. Souvatzis, O. Eriksson, M. I. Katsnelson and S. P. Rudin, Entropy Driven Stabilization of Energetically Unstable Crystal Structures Explained from First Principles Theory, Phys. Rev. Lett., 2008, 100, 095901 CrossRef CAS PubMed.
- P. Söderlind, B. Grabowski, L. Yang, A. Landa, T. Björkman, P. Souvatzis and O. Eriksson, High-Temperature Phonon Stabilization of γ-Uranium from Relativistic First-Principles Theory, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 060301 CrossRef.
- A. Perricone and H. Noël, Crystal Structure Refinements and Magnetic Behavior of U6Ni, UNi5, UNi2 and the Substitution Derivative UNi1.7Si0.3, Chem. Met. Alloys, 2008, 1, 54 CrossRef.
- J. P. Itié, J. Staun Olsen, L. Gerward, U. Benedict and J. C. Spirlet, High Pressure X-Ray Diffraction on UX2 Compounds, Physica B+C, 1986, 139–140, 330 CrossRef.
- V. Sechovský, Z. Smetana, G. Hilscher, E. Gratz and H. Sassik, Onset of Ferromagnetism in U(CoxNi1−x)2, Physica B+C, 1980, 102, 277 CrossRef.
- M. Zeleny, A. V. Andreev, W. Dreizler and V. Roskovec, Structure and Magnetic Properties of Pseudobinary Laves Phases U(CoxNi1−x)2, Phys. Status Solidi A, 1980, 57, K17 CrossRef CAS.
- P. C. Sahu, N. V. Chandra Shekar, N. Subramanian, M. Yousuf and K. Govinda Rajan, Crystal Structure of UAl2 above 10 GPa at 300 K, J. Alloys Compd., 1995, 223, 49 CrossRef CAS.
- G. Petzow, S. Steeb and G. Kiessler, Das Quasibinäre System UCo2-UAl2, J. Nucl. Mater., 1964, 12, 271 CrossRef CAS.
- G. Petzow and S. Steeb, Phase Equilibria between Intermetallic Compounds in Uranium Alloys, Proc. Int. Conf. Peaceful Uses At. Energy, 1964, 169–176 Search PubMed.
- W. Dreizler, F. Aldinger and G. Petzow, Das System Uran-UNi2-UCo2, Int. J. Mater. Res., 1979, 70, 769 CrossRef CAS.
- I. Bruno, S. Gražulis, J. R. Helliwell, S. N. Kabekkodu, B. McMahon and J. Westbrook, Crystallography and Databases, Data Sci. J., 2017, 16, 38 CrossRef.
- V. Tsvyashchenko and L. N. Fomicheva, High Pressure Synthesis of the Hexagonal Laves Phase UCoAl, J. Less-Common Met., 1991, 171, L5 CrossRef.
- V. Sechovsky, L. Havela, F. R. R. de Boer, J. J. M. J. M. Franse, P. A. A. Veenhuizen, J. Sebek, J. Stehno and A. V. V. Andreev, Systematics across the UTX Series (T = Ru, Co, Ni; X = Al, Ga, Sn) of High-Field and Low-Temperature Properties of Non-Ferromagnetic Compounds, Physica B+C, 1986, 142, 283 CrossRef CAS.
- V. Andreev, S. Daniš, J. Šebek, M. S. Henriques, J. Vejpravová, D. I. Gorbunov and L. Havela, Crystal Structure and Magnetism of UOsAl, J. Magn. Magn. Mater., 2017, 428, 144 CrossRef.
- P. Lucaci and E. Culea, Magnetic Behavior of U(TxAl1-x)2 Compounds (T = Co, Ni, Mn), Mod. Phys. Lett. B, 2006, 20, 1677 CrossRef CAS.
- D. Benea, S. Mankovsky and H. Ebert, Fully Relativistic Description of Magnetic Compton Profiles with an Application to UFe2, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 094411 CrossRef.
- J. M. Fournier, A. Boeuft, P. Fringss, M. Bonnet, J. X. Boucherle, A. Delapalme and A. Menovsky, Polarized Neutron Diffraction Study of UNi2, J. Less-Common Met., 1986, 121, 249 CrossRef CAS.
- C. Schmitzer, E. Gmelin and G. Hilscher, Low Temperature Specific Heat Measurements of UNi2, Physica B+C, 1985, 130, 237 CrossRef CAS.
- L. Havela, V. Sechovský, J. Hřebík and A. V. Andreev, Magnetic Behaviour of U(Fe,Ti)2 Compounds, J. Less-Common Met., 1985, 114, 317 CrossRef CAS.
- E. Burzo and M. Valeanu, Magnetic Properties of U(FexAl1-x)2 and U(FeyNi1-y)2 Compounds, Appl. Phys. A: Solids Surf., 1984, 35, 79 CrossRef.
- E. Burzo and P. Lucaci, Magnetic Properties of U(CoxAl1−x)2 Compounds, Solid State Commun., 1985, 56, 537 CrossRef CAS.
- E. Burzo, E. Gratz and P. Lucaci, Magnetic Behaviour of U(MnxAl1−x)2 Compounds, Solid State Commun., 1986, 60, 241 CrossRef CAS.
- E. Burzo and P. Lucaci, Magnetic Properties of U(NixAl1−x)2, Solid State Commun., 1989, 72, 305 CrossRef CAS.
- G. H. Lander, Spin and Orbital Magnetic Moments in Actinide Compounds, Phys. Scr., 1991, 44, 33 CrossRef CAS.
- B. Lebech, M. Wulff and G. H. Lander, Spin and Orbital Moments in Actinide Compounds (Invited), J. Appl. Phys., 1991, 69, 5891 CrossRef CAS.
- G. Schadler, G. Hilscher and P. Weinberger, Electronic Structure of Actinide Intermetallics of Laves Type, J. Magn. Magn. Mater., 1982, 29, 241 CrossRef CAS.
- O. Eriksson, M. S. S. Brooks and B. Johansson, Theoretical Aspects of the Magnetism in the Ferromagnetic AFe2 Systems (A =U, Np, Pu, and Am), Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 9087 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Efficiency of Ab-Initio Total Energy Calculations for Metals and Semiconductors Using a Plane-Wave Basis Set, Comput. Mater. Sci., 1996, 6, 15 CrossRef CAS.
- J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Restoring the Density-Gradient Expansion for Exchange in Solids and Surfaces, Phys. Rev. Lett., 2008, 100, 1 CrossRef PubMed.
- G. Kresse and D. Joubert, From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758 CrossRef CAS.
- H. J. Monkhorst and J. D. Pack, Special Points for Brillouin-Zone Integrations, Phys. Rev. B: Solid State, 1976, 13, 5188 CrossRef.
- M. Methfessel and A. T. Paxton, High-Precision Sampling for Brillouin-Zone Integration in Metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 40, 3616 CrossRef CAS PubMed.
- P. E. Blöchl, O. Jepsen and O. K. Andersen, Improved Tetrahedron Method for Brillouin-Zone Integrations, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 16223 CrossRef PubMed.
- A. Togo and I. Tanaka, First Principles Phonon Calculations in Materials Science, Scr. Mater., 2015, 108, 1 CrossRef CAS.
- M. Ganose, A. J. Jackson and D. O. Scanlon, Sumo: Command-Line Tools for Plotting and Analysis of Periodic Ab Initio Calculations, J. Open Source Softw., 2018, 3, 717 CrossRef.
- J. Christopher, J. Bradley and A. P. Cracknell, The Mathematical Theory of Symmetry in Solids, Clarendon Press, 1972 Search PubMed.
- L. Severin, L. Nordström, M. S. S. Brooks and B. Johansson, Theoretical Study of the Ferromagnetism in Ni2, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44, 9392 CrossRef CAS PubMed.
- L. Severin, B. Johansson, L. Nordström and M. S. S. Brooks, Calculated Spin and Orbital Moments in UNi2, J. Appl. Phys., 1991, 70, 6586 CrossRef CAS.
- J. M. Fournier, Pressure Effects on the Magnetic Properties of Actinide Intermetallics, Physica B+C, 1985, 130, 268 CrossRef CAS.
- A. Zentko, J. Hřebík, J. Šternberk and J. Turán, On the Magnetic Properties of Non-Stoichiometric UCo2 Compounds, Physica B+C, 1980, 102, 269 CrossRef CAS.
- M. Wulff, G. H. Lander, B. Lebech and A. Delapalme, Cancellation of Orbital and Spin Magnetism in UFe2, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 39, 4719 CrossRef CAS PubMed.
- B. Lebech, M. Wulff, G. H. Lander, J. Rebizant, J. C. Spirlet and A. Delapalme, Neutron Diffraction Studies of the Crystalline and Magnetic Properties of UFe2, J. Phys.: Condens. Matter, 1989, 1, 10229 CrossRef CAS.
- L. Paolasini, G. H. Lander, S. M. Shapiro, R. Caciuffo, B. Lebech, L.-P. Regnault, B. Roessli and J.-M. Fournier, Magnetic Excitations in the Itinerant Ferromagnet UFe2, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 7222 CrossRef CAS PubMed.
- C. Zhang, Z. Zhang, S. Wang, H. Li, J. Dong, N. Xing, Y. Guo and W. Li, First-Principles Study of Electronic Structure for the Laves-Phase Compounds HfFe2 and HfV2, J. Alloys Compd., 2008, 448, 53 CrossRef CAS.
- Q. Yao, J. Sun, D. Lin, S. Liu and B. Jiang, First-Principles Studies of Defects, Mechanical Properties and Electronic Structure of Cr-Based Laves Phases, Intermetallics, 2007, 15, 694 CrossRef CAS.
- L. Ma, Y. Duan and R. Li, Phase Stability, Anisotropic Elastic Properties and Electronic Structures of C15-Type Laves Phases ZrM2 (M = Cr, Mo and W) from First-Principles Calculations, Philos. Mag., 2017, 97, 2406 CrossRef CAS.
- S. Root, L. Shulenburger, R. W. Lemke, D. H. Dolan, T. R. Mattsson and M. P. Desjarlais, Shock Response and Phase Transitions of MgO at Planetary Impact Conditions, Phys. Rev. Lett., 2015, 115, 1 CrossRef PubMed.
Footnotes |
| † Notice: This manuscript has been authored by UT-Battelle, LLC, under contract DE-AC05-00OR22725 with the US Department of Energy (DOE). The US government retains and the publisher, by accepting the article for publication, acknowledges that the US government retains a nonexclusive, paid-up, irrevocable, worldwide license to publish or reproduce the published form of this manuscript, or allow others to do so, for US government purposes. DOE will provide public access to these results of federally sponsored research in accordance with the DOE Public Access Plan (https://energy.gov/downloads/doe-public-access-plan). |
| ‡ Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ra00498h |
| This journal is © The Royal Society of Chemistry 2023 |